Robust Clutter Suppression and Ground Moving Target Imaging Method for a Multichannel SAR with High-Squint Angle Mounted on Hypersonic Vehicle
Abstract
1. Introduction
- The first challenge is high-order phase error, a second-order Taylor expansion of instantaneous range history can basically meet the general resolution requirements for the side-looking SAR with an ideal trajectory [19,20]. However, the high-order phases are non-negligible for HSV, considering the errors brought by its high-squint and high-speed;
- The second challenge is motion parameter coupling. In the case of side-looking SAR, the first-order phase coupling is only associated with the radial speed (RS) of GMT [14]. However, for high-squint HSV-MC-SAR, both the speeds of GMT and HSV platform are involved in the coupling. The high-order phases together with serious motion parameter coupling, may lead to the shifting and smearing of GMT imageries [6];
- The third challenge is the Doppler ambiguity induced by high-resolution wide-swath (HRWS) and high-speed [4,11,19,21,22]. The basic clutter suppression methods, including displaced phase center antenna (DPCA) [23,24,25] and space-time adaptive processing (STAP) [26,27], are found to be particularly effective under a short coherent accumulation time (CAT) condition. However, they are only suitable for the unambiguous echo signals;
- The fourth challenge is the antenna size limitations caused by the aerodynamic characteristics of HSV. Although methods such as the extended DPCA (EDPCA) [28,29,30] and imaging STAP (ISTAP) methods [31] have long CATs and are able to improve the signal-to-clutter-and-noise ratio (SCNR), or Deramp technology [32,33] is able to minimize clutter together with its ambiguous components and recover unambiguous GMT, they both need large antennas. Limited by the antenna size of HSV, all of these methods lack sufficient degrees-of-freedom (DOF) [34], resulting in increasing system complexity and GMT integration loss. Although theoretically, the multiple-input multiple-output (MIMO) radar systems enjoy more DOF, in fact, it is difficult to directly apply to the HSV-SAR systems [35,36].
- The modified coarse-focused method with cubic CFT would alleviate the impacts of GMT Doppler ambiguity and RCM, and form a basis for the subsequent motion parameter recovery, clutter suppression, and GMT imaging;
- The robust clutter suppression method, due to that the recovered RS is developed to modify the matching between the beam-former center and GMT, reduces the unwanted integration loss in the desired GMT direction and ameliorates the SCNR;
- By alleviating or inhibiting the effects of clutter Doppler ambiguity, channel phase mismatch, and co-registration error, the RS recovery with joint-pixel model is more precise;
- The proposed GMT imaging method, due to that the parameter recovery is preprocessed and the first-order phase correction is simplified to a single-step process, has lower computational burden compared to the CFT-improved method [4]. In the case of high-squint and high-speed, the impacts of GMT 2-D speeds are accurately compensated, and accurate-focused imagery of GMT can hence be recovered.
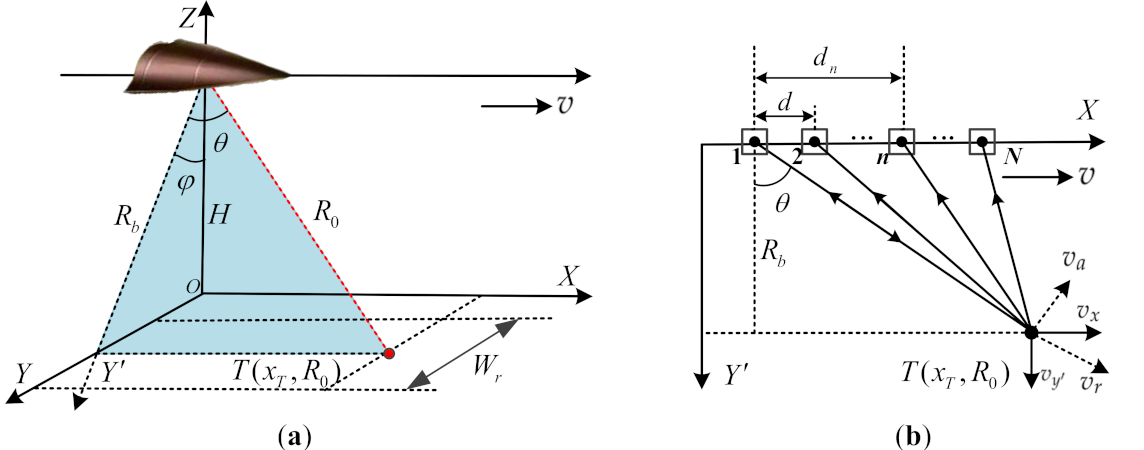
2. Signal Model
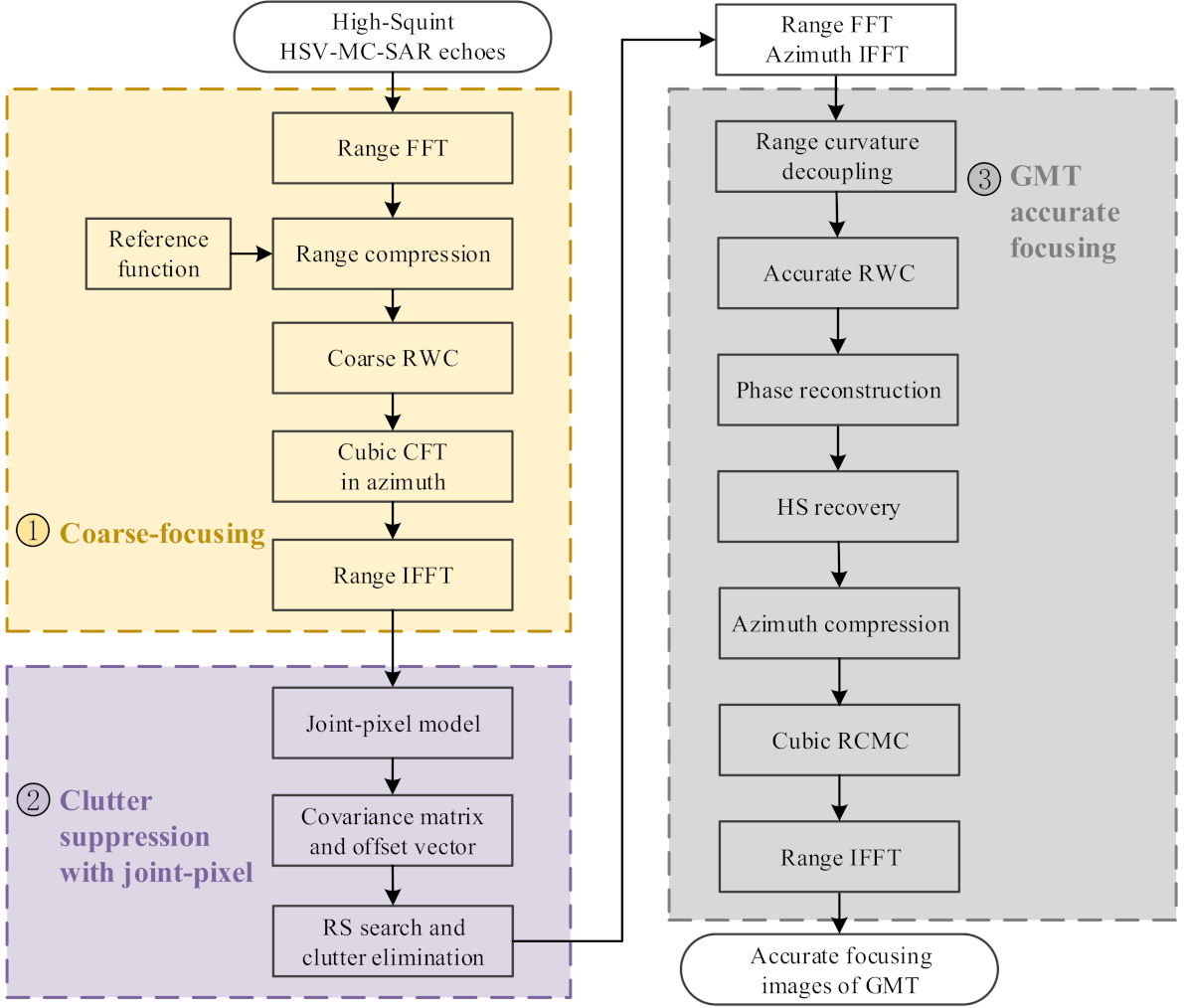
3. Robust Clutter Suppression and GMT Imaging Method for the High-Squint HSV-MC-SAR
3.1. Modified Coarse-Focusing of GMT and Clutter
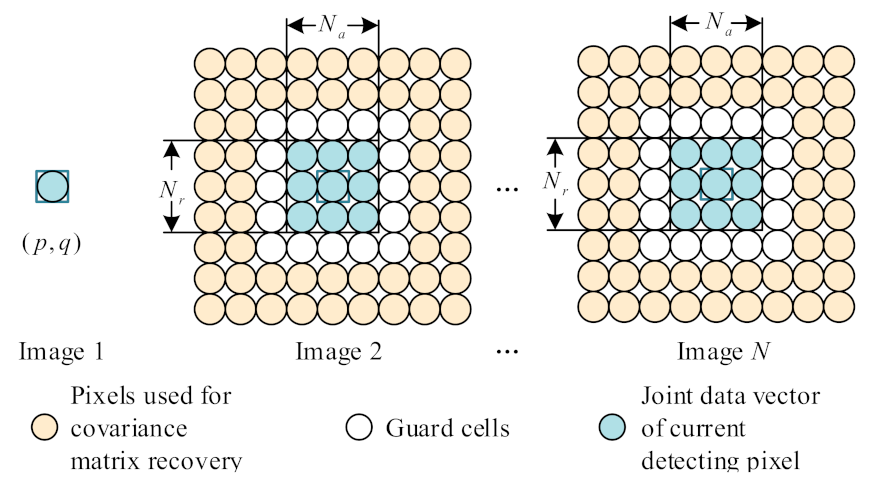
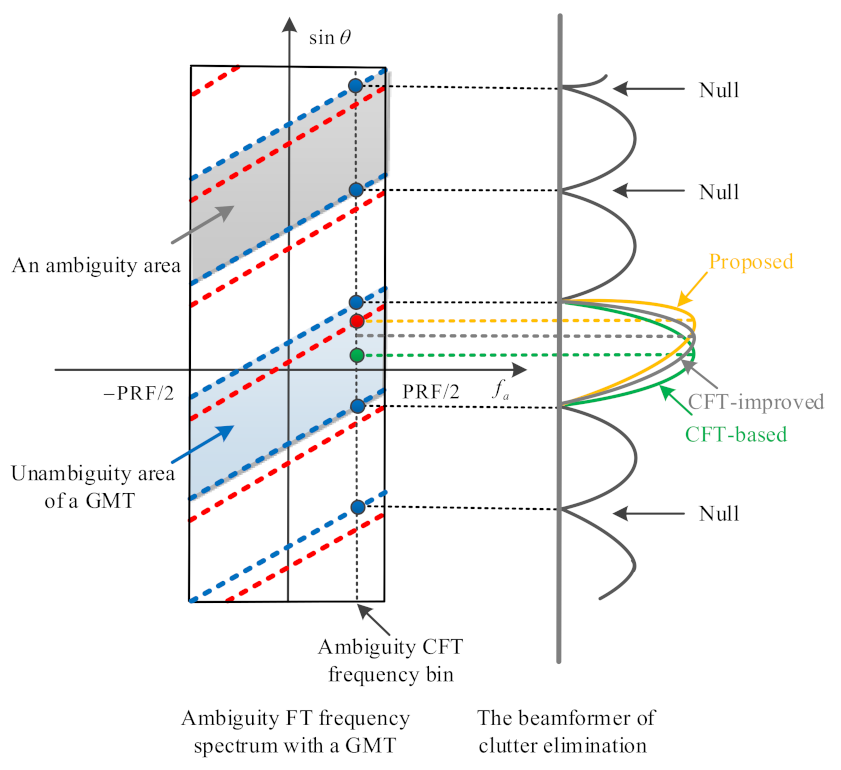
3.2. Robust Clutter Suppression Method with Joint-Pixel Model
- The RS is estimated in , an arbitrary RS component is obtained;
- Performing the RS search in , the precise RS and GMT unambiguity area can be recovered. Note that reflects the neighborhood.
3.3. GMT Accurate-Focusing
4. RCM Analysis
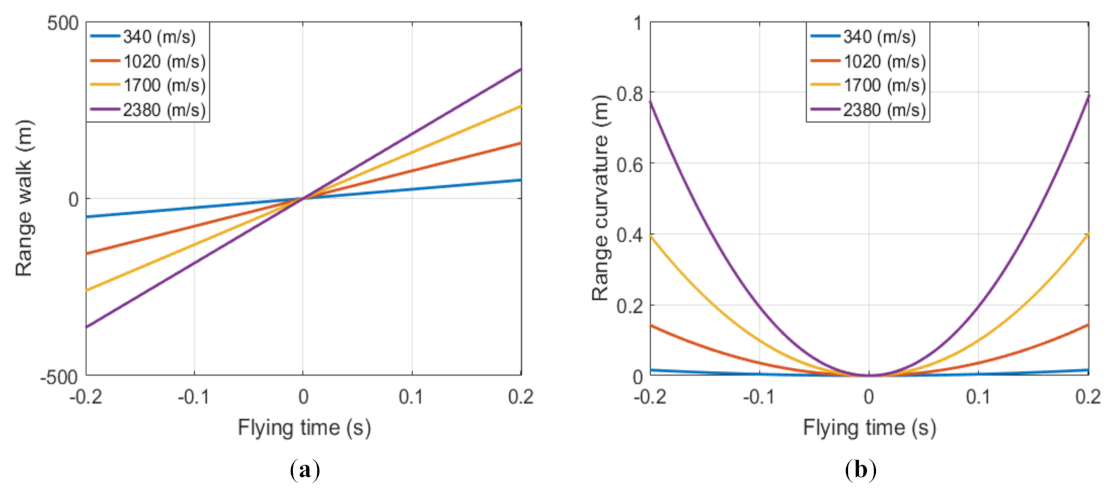
4.1. Range Walk and Range Curvature
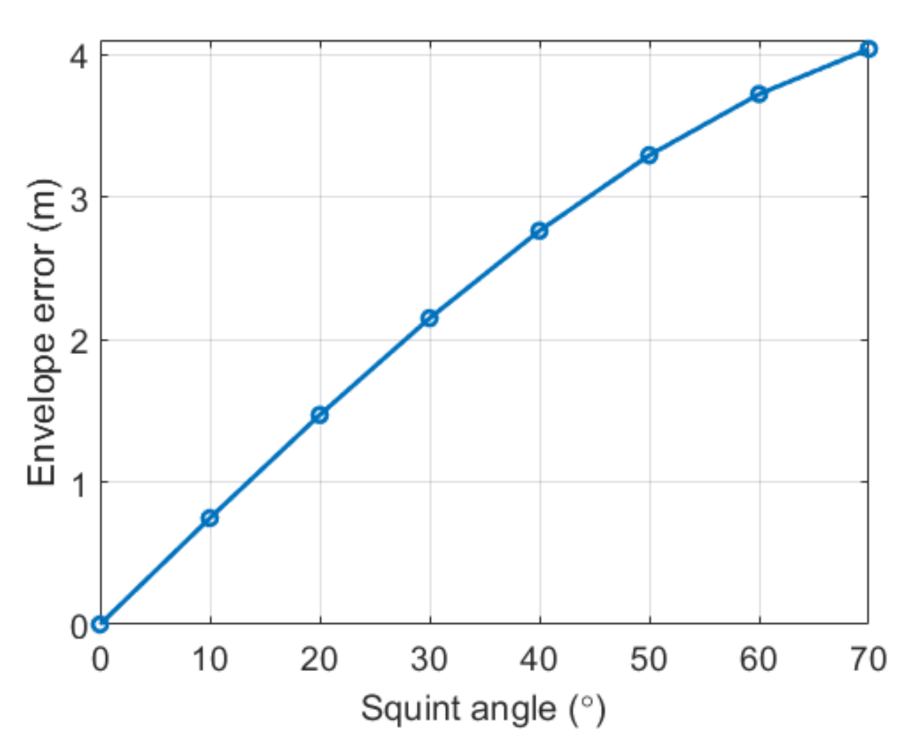
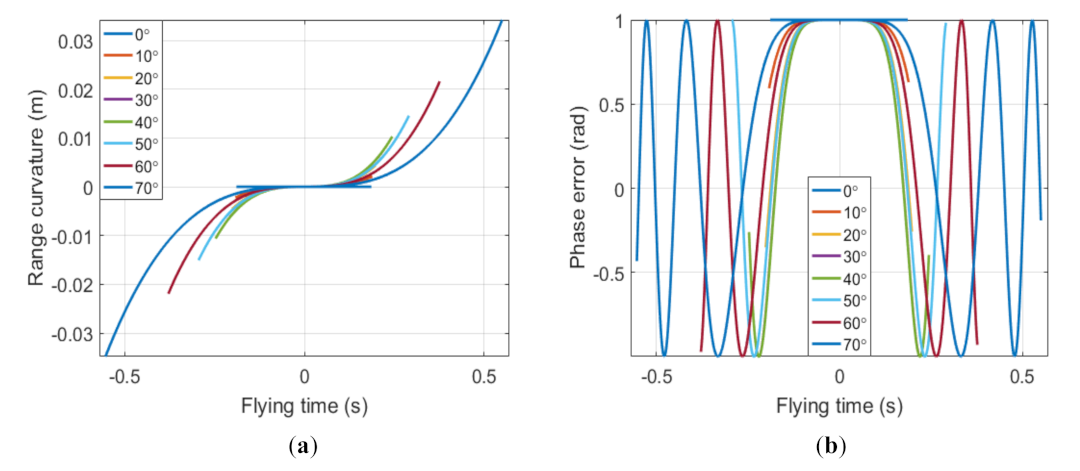
4.2. High-Order Phases
5. Simulation and Examples
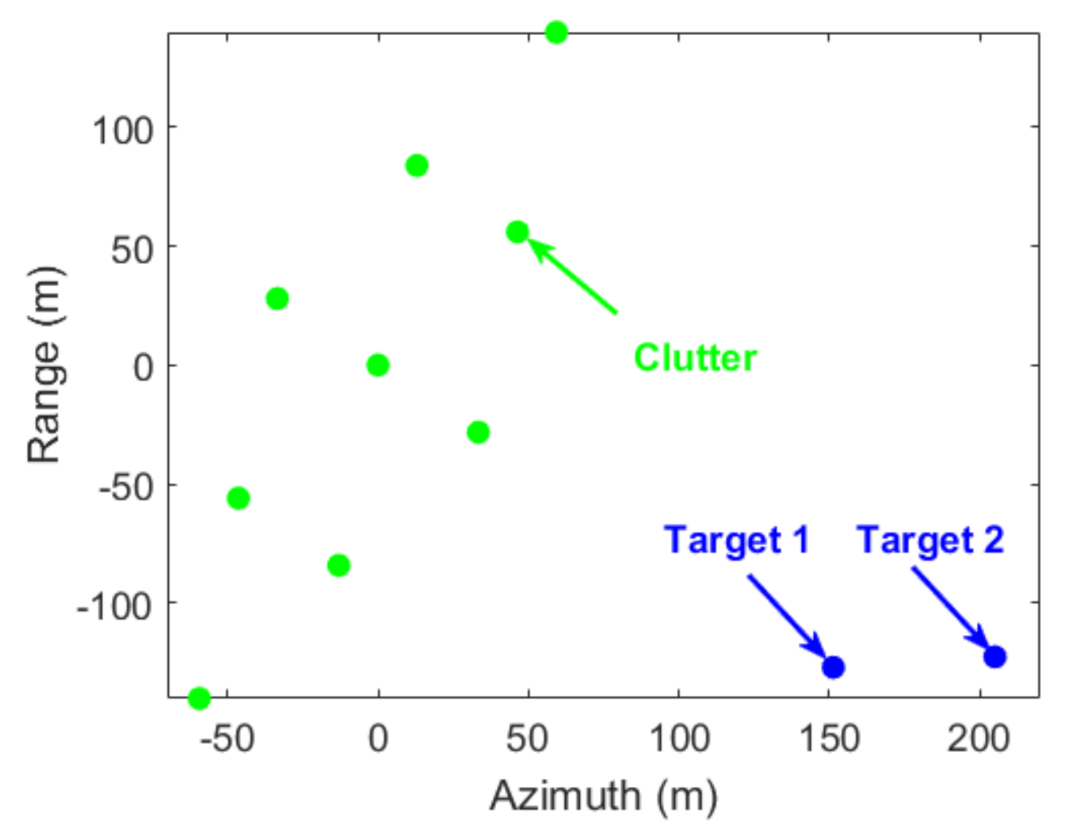
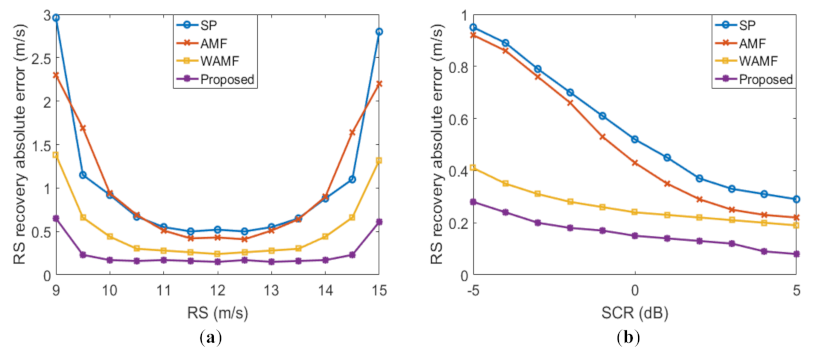
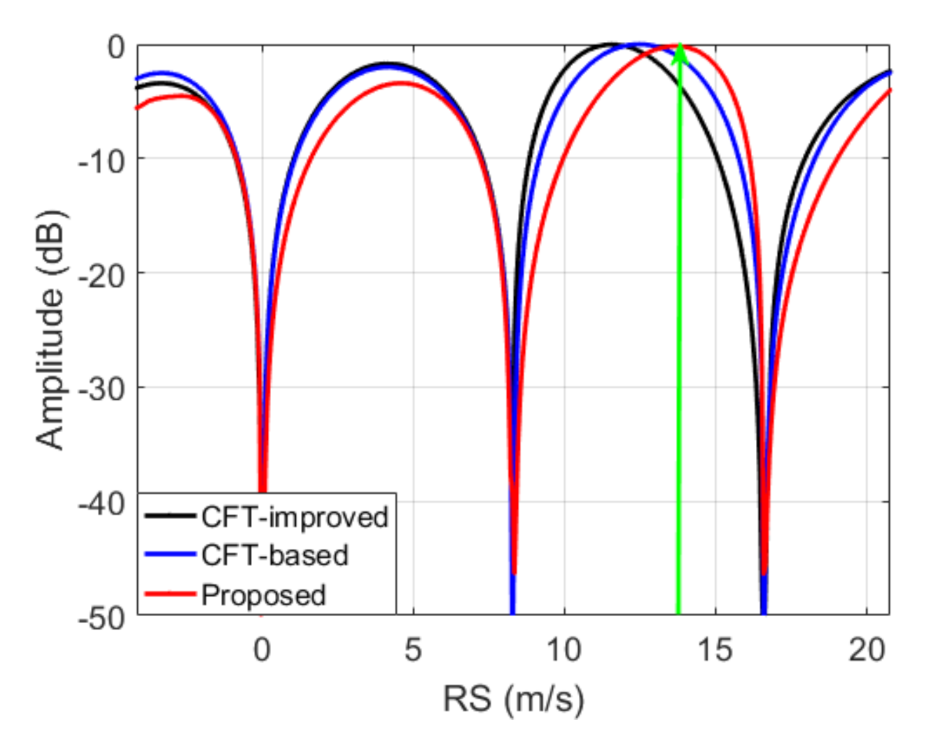
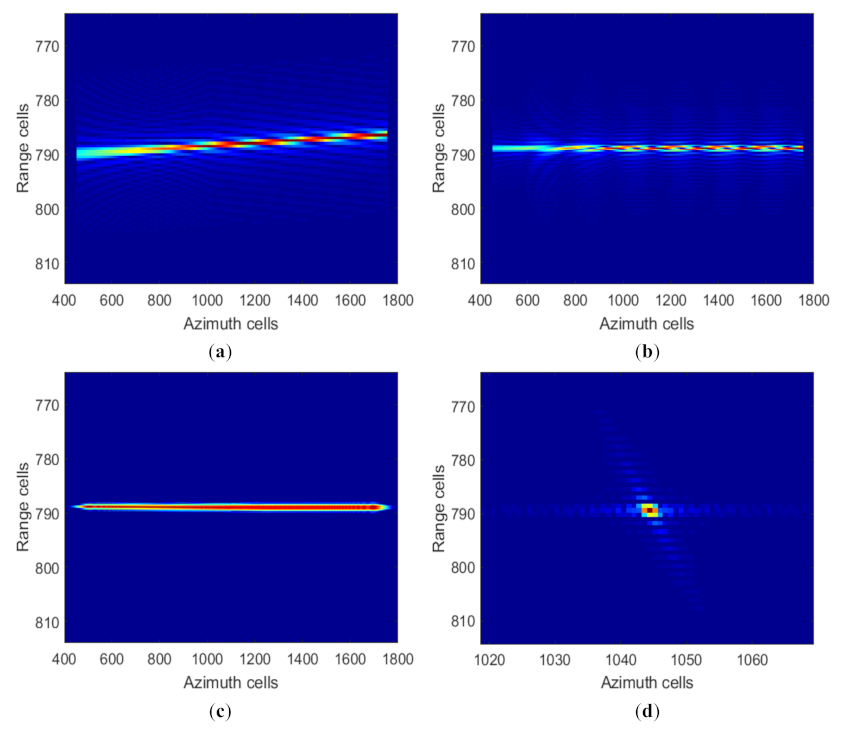
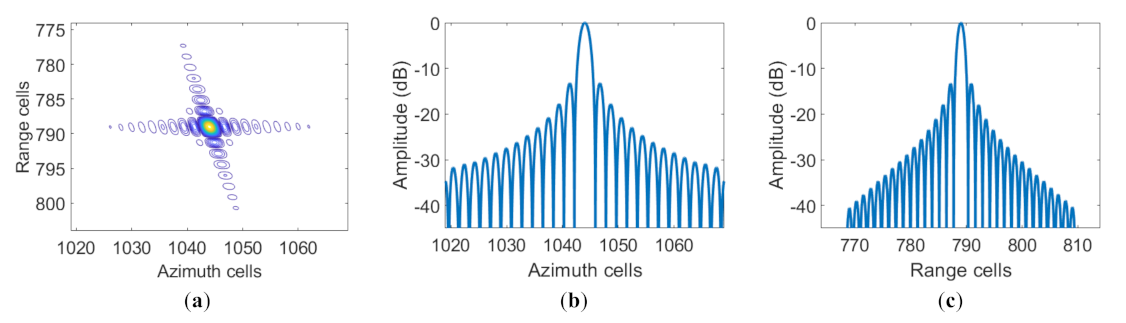
5.1. Simulation Results
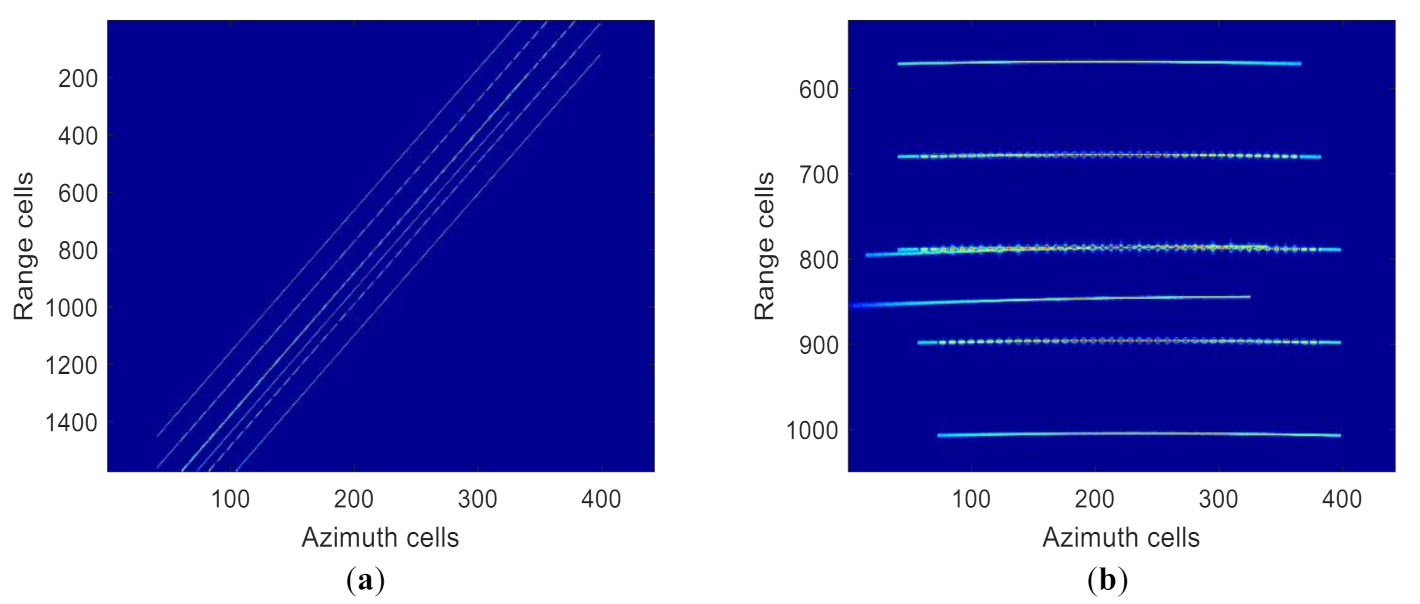
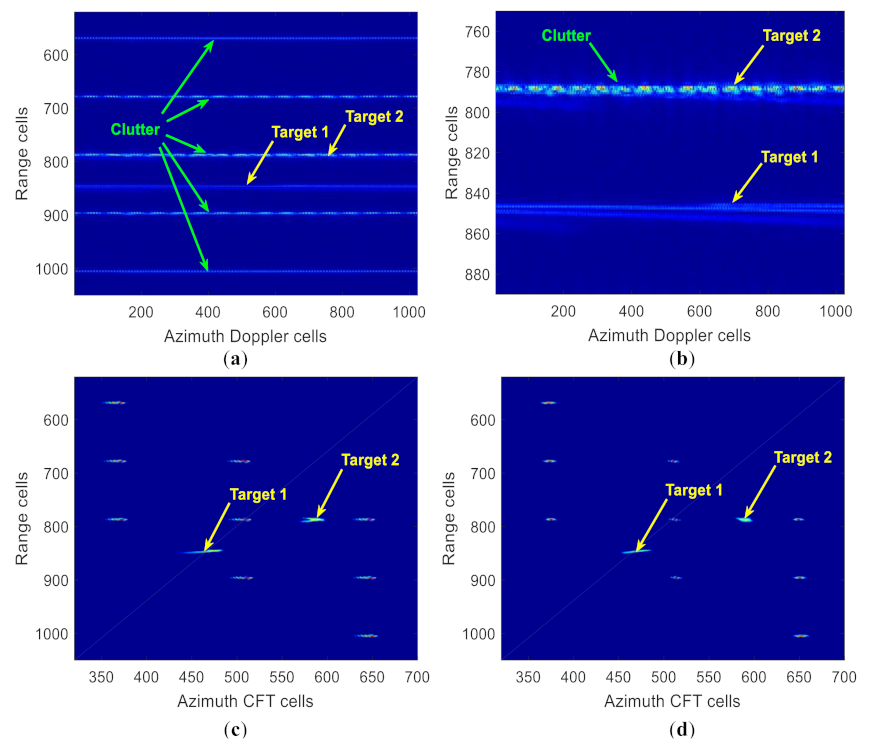
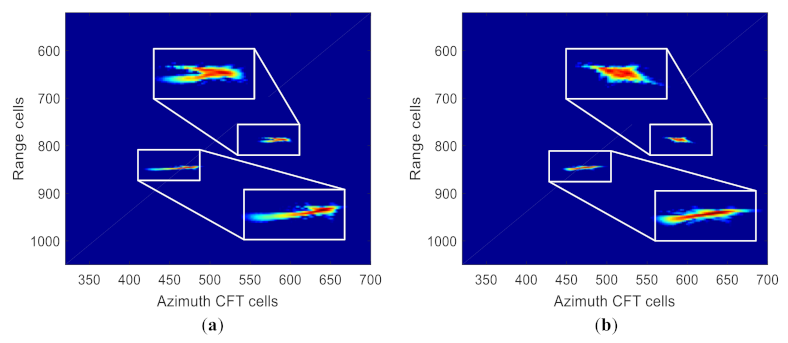
5.2. Real Data Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Cheng, X.; Dai, C.; Liu, F. Robust stability analysis of H1-SGQKF and its application to transfer alignment. Signal Process. 2015, 117, 310–321. [Google Scholar] [CrossRef]
- Wang, W. Near-space vehicle-borne SAR with reflection-antenna for high-resolution and wide-swath remote sensing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 338–348. [Google Scholar] [CrossRef]
- Tang, S.; Guo, P.; Zhang, L.; So, H.C. Focusing Hypersonic Vehicle-Borne SAR Data Using Radius/Angle Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 281–293. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Wang, S.; Su, H. Clutter Suppression and Ground Moving Target Imaging Approach for Hypersonic Vehicle borne multichannel radar based on Two-Step focusing Method. Digit. Signal Process. 2019, 85, 62–76. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Peng, Z.; Su, H. Clutter suppression and moving target imaging approach for multichannel hypersonic vehicle borne radar. Digit. Signal Process. 2017, 68, 81–92. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Zhang, L.; Lin, C.; Huang, Y.; Tang, S. Ground Moving Target Imaging and Analysis for Near-Space Hypersonic Vehicle-Borne Synthetic Aperture Radar System with Squint Angle. Remote Sens. 2018, 10, 1966. [Google Scholar] [CrossRef]
- Galletti, M.; Krieger, G.; Thomas, B.; Marquart, M.; Johannes, S.S. Concept design of a near-space radar for tsunami detection. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 34–37. [Google Scholar]
- Khedkar, S.B.; Kasav, S.M.; Khedkar, A.S.; Mahajan, S.M.; Satpute, D.R. A Review on Hypersonic Aircraft. Int. J. Adv. Technol. Eng. Sci. 2015, 3, 1566–1570. [Google Scholar]
- Xu, X.; Liao, G.; Yang, Z.; Wang, C. Moving-in-pulse duration model-based target integration method for HSV-borne high-resolution radar. Digit. Signal Process. 2017, 68, 31–43. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M. A Novel Doppler Chirp Rate and Baseline Estimation Approach in the Time Domain Based on Weighted Local Maximum-Likelihood for an MC-HRWS SAR System. IEEE Trans. Geosci. Remote Sens. Lett. 2017, 14, 299–303. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Z.; Wang, Z.; Xiao, L.; Xia, X.; Long, T. Radial Velocity Retrieval for Multichannel SAR Moving Targets with Time–Space Doppler Deambiguity. IEEE Trans. Geosci. Remote Sens. 2018, 56, 35–48. [Google Scholar] [CrossRef]
- Lv, G.; Li, Y.; Wang, G.; Zhang, Y. Ground Moving Target Indication in SAR Images with Symmetric Doppler Views. IEEE Trans. Geosci. Remote Sens. 2016, 54, 533–543. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Xu, J.; Yang, D. MIMO SAR OFDM chirp waveform design and GMTI with RPCA based method. Digit. Signal Process. 2016, 51, 184–195. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.; Wang, Y. Imaging and parameter estimation of fast-moving targets with signle-antenna SAR. IEEE Trans. Geosci. Remote Sens. Lett. 2014, 11, 529–533. [Google Scholar] [CrossRef]
- Robinson, P.N. Depth of field for SAR with aircraft acceleration. IEEE Trans. Aerosp. Electron. Syst. 1984, 20, 603–616. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Hing, S. Focusing High-Resolution Highly-Squinted Airborne SAR Data with Maneuvers. Remote Sens. 2018, 10, 862. [Google Scholar] [CrossRef]
- Jing, K.; Xu, I.; Yao, D.; Huang, Z.; Long, T. SAR Ground Moving Target Indication via Cross-Track Interferometry for a Forward-Looking Array. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 966–986. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Zhang, Y.; Li, Q.; Gu, Y.; Lin, C. Processing of monostatic SAR with general configurations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6529–6546. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.; Xia, X. Robust clutter suppression and moving target imaging approach for multichannel in azimuth high-resolution and wide-swath synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 687–709. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Huang, Y.; Liao, G.; Xu, J.; Li, J.; Yang, D. GMTI and Parameter Estimation for MIMO SAR System via Fast Interferometry RPCA Method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1174–1187. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Peng, Z. Clutter suppression and GMTI for hypersonic vehicle borne SAR system with MIMO antenna. IET Signal Process. 2017, 11, 909–915. [Google Scholar] [CrossRef]
- Makhoul, E.; Broquetas, A.; Rodon, J.R.; Zhan, Y.; Ceba, F. A performance evaluation of sar-gmti missions for maritime applications. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2496–2509. [Google Scholar] [CrossRef]
- Faubert, D.; Tam, W. Improvement in the detection performance of a space based radar using a displaced phase centre antenna. In Proceedings of the 1987 Antennas and Propagation Society International Symposium, Blacksburg, VA, USA, 15–19 June 1987; pp. 964–967. [Google Scholar]
- Lightstone, L.; Faubert, D.; Rempel, G. Multiple phase centre DPCA for airborne radar. In Proceedings of the 1991 IEEE National Radar Conference, Los Angeles, CA, USA, 12–13 March 1991; pp. 36–40. [Google Scholar]
- Klemm, R. Introduction to space-time adaptive processing. Electron. Commun. Eng. J. 1999, 11, 5–12. [Google Scholar] [CrossRef]
- Xu, L.; Gianelli, C.; Jian, L. Long-CPI multichannel SAR-based ground moving target indication. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5159–5170. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I. A Generalization of DPCA Processing for Multichannel SAR/GMTI Radars. IEEE Trans. Geosci. Remote Sens. 2013, 51, 560–572. [Google Scholar] [CrossRef]
- Delphine, C.; Ishuwa, S. Optimum GMTI processing for space-based SAR/GMTI systems—Theoretical derivation. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 390–393. [Google Scholar]
- Makhoul, E.; Broquetas, A.; Gonzalez, O. Evaluation of state-ofthe- art GMTI techniques for future space-borne SAR system-simulation validation. In Proceedings of the 9th European Conference on Synthetic Aperture Radar (EUSAR 2012), Nuremberg, Germany, 23–26 April 2012; pp. 376–379. [Google Scholar]
- Cerutti-Maori, D.; Sikaneta, I.C.H. Gierull, Optimum SAR/GMTI Processing and Its Application to the Radar Satellite RADARSAT-2 for Traffic Monitoring. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3868–3881. [Google Scholar] [CrossRef]
- Li, X.; Xing, M.; Xia, X.; Sun, G.; Yi, L.; Zheng, B. Deramp space-time adaptive processing for multichannel SAR systems. IEEE Trans. Geosci. Remote Sens. Lett. 2014, 11, 1448–1452. [Google Scholar]
- Sun, G.; Xing, M.; Xia, X.; Wu, Y.; Bao, Z. Robust ground moving-target imaging using deramp-keystone processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Duan, K.; Xu, H.; Yuan, H.; Xie, H.; Wang, Y. Reduced-DOF Three-Dimensional STAP via Subarray Synthesis for Nonsidelooking Planar Array Airborne Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3311–3325. [Google Scholar] [CrossRef]
- Zoubir, A.; Pesavento, M.; Korso, M.; So, H.C.; Jiang, X. Special Issue on Robust Multi-Channel Signal Processing and Applications: On the Occasion of the 80th Birthday of Johann F. Bhme. Signal Process. 2020, 172, 1–4. [Google Scholar] [CrossRef]
- Eedara, I.P.; Amin, M.G.; Hassanien, A. Controlling Clutter Modulation in Frequency Hopping MIMO Dual-Function Radar Communication Systems. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 28–30 April 2020; pp. 466–471. [Google Scholar]
- Xia, X.G. Discrete chirp-Fourier transform and its application to chirp rate. IEEE Trans. Signal Process. 2000, 48, 3122–3133. [Google Scholar]
- Gershman, A.B.; Pesavento, M.; Amin, M.G. Estimating parameters of multiple wideband polynomial-phase sources in sensor arrays. IEEE Trans. Signal Process. 2001, 49, 2924–2934. [Google Scholar] [CrossRef]
- Suleiman, W.; Parvazi, P.; Pesavento, M.; Zoubir, A.M. Non-Coherent Direction-of-Arrival Estimation Using Partly Calibrated Arrays. IEEE Trans. Signal Process. 2018, 66, 5776–5787. [Google Scholar] [CrossRef]
- Schenck, D.; Mester, X.; Pesavento, M. Probability of Resolution of Partially Relaxed Deterministic Maximum Likelihood: An Asymptotic Approach. IEEE Trans. Signal Process. 2021, 69, 853–866. [Google Scholar] [CrossRef]
- Xin, Z.; Korso, M.; Pesavento, M. MIMO radar target localization and performance evaluation under SIRP clutter. Signal Process. 2017, 130, 217–232. [Google Scholar]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Dragosevic, M.V.; Burwash, W.; Chiu, S. Detection and estimation with RADARSAT-2 moving-object detection experiment modes. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3527–3543. [Google Scholar] [CrossRef]
- Liao, G.; Li, H. Estimation Method for InSAR Interferometric Phase Based on Generalized Correlation Steering Vector. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1389–1403. [Google Scholar] [CrossRef]
- He, X.; Liao, G.; Xu, J.; Zhu, S. Robust radial velocity estimation based on joint-pixel normalized sample covariance matrix and shift vector for moving targets. IEEE Trans. Geosci. Remote Sens. Lett. 2019, 16, 221–225. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, B.; Wang, H.; Liao, G. Performance improvement for constellation sar using signal processing techniques. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 436–452. [Google Scholar]
- Zuo, S.S.; Xing, M.; Xia, X.G.; Sun, G. Improved Signal Reconstruction Algorithm for Multichannel SAR Based on the Doppler Spectrum Estimation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1425–1442. [Google Scholar] [CrossRef]
- Yan, H.; Wang, R.; Li, F.; Deng, Y.; Liu, Y. Ground moving target extraction in a multichannel wide-area surveillance sar/gmti system via the relaxed pcp. IEEE Trans. Geosci. Remote Sens. Lett. 2013, 10, 617–621. [Google Scholar] [CrossRef]
- Suo, Z.; Li, Z.; Bao, Z. Multi-channel sar-gmti method robust to coregistration error of sar images. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 2035–2043. [Google Scholar] [CrossRef]
- Shu, Y.; Liao, G.; Yang, Z. Robust radial velocity estimation of moving targets based on adaptive data reconstruction and subspace projection algorithm. IEEE Trans. Geosci. Remote Sens. Lett. 2014, 11, 11010–11105. [Google Scholar] [CrossRef]
- Liu, J.; Gershman, A.B.; Luo, Z.Q.; Wong, K.M. Adaptive beamforming with sidelobe control. IEEE Signal Proces. Lett. 2015, 10, 331–334. [Google Scholar]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.; Zheng, J. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 2017, 55, 320–335. [Google Scholar] [CrossRef]
- Zeng, C.; Li, D.; Luo, X.; Song, D.; Liu, H.; Su, J. Ground maneuvering targets imaging for synthetic aperture radar based on second-order keystone transform and high-order motion parameter estimation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 12, 4486–4501. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. Mimo sar processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5034–5055. [Google Scholar] [CrossRef]
- Pei, S.C.; Ding, J.J. Fractional cosine, sine, and Hartley transforms. IEEE Trans. Signal Process. 2002, 50, 1661–1680. [Google Scholar]
- Almeida, L.B. The fractional fourier transform and time-frequencyrepresentations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Wang, W.-Q. Approach of multiple moving targets detection for microwave surveillance sensors. Int. J. Inf. Acquisit. 2007, 4, 57–68. [Google Scholar] [CrossRef]
- Li, Z.; Wu, J.; Liu, Z.; Huang, Y.; Yang, J. An optimal 2-d spectrum matching method for sar ground moving target imaging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5961–5974. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I.; Machado, R.; Dammert, P.; Hellsten, H. False alarm reduction in wavelength-resolution sar change detection using adaptive noise canceler. IEEE Trans. Geosci. Remote Sens. 2016, 55, 591–599. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 10 GHz | Signal bandwidth | 150 MHz |
| Wavelength | 0.03 m | Incidence angle | 60° |
| Platform altitude | 30 km | Range resolution | 1 m |
| PRF | 554 Hz | Azimuth resolution | 1 m |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 10 GHz | Squint angle | 50° |
| Wave length | 0.03 m | Platform spend | 2380 (m/s) |
| Platform altitude | 30 km | Channel distance | 1.5 m |
| Center slant range | 60 km | Doppler bandwidth | 1530 Hz |
| Channel number | 5 | PRF | 554 Hz |
| SCNR (dB) | RS Absolute Error (m/s) | HS Absolute Error (m/s) | Calculation Time (s) | |
|---|---|---|---|---|
| ISTAP | 19.21 | 2.58 | 2.63 | 26.53 |
| CFT-based | 26.27 | 5.13 | / | 1.96 |
| CFT-improved | 28.62 | 1.91 | 1.40 | 5.46 |
| Proposed | 30.71 | 0.15 | 0.16 | 3.28 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pulse width | 10 us | PRF | 1000 Hz |
| Sampling rate | 60 MHz | Channel number | 3 |
| Bandwidth | 40 MHz | Doppler bandwidth | 417.4 Hz |
| Wavelength | 0.0339 m | Platform velocity | 115 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Cao, Y.; Yeo, T.-S.; Wang, F. Robust Clutter Suppression and Ground Moving Target Imaging Method for a Multichannel SAR with High-Squint Angle Mounted on Hypersonic Vehicle. Remote Sens. 2021, 13, 2051. https://doi.org/10.3390/rs13112051
Han J, Cao Y, Yeo T-S, Wang F. Robust Clutter Suppression and Ground Moving Target Imaging Method for a Multichannel SAR with High-Squint Angle Mounted on Hypersonic Vehicle. Remote Sensing. 2021; 13(11):2051. https://doi.org/10.3390/rs13112051
Chicago/Turabian StyleHan, Jiusheng, Yunhe Cao, Tat-Soon Yeo, and Fengfei Wang. 2021. "Robust Clutter Suppression and Ground Moving Target Imaging Method for a Multichannel SAR with High-Squint Angle Mounted on Hypersonic Vehicle" Remote Sensing 13, no. 11: 2051. https://doi.org/10.3390/rs13112051
APA StyleHan, J., Cao, Y., Yeo, T.-S., & Wang, F. (2021). Robust Clutter Suppression and Ground Moving Target Imaging Method for a Multichannel SAR with High-Squint Angle Mounted on Hypersonic Vehicle. Remote Sensing, 13(11), 2051. https://doi.org/10.3390/rs13112051







