Abstract
Slope failures pose a substantial threat to mining activity due to their destructive potential and high probability of occurrence on steep slopes close to limit equilibrium conditions, which are often found both in open pits and in waste and tailing disposal facilities. The development of slope monitoring and modeling programs usually entails the exploitation of in situ and remote sensing data, together with the application of numerical modeling, and it plays an important role in the definition of prevention and mitigation measures aimed at minimizing the impact of slope failures in mining areas. In this paper, a new methodology is presented; one that combines satellite radar interferometry and 2D finite element modeling for slope stability analysis at a regional scale, and applied within slope unit polygons. Although the literature includes many studies applying radar interferometry and modeling for slope stability analysis, the addition of slope units as input data for radar interferometry and modeling purposes has, to our knowledge, not previously been reported. A former mining area in southeast Spain was studied, and the method proved useful for detecting and characterizing a large number of unstable slopes. Out of the 1959 slope units used for the spatial analysis of the radar interferometry data, 43 were unstable, with varying values of safety factor and landslide size. Out of the 43 active slope units, 21 exhibited line of sight velocities greater than the maximum error obtained through validation analysis (2.5 cm/year). Finally, this work discusses the possibility of using the results of the proposed approach to devise a proxy for landslide hazard. The proposed methodology can help to provide non-expert final users with intelligible, clear, and easily comparable information to analyze slope instabilities in different settings, and not limited to mining areas.
1. Introduction
Mining activities frequently induce ground movements, for different reasons. In underground mining, instability normally develops as a consequence of adverse structural geology, substantial stress, weathering and/or softening of rocks, and excessive groundwater pressure or flow [1]. Such conditions may lead to the collapse of underground openings. All of these factors can give rise, in turn, to ground subsidence. In surface mining, instability is generally the result of the exposure of dominant weakness planes, although failure within intact rock is also possible in very weak rocks and formations. Instability mainly affects excavated slopes and may result in catastrophic events if appropriate measures to prevent slope failure are not undertaken. Slope instability often affects waste and tailing disposal facilities as well; which are essential in both surface and underground mining operations. These facilities consist of unconsolidated debris material arranged in waste dumps and tailing dams.
Slope failures and subsidence can cause serious problems, such as environmental impacts, damage to property, harm to the health and safety of both employees and residents of nearby communities, and economic outcomes that can either result in the premature closure of the mine [2] or compromise the reclamation and decommissioning of the mining operation. Both phenomena may occur long after the mine operations have been abandoned [3]. Moreover, unlike civil engineering projects, where the useful and expected life of the structures is very long (typically more than 10 years), mining projects only require certain facilities to have long lives (e.g., shafts, main haulage drifts, etc.).
For this reason, the safety factor (SF) used in the design of mining structures is much lower than that used in civil structures, and, in many situations, a SF ≈ 1 is used [2]. Low SFs do not imply, however, that safety is less important in mining. Rather, that profit margins are narrow and total costs must be kept to a minimum. In all mining operations, it is always a major challenge for the designers to ensure the integrity and stability of all openings and excavations, while keeping the costs low. However, in most mining projects, investing in specific ground monitoring programs early can produce major cost savings in the future. A clear example would be the case of large open-pit mines, where the slopes are designed so that they are allowed to move in order to reduce the amount of waste to be mined, while also monitoring the movements very carefully.
In order to ensure safe and stable conditions, ground monitoring in mining has been traditionally undertaken through the application of surface and subsurface techniques [4]. Recently, the development of modern monitoring systems, such as time domain reflectometers [5], terrestrial laser scanners [6], radars [7,8,9], and unmanned aerial vehicles [10,11], has spurred a rise in the use of remote sensing technologies. However, all of the methods mentioned above require in situ measurements for calibration and validation, and in some cases they represent a costly solution.
The application of satellite synthetic aperture radar interferometry (InSAR) [12] has been adopted as a supplementary technique to study mining-induced ground movements. As in the case of other remote sensing techniques, InSAR results require the validation of the measured ground movements, typically carried out using in situ monitoring data. In addition, they can be used in conjunction with numerical models reproducing the measured movements after ground truth verification [13,14,15].
In particular, case studies on the use of satellite InSAR to analyze mining-induced slope instabilities are scarce, as most of them focus on ground subsidence (e.g., [16,17,18]). Nevertheless, the application of such technique has been documented in a few mining sites in Australia [19,20], Brazil [21,22], Spain [23,24], South Africa [15], Turkey [7], and U.S.A. [14,25]. However, in most cases these works present analyses of the InSAR data at the slope scale, or include no complementary stability analyses taking into account geotechnical data through geo-mechanical modeling.
In this paper, a topography-driven methodology is proposed, aimed at analyzing slope instabilities at a regional scale, and using satellite InSAR in conjunction with 2D finite element (FE) modeling. The method is topography-driven because it makes use of slope units (SUs) as mapping units, instead of the widely used grid cells. SUs are portions of geomorphologically homogeneous terrain. The proposed approach aims to simplify the InSAR- and FE-modeling-derived results in order to provide non-expert final users with intelligible, clear, and easily comparable information.
The methodology has been implemented for the region of Sierra de Cartagena-La Unión (Murcia), hereinafter referred to as Sierra Minera, a former mining area in southeast Spain (Figure 1). A few case studies conducted in Sierra Minera through satellite InSAR are known in the literature. However, most of these focus on mapping and monitoring ground subsidence within the urban area of La Unión [26,27]; which is no longer occurring in the area, according to our InSAR data.
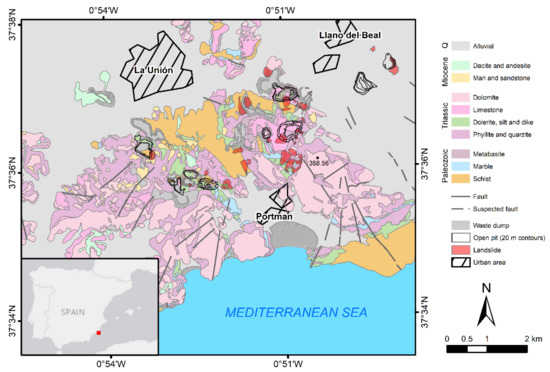
Figure 1.
Study area and geological map of Sierra de Cartagena-La Unión (adapted with permission from ref. [28]).
One of the existing studies mapped ground movements in Sierra Minera using satellite InSAR [23]. Yet, the data used in that study were obtained by processing ERS and ENVISAT satellite data. Hence, the spatial resolution of the results (80 by 80 m) and the density of measuring points (MPs) were rather low.
In contrast, our results were obtained by processing Sentinel-1 satellite data. Thus, in this work, line-of-sight (LOS) ground velocity maps over Sierra Minera were derived at a higher resolution (30 by 30 m) and with a much higher density of MPs. This improvement is not only due to the higher spatial resolution of the Sentinel-1 constellation, but also to its short revisit time (6 days). In addition, stability analyses were performed through 2D FE modeling in order to cross-reference the InSAR data.
The proposed approach builds upon previously published works aimed at detecting active deformation areas [29,30,31,32]. In those studies, however, the topography was only taken into account to discern flat areas from hill slopes; the concept of SU was not considered, and no stability analyses were performed. Moreover, whereas those studies were conceived to analyze ground deformation phenomena in general, our approach focuses exclusively on analyzing slope instability.
This paper is organized as follows. Section 2 provides an overview of the geographical, geological, and geotechnical characteristics of Sierra Minera, as well as a summary of the data used for this study, some of which were collected through fieldwork. Section 3 includes a detailed explanation of the different steps of the proposed approach. Section 4 and Section 5, respectively, describe and discuss the obtained results. Finally, Section 6 summarizes the main findings and details the conclusions of this study.
2. Study Area and Data
2.1. Geological, Lithological, and Geotechnical Setting
The study area is located in Sierra Minera, at a distance of approximately 50 km south-southeast from the city of Murcia, in the south-easternmost part of Spain (Figure 1). The region extends over an area of 50 km2, with a maximum elevation of 389 m a.s.l. at Peña del Águila. It is limited by the Mediterranean Sea to the south and by the Campo de Cartagena basin to the north.
Sierra Minera contains one of the largest Pb and Zn ore deposits in the south of Europe [33], which was exploited from the Iberian period until 1991 [34]. It is a coastal mountain range with an approximate east-west trend, and which belongs to the Internal Zones of the Betic Cordillera.
The Betic Cordillera, an Alpine chain that acquired its present configuration during the Neogene, was developed from the late Mesozoic to the Cenozoic with the convergence between the African and Iberian plates [35]. The Internal Zones comprise three complex nappes with decreasing metamorphism grade, from the lower complex to the upper one. These are, from bottom to top, the Nevado–Filábride, the Alpujárride, and the Maláguide complexes [35].
The Nevado–Filábride mainly comprises graphite schists, quartzitic schists, micaschists, marbles, and quartzites of Paleozoic to Permo-Triassic age. Discordantly overlaying this complex is the Alpujárride complex, represented by a detritic formation (epimetamorphic rocks, quartzites, and phyllites) of Permian age, and by a Triassic carbonate series containing intrusive bodies of diabases and dolerites [33]. After a significant erosional phase, these formations were covered by the Maláguide complex, made up of a post-orogenic, Neogene series of sedimentary rocks (sandstone, quartzite, silt, limestone, and conglomerate) [36]. Finally, a thin level of quaternary alluvial deposits, formed of sand, silt, and clays, overlies the complex nappes.
The mineralization is mainly represented by two sulfide deposits on the carbonate sequences in the Nevado–Filábride and Alpujárride complexes. It is characterized by a strict stratigraphic control, although many faults are also mineralized and sometimes contain thick seams. In addition, mineralizations can also be found disseminated in Miocene materials, gossans, stickworks, and veins [33].
The deposits were mainly exploited through underground mining using the room-and-pillar method until the 1960s, when large open-pit exploitations were developed. One third of the total reserves was extracted between 1940 and 1990, thanks to the application of differential flotation processes and open-pit mining [33].
Over the years, 12 open pits were excavated, 3000 wells were drilled, and hundreds of galleries and waste dumps were developed [36]. The waste dump debris material was accumulated on existing hillsides, without any particular safety measures, and remaining in a limit equilibrium situation (SF ≈ 1).
The first ecological restoration in Sierra Minera was conducted in 1982 by Benaroya SA, the mining company. It was carried out by sealing the mining tailings with a soil layer, in order to allow the growth of vegetation and to avoid the mobilization of heavy metals [37]. Later, in 1996, the Spanish Geological Survey conducted an environmental restoration project aimed at characterizing the geo-mechanical properties of dominant lithologies in the area (Table 1) [28]. For this purpose, geotechnical boreholes, as well as in situ and laboratory tests, were carried out. The pumping tests carried out in well points over the study area revealed that most of the lithologies are fairly impermeable (e.g., those formed by schists, phyllites, and marls) [28]. However, quaternary formations, Miocene sedimentary rocks, and some Alpujárride detritic units are permeable. The study concluded that the presence of schists, phyllites, and, most importantly, waste dump debris material favored the occurrence of slope instabilities. Moreover, it was found that these instabilities were induced by intense and short periods of rainfall, triggering torrential events. In Sierra Minera, these type of events are concentrated in a few days throughout the year; 20 or 30 days, mainly in autumn. New insights into the analysis of such slope instabilities are presented in this paper.

Table 1.
Geo-mechanical properties of dominant lithologies (adapted with permission from ref. [28]).
2.2. In Situ and Satellite Data
For the purpose of landslide mapping and monitoring, in situ investigations were conducted over the study area through geomorphic analysis and topographic surveying. A landslide inventory (Figure 1) was elaborated through fieldwork and aerial-photo interpretation, updating the previously published data [23]. Most of the inventoried landslides affect waste dump areas and open-pit slopes. Although some landslides, associated with the presence of phyllites and schists, seem to affect both cut and fill slopes from haul roads. Most of the mapped slope instabilities can be classified as complex movements, frequently consisting of debris roto-translational landslides, debris flows, and translational landslides, together with rockfalls and toppling [38].
In addition, in situ topographic surveying activities were performed using differential global positioning system (DGPS) instrumentation. Thus, ground monitoring data were obtained for validation purposes from two campaigns performed in 11 July 2017 and 15 November 2018, over one of the inventoried landslides.
During one of the conducted in situ monitoring campaigns, two stacks of 64 and 83 Sentinel-1 Single Look Complex (SLC) images (with a spatial resolution of 3 by 14 m) were acquired under ascending and descending passes, respectively, and considered for the investigation. These images covered the period from the 10 July 2017 to the 15 November 2018. Finally, we used a digital elevation model of the study area with a spatial resolution of 5 by 5 m, corresponding to the December 2009 acquisitions, and downloaded from the National Geographic Institute of Spain [39].
3. Methodology
The methodology presented here relies on the joint exploitation of remote sensing, and in situ and additional available data, to quantify mean LOS ground velocity, 2D safety factor SF, and 2D landslide size for a set of automatically-mapped slope instabilities. It essentially comprises three successive steps. First, LOS ground velocity maps were derived using a web-based unsupervised satellite InSAR processing chain, which were then validated with DGPS data. The unsupervised nature of the algorithm relates to the fact that it is capable of running in a fully automated manner, and thus reducing the user interaction to only few initial steps. Then, a spatial analysis of the InSAR-retrieved velocities was performed using an optimized SU map, from which an active deformation slope unit (ADSU) map was obtained. Finally, 2D FE modeling was employed to perform stability analyses on each ADSU from the optimal map. As a result, a LOS ground velocity (VLOS), a safety factor SF, and a landslide size was obtained for each ADSU (Figure 2). The results can be updated, for a continuous assessment, by repeating the analysis on a regular basis.
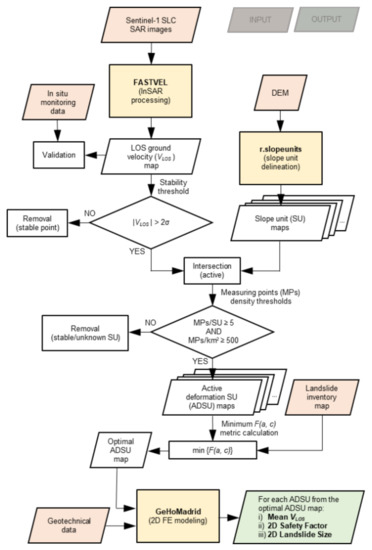
Figure 2.
Flowchart of the proposed methodology.
The input data needed to apply the proposed methodology include a stack of SAR images, a digital elevation model, a landslide inventory map, a geotechnical map, and in situ ground monitoring data for validation.
The automatic mapping procedure is based on the aggregation of the active MPs within the boundaries of different sets of morphological SUs, with varying sizes. In fact, SUs can be delineated applying different degrees of aspect homogeneity, which results in different maps containing a varying number of polygons.
An ADSU map is obtained for each SU delineation. The different ADSU maps are evaluated to find the map best matching the landslides observed in the study area. The best matching map is referred to as the optimal ADSU map. ADSUs are also used to derive 2D cross-sections through an automated procedure. Finally, stability analyses are performed for each cross-section, and taking into account their geo-mechanical properties.
The different steps of the methodology, as well as the results obtained at each step, are described in detail in the next sections.
3.1. Advanced Differential Satellite InSAR Processing and Comparison with In Situ DGPS Measurements
LOS ground velocity maps in the study area were derived by processing the aforementioned Sentinel-1 images stacks using FASTVEL [12,40], an on-demand, unsupervised processing service available on the Geohazards Exploitation Platform (GEP) [41]. GEP is part of the Thematic Exploitation Platforms initiative set up by the European Space Agency (ESA), aiming to support the exploitation of satellite Earth Observation for geohazard assessment (https://geohazards-tep.eu/) (accessed on 13 February 2020) [42,43].
FASTVEL offers two different processing modes, namely, interferogram generation and multi-temporal analysis, and aimed respectively at generating differential interferograms or mean ground velocity maps. Earth Observation sources supported by FASTVEL include ERS, Envise-ASAR, and Sentinel-1.
In multi-temporal analysis mode, the service provides the following output results: (i) a LOS ground velocity map; (ii) the updated topography, including a reference digital elevation model with height uncertainty; and (iii) a CSV file with the main LOS interferometric products. Once the SAR images covering the area of interest have been selected, the user is required to enter a few processing parameters, with the option of selecting the default parameters provided, if preferred. These account for the maximum temporal and spatial baseline, the maximum Doppler centroid difference, the maximum image Doppler centroid value, and the Goldstein phase filter exponential factor. In addition, the user must select a mean coherence threshold to set the initial grid of points, and a maximum atmospheric phase screen correlation distance for linking the initially selected points to minimize atmospheric phase screen propagation. For a detailed description of the FASTVEL service, please refer to its user guide [44].
In this study, default values were adopted for most of the parameters. Note that in the particular case of Sierra Minera, the default values provided by FASTVEL performed well, due to the fact that the area is majorly covered by sparse vegetation, the fact that the movements are slow to extremely slow, and the fact that there are no additional decorrelation sources, such as atmospheric artifacts or strong topographical variations. Thus, LOS ground velocity maps could be calculated in the study area, both in ascending and descending geometries, for the period monitored by DGPS.
Then, the DGPS ground velocities were projected onto the LOS for comparison, considering both geometries (ascending and descending), and using the following equations:
In Equations (1)–(4), and are respectively the projected and the raw ground velocities measured by DGPS; is the angle formed by the two velocity vectors; , , and are respectively the north, east, and up unitary vector components of the raw DGPS vector; is the azimuth angle of the LOS vector measured on the horizontal plane, from the east axis to the north axis in a counterclockwise direction; is the incidence angle of the LOS vector, measured on the vertical plane from the horizontal plane to the up axis in a counterclockwise direction; and , , and are respectively the north, east, and up unitary vector components of the LOS vector.
3.2. Parametric Delineation of Slope Units
Slope units are morphological terrain units, which are alternative to square grid cells, bounded by drainage and divide lines [45,46], and delineated in such a way that the terrain homogeneity is maximized within the units and inhomogeneity is maximized across neighboring units [47,48]. Terrain units are portions of terrain with similar geological and geomorphological features, and which divide a region into portions that have a set of common properties, different from the adjacent ones across definable boundaries [49]. Thus, SUs are a particular type of terrain units causally related to hydro-geomorphological conditions [47] and represent a formalization of what geomorphologists describe as slopes.
Slope units are well suited for hydrological and geomorphological studies, and for landslide susceptibility modeling and zonation [46,50,51,52,53]. SUs are, therefore, also particularly suited in the context of InSAR and FE modeling, since they encompass areas with similar slope-facing direction (i.e., aspect). SUs have been used in the literature in conjunction with optical satellite imagery for landslide mapping [54]. However, the use of SUs to either aggregate InSAR data or derive 2D FE modeling geometries has not, to our knowledge, previously been reported.
In this work, we used the software r.slopeunits of [47] for SU delineation, which is freely available from http://geomorphology.irpi.cnr.it/tools/slope-units (accessed on 9 April 2020). The software is adaptive because, as outlined in [47], no unique SU delineation exists, since there is an inherent dependence on the scale and nature of the process under investigation. Given this non-univocity, the software allows SUs to be delineated with varying sizes and different degrees of homogeneity of aspect. Then, optimized SUs can be obtained by selecting the values of the software’s input parameters that maximize fitness of the output SU set for a particular purpose. The input parameters required by the algorithm are described in detail in [47].
Here, the r.slopeunits software was first run multiple times with different combinations of the input parameters a (minimum area) and c (circular variance of aspect), namely a = (5000, 10,000, 50,000, 100,000, 150,000, 250,000, 350,000, 450,000) m2 and c = (0.01, 0.05, 0.1, 0.15, 0.25, 0.35, 0.45). Thus, we calculated 56 SU maps, corresponding to the possible (a, c) combinations. The values selected were similar to the ones used in previous works [47,55]. Flat areas were excluded from the delineation process by computing a plains map including all areas of the digital elevation model with slope gradient lower than 5°.
3.3. Determination of Active Deformation Slope Units
Once the 56 SU sets were obtained, the two InSAR datasets (ascending and descending) were filtered according to their standard deviations, selecting only the points with |VLOS| > 2σ (i.e., the moving or active MPs). Then, the active MPs were superimposed to the SUs by performing the intersection of the two InSAR datasets and the 56 SU maps; amounting to 112 intersections.
Two different criteria were applied in order to determine which SUs were active (ADSUs). The SUs (i) containing at least five active MPs, either from the ascending or descending dataset, and (ii) yielding a density of active MPs greater than or equal to 500 MPs/km2 (around half of the maximum MPs density of FASTVEL) from the corresponding dataset, were considered ADSUs. The two ADSU sets obtained in ascending and descending geometry for each combination of the input parameters a and c, were combined into a single set.
To select the best combination of the input parameters a and c of the r.slopeunits software, the error index EI, introduced by [45] and utilized in [54], was used, which is defined as follows:
where is the area of the region where either the automatically mapped ADSUs or the inventoried landslides exist (union) with the specified values of (a, c), and is the area of the region where both exist (intersection). The optimal values of the input parameters a and c (i.e., the ones corresponding to the optimal ADSU set), were obtained by minimizing Equation (5) to find the best agreement between the mapped ADSUs and the landslide inventory.
Although the optimal ADSU set was selected on the basis of the results obtained from Equation (5), we also investigated the use of the custom metric developed in [55,56] for comparison. This metric analyzes the differences between the inventoried landslides and the predicted ones (i.e., the mapped ADSUs in this case), in terms of their cumulative frequency size distributions, and is defined as follows:
where 39 is the number of inventoried landslides, is the i-th point of the distribution of the inventoried landslides, and is the corresponding i-th point of the distribution of the mapped ADSUs obtained with the specified values of (a, c), among the 56 different ADSU sets.
Lastly, the results were discussed in terms of confusion matrices. The values of the confusion matrices for the two sets of ADSUs corresponding to the minimum of Equations (5) and (6) were further compared with the values obtained for the active deformation areas (ADAs) mapped by means of the ADAFinder software package [29]. This comparison was carried out to evaluate the improvement achieved through the introduction of topographic data, since ADAFinder is an algorithm for active deformation mapping in which topography is ignored. The only input data required by the ADAFinder software are the InSAR-derived LOS ground velocity maps. In order to perform a meaningful comparison, the two ADA sets obtained with ADAFinder, corresponding to ascending and descending geometry, were likewise combined into a single set.
3.4. 2D Finite Element Modeling
Stability analyses were performed through 2D FE modeling using the shear strength reduction technique [57,58], implemented in the GeHoMadrid code [59,60]. Shear strength reduction simply reduces the soil shear strength, in terms of friction angle Φ and cohesion c, until collapse occurs. The resulting SF is the ratio of the actual soil shear strength to the reduced shear strength at failure.
In this work, the analyzed geometries were automatically derived from the optimal ADSU set using the centroid and the aspect values of each ADSU. Initially, three 400-m long cross-sections were derived for each ADSU, considering three different aspect values that were obtained using the three most common measures of central tendency (i.e., the mean, the median, and the mode; the latter calculated using integer aspect values). In addition, the middle points of the profile traces of all cross-sections were fixed on the ADSUs centroids.
Next, 2D stability analyses (plane–strain conditions) were performed over the three cross-sections obtained for each ADSU, considering a single, homogeneous material and prescribing zero pore pressure on the surface, corresponding to fully saturated conditions. Different materials were assigned for each of the ADSUs, depending on the predominant lithology within their boundaries. The geo-mechanical properties of the four materials considered were taken from [28] and are listed in Table 1. For the other boundary conditions, all displacements were fixed in the bottom plane; perpendicular displacements were fixed in the lateral planes. For the applied external load, only gravitational force was contemplated.
The cases in which the plastic strain contours resulting from the stability analyses did not properly fit the geometry obtained considering a length of 400 m, were repeated considering a length of 800 m. Even though most of the analyses were satisfactorily performed using either 400- or 800-m long cross-sections, a small number of cases needed to be repeated considering a length of 1200 m. Fine meshes made up of quadratic triangular elements were used for each geometry, in order to get well-defined failure mechanisms and precise SFs.
Once all the ADSUs were satisfactorily modeled, final results were derived from the models yielding the lowest safety factors (SFs). In addition to the SFs resulting from such models, landslide sizes were determined for each of the models by computing the surface area enclosed by the displacement contours at failure in each case. Thus, SFs and landslide sizes could be calculated for each of the ADSUs within the optimal set.
4. Results
4.1. Ground Velocity Maps and Validation
LOS ground velocity maps (Figure 3) revealed maximum positive LOS velocities (movement towards the satellite or uplift) of 5.8 and 8.7 cm/year, respectively, in ascending and descending geometry over the area of the southernmost group of inventoried landslides (Figure 1). This area also exhibited the maximum negative LOS velocity (movement away from the satellite or elevation loss) in descending geometry, with a value of −12.9 cm/year. The ascending results revealed, however, a maximum negative LOS velocity of −9.9 cm/year over the area of the south-westernmost cluster of active MPs in Figure 3.
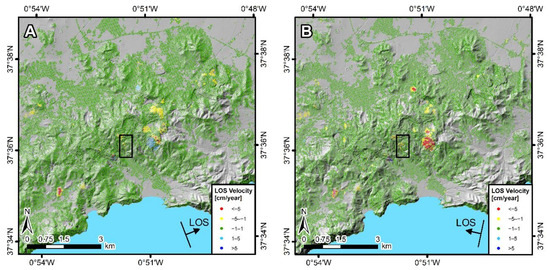
Figure 3.
LOS ground velocity maps for the period from 10 July 2017 to 15 November 2018. (A) Ascending velocities. (B) Descending velocities. The black squares show the location of the slope instability monitored by DGPS and used for the validation analysis.
The results in ascending geometry (Figure 3A) contain 72,610 MPs, with a MPs density of 712 MPs/km2, whereas the map in descending geometry (Figure 3B) contains 66,293 MPs, with a MPs density of 626 MPs/km2. Standard deviations of the LOS velocities of all the MPs from the ascending and descending datasets resulted, respectively, in 0.45 and 0.61 cm/year.
The validation analysis was performed by comparing the InSAR-retrieved LOS velocities with in situ DGPS measurements projected onto the LOS, both in ascending and descending geometry (Figure 4). Root mean square error (RMSE) values resulted in 1.06 cm/year and 2.46 cm/year, respectively, for the ascending and descending results (Figure 4F). The difference between both RMSEs is most likely related to the different levels of noise affecting the InSAR data, which is higher for the descending results, according to their standard deviation.
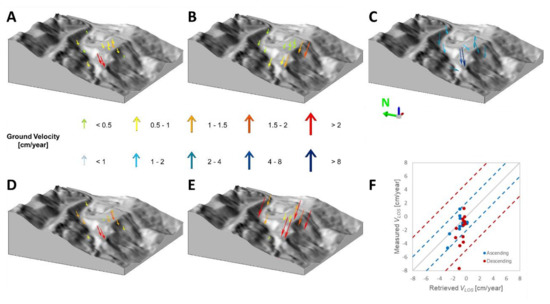
Figure 4.
Results of the validation analysis. A 3D view of the (A) InSAR ascending and (B) descending LOS ground velocities over the points monitored by DGPS, (C) raw DGPS ground velocities for the period from 11 July 2017 to 15 November 2018, and DGPS ground velocities projected onto the (D) ascending and (E) descending LOS. (F) Scatter plot of the LOS ground velocities VLOS measured by DGPS and retrieved by InSAR. The gray solid line indicates the cases where the retrieved and the measured LOS ground velocities VLOS are exactly equal. The blue (red) dashed lines denote the 95% confidence band for the ascending (descending) data (i.e., two times the RMSE).
4.2. Slope Unit Maps and Active Deformation Slope Unit Maps
The SUs and ADSUs obtained over the study area showed a high degree of variability for the different combinations of the software r.slopeunits input parameters a and c. These differences can be observed in detail in Figure 5, for nine of the 56 SU (Figure 5A) and ADSU (Figure 5B) maps obtained over the central part of the study area, and using different (a, c) combinations.
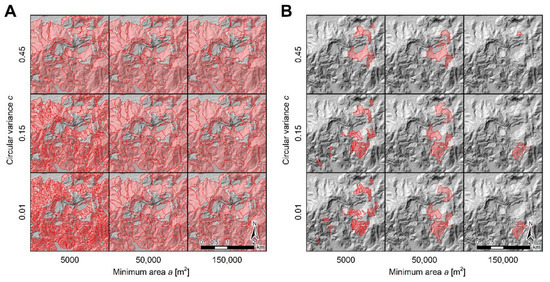
Figure 5.
(A) Detail of the slope unit (SU) maps obtained with the software r.slopeunits [47] for several combinations of the input parameters a and c. (B) Detail of the active deformation slope unit (ADSU) maps obtained from the SU maps, as described in Section 3.3.
The maximum and minimum number of SUs obtained considering the 56 SU sets resulted in 4623 and 116, respectively, for SU maps 1 (lower left corner in Figure 5A) and 56, for which the mean SU area resulted in 10,000 and 370,000 m2, respectively.
The number of ADSUs corresponding to the ADSU sets 1 (lower left corner in Figure 5B) and 56 resulted in 94 and 2, respectively, with a mean ADSU area of 10,000 and 20,000 m2, respectively.
Note that when using the finest SU partition, obtained with the smallest values of a and c, the number of ADSUs more than doubles the number of inventoried landslides. On the other hand, for the coarsest SU partition, a negligible number of ADSUs is obtained. Moreover, in most of the cases where a values greater than 150,000 m2 were used, no ADSUs were obtained due to the MPs density threshold considered (500 MPs/km2).
In the next section we evaluate the different ADSU sets to find the (a, c) combination that provides the ADSU set best matching the landslide inventory, i.e., the optimal ADSU set.
4.3. Optimal Active Deformation Slope Unit Map
The values of the two metrics F(a, c) considered in this work for optimization of the software r.slopeunits input parameters a and c, Equations (5) and (6), are shown in Figure 6. Note that the figure shows the values obtained for the 56 ADSU sets resulting from all the possible (a, c) combinations. In addition, Figure 7 shows the cumulative frequency size distributions used to calculate Equation (6), also for the 56 ADSU sets. For clarity, a few ADSU sets covering the whole range of frequency size distributions are highlighted (Figure 7A). These ADSU sets, denoted by “set 1”, “set 3”, “set 5”, “set 25”, “set 27”, “set 29”, “set 49”, “set 51”, and “set 53”, were obtained with the (a, c) combinations shown in Figure 5 (from the lower left to the upper right corner). Note that the leftmost point of all distributions is normalized to 100% by definition. The distribution of the inventoried landslides is also depicted (Figure 7B).
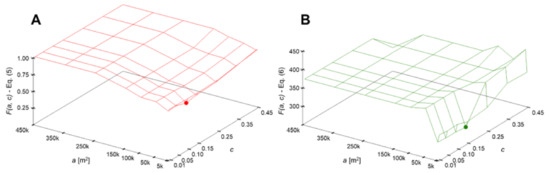
Figure 6.
Active deformation slope units (ADSUs) optimization metrics, calculated as a function of the software r.slopeunits [47] input parameters a and c, for all the possible (a, c) combinations. (A) Values of the metric F(a, c) defined by Equation (5): the optimal values are found in correspondence with the minimum value of Equation (5), indicated with a red dot. (B) Values of the metric F(a, c) defined by Equation (6): the minimum value of Equation (6) is indicated with a green dot.
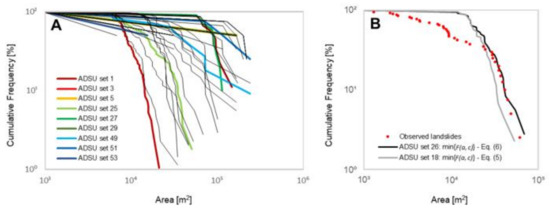
Figure 7.
(A) Cumulative frequency size distributions of the active deformation slope unit (ADSU) maps for all the possible combinations of the software r.slopeunits [47] input parameters a and c. The highlighted results are listed and described in the text. (B) Cumulative frequency size distributions of the inventoried landslides, the ADSU set corresponding to the minimum value of the metric F(a, c) defined by Equation (6) (ADSU set 26), and the optimal ADSU set (ADSU set 18), corresponding to the minimum value of the metric F(a, c) defined by Equation (5).
The results reveal that the higher the value of a, the higher the difference between the inventoried landslides and the mapped ADSUs (Figure 6). However, it can be noted that Equation (5) (Figure 6A) captures a greater variety of results than Equation (6) (Figure 6B), and increases gradually with increasing values of a, until reaching a = 250,000 m2. Starting from that value, the overlap between the mapped ADSUs and the landslide inventory becomes zero, and the error results in 100%. The set of ADSUs corresponding to the minimum of Equation (5) (ADSU set 18), shown with a red dot in Figure 6A, was derived from the SU map obtained by (a, c) = (10,000 m2, 0.10). The distribution corresponding to the ADSU set 18 is shown with a gray solid curve in Figure 7B.
On the other hand, if we analyze the results of Equation (6), we can observe that the values of this metric vary strongly until reaching a = 150,000 m2. For values above that threshold, the results become constant. The reason for this is that several ADSU maps are not comparable with our landslide inventory using cumulative frequency size distribution plots (Figure 7). These ADSU maps include a few very large ADSUs that do not match the inventoried landslides (e.g., ADSU sets 3, 5, 27, 29, 51 and 53 in Figure 7A). The set of ADSUs corresponding to the minimum of Equation (6) (ADSU set 26), shown with a green dot in Figure 6B, was derived from the SU map obtained by (a, c) = (10,000 m2, 0.10). The distribution corresponding to the ADSU set 26 is shown with a black solid curve in Figure 7B.
This means that the metric in Equation (5) allows a more accurate comparison between the inventory and the ADSU maps, even for maps containing a limited number of ADSUs. For this reason, the optimal ADSU set (ADSU set 18) was selected on the basis of the results obtained from Equation (5). Note that the (a, c) combination corresponding to the optimal set of ADSUs according to the metric of Equation (6) (ADSU set 26) is fairly similar to that of the selected optimal ADSU set (ADSU set 18). In fact, the ADSU set 18 corresponds to the second-best result obtained from Equation (6) (Figure 7B).
However, the accuracy, defined as the sum of true positives (TP) and true negatives (TN), is slightly higher for set 18 than for set 26 (99.39% compared to 99.37%) (Table 2). The total false statements are also lower for set 18 (0.62% compared to 0.63%).

Table 2.
Confusion matrices and values of the metrics defined by Equations (5) and (6) for three different outputs: the active deformation areas (ADAs) mapped by means of the so-called ADAFinder software package [29], the active deformation slope unit (ADSU) set 26, corresponding to the minimum value of the metric F(a, c) defined by Equation (5), and the ADSU set 18 (optimal ADSU set), corresponding to the minimum value of the metric F(a, c) defined by Equation (5). TN: true negatives. FN: false negatives. FP: false positives. TP: true positives.
These results suggest that the metric of Equation (5) is more appropriate than that of Equation (6) for the optimization procedure devised in this work. The ADSU maps obtained with both metrics increased by 0.5% the accuracy of the ADAs mapped by ADAFinder (Table 2), which is unable of distinguishing slope instabilities from vertical ground movements. This improvement is also reflected in the values obtained from Equations (5) and (6) for the ADSU maps 18 and 26, as well as for the ADA set (Table 2).
The total number of ADSUs that conformed to the optimal set (ADSU set 18), resulted as 43 (opaque or non-transparent polygons in Figure 8). In turn, the set of SUs obtained by (a, c) = (10,000 m2, 0.10), used to derive the optimal ADSU set, was formed by a total of 1959 SUs. From these 1959 SUs, 151 were characterized as unknown SUs. This was determined by intersecting the non-active deformation SUs with the two InSAR datasets separately. Those SUs containing less than five MPs both from the ascending and descending datasets, and yielding a density of active MPs (also from the ascending and descending datasets) lower than 500 MPs/km2, were characterized as unknown SUs (transparent pink polygons in Figure 8). These SUs were mainly located over densely vegetated hill slopes, where only few MPs were obtained (SE quadrants in Figure 3A,B). No landslides were, however, inventoried over those areas. The remaining 1756 SUs were characterized as stable SUs (transparent green polygons in Figure 8).
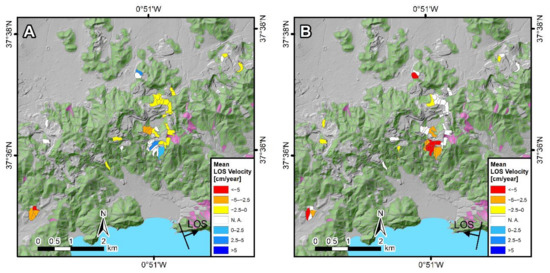
Figure 8.
Mean LOS ground velocities obtained for the 43 active deformation slope units (ADSUs) from the optimal set (ADSU set 18). All ADSUs are represented in opaque (i.e., non-transparent) colors. (A) Ascending velocities. (B) Descending velocities. ADSUs not detected in each geometry are represented in opaque white. Unknown and stable SUs are also depicted in transparent pink and transparent green, respectively.
Mean LOS velocities for the 43 ADSUs from the optimal set, both in ascending and descending geometry, are presented in Figure 8A,B, respectively. Note that the 43 ADSUs that conform to the optimal set were obtained through the combination of the ascending and descending results. Positive mean LOS velocities in Figure 8 correspond to movement towards the satellite, whereas negative values represent movement away from the satellite. ADSUs not detected in ascending, but in descending, are represented in opaque white in Figure 8A (and vice versa in Figure 8B).
The number of ADSUs derived using ascending and descending data was 31 and 20, respectively. From among these ADSUs, 10 and 15 presented absolute mean LOS velocities greater than 2.5 cm/year respectively in ascending and descending geometries. These ADSUs can be interpreted as representing slope instabilities with the highest degree of confidence, since the maximum RMSE obtained through the validation analysis resulted in 2.46 cm/year.
Positive mean LOS velocities were only obtained in ascending geometry (Figure 8A), for a total of four ADSUs. A total of eight ADSUs were detected in both geometries (ascending and descending). From among these, three ADSUs showed an opposite direction of movement in ascending and descending, a behavior typically attributed to slope movements having a strong horizontal component. Considering the 43 ADSUs conforming the optimal set, taking maximum absolute values in those ADSUs detected in both geometries, a total of 21 ADSUs presented absolute mean LOS velocities greater than 2.5 cm/year. Hence, these 21 ADSUs can most certainly be associated with slope instabilities.
4.4. 2D Stability Analyses
Out of the 43 ADSUs in the optimal set (ADSU set 18), 14 revealed 2D safety factors SFs lower than 1.2, 13 SFs between 1.2 and 1.5, and 16 SFs greater than 1.5. Only three and five ADSUs revealed SFs lower than 1 and greater than 2, respectively. Most of the ADSUs with SFs greater than 2, characterized by very low slope gradients, coincide with the south-westernmost cluster of active MPs in Figure 3. The 2D landslide sizes for the 43 ADSUs ranged from 1900 to 27,000 m2.
The median of the aspect was found to offer the best performance for the purpose of obtaining cross-sections. In many cases, however, the differences were not significant, similar results were obtained using the three different aspect values considered (mean, median, and mode), indicating a proper delineation result in terms of aspect homogeneity.
Thus, 32.56%, 53.49%, and 34.88% of the ADSUs were satisfactorily modeled using the mean, the median, and the mode of the aspect, respectively. Concerning the length of the cross-sections, 44.19%, 46.51%, and 9.30% of the ADSUs were modeled using 400-, 800-, and 1200-m long cross-sections, respectively.
Figure 9 shows detailed results of the 2D stability analyses corresponding to three cross-sections obtained for three particular ADSUs. The cross-sections corresponding to Figure 9A,B were obtained using mean aspect values, whereas the cross-section corresponding to Figure 9C was obtained using the median. For convenience, the examples integrate 2D stability analyses performed using 400-, 800-, and 1200-m long cross-sections. Note that the slope in Figure 9B corresponds to the slope instability monitored by DGPS (Figure 4).
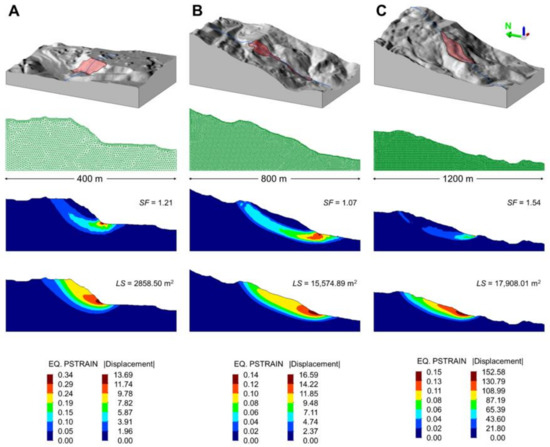
Figure 9.
Results of three 2D stability analyses performed using (A) 400-, (B) 800-, and (C) 1200-m long cross-sections derived from three particular active deformation slope units (ADSUs) from the optimal set (ADSU set 18). First row: 3D view of the three ADSUs. The blue solid lines represent each profile trace, the 1200-m long profile trace clipped to the hillshade extent. Second row: finite element meshes corresponding to each profile trace. Third row: equivalent plastic strain contours at failure corresponding to each profile trace. Fourth row: displacement contours (in m) corresponding to each profile trace. The resulting 2D safety factors SFs and 2D landslide sizes LSs are also presented. The legends for the third and fourth rows are shown at the bottom of the figure.
Finally, we elaborated two ADSU maps summarizing the results of the 2D stability analyses for the 43 ADSUs from the optimal set (ADSU set 18) (Figure 10). The map in Figure 10A shows the resulting safety factors SFs, whereas the map in Figure 10B shows the resulting landslide sizes.
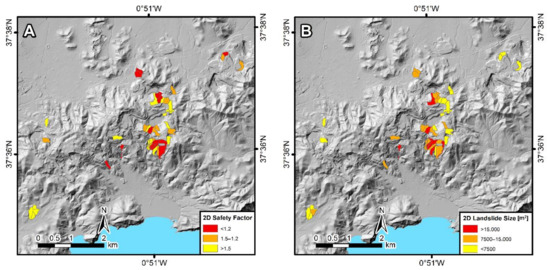
Figure 10.
Results of the 2D stability analyses for the 43 active deformation slope units (ADSUs) from the optimal set (ADSU set 18). (A) 2D safety factors, and (B) 2D landslide sizes.
5. Discussion
This work proposes a new approach for detecting and characterizing slope instabilities at a regional scale, and aimed at providing non-expert final users, such as Civil Protection authorities or risk management decision-makers, with easily intelligible products that can thus be exploited for geohazard management purposes. Although the proposed methodology has been applied here to analyze mining-induced slope instabilities, it can likewise be applied to analyze all types of slope instabilities.
Existing approaches for detecting ADAs from InSAR data [29,30,31,32] focus on the delineation of the more reliable deforming areas through the aggregation of subsets of points obtained by filtering the raw LOS ground velocity map. First, in order to filter the LOS ground velocity map, these approaches usually select the moving points using an absolute velocity threshold equal to 2σ (two times the standard deviation of the raw LOS ground velocity map). Then, groups of moving points sharing their influence area are aggregated into polygons representing the ADAs.
Given the inability of these approaches to discern between different types of ground movement, sometimes overlapping within a single ADA, it is desirable to develop new approaches that provide further partitioning of the active areas to better analyze ground movements in complex areas with large deformation footprints. In that sense, the ADSU map represents an interesting product that allows a comprehensive analysis of ground movements; in particular, of slope instabilities. Through the aggregation of the moving points within the boundaries of slopes defined by polygons with similar slope-facing direction (aspect), different mean LOS ground velocities can be determined for adjacent partitions. Using the traditional active deformation mapping approaches, such partitions would be integrated into a single polygon, with a consequent loss of information.
Furthermore, in addition to helping determine the mean LOS ground velocity of each polygon, SUs can be used to derive numerical modeling geometries, given their high aspect homogeneity. In this work, an automated procedure to obtain 2D cross-sections for each ADSU has been devised, followed by simplified stability analyses aimed at determining their SFs and landslide sizes.
The comparison between the computed SFs and the maximum absolute mean LOS velocities resulting from the InSAR data (Figure 11) provided interesting results. In principle, these two variables should be correlated, assuming that the most unstable slopes should also be the ones showing the highest slope movement rates.
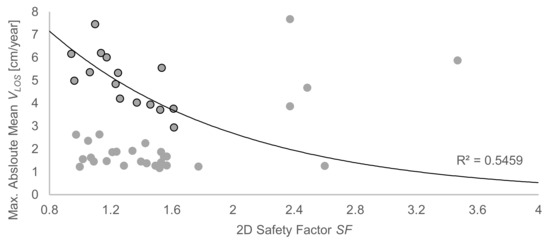
Figure 11.
Scatter plot of the maximum absolute mean LOS ground velocities VLOS and the 2D safety factors SFs for 15 active deformation slope units (ADSUs) from the optimal set (ADSU set 18). The black curve is a fit of the subset of points outlined in black.
At first glance, if we analyze the scatter plot in Figure 11, we can observe that there is no relationship between the two variables in general terms. However, the points are not randomly distributed either. In fact, if we analyze the points exhibiting SFs lower than 2, two distinct clusters are found. One is the group of 21 points with mean LOS velocities of up to 2.5 cm/year, for which there is no relationship between SF and mean LOS velocity. The other is the group of 17 points with mean LOS velocities greater than 2.5 cm/year, for which a potential relationship between the two variables is observed when excluding the two ADSUs with mean LOS velocities of 2.63 cm/year. Note that the best-fit exponential curve corresponding to the 15 points remaining, after excluding the two ADSUs with mean LOS velocities of 2.63 cm/year (black curve in Figure 11), yields a reasonably fair coefficient of determination (R2 = 0.55). Points exhibiting SFs greater than 2, which correspond to ADSUs characterized by very low slope gradients, are interpreted as outliers.
This finding is in line with the fact that the maximum RMSE obtained through the validation analysis resulted in 2.46 cm/year. For this reason, the relationship between SF and mean LOS velocity is only observed for the ADSUs exhibiting mean LOS velocities greater than 2.5 cm/year; as long as the two ADSUs with mean LOS velocities of 2.63 cm/year, close to 2.5 cm/year, are excluded. ADSUs exhibiting lower velocities cannot be interpreted as slope instabilities with absolute certainty, since they are most likely the subject of errors associated to noisy InSAR data.
These results indicate that significant further efforts are needed in order to improve the relationship between SF and mean LOS velocity. Possible solutions for this purpose could include the use of more sophisticated InSAR processing chains, providing higher resolution and time series of movement. In the case of the slope stability assessment step, the adoption of accurate lithostratigraphic geometry descriptions (considering different materials instead of a single material) and hydrogeological data (instead of assuming fully saturated conditions) and, possibly, the use of 3D FE modeling could provide an improvement.
Although the proposed methodology could be improved by modifying these aspects, it is still useful for generating easy-to-interpret products that can be integrated into the geohazard management chain. In contrast to pixel-based approaches, our methodology provides discrete, easily intelligible results, by relying on the assumption that failures cannot be bigger than the physical boundaries of the slopes. By defining the physical boundaries of the slope where the potential failure can occur, the main restriction of pixel-based approaches, related to the lack of correspondence between the landslide size and the pixel size, is overcome.
A further step towards an integrated analysis of slope stability based on these products could be the combination of mean LOS velocities, SFs, and landslide sizes into a hazard proxy. According to probabilistic models for landslide hazard assessment, landslide hazard is the probability of occurrence within a specified period and within a given area of a landslide of a given magnitude [61]. Assuming independence among the three probabilities, the landslide hazard can be defined as follows [62]:
where P(AL), P(NL), and S are respectively the probability of landslide size (magnitude), of landslide occurrence in an established period (frequency), and of landslide spatial occurrence (susceptibility), given the local environmental setting.
Here, rather than opting for a quantitative probabilistic analysis of the landslide hazard, we adopted a qualitative approach to derive a hazard proxy taking into account the results of the methodology (i.e., mean LOS velocities, SFs, and landslide sizes), which were nevertheless obtained on a deterministic basis. The slope instability hazard proxy was evaluated by combining the landslide sizes as a proxy for magnitude, the mean LOS velocity as a proxy for frequency, and the SF as a proxy for susceptibility (Figure 12). For each combination, the degree of hazard was established and expressed in qualitative terms. Figure 12A shows the maximum absolute mean LOS velocities resulting from the InSAR data. The measurement direction, indicating whether the values correspond to ascending or descending data, is also shown. The matrix defined to evaluate the slope instability hazard proxy is shown in Figure 12C.
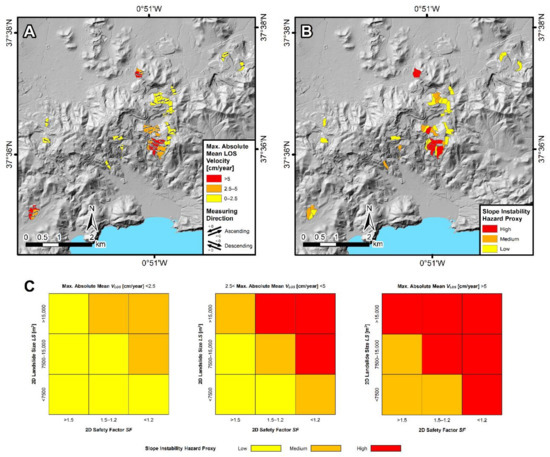
Figure 12.
(A) Maximum absolute mean LOS ground velocities for the 43 active deformation slope units (ADSUs) from the optimal set (ADSU set 18). Directions of movement are also indicated. (B) Slope instability hazard proxy obtained through the combination of the 2D landslide size LS (as a proxy for magnitude of failure), the LOS ground velocity VLOS (as a proxy for frequency of failure), and the 2D safety factor SF (as a proxy for susceptibility of failure) for each ADSU. (C) Matrix defined to evaluate the slope instability hazard proxy.
The main drawback of this analysis is the oversimplification of both the geotechnical setting and the groundwater pore-water pressure distribution, as well as the introduction of a time frame based on the mean LOS velocity. The resulting hazard proxy should therefore only be used to act as a trigger for more detailed geotechnical assessment of the identified priority areas. In contrast, this simplicity allows the approach to be fully scalable.
This last point is particularly interesting when considering that massive InSAR data will shortly be available thanks to upcoming projects, such as the Copernicus European Ground Motion Service. Once the open-access InSAR data that are to be provided by this project are available all over Europe, it will be possible to perform slope stability analysis over all mining waste disposal areas at a European scale using the proposed methodology.
To illustrate this point, we elaborated an SU map over the Region of Murcia, and focusing exclusively on mining and waste disposal areas (Figure 13). For this purpose, we extracted the mineral extraction areas and dump sites from the Corine Land Cover 2018 [63]. Note that the map only contains SUs that overlap these two land cover classes (Figure 13B). The SUs were delineated with the software r.slopeunits [47] excluding all areas with slope gradient lower than 5⁰, and using the optimal values of the input parameters a and c that we obtained for Sierra Minera, i.e., (a, c) = (10,000 m2, 0.10).
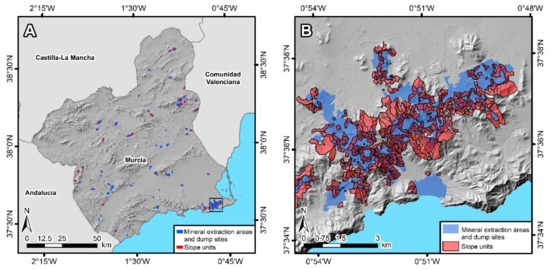
Figure 13.
(A) Mineral extraction areas and dump sites extracted from the Corine Land Cover 2018 [63] over the region of Murcia, and slope units (SUs) overlapping both classes, obtained with the software r.slopeunits [47], using the optimal values of the input parameters a and c, i.e., (a, c) = (10,000 m2, 0.10). The black square shows the location of the study area. (B) Detail of the mineral extraction areas and dump sites over the study area, and slope units (SUs) intersecting both classes.
6. Conclusions
This paper introduces a novel methodology for regional slope stability analysis in mining waste disposal areas. The methodology combines satellite InSAR, SUs, and 2D FE modeling to quantify mean LOS velocities, SFs, and landslide sizes for a set of slope instabilities derived following a semi-automated procedure.
The first step of the methodology is to generate LOS ground velocity maps through InSAR processing, which must be properly validated. The second step consists in the aggregation of the moving points within the boundaries of morphological SUs, which allows obtaining an ADSU map optimized with respect to the landslide inventory. The last step is to perform stability analyses on each of the ADSUs within the optimal map.
In this work, InSAR processing was carried out by using the unsupervised FASTVEL processing chain [12,40], and the results were validated using in situ DGPS data. The software r.slopeunits [47] and the GeHoMadrid code [59,60] were used for SU delineation and 2D FE modeling, respectively.
The methodology, was set up for Sierra Minera (Murcia), a former mining area in southeast Spain, where it has proven effective for detecting and characterizing a considerable number of slope instabilities. Out of the 1959 SUs used to derive the optimal ADSU set, a total of 43 were found to be active according to the InSAR data, whereas 1756 were found to be stable. Only 151 SUs, located in areas poorly covered by the InSAR data, were characterized as unknown. A total of 21 out of the 43 ADSUs that conform to the optimal ADSU set presented absolute mean LOS velocities greater than 2.5 cm/year. These 21 ADSUs can be interpreted as slope instabilities with absolute certainty, considering that the maximum RMSE obtained through the validation analysis resulted in 2.46 cm/year. The set of SUs used to derive the optimal ADSU set was obtained by (a, c) = (10,000 m2, 0.10).
From among the 43 ADSUs that conform to the optimal ADSU set, 14 revealed SFs lower than 1.2, 13 showed SFs between 1.2 and 1.5, and 16 showed SFs greater than 1.5. Only five ADSUs characterized by very low slope gradients revealed SFs greater than 2. Landslide sizes for the 43 ADSUs ranged from 1900 to 27,000 m2.
The comparison of the computed SFs with the maximum absolute mean LOS velocities resulting from the InSAR data led to noteworthy observations. The best-fit exponential curve obtained for the 15 ADSUs presenting SFs lower than 2 and mean LOS velocities greater than 2.5 cm/year yielded a reasonably good coefficient of determination (R2 = 0.55), indicating a potential relationship between SF and mean LOS velocity. These findings are consistent with the maximum RMSE obtained through the validation analysis (2.46 cm/year). However, the relationship between SF and mean LOS velocity was not observed for two ADSUs with mean LOS velocities of 2.63 cm/year; which is still close to 2.46 cm/year.
Possible improvements to further refine these results could include the use of more sophisticated InSAR processing chains providing LOS ground velocity maps at full resolution and time series of movement, the adoption of precise lithostratigraphic and hydrogeological data in the stability analyses, and the application of 3D FE modeling.
This paper presents the first study using FASTVEL for slope stability mapping, and providing validation results for FASTVEL. It also provides a new systematic, automated procedure based on SU delineation to aggregate InSAR data, and demonstrates the use of SUs to automatically derive 2D FE modeling geometries for the first time. Furthermore, this work discusses the possibility of evaluating the slope instability hazard through a qualitative approach combining the results of the methodology (i.e., mean LOS velocities, SFs, and landslide sizes) to derive a hazard proxy.
It should be noted that the results of the proposed methodology can be periodically updated, for continuous evaluation, by performing the analyses on a regular basis. The application of the methodology allows generating products that provide non-expert end users with intelligible, clear, and easily comparable information, which can then be integrated in the geohazard management chain. These products can thus be used by Civil Protection or risk management authorities for geohazard management purposes. Moreover, since the methodology is fully scalable, its application for slope stability analysis in all European mining waste disposal areas will soon be possible, once the upcoming massive InSAR data from ongoing projects such as the Copernicus European Ground Motion Service is made available. Even though the methodology presented here was used to analyze mining-related slope instabilities, the same can likewise be used to analyze slope instabilities affecting natural and man-made slopes in general.
Author Contributions
Conceptualization, J.L.-V., J.A.F.-M. and G.H.; methodology, J.L.-V., J.A.F.-M. and G.H.; software, J.L.-V., J.A.F.-M., A.B. and M.A.; validation, J.L.-V. and J.C.G.-D.; formal analysis, P.E. and A.B.; investigation, J.C.G.-D. and R.S.; resources, P.E. and A.B.; data curation, C.R.-C., J.A.N. and V.K.; funding acquisition, R.S. and G.H.; project administration, G.H.; supervision, J.A.F.-M. and M.A.; visualization, J.L.-V. and P.E.; writing—original draft preparation, J.L.-V., J.A.F.-M. and G.H.; writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work has received funding from the Regional Administration of Madrid (Comunidad de Madrid) in the framework of the Industrial PhD Project GEODRON (IND2017/AMB-7789).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available at IGME on request from the corresponding author.
Acknowledgments
First author shows gratitude for the working contract arranged with HEMAV SL for the development of the Industrial PhD Project GEODRON. Copernicus Sentinel-1 IW SAR data were provided via and processed in ESA’s Geohazards Exploitation Platform (GEP), in the framework of the GEP Early Adopters Programme 2015–2020 and the Geohazards Lab initiative, the latter developed under the CEOS Working Group on Disasters. Data processing was carried out with the FASTVEL service developed and integrated by TRE ALTAMIRA in the GEP. The authors thank the whole GEP Team for providing technical support and assistance to use the platform, and TRE ALTAMIRA for making the FASTVEL chain available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brown, E.T. Underground Excavations in Rock; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar] [CrossRef]
- Botin, J.A. Sustainable Management of Mining Operations. Available online: https://books.google.es/books?hl=es&lr=&id=EOq691P4oq8C&oi=fnd&pg=PR7&ots=L6cA7tNaUU&sig=2u7VTlY9KDtvhYN0c3LpQWfqdhI&redir_esc=y#v=onepage&q&f=false (accessed on 23 April 2020).
- Bell, F.G.; Stacey, T.R.; Genske, D.D. Mining subsidence and its effect in the environment: Some differing examples. Environ. Geol. 2000, 40, 135–152. [Google Scholar] [CrossRef]
- Osasan, K.S.; Afeni, T.B. Review of surface mine slope monitoring techniques. J. Min. Sci. 2010, 46, 177–186. [Google Scholar] [CrossRef]
- O’Connor, K.M.; Murphy, E.W. TDR monitoring as a component of subsidence risk assessment. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1997, 34, 619. [Google Scholar] [CrossRef]
- Zhou, D.; Wu, K.; Chen, R.; Li, L. GPS/terrestrial 3D laser scanner combined monitoring technology for coal mining subsidence: A case study of a coal mining area in Hebei, China. Nat. Hazards 2014, 70, 1197–1208. [Google Scholar] [CrossRef]
- Carlà, T.; Farina, P.; Intrieri, E.; Ketizmen, H.; Casagli, N. Integration of ground-based radar and satellite InSAR data for the analysis of an unexpected slope failure in an open-pit mine. Eng. Geol. 2018, 235, 39–52. [Google Scholar] [CrossRef]
- Dick, G.J.; Eberhardt, E.; Cabrejo-Liévano, A.G.; Stead, D.; Rose, N.D. Development of an early-warning time-of-failure analysis methodology for open-pit mine slopes utilizing ground-based slope stability radar monitoring data. Can. Geotech. J. 2015, 52, 515–529. [Google Scholar] [CrossRef]
- Osasan, K.S.; Stacey, T.R. Automatic prediction of time to failure of open pit mine slopes based on radar monitoring and inverse velocity method. Int. J. Min. Sci. Technol. 2014, 24, 275–280. [Google Scholar] [CrossRef]
- Francioni, M.; Salvini, R.; Stead, D.; Giovannini, R.; Riccucci, S.; Vanneschi, C.; Gullì, D. An integrated remote sensing-GIS approach for the analysis of an open pit in the Carrara marble district, Italy: Slope stability assessment through kinematic and numerical methods. Comput. Geotech. 2015, 67, 46–63. [Google Scholar] [CrossRef]
- Tong, X.; Liu, X.; Chen, P.; Liu, S.; Luan, K.; Li, L.; Liu, S.; Liu, X.; Xie, H.; Jin, Y.; et al. Integration of UAV-based photogrammetry and terrestrial laser scanning for the three-dimensional mapping and monitoring of open-pit mine areas. Remote. Sens. 2015, 7, 6635–6662. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote. Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ng, A.H.M.; Ge, L.; Yan, Y.; Li, X.; Chang, H.C.; Zhang, K.; Rizos, C. Mapping accumulated mine subsidence using small stack of SAR differential interferograms in the Southern coalfield of New South Wales, Australia. Eng. Geol. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Styles, T.D.; Stead, D.; Eberhardt, E.; Rabus, B.; Gaida, M.; Bloom, J. Integrated Numerical Modelling and Insar Monitoring of a Slow Moving Slope Instability at Bingham Canyon Mine. In Proceedings of the Slope Stability 2011: International Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering, Vancouver, CO, Canada, 18–21 September 2011. [Google Scholar]
- Woo, K.S.; Eberhardt, E.; Rabus, B.; Stead, D.; Vyazmensky, A. Integration of field characterisation, mine production and InSAR monitoring data to constrain and calibrate 3-D numerical modelling of block caving-induced subsidence. Int. J. Rock Mech. Min. Sci. 2012, 53, 166–178. [Google Scholar] [CrossRef]
- Alex, H.M.N.G.; Linlin, G.E.; Zhang, K.; Chang, H.C.; Li, X.; Rizos, C.; Omura, M. Deformation mapping in three dimensions for underground mining using InSAR—Southern highland coalfield in New South Wales, Australia. Int. J. Remote. Sens. 2011, 32, 7227–7256. [Google Scholar] [CrossRef]
- Samsonov, S.; D’Oreye, N.; Smets, B. Ground deformation associated with post-mining activity at the French-German border revealed by novel InSAR time series method. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 142–154. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, Z.; Zhang, Q. Time-series deformation monitoring over mining regions with SAR intensity-based offset measurements. Remote. Sens. Lett. 2013, 4, 436–445. [Google Scholar] [CrossRef]
- Carlà, T.; Intrieri, E.; Raspini, F.; Bardi, F.; Farina, P.; Ferretti, A.; Colombo, D.; Novali, F.; Casagli, N. Perspectives on the prediction of catastrophic slope failures from satellite InSAR. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Thomas, A.; Edwards, S.; Engels, J.; Mccormack, H.; Hopkins, V.; Holley, R. Earth Observation Data and Satellite InSAR for the Remote Monitoring of Tailings Storage Facilities: A Case Study of Cadia Mine, Australia. In Proceedings of the 22nd International Conference on Paste, Thickened and Filtered Tailings, Perth, Australia, 8–10 May 2019; pp. 183–195. [Google Scholar] [CrossRef]
- Paradella, W.R.; Ferretti, A.; Mura, J.C.; Colombo, D.; Gama, F.F.; Tamburini, A.; Santos, A.R.; Novali, F.; Galo, M.; Camargo, P.O.; et al. Mapping surface deformation in open pit iron mines of Carajás Province (Amazon Region) using an integrated SAR analysis. Eng. Geol. 2015, 193, 61–78. [Google Scholar] [CrossRef]
- Holden, D.; Donegan, S.; Pon, A. Brumadinho Dam InSAR study: Analysis of TerraSAR-X, COSMO-SkyMed and Sentinel-1 Images Preceding the Collapse. In Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Perth, Australia, 12–14 May 2020; pp. 293–306. [Google Scholar] [CrossRef]
- Herrera, G.; Tomás, R.; Vicente, F.; Lopez-Sanchez, J.M.; Mallorquí, J.J.; Mulas, J. Mapping ground movements in open pit mining areas using differential SAR interferometry. Int. J. Rock Mech. Min. Sci. 2010, 47, 1114–1125. [Google Scholar] [CrossRef]
- López-Vinielles, J.; Ezquerro, P.; Fernández-Merodo, J.A.; Béjar-Pizarro, M.; Monserrat, O.; Barra, A.; Blanco, P.; García-Robles, J.; Filatov, A.; García-Davalillo, J.C.; et al. Remote analysis of an open-pit slope failure: Las Cruces case study, Spain. Landslides 2020, 1–16. [Google Scholar] [CrossRef]
- Williams, C.; Ross, B.; Zebker, M.; Gaida, M.; Morkeh, J.; Robotham, M.E. Assessment of Historic InSAR Monitoring Data Prior to the Manefay Slide at the Bingham Canyon Mine Using the Latest Analytical Techniques. In Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019. [Google Scholar]
- Herrera, G.; Tomás, R.; Lopez-Sanchez, J.M.; Delgado, J.; Mallorqui, J.J.; Duque, S.; Mulas, J. Advanced DInSAR analysis on mining areas: La Union case study (Murcia, SE Spain). Eng. Geol. 2007, 90, 148–159. [Google Scholar] [CrossRef]
- Herrera, G.; Álvarez Fernández, M.I.; Tomás, R.; González-Nicieza, C.; López-Sánchez, J.M.; Álvarez Vigil, A.E. Forensic analysis of buildings affected by mining subsidence based on differential interferometry (Part III). Eng. Fail. Anal. 2012, 24, 67–76. [Google Scholar] [CrossRef]
- Instituto Geológico y Minero de España. Estudio Geotécnico para el Depósito de Residuos de la Bahía de Portman en Corta Minera, Madrid; Instituto Geológico y Minero de España: Madrid, Spain, Unpublished report; 1996.
- Barra, A.; Solari, L.; Béjar-Pizarro, M.; Monserrat, O.; Bianchini, S.; Herrera, G.; Crosetto, M.; Sarro, R.; González-Alonso, E.; Mateos, R.M.; et al. A methodology to detect and update active deformation areas based on Sentinel-1 SAR images. Remote. Sens. 2017, 9, 1002. [Google Scholar] [CrossRef]
- Tomás, R.; Pagán, J.I.; Navarro, J.A.; Cano, M.; Luis Pastor, J.; Riquelme, A.; Cuevas-González, M.; Crosetto, M.; Barra, A.; Monserrat, O.; et al. Semi-automatic identification and pre-screening of geological-geotechnical deformational processes using persistent scatterer interferometry datasets. Remote. Sens. 2019, 11, 1675. [Google Scholar] [CrossRef]
- Navarro, J.A.; Cuevas, M.; Tomás, R.; Barra, A.; Crosetto, M. A Toolset to Detect and Classify Active Deformation Areas Using Interferometric SAR Data. In Proceedings of the GISTAM, Heraklion, Greece, 3–5 May 2019; pp. 167–174. [Google Scholar] [CrossRef]
- Navarro, J.A.; Tomás, R.; Barra, A.; Pagán, J.I.; Reyes-Carmona, C.; Solari, L.; Vinielles, J.L.; Falco, S.; Crosetto, M. ADAtools: Automatic detection and classification of active deformation areas from PSI displacement maps. ISPRS Int. J. Geo Inf. 2020, 9, 584. [Google Scholar] [CrossRef]
- Manteca, J.; Ovejero, G. Los yacimientos Zn, Pb, Ag-Fe del distrito minero de la La Unión-Cartagena, Bética Oriental; CSIC: Madrid, Spain, 1992.
- Conesa, H.M.; Schulin, R.; Nowack, B. Mining landscape: A cultural tourist opportunity or an environmental problem? The study case of the Cartagena-La Unión Mining District (SE Spain). Ecol. Econ. 2008, 64, 690–700. [Google Scholar] [CrossRef]
- Sanz De Galdeano, C.; Vera, J.A. Stratigraphic record and palaeogeographical context of the Neogene basins in the Betic Cordillera, Spain. Basin Res. 1992, 4, 21–36. [Google Scholar] [CrossRef]
- Robles-Arenas, V.M.; Rodríguez, R.; García, C.; Manteca, J.I.; Candela, L. Sulphide-mining impacts in the physical environment: Sierra de Cartagena-La Unión (SE Spain) case study. Environ. Geol. 2006, 51, 47–64. [Google Scholar] [CrossRef]
- Gomez-Ros, J.M.; Garcia, G.; Peñas, J.M. Assessment of restoration success of former metal mining areas after 30 years in a highly polluted Mediterranean mining area: Cartagena-La Unión. Ecol. Eng. 2013, 57, 393–402. [Google Scholar] [CrossRef]
- Cruden, D.; Varnes, D. Landslides: Investigation and mitigation. Chapter 3—Landslide types and processes. Transp. Res. Board Spec. Rep. 1996, 247, 36–75. Available online: https://www.academia.edu/download/51081833/150TEXT_1993.pdf (accessed on 16 April 2020).
- Instituto Geográfico Nacional Centro de Descargas del CNIG. 2019. Available online: http://centrodedescargas.cnig.es/CentroDescargas/index.jsp (accessed on 10 February 2020).
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote. Sens. 2002. [Google Scholar] [CrossRef]
- Iglesias, R.; Blanco, P.; Ordoqui, P.; Lopez, A.; Balague, X.; Gili, A.; Bianchi, M.; Monells, D. Fastvel: A PSI GEP Service for Terrain Motion Velocity Map Generation. In Proceedings of the APA Fringe 2017 Workshop, Helsinki, Finland, 5–9 June 2017; p. 109. [Google Scholar]
- Galve, J.P.; Pérez-Peña, J.V.; Azañón, J.M.; Closson, D.; Caló, F.; Reyes-Carmona, C.; Jabaloy, A.; Ruano, P.; Mateos, R.M.; Notti, D.; et al. Evaluation of the SBAS InSAR service of the European space agency’s geohazard exploitation platform (GEP). Remote. Sens. 2017, 9, 1291. [Google Scholar] [CrossRef]
- Foumelis, M.; Papadopoulou, T.; Bally, P.; Pacini, F.; Provost, F.; Patruno, J. Monitoring geohazards using on-demand and systematic services on esa’s geohazards exploitation platform. Int. Geosci. Remote Sens. Symp. 2019, 5457–5460. [Google Scholar] [CrossRef]
- Terradue FASTVEL for Displacement Velocity Map Generation. Available online: https://docs.terradue.com/geohazards-tep/tutorials/fastvel.html (accessed on 1 December 2020).
- Carrara, A.; Cardinali, M.; Guzzetti, F. Uncertainty in assessing landslide hazard and risk. ITC J. 1992, 1992, 172–183. [Google Scholar]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Alvioli, M.; Marchesini, I.; Reichenbach, P.; Rossi, M.; Ardizzone, F.; Fiorucci, F.; Guzzetti, F. Automatic delineation of geomorphological slope units with r.slopeunits v1.0 and their optimization for landslide susceptibility modeling. Geosci. Model. Dev. 2016, 9, 3975–3991. [Google Scholar] [CrossRef]
- Alvioli, M.; Guzzetti, F.; Marchesini, I. Parameter-free delineation of slope units and terrain subdivision of Italy. Geomorphology 2020, 358. [Google Scholar] [CrossRef]
- Hansen, A. Landslide hazard analysis. Slope Instab. 1984, 523–602. Available online: https://ci.nii.ac.jp/naid/10024222961/ (accessed on 13 May 2020).
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS techniques and statistical models in evaluating landslide hazard. Earth Surf. Process. Landf. 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Carrara, A.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Gis Technology in Mapping Landslide Hazard; Springer: Dordrecht, The Netherlands, 1995; pp. 135–175. [Google Scholar]
- Guzzetti, F.; Galli, M.; Reichenbach, P.; Ardizzone, F.; Cardinali, M. Landslide hazard assessment in the Collazzone area, Umbria, Central Italy. Nat. Hazards Earth Syst. Sci. 2006, 6, 115–131. [Google Scholar] [CrossRef]
- Guzzetti, F.; Cardinali, M.; Reichenbach, P. Comparing landslide maps: A case study in the upper Tiber river basin, central Italy. Environ. Manag. 2000, 25, 247–263. [Google Scholar] [CrossRef]
- Alvioli, M.; Mondini, A.C.; Fiorucci, F.; Cardinali, M.; Marchesini, I. Topography-driven satellite imagery analysis for landslide mapping. Geomat. Nat. Hazards Risk 2018, 9, 544–567. [Google Scholar] [CrossRef]
- Domènech, G.; Alvioli, M.; Corominas, J. Preparing first-time slope failures hazard maps: From pixel-based to slope unit-based. Landslides 2020, 17, 249–265. [Google Scholar] [CrossRef]
- Domènech, G. Assessment of the Magnitude-Frequency Relationship of Landslides and Rockfalls: Application to Hazard Mapping. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2015. [Google Scholar]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and non-associated visco-plasticity and plasticity in soil mechanics. Geotechnique 1975. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999. [Google Scholar] [CrossRef]
- Fernández-Merodo, J.A. Une Approche à la Modélisation des Glissements et des Effondrements de Terrains: Initiation et Propagation. Ph.D. Thesis, École Centrale Paris, Châtenay-Malabry, France, 2001. [Google Scholar]
- Mira, P. Análisis por Elementos Finitos de Problemas de Rotura de Geomateriales. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2002. [Google Scholar]
- Alvioli, M.; Melillo, M.; Guzzetti, F.; Rossi, M.; Palazzi, E.; Von Hardenberg, J.; Brunetti, M.T.; Peruccacci, S. Implications of climate change on landslide hazard in Central Italy. Sci. Total Environ. 2018, 630, 1528–1543. [Google Scholar] [CrossRef] [PubMed]
- Guzzetti, F. Landslide Hazard and Risk Assessment. Ph.D. Thesis, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, Germany, 2006. [Google Scholar]
- Copernicus Land Monitoring Corine Land Cover (CLC) 2018 Version 2020_20u1. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc2018 (accessed on 15 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).