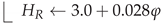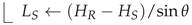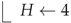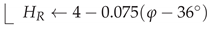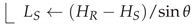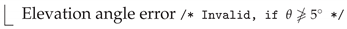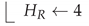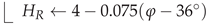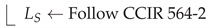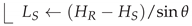A Survey of Rain Fade Models for Earth–Space Telecommunication Links—Taxonomy, Methods, and Comparative Study
Abstract
1. Introduction
- To the best of our knowledge, slant link rain fade models have not been classified broadly. In this work, we have prepared a taxonomy of the rain fade models for Earth–space links.
- A brief overview of each of the models selected is presented. In addition, we have provided algorithms of different models.
- Quantitative and qualitative characteristics of different models are organized in tables to review comparative studies.
- We noticed that each model was improved inherently and criticized the prototype by finding the inconveniences, and the specific characteristics are listed.
- Finally, the open research issues are summarized.
2. Background Study
2.1. Rain Attenuation Parameters
2.2. Earth–Space Link Budget
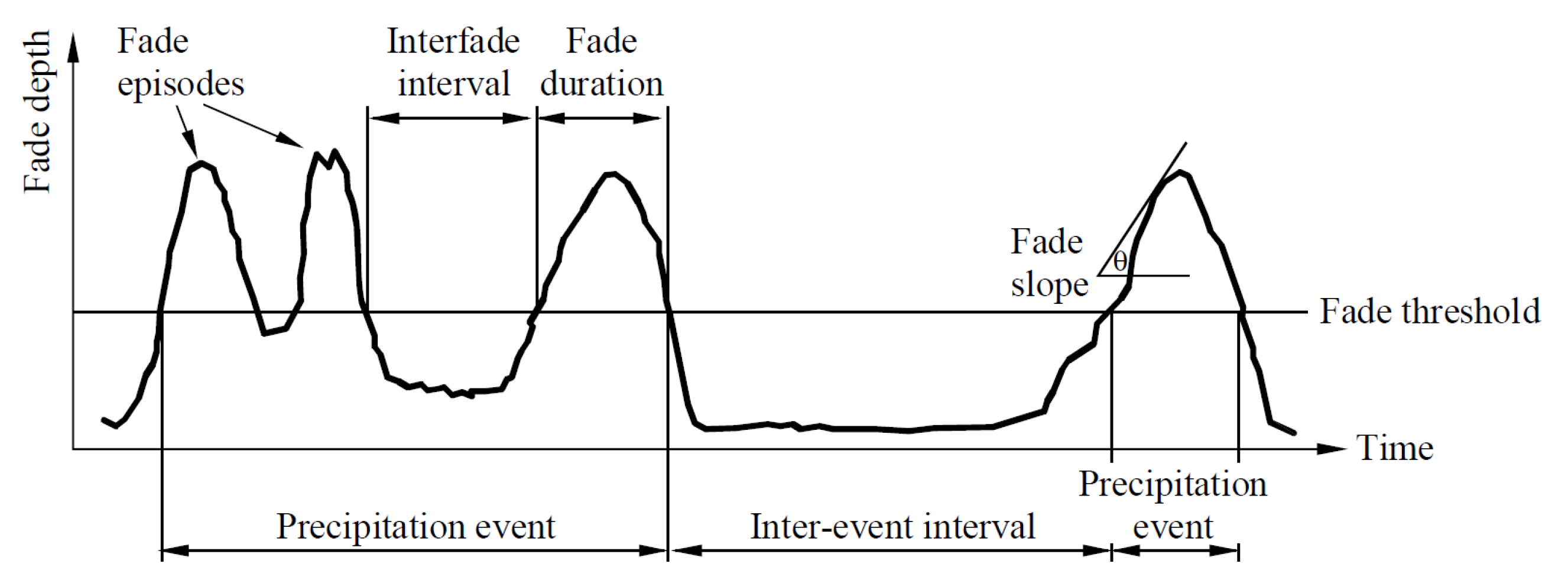
2.3. Rain Attenuation Anomalies: Breakpoint
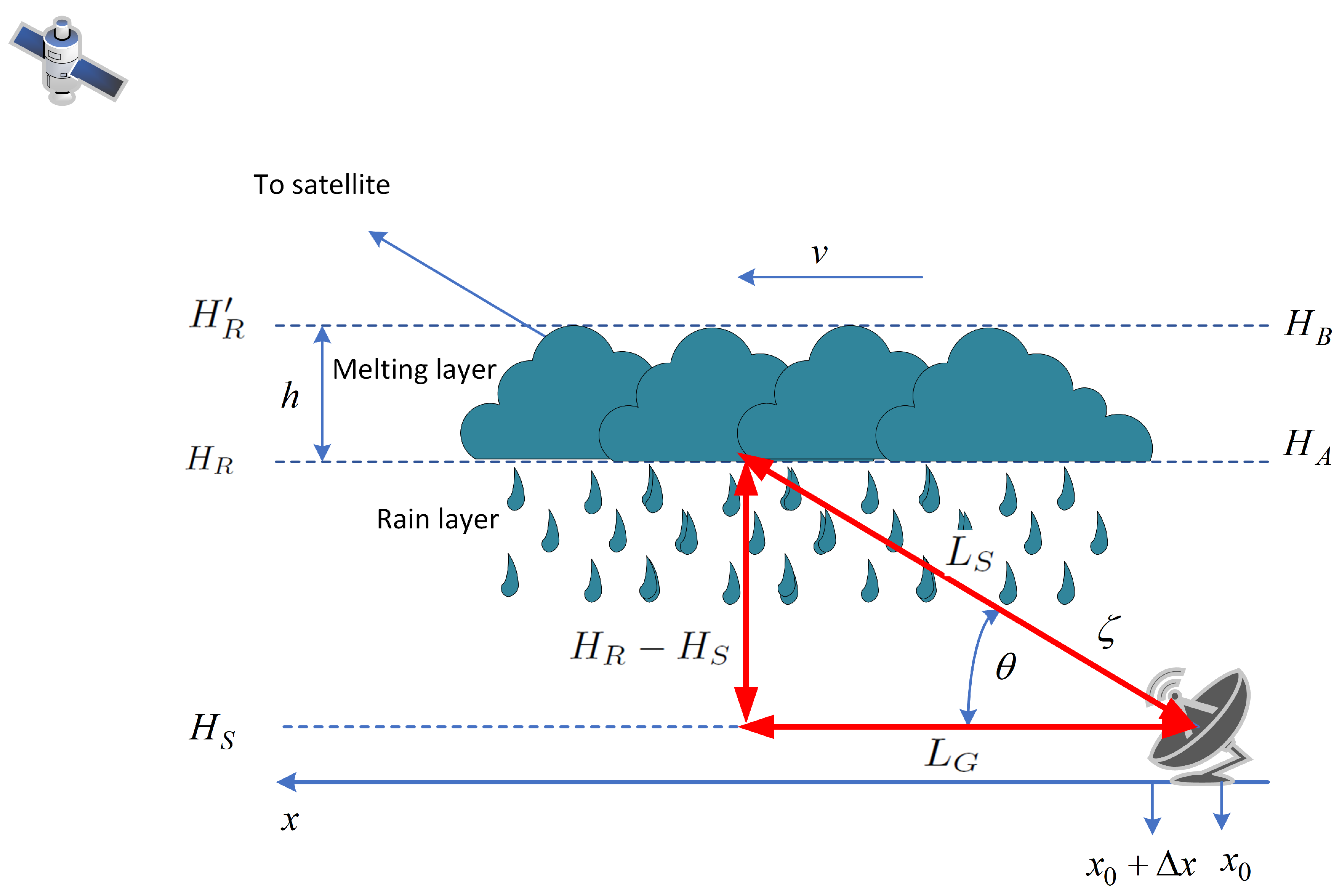
2.4. Slant Path in Rain Cell
2.4.1. Rain Height
2.4.2. Effective Slant Path
2.5. Rainfall Rate Conversion
2.6. Rain Type
2.7. Rain Cell Size
2.8. Rainfall Rate Missing Data
2.8.1. Temporal Missing: Time Series (TS)
2.8.2. Temporal Missing: Generation by Synthetic Means
2.9. Effective Rainfall Rate
2.10. Raindrop Size Distribution
3. Models to Predict Slant Link Attenuation
- Empirical models: The model depends on experimental data findings rather than mathematically describable input–output relationships.
- Physical models: In the physical model, there exists some physical resemblance between the formulated rain attenuation model and the physical structure of rain.
- Statistical models: This type of model is built on the long-term data of rain attenuation, rainfall rate, and related atmospheric parameter statistical analysis.
- Fade slope models: In the fade slope model, a change in rain attenuation is determined from the fluctuations of measured experimental rain attenuation over time. These results can subsequently be used to forecast the attenuation of rain.
- Learning-based models: The learning-based rain attenuation is new in the domain of knowledge. Long-term rain attenuation and huge datasets of related parameters are used as the input to a learning network (i.e., artificial neural network) to train, and later this trained network (e.g., optimized weights) can be used to predict rain attenuation.
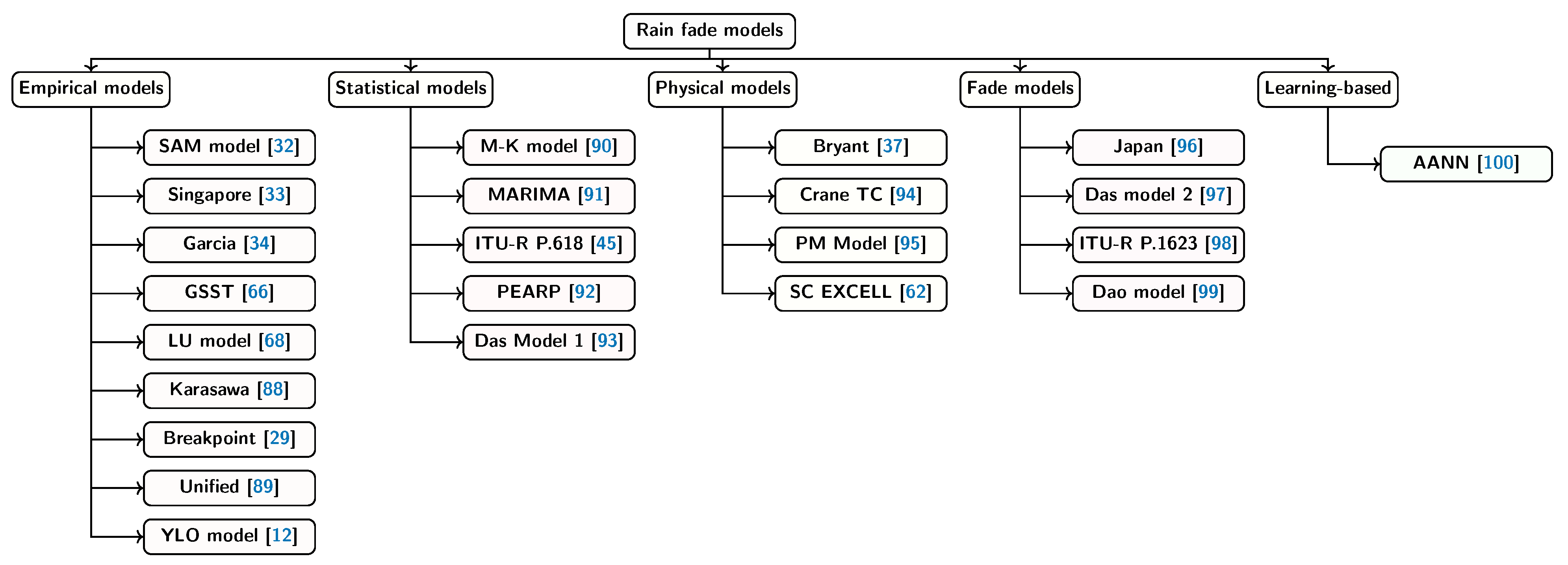
4. Review: Slant Links Rain Fade Models
4.1. Empirical Model
4.1.1. SAM
- (1)
- Calculate specific attenuation:
- (2)
- (3)
- Finally the rain attenuation is determined by Equation (19):
| Algorithm 1: SAM Model [32] |
 |
Advantages
Limitations
4.1.2. Singapore Model
Advantages
Limitations
| Algorithm 2: Singapore Model [33] |
|
4.1.3. Garcia Lopez Model
| Algorithm 3: Garcia Lopez Model [34] |
|
Advantages
Limitations
4.1.4. GSST Model
Advantages
Limitations
4.1.5. LU Model
| Algorithm 4: GSST Model [66] |
 |
- (1)
- The distribution of rainfall rate projection on the Earth is defined as:where here (km) is the same radius for which the rainfall rate is fixed .
- (2)
- The attenuation along with the slant link:where is the rain rate adjustment factor, and is the rain rate exceeded for of an average year.
- (3)
- The coefficients are taken using the genetic algorithm (GA) and annealing algorithm; thus, exploiting the rain databank of the ITU-R for the slant link:
| Algorithm 5: LU Model [68] |
| // Assumption: abrupt change more than 1 dB is neglected |
Advantages
Limitations
4.1.6. Karasawa Model
| Algorithm 6: Karasawa Model [88] |
|
Advantages
Limitations
4.1.7. Breakpoint Model
- (1)
- Calculate the “percentage of exceedance” at the breakpoint:
- (2)
| Algorithm 7: Breakpoint Model [29] |
 |
Advantages
Limitations
4.1.8. Unified Model
| Algorithm 8: Unified Model [89] |
Advantages
Limitations
4.1.9. YJ.X. Yeo, Y.H. Lee and J.T. Ong (YLO) Model
| Algorithm 9: YLO Model [12] |
 |
Advantages
Limitations
4.2. Statistical Models
4.2.1. Maseng–Bakken (M-K) Model
| Algorithm 10: M-K Model [90] |
|
Advantages
Limitations
4.2.2. Modified Genetic Algorithm-ARIMA (MARIMA) Model
| Algorithm 11: MARIMA model [91] |
 |
Advantages
Limitations
4.2.3. ITU-R P.618 Model
| Algorithm 12: ITU-R P.618 Model [45] |
 |
Advantages
Limitations
4.2.4. PEARP Model
| Algorithm 13: PEARP model [92] |
|
Advantages
Limitations
4.2.5. Das Model
| Algorithm 14: Das Model [93] |
 |
Advantages
Limitations
4.3. Physical Models
4.3.1. Bryant Model
| Algorithm 15: Bryant Model [37] |
 |
Advantages
Limitations
4.3.2. Crane TC
| Algorithm 16: Crane TC [94] |
 |
Advantages
Limitations
4.3.3. Physical-Mathematical (PM) Model
| Algorithm 17: PM Model [95] |
 |
Advantages
Limitations
4.3.4. SCEXCELL Model
| Algorithm 18: SCEXCELL Model [62] |
 |
Advantages
Limitations
4.4. Fade Slope Model
4.4.1. Japan Model
| Algorithm 19: Japan Model [96] |
| /* Choose proper sampling time to avoid aliasing effect on */ 1 Find Xlow /* Apply Equation (53) */ 2 Find Xhigh /* Apply Equation (54) */ 3 Apply FFT /* Choose number of FFT points for better visualization */ 4 Generate time domain diagram /* To observe the fluctuations */ |
Advantages
Limitations
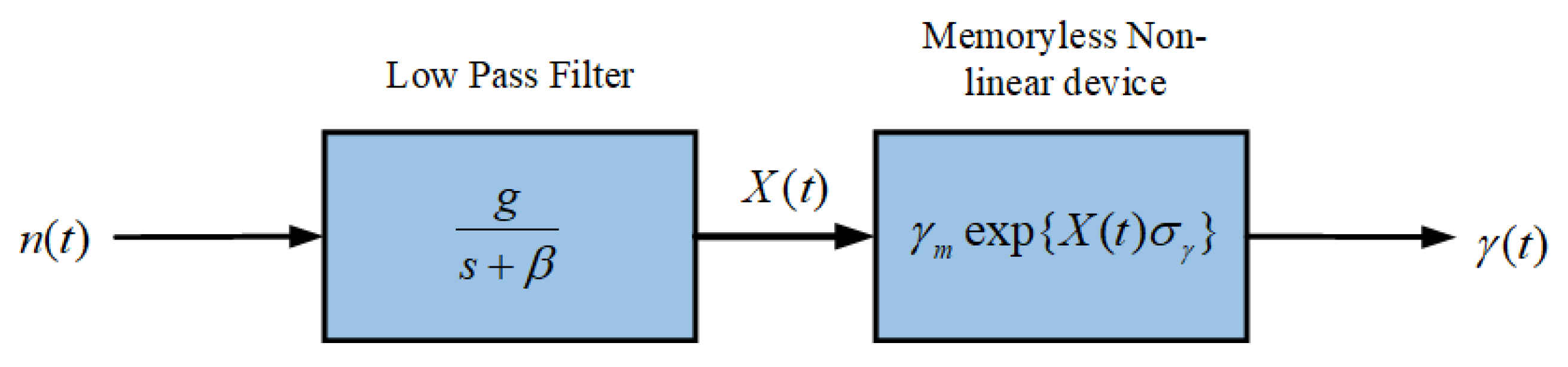
4.4.2. Das Fade Model
| Algorithm 20: Das Fade slope model [133] |
| 1 Apply LPF and MAF; 2 Find the fade slope; 3 Calculate PDF /* PDF: probability density function */ 4 Extract statistical coefficient () /* : standard deviation of */ 5 Fit polynomial to fit attenuation with 6 Use to calculate rain attenuation for time series data prediction () 7 Return |
Advantages
Limitations
4.4.3. ITU-R P.1623
| Algorithm 21: ITU-R P.1623 model [98] |
| 1 Calculate F /* Equation (59) */ 2 Calculate /* Equation (60) */ 3 Calculate /* Equation (61) */ Return A |
Advantages
Limitations
4.4.4. Dao Model
| Algorithm 22: Dao model [99] |
Advantages
Limitations
4.5. Learning-Based Model
4.5.1. Ahuna Model
Advantages
Limitations
5. Comparative Study of Slant Link Rain Fade Models
6. Future Research Scope
6.1. Scaling Improvement
6.2. Non-Uniformity of Isothermal Heights
6.3. Spatial Rainfall Distribution Along Slant Link
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2-D SST | 2-Dimentional SST |
| ARIMA | Autoregressive integrated moving average |
| BBH | Bright band height |
| BPNN | Backpropagation neural network |
| CCDF | Complementary cumulative distribution function |
| CCIR | Comité Consultatif International des Radiocommunications |
| CDF | Cumulative distribution function |
| DBSG3 | Study group 3 databanks |
| DSD | Drop size distribution |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| EMPI | Empirical |
| ERA-15 | ECMWF Re-Analysis-15 |
| ESST | Enhanced synthetic storm technique |
| EXCELL | EXponential CELL |
| FADE | Fade slope |
| FFT | Fast Fourier transform |
| FSL | Free space path loss |
| GA | Genetic algorithm |
| GE23 | General Electric 23 |
| GEO | Geostationary |
| GRV | Gaussian random variable |
| GSST | Global synthetic storm technique |
| HYCELL | Hybrid CELL |
| IDW | Inverse distance weighting |
| INTELSAT | International Telecommunications Satellite Organization |
| IoT | Internet of Things |
| ITU-R | International Telecommunication Union-Radiocommunication sector |
| LB | Learning-based |
| LEO | Low-Earth orbit |
| LPF | Low-pass filter |
| MAF | Moving average filter |
| MARIMA | Modified genetic algorithm-ARIMA |
| MEO | Medium-Earth orbit |
| M-K | Maseng–Bakken |
| MultiEXCELL | Multi-EXCELL |
| NM | Not mentioned |
| Probability density function | |
| PEARP | Prévision d’Ensemble ARPEGE |
| PHY | Physical |
| PLF | Path length factor |
| PM | Physical-mathematical |
| POR | Pacific Ocean Region |
| PRF | Path reduction factor |
| RF | Reduction factor |
| RHCP | Right-hand circular polarization |
| RMS | Root mean square |
| RMSE | Root mean square error |
| RN | Random number |
| RSL | Received signal level |
| RV | Random variable |
| SAM | Simple rain attenuation model |
| SCEXCELL | Stratiform convective exponential CELL model |
| SNR | Signal-to-noise ratio |
| SST | Synthetic storm technique |
| STAT | Statistical |
| STD | Standard deviation |
| TC | Two component |
| TS | Time series |
| UAV | Unmanned aerial vehicle |
| VDK | Van de Kamp |
| WINDS | Wideband InterNet-working engineering test and Demonstration Satellite |
| Meanings of Used Symbols | |
| A shift along horizontal axis due to the presence of layer B (Figure 2) | |
| Rainfall rate conversion factor | |
| Decay profile along horizontal axis [Equation (16)] | |
| Specific attenuation | |
| Log-normal distribution | |
| Free-space wavelength (m) | |
| Rain cell radius | |
| Elevation angle in degrees of the earth station | |
| Latitude of the earth station (degrees) | |
| Slant path | |
| Vertical adjustment factor (Algorithm 7) | |
| Horizontal length of rain cell | |
| Coefficient defined in “characteristic length” (Algorithm 6) | |
| Breakpoint attenuation [Equation (23)] | |
| Rain attenuation [Equation (13)] | |
| Slant path attenuation | |
| Slant length of rain cell | |
| B | Bandwidth (Hz) |
| Rainfall rate conversion factor | |
| D | Rain cell diameter [Equation (36)] |
| Receive antenna gain | |
| Transmit antenna gain | |
| Top of melting level | |
| Rain height | |
| Height above mean sea level of the earth station (km) | |
| isotherm height | |
| Central moments of inertia | |
| k | Boltzmann constant J / K |
| Characteristic length | |
| Average long term slant path in the precipitation | |
| Effective path length | |
| Horizontal projection length in the precipitation | |
| System loss at the receiver and transmitter | |
| Projected path-length (Table 4) | |
| l | Link distance (m) |
| L | Losses due to the presence of atmospheric gases, clouds, and fogs |
| Effective number of rain cells (Table 4) | |
| N | Number of tips [Equation (10)] |
| Probability of the mean rainfall rate is exceeded for -min | |
| Probability of the mean rainfall rate is exceeded for 1-min | |
| Transmitter power expressed in dBm) | |
| Average rainfall rate | |
| Rain rate adjustment | |
| Rain rate exceeded for p% of an average year | |
| Boundary rain rate | |
| Local peak rainfall rate | |
| Maximum rain rate for p% of an average year | |
| Path length reduction factor [Equation (13)] | |
| Point rainfall rate [Equation (10)] | |
| Point rainfall rate exceeded at of the time [Equation (13)] | |
| Root mean square (RMS) of rainfall rate | |
| Rainfall per tip (mm) [Equation (10)] | |
| , | Rainfall rate |
| T | Noise temperature (K) of the system which is assumed to be 290 K |
| T | Time gap in consecutive tips [Equation (10)] |
| Under rainy conditions temperature | |
| Under clear sky temperature | |
| Maximum rainfall in mm for time interval T-min | |
| u | Empirical constant (Table 5) |
| v (m/s) | Advection velocity of rain cells |
| Location of the ground station | |
| Rain cell gravity center | |
| Reflected signal in rainy condition | |
| Reflected signal in clear sky condition |
References
- Evans, B.; Wang, N.; Rahulan, Y.; Kumar, S.; Cahill, J.; Kavanagh, M.; Watts, S.; Chau, D.K.; Begassat, Y.; Brunel, A.P.; et al. An integrated satellite-terrestrial 5G network and its use to demonstrate 5G use cases. Int. J. Satell. Commun. Netw. 2021. [Google Scholar] [CrossRef]
- Goratti, L.; Herle, S.; Betz, T.; Garriga, E.T.; Khalili, H.; Khodashenas, P.S.; Brunel, A.P.; Chau, D.K.; Ravuri, S.; Vasudevamurthy, R.; et al. Satellite integration into 5G: Accent on testbed implementation and demonstration results for 5G Aero platform backhauling use case. Int. J. Satell. Commun. Netw. 2020. [Google Scholar] [CrossRef]
- Strinati, E.C.; Barbarossa, S.; Choi, T.; Pietrabissa, A.; Giuseppi, A.; Santis, E.D.; Vidal, J.; Becvar, Z.; Haustein, T.; Cassiau, N.; et al. 6G in the sky: On-demand intelligence at the edge of 3D networks (Invited paper). ETRI J. 2020, 42, 643–657. [Google Scholar] [CrossRef]
- Marchese, M.; Moheddine, A.; Patrone, F. IoT and UAV Integration in 5G Hybrid Terrestrial-Satellite Networks. Sensors 2019, 19, 3704. [Google Scholar] [CrossRef] [PubMed]
- Cuervo, F.; Martín-Polegre, A.; Las-Heras, F.; Vanhoenacker-Janvier, D.; Flávio, J.; Schmidt, M. Preparation of a CubeSat LEO radio wave propagation campaign at Q and W bands. Int. J. Satell. Commun. Netw. 2020. [Google Scholar] [CrossRef]
- Badron, K.; Ismail, A.F.; Din, J.; Tharek, A. Rain induced attenuation studies for V-band satellite communication in tropical region. J. Atmos. Sol. Terr. Phys. 2011, 73, 601–610. [Google Scholar] [CrossRef]
- Norouzian, F.; Marchetti, E.; Gashinova, M.; Hoare, E.; Constantinou, C.; Gardner, P.; Cherniakov, M. Rain Attenuation at Millimeter Wave and Low-THz Frequencies. IEEE Trans. Antennas Propag. 2020, 68, 421–431. [Google Scholar] [CrossRef]
- Kalaivaanan, P.M.; Sali, A.; Abdullah, R.S.A.R.; Yaakob, S.; Singh, M.J.; Al-Saegh, A.M. Evaluation of Ka-Band Rain Attenuation for Satellite Communication in Tropical Regions Through a Measurement of Multiple Antenna Sizes. IEEE Access 2020, 8, 18007–18018. [Google Scholar] [CrossRef]
- Abdulrahman, A.Y.; Rahman, T.A.; Rafiqul, I.M.; Olufeagba, B.J.; Abdulrahman, T.A.; Akanni, J.; Amuda, S.A.Y. Investigation of the unified rain Attenuation prediction method with data from tropical Climates. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1108–1111. [Google Scholar] [CrossRef]
- Khairolanuar, M.; Ismail, A.; Badron, K.; Jusoh, A.; Islam, M.; Abdullah, K. Assessment of ITU-R predictions for Ku-Band rain attenuation in Malaysia. In Proceedings of the 2014 IEEE 2nd International Symposium on Telecommunication Technologies (ISTT), Langkawi, Malaysia, 24–26 November 2014; pp. 389–393. [Google Scholar] [CrossRef]
- Chodkaveekityada, P. Comparison of spatial correlation between Japan and Thailand. In Proceedings of the 2017 International Symposium on Antennas and Propagation (ISAP), Phuket, Thailand, 30 October–2 November 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Yeo, J.X.; Lee, Y.H.; Ong, J.T. Rain Attenuation Prediction Model for Satellite Communications in Tropical Regions. IEEE Trans. Antennas Propag. 2014, 62, 5775–5781. [Google Scholar] [CrossRef]
- Lam, H.; Luini, L.; Din, J.; Capsoni, C.; Panagopoulos, A. Application of the SC EXCELL model for rain attenuation prediction in tropical and equatorial regions. In Proceedings of the 2010 IEEE Asia-Pacific Conference on Applied Electromagnetics (APACE), Port Dickson, Malaysia, 9–11 November 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Okamura, S.; Oguchi, T. Electromagnetic wave propagation in rain and polarization effects. Proc. Jpn. Acad. Ser. B 2010, 86, 539–562. [Google Scholar] [CrossRef]
- Samad, M.A.; Choi, D.Y. Learning-Assisted Rain Attenuation Prediction Models. Appl. Sci. 2020, 10, 6017. [Google Scholar] [CrossRef]
- Choi, K.S.; Kim, J.H.; Ahn, D.S.; Jeong, N.H.; Pack, J.K. Trends in Rain Attenuation Model in Satellite System. In Proceedings of the 13th International Conference on Advanced Communication Technology (ICACT2011), Gangwon, Korea, 13–16 February 2011; pp. 1530–1533. [Google Scholar]
- Samad, M.A.; Diba, F.D.; Choi, D.Y. A Survey of Rain Attenuation Prediction Models for Terrestrial Links—Current Research Challenges and State-of-the-Art. Sensors 2021, 21, 1207. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, L.; Song, Q.; Zhao, C.; Li, B. Rain Attenuation Prediction Models of 60 GHz Based on Neural Network and Least Squares-Support Vector Machine. In Proceedings of the Second International Conference on Communications, Signal Processing, and Systems; Springer International Publishing: Tianjin, China, 2013; pp. 413–421. [Google Scholar] [CrossRef]
- Alencar, G.; Caloba, L. Low statistical data processing for applications in earth space paths rain attenuation prediction by an artificial neural network. In Proceedings of the 2004 Asia-Pacific Radio Science Conference, Qingdao, China, 24–27 August 2004. [Google Scholar] [CrossRef]
- Thiennviboon, P.; Wisutimateekorn, S. Rain Attenuation Prediction Modeling for Earth-Space Links using Artificial Neural Networks. In Proceedings of the 2019 16th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Pattaya, Thailand, 10–13 July 2019. [Google Scholar] [CrossRef]
- Mpoporo, L.J.; Owolawi, P.A.; Ayo, A.O. Utilization of artificial neural networks for estimation of slant-path rain attenuation. In Proceedings of the 2019 International Multidisciplinary Information Technology and Engineering Conference (IMITEC), Vanderbijlpark, South Africa, 21–22 November 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Kvicera, V.; Grabner, M. Rain Attenuation at 58 GHz: Prediction versus Long-Term Trial Results. EURASIP J. Wirel. Commun. Netw. 2007, 2007, 046083. [Google Scholar] [CrossRef][Green Version]
- Lutz, E.; Werner, M.; Jahn, A. Satellite Systems for Personal and Broadband Communications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Csurgai-Horváth, L.; Adjei-Frimpong, B.; Riva, C.; Luini, L. Radio Wave Satellite Propagation in Ka/Q Band. Period. Polytech. Electr. Eng. Comput. Sci. 2018, 62, 38–46. [Google Scholar] [CrossRef]
- Hilt, A. Microwave Hop-Length and Availability Targets for the 5G Mobile Backhaul. In Proceedings of the 2019 42nd International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 1–3 July 2019. [Google Scholar] [CrossRef]
- Seybold, J.S. Introduction to RF propagation; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Diba, F.D.; Samad, M.A.; Ghimire, J.; Choi, D.Y. Wireless Telecommunication Links for Rainfall Monitoring: Deep Learning Approach and Experimental Results. IEEE Access 2021, 9, 66769–66780. [Google Scholar] [CrossRef]
- Best, S.R. Realized Noise Figure of the General Receiving Antenna. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 702–705. [Google Scholar] [CrossRef]
- Ramachandran, V.; Kumar, V. Modified rain attenuation model for tropical regions for Ku-Band signals. Int. J. Satell. Commun. Netw. 2006, 25, 53–67. [Google Scholar] [CrossRef]
- Mandeep, J.S. Slant path rain attenuation comparison of prediction models for satellite applications in Malaysia. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Mandeep, J.S.; Hassan, S.I.S.; Tanaka, K. Rainfall effects on Ku-band satellite link design in rainy tropical climate. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Stutzman, W.L.; Yon, K.M. A simple rain attenuation model for earth-space radio links operating at 10–35 GHz. Radio Sci. 1986, 21, 65–72. [Google Scholar] [CrossRef]
- Ong, J. Rain rate and attenuation prediction model for Singapore. In Proceedings of the Ninth International Conference on Antennas and Propagation (ICAP), Eindhoven, The Netherlands, 4–7 April 1995. [Google Scholar] [CrossRef]
- Garcia-Lopez, J.; Hernando, J.; Selga, J. Simple rain attenuation prediction method for satellite radio links. IEEE Trans. Antennas Propag. 1988, 36, 444–448. [Google Scholar] [CrossRef]
- Mandeep, J.S.; Ng, Y.Y.; Abdullah, H.; Abdullah, M. The Study of Rain Specific Attenuation for the Prediction of Satellite Propagation in Malaysia. J. Infrared Millimeter Terahertz Waves 2010. [Google Scholar] [CrossRef]
- Sharma, P.; Hudiara, I.S.; Singh, M.L. Estimation of Effective Rain Height at 29 GHz at Amritsar (Tropical Region). IEEE Trans. Antennas Propag. 2007, 55, 1463–1465. [Google Scholar] [CrossRef]
- Bryant, G.H.; Adimula, I.; Riva, C.; Brussaard, G. Rain attenuation statistics from rain cell diameters and heights. Int. J. Satell. Commun. 2001, 19, 263–283. [Google Scholar] [CrossRef]
- ITU-R Recommendation. P. 839-4: Rain Height Model for Prediction Methods; Report; International Telecommunication Union: Geneva, Switzerland, 2003. [Google Scholar]
- Sharma, P.; Hudiara, I.S.; Singh, M.L. Statistics of effective rain height by using zenith looking radiometer at 29 GHz at Amritsar (INDIA). In Proceedings of the 2006 First European Conference on Antennas and Propagation, Nice, France, 6–10 November 2006. [Google Scholar] [CrossRef]
- Abdulrahman, Y.; Rahman, T.A.; Islam, R.M.; Olufeagba, B.J.; Chebil, J. Comparison of measured rain attenuation in the 10.982-GHz band with predictions and sensitivity analysis. Int. J. Satell. Commun. Netw. 2014, 33, 185–195. [Google Scholar] [CrossRef]
- ITU-R Recommendation. P.839: Rain Height Model for Prediction Methods; Report; International Telecommunication Union: Geneva, Switzerland, 1997. [Google Scholar]
- da Silva Mello, L.; Pontes, M.S. Unified method for the prediction of rain attenuation in satellite and terrestrial links. J. Microw. Optoelectron. Electromagn. Appl. 2012, 11, 01–14. [Google Scholar] [CrossRef]
- Kang, W.G.; Kim, T.H.; Park, S.W.; Lee, I.Y.; Pack, J.K. Modeling of Effective Path-Length Based on Rain Cell Statistics for Total Attenuation Prediction in Satellite Link. IEEE Commun. Lett. 2018, 22, 2483–2486. [Google Scholar] [CrossRef]
- Argota, J.A.R.; Santamaria, L.; Larrea, A.; Anitzine, I.F. Estimation of effective path lengths of rain based on cell size distributions from meteorological radar. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014. [Google Scholar] [CrossRef]
- P.618-13:Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems; Report; International Telecommunication Union: Geneva, Switzerland, 2017.
- Emiliani, L.D.; Agudelo, J.; Gutierrez, E.; Restrepo, J.; Fradique-Mendez, C. Development of rain-attenuation and rain-rate maps for satellite system design in the Ku and Ka bands in Colombia. IEEE Antennas Propag. Mag. 2004, 46, 54–68. [Google Scholar] [CrossRef]
- Chebil, J.; Rahman, T. Development of 1 min rain rate contour maps for microwave applications in Malaysian Peninsula. Electron. Lett. 1999, 35, 1772–1774. [Google Scholar] [CrossRef]
- Ojo, J.S.; Ajewole, M.O.; Emiliani, L.D. One-Minute Rain-Rate Contour Maps for Microwave-Communication-System Planning in a Tropical Country: Nigeria. IEEE Antennas Propag. Mag. 2009, 51, 82–89. [Google Scholar] [CrossRef]
- Segal, B. The influence of raingage integration time, on measured rainfall-intensity distribution functions. J. Atmos. Ocean. Technol. 1986, 3, 662–671. [Google Scholar] [CrossRef]
- Burgueño, A.; Puigcerver, M.; Vilar, E. Influence of Rain Gauge Integration Time on the Rain Rate Statistics Used in Microwave Communications. Annales des Telecommunications; Springer: Berlin/Heidelberg, Germany, 1988; Volume 43, pp. 522–527. [Google Scholar] [CrossRef]
- Chebil, J.; Rahman, T. Rain rate statistical conversion for the prediction of rain attenuation in Malaysia. Electron. Lett. 1999, 35, 1019–1021. [Google Scholar] [CrossRef]
- Emiliani, L.D.; Luini, L.; Capsoni, C. Analysis and Parameterization of Methodologies for the Conversion of Rain-Rate Cumulative Distributions from Various Integration Times to One Minute. IEEE Antennas Propag. Mag. 2009, 51, 70–84. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, Y.S.; Kim, J.H.; Choi, Y.S. Empirical conversion process of rain rate distribution for various integration time. In Proceedings of the 2000 Asia-Pacific Microwave Conference, Proceedings (Cat. No. 00TH8522), Sydney, Australia, 3–6 December 2000; pp. 1593–1597. [Google Scholar] [CrossRef]
- Moupfouma, F.; Martin, L. Modelling of the rainfall rate cumulative distribution for the design of satellite and terrestrial communication systems. Int. J. Satell. Commun. 1995, 13, 105–115. [Google Scholar] [CrossRef]
- Lee, J.; Choi, Y.S.; Pack, J.; Ha, E. Conversion of rain rate distribution for various integration times. In Proceedings of the XXVIIth URSI General Assembly, Eindhoven, The Netherlands, 17–24 August 2002. [Google Scholar]
- ITU-R Recommendation. P.837-7: Characteristics of Precipitation for Propagation Modelling; Report; International Telecommunication Union: Geneva, Switzerland, 2017. [Google Scholar]
- Kestwal, M.C.; Joshi, S.; Garia, L.S. Prediction of Rain Attenuation and Impact of Rain in Wave Propagation at Microwave Frequency for Tropical Region (Uttarakhand, India). Int. J. Microw. Sci. Technol. 2014, 2014, 1–6. [Google Scholar] [CrossRef]
- Migliora, C.; Pontes, M.; Mello, L. Conversion of rainrate statistics with various integration times to equivalent one-minute distributions. In Proceedings of the CCECE 2003—Canadian Conference on Electrical and Computer Engineering, Toward a Caring and Humane Technology (Cat. No.03CH37436), Montreal, QC, Canada, 4–7 May 2003. [Google Scholar] [CrossRef]
- Rice, P.; Holmberg, N. Cumulative Time Statistics of Surface-Point Rainfall Rates. IEEE Trans. Commun. 1973, 21, 1131–1136. [Google Scholar] [CrossRef]
- Ito, C.; Hosoya, Y. The thunderstorm ratio as a regional climatic parameter: Its effects on different-integration-time rain rate conversion, rain attenuation, site-diversity and rain depolarization. In Proceedings of the XXVIIth URSI General Assembly, Eindhoven, The Netherlands, 17–24 August 2002. [Google Scholar]
- Ito, C.; Hosoya, Y. Proposal of a global conversion method for different integration time rain rates by using M distribution and regional climatic parameters. Electron. Commun. Jpn. (Part I Commun.) 2005, 89, 1–9. [Google Scholar] [CrossRef]
- Capsoni, C.; Luini, L.; Paraboni, A.; Riva, C.; Martellucci, A. A New Prediction Model of Rain Attenuation that Separately Accounts for Stratiform and Convective Rain. IEEE Trans. Antennas Propag. 2009, 57, 196–204. [Google Scholar] [CrossRef]
- Sanchez-Lago, I.; Fontan, F.P.; Marino, P.; Fiebig, U.C. Validation of the Synthetic Storm Technique as Part of a Time-Series Generator for Satellite Links. IEEE Antennas Wirel. Propag. Lett. 2007, 6, 372–375. [Google Scholar] [CrossRef]
- Luini, L.; Panzeri, A.; Riva, C.G. Enhancement of the Synthetic Storm Technique for the Prediction of Rain Attenuation Time Series at EHF. IEEE Trans. Antennas Propag. 2020, 68, 5592–5601. [Google Scholar] [CrossRef]
- Pastoriza-Santos, V.; Machado, F.; Nandi, D.; Sanroman, P.; Perez-Fontan, F. A Semi-2D Synthetic Storm Technique for Orbital Diversity on Earth-Space Propagation Paths. IEEE Trans. Antennas Propag. 2021, 69, 1631–1642. [Google Scholar] [CrossRef]
- Matricciani, E. Global formulation of the Synthetic Storm Technique to calculate rain attenuation only from rain rate probability distributions. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11 July 2008. [Google Scholar] [CrossRef]
- Capsoni, C.; Fedi, F.; Magistroni, C.; Paraboni, A.; Pawlina, A. Data and theory for a new model of the horizontal structure of rain cells for propagation applications. Radio Sci. 1987, 22, 395–404. [Google Scholar] [CrossRef]
- Lu, C.S.; Zhao, Z.W.; Wu, Z.S.; Lin, L.K.; Thiennviboon, P.; Zhang, X.; Lv, Z.F. A New Rain Attenuation Prediction Model for the Earth-Space Links. IEEE Trans. Antennas Propag. 2018, 66, 5432–5442. [Google Scholar] [CrossRef]
- Féral, L.; Sauvageot, H.; Castanet, L.; Lemorton, J. HYCELL—A new hybrid model of the rain horizontal distribution for propagation studies: 1. Modeling of the rain cell. Radio Sci. 2003, 38, 23-1–23-18. [Google Scholar] [CrossRef]
- Luini, L.; Capsoni, C. MultiEXCELL: A New Rain Field Model for Propagation Applications. IEEE Trans. Antennas Propag. 2011, 59, 4286–4300. [Google Scholar] [CrossRef]
- Kourogiorgas, C.; Panagopoulos, A.; Livieratos, S.; Chatzarakis, G. Rain attenuation time series synthesizer based on inverse Gaussian distribution. Electron. Lett. 2015, 51, 2162–2164. [Google Scholar] [CrossRef]
- Andrade, F.J.A.; da Silva Mello, L.A.R. Rain Attenuation Time Series Synthesizer Based on the Gamma Distribution. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1381–1384. [Google Scholar] [CrossRef]
- Adetan, O.; Afullo, T.J. Attenuation-rain rate power-law relation and critical diameters from drop size distribution measurements in Durban. In Proceedings of the 2013 Africon, Le Meridien Hotel, Mauritius, 9–12 September 2013. [Google Scholar] [CrossRef]
- Raupach, T.H.; Berne, A. Correction of raindrop size distributions measured by Parsivel disdrometers, using a two-dimensional video disdrometer as a reference. Atmos. Meas. Tech. 2015, 8, 343–365. [Google Scholar] [CrossRef]
- Katz, I. A Momentum Disdrometer for Measuring Raindrop Size from Aircraft. Bull. Am. Meteorol. Soc. 1952, 33, 365–368. [Google Scholar] [CrossRef]
- Gosset, M.; Zahiri, E.P.; Moumouni, S. Rain drop size distribution variability and impact on X-band polarimetric radar retrieval: Results from the AMMA campaign in Benin. Q. J. R. Meteorol. Soc. 2010, 136, 243–256. [Google Scholar] [CrossRef]
- Guyot, A.; Pudashine, J.; Protat, A.; Uijlenhoet, R.; Pauwels, V.R.N.; Seed, A.; Walker, J.P. Effect of disdrometer type on rain drop size distribution characterisation: A new dataset for Southeastern Australia. Preprint 2019. [Google Scholar] [CrossRef]
- Jaffrain, J.; Studzinski, A.; Berne, A. A network of disdrometers to quantify the small-scale variability of the raindrop size distribution. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Chodkaveekityada, P.; Fukuchi, H. Effect of raindrop size distribution and rain rate inhomogeneity on the relationship between attenuation and depolarization. Int. J. Satell. Commun. Netw. 2017, 36, 134–145. [Google Scholar] [CrossRef]
- Lam, H.Y.; Din, J.; Jong, S.L. Statistical and Physical Descriptions of Raindrop Size Distributions in Equatorial Malaysia from Disdrometer Observations. Adv. Meteorol. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Xie, Z.; Yang, H.; Lv, H.; Hu, Q. Seasonal Characteristics of Disdrometer-Observed Raindrop Size Distributions and Their Applications on Radar Calibration and Erosion Mechanism in a Semi-Arid Area of China. Remote Sens. 2020, 12, 262. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, L.; Zhang, Z.; Tong, Z.; Li, J.; Liu, F.; Zhang, J.; Jiang, Y. Characteristics of Clouds and Raindrop Size Distribution in Xinjiang, Using Cloud Radar Datasets and a Disdrometer. Atmosphere 2020, 11, 1382. [Google Scholar] [CrossRef]
- Mercier, F.; Chazottes, A.; Barthès, L.; Mallet, C. 4-D-VAR assimilation of disdrometer data and radar spectral reflectivities for raindrop size distribution and vertical wind retrievals. Atmos. Meas. Tech. 2016, 9, 3145–3163. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Atmos. Sci. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural Variations in the Analytical Form of the Raindrop Size Distribution. J. Appl. Meteorol. Climatol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Feingold, G.; Levin, Z. The Lognormal Fit to Raindrop Spectra from Frontal Convective Clouds in Israel. J. Appl. Meteorol. Climatol. 1986, 25, 1346–1363. [Google Scholar] [CrossRef]
- Sekine, M.; Ishii, S.; Hwang, S.I.; Sayama, S. Weibull Raindrop-Size Distribution and its Application to Rain Attenuation from 30 GHz to 1000 GHz. Int. J. Infrared Millim. Waves 2007, 28, 383–392. [Google Scholar] [CrossRef]
- Yamada, M.; Karasawa, Y.; Yasunaga, M.; Arbesser-Rastburg, B. An improved prediction method for rain attenuation in satellite communications operating at 10–20 GHz. Radio Sci. 1987, 22, 1053–1062. [Google Scholar] [CrossRef]
- da Silva Mello, L.A.R.; Pontes, M.S. Improved unified method for the prediction of rain attenuation in terrestrial and earth space links. In Proceedings of the 2009 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Belem, Brazil, 3–6 November 2009. [Google Scholar] [CrossRef]
- Maseng, T.; Bakken, P. A Stochastic Dynamic Model of Rain Attenuation. IEEE Trans. Commun. 1981, 29, 660–669. [Google Scholar] [CrossRef]
- Gong, S.; Gao, Y.; Shi, H.; Zhao, G. A practical MGA-ARIMA model for forecasting real-time dynamic rain-induced attenuation. Radio Sci. 2013, 48, 208–225. [Google Scholar] [CrossRef]
- Dahman, I.; Arbogast, P.; Jeannin, N.; Benammar, B. Rain attenuation prediction model for satellite communications based on the Météo-France ensemble prediction system PEARP. Nat. Hazards Earth Syst. Sci. 2018, 18, 3327–3341. [Google Scholar] [CrossRef]
- Das, D.; Maitra, A. Time series prediction of rain rate during rain events at a tropical location. IET Microw. Antennas Propag. 2012, 6, 1710–1716. [Google Scholar] [CrossRef]
- Crane, R.K. A two-component rain model for the prediction of attenuation statistics. Radio Sci. 1982, 17, 1371–1387. [Google Scholar] [CrossRef]
- Matricciani, E. Physical-mathematical model of the dynamics of rain attenuation based on rain rate time series and a two-layer vertical structure of precipitation. Radio Sci. 1996, 31, 281–295. [Google Scholar] [CrossRef]
- Karasawa, Y.; Matsudo, T. Characteristics of fading on low-elevation angle Earth-space paths with concurrent rain attenuation and scintillation. IEEE Trans. Antennas Propag. 1991, 39, 657–661. [Google Scholar] [CrossRef]
- Das, D.; Maitra, A. Time series prediction of rain attenuation from rain rate measurement using synthetic storm technique for a tropical location. AEU Int. J. Electron. Commun. 2014, 68, 33–36. [Google Scholar] [CrossRef]
- ITU-R Recommendations. P.1623: Prediction Method of Fade Dynamics on Earth-Space Paths; Report; International Telecommunication Union: Geneva, Switzerland, 2005. [Google Scholar]
- Dao, H.; Islam, M.R.; Al-Khateeb, K.A.S. Rain Fade Slope Model in Satellite Path Based on Data Measured in Heavy Rain Zone. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 50–53. [Google Scholar] [CrossRef]
- Ahuna, M.N.; Afullo, T.J.; Alonge, A.A. Rain Attenuation Prediction Using Artificial Neural Network for Dynamic Rain Fade Mitigation. SAIEE Afr. Res. J. 2019, 110, 11–18. [Google Scholar] [CrossRef]
- Stutzman, W.; Dishman, W. A simple model for the estimation of rain-induced attenuation along earth-space paths at millimeter wavelengths. Radio Sci. 1982, 17, 1465–1476. [Google Scholar] [CrossRef]
- Giannetti, F.; Reggiannini, R.; Moretti, M.; Adirosi, E.; Baldini, L.; Facheris, L.; Antonini, A.; Melani, S.; Bacci, G.; Petrolino, A.; et al. Real-Time Rain Rate Evaluation via Satellite Downlink Signal Attenuation Measurement. Sensors 2017, 17, 1864. [Google Scholar] [CrossRef] [PubMed]
- Acharya, R. A simple real-time frequency scaling technique for rain attenuation and its performance. Int. J. Satell. Commun. Netw. 2020, 38, 329–340. [Google Scholar] [CrossRef]
- The International Radio Consultative Committee (CCIR). Report 564, CCIR and Radiocommunication Assemblies. In Proceedings of the XVI Plenary Assembly, Dubrovnik, Croatia, 12–23 May 1986. [Google Scholar]
- Matricciani, E. A fundamental differential equation that links rain attenuation to the rain rate measured at one point, and its applications in slant paths. In Proceedings of the 2006 First European Conference on Antennas and Propagation, Nice, France, 6–10 November 2006. [Google Scholar] [CrossRef]
- CCIR. Report 564-2: Propagation Data Required for Space Telecommunications Systems; The International Radio Consultative Committee (CCIR): Geneva, Switzerland, 1982; Volume V, pp. 331–373. [Google Scholar]
- P.618-8: Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems; Report; International Telecommunication Union: Geneva, Switzerland, 2003.
- P.618-12: Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems; Report; International Telecommunication Union: Geneva, Switzerland, 2015.
- ITU-Recommendation. P.838-3: Specific Attenuation Model for Rain for Use in Prediction Methods; Report; International Telecommunication Union: Geneva, Switzerland, 2005. [Google Scholar]
- Carrie, G.; Lacoste, F.; Castanet, L. A new ‘event-on-demand’ synthesizer of rain attenuation time series at Ku-, Ka- and Q/V-bands. Int. J. Satell. Commun. Netw. 2010, 29, 47–60. [Google Scholar] [CrossRef]
- Yaccop, A.; Yao, Y.; Ismail, A.; Badron, K. Comparison of Ku-band satellite rain attenuation with ITU-R prediction models in the tropics. In Proceedings of the 2013 IEEE Antennas and Propagation Society International Symposium (APSURSI), Orlando, FL, USA, 7–13 July 2013. [Google Scholar] [CrossRef]
- Luini, L.; Riva, C.G.; Panzeri, A. On Combining Attenuation Statistics of Different Tropospheric Effects Affecting EHF Earth–Space Links. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1496–1500. [Google Scholar] [CrossRef]
- Hatsuda, T.; Aoki, Y.; Echigo, H.; Takahata, F.; Maekawa, Y.; Fujisaki, K. Ku-Band Long Distance Site-Diversity (SD) Characteristics Using New Measuring System. IEEE Trans. Antennas Propag. 2004, 52, 1481–1491. [Google Scholar] [CrossRef]
- Boulanger, X.; Gabard, B.; Casadebaig, L.; Castanet, L. Four Years of Total Attenuation Statistics of Earth-Space Propagation Experiments at Ka-Band in Toulouse. IEEE Trans. Antennas Propag. 2015, 63, 2203–2214. [Google Scholar] [CrossRef]
- Das, D.; Maitra, A. Time series predictor of Ku band rain attenuation over an Earth-space path at a tropical location. Int. J. Satell. Commun. Netw. 2011, 30, 19–28. [Google Scholar] [CrossRef]
- Crane, R. Prediction of Attenuation by Rain. IEEE Trans. Commun. 1980, 28, 1717–1733. [Google Scholar] [CrossRef]
- Lin, S.H.; Bergmann, H.J.; Pursley, M.V. Rain Attenuation on Earth-Satellite Paths-Summary of 10-Year Experiments and Studies. Bell Syst. Tech. J. 1980, 59, 183–228. [Google Scholar] [CrossRef]
- Misme, P.; Waldteufel, P. Calcul des affaiblissements dus à la pluie sur un trajet Terre-satellite. In Annales des Télécommunications; Springer: Berlin/Heidelberg, Germany, 1981; Volume 36, pp. 65–72. [Google Scholar] [CrossRef]
- Leitao, M.; Watson, P. Method for prediction of attenuation on earth-space links based on radar measurements of the physical structure of rainfall. EE Proc. F Commun. Radar Signal Process. 1986, 133, 429–440. [Google Scholar] [CrossRef]
- Capsoni, C.; Fedi, F.; Paraboni, A. A comprehensive meteorologically oriented methodology for the prediction of wave propagation parameters in telecommunication applications beyond 10 GHz. Radio Sci. 1987, 22, 387–393. [Google Scholar] [CrossRef]
- Matricciani, E. Rain attenuation predicted with a two-layer rain model. Eur. Trans. Telecommun. 1991, 2, 715–727. [Google Scholar] [CrossRef]
- Capsoni, C.; Luini, L.; Paraboni, A.; Riva, C. Stratiform and convective rain discrimination deduced from local P(R). IEEE Trans. Antennas Propag. 2006, 54, 3566–3569. [Google Scholar] [CrossRef]
- Bosisio, A.V.; Riva, C. A novel method for the statistical prediction of rain attenuation in site diversity systems: Theory and comparative testing against experimental data. Int. J. Satell. Commun. 1998, 16, 47–52. [Google Scholar] [CrossRef]
- Capsoni, C.; Luini, L. 1-min rain rate statistics predictions from 1-hour rain rate statistics measurements. IEEE Trans. Antennas Propag. 2008, 56, 815–824. [Google Scholar] [CrossRef]
- Capsoni, C.; D’Amico, M. Prediction of effective transmission loss by hydrometeor scatter through a 3D rain cell model. In Proceedings of the 1991 Seventh International Conference on Antennas and Propagation, ICAP 91 (IEE), York, UK, 15–18 April 1991; pp. 238–241. [Google Scholar]
- Mandeep, J. Fade duration statistics for Ku-band satellite links. Adv. Space Res. 2013, 52, 445–450. [Google Scholar] [CrossRef]
- van de Kamp, M. Statistical analysis of rain fade slope. IEEE Trans. Antennas Propag. 2003, 51, 1750–1759. [Google Scholar] [CrossRef]
- Dintelmann, F. Analysis of 11 GHz slant path fade duration and fade slope. Electron. Lett. 1981, 17, 267. [Google Scholar] [CrossRef]
- Adhikari, A.; Das, S.; Bhattacharya, A.; Maitra, A. Improving rain attenuation estimation: Modelling of effective path length using Ku-band measurements at a tropical location. Prog. Electromagn. Res. B 2011, 34, 173–186. [Google Scholar] [CrossRef]
- Jong, S.L.; Riva, C.; Din, J.; D’Amico, M.; Lam, H.Y. Fade slope analysis for Ku-band earth-space communication links in Malaysia. IET Microw. Antennas Propag. 2019, 13, 2330–2335. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, M.; Chakraborty, S.; Shukla, A.; Acharya, R. Experimental studies of Ka Band Rain Fade Slope at a Tropical Location of India. Adv. Space Res. 2020, 66, 1551–1557. [Google Scholar] [CrossRef]
- del Pino, P.G.; Riera, J.M.; Benarroch, A. Tropospheric Scintillation with Concurrent Rain Attenuation at 50 GHz in Madrid. IEEE Trans. Antennas Propag. 2012, 60, 1578–1583. [Google Scholar] [CrossRef]
- Das, D.; Maitra, A. Fade-slope model for rain attenuation prediction in tropical region. IEEE Geosci. Remote Sens. Lett. 2016, 13, 777–781. [Google Scholar] [CrossRef]
- Kourogiorgas, C.; Kelmendi, A.; Panagopoulos, A.D.; Vilhar, A. On Rain Attenuation Time Series Generation: A New Simple Copula-based Channel Model for Satellite Slant Paths. IEEE Trans. Antennas Propag. 2016, 64, 3206–3211. [Google Scholar] [CrossRef]
- Nandi, D.D.; Pérez-Fontán, F.; Pastoriza-Santos, V.; Machado, F. Application of synthetic storm technique for rain attenuation prediction at Ka and Q band for a temperate Location, Vigo, Spain. Adv. Space Res. 2020, 66, 800–809. [Google Scholar] [CrossRef]
- Andrade, F.J.A.; de Medeiros, A.A.M.; da Silva Mello, L.A.R. Short-Term Rain Attenuation Predictor for Terrestrial Links in Tropical Area. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1325–1328. [Google Scholar] [CrossRef]
- The European Space Agency. Satellite Frequency Bands. Available online: https://www.esa.int/Applications/Telecommunications_Integrated_Applications/Satellite_frequency_bands (accessed on 20 March 2021).
- Report ITU-R SA.2167: Factors Affecting the Choice of Frequency Bands for Space Research Service Deep-Space (Space-to-Earth) Telecommunication Links; Report; International Telecommunication Union: Geneva, Switzerland, 2009.
- P.311-17: Acquisition, Presentation and Analysis of Data in Studies of Radiowave Propagation; Report; International Telecommunication Union: Geneva, Switzerland, 2017.
- Jong, S.L.; Riva, C.; D’Amico, M.; Lam, H.Y.; Yunus, M.M.; Din, J. Performance of synthetic storm technique in estimating fade dynamics in equatorial Malaysia. Int. J. Satell. Commun. Netw. 2018, 36, 416–426. [Google Scholar] [CrossRef]
- del Pino, P.G.; Riera, J.; Benarroch, A. Fade and interfade duration statistics on an Earth-space link at 50 GHz. IET Microw. Antennas Propag. 2011, 5, 790. [Google Scholar] [CrossRef]
- Mandeep, J.S.; Hui, O.W.; Abdullah, M.; Tariqul, M.; Ismail, M.; Suparta, W.; Yatim, B.; Menon, P.S.; Abdullah, H. Modified ITU-R rain attenuation model for equatorial climate. In Proceedings of the 2011 IEEE International Conference on Space Science and Communication (IconSpace), Penang, Malaysia, 12–13 July 2011. [Google Scholar] [CrossRef]
- Yeo, J.X.; Lee, Y.H.; Ong, J.T. Modified ITU-R slant path rain attenuation model for the tropical region. In Proceedings of the 2009 7th International Conference on Information, Communications and Signal Processing (ICICS), Macau, China, 8–10 December 2009. [Google Scholar] [CrossRef]
- Dafda, A.H.; Maradia, K.G. A novel method for estimation of rainfall attenuation using coarse rainfall data and proposal of modified ITU-R rain model for India. SN Appl. Sci. 2019, 1, 379. [Google Scholar] [CrossRef]
- Mello, L.; Pontes, M.; Fagundes, I.; Almeida, M.; Andrade, F. Modified rain attenuation prediction method considering the effect of wind direction. J. Microw. Optoelectron. Electromagn. Appl. 2014, 13, 254–267. [Google Scholar] [CrossRef][Green Version]
- Badron, K.; Ismail, A.F.; Islam, M.R.; Abdullah, K.; Din, J.; Tharek, A.R. A modified rain attenuation prediction model for tropical V-band satellite earth link. Int. J. Satell. Commun. Netw. 2014, 33, 57–67. [Google Scholar] [CrossRef]
- Liu, Z.N.; Yu, X.Y.; Jia, L.F.; Wang, Y.S.; Song, Y.C.; Meng, H.D. The influence of distance weight on the inverse distance weighted method for ore-grade estimation. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef]
- Diba, F.D.; Afullo, T.J.; Alonge, A.A. Rainfall Rate and Attenuation Performance Analysis at Microwave and Millimeter Bands for the Design of Terrestrial Line-of-Sight Radio Links in Ethiopia. SAIEE Afr. Res. J. 2016, 107, 177–186. [Google Scholar] [CrossRef]
- Al-Samman, A.M.; Mohamed, M.; Ai, Y.; Cheffena, M.; Azmi, M.H.; Rahman, T.A. Rain Attenuation Measurements and Analysis at 73 GHz E-Band Link in Tropical Region. IEEE Commun. Lett. 2020, 24, 1368–1372. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V. Estimation of missing precipitation records integrating surface interpolation techniques and spatio-temporal association rules. J. Hydroinform. 2009, 11, 133–146. [Google Scholar] [CrossRef]
- Viale, M.; Garreaud, R. Orographic effects of the subtropical and extratropical Andes on upwind precipitating clouds. J. Geophys. Res. Atmos. 2015, 120, 4962–4974. [Google Scholar] [CrossRef]
- Freund, R.J.; Wilson, W.J.; Sa, P. Regression Analysis; Academic Press, Elsevier: Cambridge, MA, USA, 2006. [Google Scholar]
- Teegavarapu, R.S.; Chandramouli, V. Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]


| Ref. | Survey Concentrations |
|---|---|
| [14] | The results show that rain attenuation in horizontal polarization is slightly larger than that in vertical polarization. A differential coupling-based compensation was recommended to reduce the rain attenuation effects on polarization in the depolarization processes. |
| [15] | In this survey, the artificial-neural-network-based models were classified based on input parameters. In addition, the accuracy of the artificial-neural-network-based models was accessed through a comparative study. |
| [16] | Rain attenuation in a satellite system is more severe than in a terrestrial system, and for a good model, it should be implemented into the model through local climatic elements. |
| Factors | Earth–Space | Terrestrial |
|---|---|---|
| Rain | ✓ | ✓ |
| Cloud, sky noise, scintillation, latitude, Earth radius | ✓ | ✗ |
| Hop length | Varies according to orbit:
| Varies according to necessity:
|
| Path length reduction | Effective slant path | Effective terrestrial path |
| Ref. | Mechanism | Symbol Meanings |
|---|---|---|
| [35] | is the isotherm height, and R is the rain rate. | |
| [36] | is the medium temperature, , under clear sky, and is under rainy condition temperatures, and is the specific attenuation coefficient. | |
| [37] | R is the rain rate in the range 30–70 mm/h. | |
| [38] | , also using rain height map | is the isotherm height. |
| [32] | is the latitude in degrees. | |
| [33] | is the latitude in degrees. | |
| [34] | is the latitude in degrees. | |
| [39] | R is the rain rate. | |
| [40] | R is the rain rate. | |
| [41] | is the latitude in degrees. |
| Ref. | Mathematical Procedure |
|---|---|
| white [35] | , where R is the rain rate. |
| [42] | , where is the elevation angle, is the station height above mean sea level of the Earth, and is the horizontal projection length in the precipitation. |
| [43] | where is the projected path-length, which is defined by , a boundary rain rate. If then , and if then (Figure 1), and ‘’ is the effective number of rain cells given by , where , and ( is elevation angle). |
| [44] | The estimation of the rain path can be determined by calibrating the reflected signal in clear-sky conditions and in rainy conditions . Once rainfall events are identified the first step of the procedure involves the determination of the volume of the rain cell with . |
| Ref. | Conversion Techniques |
|---|---|
| [49] | Using the Rain rate , where , the model can convert rain between 1- and -min, where is the probability that the mean rainfall rate is exceeded for a 1 min accumulation time, and is the probability that the mean rainfall rate is exceeded for min accumulation time. |
| [50] | Using cumulative rainfall distributions, the model can convert rain between 1- and -min. |
| [51] | Using the conversion factor , where () the model can convert 60 min to a 1 min integration time rain rate, where is the conversion factor, a, b, c, d are constants, and P is the probability of rainfall rate exceedance within . It can also be used to convert between different rain rates [52]. |
| [53] | Using the equation (), min to 1 min conversion. |
| [54] | Using the equation , where the model can convert the rain rate from min to 1 min. |
| [55] | Using the equation, , where : regression component determined statistically, and . |
| [56] | In the absence of accurate long-term rainfall data, this method takes the percent of time exceedance, latitude, and longitude as input to generate a 1 min integration time rain rate. |
| [57] | The model simply calculates the rain rate , where : maximum rainfall in mm for time interval T min. |
| [58] | , R: rain rate, u: empirical constant, a, b: depending on the location and integration time of the rain gauge. |
| [59] | where M is the average annual rainfall (mm), and T is the number of hours in the year during which rain rates exceed R (mm/h). |
| [60] | where p is the percentage of the time, M is the total annual rainfall accumulation, , and are constants, which can be derived from , and is the thunderstorm ratio (), where is the rain rate due to a thunderstorm and is the rain rate without a thunderstorm. |
| [61] | where R is the rain rate in mm/h and is the regional climatic parameter. |
| Parameter | Monoaxial Rain Cell | Biaxial Rain Cell |
|---|---|---|
| Peak rainfall rate () | ✓ | ✓ |
| Cell radius/radii |
| Tpe | Ref. | Slant or Both | Rain Structure | Rainfall Rate | Frequency | Angle(Earth Station) | Rain Height | Melting Layer Height | Time Series |
|---|---|---|---|---|---|---|---|---|---|
| EMPI | [32] | Slant | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ |
| [33] | Slant | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| [34] | Slant | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| [66] | Slant | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [68] | Slant | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | |
| [88] | Slant | ✓ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | |
| [29] | Slant | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| [89] | Both | ✗ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | |
| [12] | Slant | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| STAT | [90] | Slant | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [91] | Slant | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | |
| [45] | Slant | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| [92] | Slant | ✗ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | |
| [93] | Slant | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | |
| PHY | [37] | Slant | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ |
| [94] | Both | — | ✓ | — | ✓ | ✓ | ✗ | ✗ | |
| [95] | Both | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | |
| [62] | Slant | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | |
| FADE | [96] | Slant | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [97] | Slant | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | |
| [98] | Slant | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | |
| [99] | Slant | ✗ | ✗ | — | ✓ | ✗ | ✗ | ✗ | |
| LB | [100] | Slant | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Type | Ref. | Frequency Range | Polarization | Regional Climatic Parameter | Spatial Friendly | Reported Region that Suits |
|---|---|---|---|---|---|---|
| EMPI | [32] | 10–35 GHz | ✓ | ✓ | ✓ | The USA, Europe, and Japan |
| [33] | 4–6 GHz | NM | Rainfall rate | ✗ | Singapore | |
| [34] | NM | ✓ | 4 coefficient constants called a,b,c and d depend on geographic area | NM | Best suited areas are in Europe, the USA, Japan, and Australia | |
| [66] | 10–100 GHz | ✓Circular, horizontal and vertical | Rainfall rate | ✗ | Temperate region | |
| [68] | Above 11 GHz | ✗ | Local rainfall rate | No information available | No practical information; test information is limited within DBSG3 databank | |
| [88] | 10–20 GHz | NM | Rainfall rate, the probabilities of occurrence and mean rainfalls, for cell and debris | The model considers a single volume rainfalling area and does not consider convective (cell) and stratified rain (debris) | CCIR rain zone | |
| [29] | 10.7–13 GHz (Ku band) | ✓ | Rainfall rate | NM | Fiji | |
| [89] | Terrestrial: 7–137 GHz | ✓k and | Rainfall rate | ✓ | Worldwide (ITU-R databank) | |
| [12] | 10–30 GHz | Both | Rainfall rate | ✗ | Tropical | |
| STAT | [90] | NM | ✓ | Rainfall rate | ✗ | Temperate region |
| [91] | 10–50 GHz | ✓ | Climate characteristics, link elevation angle | Has spatial dynamics of rainfall rate parameter due to Van de Kamp [127] | Xi’an, China | |
| [45] | Up to 55 GHz | ✓ | Rainfall rate | ✗ | Worldwide | |
| [92] | NM (only 20 GHz is mentioned) | NM | NM | Information NM | France | |
| [93] | NM | ✓Horizontal | Measured rain attenuation | NM | Kolkata, India | |
| PHY | [37] | Reported frequencies are 15, 30, 39.6 GHz | NM | ✓ | Rainfall rate is not a function of distance | Temperate and tropical |
| [94] | 1–100 GHz | ✗ | Cell and debris parameter | No spatial correlation function is included | Temperate region | |
| [95] | 11.6 GHz (Range NM) | ✓Circular, Linear | Rainfall rate, wind velocity | ✓(1-year rainfall rate PDF was used) | Italy | |
| [62] | 10–50 GHz | ✓ | Rainfall rate; rain height; melting layer height, etc. | ✓Vertical and horizontal | Worldwide | |
| FADE | [96] | Ku-band | RHCP, Linear polarization | ✗ | ✗ | Japan (low-elevation Earth–space path) |
| [97] | NM | Horizontal | ✓ | ✗ | Tropical area | |
| [98] | 10–50 GHz | NM | ✓ | ✗ | Designed for global perspective | |
| [99] | 10.982 GHz (Ku-band) | Vertical | s-parameter | ✗ | Malaysia | |
| LB | [100] | NM | NM | Local rainfall data: it needs to train the BPNN networks | NM | Butare, Rwanda |
| Type | Ref. | Used/Validation Databank | Remarks about Validation | Complexity Level | Constraints |
|---|---|---|---|---|---|
| EMPI | [32] | 62 experiments in the USA, Japan and Europe | Shows better prediction with minimum 2 years rainfall datasets | low | The operating frequency range is limited to 10–35 GHz |
| [33] | INTELSAT POR experiment (Singapore) | The results have been validated with CCIR model and measured attenuation | low | The recommended frequency is limited to 4–6 GHz | |
| [34] | 77 satellite links placed in Europe, the USA, Japan, and Australia (CCIR data bank) | Validated by the author | low | The model is suitable for prediction with an elevation angle ranging from 10 to 40 | |
| [66] | ITU-R databank | ITU-R databank is used to examine the behavior of m parameter at different frequencies as well as different sites | low | Not spatial friendly | |
| [68] | DBSG3 databank | The RMS value show that the new model provides the smallest rms and STD in all percentages of time except at 0.001% | high | Application area is limited by low latitudes (between 36 South and 36 North) and low elevation angles (25<) | |
| [88] | CCIR rain zone with different elevation angle | Validated by the author | medium ∔ | 10–20 GHz | |
| [29] | Used 6 tropical city’s rain databanks from ITU-R | The experimental result agreed about correction factor induced attenuation especially at elevation angle less than 60 compared to ITU-R model | medium | In this model it is assumed that rain is uniformly distributed inside a rain cell | |
| [89] | ITU-R databank | The model gives decent results with the correctness of its terrestrial and slant direction | medium | The model was not checked with actual data for attenuation | |
| [12] | ✗ | Verified with the the beacon signals from WINDS and GE23 satellites (2009 to 2012) | low | Up to 30 GHz frequency is examined | |
| STAT | [90] | ✗ | Not validated with heavy rainfall or with rainfall data around the world for different sites | low | The model is applicable only during the rain periods because no transition is included in the model to switch from rainy to clear sky conditions |
| [91] | Validated based on the measured rain attenuation data at Xi’an, China | The validation is a good agreement between measured and predicted attenuation using this model, but has not been compared with other important rain attenuation models | high | The size of the area is not defined for a specific set of parameters | |
| [92] | ✗ | Not validated | — | The probabilistic weather forecasts could be beneficial to maximize the economic value accounting the transmitted data for higher frequencies (say 50 GHz). | |
| [93] | ✗: used measured attenuation data | The validation shows a good agreement between measured and predicted attenuation using this model, but has not been compared with other important rain attenuation models | medium | It needs to derive mean and standard deviation of the Gaussian distribution for a different geographic area and find the coefficients of second-order polynomials from real measured attenuation | |
| PHY | [37] | ✓ | Validated at Lae, Papua New Guinea | low | — |
| [94] | Satellite: validated through CCIR procedure. Terrestrial: 35 terrestrial paths around the world | Both satellite and terrestrial links have been verified | high | The probabilities of incidence and mean precipitation for cells and debris are difficult to determine | |
| [95] | Experimental dataset | The experimental results show that the method show less error probability. | medium | Needs 1 min rainfall rate | |
| [62] | DBSG3 databank | Although the model does not outperform the existing ITU-R model (approximately 2.4% error), it supports a few additional facilities (e.g., site diversity) and takes account of the interference due to hydrometer scattering | high | The correctness is limited by the local values of input parameters like the melting layer and the rain plateau value, which might not be available everywhere | |
| FADE | [96] | Experimental dataset | Validated with | low | — |
| [97] | ✗ | Validated in Kolkata, India, with experimental set-up | low | To use fade margin data it needs to remove tropospheric scintillation | |
| [99] | Only experimental dataset | The resulted output agrees with the measured standard deviation of attenuation | low | The method was tested only at 10.982 GHz | |
| [98] | NM | Validated in [140,141] | low | Applicable for limited elevation angle 5–60 | |
| LB | [100] | Durban, South Africa | The model was not validated with standard DSDB3 or CCIR rain databanks | — | The model was not tested with established well-known rain databanks like DBSG3 or CCIR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samad, M.A.; Diba, F.D.; Choi, D.-Y. A Survey of Rain Fade Models for Earth–Space Telecommunication Links—Taxonomy, Methods, and Comparative Study. Remote Sens. 2021, 13, 1965. https://doi.org/10.3390/rs13101965
Samad MA, Diba FD, Choi D-Y. A Survey of Rain Fade Models for Earth–Space Telecommunication Links—Taxonomy, Methods, and Comparative Study. Remote Sensing. 2021; 13(10):1965. https://doi.org/10.3390/rs13101965
Chicago/Turabian StyleSamad, Md Abdus, Feyisa Debo Diba, and Dong-You Choi. 2021. "A Survey of Rain Fade Models for Earth–Space Telecommunication Links—Taxonomy, Methods, and Comparative Study" Remote Sensing 13, no. 10: 1965. https://doi.org/10.3390/rs13101965
APA StyleSamad, M. A., Diba, F. D., & Choi, D.-Y. (2021). A Survey of Rain Fade Models for Earth–Space Telecommunication Links—Taxonomy, Methods, and Comparative Study. Remote Sensing, 13(10), 1965. https://doi.org/10.3390/rs13101965