Maneuvering Target Detection Based on Subspace Subaperture Joint Coherent Integration

Abstract

Range cell migration and Doppler frequency migration induced by the target maneuverability are two difficulties of target signal enhancement and radar detection performance. In order to resolve them, a novel subaperture joint coherent integration (SJCI) algorithm is proposed in this article, which consists of three stages. Firstly, it divides the target signal into several subapertures, in which the Doppler frequency dispersions can be neglected. Afterward, coherent integration within each subaperture is implemented via scaled Fourier transform. Finally, correcting the Doppler frequency shifts and phase differences via axis rotation and phase compensation technology, the joint coherent integration among the subapertures can be achieved effectively. Based on the SJCI algorithm, an upgrade algorithm named subspace SJCI (SSJCI) is presented. Through acceleration space division and subspace translation, the SSJCI algorithm extends the subaperture time and optimizes the computation complexity significantly. Theoretical analyses and performance comparisons demonstrate that the SSJCI algorithm can accomplish a good trade-off among signal-to-noise ratio gain, detection capability, resolution, and computation complexity. In addition, the results of the numerical experiments further verify the effectiveness of the proposed algorithm.

1. Introduction

In recent years, a large number of weak, high-speed, and high-maneuvering targets have emerged, which is a great challenge for radar detection and parameter estimation. According to the current research, long-time integration-based algorithms can effectively accumulate their echo energy and improve the radar performance [1,2,3,4,5,6]. On the basis of the phase information utilization, they can be categorized into two kinds: incoherent integration and coherent integration [7,8]. In general, incoherent integration-based algorithms are relatively easy to implement because they do not need to achieve phase adjustments. Nevertheless, the possible signal-to-noise ratio (SNR) loss makes them unsuitable for the low SNR scenario. By contrast, coherent-integration-based algorithms are more advantageous, which have received rapid developments in the past decades. However, superior coherent-integration-based algorithms must resolve two main problems induced by the target maneuverability, i.e., range cell migration (RCM) and Doppler frequency migration (DFM) [9,10,11,12].

Keystone transform (KT) [13,14], axis rotation (AR) [15,16], and Radon Fourier transform (RFT) [17,18,19] are three conventional methods, which can effectively address RCM and achieve coherent integration for the target with uniform velocity. However, they are invalid for the high-order maneuvering target because they cannot cope with DFM. In a phased-array radar system, some methods are developed to resolve RCM. For example, the authors of [20] divide the high-range resolution range profiles into low-range resolution segments, and the authors of [21] formulate the detection problem as a multiple hypothesis test and solve it with model order selection rules. Furthermore, the code phase migration effect similar to RCM, which is induced by the motion in the direct-sequence spread-spectrum signal, is analyzed detailedly in [22].

As for DFM compensation, several representative algorithms are presented, including fractional Fourier transform (FRFT) [23] and Lv’s distribution (LVD) [24]. In the face of accelerated targets, some methods are generated via combing the RCM and DFM compensation algorithms directly, for example, second-order KT-FRFT (SKT-FRFT) [25] and improved AR-FRFT (IAR-FRFT) [26]. Apparently, in these methods, the DFM correction performance may be affected by the previous RCM correction process. In order to eliminate them simultaneously, several Radon-based methods are proposed, including generalized RFT (GRFT) [27], Radon FRFT (RFRFT) [28], and Radon LVD (RLVD) [29]. These methods obtain excellent integration performance via three-dimensional (3-D) ergodic searching in the parameter space. Unfortunately, with the extension of the 3-D parameter space, their computation complexities may become large. In addition, the blind speed side lobe may induce severe false alarm. These issues greatly limit their applications. In order to avoid searching, a variety of correlation-function-based methods are researched, including adjacent cross-correlation function (ACCF)-based [30] methods, 3-D scaled transform (TDST) [31], and 3-D coherent integration (TDCI) [32]. Nevertheless, due to the applications of the correlation functions, these methods may not be appropriate for the low SNR scenario. Moreover, the cross-terms may appear in these methods, degrading their performances.

In addition to incoherent integration and coherent integration, several methods between them are studied, including hybrid integration (HI) [33] and subspace HI (SHI) [34]. They divide the radar echoes into several subapertures. In each subaperture, the target signal stays in a single range and Doppler unit so that it can be coherently integrated via moving target detection (MTD) technology directly without any compensation. Afterward, incoherent integration is adopted among the subapertures to achieve signal enhancement further. These methods strike a good balance between integration performance and computation complexity. However, their anti-noise performance relies heavily on the subaperture length. Therefore, they may be inappropriate for the low SNR scenario also.

In this article, we propose a novel subaperture joint coherent integration (SJCI) algorithm. It divides the target signal into several subapertures, in which the proper subaperture time guarantees the Doppler frequency concentration. Thereafter, it cancels the RCM and DFM issues and achieves full coherent integrations within and among the subapertures. Therefore, the SJCI algorithm acquires significant SNR gain. Based on the SJCI algorithm, we present an upgrade algorithm, i.e., subspace SJCI (SSJCI) algorithm. Its core ideas are acceleration space division (ASD) and subspace translation (ST), which help to extend the subaperture time, optimize the detection accuracy and reduce the computation complexity. Theoretical analyses and performance comparisons are provided, leading us to the conclusion that the SSJCI algorithm can accomplish a good compromise among SNR gain, detection performance, resolution, and computation complexity. Finally, numerical experiments are carried out, which further prove the effectiveness of the SSJCI algorithm.

The remainder of this article is organized in the following manner: Section 2 establishes the mathematical model for the received target signal. Section 3 presents the theory of the SJCI algorithm. In Section 4, the SSJCI algorithm is proposed. In Section 5, theoretical subaperture time, SNR gain, detection performance, resolution, and computation complexity are analyzed and compared. In Section 6, some numerical experiments are carried out to demonstrate the effectiveness and advantages of the SSJCI algorithm. Finally, conclusions are drawn in Section 7.

Notation 1.

In the sequel, variables are denoted by the symbols in italics. Invariants and functions are denoted by the symbols in non-italics. The symbols$|·|$, $\otimes$, $\max (·)$, and${(·)}^{-1}$denote modulus value, convolution, maximum value, and inverse function, respectively.$[·,·]$and$\{·,·,\cdots ,·\}$denote interval and set, respectively.

2. Mathematical Model

Suppose the radar transmits a linear frequency modulated signal, which has the following form

$$S_{\mathrm{t}}\left(t\right)=\mathrm{rect}\left(\frac{t}{T_{\mathrm{P}}}\right)\exp \left[j2\pi \left(f_{\mathrm{c}}t+\frac{1}{2}\gamma t^2\right)\right],$$

(1)

where t denotes the fast time variable, $\mathrm{rect}\left(\frac{t}{T_{\mathrm{P}}}\right)=\left\{\begin{array}{ccc}\hfill 1& ,\hfill & \hfill \left|t\right|\le T_{\mathrm{P}}/2,\\ \hfill 0& ,\hfill & \hfill \left|t\right|>T_{\mathrm{P}}/2.\end{array}\right.$ denotes the rectangular pulse function, $T_{\mathrm{P}}$ denotes the time width, $f_{\mathrm{c}}$ denotes the carrier frequency, and $\gamma$ denotes the chirp rate.

Suppose that K maneuvering targets appear in the radar surveillance area. The received echoes from them can be formulated as

$$S_{\mathrm{r}}(t,t_{\mathrm{m}})=\sum _{k=1}^K{A}_k\mathrm{rect}\left(\frac{t-{\tau }_k}{T_{\mathrm{P}}}\right)\exp \left[j2\pi \left(f_{\mathrm{c}}(t-{\tau }_k)+\frac{1}{2}\gamma {(t-{\tau }_k)}^2\right)\right],$$

(2)

where $t_{\mathrm{m}}\in [0,T]$ denotes the azimuth slow time variable, T denotes the integration time, $A_k$ denotes the backscatter coefficient of the k-th target, $k\in \{1,···,K\}$, ${\tau }_k=\frac{2R_k\left(t_{\mathrm{m}}\right)}{c}$ denotes the time delay, $R_k\left(t_{\mathrm{m}}\right)$ denotes the instantaneous radial range between the k-th target and the radar, and c denotes the speed of light.

After down-conversion by multiplying Equation (2) with the reference signal $\exp (-j2\pi f_{\mathrm{c}}t)$, we obtain

$$S_{\mathrm{b}}(t,t_{\mathrm{m}})=\sum _{k=1}^K{A}_k\mathrm{rect}\left(\frac{t-{\tau }_k}{T_{\mathrm{P}}}\right)\exp \left[j2\pi \left(-f_{\mathrm{c}}{\tau }_k+\frac{1}{2}\gamma {(t-{\tau }_k)}^2\right)\right].$$

(3)

By performing pulse compression in the time domain, one has

$$\begin{array}{cc}\hfill S_{\mathrm{pc}}(t,t_{\mathrm{m}})& =S_{\mathrm{b}}(t,t_{\mathrm{m}})⨂\mathrm{rect}\left(\frac{t}{T_{\mathrm{P}}}\right)\exp (-j\pi \gamma t^2)\hfill \\ \hfill & =\sum _{k=1}^K{A}_{1k}\mathrm{sinc}\left[B(t-{\tau }_k)\right]\exp (-j2\pi f_{\mathrm{c}}{\tau }_k),\hfill \end{array}$$

(4)

where ⨂ denotes convolution operation, $A_{1k}$ denotes the amplitude after pulse compression, $\mathrm{sinc}(·)$ denotes the sinc function, and B denotes the bandwidth.

In order to simplify the mathematical model, we ignore the motion higher than acceleration. Then $R_k\left(t_{\mathrm{m}}\right)$ can be approximately expressed as

$$R_k\left(t_{\mathrm{m}}\right)=R_{0k}+v_k{t}_{\mathrm{m}}+\frac{1}{2}{a}_k{t}_{\mathrm{m}}^2,$$

(5)

where $R_{0k}$ denotes the initial radial range between the k-th target and the radar, $v_k$ and $a_k$ denote the radial velocity and acceleration, respectively.

Substituting Equation (5) into (4), we obtain

$$S_{\mathrm{pc}}(t,t_{\mathrm{m}})=\sum _{k=1}^K{A}_{1k}\mathrm{sinc}\left[B(t-\frac{2R_{0k}+2v_k{t}_{\mathrm{m}}+a_k{t}_{\mathrm{m}}^2}{c})\right]\exp \left(-j2\pi f_{\mathrm{c}}\frac{2R_{0k}+2v_k{t}_{\mathrm{m}}+a_k{t}_{\mathrm{m}}^2}{c}\right).$$

(6)

Then the Doppler frequency of the k-th target can be acquired, expressed as

$$f_{\mathrm{D}}=-\frac{2v_k+2a_k{t}_{\mathrm{m}}}{\lambda },$$

(7)

where $\lambda =c/f_{\mathrm{c}}$ denotes the wavelength.

It is observed from Equations (6) and (7) that due to the maneuverabilities, the envelopes and the Doppler frequencies of the targets are varying with the slow time variable, i.e., both RCM and DFM occur, which will greatly deteriorate the integration performance. Thus, they must be resolved.

3. SJCI Algorithm

By performing Fourier transform (FT) to Equation (6) with respect to t, the signal is transformed into the range frequency domain, expressed as

$$\begin{array}{cc}\hfill S_{\mathrm{f}}(f,t_{\mathrm{m}})& ={\mathrm{FT}}_t\left[S_{\mathrm{pc}}(t,t_{\mathrm{m}})\right]\hfill \\ \hfill & =\sum _{k=1}^K{A}_{2k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}+2v_k{t}_{\mathrm{m}}+a_k{t}_{\mathrm{m}}^2}{c}\right],\hfill \end{array}$$

(8)

where f denotes the range frequency variable, ${\mathrm{FT}}_t[·]$ denotes the FT operation with respect to t, and $A_{2k}$ denotes the amplitude in the range frequency domain.

Inspired by the HI algorithm [33], we divide the integration time T into $P_{\mathrm{SJCI}}$ subapertures to weaken the impacts of the accelerations. In each subaperture, the integration time can be calculated as

$$T_{\mathrm{SJCI}}=\frac{T}{P_{\mathrm{SJCI}}}.$$

(9)

Then, a 3-D signal is formed by the subapertures, which is expressed as

$$\begin{array}{cc}\hfill S_{\mathrm{s}}(f,t_{\mathrm{s}},{\tau }_{\mathrm{s}})& ={\mathrm{DIV}}_{P_{\mathrm{SJCI}}}\left[S_{\mathrm{f}}(f,t_{\mathrm{m}})\right]\hfill \\ & =\sum _{k=1}^K{A}_{2k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}}{c}\right]\hfill \\ & \times \exp \left(-j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\frac{2v_k{t}_{\mathrm{s}}+2a_k{t}_{\mathrm{s}}{\tau }_{\mathrm{s}}+a_k{t}_{\mathrm{s}}^2}{\lambda }\right)\exp \left(-j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\frac{2v_k{\tau }_{\mathrm{s}}+a_k{\tau }_{\mathrm{s}}^2}{\lambda }\right),\hfill \end{array}$$

(10)

where $t_{\mathrm{s}}\in [0,T_{\mathrm{SJCI}}]$ denotes the slow time variable in the subaperture, ${\tau }_{\mathrm{s}}=\{0,T_{\mathrm{SJCI}},2T_{\mathrm{SJCI}},···,(P_{\mathrm{SJCI}}-1)T_{\mathrm{SJCI}}\}$ denotes the lag time variable generated by the division operation, and ${\mathrm{DIV}}_{P_{\mathrm{SJCI}}}[·]$ denotes the division operation.

Define the acceleration space by $A_{\mathrm{space}}=[a_{\mathrm{L}},a_{\mathrm{R}}]$, where $a_{\mathrm{L}}$ and $a_{\mathrm{R}}$ denote its lower and upper boundaries, respectively. While $T_{\mathrm{SJCI}}$ satisfies the condition given in Equation (11), Equation (10) can be simplified, as expressed as Equation (12).

$$\frac{2a_{\max }{T}_{\mathrm{SJCI}}}{\lambda }<\frac{1}{T_{\mathrm{SJCI}}},$$

(11)

$$\begin{array}{cc}\hfill S_{\mathrm{s}}(f,t_{\mathrm{s}},{\tau }_{\mathrm{s}})=\sum _{k=1}^K& A_{2k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}}{c}\right]\hfill \\ & \times \exp \left(-j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\frac{2v_k{t}_{\mathrm{s}}+2a_k{t}_{\mathrm{s}}{\tau }_{\mathrm{s}}}{\lambda }\right)\exp \left(-j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\frac{2v_k{\tau }_{\mathrm{s}}+a_k{\tau }_{\mathrm{s}}^2}{\lambda }\right),\hfill \end{array}$$

(12)

where $a_{\max }=\max \left\{\right|a_{\mathrm{L}}|,|a_{\mathrm{R}}\left|\right\}$ denotes the maximum acceleration.

Obviously, the second-order term with respect to $t_{\mathrm{s}}$ in Equation (10) is neglected. Thus, the coherent integration along $t_s$-axis can be accomplished by scaled FT (SFT), expressed as

$$\begin{array}{cc}\hfill S_{\mathrm{SFT}}(f,f_{\mathrm{t}},{\tau }_{\mathrm{s}})& ={\mathrm{SFT}}_{t_{\mathrm{s}}}\left[S_{\mathrm{s}}(f,t_{\mathrm{s}},{\tau }_{\mathrm{s}})\right]\hfill \\ & =\int S_{\mathrm{s}}(f,t_{\mathrm{s}},{\tau }_{\mathrm{s}})\exp \left(j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}{f}_{\mathrm{t}}{t}_{\mathrm{s}}\right)d{t}_{\mathrm{s}}\hfill \\ & =\sum _{k=1}^K{A}_{3k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}}{c}\right]\exp \left(-j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\frac{2v_k{\tau }_{\mathrm{s}}+a_k{\tau }_{\mathrm{s}}^2}{\lambda }\right)\hfill \\ & \times \mathrm{sinc}\left[T_{\mathrm{SJCI}}\left(f_{\mathrm{t}}-\frac{2v_k+2a_k{\tau }_{\mathrm{s}}}{\lambda }\right)\right],\hfill \end{array}$$

(13)

where $f_{\mathrm{t}}$ denotes the scaled Doppler frequency variable, ${\mathrm{SFT}}_{t_{\mathrm{s}}}[·]$ denotes SFT operation with respect to $t_{\mathrm{s}}$, and $A_{3k}$ denotes the amplitude after SFT operation.

It can be observed from Equation (13) that the energies of the target signals are concentrated into planes $f_{\mathrm{t}}=\frac{2v_i+2a_i{\tau }_{\mathrm{s}}}{\lambda }(i=1,2,···,K)$, which are not parallel to the $f-{\tau }_{\mathrm{s}}$ plane. Thus, they cannot acquire further coherent integrations. In order to correct the planes, AR operation is employed, which is expressed as

$$S_{\mathrm{AR}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}})={\mathrm{AR}}_{k_{\mathrm{a}}}\left[S_{\mathrm{SFT}}(f,f_{\mathrm{t}},{\tau }_{\mathrm{s}})\right]=S_{\mathrm{SFT}}\left(f,f_{\mathrm{t}}-k_{\mathrm{a}}{\tau }_{\mathrm{s}},{\tau }_{\mathrm{s}}\right),$$

(14)

where $f_{\mathrm{t}}^{\prime }$ denotes the rotated scaled Doppler frequency variable, ${\mathrm{AR}}_{k_{\mathrm{a}}}[·]$ denotes the AR operation with respect to $k_{\mathrm{a}}$, and $k_{\mathrm{a}}$ denotes the rotation factor.

Thereafter, phase compensation technology is adopted, expressed as

$$S_{\mathrm{com}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}})=S_{\mathrm{AR}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}})\exp \left[j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\left(\frac{k_{\mathrm{a}}{\tau }_{\mathrm{s}}^2}{2}+f_{\mathrm{t}}^{\prime }{\tau }_{\mathrm{s}}\right)\right].$$

(15)

When $k_{\mathrm{a}}=\frac{2a_k}{\lambda }$, Equation (15) can be written as

$$\begin{array}{cc}\hfill S_{\mathrm{com}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}})=& A_{3k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}}{c}\right]\exp \left[j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right){\tau }_{\mathrm{s}}\right]\hfill \\ & \times \mathrm{sinc}\left[T_{\mathrm{SJCI}}\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right]+S_{\mathrm{com}-\mathrm{others}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}}),\hfill \end{array}$$

(16)

where $S_{\mathrm{com}-\mathrm{others}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}})$ denotes the acceleration-uncompensated target signals.

Then, the energy along the ${\tau }_{\mathrm{s}}$-axis can be accumulated via the complex addition operation. Accordingly, the dimension is reduced, represented as

$$\begin{array}{cc}\hfill S_{\mathrm{add}}(f,f_{\mathrm{t}}^{\prime })& ={\mathrm{add}}_{{\tau }_{\mathrm{s}}}\left[S_{\mathrm{com}}(f,f_{\mathrm{t}}^{\prime },{\tau }_{\mathrm{s}})\right]\hfill \\ \hfill & =A_{4k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}}{c}\right]\mathrm{sinc}\left[T\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right]\hfill \\ \hfill & \times \mathrm{sinc}\left[T_{\mathrm{SJCI}}\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right]+S_{\mathrm{add}-\mathrm{others}}(f,f_{\mathrm{t}}^{\prime }),\hfill \end{array}$$

(17)

where ${\mathrm{add}}_{{\tau }_{\mathrm{s}}}[·]$ denotes the complex addition operation with respect to ${\tau }_{\mathrm{s}}$, $A_{4k}$ denotes the amplitude after the complex addition operation, $S_{\mathrm{add}-\mathrm{others}}(f,f_{\mathrm{t}}^{\prime })$ denotes the acceleration-uncompensated target signals.

Finally, the coherent integration along the f-axis can be achieved via inverse FT (IFT), expressed as Equation (18).

$$\begin{array}{cc}\hfill S_{\mathrm{IFT}}(t^{\prime },f_{\mathrm{t}}^{\prime })& ={\mathrm{IFT}}_f\left[S_{\mathrm{add}}(f,f_{\mathrm{t}}^{\prime })\right]\hfill \\ \hfill & =\int S_{\mathrm{add}}(f,f_{\mathrm{t}}^{\prime })\exp \left(j2\pi f{t}^{\prime }\right)df\hfill \\ \hfill & =A_{5k}\exp \left[-j2\pi \frac{2R_{0k}}{\lambda }\right]\mathrm{sinc}\left[B\left(t^{\prime }-\frac{2R_{0k}}{c}\right)\right]\mathrm{sinc}\left[T\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right]\hfill \\ \hfill & \times \mathrm{sinc}\left[T_{\mathrm{SJCI}}\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right]+S_{\mathrm{IFT}-\mathrm{others}}(t^{\prime },f_{\mathrm{t}}^{\prime }),\hfill \end{array}$$

(18)

where $t^{\prime }$ denotes the new fast time variable, ${\mathrm{IFT}}_f[·]$ denotes the IFT function with respect to f, $A_{5k}$ denotes the amplitude after IFT operation, and $S_{\mathrm{IFT}-\mathrm{others}}(t^{\prime },f_{\mathrm{t}}^{\prime })$ denotes the acceleration-uncompensated target signals.

In order to illustrate the procedures above clearly, the target signal energy distributions by different processing stages are given in Figure 1, where the dark shadings represent the target signal energy.

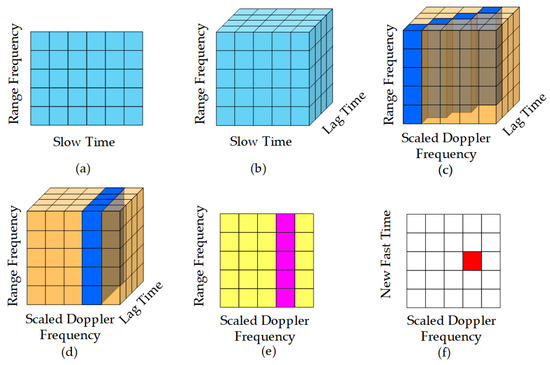
Figure 1. Target signal energy distributions by different processing stages: (a) target signal energy distribution in the range frequency domain; (b) target signal energy distribution in the subapertures; (c) target signal energy distribution after SFT operation; (d) target signal energy distribution after AR operation; (e) target signal energy distribution after phase compensation and complex addition operations; (f) target signal energy distribution after IFT operation.

It can be observed from Equation (18) that when $k_{\mathrm{a}}=\frac{2a_k}{\lambda }$, the k-th target signal is well focused by the SJCI algorithm, whereas due to the influences of the mismatched accelerations, the other target signals cannot. Therefore, in order to guarantee effective integrations for all the targets, the SJCI algorithm needs to traverse the acceleration space, which can be represented as

$$\begin{array}{cc}\hfill & S_{\mathrm{SJCI}}(t^{\prime },f_{\mathrm{t}}^{\prime },a_{\mathrm{p}})\hfill \\ \hfill & ={\mathrm{IFT}}_f\left[{\mathrm{add}}_{{\tau }_{\mathrm{s}}}\left[{\mathrm{AR}}_{\frac{2a_{\mathrm{p}}}{\lambda }}\left[{\mathrm{SFT}}_{t_{\mathrm{s}}}\left[{\mathrm{DIV}}_{P_{\mathrm{SJCI}}}\left[S_{\mathrm{f}}(f,t_{\mathrm{m}})\right]\right]\right]\exp \left[j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\left(\frac{a_{\mathrm{p}}}{\lambda }{\tau }_{\mathrm{s}}^2+f_{\mathrm{t}}^{\prime }{\tau }_{\mathrm{s}}\right)\right]\right]\right],\hfill \end{array}$$

(19)

where $a_{\mathrm{p}}\in A_{\mathrm{space}}$ denotes the potential acceleration.

Obviously, by going through the acceleration space, the SJCI algorithm generates a 3-D domain, where all the target signals can be effectively integrated into distinct peaks whose coordinates reflect their motion parameters accurately. For instance, the k-th target is integrated in $(\frac{2R_{0k}}{c},\frac{2v_k}{\lambda },a_k)$, by which $R_{0k}$, $v_k$, and $a_k$ can be estimated. The flow chart of the SJCI algorithm is given in Figure 2.

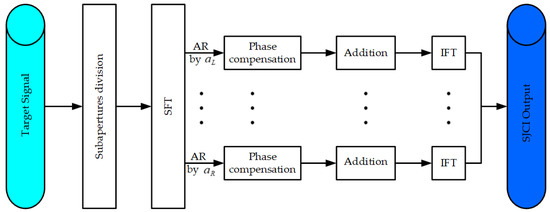
Figure 2. The flow chart of the SJCI algorithm.

In terms of the fast-moving target, due to the limited pulse repetition frequency $F_{\mathrm{p}}$, Doppler ambiguity may occur. In this case, $v_k$ should be rewritten as

$$v_k=v_{0k}+N_k{v}_{\mathrm{b}},$$

(20)

where $v_{0k}$ denotes the base band velocity of $v_k$, $N_k$ denotes the fold factor, and $v_{\mathrm{b}}=\frac{F_{\mathrm{p}}\lambda }{2}$ denotes the blind velocity.

Substituting Equation (20) and the special relationship $\exp \left(j2\pi \frac{2N_k{v}_{\mathrm{b}}{t}_{\mathrm{m}}}{\lambda }\right)=1$ into Equation (8), one has

$$\begin{array}{c}\hfill S_{\mathrm{f}}(f,t_{\mathrm{m}})=\sum _{k=1}^K{A}_{2k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}+2v_{0k}{t}_{\mathrm{m}}+a_k{t}_{\mathrm{m}}^2}{c}\right]\exp \left(-j2\pi f\frac{2N_k{v}_{\mathrm{b}}{t}_{\mathrm{m}}}{c}\right).\end{array}$$

(21)

Under this circumstance, the SJCI algorithm cannot be used directly. Thus, before the SJCI algorithm, the Doppler ambiguity must be compensated. Define a normalized matched filtering function as

$$H_{N_k}(f,t_{\mathrm{m}})=\exp \left(j2\pi f\frac{2N_k{v}_{\mathrm{b}}{t}_{\mathrm{m}}}{c}\right).$$

(22)

Multiplying Equation (21) with (22), one has

$$\begin{array}{cc}\hfill S_{\mathrm{MF}}(f,t_{\mathrm{m}})& =S_{\mathrm{f}}(f,t_{\mathrm{m}})H_{N_k}(f,t_{\mathrm{m}})\hfill \\ \hfill & =A_{2k}\mathrm{rect}\left(\frac{f}{B}\right)\exp \left[-j2\pi (f+f_{\mathrm{c}})\frac{2R_{0k}+2v_{0k}{t}_{\mathrm{m}}+a_k{t}_{\mathrm{m}}^2}{c}\right]+S_{\mathrm{MF}-\mathrm{others}}(f,t_{\mathrm{m}}),\hfill \end{array}$$

(23)

where $S_{\mathrm{MF}-\mathrm{others}}(f,t_{\mathrm{m}})$ denotes the ambiguity-uncompensated target signals.

It can be observed that the Doppler ambiguity of the k-th target is canceled by the simple multiplication. Afterward, the SJCI algorithm can be utilized normally. Notably, in order to guarantee the effective integrations for all the targets, a few searches for the fold factors based on the potential velocities are needed, which may increase the computation cost to some extent.

4. SSJCI Algorithm

According to the theory of the SJCI algorithm, the maximum acceleration determines the subaperture time. Large maximum accelerations lead to short subaperture times, few sampling points, and poor detection accuracies. In this situation, supply-zero operation for the subapertures is always needed to satisfy the detection accuracy requirement, which may induce a massive computation burden. In order to address this issue, we propose the SSJCI algorithm in this section, where ASD and ST operations are accomplished to reduce the maximum acceleration. In this way, the subaperture time is extended, the sampling points are increased, and the detection accuracy is improved, which reduce or even cancel the supply-zero operation, relieving the calculating pressure to some extent. It is proved in Section 5 that with the same detection accuracy, the SSJCI algorithm can inherit all the advantages of the SJCI algorithm with lower computation complexity. Therefore, the SSJCI algorithm can be considered as an upgrade of the SJCI algorithm. Detailed steps of the SSJCI algorithm are given as follows.

Step 1. Divide the acceleration space $A_{\mathrm{space}}$ into $K_{\mathrm{SSJCI}}$ subspaces by ASD operation, expressed as Equation (24). The diagram of ASD operation is shown in Figure 3a. The length of each subspace is $\Delta a_{\mathrm{SSJCI}}=\frac{a_{\mathrm{R}}-a_{\mathrm{L}}}{K_{\mathrm{SSJCI}}}$.

$$\begin{array}{c}\hfill A_{\mathrm{space}}\stackrel{\mathrm{ASD}}{⟶}\{A_{\mathrm{sub}-1},A_{\mathrm{sub}-2},···,A_{\mathrm{sub}-i},···,A_{\mathrm{sub}-K_{\mathrm{SSJCI}}}\},\end{array}$$

(24)

where $A_{\mathrm{sub}-i}=[a_{\mathrm{L}}+(i-1)▵a_{\mathrm{SSJCI}},a_{\mathrm{L}}+i▵a_{\mathrm{SSJCI}}]$ denotes the i-th subspace, $i\in \{1,2,\cdots ,K_{\mathrm{SSJCI}}\}$.

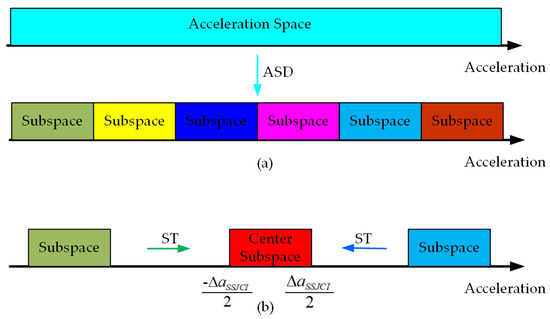
Figure 3. The diagrams of ASD and ST operations: (a) the diagram of ASD operation; (b) the diagram of ST operation.

Step 2. Translate the subspaces to the center subspace $A_{\mathrm{center}}=[-\frac{▵a_{\mathrm{SSJCI}}}{2},\frac{▵a_{\mathrm{SSJCI}}}{2}]$ by ST operation. The diagram of the ST operation is shown in Figure 3b. In this way, the maximum acceleration is maximally decreased to $\frac{▵a_{\mathrm{SSJCI}}}{2}$. Accordingly, the constraint condition given in Equation (11) is changed into Equation (25), where the subaperture time $T_{\mathrm{SSJCI}}$ is effectively improved.

$$\frac{▵a_{\mathrm{SSJCI}}{T}_{\mathrm{SSJCI}}}{\lambda }<\frac{1}{T_{\mathrm{SSJCI}}}.$$

(25)

The translation amounts can be expressed as

$$\{a_{\mathrm{ta}-1},a_{\mathrm{ta}-2},\cdots ,a_{\mathrm{ta}-i},···,a_{\mathrm{ta}-K_{\mathrm{SSJCI}}}\},$$

(26)

where $a_{\mathrm{ta}-i}$ denotes the translation amount of the i-th subspace, which can be calculated by

$$a_{\mathrm{ta}-i}=a_{\mathrm{L}}+\left(i-\frac{1}{2}\right)▵a_{\mathrm{SSJCI}}.$$

(27)

Corresponding to each subspace, the target signal must be compensated by the translation amount. For instance, the compensation for the i-th subspace can be expressed as

$$S_{\mathrm{f}-i}(f,t_{\mathrm{m}})=S_{\mathrm{f}}(f,t_{\mathrm{m}})\exp \left[j2\pi (f+f_{\mathrm{c}})\frac{a_{\mathrm{ta}-i}{t}_{\mathrm{m}}^2}{c}\right].$$

(28)

Step 3. Implement the SJCI algorithm on every subspace and acquire the SJCI results.

$$\begin{array}{cc}& S_{\mathrm{SJCI}}^i(t^{\prime },f_{\mathrm{t}}^{\prime },a_{\mathrm{pc}})\hfill \\ & ={\mathrm{IFT}}_f\left[{\mathrm{add}}_{{\tau }_{\mathrm{s}}}\left[{\mathrm{AR}}_{\frac{2a_{\mathrm{pc}}}{\lambda }}\left[{\mathrm{SFT}}_{t_{\mathrm{s}}}\left[{\mathrm{DIV}}_{P_{\mathrm{SSJCI}}}\left[S_{\mathrm{f}-i}\right(f,t_{\mathrm{m}}\left)\right]\right]\right]\exp \left[j2\pi \frac{f+f_{\mathrm{c}}}{f_{\mathrm{c}}}\left(\frac{a_{\mathrm{pc}}}{\lambda }{\tau }_{\mathrm{s}}^2+f_{\mathrm{t}}^{\prime }{\tau }_{\mathrm{s}}\right)\right]\right]\right],\hfill \end{array}$$

(29)

where $a_{\mathrm{pc}}\in A_{\mathrm{center}}$ denotes the potential acceleration in the center subspace, and $P_{\mathrm{SSJCI}}=\frac{T}{T_{\mathrm{SSJCI}}}$ denotes the number of the subapertures in the SSJCI algorithm.

Step 4. Rearrange the SJCI results by order of the subspaces and output the SSJCI result $S_{\mathrm{SSJCI}}(t^{\prime },f_{\mathrm{t}}^{\prime },a_{\mathrm{p}})$. The flow chart of the SSJCI algorithm is given in Figure 4.

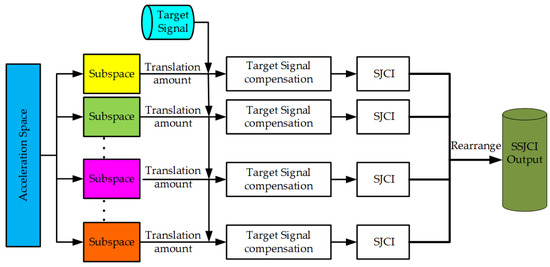
Figure 4. The flow chart of the SSJCI algorithm.

5. Theoretical Analyses and Performance Comparisons

In this section, the performances of HI, SHI, SJCI, SSJCI, and GRFT algorithms are analyzed and compared theoretically. Specifically, the five compared aspects are subaperture time, SNR gain, detection probability, resolution, and computation complexity, respectively.

5.1. Subaperture Time

The subaperture time of the HI algorithm denoted as $T_{\mathrm{HI}}$ is constrained by [33]

$$\begin{array}{cc}\hfill v_{\max }{T}_{\mathrm{HI}}+\frac{1}{2}{a}_{\max }{T}_{\mathrm{HI}}^2& <\frac{c}{2F_{\mathrm{s}}}\hfill \\ \hfill \frac{2a_{\max }{T}_{\mathrm{HI}}}{\lambda }& <\frac{1}{T_{\mathrm{HI}}},\hfill \end{array}$$

(30)

where $v_{\max }$ and $a_{\max }$ denote the maximum radial velocity and acceleration, respectively, $F_{\mathrm{s}}$ denotes the sampling frequency.

The subaperture time of the SHI algorithm denoted as $T_{\mathrm{SHI}}$ is constrained by [34]

$$\begin{array}{cc}\hfill \frac{1}{2}\left(▵v_{\mathrm{SHI}}{T}_{\mathrm{SHI}}+\frac{1}{2}▵a_{\mathrm{SHI}}{T}_{\mathrm{SHI}}^2\right)& <\frac{c}{2F_{\mathrm{s}}}\hfill \\ \hfill \frac{▵a_{\mathrm{SHI}}{T}_{\mathrm{SHI}}}{\lambda }& <\frac{1}{T_{\mathrm{SHI}}},\hfill \end{array}$$

(31)

where $▵v_{\mathrm{SHI}}$ and $▵a_{\mathrm{SHI}}$ denote the lengths of the velocity and acceleration subintervals, respectively.

The SHI algorithm is an upgrade for the HI algorithm, where $\frac{1}{2}▵v_{\mathrm{SHI}}\le v_{\max }$ and $\frac{1}{2}▵a_{\mathrm{SHI}}\le a_{\max }$. Thus, $T_{\mathrm{SHI}}\ge T_{\mathrm{HI}}$. The subaperture times of SJCI and SSJCI algorithms are constrained by Equations (11) and (25), where $\frac{1}{2}▵a_{\mathrm{SSJCI}}\le a_{\max }$. Obviously, $T_{\mathrm{SSJCI}}\ge T_{\mathrm{SJCI}}$. Due to the absence of the velocity constraint, $T_{\mathrm{SJCI}}\ge T_{\mathrm{HI}}$. Similarly, under the circumstance that $▵a_{\mathrm{SHI}}=▵a_{\mathrm{SSJCI}}$, $T_{\mathrm{SSJCI}}\ge T_{\mathrm{SHI}}$. Thanks to the complete aperture, the GRFT algorithm has the best subaperture time $T_{\mathrm{GRFT}}=T$. Since $T_{\mathrm{SJCI}}$ and $T_{\mathrm{SHI}}$ cannot be compared directly, we sort the subaperture times of the five algorithms by the following two orders

$$T_{\mathrm{GRFT}}\ge T_{\mathrm{SSJCI}}\ge T_{\mathrm{SHI}}\ge T_{\mathrm{HI}},$$

(32)

$$T_{\mathrm{GRFT}}\ge T_{\mathrm{SSJCI}}\ge T_{\mathrm{SJCI}}\ge T_{\mathrm{HI}}.$$

(33)

5.2. SNR Gain

The SNR gain of the HI algorithm is calculated as

$$G_{\mathrm{SNR},\mathrm{HI}}=\frac{SN{R}_{\mathrm{HI}}}{SN{R}_{\mathrm{PC}}}=\sqrt{P_{\mathrm{HI}}}{M}_{\mathrm{HI}}=\sqrt{M{M}_{\mathrm{HI}}},$$

(34)

where $SN{R}_{\mathrm{HI}}$ and $SN{R}_{\mathrm{PC}}$ denote the SNRs after the HI algorithm and pulse compression, respectively, $P_{\mathrm{HI}}$ denotes the number of the subapertures in the HI algorithm, $M_{\mathrm{HI}}=T_{\mathrm{HI}}{F}_{\mathrm{p}}$ denotes the number of the pulses in each subaperture, $M=T{F}_{\mathrm{p}}$ denotes the total number of the pulses.

The SNR gain of the SHI algorithm is calculated as

$$G_{\mathrm{SNR},\mathrm{SHI}}=\frac{SN{R}_{\mathrm{SHI}}}{SN{R}_{\mathrm{PC}}}=\sqrt{P_{\mathrm{SHI}}}{M}_{\mathrm{SHI}}=\sqrt{M{M}_{\mathrm{SHI}}},$$

(35)

where $SN{R}_{\mathrm{SHI}}$ denotes the SNR after the SHI algorithm, $P_{\mathrm{SHI}}$ denotes the number of the subapertures in the SHI algorithm, and $M_{\mathrm{SHI}}=T_{\mathrm{SHI}}{F}_{\mathrm{p}}$ denotes the number of the pulses in each subaperture.

In SJCI, the operations acquiring SNR gains include: SFT, complex addition, and IFT operations, which can be calculated as

$$G_{\mathrm{SNR},\mathrm{SFT}}=\frac{SN{R}_{\mathrm{SFT}}}{SN{R}_{\mathrm{f}}}=M_{\mathrm{SJCI}},$$

(36)

$$G_{\mathrm{SNR},\mathrm{add}}=\frac{SN{R}_{\mathrm{add}}}{SN{R}_{\mathrm{SFT}}}=P_{\mathrm{SJCI}},$$

(37)

$$G_{\mathrm{SNR},\mathrm{IFT}}=\frac{SN{R}_{\mathrm{SJCI}}}{SN{R}_{\mathrm{add}}}=\frac{NB}{F_{\mathrm{s}}},$$

(38)

where $SN{R}_{\mathrm{f}}$ denotes the SNR after pulse compression in the range frequency domain, $SN{R}_{\mathrm{SFT}}$, $SN{R}_{\mathrm{add}}$, and $SN{R}_{\mathrm{SJCI}}$ denote the SNRs after SFT, complex addition, and SJCI operations, respectively, $M_{\mathrm{SJCI}}=T_{\mathrm{SJCI}}{F}_{\mathrm{P}}$ denotes the number of the pulses in each subaperture, $P_{\mathrm{SJCI}}$ denotes the number of the subapertures in the SJCI algorithm, and N and B denote the number of the samplings in each pulse and bandwidth, respectively.

Considering the relationship $\frac{SN{R}_{\mathrm{f}}}{SN{R}_{\mathrm{PC}}}=\frac{F_{\mathrm{s}}}{NB}$, the SNR gain of the SJCI algorithm can be obtained by

$$G_{\mathrm{SNR},\mathrm{SJCI}}=\frac{SN{R}_{\mathrm{SJCI}}}{SN{R}_{\mathrm{PC}}}=M_{\mathrm{SJCI}}\times P_{\mathrm{SJCI}}\times \frac{NB}{F_{\mathrm{s}}}\times \frac{F_{\mathrm{s}}}{NB}=M.$$

(39)

Similarly, the SNR gain of the SSJCI algorithm can be accomplished, expressed as

$$G_{\mathrm{SNR},\mathrm{SSJCI}}=\frac{SN{R}_{\mathrm{SSJCI}}}{SN{R}_{\mathrm{PC}}}=M_{\mathrm{SSJCI}}\times P_{\mathrm{SSJCI}}\times \frac{NB}{F_{\mathrm{s}}}\times \frac{F_{\mathrm{s}}}{NB}=M,$$

(40)

where $SN{R}_{\mathrm{SSJCI}}$ denotes the SNR after the SSJCI algorithm, $M_{\mathrm{SSJCI}}=T_{\mathrm{SSJCI}}{F}_{\mathrm{P}}$ denotes the number of the pulses in each subaperture, $P_{\mathrm{SSJCI}}$ denotes the number of the subapertures in the SSJCI algorithm.

In the GRFT algorithm, the SNR gain can be calculated as

$$G_{\mathrm{SNR},\mathrm{GRFT}}=\frac{SN{R}_{\mathrm{GRFT}}}{SN{R}_{\mathrm{PC}}}=M,$$

(41)

where $SN{R}_{\mathrm{GRFT}}$ denotes the SNR after the GRFT algorithm.

Considering that $T\ge T_{\mathrm{SHI}}\ge T_{\mathrm{HI}}$, the SNR gains can be easily sorted, expressed as

$$G_{\mathrm{SNR},\mathrm{GRFT}}=G_{\mathrm{SNR},\mathrm{SSJCI}}=G_{\mathrm{SNR},\mathrm{SJCI}}\ge G_{\mathrm{SNR},\mathrm{SHI}}\ge G_{\mathrm{SNR},\mathrm{HI}}.$$

(42)

5.3. Detection Probability

HI and SHI algorithms combine the coherent and incoherent integrations. After coherent integrations, the SNRs can be expressed as $M_{\mathrm{HI}}SN{R}_{\mathrm{PC}}$ and $M_{\mathrm{SHI}}SN{R}_{\mathrm{PC}}$, respectively. The square-law detectors by their incoherent integrations among $P_{\mathrm{HI}}$ and $P_{\mathrm{SHI}}$ subapertures can be represented as

$$\sum _{m=1}^{P_{\mathrm{HI}}}{\left|z_{\mathrm{HI},m}\right|}^2\begin{array}{c}\stackrel{H_1}{>}\hfill \\ \underset{H_0}{<}\hfill \end{array}{\sigma }_{\mathrm{HI}}^2{Y}_{\mathrm{HI}},$$

(43)

$$\sum _{m=1}^{P_{\mathrm{SHI}}}{\left|z_{\mathrm{SHI},m}\right|}^2\begin{array}{c}\stackrel{H_1}{>}\hfill \\ \underset{H_0}{<}\hfill \end{array}{\sigma }_{\mathrm{SHI}}^2{Y}_{\mathrm{SHI}},$$

(44)

where $z_{\mathrm{HI},m}$ and $z_{\mathrm{SHI},m}$ denote the detection samples in the m-th subaperture by the HI and SHI algorithms, respectively, $H_1$ and $H_0$ denote the target existing and nonexisting hypotheses, ${\sigma }_{\mathrm{HI}}^2$ and ${\sigma }_{\mathrm{SHI}}^2$ denote the noise variances, and $Y_{\mathrm{HI}}$ and $Y_{\mathrm{SHI}}$ denote the normalized detection thresholds.

The false alarm probability denoted as $P_{\mathrm{FA}}$ and the normalization detection thresholds can be derived in the following relationships [35].

$$P_{\mathrm{FA}}=\mathrm{F}(P_{\mathrm{HI}},Y_{\mathrm{HI}})=\sum _{m=0}^{P_{\mathrm{HI}}-1}{e}^{-Y_{\mathrm{HI}}}\frac{Y_{\mathrm{HI}}^m}{m!},$$

(45)

$$P_{\mathrm{FA}}=\mathrm{F}(P_{\mathrm{SHI}},Y_{\mathrm{SHI}})=\sum _{m=0}^{P_{\mathrm{SHI}}-1}{e}^{-Y_{\mathrm{SHI}}}\frac{Y_{\mathrm{SHI}}^m}{m!}.$$

(46)

According to the derivation given in [35], their detection probabilities can be calculated, represented as

$$P_{\mathrm{D},\mathrm{HI}}={\mathrm{Q}}_{P_{\mathrm{HI}}}(\sqrt{2P_{\mathrm{HI}}{M}_{\mathrm{HI}}SN{R}_{\mathrm{PC}}},\sqrt{2Y_{\mathrm{HI}}})={\mathrm{Q}}_{P_{\mathrm{HI}}}(\sqrt{2MSN{R}_{\mathrm{PC}}},\sqrt{2{\mathrm{F}}^{-1}(P_{\mathrm{HI}},P_{\mathrm{FA}})}),$$

(47)

$$P_{\mathrm{D},\mathrm{SHI}}={\mathrm{Q}}_{P_{\mathrm{SHI}}}(\sqrt{2P_{\mathrm{SHI}}{M}_{\mathrm{SHI}}SN{R}_{\mathrm{PC}}},\sqrt{2Y_{\mathrm{SHI}}})={\mathrm{Q}}_{P_{\mathrm{SHI}}}(\sqrt{2MSN{R}_{\mathrm{PC}}},\sqrt{2{\mathrm{F}}^{-1}(P_{\mathrm{SHI}},P_{\mathrm{FA}})}),$$

(48)

where $\mathrm{Q}(·)$ denotes the Marcum Q function, ${\mathrm{F}}^{-1}(·)$ denotes the inverse function of $\mathrm{F}(·)$.

Despite full coherent integrations, GRFT, SSJCI, and SJCI algorithms can be regarded with incoherent integration of one sampling point. Accordingly, their square-law detectors can be represented as

$$|z_{\mathrm{GRFT}}{|}^2\begin{array}{c}\stackrel{H_1}{>}\hfill \\ \underset{H_0}{<}\hfill \end{array}{\sigma }_{\mathrm{GRFT}}^2{Y}_{\mathrm{GRFT}},$$

(49)

$$|z_{\mathrm{SSJCI}}{|}^2\begin{array}{c}\stackrel{H_1}{>}\hfill \\ \underset{H_0}{<}\hfill \end{array}{\sigma }_{\mathrm{SSJCI}}^2{Y}_{\mathrm{SSJCI}},$$

(50)

$$|z_{\mathrm{SJCI}}{|}^2\begin{array}{c}\stackrel{H_1}{>}\hfill \\ \underset{H_0}{<}\hfill \end{array}{\sigma }_{\mathrm{SJCI}}^2{Y}_{\mathrm{SJCI}},$$

(51)

where $z_{\mathrm{GRFT}}$, $z_{\mathrm{SSJCI}}$, $z_{\mathrm{SJCI}}$ denote the detection samples by GRFT, SSJCI, and SJCI algorithms, respectively, ${\sigma }_{\mathrm{GRFT}}^2$, ${\sigma }_{\mathrm{SSJCI}}^2$, ${\sigma }_{\mathrm{SJCI}}^2$ denote the noise variances, and $Y_{\mathrm{GRFT}}$, $Y_{\mathrm{SSJCI}}$, $Y_{\mathrm{SJCI}}$ denote the normalized detection thresholds.

Similarly, their detection probabilities can also be obtained, expressed as

$$P_{\mathrm{D},\mathrm{GRFT}}={\mathrm{Q}}_1(\sqrt{2MSN{R}_{\mathrm{PC}}},\sqrt{2{\mathrm{F}}^{-1}(1,P_{\mathrm{FA}})}),$$

(52)

$$P_{\mathrm{D},\mathrm{SSJCI}}={\mathrm{Q}}_1(\sqrt{2MSN{R}_{\mathrm{PC}}},\sqrt{2{\mathrm{F}}^{-1}(1,P_{\mathrm{FA}})}),$$

(53)

$$P_{\mathrm{D},\mathrm{SJCI}}={\mathrm{Q}}_1(\sqrt{2MSN{R}_{\mathrm{PC}}},\sqrt{2{\mathrm{F}}^{-1}(1,P_{\mathrm{FA}})}).$$

(54)

Considering $P_{\mathrm{HI}}\ge P_{\mathrm{SHI}}\ge 1$, the detection probabilities by the same false alarm probability can be easily sorted, expressed as

$$P_{\mathrm{D},\mathrm{GRFT}}=P_{\mathrm{D},\mathrm{SSJCI}}=P_{\mathrm{D},\mathrm{SJCI}}\ge P_{\mathrm{D},\mathrm{SHI}}\ge P_{\mathrm{D},\mathrm{HI}}.$$

(55)

5.4. Resolution

The resolutions of range, velocity, and acceleration of the HI algorithm denoted as $R_{\mathrm{r},\mathrm{HI}}$, $R_{\mathrm{v},\mathrm{HI}}$, and $R_{\mathrm{a},\mathrm{HI}}$ are expressed as [36]

$$R_{\mathrm{r},\mathrm{HI}}=\frac{c}{2B},R_{\mathrm{v},\mathrm{HI}}=\frac{\lambda }{2T_{\mathrm{HI}}},R_{\mathrm{a},\mathrm{HI}}=\frac{\lambda }{P_{\mathrm{HI}}{T}_{\mathrm{HI}}^2}=\frac{\lambda }{\frac{M{T}_{\mathrm{HI}}}{F_{\mathrm{P}}}}.$$

(56)

The resolutions of range, velocity, and acceleration of the SHI algorithm denoted as $R_{\mathrm{r},\mathrm{SHI}}$, $R_{\mathrm{v},\mathrm{SHI}}$, and $R_{\mathrm{a},\mathrm{SHI}}$ are expressed as [34]

$$R_{\mathrm{r},\mathrm{SHI}}=\frac{c}{2B},R_{\mathrm{v},\mathrm{SHI}}=\frac{\lambda }{2T_{\mathrm{SHI}}},R_{\mathrm{a},\mathrm{SHI}}=\frac{\lambda }{P_{\mathrm{SHI}}{T}_{\mathrm{SHI}}^2}=\frac{\lambda }{\frac{M{T}_{\mathrm{SHI}}}{F_{\mathrm{P}}}}.$$

(57)

In order to simplify the derivation, we take the k-th target as an example to analyze the resolutions of the SJCI algorithm. Let $f_{\mathrm{t}}^{\prime }=\frac{2v_k}{\lambda }$ and $a_{\mathrm{p}}=a_k$; therefore, $S_{\mathrm{SJCI}}\left(t^{\prime },\frac{2v_k}{\lambda },a_k\right)$ can be derived as

$$S_{\mathrm{SJCI}}\left(t^{\prime },\frac{2v_k}{\lambda },a_k\right)=A_{5k}\exp \left[-j2\pi \frac{2R_{0k}}{\lambda }\right]\mathrm{sinc}\left[B\left(t^{\prime }-\frac{2R_{0k}}{c}\right)\right].$$

(58)

Thus, the range resolution $R_{\mathrm{r},\mathrm{SJCI}}$ can be calculated as

$$R_{\mathrm{r},\mathrm{SJCI}}=\frac{c}{2B}.$$

(59)

Let $t^{\prime }=\frac{2R_{0k}}{c}$ and $a_{\mathrm{p}}=a_k$, thus $S_{\mathrm{SJCI}}\left(\frac{2R_{0k}}{c},f_{\mathrm{t}}^{\prime },a_k\right)$ can be derived as

$$S_{\mathrm{SJCI}}\left(\frac{2R_{0k}}{c},f_{\mathrm{t}}^{\prime },a_k\right)=A_{5k}\exp \left[-j2\pi \frac{2R_{0k}}{\lambda }\right]\mathrm{sinc}\left[T_{\mathrm{SJCI}}\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right]\mathrm{sinc}\left[T\left(f_{\mathrm{t}}^{\prime }-\frac{2v_k}{\lambda }\right)\right].$$

(60)

Accordingly, the velocity resolution $R_{\mathrm{v},\mathrm{SJCI}}$ can be derived as

$$R_{\mathrm{v},\mathrm{SJCI}}=\frac{\lambda }{2T}.$$

(61)

Without consideration of the AR operation, let $t^{\prime }=\frac{2R_{0k}}{c}$ and $f_{\mathrm{t}}^{\prime }=\frac{2v_k}{\lambda }$, thus $S_{\mathrm{SJCI}}\left(\frac{2R_{0k}}{c},\frac{2v_k}{\lambda },a_{\mathrm{p}}\right)$ can be derived as

$$S_{\mathrm{SJCI}}\left(\frac{2R_{0k}}{c},\frac{2v_k}{\lambda },a_{\mathrm{p}}\right)=A_{5k}\exp \left[-j2\pi \frac{2R_{0k}}{\lambda }\right]\mathrm{sinc}\left(T^2\frac{a_{\mathrm{p}}-a_k}{\lambda }\right).$$

(62)

Thus, the acceleration resolution $R_{\mathrm{a},\mathrm{SJCI}}$ can be obtained, expressed as

$$R_{\mathrm{a},\mathrm{SJCI}}=\frac{\lambda }{T^2}.$$

(63)

On the basis of the theory given in Section 4, the resolutions of range, velocity, and acceleration of the SSJCI algorithm denoted as $R_{\mathrm{r},\mathrm{SSJCI}}$, $R_{\mathrm{v},\mathrm{SSJCI}}$, and $R_{\mathrm{a},\mathrm{SSJCI}}$ can be accomplished similarly, expressed as

$$R_{\mathrm{r},\mathrm{SSJCI}}=\frac{c}{2B},R_{\mathrm{v},\mathrm{SSJCI}}=\frac{\lambda }{2T},R_{\mathrm{a},\mathrm{SSJCI}}=\frac{\lambda }{T^2}.$$

(64)

The resolutions of range, velocity, and acceleration of the GRFT algorithm denoted as $R_{\mathrm{r},\mathrm{GRFT}}$, $R_{\mathrm{v},\mathrm{GRFT}}$, and $R_{\mathrm{a},\mathrm{GRFT}}$ are expressed as [34]

$$R_{\mathrm{r},\mathrm{GRFT}}=\frac{c}{2B},R_{\mathrm{v},\mathrm{GRFT}}=\frac{\lambda }{2T},R_{\mathrm{a},\mathrm{GRFT}}=\frac{\lambda }{T^2}.$$

(65)

Based on the relationship $T\ge T_{\mathrm{SHI}}\ge T_{\mathrm{HI}}$, the resolutions can be compared, expressed as

$$\begin{array}{cc}\hfill R_{\mathrm{r},\mathrm{GRFT}}=R_{\mathrm{r},\mathrm{SSJCI}}=R_{\mathrm{r},\mathrm{SJCI}}=& R_{\mathrm{r},\mathrm{SHI}}=R_{\mathrm{r},\mathrm{HI}},\hfill \\ \hfill R_{\mathrm{v},\mathrm{GRFT}}=R_{\mathrm{v},\mathrm{SSJCI}}=R_{\mathrm{v},\mathrm{SJCI}}\le & R_{\mathrm{v},\mathrm{SHI}}\le R_{\mathrm{v},\mathrm{HI}},\hfill \\ \hfill R_{\mathrm{a},\mathrm{GRFT}}=R_{\mathrm{a},\mathrm{SSJCI}}=R_{\mathrm{a},\mathrm{SJCI}}\le & R_{\mathrm{a},\mathrm{SHI}}\le R_{\mathrm{a},\mathrm{HI}}.\hfill \end{array}$$

(66)

5.5. Computation Complexity

In this subsection, the number of the real number operation is considered as a criterion to evaluate the computation costs. Denote the numbers of the search fold factors and accelerations by $N_{\mathrm{F}}$ and $N_{\mathrm{a}}$, respectively. Then, the computation costs of the main procedures in the SJCI algorithm can be calculated and listed in Table 1.

Table 1. Computation costs of the SJCI algorithm.

Procedure	Computation Cost
Doppler ambiguity compensation	$6N_{\mathrm{F}}MN$
SFT operation	$5N_{\mathrm{F}}MN{\log }_2{M}_{\mathrm{SJCI}}$
Phase compensation	$6N_{\mathrm{F}}{N}_{\mathrm{a}}MN$
Complex addition operation	$2N_{\mathrm{F}}{N}_{\mathrm{a}}MN$
IFT operation	$5N_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SJCI}}N{\log }_{2}N$

Thus, the total computation cost of the SJCI algorithm can be concluded, expressed as

$$I_{\mathrm{SJCI}}\approx 5N_{\mathrm{F}}MN{\log }_2{M}_{\mathrm{SJCI}}+8N_{\mathrm{F}}{N}_{\mathrm{a}}MN+5N_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SJCI}}N{\log }_{2}N.$$

(67)

The computation costs of the main procedures in the SSJCI algorithm are listed in Table 2.

Table 2. Computation costs of the SSJCI algorithm.

Procedure	Computation Cost
ST compensation	$6K_{\mathrm{SSJCI}}MN$
SJCI operation	$5K_{\mathrm{SSJCI}}{N}_{\mathrm{F}}MN{\log }_2{M}_{\mathrm{SSJCI}}+8N_{\mathrm{F}}{N}_{\mathrm{a}}MN+5N_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SSJCI}}N{\log }_{2}N$

Therefore, the overall computation cost of the SSJCI algorithm can be approximately calculated by

$$I_{\mathrm{SSJCI}}\approx 5K_{\mathrm{SSJCI}}{N}_{\mathrm{F}}MN{\log }_2{M}_{\mathrm{SSJCI}}+8N_{\mathrm{F}}{N}_{\mathrm{a}}MN+5N_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SSJCI}}N{\log }_{2}N.$$

(68)

To guarantee the rationality of the comparison among HI, SHI, SJCI, SSJCI, and GRFT algorithms, the same detection accuracy is required. With the criterion of the SSJCI algorithm, the numbers of the search grids in HI, SHI, and GRFT algorithms are all set as $N_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SSJCI}}N$, and $M_{\mathrm{SJCI}}$ is supplied to $M_{\mathrm{SSJCI}}$ via supply-zero operation. Under this circumstance, the computation costs of the five algorithms are re-calculated, presented in Table 3, where Q denotes the number of the subspaces in the SHI algorithm.

Table 3. Computation costs comparison.

Method	Computation Cost
HI	$5MN{\log }_2{M}_{\mathrm{HI}}+P_{\mathrm{HI}}{N}_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SSJCI}}N$
SHI	$QMN\left[5{\log }_{2}N+5{\log }_2{M}_{\mathrm{SHI}}+6\right]+P_{\mathrm{SHI}}{N}_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SSJCI}}N$
SJCI	$5N_{\mathrm{F}}N{M}_{\mathrm{SSJCI}}{P}_{\mathrm{SJCI}}{\log }_2{M}_{\mathrm{SSJCI}}+8N_{\mathrm{F}}{N}_{\mathrm{a}}N{M}_{\mathrm{SSJCI}}{P}_{\mathrm{SJCI}}+5N_{\mathrm{F}}{N}_{\mathrm{a}}N{M}_{\mathrm{SSJCI}}{\log }_{2}N$
SSJCI	$5K_{\mathrm{SSJCI}}{N}_{\mathrm{F}}NM{\log }_2{M}_{\mathrm{SSJCI}}+8N_{\mathrm{F}}{N}_{\mathrm{a}}NM+5N_{\mathrm{F}}{N}_{\mathrm{a}}N{M}_{\mathrm{SSJCI}}{\log }_{2}N$
GRFT	$8M{N}_{\mathrm{F}}{N}_{\mathrm{a}}{M}_{\mathrm{SSJCI}}N$

Without losing generality, we give a set of typical values to analyze the computation costs of SJCI and SSJCI algorithms: $N=1200$, $M=4000$, $N_{\mathrm{F}}=3$, $N_{\mathrm{a}}=1200$, $P_{\mathrm{SJCI}}=40$. $K_{\mathrm{SSJCI}}$ varies from 1 to 100. In this case, their computation costs are numerically calculated, shown in Figure 5. It can be observed that compared with the SJCI algorithm, the SSJCI algorithm acquires significant computation cost optimization.

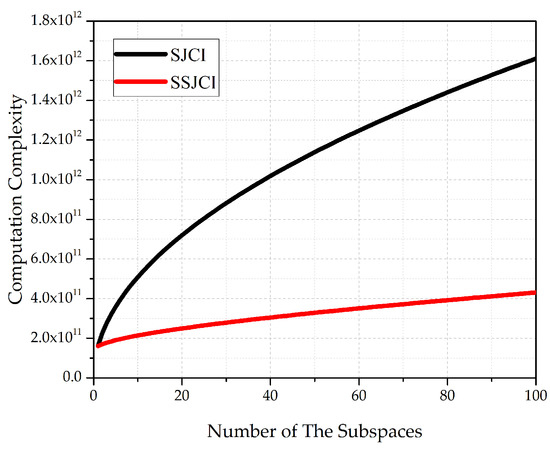
Figure 5. Computation complexity comparison between SJCI and SSJCI algorithms.

Thereafter, we compare the computation costs of HI, SHI, SJCI, SSJCI, and GRFT algorithms. Similarly, a set of typical values are given: $N=1200$, $N_{\mathrm{F}}=3$, $N_{\mathrm{a}}=1200$, $Q=256$, $K_{\mathrm{SSJCI}}=16$, $M_{\mathrm{HI}}=M_{\mathrm{SJCI}}=100$, $M_{\mathrm{SHI}}=M_{\mathrm{SSJCI}}=400$. M varies from 400 to 10,000. In this case, the computation costs of the five algorithms are numerically calculated, as shown in Figure 6.

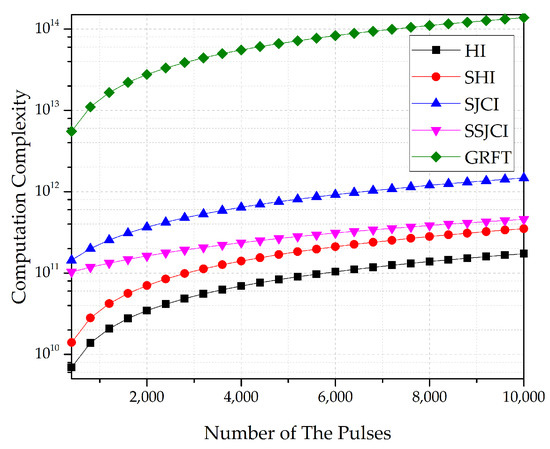
Figure 6. Computation complexity comparison among HI, SHI, SJCI, SSJCI, and GRFT algorithms.

The HI algorithm can be effectively implemented, where only fast FT (FFT) and real addition operations are employed. Apparently, it asks for the lowest computation cost. On the contrary, the implementation of the GRFT algorithm cannot be sped up, which requires the most complex addition and multiplication operations. Thus, it holds the highest computation complexity. Due to the large amount of coherent compensations and transforms, the computation burdens of SJCI and SSJCI algorithms are heavier than those of SHI and HI algorithms. Based on the typical values, we sort the computation complexities as follows

$$I_{\mathrm{GRFT}}>I_{\mathrm{SJCI}}>I_{\mathrm{SSJCI}}>I_{\mathrm{SHI}}>I_{\mathrm{HI}}.$$

(69)

6. Numerical Experiments and Results Analyses

6.1. Multiple Targets Detection

In this subsection, four targets denoted as Target A–D are simulated to demonstrate the validity of the SSJCI algorithm for multiple targets. The radar parameters are given as follows: $f_{\mathrm{c}}$ = 1 $\mathrm{GHz}$, B = 5 $\mathrm{MHz}$, $F_{\mathrm{s}}$ = 10 $\mathrm{MHz}$, $F_{\mathrm{p}}$ = 1000 $\mathrm{Hz}$, T = 2.5 $\mathrm{s}$. The parameters of the four targets are given in Table 4.

Table 4. Parameters of the four targets.

Target	Range ($\mathbf{m}$)	Velocity ($\mathbf{m}/\mathbf{s}$)	Acceleration ($\mathbf{m}/{\mathbf{s}}^2$)	SNR ($\mathbf{dB}$)
Target A	5000	540	54	−10
Target B	5000	540	45	−10
Target C	5000	630	45	−10
Target D	5450	540	45	−10

The SSJCI outputs of the four targets are shown in Figure 7. In order to present the processing results clearly, velocity–acceleration, range–acceleration, and range–velocity slices are extracted, respectively. It can be observed that the four targets are all integrated into distinct peaks, whose locations reflect their motion parameters accurately. The simulation experiment demonstrates that the SSJCI algorithm can effectively cope with the multi-target scenario.

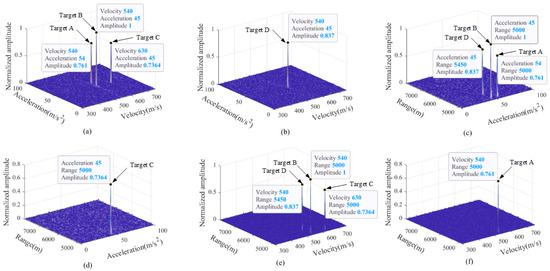
Figure 7. SSJCI outputs of the four targets: (a) the velocity–acceleration slice with the range being 5000 $\mathrm{m}$; (b) the velocity–acceleration slice with the range being 5450 $\mathrm{m}$; (c) the range–acceleration slice with the velocity being 540 $\mathrm{m}/\mathrm{s}$; (d) the range–acceleration slice with the velocity being 630 $\mathrm{m}/\mathrm{s}$; (e) the range–velocity slice with the acceleration being 45 $\mathrm{m}/{\mathrm{s}}^2$; (f) the range–velocity slice with the acceleration being 54 $\mathrm{m}/{\mathrm{s}}^2$.

6.2. Detection Performance Comparison

In this subsection, the detection probabilities of HI, SHI, SSJCI, and GRFT algorithms are compared by 1000 Monte Carlo runs. The radar parameters are the same as those of the experiment in Section 6.1. The false alarm probability is set as ${10}^{-6}$. The motion parameters of the target are given as follows: $R_0$ = 5 $\mathrm{km}$, v = 120 $\mathrm{m}/\mathrm{s}$, and a = 40 $\mathrm{m}/{\mathrm{s}}^2$. The input SNR varies from −33 dB∼−9 dB. The subaperture times of HI, SHI, and SSJCI algorithms are 0.025 s, 0.1 s, and 0.1 s, respectively. The simulation result is shown in Figure 8.

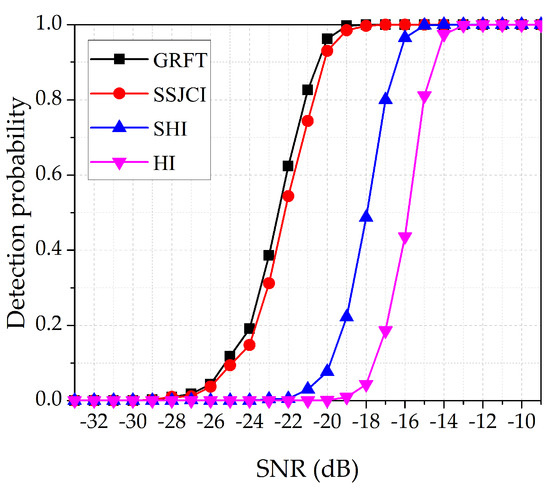
Figure 8. Detection probabilities of HI, SHI, SSJCI, and GRFT algorithms.

Thanks to the full coherent integration, GRFT and SSJCI algorithms show almost the same detection performance. However, as illustrated in Section 5.5, the computation burden of GRFT is much heavier. As to the detection probability $P_{\mathrm{D}}=0.8$, the required SNR of the SHI algorithm is 4dB higher than that of the SSJCI algorithm, which is induced by the incoherent integration among the subapertures. According to the parameters, the HI algorithm employs much more subapertures. Thus, it cannot perform as well as the SHI algorithm. Obviously, the simulation result is consistent with the theoretical analysis given in Section 5.3. The comparison reflects the excellent detection performance of the SSJCI algorithm.

6.3. Real Measured Data Processing

In this section, we investigate the performance of the SSJCI algorithm by processing a set of real measured data, which was recorded by an X-band radar whose parameters are given as follows: $f_{\mathrm{c}}$ = 8.85 $\mathrm{GHz}$, B = 40 $\mathrm{MHz}$, $F_{\mathrm{s}}$ = 60 $\mathrm{MHz}$, $F_{\mathrm{p}}$ = 1000 $\mathrm{Hz}$. In the outfield experiment, one cooperative car was tested. We extracted and processed 1000 continuous pulses from the data, the results of which are shown in Figure 9.

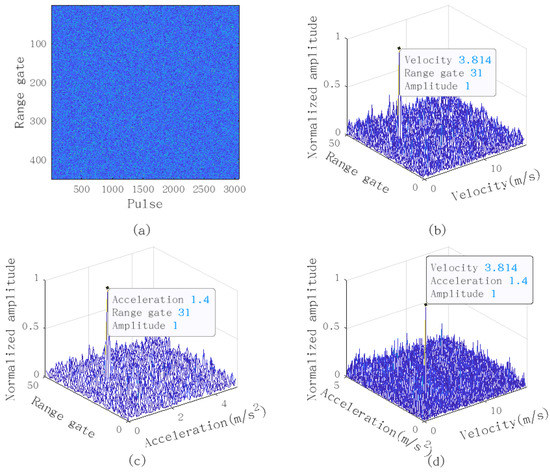
Figure 9. Real measured data processing results: (a) received radar signal after pulse compression; (b) the range–velocity slice with the acceleration being 1.4 $\mathrm{m}/{\mathrm{s}}^2$; (c) the range–acceleration slice with the velocity being 3.814 $\mathrm{m}/\mathrm{s}$; (d) the acceleration–velocity slice with the range gate being 31.

The extracted radar echoes are shown in Figure 9a, where the target signal is submerged in the powerful noise. It can be observed from Figure 9b–d that the test target is effectively integrated by the SSJCI algorithm with its motion parameters estimated accurately. Moreover, we compare the required minimum false alarm probabilities to achieve target detection by HI, SHI, SSJCI, and GRFT algorithms, the results of which are given in Table 5. Obviously, GRFT and SSJCI algorithms perform much better. It is worth noting that the SSJCI algorithm requires much lower computation complexity, which has been proved in Section 5.5. Combining the results of Section 5 and Section 6, the SSJCI algorithm can be a good candidate for the maneuvering target detection.

Table 5. Real data processing by the four algorithms.

Algorithm	HI	SHI	SSJCI	GRFT
Required false alarm probability	${10}^{-3}$	${10}^{-4}$	${10}^{-7}$	${10}^{-7}$

7. Conclusions

This article proposes a novel SJCI algorithm for the maneuvering target detection. It can effectively cope with the RCM and DFM issues and achieve full coherent integration with superior anti-noise performance. In addition, an upgraded algorithm is presented, namely, the SSJCI algorithm. It retains the advantages of the SJCI algorithm with longer subaperture time, better detection accuracy, and lower computation cost. Theoretical analyses and performance comparisons demonstrate that the SSJCI algorithm can strike a good balance among SNR gain, detection performance, resolution, and computation complexity. Finally, numerical experiment results further verify the effectiveness of the SSJCI algorithm.