Local- and Regional-Scale Forcing of Glacier Mass Balance Changes in the Swiss Alps
Abstract
1. Introduction
2. Study Area
3. Data
3.1. Mass Balance Data
3.2. Climate Data
3.3. Remotely Sensed Data
4. Methods
4.1. Statistical Analysis
4.1.1. Exploratory Data Analysis
4.1.2. Structural Change Model
4.1.3. Trend Analysis
Mann–Kendall and Sen’s Slope Estimator
Multiple Linear Regression
4.2. Remotely Sensed Data Analysis
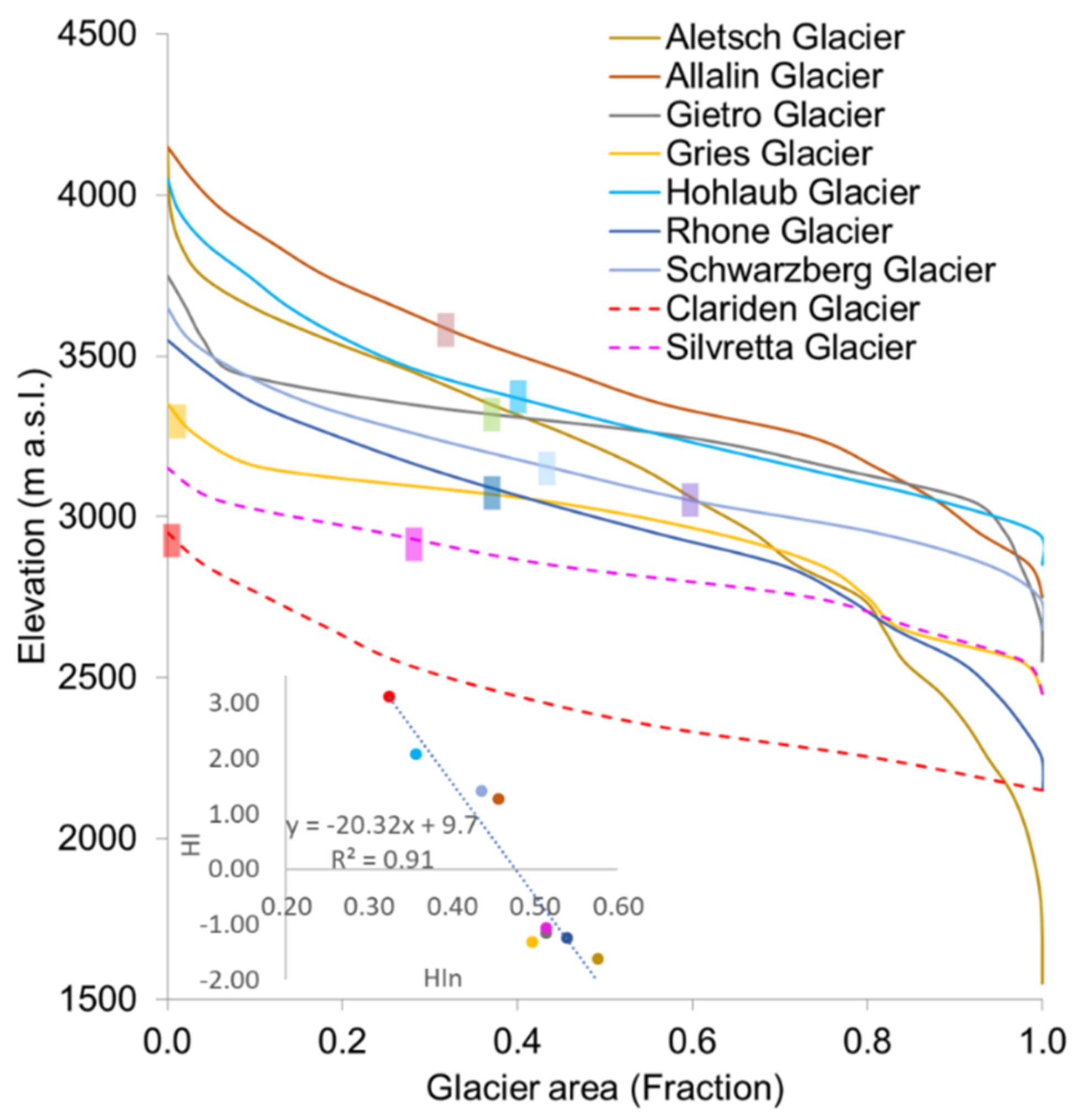
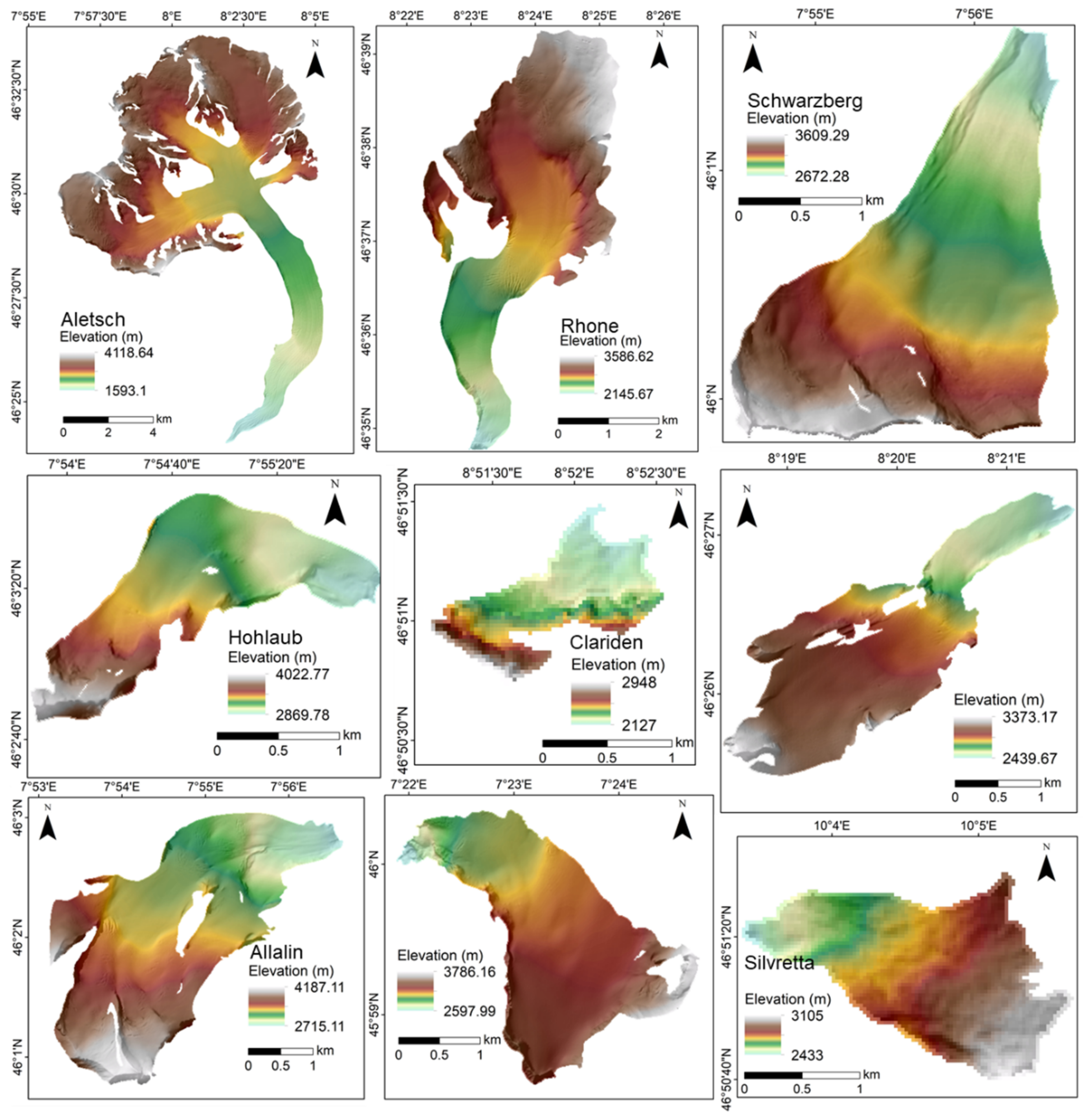
4.2.1. Hypsometric Index (HI) and Hypsometric Integral (HIn)
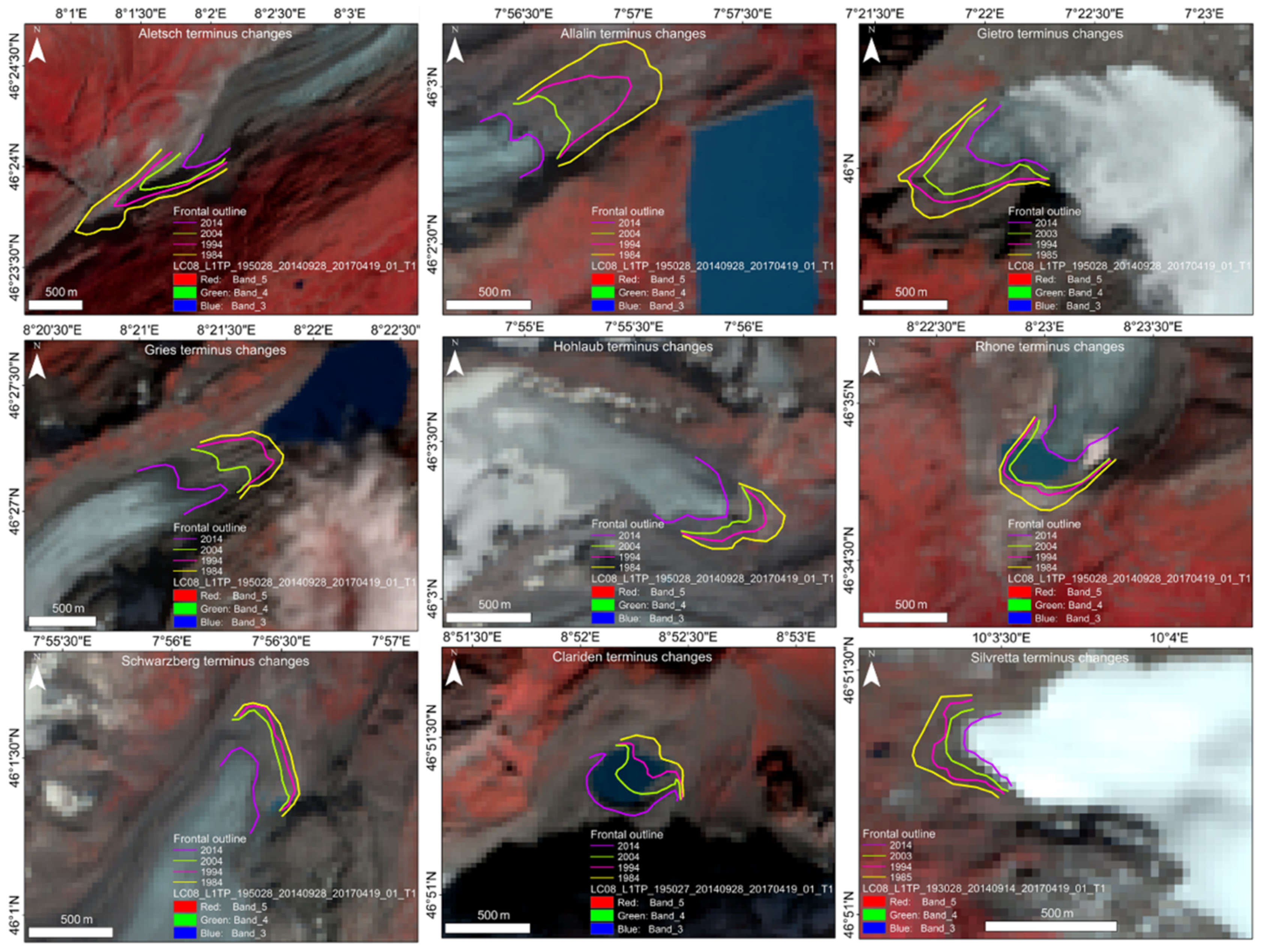
4.2.2. Glacier Terminus Delineation
5. Results and Discussion
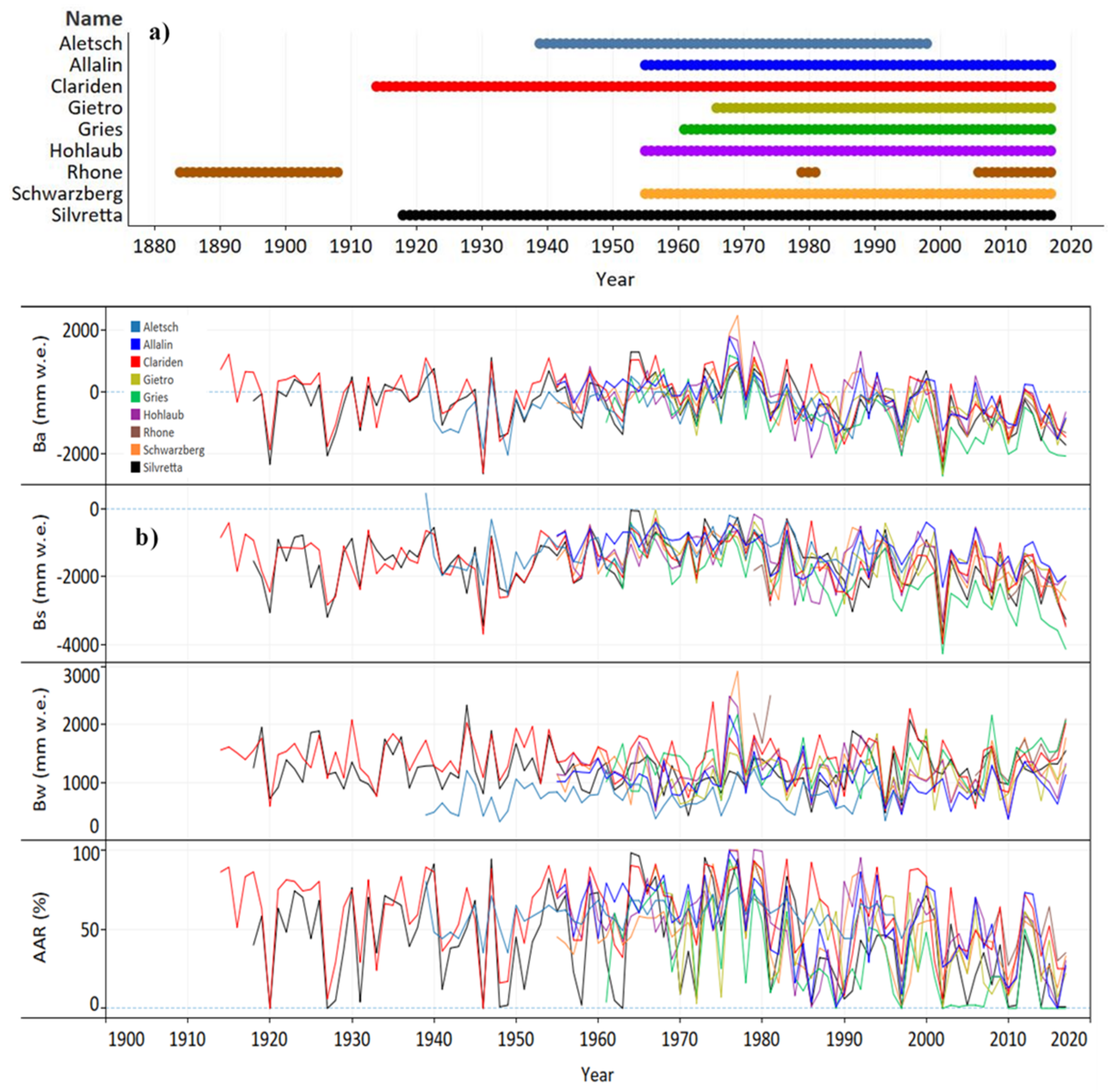
5.1. Analysis of Annual Mass Balance
5.2. Analysis of Seasonal Mass Balance and Accumulation Area
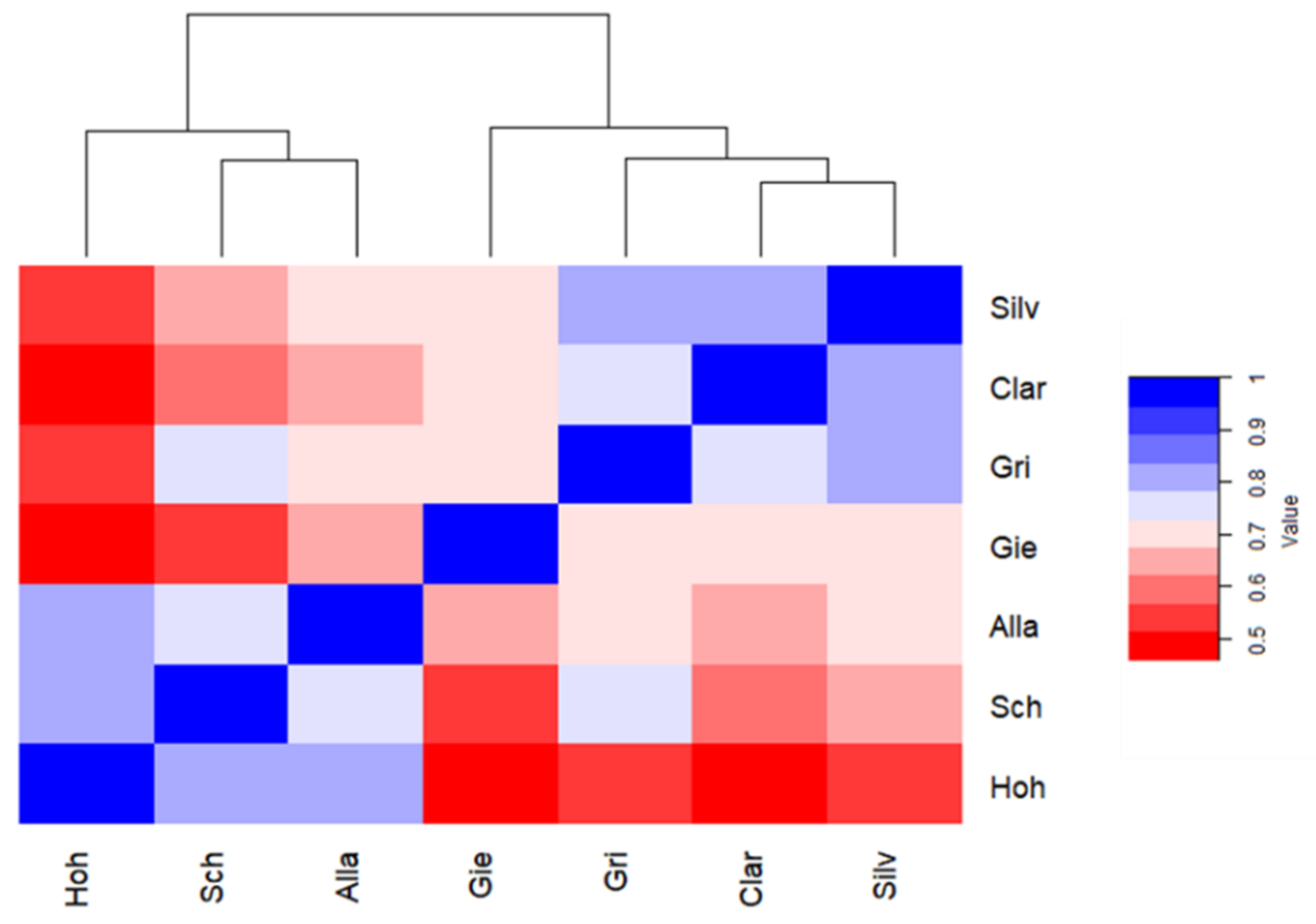
5.3. Climatic Controls
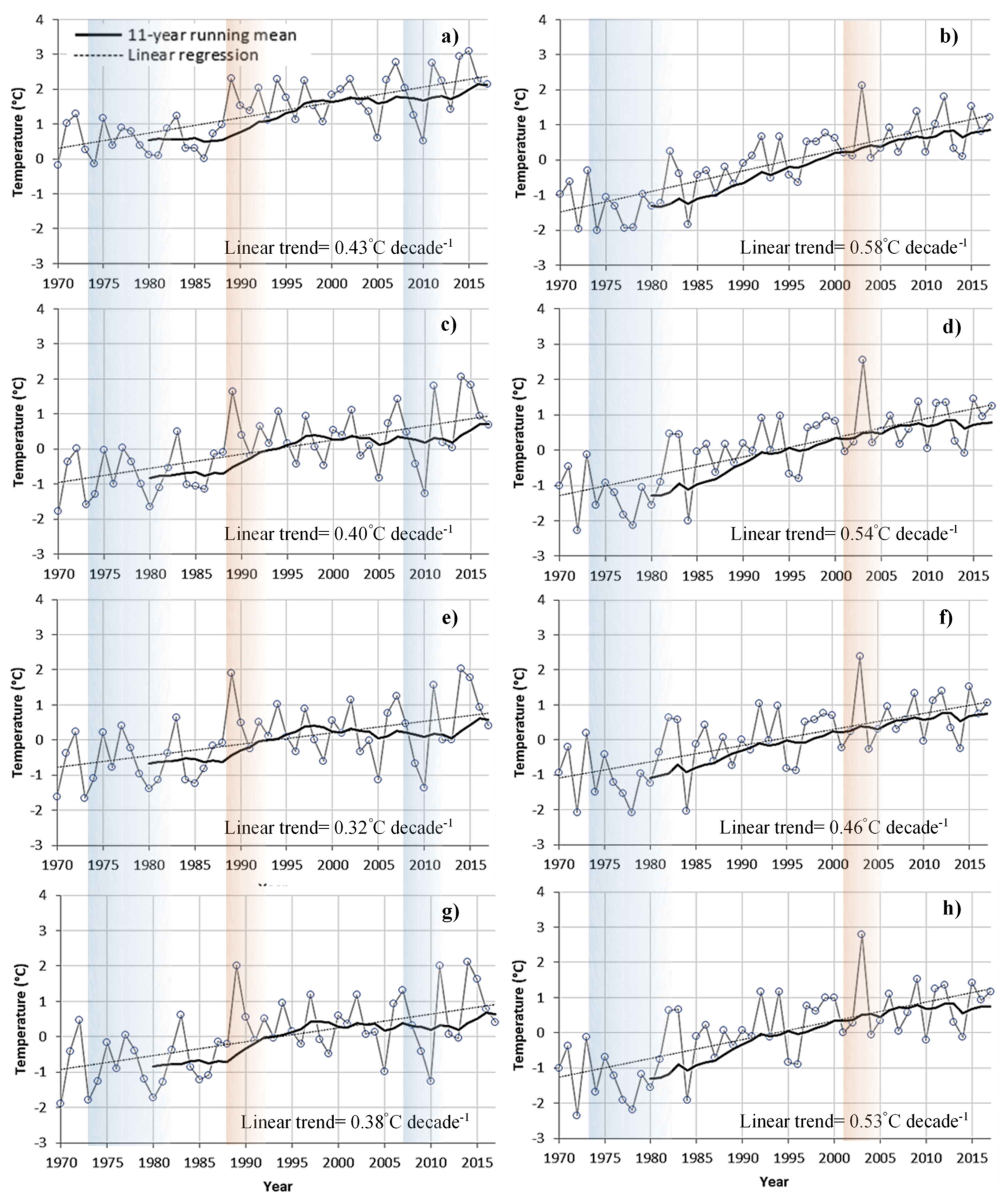
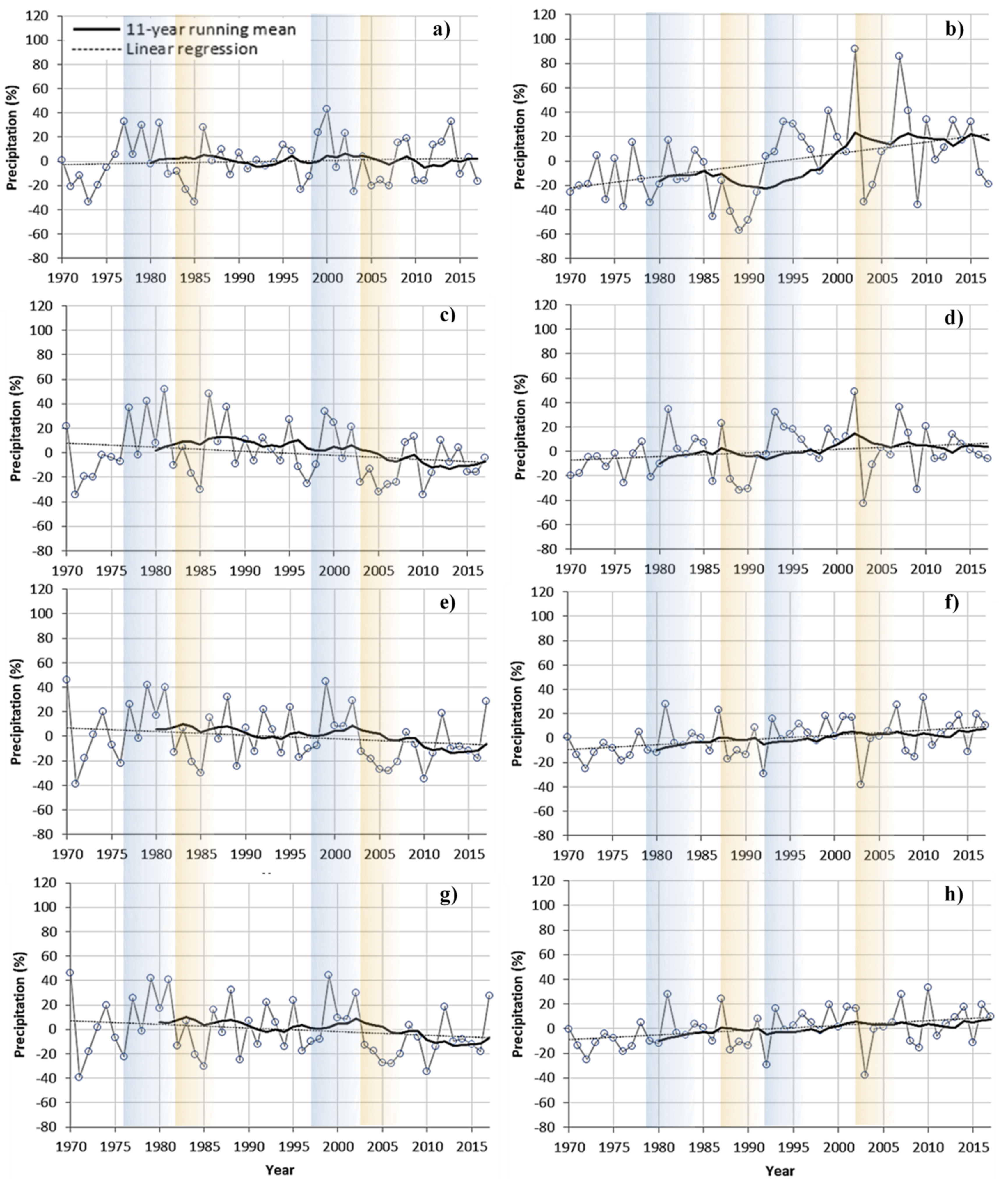
5.3.1. Local Meteorological Variables
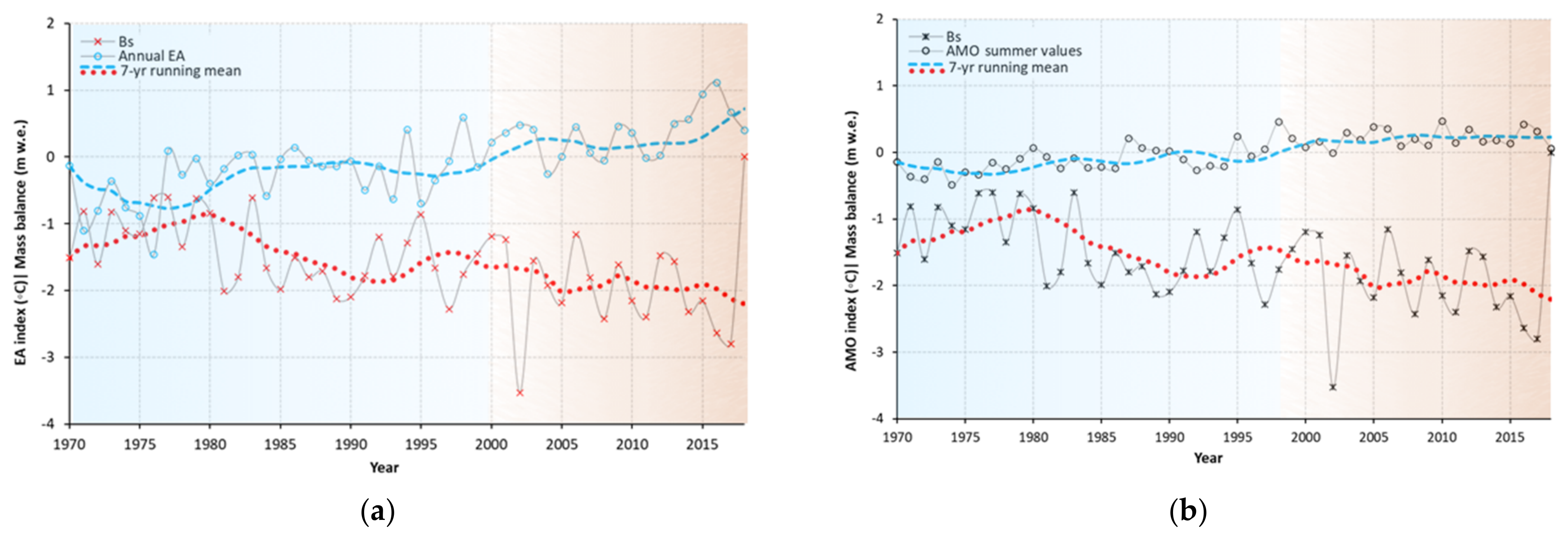
5.3.2. Large-Scale Atmospheric Circulation
5.4. Hypsometric Characteristic and Terminus Retreat
6. Conclusions
- -
- All selected glaciers have lost their equilibrium condition in the recent century, and persistent negative annual mass balance trends, accompanied by decreasing AARs, have been observed for the glaciers located in the south of Switzerland.
- -
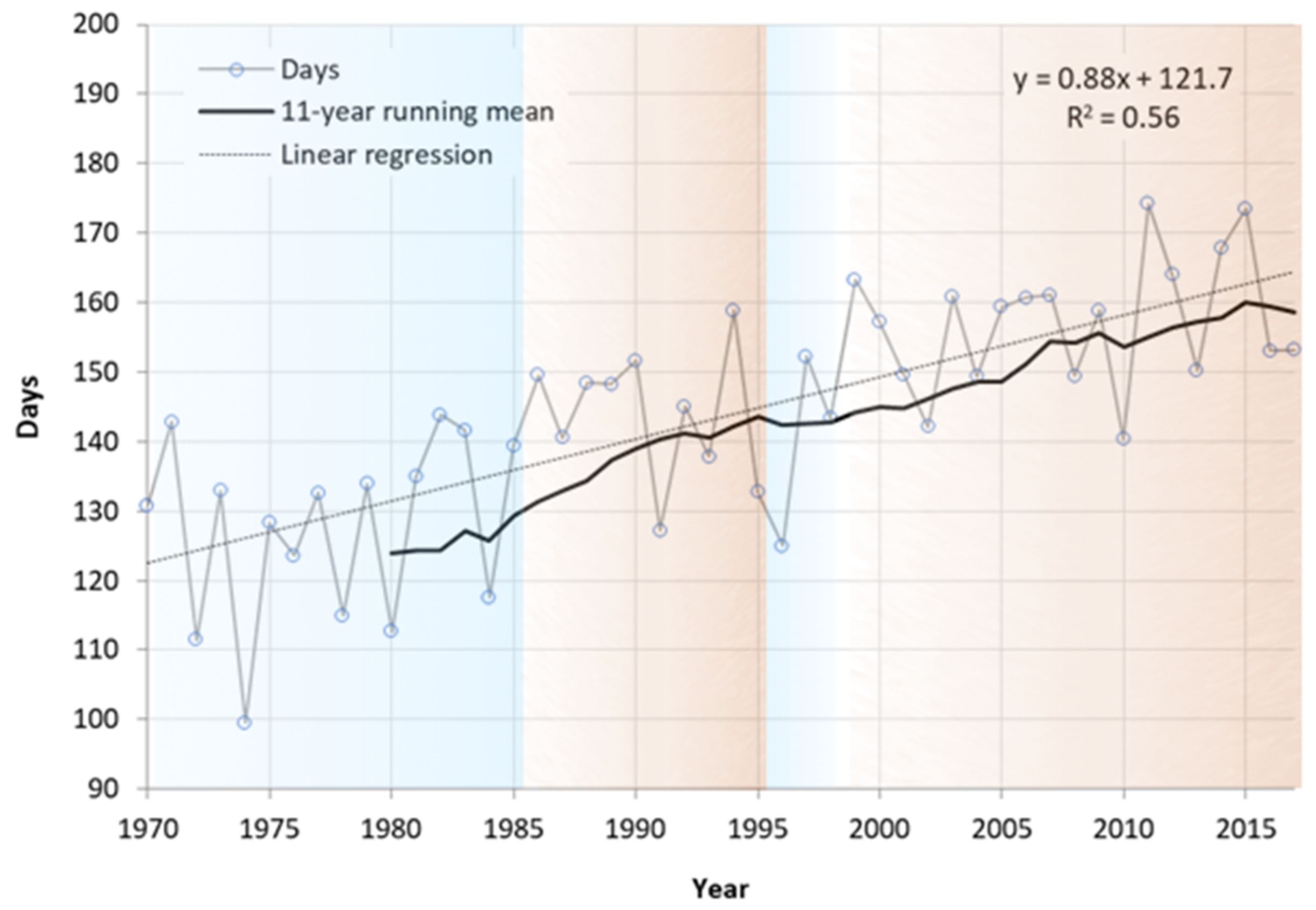
- Such imbalanced behavior is the product of ablation induced by warmer temperatures, increased melting, and acceleration of the ice-albedo feedback process. Although the precipitation trends are not significant, the increase in the number of days with the air temperature above 0 °C supports the reduction in solid precipitation over the glaciers. Additionally, rain-on-snow events may also be another contributor to the ice mass loss in these regions.
- -
- The analyzed glaciers reveal that the annual mass balances are mainly controlled by the summer mass balance, which is statistically attributed to the significant anticorrelation with summer air temperature.
- -
- Atmosphere–ocean teleconnection patterns, including AMO and EA, are strongly linked through the time to mass balance characteristics of the southern Swiss Alps, and these large-scale climatic forcings will likely continue to influence surface mass balance regime.
- -
- Most of the observed glaciers are losing accumulation area given that AAR percent has dropped from approximately 75% in 1970 to 25% in recent years, which highlights the acceleration of the melt rate.
- -
- Although a decadal frontal retreat analysis during 1984–2014 reveals significant spatiotemporal variations, nearly all glaciers have considerably receded during 2004–2014. This highlights the possibility of continuing high melt rates in the next decades and corroborates the mass balance–climate coupling in the region.
- -
- Based on the current research and the corresponding results, the negative mass balance trends cannot be simply attributed to the direct response of global warming. Hence, we emphasize that future investigations should focus on resolving complex and indirect surface–atmosphere interactions (e.g., reflectivity and impurities of glacier surfaces [93]) to more comprehensively understand physical processes driving glacier mass balance variability. In particular, the hypsometric evolution of glaciers with continued mass loss warrants considering dynamic modeling approaches to simulate the future state of glaciers as we observe glacier hypsometry and morphology playing considerable roles in defining mass balance trends. In an attempt to better understand the physical drivers of the Swiss glaciers’ mass balance, we recommend that future work provide a deeper evaluation of the spatiotemporal impacts of climatic teleconnections on the glaciers, including analyzing patterns of regional temperature advection along with wind speed and direction variations as it relates to changing glacial conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMO | Atlantic Multidecadal Oscillation |
| AARs | accumulation area ratios |
| GBI | Greenland Blocking Index |
| EA | East Atlantic pattern |
| WGMS | world glacier monitoring service |
| GTNG | global terrestrial network for glaciers |
| NAOEA | North Atlantic Oscillation |
| GLOFs | glacial lake outburst floods |
| ASTER | advanced spaceborne thermal emission and reflection radiometer |
| GDM | global digital elevation model |
| SCA | Scandinavian pattern |
| VAW/ETHZ | laboratory of hydraulics, hydrology, and glaciology at ETH Zürich |
| ELA | equilibrium line altitude |
| Ba | annual mass balance |
| Bw | winter mass balance |
| Bs | summer mass balance |
| NBCN | Swiss national basic climatological network |
| NOAA | National Oceanic and Atmospheric Administration |
| CPC | NOAA Climatic Prediction Center |
| EOF | empirical orthogonal function |
| CUSUM | cumulated sum of standard residuals |
| efp | empirical fluctuation process |
| BIC | Bayesian information criterion |
| ACF | autocorrelation |
| PACF | partial autocorrelation |
| HI | hypsometric index |
| HIn | hypsometric integral |
| RMSE | root mean square error |
References
- Fischer, M.; Huss, M.; Hoelzle, M. Surface elevation and mass changes of all Swiss glaciers 1980–2010. Cryosphere 2015, 9, 525–540. [Google Scholar] [CrossRef]
- Zemp, M.; Frey, H.; Gärtner-Roer, I.; Nussbaumer, S.U.; Hoelzle, M.; Paul, F.; Haeberli, W.; Denzinger, F.; Ahlstrøm, A.P.; Anderson, B.; et al. Historically unprecedented global glacier decline in the early 21st century. J. Glaciol. 2015, 61, 745–762. [Google Scholar] [CrossRef]
- Carturan, L.; Baroni, C.; Brunetti, M.; Carton, A.; Fontana, G.D.; Salvatore, M.C.; Zanoner, T.; Zuecco, G. Analysis of the mass balance time series of glaciers in the Italian Alps. Cryosphere 2016, 10, 695–712. [Google Scholar] [CrossRef]
- Medwedeff, W.G.; Roe, G.H. Trends and variability in the global dataset of glacier mass balance. Clim. Dyn. 2016, 48, 3085–3097. [Google Scholar] [CrossRef]
- Naegeli, K.; Huss, M. Sensitivity of mountain glacier mass balance to changes in bare-ice albedo. Ann. Glaciol. 2017, 58, 119–129. [Google Scholar] [CrossRef]
- Huss, M.; Bauder, A. 20th-century climate change inferred from four long-term point observations of seasonal mass balance. Ann. Glaciol. 2009, 50, 207–214. [Google Scholar] [CrossRef]
- Miller, J.D.; Immerzeel, W.W.; Rees, G. Climate Change Impacts on Glacier Hydrology and River Discharge in the Hindu Kush–Himalayas: A Synthesis of the Scientific Basis. Mt. Res. Dev. 2012, 32, 461–467. [Google Scholar]
- Schleiss, A.; Oberrauch, F. Flexibilisierung Der Wasserkraft in Der Schweiz Für Zukünftige Aufgaben Im Internationalen Strommarkt. Wasser Energ. Luft 2014, 106, 175–178. [Google Scholar]
- Piot, M. Wirtschaftlichkeit der Wasserkraft in der Schweiz. Wasserwirtschaft 2017, 107, 33–38. [Google Scholar] [CrossRef]
- Rahman, K.; da Silva, A.G.; Tejeda, E.M.; Gobiet, A.; Beniston, M.; Lehmann, A. An independent and combined effect analysis of land use and climate change in the upper Rhone River watershed, Switzerland. Appl. Geogr. 2015, 63, 264–272. [Google Scholar] [CrossRef]
- Rasul, G.; Molden, D. The Global Social and Economic Consequences of Mountain Cryospheric Change. Front. Environ. Sci. 2019, 7, 91. [Google Scholar] [CrossRef]
- Milner, A.M.; Khamis, K.; Battin, T.J.; Brittain, J.E.; Barrand, N.E.; Füreder, L.; Cauvy-Fraunié, S.; Gíslason, G.M.; Jacobsen, D.; Hannah, D.M.; et al. Glacier shrinkage driving global changes in downstream systems. Proc. Natl. Acad. Sci. USA 2017, 114, 9770–9778. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.P.H.; Bierkens, M.F.P. Climate change will affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar]
- Chevallier, P.; Pouyaud, B.; Suarez, W.; Condom, T. Climate change threats to environment in the tropical Andes: Glaciers and water resources. Reg. Environ. Chang. 2011, 11, 179–187. [Google Scholar] [CrossRef]
- Huggel, C.; Haeberli, W.; Kääb, A.; Bieri, D.; Richardson, S. An assessment procedure for glacial hazards in the Swiss Alps. Can. Geotech. J. 2004, 41, 1068–1083. [Google Scholar] [CrossRef]
- Klimeš, J.; Novotný, J.; Novotná, I.; De Urries, B.J.; Vilímek, V.; Emmer, A.; Strozzi, T.; Kusák, M.; Rapre, A.C.; Hartvich, F.; et al. Landslides in moraines as triggers of glacial lake outburst floods: Example from Palcacocha Lake (Cordillera Blanca, Peru). Landslides 2016, 13, 1461–1477. [Google Scholar] [CrossRef]
- Haeberli, W.; Buetler, M.; Huggel, C.; Friedli, T.L.; Schaub, Y.; Schleiss, A.J. New lakes in deglaciating high-mountain regions–opportunities and risks. Clim. Chang. 2016, 139, 201–214. [Google Scholar] [CrossRef]
- Harrison, S.; Kargel, J.S.; Huggel, C.; Reynolds, J.; Shugar, D.H.; Betts, R.A.; Emmer, A.; Glasser, N.; Haritashya, U.K.; Klimeš, J.; et al. Climate change and the global pattern of moraine-dammed glacial lake outburst floods. Cryosphere 2018, 12, 1195–1209. [Google Scholar] [CrossRef]
- Koenig, U.; Abegg, B. Impacts of Climate Change on Winter Tourism in the Swiss Alps. J. Sustain. Tour. 1997, 5, 46–58. [Google Scholar] [CrossRef]
- Spandre, P.; François, H.; Verfaillie, D.; Pons, M.; Vernay, M.; Lafaysse, M.; George, E.; Morin, S. Winter tourism under climate change in the Pyrenees and the French Alps: Relevance of snowmaking as a technical adaptation. Cryosphere 2019, 13, 1325–1347. [Google Scholar] [CrossRef]
- Spandre, P.; François, H.; Verfaillie, D.; Lafaysse, M.; Déqué, M.; Eckert, N.; George, E.; Morin, S. Climate controls on snow reliability in French Alps ski resorts. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef]
- Demiroglu, O.C.; Dannevig, H.; Aall, C. Climate change acknowledgement and responses of summer (glacier) ski visitors in Norway. Scand. J. Hosp. Tour. 2018, 18, 419–438. [Google Scholar] [CrossRef]
- Braithwaite, R.J. Glacier mass balance: The first 50 years of international monitoring. Prog. Phys. Geogr. Earth Environ. 2002, 26, 76–95. [Google Scholar] [CrossRef]
- Hall, M. II.—Les Variations Périodiques Des Glaciers. Discours Préliminaire. Par F. A. Forel, President de La Commission Internationale Des Glaciers. Archives Des Sciences Physiques et Naturelles. Genève. Vol. Xxxiv, p. 209. Geol. Mag. 1895, 2, 569–570. [Google Scholar]
- Haeberli, W.; Hoelzle, M.; Suter, S.; World Glacier Monitoring Service. Studies and reports in hydrology. In Into the Second Century of Worldwide Glacier Monitoring-Prospects and Strategies: A Contribution to the International Hydrological Programme (IHP) and the Global Environment Monitoring System (GEMS); UNESCO: Paris, France, 1998. [Google Scholar]
- World Glacier Monitoring Service (WGMS). Fluctuations of Glaciers Database; WGMS: Zurich, Switzerland, 2017. [Google Scholar]
- Holzhauser, H. Die bewegte Vergangenheit des Grossen Aletschgletschers. Bl. Aus Walliser Gesch. 2009, 47. [Google Scholar]
- Abermann, J.; Lambrecht, A.; Fischer, A.; Kuhn, M. Quantifying changes and trends in glacier area and volume in the Austrian Ötztal Alps (1969–1997–2006). Cryosphere 2009, 3, 205–215. [Google Scholar] [CrossRef]
- Carturan, L.; Filippi, R.; Seppi, R.; Gabrielli, P.; Notarnicola, C.; Bertoldi, L.; Paul, F.; Rastner, P.; Cazorzi, F.; Dinale, R.; et al. Area and volume loss of the glaciers in the Ortles-Cevedale group (Eastern Italian Alps): Controls and imbalance of the remaining glaciers. Cryosphere 2013, 7, 1339–1359. [Google Scholar] [CrossRef]
- Zemp, M.; Paul, F.; Hoelzle, M.; Haeberli, W. Glacier fluctuations in the European Alps, 1850–2000: An overview and spatio-temporal analysis of available data. In Darkening Peaks: Glacier Retreat, Science, and Society; Orlove, B., Wiegandt, E., Luckman, B.H., Eds.; University of California Press: Berkeley, CA, USA, 2008; pp. 152–167. [Google Scholar]
- Huss, M.; Usselmann, S.; Farinotti, D.; Bauder, A. Glacier mass balance in the south-eastern Swiss Alps since 1900 and perspectives for the future. Erdkunde 2010, 2010, 119–140. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R.; Bauder, A.; Funk, M. 100-year mass changes in the Swiss Alps linked to the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2010, 37, 10. [Google Scholar] [CrossRef]
- Huss, M.; Dhulst, L.; Bauder, A. New long-term mass-balance series for the Swiss Alps. J. Glaciol. 2015, 61, 551–562. [Google Scholar] [CrossRef]
- Oerlemans, J.; Anderson, B.; Hubbard, A.; Huybrechts, P.; Jóhannesson, T.; Knap, W.H.; Schmeits, M.; Stroeven, A.P.; Van De Wal, R.S.W.; Wallinga, J.; et al. Modelling the response of glaciers to climate warming. Clim. Dyn. 1998, 14, 267–274. [Google Scholar] [CrossRef]
- Braithwaite, R.J.; Zhang, Y. Sensitivity of mass balance of five Swiss glaciers to temperature changes assessed by tuning a degree-day model. J. Glaciol. 2000, 46, 7–14. [Google Scholar] [CrossRef]
- Oerlemans, J.; Reichert, B.K. Relating glacier mass balance to meteorological data by using a seasonal sensitivity characteristic. J. Glaciol. 2000, 46, 1–6. [Google Scholar] [CrossRef]
- (Lisette) Klok, E.; Oerlemans, J. Model study of the spatial distribution of the energy and mass balance of Morteratschgletscher, Switzerland. J. Glaciol. 2002, 48, 505–518. [Google Scholar] [CrossRef]
- Woul, M.D.; Hock, R. Static Mass-Balance Sensitivity of Arctic Glaciers and Ice Caps Using a Degree-Day Approach. Ann. Glaciol. 2005, 42, 217–224. [Google Scholar] [CrossRef]
- Zhu, M.; Yao, T.; Yang, W.; Xu, B.; Wu, G.; Wang, X. Differences in Mass Balance Behavior for Three Glaciers from Different Climatic Regions on the Tibetan Plateau. Clim. Dyn. 2018, 50, 3457–3484. [Google Scholar] [CrossRef]
- Huss, M.; Fischer, M. Sensitivity of Very Small Glaciers in the Swiss Alps to Future Climate Change. Front. Earth Sci. 2016, 4, 4. [Google Scholar] [CrossRef]
- McCabe, G.J.; Fountain, A.G.; Dyurgerov, M. Variability in Winter Mass Balance of Northern Hemisphere Glaciers and Relations with Atmospheric Circulation. Arct. Antarct. Alp. Res. 2000, 32, 64–72. [Google Scholar] [CrossRef]
- Shahgedanova, M.; Stokes, C.R.; Gurney, S.D.; Popovnin, V. Interactions between mass balance, atmospheric circulation, and recent climate change on the Djankuat Glacier, Caucasus Mountains, Russia. J. Geophys. Res. Space Phys. 2005, 110, 04108. [Google Scholar] [CrossRef]
- Marzeion, B.; Nesje, A. Spatial patterns of North Atlantic Oscillation influence on mass balance variability of European glaciers. Cryosphere 2012, 6, 661–673. [Google Scholar] [CrossRef]
- Thibert, E.; Eckert, N.; Vincent, C. Climatic Drivers of Seasonal Glacier Mass Balances: An Analysis of 6 Decades at Glacier de Sarennes (French Alps). Cryosphere 2013, 7, 47–66. [Google Scholar]
- Beniston, M. Variations of snow depth and duration in the swiss alps over the last 50 years: Links to changes in large-scale climatic forcings. Clim. Chang. 1997, 36, 281–300. [Google Scholar] [CrossRef]
- Gharehchahi, S.; James, W.H.M.; Bhardwaj, A.; Jensen, J.L.R.; Sam, L.; Ballinger, T.J.; Butler, D.R. Glacier Ice Thickness Estimation and Future Lake Formation in Swiss Southwestern Alps—The Upper Rhône Catchment: A VOLTA Application. Remote Sens. 2020, 12, 3443. [Google Scholar]
- Vihma, T.; Graversen, R.; Chen, L.; Handorf, D.; Skific, N.; Francis, J.A.; Tyrrell, N.; Hall, R.; Hanna, E.; Uotila, P.; et al. Effects of the Tropospheric Large-scale Circulation on European Winter Temperatures during the Period of Amplified Arctic Warming. Int. J. Climatol. 2020, 40, 509–529. [Google Scholar] [PubMed]
- Kropáček, J.; Neckel, N.; Bauder, A. Estimation of Mass Balance of the Grosser Aletschgletscher, Swiss Alps, from ICESat Laser Altimetry Data and Digital Elevation Models. Remote Sens. 2014, 6, 5614–5632. [Google Scholar] [CrossRef]
- Schwarb, M.; Schär, C.J. The Alpine Precipitation Climate. In Evaluation of a High-Resolution Analysis Scheme Using Comprehensive Rain-Gauge Data; ETH Zürich: Zürich, Switzerland, 2000. [Google Scholar]
- Spatial Climate Analyses-MeteoSwiss. Available online: https://www.meteoswiss.admin.ch/home/climate/swiss-climate-in-detail/raeumliche-klimaanalysen.html (accessed on 22 October 2019).
- Fang, Z.-F. Statistical Relationship Between the Northern Hemisphere Sea Ice and Atmospheric Circulation During Wintertime. In Observation, Theory and Modeling of Atmospheric Variability; World Scientific Series on Asia-Pacific Weather and Climate; World Scientific: Singapore, 2004; Volume 3, pp. 131–141. [Google Scholar]
- Hanna, E.; Fettweis, X.; Mernild, S.H.; Cappelen, J.; Ribergaard, M.H.; Shuman, C.A.; Steffen, K.; Wood, L.; Mote, T.L. Atmospheric and oceanic climate forcing of the exceptional Greenland ice sheet surface melt in summer 2012. Int. J. Clim. 2013, 34, 1022–1037. [Google Scholar] [CrossRef]
- Hanna, E.; Cropper, T.E.; Hall, R.J.; Cappelen, J. Greenland Blocking Index 1851–2015: A regional climate change signal. Int. J. Clim. 2016, 36, 4847–4861. [Google Scholar] [CrossRef]
- Hanna, E.; Hall, R.J.; Cropper, T.E.; Ballinger, T.J.; Wake, L.; Mote, T.; Cappelen, J. Greenland Blocking Index Daily Series 1851–2015: Analysis of Changes in Extremes and Links with North Atlantic and UK Climate Variability and Change. Int. J. Climatol. 2018, 38, 3546–3564. [Google Scholar]
- Hurrell, J.W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar]
- Kaplan, A.; Cane, M.A.; Kushnir, Y.; Clement, A.C.; Blumenthal, M.B.; Rajagopalan, B. Analyses of global sea surface temperature 1856–1991. J. Geophys. Res. Space Phys. 1998, 103, 18567–18589. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Knight, J.R.; Folland, C.K.; Scaife, A.A. Climate impacts of the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2006, 33, 17706. [Google Scholar] [CrossRef]
- Federal Office of Topography, Swisstopo Online Shop. Available online: https://shop.swisstopo.admin-.ch/en/products/height_models/alti3D (accessed on 7 October 2019).
- LP DAAC-NASA and METI Release ASTER Global DEM Version 3. Available online: https://lpdaac.usgs.gov/news/nasa-and-meti-release-aster-global-dem-version-3/ (accessed on 21 November 2019).
- USGS. Earth Explorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 28 August 2016).
- Beniston, M. Mountain Climates and Climatic Change: An Overview of Processes Focusing on the European Alps. Pure Appl. Geophys. 2005, 162, 1587–1606. [Google Scholar] [CrossRef]
- Scherrer, S.; Appenzeller, C. Swiss Alpine snow pack variability: Major patterns and links to local climate and large-scale flow. Clim. Res. 2006, 32, 187–199. [Google Scholar] [CrossRef]
- Zeileis, A.; Kleiber, C.; Krämer, W.; Hornik, K. Testing and dating of structural changes in practice. Comput. Stat. Data Anal. 2003, 44, 109–123. [Google Scholar] [CrossRef]
- Bai, J. Estimation of a Change Point in Multiple Regression Models. Rev. Econ. Stat. 1997, 79, 551–563. [Google Scholar] [CrossRef]
- Hawkins, D.M. Fitting multiple change-point models to data. Comput. Stat. Data Anal. 2001, 37, 323–341. [Google Scholar] [CrossRef]
- Sullivan, J.H. Estimating the Locations of Multiple Change Points in the Mean. Comput. Stat. 2002, 17, 289–296. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econ. 2002, 18, 1–22. [Google Scholar] [CrossRef]
- Zeileis, A. Alternative boundaries for CUSUM tests. Stat. Pap. 2004, 45, 123–131. [Google Scholar] [CrossRef]
- Andrews, D.W.K.; Ploberger, W. Optimal Tests when a Nuisance Parameter is Present Only Under the Alternative. Econometrica 1994, 62, 1383. [Google Scholar] [CrossRef]
- Kuan, C.-M.; Hornik, K. The generalized fluctuation test: A unifying view. Econ. Rev. 1995, 14, 135–161. [Google Scholar] [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for Testing the Constancy of Regression Relationships Over Time. J. R. Stat. Soc. Ser. B (Methodol.) 1975, 37, 149–163. [Google Scholar] [CrossRef]
- Ploberger, W.; Krämer, W. The Cusum Test with Ols Residuals. Econometrica 1992, 60, 271. [Google Scholar] [CrossRef]
- Kleiber, C.; Zeileis, A. Applied Econometrics with R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Chow, G.C. Tests of Equality Between Sets of Coefficients in Two Linear Regressions. Econometrica 1960, 28, 591. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Applicability of the t-Test for Detecting Trends in Water Quality Variables, by Robert H. Montgomery and Jim C. Loftis. JAWRA J. Am. Water Resour. Assoc. 1988, 24, 201–204. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Stuart, A. Rank Correlation Methods. By M. G. Kendall, 2nd Edition. Br. J. Stat. Psychol. 1956, 9, 68. [Google Scholar]
- Jiskoot, H.; Curran, C.J.; Tessler, D.L.; Shenton, L.R. Changes in Clemenceau Icefield and Chaba Group glaciers, Canada, related to hypsometry, tributary detachment, length–slope and area–aspect relations. Ann. Glaciol. 2009, 50, 133–143. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-Relief Ratio, Hypsometric Integral, and Geomorphic Area-Altitude Analysis. GSA Bull. 1971, 82, 1079. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y. Topographic and Geometric Controls on Glacier Changes in the Central Tien Shan, China, since the Little Ice Age. Ann. Glaciol. 2014, 55, 177–186. [Google Scholar] [CrossRef]
- Sam, L.; Bhardwaj, A.; Kumar, R.; Buchroithner, M.F.; Martín-Torres, F.J. Heterogeneity in topographic control on velocities of Western Himalayan glaciers. Sci. Rep. 2018, 8, 1–16. [Google Scholar] [CrossRef]
- Bjørk, A.A.; Kjær, K.H.; Korsgaard, N.J.; Khan, S.A.; Kjeldsen, K.K.; Andresen, C.S.; Box, J.E.; Larsen, N.K.; Funder, S. An aerial view of 80 years of climate-related glacier fluctuations in southeast Greenland. Nat. Geosci. 2012, 5, 427–432. [Google Scholar] [CrossRef]
- Hall, D.K.; Bayr, K.J.; Schöner, W.; Bindschadler, R.A.; Chien, J.Y. Consideration of the errors inherent in mapping historical glacier positions in Austria from the ground and space (1893–2001). Remote. Sens. Environ. 2003, 86, 566–577. [Google Scholar] [CrossRef]
- Thibert, E.; Sielenou, P.D.; Vionnet, V.; Eckert, N.; Vincent, C. Causes of Glacier Melt Extremes in the Alps Since 1949. Geophys. Res. Lett. 2018, 45, 817–825. [Google Scholar] [CrossRef]
- Rottler, E.; Kormann, C.; Francke, T.; Bronstert, A. Elevation-dependent warming in the Swiss Alps 1981–2017: Features, forcings and feedbacks. Int. J. Clim. 2019, 39, 2556–2568. [Google Scholar] [CrossRef]
- Vincent, C. Influence of climate change over the 20th Century on four French glacier mass balances. J. Geophys. Res. Space Phys. 2002, 107, ACL-4. [Google Scholar] [CrossRef]
- Comas-Bru, L.; McDermott, F. Impacts of the EA and SCA patterns on the European twentieth century NAO-winter climate relationship. Q. J. R. Meteorol. Soc. 2014, 140, 354–363. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (Area-Altitude) Analysis of Erosional Topography. Geol. Soc. Am. Bull. 1952, 63, 1117. [Google Scholar] [CrossRef]
- Lifton, N.A.; Chase, C.G. Tectonic, Climatic and Lithologic Influences on Landscape Fractal Dimension and Hypsome-try: Implications for Landscape Evolution in the San Gabriel Mountains, California. Geomorphology 1992, 5, 77–114. [Google Scholar] [CrossRef]
- Naegeli, K.; Huss, M.; Hoelzle, M. Change detection of bare-ice albedo in the Swiss Alps. Cryosphere 2019, 13, 397–412. [Google Scholar] [CrossRef]

| Glacier | Location (Alps) | Period | Δt (yr) | Elev. Range (m a.s.l.) | ELA (m a.s.l.) | Area (km2) | AAR (%) | Prevailing Aspect |
|---|---|---|---|---|---|---|---|---|
| Allalin | Valais | 1956–2017 | 62 | 2693–4180 | 3575 | 9.64 | 27 | NE |
| Hohlaub | Valais | 1956–2017 | 62 | 2843–4030 | 3365 | 2.128 | 30 | E |
| Schwarzberg | Valais | 1956–2017 | 62 | 2680–3566 | 3155 | 5.10 | 33 | NE |
| Gries | Valais | 1962–2017 | 56 | 2432–3307 | 3285 | 4.34 | 0 | NE |
| Gietro | Valais | 1966–2017 | 52 | 2751–3817 | 3315 | 5.20 | 22 | NW |
| Rhone | Bernese | 1885–2017 | 39 | 1775–3620 | 3085 | 15.10 | 35 | S |
| Aletsch | Bernese | 1940–1999 | 59 | 1560–4085 | 3055 | 83.02 | 56 | SE |
| Silvretta * | Central | 1918–2017 | 99 | 2474–3071 | 3025 | 2.60 | 1 | W |
| Clariden * | Glarus | 1914–2017 | 103 | 2534–3251 | 2935 | 4.50 | 25 | NE |
| Year | Date of Capture | Landsat Product ID | Sensor | Glaciers Covered |
|---|---|---|---|---|
| 1984, 1985 | 2 September 1984 | LT05_L1TP_194028_19840902_20170220_01_T1 | Landsat 5 Thematic Mapper (TM) | Aletsch, Allalin, Clariden, Gries, Hohlaub, Rhone, Schwarzberg |
| 2 September 1984 | LT05_L1TP_194027_19840902_20170220_01_T1 | Landsat 5 TM | Silvretta | |
| 12 September 1985 | LT05_L1TP_195028_19850912_20171212_01_T1 | Landsat 5 TM | Gietro | |
| 1994 | 4 August 1994 | LT05_L1TP_195027_19940804_20180215_01_T1 | Landsat 5 TM | Clariden |
| 4 August 1994 | LT05_L1TP_195028_19940804_20180215_01_T1 | Landsat 5 TM | Aletsch, Allalin, Gietro, Gries, Hohlaub, Rhone, Schwarzberg | |
| 6 August 1994 | LT05_L1TP_193028_19940806_20180214_01_T1 | Landsat 5 TM | Silvretta | |
| 2003, 2004 | 14 September 2003 | LT05_L1TP_195028_20030914_20161204_01_T1 | Landsat 5 TM | Gietro |
| 2 September 2004 | LT05_L1TP_193028_20040902_20161129_01_T1 | Landsat 5 TM | Silvretta | |
| 9 September 2004 | LT05_L1TP_194028_20040909_20161130_01_T1 | Landsat 5 TM | Aletsch, Allalin, Clariden, Gries, Hohlaub, Rhone, Schwarzberg | |
| 2014 | 14 September 2014 | LC08_L1TP_193028_20140914_20170419_01_T1 | Landsat 8 Operational Land Imager (OLI) | Silvretta |
| 28 September 2014 | LC08_L1TP_195027_20140928_20170419_01_T1 | Clariden | ||
| 28 September 2014 | LC08_L1TP_195028_20140928_20170419_01_T1 | Landsat 8 OLI | Aletsch, Allalin, Gietro, Gries, Hohlaub, Rhone, Schwarzberg |
| Glacier | Breaks | Chow Test | Rate of Change (Seg1) | Rate of Change (Seg2) | Rate of Change (Seg3) |
|---|---|---|---|---|---|
| Allalin | 1980 | 0.01 | 242.8 | −505.4 | - |
| Hohlaub | 1983 | 0.02 | 140.03 | −647.3 | - |
| Schwarzberg | 1971, 1980 | 0.40, 0.00 | −80.2 | 686 | −641.2 |
| Gries | 1980, 2001 | 0.04, 0.30 | −91.6 | 890 | −1561.4 |
| Gietro | 2001 | 0.20 | −224.5 | −874.8 | - |
| Silvretta | 2001 | 0.00 | −253 | −1076.6 | - |
| Clariden | 1988 | 0.01 | 17.3 | −605.5 | - |
| Glacier | Δt | Bw | Bs |
|---|---|---|---|
| Allalin | 62 | 0.42 | 0.90 |
| Hohlaub | 62 | 0.48 | 0.89 |
| Schwarzberg | 62 | 0.33 | 0.89 |
| Gries | 56 | 0.12 | 0.88 |
| Gietro | 52 | 0.15 | 0.85 |
| Rhone | 39 | 0.44 | 0.90 |
| Aletsch | 59 | 0.39 | 0.92 |
| Silvretta | 99 | 0.30 | 0.87 |
| Clariden | 103 | 0.46 | 0.88 |
| Allalin | Gietro | Gries | Hohlaub | Schwarzberg | Silvretta | Clariden | |
|---|---|---|---|---|---|---|---|
| Winter | 0.15 | 0.15 | 0.28 c | 0.05 | 0.11 | 0.22 | 0.27 b |
| Summer | 0.01 | −0.20 | −0.16 | −0.07 | −0.14 | −0.37 b | −0.43 a |
| Annual | 0.16 | 0.01 | 0.13 | −0.03 | −0.01 | 0.00 | 0.00 |
| Allalin | Gietro | Gries | Hohlaub | Schwarzberg | Silvretta | Clariden | |
|---|---|---|---|---|---|---|---|
| Winter | −0.16 | −0.19 | −0.43 a | −0.18 | −0.29 b | −0.32 a | −0.35 b |
| Summer | −0.20 | −0.23 | −0.40 a | −0.22 | −0.33 b | −0.21 | −0.06 |
| Annual | −0.25 c | −0.25 c | −0.51 a | −0.27 c | −0.40 a | −0.36 a | −0.27 c |
| Allalin | Gietro | Gries | Hohlaub | Schwarzberg | Silvretta | Clariden | |
|---|---|---|---|---|---|---|---|
| Winter precipitation | 96.69 | 130.90 | 116.80 | 62.70 | 102.34 | 131.95 | 167.76 |
| Summer temperature | −174.30 b | −123.60 | −325.32 a | −231.50 c | −317.78 a | −175.38 | −58.68 |
| Intercept | −318.00 | −648.60 | −409.60 | −89.46 | 567.42 | −500.80 | −776.65 |
| % of explained variability | 10.00 | 6.00 | 23.00 | 9.00 | 19.00 | 9.00 | 5.00 |
| Index | Bw | Bs | Ba | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Winter | Summer | Annual | Winter | Summer | Annual | Winter | Summer | Annual | |
| AMO | −0.08 | 0.01 | −0.05 | −0.80 a | −0.86 a | −0.86 a | −0.79 a | −0.82 a | −0.85 a |
| NAOCPC | 0.30 a | −0.16 | 0.26 b | −0.41 a | 0.69 a | 0.06 | −0.26 b | 0.61 a | 0.17 |
| NAOHurrell | 0.35 a | −0.25 b | 0.30 a | −0.15 | 0.39 a | −0.04 | −0.02 | 0.31 a | 0.06 |
| GBI | −0.34 a | 0.13 | −0.15 | 0.33 a | −0.68 a | −0.51 a | −0.44 a | −0.61 a | −0.55 a |
| SCA | −0.03 | −0.21 | −0.17 | 0.33 a | 0.66 a | 0.56 a | 0.25 b | 0.59 a | 0.47 a |
| EA | 0.14 | 0.03 | 0.07 | −0.86 a | −0.82 a | −0.88 a | −0.79 a | −0.77 a | −0.81 a |
| Glaciers | HIn | HI | Glacier Geometry |
|---|---|---|---|
| Aletsch | 0.58 | −1.62 | very top-heavy |
| Allalin | 0.46 | 1.26 | bottom-heavy |
| Gietro | 0.51 | −1.16 | equidimensional |
| Gries | 0.50 | −1.19 | equidimensional |
| Hohlaub | 0.36 | 2.06 | very bottom-heavy |
| Rhone | 0.54 | −1.24 | top-heavy |
| Schwarzberg | 0.44 | 1.41 | bottom-heavy |
| Clariden | 0.32 | 3.11 | very bottom-heavy |
| Silvretta | 0.51 | −1.06 | equidimensional |
| Glacier | Period | Total Retreat (m) | Retreat Rate (m/yr) |
|---|---|---|---|
| Aletsch | 1984–1994 | 433.09 | 43.31 |
| 1994–2004 | 282.11 | 28.21 | |
| 2004–2014 | 451.03 | 45.10 | |
| Allalin | 1984–1994 | 190.97 | 19.10 |
| 1994–2004 | 461.70 | 46.17 | |
| 2004–2014 | 190.06 | 19.01 | |
| Gietro | 1985–1994 | 102.59 | 11.40 |
| 1994–2003 | 78.08 | 8.67 | |
| 2003–2014 | 287.81 | 26.16 | |
| Gries | 1984–1994 | 85.06 | 8.51 |
| 1994–2004 | 209.22 | 20.92 | |
| 2004–2014 | 228.60 | 22.86 | |
| Hohlaub | 1984–1994 | 94.18 | 9.42 |
| 1994–2004 | 90.58 | 9.06 | |
| 2004–2014 | 136.15 | 13.61 | |
| Rhone | 1984–1994 | 98.81 | 9.88 |
| 1994–2004 | 38.56 | 3.86 | |
| 2004–2014 | 202.17 | 20.22 | |
| Schwarzberg | 1984–1994 | 15.43 | 1.54 |
| 1994–2004 | 30.86 | 3.09 | |
| 2004–2014 | 230.67 | 23.07 | |
| Clariden | 1984–1994 | 137.25 | 13.72 |
| 1994–2004 | 170.66 | 17.07 | |
| 2004–2014 | 193.02 | 19.30 | |
| Silvretta | 1984–1994 | 80.24 | 8.02 |
| 1994–2004 | 61.11 | 6.11 | |
| 2004–2014 | 65.78 | 6.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharehchahi, S.; Ballinger, T.J.; Jensen, J.L.R.; Bhardwaj, A.; Sam, L.; Weaver, R.C.; Butler, D.R. Local- and Regional-Scale Forcing of Glacier Mass Balance Changes in the Swiss Alps. Remote Sens. 2021, 13, 1949. https://doi.org/10.3390/rs13101949
Gharehchahi S, Ballinger TJ, Jensen JLR, Bhardwaj A, Sam L, Weaver RC, Butler DR. Local- and Regional-Scale Forcing of Glacier Mass Balance Changes in the Swiss Alps. Remote Sensing. 2021; 13(10):1949. https://doi.org/10.3390/rs13101949
Chicago/Turabian StyleGharehchahi, Saeideh, Thomas J. Ballinger, Jennifer L. R. Jensen, Anshuman Bhardwaj, Lydia Sam, Russell C. Weaver, and David R. Butler. 2021. "Local- and Regional-Scale Forcing of Glacier Mass Balance Changes in the Swiss Alps" Remote Sensing 13, no. 10: 1949. https://doi.org/10.3390/rs13101949
APA StyleGharehchahi, S., Ballinger, T. J., Jensen, J. L. R., Bhardwaj, A., Sam, L., Weaver, R. C., & Butler, D. R. (2021). Local- and Regional-Scale Forcing of Glacier Mass Balance Changes in the Swiss Alps. Remote Sensing, 13(10), 1949. https://doi.org/10.3390/rs13101949