Regional GNSS-Derived SPCI: Verification and Improvement in Yunnan, China
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area
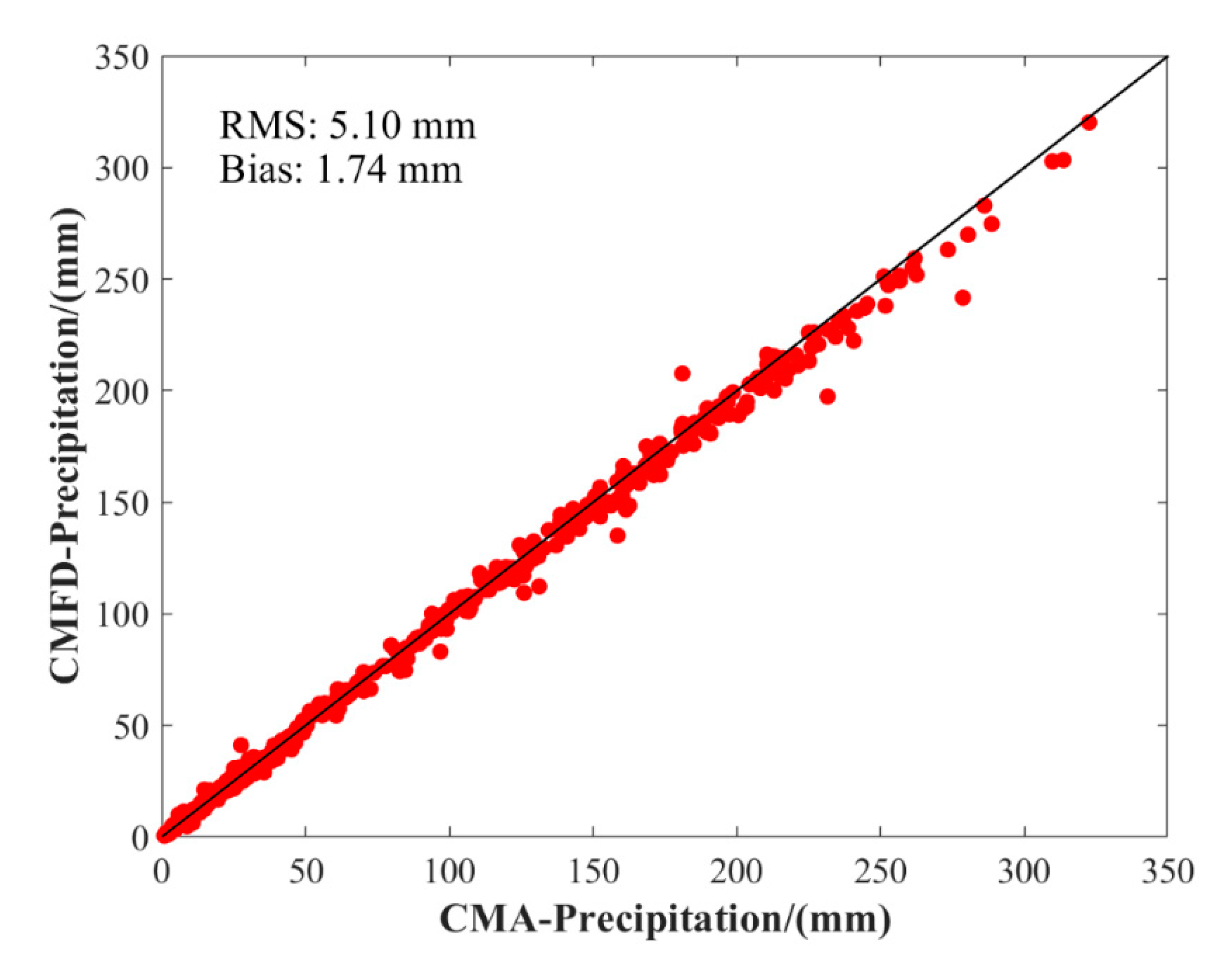
2.2. Data Description
2.3. Methodology
2.3.1. Correlation Analysis
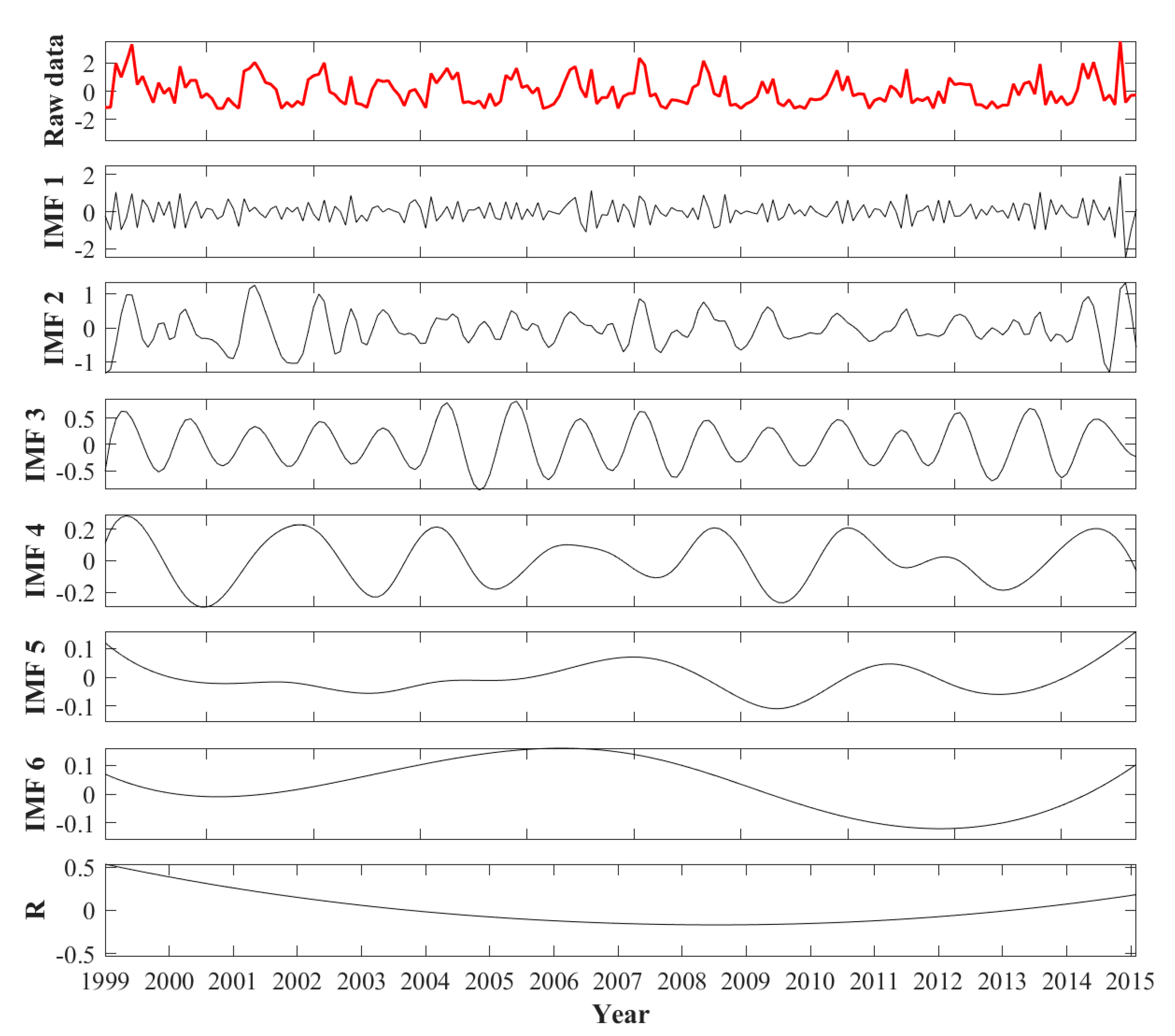
2.3.2. Ensemble Empirical Mode Decomposition (EEMD)
2.3.3. SPCI, CI, and SPEI
- (1)
- SPCI
- (2)
- SPEI
- (3)
- CI
2.3.4. Deviation Rate Calculation
3. Results
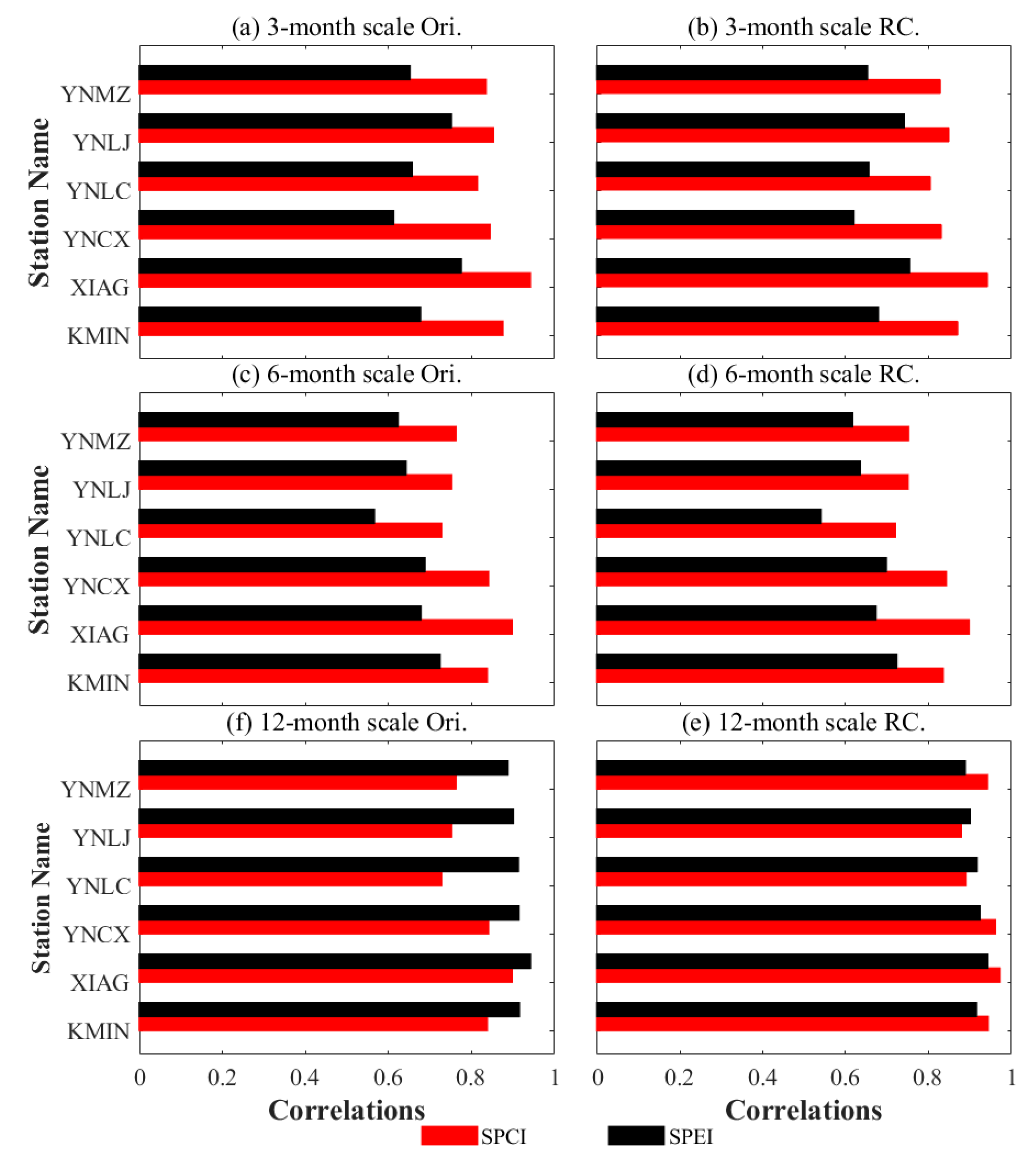
3.1. Correlation Analysis of SPCI and SPEI at Different Time Scales
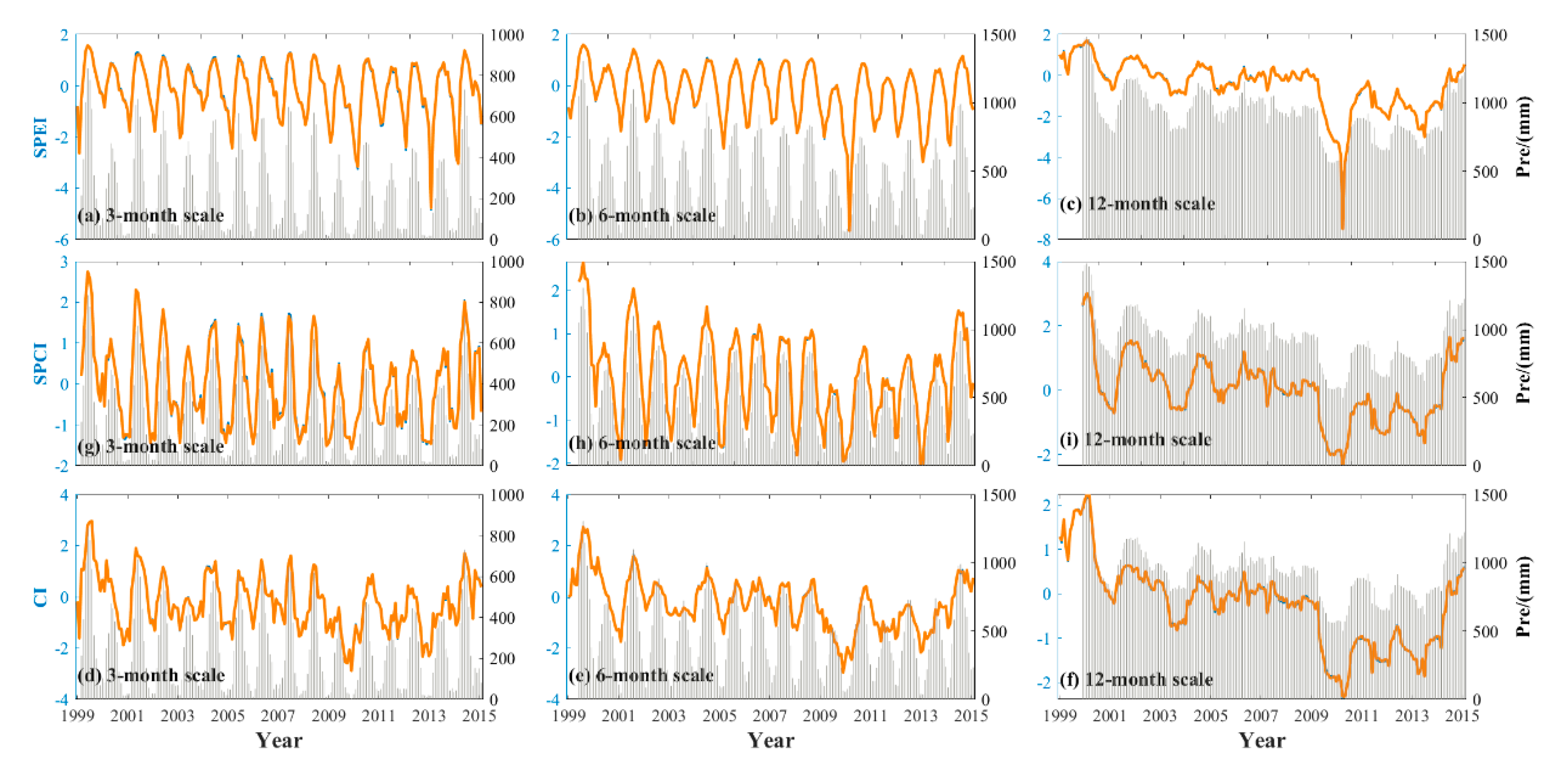
3.2. Correlation Analysis of SPCI/SPEI with CI at Different Time Scales
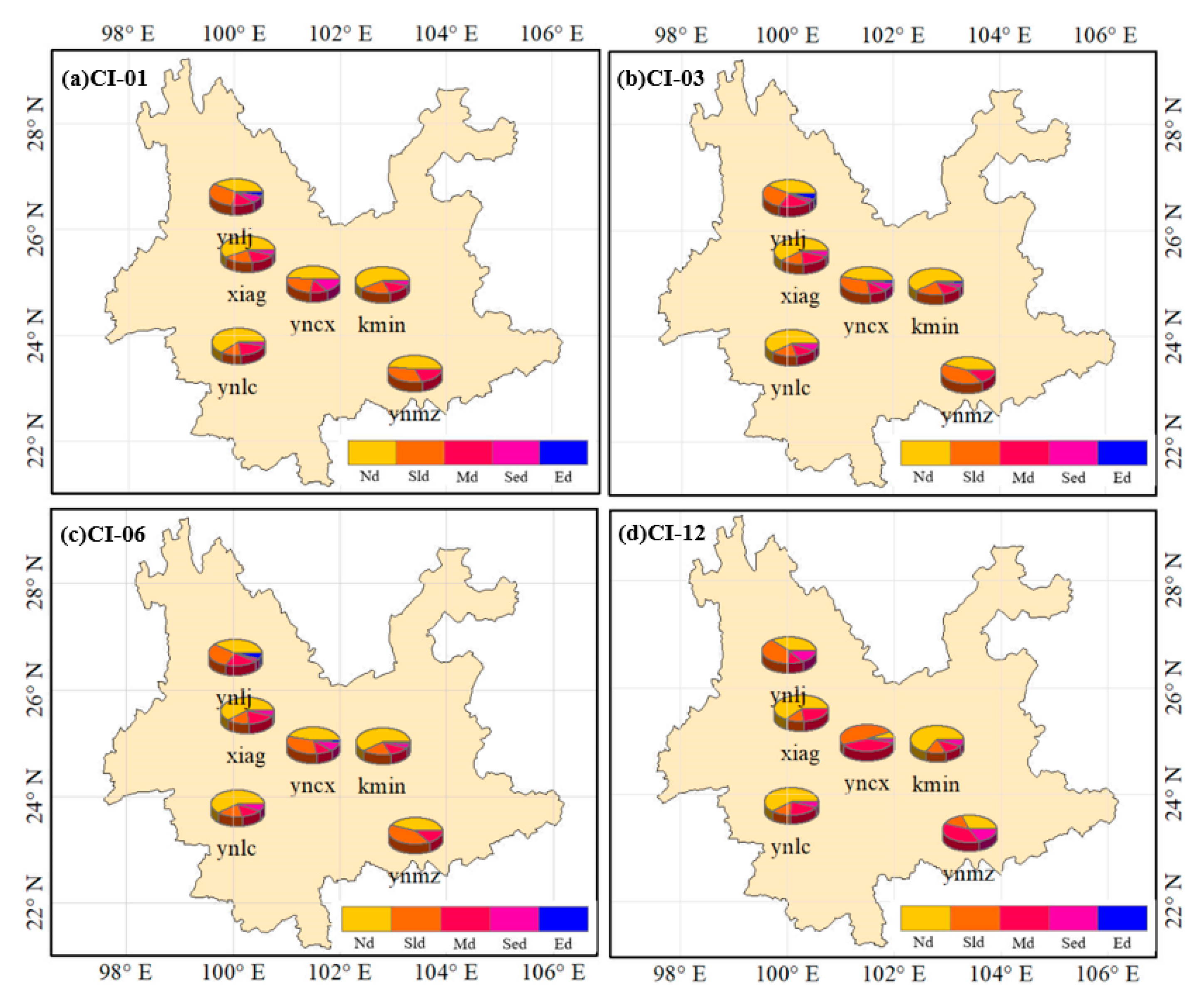
3.2.1. Determination of Multi-Time Scale CI (MCI)
3.2.2. Correlation Analysis of SPCI, SPEI, and CI
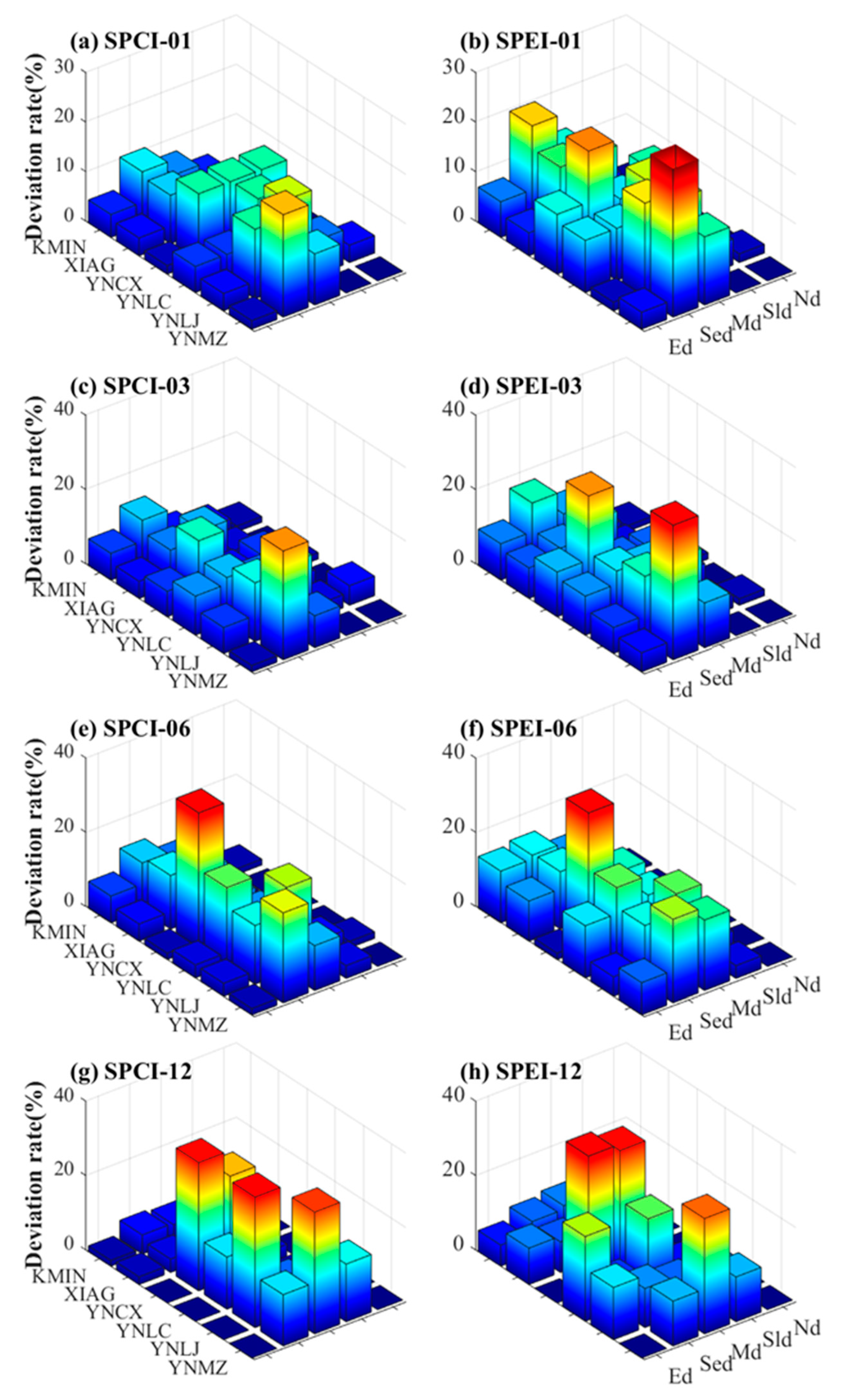
3.3. Comparison of Drought Monitoring Deviation at Different Time Scales
4. Discussion
4.1. Different Correlation Coefficients for Different Sites and Scales
4.2. Advantages of EEMD in SPEI Monitoring
4.3. Rationale for Multi-Scale CI
4.4. Necessity of Calibration
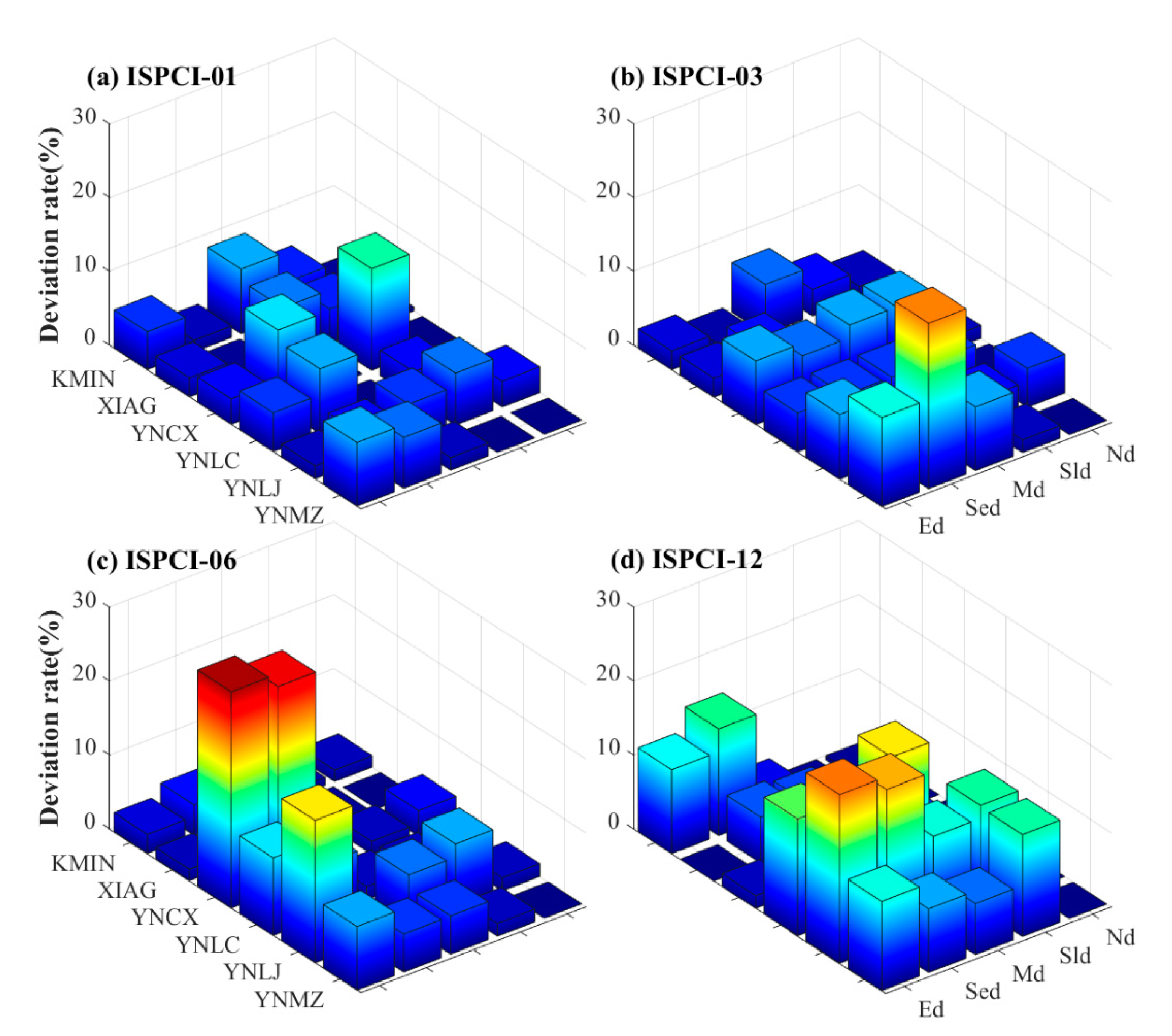
4.4.1. Improved SPCI (ISPCI) and Validation
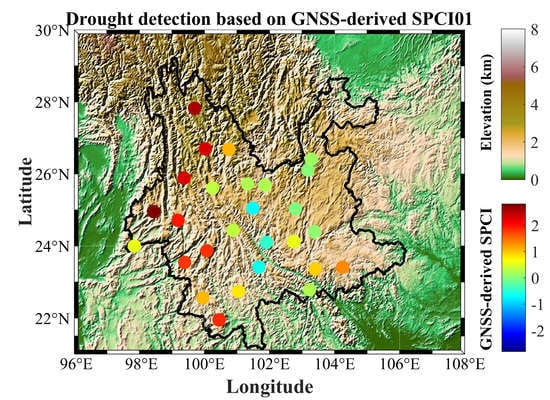
4.4.2. Spatial Comparison of ISPCI and CI in Yunnan
4.5. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, S.; Huang, Q.; Chang, J.; Leng, G. Linkages between hydrological drought, climate indices and human activities: A case study in the Columbia River basin. Int. J. Climatol. 2016, 36, 280–290. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Meng, E.; Luan, J. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Tong, S.; Lai, Q.; Zhang, J.; Bao, Y.; Lusi, A.; Ma, Q.; Li, X.; Zhang, F. Spatiotemporal drought variability on the Mongolian Plateau from 1980–2014 based on the SPEI-PM, intensity analysis and Hurst exponent. Sci. Total Environ. 2018, 615, 1557–1565. [Google Scholar] [CrossRef] [PubMed]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900–2008. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Zhang, B.; He, C. A modified water demand estimation method for drought identification over arid and semiarid regions. Agric. For. Meteorol. 2016, 230, 58–66. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.J.J. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- Reyes-Gomez, V.; Díaz, S.; Brito-Castillo, L.; Núñez-López, D. ENSO drought effects and their impact in the ecology and economy of the state of Chihuahua, Mexico. Wit Trans. Staten Art Sci. Eng. 2013, 64. [Google Scholar] [CrossRef]
- Sepulcre-Canto, G.; Horion, S.; Singleton, A.; Carrao, H.; Vogt, J. Development of a Combined Drought Indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef]
- Esfahanian, E.; Nejadhashemi, A.P.; Abouali, M.; Adhikari, U.; Zhang, Z.; Daneshvar, F.; Herman, M.R. Development and evaluation of a comprehensive drought index. J. Environ. Manag. 2017, 185, 31–43. [Google Scholar] [CrossRef]
- Rad, A.M.; Ghahraman, B.; Khalili, D.; Ghahremani, Z.; Ardakani, S.A. Integrated meteorological and hydrological drought model: A management tool for proactive water resources planning of semi-arid regions. Adv. Water Resour. 2017, 107, 336–353. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Ghale, Y.A.G.; Altunkaynak, A.; Unal, A. Investigation anthropogenic impacts and climate factors on drying up of Urmia Lake using water budget and drought analysis. Water Resour. Manag. 2018, 32, 325–337. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January1993; pp. 179–183. [Google Scholar]
- Rousta, I.; Olafsson, H.; Moniruzzaman, M.; Zhang, H.; Liou, Y.-A.; Mushore, T.D.; Gupta, A. Impacts of drought on vegetation assessed by vegetation indices and meteorological factors in Afghanistan. Remote Sens. 2020, 12, 2433. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Wood, A.W.; Hamlet, A.F.; Lettenmaier, D.P. Twentieth-century drought in the conterminous United States. J. Hydrometeorol. 2005, 6, 985–1001. [Google Scholar] [CrossRef]
- Wilhite, D.; Pulwarty, R.S. Drought and Water Crises: Integrating Science, Management, and Policy; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zhang, Q.; Cui, N.; Feng, Y.; Gong, D.; Hu, X. Improvement of Makkink model for reference evapotranspiration estimation using temperature data in Northwest China. J. Hydrol. 2018, 566, 264–273. [Google Scholar] [CrossRef]
- LI, S.; LIU, R.; SHI, L.; MA, Z.-G. Analysis on Drough tCharacteristic of He’nan in Resent 40 Year Based on MeteorologicalDrought Composite Index. J. Arid Meteorol. 2009, 27, 97–102. [Google Scholar]
- Liu, X.; Li, J.; Lu, Z.; Liu, M.; Xing, W. Dynamic changes of composite drought index in Liaoning Province in recent 50 year. Chin. J. Ecol. 2009, 28, 938–942. [Google Scholar]
- Qian, W.; Shan, X.; Zhu, Y. Ranking regional drought events in China for 1960–2009. Adv. Atmos. Sci. 2011, 28, 310–321. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bosy, J.; Rohm, W.; Sierny, J.; Kapłon, J. GNSS Meteorology. In Navigational Systems and Simulators; CRC Press: Boca Raton, FL, USA, 2011; pp. 79–83. [Google Scholar]
- Bordi, I.; Zhu, X.; Fraedrich, K. Precipitable water vapor and its relationship with the Standardized Precipitation Index: Ground-based GPS measurements and reanalysis data. Theor. Appl. Climatol. 2016, 123, 263–275. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 5874. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, K.; Wu, S.; Li, Z.; Cheng, Y.; Li, L.; Yuan, H. The correlation between GNSS-derived precipitable water vapor and sea surface temperature and its responses to El Niño–Southern Oscillation. Remote Sens. Environ. 2018, 216, 1–12. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Du, Z.; Yang, P.; Yao, Y. Improved Drought Monitoring Index Using GNSS-Derived Precipitable Water Vapor over the Loess Plateau Area. Sensors 2019, 19, 5566. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Haase, J.S.; Zhang, R.; Zheng, G.; Huang, J.; Shi, C.; Liu, J. The use of ground-based gps precipitable water measurements over china to assess radiosonde and era-interim moisture trends and errors from 1999 to 2015. J. Clim. 2017, 30, 7643–7667. [Google Scholar] [CrossRef]
- Duan, X.; Gu, Z.; Li, Y.; Xu, H. The spatiotemporal patterns of rainfall erosivity in Yunnan Province, southwest China: An analysis of empirical orthogonal functions. Glob. Planet. Chang. 2016, 144, 82–93. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, Y.; Zheng, J.; Cao, J.; Ma, T. Impacts of the vapor transportation by summer monsoon on drought and flooding in summer of Yunnan. J. Nat. Resour. 2012, 27, 293–301. [Google Scholar]
- Peng, G.; Liu, Y.; Zhang, Y. Research on Characteristics of Drought and Climatic Trend in Yunnan Province. J. Catastrophol. 2009, 24, 40–44. [Google Scholar]
- Zhang, W.; Zheng, J.; Ren, J. Climate characteristics of extreme drought events in Yunnan. J. Catastrophol. 2013, 28, 59–64. [Google Scholar]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Qiu, J. China drought highlights future climate threats: Yunnan’s worst drought for many years has been exacerbated by destruction of forest cover and a history of poor water management. Nature 2010, 465, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Dijin, W.; Bin, Z.; Yong, H.; Caihong, Z.; Kai, T.; Shaomin, Y. Horizontal crustal deformation in Chinese Mainland analyzed by CMONOC GPS data from 2009–2013. Geod. Geodyn. 2014, 5, 41–45. [Google Scholar] [CrossRef]
- Liu, R.; Li, H.; Yang, S. Regional crustal deformation characteristic before 2016 Yuncheng M4. 4 earthquake swarm based on CMONOC continuous GPS data. Geod. Geodyn. 2016, 7, 459–464. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, R.; Nie, Z.; Li, Y.; Chen, Z.; Wang, T. Research on variety characteristics of mainland China troposphere based on CMONOC. Geod. Geodyn. 2018, 9, 411–417. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Teng, Y.-T.; Van Hove, T.; Liljegren, J.C. Comparison of precipitable water observations in the near tropics by GPS, microwave radiometer, and radiosondes. J. Appl. Meteorol. 2001, 40, 5–15. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X.J.S.D. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M.J.W. A comparative study of potential evapotranspiration estimation by eight methods with FAO Penman–Monteith method in southwestern China. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- Yu, W.; Shao, M.; Ren, M.; Zhou, H.; Jiang, Z.; Li, D. Analysis on spatial and temporal characteristics drought of Yunnan Province. Acta Ecol. Sin. 2013, 33, 317–324. [Google Scholar] [CrossRef]
- Song, X.; Li, L.; Fu, G.; Li, J.; Zhang, A.; Liu, W.; Zhang, K. Spatial–temporal variations of spring drought based on spring-composite index values for the Songnen Plain, Northeast China. Theor. Appl. Climatol. 2014, 116, 371–384. [Google Scholar] [CrossRef]
- Song, X.; Song, S.; Sun, W.; Mu, X.; Wang, S.; Li, J.; Li, Y. Recent changes in extreme precipitation and drought over the Songhua River Basin, China, during 1960–2013. Atmos. Res. 2015, 157, 137–152. [Google Scholar] [CrossRef]
- Shen, R.; Huang, A.; Li, B.; Guo, J. Construction of a drought monitoring model using deep learning based on multi-source remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 48–57. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Chen, Q.; Pu, X.; Xiang, L. Multi-models for SPI drought forecasting in the north of Haihe River Basin, China. Stoch. Environ. Res. Risk Assess. 2017, 31, 2471–2481. [Google Scholar] [CrossRef]
- Shi, H.; Li, T.; Wei, J. Evaluation of the gridded CRU TS precipitation dataset with the point raingauge records over the Three-River Headwaters Region. J. Hydrol. 2017, 548, 322–332. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, C.; Chen, B.; Dai, W. Consistency evaluation of precipitable water vapor derived from ERA5, ERA-Interim, GNSS, and radiosondes over China. Radio Sci. 2019, 54, 561–571. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Wang, S.; Salahou, M.K.; Fang, Y. Analysis and Application of Drought Characteristics Based on Theory of Runs and Copulas in Yunnan, Southwest China. Int. J. Environ. Res. Public Health 2020, 17, 4654. [Google Scholar] [CrossRef]
- Paulo, A.; Rosa, R.; Pereira, L. Climate trends and behaviour of drought indices based on precipitation and evapotranspiration in Portugal. Nat. Hazards Earth Syst. Sci. 2012, 12, 1481–1491. [Google Scholar] [CrossRef]
- Lee, S.-W.; Kouba, J.; Schutz, B.; Lee, Y.J. Monitoring precipitable water vapor in real-time using global navigation satellite systems. J. Geod. 2013, 87, 923–934. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Ma, X.; Yao, W.; Yao, Y.; Li, X. An improved rainfall forecasting model based on GNSS observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4891–4900. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, Q.; Yao, Y.; Yao, W. A novel method of retrieving potential ET in China. J. Hydrol. 2021, 598, 126271. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Yao, W.; Yao, Y. Hourly rainfall forecast model using supervised learning algorithm. IEEE Trans. Geosci. Remote Sens. 2021, 1–9. [Google Scholar] [CrossRef]






| Name | Sources | Spatial Coverage | Temporal Resolution | Temporal Coverage | Sources |
|---|---|---|---|---|---|
| Temperature max; Temperature min; Wind speed; Relative humidity; Sunshine hours; Precipitation | CMA | 826 | Daily | 1949–2018 | http://data.cma.cn/; accessed on 12 May 2020 |
| PWV | CMONOC | 259 | 6-hourly | 1999–2015 | [31] |
| Precipitation | CMFD | 0.1° | Monthly | 1979–2018 | https://data.tpdc.ac.cn/; accessed on 12 May 2020 |
| Categories | SPEI Values |
|---|---|
| Extremely dryness | Less than −2 |
| Severe dryness | −1.99 to −1.5 |
| Moderate dryness | −1.49 to −1.0 |
| Near normal | −1.0 to 1.0 |
| Moderate wetness | 1.0 to 1.49 |
| Severe wetness | 1.5 to 1.99 |
| Extremely wetness | More than 2 |
| Grade | Type | Scope of Drought Effects | |
|---|---|---|---|
| 1 | No drought | −0.6 < | Precipitation is normal or higher than in normal years, moist surface, no signs of drought |
| 2 | Light drought | −1.2 < ≤ −0.6 | Precipitation is less than normal years, surface air is dry, soil moisture exhibits mild deficiencies |
| 3 | Moderate drought | −1.8 < ≤ −1.2 | Precipitation continued below normal years, soil surface is dry, soil water shortage, surfaces of plant leaves exhibit daytime wilting |
| 4 | Serious drought | −2.4 < ≤ −1.8 | Soil appear sustained severe lack of moisture, thicker dry soil, wilting plants, dry leaves, and fruit shedding. Serious negative impact on crops and ecological environment, industrial production, and drinking water |
| 5 | Special serious drought | ≤ −2.4 | Soil appeared a serious shortage of water for a long time, Surface plants withered or died, causing a serious impact on crops and ecological environment with a greater impact on drinking water and industrial production |
| Station Name | Length | SPEI-01 | SPCI-01 | ||
|---|---|---|---|---|---|
| Original | RC | Original | RC | ||
| KMIN | 1999.03–2015.04 | 0.71 | 0.72 | 0.92 | 0.92 |
| XIAG | 1999.03–2015.04 | 0.83 | 0.81 | 0.92 | 0.90 |
| YNCX | 2010.07–2015.04 | 0.61 | 0.62 | 0.87 | 0.84 |
| YNLC | 2010.08–2015.04 | 0.72 | 0.71 | 0.88 | 0.86 |
| YNLJ | 2010.8–2015.04 | 0.80 | 0.77 | 0.91 | 0.91 |
| YNMZ | 2010.07–2015.04 | 0.74 | 0.65 | 0.88 | 0.85 |
| 1-Month Scale | 3-Month Scale | 6-Month Scale | 12-Month Scale | Mean | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SPCI | SPEI | SPCI | SPEI | SPCI | SPEI | SPCI | SPEI | SPCI | SPEI | |
| Nd. | 3.41 | 6.67 | 6.34 | 8.80 | 3.72 | 9.06 | 0.60 | 8.72 | 3.52 | 8.31 |
| Sld. | 12.40 | 19.81 | 16.22 | 20.82 | 20.75 | 20.98 | 17.69 | 13.81 | 16.76 | 18.86 |
| Md. | 11.69 | 14.51 | 9.61 | 13.00 | 12.90 | 16.30 | 14.11 | 19.93 | 12.08 | 15.94 |
| Sed. | 5.60 | 4.96 | 3.81 | 4.40 | 3.10 | 3.73 | 4.88 | 6.33 | 4.35 | 4.86 |
| Ed. | 0.76 | 0.38 | 1.42 | 0.84 | 0.55 | 0.09 | 0 | 0 | 0.68 | 0.33 |
| Mean | 6.77 | 9.27 | 7.48 | 9.57 | 8.20 | 10.32 | 7.45 | 9.76 | 7.48 | 9.73 |
| 1-Month Scale | 3-Month Scale | 6-Month Scale | 12-Month Scale | Mean | |
|---|---|---|---|---|---|
| Nd | 4.47 | 6.64 | 11.98 | 10.62 | 6.72 |
| Sld | 5.26 | 6.62 | 7.87 | 10.13 | 6.10 |
| Md | 3.83 | 44.87 | 3.10 | 8.74 | 4.22 |
| Sed | 5.60 | 4.04 | 2.59 | 6.55 | 3.77 |
| Ed | 0.76 | 1.42 | 1.12 | 0.08 | 0.67 |
| Mean | 3.98 | 4.72 | 5.33 | 7.22 | 4.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Yao, Y.; Zhao, Q. Regional GNSS-Derived SPCI: Verification and Improvement in Yunnan, China. Remote Sens. 2021, 13, 1918. https://doi.org/10.3390/rs13101918
Ma X, Yao Y, Zhao Q. Regional GNSS-Derived SPCI: Verification and Improvement in Yunnan, China. Remote Sensing. 2021; 13(10):1918. https://doi.org/10.3390/rs13101918
Chicago/Turabian StyleMa, Xiongwei, Yibin Yao, and Qingzhi Zhao. 2021. "Regional GNSS-Derived SPCI: Verification and Improvement in Yunnan, China" Remote Sensing 13, no. 10: 1918. https://doi.org/10.3390/rs13101918
APA StyleMa, X., Yao, Y., & Zhao, Q. (2021). Regional GNSS-Derived SPCI: Verification and Improvement in Yunnan, China. Remote Sensing, 13(10), 1918. https://doi.org/10.3390/rs13101918