Abstract
Plant phenotyping deals with the metrological acquisition of plants in order to investigate the impact of environmental factors and a plant’s genotype on its appearance. Phenotyping methods that are used as standard in crop science are often invasive or even destructive. Due to the increase of automation within geodetic measurement systems and with the development of quasi-continuous measurement techniques, geodetic techniques are perfectly suitable for performing automated and non-invasive phenotyping and, hence, are an alternative to standard phenotyping methods. In this contribution, sequentially acquired point clouds of cucumber plants are used to determine the plants’ phenotypes in terms of their leaf areas. The focus of this contribution is on the spatio-temporal segmentation of the acquired point clouds, which automatically groups and tracks those sub point clouds that describe the same leaf. The application on example data sets reveals a successful segmentation of 93% of the leafs. Afterwards, the segmented leaves are approximated by means of B-spline surfaces, which provide the basis for the subsequent determination of the leaf areas. In order to validate the results, the determined leaf areas are compared to results obtained by means of standard methods used in crop science. The investigations reveal consistency of the results with maximal deviations in the determined leaf areas of up to 5%.
1. Introduction
In times of climate change, the topic of phenotyping has become more and more important—in order to ensure global food security, high-yielding and climate-resistant crops are required, making a profound understanding of the interaction between environmental factors and a plant’s phenotype mandatory [1]. The task of phenotyping involves the monitoring of plants’ appearances (e.g., stem height, size and inclination as well as leaf width, inclination, and area) under controlled but changing environmental influences [2]. Usually, the investigations are performed under greenhouse conditions, but field-based phenotyping is also becoming more and more important (see, for example, References [3,4]). The measurement methods traditionally used in crop science are often destructive or invasive [5], making a temporal monitoring of the plants impossible or at least complicated. Furthermore the measurements are typically performed manually and, hence, are very tedious [6]. An example of a non-destructive invasive classical method is the manual digitization of characteristic points of a plant, as presented for example, in Reference [7]. In addition to its labour-intensity, the strong simplification of the resulting plant model causes falsified values of the plant’s descriptive parameters. As the procedure is invasive, detected movements of the plant cannot be attributed solely to natural environmental influences. Because of these drawbacks and due to the demand to investigate several thousands of plants per day in order to guarantee a successful phenotyping [8], the developments towards a non-destructive (semi-)automatic phenotyping is progressing, imposing requirements on the measurement technique and on the subsequent analysis of the large amount of acquired data. Initial investigations regarding a non-destructive data acquisition almost exclusively involved two-dimensional (2D) imaging techniques (see e.g., Reference [9] or Reference [10]). However, due to occlusions within 2D data that can hardly be resolved solely on the basis of colour information [11], three-dimensional (3D) data is increasingly used for plant phenotyping [12]. Due to their relatively low costs, cameras are still the most common sensors used in phenotyping [13,14]. In order to obtain 3D information of the plants under investigation, multiview images are used to construct 3D point clouds, for example with structure from motion (see e.g., References [2,6,11,13,14]). Another possibility is to complete 2D images with depth information of a time-of-flight camera [15]. Due to the fast and contactless measuring process, laser scanners are also perfectly suitable for phenotyping tasks. Laser scanners directly yield a 3D point cloud and, hence, avoid the subsequent construction of 3D point clouds. Furthermore, they are more robust with regard to changing lighting conditions than cameras [5] and, therefore, do not require the subsequent use of post-processing algorithms to deal with different lightning conditions. However, compared to digital cameras, the purchase of a laser scanner is usually expensive. Laser scanner-based approaches for plant phenotyping can be found in References [5,12,16,17].
Although the developments at sensor level allow for a fast and automated data acquisition, the large amount of acquired data is only manageable when the data analysis is also performed automatically. One of the most crucial tasks within the processing chain is the segmentation step during which the unordered 3D point cloud is partitioned into meaningful subsets. With regard to phenotyping, the segmentation is a grouping of points that describe the same plant organ. The segmentation of digital images and laser scanner-based 3D point clouds is generally an extensively studied field of research, but the segmentation of natural objects like plants still presents a challenge—apart from their complex structure, the different forms of appearance make a segmentation difficult [11]. Although occlusions can be solved to a large extent by means of 3D data, touching or overlapping plant organs are still very difficult to separate [6]. Nevertheless, a variety of approaches for plant segmentation—either based on images or on laser scanner-based 3D point clouds—can be found in the literature. In contrast to anthropogenic objects, plant organs cannot be described sufficiently well by simple geometric primitives. For this reason, rule-based methods exist which use, for example, Lindenmayer (L)-systems (for detailed information see, for example, Reference [18]) in order to build complex models of the plants [11]. These pre-generated models are compared with the point cloud, and structures similar to these models are identified. However, the creation of suitable models requires expert knowledge of a plant’s structure and is only of limited use. Hence, hybrid approaches, which account for the complexity of different plants as well as the variability within the same plant organs, are usually proposed. In Reference [15], a pre-segmentation is achieved by a hierarchical color segmentation and is afterwards improved by fitting quadratic surfaces through the sparse 3D data provided by a time-of flight camera. In Reference [2], the point clouds are coarsely segmented by means of a region-growing algorithm. Afterwards, a primitive fitting is used to segment the stem and the petioles, whereas a clustering according to the vertices’ normal vector distribution as well as symmetry considerations are used to segment the leaves. In Reference [5], also a multi-step procedure is proposed. Based on a graph constructed from the 3D point cloud, the major intrinsic directions are detected by means of a general data clustering (spectral embedding, for more details see Reference [5]). Afterwards, a clustering groups the points that describe the same plant organ. A similar approach can be found in Reference [13]—first- and second-order tensors, which capture local point properties, are used to evaluate neighbouring points with regard to their similarity. A distinction between leaf and stem is made by means of local eigenvalues. In Reference [19], a surface feature histogram-based approach is used in order to classify grapevine stems and leaves as well as wheat ears from other plant organs.
In the case of a temporal monitoring of plants, the segmentation additionally has to be solved over time. This task has to account for a plant’s movement caused by its environmental interaction as well as by its growth, leading to non-rigid deformations of the plant organs [15]. In the context of the plant’s growth it must also be taken into account that new plant organs develop over time, whereas others decay [16]. In Reference [2] a rough alignment of the spatial segmented point clouds and a subsequent matching based on the plants’ internodes is proposed, whereas Reference [16] uses a forward-backward approach which uses future information to improve the segmentation results from previous point clouds.
In this contribution a fully automated spatio-temporal segmentation procedure for the phenotyping of cucumber plants based on 3D point clouds is proposed. The strategy focuses on the segmentation of individual leaves as they are the main organ of plants, being responsible for the energy and oxygen supply of the plant by means of photosynthesis and, hence, having a major influence on the plant’s growth [20,21]. The species under investigation is the cucumber plant, as it is characterized by large leaves with good-natured shape and, hence, is a suitable species for the initial investigations conducted within this contribution. In future, the investigations conducted may be further developed, allowing for the phenotyping of other plant species. A hybrid alternative to the spatial segmentation strategies presented above is introduced, the results of which are temporally linked in a second step, resulting in spatio-temporally segmented time series of point clouds. In contrast to the majority of segmentation strategies proposed in the literature, our strategy does not focus either on the spatial segmentation or on the temporal one, but directly provides a spatio-temporal segmentation of the acquired point clouds. Both steps are realized in a fully automatic way and do not require any user-interaction. One of its major strength is the use of information gained from the temporal segmentation to improve possible erroneous spatial segmentations. Furthermore, the segmentation strategy automatically implements a noise filtering, so that no filtering pre-processing steps are required. The segmented leaves are afterwards automatically modelled by means of best-fitting B-spline surfaces, and the leaf areas are subsequently computed. The use of best-fitting B-spline surfaces has two major advantages over leaf modelling strategies available in the literature—firstly, the use of approximating surfaces leads to a considerably better noise reduction than non-filtering modelling strategies like for example, triangulation strategies or alpha-shapes (see for example Reference [19]). Secondly, the enhanced B-spline surfaces are a a very flexible tool and, hence, are more appropriate models for complex leaves than for example, quadratic surfaces. Consequently, the chosen modelling strategy leads to more reliable leaf areas than the majority of strategies proposed in the literature. The phenotyping results yielded by the developed strategy are compared to those yielded by standard methods used in crop science. Based on this comparison the applicability of the used multi-sensor system (MSS) to plant phenotyping is evaluated. Finally, the influence of the measurement noise is investigated by applying the developed approach to a point cloud provided by a common terrestrial laser scanner.
2. Materials and Methods
2.1. Data Acquisition
The phenotyping strategy developed below is applied to two plants and which are acquired several times in different growth stages by a variety of sensors. The main focus is on the MSS for plant phenotyping introduced in Section 2.1.1, the main object capturing sensor of which is an automotive grade laser scanner. Additionally, point clouds acquired by means of a terrestrial laser scanner are investigated. Finally, sensors typically used in crop science are used to acquire reference values.
2.1.1. Multi-Sensor-System (MSS) for Plant Phenotyping
The data sets used in this methodology study are primarily captured by means of the MSS depicted in Figure 1 in order to investigate the applicability of automotive grade laser scanners to the phenotyping task. Due to the assembly of different kind of sensors on a single platform, we refer to it as an MSS.

Figure 1.
(Left): MSS on the vertical lift acquiring a plant probe. (Right): Front view of the MSS senors: (1) 2D laser scanner of type SICK LMS 500-20000 PRO-HR, (2) 2D laser scanner of type Hokuyo URG-04LX, (3) digital camera of type The Imaging Source DFK 41.
The object capturing sensors are a 2D laser scanner of type SICK LMS 500-20000 PRO-HR (SICK AG, Waldkirch, Germany) (cf. Figure 1 right no 1) and a digital camera with 1280 × 960 pixel of type The Imaging Source DFK 41 (The Imaging Source Europe GmbH, Bremen, Germany) (cf. Figure 1 right no 3). The latter is only used to enrich the laser scanner data with color information for a better visual interpretation. This 3D point cloud colouring is realized by pre-determining the relative orientation of both sensors within a system calibration procedure. The SICK laser scanner is the MSS’s core capturing sensor and is responsible for the data acquisition of the plant probe. The laser scanner’s beam is near-infrared (905 nm) with divergence of 4.7 mrad (4.7 mm diameter at 1 m distance). A value of 12 mm at 6 m (object remission of 100%) is given for the range accuracy in the manufacturer’s data sheet. In general, the 2D laser scanner provides 2D scan lines or 2D profiles which are computed by means of the raw measurements (horizontal angles and ranges). The profiles’ spatial resolution is defined by the angle increment used ( for the SICK laser scanner) and the distance to the object (approximately 1 m in this study). Due to the sensor’s mounting on the MSS with its zero direction pointing towards the plant (see Figure 1), horizontal 2D scan lines of the plant under investigation arise. By vertically moving the MSS, a 3D point cloud results. The vertical resolution is determined by the speed of the vertical movement and the scanning frequency of 25 Hz per 2D profile. The vertical movement can be obtained with an accuracy of ≈4 mm (obtained from repeated experiments). As the object capturing sensors are in motion during data acquisition and more than a single survey position is required to capture the entire plant, referencing sensors are required in order to track the individual viewpoint positions and to ease the way to an on-the-fly registration of multiple viewpoints. The core referencing sensor is a 2D laser scanner of type Hokuyo URG-04LX (Hokuyo Automatic Co., LTD., Osaka, Japan) (cf. Figure 1 right no 2), which faces downwards and, hence, measures the height above ground. The final 3D point cloud is obtained by data fusion of the horizontal scan lines provided by the object capturing laser scanner and the height component determined by the referencing laser scanner. It is worth mentioning that only relative changes in height are of interest so that a rigorous determination of the mutual orientation of the two involved laser scanners is not required. For in-depth discussion regarding the MSS see Reference [22].
A single plant is entirely acquired by means of the MSS from at least three viewpoints that are arranged at a distance of approximately 1 m from the plant at angles of to each other. The entire data acquisition takes less than min per plant. The result from each MSS position is a 3D point cloud of the acquired plant in the specific field of view. Each single 3D point cloud overlaps with the point clouds acquired from the neighbouring MSS positions. In a spatial referencing process, which is carried out in two stages, the 3D point clouds are aligned into a common coordinate frame (cf. Reference [22]): (1) a coarse registration by means of transformation parameters a priori known from the data acquisition set-up is followed by (2) a fine registration by means of the iterative closest point algorithm [23]. The temporal registration of different epochs is based on the previously performed spatial registration. In order to define a common coordinate system over time, stable areas in the spatially referenced point clouds have to be identified. In these initial studies cylindrical, retro-reflective targets are placed in the scanning area and are used to temporally register the acquired point clouds.
In order to evaluate the registration results, an accuracy assessment of the acquired 3D point cloud is performed for a representative nearly planar region of the data (cyan coloured region in Figure 2) in three subsequent epochs with an inter-epochal time span of 5 min. For the accuracy assessment a best-fitting plane is estimated for the nearly planar region. The dimension in width and height of ≈5 cm is chosen in order to keep the effect of the leaf curvature as small as possible. Statistical values for the residuals with respect to the best fitting plane are calculated for each epoch. In Table 1, the minimal and maximal values as well as the standard deviation of the residuals are summarized. These statistics reveal that the noise level of the acquired 3D point cloud is within the sensors’ specifications and, therefore, emphasize the quality of the registration procedure. Hence, plant is repeatedly scanned by the MSS in two different growth stages, resulting in eight data sets listed in Table 2. The respective names are composed of the plant’s name, the measuring epoch and the growth stage.
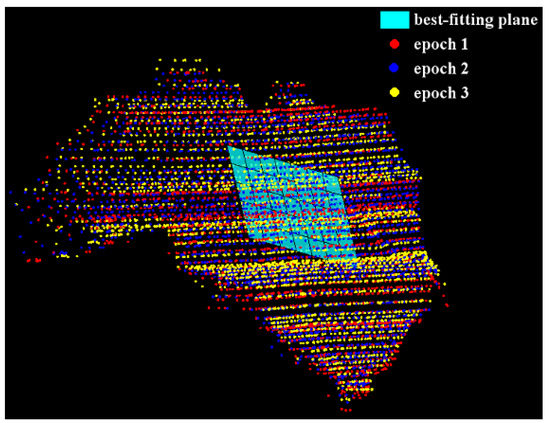
Figure 2.
Accuracy assessment. Exemplary leaf of a plant (height: 18 cm, width: 23 cm) in three subsequent epochs and the 5 cm × 5 cm patch (cyan).

Table 1.
Statistical values (minimum, maximum and standard deviation) of the residuals (res) of the plane fitting sketched in Figure 2.

Table 2.
Data sets used for the phenotyping. The data sets’ denotations are composed of the plant’s name (either or ), the measuring epoch () and the growth stage (either e (early) or l (late)).
2.1.2. Reference Measurements by Means of a Geodetic Laser Scanner
In order to investigate the influence of the noise level on the segmentation procedure and, consequently, on the phenotyping results, plant is scanned by means of a geodetic terrestrial laser scanner (TLS) of type Zoller+Fröhlich (Z + F) IMAGER 5010 (cf. Table 2). The ZF IMAGER 5010 is characterized by a range noise of 0.4 mm @ 10 m for surfaces with grey colour.
2.1.3. Reference Measurements by Means of Standard Sensors of Crop Science
The phenotyping results provided by the laser scanning point clouds are evaluated by means of reference values obtained by two standard sensors and corresponding analysis strategies used in the field of crop science. Firstly, reference measurements with a 3D digitizer (FASTRAK, Polhemus Inc., Colchester, VT, USA), representing an established method to capture static plant parameters, are conducted. The digitizer is a manual, contact-based measuring system that records single points in an electromagnetic field. The recording of the leaves is usually performed in a standardized order [7]. The accuracy of the digitizer is given with 1 mm under controlled conditions and with 10 mm under field conditions [24]. Using this strategy, each leaf is described by thirteen defined characteristic points [25] as presented in Figure 3. The leaf areas are then computed based on these generalizing models of the cucumber leaves.

Figure 3.
Digitizer model of a cucumber leaf.
Secondly, the leaf area is destructively determined by means of a leaf area meter LI-3100 (LI-COR, Lincoln, NE, USA). The last column of Table 2 gives the type of reference data that is available for the respective data set.
2.2. Spatio-Temporal Leaf Segmentation
The first step of an automatic phenotyping is the segmentation of the point cloud: according to a similarity measure, the set of the so far unordered point cloud is partitioned into disjoint and connected subsets. In the case of plant phenotyping, this task corresponds to the aggregation of points that describe the same plant organ, particularly of points that describe the same leaf. Because of the varying appearances and the complex structure of plants as well as occluded and touching leaves, the segmentation of plants is a challenging task and the use of generic segmentation algorithms is usually not satisfying. In the following sections a 3-step-segmentation algorithm is proposed, resulting in a spatio-temporal segmentation of time series of 3D point clouds, which provides the basis for the subsequent phenotyping. One of the strengths of the developed algorithm is that—apart from the registration—no further pre-processing steps are required, as the segmentation procedure as well as the subsequent B-spline-based leaf surface estimation directly implement a filtering of the noisy point clouds. The segmentation procedure, consisting of a graph-based pre-segmentation (Section 2.2.1), a statistically-based region merging (Section 2.2.2) as well as a shape matching by means of dynamic time warping (Section 2.2.3), is schematically sketched in Figure 4.
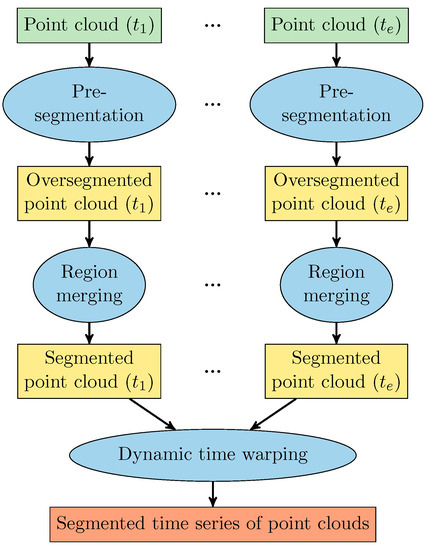
Figure 4.
Sketch of the developed segmentation procedure.
2.2.1. Spatial Segmentation: Graph-Based Pre-Segmentation
Theoretically, both spectral and geometric properties of point clouds can be used for segmentation purposes. Comparing these properties of plant leaves, it is obvious that only the latter provide an appropriate basis in order to separate touching leaves. However, geometric properties may vary to a large extent within the same leaf. For this reason, the segmentation proposed is based on the adaptive graph-based algorithm introduced in Reference [26], the strength of which is the ability to deal with varying properties within the same segment. Using this algorithm, the point cloud is interpreted to be a graph consisting of nodes and undirected edges , the weights of which express the similarity of the connected nodes. Each node corresponds to an individual segment in the initial segmentation. The respective edge list is constructed, sorted in ascending order and traversed. While traversing the edge list, it is examined whether there is evidence for an object boundary between the two nodes connected by the respective edge by comparing two values:
- The internal difference measures the variation in the properties within a segment C and is defined as the maximum weight of the minimum spanning tree (MST) constructed by the nodes of C:
- The difference between two neighbouring segments and evaluates the variation between the properties of the two segments and is defined as the minimum of the weights belonging to all edges connecting and :
The segments and remain separated if the comparison of these two values gives evidence for an object boundary:
otherwise they are merged. The threshold unit in Equation (3) controls the level of over- or undersegmentation and is calculated from the segment’s size as well as a freely chosen constant k. The success of the segmentation is to a large extent determined by a reasonable choice of the similarity measure w. In order to solve the main challenge in plant phenotyping—the separation of touching leaves—the angle between the corresponding surface normals and , the change of which indicates the transition between two touching surfaces, has proven to be an appropriate similarity measure:
However, the change of the normal direction within a leaf may be larger than the change of the normal direction between two touching leaves. Hence it is usually impossible to directly achieve a satisfying result based on this strategy; rather the point cloud is either over- or undersegmented, depending on the choice of the value of k. In this paper, the parameter k is chosen to obtain a result with only oversegmented leaves (Figure 5), providing the basis for a subsequent post-processing. The specific values for k are heuristically determined for individual growth stages of cucumber plants.

Figure 5.
Oversegmented point cloud as a result of using the algorithm proposed in Reference [26]. The points’ affiliations to the respective segments are indicated by the colouring.
2.2.2. Spatial Segmentation: Statistically-Based Region Merging
The post-processing is implemented as a region merging—segments exceeding a certain size are considered as super-segments which are extended by neighbouring segments if there is evidence that the segments describe the same leaf. The respective decision is based on two statistical hypothesis tests, whose principle ideas are given in the following. For a detailed description of the region merging we refer to Reference [27].
- The first test evaluates whether two neighbouring segments describe the same surface. For this purpose, a part of the super-segment (blue-coloured segment in Figure 6) as well as the neighbouring segment under investigation (green-coloured segment in Figure 6) are approximated by means of second-order surfaces (cyan- and green-coloured surfaces in Figure 6). Afterwards, the parameters of the best-fitting second order surfaces are statistically checked for equality according to the difference test described in Reference [28]. If the parameters do not differ significantly, the super-segment and the segment under investigation are merged.
 Figure 6. Surface-based region merging: the parameters of best-fitting second-order surfaces are statistically tested for equality.
Figure 6. Surface-based region merging: the parameters of best-fitting second-order surfaces are statistically tested for equality. - In the second test the segments’ border edges are evaluated. As motivated by Figure 7, it can be assumed that two neighbouring segments describe the same leaf if the respective border edges describe the same space curve: This is the case in Figure 7 for the two segments with the yellow-coloured border edges, whereas the two segments with the cyan-coloured border edges describe two different, but touching leaves. In order to realize this second test, the edge points of the super-segment and of the respective neighbouring segments under investigation are automatically identified by means of a variant of the Douglas-Peucker-algorithm described in Reference [27]. Afterwards, the edge points describing a joint edge between two segments are approximated by means of space curves (cf. Figure 7). Analogously to the surface-based region merging, the parameters of the two resulting space curves are statistically checked for equality. If the estimated parameters do not differ significantly, the super-segment and the segment under investigation are merged.
 Figure 7. Edge-based region merging: neighbouring segments belong to the same leaf, if their border edges describe the same space curve.
Figure 7. Edge-based region merging: neighbouring segments belong to the same leaf, if their border edges describe the same space curve.
2.2.3. Temporal Segmentation: Dynamic Time Warping
When not only geometric characteristics of plants, but also their changes over time are of interest, a time series of point clouds provides the basis for the phenotyping. The segmentation of this time series has to be consistent in time, making a temporal segmentation necessary. The strategy used is motivated by Figure 8, presenting the results of the spatial segmentations of two consecutive measuring epochs. As can be seen, in some few cases one of the point clouds may be oversegmented, leading to a segment’s splitting from one epoch to another (indicated by the white circle in Figure 8). Contrary to the segment’s centre of mass or its size, the segment’s shape is mostly unaffected by this effect, motivating the use of shape matching algorithms to track segments over time. In Reference [29] a shape matching algorithm based on dynamic time warping (DTW) is proposed, which also provides the basis for the temporal segmentation in this paper. DTW has its origin in speech recognition where it is used to align two sequences and in an optimal manner. The optimality is defined by a cost function , which measures the effort required to align the two sequences. Among all possible solutions to align the two sequences, the solution causing the minimal overall cost is found by means of dynamic programming as described in Reference [30]. In order to use DTW for temporal segmentation purposes, the boundaries of spatial segments are interpreted to be sequences and the temporal link between segments is established by applying DTW to these sequences. Hence, the segments’ tracking over time is based on the assumption that the change in a leaf’s position as well as in its shape is small from one point cloud to another. Under this assumption segments of one point cloud can be interpreted as templates. For each template possible correspondences are determined by means of a radius search. This individual search for each of the leaves allows the leaves to behave differently over time as, for example, some of the leaves may lift faster than others. Afterwards, the segments’ edges delivered by the variant of the Douglas-Peucker-algorithm are interpreted as sequences of size . Following the ideas of DTW, for each possible correspondence the normalised warping costs are computed according to
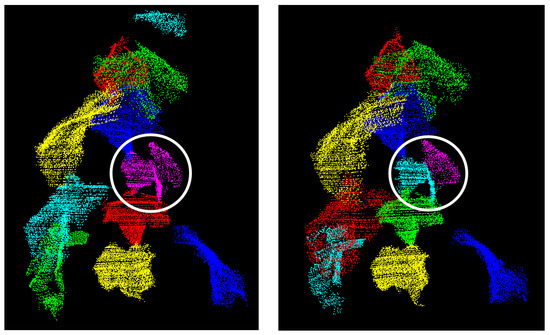
Figure 8.
Spatial segmentation of two point clouds of the same plant. Points having the same colour belong to the same segment. There is no temporal link between the segments of the two point clouds.
In this contribution, the sum of the Euclidean distances between two sequences is used as cost function . Given that exactly one matching partner to each template exists, the segment causing the smallest warping cost is the desired correspondence. However, because of the occasional oversegmentations, this assumption cannot be taken for granted. For this reason, the warping costs of combined segments are computed as well, while each segmented point cloud is alternately interpreted as a template. The result of these computations is a list of potential correspondences and the respective costs. The corresponding segments are greedily chosen from this list, starting with the combination leading to the overall smallest warping costs. In some special situations, the number of leaves may not be the same in different epochs (e.g., due to newly growing leaves or leaves that fall off the plant.) The greedy search allows an adequate handling of such situations—by linking combinations in increasing order of their warping costs, segments with no correspondence are left over and, hence, are not linked to another segment. For further details see Reference [27].
2.3. B-Spline Based Determination of the Leaf Areas
The determination of the leaf areas based on the segments resulting from Section 2.2 requires a modelling of the surfaces described by the respective sub point clouds. In Reference [27] 3D alpha shapes (developed in Reference [31] and extended to three dimensions in Reference [32]) are directly applied to the noisy point cloud as well as on a smoothed one. However, due to the measuring noise’s large influence on the alpha shapes, the leaf areas are falsified. For this reason, approximating surfaces, which reduce the measuring noise, are used to model the leaves.
2.3.1. B-Spline Based Leaf Modelling
Free form surfaces like B-splines have been proven to be appropriate to model complex shapes like leaves (see for example Reference [14], Reference [33] or Reference [34]). The mathematical definition of such a B-spline surface is given by [35]:
A surface point is computed as the weighted average of the control points . The corresponding weights are defined by the B-spline basis functions and , which can be computed recursively (cf. References [36,37]). The B-spline’s degrees p and q are usually specified a priori: the use of cubic B-splines with and is a generally accepted choice [35]. The B-splines’ domain is split into knot spans by means of the knot vectors and . Methods to determine these knot vectors can be found in Reference [35], Reference [38] or Reference [39]. Before being able to estimate the best-fitting B-spline, convenient surface parameters u and v have to be allocated to the observations. The parameterization in this paper is based on the iterative approach proposed in Reference [33]. The major strength of this parameterization approach is the definition of the surface parameter lines by means of the segments’ boundary curves. As a consequence, the approximation quality, which is directly linked to the parameterization’s quality, gains independence from the leaves’ spatial orientations.
If the number of control points is known, the unknown location of the control points can be estimated by means of a linear Gauss-Markov-Model. This assumption does not apply in the case of plant phenotyping. Commonly used intuitive trial and error procedures are not able to find the optimal balance between noise filtering and approximation quality, resulting in falsified leaf areas. For this reason, the determination of the optimal number of control points is interpreted as a model selection problem and is solved by means of structural risk minimization as proposed in References [40,41]. This strategy results in surfaces that are as simple as possible while they approximate the leaves as good as possible. As a consequence, the effects of noisy data on the surface areas to be determined are reduced to a large extent.
2.3.2. Determination of Leaf Areas
In order to determine the leaf areas of the segmented leaves, the estimated B-spline surface is partitioned into small triangles with which are assumed to be approximately planar. The overall area A corresponds to the sum of all triangle areas with :
The computation of each triangle area is based on Heron’s formula using the respective triangle’s side lengths a, b and c:
3. Results
3.1. Segmentation Results
The segmentation strategy developed in Section 2.2 is initially applied to data set (cf. Table 2).
3.1.1. Results of the Spatial Segmentation
As already indicated by Figure 5, the graph-based pre-segmentation does not provide satisfactory results, making the statistically-based region merging necessary. The surface-based region merging (cf. Figure 6) improves the segmentation result particularly by filling existing gaps in the super-segment. This behaviour can be seen in Figure 9 (left), presenting as an example a super-segment (blue), the merged segments (red) as well as the non-merged segments (green). Contrarily, the edge-based region merging detects sharp bends within a leaf, as can be seen in Figure 9 (right): This figure presents as an example a blue-coloured super-segment as well as segments that are merged due to the surface-based region merging (red), segments that are merged due to the edge-based region merging (yellow) and segments that are not merged (green). The edge-based region merging in particular leads to a considerable improvement of the segmentation result.
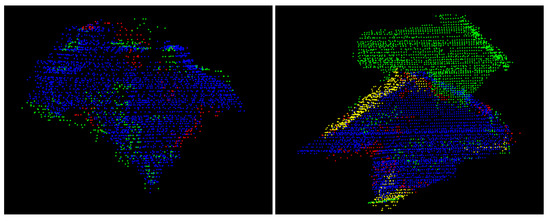
Figure 9.
Results of the region merging: surface-based region merging (left), edge-based region merging (right). The blue-coloured super-segment is complemented by the red-coloured segments (surface-based region merging) as well as by the yellow-coloured segments (edge-based region merging). For the green-coloured segments the test decision is negative.
The overall result of the spatial segmentation is presented for the early stage of plant in Figure 10. Over the entire time series, all but three leaves are completely segmented and there do not exist any undersegmentations. Altogether 38 of 41 leafs are correctly segmented (93%). Low point densities may cause oversegmentations, but in general the results are satisfying with respect to the subsequent phenotyping. However, the result’s quality strongly depends on the quality of the graph-based pre-segmentation (cf. Section 2.2.1), so that the value of the constant k in Equation (3) has to be chosen carefully. In future investigations the sensitivity of the choice of the constant k will be analysed. Finally, it is worth noting that there is no temporal link between the two point clouds in Figure 8; the same colouring of leaves in both point clouds has no meaning.
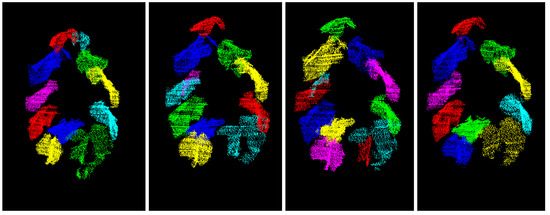
Figure 10.
Result of the spatial segmentation of plant (the same colours in different point clouds do not have a meaning).
3.1.2. Results of the Temporal Segmentation
The result of the shape matching and as a consequence the final spatio-temporal segmentation can be seen in Figure 11 for point clouds and . Contrary to Figure 8 and Figure 10, leaves with the same colour in both point clouds are now temporally linked to each other. In Figure 11, all the leaves are successfully tracked over time. Furthermore, the original spatial segmentation (cf. Figure 8 is improved by the shape matching: by taking into account the information provided by the spatial segmentations of the remaining epochs, the amount of oversegmentation is reduced. Just as in the spatial segmentation, it has to be guaranteed, that the initial segmentations are not undersegmented.
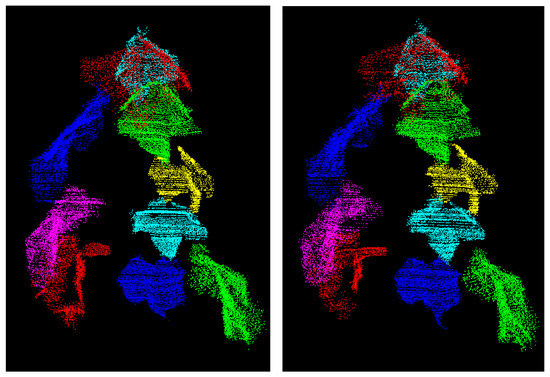
Figure 11.
Temporal segmentation of two point clouds of the same plant. Points having the same colour belong to the same segment.
3.2. Phenotyping Results
The segmented time series provide the basis for the subsequent phenotying. The phenotyping strategy introduced in Section 2.3 is applied to the entirety of data sets listed in Table 2. Plant is scanned at an early and at a late growth stage during four measuring epochs each and, hence, allows for the evaluation of the developed strategies’ performance on different growth stages of cucumber plants. Furthermore, the multi-epochal point clouds are used to gain information about the results’ stability over different realizations. The final phenotyping results of plant are compared to the results yielded by reference methods used in crop science (the digitizer results in the case of the early growth stage and the leaf area meter results in the case of the late growth stage). Finally, the influence of the measuring noise on the phenotyping is investigated by means of the point cloud representing the plant which—contrary to the plant —is captured by means of a terrestrial laser scanner rather than with an automotive grade laser scanner. Before the results of the B-spline-based phenotyping are analysed, a comparison of the reference methods is conducted.
3.2.1. Phenotyping Results Delivered by the Reference Methods
With the 3D digitizer and the leaf area meter two reference sensors with strongly different characteristics are available. The 3D digitizer allows for a non-destructive phenotyping and, hence, for a temporal monitoring of the plants’ leaf areas. However, the digitization results in generalizing models of the leaves (cf. Figure 3) and, hence, in leaf areas which can be assumed to be too small. On the contrary, the leaf area meter allows for a very precise determination of the leaf areas, but requires the plants to be destroyed. Hence, it is not suitable for monitoring plants over time. In order to investigate to what extent the generalization of the digitizer—which is the only reference method for evaluating the temporal phenotyping—affects the determined leaf areas, the results of the two reference methods are initially compared: For the late growth stage of plant measurements of both reference sensors are available (cf. Table 2 and Section 2.1.3), allowing for such a comparison. In Table 3 the respective results for six leaves of plant are contrasted (It is worth noting that only complete leaves are investigated in this study as leaf areas of damaged leaves cannot be appropriately determined by means of the digitizer and, hence, no reference values are available.). For all investigated leaves the area , which is determined by means of the digitizer, is significantly smaller than the area , which is determined by means of the leaf area meter. The exceptionally large discrepancy of the area of leaf 4 can only explained by means of incorrect measurements, whereas the discrepancies of the remaining leaf areas are caused by the generalization during digitization (see Figure 3 for an example for a digitizer model of a leaf). The leaf areas in Table 3 indicate that the generalization results in leaf areas that are up to 13% smaller than the actual leaf area which can be determined by means of the leaf area meter. This underestimation of the leaf area has to be taken into account when only the values of the digitizer are available as a reference.

Table 3.
Comparison of the results provided by the reference methods for data set . Leaf areas given by the digitizer and by the leaf area meter .
3.2.2. Results of the B-Spline-Based Phenotyping
Multiple point clouds of plant in both growth stages are acquired by means of the MSS, each in a time span of hours. As the leaf area is not expected to change within hours, in a first step the determined leaf areas are averaged (second column in Table 4 for the early growth stage and in Table 5 for the late growth stage) in order to get an impression about the results’ stability. The corresponding standard deviations in the subsequent column are a quality criterion of the B-spline based leaf area determination. For both growth stages some of the determined leaf areas considerably vary between the measuring epochs with the phenotyping results of the late stage showing a considerably stronger variation. The fourth columns of Table 4 and Table 5 compare the results of the B-spline-based phenotyping with the results of the reference method available for the specific data set (digitizer results for the early growth stage and leaf area meter results for the late growth stage):

Table 4.
Averaged leaf areas over the time series of plant , acquired by the MSS as well as differences between the B-spline based leaf area determination and the digitizer results.

Table 5.
Averaged leaf areas over the entire time series of plant , acquired by the MSS as well as differences between the B-spline based leaf area determination and the results of the leaf area meter.
The last column, listing the ratio between these differences and the determined leaf areas , complements the comparison of the B-spline-based phenotyping with the reference values. The results listed vary considerably: For both growth stages there exist leaf areas which perfectly match the reference values, while other leaf areas show large discrepancies. The results of plant , which is scanned by means of a TLS in order to investigate the influence of the MSS’s high measuring noise on the results, are summarized in Table 6. The plant is scanned once so that no mean values or standard deviations can be determined, and only leaf areas of the digitizer are available as a reference. The results of plant are much more stable, with discrepancies with respect to the reference values of up to 11%.

Table 6.
Computed leaf areas of the plant , acquired by the terrestrial laser scanner (TLS) as well as differences between the B-spline based leaf area determination and the digitizer results.
4. Discussion
4.1. Discussion of the Segmentation Results
The segmentation procedure is initially demonstrated on a cucumber plant at a relatively early growth stage in Section 3.1. As shown in Figure 9, Figure 10 and Figure 11, the developed segmentation chain leads to very satisfying results in the case of this plant: Admittedly, there are always small point groups that are not allocated to any leaf (green points within the blue point cloud in Figure 9), but their influence on the phenotyping can be assumed to be minimal. Rather, the non-allocation of these point groups can be seen as an outlier-detection—obviously, the surface characteristics of these sub groups do not match with the surface characteristics of the entire leaf. Taking into account these outlier groups during the phenotyping would falsify the leaf areas to a large extent. However, some problems may occur when acquiring point clouds representing a plant at a later growth stage as can be seen in Figure 12, presenting the segmented time series of the later growth stage of plant : Only 49 of 59 leafs are correctly segmented (83%).
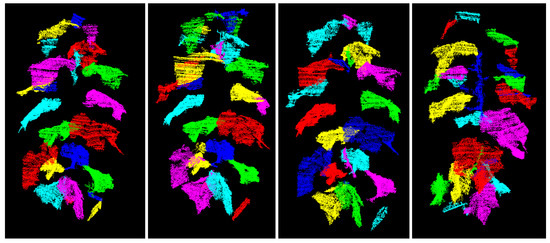
Figure 12.
Result of the spatial segmentation of plant .
These poorer results are caused by the current measurement configuration as well as by the laser scanner used. There are two essential differences between cucumber plants of different growth stages:
- Firstly, there is the obvious relation that the older the plant is, the larger the leaves become, leading to an increased amount of occlusion. In combination with the relatively low point density, these occlusions cause data gaps which impede the merging of neighbouring segments as can be seen in Figure 13 (left): the yellow- and the green-coloured segment obviously belong to the same leaf, but are not merged, as they are separated by a relatively large data gap (circled in red).
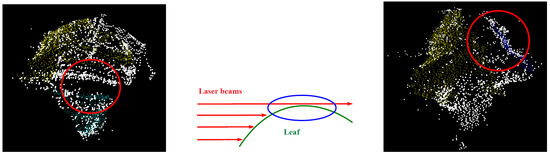 Figure 13. (Left): A data gap impedes the merging of the yellow- and green-coloured segments. The white class consists of points which are not allocated to any leaf. (Middle): Horizontal laser beams fail to acquire horizontal oriented leafs. (Right): Oversegmentation caused by the horizontal laser beam.
Figure 13. (Left): A data gap impedes the merging of the yellow- and green-coloured segments. The white class consists of points which are not allocated to any leaf. (Middle): Horizontal laser beams fail to acquire horizontal oriented leafs. (Right): Oversegmentation caused by the horizontal laser beam. - Secondly, the plant raises its leaves from an almost vertical position to a nearly horizontal one when becoming older. As the laser beam is currently also horizontally oriented, those horizontal parts of the leaves cannot be acquired as is schematically shown in Figure 13 (middle). As a consequence, the leaves of later growth stages are incompletely acquired as can be seen in Figure 13 (right), presenting such a partly horizontally oriented leaf from above. The red circled part of the leaf is the critical part that impedes the merging of the blue- and the yellow-coloured segments.
Although both aforementioned problems cause oversegmented leaves which falsify the results of the phenotyping, they are not caused by the segmentation process, but rather by the measuring configuration and the laser scanner used. An adapted orientation of the laser scanner as well as an increase of the point density should be sufficient to reduce these negative effects.
4.2. Discussion of the Phenotyping Results
As already indicated in Section 4.1, the segmentation of a plant in a later growth stage is much more challenging than the segmentation of a plant in an earlier growth stage. This finding directly explains the larger variability of the phenotyping results in Table 5 (late growth stage) than in Table 4 (early growth stage). However, the results of both grow stages are characterized by an unexpectedly large standard deviation. The quality of the phenotyping results and, hence, their stability over different realizations has three influencing factors: (1) the data quality due to the measuring process, (2) the segmentation quality and (3) the quality of the B-spline estimation. A detailed investigation of the early stage’s results (Table 4) reveals that in at least one of the four measuring epochs either data gaps or the large measuring noise cause erroneous segmentations. This holds especially for the leaves 4, 5 and 7. When these erroneous segmentation results are excluded from the averaging, the respective standard deviations immediately decrease to ≈7 cm. The higher the leaves’ positions on the plant is, the more challenging is the data acquisition (leaves 9, 10 and 11)—due to occlusions, these leaves are incompletely acquired. Especially leaf 10 has large data gaps, making a reasonable determination of the leaf area impossible. The incomplete acquisition of these leaves is also apparent when comparing the respective leaf areas with the results of the digitizer. The difference (Table 4, fourth column) being negative (leaves 5, 9 and 10) is an indicator that either the measuring process or the segmentation result in incomplete descriptions of the leaves so that the respective leaf areas are not meaningful. For the remaining five leaves with a positive difference however, the determined leaf areas correspond very well with the reference values yielded by the digitizer. As indicated by the last column in Table 4, the B-spline-based leaf area determination yields results that are up to larger than the results given by the digitizer. Taking into account that the digitizer’s results tend to be too small (cf. Table 3), the results of the B-spline-based leaf area determination can be assumed to represent the true leaf areas better than the digitizer’s results. The variation within these five results (discrepancies varying between 0.0% and 8.0%) is comparable to the variation within the results in Table 3, presenting the discrepancies between the reference methods. The leaf area meter, as a very precise measuring instrument, is not responsible for the variation visible in Table 3. Hence, the results’ variability indicates that the amount of generalization due to the digitization differs. Depending on the leaf’s actual shape, the leaf area can be determined very well by means of the digitizer (e.g., leaf 3 in Table 3 with ) or it is determined considerably too small (e.g., leaf 1 in Table 3 with ). The instability of the leaf areas determined by means of the digitizer is also the reason for the results’ variability in Table 4. In the case of the later growth stage of plant (Table 5), a comparison of the determined leaf areas with the results given by the leaf area meter is possible. Particularly conspicuous are the large discrepancies between the results yielded by the B-spline-based leaf area determination and the results of the leaf area meter for the leaves 3 and 4. For these two leaves, the segmentation problems that are discussed in Section 4.1 apply: the leaves are incompletely acquired, making a successful segmentation and, consequently, a meaningful determination of the leaf areas impossible. For the majority of the remaining leaf areas, the B-spline-based leaf area determination yields results that are smaller than those of the leaf area meter. In addition to the acquisition and segmentation problems caused by the laser scanner’s high noise level, which are already discussed in Section 4.1, this is caused by the parameterization process during the B-spline estimation. In order to prevent a degeneration of the estimated surfaces, the surfaces’ boundaries are forced to a priori determined boundary curves of the point cloud (see Reference [33] for more details).
The large measuring noise complicates the determination of boundary points which provide the basis for the modelling of the boundary curves. This in combination with the leaves’ complex shapes lead to a generalization of the actual shape of the respective leaf and the leaves’ edges are partially cropped (indicated as an example by the green circle in Figure 14). When point clouds with less ragged boundaries are available, a more realistic modelling of the boundaries is possible. Nevertheless, the results of the B-spline based determination of the leaf areas are considerably closer to the results of the leaf area meter and, hence, to the nominal values, than the digitizer’s results. Thus, even in the case of very noisy data sets, which considerably complicate the determination of the leaf areas, the respective results are much more satisfying than the results of the digitizer.
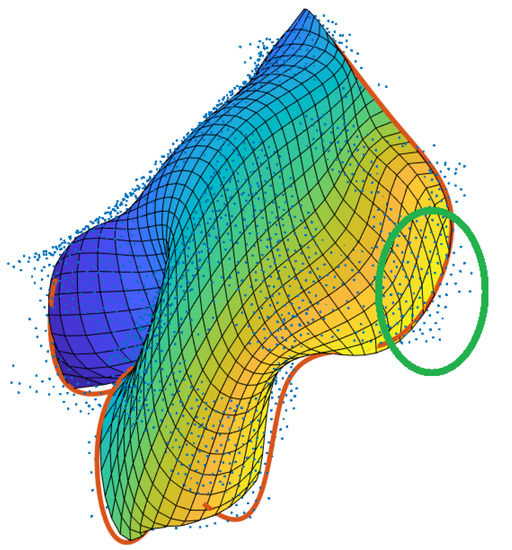
Figure 14.
Cropping of a leaf’s area due to the estimated boundary curve.
Table 6, listing the results achieved by means of less noisy point clouds, supports the conclusions drawn above: As can be expected, the B-spline based leaf areas are larger than the reference values of the digitizer. The comparison of the results listed in column 4 of Table 6 with the corresponding ratios provided by Table 3 reveals a very similar behaviour of the ratios, both in magnitude and variability. This finding supports the assumption that the high noise level of the automotive grade laser scanner has indeed a large influence on the leaf area determination and that an acquisition by means of a TLS yields leaf areas that are considerably closer to the true values than those yielded by the automotive grade laser scanner.
5. Conclusions
5.1. Summary
Geodetic measurement techniques become more and more important in plant phenotyping. In this contribution an MSS for plant phenotyping is used that acquires time series of 3D point clouds of cucumber plants by means of an automotive grade laser scanner. The focus of this contribution is on the fully automated spatio-temporal segmentation of the acquired point clouds by means of a three-stage procedure:
- Each point cloud is pre-segmented by means of a graph-based segmentation algorithm.
- A statistically-based region merging procedure is applied to the undersegmented point clouds, yielding spatially segmented leaves.
- The leaves are tracked over time by means of a shape matching which simultaneously improves possible erroneous spatial segmentations by using information from temporally neighbouring point clouds.
The strength of the algorithm that should be emphasized comes from the third step—not only does the temporal segmentation step successfully link segments over time regardless of newly developing or decaying leaves, but it also improves undersegmented spatial segmentation results. The segmented leaves are afterwards modelled by means of B-spline surfaces, providing the basis for the leaf area determination. The use of the flexible B-spline surfaces has proven to be particularly suitable at this point—in addition to the ability to appropriately model the complex leaf structures, the noise contained in the point clouds is considerably filtered by estimating best-fitting B-spline surfaces. Hence, this approach outperforms approaches that directly build the models on the noisy point clouds like, for example, alpha shapes. Therefore, even in the case of very noisy 3D point clouds acquired by the automotive grade laser scanner, the leaf areas are more accurately determined than those obtained by the non-destructive standard method from crop science used for comparison purposes. However, as the large measuring noise impedes the segmentation procedure as well as the subsequent modelling of the the leaves, the leaf areas are slightly underestimated. Nevertheless, the use of a 3D point cloud acquired by means of a geodetic TLS with a considerably lower noise level clarifies the potential of the presented fully automated phenotyping method.
5.2. Outlook
Despite of the successful application of the developed algorithm on the test data sets, future investigations need to be conducted—firstly, the constant k of the spatial pre-segmentation has so far been determined heuristically for different growth stages of cucumber plants. This heuristic choice needs to be validated, for example, by means of a sensitivity analysis. Secondly, only two plants, yielding nine different point clouds, are investigated in this methodology study. The results are very promising, but need to be validated by means of a larger amount of suitable 3D point clouds. In these future investigations, however, the data acquisition needs to be adapted to reduce the segmentation problems of horizontally oriented leaves caused by the horizontal laser beam. Finally the developed strategy is only applied to data sets acquired under controlled green house conditions until now. Taking into account that in-field phenotyping becomes more and more important, the applicability of the developed approach to outdoor tasks need to be investigated in future. Especially the temporal segmentation has to be adjusted for in-field phenotyping tasks in order to account for the leaves’ movements due to wind or their damage due to pest infestation.
Author Contributions
Conceptualization, C.H. and J.-A.P.; Methodology, C.H.; Formal Analysis, C.H. and J.-A.P.; Investigation, C.H.; Resources, J.-A.P.; Writing—Original Draft Preparation, C.H.; Writing—Review & Editing, J.-A.P.; Visualization, C.H.; Supervision, J.-A.P.; Project Administration, J.-A.P. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the support by the Open Access Publishing Fund of Clausthal University of Technology.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Furbank, R.T.; Tester, M. Phenomics–technologies to relieve the phenotyping bottleneck. Trends Plant Sci. 2011, 16, 635–644. [Google Scholar] [CrossRef] [PubMed]
- Paproki, A.; Sirault, X.; Berry, S.; Furbank, R.; Fripp, J. A novel mesh processing based technique for 3D plant analysis. BMC Plant Biol. 2012, 12, 63. [Google Scholar] [CrossRef] [PubMed]
- Becirevic, D.; Klingbeil, L.; Honecker, A.; Schumann, H.; Rascher, U.; Léon, J.; Kuhlmann, H. On the derivation of Crop heights from multitemporal UAV imagery. ISPRS Ann. Photogram. Remote Sens. Spat. Inf. Sci. 2019, IV-2/W5, 95–102. [Google Scholar] [CrossRef]
- Johansen, K.; Morton, M.J.L.; Malbeteau, Y.; Aragon, B.; Al-Mashharawi, S.; Ziliani, M.; Angel, Y.; Fiene, G.; Negrao, S.; Mousa, M.A.A.; et al. Predicting biomass and yield at harvest of salt-stressed tomato plants using UAV imagery. ISPRS Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 407–411. [Google Scholar] [CrossRef]
- Hétroy-Wheeler, F.; Casella, E.; Boltcheva, D. Segmentation of tree seedling point clouds into elementary units. Int. J. Remote Sens. 2016, 37, 2881–2907. [Google Scholar] [CrossRef]
- Lou, L.; Liu, Y.; Shen, M.; Han, J.; Corke, F.; Doonan, J.H. Estimation of Branch Angle from 3D Point Cloud of Plants. In Proceedings of the IEEE 2015 International Conference on 3D Vision, Lyon, France, 19–22 October 2015; pp. 554–561. [Google Scholar] [CrossRef]
- Kahlen, K.; Stützel, H. Estimation of Geometric Attributes and Masses of Individual Cucumber Organs Using Three-dimensional Digitizing and Allometric Relationships. J. Am. Soc. Hortic. Sci. 2007, 132, 439–446. [Google Scholar] [CrossRef]
- Eberius, M.; Lima-Guerra, J. High-Throughput Plant Phenotyping—Data Acquisition, Transformation, and Analysis. In Bioinformatics; Edwards, D., Stajich, J., Hansen, D., Eds.; Springer: New York, NY, USA, 2009; Volume 88, pp. 259–278. [Google Scholar] [CrossRef]
- Hartmann, A.; Czauderna, T.; Hoffmann, R.; Stein, N.; Schreiber, F. HTPheno: An image analysis pipeline for high-throughput plant phenotyping. BMC Bioinf. 2011, 12, 148. [Google Scholar] [CrossRef]
- Iyer-Pascuzzi, A.S.; Symonova, O.; Mileyko, Y.; Hao, Y.; Belcher, H.; Harer, J.; Weitz, J.S.; Benfey, P.N. Imaging and analysis platform for automatic phenotyping and trait ranking of plant root systems. Plant Physiol. 2010, 152, 1148–1157. [Google Scholar] [CrossRef]
- Quan, L.; Tan, P.; Zeng, G.; Yuan, L.; Wang, J.; Kang, S.B. Image-based plant modeling. ACM Trans. Graph. 2006, 25, 599. [Google Scholar] [CrossRef]
- Paulus, S.; Schumann, H.; Kuhlmann, H.; Léon, J. High-precision laser scanning system for capturing 3D plant architecture and analysing growth of cereal plants. Biosyst. Eng. 2014, 121, 1–11. [Google Scholar] [CrossRef]
- Elnashef, B.; Filin, S.; Lati, R.N. Tensor-based classification and segmentation of three-dimensional point clouds for organ-level plant phenotyping and growth analysis. Comput. Electr. Agric. 2019, 156, 51–61. [Google Scholar] [CrossRef]
- Gelard, W.; Devy, M.; Herbulot, A.; Burger, P. Model-based Segmentation of 3D Point Clouds for Phenotyping Sunflower Plants. In Proceedings of the 12th International Joint Conference on Computer Vision, Porto, Portugal, 1 January 2017; pp. 459–467. [Google Scholar] [CrossRef]
- Alenya, G.; Dellen, B.; Torras, C. 3D modelling of leaves from color and ToF data for robotized plant measuring. In Proceedings of the IEEE International Conference on Robotics and Automation 2011, Shanghai, China, 9–13 May 2011; pp. 3408–3414. [Google Scholar] [CrossRef]
- Li, Y.; Fan, X.; Mitra, N.J.; Chamovitz, D.; Cohen-Or, D.; Chen, B. Analyzing growing plants from 4D point cloud data. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Rist, F.; Herzog, K.; Mack, J.; Richter, R.; Steinhage, V.; Töpfer, R. High-Precision Phenotyping of Grape Bunch Architecture Using Fast 3D Sensor and Automation. Sensors 2018, 18, 763. [Google Scholar] [CrossRef] [PubMed]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer: New York, NY, USA, 1990. [Google Scholar] [CrossRef]
- Paulus, S.; Dupuis, J.; Mahlein, A.K.; Kuhlmann, H. Surface feature based classification of plant organs from 3D laserscanned point clouds for plant phenotyping. BMC Bioinf. 2013, 14, 238. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Short, T.H.; Fox, R.D.; Bauerle, W.L. Plant architectural parameters of a greenhouse cucumber row crop. Agric. Forest Meteorol. 1990, 51, 93–105. [Google Scholar] [CrossRef]
- Qian, T.; Zheng, X.; Guo, X.; Wen, W.; Yang, J.; Lu, S. Influence of temperature and light gradient on leaf arrangement and geometry in cucumber canopies: Structural phenotyping analysis and modelling. Inf. Process. Agric. 2019, 6, 224–232. [Google Scholar] [CrossRef]
- Paffenholz, J.A.; Harmening, C. Spatiotemporal monitoring of natural objects in occluded scenes. In 4th International Conference on Machine Control & Guidance; Schattenberg, J., Minßen, T.F., Eds.; Institut für mobile Maschinen und Nutzfahrzeuge: Braunschweig, Germany, 2014; pp. 63–74. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- SINOQUET, H. Characterization of the Light Environment in Canopies Using 3D Digitising and Image Processing. Ann. Botany 1998, 82, 203–212. [Google Scholar] [CrossRef]
- Wiechers, D.; Kahlen, K.; Stützel, H. A method to analyse the radiation transfer within a greenhouse cucumber canopy (Cucumis sativus L.). Acta Hortic. 2006, 75–80. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient Graph-Based Image Segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Harmening, C.; Brenner, C.; Paffenholz, J.A. Raumzeitliche Segmentierung von Pflanzen in stark verdeckten Szenen. In Photogrammetrie—Laserscanning—Optische 3D-Messtechnik; Luhmann, T., Müller, C., Eds.; Wichmann: Berlin, Germany, 2014; pp. 334–341. [Google Scholar]
- Heunecke, O.; Kuhlmann, H.; Welsch, W.; Eichhorn, A.; Neuner, H. Handbuch Ingenieurgeodäsie: Auswertung geodätischer Überwachungsmessungen, 2nd ed.; Wichmann: Heidelberg, Germany, 2008. [Google Scholar]
- Brendel, W.; Todorovic, S. Video object segmentation by tracking regions. In Proceedings of the IEEE 12th International Conference on Computer Vision (ICCV), Kyoto, Japan, 29 September–2 October 2009; pp. 833–840. [Google Scholar] [CrossRef]
- Müller, M. Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germny, 2007. [Google Scholar]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mücke, E.P. Three-dimensional alpha shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Harmening, C.; Neuner, H. A constraint-based parameterization technique for B-spline surfaces. J. Appl. Geodesy 2015, 9, 143–161. [Google Scholar] [CrossRef]
- Beardsley, P.; Chaurasia, G. Editable Parametric Dense Foliage from 3D Capture. In Proceedings of the IEEE 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5315–5324. [Google Scholar] [CrossRef]
- Piegl, L.A.; Tiller, W. The NURBS book. In Monographs In Visual Communications, 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 1997. [Google Scholar]
- Cox, M.G. The Numerical Evaluation of B-Splines. IMA J. Appl. Math. 1972, 10, 134–149. [Google Scholar] [CrossRef]
- Boor, C.d. On calculating with B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- Schmitt, C.; Neuner, H. Knot estimation on B-Spline curves. Österreichische Z. Vermessung Geoinf. (VGI) 2015, 103, 188–197. [Google Scholar]
- Bureick, J.; Alkhatib, H.; Neumann, I. Robust Spatial Approximation of Laser Scanner Point Clouds by Means of Free-form Curve Approaches in Deformation Analysis. J. Appl. Geodesy 2016, 10, 27–35. [Google Scholar] [CrossRef]
- Harmening, C.; Neuner, H. Choosing the Optimal Number of B-spline Control Points (Part 1: Methodology and Approximation of Curves). J. Appl. Geodesy 2016, 10, 139–157. [Google Scholar] [CrossRef]
- Harmening, C.; Neuner, H. Choosing the optimal number of B-spline control points (Part 2: Approximation of surfaces and applications). J. Appl. Geodesy 2017, 11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).