Abstract
This paper presents an application of an Msplit estimation in the determination of terrain profiles from terrestrial laser scanning (TLS) data. We consider the squared Msplit estimation as well as the absolute Msplit estimation. Both variants have never been used to determine terrain profiles from TLS data (the absolute Msplit estimation has never been applied in any TLS data processing). The profiles are computed by applying polynomials of a different degree, determining which coefficients are estimated using the method in question. For comparison purposes, the profiles are also determined by applying a conventional least squares estimation. The analyses are based on simulated as well as real TLS data. The actual objects have been chosen to contain terrain details (or obstacles), which provide some measurements which are not referred to as terrain surface; here, they are regarded as outliers. The empirical tests prove that the proposed approach is efficient and can provide good terrain profiles even if there are outliers in an observation set. The best results are obtained when the absolute Msplit estimation is applied. One can suggest that this method can be used in a vertical displacement analysis in mining damages or ground disasters.
1. Introduction
Laser scanning is a popular technique of data acquisition nowadays. Laser scanning data are acquired as point clouds of varying resolution. Depending on the type of platform, there is airborne laser scanning (ALS), terrestrial laser scanning (TLS), satellite laser scanning (SLS) and mobile laser scanning (MLS) [1,2]. All types of laser scanning have a wide range of applications, e.g., terrain surface and vegetation cover measurements and digital terrain model (DTM) generation [3,4,5,6,7], building detection and their condition diagnosis [8,9,10,11,12], displacement detection [13,14,15], modeling of cultural heritage sites or object structures [2,13,16], registration roads, railways or power lines [17,18], monitoring coastal zones [19], mining damages and ground disasters [20,21].
Here, we consider the classical application of TLS, namely acquiring data of terrain surface. However, grass, roots, fallen leaves, fallen tree branches, shoots (in general vegetation cover), or other terrain details situated on this surface might disturb such TLS measurements. The problem of how to separate such obstacles from the point clouds or how to deal with observations that might be considered as outliers (distinguishing positive and negative outliers) was addressed in several publications, e.g., [22,23,24]. Generally, TLS data (point cloud) might require a separation of observations related to the terrain surface from observations related to terrain details. Such a separation might be done by segmentation, e.g., region-based methods, Hough transform and Random Sample Consensus (RANSAC) [11,17,25,26,27]. Obviously, there are also other different methods of point cloud filtering, e.g., surface-based adjustment, morphology-based filtering, Triangulated Irregular Network (TIN)-based refinement or adaptive TIN (ATIN)-based refinement [1,5,7,28]. Another possible approach to such a separation is the application of Msplit estimation [1].
Msplit estimation, which is a development of M-estimation, was introduced in [29]. The primary assumption is that an observation set is an unrecognized mixture of realizations of different random variables [29,30]. The idea behind the method is to estimate such variables’ location parameters without dividing the observation set into the respective number of subsets (observation aggregations). In many practical cases, such an a priori division would be hard or almost impossible. The basic variant of Msplit estimation assumes two such variables; thus, the classical functional model is split into two competitive functional models. It is also worth noting that the observations’ assignment to the particular variable (and thus to the specific variant of the split functional model) is automatic during the iterative process. In the context of this paper, a point cloud obtained from TLS includes points related to the terrain surface and terrain details. Msplit estimation allows us to process data without dividing a point cloud into two clouds representing selected surfaces. In general, the method in question will enable us to process a point cloud and approximate two surfaces by estimating surfaces’ parameters. In some special cases, one can approximate not the whole surfaces, but rather chosen profiles. Such an approach would be advisable in deformation analysis when one wants to control how the terrain heights are changing between measurement epochs. This might concern, e.g., monitoring landslides or mining damages. In this context, the terrain profile as well as terrain details can be approximated by, e.g., polynomials of a single indeterminate, of which the coefficients can be estimated by different methods, including Msplit estimation.
Applications of Msplit estimation concerned so far not only processing of TLS data (presented in [1,15,22,31]) but also deformation analyses [29,30,32,33,34,35,36], direct identification of gross errors [37], linear regression analyses [30,34], robust coordinate transformation [38], S-transformation [39] and marine navigation [40]. Most of these applications applied only the squared Msplit estimation (SMS), of which the objective functions stem from the assumption that observation errors are normally distributed. However, there is also an alternative variant of Msplit estimation in which objective functions are based on the L1 norm condition, which refers to the minimization of L1 norm of error vector [41,42]. Such a variant is called the absolute Msplit estimation (AMS) [34,43], and it has not been used in laser scanning data analysis so far. Due to that fact, it seems interesting to apply this method in such a context, especially since some previous papers proved that AMS estimation is generally less sensitive to outliers than SMS estimation [34,35]. Thus, the paper’s main objective is to analyze both variants of Msplit estimation in the context of the determination of terrain and terrain details profiles based on TLS data. The paper presents the squared and absolute Msplit estimation foundations, their application in profile approximation and the empirical analyses based on simulated and real TLS data.
2. Related Work
As mentioned earlier, one of the variants of Msplit estimation, namely SMS estimation, was applied in several laser scanning data analyses [1,15,22,31]. We will discuss them in chronological order.
One paper [22] proposed an application of the SMS estimation to fit planes and to detect the edge of adjacent planes. The analyses presented were based on the simulated as well as real ALS data. Good results obtained in both considered cases prove that the method in question can be successfully used in laser scanning data processing.
Another paper presents an application of the SMS estimation for filtering point clouds obtained from ALS [1] and used to determine DTMs. In the first approach (the quality method), the DTM is obtained by applying the terrain surface’s estimated parameters. The second way (the quantity method) considers the division of the point cloud into two subsets. The first subset contains observations that are qualified for the creation of DTM, whereas the second subset includes points representing terrain details. Then, DTM is created based on the observations from the first subset. The obtained results prove that SMS estimation can be used for filtering ALS data. The correctness of the results was verified successfully by the ATIN method. This statement is essential for the objective of this study.
One paper [31] showed the SMS estimation application in the case of filtration and aggregation of point clouds that contain a known number of elliptical shapes (e.g., tree trunks, columns, gutters) with preliminary unknown locations and dimensions, respectively. The theoretical considerations related to such a problem are satisfactory.
The SMS estimation’s newest application in the context of laser scanning data processing is the detection and dimensioning of the displacement of adjacent planes in a point cloud acquired from TLS [15]. The paper presents tests which concerned the objects representing vertical planes (namely the fragment of the precast concrete wall and the fragment of the concrete slabs of a retaining wall) as well as the objects representing horizontal planes (namely the segment of the asphalt road and the fragment of the pavement). The results show that the SMS estimation can distinguish the planes in a point cloud obtained from TLS. However, in some cases where there is no displacement of the planes relative to other planes, two overlapping planes were determined.
Generally, current research has proved that the SMS estimation could give promising results in laser scanning data processing. Thus, one can suppose that Msplit estimation might also give satisfactory outcomes in determining the terrain profiles. This paper will discuss both known variants of Msplit estimation in the context of TLS data analysis.
3. Theoretical Foundations of Msplit Estimation
In Msplit estimation, the classical linear functional model is split into two competitive ones [29]:
where y—observation vector, A—coefficient matrix, X—parameter vector and v—measurement error vector. The split models concern the same observation y, and they differ from each other in the competitive versions and of the parameter vector X and also the competitive versions and of the measurement error vector v. Msplit estimation can be applied when the observation vector is an unknown mixture of realizations of two random variables that differ from each other at least in location parameters. The assignment of a particular observation to the respective version of the parameter vector is unknown. In other words, there is no supposition about dividing the observations into two aggregations.
The general optimization problem of Msplit estimation can be formulated as follows:
where —objective function and —arbitrarily chosen function. Let us introduce two variants of Msplit estimation: the squared Msplit estimation (SMS) and the absolute Msplit estimation (AMS). In the case of the SMS estimation, the objective function can be defined as [29,30]:
Such a formula can be derived from a general assumption that the observation errors are normally distributed. The optimization problem (Equation (2)) of the SMS estimation can be solved by applying the Newton method. The iterative process of the SMS estimation, namely the traditional one [43], is as follows [29]:
where Hessians——and gradients——are computed in the following way [29]:
where —diagonal matrix and —matrices of the weight functions. The objective function of the SMS estimation leads to the following forms of weight functions [29]:
Since the first variant’s weight function depends only on the second one’s errors (and vice versa), one can call this relationship a mutual cross-weighting.
On the other hand, the AMS estimation is based on application L1 norm condition [41,42]; thus, its objective function is defined in the following way [34,43]:
Such an objective function leads to the following weight functions:
They both depend on both variants of the error vectors; hence, there is no mutual cross-weighting in this case. Thus, the iterative process of the AMS estimation is a little bit different than the respective iterative process of the SMS estimation. The iterative process of the AMS estimation can be described as [34,43]:
where:
Such an iterative process might be called parallel [43]. Because the original weight functions of the AMS estimation are not defined for measurement errors equal to zero, which may cause singularity, in practice, we can apply the following modified weight functions:
where b—assumed small positive constant.
Both types of iterative processes require a proper choice of starting points [43], and they should both be stopped for such a j = k for which and also , [29,34].
Previous papers [34,35,43] showed that differences in the SMS and AMS estimations’ objective functions also result in slightly different general properties. As was shown, both methods’ weight functions differ from each other, which leads to the necessity of two different iterative processes. The more significant differences stem from the influence functions [32,39] and conclude that the AMS estimation is less sensitive to the outlying observations of moderate magnitude. This property seems especially interesting in TLS data processing, where observations (points in point clouds) might represent different surfaces and just obstacles.
4. Experiments and Results
Let us apply Msplit estimation in TLS data processing, namely in the approximation of terrain profiles. Such profiles might describe the terrain surface, but they are also useful in deformation analysis. One can obtain interesting information about vertical movements by comparing terrain profiles determined at different epochs. The essential information is that a point cloud, obtained from TLS measurements, may contain terrain points and points of terrain details or obstacles. Application of Msplit estimation allows us to get terrain profiles without division of the point cloud in subsets containing points of the mentioned types. In such a context, this approach avoids, for example, errors in the assignment of points to the respective subsets.
To examine the method proposed, we consider simulated as well as real TLS data. In both cases, measurements concern terrain surface and terrain details, and generally, we do not know which points should be assigned to the particular surface.
4.1. Simulated Data
The first test concerns the determination of a terrain profile P based on the simulated TLS data. We assume that a chosen polynomial defines the profile. Let us consider three variants of such polynomials: a second-degree polynomial (a parabola), a third-degree polynomial (a cubic curve) and a fourth-degree polynomial. The simulated polynomial coefficients are presented in Table 1.

Table 1.
Simulated coefficients of the polynomials.
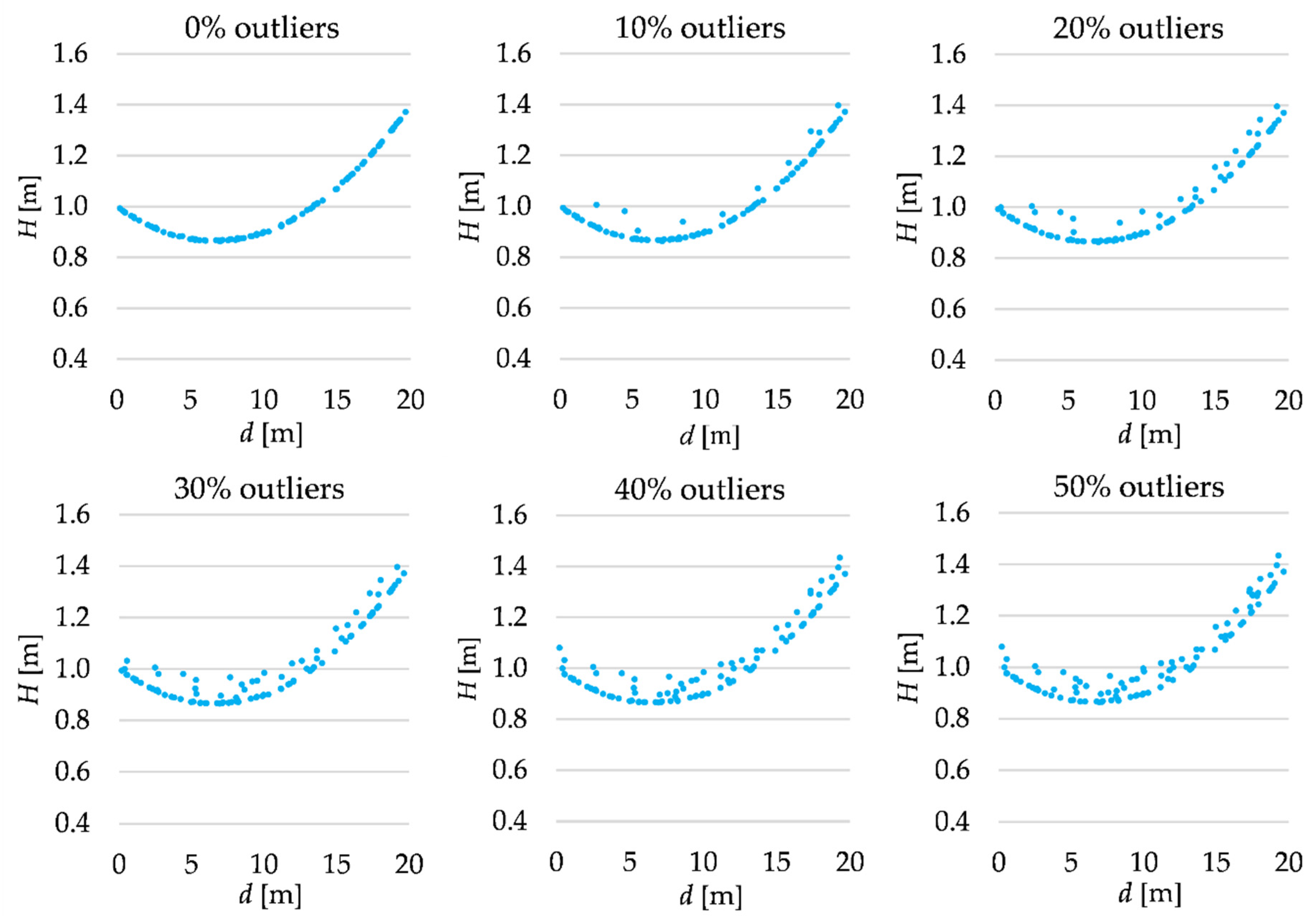
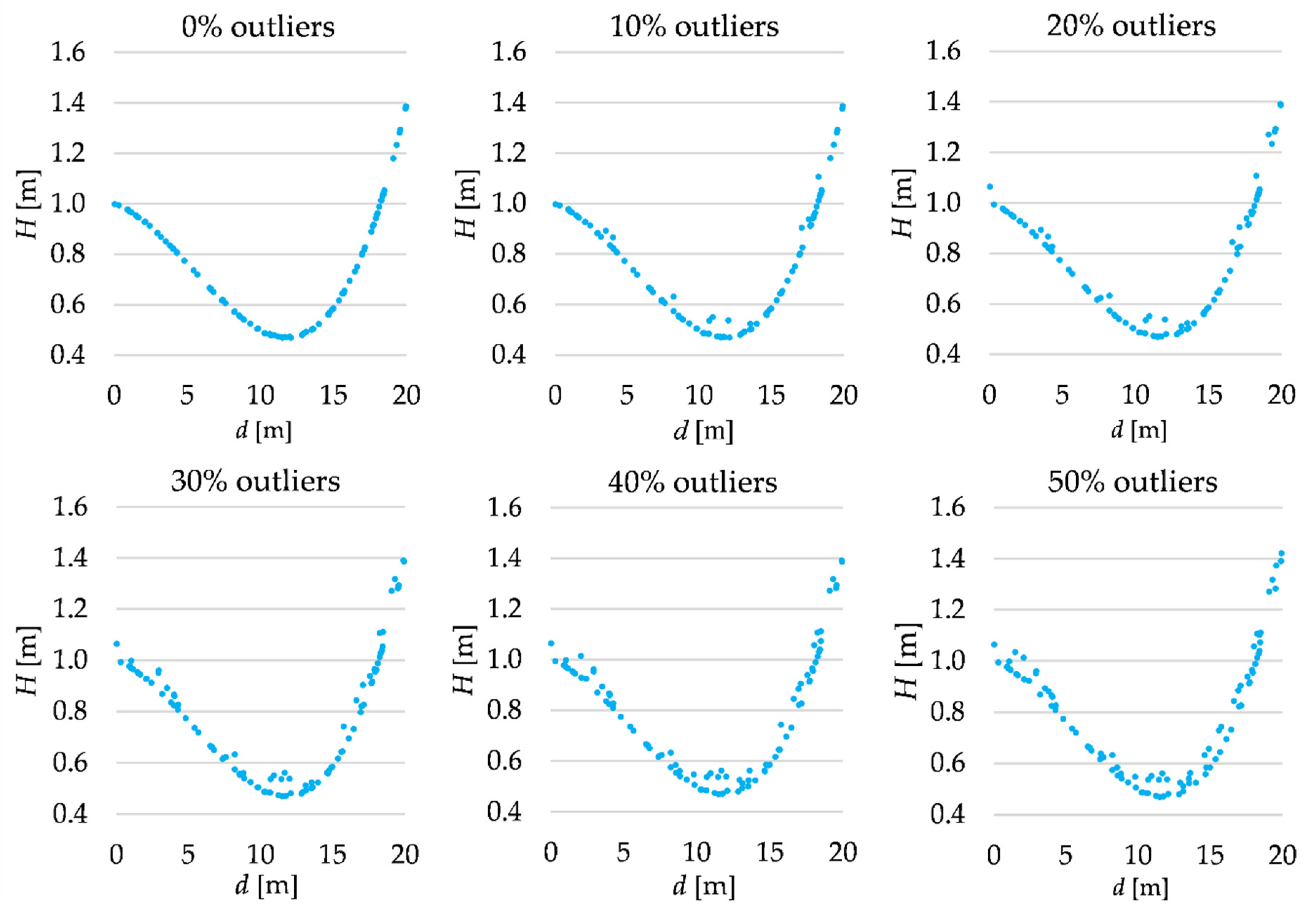
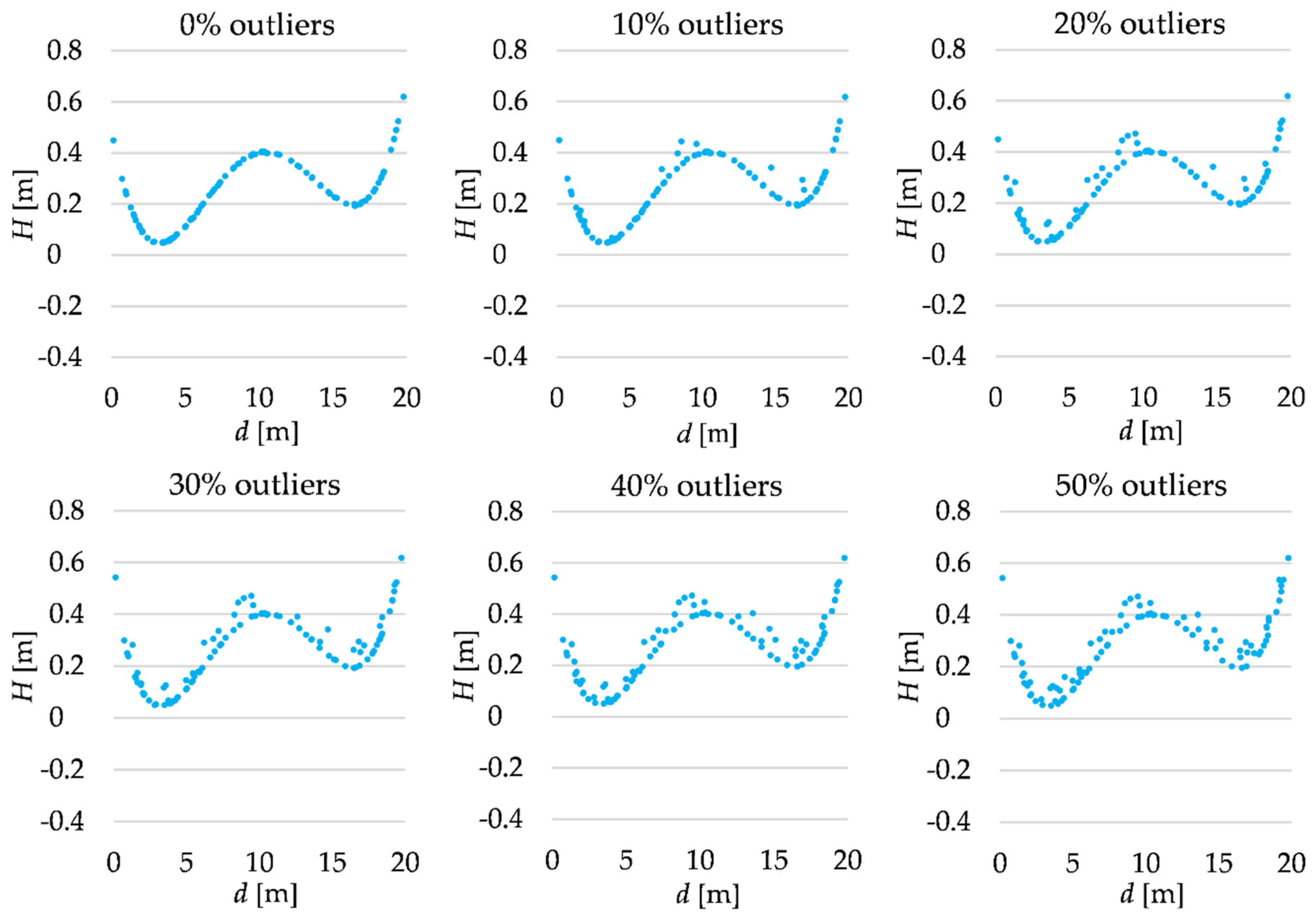
We assume that each terrain profile is 20 m in length, and we try to approximate it based on 100 points simulated from the laser scanning measurements. The distance di from the profile beginning to each point is randomly generated from the uniform distribution within the range . The theoretical height Hi of each point is computed using the polynomial chosen that is assumed as a “real” terrain surface. Then, such heights are affected by random errors generated from the normal distribution . The analyzes are conducted for several variants that differ in the share of outliers in the simulated observation set. Such types of observations are obtained by adding gross errors to the randomly chosen points. Gross errors follow the uniform distribution within the range of . The outliers simulate the occurrence of the terrain details. The percentage of outliers in the observation sets in the subsequent cases is equal to 0%, 10%, 20%, 30%, 40% or 50%. All simulated observation sets are presented in Figure 1, Figure 2 and Figure 3.
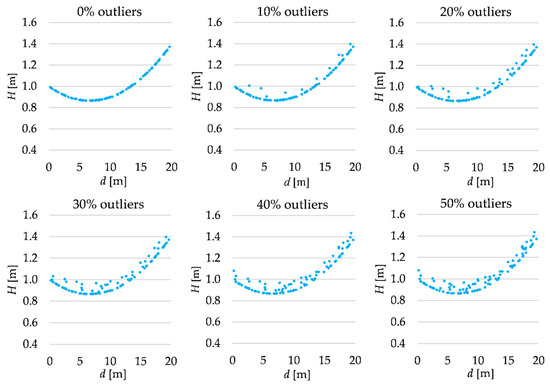
Figure 1.
Simulated observation set (the second-degree polynomial).
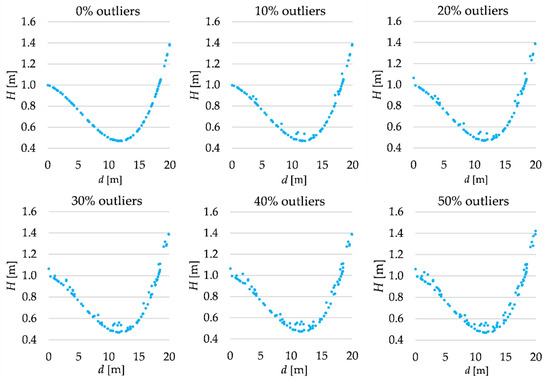
Figure 2.
Simulated observation set (third-degree polynomial).
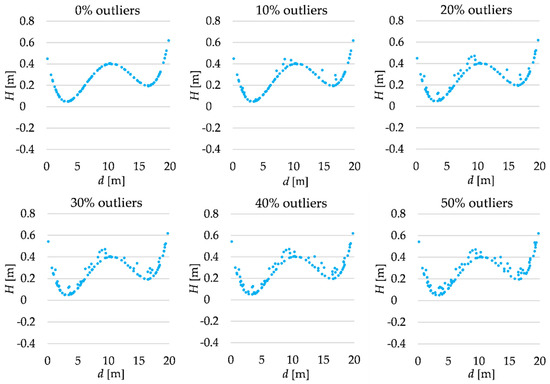
Figure 3.
Simulated observation set (fourth-degree polynomial).
In the functional model of Equation (1), the parameter vector (in two competitive variants ) includes the respective polynomial coefficients, and the coefficient matrix A includes indeterminates , raised to the respective powers. Thus, the terrain profiles are determined based on the polynomial coefficients estimated by applying Msplit estimation (SMS or AMS estimation) and for the comparison purpose by the least squares method (LS).
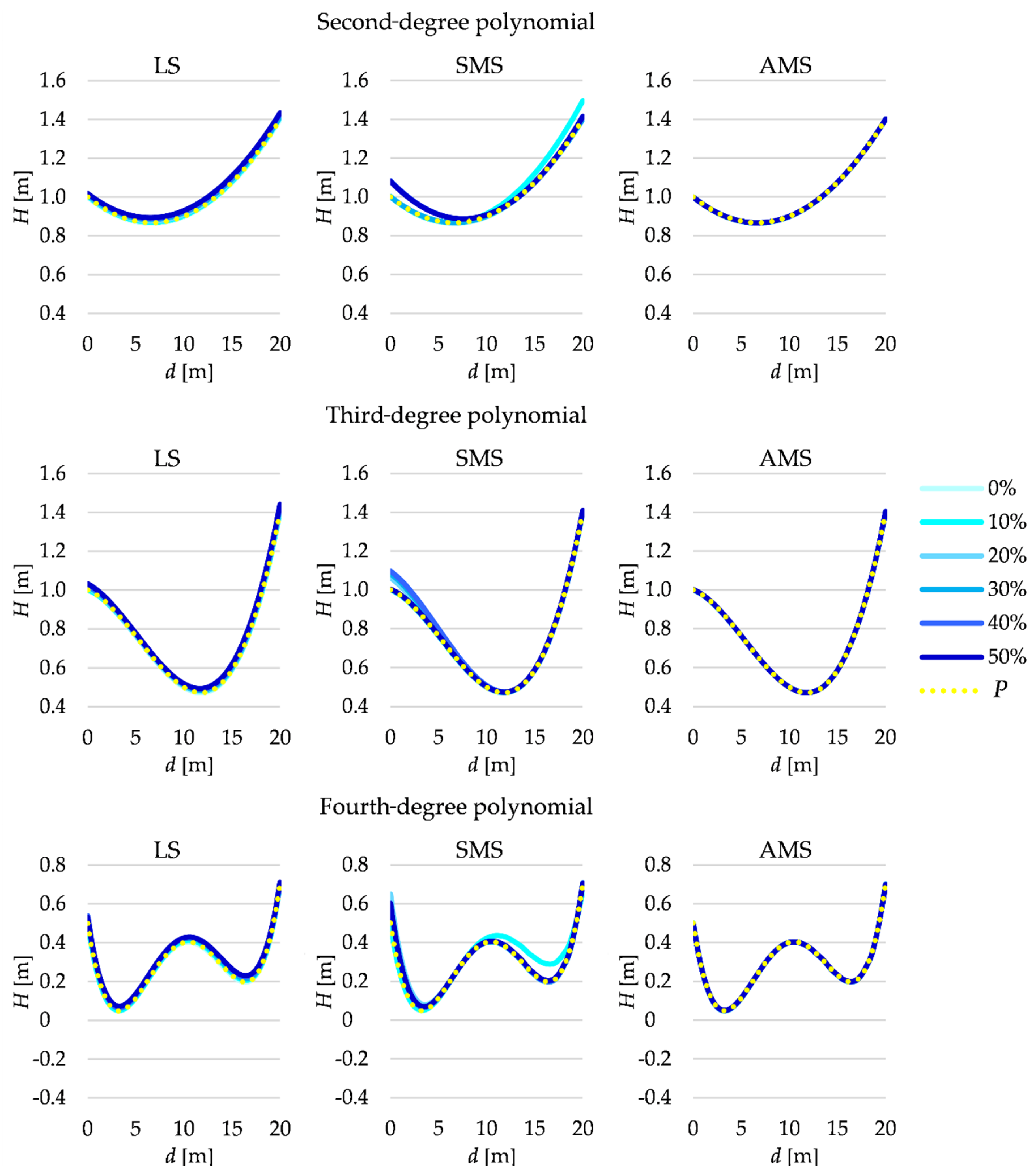
The main objective of that test is to examine how the increasing percentage of outliers influences the estimation results. The estimated polynomial coefficients are the basis for the estimated terrain profiles; hence, we can compute the terrain profiles by applying the LS, SMS and AMS estimates, respectively. The estimated profiles are presented in Figure 4 in comparison to simulated profile P. It is worth noting that in the SMS as well as the AMS estimation, there is also the second solution (based on the second variant of the estimated parameter vector). Here, in contrast to the typical applications of Msplit estimation, we are not interested in such a solution. Its task is just “absorbing” the outliers and reducing their influence on the estimated terrain profile; thus, the second estimated profiles are not shown in Figure 4.
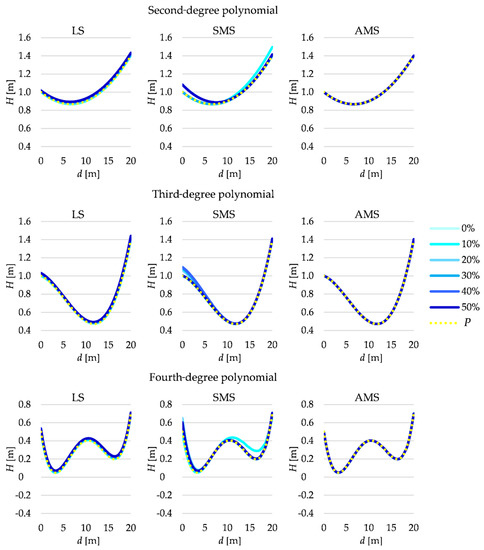
Figure 4.
Estimated terrain profiles for LS, SMS and AMS estimates for different percentages of outliers.
Generally, the superior results are obtained for the AMS estimation for all three polynomials simulated. For such a method, even for 50% outliers in the observation set, the estimated terrain profile is comparable to the simulated one. Such good outcomes are not always obtained for SMS estimation. In the case of the second-degree polynomial, the SMS estimation gives good results for the whole terrain profile for the 0%, 20% and 30% outliers in the observation set; in the case of the third-degree polynomial, it gives good results for the 0%, 10% and 50% outliers; in the case of a fourth-degree polynomial, it only gives good results when there is a lack of outliers. It is also worth noting that in the other variants, the estimated profiles are similar to the simulated ones only for the particular values of the distance d. However, these estimated terrain profiles cannot be considered as satisfactory ones. In the LS estimation case, only for 0% and 10% outliers in the observation set, the obtained profiles are similar to the simulated ones. The shape of the estimated profiles is acceptable in the other variants, but the profiles seem to be lifted about the respective simulated terrain profiles. Thus, the results prove that Msplit estimation, especially the AMS estimation, may give better results than the LS estimation when the observation set is affected by gross errors.
To assess how the estimated profiles fit the simulated ones, we compute root-mean-square deviations by applying the following formula:
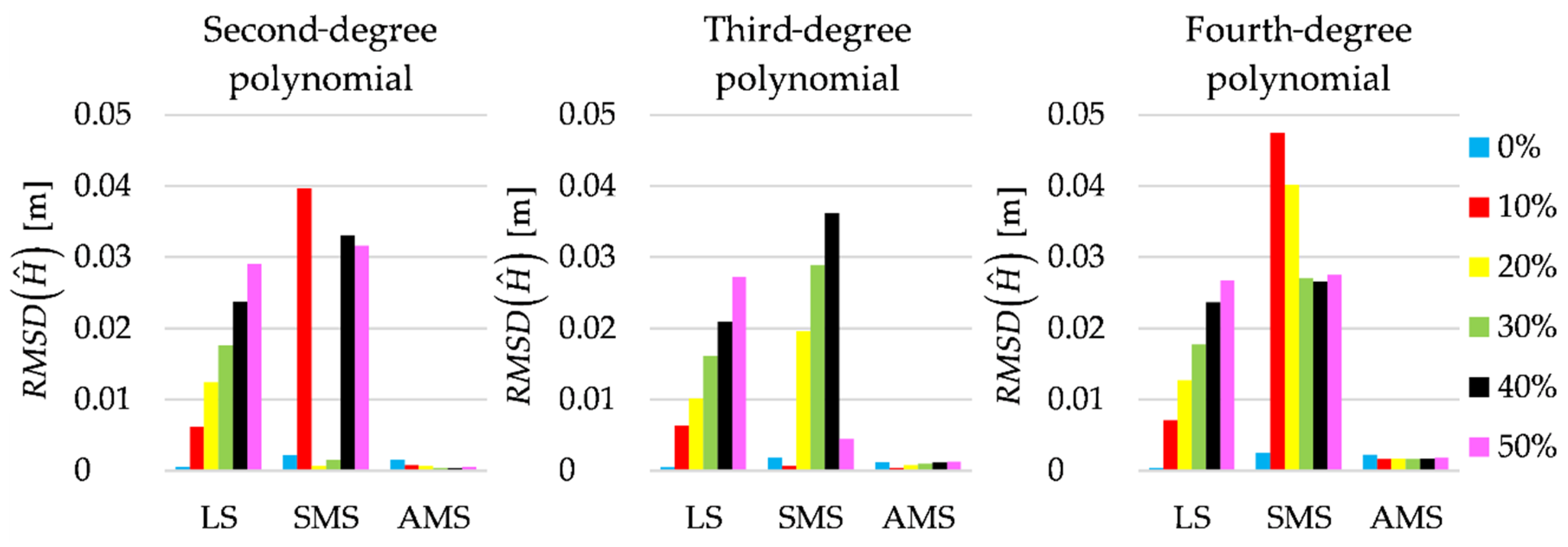
where: —estimated height, —simulated height and n = 41—number of points for which heights are determined for . which are obtained for all estimation methods and all observation sets are shown in Figure 5. The results confirm the conclusions from the analysis of Figure 4.
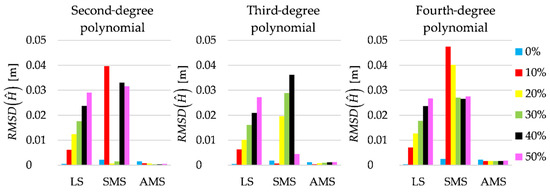
Figure 5.
for LS, SMS and AMS estimates for different percentages of outliers.
The estimated terrain profiles are best fitted when they are computed by applying the AMS estimates of the polynomial coefficients. The only exception is when the observation sets are free of outliers. Then, unsurprisingly, slightly better fits are obtained by using the LS method. Here, all observations are related to one profile, and hence, the observations do not create two real subsets related to their version of the parameter vector. Thus, the assignment of each observation to either version of the parameters during the Msplit estimation process seems somewhat random, and it depends on the particular observation error. In such cases, both versions of the SMS and AMS estimates obtain values close to the theoretical values; however, the accuracy of the estimates is lower than the accuracy of the LS estimates [44]. For the growing percentage of outliers, the fit of the estimated profiles based on the LS estimates becomes worse and worse, which is in line with that method’s general properties. The most surprising results are those of the SMS estimation. In some variants, the fit is very good, but in others, the fit is even worse than for the profiles obtained for the LS method. The worst fit is usually obtained in the variants with a higher percentage of outliers, which confirms that the SMS estimation is sensitive to outliers.
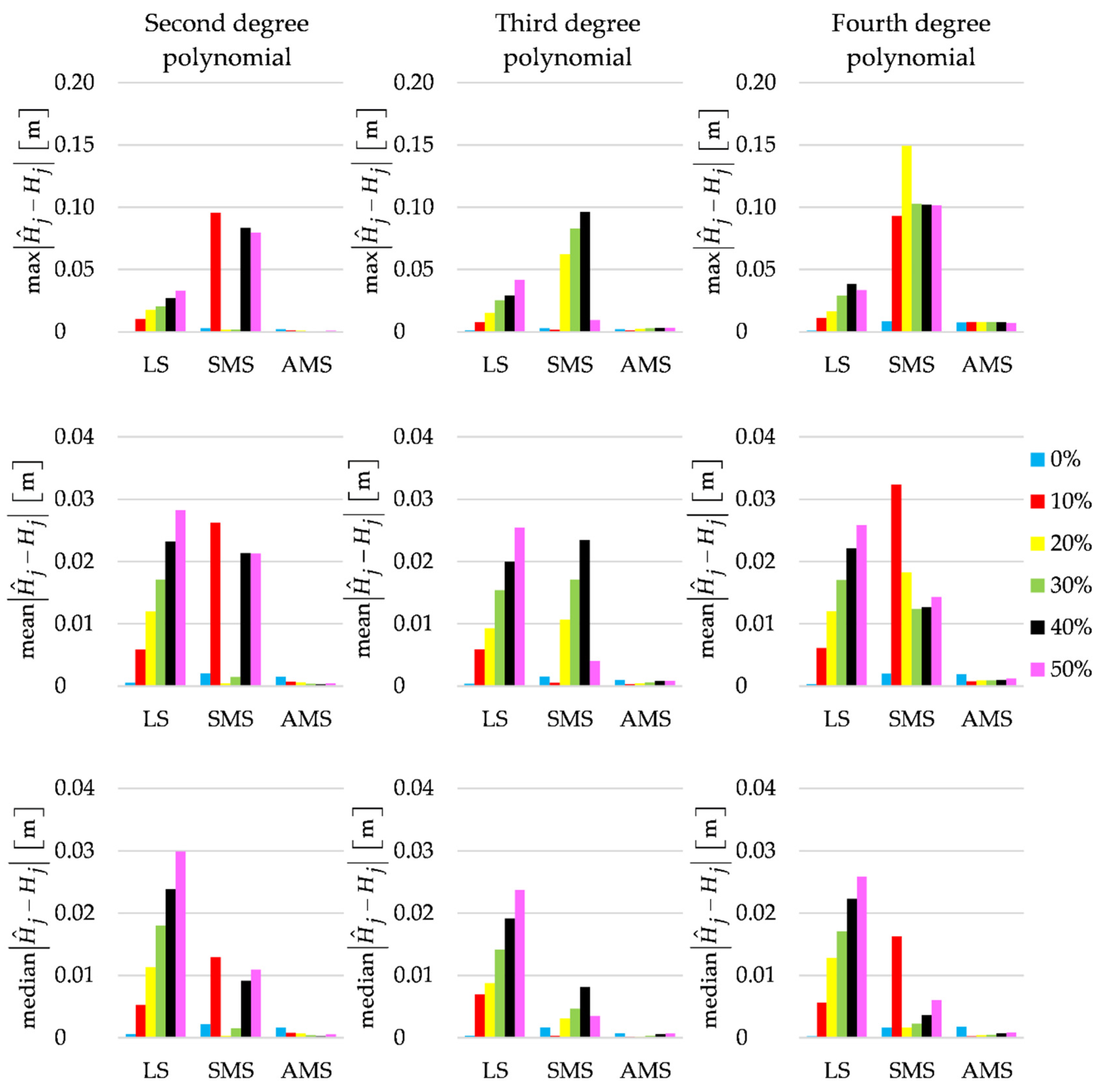
Finally, to better describe the fit in question, Figure 6 presents the maximum, mean and median height differences between the estimated terrain profiles and the simulated profile.
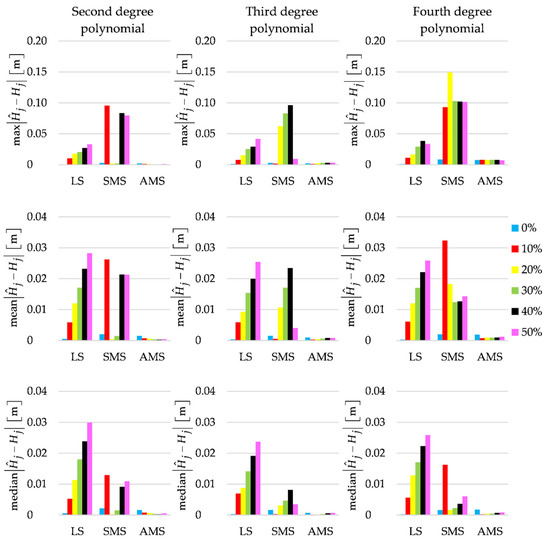
Figure 6.
Maximum, mean and median values of for LS, SMS and AMS estimates for different percentages of outliers.
The values, especially confirm that the best fits are for the profiles obtained by applying the AMS estimates of the polynomial coefficients.
Overall, Msplit estimation proves that it may give satisfactory results in the context of processing TLS data. The estimated terrain profiles by applying the AMS estimation are similar to the simulated one, even for 50% outliers in the observation sets for all three polynomials examined.
4.2. Real TLS Data
Further tests concern real TLS data. We considered two testing objects. The terrain at the first area is covered by small or medium height shrubs, whereas the second area’s terrain is covered by fallen leaves, fallen tree branches and low height grass. Both areas were scanned by applying the Leica ScanStation C10 scanner with a resolution of 5 mm at 30 m. We considered two terrain profiles (each 15 m long) at the first object and two at the second one (each 20 m long). Each profile was measured by the electronic level Leica Sprinter to verify the results obtained from TLS data processing. The profile heights were measured every half meter. We regarded the heights obtained from such a leveling as reference heights. The scanning results, namely point clouds, were imported into Leica Cyclone to create the point set related to each profile. The sets obtained contained about 1300 points for the profiles on the first objects or 950 as for the second object profiles (such a difference in results from the scanner location). The final step was to process such observation sets in Mathcad 15.0 by applying the Msplit estimation to determine terrain profile P.
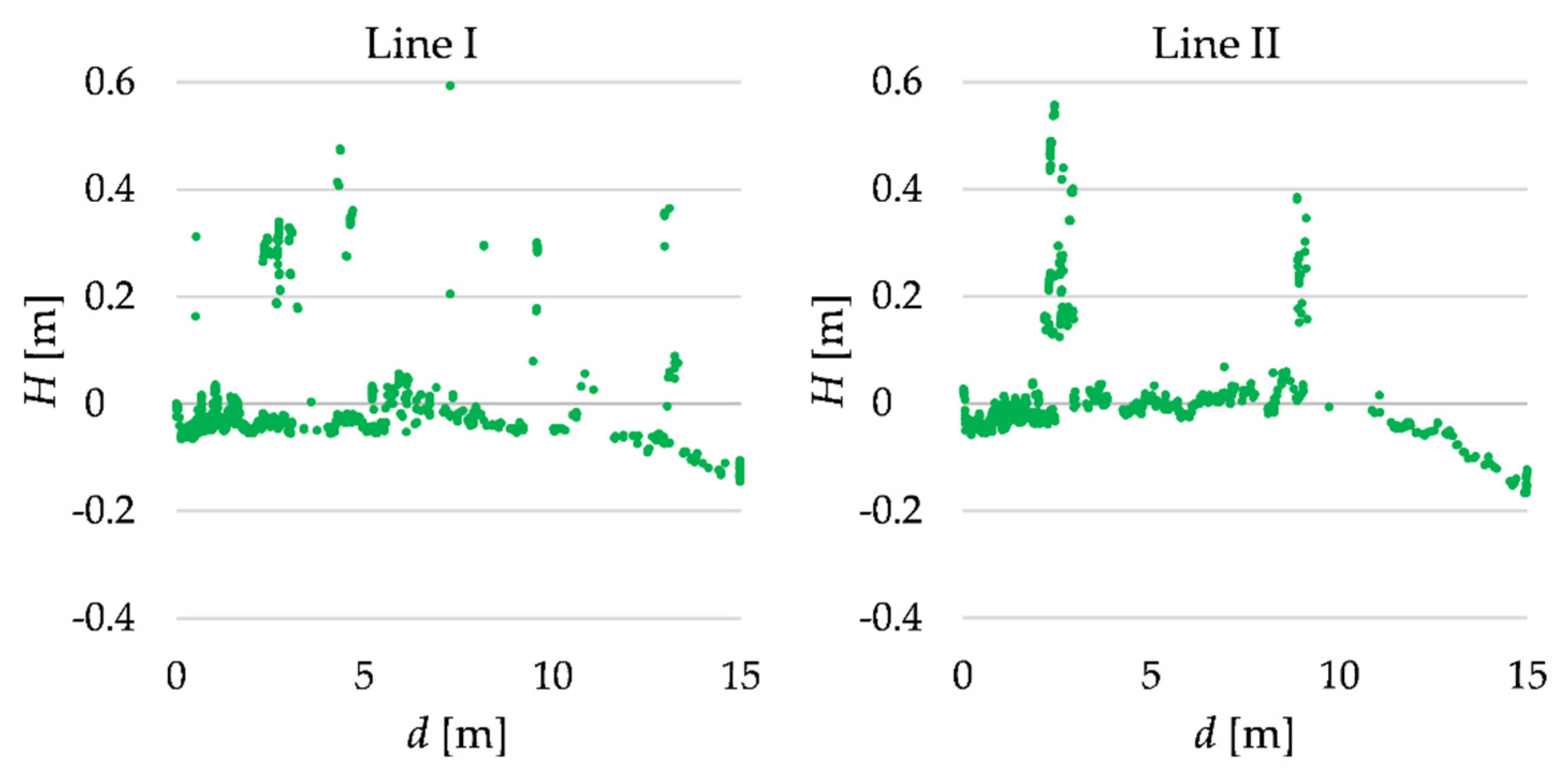
Let us first consider two profiles at the first object. The cutouts of the original point clouds related to the profiles at lines I and II are presented in Figure 7. There were some shrubs on these measurement lines.
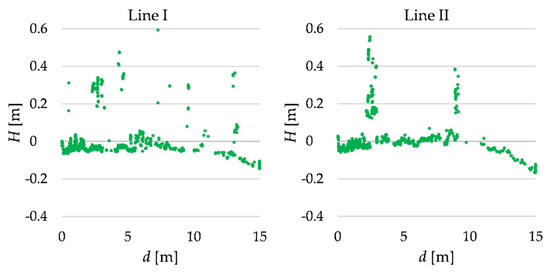
Figure 7.
TLS data related to lines I and II.
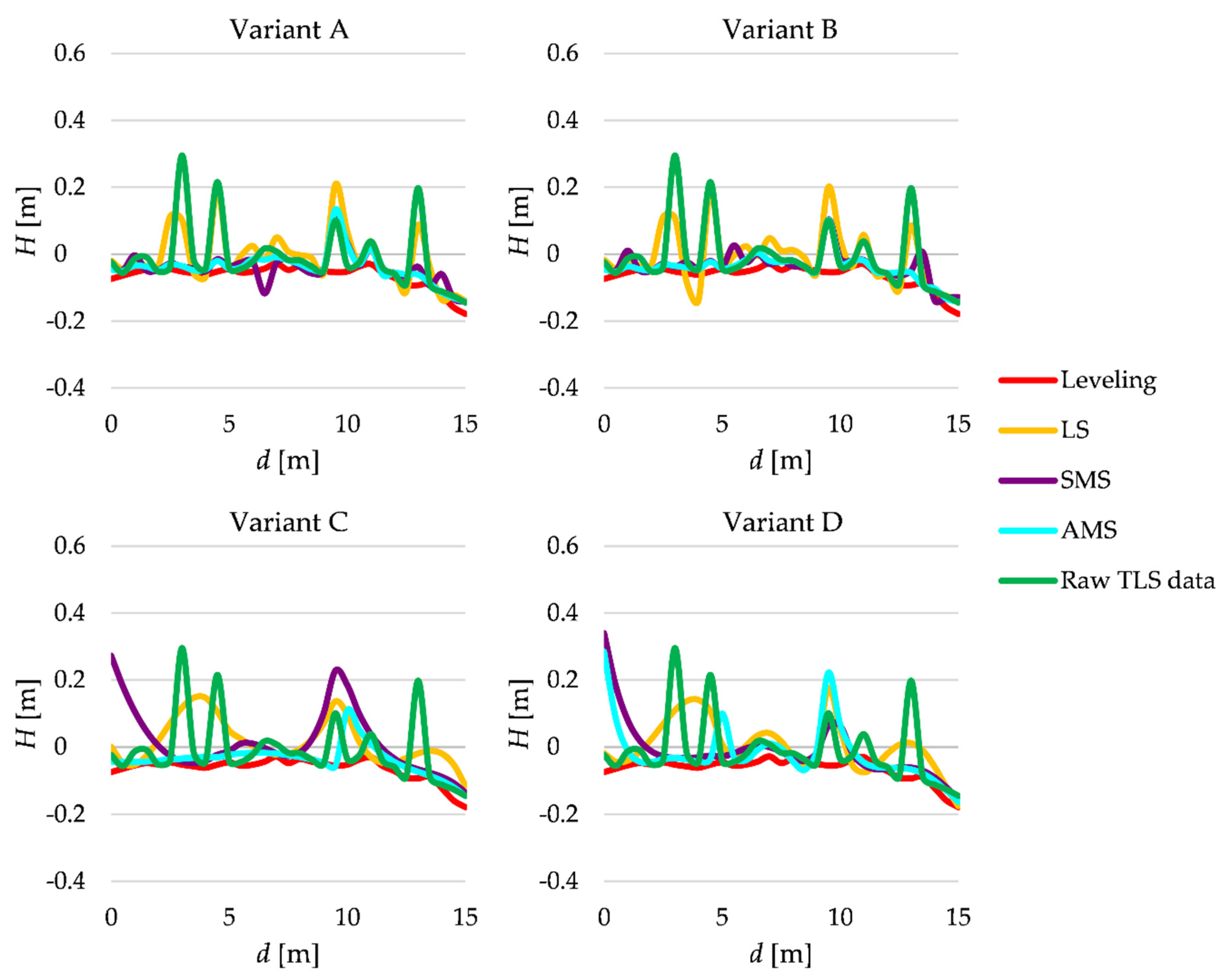
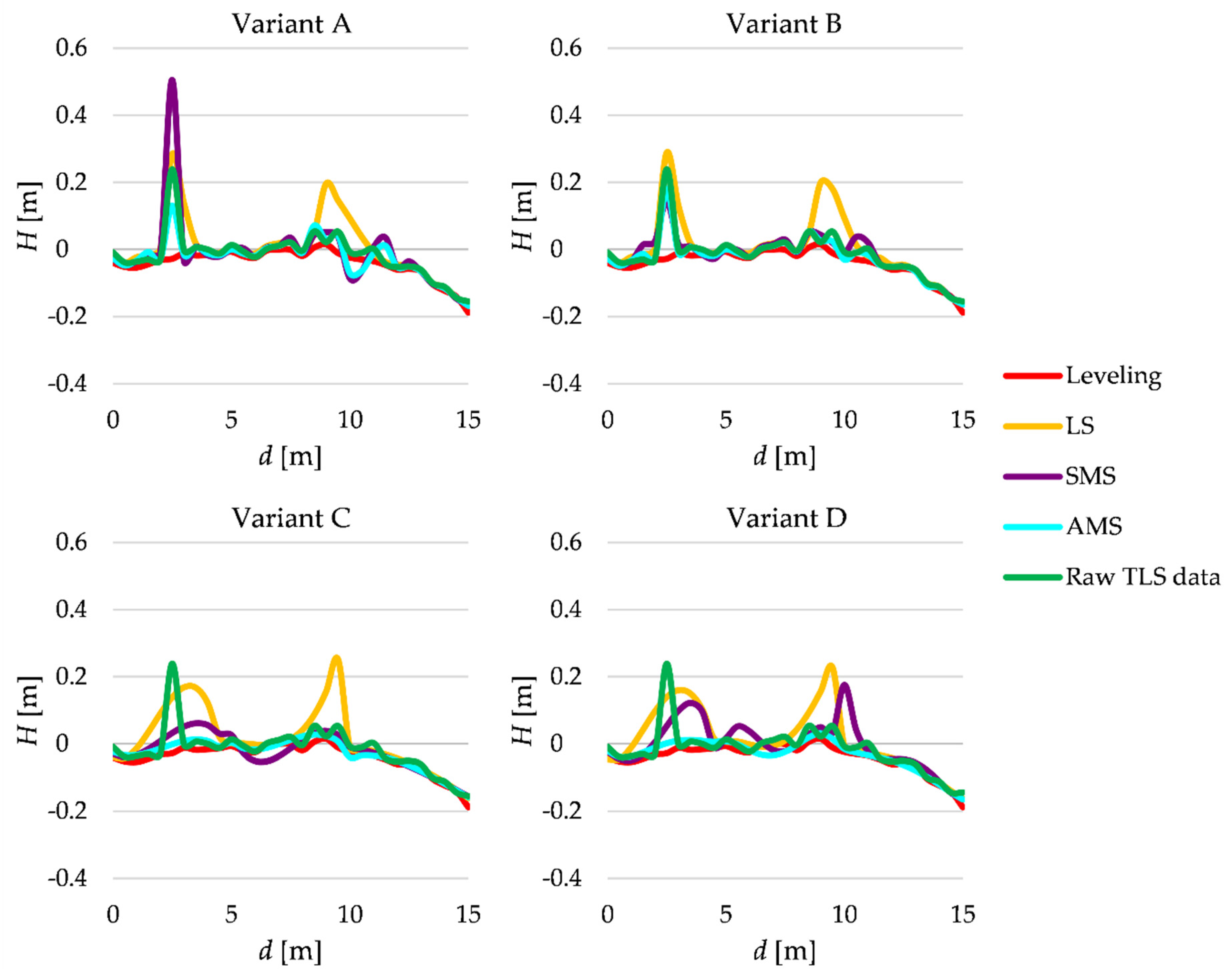
The profiles are supposed to be approximated by polynomials; hence, we assume two different polynomials, namely a third-degree polynomial and a fourth-degree polynomial. Because of the complexity of the real terrain profiles, we propose to process measurements in arbitrarily chosen intervals of the distances d. The first distance intervals are of the length 1.5 m; thus, we consider the intervals , , etc. In the second variant, the length is 5.5 m. We estimated the polynomial coefficients within each interval, which were the basis for computing the profile heights. Such heights were calculated at the points for which heights were earlier determined by geometric leveling. Hence, we consider four different variants: A—third-degree polynomial, interval length 1.5 m; B—fourth-degree polynomial, interval length 1.5 m; C—third-degree polynomial, interval length 5.5 m; D—fourth-degree polynomial, interval length 5.5 m. The terrain profiles are obtained in these four variants (by applying the SMS, AMS or LS estimation, respectively). Moreover, we determine the terrain profiles based on raw TLS data obtained by using the linear interpolation at every half meter (at the same distances dj as for the leveling measurements). The terrain profiles at line I are presented in Figure 8 (the second version of the profiles for the SMS and AMS estimations are not shown here).
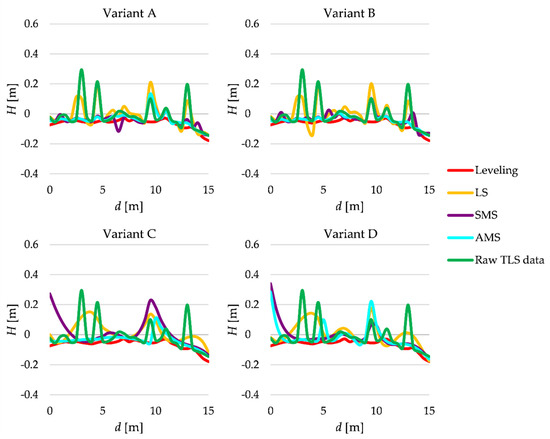
Figure 8.
Estimated terrain profiles of line I.
Generally, the best results are obtained by applying the AMS estimation. These terrain profiles seem to the most similar to the profile obtained from the leveling. SMS estimation gives worse outcomes, but they are still better than the results of the LS estimation (or the profiles based on raw TLS data). The superior results are these of Variant B or A. However, for d equal 9.5 m, even the AMS estimation fails. The reason is that almost all measurements from TLS, which are close to that point, concern terrain details (a shrub), not terrain surface. It is worth noting that there are also other intervals where TLS data comes mostly from the terrain details (see the green line and d equal 3, 4.5 or 13 m). In these cases, there were also a few points from the terrain, making it possible to estimate the profile acceptably, but only by applying the SMS or especially AMS estimation (the LS estimation provides much worse results). Thus, if the number of points related to terrain is much too small, then the methods examined, even the variants of Msplit estimation, might not give us satisfactory results (regardless of the variant considered here).
The terrain profiles of line II are shown in Figure 9. Again, the best-fitted profiles are obtained by applying the AMS estimation. Let us focus on Variants A and B. When d is equal to 2.5 m, all estimated profiles represent terrain details rather than the terrain itself. It also means that the number of points related to the terrain were too small. As for the SMS estimation and especially for AMS estimation, such a problem disappears in Variants C and D. Thus, the widening of the interval considered allows us to obtain satisfactory results, especially for the AMS estimation. One can say that in such a wider interval, a few points related to the terrain “appear,” which allows the AMS estimation to “catch” terrain and determine the terrain profile in a better way.
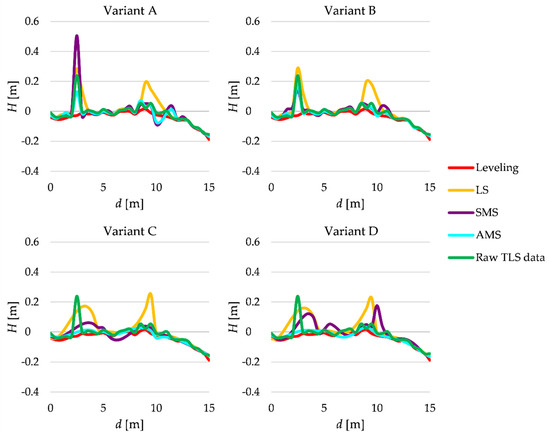
Figure 9.
Estimated terrain profiles of line II.
The simple graphical analyses of the estimated profiles of lines I and II show that the profiles obtained by applying the AMS estimation are the most fitted in the profile determined by the leveling measurements. However, it is not generally apparent in which variant the AMS estimation gives the best results; in fact, it depends on the shape of the terrain and terrain details and the number of TLS points related to them.
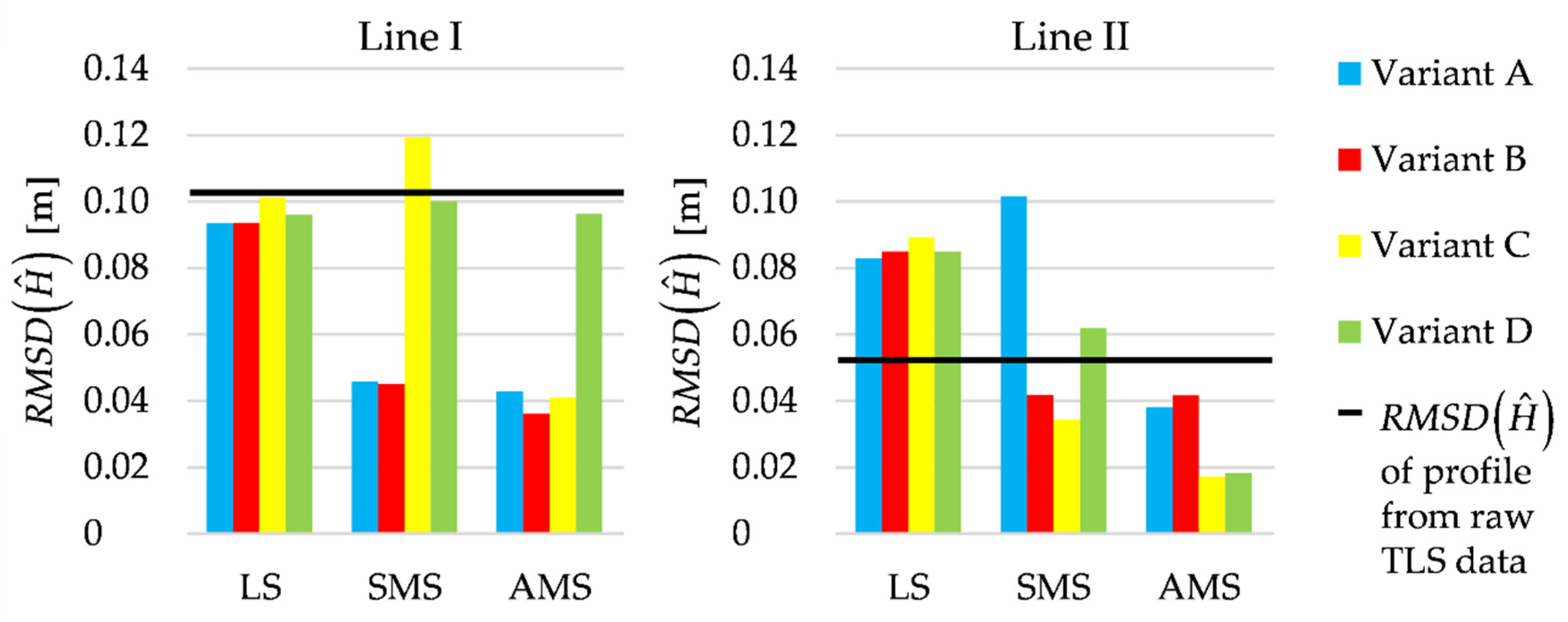
The analyses of the terrain profiles determined at lines I and II are supplemented with the estimated accuracy of the fit, namely, , which is computed by applying Equation (12) (—estimated height, —height from leveling measurements, ). The respective accuracies, calculated for all variants considered, are presented in Figure 10. In the LS estimation case, the differences between the values that are obtained for each variant are small and insignificant. As for both variants of Msplit estimation, such differences are more evident. For line I, the superior accuracy, approximately 0.04 m, is obtained for the AMS estimation in Variants A, B and C; superior accuracy for the SMS estimation is obtained in Variants A and B. Similar values of are also obtained for line II, namely, for the SMS estimation in Variants B and C and for the AMS estimation in Variants A and B. The fit’s highest accuracy is obtained for the AMS estimation in Variants C and D (approximately 0.02 m, line II). One should realize that RMSD is a measure of accuracy that is not robust against outliers. Here, its values are sensitive to the high discrepancies between the estimated and reference profile, even if such discrepancies concern only a single point (or a few points). For that reason, to better describe the fit of the estimated profiles to the reference one, Table 2 shows the maximum, mean and median of the absolute differences
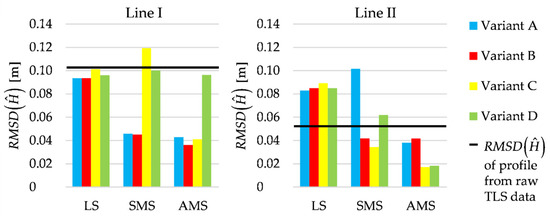
Figure 10.
Lines I and II; accuracy of the estimated profiles compared to accuracy of the profile obtained from raw TLS data.

Table 2.
Maximum, mean and median of for lines I and II.
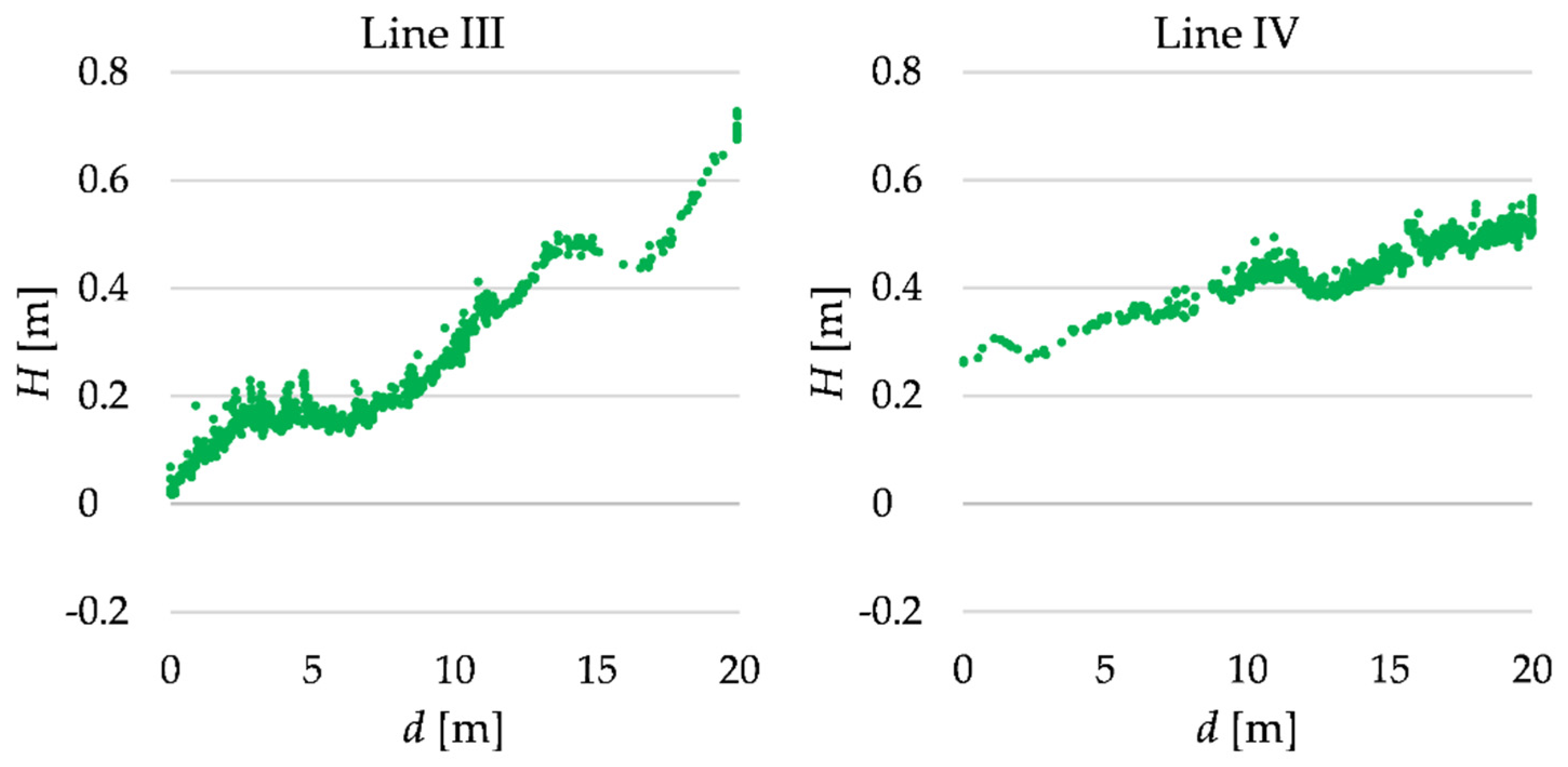
Let us now consider terrain profiles at the second object. Let us recall that the object area was covered by fallen leaves and small fallen tree branches. We consider two profiles measured 20 m in length. The cutouts of the original point clouds related to the profiles at lines III and IV are shown in Figure 11.
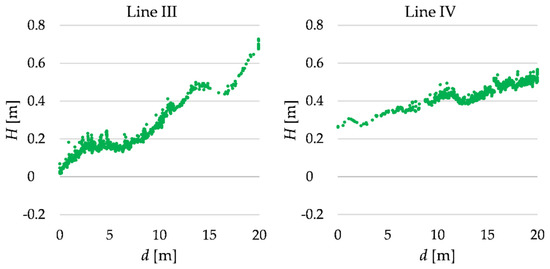
Figure 11.
TLS data related to lines III and IV.
The profiles are later estimated in the same way as in the previous test. We also consider the same variants of estimation of the polynomial coefficients, namely A, B, C and D. As on the last test, the profile which was determined by geometric leveling was regarded as a reference.
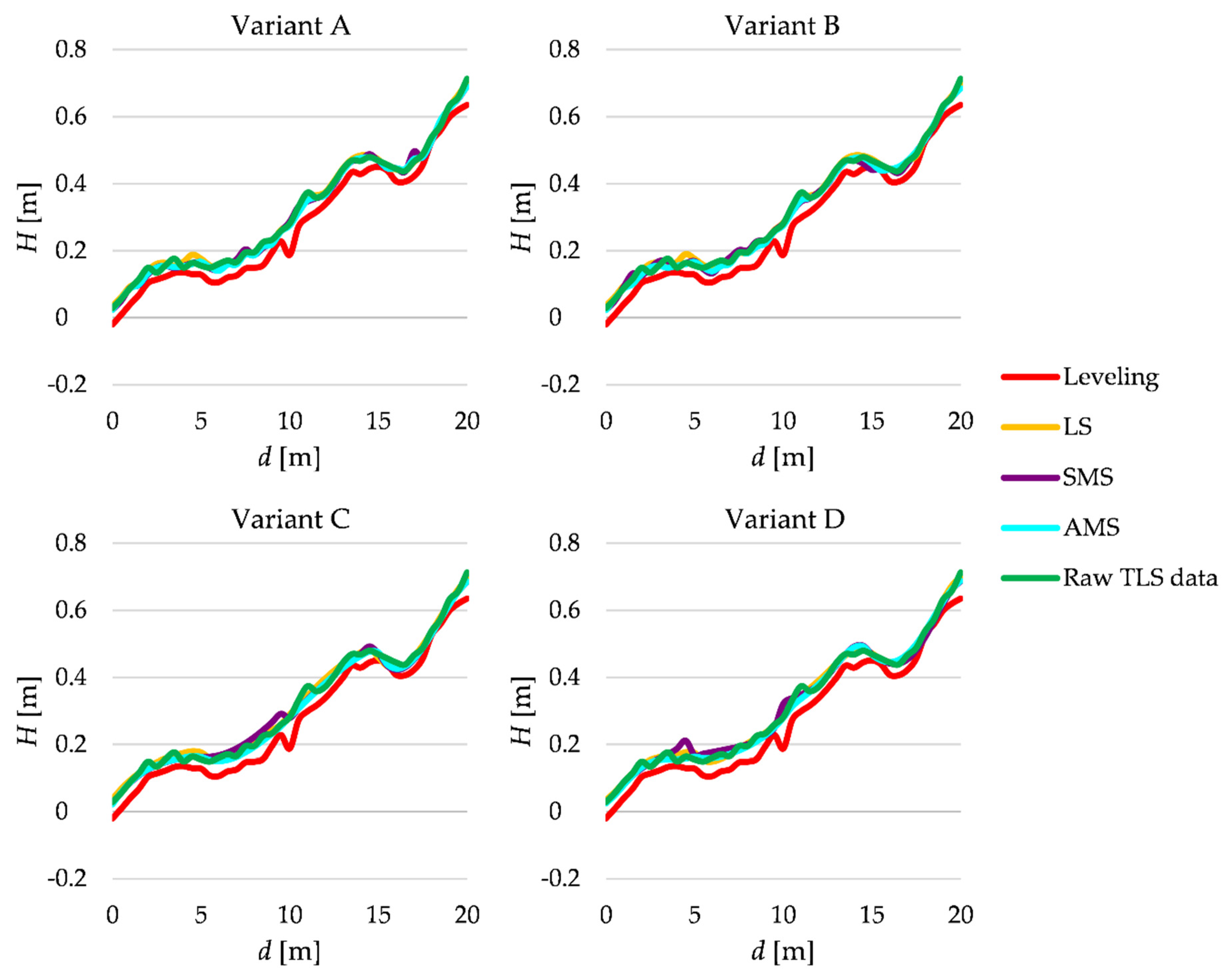
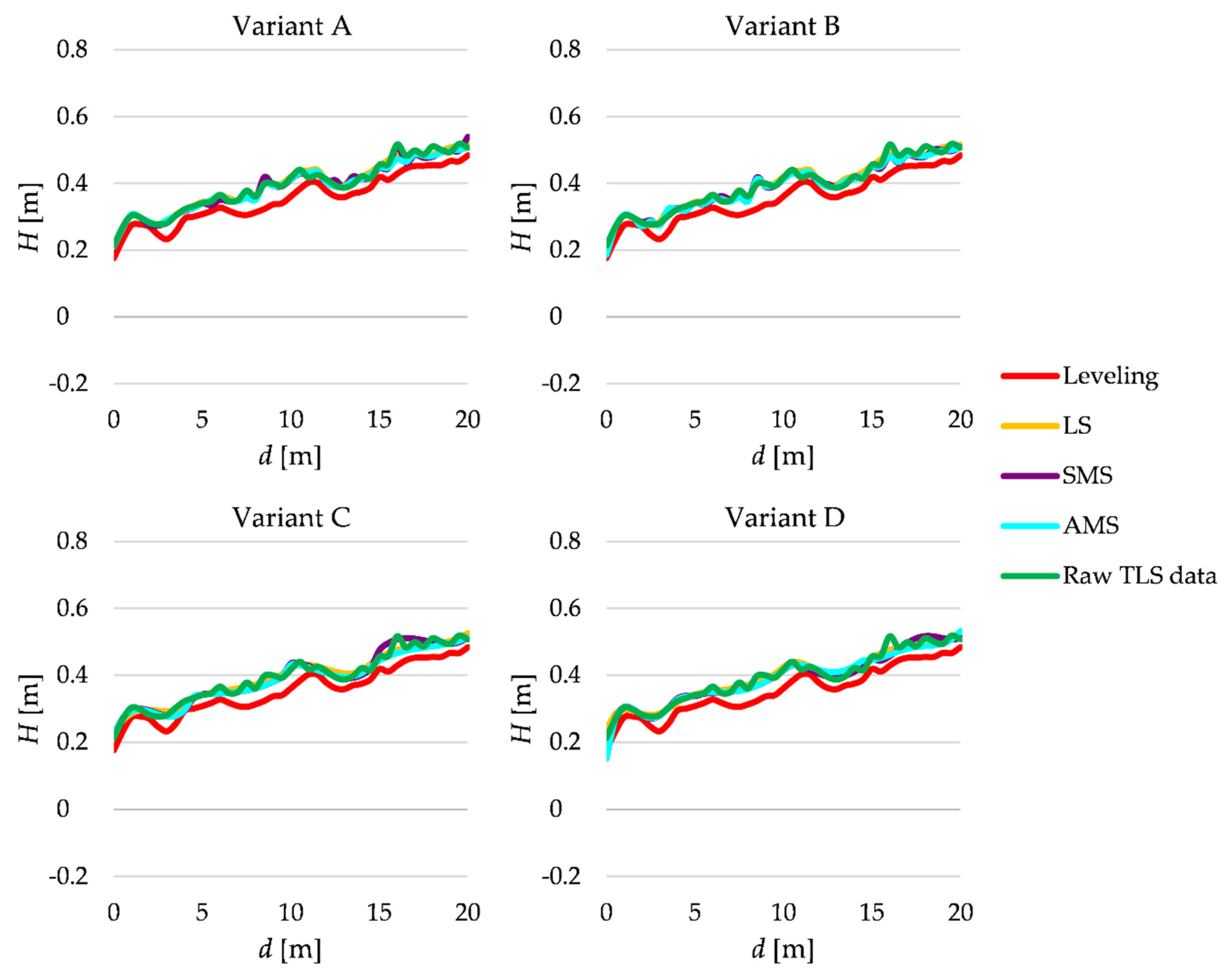
Figure 12 presents the estimated terrain profiles at the first line, which was considered in that test, i.e., line III.
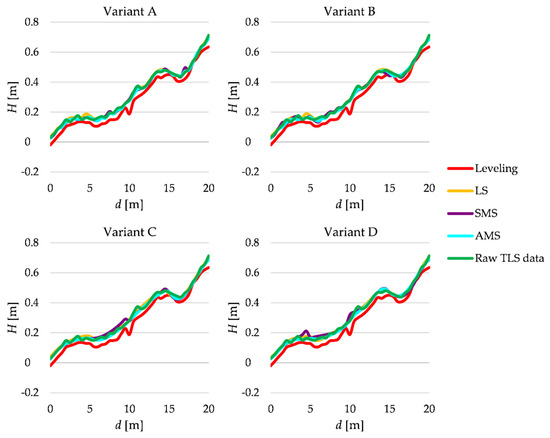
Figure 12.
Estimated terrain profiles of line III.
The terrain profiles obtained from raw TLS data and by applying the LS, SMS and AMS methods are quite similar. They seem to be shifted up a few centimeters above the reference terrain profile. The reason is that the fallen leaves cover the terrain surface almost uniformly. One can also observe the same effect for the estimated profiles at line IV (see, Figure 13). To assess such a shift, we compute the mean of the differences which are presented in Table 3 (in this test ).
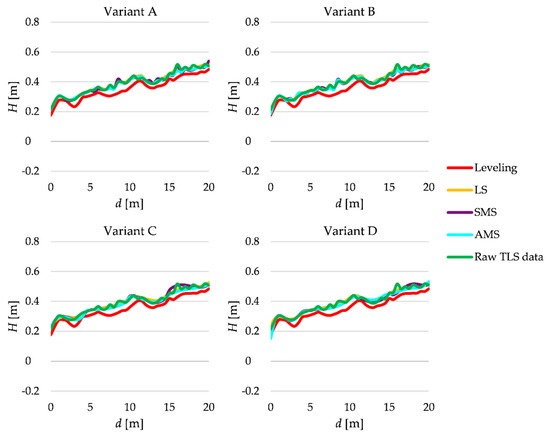
Figure 13.
Estimated terrain profiles of line IV.

Table 3.
Mean of for lines III and IV.
For both lines, the shift values are close to each other; thus, one can conclude that, in fact, it is the thickness of the fallen leave layer. It is also worth noting that TLS data contained some points related to the terrain details (some small “hills,” see the green lines in Figure 12 and Figure 13). Usually, such data irregularities are smoothed in the estimated profiles, especially those obtained by applying the AMS estimation in Variants C and D.
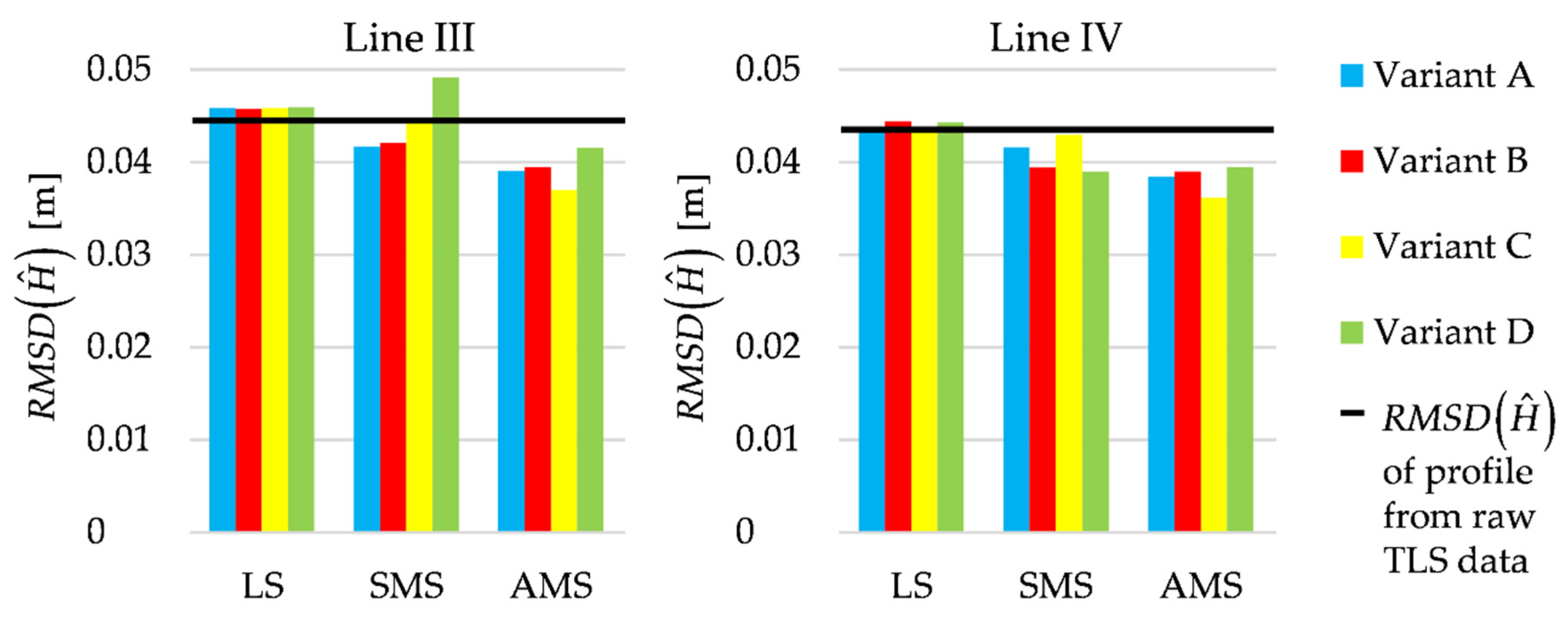
To compare the estimated profiles with each other, Figure 14 presents RMSDs of the profile fits (they are computed by applying Equation (12) and taking ).
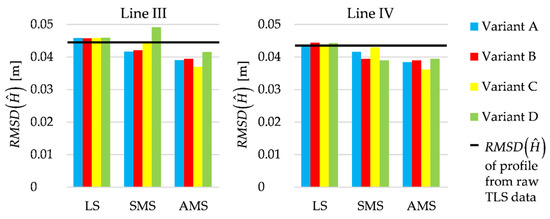
Figure 14.
Lines III and IV; accuracy of the estimated profiles compared to accuracy of the profile obtained from raw TLS data.
The differences in RMSDs between the estimation methods are much smaller than in the previous tests. This is because there were only a few small terrain details; hence, there was a small number of outlying observations. It is worth noting that the values of RMSDs are like those obtained in the previous test (in which the number and the height of the terrain details were more significant) for the profiles estimated by applying Msplit estimation. Undoubtedly, all RMSDs are strongly influenced by the systematic error (the shift of the estimated profiles).
Let us now consider the application of the proposed approach to deformation analysis. Generally, such an application would concern TLS measurements and the estimation of terrain profiles at different epochs. These profiles can then be compared with each other to determine the vertical displacements of the terrain surface. Such an application of Msplit estimation would be novel. Currently, such a method was used in the deformation analysis in a different context, namely when the observation set was a disordered mixture of the same object’s observations from two different measurement epochs [29,32,35,45].
Here, we do not have measurements at two different epochs; however, we do have two different terrain profiles of the same length. We can apply the approach at hand to estimate the vertical differences between the profiles in question. This experiment allows us to assess whether the method proposed in the paper can be used in such a case. Note that the estimation of the vertical displacements (differences between the same profile at different measurement epochs) would be performed very similarly.
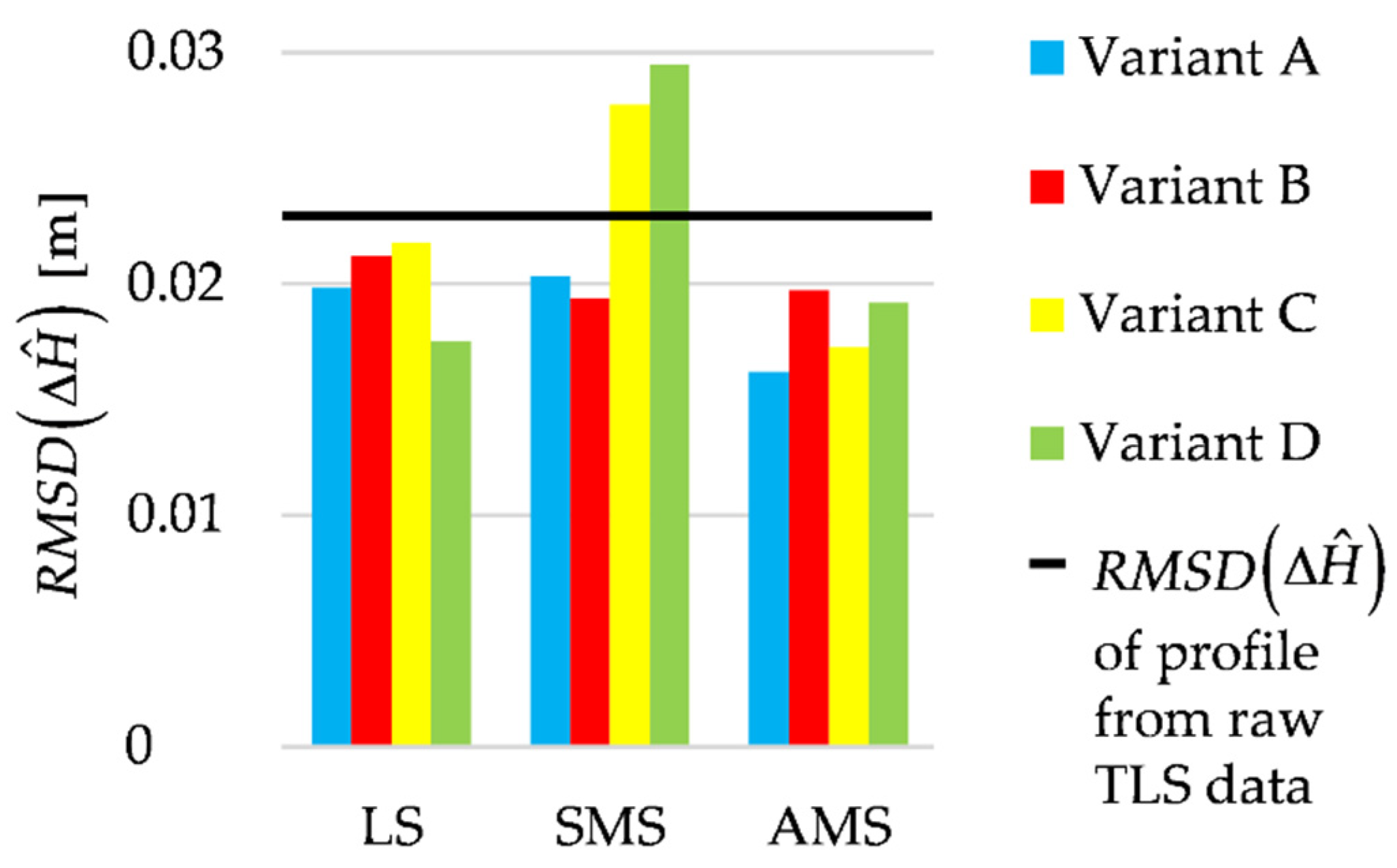
Let us analyze the estimated height differences ( and —heights at the estimated profile of line III or IV, respectively, at the distance , ). Figure 15 presents RMSDs computed like in the previous test but related to the estimated height differences. Here, as a reference, we assume the height differences obtained from the geometric leveling.
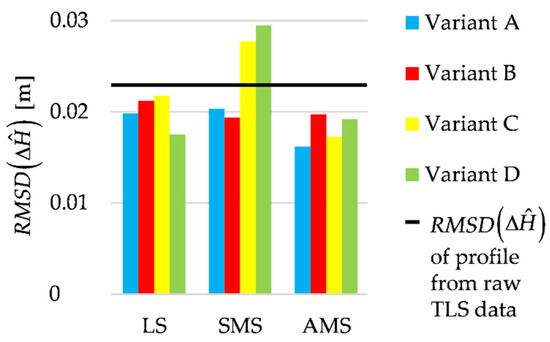
Figure 15.
Lines III and IV; accuracy of the differences between the estimated profiles compared to accuracy of the differences obtained from raw TLS data.
The values of RMSD are usually close to one another. The smallest RMSD is obtained when the differences between profiles are based on the AMS estimates (Variant A). In contrast, the highest RMSDs are obtained by applying the SMS estimates (Variants C and D). Except for these two cases, RMSDs are lower than RMSDs obtained for the profiles determined from the raw TLS data. Moreover, they are twice as small as the respective RMSDs of the terrain profiles of lines III and IV. This means that during the estimation of height differences, the influence of the systematic error (shift) was significantly reduced.
Table 4 shows the maximum, mean and median values of the absolute differences to describe the height differences obtained in the different variants.

Table 4.
Maximum, mean and median of between the terrain points of lines III and IV.
The mean and median values confirm the conclusions drawn from the RMSD values. The smallest discrepancies are obtained when the profiles are estimated by applying the AMS estimation. On average, the discrepancies between the estimated and the reference profile are close to 10–15 mm. For the other methods, the discrepancies are usually bigger, about 2–3 mm.
5. Discussion
This paper presents an application of two variants of Msplit estimation, i.e., the SMS and AMS estimation, in the context of the determination of profiles of the terrain surface based on TLS data. Let us recall that up to now, the SMS estimation was applied in several problems of the laser scanning data analysis [1,15,22,31]. It was proved that the method in question could provide satisfactory results in the context mentioned.
The empirical tests were based on two types of data: simulated or real TLS data, respectively. The processing of the simulated TLS data by applying Msplit estimation, especially the AMS estimation, gives very promising results for all three polynomials examined. The fit of the estimated profile for the simulated data is very good. The AMS estimation does not fail even for 50% outliers in the observation set. It confirms the results presented in the previous papers, which indicate that such a method is generally less sensitive to outliers of the moderate magnitude than the SMS estimation [34,35].
In real TLS data, we chose the areas with many terrain details (i.e., shrubs and fallen tree branches) or where fallen leaves covered the terrain surface. Thus, we considered the objects for which it was not so easy to determine terrain profiles because many points in a point cloud did not refer to the real terrain surface. For the first object, where there were many shrubs and fallen tree branches, Msplit estimation was able to provide the terrain profiles which were better fitted in the real profile (determined by geometric leveling) than the profiles provided by the LS estimation. The profiles in question are also better fitted than the profiles determined directly from the raw TLS data. The best-fitted profiles were obtained by applying the AMS estimation; the accuracy of the fit is from 0.02 m to 0.04 m, which depends on the estimation variant. One can say that such accuracy is twice as small as the accuracy of the fit of the profiles obtained by applying the LS estimation or determined directly from the raw TLS data. Unfortunately, if the obstacles “obscure” the terrain surface to a large extent and hence the number of TLS points related to the terrain was very small, then even the variants of the Msplit estimation examined might not give us satisfactory results.
For the second object, there were only fallen leaves and fallen small tree branches (no high obstacles). The fallen leaves covered the terrain surface almost uniformly. Hence, the point cloud included only a few points related to the terrain surface. In many intervals considered, there were no such points at all. It was impossible to determine the real terrain profile from the TLS data in such a case. The shapes of estimated profiles were close to the real terrain profile; however, all determined profiles seemed to be shifted up for about 0.03–0.04 m. The accuracy of the fit for all estimated profiles was usually close to 0.04 m, which appeared to be strongly influenced by the systematic error (the shift). The accuracy was the highest when the profile was estimated by applying the AMS estimation. However, the differences between all estimation methods were much smaller than for the first object. Generally, the accuracy of fit of the estimated profile was a little bit better than the accuracy obtained for the profile determined from the raw TLS data.
As we considered applying the proposed approach in deformation analysis, we estimated differences between two terrain profiles at the second object. When estimating such differences, the systematic error was reduced in a significant way. The accuracy of the fit increased to 0.02 m, which is twice smaller than in the case of a single profile. We can expect much higher accuracy when the terrain would not be covered by a “contamination layer.” In such a context, the approach presented can be applied in, e.g., assessing the mining damages and ground disasters [20,21].
Another interesting issue is the analysis of the Msplit estimation itself. A study with a focus on profile estimation has never been done before. The results confirm the general properties of the SMS and AMS estimations. Firstly, the results are better when the difference between profiles of terrain or terrain details are more significant [34,44,45]. Secondly, the AMS estimation proved its robustness against outliers of the moderate magnitude, in contrast to the SMS estimation and, of course, the LS estimation. It is worth noting that the presented application of both Msplit estimations is not a usual one. Here, we were especially interested in one estimated profile (the terrain profile). The second profile (the profile of the terrain details) is out of our interest. Its main objective is to attract the outlying observations (observations related to terrain details or observations disturbed with gross errors) and reduce the influence of such observations on the terrain profile estimation. Such an approach is similar to the variant of the SMS estimation proposed in [46].
Here, we consider four variants that were applied in the profile estimation. They differ from each other in the length of the distance interval considered and the polynomial degree used. Although there are some differences between the respective variants’ results, it is hard to indicate the most suitable variant for profile estimation. Generally, one can suggest that polynomials of the third degree and shorter rather than longer intervals should be applied when there are many terrain details of medium height (e.g., shrubs).
Furthermore, an interesting issue to consider in the future is the application of Msplit(q) estimation [30] for more than two competitive models for processing TLS or ALS point cloud. Another option would be the application of Msplit estimation to determine horizontal displacements from TLS data, based on an analysis of changing terrain details location.
6. Conclusions
The paper presents an application of Msplit estimation in the determination of terrain profiles from TLS point clouds. The profiles in question are determined by applying the polynomials, of which the coefficients are estimated by the respective estimation method. The analysis presented in the paper proves that such an approach is efficient and can provide good terrain profiles even if there are outliers in an observation set. In other words, if there are many shrubs or other significant terrain details, namely if the difference between terrain heights and terrain details heights is vivid, Msplit estimation might be applied successfully to the determination of the terrain profile. The obtained results suggest that in the application at hand, AMS estimation is a better option than SMS estimation. Regardless of the methods analyzed in this paper, too few terrain data due to terrain obstacles may lead to unacceptable results; however, other methods cannot provide satisfactory results in such a case.
The application of Msplit estimation, especially the AMS estimation, yields profiles that are better fitted in the real terrain profile compared to profiles obtained by applying the LS estimation or computed from the raw TLS data.
Author Contributions
Conceptualization, R.D. and P.W.; methodology, R.D., P.W. and A.D.; software, P.W. and A.D.; validation, R.D. and P.W.; formal analysis, R.D.; investigation, P.W.; data acquisition, A.D. and P.W.; data curation, P.W.; writing—original draft preparation, P.W. and R.D.; writing—review and editing, R.D. and P.W.; visualization, P.W.; supervision, R.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Department of Geodesy, University of Warmia and Mazury in Olsztyn, Poland, statutory research no. 28.610.002-110.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Błaszczak-Bąk, W.; Janowski, A.; Kamiński, W.; Rapiński, J. Application of the Msplit method for filtering airborne laser scanning data-sets to estimate digital terrain models. Int. J. Remote Sens. 2015, 36, 2421–2437. [Google Scholar] [CrossRef]
- Rodríguez-Gonzálvez, P.; Jiménez Fernández-Palacios, B.; Muñoz-Nieto, Á.L.; Arias-Sanchez, P.; Gonzalez-Aguilera, D. Mobile LiDAR System: New possibilities for the documentation and dissemination of large cultural heritage sites. Remote Sens. 2017, 9, 189. [Google Scholar] [CrossRef]
- Forlani, G.; Nardinocchi, C. Adaptive filtering of aerial laser scanning data. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; pp. 130–135. [Google Scholar]
- Spaete, L.P.; Glenn, N.F.; Derryberry, D.R.; Sankey, T.T.; Mitchell, J.J.; Hardegree, S.P. Vegetation and slope effects on accuracy of a LiDAR-derived DEM in the sagebrush steppe. Remote Sens. Lett. 2011, 2, 317–326. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Tompalski, P.; Coops, N.C.; Ruiz, L.Á. Characterizing understory vegetation in Mediterranean forests using full-waveform airborne laser scanning data. Remote Sens. Environ. 2018, 217, 400–413. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A fast global interpolation method for digital terrain model generation from large LiDAR-derived data. Remote Sens. 2019, 11, 1324. [Google Scholar] [CrossRef]
- Wang, C.; Hsu, P.-H. Building detection and structure line extraction from airborne LiDAR data. J. Photogramm. Remote Sens. 2007, 12, 365–379. [Google Scholar]
- He, M.; Zhu, Q.; Du, Z.; Hu, H.; Ding, Y.; Chen, M. A 3D shape descriptor based on contour clusters for damaged roof detection using airborne LiDAR point clouds. Remote Sens. 2016, 8, 189. [Google Scholar] [CrossRef]
- Zhang, Z.; Vosselman, G.; Gerke, M.; Persello, C.; Tuia, D.; Yang, M.Y. Detecting building changes between Airborne Laser Scanning and photogrammetric data. Remote Sens. 2019, 11, 2417. [Google Scholar] [CrossRef]
- Zhao, R.; Pang, M.; Liu, C.; Zhang, Y. Robust normal estimation for 3D LiDAR point clouds in urban environments. Sensors 2019, 19, 1248. [Google Scholar] [CrossRef]
- Błaszczak-Bąk, W.; Suchocki, C.; Janicka, J.; Dumalski, A.; Duchnowski, R.; Sobieraj-Żłobińska, A. Automatic threat detection for historic buildings in dark places based on the modified OptD method. ISPRS Int. J. Geo Inf. 2020, 9, 123. [Google Scholar] [CrossRef]
- Yang, H.; Omidalizarandi, M.; Xu, X.; Neumann, I. Terrestrial laser scanning technology for deformation monitoring and surface modeling of arch structures. Compos. Struct. 2017, 169, 173–179. [Google Scholar] [CrossRef]
- Zhao, X.; Kargoll, B.; Omidalizarandi, M.; Xu, X.; Alkhatib, H. Model selection for parametric surfaces approximating 3D point clouds for deformation analysis. Remote Sens. 2018, 10, 634. [Google Scholar] [CrossRef]
- Janicka, J.; Rapiński, J.; Błaszczak-Bąk, W.; Suchocki, C. Application of the Msplit estimation method in the detection and dimensioning of the displacement of adjacent planes. Remote Sens. 2020, 12, 3203. [Google Scholar] [CrossRef]
- Corso, J.; Roca, J.; Buill, F. Geometric analysis on stone façades with terrestrial laser scanner technology. Geosciences 2017, 7, 103. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Belton, D.; West, G. Robust statistical approaches for local planar surface fitting in 3D laser scanning data. ISPRS J. Photogramm. Remote Sens. 2014, 96, 106–122. [Google Scholar] [CrossRef]
- Kwoczyńska, B.; Dobek, J. Elaboration of the 3D model and survey of the power lines using data from airborne laser scanning. J. Ecol. Eng. 2016, 17. [Google Scholar] [CrossRef]
- Suchocki, C. Conception of monitoring of cliff shores. Rep. Geod. 2011, 90, 461–467. [Google Scholar]
- Lian, X.; Hu, H. Terrestrial laser scanning monitoring and spatial analysis of ground disaster in Gaoyang coal mine in Shanxi, China: A technical note. Environ. Earth Sci. 2017, 76, 287. [Google Scholar] [CrossRef]
- Szwarkowski, D.; Moskal, M. Assessment of deformations in mining areas using the Riegl VZ-400 terrestrial laser scanner. E3S Web Conf. 2018, 36, 02009. [Google Scholar] [CrossRef]
- Janowski, A.; Rapiński, J. M-split estimation in laser scanning data modeling. J. Indian Soc. Remote Sens. 2013, 41, 15–19. [Google Scholar] [CrossRef]
- Carrilho, A.C.; Galo, M.; Santos, R.C. Statistical outlier detection method for airborne LiDAR data. In Proceedings of the ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Karlsruhe, Germany, 10–12 October 2018; Copernicus GmbH: Göttingen, Germany, 2018; Volume XLII–1, pp. 87–92. [Google Scholar]
- Carrilho, A.C.; Galo, M. Automatic object extraction from high resolution aerial imagery with simple linear iterative clustering and convolutional neural networks. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W16, 61–66. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Nguyen, A.; Le, B. 3D point cloud segmentation: A survey. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Phillippines, 12–15 November 2013; pp. 225–230. [Google Scholar]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An improved RANSAC for 3D point cloud plane segmentation based on normal distribution transformation cells. Remote Sens. 2017, 9, 433. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-art: DTM generation using airborne LIDAR data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed]
- Wiśniewski, Z. Estimation of parameters in a split functional model of geodetic observations (Msplit estimation). J. Geod. 2009, 83, 105–120. [Google Scholar] [CrossRef]
- Wiśniewski, Z. Msplit(q) estimation: Estimation of parameters in a multi split functional model of geodetic observations. J. Geod. 2010, 84, 355–372. [Google Scholar] [CrossRef]
- Janowski, A. The circle object detection with the use of Msplit estimation. E3S Web Conf. 2018, 26, 00014. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H.; Baryła, R. Determination of vertical indicators of ground deformation in the Old and Main City of Gdansk area by applying unconventional method of robust estimation. Acta Geodyn. Geomater. 2015, 12, 249–257. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H.; Hejbudzka, K.; Dumalski, A. Multi split functional model of geodetic observations in deformation analyses of the Olsztyn castle. Acta Geodyn. Geomater. 2017, 14, 195–204. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Msplit estimation based on L1 norm condition. J. Surv. Eng. 2019, 145, 04019006. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Performance of Msplit estimates in the context of vertical displacement analysis. J. Appl. Geod. 2020, 14, 149–158. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Systematic bias of selected estimates applied in vertical displacement analysis. J. Geod. Sci. 2020, 10, 41–47. [Google Scholar] [CrossRef]
- Li, J.; Wang, A.; Xinyuan, W. Msplit estimate the relationship between LS and its application in gross error detection. Mine Surv. 2013, 2, 57–59. [Google Scholar] [CrossRef]
- Janicka, J.; Rapiński, J. Msplit transformation of coordinates. Surv. Rev. 2013, 45, 269–274. [Google Scholar] [CrossRef]
- Nowel, K. Squared Msplit(q) S-transformation of control network deformations. J. Geod. 2019, 93, 1025–1044. [Google Scholar] [CrossRef]
- Czaplewski, K.; Wąż, M.; Zienkiewicz, M.H. A novel approach of using selected unconventional geodesic methods of estimation on VTS areas. Mar. Geod. 2019, 42, 447–468. [Google Scholar] [CrossRef]
- Marshall, J.; Bethel, J. Basic concepts of L1 norm minimization for surveying applications. J. Surv. Eng. 1996, 122, 168–179. [Google Scholar] [CrossRef]
- Marshall, J. L1-norm pre-analysis measures for geodetic networks. J. Geod. 2002, 76, 334–344. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Iterative process of Msplit(q) estimation. J. Surv. Eng. 2020, 146, 06020002. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Robustness of squared Msplit(q) estimation: Empirical analyses. Stud. Geophys. Geod. 2020, 64, 153–171. [Google Scholar] [CrossRef]
- Wiśniewski, Z.; Duchnowski, R.; Dumalski, A. Efficacy of Msplit estimation in displacement analysis. Sensors 2019, 19, 5047. [Google Scholar] [CrossRef] [PubMed]
- Zienkiewicz, M.H. Application of Msplit estimation to determine control points displacements in networks with unstable reference system. Surv. Rev. 2015, 47, 174–180. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).