A Study of Lunar Microwave Radiation Based on Satellite Observations
Abstract
1. Introduction
2. Lunar Microwave Tb Derived from Satellite Observations
2.1. General Description of Satellite Lunar Microwave Tb Retrieval Algorithms
2.2. Retrieval of the Lunar Microwave Tb Spectrum from NOAA-20 ATMS 2D Raster Scans of the Moon’s Disk
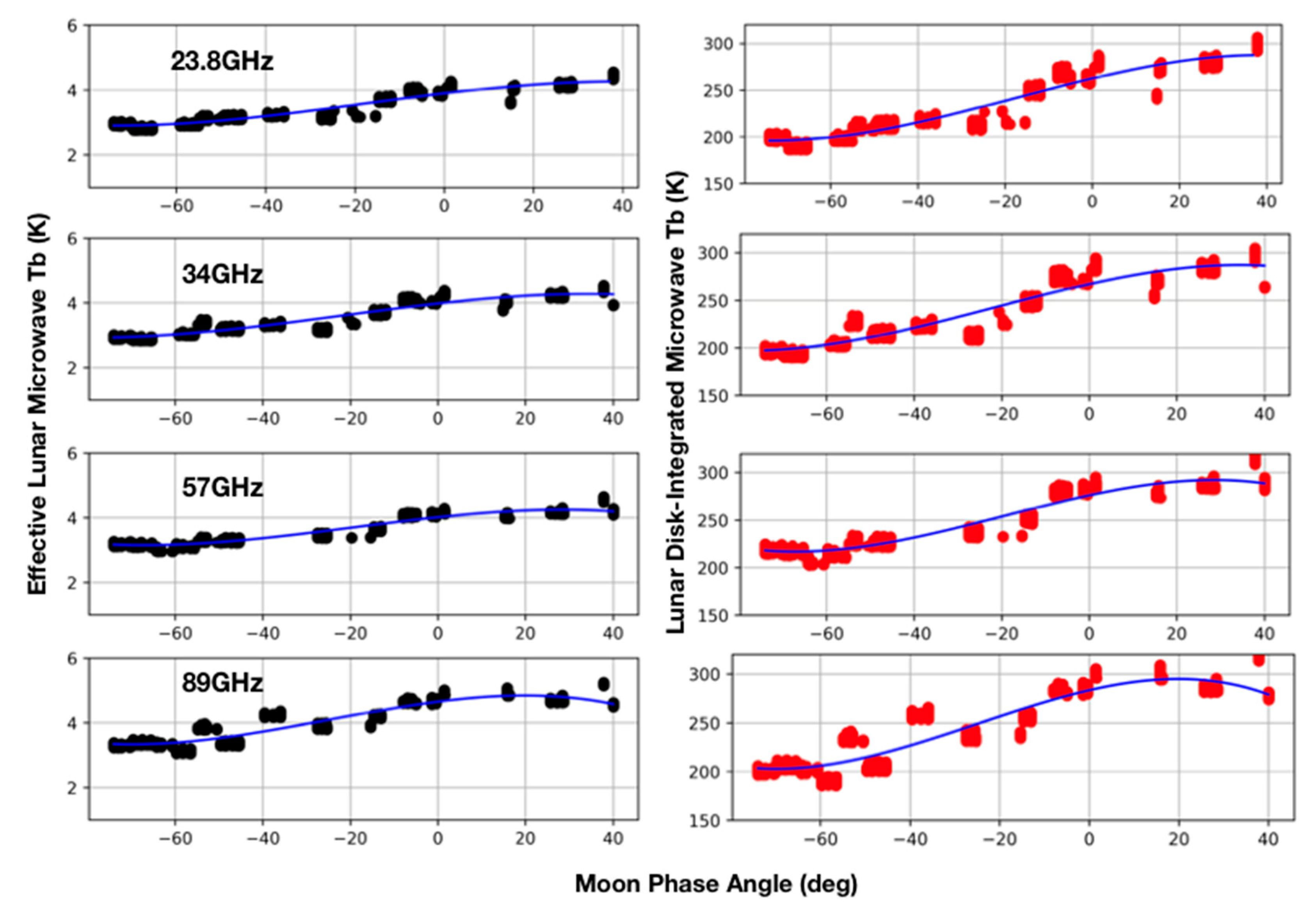
2.3. Lunar Microwave Tb 23–89-GHz Retrieval Results from AMSU-A
2.4. Lunar Microwave Tb 89–183-GHz Retrieval Results from AMSU-B/MHS
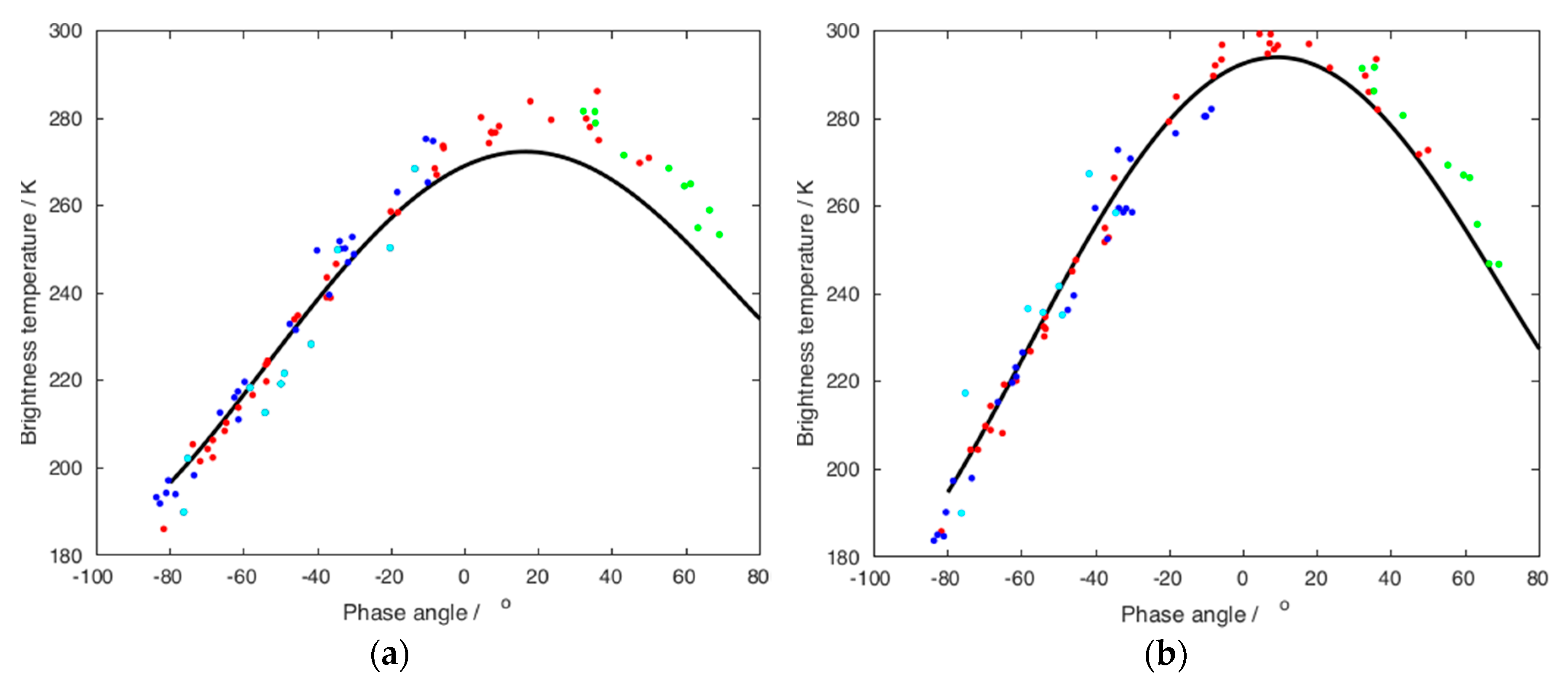
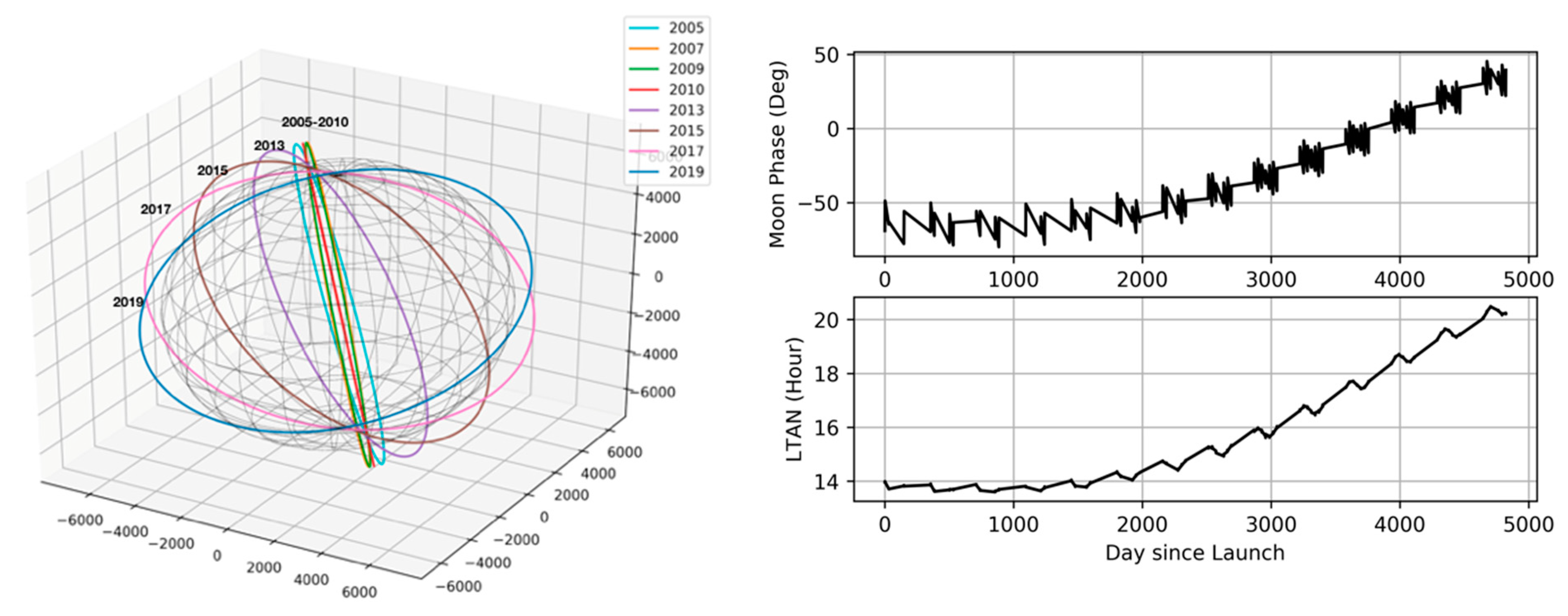
3. Moon Phase Lag Angle Observed from the Drifting Orbit of NOAA-18 AMSU/MHS
4. Uncertainty of the Retrievals
4.1. Random Error in AMSU-B/MHS Retrievals
4.2. Systematic Uncertainties of AMSU-B and MHS Retrievals
- Channel frequency ν: BνMoon is a spectral radiance that is converted to a Tb using the Planck function. To do this, one needs to know the effective frequency midpoint of the channel, which depends on the shape of its relative spectral response function (RSRF). The RSRFs were determined on the ground. Tests with the Atmospheric Transfer Radiance Simulator [31] showed that replacing the actual RSRF with a simple step function changes the Tb corresponding to a given spectral radiance by only 0.1 K. Given that the dilution factor scales the flux density from the Moon, we also multiply this uncertainty by a factor of five, obtaining a contribution of 0.5 K from the RSRF to the overall uncertainty.
- Gain G: The gain is the slope of the function that relates counts to scene radiances. It is determined from two points: the cosmic microwave background (CMB) and the internal calibration target (ICT). The temperature of the ICT is measured with five (MHS) or seven (AMSU-B) platinum resistance thermometers, each one with a systematic uncertainty of 0.1 K [32]. This is smaller than the uncertainties of the cold-space and warm-load correction factors. The warm-load correction factor has an uncertainty of 0.16 K [33], and the cold-space correction is in the order of 1 K, so we adopt these values for the uncertainty. Because the radiance of the CMB is very small, its uncertainty has only a small impact on the gain. We estimate that the systematic uncertainty of the gain is less than 0.3%.
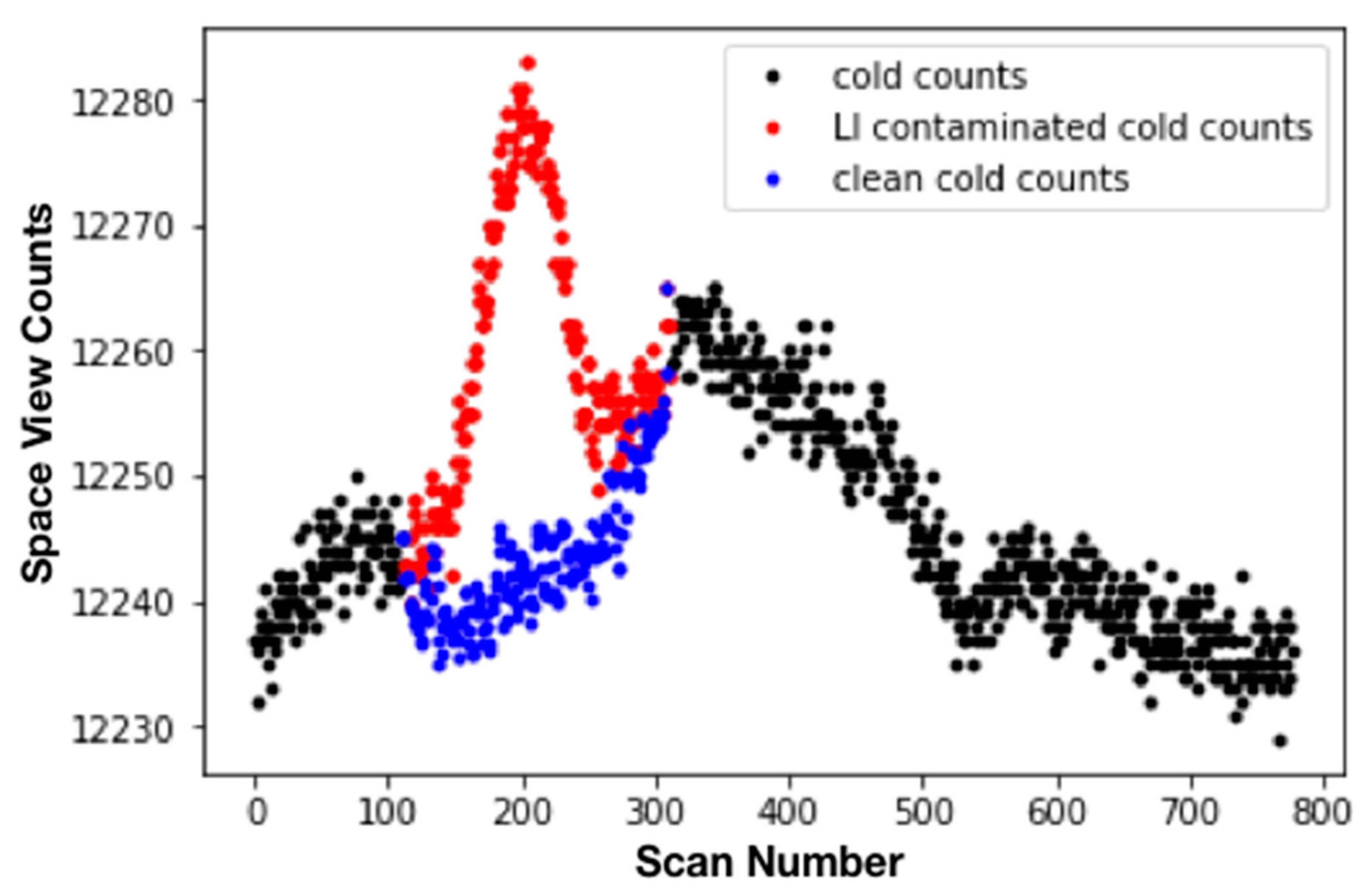
- Dilution factor Fch: The dilution factor is the fraction of the beam covered by the Moon, taking into account directivity. We assume that the directivity has the shape of a rotationally symmetric Gaussian, with its center being the pointing direction of the DSV. Hence, a single number, i.e., its FWHM, specifies it. Even though its uncertainty is estimated to be 0.01° [34,35], the values provided during ground tests sometimes differ by more than 0.2° from those found in flight. The FWHM of the beam is determined with the Moon intrusions themselves, using a method similar to the one employed by [37] to measure the pointing alignment of different channels. It relies on the fact that the width of the light curve we get from plotting the number of DSV counts as a function of scan number is proportional to the beam size. With every new scan, the pointing direction shifts slightly in the along-track direction, and by using Equation (A2), one can convert the width of the light curve from scans to angle. The random uncertainty of the FWHM is determined from the scatter of FWHM values obtained from different Moon intrusions. It is typically 0.01° for an average FWHM calculated from a dozen Moon intrusions in the DSV. Because Tb is inversely proportional to the dilution factor, which is more or less inversely proportional to the square of the FWHM of the beam, the systematic uncertainty of Fch is about 2%. This is the dominant contribution to the systematic uncertainty of the measured Tbs of the Moon.
- All contributions combined, we find an overall 1σ uncertainty of the Tb of the Moon when measured with a single instrument, e.g., the MHS onboard NOAA-18, namely, 3% or ~8 K. This means that the values from different instruments in Table 3 are in agreement.
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wang, Z.; Li, Y.; Jiang, J.; Li, D. Lunar surface dielectric constant, regolith thickness, and 3He abundance distributions retrieved from the microwave brightness temperatures of CE-1 Lunar Microwave Sounder. Sci. China 2010, 53, 1365–1378. [Google Scholar] [CrossRef]
- Olhoeft, G.R.; Strangway, D.W. Dielectric properties of the first 100 meters of the Moon. Earth Planet. Sc. Lett. 1975, 24, 394–404. [Google Scholar] [CrossRef]
- Anderson, R.C.; Buehler, M.; Seshadri, S.; Kuhlman, G.; Schaap, M. Dielectric constant measurements for characterizing lunar soils. Lunar Planet. Sci. XXXVI 2005. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20050165132.pdf (accessed on 15 December 2019).
- Ryadov, V.Y.; Furashov, N.I.; Sharonov, G.A. Measurements of the Moon’s natural infrared thermal radiation. Sov. Astron. 1964, 8, 82–84. [Google Scholar]
- Sandor, B.J.; Clancy, R.T. Microwave observations and modelling of a lunar eclipse. Icarus 1995, 115, 387–398. [Google Scholar] [CrossRef]
- Hu, G.; Zheng, Y.; Cu, A.; Tang, Z. Microwave brightness temperature of the Moon: The possibility of setting a calibration source of the lunar surface. IEEE Geosci. Remote Sens. Lett. 2016, 13, 182–186. [Google Scholar] [CrossRef]
- Wu, J.; Li, D.; Zhang, X.; Jiang, J.; Altyntesev, A.T.; Lubyshev, B.I. Microwave brightness temperature imaging and dielectric properties of lunar soil. J. Earth Syst. Sci. 2016, 114, 627–632. [Google Scholar]
- Maghrabi, A.H. On the measurements of the moon’s infrared temperature and its relation to the phase angle. Adv. Space Res. 2014, 53, 339–347. [Google Scholar] [CrossRef]
- Williams, J.-P.; Paige, D.A.; Greenhagen, B.T.; Sefton-Nash, E. The global surface temperatures of the Moon as measured by the Diviner Lunar Radiometer Experiment. Icarus 2016, 283, 300–325. [Google Scholar] [CrossRef]
- Krotikov, V.D.; Troitskii, V.S. Radio emission and nature of the Moon. Sov. Phys. Uspekhi 1964, 6, 841–871. [Google Scholar] [CrossRef]
- Piddington, H.; Minnett, H.C. Microwave thermal radiation from the Moon. Aust. J. Sci. Res. Ser. A 1949, 2, 63–77. [Google Scholar] [CrossRef]
- Zheng, Y.C.; Tsang, K.T.; Chan, K.L.; Zou, Y.L.; Zhang, F.; Ouyang, Z.Y. First microwave map of the Moon with ChangE-1 data: The role of local time in global imaging. Icarus 2012, 219, 194–210. [Google Scholar] [CrossRef]
- Montopoli, M.; Carlofelice, A.D.; Cicchinelli, M.; Tognolatti, P.; Marzano, F.S. Lunar microwave brightness temperature: Model interpretation and inversion of spaceborne multifrequency observations by a neural network approach. IEEE Geosci. Remote Sens. 2011, 49, 3350–3358. [Google Scholar] [CrossRef]
- Montopoli, M.; Carlofelice, A.D.; Tognolatti, P.; Marzano, F.S. Remote sensing of the Moon’s subsurface with multifrequency microwave radiometers: A numerical study. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Keihm, S.J. Interpretation of the lunar microwave brightness temperature spectrum. Icarus 1984, 60, 568–589. [Google Scholar] [CrossRef]
- Yu, S.; Fa, W. Thermal conductivity of surficial lunar regolith estimated from Lunar Reconnaissance Orbiter Diviner Radiometer data. Planet. Space Sci. 2016, 124, 48–61. [Google Scholar] [CrossRef]
- Lucey, P.G.; Blewett, D.T.; Jolliff, B.L. Lunar iron and titanium abundance algorithms based on final processing of Clementine ultraviolet-visible images. J. Geophys. Res. Planets 2000, 105. [Google Scholar] [CrossRef]
- Fa, W.; Jin, Y.Q. Simulation of brightness temperature from lunar surface and inversion of regolith-layer thickness. J. Appl. Geophys. 2007, 112. [Google Scholar] [CrossRef]
- Liu, N.; Jin, Y.Q. Calibration of multi-channel millimeter-wave radiometer of FY-4M based on real time brightness temperature along the equator of lunar surface. Chin. Sci. Bull. 2019, in press. [Google Scholar]
- Yang, H.; Weng, F. On-orbit ATMS lunar contamination corrections. IEEE Geosci. Remote Sens. 2016, 54, 1–7. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, J.; Weng, F.; Sun, N.; Anderson, K.; Liu, Q.; Kim, E.J. Developing vicarious calibration for microwave sounding instruments by using lunar radiation. IEEE Geosci. Remote Sens. 2018, 56, 6723–6733. [Google Scholar] [CrossRef]
- Burgdorf, M.J.; Buehler, S.A.; Lang, T.; Michel, S.; Hans, I. The Moon as a photometric calibration standard for microwave sensors. Atmos. Meas. Tech. 2016, 9, 3467–3475. [Google Scholar] [CrossRef]
- Burgdorf, M.J.; Buehler, S.A.; Hans, I.; Prange, M. Disk-integrated lunar brightness temperatures between 89 and 190 GHz. Adv. Astron. 2019, 2019. [Google Scholar] [CrossRef]
- Yang, F.; Xu, Y.; Chan, K.L.; Zhang, X.; Hu, G.; Li, Y. Study of Chang’E-2 microwave radiometer data in the lunar polar region. Adv. Astron. 2019, 2019. [Google Scholar] [CrossRef]
- Kigawa, S.; Mo, T. An Algorithm for Correction of Lunar Contamination in AMSU-A Data. NOAA Technical Report, NESDIS 111. 2002. Available online: https://repository.library.noaa.gov/view/noaa/12824 (accessed on 5 December 2019).
- Labrot, T.; Lavanant, L.; Whyte, K.; Atkinson, N.; Brunel, P. AAPP Documentation Scientific Description. In Satellite Application Facility for Numerical Weather Prediction; NWPSAF-MF-UD-001; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2019. [Google Scholar]
- Robel, J.; Graumann, A. NOAA KLM User’s Guide; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2014.
- Keihm, S.J.; Cutts, J.A. Vertical-structure effects on planetary microwave brightness temperature measurements: Applications to the lunar regolith. Icarus 1981, 48, 201–229. [Google Scholar] [CrossRef]
- Hans, I.; Burgdorf, M.; John, V.O.; Mittaz, J.; Buehler, S.A. Noise performance of microwave humidity sounders over their lifetime. Atmos. Meas. Tech. 2017, 10, 4927–4945. [Google Scholar] [CrossRef]
- Hans, I. Personal Communication; EUMETSAT: Darmstadt, Germany, 2017. [Google Scholar]
- Buehler, S.A.; Mendrok, J.; Eriksson, P.; Perrin, A.; Larsson, R.; Lemke, O. ARTS, the Atmospheric Radiative Transfer Simulator. Geosci. Model Dev. 2018, 11, 1537–1556. [Google Scholar] [CrossRef]
- Hans, I.; Burgdorf, M.; Buehler, S.A.; Prange, M.; Lang, T.; John, V.O. An uncertainty quantified fundamental climate data record for microwave humidity sounders. Remote Sens. 2019, 11, 548. [Google Scholar] [CrossRef]
- Hans, I.; Burgdorf, M.; Woolliams, E. FIDUCEO Product User Guide—Microwave FCDR Release 4.1. 2019. Available online: http://cedadocs.ceda.ac.uk/1415/ (accessed on 5 December 2019).
- Whatling, C.A. Microwave Humidity Sounder Instrument End Item Data Package, 3175-JA291-DPQ, MHS-DP-JA291-MMP; Matra Marconi Space: Toulouse, France, 1999. [Google Scholar]
- Whatling, C.A. Microwave Humidity Sounder Instrument End Item Data Package, 3175-JA292-DPF, MHS-DP-JA292-MMP; Matra Marconi Space: Toulouse, France, 1999. [Google Scholar]
- Hewison, T.J. AMSU-B Antenna Test Results, Met O(RSI) Branch Technical Note No. 2; Met Office (RS) Branch Memorandum 21: Farnborough, UK, 1993.
- Bonsignori, R. In-orbit verification of microwave humidity sounder spectral channels coregistration using the moon. J. Appl. Remote Sens. 2018, 12. [Google Scholar] [CrossRef]
- Appel, J.W.; Xu, Z.; Padilla, I.L.; Harrington, K.; Marquez, B.P.; Ali, A.; Bennett, C.L.; Brewer, M.K.; Bustos, R.; Chan, M.; et al. On-sky performance of the CLASS Q-band telescope. Astrophys. J. 2019, 876, 126. [Google Scholar] [CrossRef]
| Center Frequency (GHz) | Beam Width (°) | |
|---|---|---|
| 23.8 | 5.1 | 267 |
| 31.4 | 4.9 | 278 |
| 50.3–55.5 | 2.2 | 284 |
| 57 | 2.2 | 287 |
| 88.2 | 2.1 | 289 |
| 165.5 | 1.1 | 296 |
| 183.3 | 1.1 | 300 |
| AMSU-B | MHS | ATMS | |
|---|---|---|---|
| Channel 16/1/16 | 89.0 | 89.0 | 89.5 |
| Channel 17/2/17 | 150.0 | 157.0 | 165.5 |
| Channel 18/3/18 | 183.31 ± 1.0 | 183.31 ± 1.0 | 183.31 ± 7.0 |
| Channel 19/4/19 | 183.31 ± 3.0 | 183.31 ± 3.0 | 183.31 ± 4.5 |
| Channel 20/5/20 | 183.31 ± 7.0 | 190.31 | 183.31 ± 3.0 |
| Channel -/-/21 | 183.31 ± 1.8 | ||
| Channel -/-/22 | 183.31 ± 1.0 |
| T89max | T89full | Φ89 | T183max | T183full | Φ183 | |
|---|---|---|---|---|---|---|
| AMSU-B and MHS | 282 K | 276 K | 23° | 297 K | 295 K | 12° |
| AMSU-A or ATMS | 295 K | 289 K | 20° | 300 K | ||
| Keihm [15] | 272 K | 269 K | 16° | 294 K | 293 K | 9° |
| Center Frequency (GHz) | Peak Tb (K) | Phase Lag Angle (°) |
|---|---|---|
| 23.8 | 287 | 37 |
| 31.4 | 287 | 34 |
| 50.3–55.5 | 292 | 31 |
| 57 | 294 | 28 |
| 89 | 295 | 20 |
| 183 (MHS) | 297 | 12 |
| AMSU-B NOAA-16 | MHS NOAA-18 | MHS NOAA-19 | MHS MetOp-A | |
|---|---|---|---|---|
| 89 GHz | 5.8 K | 2.7 K | 3.5 K | 2.5 K |
| 183 GHz | 5.2 K | 3.3 K | 4.5 K | 3 K |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Burgdorf, M. A Study of Lunar Microwave Radiation Based on Satellite Observations. Remote Sens. 2020, 12, 1129. https://doi.org/10.3390/rs12071129
Yang H, Burgdorf M. A Study of Lunar Microwave Radiation Based on Satellite Observations. Remote Sensing. 2020; 12(7):1129. https://doi.org/10.3390/rs12071129
Chicago/Turabian StyleYang, Hu, and Martin Burgdorf. 2020. "A Study of Lunar Microwave Radiation Based on Satellite Observations" Remote Sensing 12, no. 7: 1129. https://doi.org/10.3390/rs12071129
APA StyleYang, H., & Burgdorf, M. (2020). A Study of Lunar Microwave Radiation Based on Satellite Observations. Remote Sensing, 12(7), 1129. https://doi.org/10.3390/rs12071129





