1. Introduction
The introduction of Unmanned Aerial Vehicles (UAV), also referred to as Unmanned Aerial Systems (UAS), as platforms for the acquisition of high-resolution 3D data has fundamentally changed the mapping sector in recent years. UAVs flying at low altitudes combine the advantages of small sensor-to-object distances (i.e., close range) and agility. The latter is achieved via remotely controlling the unmanned sensor platform either manually by a pilot within the Visual Line-Of-Sight (VLOS) or by autonomously flying predefined routes based on waypoints, allowing both within and beyond VLOS operation.
UAV-based 3D data acquisition was first accomplished using light-weight camera systems, where advancements in digital photogrammetry and computer vision-enabled automatic data processing workflows for the derivation of dense 3D point clouds based on Structure-from-Motion (SfM) and Dense Image Matching (DIM). Due to advancements in UAV-platform technology and ongoing sensor miniaturization, today compact LiDAR sensors are increasingly integrated on both multi-copter and fixed-wing UAVs, enabling 3D mapping with unprecedented spatial resolution and accuracy. The tackled applications include topographic mapping, geomorphology, infrastructure inspection, environmental monitoring, forestry, and precision farming. While UAV-borne laser scanning (ULS) can already be considered state-of-the-art for mapping tasks above the water table, UAV-based bathymetric LiDAR still lacks behind, mainly due to payload restrictions.
The established techniques for mapping bathymetry are single- or multi-beam echo sounding (SBES/MBES), including Acoustic Doppler Current Profiling (ADCP). This holds for both coastal and inland water mapping. MBES is the prime acquisition method for area-based charting of water bodies deeper than approximately two times the Secchi depth (SD), and the productivity of this technology is best in deeper water because the width of the scanned swath increases with water depth. For mapping shallow water bathymetry including shallow running waters, boat-based echo sounding is less productive and furthermore, safety issues arise. For relatively clear and shallow water bodies, airborne laser bathymetry (ALB) constitutes a well-proven alternative. This active, optical, polar measurement technique features the following advantages: (i) areal coverage only depending on the flying height but not on the water depth; (ii) homogeneous point density; (iii) simultaneous mapping of water bottom, water surface, and dry land area in a single campaign, referred to as topo-bathymetric LiDAR; and (iv) non-contact remote sensing approach with clear benefits for mapping nature conservation areas.
ALB performed from manned platforms [
1] has a long history in under-water object detection and charting of coastal areas including characterization of benthic habitats [
2]. In the recent past, the technology is increasingly used for inland waters [
3,
4,
5]. In order to ensure eye safety, the employed laser beam divergence is typically in the range of 1–10 mrad. For a typical flying altitude of 500 m or higher the resulting laser footprint diameter on the ground measures at least 50–500 cm. Thus, the spatial resolution of ALB from manned aerial platforms is limited. Due to the shorter measurement ranges, ULS promises a better resolution and allows users to capture and reconstruct smaller structures like boulders, submerged driftwood, and the like, with potential applications for the characterization of flow resistance in hydrodynamic numerical (HN) models.
To date, only a few UAV-borne LiDAR sensors are available. The
RIEGL BathyDepthFinder is a bathymetric laser range finder with a fixed laser beam axis (i.e., no scanning). Like most of the bathymetric laser sensors, the system utilizes a green laser (
= 532 nm) and allows for the capture of river cross-sections constituting an appropriate input for 1D-HN models. The ASTRALiTe sensor is a scanning polarizing LiDAR [
6]. The employed 30 mW laser only allows low flying altitudes and therefore provides limited areal measurement performance and the depth performance is moderate (1.2 -fold SD). The RAMMS (Rapid Airborne Multibeam Mapping System) was recently developed by Fugro Inc. and Areté Associates [
7]. It is a relatively lightweight, 14 kg push-broom ALB sensor featuring a measurement rate of 25 kHz and promising a penetration performance of 3 SD according to the company’s web site [
8]. The sensor is operated by Fugro for delivering high-resolution bathymetric services, but independent performance and accuracy assessments are not available.
In 2018,
RIEGL introduced the VQ-840-G, a lightweight topo-bathymetric full-waveform scanner [
9] with a maximum pulse repetition rate (PRR) of 200 kHz. The scanner is designed for installation on various platforms including UAVs and carries out laser range measurements for high resolution, survey-grade mapping of underwater topography with a narrow, visible green laser beam. The system is optionally offered with an integrated and factory-calibrated IMU/GNSS system, and with an optional camera or IR rangefinder. As such, it constitutes a compact, comprehensive, and full-featured ALB system for mapping coastal and inland waters from low flying altitudes.
The inherent advantage of such a design is twofold: (i) the short measurement ranges and high scan rates enable surface description in high spatial resolution as a consequence of high point density and relatively small laser footprint; and (ii) integration on UAV platforms or lightweight manned aircraft reduces mobilization costs and enables agile data acquisition. In the context of ALB, the prior holds out the prospect of reconstructing submerged surface details below the size of boulder (i.e., dm-level) which is not feasible from flying altitudes of 500 m or higher due to the large laser footprint diameter, and the latter is especially beneficial for capturing medium-sized, meandering running waters with moderate widths (<50 m) and depth (<5 m) which would require a complex flight plan with many potentially short flight strips and a multitude of turning maneuvers for a conventional manned ALB survey. Thus, UAV-borne bathymetric LiDAR is considered a major leap forward for river mapping with an expected positive stimulus on a variety of hydrologic and hydraulic applications like flood risk simulations, sediment transport modeling, monitoring of fluvial geomorphology, eco-hydraulics, and the like.
In this article, we present the first rigorous accuracy and performance assessment of a UAV-borne ALB system by evaluating the 3D point clouds acquired at the pre-Alpine Pielach River and an adjacent freshwater pond. We compare the LiDAR measurements with ground truth data obtained from terrestrial survey with a total station in cm-accuracy and provide objective measures describing the precision, accuracy, and depth performance of the system. Furthermore, we discuss the fields of application, limits, and challenges of UAV-borne LiDAR bathymetry including potential fusion with complementary sensors (RGBI cameras, thermal IR cameras), widening the scope beyond pure bathymetric mapping towards discharge estimation, flow resistance characterization, etc.
Our main contribution is providing an in-depth evaluation of topo-bathymetric UAV-LiDAR including a discussion of limitations on the one side and benefits compared to manned ALB on the other side. Next to accuracy and performance assessment, our focus is on an objective evaluation of achievable spatial resolution, especially addressing the question to which extent the shorter measurement ranges and smaller nominal laser footprints directly induce higher resolution. Furthermore, we put the presented full-waveform scanner in context with existing line scanning technologies.
The remainder of the manuscript is structured as follows. In
Section 2, we review the state-of-the-art in UAV-based bathymetry followed by a description of the senor concept in
Section 3.
Section 4 introduces the study area and existing datasets, and details the employed data processing and assessment methods. The evaluation results are presented in
Section 5 along with critical discussion in
Section 6. The paper concludes with a summary of the main findings in
Section 7.
3. Sensor Concept
The RIEGL VQ-840-G is a fully integrated compact airborne laser scanner for combined topographic and bathymetric surveying. The instrument can be equipped with an integrated and factory-calibrated IMU/GNSS system and with an integrated industrial camera, thereby implementing a full airborne laser scanning system. The VQ-840-G LiDAR has a compact volume of 20.52 L with a weight of 12 kg and, thus, can be installed on various platforms including UAVs.
The laser scanner comprises a frequency-doubled IR laser, emitting pulses with about 1.5 ns pulse duration at a wavelength of 532 nm and at a PRR of 50–200 kHz. At the receiver side, the incoming optical echo signals are converted into an electrical signal, they are amplified and digitized at a digitization rate of close to 2G samples/s. The laser beam divergence can be selected between 1 mrad and 6 mrad in order to be able to maintain a constant energy density on the ground for different flying altitudes and therefore balancing eye-safe operation with spatial resolution. The receiver’s iFOV (instantaneous Field of View) can be chosen between 3 mrad and 18 mrad. For topographic measurements and very clear or shallow water, a smaller setting is suitable while for turbid water it is better to increase the receiver’s iFOV in order to collect a larger amount of light scattered by the water body.
The VQ-840-G employs a Palmer scanner generating an elliptical scan pattern on the ground. The scan range is ±20 across and ±14 along the intended flight direction and consequently, the laser beam hits the water surface at an incidence angle with low variation. The scan speed can be set between 10–100 lines/s to generate an even point distribution in the center of the swath. Towards the edge of the swath, where the consecutive lines overlap, an extremely high point density with strongly overlapping footprints is produced.
The onboard distance measurement is based on time-of-flight measurement through online waveform processing of the digitized echo signal [
62]. A real-time detection algorithm identifies potential targets within the stream of the digitized waveform and feeds the corresponding sampling values to the signal processing unit, which is capable of performing system response fitting (SRF) in real-time at a rate of up to 2.5M targets per second. These targets are represented by the basic attributes of range, amplitude, reflectance, and pulse shape deviation and are saved to the storage device, which can be the internal SSD a removable CFast© card, or an external data recorder via an optical data transmission cable.
Besides being fed to target detection and online waveform processing, the digitized echo waveforms can also be stored on disc for subsequent off-line full waveform analysis. For every laser shot, sample blocks with a length of up to 75 m are stored unconditionally, i.e., without employing any target detection. This opens up a range of possibilities including pre-detection averaging (waveform stacking), variation of the target detection parameters or algorithm, and employing different sorts of full-waveform analysis. For the work presented here, offline SRF with modified target detection parameters was employed for optimized results. The depth performance of the instrument has been demonstrated to be in the range of 2 Secchi depths for single measurements, i.e., without waveform stacking.
Instead of or in addition to the internal camera, a high-resolution camera can be externally attached and triggered by the instrument. This option was chosen for the experiments in this study using a nadir looking Sony Alpha 7RM3.
Figure 1 and
Figure 2 show conceptual drawings of the sensor and the general data acquisition concept, respectively. respectively.
Table 1 summarizes the main sensor parameters.
6. Discussion
The presented compact topo-bathymetric laser scanner exhibits a weight of 12 kg and a power consumption of 160 W. This makes the instrument suitable for integration on light manned aircraft, gyrocpters, and helicopters as well as on larger UAV platforms, as was the case for our data acquisition. The considerable payload and power consumption, however, limit UAV flight endurance with the selected UAV. The longest net acquisition airtime in our experiment was about 10 min excluding starting, landing, and IMU/GNSS initialization. This might be sufficient endurance for corridor mapping in a visual line of sight (VLOS) context, but poses hard constraints for larger project areas and beyond VLOS operation. Thus, our UAV-borne experiment is regarded as a successful proof-of-concept, but further sensor miniaturization is needed for integration on mainstream UAV platforms like the DJI Matrice 600 Pro or comparable platforms. No matter if the sensor is integrated on a light manned or unmanned aerial platform, in both cases the mobilization costs are considerably lower compared to traditional ALB surveys and smaller aircraft feature a higher maneuverability. The sensor, therefore, constitutes a cost-effective alternative, especially for mapping bathymetry of narrow river channels, as a supplement to area-wide topographic laser scanning which is today often available on a country-wide level.
A major benefit of the sensor design is the adjustable pulse repetition rate, laser beam divergence, and receiver iFoV, making eye-safe operation possible for low flying altitudes like the standard 50 m altitude in our experiment. Due to the smaller sensor-to-target distances and the narrow laser cone, the resulting nominal laser footprint diameter in the dm-range is much smaller compared to existing topo-bathymetric sensors operated on manned aircraft featuring footprint sizes of about half a meter. This gain in spatial resolution opens new applications in the context of hydraulic engineering (roughness estimation) for reliable flood simulations, eco-hydraulics (habitat modelling), fluvial geomorphology, and many more.
As stated before, the limiting factor for spatial resolution in the lateral direction of the laser beam is the
laser footprint, i.e., the illuminated area on the target. As reported in
Section 5.4, this is not the same as the area resulting from the vendor specifications. The power distribution in the laser footprint has Gaussian shape and it is common practice to specify the beam diameter by twice the radius where the optical power has decreased by a factor of
. For a beam diameter
w, the power distribution
as a function of off-axis distance
r is given by
with
the power at the center. The power level at
is
% of the power level at the maximum. Expressing the power level at
in Decibels gives
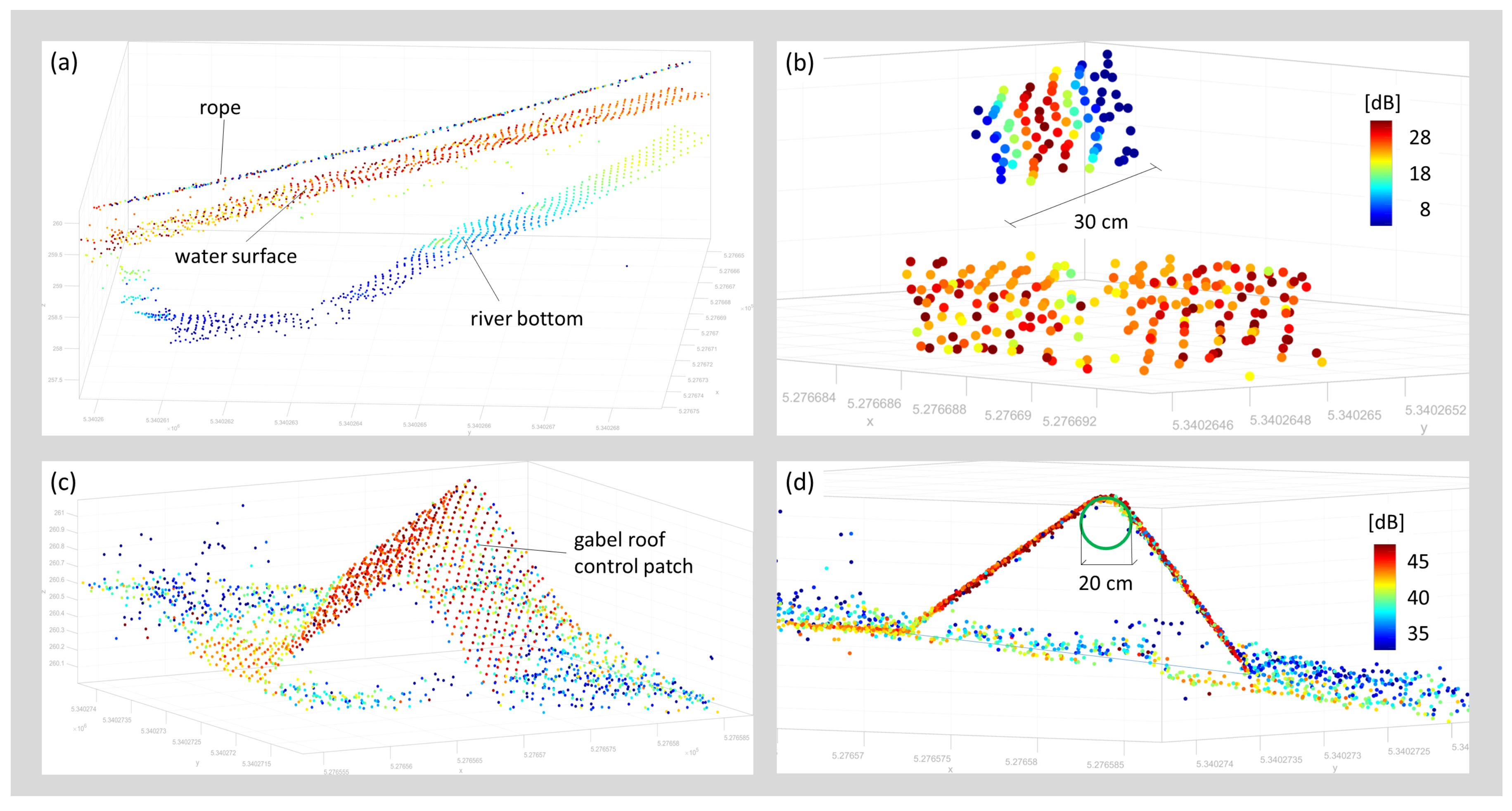
A signal causing a return strength in the center of the beam that is more than 8.7 dB above the receiver detection threshold will cause a detectable signal in an adjacent measurement even when further apart than the nominal beam diameter radius. The effective size of the footprint, thus, is determined not only by the properties of the laser beam but also by the sensitivity of the receiver circuitry and the iFOV. A small isolated object will be seen in adjacent laser points until it is too weak to be detected. However, the object will appear with diminishing amplitudes towards the edges (cf.
Figure 14b).
The finite footprint and high receiver sensitivity also cause smoothing effects if the target’s shape is not flat within the illuminated area. This applies to discontinuities in height (cliff, wall) or slope (sharp edge), or in case of high curvature (e.g., small boulders). In any case, this leads to rounding artifacts as exemplified in
Figure 14d for a sharp edge. In the context of mapping river channel bathymetry, this limits the ability to precisely reconstruct objects smaller than ≈20 cm. While the instrument’s spatial resolution is too low for roughness estimation on grain size level, it is suitable for the detection of blocks, boulders, and other flow resistance relevant objects. As an example, the circular underwater reference targets clearly stood out from the surrounding river bottom although they were firmly anchored in the ground and, thus, only protruded from the ground surface by a few cm.
For smooth surfaces, the sensor showed a measurement noise below 1 cm verified at horizontal asphalt surfaces (cf. surface patch A1 in
Figure 8 and
Table 4) as well as on tilted surfaces (cf.
Table 5, e.g., points 1001–1020). Beyond the local level, this also holds for the strip fitting precision of the entire flight block, which even outperformed comparable data acquisitions with a state-of-the-art topographic UAV laser scanner employed in the same study area in the previous work [
66,
71]. High relative accuracy is of special importance, e.g., for detailed hydrodynamic-numerical modeling in flat areas where a few cm can determine whether or not certain areas are flooded.
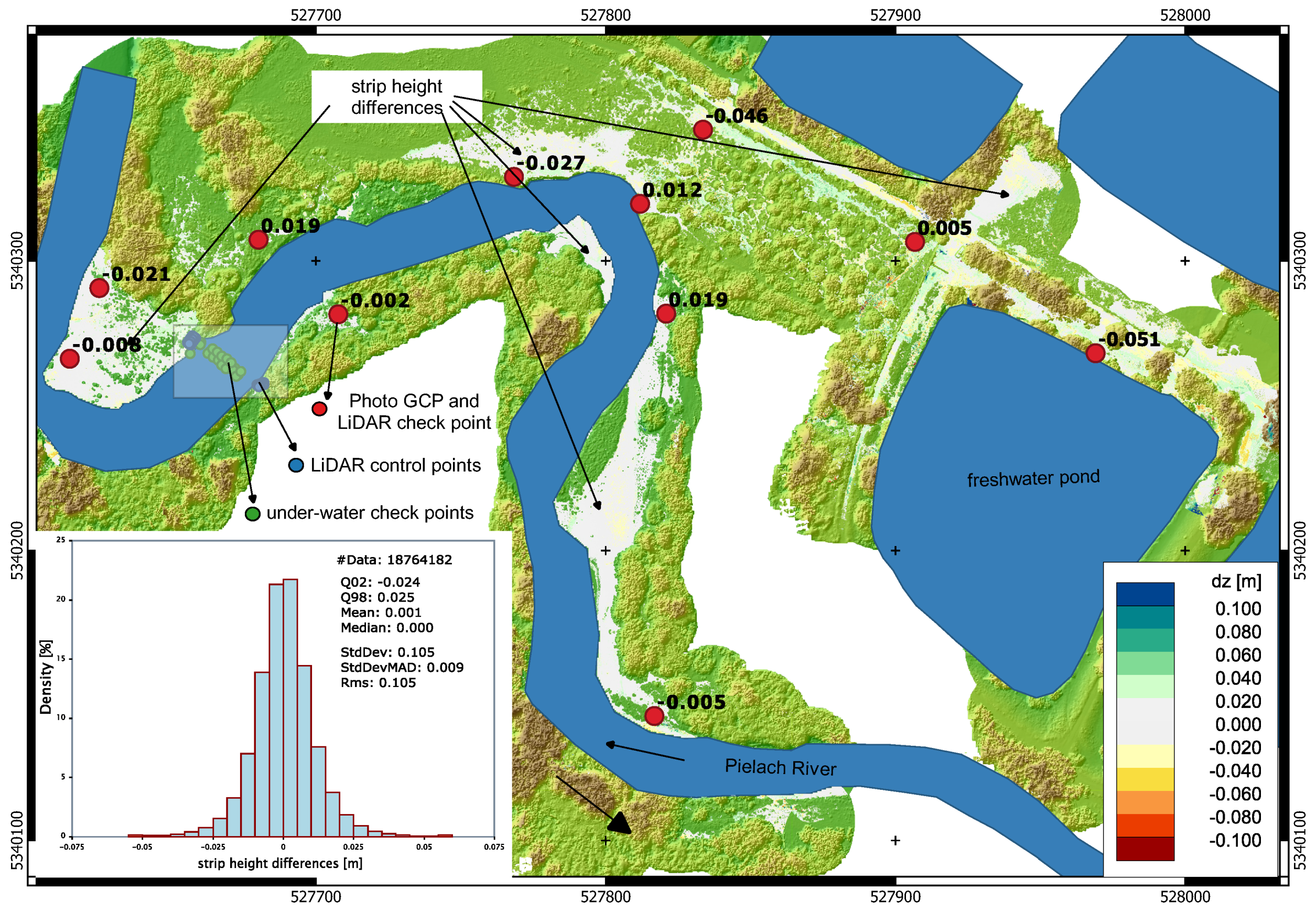
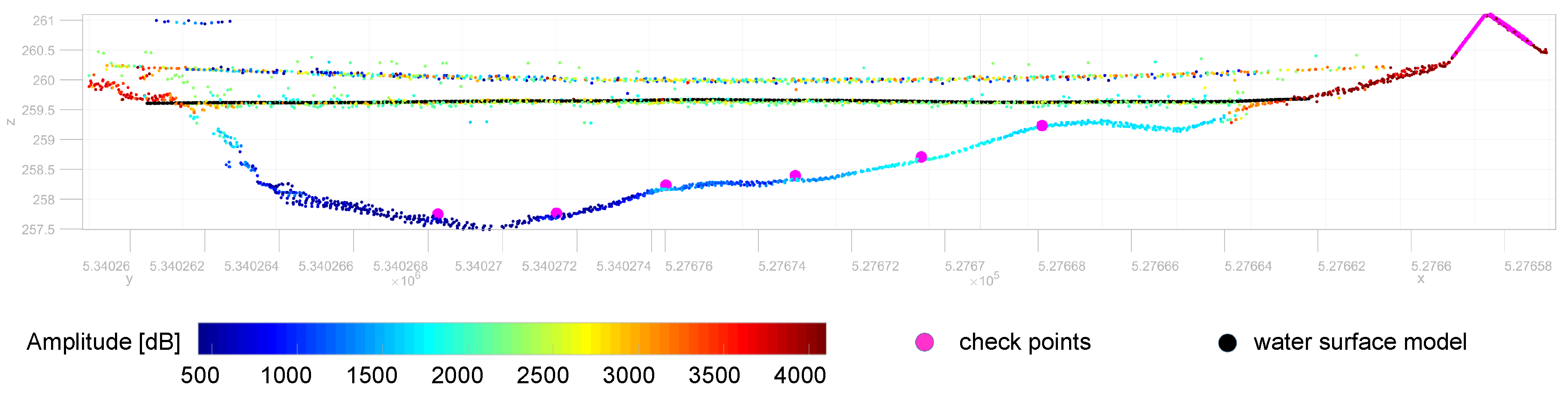
While the absolute accuracy of the flight block, measured as point-to-plane distances between terrestrially surveyed reference targets and the LiDAR point cloud, is generally better than 3 cm on land (cf. red dots in
Figure 9), systematic deviations were observed for submerged checkpoints. In addition to geometric calibration of the sensor system and (ranging, scanning, lever arms, boresight angles, trajectory), the overall accuracy of LiDAR-derived bathymetry depends on the accuracy of (i) the modeled water surface and (ii) the refraction coefficients for run-time correction. Data analysis has revealed that laser echoes from the water surface are dense (i.e., practically every laser shot returned an echo from the surface) and the signal amplitude is sufficiently strong to enable reliable range measurement.
Figure 11 and
Figure 14a,b illustrate that (i) the recorded signal amplitudes are around 20 dB; (ii) the point density is high; and (iii) the vertical spread is remarkably low. It is well known from literature including our own work [
1,
57,
77,
78] that the laser signal reflected from water surfaces is a mixture of reflections from the surface and volume backscattering from the water column beneath the surface. Surface data obtained from conventional green-only ALB sensors operated from manned platforms in flying altitudes of around 600 m often show a fuzzy appearance. In contrast, surface data acquired in this experiment are concise and the point clouds show a vertical spread of only a few cm. Independent validation of the modeled water surface with terrestrially surveyed checkpoints at the water-land-boundary (cf.
Table 5) also confirmed the accuracy of the water surface model. Thus, we rule out that inaccuracies of the modeled water surface are responsible for the detected depth-dependent bias.
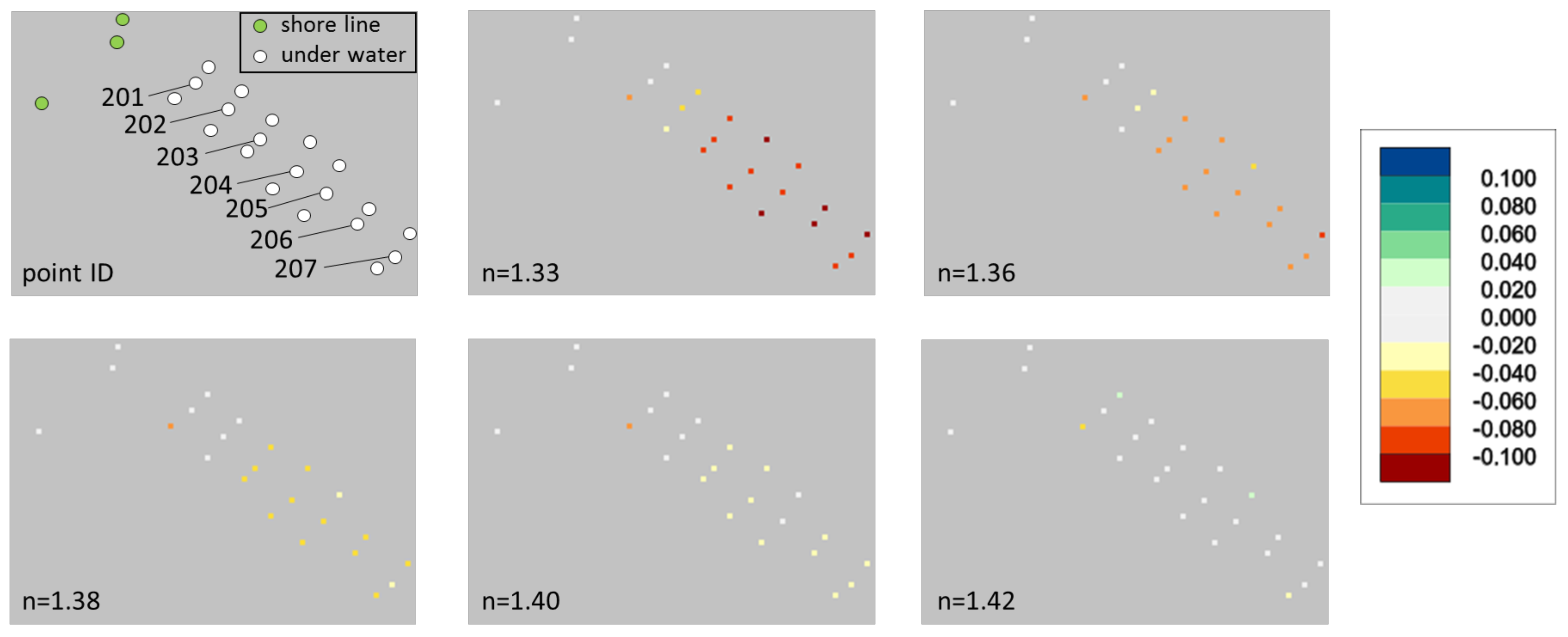
Concerning run-time correction, we first started with standard values documented in the literature. [
76] reports a valid range of
n = 1.329–1.367, but the upper bound is only valid for extreme salinity and temperature conditions. In recent work, [
75] reported that group velocity is relevant for run-time correction of pulsed lasers rather than the phase velocity of the underlying laser wavelength (
= 532 nm). With a respective experiment, they showed that a value of around 1.36 is valid for freshwater conditions. Therefore, this value was also used for run-time correction in this work, but comparison with the reference points still showed a systematic, depth-dependent error. The bias only disappeared when using a hypothetical refraction coefficient of
. As there is no physical explanation for such a high refractive index, the question for the reason of the systematic deviation still remains. Multi-path effects due to complex forward scattering within the water columns are the most likely explanation for the observed phenomenon. As documented in
Table 2 and as can be seen from the on-site photographs in
Figure 6, the turbidity level was high (Secchi depth in the river: 1.1 m) due to a thunderstorm event in the days before data acquisition. This resulted in a high load of suspended sediment. Scattering at the sediment particles leads to a widening of the laser footprint, which entails non-linearity of the ray paths leading to elongated path lengths in water, which might result in the observed underestimation of the river bottom height. Following this line of argument, a repeat survey is planned in the winter season 2020 in clear water conditions to verify and quantify the influence of turbidity on the UAV-LiDAR derived depth measurements.
The depth performance of 2 SD stated by the manufacturer was confirmed in the conducted evaluation. All results relied on online waveform processing [
62] and did not make use of sophisticated waveform processing [
79,
80]. Processing of data acquired with different iFoV settings confirmed an increased depth performance using the widest possible setting of 18 mrad compared to the default setting of 6 mrad. The gain measures 0.3 SD or 15% but comes at the price of a reduced spatial resolution as the receiver’s perceivable target area is larger, exemplary illustrated in
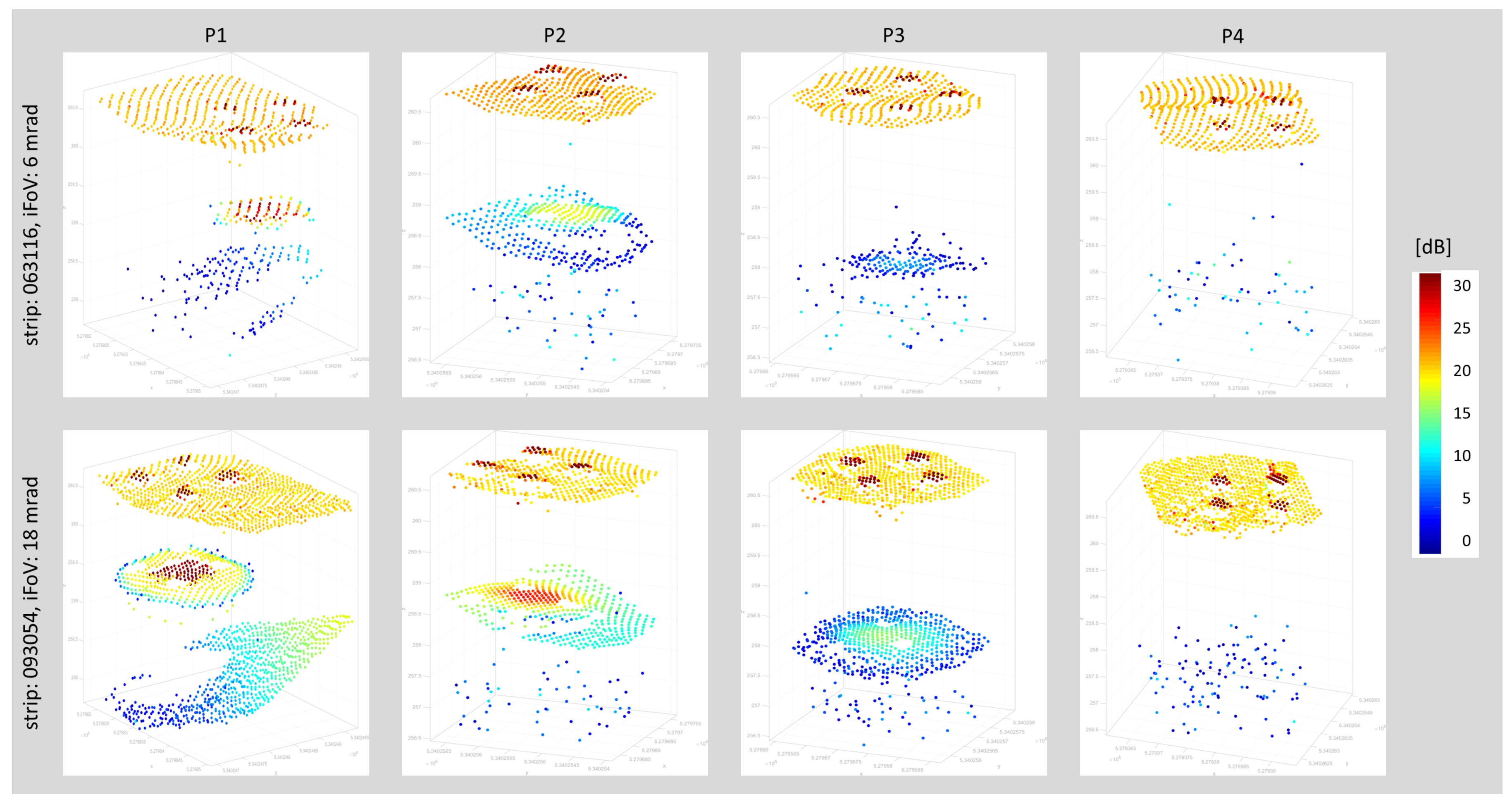
Figure 12 at plate P1. In a practical context, this clearly shows that a trade-off between high spatial resolution and maximum depth performance needs to be found. A potential best practice procedure may include a repeat survey of the same flight lines first with scanner settings optimized for spatial resolution (high PRR, narrow beam divergence and iFoV) and second with parameters optimized for maximum depth penetration. With the studied instrument, this can be achieved in a single flight mission as individual sensor settings are feasible on a per flight line basis.
The conducted depth performance assessment based on the four lowered metal plates yielded that plate P4 at a depth of 2.2 SD could not be identified in any of the flight strips including the ones with 18 mrad iFoV. This is astonishing, as the natural bottom of the pond could be measured at approximately the same depth (cf. blue points in
Figure 13). By extrapolating the signal amplitude decrease from plate P3 (14.5 dB), enough signal should have been available to also detect P4. One of the plausible reasons is an abrupt turbidity increase within the freshwater pond at a water depth of around 3 m. We consider this the most likely explanation as the pond is mainly used for fishing purposes and the dominating species (
Cyprinus carpio) tends to dig into the mud at the bottom of the pond potentially swirling up mud particles.
Beyond the pure sensor settings, an additional increase of depth performance is expected via sophisticated waveform processing. [
81] reported an increased areal coverage when employing a surface-volume-bottom based exponential decomposition approach, in both very shallow and deeper water areas. [
5,
82] use waveform stacking, i.e., averaging of neighboring waveforms, to enhance ALB depth performance reporting an increase of 30%. The presented sensor is specifically well suited for the application of waveform stacking, also referred to as pre-detection averaging, as waveform recording does not depend on a trigger event (i.e., echo detection) during data acquisition but waveforms are continuously stored within a certain range gate. While this is not possible for typical ALB flying altitudes of 600 m due to storage capacity limits, it is well possible for the shorter ranges in UAV-borne laser bathymetry. By combining the possibilities offered by the sensor (PRR, beam divergence, iFoV) with data processing based on the cited strategies, a maximum depth penetration of about 2.9 SD can be expected, but further experiments are required to verify this value.
Further advantages arise from the integration of active and passive sensors in a single hybrid system. Examples for applications benefiting from the concurrent acquisition of laser and image data are water body detection [
83] and discharge estimation [
46].
7. Conclusions
In this paper, we introduced the concept of a novel compact topo-bathymetric laser scanner and presented a comprehensive assessment evaluating measurement noise, strip fitting precision, accuracy compared to terrestrially measured reference data, depth performance, and spatial resolution. With a weight of 12 kg the sensor is suitable for integration on light manned as well as powerful unmanned platforms, reducing the mobilization costs compared to conventional ALB. The scanner features an adjustable pulse repetition rate (50–200 kHz), scan rate (10–100 lines/s), beam divergence (1–6 mrad), and receiver’s iFoV (of 3–18 mrad). With nominal flying altitudes from 50–150 m, this enables flexible flight planning and full user control concerning the properties of the resulting 3D point clouds w.r.t. point density, spatial resolution, achievable depth performance, and aerial coverage.
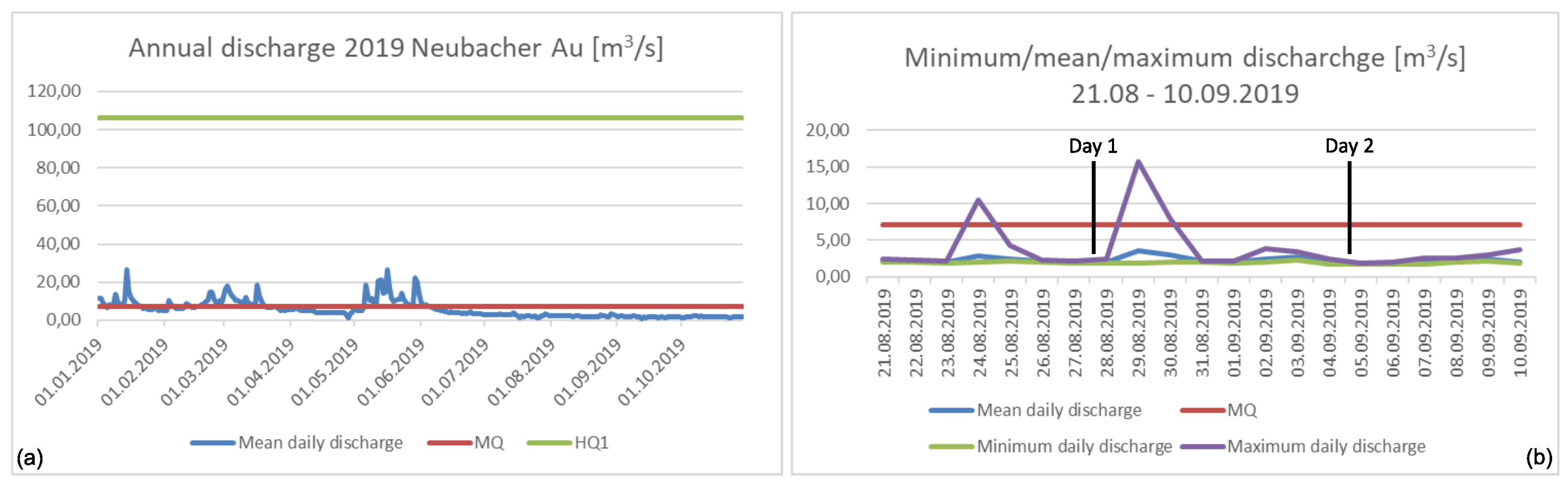
For assessing the overall quality, a flight mission was designed and carried out on 28 August 2019, at the pre-Alpine Pielach River (Austria) with the sensor mounted on an octocopter UAV platform. After geometric calibration and refraction correction, the resulting 3D point clouds were compared to reference points obtained by terrestrial surveys with RTK GNSS and total station. The evaluations exhibited a local measurement noise at smooth asphalt surfaces of 1–3 mm, a relative strip fitting precision of about 1 cm, and an absolute flight block accuracy of 2–3 cm compared to check points on dry land.
Assessment of the bathymetric accuracy yielded a depth-dependent bias when employing a representative refraction coefficient of n = 1.36 for run-time correction in water. The maximum deviation of 7.8 cm at a water depth of 2.1 m only disappeared when using a hypothetical refraction coefficient of n = 1.42, which is physically implausible. We hypothesize that the bias results from multi-path effects caused by forward scattering at dissolved sediment particles, as turbidity was high (SD: ≈1.1 m) due to thunderstorm events in the days before data acquisition.
Depth performance evaluation, based on four metal plates lowered into a freshwater pond in different depths, confirmed a maximum water penetration depth of 2 SD for the laser echoes derived with online waveform processing. In addition to that, the entire echo waveform is also stored for off-line waveform analysis. Waveform recording does not depend on a triggering event but the entire waveform is rather captured within a user-definable range gate. This enables waveform stacking by summing up the waveforms of neighboring laser shots, which potentially increases the depth performance to 2.5–2.8 SD. Respective experiments addressing these open questions are currently in preparation.
To sum up, the presented compact topo-bathymetric laser scanner is well suited for mapping river channel bathymetry. The sensor system poses an alternative to conventional ALB for mapping smaller rivers and shallow lakes when mounted on flexible UAV-platforms and also for larger coastal environments when integrated on light manned aircraft. One of the main benefits compared to other UAV-based bathymetric laser sensors is the full adjustability of the sensor parameters enabling the end-user to balance accuracy, depth performance, spatial resolution, and aerial coverage.