Abstract
BIOMASS is ESA’s seventh Earth Explorer mission, scheduled for launch in 2022. The satellite will be the first P-band SAR sensor in space and will be operated in fully polarimetric interferometric and tomographic modes. The mission aim is to map forest above-ground biomass (AGB), forest height (FH) and severe forest disturbance (FD) globally with a particular focus on tropical forests. This paper presents the algorithms developed to estimate these biophysical parameters from the BIOMASS level 1 SAR measurements and their implementation in the BIOMASS level 2 prototype processor with a focus on the AGB product. The AGB product retrieval uses a physically-based inversion model, using ground-canceled level 1 data as input. The FH product retrieval applies a classical PolInSAR inversion, based on the Random Volume over Ground Model (RVOG). The FD product will provide an indication of where significant changes occurred within the forest, based on the statistical properties of SAR data. We test the AGB retrieval using modified airborne P-Band data from the AfriSAR and TropiSAR campaigns together with reference data from LiDAR-based AGB maps and plot-based ground measurements. For AGB estimation based on data from a single heading, comparison with reference data yields relative Root Mean Square Difference (RMSD) values mostly between 20% and 30%. Combining different headings in the estimation process significantly improves the AGB retrieval to slightly less than 20%. The experimental results indicate that the implemented retrieval scheme provides robust results that are within mission requirements.
Keywords:
BIOMASS; SAR; polarimetry; tomography; interferometry; forest height; forest disturbance; earth explorer; DTM 1. Introduction
There is an urgent need to improve our understanding of the global carbon cycle, in which anthropogenic carbon dioxide (CO2) emissions into the atmosphere are the dominant factor driving climate change. Terrestrial ecosystems play a crucial role in the mitigation of climate warming [1]. Global forests are responsible for the sequestration of approximately 29% of the emitted CO2 [2], but forest areas are also an important source of CO2 emissions to the atmosphere through deforestation and forest degradation. Despite the importance of forests in the global carbon cycle, the spatial distribution of forest carbon stocks and related fluxes is not yet well-quantified [3,4]. Above-ground biomass (AGB) in forests, which contains about 50% of carbon [5], is a central factor in the carbon budget, but in many parts of the planet AGB is poorly quantified due to the difficulty in collecting sufficient field measurements.
Measurements of AGB from spaceborne sensors have relied on sensors of opportunity so far, since no mission was designed for this specific purpose [6]. Several studies deal with either the combination of forest height (FH) estimates from laser altimeters with other Earth observation (EO) measurements (e.g., [7]) or with time series of Synthetic Aperture Radar (SAR) data to estimate AGB and its change over time (e.g., [8]). Limitations of these studies mainly come from the very coarse scale at which reliable estimation is possible or the availability of a limited amount of data both in time and space due to the lack of systematic acquisition strategies over forested areas. Moreover, as regards SAR sensors, the higher frequencies at which some in-orbit platforms operate (e.g., Sentinel-1, Tandem-X) are only sensitive to the uppermost layer of the forest canopy (mainly leaves) and thus have only limited retrieval capabilities, while the sensitivity to AGB of L-band sensors (ALOS-PALSAR, SAOCOM) tends to saturate at higher levels of AGB [3,4].
The European Space Agency (ESA) Earth Explorer missions focus on the most challenging issues identified by the scientific community regarding the study of our planet using innovative satellite technologies. In this framework the BIOMASS mission was selected as the seventh Earth Explorer in May 2013 [3,4]. The scientific goal of BIOMASS is to provide frequent global maps of AGB, FH and forest disturbance (FD) at a resolution and accuracy compatible with the needs of international reporting on carbon stocks [9] and terrestrial carbon modeling [1,6]. BIOMASS will carry the first P-band radar in space (435 MHz) with multi-baseline interferometric and fully-polarimetric capabilities. This configuration will provide unprecedented sensitivity to forest AGB and penetration capability down to the underlying terrain [4,10].
The mission preparatory activities include the definition and implementation of the main algorithms of the Prototype Processor for generating global biophysical mission products [11]. In this paper, the scientific basis and the outline and operational flow of the level 2 prototype processor are presented. Section 2 contains a summary of BIOMASS mission and product characteristics. Section 3 presents the scientific concepts and rationale behind the AGB inversion implemented in the processor, as well as for the other mission products. In Section 4 the processor outline and operational flow are presented, with a focus on global AGB estimation. In Section 5 experimental results from level 2 product generation obtained with campaign data are discussed, highlighting the current status and open issues in Section 6.
2. BIOMASS Mission and Products Summary
2.1. BIOMASS Products
The data products to be retrieved in order to accomplish the primary mission objectives are defined in the BIOMASS Mission Requirements Document [12] and are defined as:
- AGB, defined as dry weight of woody matter per unit area, expressed in t/ha = Mg/ha. AGB is defined as the mass of live organic matter above the soil including stem, stump, branches, bark, seeds and foliage, it does not include dead mass, litter and below-ground biomass [13].
- FH, defined as upper canopy height according to the H100 standard used in forestry expressed in m. H100 is defined as the average height of the 100 tallest trees/ha [14].
- FD, defined as an area where an intact patch of forest has been cleared, expressed as a binary classification of intact versus deforested or logged areas.
The accuracy and spatial resolution of these products are defined in Table 1. The higher resolution of the FD product with respect to the AGB and FH products is due to two facts: (a) logging and disturbance activities often occur at small scale requiring higher resolution to detect them; (b) deforestation is expected to cause large changes in the radar return which is expected to be detectable with a much smaller number of looks (i.e., independent samples in a spatial estimation window and hence finer spatial resolution) than is needed to estimate AGB. The temporal sampling of products is one map every global observation cycle, where the length of the global observation cycle depends on the specific mission phase. The latency of the data products will be shorter than 1 month. The products are intended to be global, covering forested land areas between 75°N and 56°S but subject to United States Department of Defense Space Object Tracking Radar (SOTR) restrictions [15]. These restrictions exclude coverage of North America and Europe.

Table 1.
Summary of primary level 2 products.
2.2. BIOMASS Mission Characteristics
The spatial resolution of the BIOMASS level 1 single-look complex images will be about 8.3 m in azimuth and 59 m in-ground range (25 m in slant range), where the range resolution is limited by the 6 MHz bandwidth of the system considering an incidence angle of 25°. The 50 × 50 m2 product will hence be based on six equivalent numbers of looks (ENL) [4].
The system will observe during both ascending and descending passes, thus providing for each point within the observation mask at least two stacks of level 1 data within one global coverage cycle. BIOMASS will be in a sun-synchronous orbit with a near dawn-dusk equator crossing time (Local Time of the Ascending Node of 06:00 ± 15 min), chosen to minimize scintillation effects that occur in the post-sunset equatorial ionosphere [16]. The system will be left-looking and the orbit inclination will be 98°, with the highest latitude in the northern hemisphere attained on the night-side.
The BIOMASS orbital pattern will be organized into three phases. The three month Commissioning Phase (CP) is designed to allow 21 passes over a transponder at different incidence angles in order to measure the 2-D antenna pattern and test the polarimetric calibration [17]. The subsequent Tomographic Phase (TOM) will provide 3D tomographic mapping of all forest areas (in fact, all continental areas) outside the SOTR zone. A TOM stack will be composed of seven acquisitions, each one separated by three days and a baseline of 15% of the critical baseline (approximately 0.823 km at the Equator [4]) which will be achieved through orbital drift [18]. This mission phase will require 425 days or approximately 14 months in order to cover the globe. The temporal and spatial separation of the tracks was designed in order to preserve coherence at P-band with a repeat pass system [19]. The TOM phase will also provide the mission’s first global maps of AGB and FH. The remainder of the five-year mission will be taken up by the Interferometric Phase (INT). During the INT phase each interferometric stack will consist of three acquisitions, thus allowing for faster global coverage of 228 days (approximately seven months). Similar to the TOM phase, each acquisition will be separated by three days and a baseline of 15% of the critical baseline.
Both ascending and descending data will be used to provide more independent samples in the estimation, to reduce topographic effects and to acquire data with large enough ENL to meet the strict accuracy requirements. This means that the time to produce a final product at any given location within the TOM phase and each cycle of the INT phase will depend on the interval between the ascending and descending acquisitions at that point.
A peculiar feature of BIOMASS is the way the global coverage is obtained, as it is built up systematically by a sequence of roll and repositioning maneuvers. This is due to the relatively small swath width of approximately 50 km that can be achieved at P-band while maintaining the performance requirements and a requirement for a three-day repeat cycle to maintain high coherence. Roll maneuvers will allow the satellite to successively generate three sub-swaths of width 54.32, 54.41 and 46.06 km, giving a range of incidence angles across the combined swath from 23° to 34°. After acquiring the three subswaths, the satellite will conduct an orbit maneuver to move to the next swath and start again to acquire a sequence of three subswaths. This strategy implies that adjacent swaths used to build up the global coverage are gathered at different times. Consequently, the algorithms retrieving the biophysical parameters will encounter differences in the environmental conditions between adjacent swaths acquired during one global coverage cycle. It is thus of paramount importance that the proposed algorithms are robust to or can compensate for these variations to avoid introducing systematic biases in the final global products.
3. Scientific Background
3.1. AGB Retrieval
The relationship between P-band SAR backscatter intensity of forests and forest AGB is governed by a large number of factors related to both forest characteristics (3D structure, species, growth stage, leaf and wood water content, etc.) and the environment (topography, soil moisture and surface roughness). An inversion taking into account all these parameters is ill-posed, as mentioned in the following. Existing studies are usually based on data obtained on a limited number of test sites and for one point in time. For these, extensive reference data available within the same scene were used in the training process of some inversion scheme. The extension from reference plots to the entire scene was performed using statistical methods (e.g., Random Forest), or using simplified physical models [20,21,22,23,24]. In those models effort was made to reduce or take into account the various effects disturbing the relation between vegetation AGB and backscatter (including system effects, such as radiometric accuracy and incidence angle, and environmental effects, such as soil and vegetation moisture, surface roughness and ground topography).
The following approaches to retrieve AGB from P-Band SAR data have been identified:
- in the tropics, regression of VH tomographic intensity from a height around 30 m above the ground against reference data using a log-linear regression relation [20];
- in the tropics, regression of a VH polarimetric power index of some form (σ0, γ0 or t0) against reference data using a power law [21];
- in the boreal zone, regression of a polarimetric relation involving all three polarimetric terms (HH, VV and VH) [25] against reference data [22];
- a physics-based approach based on a semi-empirical scattering model [23];
- conversion of height estimates into AGB using allometric relations [24], which does not rely on regression or reference data for its primary height estimate, but thereafter is dependent on the accuracy of the height-to-AGB allometric relationships used.
However, these approaches are subject to severe limitations. The data on which tropical inversion schemes were based covered a very limited range of conditions: almost all the reference plots had high AGB and the environmental conditions during the acquisitions of the airborne data used to develop the algorithms showed little variation. Topography was the major disturbing factor and methods were developed to minimize its impact [21], even though significant sensitivity to AGB could mostly be demonstrated using tomographic techniques [20]. Boreal campaigns were specifically designed to include substantial environmental changes, and the study areas included significant topographic variation. This allowed the development of relations that mitigated both moisture and slope effects by the use of the HH/VV ratio [22]. However, establishing the regressions or parametrizing the models relied (both for tropics and boreal) on substantial amounts of reference data, so the generality of these relations was of great concern. Boreal studies [22] indicated that the regression could be successfully transferred between sites to some extent. However, satisfactory accuracy across all boreal datasets could only be achieved by increasing the number of regression parameters, and extra parameters are to be handled with care for a global algorithm, especially when they have no clear physical meaning.
The model presented in [23] is more grounded in scattering physics but its initial assessment suggested that it involved too many parameters, required too much reference data and was algorithmically unstable. Regarding AGB estimation from height, particularly in the tropics, the allometric relations between height and AGB are not mature enough to yield accurate AGB estimates, especially when the uncertainty in the height estimate from Pol-InSAR is taken into account. Moreover, the application of allometric equations without precisely knowing the diameter causes errors as, in many tree species, the variation of diameter and tree height is not correlated after a certain point [26]. To overcome this issue, it would be useful to add optical-based variables (e.g., multispectral data [27]) or structural-related variables (e.g., heterogeneity from LiDAR [28]), but this would add more requirements on external/training data to the algorithm, weakening the desired self-containedness.
Circumventing these limitations and making full use of the BIOMASS interferometric observation capabilities requires a fundamentally new conceptual design of the retrieval. This revision is based on three research results of the mission preparatory activities:
- The observational and modeling evidence that 30−40% of the total AGB in a dense tropical forest is contained in the canopy region 25–35 m above the ground [20], and that the biomass in this region is highly correlated with the total AGB [29];
- The development of signal processing techniques (i.e., ground cancellation) to cancel out the backscatter signal from the ground layer using interferometric stacks of P-band data to isolate the volume scattering element of the forest canopy;
- The development of an optimization approach to solve the model [23] that minimizes the need for reference data.
Studies comparing tomographic SAR data to in situ observations of AGB show that the backscatter of a layer located at 30 m above ground shows higher sensitivity to and correlation with AGB than the total backscatter of the whole canopy [20]. The explanation for this observation is twofold. First, the effectiveness of SAR tomography in achieving good sensitivity to AGB is due to the fact that by reconstructing the full 3D image of the forest it is possible to single out the canopy layer, which is hardly contaminated by any contribution from the ground layer as long as the vertical resolution is sufficient. Second, recent ecological studies in dense tropical forests reveal that the correlation between AGB and the area occupied at different heights by large trees (as derived from terrestrial LiDAR measurements) is maximal at a height of about 30 m [29], and about one-third of the total volume tends to be concentrated at the same height above the ground [30]. These findings provide a sound basis for the very good results obtained with tomographic regression [20]. These results are further confirmed by the prediction obtained with the TROLL ecological model that for dense tropical forests the fraction of biomass contained between 20 and 40 m accounts for about 35% to 40% of the total AGB. This relation is stable over a large range of AGB values. It has to be noted however that the relevance of the layer of vegetation around 30 m was demonstrated for dense tropical forests [31], in other types of forests with different structures the most representative layer height may be different. These results, along with the evidence that the ground mostly acts as a noise source to the AGB retrieval (being influenced mainly by soil moisture, the micro-relief of the surface and tree-ground interaction) [32] and the limited availability of baselines during the INT mission phase compared to the TOM phase, motivated the development of ground cancellation techniques. Finally, from [23] the backscattering coefficient in each polarimetric channel can be expressed as the incoherent summation of three main contributions: volume (related to the forest canopy), surface, and double-bounce scattering (related to the ground). With ground cancellation the volume component can be isolated which, as noted above, is well correlated with AGB.
Volume separation can be obtained through model-based ground and volume decomposition techniques [33,34], although the decomposition does not have a unique solution and the preferred solution is obtained by imposing physical constraints on the model [35,36]. Interferometric ground cancellation [37] instead relies purely on geometry. Consider two acquisitions separated by an interferometric baseline that has been previously phase-calibrated [38,39] and phase-steered, so that the sensor-terrain distance is compensated, and the ground level corresponds to zero. By subtracting these two acquisitions, cancellation of the ground, as well as the emphasis of a certain height layer, is automatically achieved with a vertical impulse response function (IRF) that weights backscatter within the resolution cell depending on the interferometric baseline:
where z is the elevation and is the phase-to-height conversion factor. As , terrain scattering is canceled out. The value of determines the position of the peak of the vertical IRF, that is , with being the height of ambiguity [40]. With more than two acquisitions a specific elevation can be emphasized in the processing, while at the same time removing the ground echo. A synthetic SLC image emphasizing the desired can be produced by linearly interpolating the stack to the position . Ground cancellation for each polarization is then obtained as . It must be noted that unlike extracting a tomographic layer at a specific height, ground cancellation emphasizes an interval of heights and it is thus less sensitive to change of the average canopy height depending on the specific type of forest.
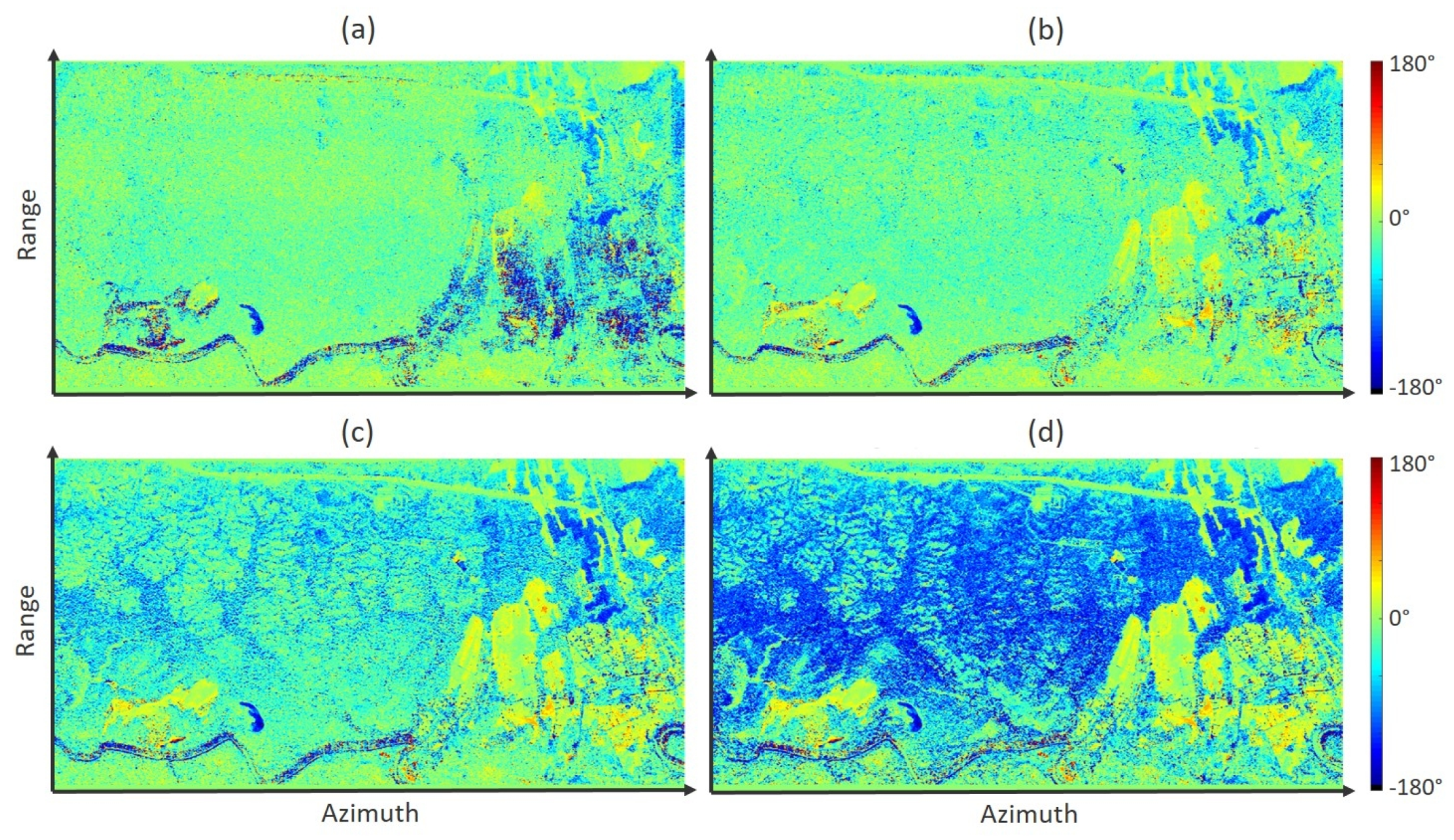
The effectiveness of ground cancellation is shown in Figure 1. The two top panels show ground-canceled data produced by using image pairs which correspond to a short and long interferometric baseline, respectively. As a reference, we show in the two bottom panels the HH-VV phase difference obtained using the original SLC data (bottom left) and the tomographic section corresponding to the ground elevation (bottom right). Double bounce scattering from ground-trunk interactions is associated with a value of the HH-VV phase approaching 180°. This phenomenon is significant at Paracou, a tropical forest site in French Guiana, and strongly connected to local ground topography [32]. It is immediate to see that the HH-VV phase of both ground-canceled images is nearly zero everywhere on forested areas, while the presence of double bounce scattering is clearly observable in the phase of original SLC data and (especially) in tomographic data.
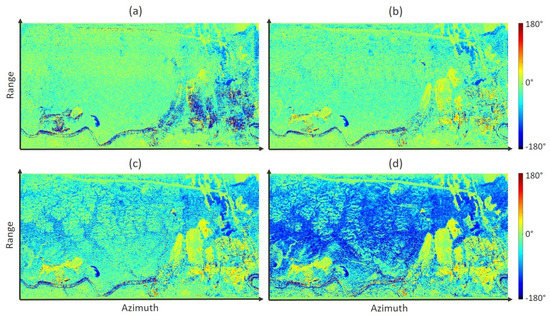
Figure 1.
HH-VV phase: (a) ground-cancelled data obtained from a short-baseline pair; (b) ground-cancelled data obtained from a long-baseline pair; (c) original SLC data; (d) tomographic section corresponding to terrain height. Dataset: Paracou, ONERA [20].
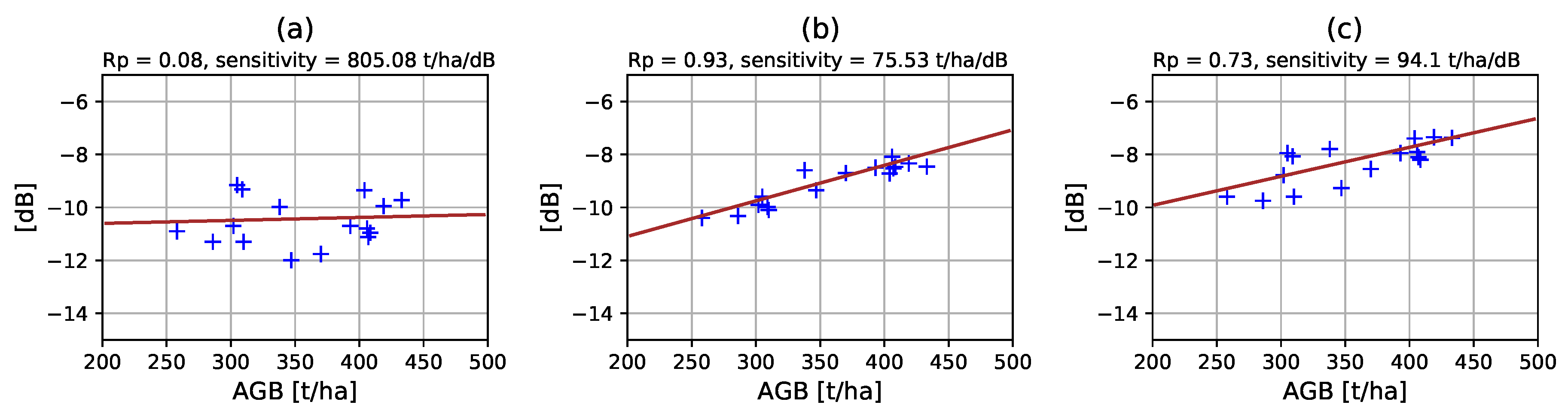
The effectiveness of ground cancellation in enhancing the backscatter-AGB correlation is highlighted in Figure 2. Ground truth AGB plots are represented against σ0 [41] for the same area in three cases: the VH channel power from SLC (left plot), the tomographic power at 30 m layer (center plot) and the power of the volume-only component as obtained through ground cancellation. It is evident that while from a single acquisition we get no sensitivity to AGB, ground cancellation greatly improves correlation and sensitivity, with tomography giving the best results.
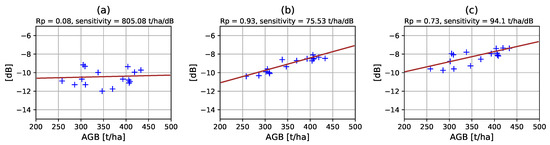
Figure 2.
Correlation and sensitivity of backscattered power with respect to above-ground biomass (AGB). (a) VH channel power from SLC, (b) tomographic power at 30 m above ground (center plot), (c) power of the volume only component obtained through ground cancellation. Dataset: Paracou, ONERA [20].
A critical point regarding the application of ground cancellation is the availability of a precise Digital Terrain Model (DTM). Equation (1) shows that if data are steered in phase with an incorrect DTM, the elevation canceled out will not correspond to the true terrain, thus resulting in errors. Since commonly available global Digital Elevation Models (DEM) are estimated from sensors operating at higher frequencies than P-band (e.g., Tandem-X or SRTM [42]), the elevation model may not correspond to the real terrain level, due to the limited penetration capabilities of higher frequencies into natural media. Thus, a suitable DTM will be produced from BIOMASS data themselves by using the full 3D information achievable from multi-baseline tomographic data [43] in the TOM phase.
Once the backscattering terms related to the ground (surface scattering and double bounce) are removed from the model formulation [23], the volume only scattering term related to the canopy can be expressed in simplified form (both for low and high attenuation vegetation [4]) as:
where is the polarization combination, is a scaling coefficient, W is the AGB, is a coefficient determined by forest structure, and is the local incidence angle accounting for topography [21]. is a coefficient accounting for the volumetric scattering within the resolution cell [20]. Modeling the in this way is consistent with previous literature, which states that the most appropriate backscattering coefficient correction for uniform volumetric scattering is [20,21,22]. The difference of n from 1 is an empirical correction which allows for more flexibility when accounting for multiple volumetric effects [21].
The model presented in Equation (2) contains many fewer parameters than the original formulation in [23]. It can be solved from ground-cancelled data by constraining the dimensionality of the unknown parameters. AGB is not polarization-dependent and we assume that , , and are slowly varying in time and space. All model parameters can be simultaneously estimated by a non-linear iterative minimization scheme without model training [44]. However, there is a scaling ambiguity since the same prediction is obtained if the model parameters , are scaled versions of the true parameters. The parameters are also sensitive to canopy moisture changes although this effect is ignored in [23]. Therefore, it is not possible to obtain an unambiguous estimate of the true AGB value without calibration. Reference data are needed, but these data do not need to cover a wide range of backscatter, slope and incidence angle conditions, as would be required if any of the models such as [23], were to be trained directly. Several options exist for reference data, e.g., in situ data and LiDAR AGB estimates, though a systematic network of calibration super-sites with suitable characteristics for AGB is yet to be established (this is mainly due to the limited number of sites available, mostly in the tropics, and the different spatial scale of the measurements with respect to that of AGB). Among the pre-launch activities, the Forest Observation System [45] database is being developed with that aim and possible benefits will come also from the cooperation between ESA BIOMASS and the NASA GEDI [46] and NISAR initiatives [47].
3.2. FH Product
The FH product is generated in both the TOM and INT phases. The baseline methodology for the INT phase is implemented by means of Pol-InSAR which in recent years has evolved into a well-established method [33].
Polarimetric-interferometric correlations estimated from data are linked to forest structural parameters such as FH, terrain height, ground-to-volume ratio, canopy extinction and scalar temporal decorrelation used to model environmental changes through the Random Volume over Ground (RVoG) model. This model assumes that forest scattering comes from an extended layer of height equal to the canopy height above an opaque ground layer. The vertical distribution of scatterers is weighted by an extinction function, accounting for electromagnetic attenuation through the vegetation. The propagation through the volume is assumed to be independent of polarization. Two approaches are possible for ground and volume separation in order to fit the volume-only correlations: the classic coherence region-based approach, performing the separation for each interferometric pair independently [33] and the algebraic decomposition-based approach [34], performing the separation for all interferometric pairs simultaneously. While the former provides the flexibility of accounting for the temporal decorrelation between each interferometric pair, the latter estimates the average polarimetric-interferometric properties of the volumetric scattering mechanism within the timespan needed to acquire the stack.
Pros and cons of Pol-InSAR are well known from the literature, thanks to extensive studies and validation. The main challenges for BIOMASS are the presence of ground scattering in all polarizations due to the limited extinction at P-band [34], the limited ENL available at 6 MHz and temporal decorrelation due to the three-day repeat cycle. Thus, the design of the inversion scheme accounts for scalar temporal decorrelation and three-dimensional polarimetric ground scattering. Another critical point is that an accurate DTM is required for the height estimation algorithm to be unbiased. To minimize the impact of this uncertainty the algorithm is expected to use the terrain elevation of the DTM derived during the tomographic phase [43], similarly to the ground cancellation described in Section 3.1.
During the TOM phase FH will be estimated from the upper envelope of the tomographic voxel intensity, as is done for instance in [35] for boreal forests. This is done by employing ground/volume separation to isolate volume-only contributions from data and computing tomographic voxels from them [34].
3.3. FD Product
The disturbance product generation is based on level 1 instead of level 2 products: the restriction to severe disturbance allows the spatial resolution to be much finer than the other products since the associated changes in backscatter are expected to be several dBs in each intensity channel. As numerous other sensors are used to detect severe disturbance with higher temporal revisit and spatial resolution (Sentinel-1, optical [48]), the BIOMASS disturbance product will be a complement to their capabilities that allows for the detection of selective logging.
The detection of changes in the polarimetric time series is based on hypothesis testing, where the null hypothesis is that in a time series of polarimetric data no change has occurred (at a given position and up to a given time). If this hypothesis fails at a given level of significance (assuming a Wishart distribution for the complex covariance data), then we assume a change has occurred [49]. Note that this approach does not specify the detection probability, which depends on the form of the multi-variate probability distribution function associated with disturbed forest. Unlike the distribution for the unchanged forest, this distribution cannot be specified a priori because change may affect the covariance matrix in many different ways. Instead, the approach provides a statistically well-defined way to determine how sure we are that change has occurred. Note that it is closely related to the constant false alarm rate approach to target detection, in which the probability that an undisturbed pixel is incorrectly classified as disturbed is fixed. The estimates are updated each time a new acquisition is added to the stack, and significance levels can be attached to the test statistics.
An open issue in generating the BIOMASS disturbance product in this way is that changes in the signal caused by disturbance occur against a general background of non-forest and environmental changes. Further work is required to quantify how much these nuisance changes will increase the false detection rate. An important requirement is also to have an initial forest mask, derived from the BIOMASS data themselves or from some other source, in order to mask out detections in the non-forest areas.
4. Processor Architecture and Current Implementation
All software modules of the BIOMASS level 2 processor are implemented in the Python language and are integrated as open-source libraries in the BIOMASS Mission Algorithm and Analysis Platform (BMAAP) [50], which is the official platform for BIOMASS data analysis and algorithm development that will be opened along with the mission launch.
In the following, the main processing chains for AGB, FH and FD product generation are presented. Particular focus is dedicated to the AGB retrieval, as most research effort was committed to the generation of this product.
4.1. AGB Product Generation
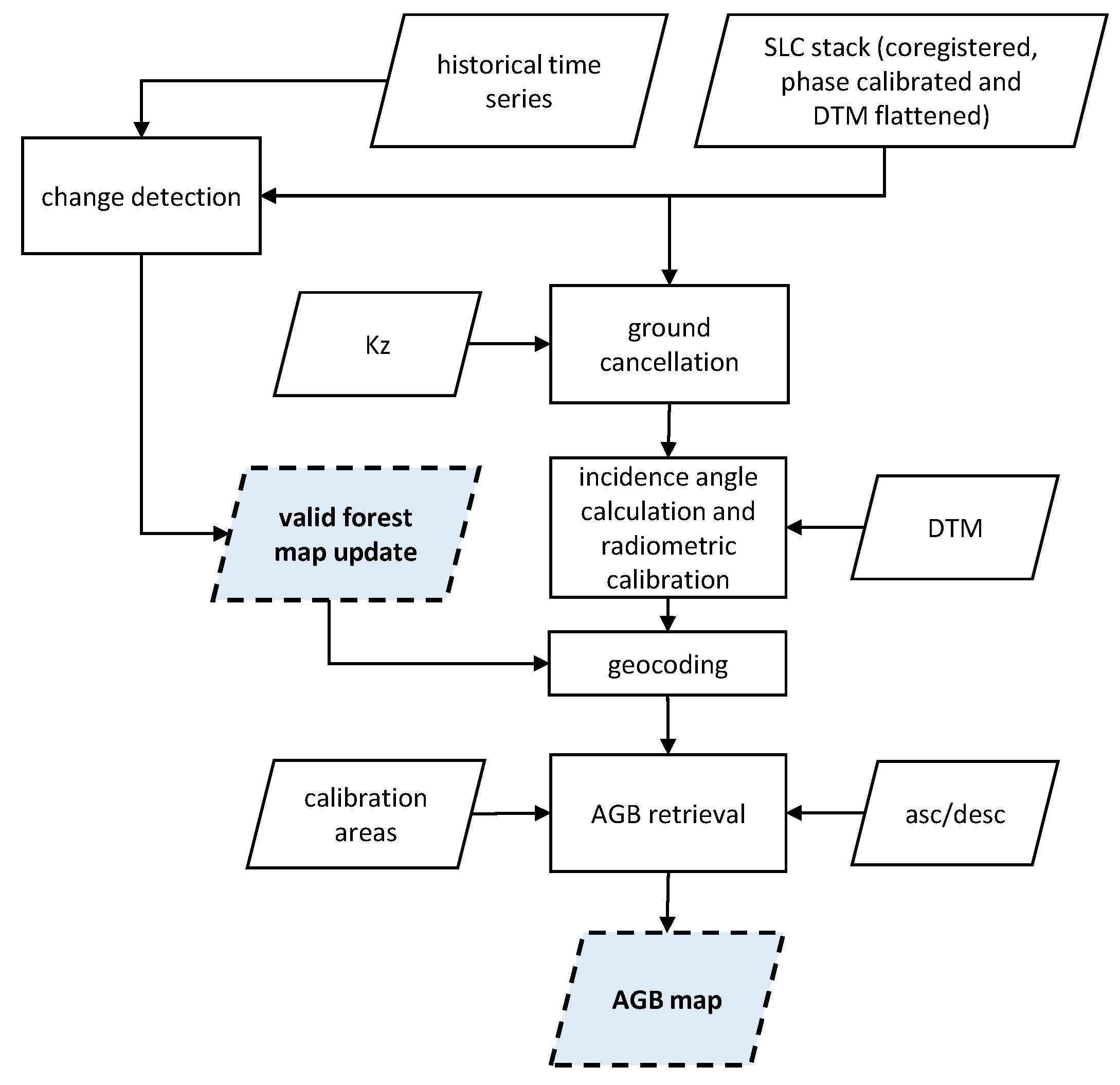
The processing chain for the AGB product generation is outlined in Figure 3.
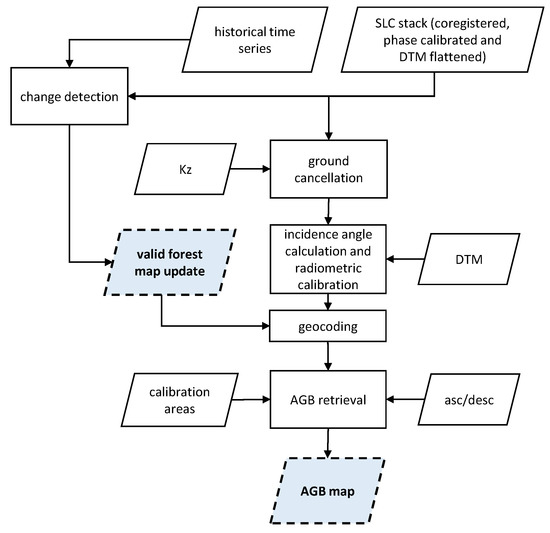
Figure 3.
Main outline of the AGB product generation chain.
4.1.1. Data Pre-Processing
The starting point is a full-polarimetric stack of multi-baseline SLC data(reciprocity can be assumed so that HV = VH), coregistered to a common master geometry, and calibrated both radiometrically and in-phase (which will be denoted by level 1c). This will correspond to three acquisitions with a different baseline in the INT phase and seven acquisitions during the TOM phase for a given cycle and ascending or descending pass. The data stack is phase-calibrated, which means that all the noise related to atmospheric effects (mainly ionosphere) and orbital inaccuracies are compensated for and the phase of the complex data is related directly to the geometric sensor-to-target distance [38,39]. Moreover, the data are DTM flattened, i.e., the sensor-to-ground distance has been compensated so that the ground level corresponds to zero elevation. As already mentioned in Section 3.1 this implies having a precise DTM available, which will be generated using the full 3D information of the TOM phase.
The first processing step applied to data is ground cancellation [37]. As explained in Section 3.1, ground cancellation is a way to combine two or more images in order to attenuate the ground return from interferometric data and at the same time enhance a vegetation layer well correlated with the AGB, depending on the baseline. This can be done by simply subtracting two calibrated and ground steered acquisitions in the case of a single baseline or by subtracting from the master an acquisition synthesized at a desired interferometric vertical wavenumber by interpolation from multi-baseline data, corresponding to the height of interest . In this way a set of three polarimetric images representative of the forest canopy will be obtained.
Subsequently, compensation of the radiometric variations due to the variation of the incidence angle over the swath is carried out in order to go from backscattering coefficient to [51], using precise local incidence angle estimation from the tomographic DTM. The polarimetric data are then geocoded to map coordinates. A fixed grid reference system is chosen in order to ease merging of subsequent ascending and descending products and AGB calibration (e.g., [52]).
An up to date forest/non-forest map (from the disturbance product presented in Section 3.3) is computed during the INT phase by change detection between the current stack and historical time series, in order to aid the AGB estimation algorithm. For the TOM phase an initial map will be available from the BIOMASS data themselves or from some other source, to be updated during the INT phase.
4.1.2. Global AGB Estimation
After geocoding to a fixed global grid, AGB estimation is performed. The model described in Equation (2) is inverted by iteratively minimizing a cost function of the form:
In Equation (3), is the base 10 logarithm, is the vector collecting the AGB values, known for at least two calibration (CAL) points, to be estimated for a grid of regions-of-interest (ROIs); is the model parameter vector (, , ) to be estimated for all the points; is the vector of observables, i.e., for all the three polarizations after ground cancellation; is the vector of local incidence angle values accounting for local topography; is the model of Equation (2).
The dimensionality of the inversion problem is reduced considering that:
- AGB, i.e., W, varies in space, but not with polarization or between ascending and descending passes (as long as no disturbance occurred between the acquisition times);
- the local incidence angle varies only in space and between ascending and descending passes;
- model parameters (, , ) vary with polarization, but slowly in space, so that they can be assumed constant within a grid region (see below for more details). Generally, they can also vary between ascending and descending passes due to, e.g., vegetation moisture variability and residual -dependent ground contributions. Since the differences between ascending and descending passes and between repeat swaths gathered in different cycles are uncertain, the algorithm has the flexibility to alter whether these parameters should vary or be constant across swaths. One approach to this is to first assume that both and are constant. The inversion is then run and AGB is estimated for both swaths. If AGB estimates over unchanged areas are similar, without any visible trends or biases, then the assumption is taken to be correct. Otherwise, the assumptions may need to be reviewed and the inversion has to be performed using different assumptions about the variability of model parameters across swaths. If an ascending-descending pair is used, then is assumed to be constant between these two swaths and can be estimated with better confidence. If only a single heading is available, should be fixed to an empirical value to reduce the dimensionality of the inversion and avoid ambiguity [53,54].
The provided ROIs must represent the diversity of AGB, backscatter and incidence angle conditions across the scene. These ROIs can be stands, plots or even individual pixels. Larger ROIs are preferred because they give a larger number of looks and less speckle. A large number of ROIs is preferred because this represents a larger number of backscatter-AGB combinations, at the price of a larger computational load. A regular sampling of ROIs is preferred because this gives a better representation of incidence angle scenarios.
To obtain low bias, the estimation algorithm requires at least two calibration areas with known AGB. For this reason, global estimation begins over areas with existing reference AGB data, e.g., well-known test sites. Subsequently, AGB is estimated using regions in overlap zones without significant forest disturbance and associated AGB estimates obtained in the previous steps, but now used as calibration references. For this, a global regular ROI grid is set up, from which ROIs in overlap regions are selected as calibration areas for adjacent acquisitions. The BIOMASS disturbance detection is carried out prior to calibration area selection from the ROIs to discard deforested and severely changed areas. Accordingly, a global grid of model parameters (, , ) is established and subsequently filled. It will have a coarser spatial sampling than the ROI grid, as model parameters are assumed to vary more slowly in space than AGB. The best model parameter grid size will be dealt with in a separate study, as further understanding is required to shed light on the variability of model parameters from area to area and from forest to forest [54] (the reader is also referred to Section 5.3 and Section 6.2). The procedure is repeated until global coverage is achieved and both grids are filled. This process results in the global level-2 AGB product, which can be further refined by combining ascending and descending tracks in the estimation step. The processor is able to deal with data both from individual and combined acquisitions.
4.2. FH Product Generation
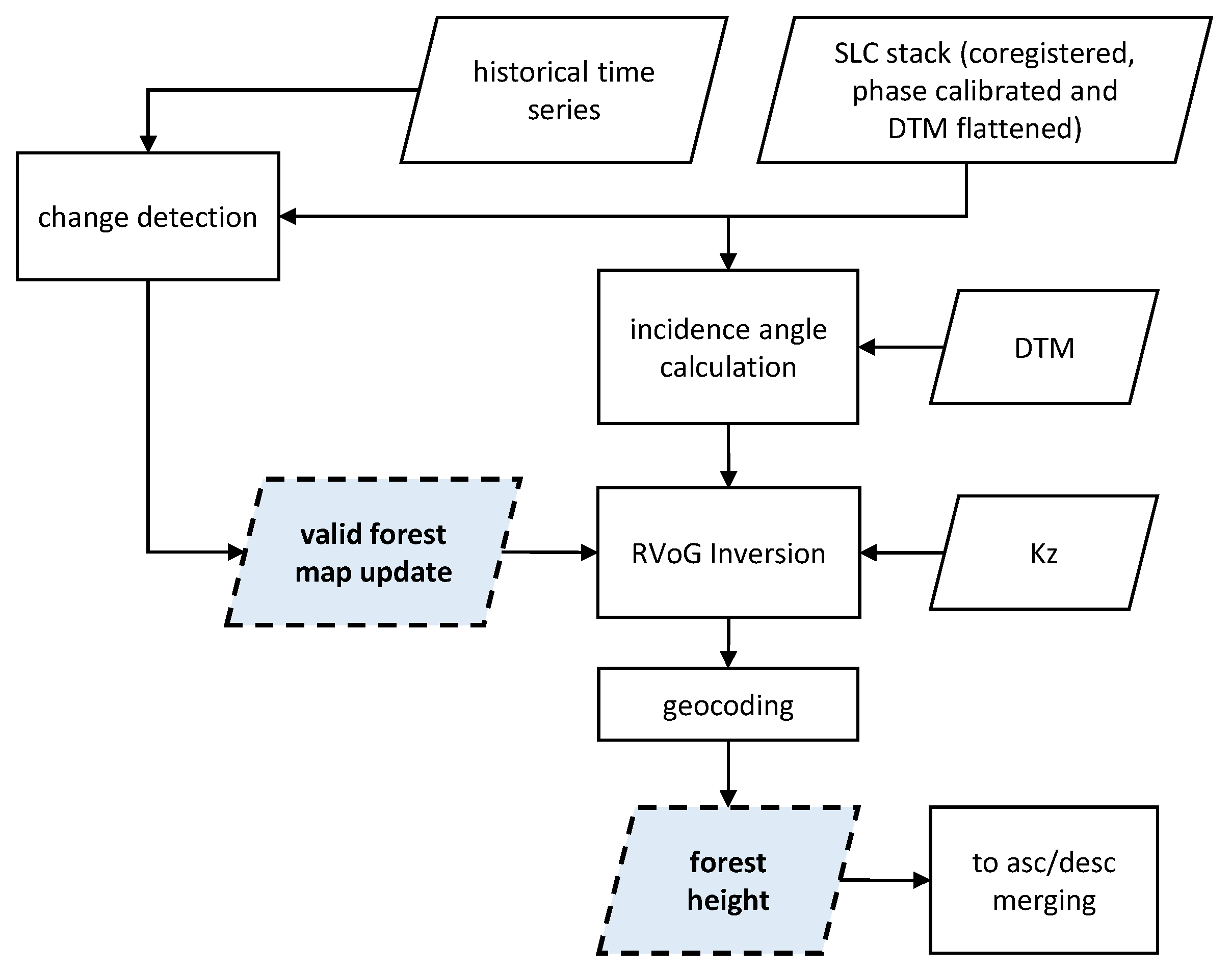
The FH product generation in the INT phase is depicted in Figure 4. The level 1c stack is fed into the RVoG inversion, after computing precise incidence angles from the DTM. Again an up to date forest/non-forest map provides additional input in order to mask out non-valid points.
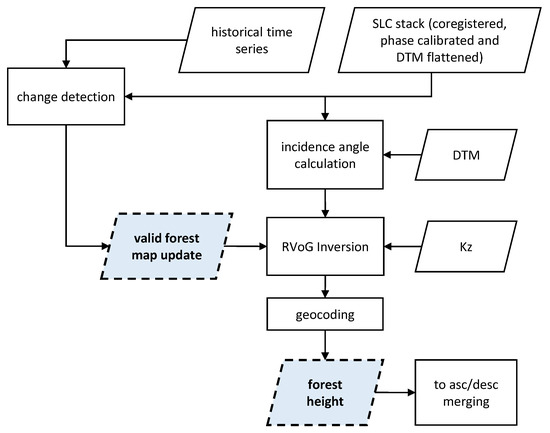
Figure 4.
Main outline of the forest height (FH) product generation chain (Interferometric Phase (INT) phase).
The RVoG module computes the complex polarimetric correlation between each acquisition pair (i.e., the three possible pairs in each triplet), perform ground and volume separation and fits the model to volume-only correlation as a function of FH, extinction, ground-to-volume ratio and temporal decorrelation for each baseline. The inversion includes correction of topographic effects [55] that affect both and the estimated FH. In particular, terrain slopes tilted in range towards the radar decrease the local incidence angle and increase the vertical wavenumber. Slopes tilted away from the radar have the opposite effect. Accordingly, for the same volume height, on positive slopes the interferometric correlation decreases and FH (if estimated without terrain correction) is overestimated while on negative slopes the interferometric coherence increases and FH is underestimated. Hence for unbiased FH inversion, the dependence of on range terrain slopes has to be accounted for. After inversion, the estimated volume heights have to be transformed into FH, as the terrain slope correction by means of the local incidence angle also tilts the reference ground level [55].
The output FH map is then geocoded to map coordinates. If available, ascending and descending passes are processed separately for the same area and then merged at the map level. Merging is done on the basis of the accuracy requirements outlined in Section 2. For each geometry (ascending or descending) the areas associated with vertical wavenumbers lower than a minimum threshold or higher than a maximum threshold are masked out. The maximum threshold is defined by the minimum number of looks (assumed as 20) required to meet the performance and is set at 60% of the critical wavenumber [56,57]. The minimum threshold is defined by the lower FH that has to fulfill the performance specifications (set at 10 m). Three cases are possible: one of the two solutions is masked out (combined FH will be given by the single solution); both solutions are available (combined FH will be given by the mean or alternatively by a weighted combination of the two FHs); both solutions are masked out, in which case we either do not provide any solution, or use only one solution and flag a warning. The final strategy is still to be decided based on further investigations.
In the TOM phase, FH is retrieved from tomographic voxels. Volume-only contributions are computed using algebraic decomposition [34]. Then volume-only data are focused in 3D and FH is estimated from the upper envelope of tomographic voxel intensity by setting a threshold to the power decay at each range-azimuth bin.
4.3. FD Product Generation
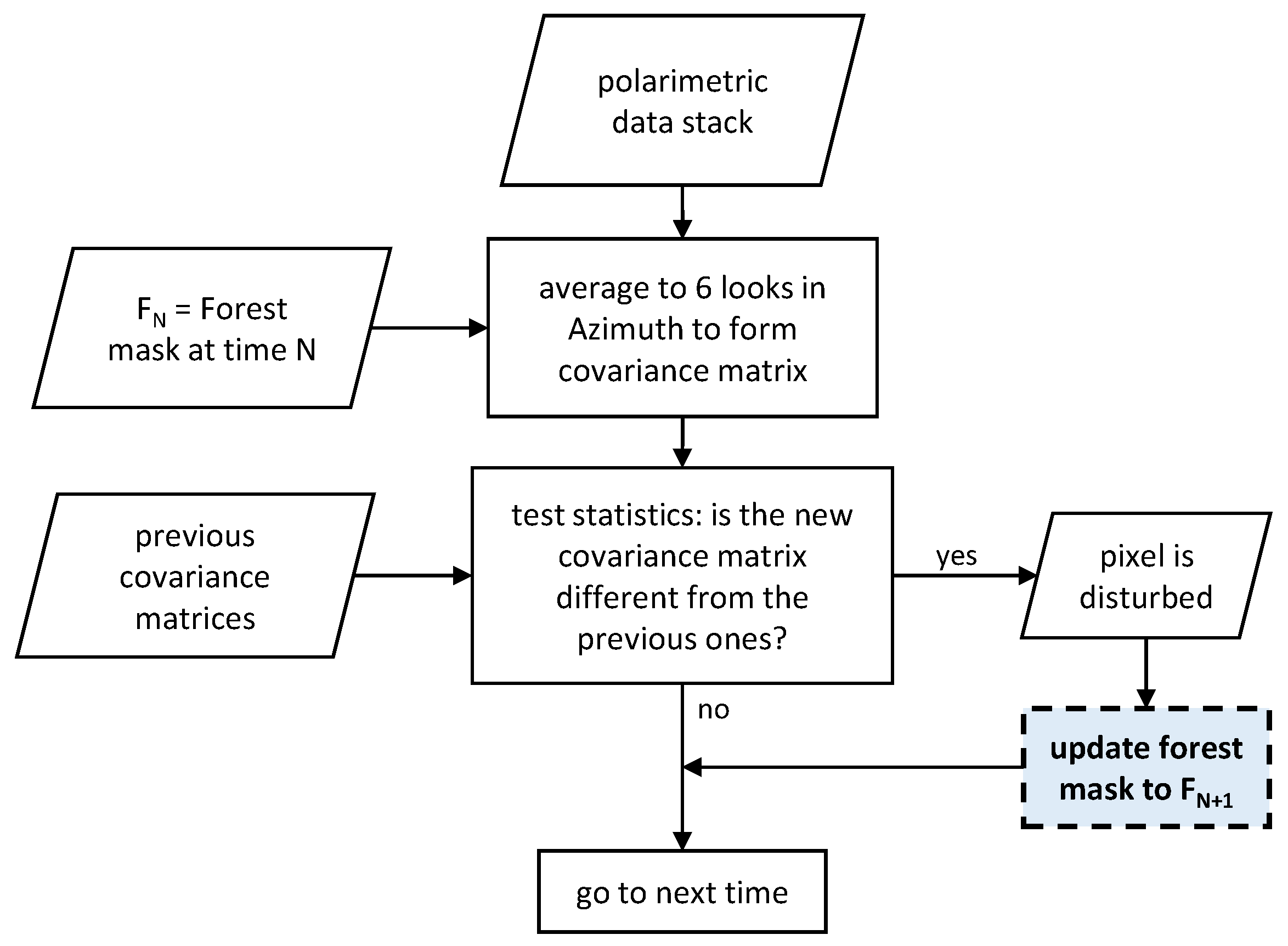
The generation of the FD product is summarised in Figure 5. The process takes as input a stack of polarimetric data, which are averaged to 6 looks in azimuth to reach the target resolution of 50 m (see Table 1) and to allow the calculation of scattering statistics expressed by the covariance matrix [25]. This process is only run for pixels within a forest mask at a given time N. For the initial run, the forest mask generated during the TOM phase will be used (see Section 4.1.1). Assuming a Wishart distribution for the complex covariance data, hypothesis testing [49] is then applied to determine whether the new matrix is different from the previous n matrices at that pixel at a given significance level. If the null hypothesis (no change occurred) is rejected, we assume that the given pixel is disturbed. The pixel is then removed from the forest mask at time , i.e., the currently completed global cycle.
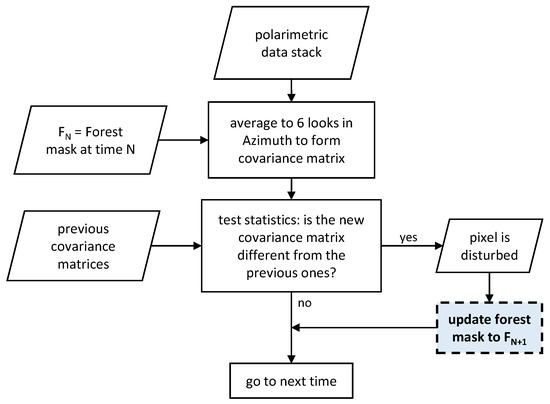
Figure 5.
Main outline of the FD product generation chain (INT phase).
4.4. Product Quality Considerations
All three forest products (AGB, FH and FD) are intended to be provided with an additional layer. This contains information about the quality of the estimates obtained from the error budget of the overall end-to-end processing chain for each pixel. The definition of the best quality metrics for each product is still being investigated, but some general consideration about the main sources of error is already possible.
For AGB and FH, in particular, the focus is on determining the impact of errors mainly in the DTM and covariance/multi-look statistics. Both systematic and random DTM errors must be precisely quantified, as both ground notching employed in AGB estimation and RVoG inversion for height estimation relies on a precise estimate of the height level of the terrain, as explained in Section 3.1 and Section 3.2. A dedicated study is ongoing to determine the quality of the DTM estimate from tomography [58]. Concerning the estimation of covariance/multi-look statistics, classical bounds from the interferometric literature already provide consistent metrics [40]. For AGB, a further point is represented by the errors on the ground plots used to calibrate AGB estimation, thus confidence intervals on the AGB estimates from ground plots through allometric equations have to be accounted for in the error budget [45]. The impact of the spatial distribution (or better the representativeness of geometric and environmental conditions) and size of the calibration plots and propagation of the errors when propagating the estimates through overlaps is a particularly delicate point, that will be assessed in a dedicated study [54]. For FD, the error budget is based on the statistics of multi-look estimated covariance matrices.
The end-to-end error budget to form the quality indicators is derived through sensitivity analysis of the end-to-end error model, in order to transfer the uncertainties in the inputs to the outputs. Wherever the complexity of the model is too demanding, an alternative would be to use statistical procedures such as bootstrapping [59], where confidence intervals on the estimates are built by random sampling with replacement of the inputs based on their errors. A comprehensive reference on uncertainty estimation for biomass retrieval can be found in [60].
5. Experimental Results
In this section, experimental results obtained by testing the algorithms on campaign data are presented. The scope of the analyses shown is to gain preliminary insights into the performance of the level 2 product generation under conditions we consider realistic for the operational BIOMASS mission. For a complete validation of the algorithms, as well as intermediate products and in-depth analysis of the behavior of model parameters for AGB retrieval, dedicated publications are envisaged [54,61].
Tests were executed on data from ESA airborne campaigns collected at tropical forest sites: TropiSAR [20] and AfriSAR [44]. The airborne campaign datasets used for the initial tests are summarized in Table 2.

Table 2.
Summary of airborne campaign datasets.
LiDAR-based DTMs, forest height and AGB maps, as well as plot-based ground measurements of AGB, were used as reference data [62]. The current focus of the project is mainly on tropical forests, since these are the main areas of interest for the mission, as they contain two-thirds of global AGB carbon stocks [15]. Moreover, the tropics contain areas with large AGB values, for which it is hardest to obtain sensitivity [21], thus representing a suitable scenario for performance assessment. Note that the FD product generation is not tested as no reference dataset documenting notable forest disturbance with associated polarimetric data is currently available.
Data were reprocessed from the original campaign datasets in order to make them compliant with the input specification of the processor. In particular, the data stacks (originally coregistered to a common master geometry) were phase-calibrated following the methodology presented in [39] and a precise DTM was estimated using tomographic techniques [43] for all the scenarios. As a last preparatory step, data were also filtered to the single-look BIOMASS resolution by reducing the bandwidth [57]. This implies that the significant variation in the local incidence angle over the swath due to airborne geometry is not compensated for at this stage. Compensation is later carried out through ground cancellation and radiometric calibration, as explained in Section 4. The same DTM was used for compensating the data in phase so that the ground level corresponds to zero. Data were also harmonized with regard to formats and annotations, so as to process them within the same algorithmic platform. Reprocessed data were delivered for integration into the BMAAP [50]. Ground truth and reference data were available from ground plots collected within the framework of the aforementioned campaigns or from LiDAR data provided by the Evolution and Biological Diversity Laboratory (EDB) [46].
It is worth remarking that, although the data used for testing contain significant topographic, incidence angle and AGB variation, these are unlikely to be representative of all the possible set of conditions the algorithms will face during operations. This is especially true as regards environmental effects as, though the data were collected in several years, no suitable time series over the same scenario was available, for example, to test the disturbance product algorithm. AfriSAR data contain a higher range of AGB than TropiSAR data, a wider range of scenario conditions and were collected in two different years and seasons, from ONERA in July 2015 and from DLR in February 2016. However, the relative calibration of the DLR and ONERA datasets resulted in differences in the dynamic range when comparing data from same scenes, suggesting not mixing the two datasets. This means that the tests being performed are only for estimators operating under a limited set of the conditions that will be met by BIOMASS. Hence this preliminary testing of the level 2 performance for the tropics can only be considered interim.
In the following, selected results from the tests are presented according to different scenarios, with a focus on the AGB product. We assume that the estimated products, , are to be compared to a reference dataset, , with samples . Since the reference dataset may contain errors [45] we cannot measure the true error in the product estimates, only their difference from the reference. The applied statistical measures are the bias or mean difference (MD) and the root mean square difference (RMSD, containing both bias and dispersion):
Both can be expressed in the form of Equation (4) or in equivalent percentage form with respect to the reference measurements. Additionally, for some of the results the Pearson correlation coefficient is computed, defined as:
where represents the average.
5.1. AGB Estimation Accuracy
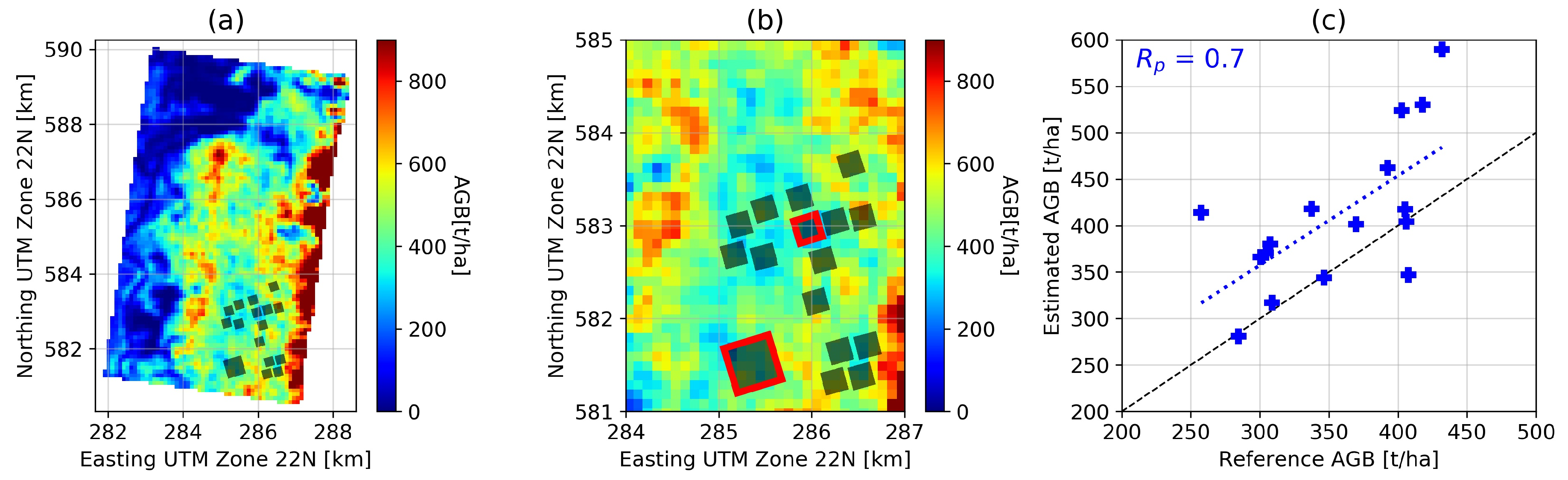
The accuracy of AGB estimation with respect to the target requirements is tested at the Paracou site in French Guiana from TropiSAR data. Paracou is characterized by hilly topography and high AGB range with a mean value of 345 t/ha (with a dispersion of 73 t/ha). In situ surveys provided 16 ground plots, one of which has size 25 ha, the rest being 6.25 ha, all measured in the same year as the SAR campaign.
AGB inversion is run on calibrated ground-cancelled data geocoded to a UTM grid. The AGB estimation ROIs are 200 m × 200 m wide and with 250 m × 250 m spacing. The height emphasized by ground cancellation corresponds to 30 m above ground level [20]. Results are shown in Figure 6. Two of the ground plots were chosen as calibration points for the algorithm, as representative of the higher and lower AGB regions. Since only one heading is available, the model parameter is fixed to 0.5 (see Section 4.1.2) as this configuration proved to produce the best results in the framework of this initial performance assessment.
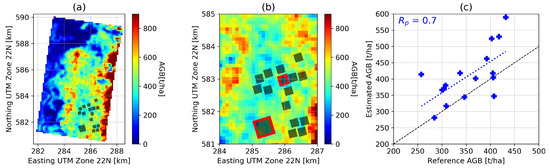
Figure 6.
(a) Estimated AGB map, (b) zoom of the area showing the ground plots location and the calibration plots (red frame), (c) estimated against reference AGB.
In plot (a) the estimated AGB map is represented in UTM, with the ground plot locations superimposed in grey boxes. In near range, corresponding to the right side of the plot, the estimation saturates, possibly due to residual uncompensated incidence angle effects. In plot (b), zoom of the area corresponding to the ground plot location is represented, highlighting also the two plots used for calibration. In (c) the estimated AGB is plotted against reference AGB. The RMSD is 82 t/ha, corresponding to about 23% for this range of AGB values, close to target requirements, while the Pearson correlation coefficient is 0.7. By comparing the blue line corresponding to the fit with the black one-to-one line, a bias is evident, amounting to about 55 t/ha for the entire range of AGB values. The bias could be introduced by the two calibration areas being at very similar range and incidence angles, thus not representing the whole range of scenarios.
5.2. Effects of Topography and Multi-Pass Combination on AGB Estimation
This test used the dataset acquired at the La Lope site in Gabon from four different headings by DLR in the framework of the AfriSAR campaign (see Table 2). The terrain at La Lope has topographic variations from moderately flat to steep slopes, and the AGB range follows a bimodal distribution around low AGB values (50 t/ha) and high AGB values (450 t/ha), with mean value 298 t/ha (dispersion 172 t/ha). Ground plots were collected, but found to be not fully representative of the full range of forest conditions. Hence, LiDAR-derived AGB maps are used as the main data source for reference data.
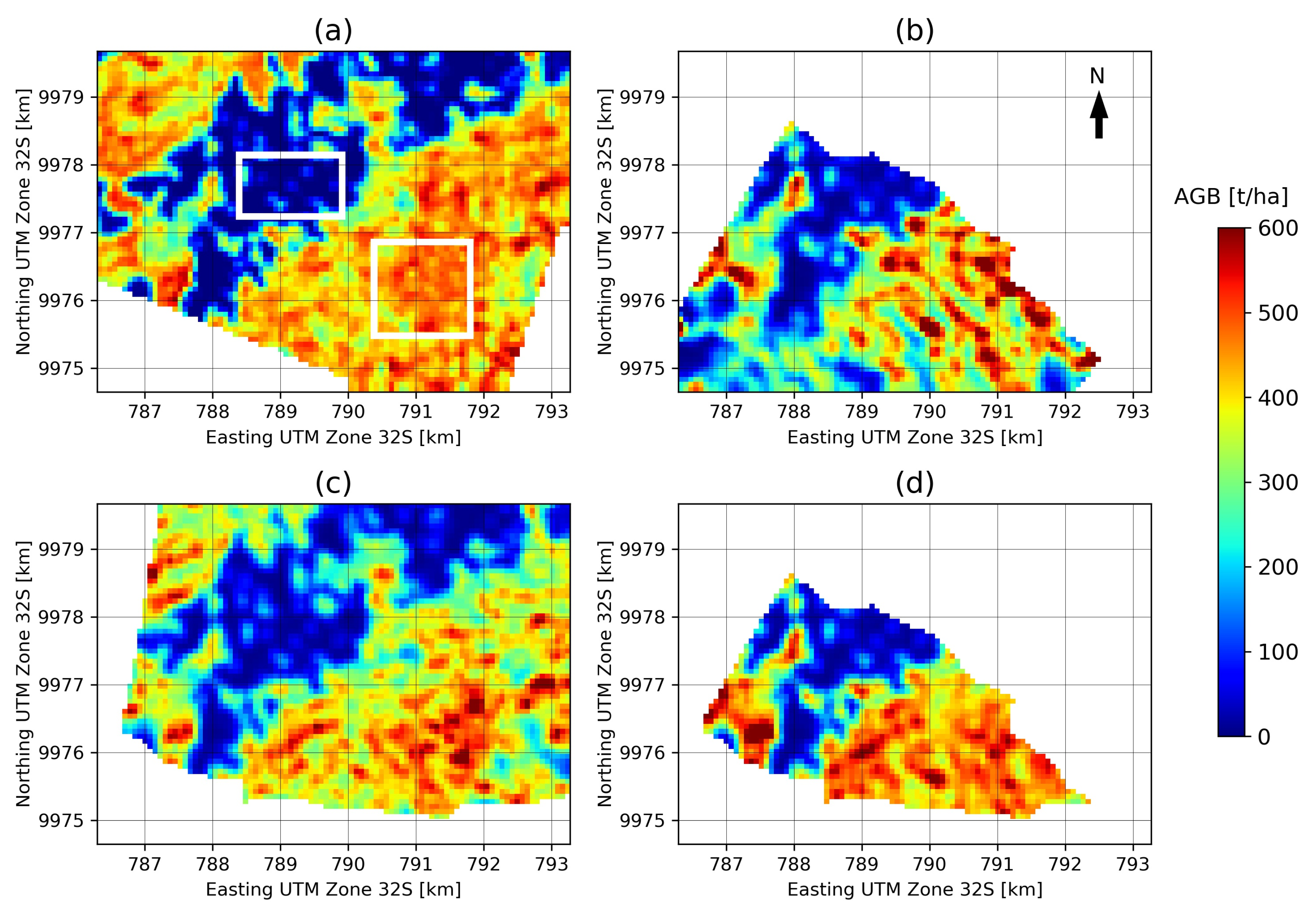
AGB inversion was run on calibrated ground-cancelled data geocoded to the UTM grid. The AGB estimation ROIs are 200 m × 200 m wide and spaced at 250 m × 250 m. The height emphasized by ground cancellation corresponds to 50 m above ground level, as taller trees are found in La Lope than Paracou. Two areas from the LiDAR AGB maps are chosen as calibration points for the algorithm, as representative of the higher and lower AGB regions, shown in Figure 7a. As for the Paracou scenario, the model parameter is fixed to 0.5.
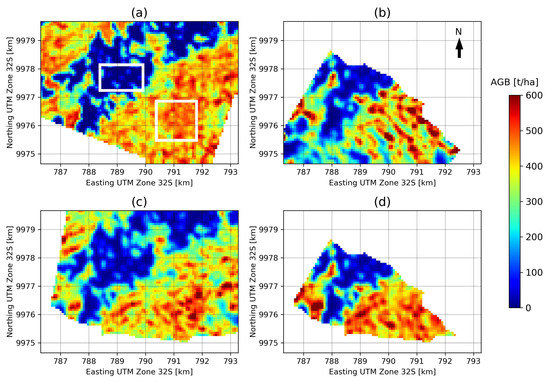
Figure 7.
(a) Reference AGB map for La Lope. The locations of the calibration areas are shown in white boxes. (b) AGB estimation for heading 1 (124°). (c) AGB estimation for heading 2 (275°). (d) AGB estimation for both headings combined.
AGB was estimated for two headings separately and then both headings were combined. We selected two headings with contrasting look-angles in order to simulate an ascending/descending combination representing an operational BIOMASS scenario. The effects of further combinations of headings are studied in [54]. Note that when combining data from two or more headings, the algorithm still produces one AGB map for each backscatter dataset with parameters estimated from the joint inversion. For this test, the maps are then averaged to provide one output product. In Figure 7b–d the estimated AGB maps are represented for the two individual headings as well as for the combination of headings. Note that the AGB estimation for the combined headings has a smaller extent due to the limited overlap of the opposing acquisitions. It can be seen that while all three estimated AGB maps reproduce the general patterns of the reference map, the estimation based on two headings shows the most homogeneous result and the best agreement with the reference LiDAR-based AGB map. The patterns of AGB estimates from single headings show some local differences whose explanation can be twofold: sensitivity to AGB may depend in part on the acquisition geometry heading (thus on incidence angle and local slopes) and incidence angle variation for the considered area may be attributed to AGB variation by the model. This is further analyzed in [54], where plots of bias and RMSE against incidence angle are presented.
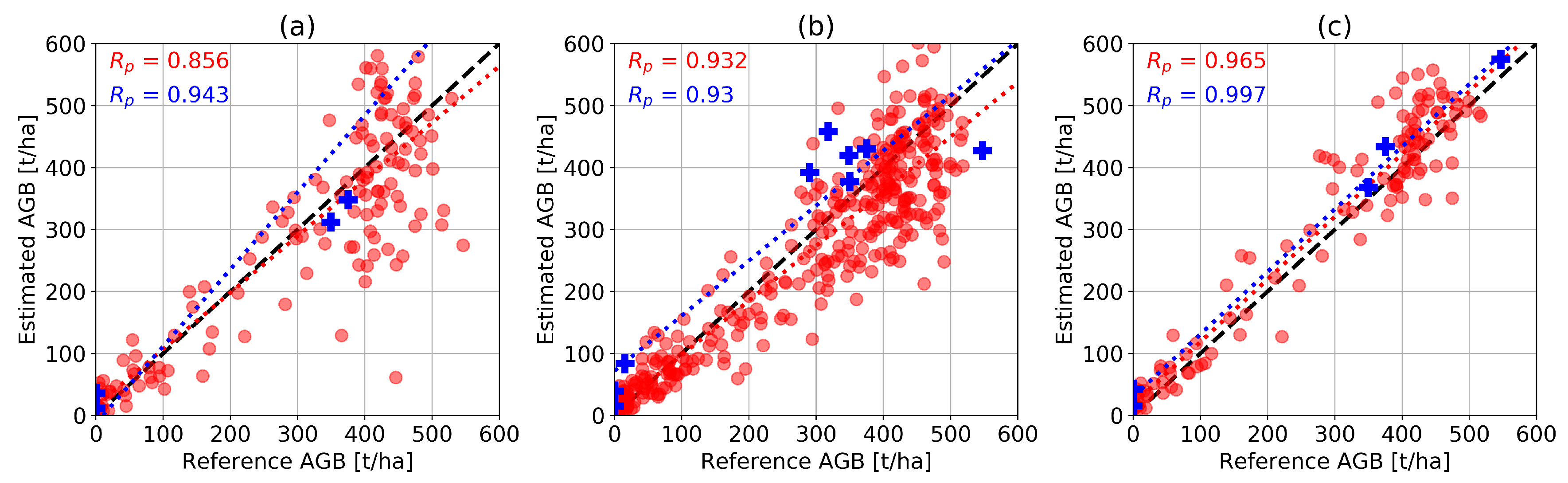
Figure 8 compares the AGB estimates for two individual headings (a) and (b) as well as for the combined headings (c), with the LiDAR- and ground-based reference data. The red circles indicate the results for the estimation ROIs with a size of 200 m × 200 m; here the LiDAR-based map is used to extract reference AGB values. Reference values and estimation results for the ground plots are indicated by blue crosses. For the individual headings, dispersion in the high AGB region leads to RMSD values of 25.4% to 32.8% (LiDAR-based) and 32.5% to 47.5% (ground-based). The combination of headings substantially reduces the RMSD to 18.9% (LiDAR-based) and 14.2% (ground-based). A small bias relative to LiDAR ROIs can be seen in the high AGB region of plot (b), which is significantly mitigated in the combined headings case (c).
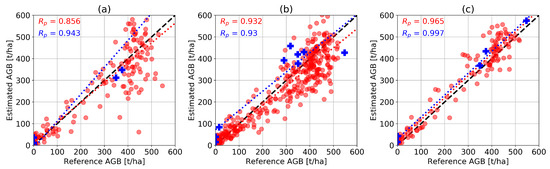
Figure 8.
Results for AGB estimation based on (a) heading 124°, (b) heading 275°, (c) both headings combined. Red circles indicate the 200 m × 200 m regions-of-interest (ROIs) using the LiDAR-based AGB map as a reference. Blue crosses indicate the ground measurements. The 1-1 line is indicated by the black dashed line, the blue and red dotted lines show the linear regression for the corresponding reference dataset.
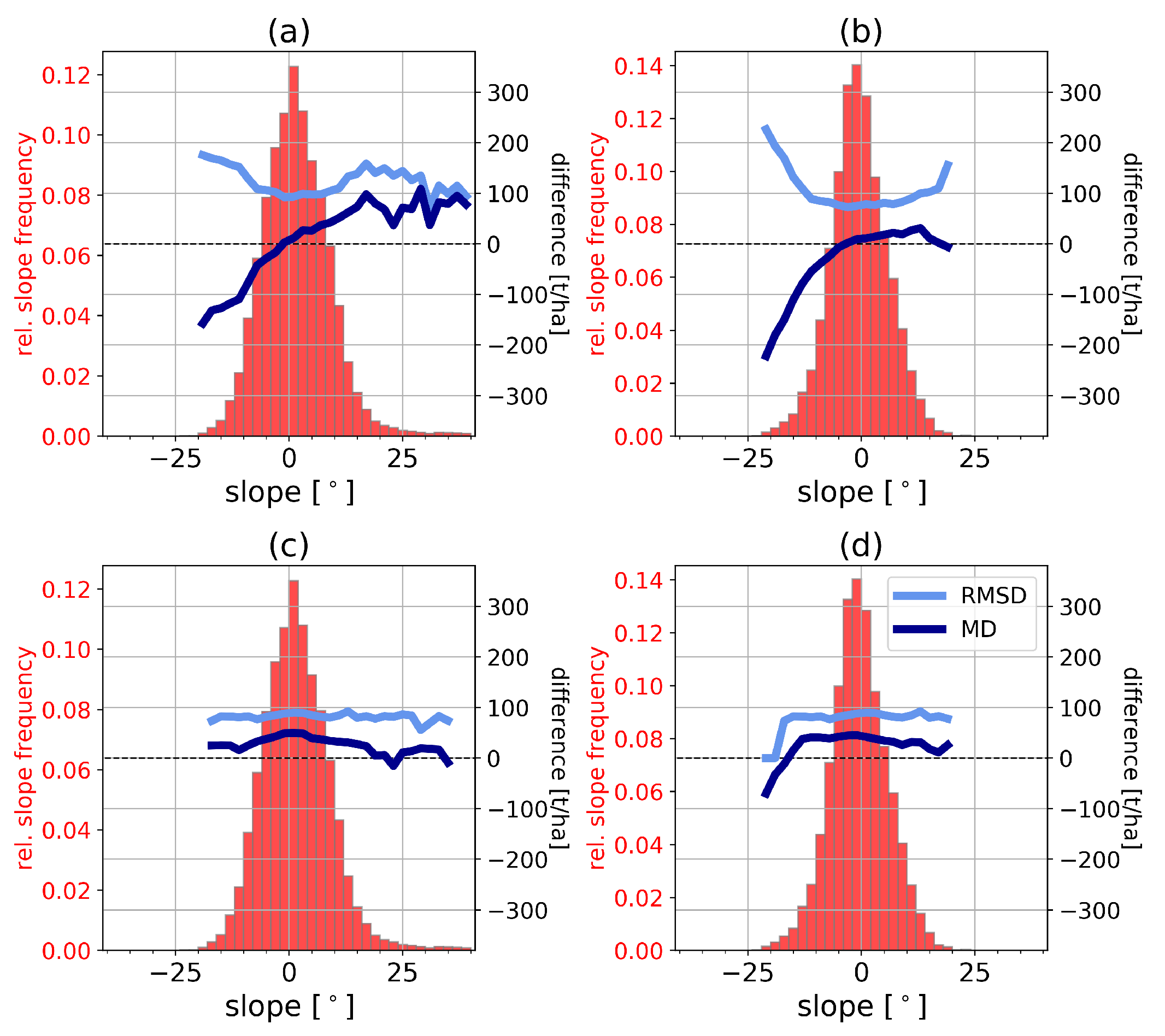
To study the influence of topography, the dependence of MD and RMSD on the terrain slope (calculated using the LiDAR AGB map) is visualized in Figure 9. Since azimuth slopes have only a secondary impact on estimation performance by moderately increasing the dispersion, only range slopes are considered in this test. It is clear in Figure 9a,b that increasing slopes degrade AGB estimation, especially for slopes facing away from the sensor (indicated as negative slopes). Note that using a combination of headings for model parameter estimation still produces one AGB map for each of the input headings. Hence, Figure 9c,d show the results of AGB estimation based on combined headings for headings 124° and 275° respectively. In these cases, the impact of slopes is much less severe as the RMSD values remain stable across different slope values, although a small bias (expressed by the MD) is introduced. Nevertheless, the combination of headings clearly leads to improved AGB estimation.
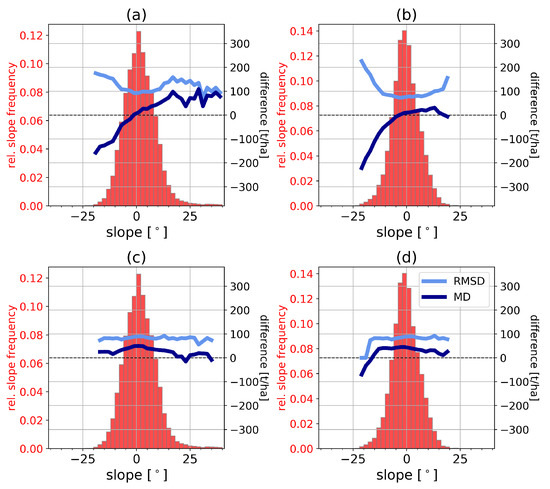
Figure 9.
Root Mean Square Difference (RMSD) (light blue) and mean difference (MD) (dark blue) as a function of terrain slope (histogram in red) for AGB estimation based on (a) heading 124° (b) and heading 275°. The results for AGB estimation based on both headings combined are shown in (c) for heading 124° and in (d) for heading 275°. All figures are based on the shared extent of both headings. The histograms differ between (a)/(c) and (b)/(d) because the slope is defined in range direction, which changes with different headings.
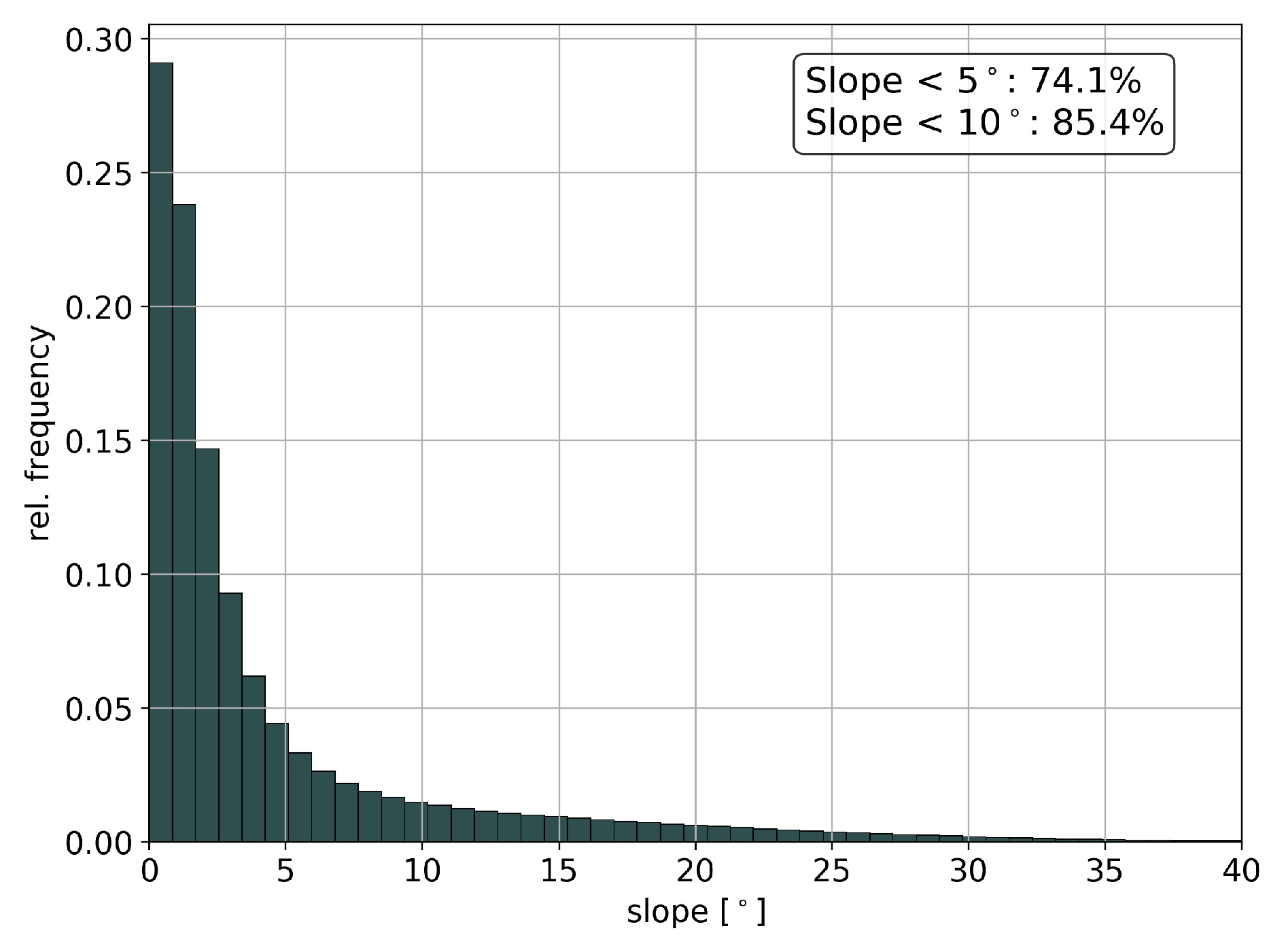
To estimate the expected impact of slopes under operational BIOMASS conditions, the global distribution of slopes in the tropics is evaluated from available datasets. A slope map covering the tropical land surface is generated from the SRTM 3-arc second (approximately 100 m) V3 void-filled DEM according to the methods described in [63]. To define a forest mask, both the GLC-SHARE global tree cover map (pixel size about 1 km2) [64] and a global forest canopy height map derived from data from the Geoscience Laser Altimeter System (GLAS) onboard the ICESat mission (pixel size about 1 km2) [65] are used. Both forest parameter maps are resampled to match the higher DEM resolution to avoid the smoothing of the slopes. Following the forest definition of the Food and Agriculture Organization of the United Nations (FAO), slope statistics are calculated for areas with a canopy cover of more than 10% and a tree height of more than 5 m [66]. Note that the X and C band radar acquisition frequency of SRTM is likely to lead to overestimation of slopes at forest edges, as in these areas the DEM represents the transition from canopy to ground layer. From Figure 10 it can be seen that 74% of the tropical forest areas have less than 5° slope and more than 85% have less than 10° slope, representing favourable conditions for AGB estimation.
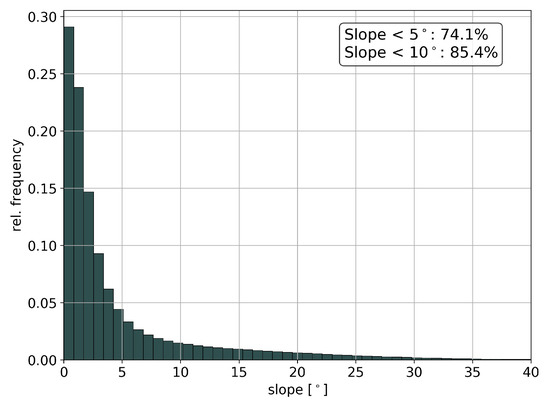
Figure 10.
Distribution of slopes in tropical forest areas.
5.3. Transfer of Model Parameters for AGB Estimation
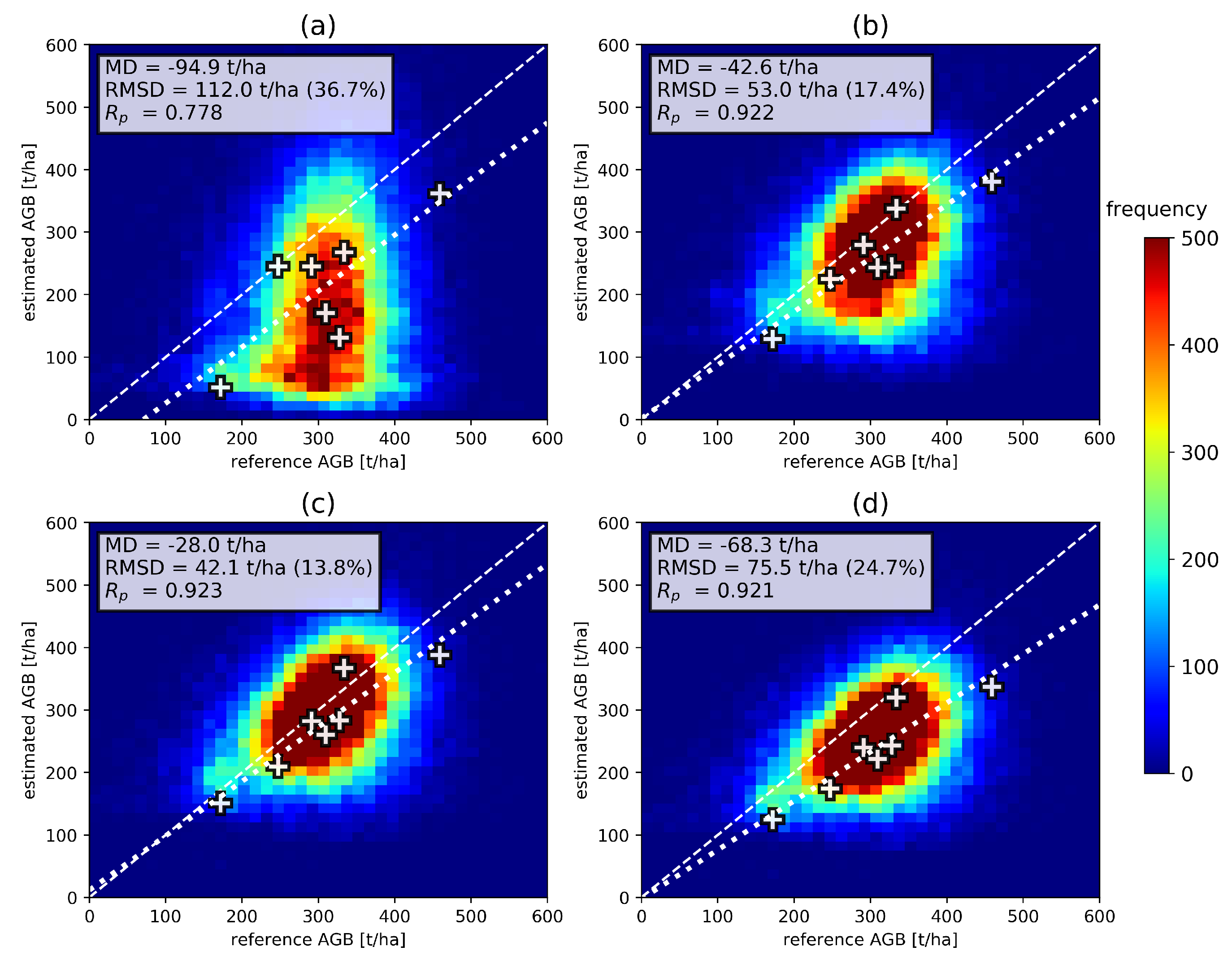
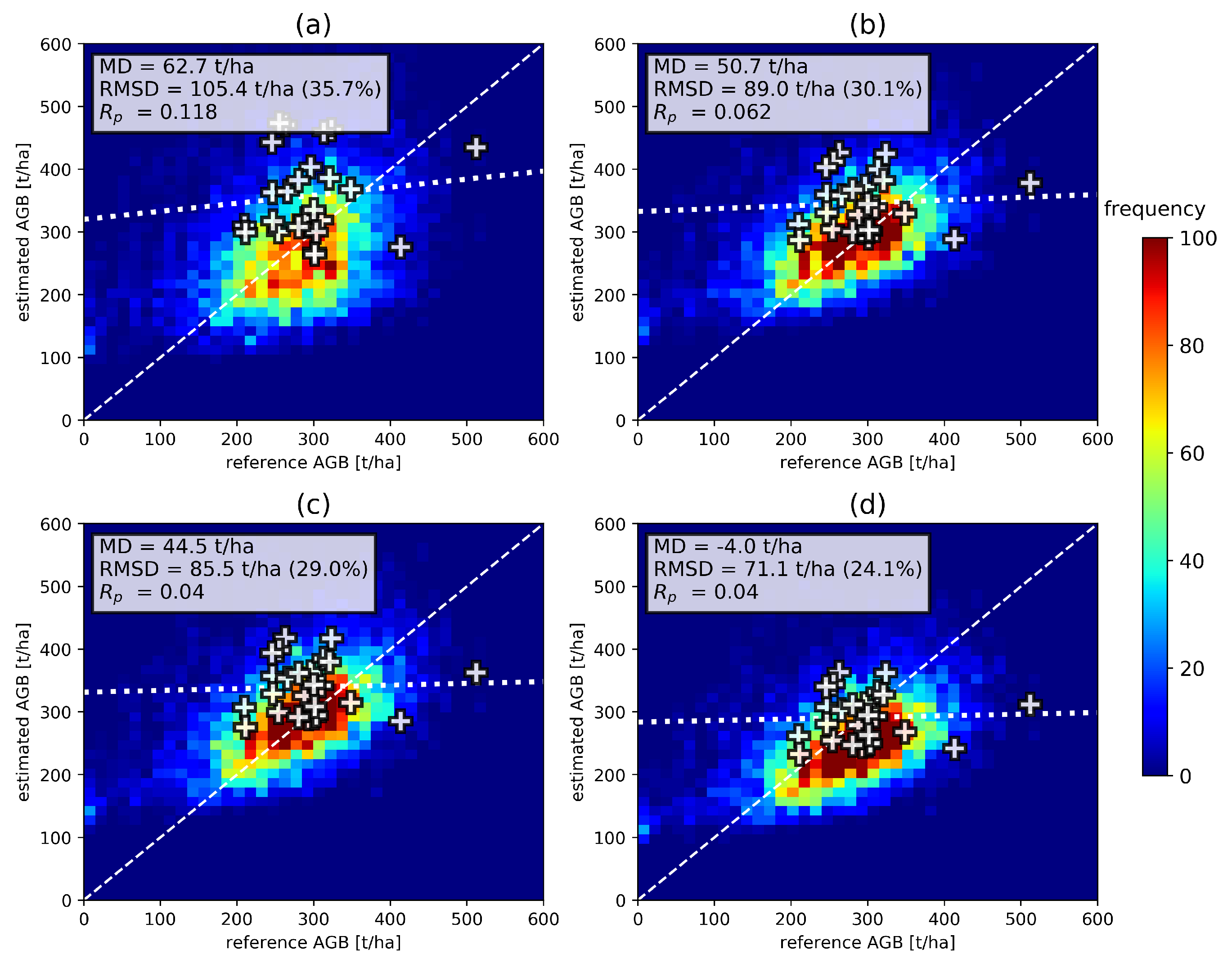
The transferability of model parameters for AGB estimation is tested for three sites from the AfriSAR campaign. Transferability is tested as an alternative to model parameter estimation through overlap propagation. Model parameters estimated at the La Lope site are transferred to backscatter data from Mabounie and Rabi. The Mabounie site lies 130 km southwest of La Lope and is characterized by swampy tropical rainforest with high AGB values, with a unimodal distribution around 332 t/ha, a mean of 328 t/ha and dispersion of 93 t/ha. Rabi is located 270 km southwest of La Lope, rainforest AGB is distributed unimodally around 280 t/ha with a mean of 275 t/ha and a dispersion of 78 t/ha. LiDAR-based AGB maps, as well as ground measurements, are available as a reference for both campaign sites. Note that the LiDAR acquisition at Mabounie was carried out in 2007, while for La Lope and Rabi it was 2015 [62]. Hence, forest changes may have occurred at Mabounie between the LiDAR and radar acquisitions, possibly causing mismatches between reference and estimated values.
For this test, model parameters are estimated for data from four individual headings at La Lope (see Section 5.2), using the same calibration areas (see Figure 7) and fixing to 0.5. They are then applied to the ground-canceled backscatter data from Mabounie and Rabi to generate AGB maps.
Figure 11 shows scatterplots of the resulting AGB maps against reference data. Note that differences between the plots (a) to (d) are caused entirely by varying model parameters. The transfer results in good agreement with the LiDAR-based reference data for cases (b) and (c), where model parameters are estimated based on La Lope headings 230° and 275°. However a large bias is visible in case (a), and a smaller bias in case (d), corresponding to parameter estimation at La Lope headings 124° and 320°. The comparison to the ground measurements shows a good agreement in cases (b) and (c), with RMSD values below 20%. Larger differences due to biases are visible in the other two cases. Similar patterns occur in Figure 12, where the results of the model parameter transfer to Rabi are shown. A good general agreement based on LiDAR reference data can be stated, but biases are present for test cases (a) and (d). Comparison to ground data shows a large dispersion with RMSD values between 24.1% and 35.7%. Furthermore, the sensitivity of backscatter to ground-measured AGB is very low. Similar tests were carried out transferring model parameters the other way around from Rabi and Mabounie to La Lope, resulting in larger biases than reported in Figure 11 and Figure 12, especially in low AGB regions. This can be explained by the fact that Rabi and Mabounie only cover a limited AGB range in the high AGB region and the model parameters are therefore also optimized for this scenario. The La Lope site, however, covers both low and high AGB values. Hence, it is assumed that model parameter transfer is performed under more representative conditions using La Lope data as the initial set for parameter estimation.
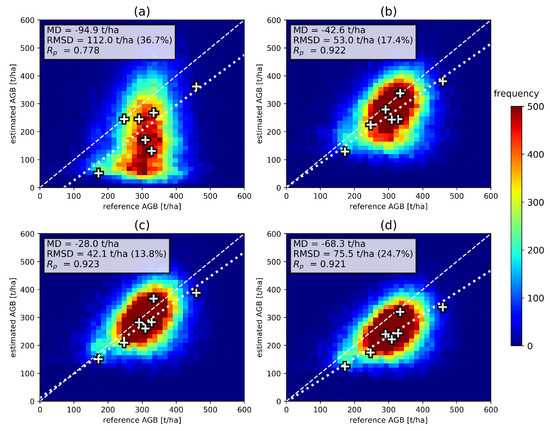
Figure 11.
Evaluation of AGB maps at Mabounie with model parameters estimated at La Lope (a) heading 124°, (b) heading 230°, (c) heading 275°, (d) heading 320°. Comparison is based on the reference LiDAR-based AGB map (2D-histogram) and ground measurements (white crosses).
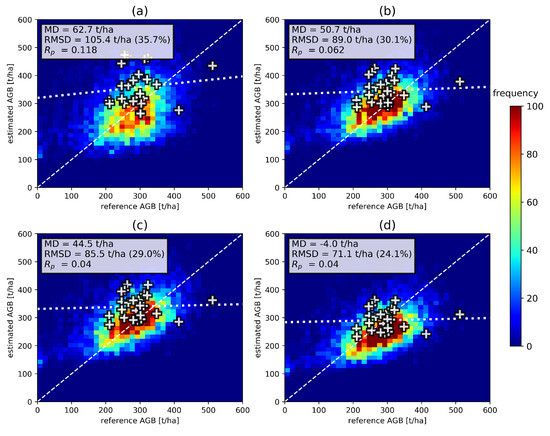
Figure 12.
Evaluation of AGB maps at Rabi with model parameters estimated at La Lope (a) heading 124°, (b) heading 230°, (c) heading 275°, (d) heading 320°. Comparison is based on the reference LiDAR-based AGB map (2D-histogram) and ground measurements (white crosses).
This test indicates that model parameters are generally transferable to sites with similar forest types and comparable terrain conditions. Biases may be introduced, especially if AGB is estimated based on one heading only, as is the case for this test. However, general conclusions on the spatial variation of model parameters cannot be drawn from this preliminary assessment, and further research is required on this issue.
5.4. FH Estimation
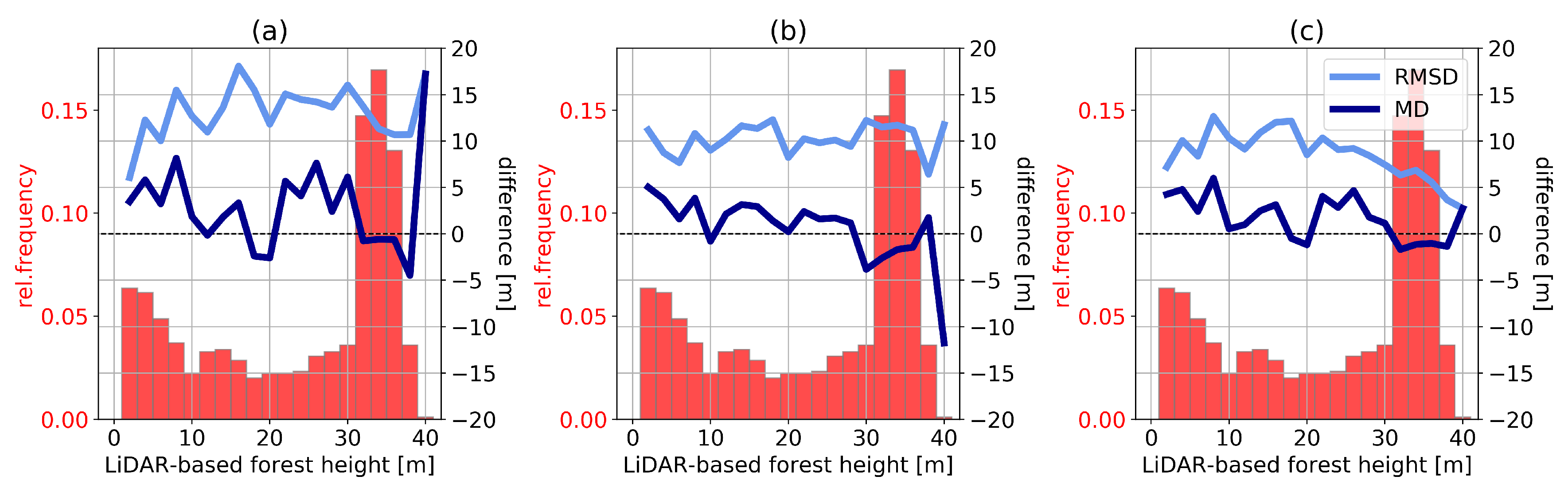
FH estimation is preliminarily tested on the La Lope multi-heading dataset presented in Section 5.2. To simulate an ascending/descending scenario, FH is estimated individually for two different headings and the average of both products is calculated (see Section 4.2). Figure 13 reports the RMSD depending on the LiDAR-based reference FH for two individual different headings as well as for their combination.
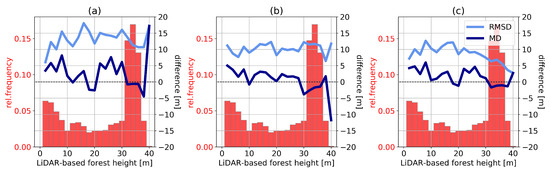
Figure 13.
RMSD as a function of reference LiDAR-based FH for La Lope data estimated from (a) heading 124°, (b) heading 275°, (c) both headings combined. Reference FH distribution is shown in red.
For heights from about 10 m to 40 m RMSD is about 8-15 m when only one heading is used for estimation. This is slightly larger than target requirements but the performance improves, especially at high FH values, with the merging of ascending and descending acquisitions. A comparable effect is found for the MD, as a strong bias for high FH values is visible in case (b), which is neutralized by the combination of headings. Further analysis shows that similarly to AGB estimation, higher errors (in terms of both bias and RMSD) are found for steeper slopes, with RMSD around 10 m and 40% bias for gentle slopes and RMSD around 20 m and bias 60% for steep slopes. This confirms that sloping terrain represents a challenge for FH estimation, but based on the tests in Section 5.2, the impact is mitigated by merging of ascending and descending data.
6. Discussion
6.1. Comparison with Other Forest Biomass Retrieval Approaches
In this section, we compare the methodology chosen for AGB estimation implemented in the processor with other popular AGB estimation methodologies found in the literature. The discussion again focuses on AGB, due to its relevance and the novelty of the approach. Forest height estimation and forest disturbance detection rely on more consolidated techniques and their main innovations are related to the tailoring of the chosen algorithms to the BIOMASS case.
Since comparison with AGB inversion techniques tailored to particular scenarios is already done in Section 3.1 when explaining where the current approach originated from, the purpose of this section is to put the AGB estimation proposed within the L2 processor in a broader context of global AGB estimation methodologies. The discussion here considers only general methodologies for AGB estimation, without going into the details of any particular approach.
Following [67,68], the techniques for AGB estimation commonly found in the literature can be divided roughly into:
- Parametric empirical regression models: the backscatter-AGB relationship is modeled by some simple mathematical law (linear, power-law) as a function of a few regression parameters and is then inverted. This simple approach is effective when the chosen mathematical law corresponds to the relationship observed in the data. Drawbacks include that it requires a lot of training data and when the estimation procedure is applied to regions too far from the training area or which include a substantial amount of environmental variation (not accounted for in the training data), the estimates become questionable. As a last point, the inversion parameters cannot generally be transferred as they usually do not have physical meaning. Rodríguez-Veiga et al. [67], in particular, discusses how problems of overestimation of low AGB and underestimation of high AGB very often occur in practice, due to the simplicity of the chosen mathematical law (often linear or with too few parameters) describing the AGB-backscatter relationship or to unaccounted environmental variation in training data. Techniques 1-3 described at the beginning of Section 3.1 belong to this class.
- Parametric semi-empirical physically-based model: the backscatter-AGB relationship is modeled with some physical law as a function of a few parameters that have a clear physical meaning. In this case the model is more adaptable than empirical regression models, due to the physical meaning of the parameters. Parameters can moreover be transferred between sites (at least in principle) and there is less need for training data. Parameters can be tuned in order to control the inversion, but direct inversion can be hindered by the complexity of the model. Moreover, the model may not be able to fully capture the complexity of the scattering mechanisms. Techniques 4-5 described at the beginning of Section 3.1 belong to this class.
- Non-parametric techniques (e.g., Neural Networks, Random Forest): these do not require any data model, can ingest multiple predictors and adapt much better than model-based approaches. However, it is much more difficult to control their behavior and they require a substantial amount of reference data to account for all the possible conditions.
The discussion presented in this paper makes clear that the global algorithm proposed for implementation in the BIOMASS L2 prototype processor belongs to the second class, i.e., it is based on a semi-empirical physically-based model. This choice is motivated, as explained in Section 3.1, by the necessity to keep the complexity at a reasonable level, limit the amount of training data required and at the same time preserve the physical meaning of the parameters in order to allow transferability and to control the model behavior. Significant effort has been made to reduce the parametrization of the scattering model through ground cancellation techniques, which are of major benefit to the model inversion, though further investigations are required to determine both the impact of ground cancellation errors (due to for instance a non-precise DTM knowledge) and whether the simple model Equation (2) is sufficient to describe all the environmental conditions to be met by BIOMASS. Moreover, significant efforts are being made to design an effective global estimation scheme that relies on propagating the estimates through overlapping regions, starting from calibration points (as described briefly in Section 4.1.2). This requires further investigations to determine the impact of both the initial calibration points and the propagation of errors through overlaps as discussed in [54]. Further investigation of model parameter transferability is also required as the results reported in Section 5.3 are mixed.
Regarding the non-parametric class of biomass estimation methods, it is worth mentioning that besides the official L2 product delivery, BIOMASS P-band L1 data will be available for use in the broader context of multi-sensor data fusion. This kind of approach is not self-contained and is less intuitive than the approach proposed for BIOMASS. However, it may be able to exploit the varying sensitivity of other radar frequencies (as well as that of optical and LiDAR sensors) to different forest properties (including forest horizontal structural information provided by LiDAR and optical data), potentially improving the accuracy of and reducing the uncertainties in AGB estimation.
6.2. Open Points
The experimental results suggest that AGB accuracy is close to the target requirement when good calibration data are available and terrain slopes are moderate (as for example is the case for Paracou). They further imply that AGB estimation is significantly improved by combining acquisitions from multiple headings, as will be the case when combining data from ascending and descending orbits. Similar results apply also for height estimation. However, these results do not represent an exhaustive validation, because tests are carried out only for a few scenarios and not the full range of available campaign data and their combinations. A dedicated study is currently tackling this issue [54]. Furthermore, no effort is committed to evaluating the performance of the individual modules of the processor, as only the accuracy of the final level 2 products is assessed. Validation of interferometric ground cancellation is carried out in [61]. Nevertheless, several open issues can be identified from the experimental results in Section 5 that are required to improve the robustness of the algorithms, especially in a global perspective.
The first concerns the limited AGB range and range of weather conditions within the campaign data available for testing, which are only partially representative of the range of AGB and environmental conditions that will be met by BIOMASS. In this context, it is important to note that other technology, such as L-band [47], can be effective in measuring AGB. Campaign data used for testing mainly contains variation across high AGB values which is the range for which the BIOMASS mission is particularly designed. In addition, the environmental conditions did not vary much across the tropical campaigns as they were collected at a limited number of sites and times. This limited the testing of the AGB inversion and meant that testing of the disturbance product relied on simulation, as no data representative of a BIOMASS-like case was available. Efforts to provide more thorough testing of the disturbance product are now focused on using additional datasets, such as multi-temporal L-band airborne polarimetric data collected by DLR at the Traunstein site [69] or polarimetric time series data collected during tower experiments to study seasonal effects [70,71] (however the latter are collected in a slightly different geometry than airborne and spaceborne systems and the coverage is much more limited in space).
Connected to the use of campaign data is also the fact that the suggested approach to area extension using grid region overlaps could not be tested, as the test scenarios available are localized in different areas separated by hundreds of kilometers, even in the best case (AfriSAR). Splitting a scenario in smaller blocks is not a viable option, as the scales would not be representative for BIOMASS. A dedicated study is currently being performed to address this issue. The strategy foreseen is to study the variability of model parameters, AGB and environmental conditions across AfriSAR sites, simulate data in between and test the propagation through overlaps from one scene to another. This will help also in assessing how to extend the solution away from regions with calibration data without causing excessive error propagation. The study of model parameters should also shed more light on model parameter transferability, see Section 5.3.
The implementation of a fixed grid will support the merging of ascending and descending data and simplify model calibration. Here a UTM grid was used to process campaign data, but the Equi7 grid [52] represents a valid alternative that minimizes projection distortions for each continent.
The AGB estimation algorithm relies on some calibration data, but these have not yet properly defined for BIOMASS and further work is required to define proper calibration strategies (e.g., supersites with stratification, etc.).
The framework and algorithms for height estimation are well-defined and understood. More effort should be devoted to comparing the performance of different proposed algorithms with respect to the effects of temporal decorrelation, and optimizing the spatial baseline ratios to maximize the FH range over which the inversion performance meets BIOMASS requirements.
The impact of the tomographic DTM on error propagation of level 2 estimates will be assessed in a dedicated study [58].
More effort is needed to investigate AGB estimation in boreal and temperate forests. These forests are not as tall as in the tropics and the tomographic resolution of BIOMASS is unlikely to allow clear separation of the ground and canopy. In addition, double-bounce scattering is much more relevant for these types of forests, so ground cancellation may remove pertinent information. Preliminary results from the level 2 study do not give any clear indication that AGB estimation is improved by ground-cancellation [4].
Finally, consistency between the estimated FH and AGB will be addressed. This implies converting the FH estimates into AGB through an allometric equation and then comparing the derived AGB map with that estimated from the BIOMASS algorithm.
7. Conclusions
In this paper, we present the theoretical basis, implementation design and global coverage strategy for the level 2 products created in the framework of ESA’s P-Band SAR mission BIOMASS. The generation of global above-ground biomass (AGB) maps relies on fundamental findings from the level 2 prototype processor development. For tropical forests, tomographic analysis and biophysical evidence show that biomass in the 25 m to 35 m canopy layer is highly correlated with total AGB and that backscatter attributed to the ground represents an obstacle for AGB retrieval. This is exploited in the level 2 prototype processor by applying interferometric ground cancellation, a novel technique developed in the course of the level 2 activities, that strongly attenuates the signal contribution from the ground by combining two or more acquisitions separated by an interferometric baseline. The resulting signal can be attributed to the vegetation layer. Because of this, the semi-empirical model used to establish a relationship between AGB and backscatter [23] can be simplified to describe only the volume scattering terms. In this way the number of model parameters and hence the dimensionality of the inversion problem is greatly reduced, thus permitting a stable numerical inversion procedure.
Furthermore, we present the implementation of the FH product generation. While the data acquired in the TOM phase allows the estimation of FH through a tomographic voxel dataset, Pol-InSAR methods are applied together with the RVoG-model in the INT phase. It is envisaged to merge FH maps generated from ascending and descending orbits to improve accuracy and mitigate negative effects of slopes.
We test AGB and FH retrieval using airborne P-Band data from the AfriSAR and TropiSAR campaigns together with reference data from LiDAR-based AGB maps and plot-based ground measurements. For AGB estimation based on data from a single heading, comparison with reference data yields relative RMSD values mostly between 20% and 30%. Combining different headings in the estimation process, as will be possible with the ascending/descending pattern of the BIOMASS satellite, significantly improves performance and relative RMSD values of less than 20% are achieved. RMSDs of 8–15 m are achieved for FH retrieval which improve to 3–11 m when combining data from different headings.
The experiments suggest that the implemented retrieval scheme provides robust results that are within target requirements. However, testing was carried out only for a very limited number of reference sites and further research is currently dedicated to algorithm validation. On top of this, ongoing preparatory research activities include simulation-based analyses on the spatial variation of model parameters as well as the development of a validation strategy for the FD product.
Author Contributions
Conceptualization, S.Q., K.P., L.U., L.V., T.L.T., S.T., M.S., F.B., M.M.d., D.G. and K.S.; methodology, S.Q., K.P., L.U., L.V., T.L.T., S.T., M.S., M.M.d., F.B. and K.S.; software, M.S., M.M., G.R. and F.B.; validation, M.S., F.B. and G.R.; formal analysis, M.S., L.V., M.M., G.R. and F.B.; investigation, S.Q., K.P., L.U., L.V., T.L.T., S.T., M.S., M.M., G.R. and F.B.; resources, S.Q., K.P., L.U., L.V., T.L.T, S.T. and M.M.d.; data curation, M.S., S.T., M.M.d., L.V. and F.B.; writing—original draft preparation, F.B., S.Q. and G.R.; writing—review and editing, K.P., L.V., T.L.T., S.T., M.S., M.M.d., F.B., S.Q., G.R. and K.S.; visualization, S.Q., L.U., L.V., T.L.T., S.T., M.S., M.M.d., F.B. and G.R.; Supervision, K.S. and S.Q.; project administration, D.G. and F.B.; funding acquisition, S.Q., K.P., L.U., L.V., T.L.T., S.T., M.S., M.M., D.G. and F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Space Agency through contract 4000119231 BIOMASS Level 2 Implementation Study.
Acknowledgments
The authors would like to acknowledge Jun Su Kim (DLR) for providing core implementation of height inversion, Emanuele Giorgi (Aresys) for helping in the execution of the experimental tests and data preparation, Jerome Chave, Nicolas Labriere (EDB) and Sassan Saatchi (NASA) for providing LiDAR data and for consultancy on the project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reichstein, M.; Carvalhais, N. Aspects of Forest Biomass in the Earth System: Its Role and Major Unknowns. Surv. Geophys. 2019, 40, 693–707. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Hauck, J.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; Le Quéré, C.; et al. Global Carbon Budget 2019. Earth Syst. Sci. Data 2019, 11, 1783–1838. [Google Scholar] [CrossRef]
- ESA. BIOMASS—Report for Mission Selection—An Earth Explorer to Observe Forest Biomass; SP-1324/1; European Space Agency: Noordwijk, The Netherlands, 2012. [Google Scholar]
- Quegan, S.; Le Toan, T.; Chave, J.; Dall, J.; Exbrayat, J.F.; Ho Tong Minh, D.; Lomas, M.; Mariotti d’Alessandro, M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Exbrayat, J.F.; Bloom, A.A.; Carvalhais, N.; Fischer, R.; Huth, A.; MacBean, N.; Williams, M. Understanding the Land Carbon Cycle with Space Data: Current Status and Prospects. Surv. Geophys. 2019, 40, 735–755. [Google Scholar] [CrossRef]
- Saatchi, S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.; Salas, W.; Zutta, B.; Buermann, W.; Lewis, S.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Santoro, M.; Beer, C.; Cartus, O.; Schmullius, C.; Shvidenko, A.; McCallum, I.; Wegmüller, U.; Wiesmann, A. Retrieval of growing stock volume in boreal forest using hyper-temporal series of Envisat ASAR ScanSAR backscatter measurements. Remote Sens. Environ. 2011, 115, 490–507. [Google Scholar] [CrossRef]
- Herold, M.; Carter, S.; Avitabile, V.; Espejo, A.B.; Jonckheere, I.; Lucas, R.; McRoberts, R.E.; Næsset, E.; Nightingale, J.; Petersen, R.; et al. The Role and Need for Space-Based Forest Biomass-Related Measurements in Environmental Management and Policy. Surv. Geophys. 2019, 40, 757–778. [Google Scholar] [CrossRef]
- Banda, F.; Dall, J.; Tebaldini, S. Single and Multipolarimetric P-Band SAR Tomography of Subsurface Ice Structure. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2832–2845. [Google Scholar] [CrossRef]
- Banda, F.; Giudici, D.; Quegan, S.; Scipal, K. The Retrieval Concept of the Biomass Forest Biomass Prototype Processor. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8582–8585. [Google Scholar]
- ESA. Biomass Mission Requirements Document; EOP-SM/1645; European Space Agency: Noordwijk, The Netherlands, 2015. [Google Scholar]
- FAO. Assessment of the Status of the Development of the Standards for the Terrestrial Essential Climate Variables; GTOS Secretariat, UN Food and Agriculture Organisation: Rome, Italy, 2009. [Google Scholar]
- Philip, M. Measuring Trees and Forests, 2nd ed.; CAB International: Oxon, UK, 1994. [Google Scholar]
- Carreiras, J.M.B.; Quegan, S.; Le Toan, T.; Ho Tong Minh, D.; Saatchi, S.; Carvalhais, N.; Reichstein, M.; Scipal, K. Coverage of high biomass forests by the ESA BIOMASS mission under defense restrictions. Remote Sens. Environ. 2017, 196, 154–162. [Google Scholar] [CrossRef]
- Rogers, N.C.; Quegan, S.; Kim, J.S.; Papathanassiou, K.P. Impacts of Ionospheric Scintillation on the BIOMASS P-Band Satellite SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1856–1868. [Google Scholar] [CrossRef]
- Quegan, S.; Lomas, M.; Papathanassiou, K.P.; Kim, J.; Tebaldini, S.; Giudici, D.; Scagliola, M.; Guccione, P.; Dall, J.; Dubois-Fenandez, P.; et al. Calibration Challenges for the Biomass P-Band SAR Instrument. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8575–8578. [Google Scholar]
- Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Le Toan, T. The Impact of Temporal Decorrelation on BIOMASS Tomography of Tropical Forests. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1297–1301. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Le Toan, T.; Rocca, F.; Tebaldini, S.; Mariotti d’Alessandro, M.; Villard, L. Relating P-Band Synthetic Aperture Radar Tomography to Tropical Forest Biomass. IEEE Trans. Geosci. Remote Sens. 2014, 52, 967–979. [Google Scholar] [CrossRef]
- Villard, L.; Le Toan, T. Relating P-Band SAR Intensity to Biomass for Tropical Dense Forests in Hilly Terrain: γ0 or t0? IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 214–223. [Google Scholar] [CrossRef]
- Soja, M.J.; Sandberg, G.; Ulander, L.M.H. Regression-Based Retrieval of Boreal Forest Biomass in Sloping Terrain Using P-Band SAR Backscatter Intensity Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2646–2665. [Google Scholar] [CrossRef]
- Truong-Loi, M.L.; Saatchi, S.; Jaruwatanadilok, S. Soil Moisture Estimation Under Tropical Forests Using UHF Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1718–1727. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Lee, J.S. and Pottier, E.. Polarimetric Radar Imaging: From Basics to Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Brandl, S.; Mette, T.; Falk, W.; Vallet, P.; Rötzer, T.; Pretzsch, H. Static site indices from different national forest inventories: harmonization and prediction from site conditions. Ann. For. Sci. 2018, 75. [Google Scholar] [CrossRef]
- Kukkonen, M.; Maltamo, M.; Korhonen, L.; Packalen, P. Multispectral Airborne LiDAR Data in the Prediction of Boreal Tree Species Composition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3462–3471. [Google Scholar] [CrossRef]
- Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A Benchmark of Lidar-Based Single Tree Detection Methods Using Heterogeneous Forest Data from the Alpine Space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
- Meyer, V.; Saatchi, S.; Clark, D.B.; Keller, M.; Vincent, G.; Ferraz, A.; Espírito-Santo, F.; d’Oliveira, M.V.N.; Kaki, D.; Chave, J. Canopy area of large trees explains aboveground biomass variations across neotropical forest landscapes. Biogeosciences 2018, 15, 3377–3390. [Google Scholar] [CrossRef]
- Tang, S. Quantifying Differences in Forest Structures with Quantitative Structure Models from TLS Data. Master’s Thesis, UCL, London, UK, 2017. [Google Scholar]
- Saatchi, S.; Ramachandran, N.; Tebaldini, S.; Quegan, S.; Le Toan, T.; Papathanassiou, K.; Chave, J.; Shugart, H.; Jeffery, K.; White, L. Estimation of Tropical Forest Structure and Biomass from Airborne P-band Backscatter and TomoSAR Measurements. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Mariotti d’Alessandro, M.; Tebaldini, S.; Rocca, F. Phenomenology of Ground Scattering in a Tropical Forest Through Polarimetric Synthetic Aperture Radar Tomography. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4430–4437. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. IEE Proc. Radar, Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Tebaldini, S. Algebraic Synthesis of Forest Scenarios From Multibaseline PolInSAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4132–4142. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- Banda, F.; Mariotti d’Alessandro, M.; Tebaldini, S. Ground and Volume Decomposition as a Proxy for AGB from P-Band SAR Data. Remote Sens. 2020, 12, 240. [Google Scholar] [CrossRef]
- Mariotti d’Alessandro, M.; Tebaldini, S.; Quegan, S.; Soja, M.; Ulander, L.M.H. Interferometric Ground Notching of SAR Images for Estimating Forest Above Ground Biomass. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8797–8800. [Google Scholar]
- Mancon, S.; Giudici, D.; Tebaldini, S. The ionospheric effects mitigation in the BIOMASS mission exploiting multi-squint coherence supported by Faraday rotation. In Proceedings of the EUSAR 2018, 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018; pp. 1–6. [Google Scholar]
- Tebaldini, S.; Rocca, F.; Mariotti d’Alessandro, M.; Ferro-Famil, L. Phase Calibration of Airborne Tomographic SAR Data via Phase Center Double Localization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1775–1792. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Small, D. Flattening Gamma: Radiometric Terrain Correction for SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Deo, R.; Rossi, C.; Eineder, M.; Fritz, T.; Rao, Y.S. Framework for Fusion of Ascending and Descending Pass TanDEM-X Raw DEMs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3347–3355. [Google Scholar] [CrossRef]
- Mariotti d’Alessandro, M.; Tebaldini, S. Digital Terrain Model Retrieval in Tropical Forests Through P-Band SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Soja, M.J.; Mariotti d’Alessandro, M.; Quegan, S.; Tebaldini, S.; Ulander, L.M.H. Model-Based Estimation of Tropical Forest Biomass from Notch-Filtered P-Band Sar Backscatter. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8617–8620. [Google Scholar]
- Chave, J.; Davies, S.J.; Phillips, O.L.; Lewis, S.L.; Sist, P.; Schepaschenko, D.; Armston, J.; Baker, T.R.; Coomes, D.; Disney, M.; et al. Ground Data are Essential for Biomass Remote Sensing Missions. Surv. Geophys. 2019, 40, 863–880. [Google Scholar] [CrossRef]
- Silva, C.A.; Saatchi, S.; Garcia, M.; Labrière, N.; Klauberg, C.; Ferraz, A.; Meyer, V.; Jeffery, K.J.; Abernethy, K.; White, L.; et al. Comparison of Small- and Large-Footprint Lidar Characterization of Tropical Forest Aboveground Structure and Biomass: A Case Study From Central Gabon. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3512–3526. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Shaffer, S.; Edelstein, W.; Kim, Y.; Kumar, R.; Misra, T.; Bhan, R.; Sagi, R. The NASA-ISRO SAR (NISAR) mission dual-band radar instrument preliminary design. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3832–3835. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.A.; Skriver, H. Determining the Points of Change in Time Series of Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3007–3024. [Google Scholar] [CrossRef]
- Albinet, C.; Whitehurst, A.; Jewell, L.A.; Bugbee, K.; Laur, H.; Murphy, K.; Frommknecht, B.; Scipal, K.; Costa, G.; Jai, B.; et al. A Joint ESA-NASA Multi-mission Algorithm and Analysis Platform (MAAP) for Biomass, NISAR, and GEDI. Surv. Geophys. 2019, 40, 1017–1027. [Google Scholar] [CrossRef]
- Ulander, L.M.H. Radiometric Slope Correction of Synthetic-Aperture Radar Images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1115–1122. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Sabel, D.; Wagner, W. Optimisation of global grids for high-resolution remote sensing data. Comput. Geosci. 2014, 72, 84–93. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence Angle Normalization of Radar Backscatter Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1791–1804. [Google Scholar] [CrossRef]
- Soja, M.J.; Banda, F.; Ulander, L.M.H.; Mariotti d’Alessandro, M.; Tebaldini, S.; Quegan, S.; Scipal, K. Above-Ground Biomass Estimation with ESA’s 7th Earth Explorer Mission BIOMASS: Algorithm Basics and Performance over Tropical Forests. Remote Sens. Environ. in review.
- Kugler, F.; Lee, S.; Hajnsek, I.; Papathanassiou, K.P. Forest Height Estimation by Means of Pol-InSAR Data Inversion: The Role of the Vertical Wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Gatelli, F.; Monti Guamieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Le Toan, T.; Villard, L.; Dubois-Fernandez, P.C. Capabilities of BIOMASS Tomography for Investigating Tropical Forests. IEEE Trans. Geosci. Remote Sens. 2015, 53, 965–975. [Google Scholar] [CrossRef]
- DLR; Aresys; Politecnico di Milano. BIOMASS DEM Product Prototype Processor Critical Review of CoSCS and DEM Algorithms; ESA, ESTEC: Noordwijk, The Netherlands, 2019. [Google Scholar]
- Dixon, P.M. Bootstrap Resampling. In Encyclopedia of Environmetrics; American Cancer Society: Atlanta, GA, USA, 2006. [Google Scholar] [CrossRef]
- Flores, A.; Herndon, K.; Thapa, R.; Cherrington, E. The SAR Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; NASA Marshall Space Flight Center: Huntsville, AL, USA, 2019. [Google Scholar] [CrossRef]
- Mariotti d’Alessandro, M.; Tebaldini, S.; Soja, M.J.; Ulander, L.M.H.; Quegan, S.; Scipal, K. Interferometric Ground Cancellation for Above Ground Biomass Estimation. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Labrière, N.; Tao, S.; Chave, J.; Scipal, K.; Le Toan, T.; Abernethy, K.; Alonso, A.; Barbier, N.; Bissiengou, P.; Casal, T.; et al. In Situ Reference Datasets From the TropiSAR and AfriSAR Campaigns in Support of Upcoming Spaceborne Biomass Missions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3617–3627. [Google Scholar] [CrossRef]
- Verdin, K.L.; Godt, J.W.; Funk, C.; Pedreros, D.; Worstell, B.; Verdin, J. Development of a Global Slope Dataset for Estimation of Landslide Occurence Resulting from Earthquakes; U.S. Geological Survey, Open-File Report 2007-1188; U.S. Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Latham, J.; Cumani, R.; Rosati, I.; Bloise, M. FAO Global Land Cover (GLC-SHARE) Beta-Release 1.0 Database; Land and Water Division: Rome, Italy, 2014. [Google Scholar]
- Simard, M.; Naiara, P.; Fisher, J.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- FAO. The Forest Resources Assessment Programme (FRA) 2020—Terms and Definitions; FRA Working Paper 188; FAO: Rome, Italy, 2018. [Google Scholar]
- Rodríguez-Veiga, P.; Quegan, S.; Carreiras, J.; Persson, H.J.; Fransson, J.E.; Hoscilo, A.; Ziółkowski, D.; Stereńczak, K.; Lohberger, S.; Stängel, M.; et al. Forest biomass retrieval approaches from earth observation in different biomes. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 53–68. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. Research Pathways of Forest Above-Ground Biomass Estimation Based on SAR Backscatter and Interferometric SAR Observations. Remote Sens. 2018, 10, 608. [Google Scholar] [CrossRef]
- Tello, M.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Forest Structure Characterization From SAR Tomography at L-Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3402–3414. [Google Scholar] [CrossRef]
- Bai, Y.; Tebaldini, S.; Ho Tong Minh, D.; Yang, W. An Empirical Study on the Impact of Changing Weather Conditions on Repeat-Pass SAR Tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3505–3511. [Google Scholar] [CrossRef]
- Monteith, A.R.; Ulander, L.M.H. Temporal Survey of P- and L-Band Polarimetric Backscatter in Boreal Forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3564–3577. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).