A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam
Abstract
:1. Introduction
2. Materials and Methods
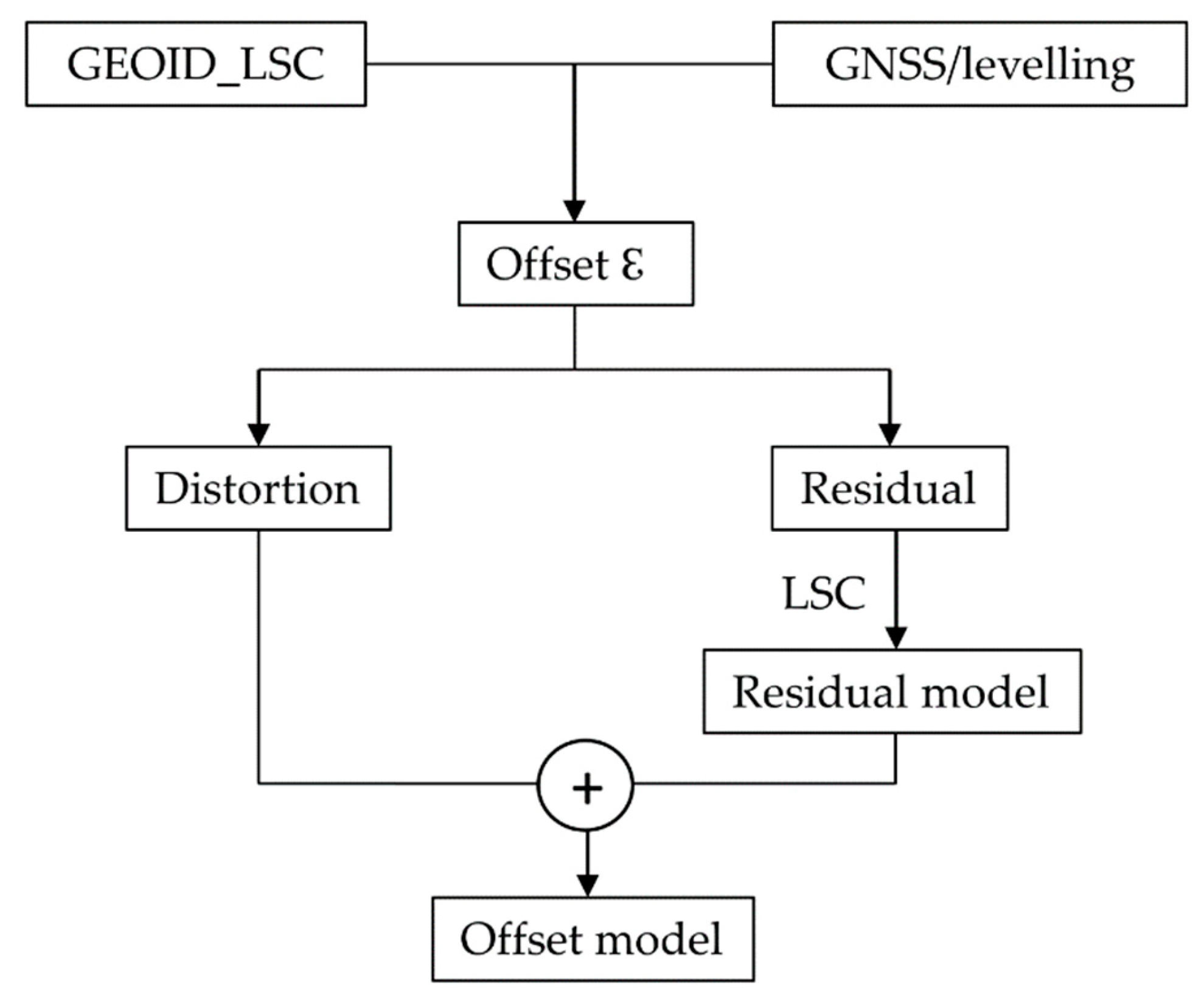
2.1. Offset Model Determination Methodology
- linear in φ and λ model:
- second-order polynomial model:
- third-order polynomial model:
- four parameter Helmert model:
2.2. Data for the Determination of the Offset Model
2.2.1. Gravimetric Quasigeoid Model (GEOID_LSC)
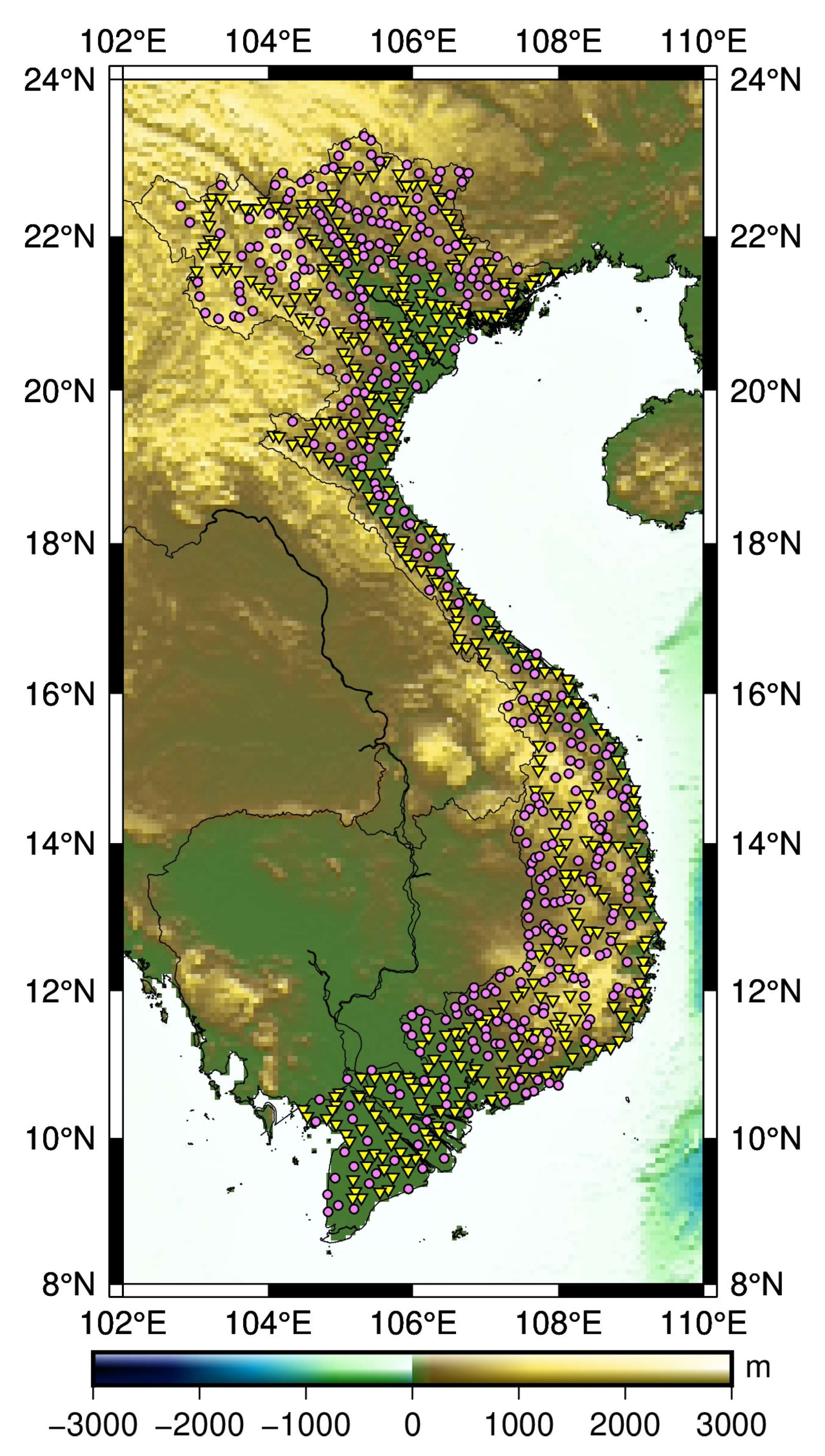
2.2.2. GNSS/Levelling Data
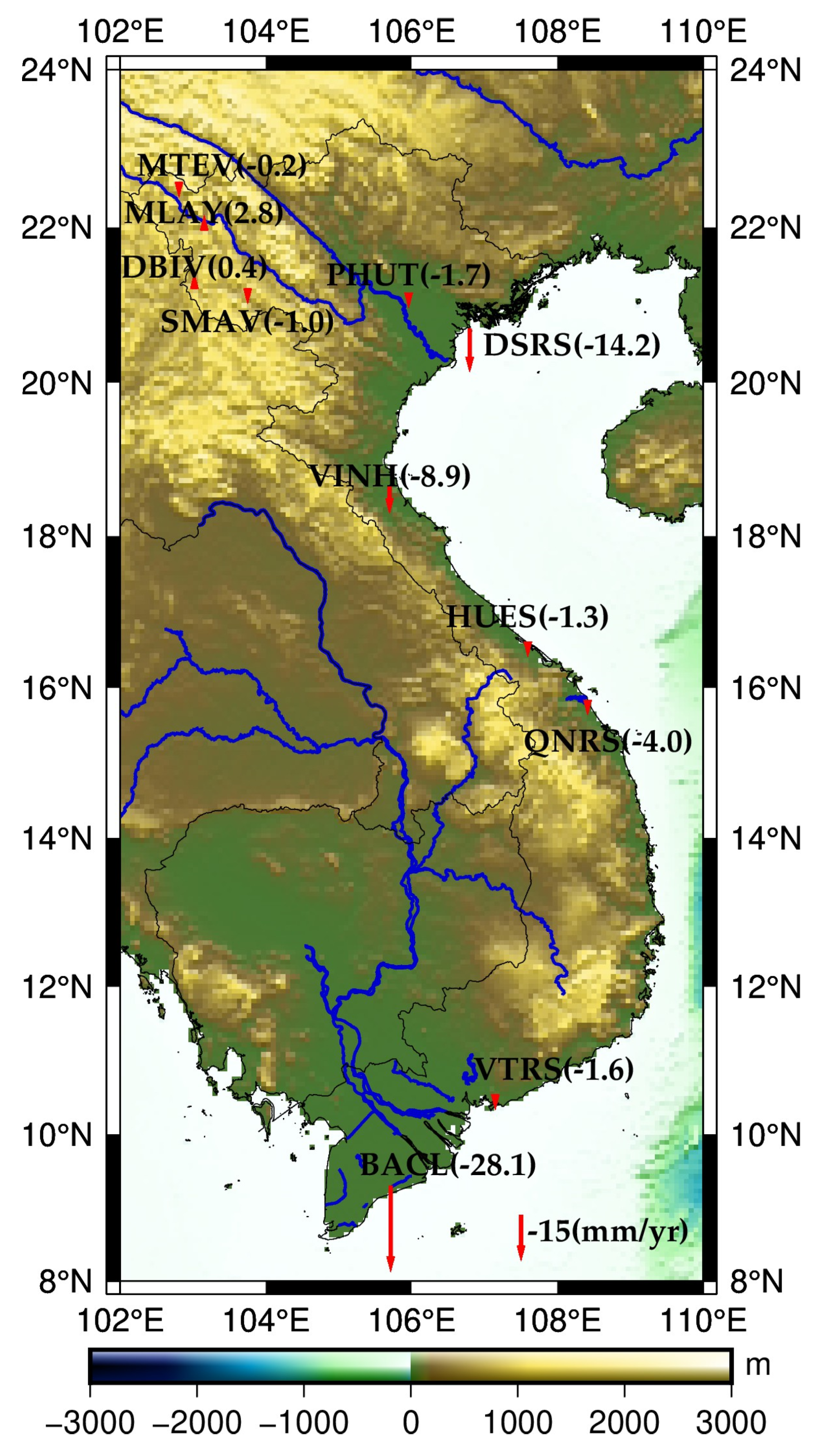
3. Land Subsidence in Vietnam
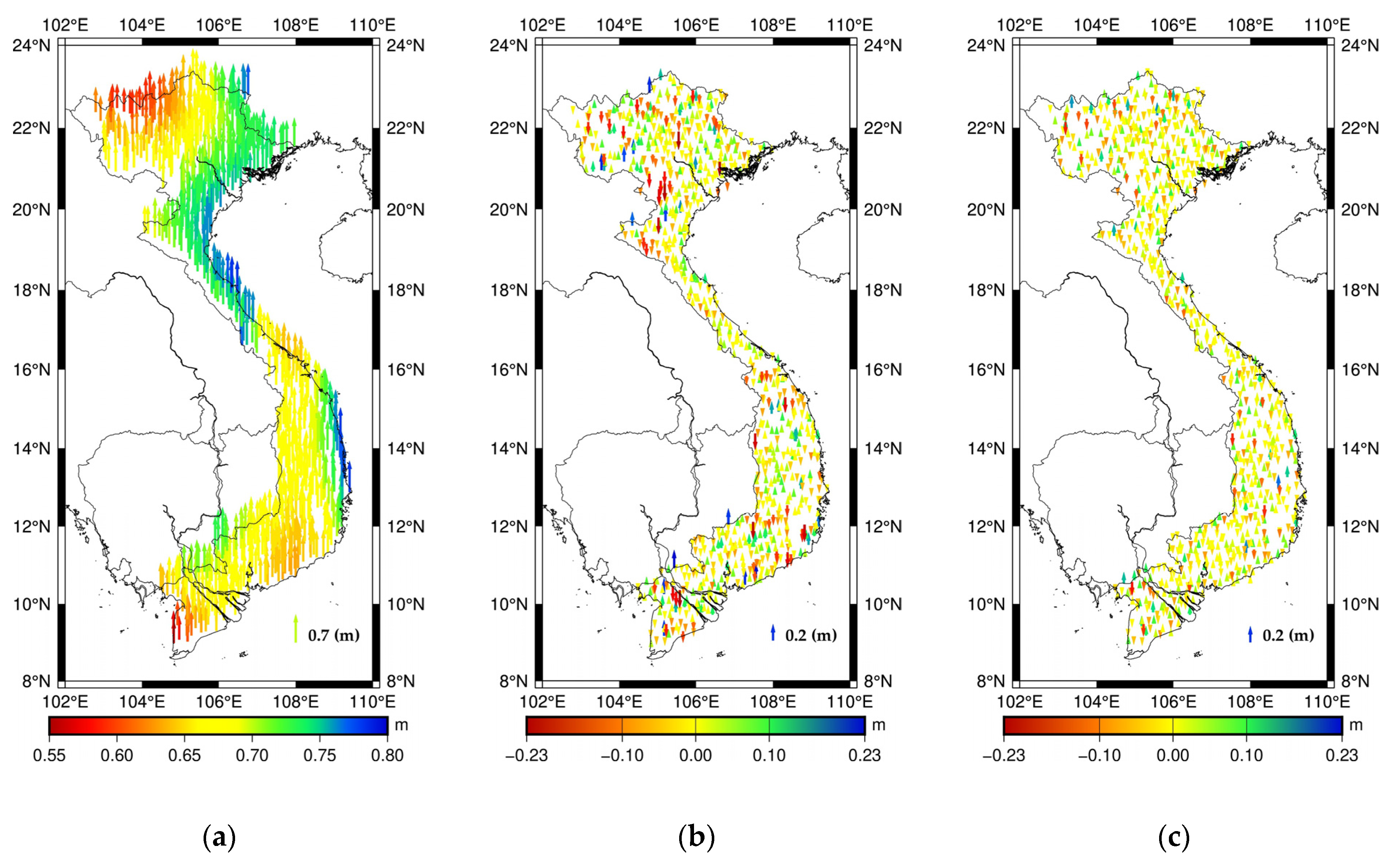
3.1. GNSS and InSAR Data
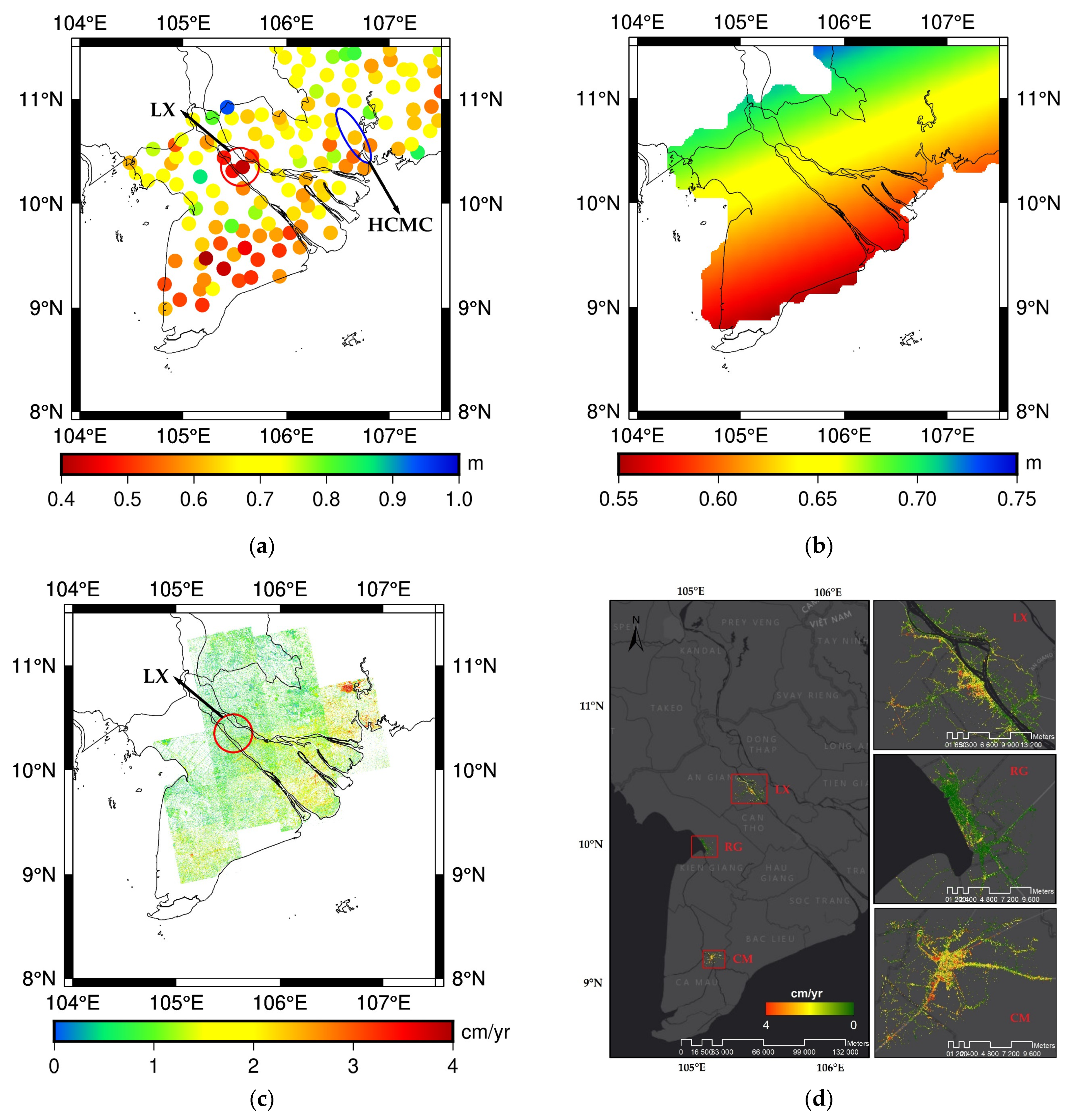
3.2. Land Subsidence and Correcting GNSS/Levelling Data in the Mekong Delta
- using all 802 GNSS/levelling points and calculating the homogeneous distortion parameter (case 1);
- using all 802 GNSS/levelling points and calculating two distortion parameters for two regions: southern (<17° in latitude) and northern part (>17° in latitude) (case 2).
4. Results and Discussion
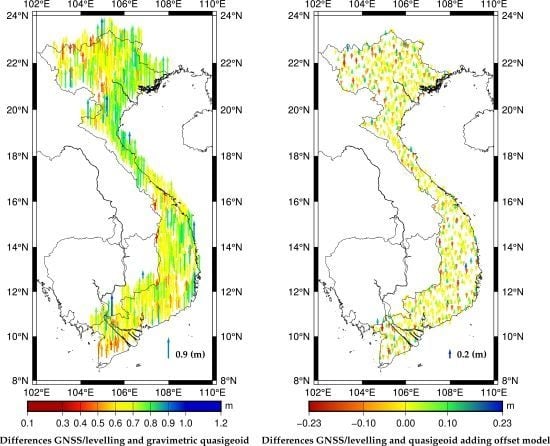
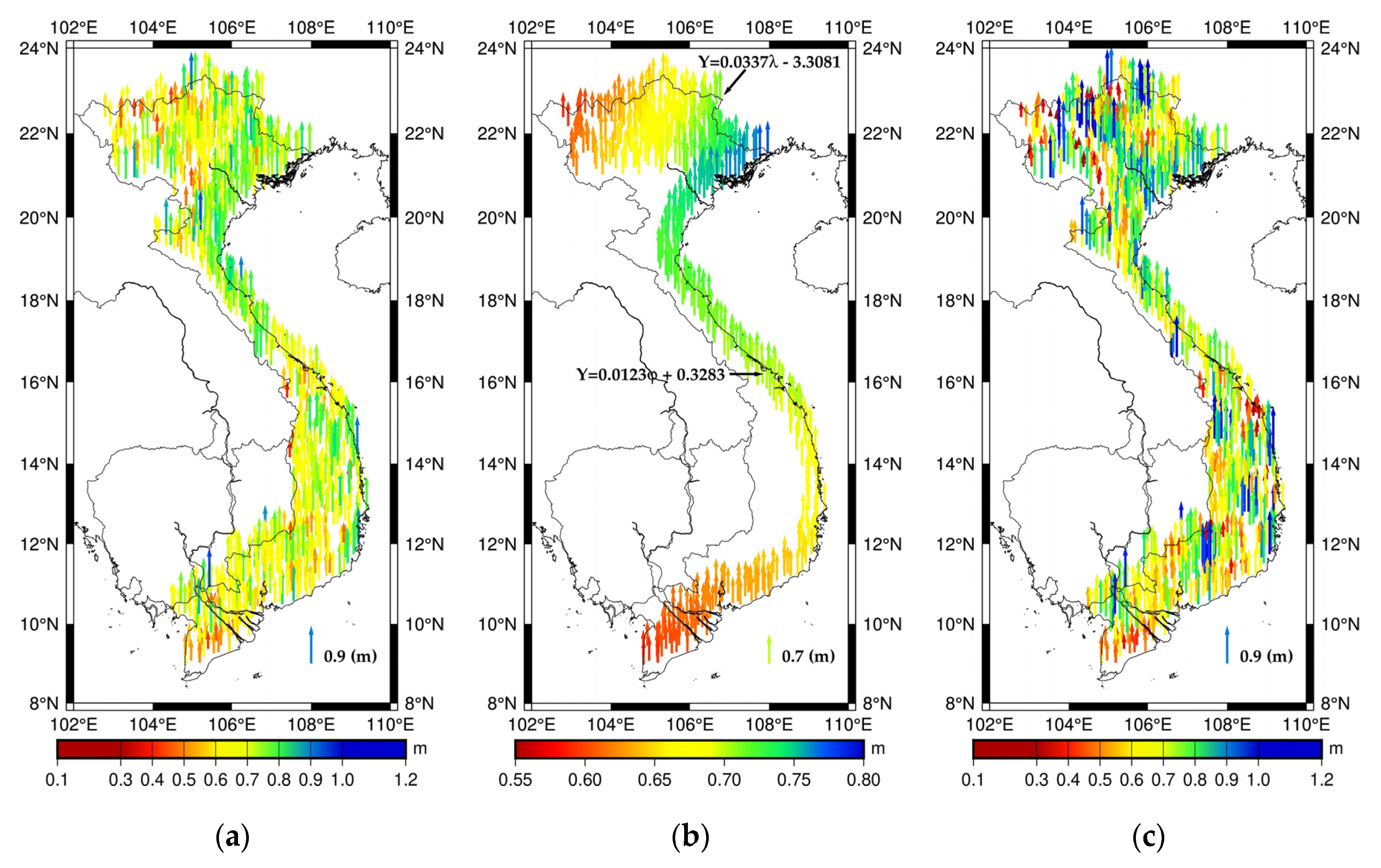
4.1. Offset Model Estimation and Validation
4.2. Estimation of the Geopotential Value W0 for the VLVD
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lemoine, F.G.; Kenyon, S.C.; Factor, J.K.; Trimmer, R.G.; Pavlis, N.K.; Chinn, D.S.; Cox, C.M.; Klosko, S.M.; Luthcke, S.B.; Torrence, M.H.; et al. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96. 1998; p. 584. Available online: https://ntrs.nasa.gov/search.jsp?R=19980218814 (accessed on 28 January 2020).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S. A high-resolution gravimetric quasigeoid model for Vietnam. Earth Planets Space 2019, 71, 65. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Sproule, D.; Goos, J.; Kirby, J.; Kuhn, M.; Claessens, S.J. Towards the new AusGeoid model. In Proceedings of SSC2005 Spatial Intelligence, Innovation and Praxis: The National Biennial Conference of the Spatial Sciences Institute, September 2005; Spatial Sciences Institute: Melbourne, Australia, 2005; ISBN 0-9581366-2-9. [Google Scholar]
- Brown, N.J.; Featherstone, W.E.; Hu, G.; Johnston, G.M. AUSGeoid09: A more direct and more accurate model for converting ellipsoidal heights to AHD heights. J. Spat. Sci. 2011, 56, 27–37. [Google Scholar] [CrossRef]
- Brown, N.J.; McCubbine, J.C.; Featherstone, W.E.; Gowans, N.; Woods, A.; Baran, I. AUSGeoid2020 combined gravimetric–geometric model: Location-specific uncertainties and baseline-length-dependent error decorrelation. J. Geod. 2018, 92, 1457–1465. [Google Scholar] [CrossRef] [Green Version]
- Kuroishi, Y.; Ando, H.; Fukuda, Y. A new hybrid geoid model for Japan, GSIGEO2000. J. Geod. 2002, 76, 428–436. [Google Scholar] [CrossRef]
- Miyahara, B.; Kodama, T.; Kuroishi, Y. Development of New Hybrid Geoid Model for Japan, “GSIGEO2011”. 2014, Volume 10. Available online: https://www.semanticscholar.org/paper/Development-of-new-hybrid-geoid-model-for-Japan-%2C-%E2%80%9C-Miyahara-Kodama/9218fa00c80813084355b096ea1efe84c2d21f1c (accessed on 28 January 2020).
- Lee, S.B.; Auh, S.C.; Seo, D.Y. Evaluation of global and regional geoid models in South Korea by using terrestrial and GNSS data. KSCE J. Civ. Eng. 2017, 21, 1905–1911. [Google Scholar] [CrossRef]
- Dumrongchai, P.; Wichienchareon, C.; Promtong, C. Local geoid modeling for Thailand. Int. J. Geoinform. 2012, 8, 15–26. [Google Scholar]
- Gatchalian, R.; Forsberg, R.; Olesen, A. PGM2016: A New Geoid Model for the Philippines; Report of National Mapping and Resource Information Authority (NAMRIA). Department of Environmental and Natural Resources, Republic of The Philippines: Quezon City, Philippines, 2016; p. 27. Available online: http://www.isgeoid.polimi.it/Geoid/Asia/Philippines/new_geoid_for_the_philippines.pdf (accessed on 28 January 2020).
- Ismail, M.K.; Din, A.H.M.; Uti, M.N.; Omar, A.H. Establishment of New Fitted Geoid Model in Universiti Teknologi Malaysia. Available online: https://www.researchgate.net/publication/328683742 (accessed on 22 November 2018).
- Chen, Y.-Q.; Luo, Z. A hybrid method to determine a local geoid model—Case study. Earth Planets Space 2004, 56, 419–427. [Google Scholar] [CrossRef] [Green Version]
- Entin, I.I. Main systematic errors in precise levelling. Bull. Geod. 1959, 52, 37–45. [Google Scholar] [CrossRef]
- Geodetic Leveling and Its Applications—Vanicek—1980—Reviews of Geophysics—Wiley Online Library. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/RG018i002p00505 (accessed on 22 November 2019).
- Amos, M. New Zealand vertical datum 2009. New Zealand Surv. 2010, 300, 5–16. [Google Scholar]
- Hayden, T.; Amjadiparvar, B.; Rangelova, E.; Sideris, M.G. Estimating Canadian vertical datum offsets using GNSS/levelling benchmark information and GOCE global geopotential models. J. Geod. Sci. 2013, 2, 257–269. [Google Scholar] [CrossRef] [Green Version]
- Amjadiparvar, B.; Rangelova, E.V.; Sideris, M.G.; Véronneau, M. North American height datums and their offsets: The effect of GOCE omission errors and systematic levelling effects. J. Appl. Geod. 2013, 7, 39–50. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Filmer, M.S. A New GPS-based evaluation of distortions in the Australian Height Datum in Western Australia. J. R. Soc. West. Aust. 2008, 91, 199–206. [Google Scholar]
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A. Groundwater extraction, land subsidence, and sea-level rise in the Mekong Delta, Vietnam. Environ. Res. Lett. 2014, 9, 084010. [Google Scholar] [CrossRef]
- Minderhoud, P.S.J.; Erkens, G.; Pham, V.H.; Bui, V.T.; Erban, L.; Kooi, H.; Stouthamer, E. Impacts of 25 years of groundwater extraction on subsidence in the Mekong delta, Vietnam. Environ. Res. Lett. 2017, 12, 064006. [Google Scholar] [CrossRef]
- Reyes, R.B.; Nagai, M.; Kamiya, Y.; Tipdecho, T.; Ninsawat, S. Effect of sea level rise in the validation of geopotential/geoid models in Metro Manila, Philippines. Surv. Rev. 2015, 47, 211–219. [Google Scholar] [CrossRef]
- Kasenda, A.; Kearsley, A.H.W. Towards the Establishment of an Indonesian Unified Vertical Datum. In Vertical Reference Systems; Drewes, H., Dodson, A.H., Fortes, L.P.S., Sánchez, L., Sandoval, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 334–338. [Google Scholar]
- Amos, M.J.; Featherstone, W.E. Unification of New Zealand’s local vertical datums: Iterative gravimetric quasigeoid computations. J. Geod. 2009, 83, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Rapp, R.H.; Balasubramania, N. A Conceptual Formulation of a World Height System; Department of Geodetic Science and Surveying, The Ohio State University: Columbus, OH, USA, 1992. [Google Scholar]
- Tran, T.; Nguyen, X.H.; Le, Q.H.; Doan, T.T.H. Updated trend of change of sea level of the east sea, Vietnam. Sci. Tech. Hydro-Meteorol. J. 2015, 657, 25–30. [Google Scholar]
- Sánchez, L.; Čunderlík, R.; Dayoub, N.; Mikula, K.; Minarechová, Z.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. A conventional value for the geoid reference potential $$W {0}$$W0. J. Geod. 2016, 90, 815–835. [Google Scholar] [CrossRef]
- Fotopoulos, G. An Analysis on the Optimal Combination of Geoid, Orthometric and Ellipsoidal Height Data. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, December 2003. [Google Scholar]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-211-33544-4. [Google Scholar]
- NIMA. Deparment of Defense World Geodectic System 1984. 2000, p. 169. Available online: https://earth-info.nga.mil/GandG/publications/tr8350.2/wgs84fin.pdf (accessed on 28 January 2020).
- Iliffe, J.C.; Ziebart, M.; Cross, P.A.; Forsberg, R.; Strykowski, G.; Tscherning, C.C. Osgm02: A New Model for Converting Gps-Derived Heights to Local Height Datums in Great Britain and Ireland. Surv. Rev. 2003, 37, 276–293. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs; DTU Space: Copenhagen, Denmark, 2008. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2005RG000183 (accessed on 28 January 2020). [CrossRef] [Green Version]
- Becker, J.J.; Sandwell, D.T.; Smith, W.H.F.; Braud, J.; Binder, B.; Depner, J.; Fabre, D.; Factor, J.; Ingalls, S.; Kim, S.-H.; et al. Global Bathymetry and Elevation Data at 30 Arc Seconds Resolution: SRTM30_PLUS. Mar. Geod. 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Pham, H.L. Final Report: Research on Establishing the Height System Unification for Vietnam on the Basis without Using the Mean Sea Level; The Vietnam Institute of Geodesy and Cartography (VIGAC): Hanoi, Vietnam, 2009. (In Vietnamese) [Google Scholar]
- Wessel, P.; Smith, W.H.F. New, improved version of generic mapping tools released. EOS Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]
- Drinkwater, M.R.; Floberghagen, R.; Haagmans, R.; Muzi, D.; Popescu, A. GOCE: ESA’s First Earth Explorer Core Mission. In Earth Gravity Field from Space—From Sensors to Earth Sciences; Space Sciences Series of ISSI; Springer: Berlin/Heidelberg, Germany, 2003; pp. 419–432. ISBN 978-90-481-6334-2. [Google Scholar]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Lemoine, J.-M.; Marty, J.-C.; Mulet, S.; Rio, M.-H.; Bonvalot, S. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys. Res. Lett. 2014, 41, 7508–7514. [Google Scholar] [CrossRef] [Green Version]
- Featherstone, W.E.; Lyon, T.J.; McCubbine, J.C. Potentially Misleading GPS Leveling–Based Assessment of Gravimetric Geoid or Quasigeoid Models due to Vertical Land Motion and Different GPS Processing Software. J. Surv. Eng. 2019, 145, 04019015. [Google Scholar] [CrossRef]
- Marty, J.C. Algorithmic Documentation of the GINS Software. Available online: https://www5.obs-mip.fr/wp-content-omp/uploads/sites/28/2017/11/GINS_Algo_2013.pdf (accessed on 28 January 2020).
- Copernicus Emergency Management Service. Available online: https://emergency.copernicus.eu/mapping/list-of-components/EMSN057 (accessed on 19 November 2019).
- Minh, D.H.T.; Van Trung, L.; Toan, T.L. Mapping Ground Subsidence Phenomena in Ho Chi Minh City through the Radar Interferometry Technique Using ALOS PALSAR Data. Remote Sens. 2015, 7, 8543–8562. [Google Scholar] [CrossRef] [Green Version]
- Kotsakis, C.; Katsambalos, K.; Ampatzidis, D. Estimation of the zero-height geopotential level WoLVDin a local vertical datum from inversion of co-located GPS, leveling and geoid heights: A case study in the Hellenic islands. J. Geod. 2012, 86, 423–439. [Google Scholar] [CrossRef]
- Tocho, C.; Vergos, G.S. Estimation of the Geopotential Value W0 for the Local Vertical Datum of Argentina Using EGM2008 and GPS/Levelling Data W0LVD. In IAG 150 Years; Rizos, C., Willis, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 271–279. [Google Scholar]
- Vergos, G.S.; Erol, B.; Natsiopoulos, D.A.; Grigoriadis, V.N.; Işık, M.S.; Tziavos, I.N. Preliminary results of GOCE-based height system unification between Greece and Turkey over marine and land areas. Acta Geod. Geophys. 2018, 53, 61–79. [Google Scholar] [CrossRef]
- Gerlach, C.; Rummel, R. Global height system unification with GOCE: A simulation study on the indirect bias term in the GBVP approach. J. Geod. 2013, 87, 57–67. [Google Scholar] [CrossRef]
- Gatti, A.; Reguzzoni, M.; Venuti, G. The height datum problem and the role of satellite gravity models. J. Geod. 2013, 87, 15–22. [Google Scholar] [CrossRef]
- Amjadiparvar, B.; Rangelova, E.; Sideris, M.G. The GBVP approach for vertical datum unification: Recent results in North America. J. Geod. 2016, 90, 45–63. [Google Scholar] [CrossRef]
| No | Country, Region | Name | Year | STD (cm) | Geoid Type | Reference |
|---|---|---|---|---|---|---|
| 1 | Australia | AUSGeoid98 | 2005 | 11.8 | Hybrid quasigeoid | [4] |
| AUSGeoid09 | 2009 | 3.0 | Hybrid quasigeoid | [5] | ||
| AUSGeoid2020 | 2018 | 2.7 | Hybrid quasigeoid | [6] | ||
| 2 | Japan | GSIGEO2000 | 2002 | 4.0 | Hybrid geoid | [7] |
| GSIGEO2011 | 2014 | 1.8 | Hybrid geoid | [8] | ||
| 3 | South Korea | KNGeoid13 | 2013 | 5.4 | Hybrid geoid | [9] |
| KNGeoid14 | 2014 | 5.2 | Hybrid geoid | [9] | ||
| 4 | Thailand | THAI12H | 2012 | 15.8 | Hybrid geoid | [10] |
| 5 | Philippines | PGM2016 | 2016 | 2.2 | Hybrid geoid | [11] |
| 6 | Peninsular (Malaysia) | VMGEOID04 | 2018 | 5.0 | Hybrid geoid | [12] |
| Sabah and Sarawak (Malaysia) | EMGEOID05 | 2018 | 10.0 | Hybrid geoid | [12] | |
| 7 | Hong Kong | HKGEOID-2000 | 2004 | 1.7 | Hybrid geoid | [13] |
| 8 | Shenzhen | SZGEOID-2001 | 2004 | 1.4 | Hybrid geoid | [13] |
| Absolute Differences | ||||||
| Mean | STD | Max | Min | Outlier Points | ||
| ζGNSS/levelling – ζLSC (812 points) | 0.680 | 0.097 | 0.987 | 0.310 | 9 | |
| ζGNSS/levelling – ζLSC (excluding outliers) (803 points) | 0.682 | 0.092 | 0.937 | 0.396 | 0 | |
| ζGNSS/levelling – ζDIR/EGM+RTM (803 points) | 0.682 | 0.168 | 1.138 | 0.119 | ||
| ζGNSS/levelling – ζLSC (North-east part) (190 points) | 0.705 | 0.077 | 0.879 | 0.459 | ||
| ζGNSS/levelling – ζLSC (Southern, <11°) (120 points) | 0.634 | 0.092 | 0.937 | 0.402 | ||
| Relative Differences | ||||||
| Mean | STD | Max | Min | Outlier third-order | Outlier fourth-order | |
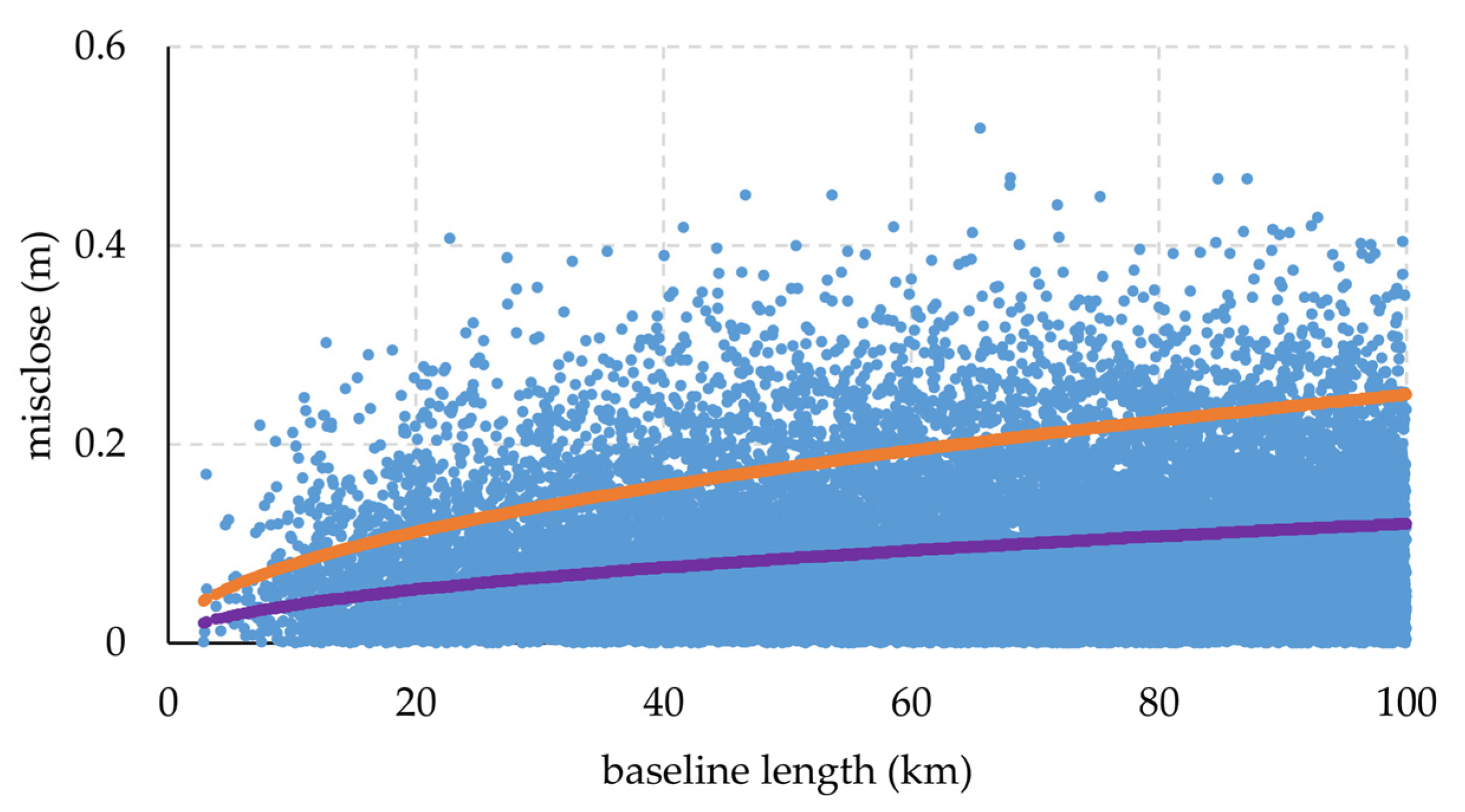
| ∆ζGNSS/levelling – ∆ζLSC (803 points) (21,423 baselines) | 0.087 | 0.071 | 0.518 | 0 | 8153 (38.06%) | 2052 (9.58%) |
| 10 km | 20 km | 30 km | 40 km | 50 km | 60 km | 70 km | 80 km | 90 km | 100 km | All | |
| NoB | 96 | 760 | 1356 | 1776 | 2215 | 2505 | 2845 | 3068 | 3334 | 3468 | 21,423 |
| mean | 0.055 | 0.065 | 0.077 | 0.082 | 0.084 | 0.089 | 0.089 | 0.091 | 0.090 | 0.093 | 0.087 |
| STD | 0.045 | 0.055 | 0.063 | 0.066 | 0.070 | 0.072 | 0.073 | 0.072 | 0.073 | 0.074 | 0.071 |
| Max | 0.219 | 0.302 | 0.407 | 0.394 | 0.451 | 0.451 | 0.518 | 0.449 | 0.467 | 0.428 | 0.518 |
| min | 0.001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Northern Part | |||||||||||
| NoB | 34 | 231 | 376 | 530 | 647 | 751 | 854 | 868 | 1004 | 998 | 6294 |
| mean | 0.044 | 0.075 | 0.080 | 0.084 | 0.083 | 0.089 | 0.092 | 0.094 | 0.093 | 0.093 | 0.089 |
| STD | 0.030 | 0.061 | 0.066 | 0.066 | 0.069 | 0.071 | 0.071 | 0.069 | 0.072 | 0.072 | 0.070 |
| Max | 0.120 | 0.295 | 0.322 | 0.316 | 0.390 | 0.400 | 0.468 | 0.396 | 0.392 | 0.404 | 0.468 |
| min | 0.001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Points Near the Coast (within 50 km from the coastline) | |||||||||||
| NoB | 18 | 202 | 312 | 357 | 380 | 369 | 347 | 361 | 336 | 321 | 3003 |
| mean | 0.042 | 0.055 | 0.067 | 0.073 | 0.072 | 0.079 | 0.078 | 0.074 | 0.074 | 0.75 | 0.073 |
| STD | 0.037 | 0.049 | 0.055 | 0.066 | 0.067 | 0.067 | 0.065 | 0.060 | 0.069 | 0.069 | 0.064 |
| Max | 0.138 | 0.290 | 0.388 | 0.333 | 0.418 | 0.363 | 0.384 | 0.408 | 0.467 | 0.352 | 0.467 |
| min | 0.007 | 0 | 0 | 0 | 0 | 0.001 | 0 | 0 | 0 | 0 | 0 |
| Mean | STD | Max | Min | Outlier Points | |
|---|---|---|---|---|---|
| ζGNSS/levelling – ζLSC (Southern, <11°) (120 points) | 0.634 | 0.092 | 0.937 | 0.402 | |
| ζGNSS/levelling – ζLSC (>11°) (683 points) | 0.690 | 0.089 | 0.933 | 0.396 | |
| ζGNSS/levelling_cor – ζLSC (Southern, <11°) (120 points) | 0.664 | 0.085 | 0.937 | 0.459 | |
| ζGNSS/levelling_cor – ζLSC (803 points) | 0.686 | 0.089 | 0.937 | 0.396 | 1 |
| ζGNSS/levelling_cor – ζLSC (excluding outliers) (802 points) | 0.687 | 0.088 | 0.937 | 0.423 |
| Mean | STD | Max | Min | Outlier Points | |
|---|---|---|---|---|---|
| Linear (802 points) | 0 | 0.087 | 0.285 | −0.296 | |
| Second-order (802 points) | 0 | 0.085 | 0.265 | −0.326 | |
| Third-order (802 points) | 0 | 0.082 | 0.262 | −0296 | |
| Helmert model (802 points) | 0 | 0.086 | 0.285 | −0.316 | |
| case 2 (Third-order) (802 points) | 0 | 0.078 | 0.252 | −0.288 | 6 |
| case 2 (Third-order) outlier (796 points) | 0 | 0.075 | 0.225 | −0.223 |
| Absolute Differences | ||||||
| Mean | STD | Max | Min | Outlier Points | ||
| ζGNSS/levelling – ζLSC-ε (796 points) (cross-validation) | 0 | 0.065 | 0.250 | −0.291 | 17 | |
| ζGNSS/levelling – ζLSC-ε (779 points) (excluding outliers) (cross-validation) | 0 | 0.059 | 0.170 | −0.170 | ||
| ζGNSS/levelling – ζLSC-ε (779 points) | 0 | 0.034 | 0.099 | −0.109 | ||
| ζGNSS/levelling – ζLSC-ε (Hanoi) (32 points) | −0.004 | 0.047 | 0.109 | −0.092 | ||
| ζGNSS/levelling – ζLSC-ε (HCMC) (29 points) | −0.001 | 0.055 | 0.104 | −0.139 | ||
| Relative Differences | ||||||
| Mean | STD | Max | Min | Outlier 3rd Order | Outlier 4th Order | |
| ∆ζGNSS/levelling – ∆ζLSC-∆ε (779 points) (20,243 baselines) | 0.026 | 0.020 | 0.109 | 0 | 377 (1.86%) | 14 (0.07%) |
| ∆ζGNSS/levelling – ∆ζLSC-∆ε (Hanoi) (469 baselines) | 0.024 | 0.018 | 0.074 | 0.003 | 8 | 0 |
| ∆ζGNSS/levelling – ∆ζLSC-∆ε (HCMC) (384 baselines) | 0.025 | 0.019 | 0.085 | 0.085 | 13 | 0 |
| Mean | STD | Max | Min | |
|---|---|---|---|---|
| Null model | 0.688 | 0.083 | 0.912 | 0.435 |
| Third-order | 0.693 | 0.075 | 0.897 | 0.458 |
| Third-order (two parameters) | 0.689 | 0.071 | 0.902 | 0.478 |
| 6.60 ± 0.70 (m2s−2) | 62,636,846.81 ± 0.70 (m2s−2) | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, D.T.; Bruinsma, S.; Bonvalot, S.; Remy, D.; Vergos, G.S. A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam. Remote Sens. 2020, 12, 817. https://doi.org/10.3390/rs12050817
Vu DT, Bruinsma S, Bonvalot S, Remy D, Vergos GS. A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam. Remote Sensing. 2020; 12(5):817. https://doi.org/10.3390/rs12050817
Chicago/Turabian StyleVu, Dinh Toan, Sean Bruinsma, Sylvain Bonvalot, Dominique Remy, and Georgios S. Vergos. 2020. "A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam" Remote Sensing 12, no. 5: 817. https://doi.org/10.3390/rs12050817
APA StyleVu, D. T., Bruinsma, S., Bonvalot, S., Remy, D., & Vergos, G. S. (2020). A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam. Remote Sensing, 12(5), 817. https://doi.org/10.3390/rs12050817