Abstract
The goal of this work is to present a set of statistical tests that offer a formal procedure to make a decision as to whether a set of thematic quality specifications of a product is fulfilled within the philosophy of a quality control process. The tests can be applied to classification data in thematic quality control, in order to check if they are compliant with a set of specifications for correctly classified elements (e.g., at least 90% classification correctness for category A) and maximum levels of poor quality for confused elements (e.g., at most 5% of confusion is allowed between categories A and B). To achieve this objective, an accurate reference is needed. This premise entails changes in the distributional hypothesis over the classification data from a statistical point of view. Four statistical tests based on the binomial, chi-square, and multinomial distributions are stated, to provide a range of tests for controlling the quality of product per class, both categorically and globally. The proposal is illustrated with a complete example. Finally, a guide is provided to clarify the use of each test, as well as their pros and cons.
1. Introduction
The thematic component of a spatial data product is expressed as a set of classes, or category assignments (e.g., land-cover and land-use classes, geological and pedological classes, and so on). This thematic component of spatial data is of great importance in environmental modeling, decision making, climate change assessment, and so on. It is well known that spatial data are not error-free [1,2,3], and that spatial data sets represent a significant source of error in any analysis that uses them as input [4,5].
The term thematic accuracy has been broadly used when speaking about the quality of the thematic component of spatial data. The International Standard ISO 19,157 [6] defines it as the accuracy of quantitative attributes and the correctness of non-quantitative attributes and the classifications of features and their relationships. Classification correctness is defined, by the same standard, as the comparison of the classes assigned to features or their attributes to a universe of discourse (e.g., ground truth or reference data) [6]. Thus, prior to a classification correctness assessment, a well-defined classification scheme is needed. A classification scheme has two critical components [7]: (i) a set of labels, and (ii) a set of rules for assigning labels. In this way, in the case of a crisp classification, a unique assignment of classes is achieved if the classes (labels) are mutually exclusive (there are no overlaps) and exhaustive (there are no omissions or commissions of classes).
Evaluation of the thematic accuracy of spatial data is a subject of interest [8]. ISO 19,157 provides a general quality evaluation method which can be applied to thematic data and several measures for reporting the results of a thematic accuracy evaluation. For instance, Appendix D of ISO 19,157 contains some measures that can be used for thematic accuracy assessment, one of them being the error matrix or confusion matrix (see measure #62 in ISO 19157).
On the other hand, a data product specification must also include a quality evaluation method [9] to assure standardization of the assessment procedure. Considering thematic quality control, users or experts can establish a set of quality requirements that agree with the goal of the product. In addition, the fulfillment of these quality requirements has to be carried out using statistical procedures. For instance, in remote sensing, thematic correctness requirements/specifications are typically on the order of 85%–90%, as suggested by the United States Geological Survey Circular 671 [10]. Other examples of thematic quality requirements for attributes and classifications are those established by the United States Department of Agriculture for Physiognomic classes and subclasses, alliance types and associations, cover and dominance types, and tree canopy closure and diameter classes [11].
Both elements (classification scheme and quality requirements) must be a key part of the specifications of the product, in the sense of ISO 19,131 [12]. These specifications should contain a complete and well-explained classification scheme as well as a set of quality levels required for each category and each misclassification between categories. To provide measures for the thematic accuracy assessment and to determine whether a set of specifications are fulfilled through formal procedures, statistical tools must be applied. Thus, both the measures and procedures have to be based on the distributional hypothesis of the thematic classification results.
At this point, it should be pointed out that there is a difference between the appropriate statistical analysis for comparing two data sets, neither of which is considered correct, and that for comparing a product with a reference set that is considered accurate. In the first situation, assuming independence and randomness, the sample units are classified according to two criteria/analysts/times or similar and the results of the cross-classification are random by nature, as no restriction exists in their distribution. Such classification results are commonly expressed using a contingency table/confusion matrix, in order to summarize them. In this case, the multinomial distribution is the appropriate statistical base to deal with any subsequent statistical technique/method. In this context, it is included the global indexes in Append D of ISO 19,157 as the overall accuracy index, the kappa index, and so on.
However, if any kind of restriction in the classification procedure is present, the previous distributional hypothesis is false and another way to analyze the data properly is needed. One example of such a restriction is having an accurate reference. Very briefly, the reason for this is that the knowledge of the “true/accurate” label of sample units creates the posterior classification to only produce “agreement” with classes or “confusions” with other classes in the same column (supposing reference data is by column). So, complete randomness is not possible, and the multinomial distribution only can be assumed by columns, not globally (see [13] for a detailed explanation). When a reference can be considered accurate, the consequence of this fact is the key, as it provokes a change in the distributional hypothesis for the classification results. An understanding of this assumption is crucial and, for this reason, readers are referred to [13] for a deeper justification. Having a simple random sampling permits us to define a multinomial (binomial, if needed) distribution. This is a crucial assumption in hypothesis testing procedures. However, other sampling designs can be conducted (e.g., stratified sampling, clustering sampling, and so on) when the goal is to carry out estimations. An example of this is to estimate area or a land cover class (see formula 2 in [14,15], among many other papers). This latter situation is associated with the context of finite population sampling, and testing problems do not make sense here. Thus, our proposal must be understood as belonging to hypothesis testing procedures. In light of the above, a change in the statistical foundation forces a new approach for thematic accuracy assessment and thematic quality control procedures.
Regarding thematic quality control, we assume that such a control can be made by establishing a set of specifications for the product that apply two criteria: (i) minimum quality levels for the correctly classified elements (e.g., at least 90% of classification correctness for category A), and (ii) maximum levels of poor quality for confused elements (e.g., at most 5% of confusion allowed between categories A and B; for an example see Table 2 of the next section). Note that not all quality levels for confusions involve individual categories. We claim the possibility of allowing confusions between a particular category and the combination of two or more categories.
Therefore, in what follows, we will assume that an accurate reference and a set of quality specifications are given. The goal of this work is to propose a set of statistical tests for determining whether a set of quality requirements are fulfilled. This addresses the question: Does the product agree with the reference, according to the set of established specifications? Conclusions about the thematic quality derived from the proposal are not directly comparable with those obtained from the classical methods. The reason is obvious: the statistical foundation is different. As will be seen, our approach is more restrictive and demanding, as it involves the fulfillment of a set of quality specifications by columns and/or globally. In this sense, our proposal offers a new way to deal with thematic quality control.
To achieve this objective, Section 2 presents the statistical base needed to deal with classification data when the reference data are accurate. Section 3 presents four statistical tests and their use for thematic quality control, in the sense of agreement with the set of specifications of the product. Section 4 presents an example of applications of the tests, based on an example of classification data and a set of specifications defined for this purpose. A discussion about the statistical tests and results is presented in Section 5 and, finally, some general conclusions are included in Section 6.
2. Statistical Foundation of Proposal
A classification data set is a set of values accounting for the degree of agreement between paired observations in classes/categories of a controlled data set (CDS), and the same classes/categories of a reference data set (RDS). The usual way to summarize them is by using a contingency table. Table 1 shows an example with four classes, where the reference is located by columns and the product (or data classification) is located by rows.

Table 1.
Example of confusion matrix (see [16], pg. 242).
Having an accurate reference alters the statistical foundation when managing classification results. The reader is referred to [13] for a better understanding of the role of an accurate reference. For the sake of completeness, we briefly summarize this key point: Suppose the accurate RDS is located by column. If the reference data are considered as the truth, the total number of elements we know that belong to a particular category can be correctly classified or confused with other categories, but will always be located in the same column and never in another different column (category). So, the fact of having fixed the column marginal (and not randomly), from a statistical point of view, invalidates the background model of a global multinomial (for the entire confusion matrix), but allows us to deal with the classifications by columns as independent multinomial distributions. In [13], such a situation was called a Quality Control Column Set (QCCS). Figure 1 applies this idea to Table 1.
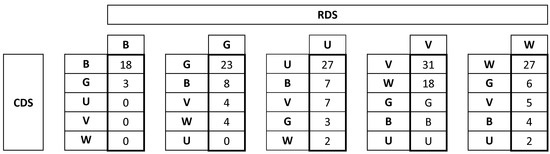
Figure 1.
The QCCS applied to data from Table 1.
The QCCS approach provides a new perspective, which allows (i) carrying out controls centered on categories; (ii) establishing quality levels on each category; and (iii) establishing limits to the presence of confusions between categories. To illustrate this idea, let us consider the set of specifications given in Table 2. These specifications are associated with classification data in Table 1 and are chosen only for the purpose of providing an example.

Table 2.
Example of specifications: quality levels required for each category and the percentage of misclassifications allowed between classes.
As can be seen in Table 2, we have supposed high percentages of correctly classified items (from ≥70% to ≥85%), a range of percentages in some misclassifications (from ≤10% to ≤20%), and some other, almost non-existent misclassifications (around ≤2%). Note that it has been decided to group the classes “Grazing Land” and “Vegetation” into a single class, “Grazing Land/Vegetation”. Part of the misclassification levels group two or more categories. To our knowledge, this type of thematic quality control is possible only when using an accurate RDS; that is, under a QCCS.
3. Notation for the Application of QCCS
In this section, we recall the mathematical notation underlying a contingency table and under a multinomial distribution. Let be the labels of the true categories in the RDS and be the labels of assigned categories in the CDS by the classification process. The most frequent number of categories, , is between 3 and 7, although there are matrices that reach up to 40 categories [17]. Usually, RDS and CDS are located by columns and by rows, respectively. Thus, the contingency table is a squared matrix when the adscription of an item into the cell implies that an element belonging to category j of the RDS is classified as belonging to category i of the CDS, and indicates the number of items assigned into the cell , . The diagonal elements contain the correctly classified items in each category, and the off-diagonal elements contain the number of confusions between categories. Table 3 shows the corresponding notation.

Table 3.
Notation in a contingency table.
Recall that, for each category , we will call the class that gives the name to the category the “main class”, and the “rest of the classes” could be any of the rest of the initial classes or could be a new class obtained after merging two or more initial classes belonging to the rest. This fact provides us with the possibility of carrying out a more specific thematic quality control. For example, for the class “Woodland” in Table 2, the expert is more worried about a misclassification with both “Grazing/Vegetation” (Sp-W#2) than a misclassification with “Bare Area” or “Urban” (Sp-W#3 or Sp-W#4).
For each category , we denote by the number of elements to be classified and define as the number of elements correctly classified in the main class j; and , as the number of misclassifications between the main class and the rest of the classes. If, for category j, the rest of the classes are the initial ones, then ; otherwise, if two or more classes of the rest are merged, then or , and so on, depending on the number of merged classes. In this way, each vector is modeled by a multinomial distribution with parameters and probability vector . The probability vector represents the probability of proper classification of the jth main class and the probabilities of misclassification between the jth main class and the rest of the classes. After the classification procedure, and following the same indices in the notation, the elements in are allocated as the following the observed frequencies . Note that if all the classes belonging to “the rest of the classes” (e.g., Sp-U#2) are merged, a binomial distribution is obtained ().
As will be seen in later sections, our proposal of an exact multinomial test will require an order in the probabilities. Therefore, in what follows, we will assume one order in the misclassifications according to the set of specifications. Such an order is established “ad hoc” by the expert and its objective is to state priorities in the misclassification levels. As an example, the assumed order in Table 2 means that, for the category “Woodland”, the specification Sp-W#1 is the most important to be fulfilled; after that, the specification Sp-W#2; after that, Sp-W#3; and, finally, the specification Sp-W#4. Any other order could be considered, however.
The idea of merging classes is motivated by the set of specifications. Such specifications represent the minimum levels of correct classifications for the main classes and the set of maximum levels of misclassifications between the main classes and the rest of the classes. These values provide the base of several testing problems that allow us to determine statistically whether the assessment results achieve the thematic quality levels previously stated. To follow the same line in the notation, the set of specifications established for the product (Table 2) can be also displayed in terms of a set of columns which we call a QCHS (quality control hypothesis set). Of course, there is a one-to-one relationship between the elements of a QCCS and a QCHS and, column by column, the values of a QCHS are considered as the fixed values of the probability vector of the corresponding multinomial distributions (or even the parameter of the binomial distribution, if the needed classes are merged). So, the particular value of each probability vector stated in the specifications is denoted by . Figure 2 presents the notation used to refer the elements of the QCCS and QCHS for any category , and for the particular case of the category “Woodland”, following the specifications in Table 2 involving the merging of two classes.
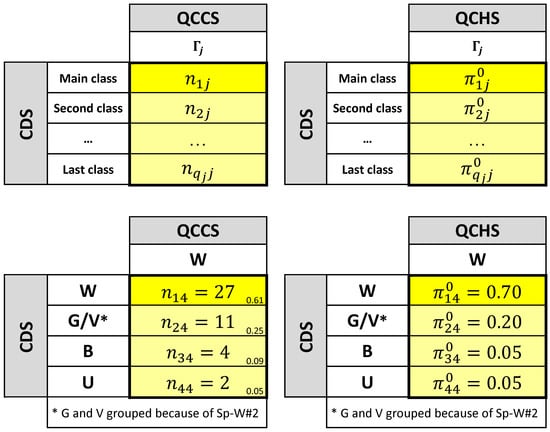
Figure 2.
Notation in a QCCS for any category and for the particular case of “Woodland”. For an easier comparison between QCCS and QCHS, this latter case includes the observed probabilities in small font.
Overall, we have defined a set of independent multinomial (or binomial) distributions and proposed values for these probability vectors through a set of quality levels.
4. Proposed Tests for QCCS
As stated previously, the goal of this work is to present a set of statistical tests that can be applied over a QCCS to perform thematic accuracy quality controls when an adequate RDS exists. As the distributions underlying of a QCCS are a set of multinomial/binomial distributions, the hypothesis tests are also based on them and, in particular, on the fixed values for the probability vectors which are given by the QCHS. From the classification results (observed QCCS) and the set of specifications (fixed values of QCHS), we wish to contrast whether the product is acceptable in accordance with the declared quality levels or, to the contrary, whether it must be rejected. In this situation, the use of a QCCS and a QCHS allows us to treat the problem of the quality of a thematic product as a set of statistical testing problems, where each column of a QCCS is compared with the values proposed by its corresponding column in a QCHS.
Four tests are presented for this purpose. Some of them focus on the percentage of correct classification in the main classes, while others focus on the whole classification (i.e., including the misclassification levels). The statistical basis of all of them exists and is well-known. Here, we systematize their use for thematic quality control and pay attention to their usefulness, in order to improve the current methodology.
The tests are organized into two groups:
- First group: There is a single quality specification for each category, always related to the correctly classified elements (e.g., at least 90% well-assigned elements in class A). Two tests for the main classes in a QCCS are presented in Section 4.1.
- Second group: There is more than one specification per category, some corresponding to the correctly classified elements and others related to maximum limits in the misclassified elements with the rest of the classes (or, even, in mixtures between some of the rest of the classes). Two tests for the complete QCCS are presented in Section 4.2.
Next, both groups of tests are presented using the notation given for the QCCS and the QCHS, and practical examples of applications and general rules of use will be provided in the following sections.
4.1. First Group: Tests for the Proportions of Correctly Classified Elements
4.1.1. Binomial Tests
Suppose that, for each category, only the number of well-assigned elements is of interest. Consider , the variable “number of correctly classified elements in the category ”. This variable follows a binomial distribution with parameters , the total elements in the category , and , the proportion of correctly classified elements. Note that each category may have a different expected probability and different sample size.
According to the QCHS, for each j, the minimum percentage of well-assigned elements to be tested is , such that a binomial test can be carried out based on the observed value, , with the null hypothesis:
against the alternative hypothesis (see [18] for details).
The p-value associated with each , say , is obtained as:
From this statistical base, we proceed as follows:
- Step 1:
- State the null hypotheses to be tested, , and obtain the corresponding p-values, .
- Step 2:
- Making use of the independence among them, decide whether (globally) all null hypotheses can be considered true or not; in other words, whether the quality levels are achieved for all the proportions of elements correctly classified or not. To do this and guarantee the global significance level, a method for multiple hypothesis testing (MMHT) is needed. In particular, Bonferroni’s Method (BM) is applied. Once the p-values are calculated, the global null hypothesis is rejected if at least one p-value is less than [19].
4.1.2. Global Binomial-Test
In the same context as the previous case, it is possible to propose an overall test which gathers all the information about differences from the specified proportions in a single quantity. In this case, the single null hypothesis to be tested is:
versus the alternative that at least one of the equalities is not true, .
To achieve this goal, taking advantage of the approximation of the binomial distribution to the standard normal distribution, we consider the following test statistic:
Under the null hypothesis, is distributed as a chi-squared distribution with degrees of freedom. takes values which are positive or zero and, under the null hypothesis, and, so, is rejected at the significance level α for large values of ; that is, if the p-value , where represents the observed value of .
This single test has the advantage of avoiding a MMHT. Note that the null hypothesis can be rejected if the relative frequencies are worse than those which are proposed, but also if they are much better. Therefore, if the null hypothesis is rejected, in a second step, we detect which category (or categories) are responsible for the rejection; that is, for which category j, the value of is higher and what is its sign. A negative sign means that the observed percentage of correctly classified elements in the main class is lower than the one established in the corresponding value in QCHS and, so, the category does not verify the quality level. On the contrary, if the sign is positive, for the category j, the quality level is exceeded.
In short, a brief summary of these tests is:
- (1)
- The null hypothesis in test 4.1.1 establishes inferior limits for the percentage of correctly classified elements (we have k testing problems, and globally make a decision with a MMHT); whereas, in test 4.1.2, the null hypothesis is the equality of all the percentages (all together).
- (2)
- Test 4.1.1 is more powerful than test 4.1.2, in the sense of rejecting the null hypothesis when it is false (that is to say, it can detect small deviations from the null values of quality for the correctness in the classification for each category).
- (3)
- If the null hypothesis of test 4.1.2 is rejected, the sign of each informs us about whether the observed percentage of correctly classified elements is greater/lower than that in the null hypothesis for the category j. Furthermore, it could be the basis for a posterior new hypothesis test, based on the fact that is distributed as a chi-square variable with one degree of freedom (similarly to the ANOVA multiple range tests)
4.2. Second Group: Tests for the Complete Classification Results
Two tests are proposed to determine statistically whether the observed classification results agree with the complete set of quality levels defined previously (for the main class and for the others).
4.2.1. Global Multinomial Test
Given the observed classification results (QCCS) and the summarized quality levels (QCHS), testing whether the QCCS and the QCHS agree is equivalent to testing if all the minimum quality levels for well-defined elements (e.g., at least 90% well-assigned elements in class A) and all the limits to the maximum percentage of mixture between the main class and the rest of the classes (e.g., not more than 4% of allowed confusion between class A and B) are fulfilled or not.
This goal is achieved by testing whether the probability vectors of the independent multinomial distributions (or even binomial distributions) in a QCCS agree with the quality levels specified in a QCHS; say, if or, equivalently, . In other words, all the probability vectors are those specified in the QCHS. Thus, the null hypothesis is now as follows:
versus the alternative .
To test , we take the following test statistic:
whose distribution under the null hypothesis is a chi-squared variable with degrees of freedom [18], when For each column j, when merging classes provides a binomial distribution instead of a multinomial distribution, the corresponding term in the sum must be changed by the following one:
Finally, is rejected at the significance level α for large values of ; that is, if the p-value, , where represents the observed value of T’.
If the null hypothesis is rejected in a posterior analysis, the test permits us to know for which category (or categories) the null hypothesis is rejected as, for a fixed j, we get:
An additional partial null hypothesis can then be stated (i.e., ) and can be solved in a similar manner, as stated previously for the second step of Section 4.1.2.
4.2.2. Multinomial Exact Tests
This test is also applicable when a complete QCHS is tested. In contrast to the previous one, in this test, we make use of probability vectors formed with an assumed order (in all the categories). This order is related to the specifications in QCHS and the preferences among them.
The criterion we will adopt is that the set of specifications for a category j is not fulfilled when:
- (i)
- the percentage of elements correctly classified in the jth main class is lower than that specified in the jth column of QCHS; or,
- (ii)
- the percentage of elements correctly classified in the jth main class is equal to that specified in the jth column of QCHS and the percentage of misclassification with the second class is greater than the corresponding one in the jth column of QCHS; or,
- (iii)
- the percentage of correct elements in the jth main class and the percentage of misclassification with the second class are equal to those indicated in the jth column QCHS and the percentage of misclassification with the third class is greater than the corresponding one in the jth column of QCHS;
- (iv)
- and so on.
For the jth category, the null hypothesis, in this case, is expressed as:
According to the criterion stated, and given that each follows a multinomial distribution, an exact test for testing Equation (9) is proposed. Such type of test is obtained ad hoc.
From this statistical base, we proceed as follows:
- Step 1:
- State the null hypotheses to be tested, , and obtain the corresponding p-values, , by means of exact multinomial tests.
- Step 2:
- Making use of independence among them, decide whether (globally) all the null hypotheses are fulfilled by using a MMHT.
The exact test for Equation (9) implies calculating the empirical probability of getting an outcome different from the null hypothesis as the outcome observed in the data, so for any fixed category , the p-value is computed by summing the probabilities of feasible outcomes in (say, ) under the alternative hypothesis. So, we have to determine the feasible outcomes under the alternative hypothesis by establishing when a classification result is considered better or worse than the other, following steps (i) to (iv).
Finally, the p-value is the sum of these probabilities; that is, for each j:
where denotes the probability mass function under (i.e., that corresponding to the ) and stands for the set of feasible outcomes (see [13]). Appendix I in [13] presents an example of the calculation of the p-value of the exact test. It is interesting to notice that [20,21] also applied this exact test for positional accuracy quality control by considering error tolerances.
A brief summary of these tests is as follows:
- (1)
- Test 4.2.1 is more demanding than the test 4.1.2, as the former involves the whole multinomial, whereas the latter involves only the diagonal percentages. So, the quality requirements to be fulfilled are different.
- (2)
- Although the test statistics are based on a chi-square variable in both cases, one is obtained from a binomial distribution and the other from a multinomial.
- (3)
- The goal of each test is different. In test 4.1.2, the goal is the fulfillment of a set of quality requirements related to the percentage of correctly classified elements, while test 4.2.1 involves not only the correctly classified elements but also the misclassifications.
5. Example Applications
The proposed four tests are applied to the data of Table 1. The data come from [16] and were used for the thematic accuracy control of a 5-class crisp Boolean classification. The study area (around the port of Tripoli, Libya) was divided into 21 blocks and the RDS was collected by a field survey, where a simple random sample of 10 locations was taken in each block (approximately 100 km2 in size). Each sample location represents a 30 × 30 m2 pixel where the overall land cover was determined.
For our purposes, the first assumption is that the RDS used in this assessment does have the quality to be a reference for our new approach of thematic accuracy control. Therefore, the new structure QCCS (Figure 1) has to be considered, instead of the classical method based on the confusion matrix (Table 1).
Taking into account the specifications of Table 2, the observed classification results from Figure 1 are rewritten, in Figure 3, after merging some classes. The corresponding QCHS is shown in Figure 4, which refers to the minimum proportions for correctly classified elements (for each category/column) and the maximum proportions of misclassifications (for each category/column).
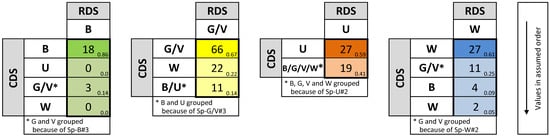
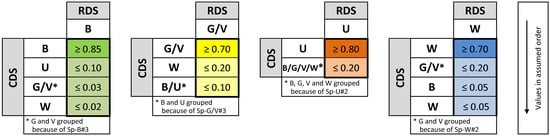
Figure 4.
QCHS derived from Table 2. B, “Bare Area”; G/V, “Grazing Land/Vegetation”; U, “Urban”; and W, “Woodland”.
In the application of the four tests proposed, the indices 1–4 correspond to the categories 1 = B, 2 = G/V, 3 = U, and 4 = W.
Next, we apply the tests described in the previous section, in the same order and using the same data set and specifications.
5.1. Application. First Group of Tests
5.1.1. Binomial Tests
In this case, we are only interested in the thematic accuracy of correctly classified elements, which means working with the first value of each column in the QCCS and QCHS shown in Figure 3 and Figure 4. The four null hypotheses are expressed, using (1), in the following way:
To apply the binomial test for proportions in each category means, the number of correctly classified elements follows a binomial distribution, say:
Given the observed values of the number of correctly classified elements in each category, , the corresponding p-values for each null hypothesis are (found using the function pbinom in the R language [22]):
Individual decisions can be taken. In this case, all specifications for the proportions of correctly classified elements are clearly fulfilled for each category, except for the category “Urban”. Furthermore, the global decision will be taken using the BM and we will reject at the level if at least one p-value is less than . As such a condition occurs, for this example, the minimum level of elements correctly classified is not achieved globally for all categories.
5.1.2. χ2 Global Binomial Test
With the same data, we can state the following single null hypothesis:
In this case, the observed value for T is:
and the p-value is . In consequence, for this example, we reject at the level . This means the requirement about the levels of elements correctly classified is not fulfilled at 5% of the significance level.
5.2. Application. The Second Group of Tests
5.2.1. χ2 Global Multinomial Test
In this case, we are interested in testing the complete fulfillment of all specifications, which means working with the complete QCCS and QCHS shown in Figure 3 and Figure 4.
The null hypothesis is: The observed value of the statistic T’ is given by:
Note that the degrees of freedom are = 9, with and and the corresponding p-value is As a consequence, we reject the null hypothesis and the set of quality levels expressed throughout the values in the QCHS is not fulfilled (involving both the specifications for the correctly classified elements and those for the misclassifications).
5.2.2. Multinomial Exact Tests
As in the previous case, we are interested in testing the complete fulfillment of all specifications, which means working with the complete QCCS and QCHS, but also applying several exact multinomial tests—one for each category (column).
Each test can be interpreted individually, as well as jointly after using a MMHT as the BM. The null hypotheses are:
Next, we show the results of the corresponding exact tests:
- Urban. In this case, from Figure 4 (column U), the maximum percentage of misclassified elements is 20%, so the classification results lead us to define a binomial distribution with parameters: the number of elements to be classified (m1 = 46) and the probability of correctness in the classification is p = 0.80; in short, we get B(46,0.80). The observed classification is (see Figure 3, column U) and the p-value obtained is 0.0007 (calculated, for instance, by means of the pbinom function in R [22]).
The individual exact multinomial tests reveal it is only the null hypothesis for the category “Urban” that is rejected. For the rest of categories, we do not reject the null hypotheses, so, it means that for such categories, the set of specifications in Table 2 is achieved. In addition, after applying a MMHT (for example, the BM, as not all the p-values are greater than , it cannot be concluded that, globally, all the specifications involving the quality of the product are fulfilled, as stated in Table 2.
6. Discussion
This section presents the discussion, divided into two parts. The first is focused on the results of the example that has been presented, and the second mainly focuses on comparing the proposal of tests based on the QCCS with the methods and indices based on the whole confusion matrix; in this case, the argument is qualitative, as methods based on the confusion matrix cannot be applied to the presented example.
In terms of the example, we considered a variety of cases: (i) at category level, from the initial multinomial case (Urban category) to a new definition of the category “Urban” after collapsing Grazing Land, Vegetation, Bare area and Woodland (binomial case) and (ii) at class level, we allowed the merging of classes in the classified categories (e.g., Grazing land and Vegetation for the categories Bare area and Woodland). This is an example of the flexibility of the proposed approach. The four tests here presented offer the user a variety of statistical tools that can cover different quality controls. The first two tests focused on the correctly classified elements and the quality control related to this topic, while the latter two tests focused on the fulfillment of a complete set of specifications. Furthermore, users should pay attention to the type of null hypothesis to be tested. The tests in 4.1.2 and 4.2.1 involved a single null hypothesis, whereas the other two tests involved a set of null hypotheses and the application of a MMHT. Nevertheless, the statistical calculations to be carried out are simple. The only test that presents some complexity is the last one, as, being an exact test, it requires specification of the entirety of the possible solution space. In any case, this can be easily calculated with a script written in the R Language, as shown in Appendix I (see [13] for details).
In addition, it is important to take care with the relationship between the sample size and the power of any hypothesis test. If one increases the sample size, the hypothesis test gains a greater ability to detect small effects. However, larger sample sizes cost more money. And, there is a point where an effect becomes so minuscule that it is meaningless in a practical sense. Considerations about the power involve that the desired values of the significance level and the minimum significant difference that we want to detect have to be previously established. As a first approximation, we recommend to use formulae for the binomial case (see [18] for details).
Concerning the methods and indices based on the confusion matrix, comparison between those indices and the tests proposed does not make sense, as the distributional hypothesis is different and, hence, the way to deal with the classification results differs. Furthermore, the classical indices based on a confusion matrix are accompanied by a confidence interval, whereas, in our proposal, the inference is made in terms of hypothesis tests and refers to the adequacy (or not) of all categories with respect to previous quality specifications. The first two tests (cases 4.1.1 and 4.1.2) focused on the proportion of correctly classified elements. In this case, one can see a subtle relation to the classical inference about the producer’s accuracy and conditional kappa (producer’s) indices. The last two tests (4.2.1 and 4.2.2) represent a novel idea in thematic quality control. They involve the fulfillment of a set of quality specifications, by columns and/or globally. In summary, the proposed approach offers a new way to deal with thematic quality control.
As a guide to characterize and facilitate the application, Table 4 presents a summary of the four proposed tests.

Table 4.
Summary of the proposed test for quality control based on QCCS.
7. Conclusions
A new framework has been proposed for the thematic accuracy quality control of spatial data products. The presented approach is different from the traditional one based on a confusion matrix, where the RDS and the CDS are simply two data sets. The availability of a RDS of higher accuracy than the data to be evaluated is the critical and differentiating aspect of the proposed approach. The application of this new proposal also entails the opportunity and need to establish more complete specifications for the products, such that they can not only establish the minimum required quality level for each category, but also limit the maximum misclassification level between categories.
This perspective is centered on quality control and is supported by well-known statistical hypothesis testing methods, the objective of which is to make a decision about the fulfillment or not (acceptation or rejection) of a set of thematic quality specifications. This perspective allows class-by-class quality control, including some degree of mixing or relaxation (confusions between classes). The four presented cases comprise a very flexible set of statistical tests, where a specific application can be selected depending on the specifications to control. As an example, this flexibility allows us to set different quality specifications for each class, as well as restrict the contrasts only for a subset of the classes. In general, the statistical implementation of the proposed tests is not difficult; only the multinomial overall test is a little more complex, as it is an exact test.
As we do not address an estimation problem, only simple random sampling (SRS) is required and, besides, the sample size does not play a relevant role in assuring the significance level of the tests proposed. The required SRS permits us to define the multinomial (or binomial, if needed) distribution. This is a crucial assumption in hypothesis testing procedures. Other sampling designs (e.g., stratified sampling, clustering sampling, and so on) are common when the goal is to carry out estimation.
From a methodological point of view, given that the RDS is in columns and the CDS is in rows, the tests also work if the SRS changes from columns to rows. However, the meaning of these tests and their conclusions change radically. In our opinion, only by columns make sense (the quality requirements of the product agrees with reality, not the opposite). This point of view is analogous to that of the producer’s accuracy.
With respect to the developed example, it has been proved that the calculations are not complex and that all the results of the tests are congruent with each other. Finally, as has been shown, the proposed approach is directly applicable to crisp classification, but we also consider that it is extensible to fuzzy classification. This is the next challenge we are going to address.
Author Contributions
This research was done by several authors: conceptualization, F.J.A.-L. and J.R.-A.; methodology, J.R.-A., M.V.A.-F., and F.J.A.-L.; software, J.R.-A. and M.V.A.-F.; investigation, F.J.A.-L., J.R.-A., M.V.A.-F., and J.L.G.-B.; resources, F.J.A.-L. and J.L.G.-B.; writing—original draft preparation, F.J.A.-L., J.R.-A., M.V.A.-F., and J.L.G.-B.; resources, F.J.A.-L. and J.L.G.-B.; writing—review and editing, M.V.A.-F.; funding acquisition, M.V.A.-F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science and Innovation, grant number CTM2015-68276-R.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Veregin, H. Taxonomy of Errors in Spatial Databases; NCGIA, Technical Report 89-12; National Center for Geographic Information and Analysis: Buffalo, NY, USA, 1989.
- Guptill, S.C.; Morrison, J.L. Elements of Spatial Data Quality; Pergamon Press: Oxford, UK, 1995. [Google Scholar]
- Ariza-López, F.J. Calidad en la Producción Cartográfica; Ra-Ma: Venice, CA, USA, 2002. [Google Scholar]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Climatol. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Strahler, A.H.; Boschetti, L.; Foody, G.M.; Friedl, M.A.; Hansen, M.C.; Herold, M.; Mayaux, P.; Morisette, J.T.; Stehman, S.V.; Woodcock, C.E. Global Land Cover Validation: Recommendations for Evaluation and Accuracy Assessment of Global Land Cover Maps; GOFC-GOLD Report No. 25; Office for Official Publications of the European Communities: Brussels, Belgium, 2006. [Google Scholar]
- ISO. ISO 19157:2013 Geographic Information—Data Quality; International Organization for Standardization: Geneva, Switzerland, 2013. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; Lewis Publishers: Boca Raton, FL, USA, 2009. [Google Scholar]
- Devillers, R.; Stein, A.; Bédard, Y.; Chrisman, N.; Fisher, P.; Shi, W. Thirty Years of Research on Spatial Data Quality: Achievements, Failures, and Opportunities. Trans. GIS 2010, 14, 387–400. [Google Scholar] [CrossRef]
- Ariza-López, F.J. (Ed.) Fundamentos de evaluación de la calidad de la información geográfica; Universidad de Jaén: Jaén, Spain, 2013. [Google Scholar]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T. A Land-Use Classification System for Use with Remote Sensor Data; USGS Circular 671; U.S. Government Printing Office: Washington, DC, USA, 1972.
- USDA. Existing Vegetation Classification and Mapping Technical Guide Version 1.0; USDA: Washington, DC, USA, 2005.
- ISO. ISO 19131:2007 Geographic Information—Data Product Specifications; International Organization for Standardization: Geneva, Switzerland, 2007. [Google Scholar]
- Ariza-López, F.J.; Rodríguez-Avi, J.; Alba-Fernández, M.V.; García-Balboa, J.L. Thematic accuracy quality control by means of a set of multinomials. Appl. Sci. 2019, 9, 4240. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area and map accuracy for stratified random sampling when strata are different form the map classes. Int. J. Remote Sens. 2014, 35, 923–4939. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcok, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using stratified estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Comber, A.; Fisher, P.; Brunsdom, C.; Khmag, A. Spatial analysis of remote sensing image classification accuracy. Remote Sens. Environ. 2012, 127, 237–246. [Google Scholar] [CrossRef]
- Liu, C.; Frazier, P.; Kumar, L. Comparative assessment of the measures of thematic classification accuracy. Remote Sens. Environ. 2007, 107, 606–616. [Google Scholar] [CrossRef]
- Rohatgi, V.K. Statistical Inference; Dover Publications: Mineola, NY, USA, 2003. [Google Scholar]
- Shaffer, J.P. Multiple hypothesis testing. Ann. Rev. Psychol. 1995, 46, 561–584. [Google Scholar] [CrossRef]
- Ariza-López, F.J.; Rodríguez-Avi, J.; Alba-Fernández, V. A Positional Quality Control Test Based on Proportions. In Geospatial Technologies for All. AGILE 2018. Lecture Notes in Geoinformation and Cartography; Mansourian, A., Pilesjö, P., Harrie, L., van Lammeren, R., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Ariza-López, F.J.; Rodríguez-Avi, J.; González-Aguilera, D.; Rodríguez-González, P. A new method for positional accuracy control for non-normal errors applied to Airborne Laser Scanner data. Appl. Sci. 2019, 9, 3887. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).