Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution
Abstract
1. Introduction
2. Materials and Methods
2.1. GPT Series Model
2.2. TropGrid2 Model
2.3. ITG Model
2.4. The proposed WGTEM
- (1)
- Search for 10 adjacent modeling epochs close to the t epoch to be evaluated , ~ , the epoch t is between and .
- (2)
- The tropospheric parameters at these 10 epochs are then calculated using the model expression (6) and the model coefficient.
- (3)
- The distance-dependent interpolation algorithm is subsequently employed to obtain the value at the t epoch.
3. Results and Discussion
3.1. Evaluation of Model Expression
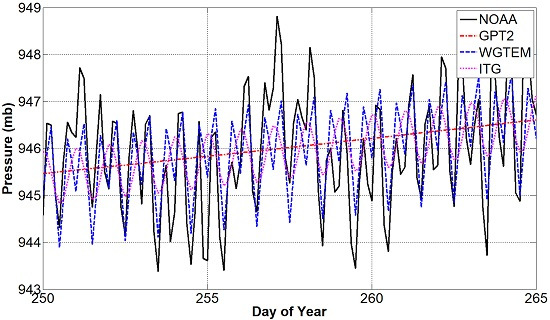
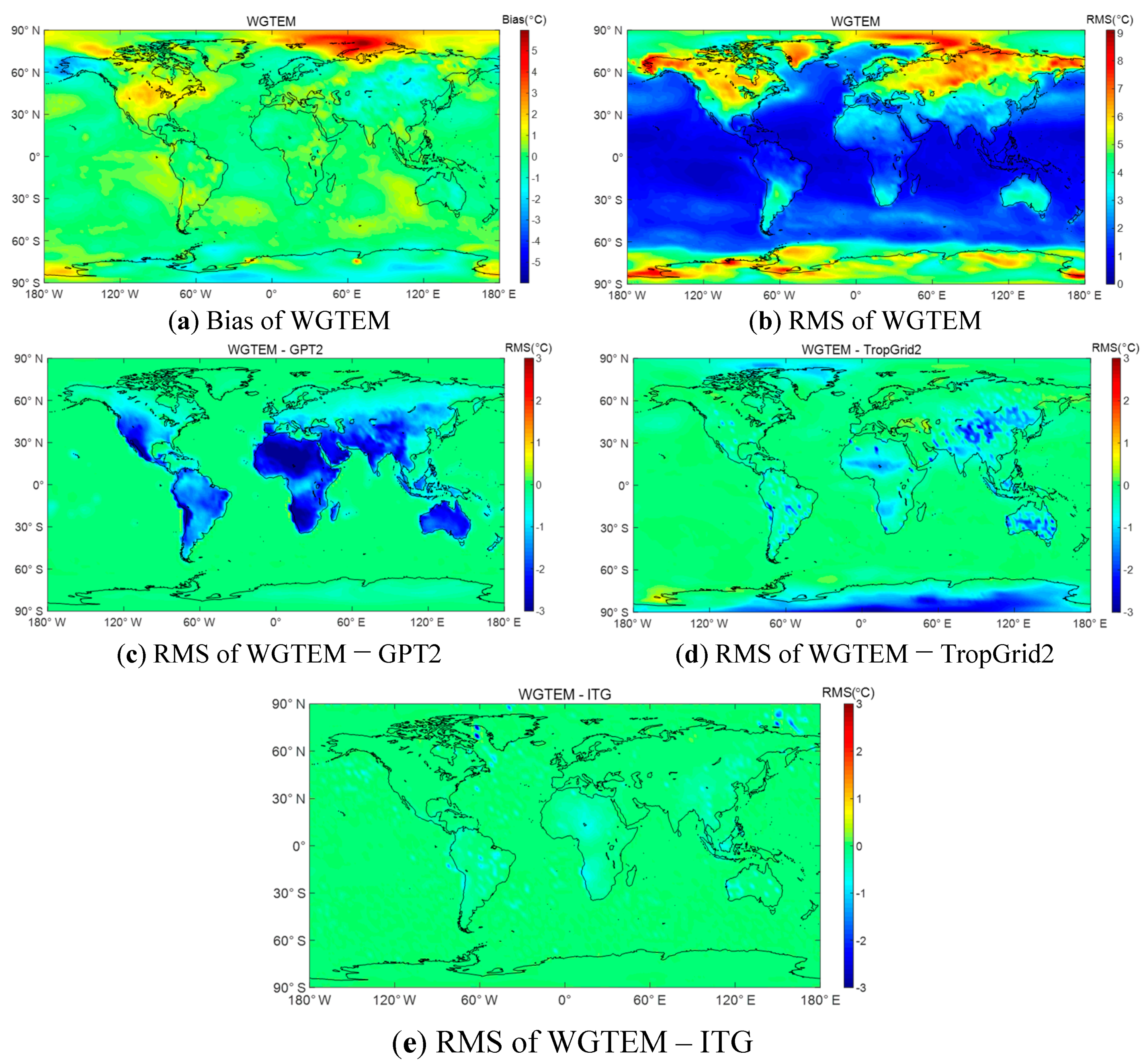
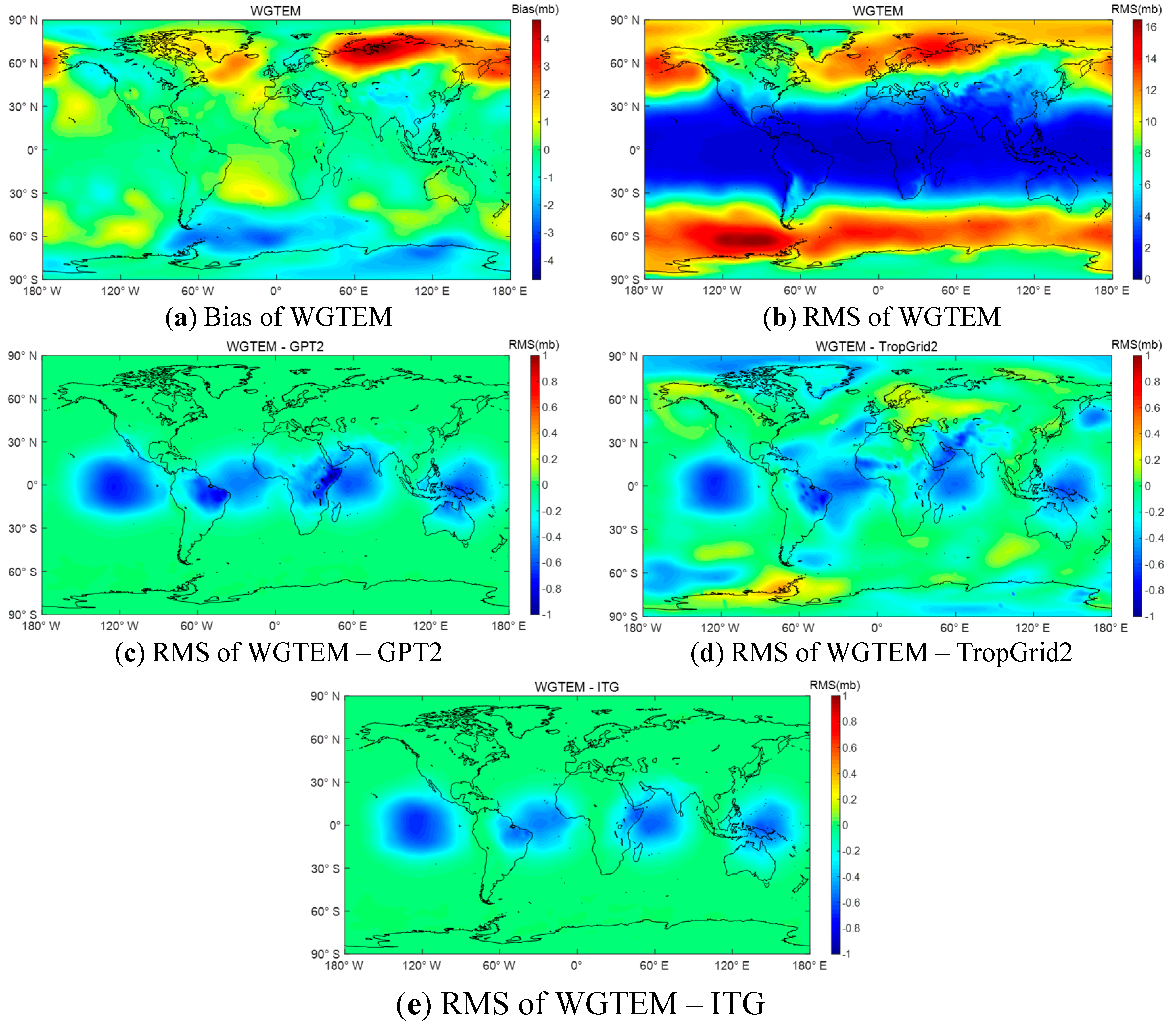
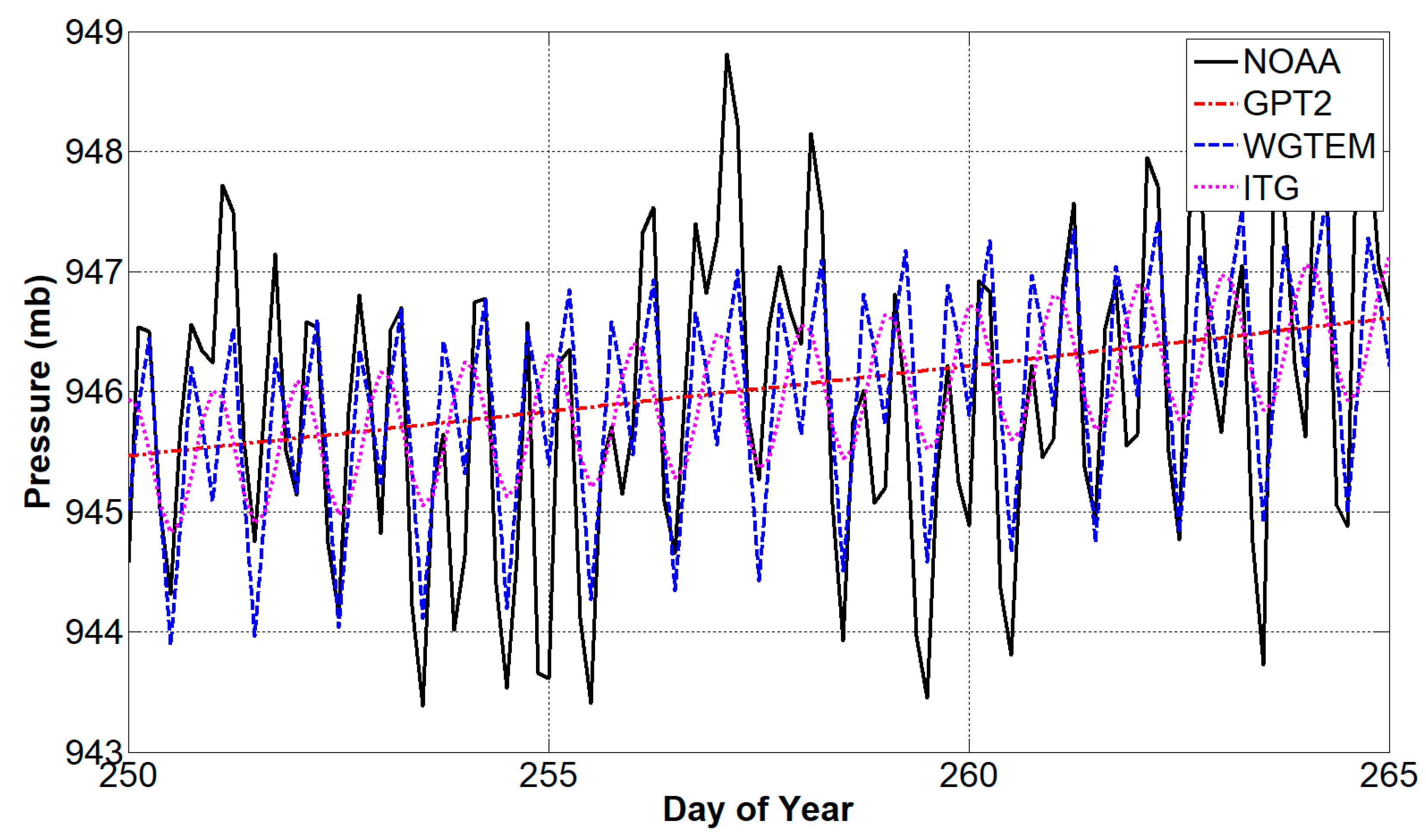
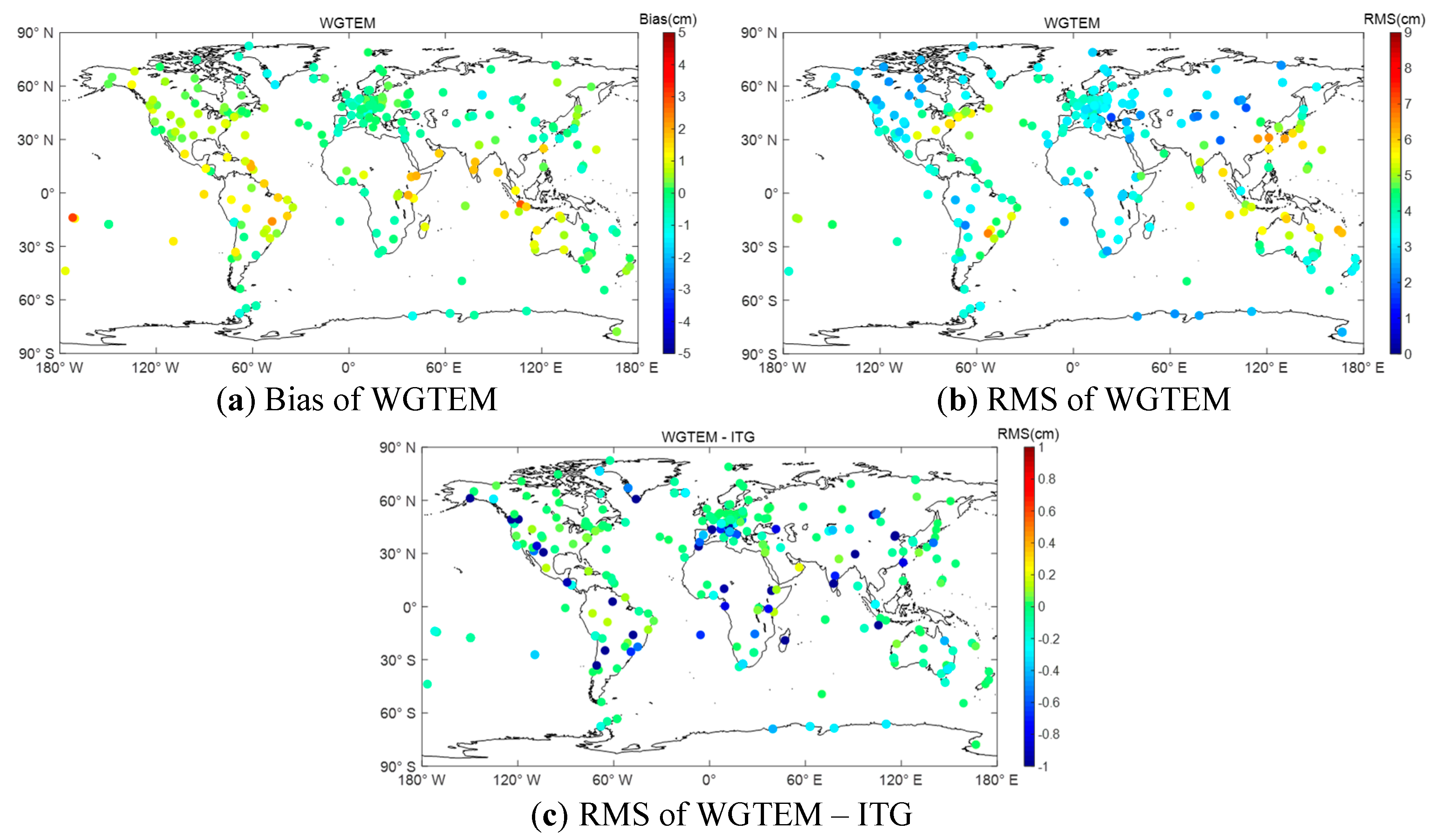
3.2. External Accuracy Evaluation of WGTEM
4. Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Rocken, C.; Van Hove, T.; Ware, R. Near real—Time GPS sensing of atmospheric water vapor. Geophys. Res. Lett. 1997, 24, 3221–3224. [Google Scholar] [CrossRef]
- Allan, R.P. The role of water vapour in Earth’s energy flows. Surv. Geophys. 2012, 33, 557–564. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; McClusky, S. GPS meteorology: Direct estimation of the absolute value of precipitable water. J. Appl. Meteorol. Clim. 1996, 35, 830–838. [Google Scholar] [CrossRef]
- Jacob, D. The role of water vapour in the atmosphere. A short overview from a climate modeller’s point of view. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 523–527. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Precise point positioning using combined GPS and GLONASS observations. Positioning 2007, 1, 13–22. [Google Scholar] [CrossRef]
- Collins, P.; Lahaye, F.; Héroux, P.; Bisnath, S. Precise point positioning with ambiguity resolution using the decoupled clock model. In Proceedings of the 21st international technical meeting of the satellite division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Li, X.; Ge, M.; Zhang, H.; Wickert, J. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J. Geod. 2013, 87, 405–416. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Lu, C.; Zus, F.; Ge, M.; Heinkelmann, R.; Dick, G.; Wickert, J.; Schuh, H. Tropospheric delay parameters from numerical weather models for multi-GNSS precise positioning. Atmos. Meas. Tech. 2016, 9, 5965. [Google Scholar] [CrossRef]
- Hopfield, H.S. Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Ifadis, I. The Atmospheric Delay of Radio Waves: Modelling the Elevation Dependence on a Global Scale; Technical Report No. 38L; School of Electrical and Computer Engineering, Chalmers University of Technology: Goteburg, Sweden, 1986. [Google Scholar]
- Askne, J.; Nordius, H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Wang, G.Q. Millimeter-accuracy GPS landslide monitoring using Precise Point Positioning with Single Receiver Phase Ambiguity (PPP-SRPA) resolution: A case study in Puerto Rico. J. Geod. Sci. 2013, 3, 22–31. [Google Scholar] [CrossRef]
- Rabbou, M.A.; El-Rabbany, A. PPP accuracy enhancement using GPS/GLONASS observations in kinematic mode. Positioning 2015, 6, 1–6. [Google Scholar] [CrossRef]
- Maciuk, K. GPS-only, GLONASS-only and combined GPS + GLONASS absolute positioning under different sky view conditions. Tehnički Vjesnik 2018, 25, 933–939. [Google Scholar]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of multi-GNSS precise point positioning time and frequency transfer with clock modeling. Remote Sens. 2019, 11, 347. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, M.; Zhou, C.; Zhang, P. Precise point positioning using dual-frequency GNSS observations on smartphone. Sensors 2019, 19, 2189. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A troposphere constraint method to improve PPP ambiguity-resolved height solution. J. Navig. 2014, 67, 249–262. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Local troposphere augmentation for real-time precise point positioning. Earth Planets Space 2014, 66, 30. [Google Scholar] [CrossRef]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
- Collins, J.P.; Langley, R. The residual tropospheric propagation delay: How bad can it get? Proceedings of Ion GPS; Institute of Navigation: Manassas, VA, USA, 1998; Volume 11, pp. 729–738. [Google Scholar]
- Penna, N.; Dodson, A.H.; Chen, W. Assessment of EGNOS Tropospheric Correction Model; ION GPS: Nashville, TN, USA, 1999; pp. 14–17. [Google Scholar]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS tropospheric correction model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef]
- Ueno, M.; Hoshinoo, K.; Matsunaga, K.; Kawai, M.; Nakao, H.; Langley, R.B.; Bisnath, S.B. Assessment of atmospheric delay correction models for the Japanese MSAS. In Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation, Salt Lake City, UT, USA, 11–14 September 2001; pp. 2341–2350. [Google Scholar]
- Krueger, E.; Schueler, T.; Hein, G.W.; Martellucci, A.; Blarzino, G. Galileo Tropospheric Correction Approaches Developed within GSTB-V1. Proceedings of ENC-GNSS 2004, Rotterdam, The Netherlands, 16–19 May 2004; Available online: https://www.researchgate.net/profile/Torben_Schueler/publication/228730717_Galileo_Tropospheric_Correction_Approaches_Developed_within_GSTB-V1/links/09e4150880fbbbaca7000000/Galileo-Tropospheric-Correction-Approaches-Developed-within-GSTB-V1.pdf (accessed on 14 February 2020).
- Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Böhm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Kouba, J. Testing of Global Pressure/Temperature (GPT) Model and Global Mapping Function (GMF) in GPS analyses. J. Geod. 2009, 83, 199–208. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Boehm, J.; Krasna, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in then troposphere (GPT2w). GPS Solut. 2015. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, C.; Shi, J.; Cao, N.; Zhang, B.; Yang, J. ITG: A new global GNSS tropospheric correction model. Sci. Rep. 2015, 5, 10273. [Google Scholar] [CrossRef]
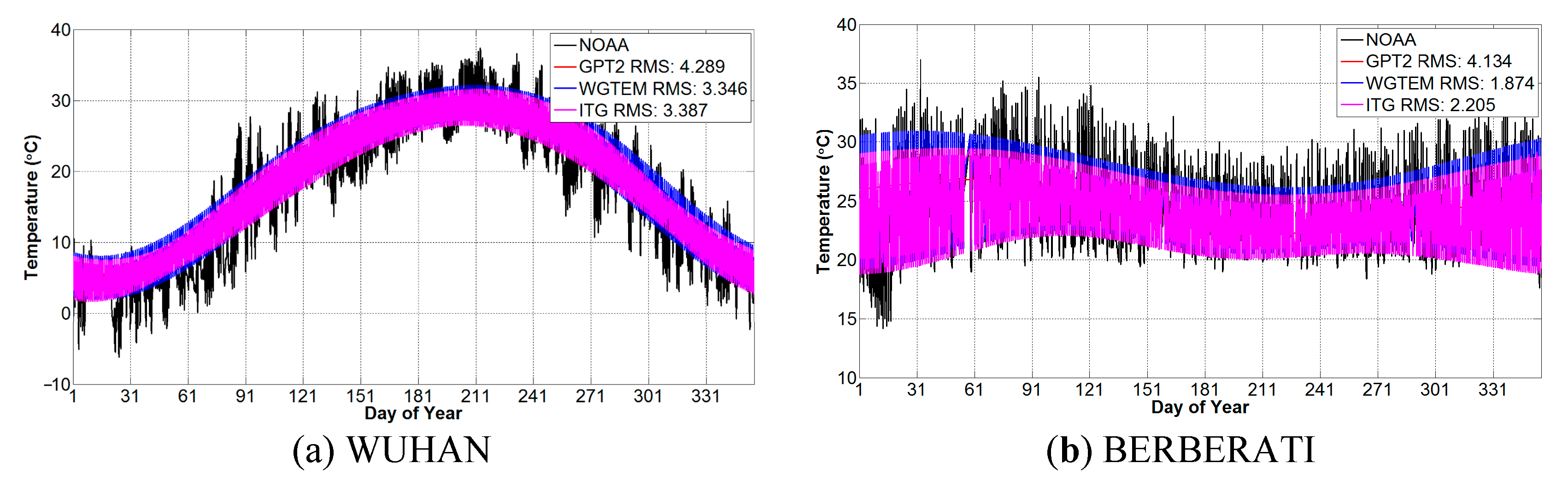
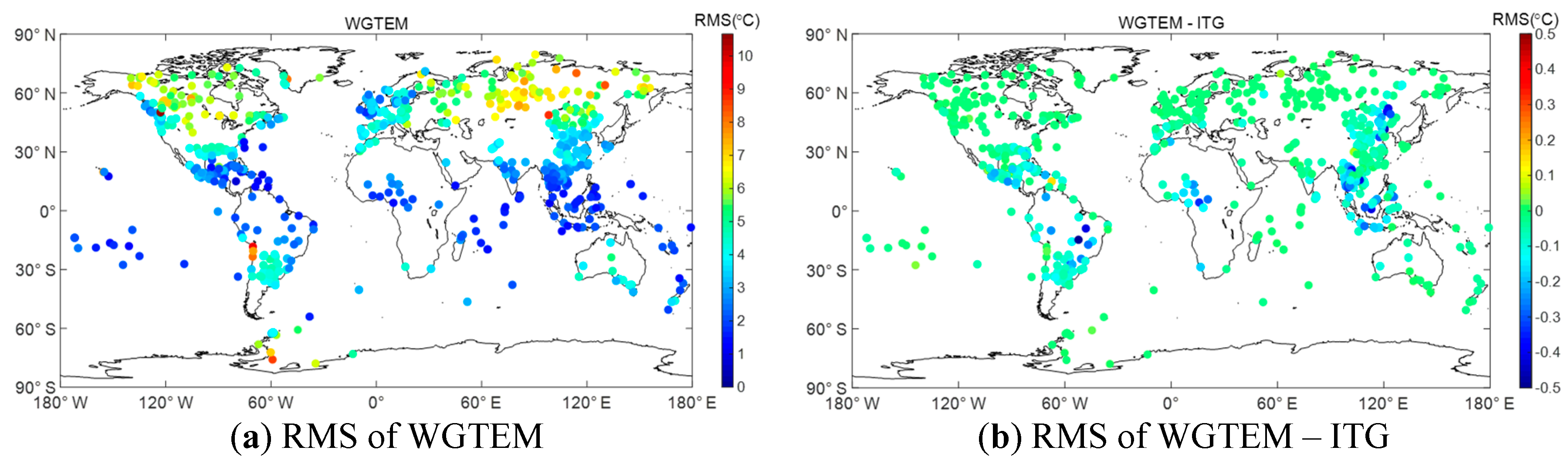
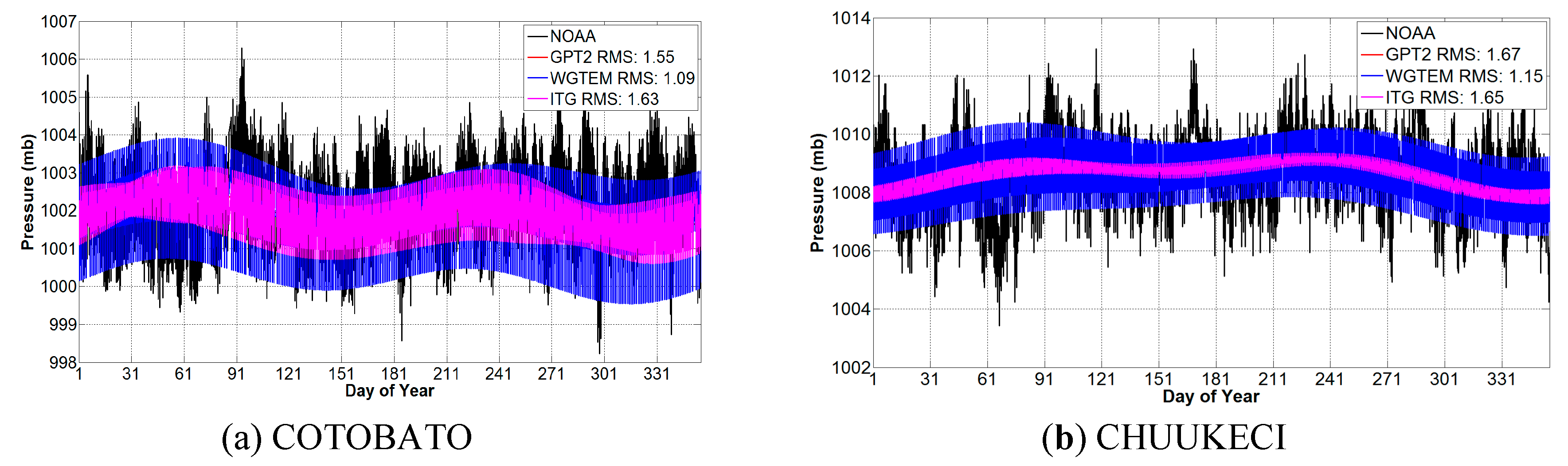
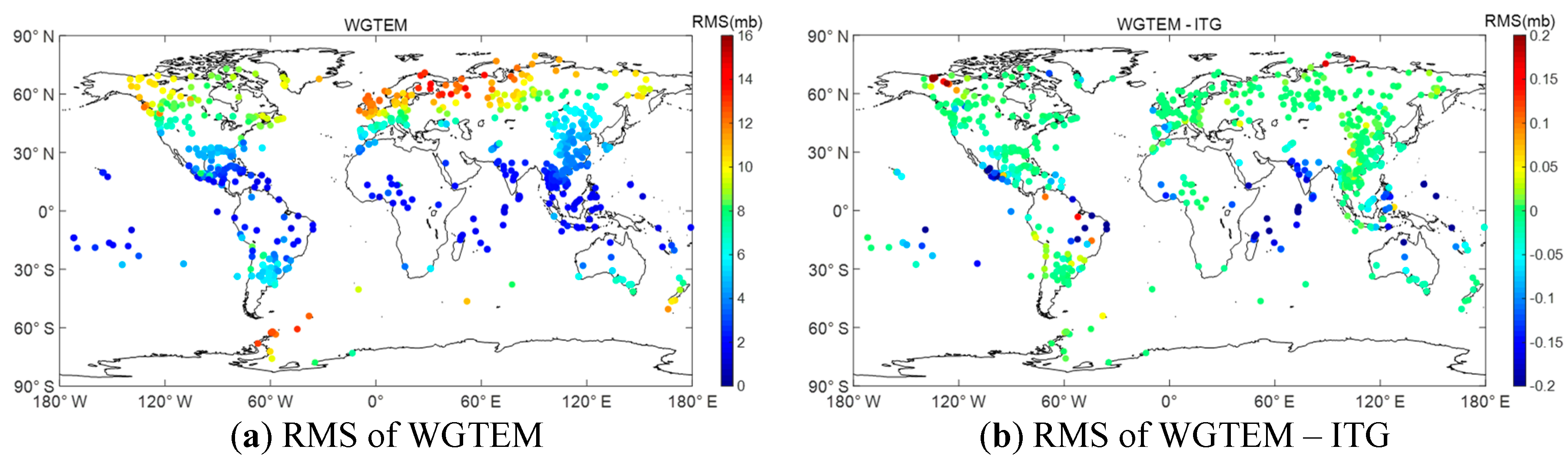
| Model | RMS (°C) | ||
|---|---|---|---|
| Mean | Max | Min | |
| GPT2 | 3.20 | 9.32 | 0.46 |
| TropGrid2 | 3.11 | 9.07 | 0.47 |
| ITG | 2.89 | 9.11 | 0.44 |
| WGTEM | 2.85 | 9.10 | 0.43 |
| Model | RMS (mb) | ||
|---|---|---|---|
| Mean | Max | Min | |
| GPT2 | 7.04 | 16.45 | 0.82 |
| TropGrid2 | 7.10 | 16.63 | 0.77 |
| ITG | 7.03 | 16.40 | 0.78 |
| WGTEM | 6.95 | 16.45 | 0.75 |
| Model | Bias (°C) | RMS (°C) | ||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| WGTEM | −0.26 | 6.86 | −9.14 | 3.81 | 10.66 | 0.67 |
| ITG | −0.27 | 6.84 | −9.14 | 3.87 | 10.66 | 0.69 |
| Model | Bias (hPa) | RMS (hPa) | ||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| WGTEM | −0.2 | 7.8 | −8.3 | 5.9 | 14.5 | 1.1 |
| ITG | −0.2 | 7.8 | −8.3 | 6.0 | 14.6 | 1.4 |
| Model | ZTD Bias (cm) | ZTD RMS(cm) | ||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| WGTEM | 0.18 | 3.07 | −1.54 | 3.82 | 6.62 | 1.65 |
| ITG | 0.05 | 4.71 | −4.57 | 4.04 | 6.62 | 1.70 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Yao, Y.; Shi, J.; Zhang, Q.; Peng, W. Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution. Remote Sens. 2020, 12, 721. https://doi.org/10.3390/rs12040721
Xu C, Yao Y, Shi J, Zhang Q, Peng W. Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution. Remote Sensing. 2020; 12(4):721. https://doi.org/10.3390/rs12040721
Chicago/Turabian StyleXu, Chaoqian, Yibin Yao, Junbo Shi, Qi Zhang, and Wenjie Peng. 2020. "Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution" Remote Sensing 12, no. 4: 721. https://doi.org/10.3390/rs12040721
APA StyleXu, C., Yao, Y., Shi, J., Zhang, Q., & Peng, W. (2020). Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution. Remote Sensing, 12(4), 721. https://doi.org/10.3390/rs12040721