Potential of Using Phase Correlation in Distributed Scatterer InSAR Applied to Built Scenarios
Abstract
1. Introduction
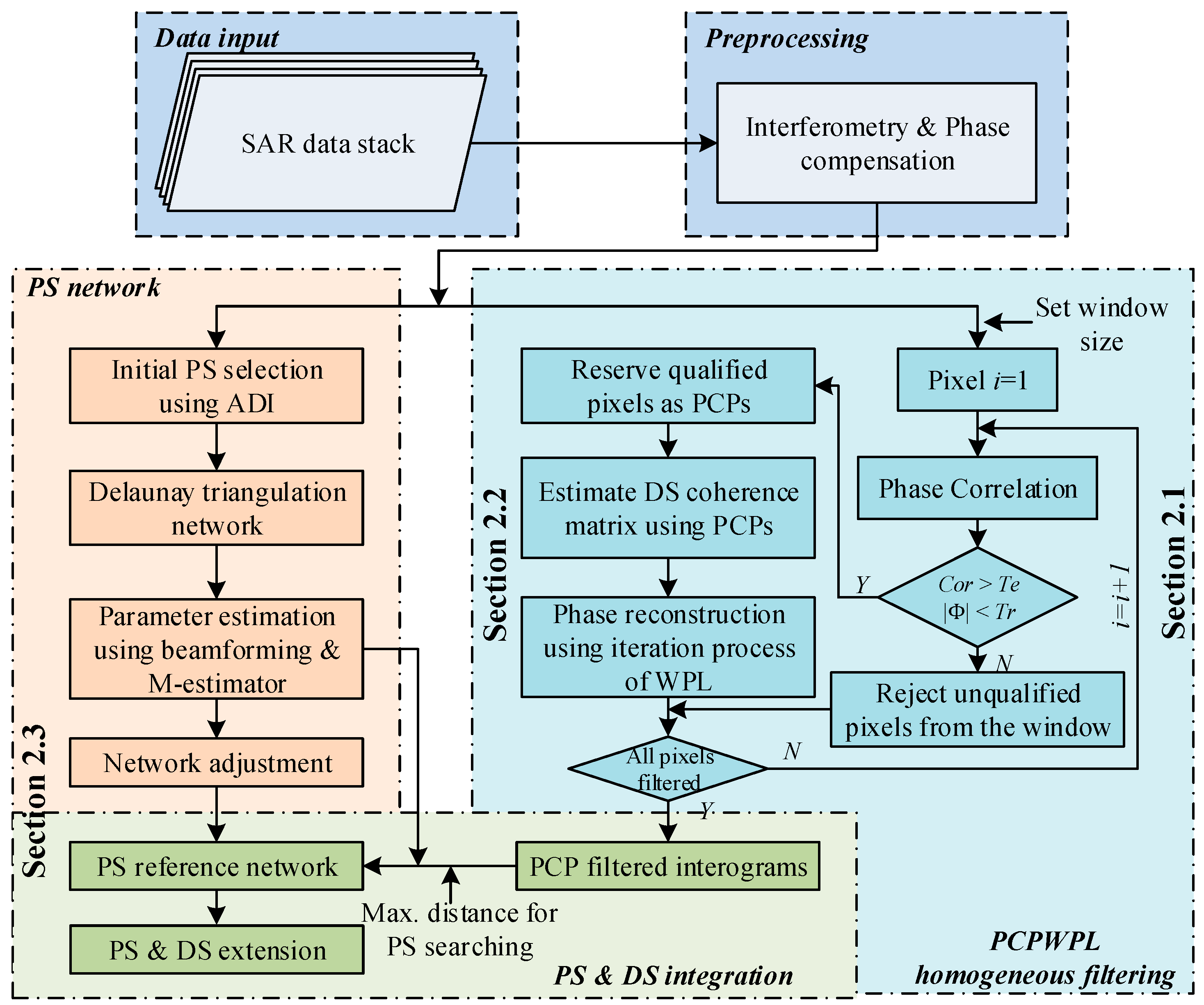
2. Methodologies
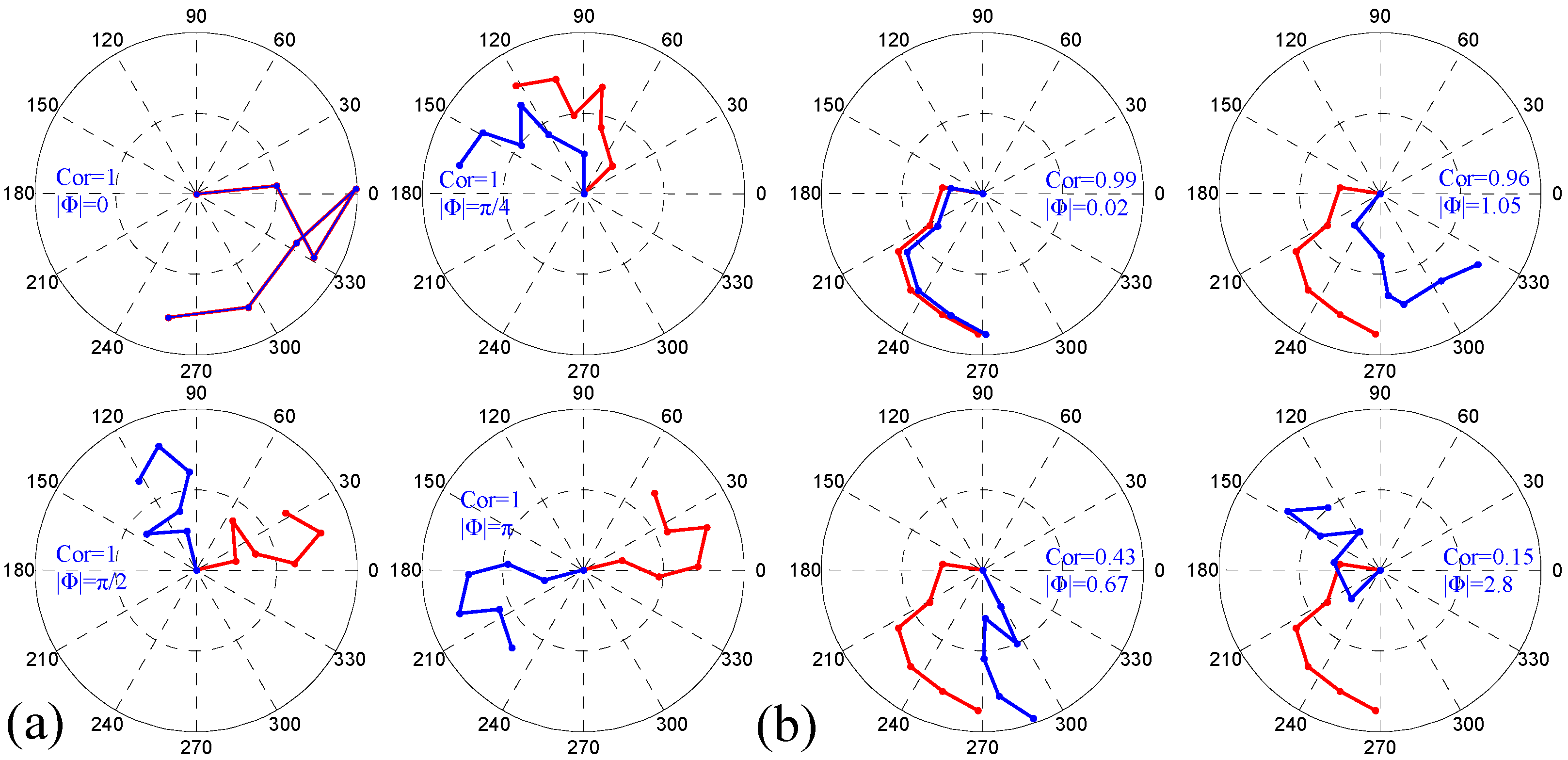
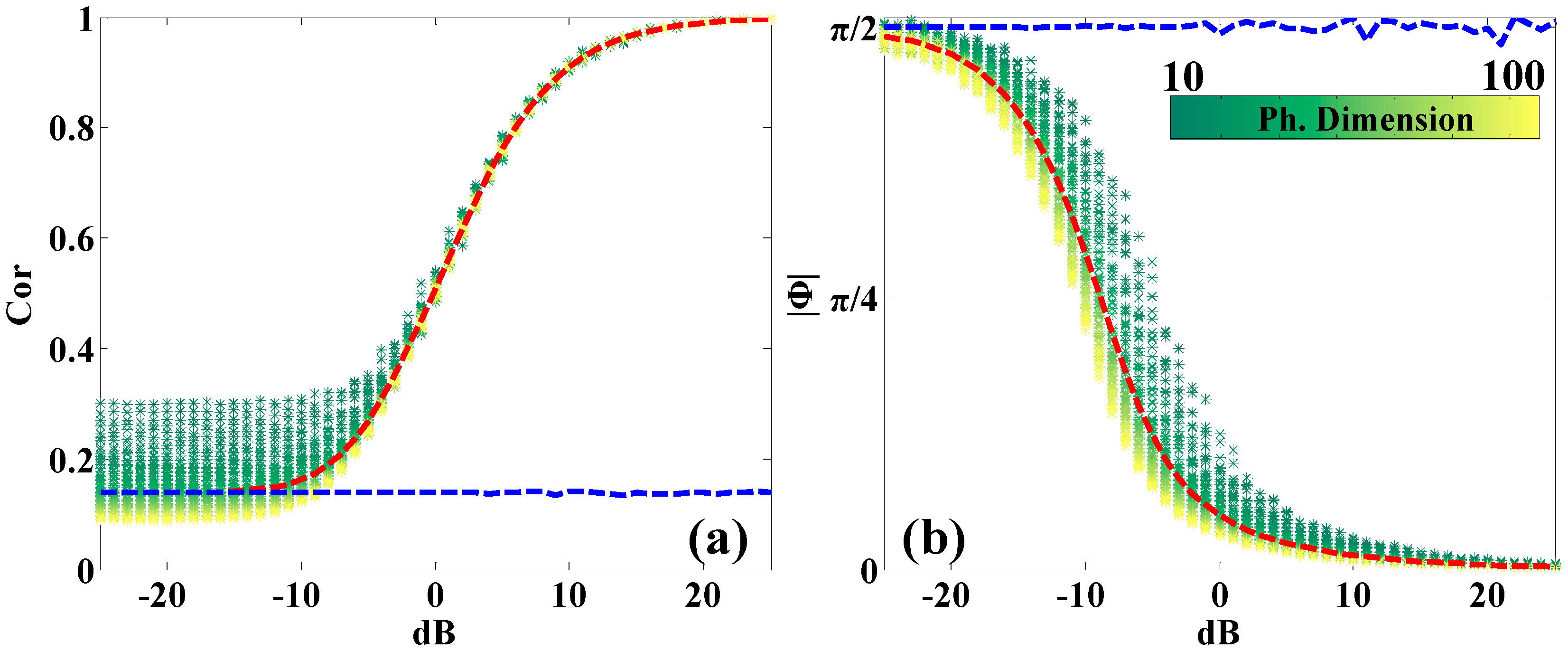
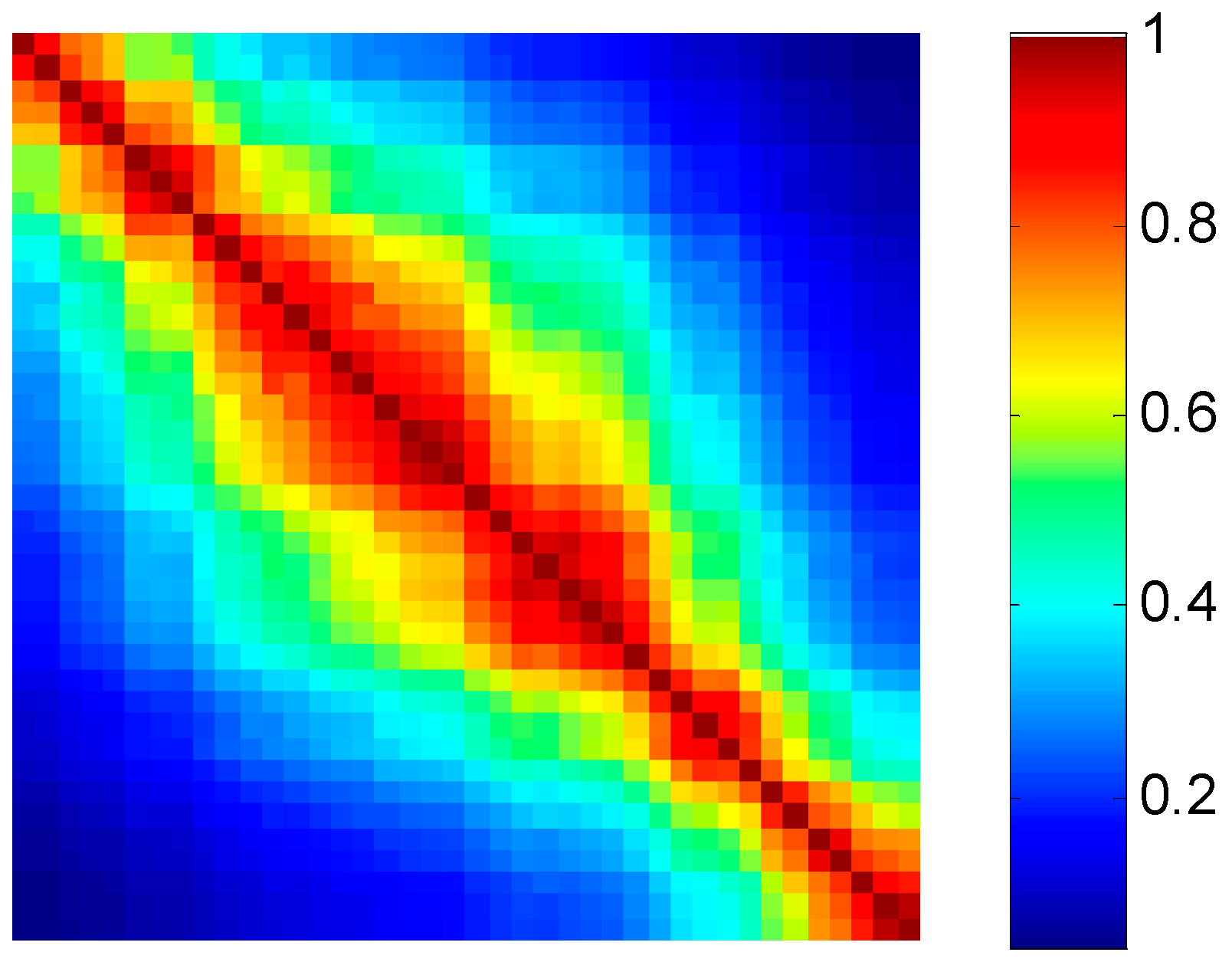
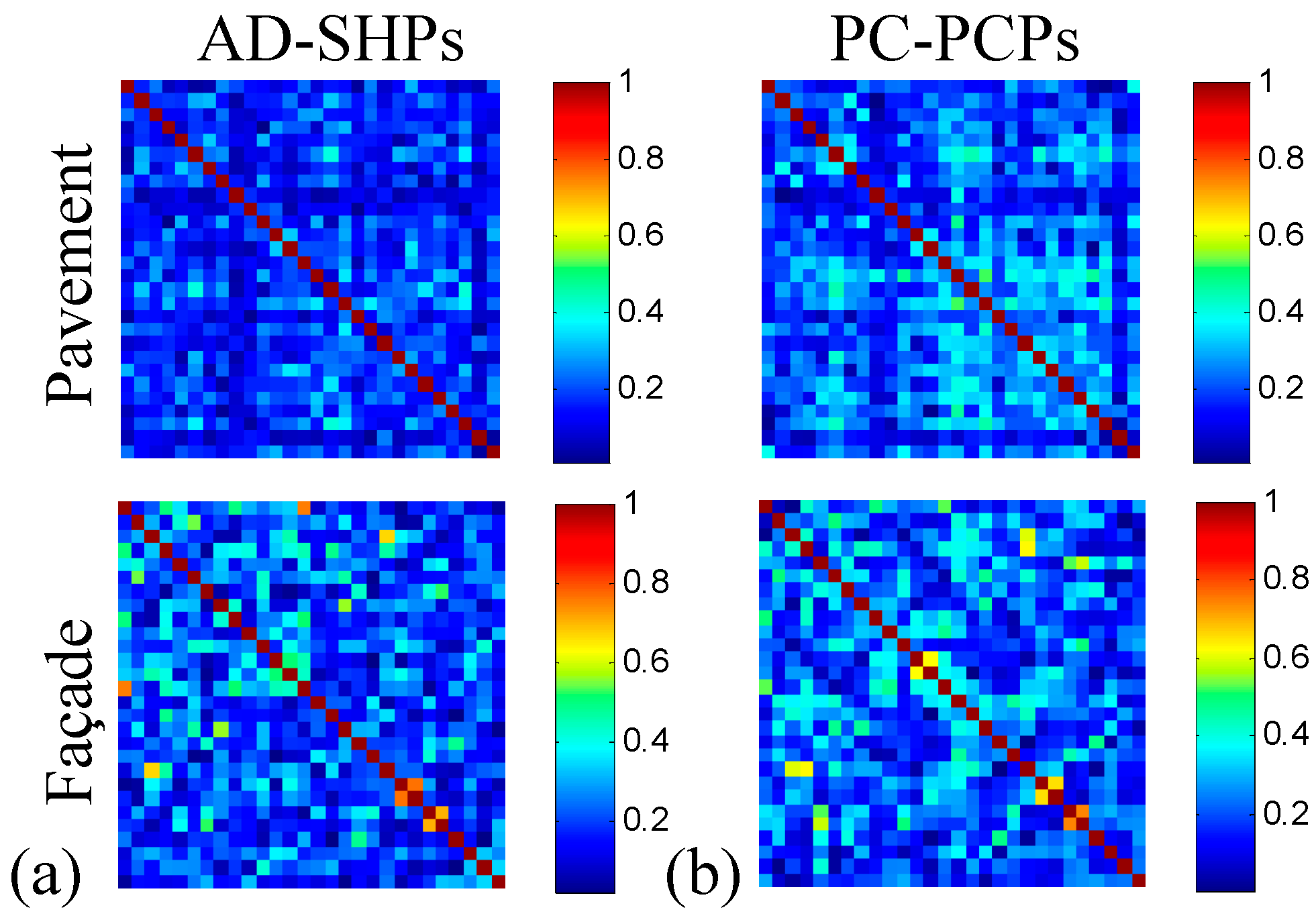
2.1. Homogeneous Clustering of Phase-Correlated Pixels (PCPs)
2.2. Phase Reconstruction Using Coherence Weighted Phase Link (WPL)
2.3. Combined Processing of PS and DS
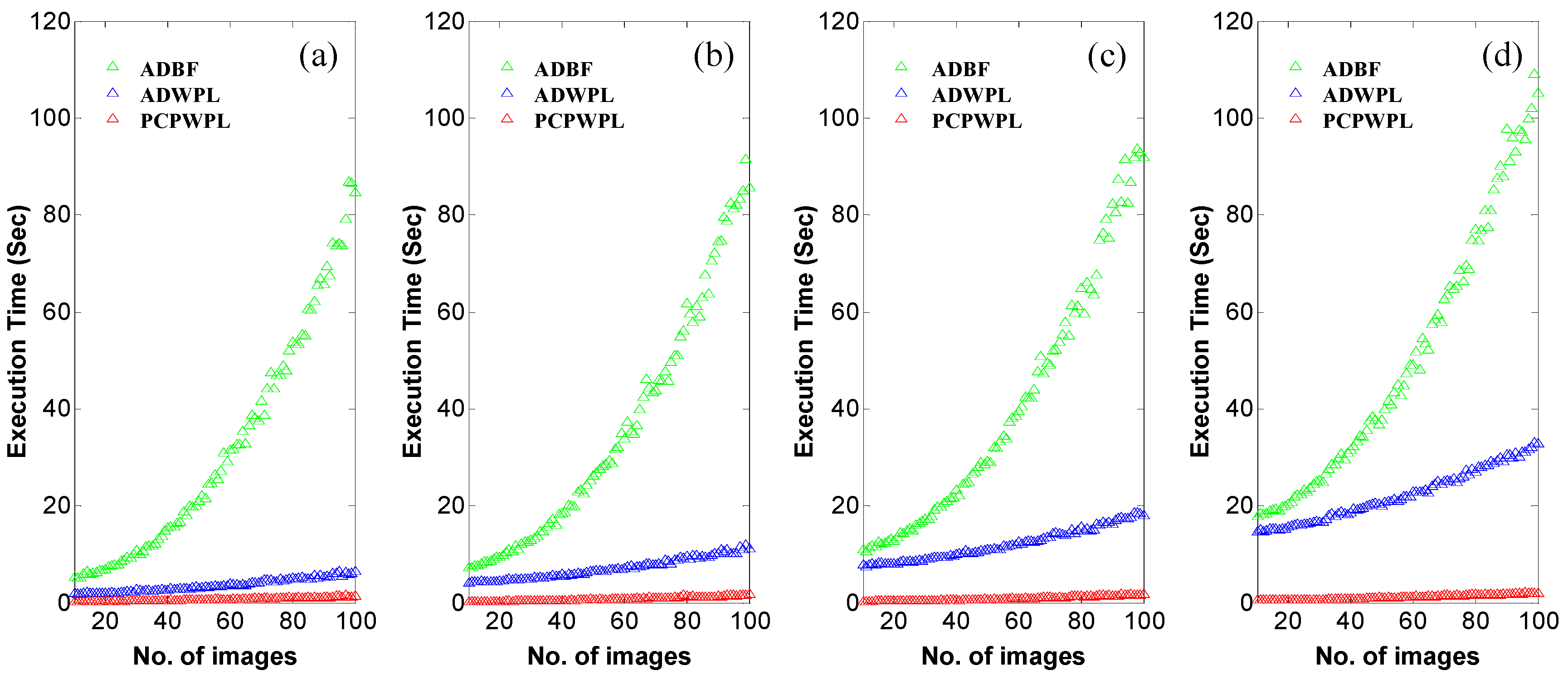
3. Simulated Experiments
4. Real Data Experiment
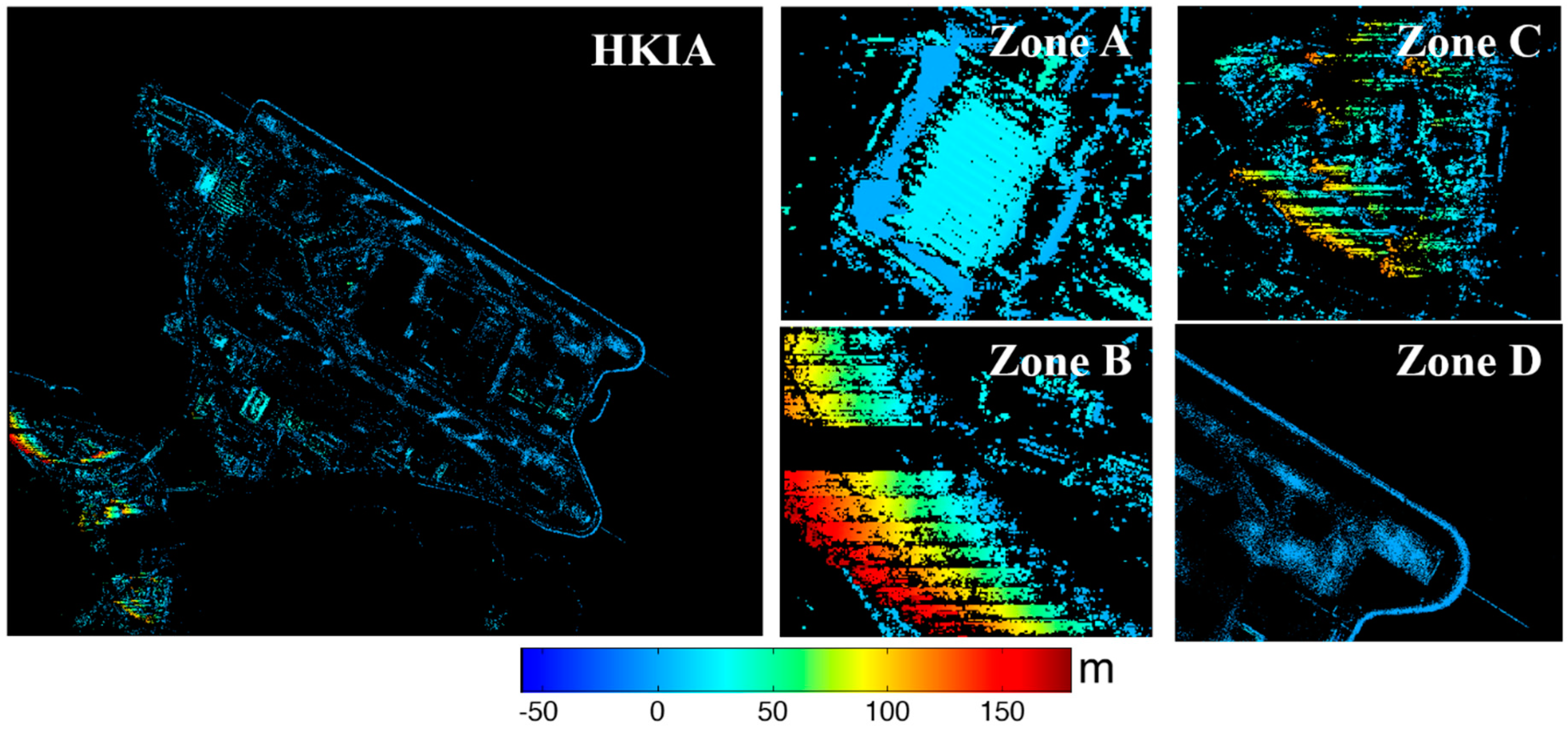
4.1. Study Area and Data
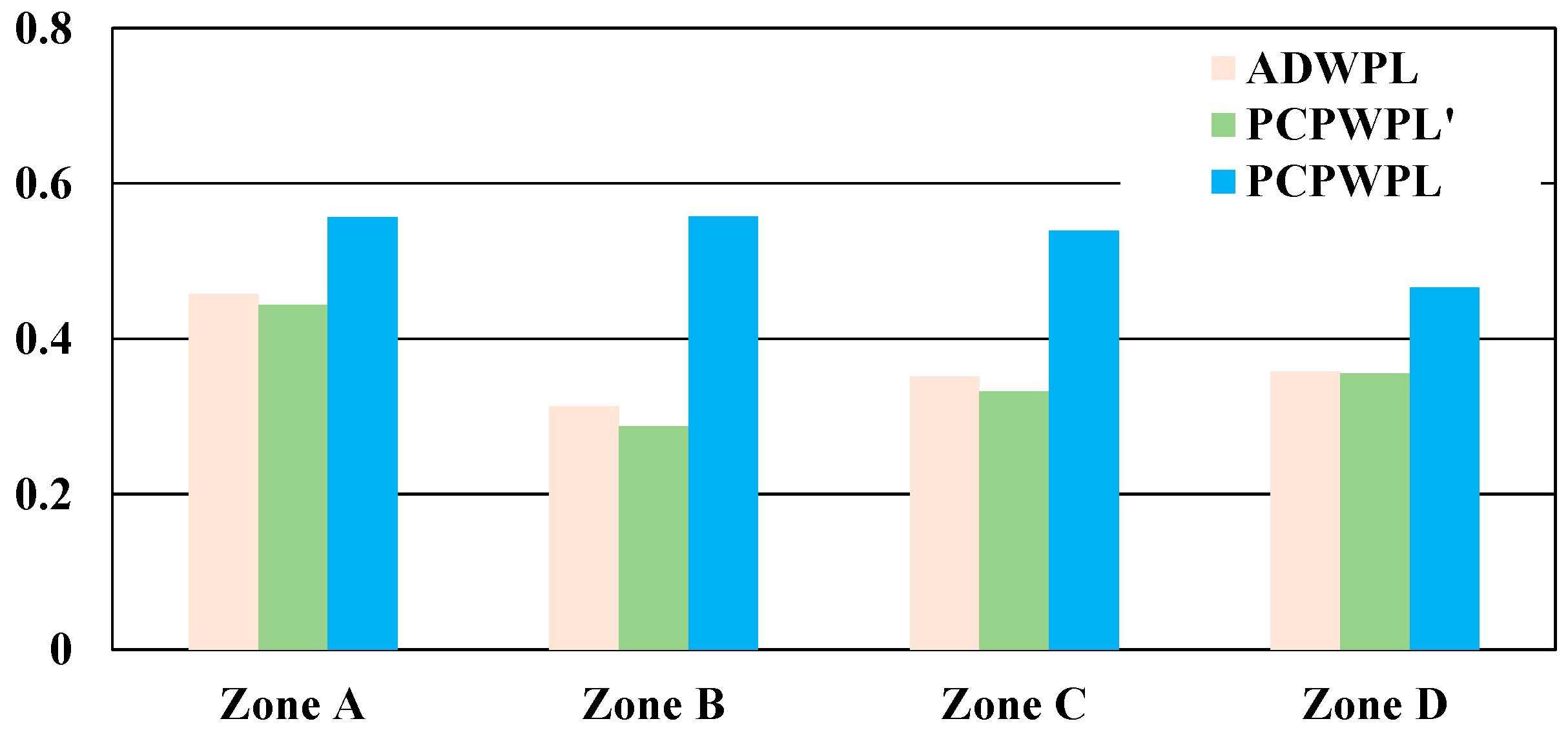
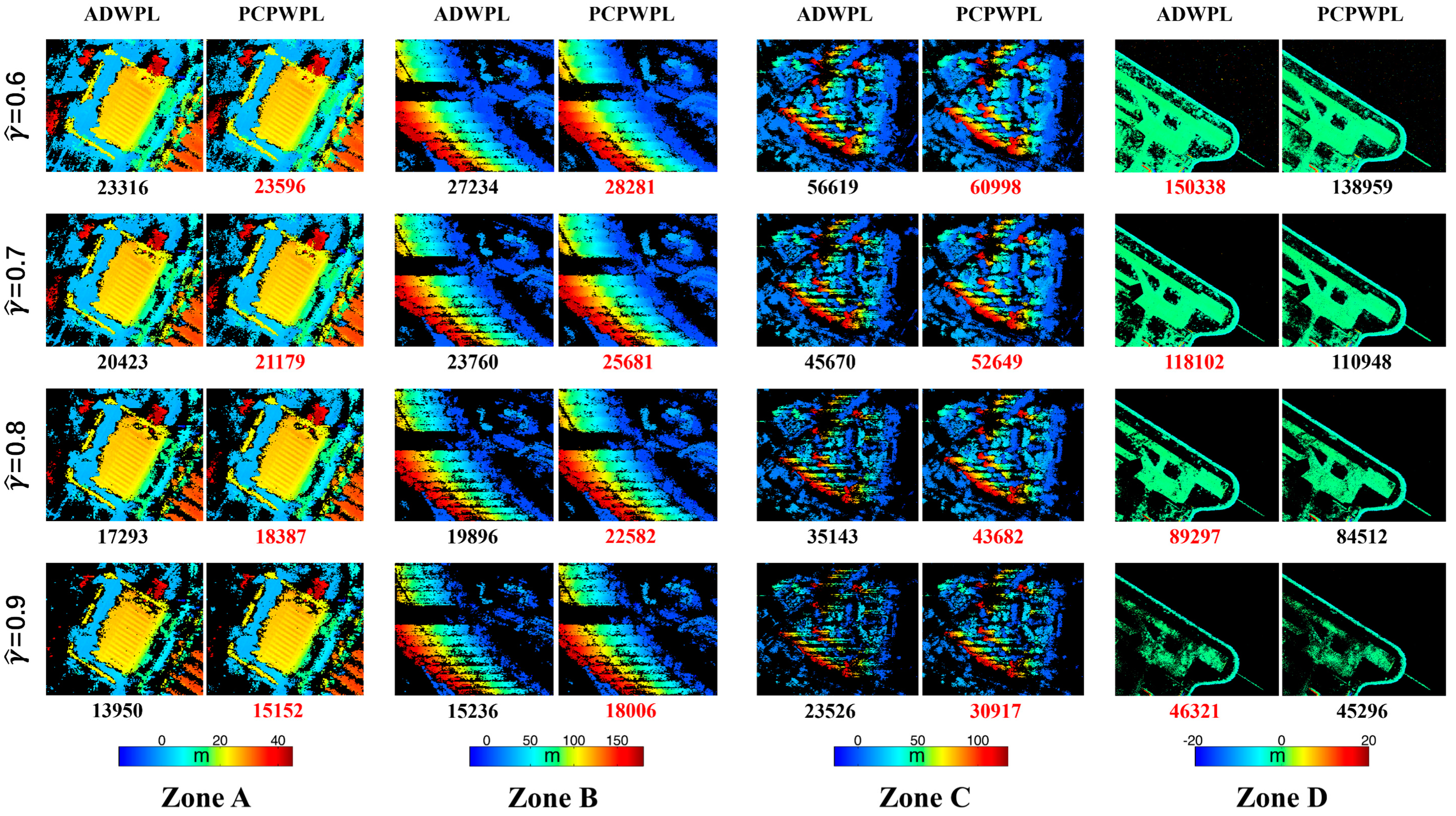
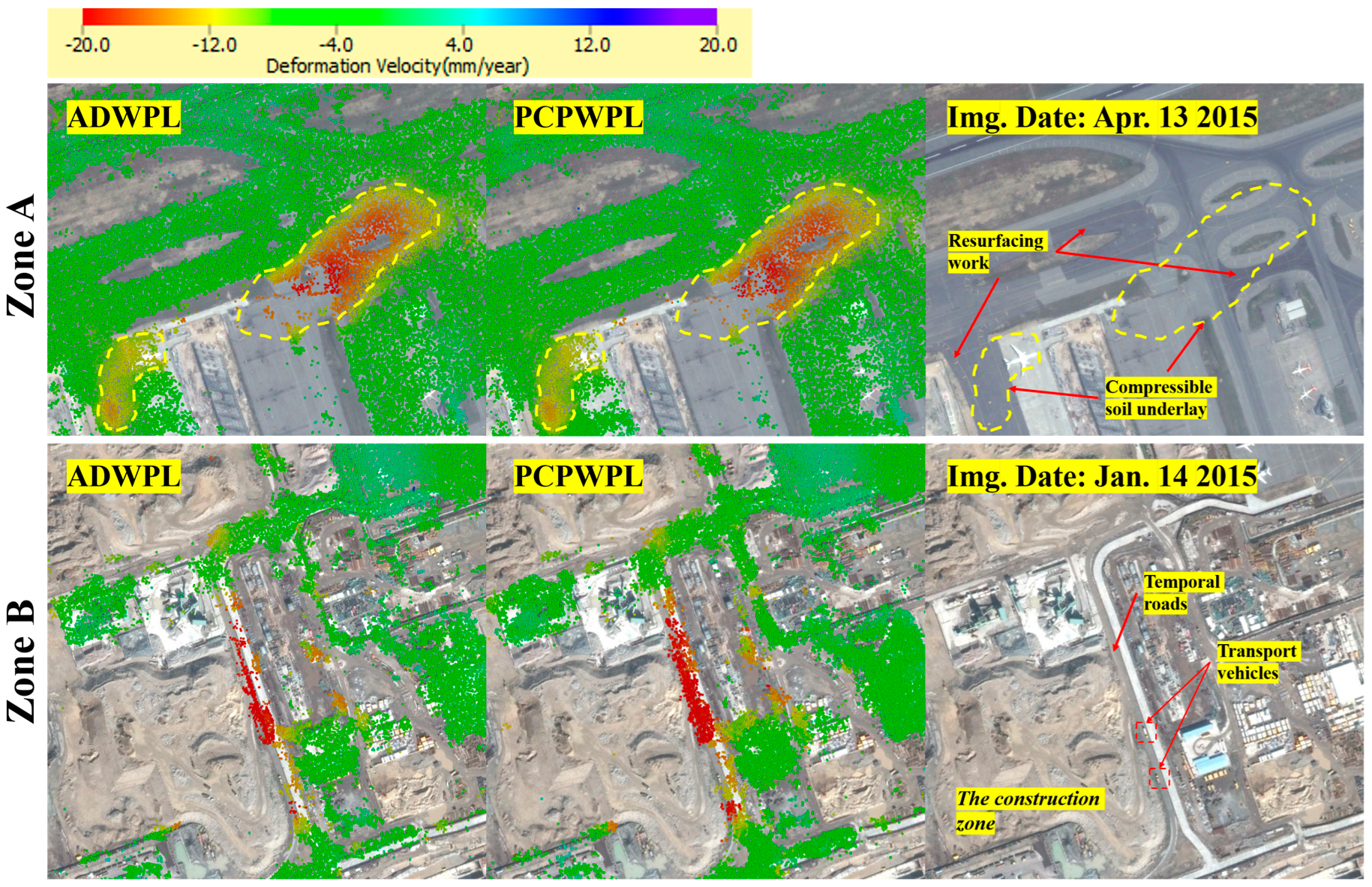
4.2. Experimental Results
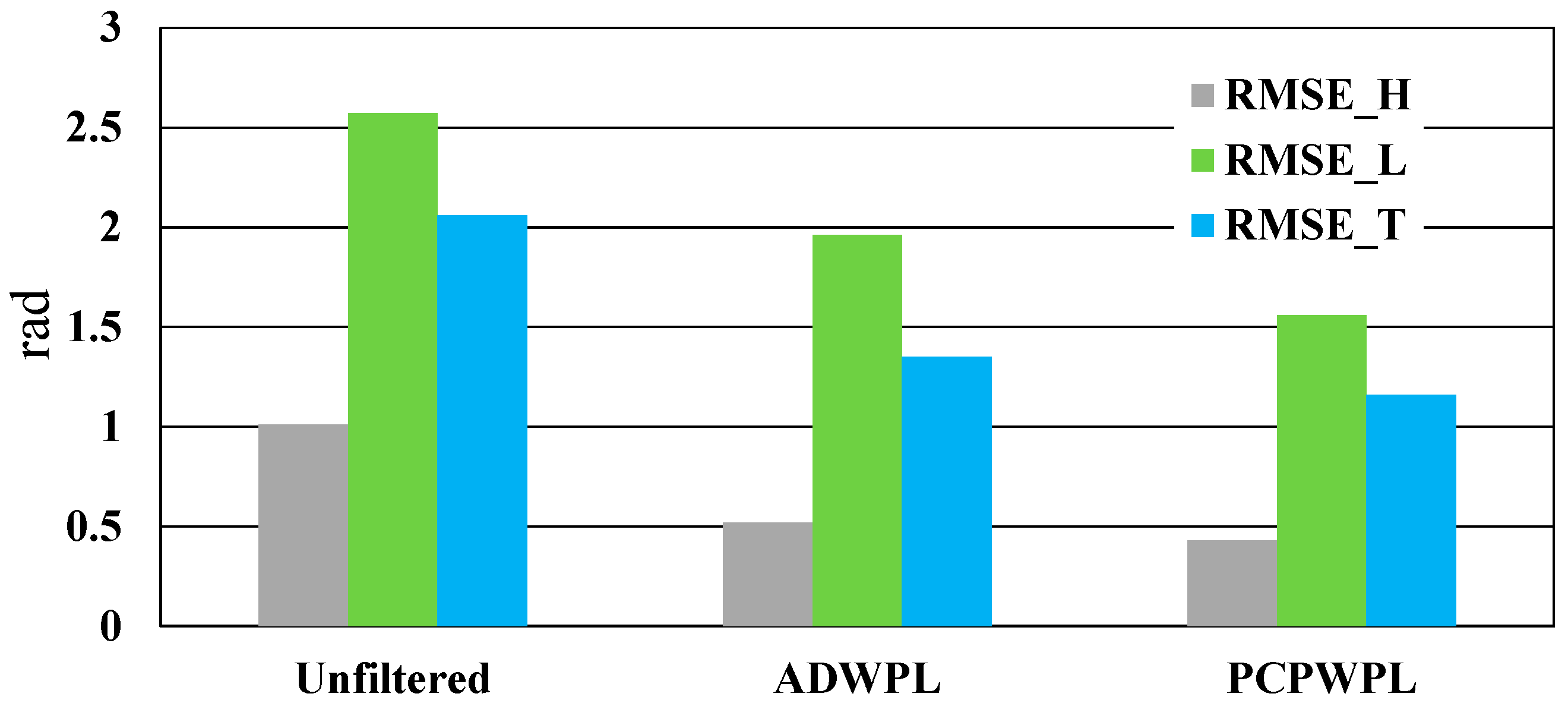
4.3. Deformation Estimates and Cross-Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Even, M.; Schulz, K. InSAR Deformation Analysis with Distributed Scatterers: A Review Complemented by New Advances. Remote Sens. 2018, 10, 744. [Google Scholar] [CrossRef]
- Yu, H.; Lee, H.; Yuan, T.; Cao, N. A novel method for deformation estimation based on multibaseline InSAR phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5231–5243. [Google Scholar] [CrossRef]
- Yu, H.; Lan, Y.; Yuan, Z.; Xu, J.; Lee, H. Phase unwrapping in InSAR: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 40–58. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ma, P.; Lin, H.; Lan, H.; Chen, F. Multi-dimensional SAR tomography for monitoring the deformation of newly built concrete buildings. ISPRS J. Photogramm. Remote Sens. 2015, 106, 118–128. [Google Scholar] [CrossRef]
- Lin, H.; Ma, P. Urban infrastructural health diagnosis with satellite-terrestrial sensing technologies. Ann. GIS 2017, 23, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Zeisl, B.; Pollefeys, M. Fusing meter-resolution 4-D InSAR point clouds and optical images for semantic urban infrastructure monitoring. IEEE Trans. Geosci. Remote Sens. 2017, 55, 14–26. [Google Scholar] [CrossRef]
- Zhu, X.; Ge, N.; Shahzad, M. Joint Sparsity in SAR Tomography for Urban Mapping. IEEE J. Sel. Top. Signal Process. 2015, 9, 1498–1509. [Google Scholar] [CrossRef]
- Kang, J.; Wang, Y.; Körner, M.; Zhu, X. Robust object-based multipass InSAR deformation reconstruction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4239–4251. [Google Scholar] [CrossRef]
- Kang, J.; Wang, Y.; Schmitt, M.; Zhu, X. Object-Based Multipass InSAR via Robust Low-Rank Tensor Decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3062–3077. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, 96–106. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Bamler, R. Retrieval of phase history parameters from distributed scatterers in urban areas using very high resolution SAR data. ISPRS J. Photogramm. Rem. Sens. 2012, 73, 89–99. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N. Fusion of Monostatic/Bistatic InSAR Stacks for Urban Area Analysis via Distributed Scatterers. IEEE Geosci. Remote Sens. Lett. 2013, 11, 733–737. [Google Scholar] [CrossRef]
- Soergel, U. Potential and limits of InSAR data for building reconstruction in built-up areas. ISPRS J. Photogramm. Rem. Sens. 2003, 58, 113–123. [Google Scholar]
- Karathanassi, V.; Iossifidis, C.; Rokos, D. A texture-based classification method for classifying built areas according to their density. Int. J. Remote Sens. 2000, 21, 1807–1823. [Google Scholar] [CrossRef]
- Shi, G.; Lin, H.; Ma, P. A Hybrid Method for Stability Monitoring in Low-Coherence Urban Regions Using Persistent and Distributed Scatterers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3811–3821. [Google Scholar] [CrossRef]
- Schmidt, D.; Bürgmann, R. Time-dependent land uplift and subsidence in the Santa Clara valley, California, from a large interferometric synthetic aperture radar data set. J. Geophys. Res. Solid Earth 2003, 108, 1–13. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
- Wang, H.; Wright, T.; Yu, Y.; Lin, H.; Jiang, L.; Li, C.; Qiu, G. InSAR reveals coastal subsidence in the Pearl River Delta, China. Geophys. J. Int. 2012, 191, 1119–1128. [Google Scholar] [CrossRef]
- Perissin, D.; Wang, T. Time-Series InSAR applications over urban areas in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 92–100. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Lu, Z. Ground settlement monitoring based on temporarily coherent points between two SAR acquisitions. ISPRS J. Photogramm. Rem. Sens. 2011, 66, 146–152. [Google Scholar] [CrossRef]
- Fornaro, G.; Verde, S.; Reale, D.; Pauciullo, A. CAESAR: An approach based on covariance matrix decomposition to improve multibaseline–multitemporal interferometric SAR processing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2050–2065. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, H. A phase-decomposition-based PSInSAR processing method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1074–1090. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Tang, M.; Liao, M.; Xu, Q.; Gong, J.; Ao, M. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: A case study of Jiaju landslide in Danba, China. Remote Sens. Environ. 2018, 205, 180–198. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR stack multilooking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Hanssen, R.; Malhotra, R.; Chang, L. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Song, H.; Sun, Y.; Wang, R.; Li, N.; Zhang, B.; Wang, Y.; Fei, W. An Adaptive Multilook Approach for Small Sets of Multitemporal SAR Data Based on Adaptive Joint Data Vector. IEEE Geosci. Rem. Sens. Lett. 2017, 14, 1161–1165. [Google Scholar] [CrossRef]
- Schmitt, M.; Schönberger, J.; Stilla, U. Adaptive Covariance Matrix Estimation for Multi-Baseline InSAR Data Stacks. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6807–6817. [Google Scholar] [CrossRef]
- Jiang, M.; Yong, B.; Tian, X.; Malhotra, R.; Hu, R.; Li, Z.; Yu, Z.; Zhang, X. The potential of more accurate InSAR covariance matrix estimation for land cover mapping. ISPRS J. Photogramm. Rem. Sens. 2017, 126, 120–128. [Google Scholar] [CrossRef]
- Narayan, A.; Tiwari, A.; Dwivedi, R.; Dikshit, O. A Novel Measure for Categorization and Optimal Phase History Retrieval of Distributed Scatterers for InSAR Applications. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5843–5849. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, H. Mathematical framework for phase-triangulation algorithms in distributed-scatterer interferometry. IEEE Geosci. Rem. Sens. Lett. 2015, 12, 1838–1842. [Google Scholar]
- Hanson, B.; Klink, K.; Matsuura, K.; Robeson, S.; Willmott, C. Vector Correlation: Review, Exposition, and Geographic Application. Ann. Assoc. Am. Geogr. 1992, 82, 103–116. [Google Scholar] [CrossRef]
- Schreier, P. A Unifying Discussion of Correlation Analysis for Complex Random Vectors. IEEE Trans. Signal Process. 2008, 56, 1327–1336. [Google Scholar] [CrossRef]
- Guarnieri, A.; Tebaldini, S. On the exploitation of target statistics for SAR interferometry applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3436–3443. [Google Scholar] [CrossRef]
- Zhang, K.; Song, R.; Wang, H.; Wu, D.; Wang, H. Interferometric phase reconstruction using simplified coherence network. ISPRS J. Photogramm. Rem. Sens. 2016, 119, 1–9. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, R.; Deng, Y.; Ma, P.; Lin, H.; Wang, J. Mapping the Yellow River Delta land subsidence with multitemporal SAR interferometry by exploiting both persistent and distributed scatterers. ISPRS J. Photogramm. Remote Sens. 2019, 148, 157–173. [Google Scholar] [CrossRef]
- Ma, P.; Lin, H. Robust detection of single and double persistent scatterers in urban built environments. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2124–2139. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer InSAR for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112, 19. [Google Scholar] [CrossRef]
- Hotelling, H. Relations between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Kettenring, J. Canonical analysis of several sets of variables. Biometrika 1971, 58, 433–451. [Google Scholar] [CrossRef]
- Samiei-Esfahany, S. Exploitation of Distributed Scatterers in Synthetic Aperture Radar Interferometry. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Deledalle, C.; Denis, L.; Tupin, F. NL-InSAR: Nonlocal Interferogram Estimation. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1441–1452. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, Y.; Fei, W.; Wang, R.; Song, H.; Wang, J.; Li, N. Modified statistically homogeneous pixels’ selection with multitemporal SAR images. IEEE Geosci. Rem. Sens. Lett. 2016, 13, 1930–1934. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Bamler, R. Advanced coherence stacking technique using high resolution TerraSAR-X spotlight data. In Proceedings of the 2011 Joint Urban Remote Sensing Event (IEEE), Munich, Germany, 11–13 April 2011; pp. 233–236. [Google Scholar] [CrossRef]
- Sun, Q.; Jiang, L.; Jiang, M.; Ma, P.; Wang, H. Monitoring Coastal Reclamation Subsidence in Hong Kong with Distributed Scatterer Interferometry. Remote Sens. 2018, 10, 1738. [Google Scholar] [CrossRef]
- Jiang, L.; Lin, H. Integrated analysis of SAR interferometric and geological data for investigating long-term reclamation settlement of Chek Lap Kok Airport, Hong Kong. Eng. Geol. 2010, 110, 77–92. [Google Scholar] [CrossRef]
- Chen, F.; Lin, H. Multi-baseline differential SAR interferometry analysis of Lantau Highway, Hong Kong, using ENVISAT ASAR data. Remote Sens. Lett. 2011, 2, 167–173. [Google Scholar] [CrossRef]
- Berry, P. Application of consolidation theory for peat to the design of a reclamation scheme by preloading. Q. J. Eng. Geol. Hydrogeol. 1983, 16, 103–112. [Google Scholar] [CrossRef]
- Mimura, M.; Shibata, T.; Nozu, M.; Kitazawa, M. Deformation analysis of a reclaimed marine foundation subjected to land construction. Soils Found. 1990, 30, 119–133. [Google Scholar] [CrossRef]
- Kim, S.; Wdowinski, S.; Dixon, T.; Amelung, F.; Kim, J.; Won, J. Measurements and predictions of subsidence induced by soil consolidation using persistent scatterer InSAR and a hyperbolic model. Geophys. Res. Lett. 2010, 37, 87–105. [Google Scholar] [CrossRef]
- Shi, G.; Lin, H.; Bürgmann, R.; Ma, P.; Wang, J.; Liu, Y. Early soil consolidation from magnetic extensometers and full resolution SAR interferometry over highly decorrelated reclaimed lands. Remote Sens. Environ. 2019, 231, 111231. [Google Scholar] [CrossRef]
- Zhao, Q.; Lin, H.; Gao, W.; Zebker, H.; Chen, A.; Yeung, K. InSAR detection of residual settlement of an ocean reclamation engineering project: A case study of Hong Kong International Airport. J. Oceanogr. 2011, 67, 415–426. [Google Scholar] [CrossRef]




| No. | Date | No. | Date | ||||
|---|---|---|---|---|---|---|---|
| 1 | 04/10/2013 | −570.273 | −428 | 15 | 06/12/2014 | 0 | 0 |
| 2 | 16/10/2013 | 167.686 | −416 | 16 | 23/01/2015 | −203.352 | 48 |
| 3 | 17/11/2013 | −407.913 | −384 | 17 | 08/02/2015 | −32.422 | 64 |
| 4 | 19/12/2013 | −434.414 | −352 | 18 | 12/03/2015 | 600.770 | 96 |
| 5 | 08/01/2014 | 446.206 | −332 | 19 | 29/04/2015 | 10.405 | 144 |
| 6 | 21/02/2014 | 192.603 | −288 | 20 | 31/05/2015 | −450.135 | 176 |
| 7 | 13/03/2014 | 378.852 | −268 | 21 | 20/06/2015 | −632.838 | 196 |
| 8 | 28/05/2014 | −315.396 | −192 | 22 | 02/07/2015 | −625.484 | 208 |
| 9 | 29/06/2014 | −608.571 | −160 | 23 | 03/08/2015 | 260.131 | 240 |
| 10 | 19/07/2014 | −543.693 | −140 | 24 | 08/09/2015 | 259.052 | 276 |
| 11 | 04/08/2014 | 284.433 | −124 | 25 | 10/10/2015 | 567.223 | 308 |
| 12 | 17/09/2014 | −757.191 | −80 | 26 | 23/11/2015 | −118.312 | 352 |
| 13 | 03/10/2014 | −681.466 | −64 | 27 | 09/12/2015 | 482.739 | 368 |
| 14 | 20/11/2014 | −538.350 | −16 | 28 | 14/01/2016 | 723.162 | 404 |
| Items | ADWPL | PCPWPL |
|---|---|---|
| Computational cost | Higher | Lower |
| value | Lower | Higher |
| Number of detected points (road surface and grass) | Higher | Lower |
| Number of detected points (complex built area) | Lower | Higher |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Ma, P.; Lin, H.; Huang, B.; Zhang, B.; Liu, Y. Potential of Using Phase Correlation in Distributed Scatterer InSAR Applied to Built Scenarios. Remote Sens. 2020, 12, 686. https://doi.org/10.3390/rs12040686
Shi G, Ma P, Lin H, Huang B, Zhang B, Liu Y. Potential of Using Phase Correlation in Distributed Scatterer InSAR Applied to Built Scenarios. Remote Sensing. 2020; 12(4):686. https://doi.org/10.3390/rs12040686
Chicago/Turabian StyleShi, Guoqiang, Peifeng Ma, Hui Lin, Bo Huang, Bowen Zhang, and Yuzhou Liu. 2020. "Potential of Using Phase Correlation in Distributed Scatterer InSAR Applied to Built Scenarios" Remote Sensing 12, no. 4: 686. https://doi.org/10.3390/rs12040686
APA StyleShi, G., Ma, P., Lin, H., Huang, B., Zhang, B., & Liu, Y. (2020). Potential of Using Phase Correlation in Distributed Scatterer InSAR Applied to Built Scenarios. Remote Sensing, 12(4), 686. https://doi.org/10.3390/rs12040686






