Deep Quadruplet Network for Hyperspectral Image Classification with a Small Number of Samples
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Training Data
2.1.2. Testing Data
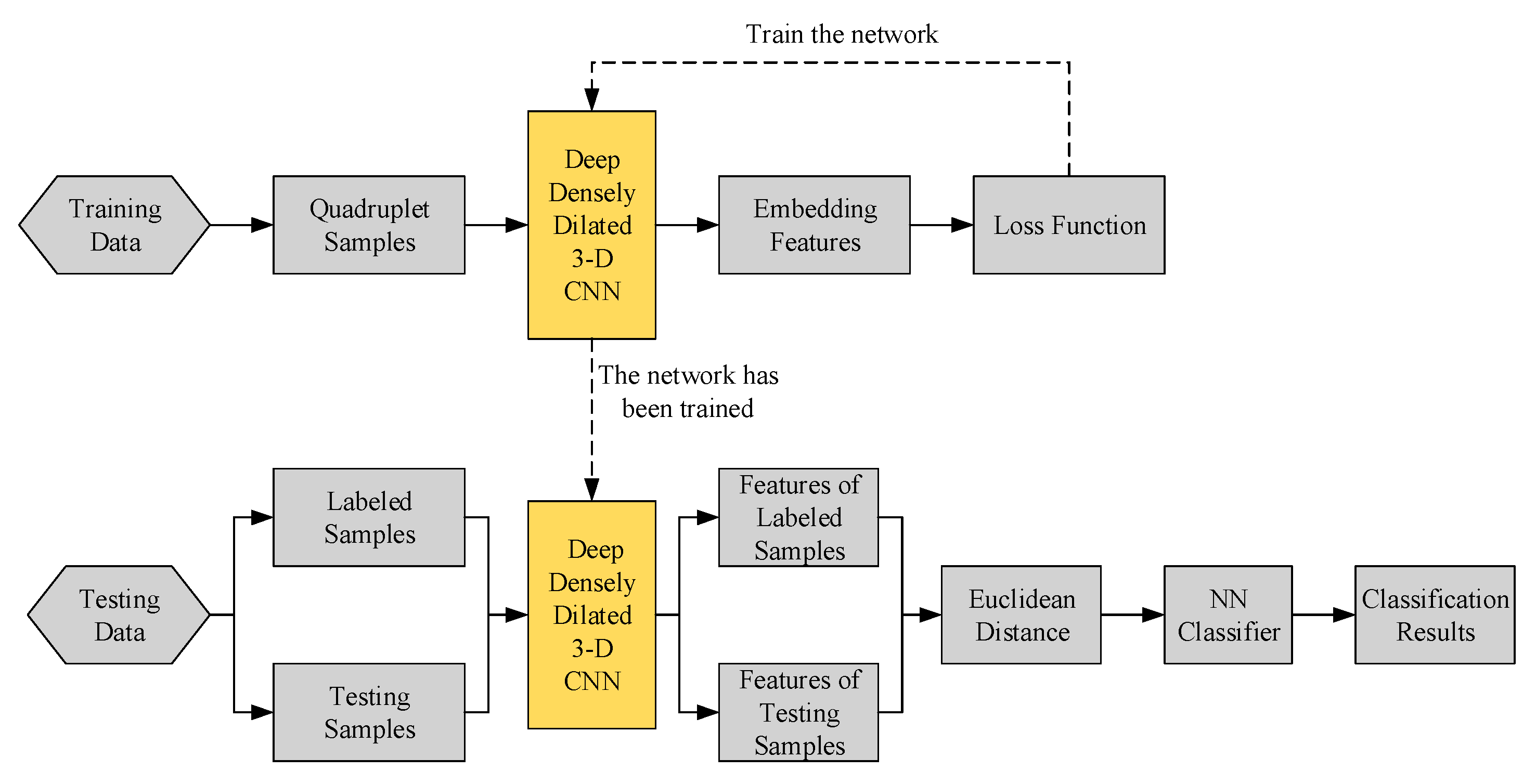
2.2. Structure of the Proposed Method
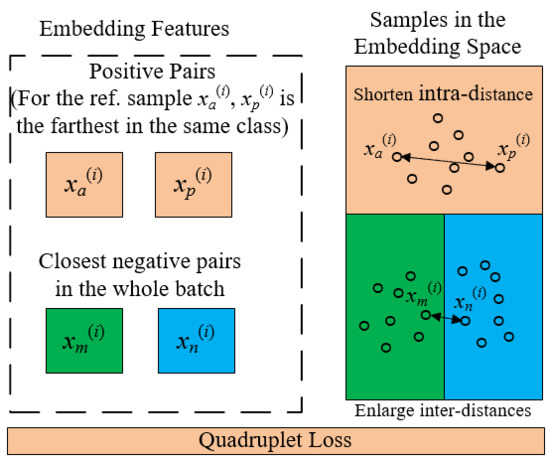
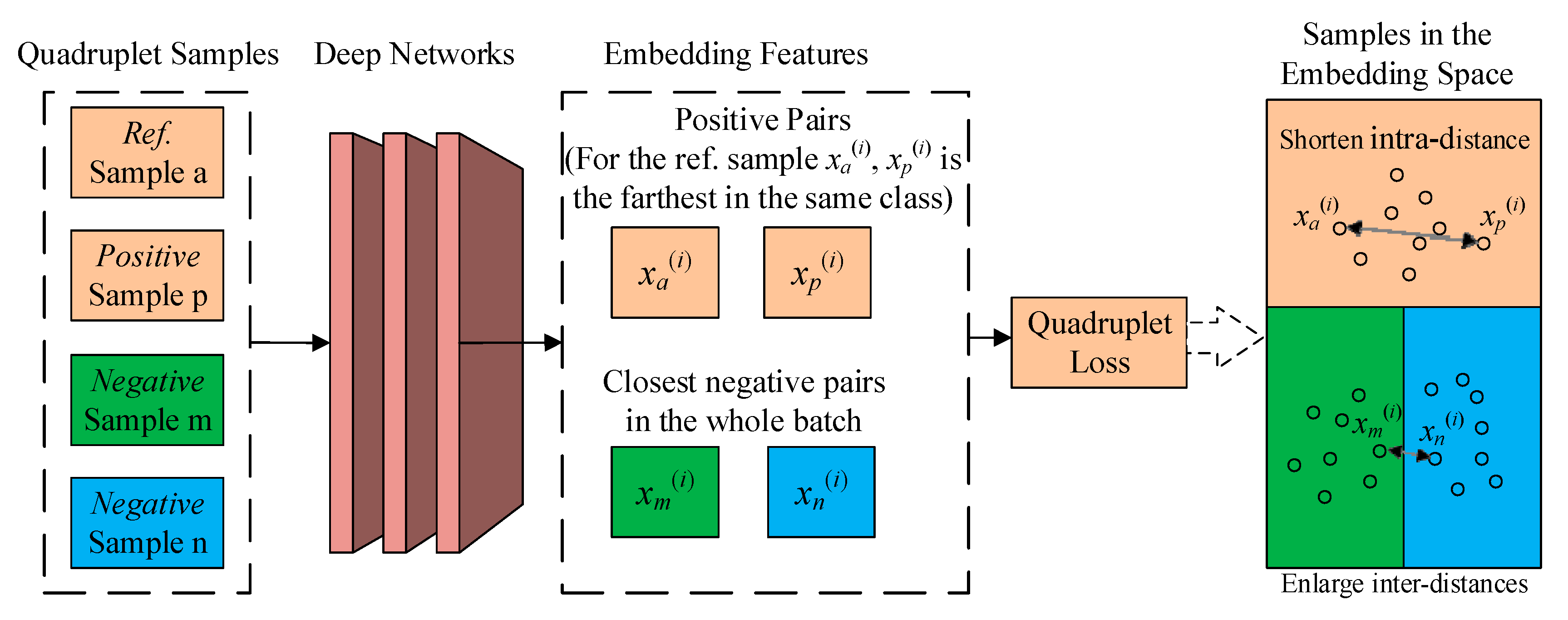
2.3. Quadruplet Learning
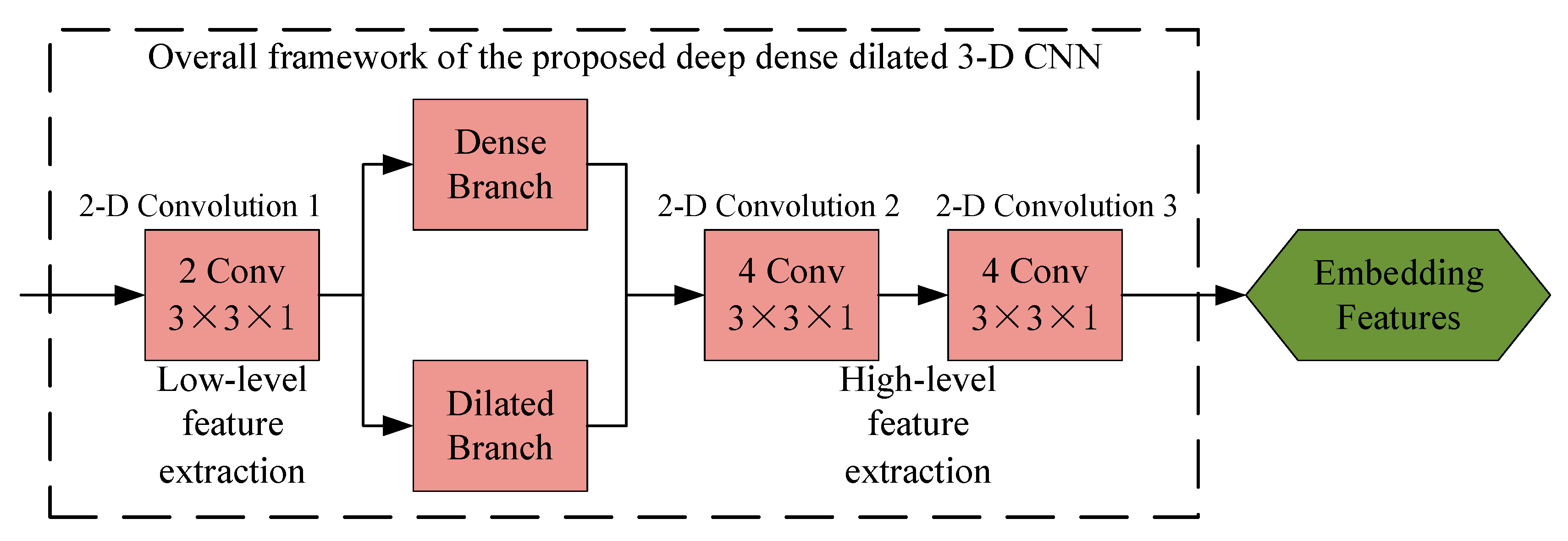
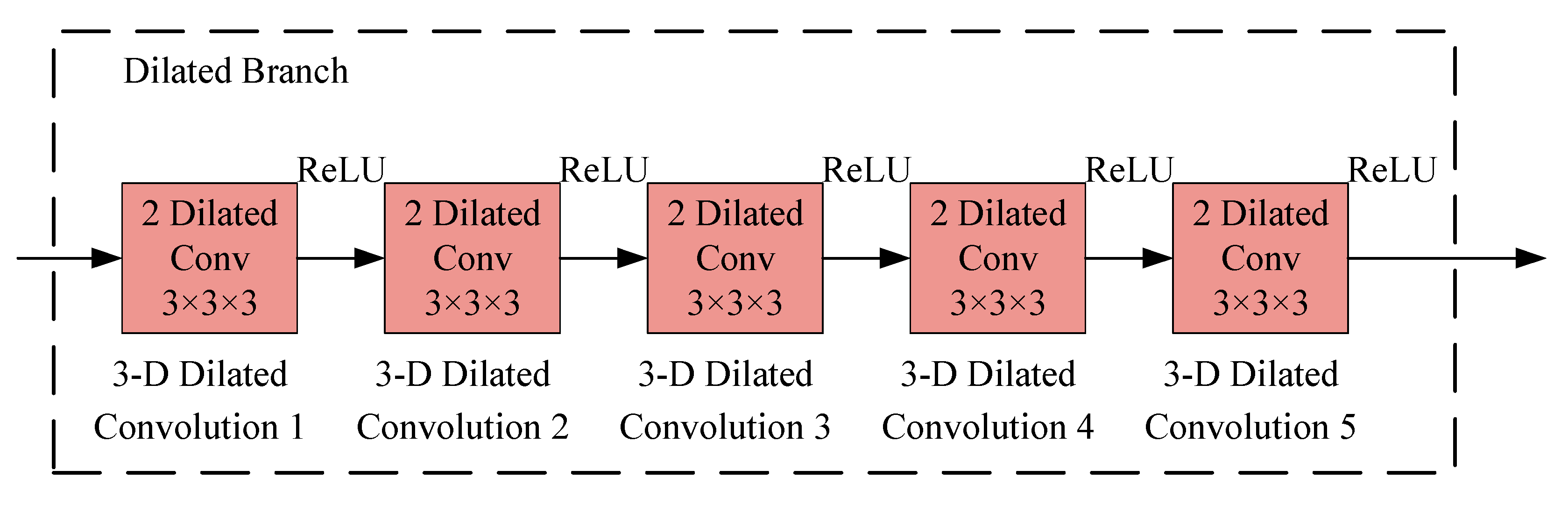
2.4. Deep Dense Dilated 3-D CNN
2.4.1. Deep Network Framework
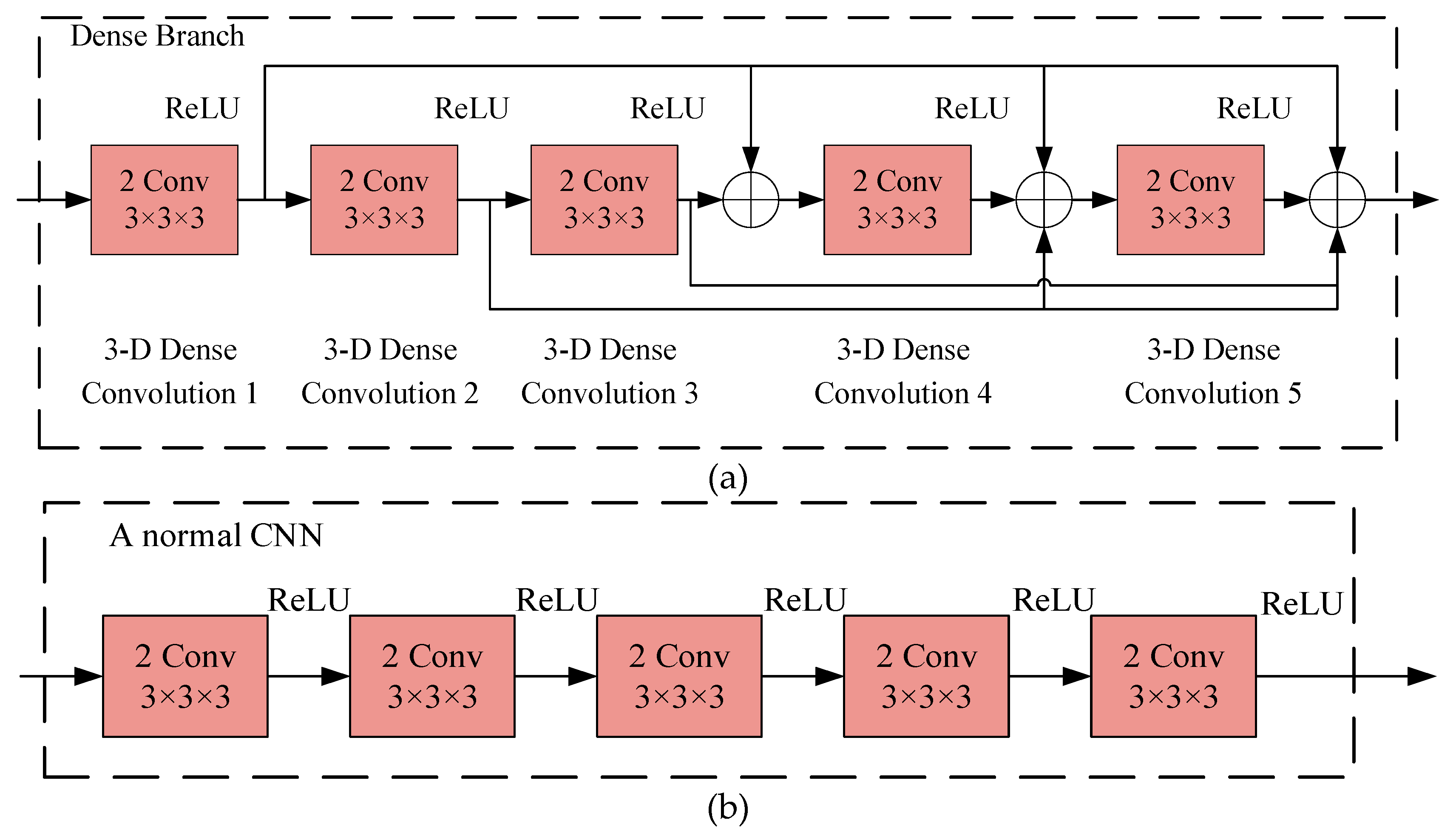
2.4.2. Dense CNN
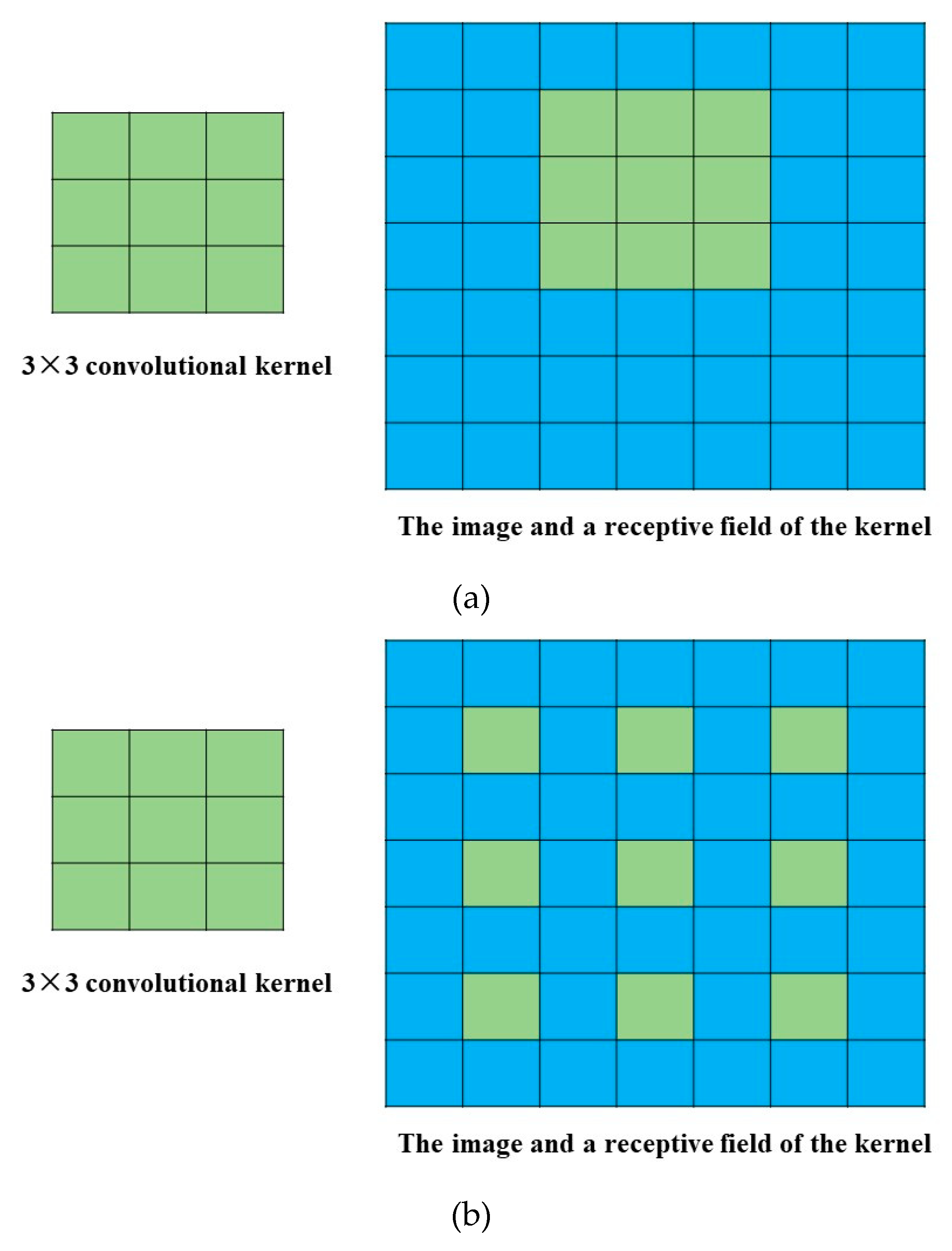
2.4.3. Dilated CNN
2.5. Nearest Neighbor (NN) for Classification
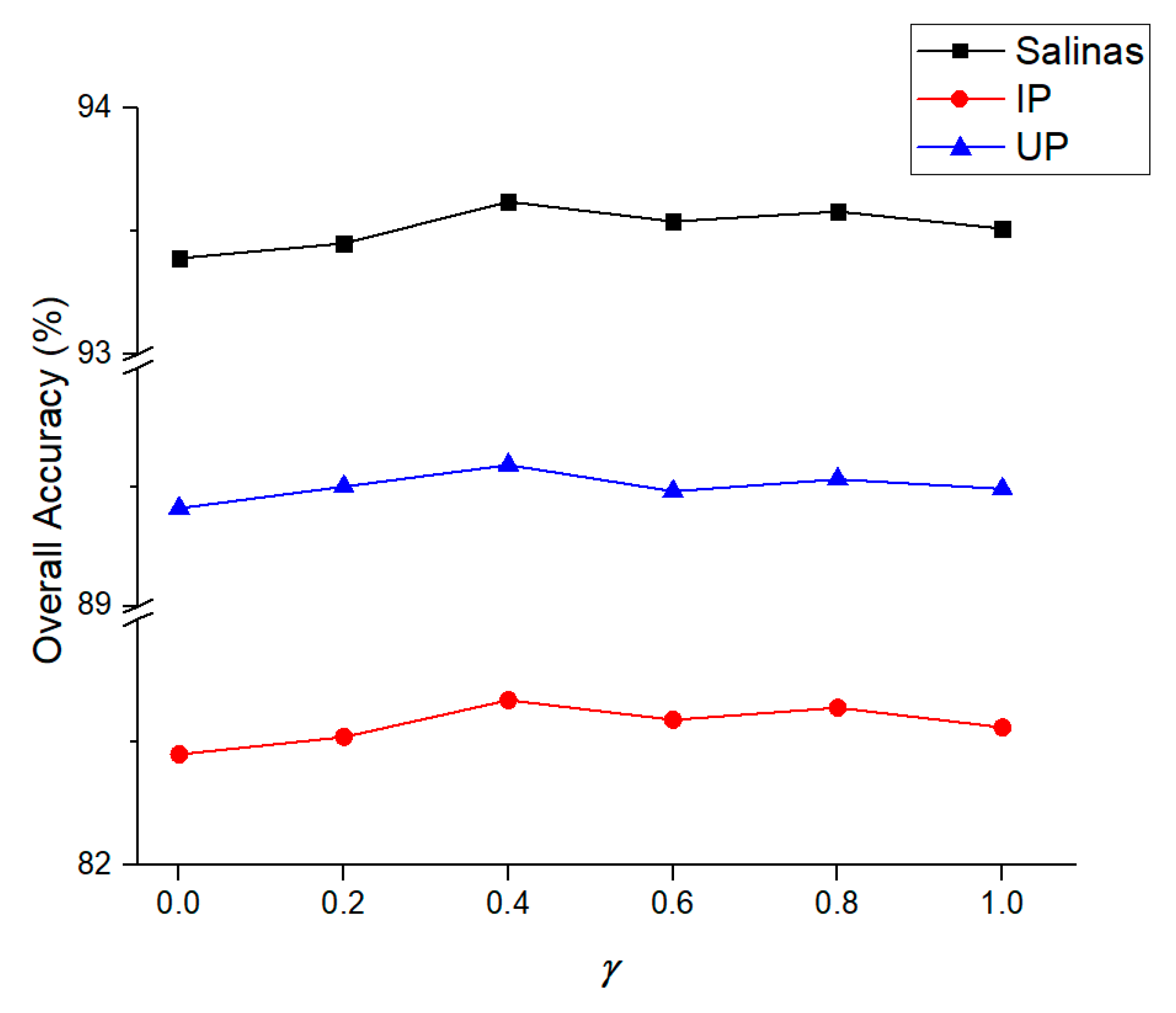
2.6. Parameters Setting
3. Results and Discussion
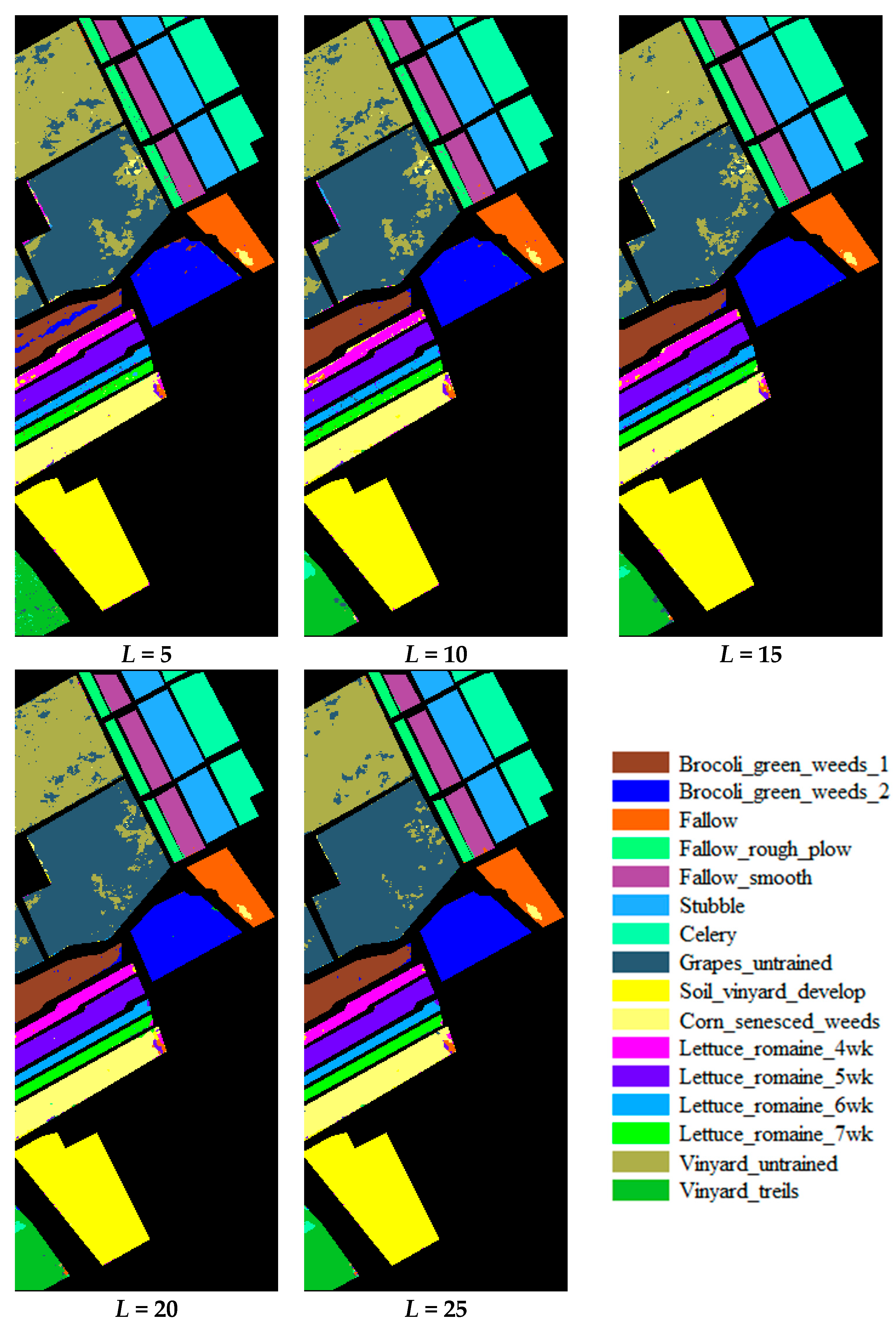
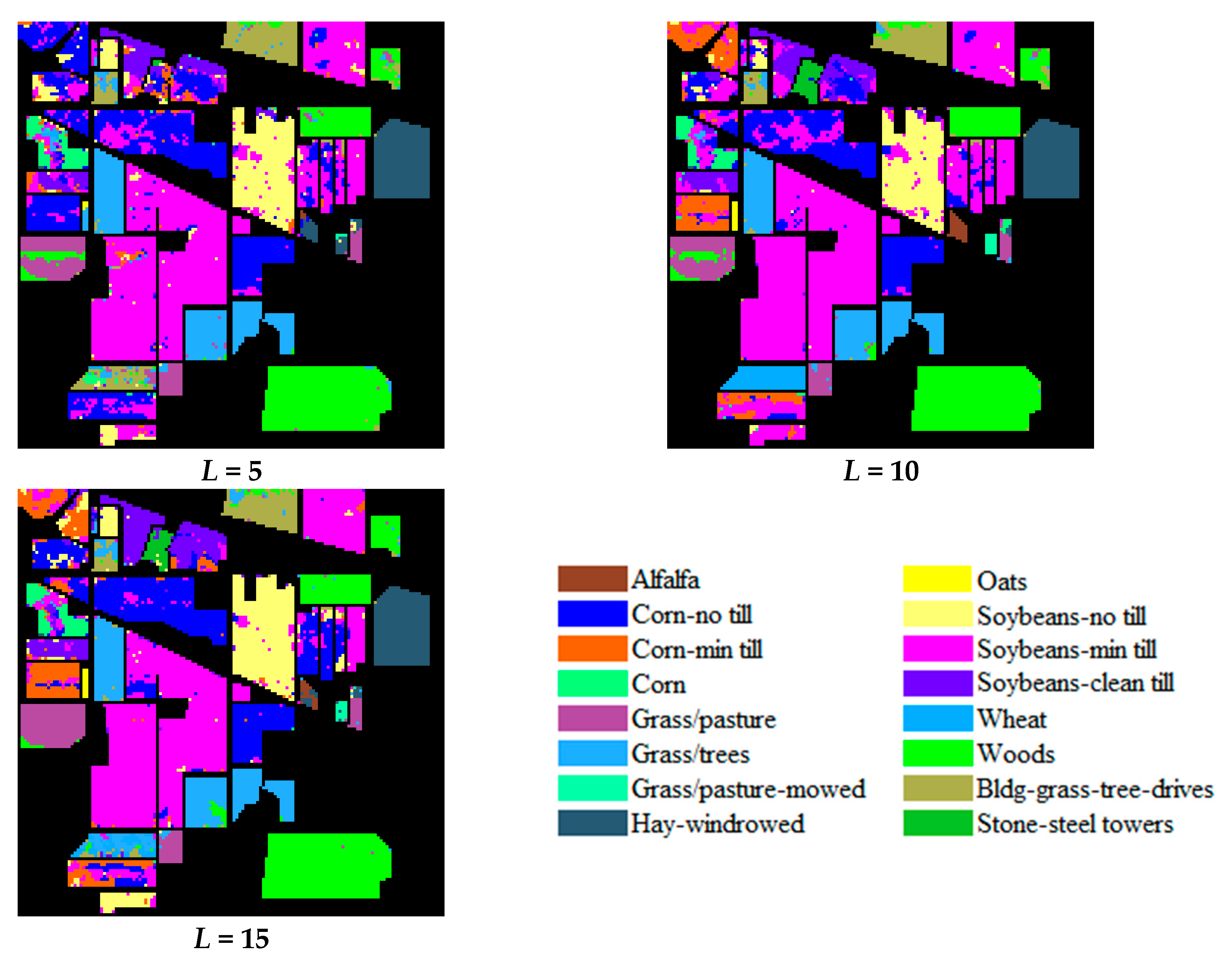
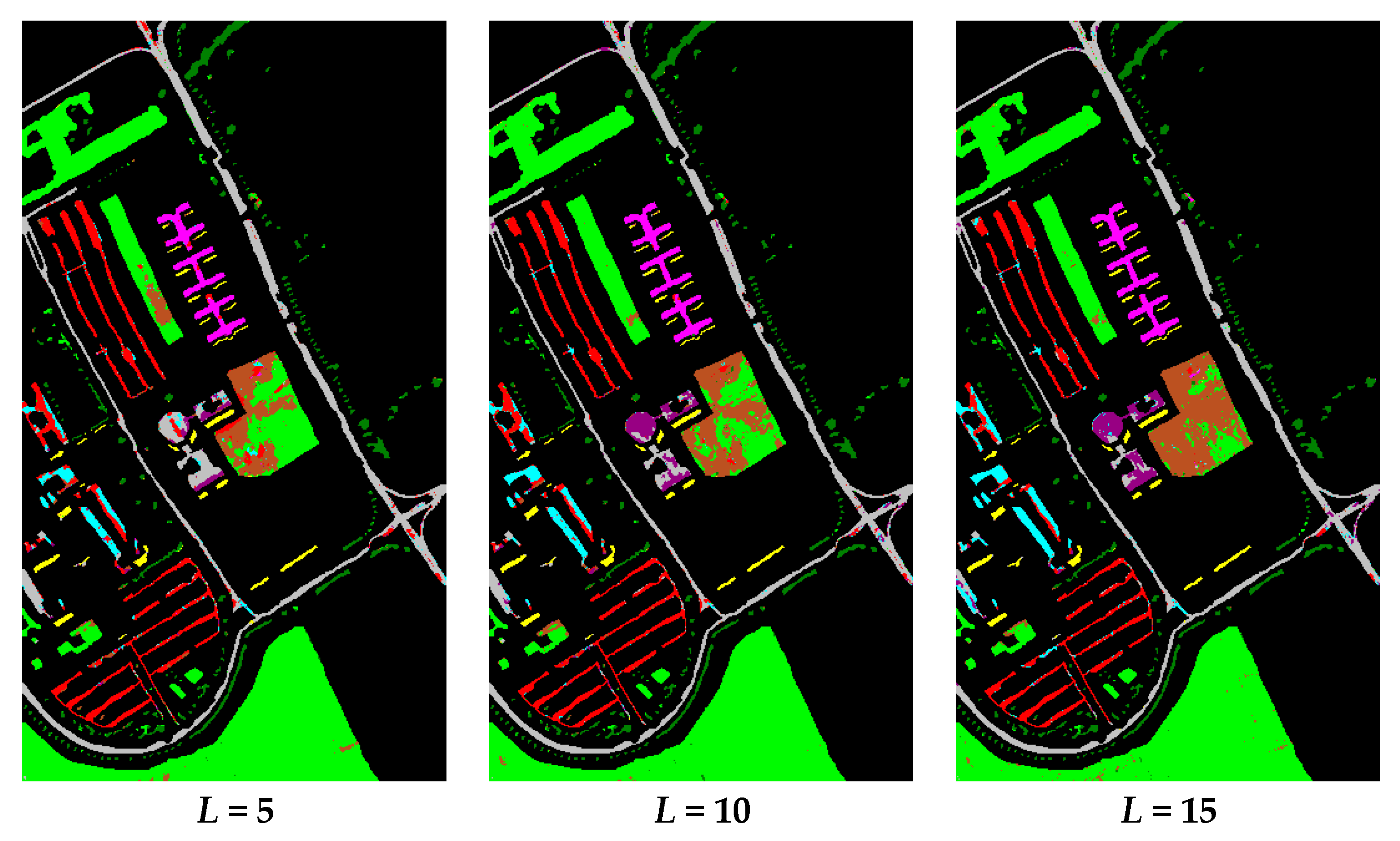
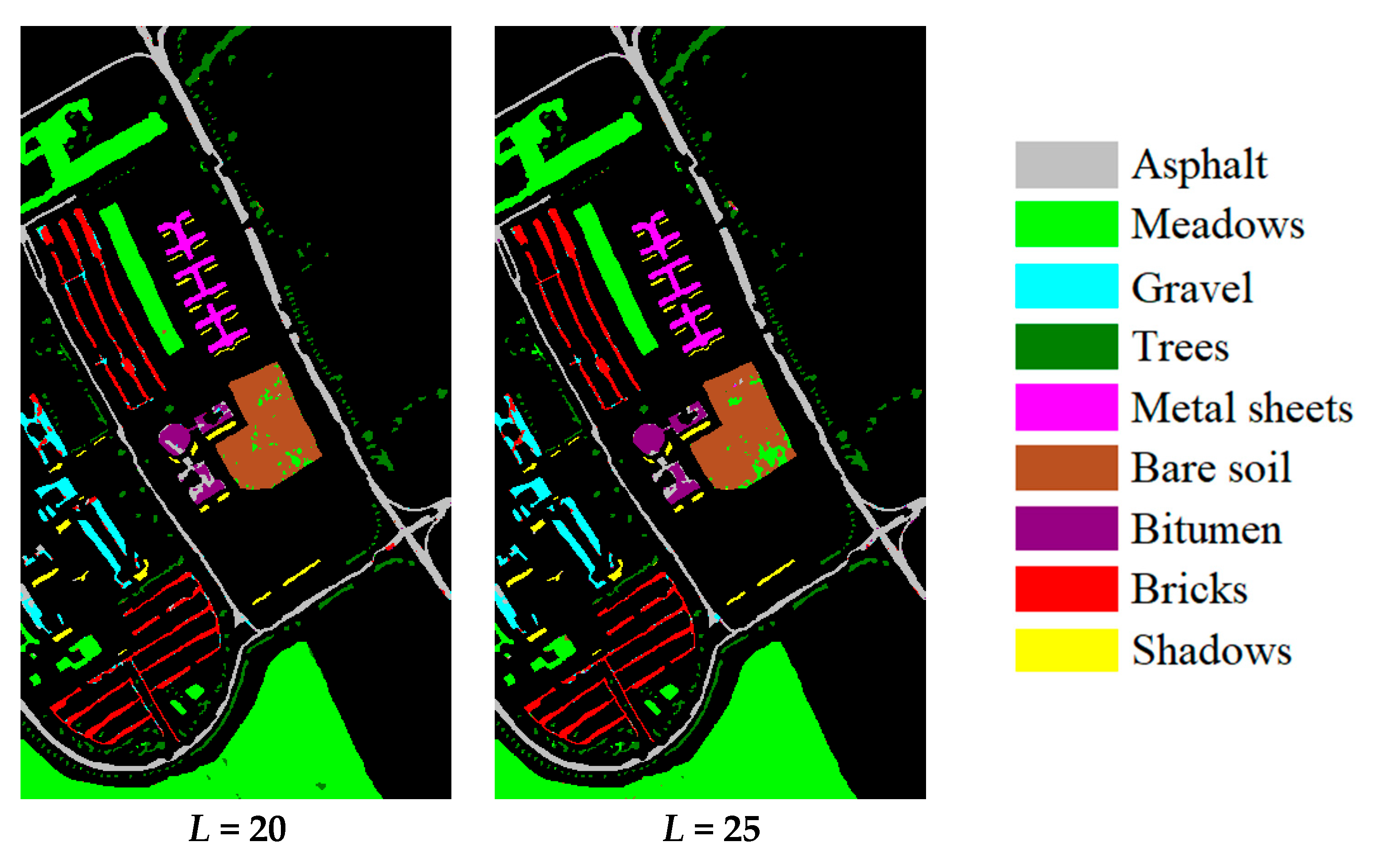
3.1. Accuracy
3.2. Ablation Study
3.3. Time Consumption
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magendran, T.; Sanjeevi, S. Hyperion image analysis and linear spectral unmixing to evaluate the grades of iron ores in parts of Noamundi, Eastern India. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 413–426. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, Q.; Chen, L.; Wang, N.; Zhao, S.; Hui, J. Rapid determination of coalbed methane exploration target region utilizing hyperspectral remote sensing. Int. J. Coal Geol. 2015, 150, 19–34. [Google Scholar] [CrossRef]
- Kruse, F. Preliminary results—Hyperspectral mapping of coral reef systems using EO-1 Hyperion. In Proceedings of the 12th JPL Airborne Geoscience Workshop, Buck Island and U.S. Virgin Islands, Buck Island, USVI, USA, 24–28 February 2003. [Google Scholar]
- Van der Meer, F.D.; Van der Werff, H.M.A.; Van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; de Smeth, J.B.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Swain, P.H.; Ersoy, O.K. Neural Network Approaches Versus Statistical Methods in Classification of Multisource Remote Sensing Data. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; pp. 489–492. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Gao, L.; Li, J.; Khodadadzadeh, M.; Plaza, A.; Zhang, B.; He, Z.; Yan, H. Subspace-Based Support Vector Machines for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 349–353. [Google Scholar]
- Ham, J.; Chen, Y.C.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Z.; Yue, J.; Zhang, X.; Luo, L. On combining multiscale deep learning features for the classification of hyperspectral remote sensing imagery. Int. J. Remote Sens. 2015, 36, 3368–3379. [Google Scholar] [CrossRef]
- Yue, J.; Mao, S.; Li, M. A deep learning framework for hyperspectral image classification using spatial pyramid pooling. Remote Sens. Lett. 2016, 7, 875–884. [Google Scholar] [CrossRef]
- Singhal, V.; Majumdar, A. Row-Sparse Discriminative Deep Dictionary Learning for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 5019–5028. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral-Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarabalka, Y.; Moser, G.; De Giorgi, A.; Fang, L.; Chen, Y.; Chi, M.; et al. New Frontiers in Spectral-Spatial Hyperspectral Image Classification The latest advances based on mathematical morphology, Markov random fields, segmentation, sparse representation, and deep learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- Li, J.; Xi, B.; Du, Q.; Song, R.; Li, Y.; Ren, G. Deep Kernel Extreme-Learning Machine for the Spectral-Spatial Classification of Hyperspectral Imagery. Remote Sens. 2018, 10, 2036. [Google Scholar] [CrossRef]
- Song, A.; Choi, J.; Han, Y.; Kim, Y. Change Detection in Hyperspectral Images Using Recurrent 3D Fully Convolutional Networks. Remote Sens. 2018, 10, 1827. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Ben Amar, C. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Du, B.; Zhang, F. Spectral-Spatial Unified Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5893–5909. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, M.; Li, J.; Yuan, Q.; Wei, Y.; Zhang, L. Spatial-Spectral Fusion by Combining Deep Learning and Variational Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6169–6181. [Google Scholar] [CrossRef]
- Choe, J.; Park, S.; Kim, K.; Park, J.H.; Kim, D.; Shim, H. Face Generation for Low-shot Learning using Generative Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision, ICCV 2017, Venice, Italy, 22–29 October 2017; pp. 1940–1948. [Google Scholar]
- Dong, X.; Zhu, L.; Zhang, D.; Yang, Y.; Wu, F. Fast Parameter Adaptation for Few-shot Image Captioning and Visual Question Answering. In Proceedings of the ACM Multimedia Conference on Multimedia Conference, Seoul, Korea, 22–26 October 2018; pp. 54–62. [Google Scholar]
- Shaban, A.; Bansal, S.; Liu, Z.; Essa, I.; Boots, B. One-Shot Learning for Semantic Segmentation. In Proceedings of the British Machine Vision Conference (BMVC), London, UK, 4–7 September 2017; Available online: https://kopernio.com/viewer?doi=arXiv:1709.03410v1&route=6 (accessed on 12 February 2020).
- Schwartz, E.; Karlinsky, L.; Shtok, J.; Harary, S.; Marder, M.; Kumar, A.; Feris, R.; Giryes, R.; Bronstein, A.M. Delta-encoder: An effective sample synthesis method for few-shot object recognition. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.S.; Hospedales, T.M. Learning to Compare: Relation Network for Few-Shot Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015. [Google Scholar]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2290–2304. [Google Scholar] [CrossRef]
- Xu, S.; Li, J.; Khodadadzadeh, M.; Marinoni, A.; Gamba, P.; Li, B. Abundance-Indicated Subspace for Hyperspectral Classification With Limited Training Samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1265–1278. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X.; Zhang, J.; Huang, K. Beyond triplet loss: A deep quadruplet network for person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1704–1719. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Lecture Notes in Computer Science; Feragen, A., Pelillo, M., Loog, M., Eds.; Springer: New York, NY, USA, 2015; Volume 9370, pp. 84–92. [Google Scholar]
- Xiao, Q.; Luo, H.; Zhang, C. Margin Sample Mining Loss: A Deep Learning Based Method for Person Re-Identification. 2017. Available online: https://arxiv.org/pdf/1710.00478.pdf (accessed on 22 October 2019).
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated Residual Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 636–644. [Google Scholar]
- Sun, K.; Geng, X.; Chen, J.; Ji, L.; Tang, H.; Zhao, Y.; Xu, M. A robust and efficient band selection method using graph representation for hyperspectral imagery. Int. J. Remote Sens. 2016, 37, 4874–4889. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Joachims, T. Transductive inference for text classification using Support Vector Machines. In Proceedings of the 16th International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; pp. 200–209. [Google Scholar]
- Kuo, B.; Huang, C.; Hung, C.; Liu, Y.; Chen, I. Spatial information based support vector machine for hyperspectral image classification. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Honolulu, Hawaii, USA, 25–30 July 2010; pp. 832–835. [Google Scholar]
- Wang, L.; Hao, S.; Wang, Q.; Wang, Y. Semi-supervised classification for hyperspectral imagery based on spatial-spectral Label Propagation. ISPRS J. Photogra. Remote Sens. 2014, 97, 123–137. [Google Scholar] [CrossRef]
- Tan, K.; Hu, J.; Li, J.; Du, P. A novel semi-supervised hyperspectral image classification approach based on spatial neighborhood information and classifier combination. ISPRS J. Photogra. Remote Sens. 2015, 105, 19–29. [Google Scholar] [CrossRef]
- Dópido, I.; Li, J.; Marpu, P.R.; Plaza, A.; Dias, J.M.B.; Benediktsson, J.A. Semisupervised Self-Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4032–4044. [Google Scholar]
- Wang, Y.A.; Kwok, J.; Ni, L.M.; Yao, Q. Generalizing from a Few Examples: A Survey on Few-Shot Learning. 2019. Available online: https://arxiv.org/pdf/1904.05046.pdf (accessed on 1 February 2020).
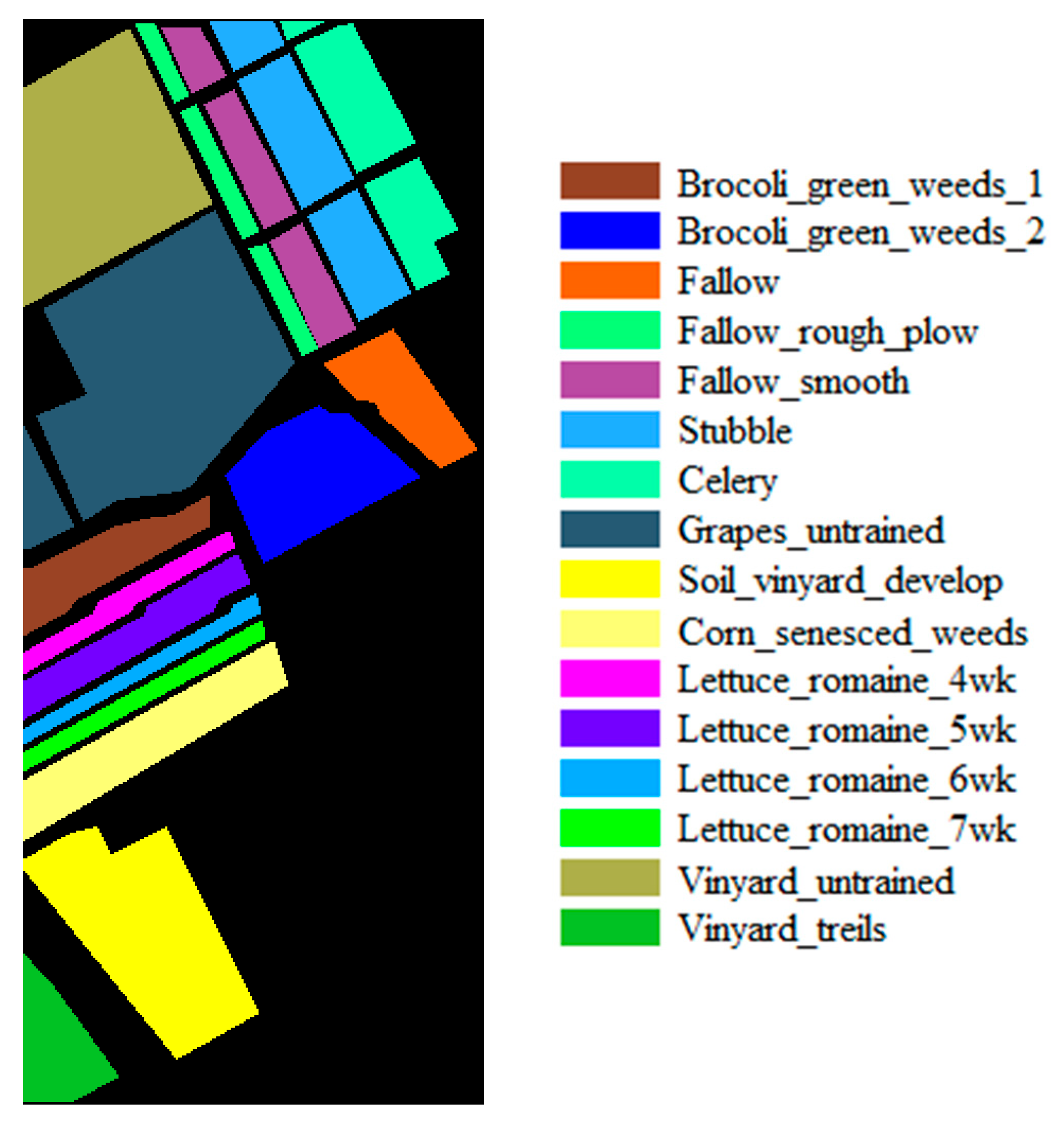
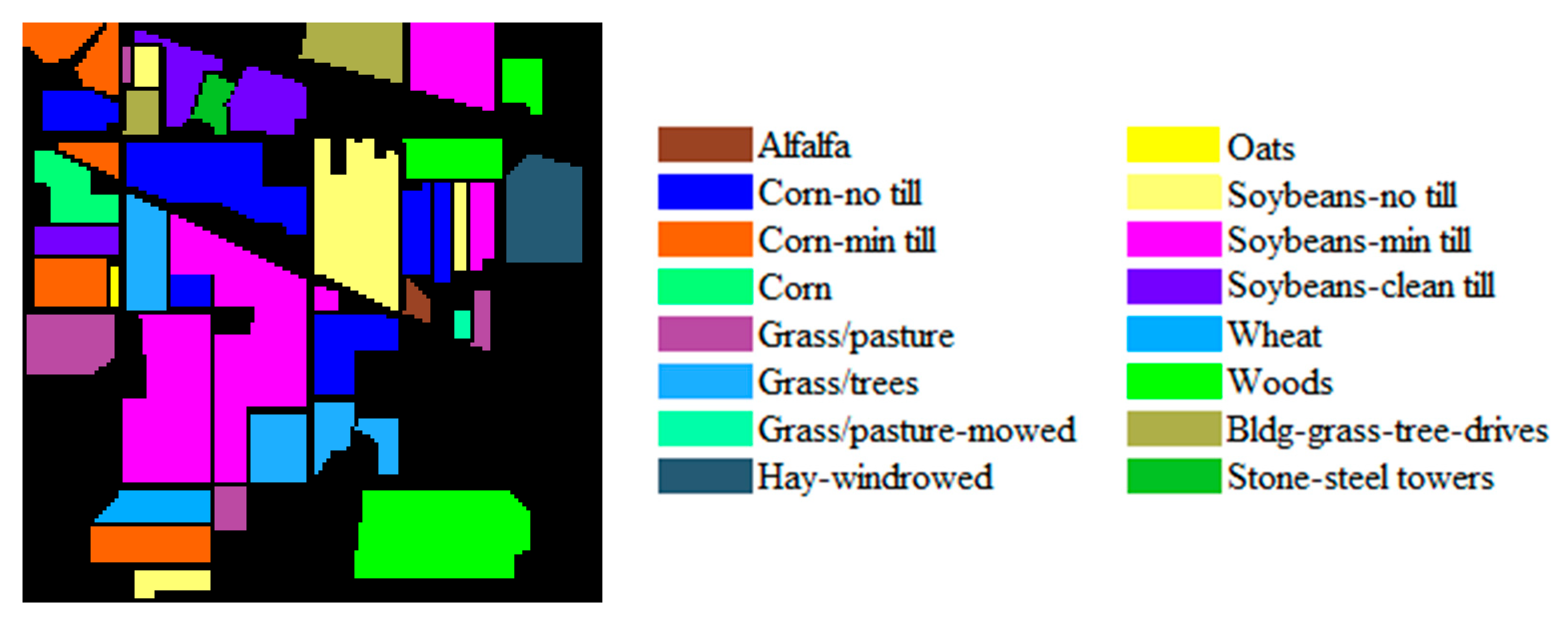
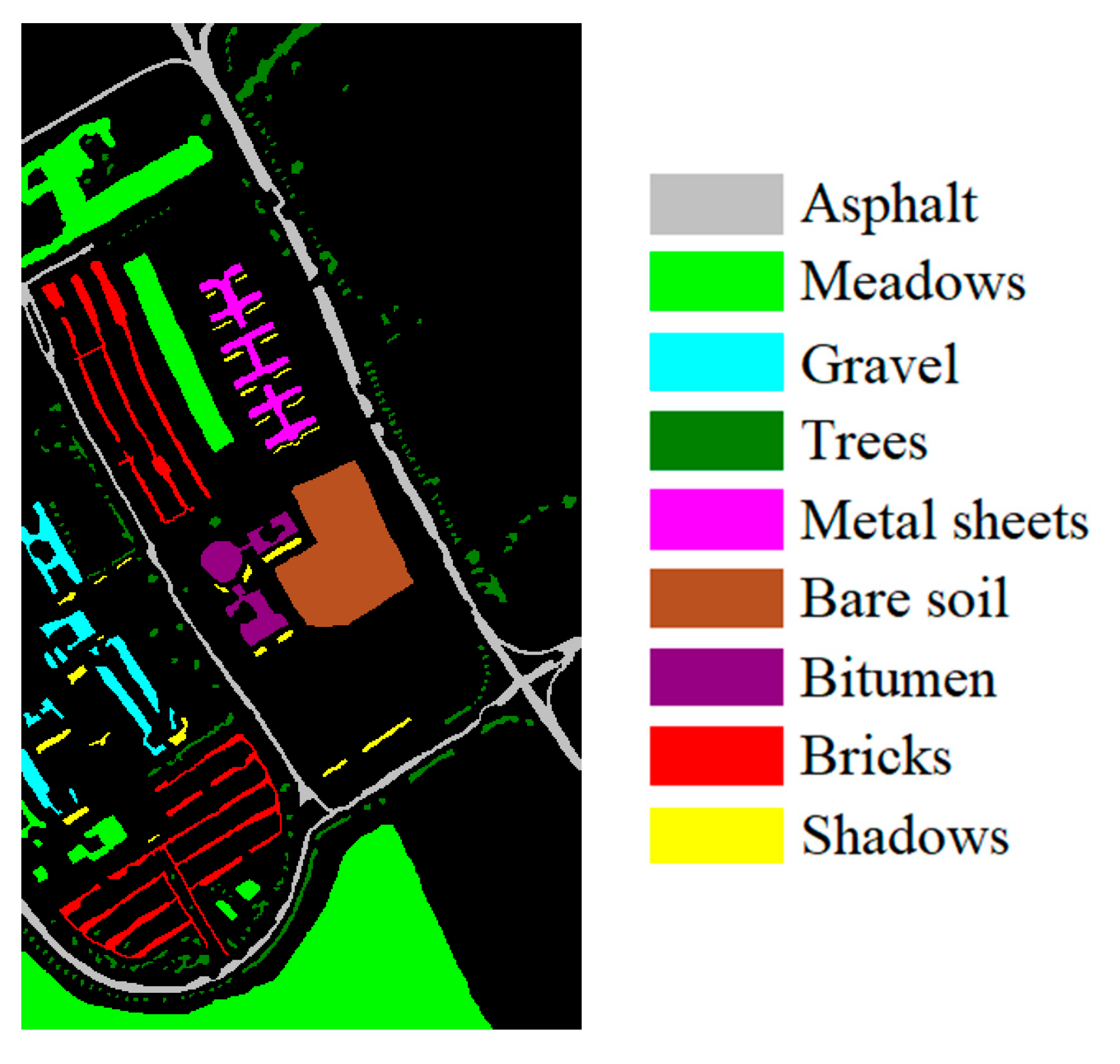
| Dataset Name | Houston | Chikusei | KSC | Botswana |
|---|---|---|---|---|
| Location | Houston | Chikusei | Florida | Botswana |
| Height | 349 | 2517 | 512 | 1476 |
| Width | 1905 | 2335 | 614 | 256 |
| Bands | 144 | 128 | 176 | 145 |
| Spectral Range (nm) | 380–1050 | 363–1018 | 400–2500 | 400–2500 |
| Spatial Resolution (m) | 2.5 | 2.5 | 18 | 30 |
| Num. of Classes | 31 | 19 | 13 | 14 |
| Dataset Name | Salinas | IP | UP |
|---|---|---|---|
| Location | California | Indiana | Pavia |
| Height | 512 | 145 | 610 |
| Width | 217 | 145 | 340 |
| Bands | 204 | 200 | 103 |
| Spectral Range (nm) | 400–2500 | 400–2500 | 430–860 |
| Spatial Resolution (m) | 3.7 | 20 | 1.3 |
| Num. of Classes | 16 | 16 | 9 |
| Input: The training dataset for this batch T={t1, t2, t3, …, ts} The initialized or updated learnable parameter θ |
|---|
| For all pairs of samples (tj, tk) in T Do |
| Calculate the Euclidean distance d (fθ (tj), fθ (tk)) |
| End For |
| Set the loss Lnq = 0 |
| Set , under the condition C(tj) ≠ C(tk) |
| xm = fθ (tm), xn = fθ (tn). (Transfer tm, tn to xm, xn by the network fθ: RF→RD) |
| Forta in the dataset T DO |
| xa = fθ (ta). (Transfer ta to xa by the network fθ: RF→RD) |
| Set , under the condition C(tj) = C(ta) |
| xp = fθ (tp). (Transfer tp to xp by the network fθ: RF→RD) |
| Update: |
| End For |
| Update: |
| Output:θ, Lnq |
| Layer Name | Input Layer | Filter Size | Padding | Output Shape |
|---|---|---|---|---|
| Input | / | / | / | 9 × 9 × N |
| 2-D Convolution 1 | Input | 3 × 3 × 1 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dense Convolution 1 | 2-D Convolution 1 | 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dense Convolution 2 | 3-D Dense Convolution 1 | 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dense Convolution 3 | 3-D Dense Convolution 2 | 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dense Shortcut 1 | 3-D Dense Convolution 1&3 | 3-D Dense Convolution 1 + 3-D Dense Convolution 3 | 9 × 9 × N × 2 | |
| 3-D Dense Convolution 4 | 3-D Dense Shortcut 1 | 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dense Shortcut 2 | 3-D Dense Convolution 1&2&4 | 3-D Dense Convolution 1 + 3-D Dense Convolution 2 + 3-D Dense Convolution 4 | 9 × 9 × N × 2 | |
| 3-D Dense Convolution 5 | 3-D Dense Shortcut 2 | 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dense Shortcut 3 | 3-D Dense Convolution 1&2&3&5 | 3-D Dense Convolution 1 + 3-D Dense Convolution 2 + 3-D Dense Convolution 3 + 3-D Dense Convolution 5 | 9 × 9 × N × 2 | |
| Max Pooling 1 | 3-D Dense Shortcut 3 | 2 × 2 × 2 | No | 5 × 5×ceil (N/2)×2 |
| 3-D Dilated Convolution 1 | 2-D Convolution 1 | 3-D Dilated 3 ×3 × 3× 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dilated Convolution 2 | 3-D Dilated Convolution 1 | 3-D Dilated 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dilated Convolution 3 | 3-D Dilated Convolution 2 | 3-D Dilated 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dilated Convolution 4 | 3-D Dilated Convolution 3 | 3-D Dilated 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| 3-D Dilated Convolution 5 | 3-D Dilated Convolution 4 | 3-D Dilated 3 × 3 × 3 × 2 | Yes | 9 × 9 × N × 2 |
| Max Pooling 2 | 3-D Dilated Convolution 5 | 2 × 2 × 2 | No | 5 × 5×ceil (N/2) × 2 |
| Concatenation | Max Pooling 1&2 | / | / | 5 × 5 × ceil (N/2) × 4 |
| 2-D Convolution 2 | Concatenation | 3 × 3 × 1 × 4 | No | 3 × 3 × ceil (N/2) × 4 |
| 2-D Convolution 3 | 2-D Convolution 2 | 3 × 3 × 1 × 4 | No | 1 × 1 × ceil (N/2) × 4 |
| Full Connected | 2-D Convolution 3 | / | / | 150 |
| Method 1 | L = 5 | L = 10 | L = 15 | L = 20 | L = 25 |
|---|---|---|---|---|---|
| SVM | 73.90 ± 1.91 | 75.62 ± 1.73 | 79.08 ± 1.45 | 77.89 ± 1.20 | 78.05 ± 1.49 |
| LapSVM | 75.31 ± 2.31 | 76.34 ± 1.77 | 77.93 ± 2.42 | 79.40 ± 0.73 | 80.56 ± 1.33 |
| TSVM | 60.43 ± 1.40 | 67.47 ± 1.05 | 69.12 ± 1.32 | 71.03 ± 1.78 | 71.83 ± 1.16 |
| SCS3VM | 74.12 ± 2.44 | 78.49 ± 2.02 | 81.83 ± 0.93 | 81.22 ± 1.27 | 77.08 ± 0.80 |
| SS-LPSVM | 86.79 ± 1.75 | 90.36 ± 1.35 | 90.86 ± 1.36 | 91.77 ± 0.96 | 92.11 ± 1.07 |
| KNN + SNI | 80.39 ± 1.58 | 84.64 ± 1.54 | 86.94 ± 1.52 | 88.28 ± 1.49 | 87.64 ± 1.72 |
| MLR + RS | 78.29 ± 2.16 | 85.03 ± 1.43 | 87.20 ± 1.74 | 88.76 ± 1.87 | 89.42 ± 0.85 |
| SVM + S-CNN | 12.66 ± 2.75 | 50.04 ± 14.34 | 60.72 ± 4.85 | 70.30 ± 2.61 | 71.62 ± 12.05 |
| 3D-CNN | 85.58 ± 2.18 | 86.26 ± 1.84 | 88.01 ± 1.47 | 88.94 ± 1.38 | 91.21 ± 1.23 |
| DFSL + NN | 88.40 ± 1.54 | 89.86 ± 1.69 | 92.15 ± 1.24 | 92.69 ± 0.98 | 93.61 ± 0.83 |
| DFSL + SVM | 85.58 ± 1.87 | 89.73 ± 1.24 | 91.21 ± 1.64 | 93.42 ± 1.25 | 94.28 ± 0.80 |
| New Approach | 89.92 ± 1.87 | 91.11 ± 1.50 | 93.66 ± 1.68 | 94.46 ± 1.17 | 95.85 ± 1.14 |
| Method 1 | L = 5 | L = 10 | L = 15 |
|---|---|---|---|
| SVM | 50.23 ± 1.74 | 55.56 ± 2.04 | 58.58 ± 0.80 |
| LapSVM | 52.31 ± 0.67 | 56.36 ± 0.71 | 59.99 ± 0.65 |
| TSVM | 62.57 ± 0.23 | 63.45 ± 0.17 | 65.42 ± 0.02 |
| SCS3VM | 55.42 ± 0.35 | 60.86 ± 5.08 | 67.24 ± 0.47 |
| SS-LPSVM | 56.95 ± 0.95 | 64.74 ± 0.39 | 78.76 ± 0.04 |
| KNN + SNI | 56.39 ± 1.03 | 74.88 ± 0.54 | 78.92 ± 0.61 |
| MLR + RS | 55.38 ± 3.98 | 69.28 ± 2.63 | 75.15 ± 1.43 |
| SVM + S-CNN | 10.02 ± 1.48 | 17.71 ± 4.90 | 44.00 ± 5.73 |
| 3D-CNN | 63.54 ± 2.72 | 71.25 ± 1.64 | 76.25 ± 2.17 |
| DFSL + NN | 67.84 ± 1.29 | 76.49 ± 1.44 | 78.62 ± 1.59 |
| DFSL + SVM | 64.58±2.78 | 75.53 ± 1.89 | 79.98 ± 2.23 |
| New Approach | 70.24 ± 1.26 | 78.20 ± 1.64 | 82.65 ± 1.82 |
| Method 1 | L = 5 | L = 10 | L = 15 | L = 20 | L = 25 |
|---|---|---|---|---|---|
| SVM | 53.73 ± 1.30 | 61.53 ± 1.14 | 60.43 ± 0.94 | 64.89 ± 1.14 | 68.01 ± 2.62 |
| LapSVM | 65.72 ± 0.34 | 68.26 ± 2.20 | 68.34 ± 0.29 | 65.91 ± 0.45 | 68.88 ± 1.34 |
| TSVM | 63.43 ± 1.22 | 63.73 ± 0.45 | 68.45 ± 1.07 | 73.72 ± 0.27 | 69.96 ± 1.39 |
| SCS3VM | 56.76 ± 2.28 | 64.25 ± 0.40 | 66.87 ± 0.37 | 68.24 ± 1.18 | 69.45 ± 2.19 |
| SS-LPSVM | 69.60 ± 2.30 | 75.88 ± 0.22 | 80.67 ± 1.21 | 78.41 ± 0.26 | 85.56 ± 0.09 |
| KNN + SNI | 70.21 ± 1.29 | 78.97 ± 2.33 | 82.56 ± 0.51 | 85.18 ± 0.65 | 86.26 ± 0.37 |
| MLR + RS | 69.73 ± 3.15 | 80.30 ± 2.54 | 84.10 ± 1.94 | 83.52 ± 2.13 | 87.97 ± 1.69 |
| SVM + S-CNN | 23.68 ± 6.34 | 66.64 ± 2.37 | 68.35 ± 4.70 | 78.43 ± 1.93 | 72.87 ± 7.36 |
| 3D-CNN | 71.58 ± 3.58 | 79.63 ± 1.75 | 83.89 ± 2.93 | 85.98 ± 1.76 | 89.56 ± 1.20 |
| DFSL + NN | 80.81 ± 3.12 | 84.79 ± 2.27 | 86.68 ± 2.61 | 89.59 ± 1.05 | 91.11 ± 0.83 |
| DFSL + SVM | 72.57 ± 3.93 | 84.56 ± 1.83 | 87.23 ± 1.38 | 90.69 ± 1.29 | 93.08 ± 0.92 |
| New Approach | 81.03 ± 1.52 | 86.10 ± 0.97 | 89.55 ± 1.28 | 93.11 ± 1.23 | 94.71 ± 1.11 |
| L = 5 | L = 10 | L = 15 | L = 20 | L = 25 | |
|---|---|---|---|---|---|
| Method | New Approach | ||||
| OA (%) | 89.92 ± 1.87 | 91.11 ± 1.50 | 93.66 ± 1.68 | 94.46 ± 1.17 | 95.85 ± 1.14 |
| Method | The proposed quadruplet loss was replaced by the siamese loss. | ||||
| OA (%) | 88.93 ± 2.18 | 90.31 ± 1.88 | 92.85 ± 1.94 | 93.68 ± 1.59 | 94.79 ± 1.48 |
| Method | The proposed quadruplet loss was replaced by the triplet loss. | ||||
| OA (%) | 89.21 ± 1.96 | 90.58 ± 1.82 | 93.01 ± 1.53 | 93.87 ± 1.46 | 94.96 ± 1.34 |
| Method | The proposed quadruplet loss was replaced by the original quadruplet loss. | ||||
| OA (%) | 89.34 ± 2.04 | 90.62 ± 1.95 | 93.30 ± 1.62 | 94.06 ± 1.57 | 95.14 ± 1.43 |
| Method | The dense branch was replaced by a normal CNN module. | ||||
| OA (%) | 89.36 ± 2.15 | 90.75 ± 1.96 | 93.34 ± 1.91 | 94.15 ± 1.69 | 95.25 ± 1.57 |
| Method | The dilated branch was replaced by a normal CNN module. | ||||
| OA (%) | 89.50 ± 2.36 | 90.97 ± 2.04 | 93.52 ± 1.96 | 94.21 ± 1.54 | 95.47 ± 1.39 |
| L = 5 | L = 10 | L = 15 | |
|---|---|---|---|
| Method | New Approach | ||
| OA (%) | 70.24 ± 1.26 | 78.20 ± 1.64 | 82.65 ± 1.82 |
| Method | The proposed quadruplet loss was replaced by the siamese loss. | ||
| OA (%) | 68.19 ± 1.59 | 77.12 ± 1.71 | 80.35 ± 1.87 |
| Method | The proposed quadruplet loss was replaced by the triplet loss. | ||
| OA (%) | 68.58 ± 1.62 | 77.37 ± 2.09 | 81.19 ± 1.58 |
| Method | The proposed quadruplet loss was replaced by the original quadruplet loss. | ||
| OA (%) | 68.72 ± 1.75 | 77.62 ± 1.84 | 81.38 ± 1.57 |
| Method | The dense branch was replaced by a normal CNN module. | ||
| OA (%) | 68.71 ± 1.68 | 77.58 ± 2.07 | 81.22 ± 1.69 |
| Method | The dilated branch was replaced by a normal CNN module. | ||
| OA (%) | 68.85 ± 1.56 | 77.64 ± 2.14 | 81.39 ± 1.62 |
| L = 5 | L = 10 | L = 15 | L = 20 | L = 25 | |
|---|---|---|---|---|---|
| Method | New Approach | ||||
| OA (%) | 81.03 ± 1.52 | 86.10 ± 0.97 | 89.55 ± 1.28 | 93.11 ± 1.23 | 94.71 ± 1.11 |
| Method | The proposed quadruplet loss was replaced by the siamese loss. | ||||
| OA (%) | 80.07 ± 2.25 | 84.13 ± 2.08 | 88.17 ± 1.67 | 91.09 ± 1.54 | 93.02 ± 1.28 |
| Method | The proposed quadruplet loss was replaced by the triplet loss. | ||||
| OA (%) | 80.31 ± 1.87 | 84.69 ± 1.54 | 88.53 ± 1.73 | 91.78 ± 1.70 | 93.19 ± 1.58 |
| Method | The proposed quadruplet loss was replaced by the original quadruplet loss. | ||||
| OA (%) | 80.54 ± 1.95 | 84.88 ± 1.73 | 88.71 ± 1.76 | 91.96 ± 1.69 | 93.27 ± 1.52 |
| Method | The dense branch was replaced by a normal CNN module. | ||||
| OA (%) | 80.64 ± 2.28 | 84.94 ± 2.09 | 88.78 ± 1.89 | 92.12 ± 1.75 | 93.35 ± 1.54 |
| Method | The dilated branch was replaced by a normal CNN module. | ||||
| OA (%) | 80.90 ± 2.11 | 85.47 ± 1.87 | 88.96 ± 1.80 | 92.34 ± 1.67 | 93.47 ± 1.64 |
| L = 5 | L = 10 | L = 15 | L = 20 | L = 25 | |
|---|---|---|---|---|---|
| Method | New Approach | ||||
| AA | 90.19 ± 1.69 | 90.75 ± 1.59 | 93.54 ± 1.79 | 94.37 ± 1.26 | 95.58 ± 1.26 |
| Kappa | 89.68 ± 1.47 | 91.06 ± 1.28 | 93.26 ± 1.59 | 94.28 ± 1.32 | 95.46 ± 1.17 |
| Method | The proposed quadruplet loss was replaced by the siamese loss. | ||||
| AA | 88.86 ± 1.88 | 90.22 ± 2.02 | 92.93 ± 1.86 | 93.79 ± 1.53 | 94.86 ± 1.36 |
| Kappa | 88.72 ± 2.39 | 89.94±1.97 | 92.78 ± 2.14 | 93.59 ± 1.68 | 94.68 ± 1.54 |
| Method | The proposed quadruplet loss was replaced by the triplet loss. | ||||
| AA | 89.14 ± 1.87 | 90.39 ± 1.98 | 93.16 ± 1.56 | 93.89 ± 1.50 | 95.02 ± 1.42 |
| Kappa | 89.06 ± 2.16 | 90.24 ± 2.03 | 92.86 ± 1.69 | 93.72 ± 1.54 | 94.89 ± 1.57 |
| Method | The proposed quadruplet loss was replaced by the original quadruplet loss. | ||||
| AA | 89.19 ± 1.96 | 90.44 ± 1.89 | 93.21 ± 1.59 | 93.93 ± 1.52 | 95.11 ± 1.54 |
| Kappa | 89.26 ± 2.17 | 90.32 ± 2.14 | 92.99 ± 1.73 | 93.85 ± 1.69 | 94.92 ± 1.63 |
| Method | The dense branch was replaced by a normal CNN module. | ||||
| AA | 89.29 ± 1.99 | 90.56 ± 1.89 | 93.35 ± 1.88 | 94.09 ± 1.74 | 95.17 ± 1.69 |
| Kappa | 89.24 ± 2.06 | 90.43 ± 2.03 | 93.08 ± 2.07 | 93.91 ± 1.78 | 95.13 ± 1.70 |
| Method | The dilated branch was replaced by a normal CNN module. | ||||
| AA | 89.43 ± 2.07 | 90.59 ± 2.36 | 93.44 ± 2.06 | 94.18 ± 1.65 | 95.29 ± 1.45 |
| Kappa | 89.36 ± 2.41 | 90.50 ± 2.13 | 93.13 ± 2.56 | 94.04 ± 1.77 | 95.31 ± 1.46 |
| Method | 3D-CNN | ||||
| AA | 84.63 ± 2.06 | 86.36 ± 1.82 | 87.76 ± 1.68 | 89.36 ± 1.56 | 91.03 ± 1.54 |
| Kappa | 85.36 ± 2.43 | 86.14 ± 2.03 | 87.96 ± 1.85 | 88.76 ± 1.89 | 90.96 ± 1.63 |
| L = 5 | L = 10 | L = 15 | |
|---|---|---|---|
| Method | New Approach | ||
| AA | 70.35 ± 1.32 | 78.58 ± 1.71 | 82.77 ± 1.88 |
| Kappa | 70.15 ± 1.16 | 77.84 ± 1.54 | 82.59 ± 1.69 |
| Method | The proposed quadruplet loss was replaced by the siamese loss. | ||
| AA | 67.95 ± 2.07 | 77.75 ± 1.69 | 80.78 ± 1.68 |
| Kappa | 68.12 ± 1.68 | 77.05 ± 1.74 | 80.29 ± 2.13 |
| Method | The proposed quadruplet loss was replaced by the triplet loss. | ||
| AA | 68.39 ± 1.85 | 77.96 ± 1.95 | 81.26 ± 1.64 |
| Kappa | 68.45 ± 1.77 | 77.28 ± 1.86 | 80.93 ± 1.89 |
| Method | The proposed quadruplet loss was replaced by the original quadruplet loss. | ||
| AA | 69.16 ± 1.69 | 78.08 ± 1.63 | 81.67 ± 1.65 |
| Kappa | 68.65 ± 2.14 | 77.54 ± 1.91 | 81.26 ± 1.91 |
| Method | The dense branch was replaced by a normal CNN module. | ||
| AA | 68.89 ± 1.64 | 77.74 ± 1.86 | 81.43 ± 1.60 |
| Kappa | 68.64 ± 1.79 | 77.47 ± 2.15 | 80.86 ± 1.88 |
| Method | The dilated branch was replaced by a normal CNN module. | ||
| AA | 69.14 ± 1.68 | 77.96 ± 1.98 | 81.57 ± 1.58 |
| Kappa | 68.73 ± 2.03 | 77.53 ± 2.36 | 81.32 ± 1.89 |
| Method | 3D-CNN | ||
| AA | 64.35 ± 2.58 | 71.69 ± 1.78 | 76.64 ± 2.04 |
| Kappa | 63.48 ± 2.87 | 71.26 ± 1.95 | 76.21 ± 2.36 |
| L = 5 | L = 10 | L = 15 | L = 20 | L = 25 | |
|---|---|---|---|---|---|
| Method | New Approach | ||||
| AA | 81.15 ± 1.59 | 86.23 ± 1.04 | 89.68 ±1.36 | 93.05 ± 1.21 | 94.57 ± 1.25 |
| Kappa | 80.97 ± 1.41 | 86.05 ± 1.08 | 89.49 ± 1.30 | 92.97 ± 1.13 | 94.42 ± 1.18 |
| Method | The proposed quadruplet loss was replaced by the siamese loss. | ||||
| AA | 80.16 ± 2.16 | 84.36 ± 1.89 | 87.86 ± 1.69 | 90.87 ± 1.63 | 92.86 ± 1.46 |
| Kappa | 79.95 ± 2.37 | 84.16 ± 1.95 | 87.93 ± 1.86 | 90.94 ± 1.78 | 92.78 ± 1.53 |
| Method | The proposed quadruplet loss was replaced by the triplet loss. | ||||
| AA | 80.39 ± 1.75 | 84.56 ± 1.78 | 88.40 ± 1.84 | 91.56 ± 1.89 | 92.94 ± 1.63 |
| Kappa | 80.06 ± 1.94 | 84.37 ± 1.85 | 88.26 ± 2.02 | 91.36 ± 1.86 | 92.89 ± 1.74 |
| Method | The proposed quadruplet loss was replaced by the original quadruplet loss. | ||||
| AA | 80.46 ± 1.86 | 84.69 ± 1.96 | 88.46 ± 1.86 | 91.83 ± 1.76 | 93.05 ± 1.69 |
| Kappa | 80.25 ± 2.03 | 84.59 ± 2.03 | 88.37 ± 1.94 | 91.58 ± 1.88 | 92.93 ± 1.82 |
| Method | The dense branch was replaced by a normal CNN module. | ||||
| AA | 80.58 ± 1.89 | 85.03 ± 1.94 | 88.59 ± 1.98 | 91.06 ± 1.89 | 93.16 ± 1.66 |
| Kappa | 80.41 ± 2.36 | 84.76 ± 2.18 | 88.44 ± 2.14 | 92.10 ± 1.83 | 92.97 ± 1.56 |
| Method | The dilated branch was replaced by a normal CNN module. | ||||
| AA | 80.68 ± 2.23 | 85.34 ± 1.94 | 88.77 ± 1.94 | 92.16 ± 1.75 | 93.36 ± 1.79 |
| Kappa | 80.49 ± 2.56 | 85.23 ± 2.00 | 88.69 ± 2.03 | 91.95 ± 1.84 | 93.15 ± 1.84 |
| Method | 3D-CNN | ||||
| AA | 71.26 ± 3.64 | 80.02 ± 1.69 | 83.52 ± 3.14 | 85.53 ± 1.89 | 89.23 ± 1.36 |
| Kappa | 70.89 ± 3.85 | 79.38 ± 1.87 | 83.46 ± 3.26 | 85.06 ± 2.03 | 88.91 ± 1.41 |
| Number of Labeled Samples | L = 5 | |||
| Method | Proposed | DFSL + NN | DFSL + SVM | 3D-CNN + NN |
| Time | 10.08 s + 0.30 s | 11.09 s + 0.34 s | 11.09 s + 2.09 s | 13.59 s + 0.38 s |
| Number of Labeled Samples | L = 25 | |||
| Method | Proposed | DFSL + NN | DFSL + SVM | 3D-CNN + NN |
| Time | 10.08 s + 0.75 s | 11.09 s + 0.78 s | 11.09 s + 123.48 s | 13.59 s + 0.84 s |
| Configuration and Program | Details |
|---|---|
| Processor | Intel (R) Core (TM) i5-9400 @ 2.90 GHz |
| Memory | Crucial DDR4 2666MHz, 8.00 GB |
| Graphics | NVIDIA GeForce GTX 1060, 6 GB |
| CUDA | Version 9.1.0 |
| Programming Language | Python, Version 3.6.10 |
| Deep Learning Platform | Google TensorFlow, Version 1.9.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Yue, J.; Qin, Q. Deep Quadruplet Network for Hyperspectral Image Classification with a Small Number of Samples. Remote Sens. 2020, 12, 647. https://doi.org/10.3390/rs12040647
Zhang C, Yue J, Qin Q. Deep Quadruplet Network for Hyperspectral Image Classification with a Small Number of Samples. Remote Sensing. 2020; 12(4):647. https://doi.org/10.3390/rs12040647
Chicago/Turabian StyleZhang, Chengye, Jun Yue, and Qiming Qin. 2020. "Deep Quadruplet Network for Hyperspectral Image Classification with a Small Number of Samples" Remote Sensing 12, no. 4: 647. https://doi.org/10.3390/rs12040647
APA StyleZhang, C., Yue, J., & Qin, Q. (2020). Deep Quadruplet Network for Hyperspectral Image Classification with a Small Number of Samples. Remote Sensing, 12(4), 647. https://doi.org/10.3390/rs12040647