Improving the Applicability of Hydrologic Models for Food–Energy–Water Nexus Studies Using Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
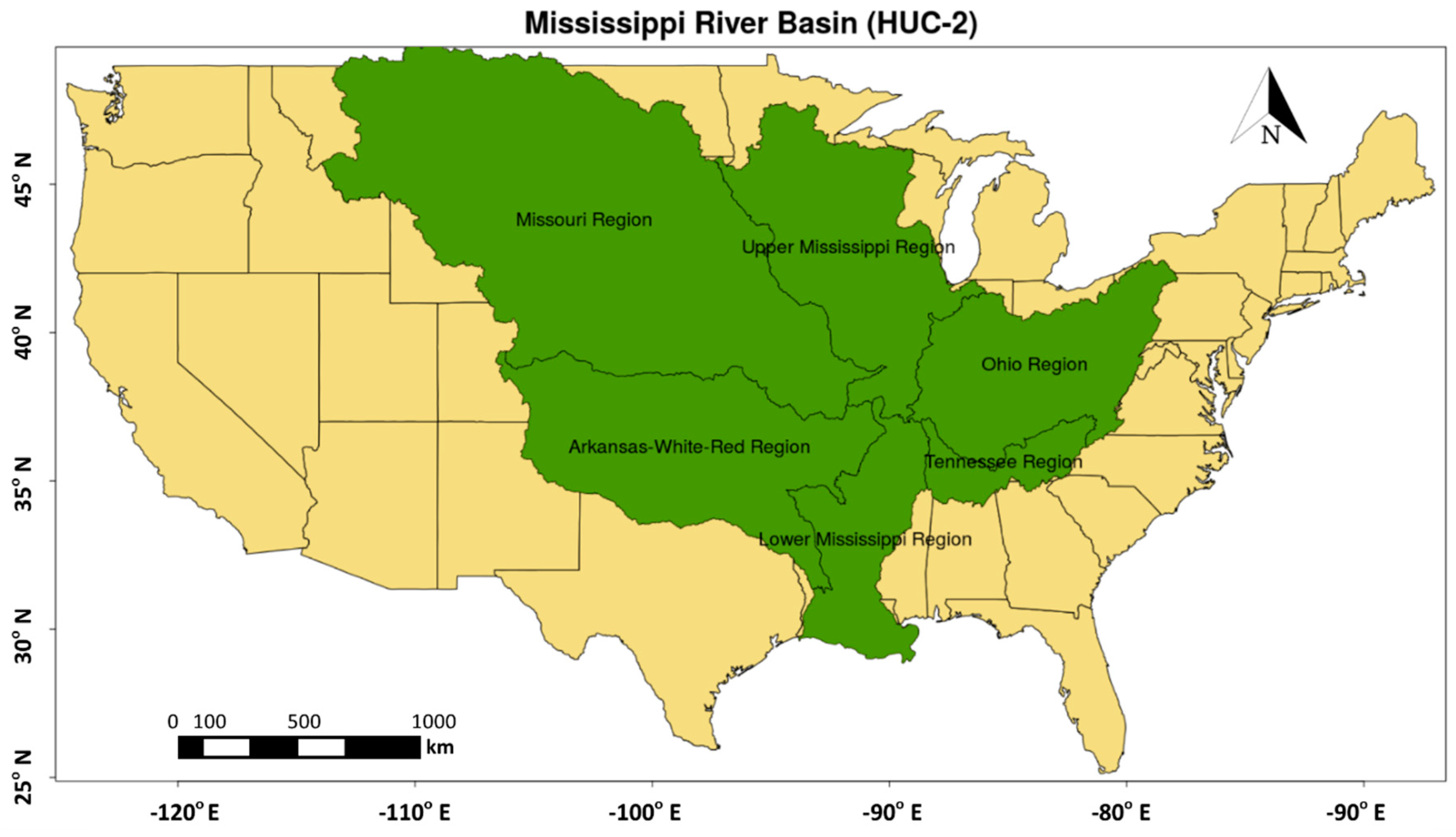
2.1. Study Area
2.2. Observational Data
2.3. Hydrologic Model Setup
2.4. Univariate Calibration
2.5. Multivariate Calibration
2.6. Methods Used for Analysis of Results
3. Results
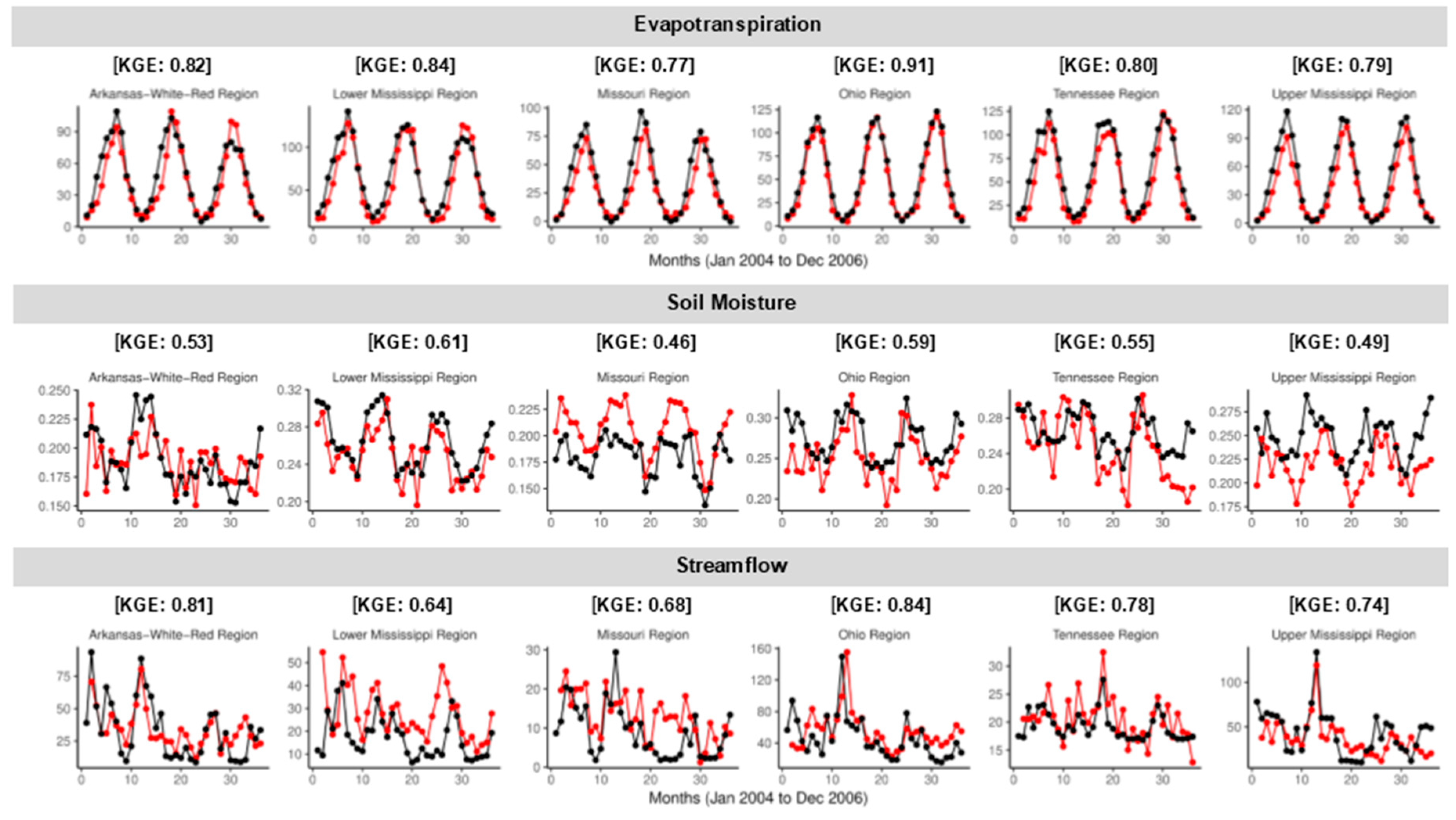
3.1. Validation of the Noah-MP Hydrologic Model
3.2. Univariate Calibration
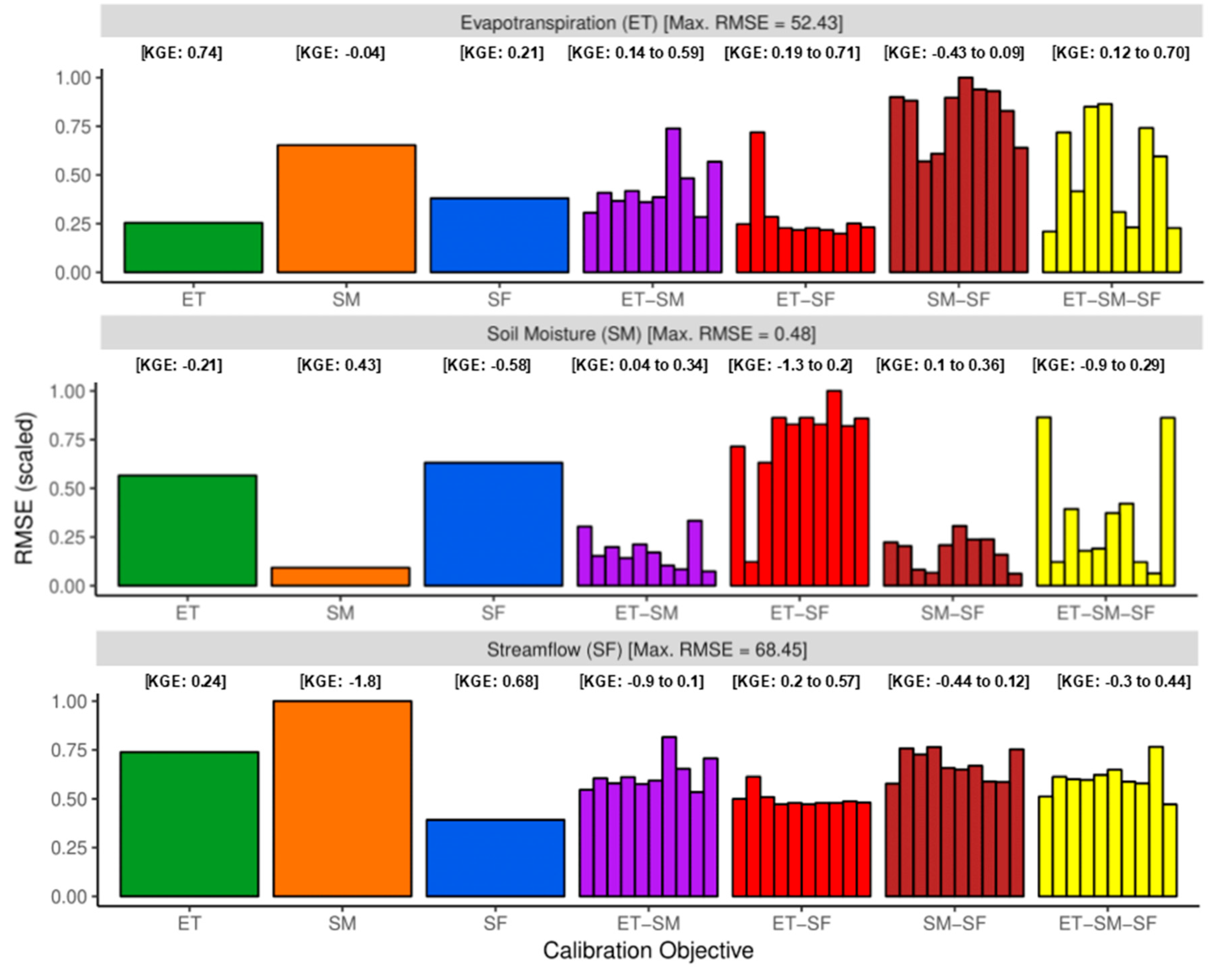
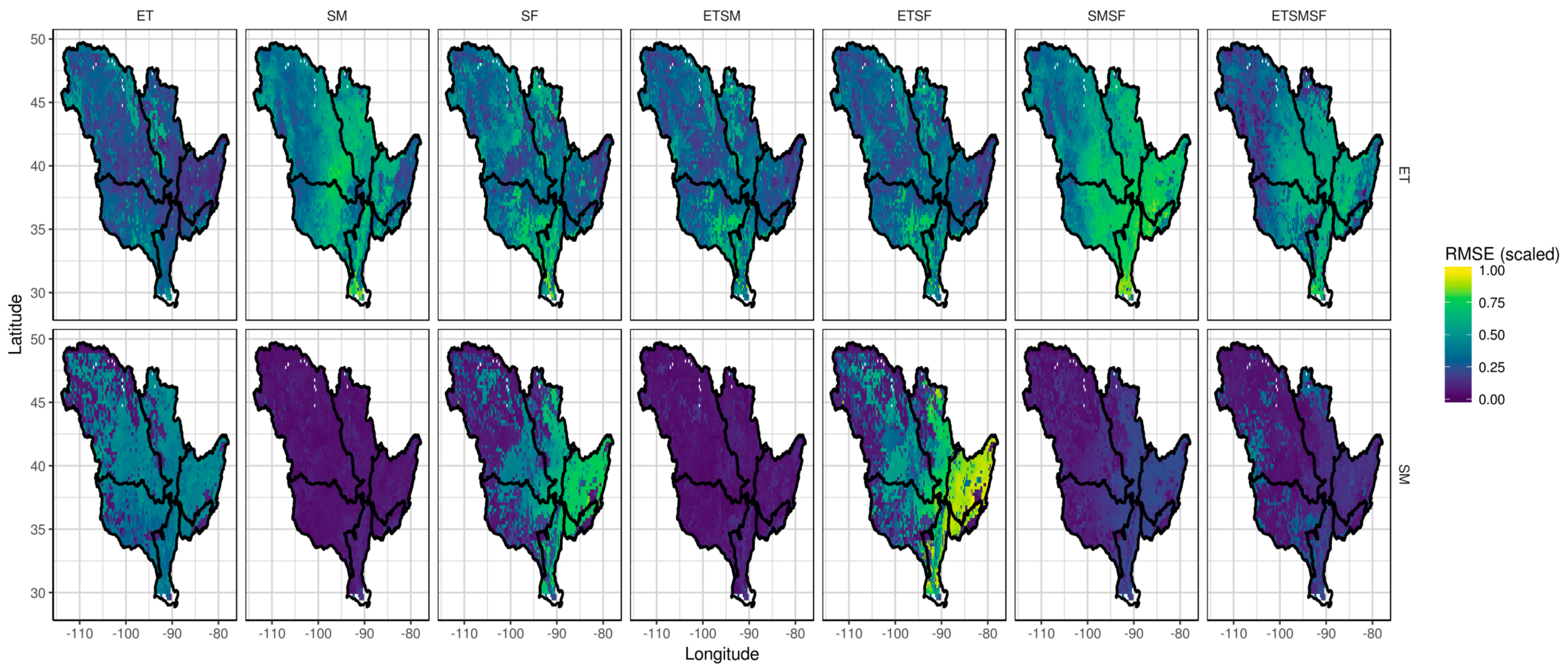
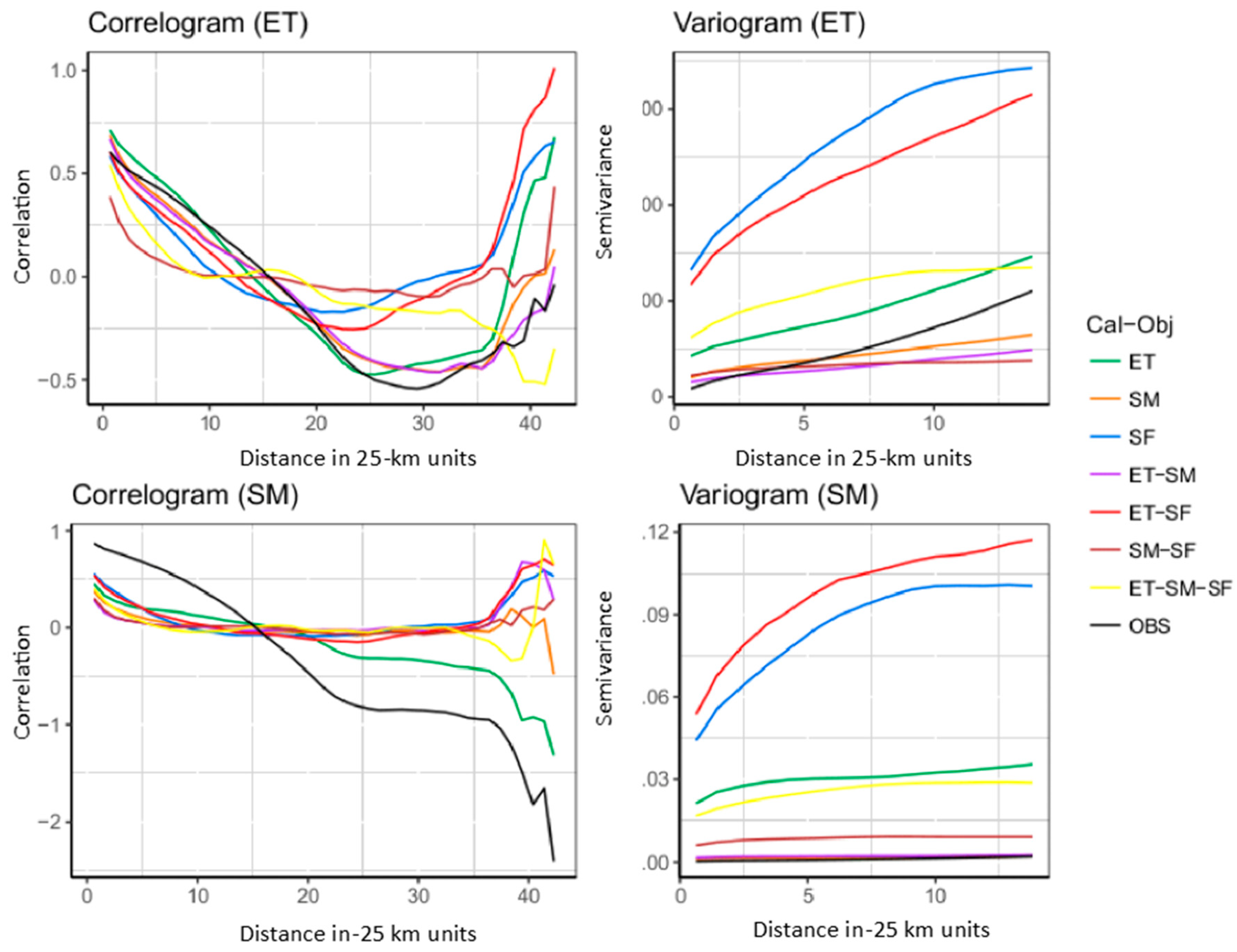
3.3. Multivariate Calibration
4. Discussion
- ET: If the nexus study only requires ET as the primary input (for example, calculation of water demand), then calibration of a hydrologic model using only observed ET gives the best results in terms of spatial and temporal accuracy. However, increased accuracy in ET comes at the cost of degrading SM and SF estimates. In the absence of SF estimates, calibration with observed ET offers the best alternative for reliably simulating SF [42,43].
- SM: Calibration of a hydrologic model with SM observations improves SM simulations significantly at considerable cost to the accuracy of both ET and SF simulations. Based on the results of this study, SM-calibration is not a viable variable for FEW nexus studies which need either water availability (SF) or water use (ET) information. SM-calibration maybe required for FEW studies in drought-affected regions where water availability is government by SM.
- SF: Using a sparse network of streamflow gages for calibration adversely affects the spatio-temporal accuracy of ET and SM. If no ET observations are available, then SF is a viable alternative for reliably simulating mean ET over the basin but not the spatial patterns which are necessary for most FEW nexus studies.
- ET–SM: Including ET and SM together in calibration not only improves the simulations of ET and SM but also has a positive impact on SF estimates compared to univariate calibration cases. This scenario exhibits the advantages of combining state-of-art remote sensing-based estimates of hydrologic variables with models for FEW nexus studies, especially for FEW nexus studies in data-scarce regions.
- ET–SF: Incorporating both ET and SF in calibration trades accuracy in SF simulation to improve ET estimates compared to univariate SF calibration. If ET and SF variables are needed for the FEW study, then this scenario is the best calibration strategy. However, combining and ET and SF does not improve soil moisture simulation (even compared to univariate ET or SF calibration).
- SM–SF: In the absence of ET observations or estimates, SM and SF are seen to be poor alternatives. Therefore this calibration scenario cannot be used for FEW nexus studies that require ET. However, this strategy can be used in nexus studies in regions which suffer from episodic droughts where both SM and SF are needed to quantify water availability.
- ET–SM–SF: Incorporating all the water balance components (ET, SM, SF) for calibration provides the best compromise solution to preserve the accuracies in simulating each of the three components.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
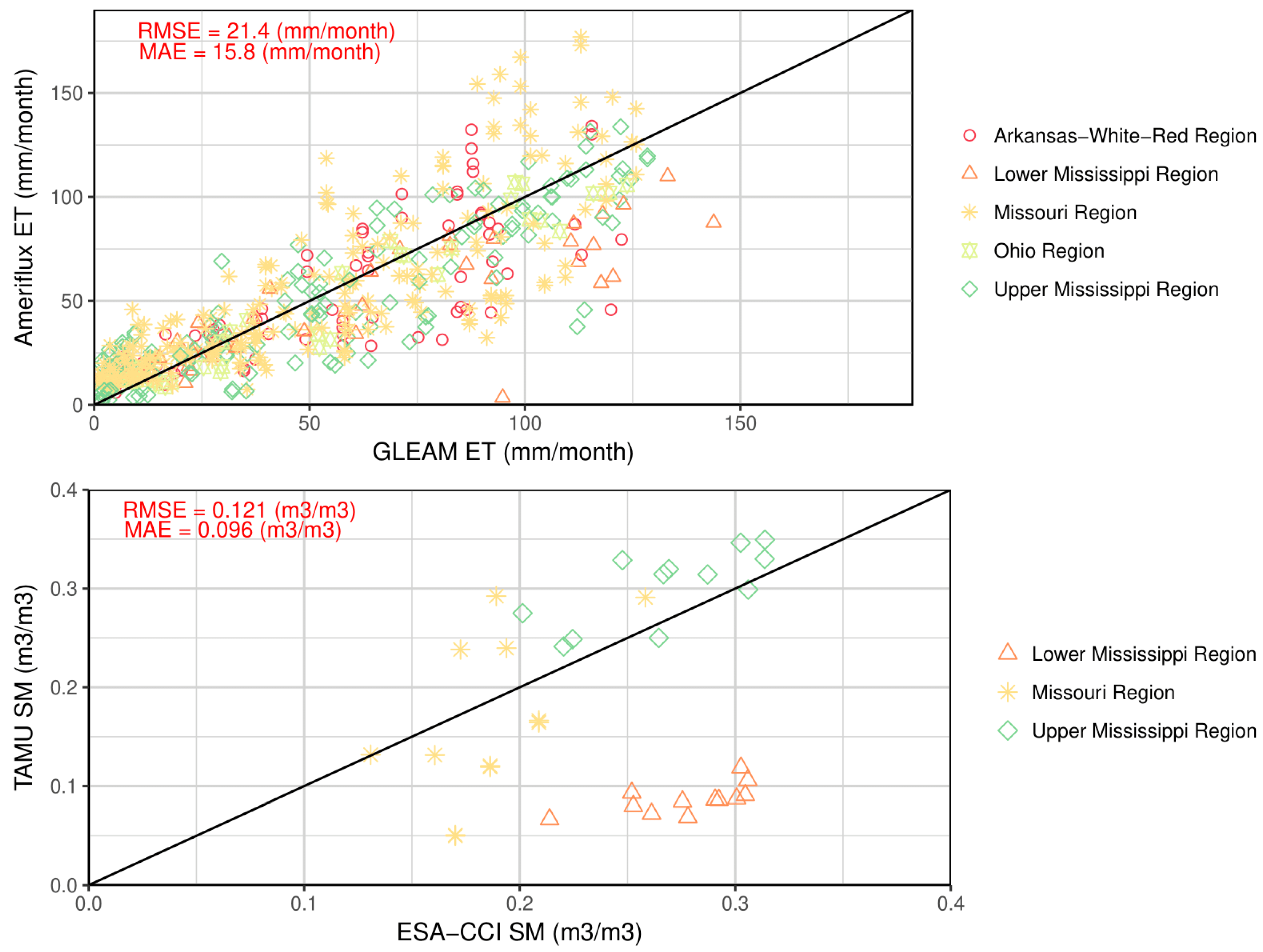
Appendix B
References
- D’Odorico, P.; Davis, K.F.; Rosa, L.; Carr, J.A.; Chiarelli, D.; Dell’Angelo, J.; Gephart, J.; MacDonald, G.K.; Seekell, D.A.; Suweis, S.; et al. The Global Food-Energy-Water Nexus. Rev. Geophys. 2018, 56, 456–531. [Google Scholar] [CrossRef]
- Mcnally, A.; Mccartney, S.; Ruane, A.C.; Mladenova, I.E.; Mcnally, A. Hydrologic and Agricultural Earth Observations and Modeling for the Water-Food Nexus. Front. Environ. Sci. 2019, 7, 23. [Google Scholar] [CrossRef]
- McCallum, I.; Montzka, C.; Bayat, B.; Kollet, S.; Kolotii, A.; Kussul, N.; Lavreniuk, M.; Lehmann, A.; Maso, J.; Mazzetti, P.; et al. Developing food, water and energy nexus workflows. Int. J. Digit. Earth 2020, 13, 299–308. [Google Scholar] [CrossRef]
- Momblanch, A.; Papadimitriou, L.; Jain, S.K.; Kulkarni, A.; Ojha, C.S.P.; Adeloye, A.J.; Holman, I.P. Untangling the water-food-energy-environment nexus for global change adaptation in a complex Himalayan water resource system. Sci. Total Environ. 2019, 655, 35–47. [Google Scholar] [CrossRef]
- Alam, S.; Gebremichael, M.; Li, R. Remote Sensing-Based Assessment of the Crop, Energy and Water Nexus in the Central Valley, California. Remote Sens. 2019, 11, 1701. [Google Scholar] [CrossRef]
- Koppa, A.; Gebremichael, M.; Yeh, W.W.-G. Multivariate calibration of large scale hydrologic models: The necessity and value of a Pareto optimal approach. Adv. Water Resour. 2019, 130, 129–146. [Google Scholar] [CrossRef]
- Wanders, N.; Bierkens, M.F.P.; de Jong, S.M.; de Roo, A.; Karssenberg, D. The benefits of using remotely sensed soil moisture in parameter identification of large-scale hydrological modelss. Water Resour. Res. 2014, 50, 6874–6891. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Zink, M.; Mai, J.; Cuntz, M.; Samaniego, L. Conditioning a Hydrologic Model Using Patterns of Remotely Sensed Land Surface Temperature. Water Resour. Res. 2018, 54, 2976–2998. [Google Scholar] [CrossRef]
- López, P.L.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Beven, K. Searching for the Holy Grail of scientific hydrology: Qt = (S, R, Δt) A as closure. Hydrol. Earth Syst. Sci. 2006, 10, 609–618. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.L.; David, C.H.; Niu, G.Y.; Rodell, M. Hydrological evaluation of the Noah-MP land surface model for the Mississippi River Basin. J. Geophys. Res. 2014, 119, 23–38. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Koppa, A.; Gebremichael, M. A Framework for Validation of Remotely Sensed Precipitation and Evapotranspiration Based on the Budyko Hypothesis. Water Resour. Res. 2017, 53, 8487–8499. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; et al. Land information system: An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Cuntz, M.; Mai, J.; Samaniego, L.; Clark, M.; Wulfmeyer, V.; Branch, O.; Attinger, S.; Thober, S. The impact of standard and hard-coded parameters on the hydrologic fluxes in the Noah-MP land surface model. J. Geophys. Res. 2016, 121, 10676–10700. [Google Scholar] [CrossRef]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis under Different Environmental Conditions. In Progress in Photosynthesis Research; Springer: Dordrecht, The Netherlands, 1987; pp. 221–224. [Google Scholar] [CrossRef]
- Chen, F.; Janjić, Z.; Mitchell, K. Impact of atmospheric surface-layer parameterizations in the new land-surface scheme of the NCEP mesoscale Eta model. Bound.-Layer Meteorol. 1997, 85, 391–421. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E.; Su, H. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L. Effects of frozen soil on snowmelt runoff and soil water storage at a continental scale. J. Hydrometeorol. 2006, 7, 937–952. [Google Scholar] [CrossRef]
- Yang, R.; Friedl, M.A. Modeling the effects of three-dimensional vegetation structure on surface radiation and energy balance in boreal forests. J. Geophys. Res. D Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Verseghy, D.L.; McFarlane, N.A.; Lazare, M. Class—A Canadian land surface scheme for GCMS, II. Vegetation model and coupled runs. Int. J. Climatol. 1993, 13, 347–370. [Google Scholar] [CrossRef]
- Jordan, R. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM.89; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1991. [Google Scholar]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Improved evolutionary optimization from genetically adaptive multimethod search. Proc. Natl. Acad. Sci. USA 2007, 104, 708–711. [Google Scholar] [CrossRef] [PubMed]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C.; Shi, Y.; Jacob, C.; Koza, J.R.; Iii, F.H.B.; Andre, D.; Keane, M. Swarm Intelligence. The Morgan Kaufmann Series in Evolutionary Computation; Morgan Kaufmann: Burlington, MA, USA, 2001; ISBN 1558605959. [Google Scholar]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mendoza, P.A.; Clark, M.P.; Barlage, M.; Rajagopalan, B.; Samaniego, L.; Abramowitz, G.; Gupta, H. Are we unnecessarily constraining the agility of complex process-based models? Water Resour. Res. 2015, 51, 716–728. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Stisen, S.; Koch, J.; Sonnenborg, T.O.; Refsgaard, J.C.; Bircher, S.; Ringgaard, R.; Jensen, K.H. Moving beyond run-off calibration-Multivariable optimization of a surface-subsurface-atmosphere model. Hydrol. Process. 2018, 32, 2654–2668. [Google Scholar] [CrossRef]
- Dembélé, M.; Hrachowitz, M.; Savenije, H.H.G.; Mariéthoz, G.; Schaefli, B. Improving the Predictive Skill of a Distributed Hydrological Model by Calibration on Spatial Patterns with Multiple Satellite Data Sets. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Rakovec, O.; Kumar, R.; Attinger, S.; Samaniego, L. Improving the realism of hydrologic model functioning through multivariate parameter estimation. Water Resour. Res. 2016, 52, 7779–7792. [Google Scholar] [CrossRef]
- Koppa, A.; Gebremichael, M.; Zambon, R.C.; Yeh, W.W.-G.; Hopson, T.M. Seasonal Hydropower Planning for Data-Scarce Regions Using Multimodel Ensemble Forecasts, Remote Sensing Data, and Stochastic Programming. Water Resour. Res. 2019, 55, 8583–8607. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; aus der Beek, T.; Schüth, C. Spatially distributed model calibration of a highly managed hydrological system using remote sensing-derived ET data. J. Hydrol. 2019, 577, 123944. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Quiring, S.M.; Ford, T.W.; Wang, J.K.; Khong, A.; Harris, E.; Lindgren, T.; Goldberg, D.W.; Li, Z. The North American soil moisture database development and applications. Bull. Am. Meteorol. Soc. 2016, 97, 1441–1459. [Google Scholar] [CrossRef]
| Model Physics | Selected Physics Option |
|---|---|
| Vegetation model | Use table Leaf Area Index (4) |
| Canopy stomatal resistance | Ball-Berry (1) [23] |
| Soil moisture factor for stomatal resistance | Original Noah (1) [24] |
| Runoff and groundwater | TOPMODEL with groundwater (1) [25] |
| Surface layer drag coefficient | Original Noah (2) [24] |
| Frozen soil permeability | Linear effects, more permeable (1) [26] |
| Radiation transfer | Modified two-stream (1) [27] |
| Snow surface albedo | CLASS (2) [28] |
| Rainfall and snowfall Partitioning | Jordan Scheme (1) [29] |
| Lower boundary of soil temperature | Original Noah (2) [24] |
| Snow and soil temperature time scheme | Semi-implicit (1) |
| Super-cooled liquid water | No iteration (1) [26] |
| Parameters | Description | Sensitive Variable | Total Parameters | Units | Minimum | Maximum |
|---|---|---|---|---|---|---|
| REFDK | Surface runoff parameter | SF | 1 | m/s | 1.4 × 10−6 | 6.5 × 10−6 |
| REFKDT | Surface runoff parameter | SF | 1 | No Units | 1.0 | 5.0 |
| BB1-BB12 | Exponent in the Brooks Corey Equation | SF, ET | 12 | No Units | 0.5 | 12.0 |
| MAXSMC1-MAXSMC12 | Soil porosity | SF, ET, SM | 12 | No units | 0.1 | 0.7 |
| SATDK1-SATDK12 | Saturated hydraulic conductivity | SF, SM | 12 | m/s | 2.0 × 10−6 | 7.0 × 10−2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koppa, A.; Gebremichael, M. Improving the Applicability of Hydrologic Models for Food–Energy–Water Nexus Studies Using Remote Sensing Data. Remote Sens. 2020, 12, 599. https://doi.org/10.3390/rs12040599
Koppa A, Gebremichael M. Improving the Applicability of Hydrologic Models for Food–Energy–Water Nexus Studies Using Remote Sensing Data. Remote Sensing. 2020; 12(4):599. https://doi.org/10.3390/rs12040599
Chicago/Turabian StyleKoppa, Akash, and Mekonnen Gebremichael. 2020. "Improving the Applicability of Hydrologic Models for Food–Energy–Water Nexus Studies Using Remote Sensing Data" Remote Sensing 12, no. 4: 599. https://doi.org/10.3390/rs12040599
APA StyleKoppa, A., & Gebremichael, M. (2020). Improving the Applicability of Hydrologic Models for Food–Energy–Water Nexus Studies Using Remote Sensing Data. Remote Sensing, 12(4), 599. https://doi.org/10.3390/rs12040599







