Mean Sea Surface Model over the Sea of Japan Determined from Multi-Satellite Altimeter Data and Tide Gauge Records
Abstract
1. Introduction
2. Study Area, Data Sources, and Methodology
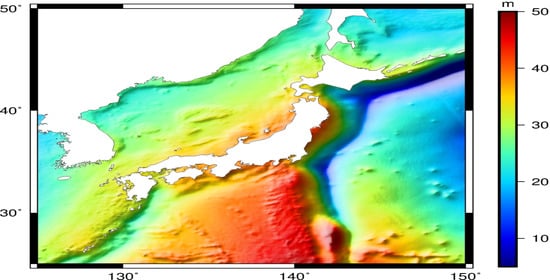
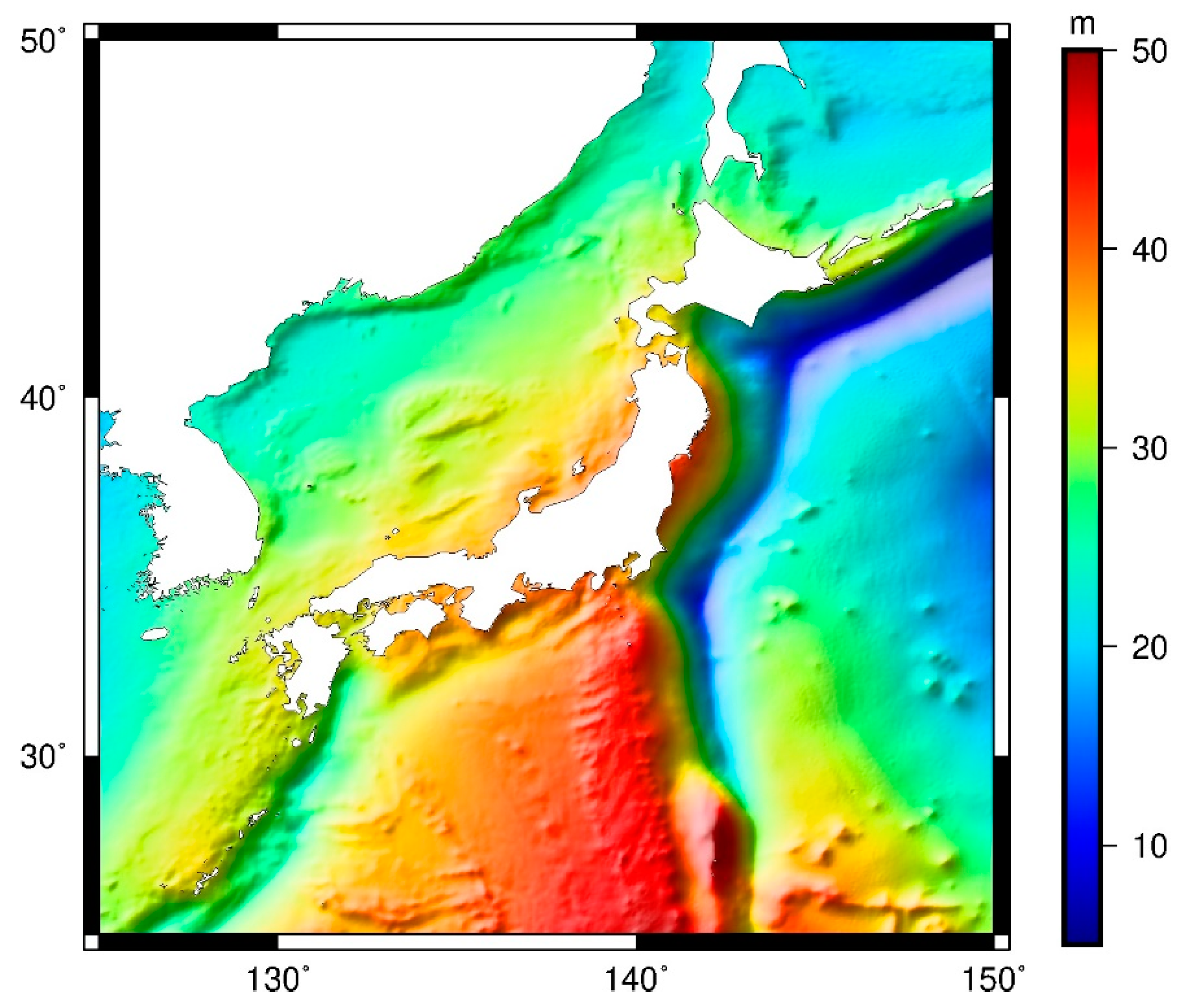
2.1. Study Area
2.2. Data Sources
2.2.1. Satellite Altimeter Data
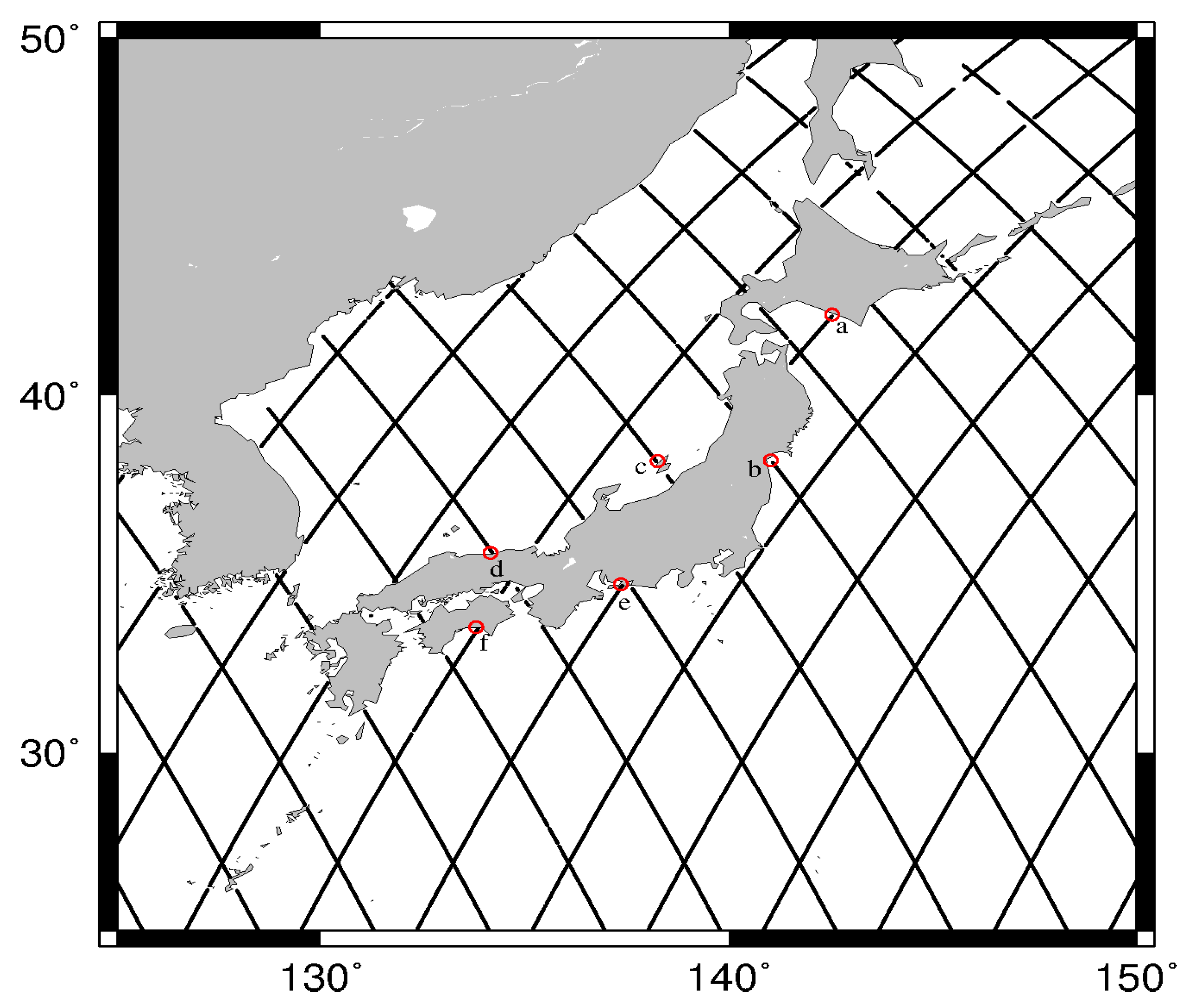
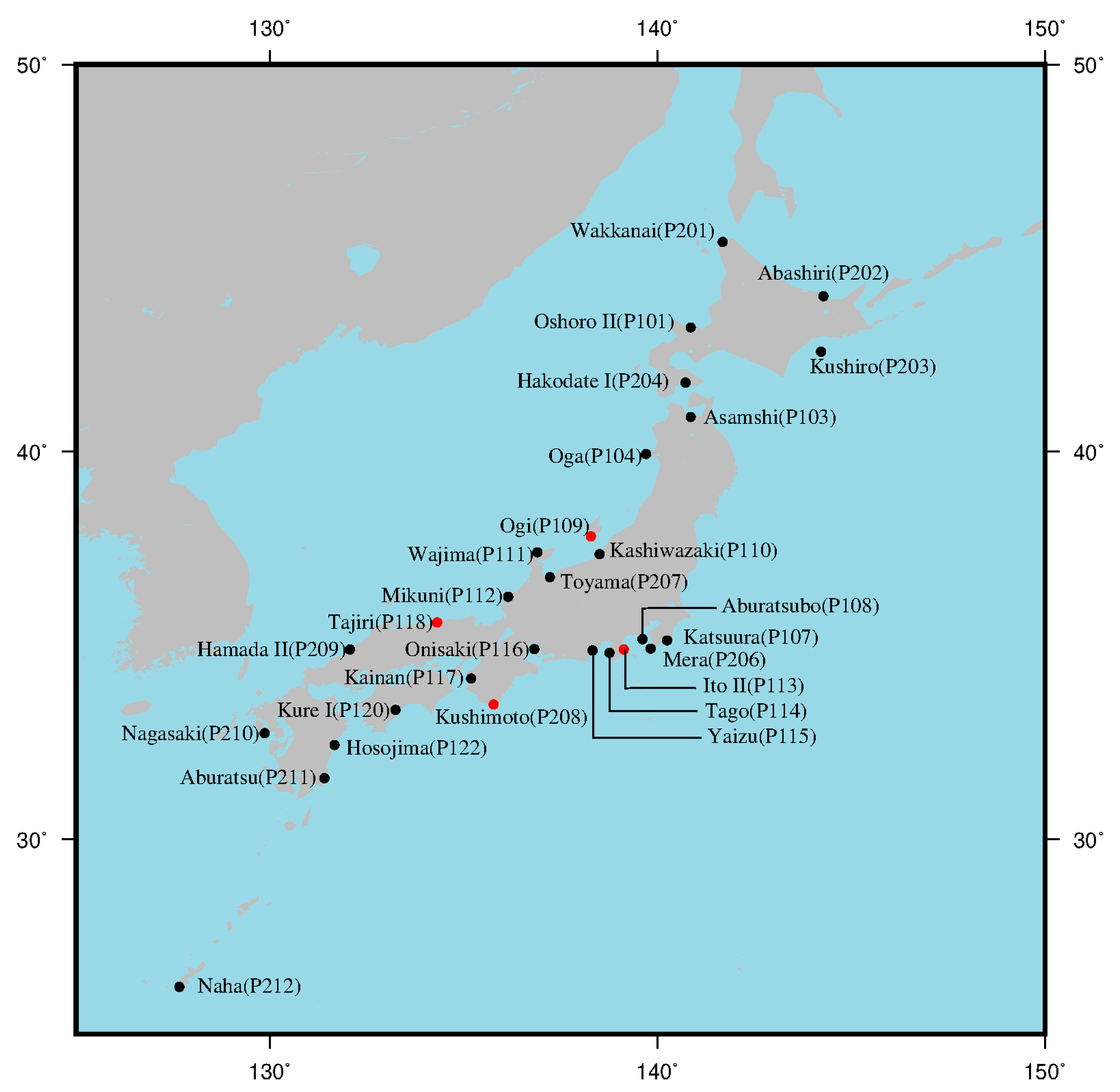
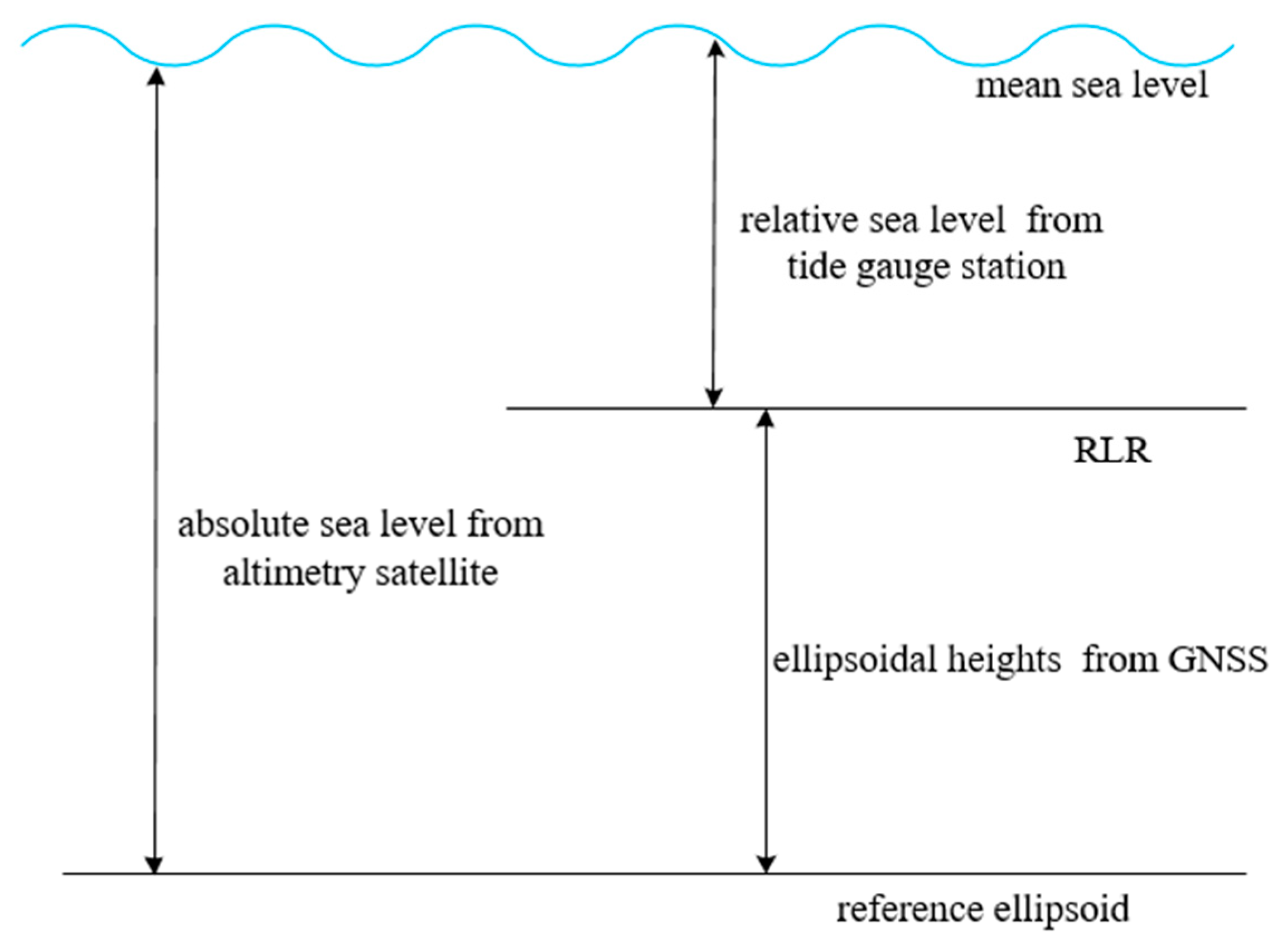
2.2.2. Tide Gauge Records
2.2.3. GNSS Data
2.3. Methodology
2.3.1. Collinear Adjustment of Exact Repeat Mission (ERM) Data
2.3.2. Temporal Oceanic Variability Corrections of GM Data
2.3.3. Crossover Adjustment
2.3.4. Least-Squares Collocation Technique for Gridding
2.3.5. Nineteen-Year Moving Average Method
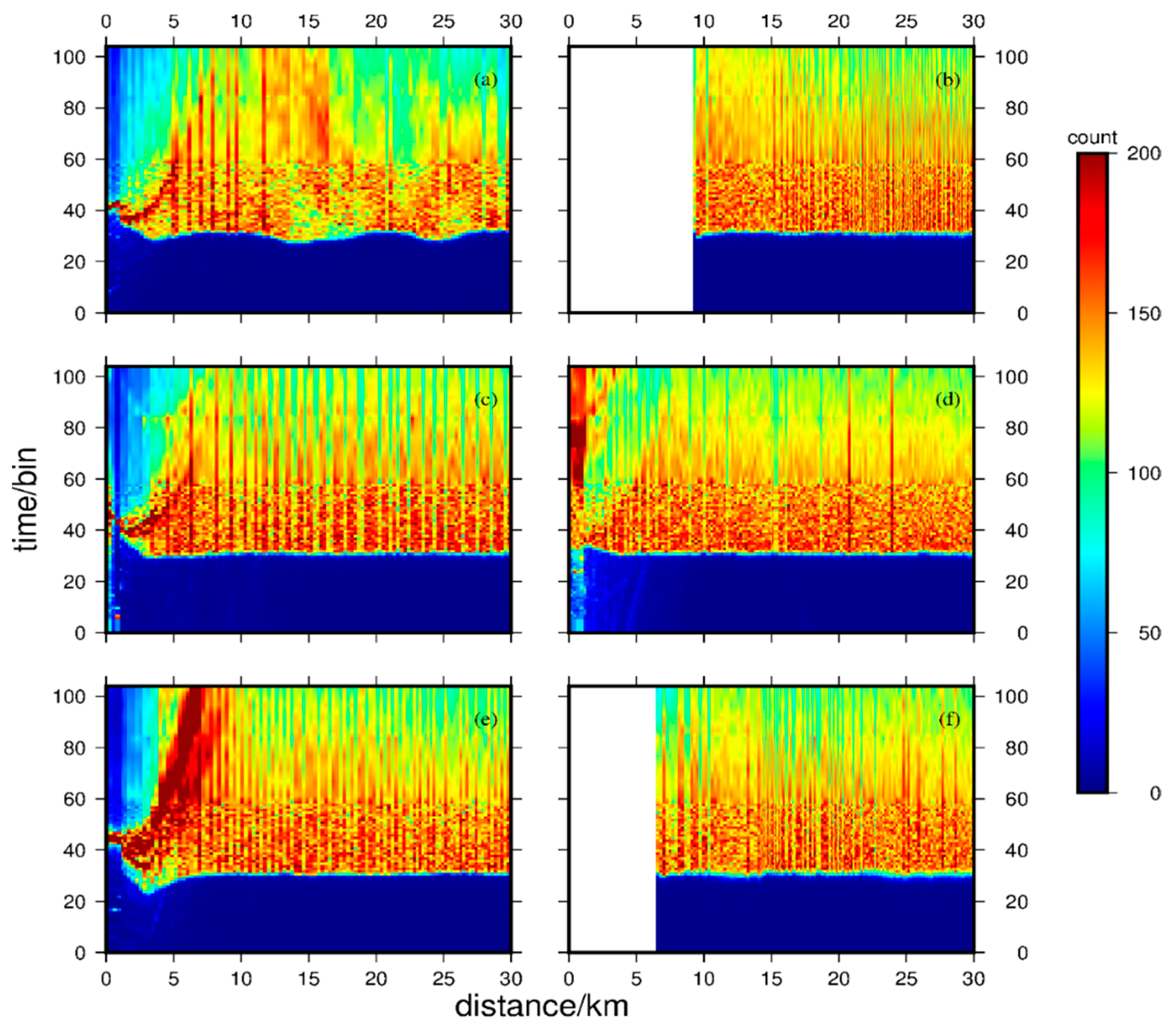
2.3.6. The Method for Improving the Coastal Accuracy of the Model
3. Results and Analysis
3.1. Establishment of the MSS Model Based on Satellite Altimeter
3.1.1. Correction of Temporal Oceanic Variability
3.1.2. The Results of the Crossover Adjustment
3.1.3. Establishment of the Model
3.2. Improvement of Model Coastal Accuracy
3.3. Accuracy Assessment of SJAO2020
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Tide Gauge | Longitude Latitude | Missing Rate of Records | RLR 1 (m) | Tide Gauge | Longitude Latitude | Missing Rate of Records | RLR 1 (m) |
|---|---|---|---|---|---|---|---|
| Wakkanai | 141.685 45.407 | 0 | 19.9807 | Aburatsubo | 139.615 35.160 | 0 | 28.8722 |
| Abashiri | 144.285 44.019 | 0.137% | 23.2246 | Katsuura | 140.249 35.129 | 0.137% | 26.2751 |
| Oshoro II | 140.858 43.209 | 0 | 25.7054 | Hamada II | 132.066 34.897 | 0 | 26.6065 |
| Kushiro | 144.371 42.975 | 0 | 22.2085 | Onisaki | 136.823 34.903 | 0 | 31.0473 |
| Hakodate I | 140.724 41.781 | 0 | 27.3744 | Yaizu | 138.327 34.870 | 0.137% | 33.1441 |
| Asamshi | 140.859 40.897 | 0.137% | 30.0906 | Mera | 139.825 34.918 | 0 | 29.3934 |
| Oga | 139.705 39.942 | 0.137% | 306029 | Ito II | 139.133 34.895 | 0 | 33.3934 |
| Ogi | 138.281 37.814 | 0 | 31.1457 | Tago | 138.764 34.806 | 0.137% | 33.3729 |
| Kashiwazaki | 138.508 37.356 | 0.275% | 32.1022 | Kainan | 135.191 34.144 | 0 | 31.2235 |
| Wajima | 136.901 37.405 | 0 | 30.4164 | Kure I | 133.243 33.333 | 0 | 29.1527 |
| Toyama | 137.224 36.762 | 0 | 31.2808 | Kushimoto | 135.773 33.475 | 0 | 31.8860 |
| Mikuni | 136.148 36.254 | 0 | 29.3105 | Nagasaki | 129.866 32.735 | 0 | 25.6219 |
| Tajiri | 134.315 35.593 | 0 | 28.8719 | Hosojima | 131.669 32.428 | 0.137% | 22.7373 |
| Aburatsu | 131.409 31.576 | 0 | 21.3963 | Naha | 127.665 26.213 | 0 | 24.5357 |
Appendix B
| GNSS Station | Receiver INFORMATION | Antenna Information | Total Number of Sessions |
|---|---|---|---|
| P101 | TRIMBLE 5700/TPS NETG3/TPS NET-G5 | TRM29659.00 DOME | 3732 |
| P103 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3849 |
| P104 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3754 |
| P107 | TRIMBLE 5700/TRIMBLE NetRS/TPS NETG3/TPS NET-G5 | TRM29659.00 DOME | 3762 |
| P108 | TRIMBLE 5700/TPS NETG3/TPS NET-G5 | TRM29659.00 DOME | 3838 |
| P109 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3783 |
| P110 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3711 |
| P111 | TRIMBLE 5700/TPS NETG3/TPS NET-G5 | TRM29659.00 DOME | 3762 |
| P112 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3768 |
| P113 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3730 |
| P114 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3734 |
| P115 | TRIMBLE 5700/TRIMBLE NetRS/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3741 |
| P116 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3762 |
| P117 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3754 |
| P118 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3706 |
| P120 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3753 |
| P122 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3785 |
| P201 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3764 |
| P202 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3733 |
| P203 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3802 |
| P204 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3781 |
| P206 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3734 |
| P207 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3731 |
| P208 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME | 3794 |
| P209 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3367 |
| P210 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3765 |
| P211 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3394 |
| P212 | TRIMBLE 5700/TPS NETG3/TPS NETG5 | TRM29659.00 DOME TRM59800.80 DOME | 3708 |
Appendix C
References
- Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. Ocean. 2009, 114, 327–432. [Google Scholar] [CrossRef]
- Qiu, H.; Jin, S. Global Mean Sea Surface Height Estimated from Spaceborne Cyclone-GNSS Reflectometry. Remote Sens. 2020, 12, 356. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, J.; Hwang, C.; Gao, J.; Yuan, J.; Liu, X. How HY-2A/GM altimeter performs in marine gravity derivation: Assessment in the South China Sea. Geophys. J. Int. 2019, 219, 1056–1064. [Google Scholar]
- Zhu, C.; Guo, J.; Gao, J.; Liu, X.; Hwang, C.; Yu, S.; Yuan, J.; Ji, B.; Guan, B. Marine gravity determined from multi-satellite-GM/ERM altimeter data over the South China Sea: SCSGA V1.0. J. Geod. 2020, 94, 50. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Hu, Z.; Liu, X.; Kong, Q.; Zhao, C. Vertical land movement over China coasts determined by tide gauge and satellite altimetric data. Arab. J. Geosci. 2016, 9, 168. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Hu, Z.; Hwang, C.; Chen, C.; Gao, Y. Temporal-spatial variations of sea level over Chinese seas derived from altimeter data of TOPEX/Poseidon, Jason-1 and Jason-2 from 1993 to 2012. Chin. J. Geophys. Chin. Ed. 2015, 58, 3103–3120. [Google Scholar]
- Dufau, C.; Orstynowicz, M.; Dibarboure, G.; Morrow, R.; La Traon, P.-Y. Mesoscale resolution capability of altimetry: Present & future. J. Geophys. Res. Ocean. 2016, 121, 4910–4927. [Google Scholar]
- Marsh, J.G.; Koblinsky, C.J.; Zwally, H.J.; Brenner, A.C.; Beckley, B.D. A global mean sea surface based upon GEOS 3 and Seasat altimeter data. J. Geophys. Res. 1992, 97, 4915–4921. [Google Scholar] [CrossRef]
- Hernandez, F.; Schaeffer, P. The CLS01 Mean Sea Surface: A Validation with the GSFC00.1 Surface; CLS: Ramonville St Agne, France, 2001. [Google Scholar]
- Schaeffer, P.; Ollivier, A.; Faugere, Y.; Bronner, E.; Picot, N. The new CNES CLS 2010 mean sea surface. In Proceedings of the Oral Presentation at OSTST Meeting, Lisbon, Portugal, 18–22 October 2010; pp. 21–22. [Google Scholar]
- Schaeffer, P.; Faugére, Y.; Legeais, J.F.; Ollivier, A.; Guinle, T.; Picot, N. The CNES_CLS11 Global Mean Sea Surface Computed from 16 Years of Satellite Altimeter Data. Mar. Geod. 2012, 35, 3–19. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Schaeffer, P.; Faugère, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the improvement of recent mean sea surface models: A new approach for identifying and quantifying their errors. J. Geophys. Res. Ocean. 2018, 123, 5889–5911. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P.; Stenseng, L. The DTU13 MSS (mean sea surface) and MDT (mean dynamic topography) from 20 years of satellite altimetry. In Proceedings of the 3rd International Gravity Field Service (IGFS), Shanghai, China, 30 June–6 July 2014; Jin, S., Barzaghi, R., Eds.; Springer: Cham, Switzerland, 2015; Volume 144, pp. 111–121. [Google Scholar]
- Andersen, O.B.; Piccioni, G.; Stenseng, L.; Knudsen, P. The DTU15 MSS (mean sea surface) and DTU15LAT (lowest astronomical tide) reference surface. In Proceedings of the ESA Living Planet Symposium 2016, Prague, Czech Republik, 9–13 May 2016. [Google Scholar]
- Andersen, O.B.; Knudsen, P.; Stenseng, L. A new DTU18 MSS mean sea surface—Improvement from SAR altimetry. 172. In Proceedings of the 25 Years of Progress in Radar Altimetry Symposium, Ponta Delgada, São Miguel Island, Azores Archipelago, Portugal, 24–29 September 2018; Volume 172, pp. 24–26. [Google Scholar]
- Jiang, W.; Li, J.; Wang, Z. Determination of global mean sea surface WHU2000 using multi-satellite altimetric data. Chin. Sci. Bull. 2002, 47, 1664–1668. [Google Scholar] [CrossRef]
- Jin, T.Y.; Li, J.C.; Jiang, W.P.; Wang, Z.T. The new generation of global mean sea surface height model based on multi-altimetric data. Acta Geod. Et Cartogr. Sin. 2011, 40, 723–729. [Google Scholar]
- Jin, T.Y.; Li, J.C.; Jiang, W.P. The global mean sea surface model WHU2013. Geod. Geodyn. 2016, 7, 202–209. [Google Scholar] [CrossRef]
- Guo, J.; Gao, Y.; Hwang, C.; Sun, J. A multi-subwaveform parametric retracker of the radar satellite altimetric waveform and recovery of gravity anomalies over coastal oceans. Sci. China Earth Sci. 2010, 53, 610–616. [Google Scholar] [CrossRef]
- Yuan, J.; Guo, J.; Niu, Y.; Zhu, C.; Li, Z.; Liu, X. Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea. J. Mar. Sci. Eng. 2020, 8, 426. [Google Scholar] [CrossRef]
- Menéndez, M.; Woodworth, P.L. Changes in extreme high water levels based on a quasi-global tide-gauge data set. J. Geophys. Res. Oceans 2010, 115, C10011. [Google Scholar] [CrossRef]
- Iliffe, J.C.; Ziebart, M.K.; Turner, J.F. A New Methodology for Incorporating Tide Gauge Data in Sea Surface Topography Models. Mar. Geod. 2007, 30, 271–296. [Google Scholar] [CrossRef]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F.; Cancet, M.; Guillot, A.; Dupuy, S. FES 2014: A new global tidal model. In Proceedings of the OSTST Meeting, Lake Contance, Germany, 28–31 October 2014. [Google Scholar]
- Yuan, J.; Guo, J.; Liu, X.; Zhu, C.; Niu, Y.; Li, Z.; Ji, B.; Ouyang, Y. Mean sea surface model over China seas and its adjacent ocean established with the 19-year moving average method from multi-satellite altimeter data. Cont. Shelf Res. 2020, 192, 104009. [Google Scholar] [CrossRef]
- Bird, P. An updated digital model of plate boundaries. Geochem. Geophy. Geosy. 2003, 4, 1027. [Google Scholar] [CrossRef]
- Ishii, M.; Kimoto, M.; Sakamoto, K.; Iwasaki, S.-I. Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses. J. Oceanogr. 2006, 62, 155–170. [Google Scholar] [CrossRef]
- CNES. Along-Track Level-2+ (L2P) SLA Product Handbook; SALP-MU-P-EA-23150-CLS, Issue1.0; CNES: Paris, France, 2017.
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New data systems and products at the permanent service for mean sea level. J. Coast. Res. 2013, 29, 493–504. [Google Scholar]
- Hassani, H. Singular spectrum analysis: Methodology and comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar]
- Shen, Y.; Guo, J.; Liu, X.; Kong, Q.; Guo, L.; Li, W. Long-term prediction of polar motion using a combined SSA and ARMA model. J. Geod. 2018, 92, 333–343. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Collilieux, X.; Guichard, M.; Míguez, B.M.; Tiphaneau, P.; Wöppelmann, G. Mitigating the effects of vertical land motion in tide gauge records using state-of-the-art GPS velocity field. Global. Planet. Change 2012, 98–99, 6–17. [Google Scholar]
- Santamaría-Gómez, A.; Gravelle, M.; Dangendorf, S.; Marcos, M.; Spada, G.; Wöppelmann, G. Uncertainty of the 20th century sea-level rise due to vertical land motion errors. Earth. Planet. Sc. Lett. 2017, 473, 24–32. [Google Scholar] [CrossRef]
- Huang, M.; Guan, Z.; Zhai, G.; Ouyang, Y. On the compensation of systematic errors in marine gravity measurements. Mar. Geod. 1999, 22, 183–194. [Google Scholar]
- Huang, M.; Zhai, G.; Ouyang, Y.; Lu, X.; Liu, C.; Wang, R. Integrated Data Processing for Multi-Satellite Missions and Recovery of Marine Gravity Field. Terr. Atmos. Ocean. Sci. 2008, 19, 103. [Google Scholar] [CrossRef]
- Wagner, C.A. Radial variations of a satellite orbit due to gravitational errors: Implications for satellite altimetry. J. Geophys. Res. Sol. Earth 1985, 90, 3027–3036. [Google Scholar] [CrossRef]
- Rummel, R. Principle of satellite altimetry and elimination of radial orbit errors. In Satellite Altimetry in Geodesy and Oceanography; Rummel, R., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; Volume 50, pp. 190–241. [Google Scholar]
- Knudsen, P.; Brovelli, M. Collinear and cross-over adjustment of Geosat ERM and Seasat altimeter data in the Mediterranean Sea. Surv. Geophys. 1993, 14, 449–459. [Google Scholar] [CrossRef]
- Wunsch, C.; Zlotnicki, V. The accuracy of altimetric surfaces. Geophys. J. Int. 1984, 78, 795–808. [Google Scholar] [CrossRef]
- Hwang, C.; Parsons, B. Gravity anomalies derived from Seasat, Geosat, ERS-1 and TOPEX/POSEIDON altimetry and ship gravity: A case study over the Reykjanes Ridge. Geophys. J. Int. 1995, 122, 551–568. [Google Scholar] [CrossRef]
- Yi, Y. Determination of Gridded Mean Sea Surface from Topex, ERS-1 and Geosat Altimeter Data. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 1995. [Google Scholar]
- Small, H. A Comparison of Techniques for the Gridding of Satellite Altimeter Data. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 1992. [Google Scholar]
- Jordan, S.K. Self-consistent statistical models for the gravity anomaly, vertical deflections, and undulation of the geoid. J. Geophys. Res. 1972, 77, 3660–3670. [Google Scholar]
- Andersen, O.B. Marine gravity and geoid from satellite altimetry. In Geoid Determination Theory and Methods; Sansô, F., Sideris, M.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 401–451. [Google Scholar]
- Moritz, H. Least-squares collocation. Rev. Geophys. 1978, 16, 421. [Google Scholar] [CrossRef]
- Basic, T.; Rapp, R.H. Oceanwide Prediction of Gravity Anomalies and Sea Surface Heights Using Geos-3, Seasat, and Geosat Altimeter Data and ETOPO5U Bathymetric Data; Ohio State University: Columbus, OH, USA, 1992; Volume 416, pp. 1–89. [Google Scholar]
- Smith, W.H.F.; Wessel, P. Gridding with continuous curvature splines in tension. Geophysics 1990, 55, 293–305. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophy. Geosy. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]


| Satellite | Start and End Date | Cycles | Satellite | Start and End Date | Cycles |
|---|---|---|---|---|---|
| TOPEX/A | December 1992–April 2004 | 11–353 | Envisat/B | February 2011–February 2012 | 100–111 |
| Jason-1/A | April 2004–October 2008 | 11–249 | SRL | March 2013–March 2015 | 1–21 |
| Jason-2/A | October 2008–May 2016 | 11–290 | HY-2A | April 2013–March 2016 | 67–117 |
| Jason-3/A | May 2016–December 2018 | 11–106 | Sentinel-3A | December 2016–January 2019 | 12–39 |
| TOPEX/B | September 2002–September 2005 | 369–479 | ERS-1/GM | April 1994–March 1995 | 30–40 |
| Jason-1/B | February 2009–February 2012 | 262–372 | Jason-1/GM | May 2012–June 2013 | 500–537 |
| ERS-1/35 | November 1992–December 1993 March 1995–March 1996 | 16–27 41–51 | CryoSat-2/LRM | January 2011–December 2018 | 14–113 |
| ERS-2 | December 1995–December 2003 | 7–80 | SRL/DP | July 2016–December 2018 | 100–125 |
| GFO | May 2000–May 2008 | 45–215 | HY-2A/GM | March 2016–January 2019 | 118–230 |
| Envisat/A | May 2002–May 2010 | 6–89 |
| GM Observations | Corresponding ERM Data | ||||
|---|---|---|---|---|---|
| Missions | Cycles | Observation Periods | Missions | Cycles | Observation Periods |
| ERS-1/GM | 100–111 | 10 April 1994–21 March 1995 | T/P | 57–93 | 1 April 1994–3 April 1995 |
| CryoSat-2 | 14–113 | 28 January 2011–30 December 2018 | Jason-2 | 94–303 | 20 January 2011–2 October 2016 |
| Jason-3 | 1–106 | 17 February 2016–3 January 2019 | |||
| Jason-1/GM | 500–537 | 7 May 2012–21 June 2013 | Jason-2 | 140–183 | 20 April 2012–3 June 2013 |
| HY-2A/GM | 118–230 | 30 March 2016–4 January 2019 | Jason-2 | 284–303 | 18 March 2016–2 October 2016 |
| Jason-3 | 4–107 | 18 March 2016–13 January 2019 | |||
| SRL/DP | 100 | 4 July 2016–31 December 2018 | Jason-2 | 294–303 | 25 June 2016–2 October 2016 |
| Jason-3 | 14–106 | 25 June 2016–2 October 2019 | |||
| Altimetric Satellite | Before Temporal Oceanic Variability Correction (m) | After Temporal Oceanic Variability Correction (m) | ||||
|---|---|---|---|---|---|---|
| Mean | STD | RMS | Mean | STD | RMS | |
| TOPEX/A + Jason-1/A + Jason-2/A + Jason-3/A | −0.0003 | 0.1971 | 0.1971 | 0.0018 | 0.0179 | 0.0179 |
| TOPEX/B + Jason-1/B | 0.0122 | 0.1598 | 0.1602 | −0.0023 | 0.0291 | 0.0292 |
| ERS-1 | −0.0095 | 0.1983 | 0.1985 | 0.0017 | 0.0452 | 0.0453 |
| ERS-2 | −0.0090 | 0.2216 | 0.2185 | −0.0049 | 0.0815 | 0.0816 |
| GFO | 0.0164 | 0.1818 | 0.1825 | 0.0034 | 0.0277 | 0.0279 |
| Envisat/A | 0.0191 | 0.1898 | 0.1908 | −0.0024 | 0.0258 | 0.0260 |
| Envisat/B | 0.0065 | 0.1692 | 0.1693 | 0.0023 | 0.0632 | 0.0632 |
| SRL | −0.0094 | 0.1842 | 0.1844 | 0.0015 | 0.0444 | 0.0444 |
| HY-2A | 0.0012 | 0.1867 | 0.1867 | 0.0005 | 0.0328 | 0.0328 |
| Sentinel-3A | 0.0064 | 0.1801 | 0.1802 | −0.0030 | 0.0293 | 0.0295 |
| ERS-1/GM | −0.0016 | 0.1883 | 0.1883 | −0.0080 | 0.1202 | 0.1204 |
| Jason-1/GM | 0.0282 | 0.1882 | 0.1861 | −0.0016 | 0.1120 | 0.1120 |
| Cryosat-2/LRM | −0.0189 | 0.1866 | 0.1876 | 0.0002 | 0.1109 | 0.1109 |
| SRL/DP | 0.0011 | 0.1851 | 0.1851 | 0.0010 | 0.1128 | 0.1128 |
| HY-2A/GM | 0.0016 | 0.2021 | 0.2021 | −0.0010 | 0.1235 | 0.1235 |
| Altimetry Satellite | After Crossover Adjustment (m) | ||
|---|---|---|---|
| Mean | STD | RMS | |
| TOPEX/A + Jason-1/A + Jason-2/A + Jason-3/A | 0.0003 | 0.0068 | 0.0068 |
| TOPEX/B + Jason-1/B | −0.0015 | 0.0245 | 0.0245 |
| ERS-1 | 0.0004 | 0.0246 | 0.0246 |
| ERS-2 | −0.0003 | 0.0444 | 0.0444 |
| GFO | 0.0008 | 0.0155 | 0.0155 |
| Envisat/A | −0.0002 | 0.0159 | 0.0159 |
| Envisat/B | 0.0015 | 0.0372 | 0.0372 |
| SRL | 0.0003 | 0.0270 | 0.0270 |
| HaiYang-2A | 0.0003 | 0.0266 | 0.0266 |
| Sentinel-3A | 0.0003 | 0.0257 | 0.0257 |
| ERS-1/GM | 0.0002 | 0.0985 | 0.0985 |
| Jason-1/GM | −0.0007 | 0.0942 | 0.0942 |
| Cryosat-2/LRM | 0.0001 | 0.0917 | 0.0917 |
| SRL/DP | 0.0004 | 0.0951 | 0.0951 |
| HY-2A/GM | −0.0009 | 0.1021 | 0.1021 |
| All satellite | 0.0001 | 0.0811 | 0.0811 |
| Tide | Improvements 1 | |||||
|---|---|---|---|---|---|---|
| Ogi | 38.8718 | 38.8410 | 38.8410 | 38.8348 | 38.8917 | 45.80% |
| Tajiri | 36.6258 | 36.2451 | 36.1905 | 36.6799 | 36.6399 | 73.94% |
| Ito II | 40.5066 | 40.4290 | 40.4480 | 40.3941 | 40.4708 | 68.17% |
| Kushimoto | 39.6676 | 39.7407 | 39.7298 | 39.7160 | 39.6874 | 59.09% |
| Altimetric Satellite | SJAO2020 | CLS15 | DTU18 | DTU15 | WHU13 | CLS11 |
|---|---|---|---|---|---|---|
| T/P+Japan-1 + Japan-2 + Japan-3 (31 December 1992–31 December 2018) | 0.0138 | 0.0177 | 0.0186 | 0.0196 | 0.0265 | 0.0292 |
| ERS-1 (27 November 1992–30 December 1993 | 0.0217 | 0.0224 | 0.0223 | 0.0224 | 0.0226 | 0.0222 |
| HY-2A (12 April 2014–15 March 2016) | 0.0201 | 0.0220 | 0.0222 | 0.0228 | 0.0255 | 0.0264 |
| Sentinel-3B (27 November 2018–5 November 2019) | 0.0292 | 0.0312 | 0.0319 | 0.0320 | 0.0342 | 0.0358 |
| SRL (19 March 2015–4 July 2016) | 0.0435 | 0.0421 | 0.0443 | 0.0449 | 0.0517 | 0.0529 |
| Jason-2/GM (29 July 2017–14 September 2017) | 0.0414 | 0.0425 | 0.0426 | 0.0430 | 0.0494 | 0.0497 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Guo, J.; Niu, Y.; Zhu, C.; Li, Z. Mean Sea Surface Model over the Sea of Japan Determined from Multi-Satellite Altimeter Data and Tide Gauge Records. Remote Sens. 2020, 12, 4168. https://doi.org/10.3390/rs12244168
Yuan J, Guo J, Niu Y, Zhu C, Li Z. Mean Sea Surface Model over the Sea of Japan Determined from Multi-Satellite Altimeter Data and Tide Gauge Records. Remote Sensing. 2020; 12(24):4168. https://doi.org/10.3390/rs12244168
Chicago/Turabian StyleYuan, Jiajia, Jinyun Guo, Yupeng Niu, Chengcheng Zhu, and Zhen Li. 2020. "Mean Sea Surface Model over the Sea of Japan Determined from Multi-Satellite Altimeter Data and Tide Gauge Records" Remote Sensing 12, no. 24: 4168. https://doi.org/10.3390/rs12244168
APA StyleYuan, J., Guo, J., Niu, Y., Zhu, C., & Li, Z. (2020). Mean Sea Surface Model over the Sea of Japan Determined from Multi-Satellite Altimeter Data and Tide Gauge Records. Remote Sensing, 12(24), 4168. https://doi.org/10.3390/rs12244168