PyTirCam-1.0: A Python Model to Manage Thermal Infrared Camera Data
Abstract
1. Introduction
2. Materials and Methods
2.1. The Case Study, the TIR Sensors, and the Data Acquisition Procedure
2.2. Theoretical Background
2.2.1. Blackbody Radiation and Emissivity
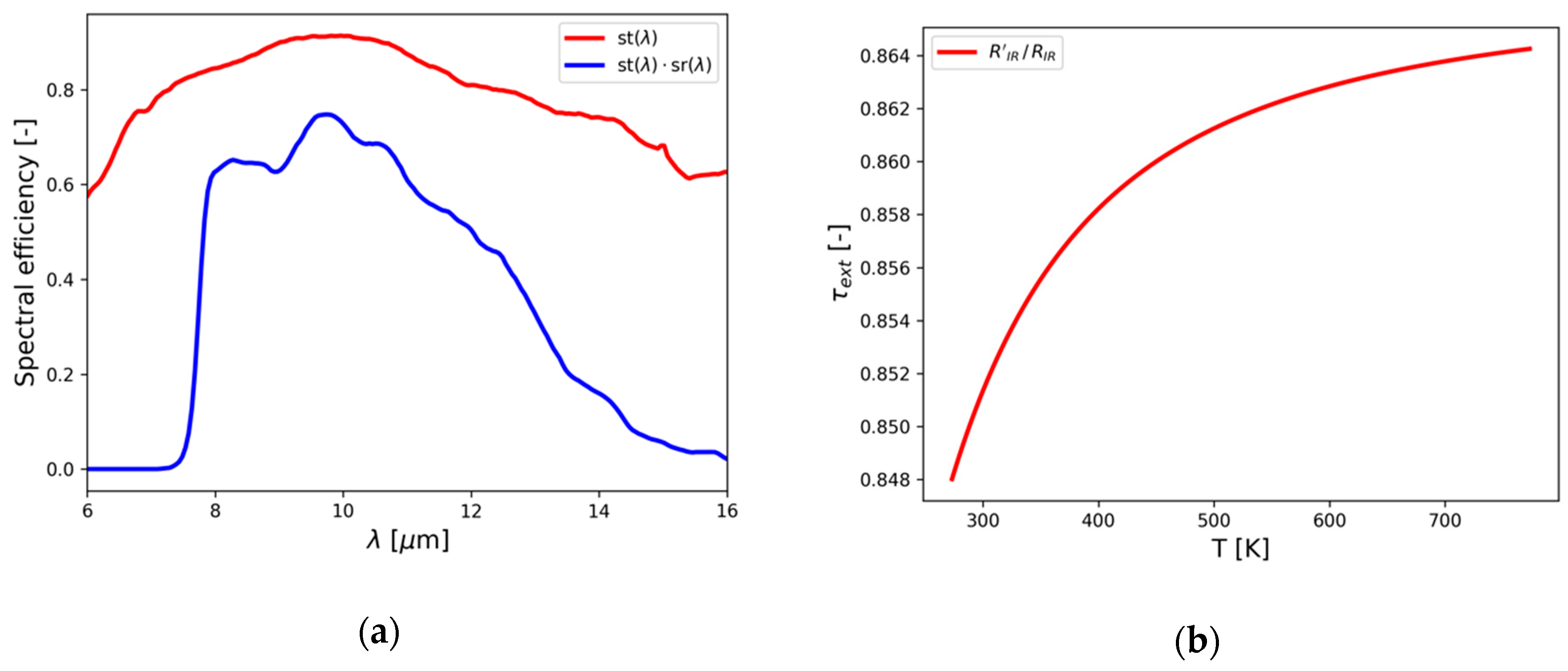
2.2.2. Camera Sensor Spectral Response
2.2.3. Atmospheric Emission and Absorption
2.2.4. Effect of a Protective Germanium Lens on IR Measurements
2.2.5. Effect of the Internal Optics
2.3. Radiance and Brighness Temperature Conversion Used by the FLIR Camera
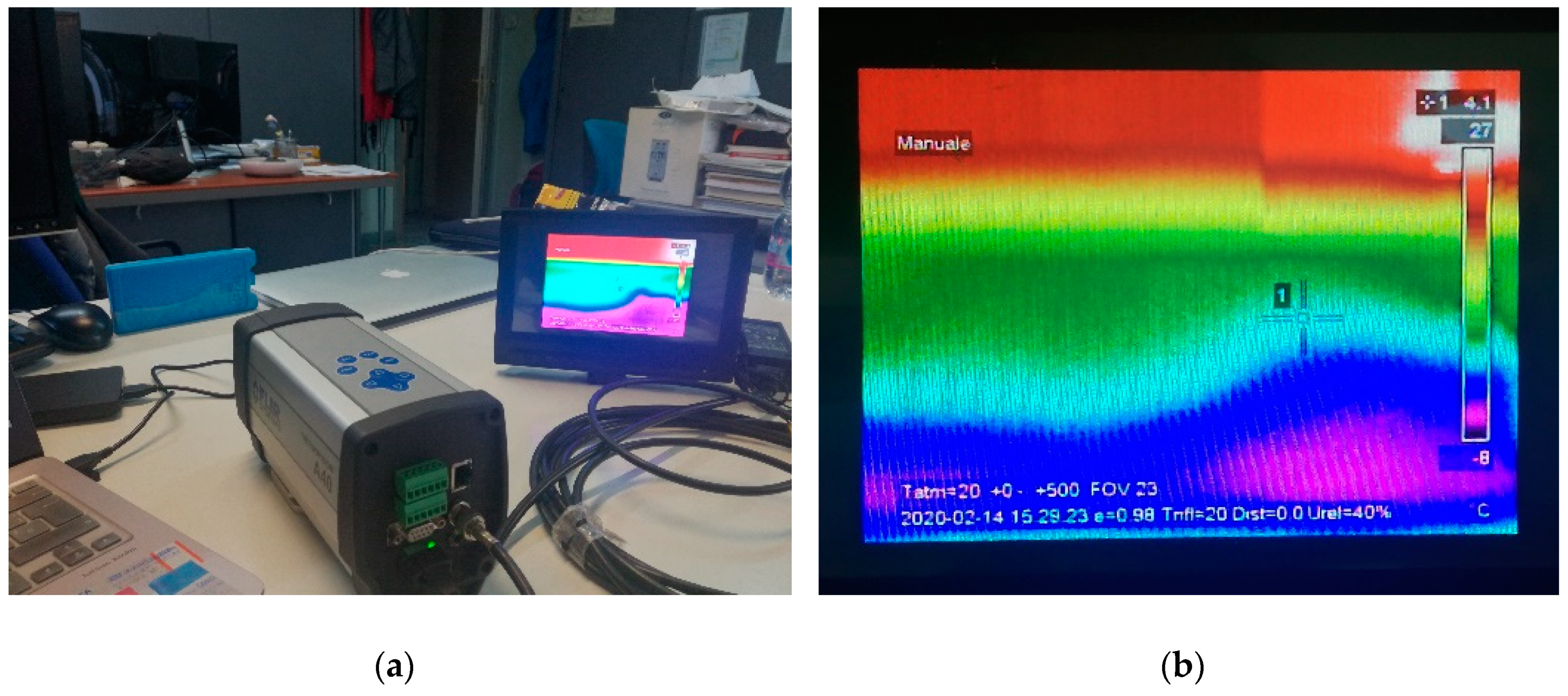
2.4. Experimental Procedure with the FLIR A40 M Camera
- Temperature range, [0, 500] °C;
- display scale range, [−10, 60] °C;
- emissivity, 0.98;
- atmospheric and reflected temperatures, 20 °C;
- relative humidity, 40%;
- distance, 3047 m;
- no external optics .
2.5. From .jpg Images to Brightness Temperature
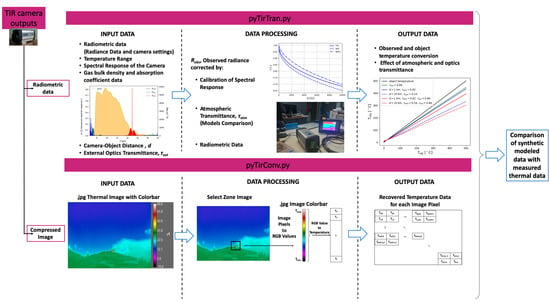
2.6. Description of Python Scripts
- PyTirCam-1.0/pyTirTran: A transmission and conversion algorithm based on the spectral properties of atmospheric gases and of the TIR camera.
- PyTirCam-1.0/jpgToTIR: An algorithm based on Python PIL library to recover the radiometric thermal data from compressed images.
2.6.1. PyTirCam-1.0/pyTirTran
- The required input and functions to run PyTirTran.py:
- input.py is the input file of pyTirTran.py. The required inputs are (symbols used in the script are reported in brackets): Temperature range in K (Tmin and Tmax), length of the temperature linear space (len_T), CO2 bulk density (rhoCO2), maximum value of the camera spectral response (SpR_max), minimum and maximum wavelength of the spectral response defined as a step function (lambda_min, lambda_max), the camera-object distance (L), external optics transmittance (tauext), and the local path of the H2O and CO2 absorption coefficient data, beside the camera spectral response data (fileIn_*).
- functions/__init__.py is the file containing: Fit, the function to perform curve fittings and provide optimal parameters; T_func, the function approximating as a combination of linear and power laws (see Section 2.3 and Table 1); ps, the saturation pressure of water; rhow and rhowThC, the water vapor bulk density (as in Equations (A3) and (A6), respectively); Planck and RIR, the Planck function and the Stefan-Boltzmann law corrected with the camera spectral response (Equations (1) and (5), respectively); Step, the spectral response as a step function (Section 3.1); tauA and tauThC, the atmospheric transmittances (Equations (10) and (A5), respectively); Rtot, the total radiance received by the camera sensor (Equation (16)).
- pyTirTran.py is the Python script to be executed. The script can be run to:
- Use the spectral response of the camera or defined as step function by choosing the flag step = False or True, respectively.
- Save the plot of the results reported and discussed in Section 3.2 (atmoAndOptics.png) and a plot showing the goodness of the approximation used in Equation (10) for the atmospheric transmittance (tauObjOnTauAtm.png), by selecting the flag results = “Figure 8”.
2.6.2. PyTirCam-1.0/jpgToTIR
- The required input and functions to run PyTirConv.py:
- input.py is the input file of pyTirConv.py. The required inputs are the radiometric image containing the colorbar (InputImage.jpg), the bounds pixel coordinates (width “w” going left-right and height “h” going top-bottom) of both the colorbar (bar_wi, bar_wf, bar_hi, bar_hf) and the zone of the image to be analyzed (wi, wf, hi, hf), and the range of the colorbar (Tmin, Tmax).
- InputData.dat is the file containing the source radiometric temperature data corresponding to the compressed image (InputImage.jpg). This is the file used to evaluate the accuracy of the conversion algorithm.
- functions/__init__.py is the file containing the functions needed to retrieve the temperature data from the compressed image. The conversion can be done both with the image colorbar and the analytical colorbar. In particular, the following functions are defined: closest_color, finds the colorbar index corresponding to the closest color (by means of the Euclidean distance); analyticBar, defines a specific analytical colorbar; fromJpgToBar, finds the colorbar directly from the image; and fromJpgToArray, extract the temperature values from the compressed image.
- pyTirConv.py is the Python script to be executed. The script can be run to:
- Covert each pixel of the selected image zone to a temperature value by finding the closest color to the RGB triplet. The temperature data and the corresponding .jpg image are saved as Temperature.dat and OutputImage.jpg, respectively. By choosing the flag load = True, it is possible to run the part of the script related only to the data analysis by loading the previously recovered temperature data beside their corresponding image.
- Save an image (difference.jpg) showing the difference between the colors of the input image (InputImage.jpg) and those of the recovered one (OutputImage.jpg), by selecting the flag evalConv = True.
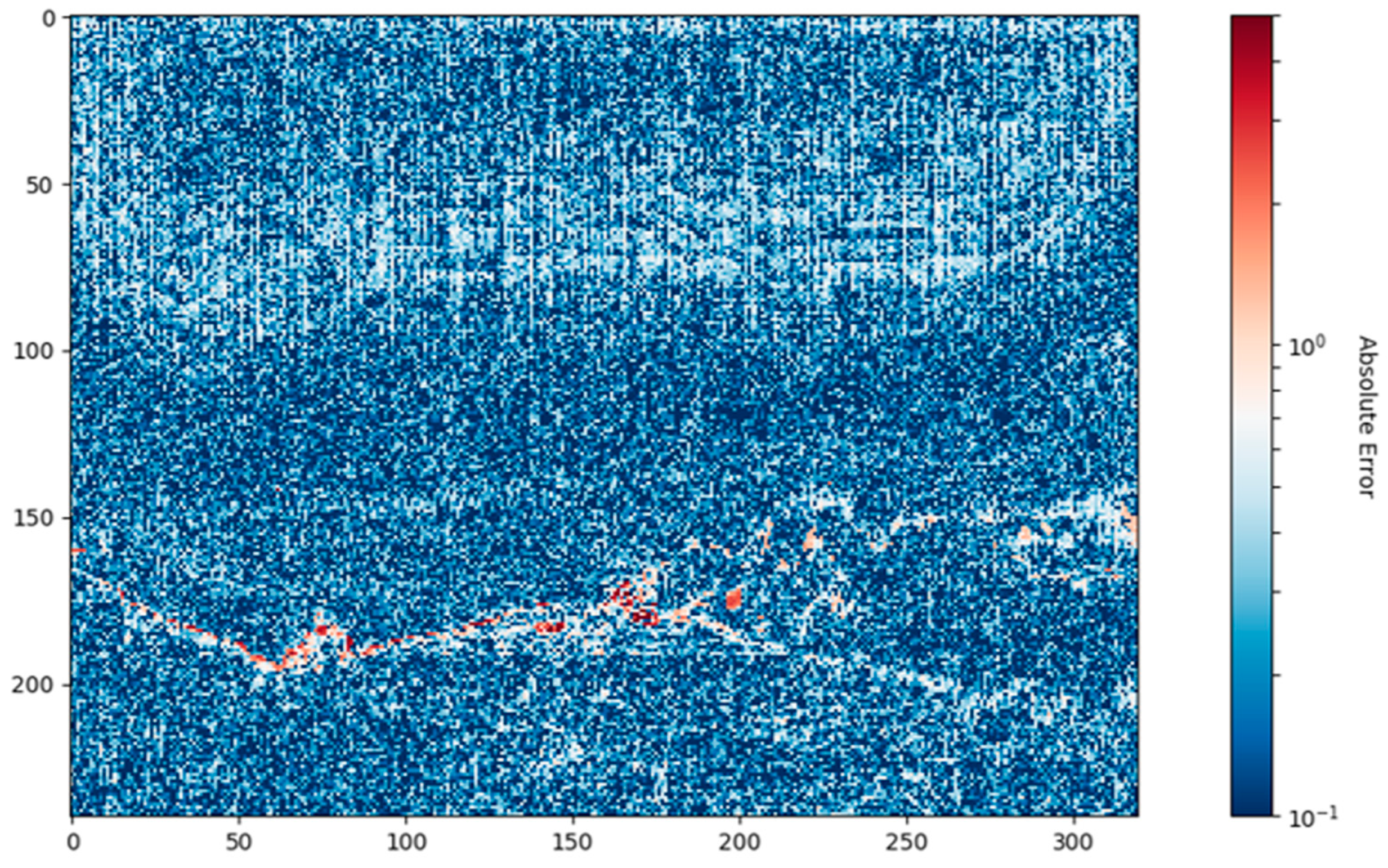
- Compute the absolute error between the radiometric (InputData.dat) and the recovered data (Temperature.dat) by selecting the flag evalRadio = True. Moreover, this flag prints the maximum, average, and minimum temperature error.
- Do the above operations (1–3), also with the analytical colorbar, by choosing the flag analytic = True. This flag shows also the comparison of the two colorbars.
- Output files: The recovered temperature data and image from both the image and analytic colorbars (Temperature.dat, Temperature_analytic.dat, OutputImage.jpg, OutputImage_analytic.jpg) and the difference between the radiometric and recovered data using both colorbars (difference.jpg, difference_analytic.jpg).
3. Results and Discussion
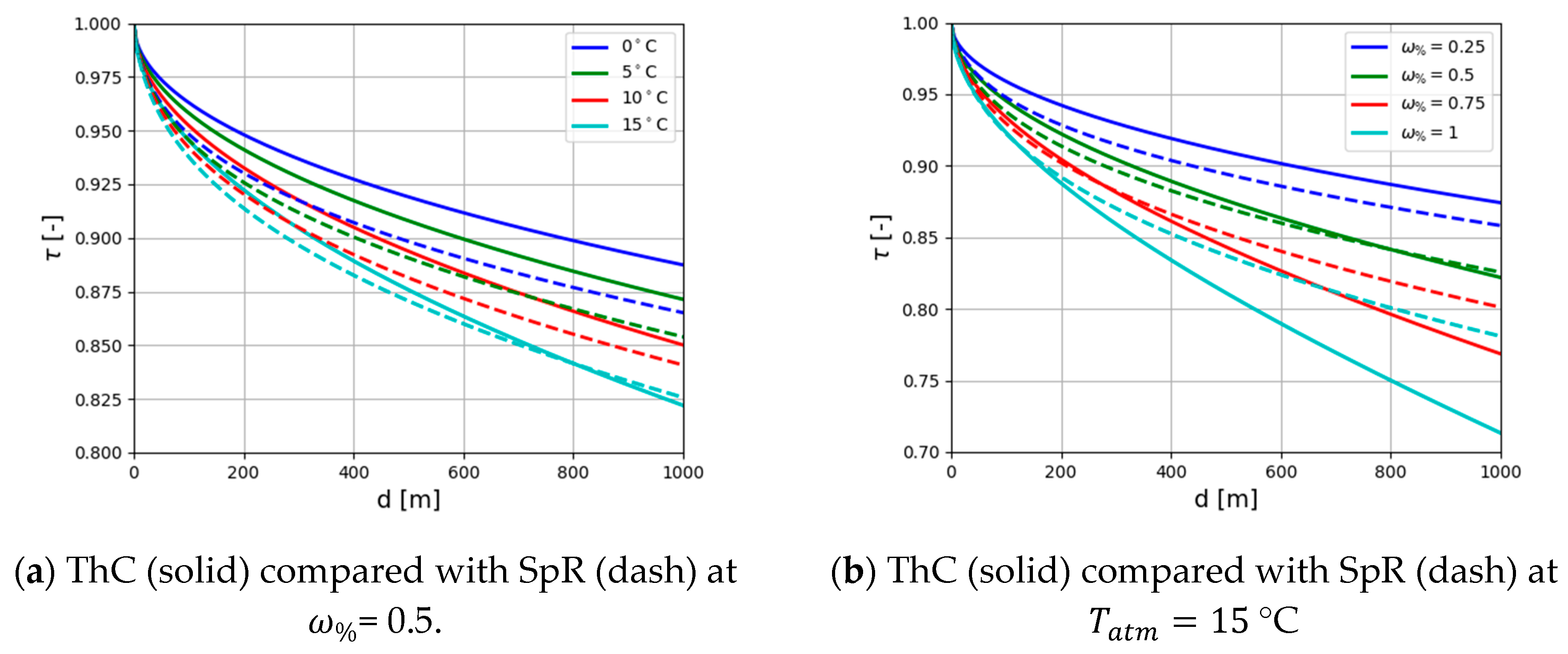
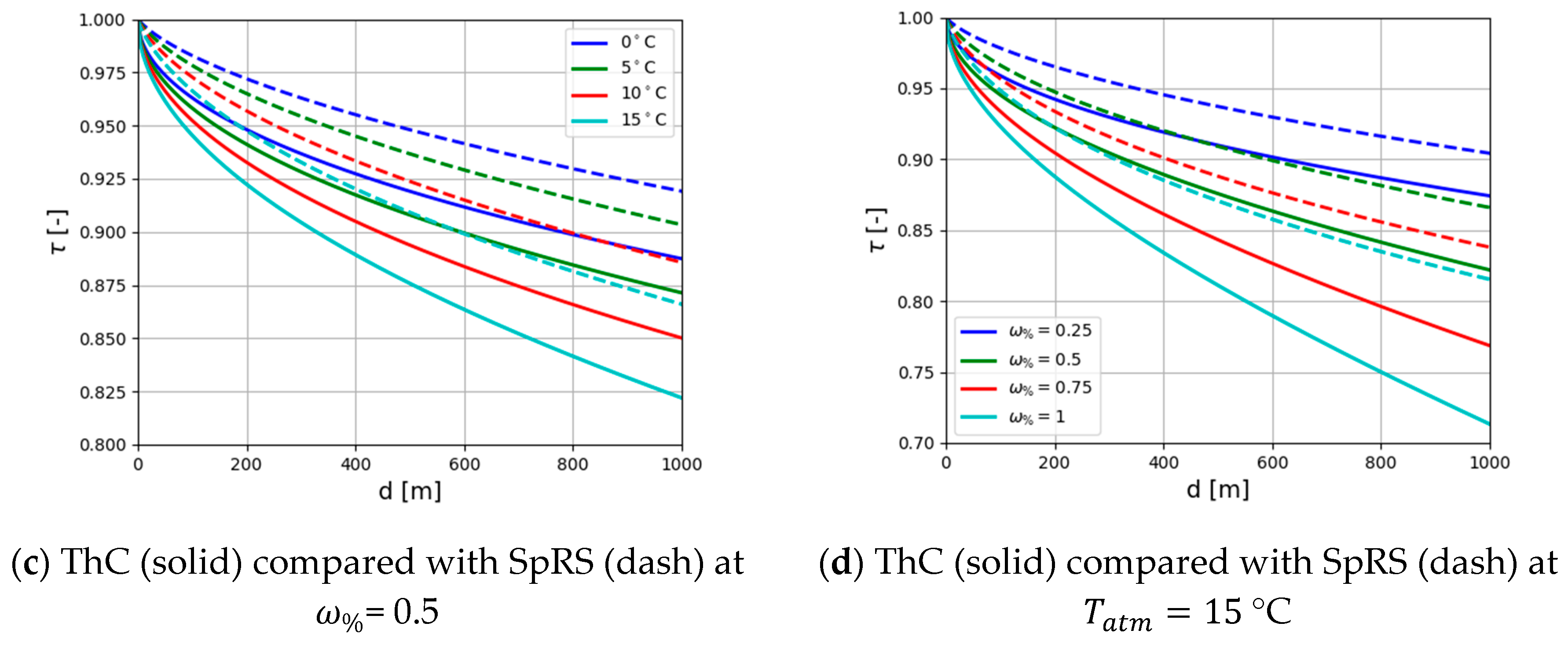
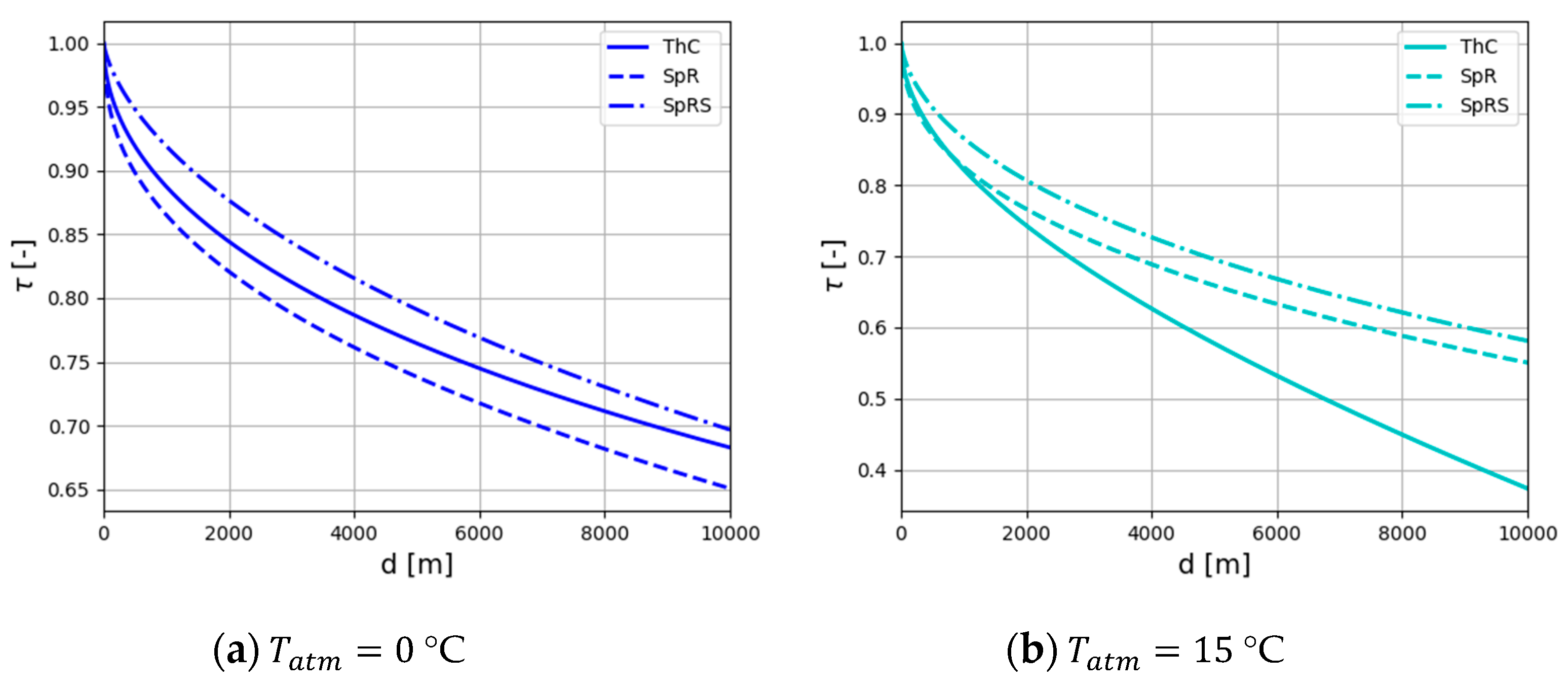
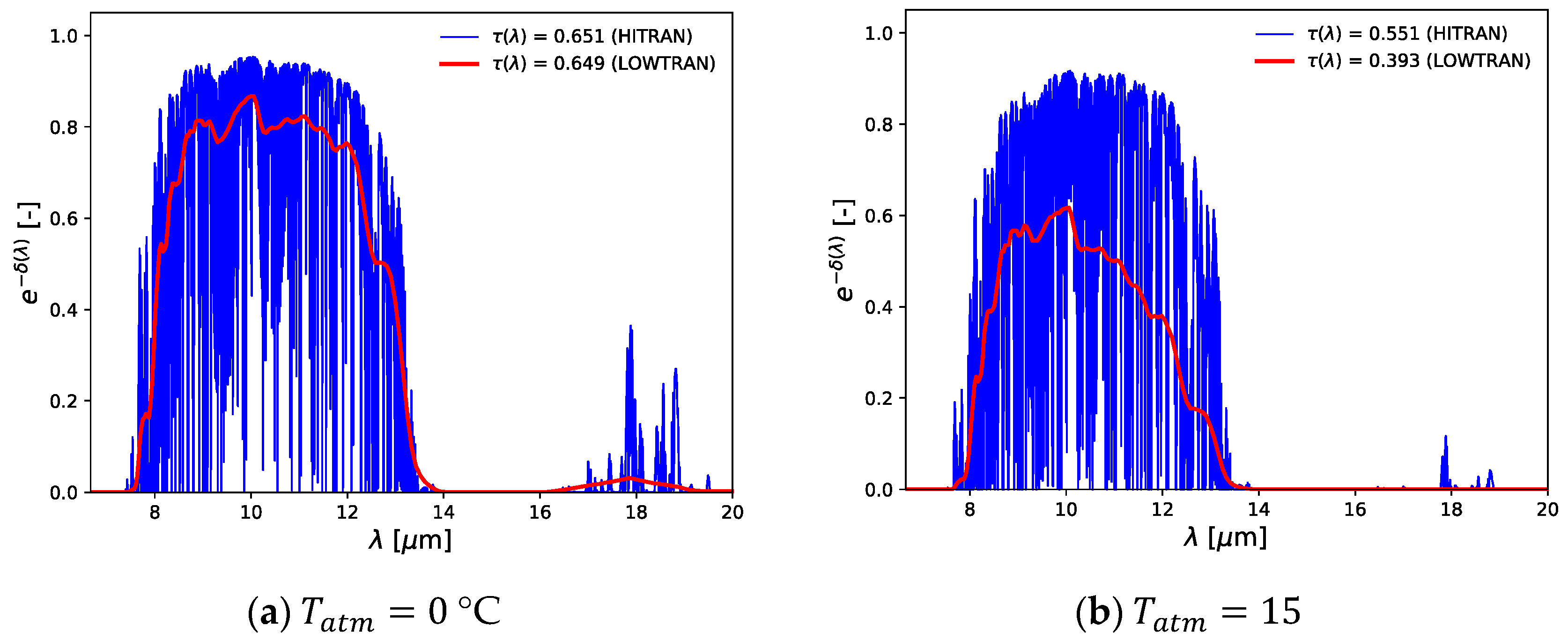
3.1. Atmospheric Transmittance Models Comparison
3.2. Effect of the Atmospheric and External Optics Corrections on High Temperature Measurements
3.3. Comparison between Experimental Data and Theoretical Atmospheric Correction
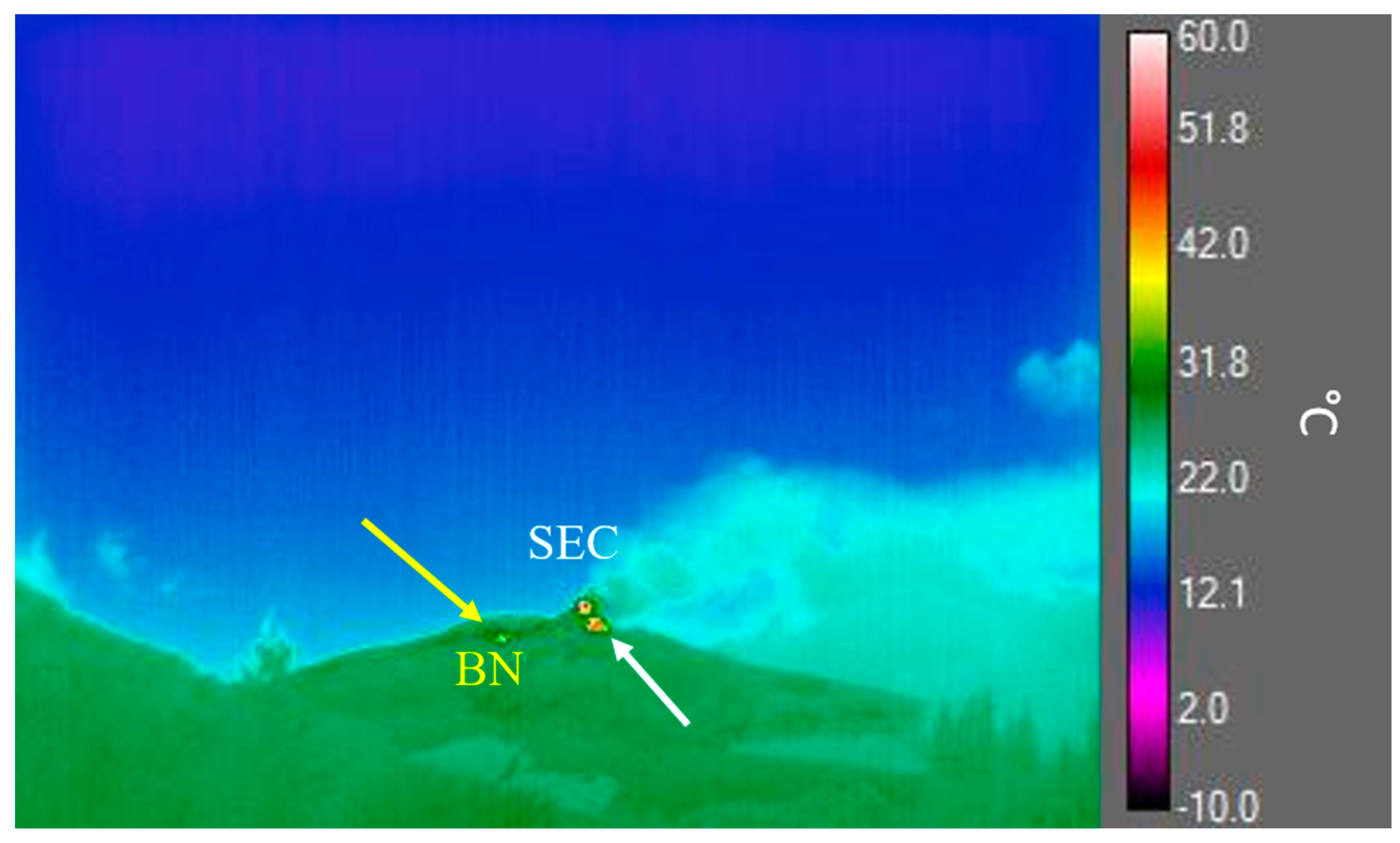
3.4. Brightness Temperature from a .jpg Image Acquired on 16 November 2006
4. Conclusions
Author Contributions
Funding
Software Availability
Acknowledgments
Conflicts of Interest
Appendix A. Transmittance Coefficients
Appendix B
References
- Flynn, L.P.; Mouginis-Mark, P.J.; Gradie, J.C.; Lucey, P.G. Radiative temperature measurements at Kupaianaha Lava Lake, Kilauea Volcano, Hawaii. J. Geophys. Res. Solid Earth 1993, 98, 6461–6476. [Google Scholar] [CrossRef]
- Pinkerton, H.; James, M.; Jones, A. Surface temperature measurements of active lava flows on Kilauea volcano, Hawai’i. J. Volcanol. Geotherm. Res. 2002, 113, 159–176. [Google Scholar] [CrossRef]
- Calvari, S.; Pinkerton, H. Birth, growth and morphologic evolution of the “Laghetto” cinder cone during the 2001 Etna eruption. J. Volcanol. Geotherm. Res. 2004, 132, 225–239. [Google Scholar] [CrossRef]
- Calvari, S.; Spampinato, L.; Lodato, L.; Harris, A.J.L.; Patrick, M.R.; Dehn, J.; Burton, M.R.; Andronico, D. Chronology and complex volcanic processes during the 2002-2003 flank eruption at Stromboli volcano (Italy) reconstructed from direct observations and surveys with a handheld thermal camera. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Harris, A. Thermal Remote Sensing of Active Volcanoes: A User’s Manual; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Platt, U.; Bobrowski, N.; Butz, A. Ground-Based Remote Sensing and Imaging of Volcanic Gases and Quantitative Determination of Multi-Species Emission Fluxes. Geosciences 2018, 8, 44. [Google Scholar] [CrossRef]
- Prata, F.J.; Bernardo, C. Retrieval of volcanic ash particle size, mass and optical depth from a ground-based thermal infrared camera. J. Volcanol. Geotherm. Res. 2009, 186, 91–107. [Google Scholar] [CrossRef]
- Prata, F.J.; Bernardo, C. Retrieval of sulphur dioxide from a ground-based thermal infrared imaging camera. Atmos. Meas. Tech. Discuss. 2014, 7, 1153–1211. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Ripepe, M. Temperature and dynamics of degassing at Stromboli. J. Geophys. Res. 2007, 112, B03205. [Google Scholar] [CrossRef]
- Blackett, M. An Overview of Infrared Remote Sensing of Volcanic Activity. J. Imaging 2017, 3, 13. [Google Scholar] [CrossRef]
- Coppola, D.; Laiolo, M.; Cigolini, C.; Massimetti, F.; Delle Donne, D.; Ripepe, M.; Arias, H.; Barsotti, S.; Parra, C.B.; Centeno, R.G.; et al. Thermal Remote Sensing for Global Volcano Monitoring: Experiences From the MIROVA System. Front. Earth Sci. 2020, 7, 362. [Google Scholar] [CrossRef]
- Spampinato, L.; Calvari, S.; Oppenheimer, C.; Boschi, E. Volcano surveillance using infrared cameras. Earth Sci. Rev. 2011, 106, 63–91. [Google Scholar] [CrossRef]
- Calvari, S.; Lodato, L.; Steffke, A.; Cristaldi, A.; Harris, A.J.L.; Spampinato, L.; Boschi, E. The 2007 stromboli eruption: Event chronology and effusion rates using thermal infrared data. J. Geophys. Res. Solid Earth 2010, 115, 1–20. [Google Scholar] [CrossRef]
- Andronico, D.; Taddeucci, J.; Cristaldi, A.; Miraglia, L.; Scarlato, P.; Gaeta, M. The 15 March 2007 paroxysm of Stromboli: Video-image analysis, and textural and compositional features of the erupted deposit. Bull. Volcanol. 2013, 75, 733. [Google Scholar] [CrossRef]
- Tran, Q.H.; Han, D.; Kang, C.; Haldar, A.; Huh, J. Effects of Ambient Temperature and Relative Humidity on Subsurface Defect Detection in Concrete Structures by Active Thermal Imaging. Sensors 2017, 17, 1718. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Menzel, W.P.; Tobin, D.C.; Revercomb, H.E. Infrared Remote Sensing with Meteorological Satellites. Adv. At. Mol. Opt. Phys. 2016, 65, 193–264. [Google Scholar] [CrossRef]
- Du, X.; Cao, D.; Mishra, D.; Bernardes, S.; Jordan, T.R.; Madden, M. Self-adaptive gradient-based thresholding method for coal fire detection using ASTER thermal infrared data, Part I: Methodology and decadal change detection. Remote Sens. 2015, 7, 6576–6610. [Google Scholar] [CrossRef]
- Ren, H.; Du, C.; Liu, R.; Qin, Q.; Meng, J.; Li, Z.L.; Yan, G. Evaluation of radiometric performance for the Thermal Infrared Sensor onboard Landsat 8. Remote Sens. 2014, 6, 12776–12788. [Google Scholar] [CrossRef]
- Pfeffer, M.A.; Bergsson, B.; Barsotti, S.; Stefánsdóttir, G.; Galle, B.; Arellano, S.; Conde, V.; Donovan, A.; Ilyinskaya, E.; Burton, M.; et al. Ground-Based measurements of the 2014-2015 holuhraun volcanic cloud (Iceland). Geosciences 2018, 8, 29. [Google Scholar] [CrossRef]
- Andò, B.; Pecora, E. An advanced video-based system for monitoring active volcanoes. Comput. Geosci. 2006, 32, 85–91. [Google Scholar] [CrossRef]
- Corradino, C.; Ganci, G.; Cappello, A.; Bilotta, G.; Calvari, S.; Negro, C.D. Recognizing eruptions of Mount Etna through machine learning using multiperspective infrared images. Remote Sens. 2020, 12, 970. [Google Scholar] [CrossRef]
- Cerminara, M.; Esposti Ongaro, T.; Valade, S.; Harris, A.J.L. Volcanic plume vent conditions retrieved from infrared images: A forward and inverse modeling approach. J. Volcanol. Geotherm. Res. 2015, 300, 129–147. [Google Scholar] [CrossRef]
- Valade, S.; Harris, A.J.L.; Cerminara, M. Plume Ascent Tracker: Interactive Matlab software for analysis of ascending plumes in image data. Comput. Geosci. 2014, 66, 132–144. [Google Scholar] [CrossRef]
- Sansivero, F.; Scarpato, G.; Vilardo, G. The automated infrared thermal imaging system for the continuous long-term monitoring of the surface temperature of the Vesuvius crater. Ann. Geophys. 2013, 56, S0454. [Google Scholar] [CrossRef]
- Sansivero, F.; Vilardo, G. Processing thermal infrared imagery time-series from volcano permanent ground-based monitoring network. Latest methodological improvements to characterize surface temperatures behavior of thermal anomaly areas. Remote Sens. 2019, 11, 553. [Google Scholar] [CrossRef]
- Russo, G.; Reitano, D.; Pecora, E.; Biale, E. Thermal Camera Data Tool (T.C.D.) per L’Analisi Dei Dati da Telecamera Termica. Rapporti Tecnici INGV 2008, 84. Available online: http://hdl.handle.net/2122/4652 (accessed on 5 December 2020).
- Gaudin, D.; Taddeucci, J.; Scarlato, P.; Harris, A.J.L.; Bombrun, M.; Del Bello, E.; Ricci, T. Characteristics of puffing activity revealed by ground-based, thermal infrared imaging: The example of Stromboli Volcano (Italy). Bull. Volcanol. 2017, 79, 24. [Google Scholar] [CrossRef]
- Labazuy, P.; Gouhier, M.; Harris, A.; Guéhenneux, Y.; Hervo, M.; Bergès, J.C.; Fréville, P.; Cacault, P.; Rivet, S. Near real-time monitoring of the April-May 2010 Eyjafjallajökull ash cloud: An example of a web-based, satellite data-driven, reporting system. Int. J. Environ. Pollut. 2012, 48, 262–272. [Google Scholar] [CrossRef]
- Wright, R.; Flynn, L.; Garbeil, H.; Harris, A.; Pilger, E. Automated volcanic eruption detection using MODIS. Remote Sens. Environ. 2002, 82, 135–155. [Google Scholar] [CrossRef]
- Minkina, W.; Klecha, D. Atmospheric transmission coefficient modelling in the infrared for thermovision measurements. J. Sens. Sens. Syst. 2016, 5, 17–23. [Google Scholar] [CrossRef]
- Minkina, W.; Klecha, D. Modeling of Atmospheric Transmission Coefficient in Infrared for Thermovision Measurements. In Proceedings of the AMA Conferences 2015, Nürnberg, Germany, 19–21 May 2015; pp. 903–907. [Google Scholar] [CrossRef]
- Ball, M.; Pinkerton, H. Factors affecting the accuracy of thermal imaging cameras in volcanology Factors affecting the accuracy of thermal imaging cameras in volcanology. J. Geophys. Res. Solid Earth 2006. [Google Scholar] [CrossRef]
- Sawyer, G.M.; Burton, M.R. Effects of a volcanic plume on thermal imaging data. Geophys. Res. Lett. 2006, 33, L14311. [Google Scholar] [CrossRef]
- HITRANonline. Available online: http://hitran.org/ (accessed on 6 November 2020).
- Wilkes, T.C.; Stanger, L.R.; Willmott, J.R.; Pering, T.D.; McGonigle, A.J.S.; England, R.A. The development of a low-cost, near infrared, high-temperature thermal imaging system and its application to the retrieval of accurate lava lake temperatures at Masaya volcano, Nicaragua. Remote Sens. 2018, 10, 450. [Google Scholar] [CrossRef]
- Bonadonna, C.; Folch, A.; Loughlin, S.; Puempel, H. Future developments in modelling and monitoring of volcanic ash clouds: Outcomes from the first IAVCEI-WMO workshop on Ash Dispersal Forecast and Civil Aviation. Bull. Volcanol. 2012, 74, 1–10. [Google Scholar] [CrossRef]
- Bonadonna, C.; Costa, A. Modeling tephra sedimentation from volcanic plumes. In Modeling Volcanic Processes: The Physics and Mathematics of Volcanism; Cambridge University Press: Cambridge, UK, 2013; pp. 173–202. [Google Scholar]
- Costa, A.; Macedonio, G.; Folch, A. A three-dimensional Eulerian model for transport and deposition of volcanic ashes. Earth Planet. Sci. Lett. 2006, 241, 634–647. [Google Scholar] [CrossRef]
- Folch, A.; Costa, A.; Macedonio, G. FALL3D: A computational model for transport and deposition of volcanic ash. Comput. Geosci. 2009, 35, 1334–1342. [Google Scholar] [CrossRef]
- Zehner, C. Monitoring Volcanic Ash From Space. In Proceedings of the ESA-EUMETSAT Workshop on the 14 April to 23 May 2010 Eruption at the Eyjafjöll Volcano, South Iceland, Frascati, Italy, 26–27 May 2010; Zehner, C., Ed.; ESA: Frascati, Italy, 2012. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- How to Calculate Absorption Coefficient (or Absorbance) from HITRAN Data. Available online: http://home.pcisys.net/~bestwork.1/CalcAbs/CalcAbsHitran.html (accessed on 8 November 2020).
- Schreier, F.; Gimeno García, S.; Hochstaffl, P.; Städt, S. Py4CAtS—PYthon for Computational ATmospheric Spectroscopy. Atmosphere 2019, 10, 262. [Google Scholar] [CrossRef]
- Kneizys, F.X.; Shettle, E.; Abreu, L.W.; Chetwynd, J.H.; Anderson, G.P. User guide to LOWTRAN 7. Environ. Res. Pap. 1988, 1010, 1–137. [Google Scholar]
- Hirsch, M. LOWTRAN: Python Module for Atmospheric Absorption Modeling. Available online: https://zenodo.org/record/213475/export/xd#.X84WOrOxVPY (accessed on 5 December 2020).
- Pecora, E.; Biale, E. Applicazioni delle telecamere termiche Flir A 40 M e Flir 320 M al monitoraggio di Stromboli e dell’Etna. Report INGV 2004. Prot. int. n° UFVG2004/036. Available online: http://hdl.handle.net/2122/10088 (accessed on 5 December 2020).
- Pecora, E.; Biale, E.; Reitano, D. Evoluzione E Sviluppo Della Rete Permanente di Telecamere Fisse per Il Monitoraggio Video Dell’Etna. Rapporti Tecnici INGV 2006, 32. Available online: http://hdl.handle.net/2122/4663 (accessed on 5 December 2020).
- Video Sorveglianza Vulcanica Etna. Available online: http://www.ct.ingv.it/index.php/monitoraggio-e-sorveglianza/segnali-in-tempo-reale/video-sorveglianza-vulcanica-etna (accessed on 3 November 2020).
- Andronico, D.; Spinetti, C.; Cristaldi, A.; Buongiorno, M.F. Observations of Mt. Etna volcanic ash plumes in 2006: An integrated approach from ground-based and polar satellite NOAA-AVHRR monitoring system. J. Volcanol. Geotherm. Res. 2009, 180, 135–147. [Google Scholar] [CrossRef]
- Andronico, D.; Scollo, S.; Cristaldi, A.; Ferrari, F. Monitoring ash emission episodes at Mt. Etna: The 16 November 2006 case study. J. Volcanol. Geotherm. Res. 2009, 180, 123–134. [Google Scholar] [CrossRef]
- FLIR Systems, Inc. User’s Manual FLIR Tools/Tools+ 5.1; FLIR: Wilsonville, OR, USA, 2015; p. T810209. Available online: http://91.143.108.245/Downloads/Flir/Dokumentation/t810209-en-us_a4.pdf (accessed on 5 December 2020).
- FLIR Systems, Inc. ResearchIR 4 User’s Guide; FLIR: Wilsonville, OR, USA, 2015; p. 29354-000. Available online: https://assets.tequipment.net/assets/1/26/FLIR_ResearchIR_User_Manual.pdf (accessed on 5 December 2020).
- CorDEX Instruments. Ir Window Transmission Guide Book; CorDEX Instruments Ltd.: Houston, TX, USA, ID 4015 Rev A; Available online: http://www.grupoalava.com/repositorio/97d2/pdf/5436/2/cordex-instruments----ir-window-transmission-guidebook.pdf?d=1 (accessed on 5 December 2020).
- Holliday, T.; Kay, J.A. Inaccuracies introduced using infrared windows and cameras. In IEEE Petroleum and Chemical Industry Technical Conference (PCIC); IEEE: San Francisco, CA, USA, 2014; pp. 53–59. [Google Scholar] [CrossRef]
- Danjoux, B.R. Window and External Optics Transmittance Window and External Optics Transmittance. Flir Syst. Infrared Train. Cent. Tech. Pub. 2012, 60, 1–9. [Google Scholar]
- Madding, R.P. Infrared Window Transmittance Temperature Dependence. Flir Syst. Infrared Train. Cent. InfraMation 2004, 104, 1–10. [Google Scholar]
- EOT-Start Page. Available online: http://www.eot.it/ (accessed on 3 November 2020).
- Clark, A. Pillow (PIL Fork). 2020. Available online: http://www.10.5281/zenodo.4118627 (accessed on 5 December 2020).
- Clough, S.A.; Kneizys, F.X.; Davies, R.W. Line shape and the water vapor continuum. Atmos. Res. 1989, 23, 229–241. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Payne, V.H.; Moncet, J.L.; Delamere, J.S.; Alvarado, M.J.; Tobin, D.C. Development and recent evaluation of the MT-CKD model of continuum absorption. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 2520–2556. [Google Scholar] [CrossRef]


| Temperature Range 1 | Fit Function | Coefficient 2 | Relative Error 3 | ||
|---|---|---|---|---|---|
| Tmin = 273.15 Tmax = 773.15 | Fourth-order polynomial | aR,4 = −7.11311987 × 10−11 | 0.0004 | 0.815 ± 0.007 | |
| aR,3 = −1.99517684 × 10−6 | |||||
| aR,2 = 5.88365541 × 10−3 | |||||
| aR,1 = −2.26002901 | |||||
| aR,0 = 2.49847011 × 102 | |||||
| Power law + Linear | aT,3 = 0.28866532 | 3.54 × 10−5 | |||
| aT,2 = 62.13601814 | |||||
| aT,1 = 0.19139056 | |||||
| aT,0 = 102.13108565 | |||||
| Tmin = 263.15 Tmax = 333.15 | Fourth-order polynomial | aR,4 = −1.60911201 × 10−8 | 9.50 × 10−7 | 0.816 ± 0.004 | |
| aR,3 = 2.14116836 × 10−5 | |||||
| aR,2 = −7.01042439 × 10−3 | |||||
| aR,1 = 9.03965543 × 10−1 | |||||
| aR,0 = −4.09879935 × 101 | |||||
| Power law + Linear | aT,3 = 0.27353948 | 9.10 × 10−7 | |||
| aT,2 = 68.18718076 | |||||
| aT,1 = 0.21251257 | |||||
| aT,0 = 94.483686 | |||||
| Measurement Group | ε | d (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| M1 | 20 | 0.98 | 20 | 3047 | 40% | 49.7 | 41.6 | 40.0 |
| 40 | 1 | 40 | 0 | 0% | 39.0 | 39.0 | 39.0 | |
| 20 | 0.98 | 20 | 3047 | 40% | 47.3 | 39.8 | 38.4 |
| Measurement Group | ε | d (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| M1 | 20 | 0.98 | 20 | 0 | 40% | −4.5 | −3.94 | −3.94 |
| 20 | 0.98 | 20 | 3047 | 40% | <−10.0 | 0.10 | 1.87 | |
| M2 | 20 | 0.98 | 20 | 3047 | 40% | −6.0 | 2.60 | 4.12 |
| 20 | 0.98 | 20 | 0 | 40% | 4.0 | 4.34 | 4.34 | |
| M3 | 20 | 0.98 | 20 | 0 | 40% | 4.5 | 4.82 | 4.82 |
| 20 | 0.98 | 20 | 3047 | 40% | −4.0 | 3.87 | 5.27 |
| Measurement Group | ε | d (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| M1 | 20 | 0.98 | 20 | 3047 | 40% | −5.3 | 3.04 | 4.52 |
| 20 | 0.98 | 20 | 0 | 40% | 4.3 | 4.63 | 4.63 | |
| M2 | 20 | 0.98 | 20 | 0 | 40% | 4.7 | 5.02 | 5.02 |
| 20 | 1 | 20 | 0 | 40% | 5.0 | 4.99 | 4.99 | |
| M3 | 20 | 0.98 | 20 | 0 | 40% | −0.3 | 0.14 | 0.14 |
| 20 | 0.98 | 20 | 0 | 0% | −0.3 | 0.14 | 0.14 | |
| 20 | 0.98 | 20 | 3047 | 0% | −3.8 | −0.47 | 0.12 | |
| 20 | 0.98 | 20 | 3047 | 40% | −13 | −1.73 | 0.22 | |
| 20 | 1 | 20 | 0 | 40% | −0.2 | −0.21 | −0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calusi, B.; Andronico, D.; Pecora, E.; Biale, E.; Cerminara, M. PyTirCam-1.0: A Python Model to Manage Thermal Infrared Camera Data. Remote Sens. 2020, 12, 4056. https://doi.org/10.3390/rs12244056
Calusi B, Andronico D, Pecora E, Biale E, Cerminara M. PyTirCam-1.0: A Python Model to Manage Thermal Infrared Camera Data. Remote Sensing. 2020; 12(24):4056. https://doi.org/10.3390/rs12244056
Chicago/Turabian StyleCalusi, Benedetta, Daniele Andronico, Emilio Pecora, Emilio Biale, and Matteo Cerminara. 2020. "PyTirCam-1.0: A Python Model to Manage Thermal Infrared Camera Data" Remote Sensing 12, no. 24: 4056. https://doi.org/10.3390/rs12244056
APA StyleCalusi, B., Andronico, D., Pecora, E., Biale, E., & Cerminara, M. (2020). PyTirCam-1.0: A Python Model to Manage Thermal Infrared Camera Data. Remote Sensing, 12(24), 4056. https://doi.org/10.3390/rs12244056