4.2.1. Monthly Streamflow Simulations
The DWBM, GR4J, RCCC-WBM, and VIC hydrological models, driven by the 7 precipitation estimates, including gauge-based CMA and other 6 SDFE or RA datasets, were used to perform streamflow simulations from 1998 to 2016, at four hydrometric stations in the UYRB. Due to the negative effects of their associated uncertainties on the hydrological modeling process, the comparative analysis was divided into two periods, which were the calibration (1998–2008) and the validation (2009–2014) periods. This was to investigate and characterize precipitation patterns and error quantification of the various precipitation estimate products over the UYRB region.
Table 7 lists the mean annual runoff at 4 hydrometric stations in the UYRB, in both the calibration and validation periods. They indicate that the runoff increased a lot during the past two decades and the increase of mean annual runoff was most pronounced in the source area (JIMA station) of the UYRB, with an increment of 46.9%.
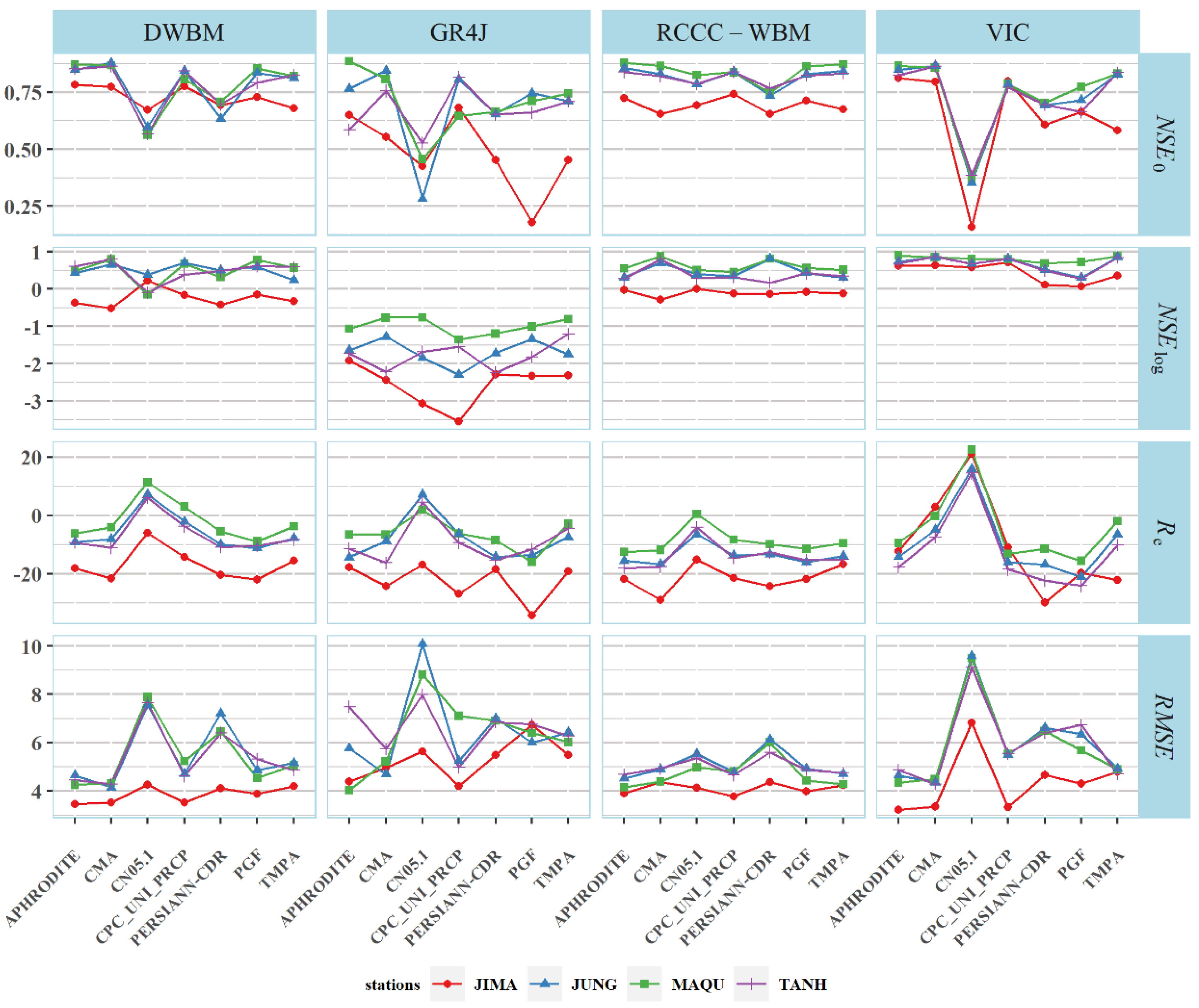
The simulated streamflow using the various precipitation inputs was compared with the observed streamflow at the monthly scale, to evaluate the hydrological utility of the satellite precipitation products, with the hydrological performance evaluation indices calculated and demonstrated in
Figure 7 and
Figure 8, for the calibration and validation periods, respectively.
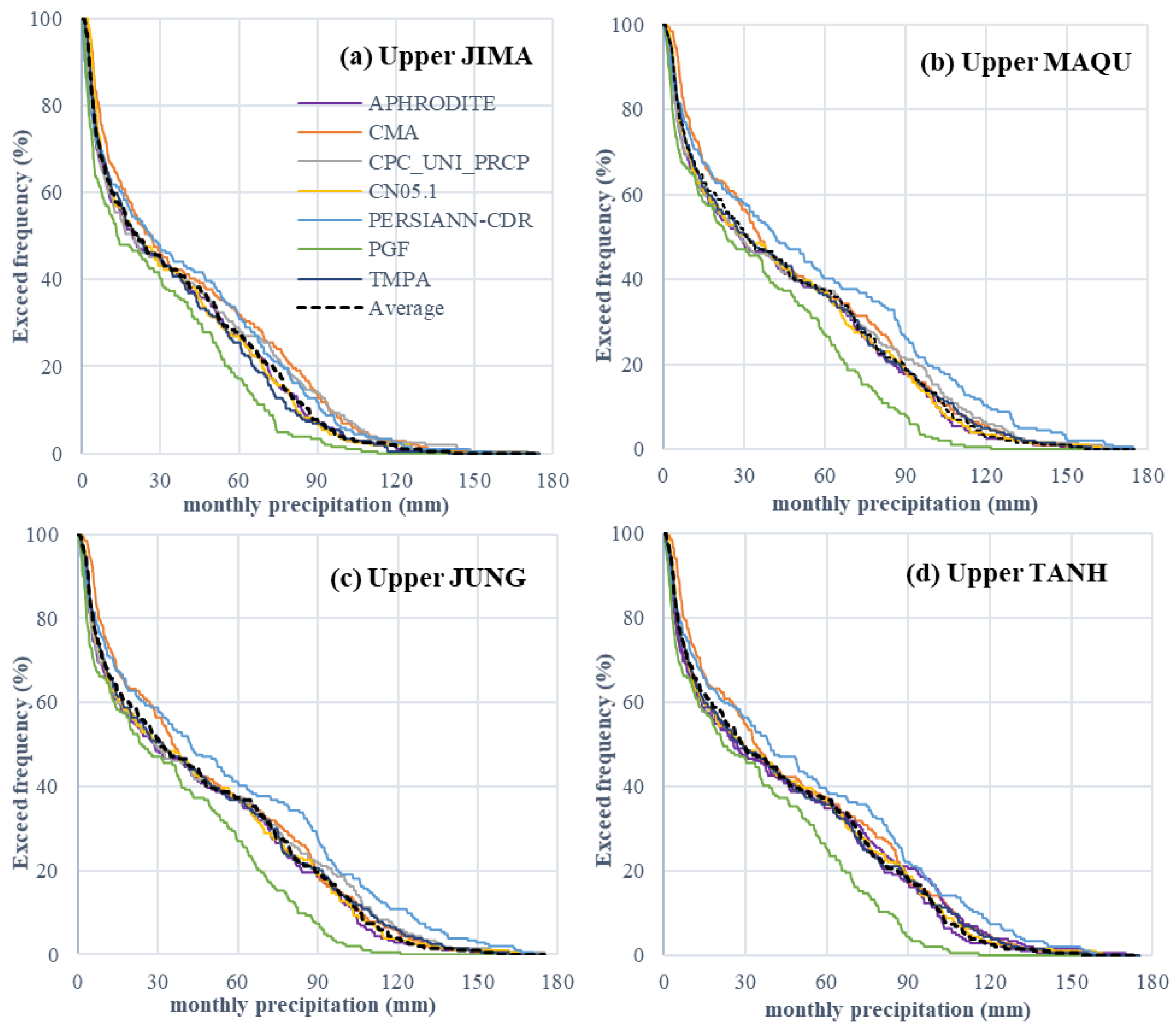
Figure 9 presents the exceed frequency curves of the simulated and observed monthly streamflow series (1998–2014), at the TANH station, as reference.
On the whole, the 7 precipitation estimates showed a great difference in monthly streamflow simulation in the UYRB, and the effects of diverse hydrological model structures in simulation performance were noticeable. In most scenarios (different precipitation products and models), the
NSE0 and
NSElog calculated at the validation period (2009–2014) were higher than those in the calibration period. One of the reasons might be that both rain observation gauges and satellite-based sensors had a much greater potential to capture heavy rains in the wet seasons or climate condition [
16,
51]. At the same time, according to previous experience, using these 4 hydrological models to simulate streamflow in humid watersheds was much better than in arid watersheds [
29,
32,
39,
52], meaning that the models might have better streamflow simulation performance in wet conditions for one watershed.
All precipitation products except the PERSIANN-CDR and CPC_UNI_PCP, showed good applicability in streamflow simulation based on the DWBM model, and obtained a “very good” rate with
NSE0 over 0.75, during the calibration period. Comparing the results of simulated and observed monthly streamflow at the TANH station (
Figure 9) as an illustration, the excess frequency curves for simulated streamflow, based on the 4 models driven by the APHRODITE, CMA, and TMPA precipitation estimates, were greatly consistent with that for the observed streamflow process. In this case, the relative errors in the CMA mainly occurred at the 40–80% quantile level (
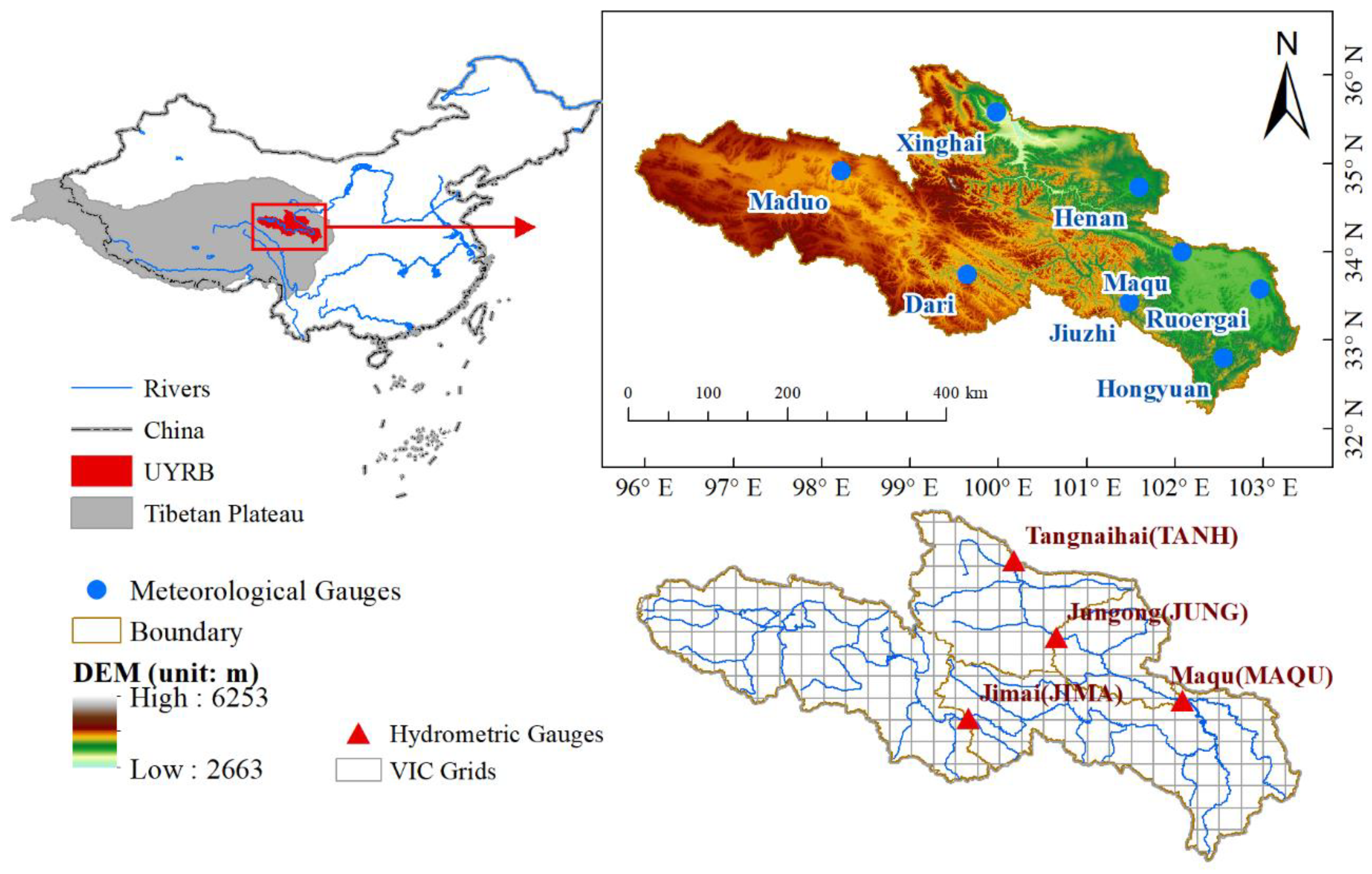
Figure 9b) and the CMA did not perform well at the JIMA station, mainly because there was only one rain gauge in the upper JIMA region (
Figure 1), resulting in larger relative errors in basin-average precipitation estimation. The PERSIANN-CDR’s performance in streamflow simulation in the UYRB, was inferior to other precipitation products overall. The 4 hydrological models forced by the PERSIANN-CDR underestimated the streamflow at the 60–90% quantile level (low flows) and overestimated at the lower quantile level (<10%, high flows). As for the CN05.1 product, it showed good performance in the streamflow simulation in the calibration period (
Figure 7), while in the validation period, the
NSE0 values in the DWBM, GR4J, and VIC models dropped a lot and the
Re and
RMSE values increased greatly, compared to those in the calibration period (
Figure 8).
From the perspective of hydrological models of different structures, the 4 selected hydrological models, used in this study on precipitation products evaluation showed great difference in reliability and stability of hydrological process simulations in the UYRB. Intuitively, the RCCC-WBM and VIC models could satisfactorily simulate the low flows in the UYRB; the NSElog values were over 0.5 at both the calibration and validation periods, and the differences in NSElog values among results from different precipitation products were small. Among the 4 hydrological models, the GR4J model showed the least stability in streamflow simulation from various precipitation estimate datasets, especially in the low-flow processes, with most NSElog values below 0 and −1, at the calibration and validation period, respectively.
The DWBM obtained a “good” performance grade in streamflow modeling, just below that of the RCCC-WBM and above that of the VIC and GR4J models. The RCCC-WBM showed the most stable and reliable streamflow simulation capacity in the UYRB, with
NSE0 values between 0.7 and 0.8,
NSElog over 0.5 and small
Re and
RMSE in both the calibration and validation periods (see
Figure 7 and
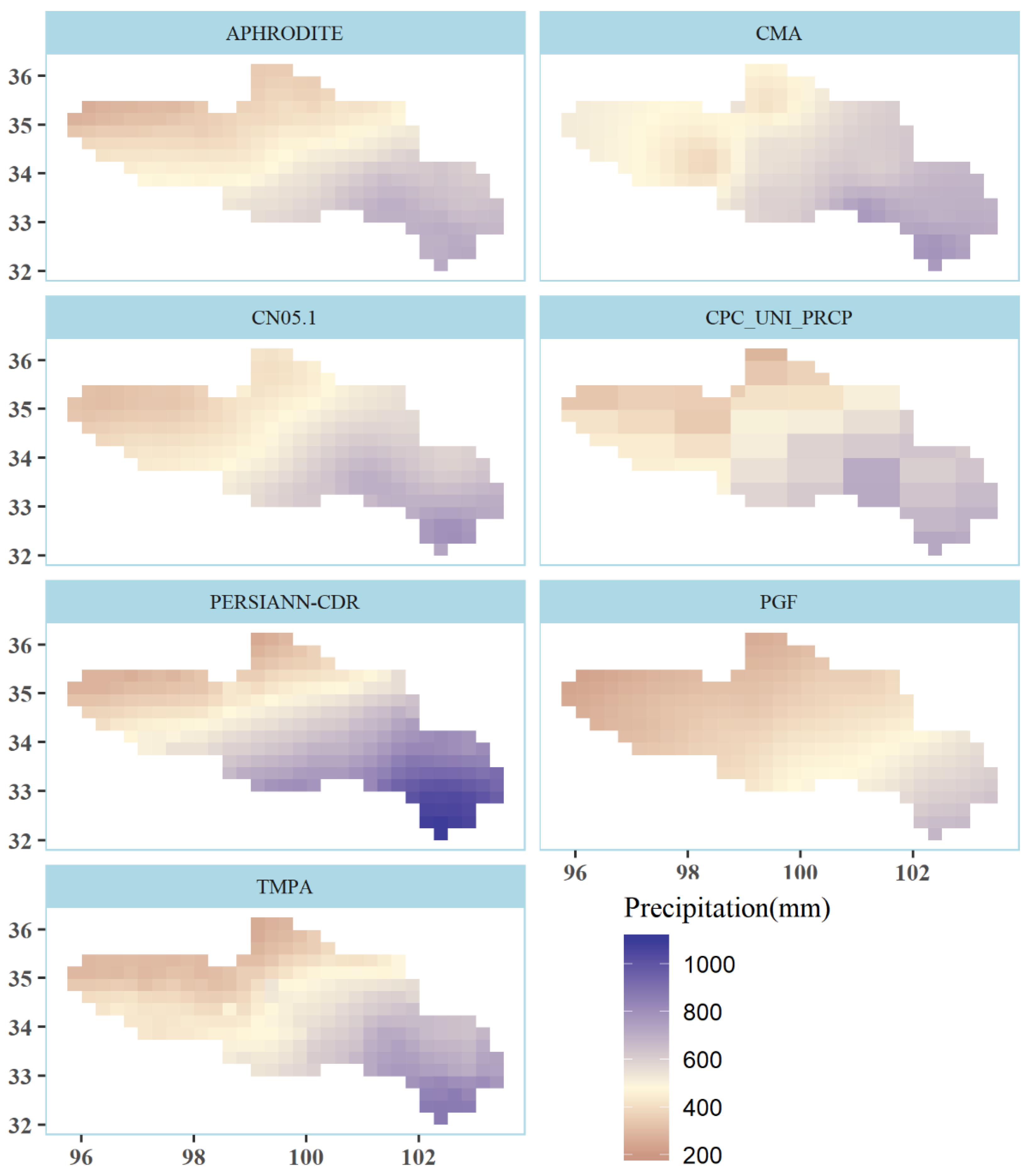
Figure 8). The difference and deviation between precipitation estimates from different products had little influence on the performance of the RCCC-WBM in streamflow simulation at 4 typical hydrometric stations over the UYRB. The only exception was that the results simulated by the PERSIANN-CDR precipitation estimates, based on the RCCC-WBM, were not as good as those forced by the other 6 precipitation products, mainly because of the poor performance of the PERSIANN-CDR in both the grid-based and basin-averaged precipitation estimation, as shown in
Figure 4 and
Figure 5. While the PGF also showed obvious errors in precipitation estimation at both gauge-located and basin-averaged scale, it obtained much better performance with higher
NSE values and lower
Re and
RMSE than the PERSIANN-CDR in the calibration period. This might be because the PGF spatially uniformly underestimated the precipitation (
Figure 4 and
Figure 5) and the Cv values of annual precipitation were few and uniformly distributed (
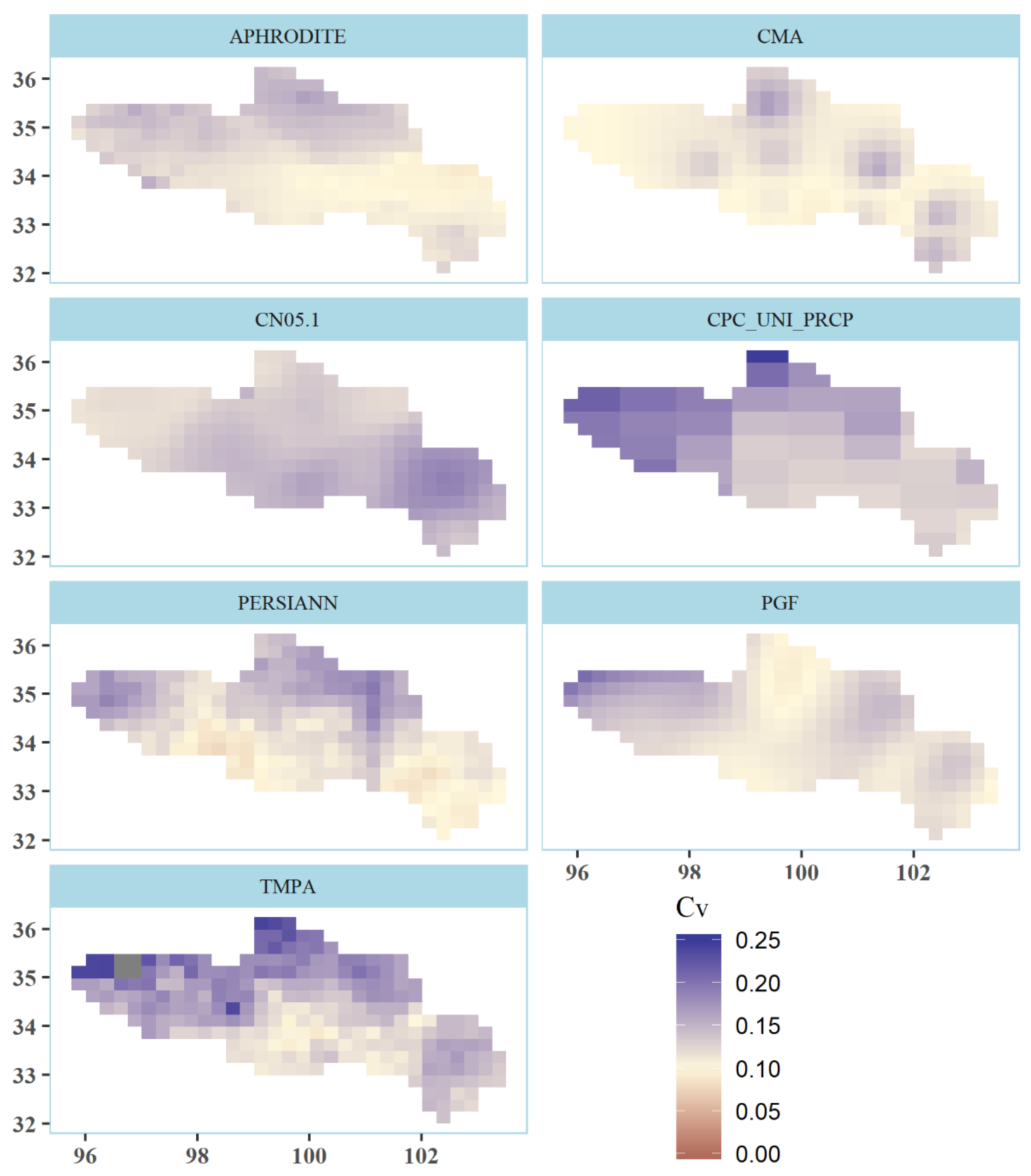
Figure 3) over the UYR. It might also be that the daily precipitation estimated by the PGF shared a better relationship (higher
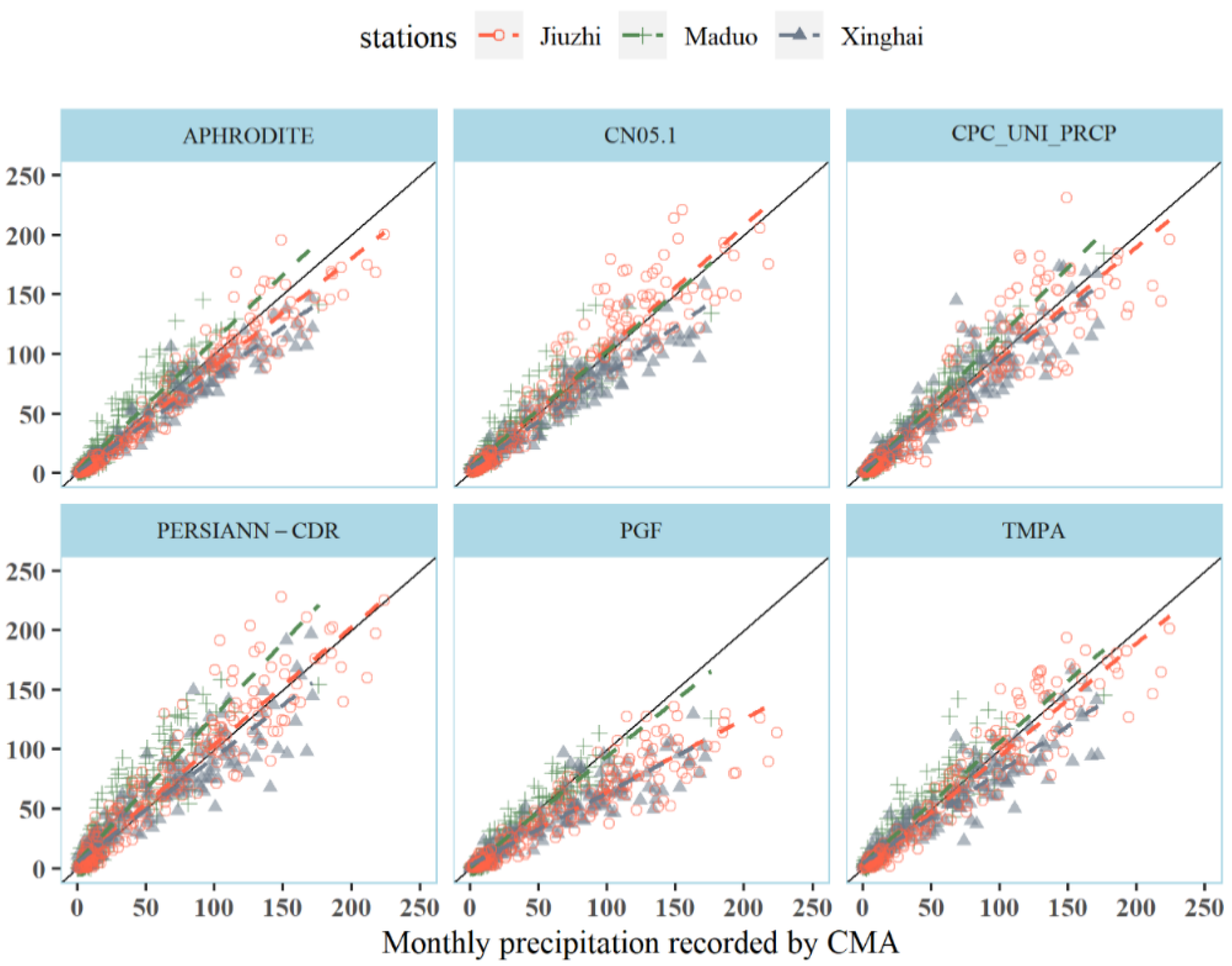
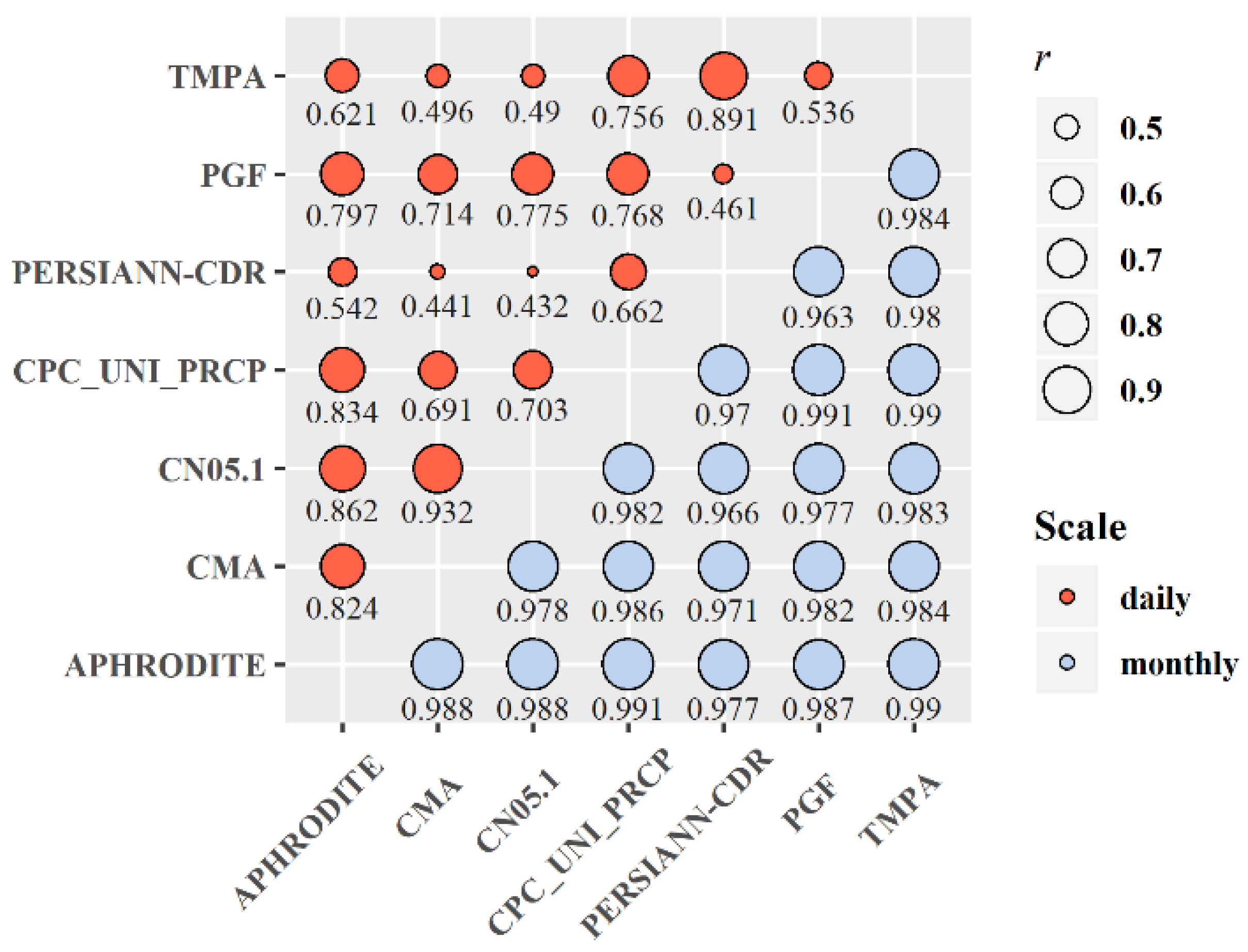
r values) with that obtained by the other 5 precipitation products, except the PERSIANN-CDR (
Figure 6), so the RCCC-WBM had the potential to reproduce the streamflow by adjusting the model parameters to offset the negative errors in precipitation estimation by the PGF.
The streamflow process at the JIMA (the uppermost hydrometric station in the UYRB) was difficult for not only the VIC but also the other 3 conceptual hydrological models to reproduce, with lower
NSE values than those at 3 other stations, in both the calibration (
Figure 7) and validation (
Figure 8) periods. The simulation results showed significant uncertainty at the JIMA station based on the VIC model, mainly because the VIC model was only calibrated with streamflow data observed at the TANH station, with lower
NSE0 and higher
Re in the period of 1998–2008, as shown in
Figure 7. What was more, all 4 models showed some uncertainty and negative errors in low-flow simulation at the TANH station, namely at higher quantile levels, with excess frequency curves in
Figure 9, and the phenomenon might be more noticeable at upper hydrometric stations, like the JIMA and MAQU stations. One of the reasons that the gauge-based precipitation (CMA), and SDFE or RA precipitation estimates generate smaller streamflow in the dry season or regions is the lack of a complex method or proper algorithm in the 4 models, to handle frozen soil. In dry conditions, when the amounts of precipitation and streamflow were small, the streamflow melted from frozen soil could account for a significant proportion of the total streamflow. In other words, the frozen soil melt could significantly influence the streamflow simulation results.
4.2.2. Precipitation Products Evaluation Based on Multi-Objective Optimum Fuzzy Model
The hydrological evaluation of SDFE or RA precipitation estimates products was subject to not only the accuracy of precipitation estimates but also the structural effects of different hydrological models, as discussed in detail above. The comprehensive evaluation of precipitation products requires cross-comparison between different models. The multi-objective optimum fuzzy model was used in this research and the performance indicators are listed in
Section 3.4, including two indicators reflecting the consistency and accuracy between the simulated and observed streamflow (
NSE0 and
NSElog), and two metrics controlling the water balance in streamflow simulation—
RMSE and
Re. Under the fuzzy model, the weights of the 4 metrics were assigned a vector of (0.35, 0.35, 0.15, 0.15)
T , based on experts’ experience and previous studies [
16]. The relative membership degree (
u) of the different precipitation products at 4 hydrometric stations in both the calibration and validation periods are shown in
Figure 10.
It could be seen that the two hydrological models (DWBM and RCCC-WBM), when modeling the runoff process at a monthly scale, obtained more stable and higher
u values than the GR4J (daily conceptual model) and VIC models. The difference in precipitation estimates from various precipitation datasets had more influence in the GR4J and VIC models. In most scenarios, the RCCC-WBM performed best in streamflow simulation with diverse precipitation estimates sources. For the RCCC-WBM model, the
u values were around 0.9 in the calibration period and 0.8 in the validation period. As for the GR4J model, the
u values dropped a lot at the validation period, compared to that in the calibration period, especially at the JIMA station. Even in the calibration period, the
u values obtained in the GR4J model were generally lower than those obtained by three other models, which all indicated the less suitability and high uncertainty of the GR4J model, coupled with snowmelt module in streamflow process simulation, based on the SDFE or RA precipitation datasets in the alpine UYRB. The results were similar when the hydrological processes were simulated at daily scale, with the distributed VIC model performing much better than the GR4J, with higher
u values over the whole research period (1998–2014). The exception was for the CN05.1 dataset because the errors of precipitation estimates in the CN05.1 dataset after 2009 were more influential in the VIC model than the DWBM and RCCC-WBM, as shown in both
Figure 8 and
Figure 10.
From the perspective of precipitation products, the APHRODITE, CMA, and TMPA datasets obtained much higher scores than other datasets, with the average relative membership degree (
u) values at 4 hydrometric stations from 4 hydrological models of 0.872, 0.872, and 0.887 in the calibration period and 0.787, 0.803, and 0.766 in the validation period, respectively. The precipitation estimates products (like PGF) tended to show better performance in streamflow simulation at the hydrometric stations, downstream of the UYRB (JUNG and TANH station), with an average
u of 0.804 at the research period, as shown in
Figure 7 and
Figure 8.
4.2.3. Effect of Snowmelt Module Parameters Recalibration on Hydrological Modeling
As shown above, the GR4J model showed significant uncertainty in streamflow simulation from the diverse precipitation estimates datasets. One of the reasons was that the GR4J model was forced with the daily precipitation data series, and the daily precipitation was harder to estimate accurately than monthly datasets from the SDFE or RA products. The basin-average daily precipitation data series from the 7 products showed various relationships between each other (
Figure 6). On the other hand, the snowmelt modules in the DWBM and RCCC-WBM had only two parameters regulating the rainfall–snowfall partition and the two parameters were all air temperature-based, and free from the influence of watershed characteristics like the spatial pattern of snow depth. Meanwhile, the GR4J model had 4 parameters in runoff yield and routing, and incorporated the SWAT snowmelt module with 7 parameters included in model calibration, which might result in uncertainty and instability in streamflow simulation. Li et al. [
39] found that little improvement was acquired when the GR4J was incorporated with the SWAT snowmelt module than the original 4 parameters GR4J model in runoff prediction in ungauged catchments. Guan, et al. [
33] applied the GR4J model excluding snowmelt module in 6 typical watersheds in the Yellow River basin including the UYRB, and found that the GR4J performed well in streamflow simulation under the changing environment. Therefore, in this study, the effects of the snowmelt module were incorporated into the 3 conceptual models in hydrological evaluation of SDFE or the RA precipitation products. According to the results of the evaluation metrics as shown in
Figure 7 and
Figure 8, the snowmelt module parameters in the DWBM, GR4J, and RCCC-WBM models for each hydrometric station were assigned the values from the calibration results, driven by the CMA dataset and then the models’ runoff generation and routing parameters (shown in
Table 3) were recalibrated with the snowmelt module parameter fixed. The evaluation metrics were calculated and compared to those (snowmelt module parameters non-fixed in model calibration) in
Figure 7 and
Figure 8. The comparison scatter plots are shown in
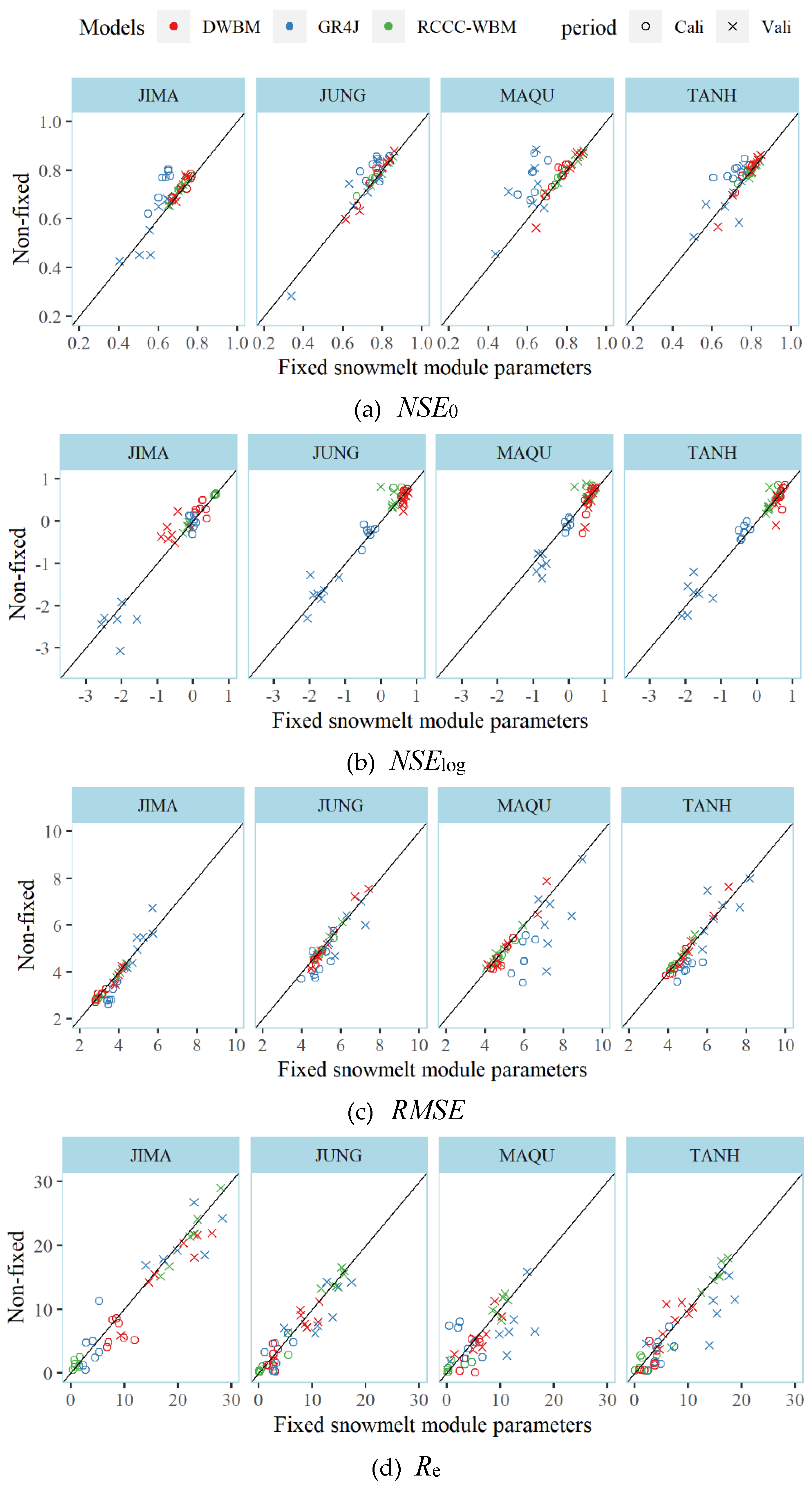
Figure 11, where the shapes of the points stand for the research periods (calibration and validation) and the colors of the points distinguish the 3 hydrological models.
As shown in
Figure 11, the snowmelt modules were less influential in the DWBM and RCCC-WBM models in terms of
NSE0 and
NSElog, with the green and red points in
Figure 11a,b located in higher value ranges and near the 1:1 line (black solid line). As for the GR4J model, the blue scatter points standing for the
NSE0 values in
Figure 11a were mostly above the 1:1 line, meaning that the streamflow simulation capacity of the GR4J model decreased with the snowmelt module parameter fixed for each hydrometric station at the calibration period. The points below the 1:1 line mainly occurred at the validation period, which was more noticeable for
NSElog in
Figure 11b. In addition, the GR4J excluding the snowmelt parameter in calibration raised the
RMSE metrics as some cross-shaped points were distributed above the 1:1 line. Overall, the RCCC-WBM and DWBM models, forced by monthly precipitation and potential evapotranspiration, can regulate the runoff generation amount and process, mainly based on the original model parameters. The temperature-based snowmelt modules are less influential to the simulation results. In the GR4J model, the snowmelt module (transferred from the SWAT model) played a more important role in streamflow simulation and improved the evaluation metrics in the calibration period. However, the SWAT snowmelt module also had 7 parameters, which might result in great uncertainty in model application in future runoff projection or just at the validation period.