Quantification and Mapping of Satellite Driven Surface Energy Balance Fluxes in Semi-Arid to Arid Inter-Mountain Region
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
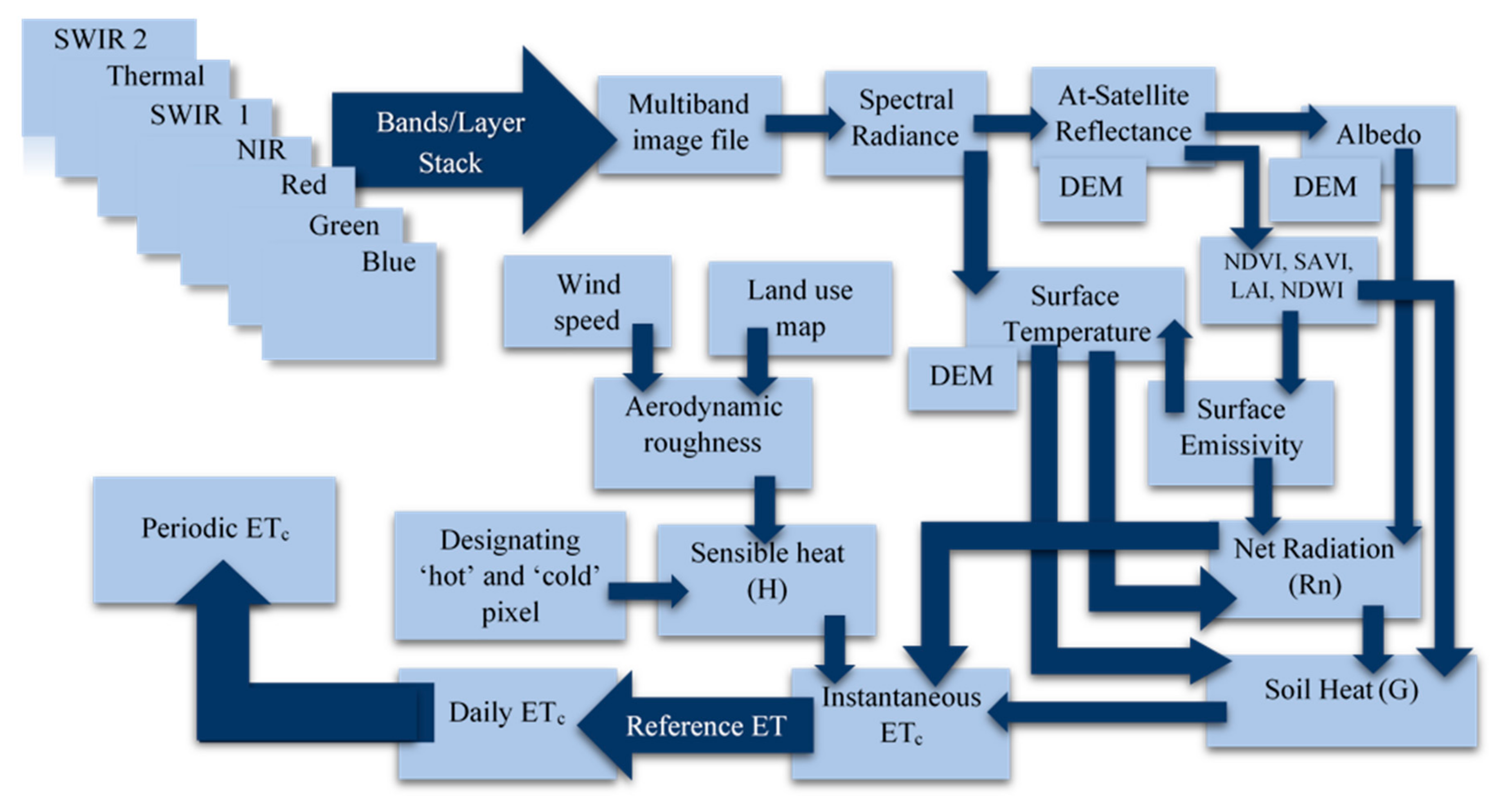
2.2. Satellite Datasets and Image Processing
2.3. METRIC Model
2.3.1. Net Radiation (Rn)
2.3.2. Soil Heat Flux (G)
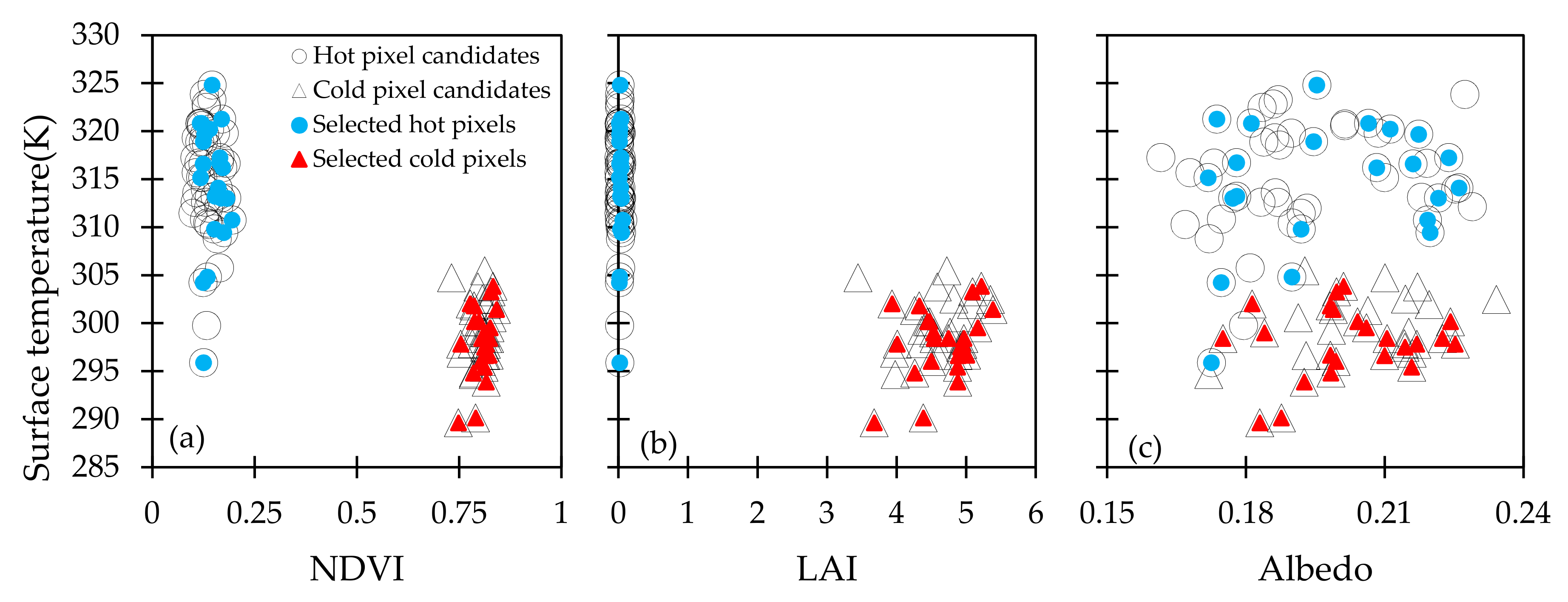
2.3.3. Sensible Heat Flux (H)
2.3.4. Estimation of Instantaneous, Daily, Monthly and Seasonal Crop Evapotranspiration (ETc)
3. Result and Discussions
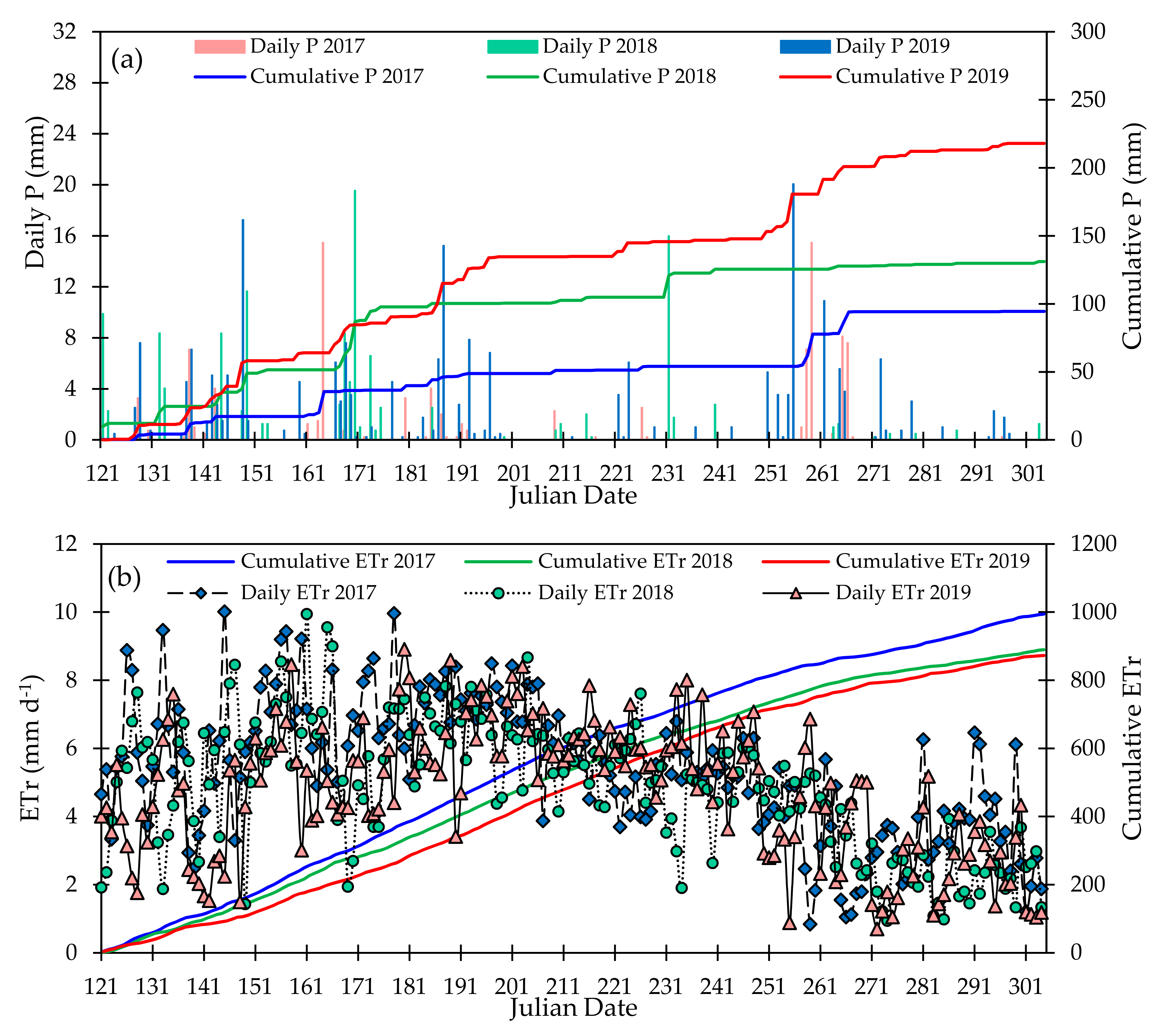
3.1. Weather Conditions
3.2. Comparison of METRIC Estimated and Measured Surface Energy Balance Fluxes
3.2.1. Instantaneous ETc (ETinst)
3.2.2. Net Radiation (Rn)
3.2.3. Sensible Heat Flux (H)
3.2.4. Soil Heat Flux (G)
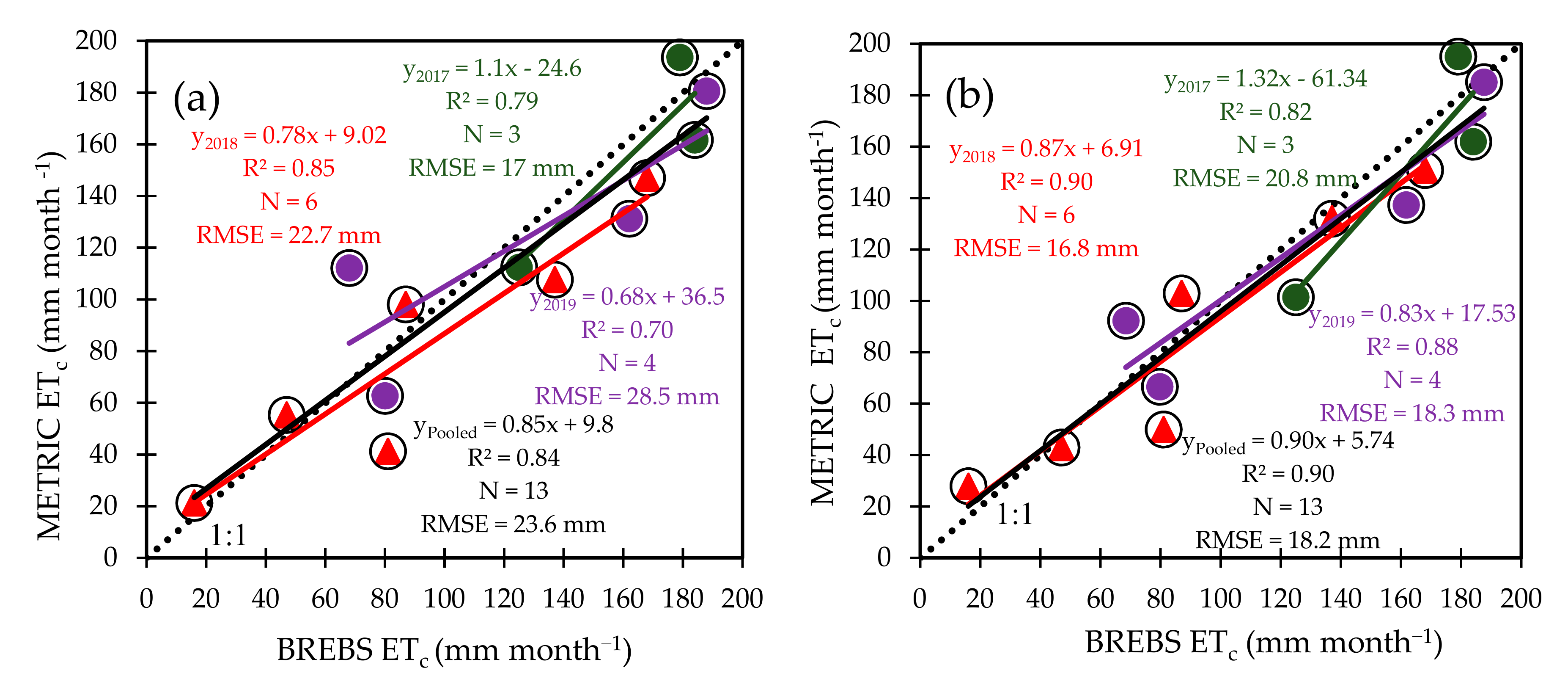
3.3. Comparison of METRIC Estimated and BREBS Measured Monthly ETc
3.4. Mapping Spatio-Temporal Variation of Surface Energy Balance Components
3.4.1. Spatio-Temporal Variation of Net Radiation (Rn), Sensible Heat (H), and Soil Heat (G) Flux
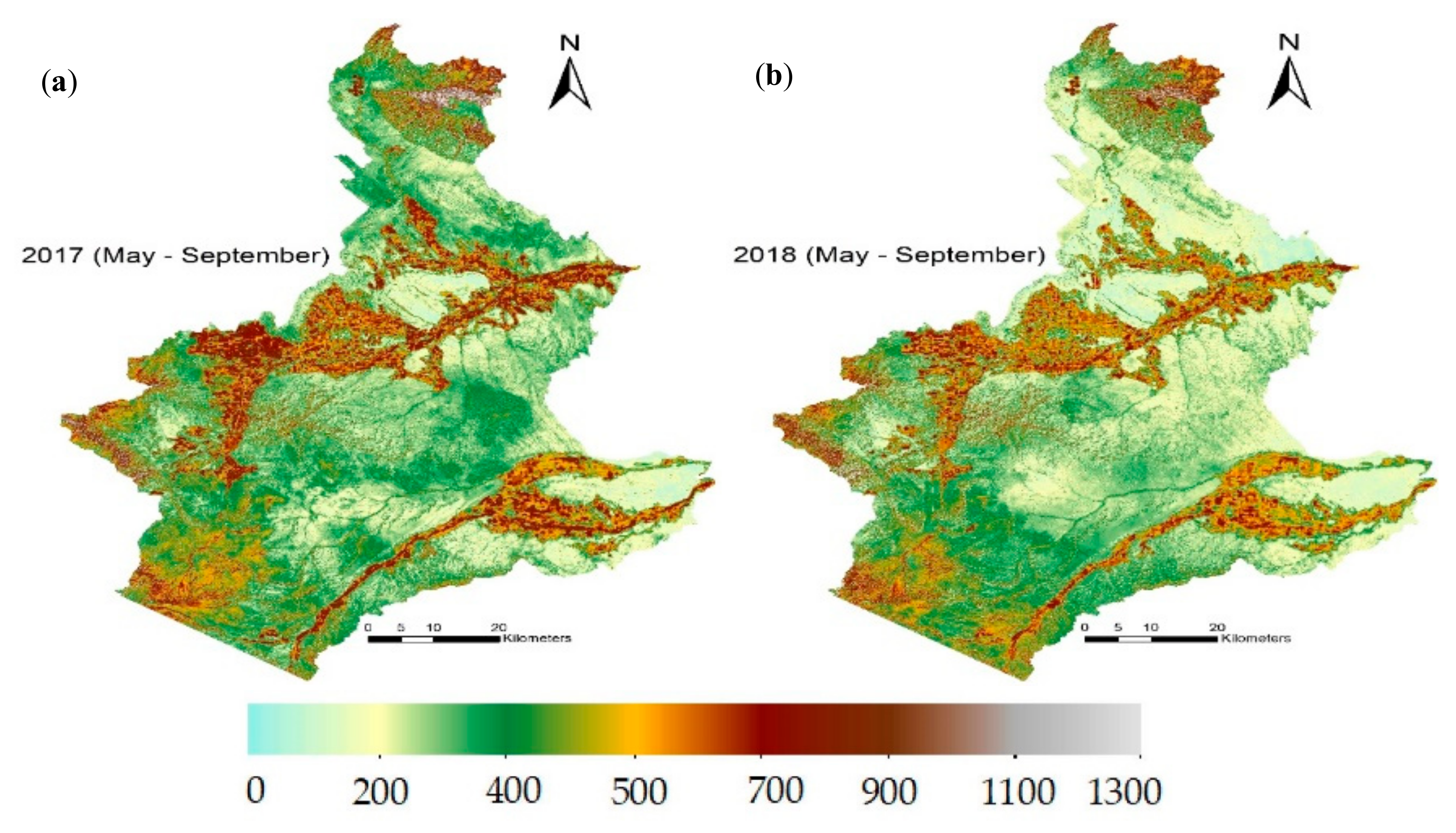
3.4.2. Spatio-Temporal Variation of Evapotranspiration (ETc)
3.5. Mapping Spatio-Temporal Variation of Cumulative Seasonal Evapotranspiration
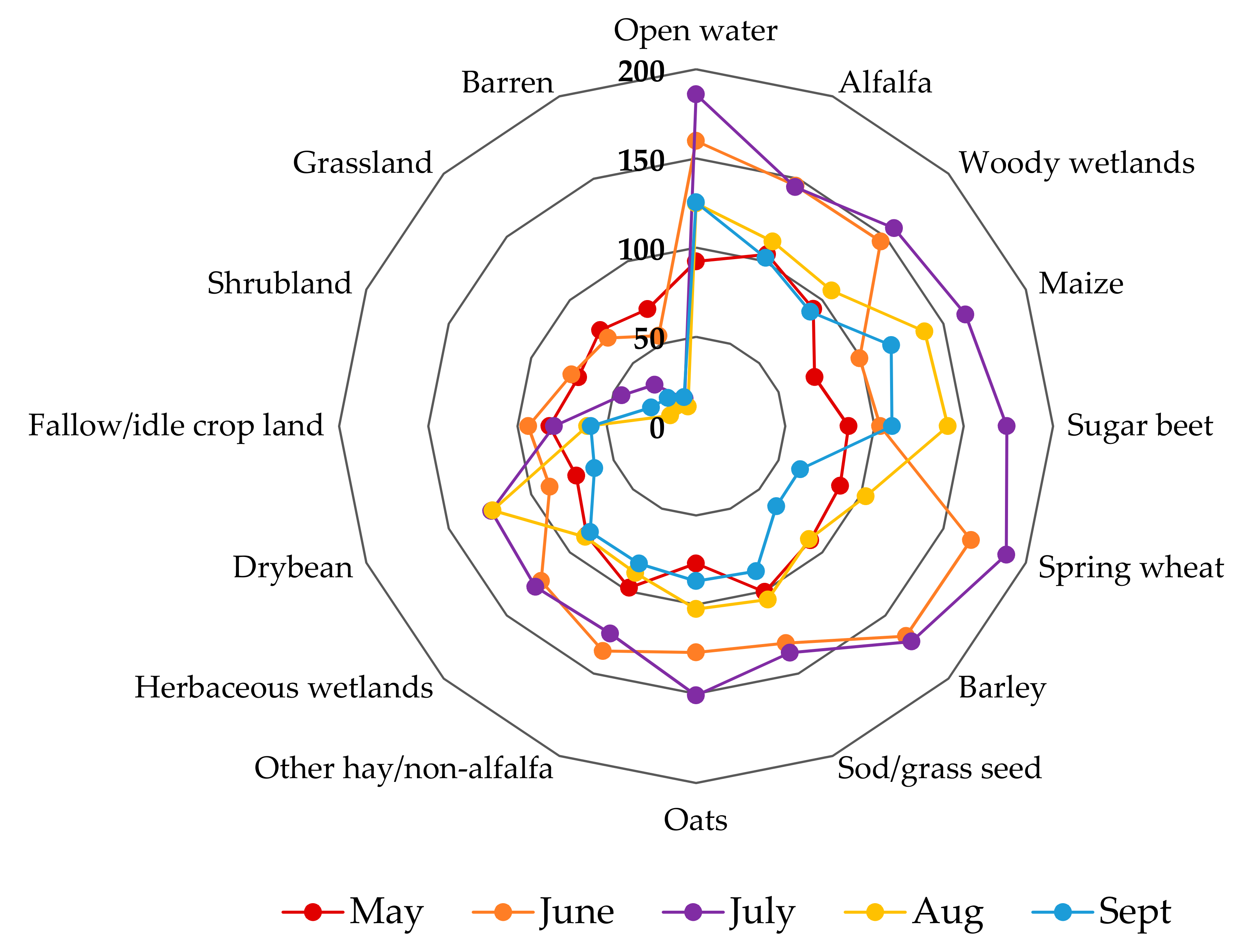
3.6. Comparison of METRIC Estimated Mean Monthly Evapotranspiration for Different Land Cover Type
3.7. Irrigation District Average Water Consumption
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Sharma, V.; Nicholson, C.; Bergantino, A.; Irmak, S.; Peck, D. Temporal Trend Analysis of Meteorological Variables and Reference Evapotranspiration in the Inter-mountain Region of Wyoming. Water 2020, 12, 2159. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Census of Agriculture. Available online: https://www.nass.usda.gov/Publications/AgCensus/2012/Full_Report/Volume_1,_Chapter_1_State_Level/ (accessed on 14 July 2020).
- Jacobs, J.J.; Brosz, D.J. Wyoming Water Law: A Summary; Bulletin B-969; C; Cooperative Extension Service, College of Agriculture and Wyoming Water Research Center, University of Wyoming: Laramie, WY, USA, 1993. [Google Scholar]
- Hansen, K.; Nicholson, C.M.; Paige, G. Wyoming’s Water: Resources & Management; University of Wyoming Extension: Laramie, WY, USA, 2015. [Google Scholar]
- Irmak, S. Nebraska Water and Energy Flux Measurement, Modeling, and Research Network (NEBFLUX). Trans. ASABE 2010, 53, 1097–1115. [Google Scholar] [CrossRef]
- Gowda, P.H.; Chavez, J.L.; Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. ET mapping for agricultural water management: Present status and challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar] [CrossRef]
- Wagle, P.; Gowda, P.H. Editorial for the Special Issue “Remote Sensing of Evapotranspiration (ET)”. Remote Sens. 2019, 11, 2146. [Google Scholar] [CrossRef]
- Sharma, V.; Irmak, S. Mapping spatially interpolated precipitation, reference evapotranspiration, actual crop evapotranspiration, and net irrigation requirements in Nebraska: Part II. Actual crop evapotranspiration and net irrigation requirements. Trans. ASABE 2012, 55, 907–921. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.T.; Trezza, R. A Landsat-based energy balance and evapotranspiration model in Western US water rights regulation and planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56: Crop Evapotranspiration; FAO: Rome, Italy, 1998. [Google Scholar]
- Moorhead, J.E.; Marek, G.W.; Gowda, P.H.; Lin, X.; Colaizzi, P.D.; Evett, S.R.; Kutikoff, S. Evaluation of Evapotranspiration from Eddy Covariance Using Large Weighing Lysimeters. Agronomy 2019, 9, 99. [Google Scholar] [CrossRef]
- Howell, T.A.; Schneider, A.D.; Jensen, M.E. History of Lysimeter Design and Use for Evapotranspiration Measurements. In Proceedings of the Lysimeters for Evapotranspiration and Environmental Measurements, Honolulu, HI, USA, 23–25 July 1991; pp. 1–9. [Google Scholar]
- Sharma, V.; Kilic, A.; Irmak, S. Impact of scale/resolution on evapotranspiration from Landsat and MODIS images. Water Resour. Res. 2016, 52, 1800–1819. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Meneti, M.; Choudhary, B.J. Parameterization of land surface evapotranspiration using a location dependent potential evapotranspiration and surface temperature range. Exch. Process. Land Surf. A Range Space Time Scales 1993, 212, 561–568. [Google Scholar]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets—A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.T.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)- Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. Regionalization of Surface Flux Densities and Moisture Indicators in Composite Terrain: A Remote Sensing Approach under Clear Skies in Mediterranean Climates. Ph.D. Thesis, CIP Data Koninklijke Bibliotheek, Den Haag, The Netherlands, 1995. [Google Scholar]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.; Roerink, G.J.; van der Wal, T. The surface energy balance algorithm for land (SEBAL): 2. Validation. J. Hydrol. 1998, 212, 213–229. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Tasumi, M.; Trezza, R.; Allen, R.G.; Wright, J.L. Operational aspects of satellite-based energy balance models for irrigated crops in the semi-arid US. Irrig. Drain. Syst. 2005, 19, 355–376. [Google Scholar] [CrossRef]
- Trezza, R.; Allen, R.G.; Tasumi, M. Estimation of actual evapotranspiration along the Middle Rio Grande of New Mexico Using MODIS and landsat imagery with the METRIC model. Remote Sens. 2013, 5, 5397–5423. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Thorp, K.R. Remote sensing of evapotranspiration over cotton using the TSEB and METRIC energy balance models. Remote Sens. Environ. 2015, 158, 281–294. [Google Scholar] [CrossRef]
- Dhungel, R.; Allen, R.G.; Trezza, R.; Robison, C.W. Evapotranspiration between satellite overpasses: Methodology and case study in agricultural dominant semi-arid areas. Meteorol. Appl. 2016, 23, 714–730. [Google Scholar] [CrossRef]
- Numata, I.; Khand, K.; Kjaersgaard, J.; Cochrane, M.A.; Silva, S.S. Evaluation of landsat-based METRIC modeling to provide high-spatial resolution evapotranspiration estimates for amazonian forests. Remote Sens. 2017, 9, 46. [Google Scholar] [CrossRef]
- Khand, K.; Kjaersgaard, J.; Hay, C.; Jia, X. Estimating Impacts of Agricultural Subsurface Drainage on Evapotranspiration Using the Landsat Imagery-Based METRIC Model. Hydrology 2017, 4, 49. [Google Scholar] [CrossRef]
- Gowda, P.H.; Chávez, J.L.; Howell, T.A.; Marek, T.; New, L.L. Surface Energy Balance Based Evapotranspiration Mapping in the Texas High Plains. Sensors 2008, 8, 5186–5201. [Google Scholar] [CrossRef]
- Madugundu, R.; Al-Gaadi, K.A.; Tola, E.K.; Hassaballa, A.A.; Patil, V.C. Performance of the METRIC model in estimating evapotranspiration fluxes over an irrigated field in Saudi Arabia using Landsat-8 images. Hydrol. Earth Syst. Sci. 2017, 21, 6135–6151. [Google Scholar] [CrossRef]
- Tasumi, M. Estimating evapotranspiration using METRIC model and Landsat data for better understandings of regional hydrology in the western Urmia Lake Basin. Agric. Water Manag. 2019, 226. [Google Scholar] [CrossRef]
- Singh, R.K.; Senay, G.B. Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States. Water 2015, 8, 9. [Google Scholar] [CrossRef]
- Singh, R.K.; Liu, S.; Tieszen, L.L.; Suyker, A.E.; Verma, S.B. Estimating seasonal evapotranspiration from temporal satellite images. Irrig. Sci. 2012, 30, 303–313. [Google Scholar] [CrossRef]
- Mokhtari, M.H.; Ahmad, B.B.; Hoveidi, H.; Busu, I. Sensitivity Analysis of METRIC-Based Evapotranspiration Algorithm. Int. J. Environ. Res. 2013, 7, 407–422. [Google Scholar] [CrossRef]
- Tang, Q.; Peterson, S.; Cuenca, R.H.; Hagimoto, Y.; Lettenmaier, D.P. Satellite-based near-real-time estimation of irrigated crop water consumption. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- De la Fuente-Sáiz, D.; Ortega-Farías, S.; Fonseca, D.; Ortega-Salazar, S.; Kilic, A.; Allen, R. Calibration of METRIC Model to Estimate Energy Balance over a Drip-Irrigated Apple Orchard. Remote Sens. 2017, 9, 670. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.A.; Cunha, M.; Andrade, J.A.; Silvestre, J.; Sousa, A.; Santos, F.L.; Pereira, L.S.; Allen, R.G. Satellite-based evapotranspiration of a super intensive olive orchard: Application of METRIC algorithms. Biosyst. Eng. 2014, 128, 69–81. [Google Scholar] [CrossRef]
- Paço, T.A.; Pôças, I.; Cunha, M.; Silvestre, J.C.; Santos, F.L.; Paredes, P.; Pereira, L.S. Evapotranspiration and crop coefficients for a super intensive olive orchard. An application of SIMDualKc and METRIC models using ground and satellite observations. J. Hydrol. 2014, 519, 2067–2080. [Google Scholar] [CrossRef]
- Allen, R.G.; Irmak, A.; Trezza, R.; Hendrickx, J.; Bastiaanssen, W. Satellite Based ET Estimation in Agriculture using SEBAL and METRIC. J. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Climate at a Glance. Available online: https://www.ncdc.noaa.gov/cag/national/rankings (accessed on 3 March 2020).
- Sharma, V.; Nicholson, C.; Bergantino, T.; Cowley, J.; Hess, B.; Tanaka, J. Wyoming Agricultural Climate Network (WACNet). In Agricultural Experiment Station 2018 Field Days Bulletin; University of Wyoming: Laramie, WY, USA, 2018; pp. 52–53. [Google Scholar]
- Fritschen, L.J. Evapotranspiration Rates of Field Crops Determined by the Bowen Ratio Method. Agron. J. 1966, 58, 339–342. [Google Scholar] [CrossRef]
- Huete, A.R.; Jackson, R.D.; Post, D.F. Spectral response of a plant canopy with different soil backgrounds. Remote Sens. Environ. 1985, 17, 37–53. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1991. [Google Scholar]
- Starks, P.J.; Norman, J.M.; Blad, B.L.; Walter-Shea, E.A.; Walthall, C.L. Estimation of shortwave hemispherical reflectance (albedo) from bidirectionally reflected radiance data. Remote Sens. Environ. 1991, 38, 123–134. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R. At-surface albedo from Landsat and MODIS satellites for use in energy balance studies of evapotranspiration. J. Hydrol. Eng. 2008, 13, 51–63. [Google Scholar] [CrossRef]
- Olmedo, G.F.; Ortega-Farías, S.; Fuente-Sáiz, D.; Fonseca-Luego, D.; Fuentes-Peñailillo, F. Water: Tools and Functions to Estimate Actual Evapotranspiration Using Land Surface Energy Balance Models in R. R J. 2016, 8, 352–369. [Google Scholar] [CrossRef]
- Tasumi, M. Progress in Operational Estimation of Regional Evapotranspiration Using Satellite Imagery. Ph.D. Thesis, University of Idaho, Moscow, ID, USA, 2003. [Google Scholar]
- Tasumi, M.; Allen, R.G.; Trezza, R.; Wright, J.L. Satellite-based energy balance to assess within population variance of crop coefficient curves. J. Irrig. Drain. Eng. 2005, 131, 94–109. [Google Scholar] [CrossRef]
- ASCE-EWRI. The ASCE standardized reference evapotranspiration equation. In ASCE-EWRI Standardization of Reference Evapotranspiration Task Committee Report; ASCE Bookstore: Reston, VA, USA, 2005. [Google Scholar]
- Romero, M.G. Daily Evapotranspiration Estimation by Means of Evaporative Fraction and Reference ET Fraction. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2004. [Google Scholar]
- Singh, R.K.; Irmak, A. Estimation of crop coefficient using satellite remote sensing. J. Irrig. Drain. Eng. 2009, 135, 597–608. [Google Scholar] [CrossRef]
- Wright, J.L. New Evapotranspiration Crop Coefficients. J. Irrig. Drain. Div. 1982, 108, 57–74. [Google Scholar]
- Horton, R.; Bristow, K.L.; Kluitenberg, G.; Sauer, T.J. Crop residue effects on surface radiation and energy balance: Review. Theor. Appl. Climatol. 1996, 54, 27–37. [Google Scholar] [CrossRef]
- Sharma, V.; Irmak, S.; Kilic, A.; Mutiibwa, D. Application of remote sensing for quantifying and mapping surface energy fluxes in south central Nebraska: Analyses with respect to field measurements. Trans. ASABE 2015, 58, 1265–1285. [Google Scholar]
- Mu, Q.; Jones, L.A.; Kimball, J.S.; McDonald, K.C.; Running, S.W. Satellite assessment of land surface evapotranspiration for the pan-Arctic domain. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Kilic, A.; Ratcliffe, I.; Ranade, P.; Hubbard, K.; Singh, R.K.; Kamble, B.; Kjaersgaard, J. Estimation of Land Surface Evapotranspiration with a Satellite Remote Sensing Procedure. Great Plains Res. J. Nat. Soc. Sci. 2011, 21, 73–88. [Google Scholar]
- Irmak, A.; Singh, R.; Walter-Shea, E.A.; Verma, S.; Suyker, A.E. Comparison and analysis of empirical equations for soil heat flux for different cropping systems and irrigation methods. Trans. ASABE 2011, 53, 67–80. [Google Scholar] [CrossRef][Green Version]
- Barr, A.G.; King, K.M.; Gillespie, T.J.; Hartog, G.D.; Neumann, H.H. A comparison of bowen ratio and eddy correlation sensible and latent heat flux measurements above deciduous forest. Bound. Layer Meteorol. 1994, 71, 21–41. [Google Scholar] [CrossRef]
- McBean, G.A. Role of Active-Passive Scalar Relationships in Evaporation from Vegetated Surfaces. In Advances in Theoretical Hydrology; O’Kane, J.R., Ed.; Elsevier Science: Amsterdam, The Netherlands, 1992; pp. 47–58. [Google Scholar]
- Monteith, J.L. Dew. Q. J. R. Meteorol. Soc. 1957, 83, 322–341. [Google Scholar] [CrossRef]
- Sharma, M.L. Contribution of dew in the hydrologic balance of semi-arid grassland. Agric. Meteorol. 1976, 17, 321–331. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. National Weather Service. Available online: https://www.weather.gov/cle/seasons (accessed on 2 August 2020).
- McGowan, H.A.; Sturman, A.P.; Mackellar, M.C.; Weibe, A.H.; Neil, D.T. Measurements of the local energy balance over a coral reef flat, Heron Island, southern Great Barrier Reef, Australia. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Stannard, D.I.; Gannett, M.W.; Polette, D.J.; Cameron, J.M.; Waibel, M.S.; Spears, J.M. Evapotranspiration from wetland and open-water sites at Upper Klamath Lake, Oregon, 2008–2010. In Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2013; p. 66. [Google Scholar]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J.; Kimball, B.A.; Nakayama, F.S. The Dependence of Bare soil albedo on soil water content. J. Appl. Meteorol. Climatol. 1975, 14, 109–113. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of cliumatological temperature and precipitation across the conterminous United States. Int. J. Climatol. 2007, 28, 2031–2064. [Google Scholar] [CrossRef]



| Date | ID | Julian Date | Tmin (°C) | Tmax (°C) | RHmin (%) | RHmax (%) | u2 (ms−1) | Rs (W m−2) | P (mm) | ETr (mm d−1) |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 May 2017 | L07 | 124 | 1.4 | 17.7 | 22.9 | 84.8 | 2.0 | 324.0 | 0 | 5.47 |
| 5 June 2017 | L07 | 156 | 12.2 | 32.7 | 11.2 | 65.3 | 2.0 | 336.0 | 0 | 9.23 |
| 21 June 2017 | L07 | 172 | 10.8 | 31.4 | 19.0 | 80.0 | 2.1 | 268.4 | 0.254 | 7.95 |
| 15 July 2017 | L08 | 196 | 15.9 | 36.8 | 13.0 | 66.2 | 1.2 | 280.1 | 0 | 7.28 |
| 31 July 2017 | L08 | 212 | 10.8 | 33.3 | 12.4 | 84.3 | 0.9 | 306.0 | 0 | 6.3 |
| 16 August 2017 | L08 | 228 | 9.7 | 25.3 | 22.6 | 82.6 | 0.8 | 217.8 | 0 | 4.14 |
| 1 September 2017 | L08 | 244 | 15.0 | 31.4 | 17.6 | 68.4 | 1.2 | 178.3 | 0 | 5.15 |
| 9 September 2017 | L07 | 252 | 8.1 | 30.2 | 11.6 | 65.6 | 0.8 | 198.2 | 0 | 4.25 |
| 15 May 2018 | L08 | 135 | 6.2 | 19.9 | 33.8 | 100 | 1.4 | 235.9 | 0 | 4.33 |
| 8 June 2018 | L07 | 159 | 10.7 | 27.0 | 24.6 | 82.1 | 1.4 | 230.4 | 0 | 5.55 |
| 2 July 2018 | L08 | 183 | 10.4 | 27.8 | 16.2 | 81.7 | 0.8 | 300.0 | 0 | 5.55 |
| 18 July 2018 | L08 | 199 | 11.8 | 29.5 | 23.6 | 84.0 | 0.7 | 210.6 | 0.254 | 4.55 |
| 26 July 2018 | L07 | 207 | 14.6 | 28.8 | 26.8 | 69.6 | 1.5 | 262.7 | 0 | 6.36 |
| 11 August 2018 | L07 | 223 | 12.4 | 36.4 | 9.0 | 68.2 | 0.7 | 302.5 | 0 | 5.95 |
| 4 September 2018 | L08 | 247 | 6.8 | 30.7 | 11.6 | 77.8 | 1.3 | 261.8 | 0 | 6.03 |
| 12 September 2018 | L07 | 255 | 8.7 | 24.7 | 18.1 | 69.6 | 1.0 | 207.3 | 0 | 4.12 |
| 22 October 2018 | L08 | 295 | −0.2 | 21.6 | 16.8 | 74.0 | 0.9 | 151.5 | 0 | 2.49 |
| 3 June 2019 | L08 | 154 | 8.9 | 27.3 | 20.3 | 84.4 | 1.1 | 301.2 | 0 | 5.97 |
| 13 July 2019 | L07 | 194 | 13.3 | 33.4 | 20.8 | 82.5 | 0.9 | 300.5 | 0 | 6.26 |
| 21 July 2019 | L08 | 202 | 12.0 | 27.5 | 21.8 | 57 | 1.9 | 332.8 | 0 | 7.63 |
| 14 August 2019 | L07 | 226 | 9.5 | 28.3 | 19.4 | 77.8 | 1.2 | 298.5 | 0 | 6.01 |
| 15 September 2019 | L07 | 258 | 8.6 | 29.1 | 13.9 | 80.7 | 1.9 | 192.3 | 0 | 5.99 |
| Flux | Year | Surface | N | R2 | Avg. BREBS | Avg. METRIC | SD BREBS | SD METRIC | S | RMSE | NSE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ETc | 2017 | Sugarbeet | 5 | 0.21 | 0.75 | 0.76 | 0.11 | 0.05 | 0.20 | 0.09 | 0.20 |
| 2018 | Dry Bean | 9 | 0.95 * | 0.33 | 0.38 | 0.23 | 0.23 | 0.99 * | 0.07 | 0.89 | |
| 2019 | Barley | 5 | 0.80 * | 0.54 | 0.54 | 0.15 | 0.18 | 1.1 * | 0.08 | 0.67 | |
| Pooled | 19 | 0.91 * | 0.49 | 0.52 | 0.25 | 0.24 | 0.91 * | 0.08 | 0.90 | ||
| Rn | 2017 | Sugarbeet | 5 | 0.94 * | 492.8 | 544.3 | 58.8 | 40 | 0.66 * | 55.3 | 0.95 |
| 2018 | Dry Bean | 9 | 0.83 * | 506.9 | 522 | 113.2 | 77.9 | 0.62 * | 52.7 | 0.76 | |
| 2019 | Barley | 5 | 0.96 * | 520.5 | 554.5 | 74.7 | 73.8 | 0.97 * | 36.2 | 0.70 | |
| Pooled | 19 | 0.81 * | 506.8 | 536.4 | 88.4 | 66.9 | 0.68 * | 49.6 | 0.67 | ||
| G | 2017 | Sugarbeet | 5 | 0.72 | 32.2 | 39.9 | 23.4 | 11 | 0.4 | 15.7 | 0.44 |
| 2018 | Dry Bean | 9 | 0.46 * | 78.3 | 78.8 | 44.2 | 29.9 | 0.46 * | 30.8 | 0.46 | |
| 2019 | Barley | 5 | 0.23 | 66.5 | 55.8 | 34.3 | 17.6 | 0.24 | 29.1 | 0.1 | |
| Pooled | 19 | 0.53 * | 63.04 | 62.5 | 40.5 | 28 | 0.50 | 27.1 | 0.53 | ||
| H | 2017 | Sugarbeet | 5 | 0.21 | −46.9 | −6.4 | 75.4 | 30.5 | 0.19 | 72.5 | −0.15 |
| 2018 | Dry Bean | 9 | 0.90 * | 205.1 | 186.4 | 127.9 | 102 | 0.75 | 46.8 | 0.85 | |
| 2019 | Barley | 5 | 0.24 | 87.6 | 132 | 52.3 | 50 | 0.47 | 64 | −0.87 | |
| Pooled | 19 | 0.86 * | 107.8 | 121.4 | 143.7 | 109.9 | 0.71 * | 59.2 | 0.82 | ||
| Year | Month | Surface | BREBS ETc | METRIC ETc (C. Spline) | METRIC ETc (Linear) | % Error (C. Spline) | % Error (Linear) |
|---|---|---|---|---|---|---|---|
| 2017 | July | Sugarbeet | 179 | 195.1 | 193.7 | 9 | 8.2 |
| 2017 | August | Sugarbeet | 184 | 162 | 161.7 | −12 | −12.1 |
| 2017 | September | Sugarbeet | 125 | 101.5 | 112.5 | −18.8 | −10 |
| 2017 | (July–September) | Sugarbeet | 488 | 459 | 468 | −6 | −4 |
| 2018 | May | Dry bean | 47 | 43 | 55.4 | −8.5 | 18 |
| 2018 | June | Dry bean | 81 | 50 | 41.3 | −38.3 | −49 |
| 2018 | July | Dry bean | 137 | 132 | 107.7 | −3.6 | −21.4 |
| 2018 | August | Dry bean | 168 | 151 | 147 | −10.1 | −12.5 |
| 2018 | September | Dry bean | 87 | 103 | 98.1 | 18.4 | 12.8 |
| 2018 | October | Dry bean | 16 | 28 | 21.4 | 75 | 33.4 |
| 2018 | (May–October) | Dry bean | 536 | 507 | 471 | −5.4 | −12 |
| 2019 | June | Barley | 161.7 | 137.4 | 131.3 | −15.1 | −19 |
| 2019 | July | Barley | 187.6 | 185.1 | 180.7 | −1.3 | −3.9 |
| 2019 | August | Barley | 68.4 | 92.3 | 112.2 | 34.9 | 65 |
| 2019 | September | Barley | 79.7 | 66.7 | 62.8 | −16.4 | −21 |
| 2019 | (June–September) | Barley | 497.5 | 481.5 | 487 | −3.2 | −2 |
| Irrigation District | Year | Avg. ETc (mm) | A (km2) | Area Wise Total ETc (km3) | P (mm) | Area Wise Total P (km3) | Irrigation (ETc-P) (km3) | % of Irrigation Contributing to ETc | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Cody Canal | 2017 | 699 | 157 | 0.11 | 158 | 0.02 | 0.08 | 77 |
| 2018 | 653 | 157 | 0.10 | 204 | 0.03 | 0.07 | 69 | ||
| 2 | Deaver | 2017 | 666 | 277 | 0.18 | 117 | 0.03 | 0.15 | 82 |
| 2018 | 610 | 277 | 0.17 | 158 | 0.04 | 0.13 | 74 | ||
| 3 | Greybull Valley | 2017 | 609 | 1284 | 0.78 | 125 | 0.16 | 0.62 | 79 |
| 2018 | 587 | 1284 | 0.75 | 162 | 0.21 | 0.54 | 72 | ||
| 4 | Heart Mountain | 2017 | 713 | 584 | 0.42 | 146 | 0.09 | 0.33 | 80 |
| 2018 | 665 | 584 | 0.39 | 197 | 0.11 | 0.27 | 70 | ||
| 5 | Hunt & Godfrey | 2017 | 717 | 51 | 0.04 | 124 | 0.01 | 0.03 | 83 |
| 2018 | 658 | 51 | 0.03 | 177 | 0.01 | 0.02 | 73 | ||
| 6 | Lovell | 2017 | 678 | 30 | 0.02 | 121 | 0.00 | 0.02 | 82 |
| 2018 | 658 | 30 | 0.02 | 164 | 0.00 | 0.01 | 75 | ||
| 7 | Shoshone | 2017 | 620 | 538 | 0.33 | 125 | 0.07 | 0.27 | 80 |
| 2018 | 606 | 538 | 0.33 | 167 | 0.09 | 0.24 | 72 | ||
| 8 | Sidon | 2017 | 637 | 207 | 0.13 | 121 | 0.03 | 0.11 | 81 |
| 2018 | 628 | 207 | 0.13 | 151 | 0.03 | 0.10 | 76 | ||
| 9 | Willwood | 2017 | 642 | 196 | 0.13 | 124 | 0.02 | 0.10 | 81 |
| 2018 | 673 | 196 | 0.13 | 153 | 0.03 | 0.10 | 77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharya, B.; Sharma, V.; Heitholt, J.; Tekiela, D.; Nippgen, F. Quantification and Mapping of Satellite Driven Surface Energy Balance Fluxes in Semi-Arid to Arid Inter-Mountain Region. Remote Sens. 2020, 12, 4019. https://doi.org/10.3390/rs12244019
Acharya B, Sharma V, Heitholt J, Tekiela D, Nippgen F. Quantification and Mapping of Satellite Driven Surface Energy Balance Fluxes in Semi-Arid to Arid Inter-Mountain Region. Remote Sensing. 2020; 12(24):4019. https://doi.org/10.3390/rs12244019
Chicago/Turabian StyleAcharya, Bibek, Vivek Sharma, James Heitholt, Daniel Tekiela, and Fabian Nippgen. 2020. "Quantification and Mapping of Satellite Driven Surface Energy Balance Fluxes in Semi-Arid to Arid Inter-Mountain Region" Remote Sensing 12, no. 24: 4019. https://doi.org/10.3390/rs12244019
APA StyleAcharya, B., Sharma, V., Heitholt, J., Tekiela, D., & Nippgen, F. (2020). Quantification and Mapping of Satellite Driven Surface Energy Balance Fluxes in Semi-Arid to Arid Inter-Mountain Region. Remote Sensing, 12(24), 4019. https://doi.org/10.3390/rs12244019







