Abstract
With new Ice, Cloud, and land Elevation Satellite (ICESat)-2 lidar (Light detection and ranging) datasets and classical Landsat imagery, a method was proposed to monitor annual changes of lake water levels and volumes for 35 years dated back to 1980s. Based on the proposed method, the annual water levels and volumes of Lake Mead in the USA over 1984–2018 were obtained using only two-year measurements of the ICESat-2 altimetry datasets and all available Landsat observations from 1984 to 2018. During the study period, the estimated annual water levels of Lake Mead agreed well with the in situ measurements, i.e., the R2 and RMSE (Root-mean-square error) were 1.00 and 1.06 m, respectively, and the change rates of lake water levels calculated by our method and the in situ data were −1.36 km3/year and −1.29 km3/year, respectively. The annual water volumes of Lake Mead also agreed well with in situ measurements, i.e., the R2 and RMSE were 1.00 and 0.36 km3, respectively, and the change rates of lake water volumes calculated by our method and in situ data were −0.57 km3/year and −0.58 km3/year, respectively. We found that the ICESat-2 exhibits a great potential to accurately characterize the Earth’s surface topography and can capture signal photons reflected from underwater bottoms up to approximately 10 m in Lake Mead. Using the ICESat-2 datasets with a global coverage and our method, accurately monitoring changes of annual water levels/volumes of lakes—which have good water qualities and experienced significant water level changes—is no longer limited by the time span of the available satellite altimetry datasets, and is potentially achievable over a long-term period.
1. Introduction
Although lakes and reservoirs only cover a small portion of the Earth’s surface, they are of great importance for human well-being, biodiversity, and ecosystem from local to global scales [1]. Fresh water stored in lakes and reservoirs is essential for human life, agricultural irrigation, and economic development, particularly in populous areas and arid/semi-arid areas [2]. Lakes/reservoirs’ water levels and volumes are fundamental information for earth system modelling, especially for hydrological modelling (e.g., atmospheric, cryospheric, and biospheric components) [3]. Additionally, the change of lake water volumes can act as sentinels of climate changes (e.g., global warming, glacier melting, and drought) and anthropogenic activities (e.g., reservoir regulation, agricultural irrigation, and damming) [4]. Hence, it is necessary to better monitor and understand water level/volume changes in lakes/reservoirs for water resource development, utilization, management, and protection under future global warming and intensive human induced disturbance [5].
Traditionally, in situ measurements were used to obtain water levels/volumes of some specific lakes [6]. Unfortunately, in situ data of water levels/volumes of lakes across the globe are very limited, especially for developing countries and some remote areas. Previous studies also reported that the lake water level and volume can be obtained by the bathymetric data derived from various sensors [6], e.g., ship-borne singlebeam or multibeam echo sounders, and airborne bathymetric lidars (Light detection and ranging) [7,8,9]. However, the high cost of those accurate bathymetric data limits the use of this approach at a global scale [10]. Currently, multiple satellite sensors have a potential for monitoring lake water levels and volumes at a global scale owing to their global spatial coverage. Using multiple satellite data, many methods were proposed and exhibited a good performance for monitoring lake water levels and volumes [6,11,12,13,14,15,16]. These previous methods have the potential to conduct a long-term monitoring of lake water levels using the linear or non-linear relationship between water level and surface area. For example, Zhang et al. obtained Tibetan Plateau’s lake level and volume changes by using Ice, Cloud, and land Elevation Satellite (ICESat)/ICESat-2 and Landsat data. Specifically, the relationship between lake level and area was constructed over 2003–2009 and 2018, and then the corresponding lake levels over 2010–2017, were derived using the lake level/area relationship and the Landsat-derived areas over 2010–2017 [16]. A precise lake level/area relationship needs an amount of water level observations over multiple years. For some remote lakes without in situ measurements, spaceborne altimeters can provide water level observations. However, for some small lakes, water level observations from ICESat and radar altimeters may be very limited due to their large footprints (i.e., 70 m and hundreds of meters in diameter) and their limited time coverages of satellite altimetry data [2,17].
The new generation of the ICESat-2 (Ice, Cloud, and land Elevation Satellite-2) photon-counting lidar provides an alternative way to monitor the lake water levels/volumes. The ICESat-2 lidar has much denser footprints in its along-track and cross-track directions [18]. The ICESat-2 has six beams (from one laser source) in the cross-track direction. The laser footprint is less than 17 m in diameter, and the footprint interval in the along-track direction is only 0.7 m [19], i.e., the ICESat-2 photon-counting lidar can provide several accurate surface profiles where it flew over. In addition, equipped with a laser source at 532 nm, the bathymetric information can also be captured by the ICESat-2 in shallow waters. Given that the Landsat data are available from 1984, the lake boundary of each year can be precisely obtained. The lake water level of each year is very promising to be obtained by matching Landsat-derived lake boundaries with the ICESat-2 derived surface profiles.
In this study, all available Landsat Thematic Mapper (TM)/Enhanced Thematic Mapper Plus (ETM+) data covering the study area over 1984–2018 were used. The Landsat pixel_qa band was utilized to generate the yearly MNDWI (modification of the normalized difference water index) composites without clouds and shadows. The yearly cloud-free MNDWI time-series during 1984–2018 were used to further obtain the annual lake boundaries. Then, after noise filtering and error correction, the ICESat-2 data were used to generate along-track surface profiles (i.e., the ground and underwater bottom) around the lake shore. The NLCD (National Land Cover Database) product was used to filter out the interference of shrubs/scrubs on available surface profiles. The lake water levels were obtained by matching Landsat-derived lake boundaries and ICESat-2-derived surface profiles. The relationship between lake areas and water levels was established to calculate water levels during 1984–2018. Afterwards, lake areas and water levels were integrated to estimate temporal changes of water volumes of Lake Mead in the USA from 1984 to 2018. Finally, the estimated annual water levels and volumes were compared with yearly-averaged in situ observations from Lake Mead Water Database website (https://lakemead.water-data.com) and the yearly-averaged water level/volume results derived from multiple altimeters in Hydroweb (http://hydroweb.theia-land.fr/).
2. Study Area and Data
2.1. Study Area and In Situ Measurements
Lake Mead [35°56′50″N~36°28′33″N, 114°03′23″W~114°50′59″W] (as illustrated in Figure 1) is the largest reservoir in the USA, which was formed by the impoundment of Hoover Dam [20]. It is located southeast of the city of Las Vegas and serves as the main water supply for surrounding residents [21]. Driven by climate changes under global warming [22], dramatic decline in Lake Mead’s water levels and volumes has been observed in recent years, according to in situ measurements (https://lakemead.water-data.com). Rocks and bare lands dominate Lake Mead’s shore based on Google Earth images. Moreover, based on the land-cover map from NLCD 2016 product (https://www.mrlc.gov/viewer/), shrubs/scrubs can be clearly observed around the Lake Mead’s shore. Additionally, no significant land-cover changes can be found around Lake Mead, according to NLCD 2001 and 2016 products. Lake Mead Water Database website provides in situ measurements of yearly water levels and volumes, which are used to validate water levels and volumes between 1984 and 2018 obtained by our method. The in situ water levels and volumes are in units of feet and acre feet, respectively. Here, the in situ data are converted to water levels in units of meter and water volumes in units of km3.
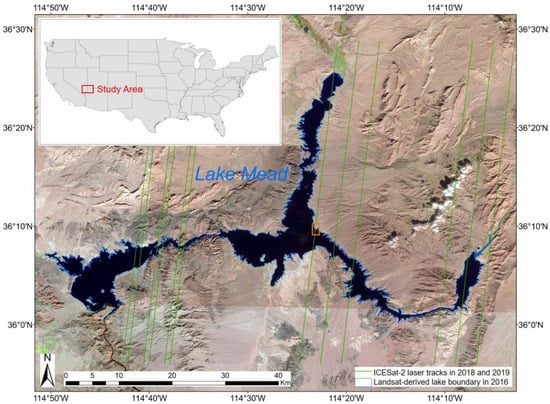
Figure 1.
Ice, Cloud, and land Elevation Satellite (ICESat)-2 laser ground tracks (i.e., twelve green lines) in Lake Mead in 2018 and 2019 used in this study. Note that the Sentinel-2 images with a 10 m resolution were collected from the earthexplorer website (https://earthexplorer.usgs.gov/) as the basemap, and Lake Mead’s boundary in 2016 (using blue curves) was obtained by the modification of the normalized difference water index (MNDWI) method. ICESat-2 flew over Lake Mead four times in 2018 and 2019 and twelve laser ground tracks of raw data points were recorded. The ICESat-2 photon-counting lidar (Light detection and ranging) has three strong laser beams; therefore, one flight route corresponds to three laser ground tracks. These data photons were captured at night when less noise photons were included. The inset shows the location of the study area in the USA. The brown box is the case area to show the ICESat-2 data photons, and to illustrate the matching procedure in detail.
2.2. Landsat Imagery
In this study, 1855 scenes of Landsat Collection 1 Tier 1 surface reflectance data, including 1013 Landsat 5 Thematic Mapper (TM) images and 842 Landsat 7 Enhanced Thematic Mapper Plus (ETM+) images, were used to monitor long-term changes of Lake Mead’s water levels and volumes at an annual scale from 1984 to 2018. The number of used Landsat images for each year is listed in Table 1 in detail. All these Landsat data are available on the Google Earth Engine (GEE) platform (https://earthengine.google.org/). The Landsat imagery is the atmospherically and geometrically corrected surface reflectance from Landsat TM/ETM sensors. The Landsat data can provide 30-m and 16-day observations for Lake Mead (path = 39, row = 35; path = 39, row = 34). To avoid the impact on the extraction of lake boundaries from Landsat imagery, pixels covered by clouds and shadows were removed using pixel_qa band, which was derived from the quality assessment algorithm and available in GEE [23].

Table 1.
Detailed information on Landsat imagery used in this study. TM: Thematic Mapper and ETM+: Enhanced Thematic Mapper Plus.
2.3. ICESat-2 Data Photons
ICESat-2 carries the first satellite photon-counting lidar, i.e., the ATLAS (Advanced Topographic Laser Altimeter System) [19]. ATLAS has six laser beams (including three strong beams and three weak beams) at the wavelength of 532 nm, which can penetrate water column. The transmitted energy of the laser pulse of weak beams is approximately 1/4 compared to the strong laser beams. The strong beams correspond to higher bathymetric capacity; therefore, in this study, only the strong beams were involved. The cross-track distance between adjacent strong beams is approximately 3.3 km and the interval between along-track adjacent footprints on Earth’s surface is approximately 0.7 m [24]. Four flight routes (including twelve strong beam tracks illustrated in Figure 1 using green lines) that flew across Lake Mead were found from ICESat-2 available datasets. These data were captured on 10/15/2018, 12/12/2018, 02/12/2019, and 04/15/2019 (Month/Day/Year) at night, when noise photons are much less than those in the daytime. The brown box in Figure 1 is the case area to demonstrate the details of ICESat-2 data photons in Figure 4.
The ICESat-2 ATL03 datasets were used in this study, which contain the raw data points recorded with unique time tag, latitude, longitude, and WGS84 ellipsoid elevation [25]. The horizontal and vertical errors of captured photons have been corrected, and the vertical and horizontal accuracy for land areas is better than 0.85 m and approximately 5 m, respectively [26]. However, the signal photons on underwater bottoms and grounds should be extracted from the noisy raw data points, and the bathymetric error should be further corrected. In ATL03 datasets, the confidence parameter (from 0 to 4) is provided to distinguish signal photons (corresponding to higher confidence values) from noise ones [25], but it does not always perform well. Hence, a DBSCAN (density-based spatial clustering of applications with noise) method was used to detect signal photons in this study. The DBSCAN algorithm was first proposed to detect clusters in large noisy spatial databases [27], and was modified to detect signal photons from the noisy data photons captured by photon-counting lidars [28]. The basic criteria of the DBSCAN algorithm are as follows. For each point in a cluster, if the point density in its neighborhood is larger than a given threshold, this point will be identified as a “signal point”. The neighborhood is normally defined as the Euclidean distance. For example, the neighborhood can be set as a circle with a radius of Ra. The threshold (called MinPts) normally corresponds to the minimum number of points within the neighborhood range.
2.4. NLCD Land-Cover Data
The National Land Cover Database (NLCD) is supported by the Multi Resolution Land Characteristics (MRLC) Consortium (http://www.mrlc.gov), which has been widely used [29]. A classification system modified from the Anderson Land Cover Classification System was used for generating the NLCD 2016 product, which provides eight land-cover types (i.e., barren, developed, forest, herbaceous, planted/cultivated, shrubland, wetlands, and water) with a 30 m spatial resolution at a national scale. For each land-cover type, the NLCD 2016 product also provides several sub-types. For example, shrubland contains two sub-types: dwarf scrub and shrub/scrub. Dwarf scrub is mainly composed of shrubs that are less than 0.2 m tall and it is found primarily in Alaska, USA, whereas shrub/scrub is dominated by shrubs that are lower than 5 m. The type of shrub/scrub includes true shrubs, young trees in an early stage or lower trees subjected to environmental conditions. In this study, shrub/scrub areas around the shore of Lake Mead were extracted to remove their influence on the estimation of water levels/volumes.
3. Methods
3.1. Extraction of Lake Boundaries from Landsat Data
This study focused on a method to calculate annual water levels and volumes over 1984–2018. Hence, for each year, only one lake boundary was required. Before extracting annual lake boundaries from Landsat imagery, land-water classification was needed. Here, the MNDWI was utilized to enhance the water information using Landsat 5 TM and Landsat 7 ETM+ reflectance data [30]. The MNDWI can be calculated as follows.
where Green is the band 2 for the Landsat TM/ETM+ data, and MIR (middle infrared) is the band 5 for the Landsat TM/ETM+ data.
Based on Equation (1), the MNDWI can be obtained for each Landsat image. Next, the Landsat pixel_qa band (i.e., the band for quality assessment) available on the GEE was utilized to generate the yearly clear MNDWI composites without clouds and shadows. According to the pixel_qa band derived from the quality assessment algorithm, pixels labeled with different values represent different classes, i.e., cloud, cloud shadow, snow/ice, water, and clear observations. Hence, the pixel_qa band can be used to identify and remove bad observations (e.g., pixels with clouds and shadows). Then, for each pixel, all available MNDWI values (without clouds and shadows) were used to determine the median as the composite value within this year, which can well eliminate the noise [31]. The yearly MNDWI composites can also effectively reduce the positional variability of lake boundaries (i.e., the land-water boundary) arising from seasonal water level fluctuations within a year [32]. Then, the yearly cloud-free MNDWI time series during 1984–2018 can be generated on the GEE platform.
Then, based on the yearly MNDWI images, a dynamic thresholding method was applied to extract yearly lake extent from other land-covers. In Figure 2, an example was used to demonstrate land-water classification and to clarify the method of generating land-water map from the MNDWI composite image in 2018. For each year, a threshold was determined based on the yearly MNDWI histogram. Specifically, the valley between two peaks of the histogram (i.e., corresponding to the water surface on lakes and the surrounding lands) was identified and the corresponding MNDWI value was defined as the threshold for land-water classification [33]. Based on the land-water binary maps, noises and other small water bodies were eliminated via the MATLAB function “bwareaopen” to produce the lake maps. Finally, we achieved yearly Lake Mead maps during 1984–2018 with a spatial resolution of 30-m. Areas of Lake Mead were estimated by Landsat-derived lake maps with a binary raster format (1 represents the lake and 0 represents surrounding lands). Those binary lake maps were then converted to lake boundary with shapefile format (i.e., polyline: a series points with longitude and latitude information) via ArcGIS 10.2, for further matching with the ICESat-2 along-track profiles.

Figure 2.
(a) Example of generating land-water map using the thresholding method based on the MNDWI composite image in 2018. The color bar shows the composite value in each pixel. (b) Land-water map in 2018 derived from (a). In sub-figure (b), the land and water areas were labeled by blue and yellow, respectively. (c) Histogram of the MNDWI composite image in 2018. The threshold that was used to classify the land and water was determined at the valley between two peaks (i.e., corresponding to the land and water). (d) Enlarged result of the MNDWI composite image in 2018. The range of the number of pixels (Y-axis) was set from 0 to 1500 to clearly show the valley in (c).
3.2. Detection of Surface Profiles from ICESat-2 Data
For different land-covers, many methods were proposed to detect signal photons from raw noisy points [34,35,36,37]. The previous study proposed a DBSCAN method and performed well in the airborne MABEL (Multiple Altimeter Beam Experimental Lidar) raw data points in coastal areas [38]. The MABEL is a technique indicator of ICESat-2 sensor [18], and its sensors and corresponding data exhibit some differences. For example, the vertical window of the MABEL datasets is normally 1500 m, whereas the ICESat-2’s vertical window is from several tens to many hundreds of meters [19]. This method was adjusted to detect the signal photons from ICESat-2 raw data points. From the ICESat-2 ATL03 datasets, every continuous 10,000 raw data points in the along-track direction were used to calculate their corresponding adaptive threshold MinPts (which was used to identify signal or noise) using Equation (2). This equation of MinPts was based on the classical study by Degnan [39], which was derived from equations of the probability of detecting signals and the probability of false alarm.
SN1 represents the estimated total number of photons (including noise photons and signal photons) within the given circular neighborhood. Within a given radius Ra of 2.5 m for ICESat-2 datasets, SN1 was calculated in Equation (3), where N1 is the total number of the noise and signal photons in current 10,000-point segment, i.e., N1 = 10,000 in this study. h is the vertical range in current segment, and l is the along-track range in current segment.
SN2 represents the estimated number of noise photons within the given neighborhood. The size of the ICESat-2’s vertical window varies from several tens to many hundreds of meters in different areas, terrain types, and elevation variations [19]. Normally, the signal photons from the Earth’s surface concentrate in the middle of the vertical window while the noise photons distribute in the whole vertical window, i.e., in the top and bottom of the vertical window, nearly all photons are noise ones. The solar-induced background noise photons scattered by particles in atmosphere and water column were the dominant noise source [40], and the density of noise photons would be larger in water column. Since the underwater bottom corresponds to lower elevation values compared to the ground surface, the density of noise photons that locate in the lowest elevations should be larger. Near coastal areas, the size of the ICESat-2’s vertical window is usually only several tens of meters. To make this method satisfy different areas and surface types, we used the photons that locate in the lowest 5 m elevations within the ICESat-2’s vertical window (because most photons in this layer are noise ones) to estimate noise photons SN2 within the given neighborhood as shown in Equation (4).
N2 is the number of photons that correspond to the lowest 5-m elevations in current segment and h2 is the height of the 5-m lowest layer, i.e., h2 = 5 m. With the given radius Ra and adaptive threshold MinPts, for every along-track 10,000 raw data points, the signal photons were distinguished from noise ones by the DBSCAN calculator [27] and its basic criteria are as follows. For each point p in a cluster, the point density in its neighborhood within a circle is calculated, and if the point density exceeds the threshold parameter Minpts, the point p would be identified as a “signal point”. The circular neighborhood is defined as the Euclidean distance for given points p and q, i.e., dist(p, q). Then, a few remaining noise photons were discarded manually.
Next, the elevation of detected signal photons that are below the local water level was corrected. The elevation of signal photon returned by lake bottom (underwater surface) is influenced by three factors, including the incident angle of laser beam, the retraction of water column, and the wave effect of water surface. The incident angle for the central beam of ICESat-2 is nearly 0°, whereas the outer beams of the ICESat-2 are only 0.38°. Based on Parrish’s method, when the water depth is 15 m, the difference of bathymetric errors with 0° and 0.38° incident angles is approximately 1 mm [24]. As a result, the bathymetric error arising from the incidence angle is negligible, but the refraction effect in water column should be carefully corrected (because light travels slower in water than in air). Parrish et al. well investigated satellite-derived bathymetry using a photon-counting lidar and proposed an effective method to correct the refraction effect (that may introduce bathymetric error up to of meters) [24]. However, in Parrish’s study, the water surface was assumed as a flat surface. In real situation, the surface undulation caused by waves could be up to tens of centimeters or even meters when the surface water is driven by strong winds. In this case, the effects of waves cannot be neglected. As shown in the schematic diagram in Figure 3, the blue horizontal dashed line represents the flat-water surface, while the blue solid curve represents the water surface with waves. If the wave effect on the water surface was not corrected, some errors would be introduced to bathymetric results.
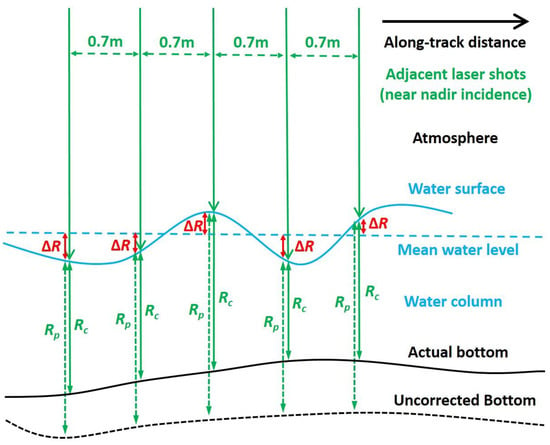
Figure 3.
Schematic diagram of the bathymetric error correction for the wave effect on the water surface.
Based on Parrish’s approach, the wave effect on the water surface was further considered and corrected as follows. For each laser shot (with a unique time tag), the bathymetric error was corrected by the ray tracing method. The preliminary laser range Rp in water column for all underwater bottom photons can be calculated by subtracting the current water level Lc from the elevation of bottom photons, where the current water level Lc is equal to the mean value of the signal photons on the water surface at the current laser shot. The corrected laser range Rc can be expressed as Rc = Rp·N1/n2 ≈ 0.75 Rp [24], where N1 is the refractive index in atmosphere (nearly equal to 1) and n2 is the refractive index in water (nearly equal to 1.334 at 532 nm). Finally, the corrected elevation of detected signal photons Hc that are below the local water level can be expressed as Hc = Huc + Rp − Rc or Equation (5), where Huc is the original elevation. After detecting along-track signal photons and calibrating the bathymetric errors, the surface profiles that are composed of lidar points were obtained.
3.3. Estimation of Lake Water Levels
During the past 30 years, the surrounding topography near the shore of Lake Mead has been proved to be slightly changed or nearly unchanged [14]. From 1984 to 2018, the lake water level in each year was estimated by matching the twelve along-track profiles from the ICESat-2 data in 2018 and 2019 with the lake boundary from Landsat datasets in that year, i.e., if a lidar point was within the 10 m radius of any lake boundaries in horizontal (under the identical coordinate system), this lidar point was identified near the water surface in that year and was selected. Then, the median elevation value of those identified lidar points can represent the water level in that year.
However, from satellite images and detected surface profiles from ICESat-2 data, some shrub/scrub areas can be clearly observed around the shore of Lake Mead. Those shrubs/scrubs on lidar profiles can inevitably influence the estimation of lake water levels. Hence, the land-cover map around Lake Mead from the NLCD 2016 product was used to identify the extent of shrubs/scrubs and to filter out the Landsat-derived lake boundaries covered by shrubs/scrubs. In each year between 1984 and 2018, the percentage of lake boundary covered by shrubs/scrubs (from the NLCD 2016 product) was calculated as the result of the number of pixels covered by shrubs/scrubs divided by the number of all pixels not covered by water along the lake boundary of this year. The estimated water levels during the years with a lower percentage of lake boundary covered by shrubs/scrubs (i.e., <10%) were considered as reliable. Then, the relationship between Landsat-derived lake areas and estimated water levels during those reliable years was established using a linear regression model [41], which is normally called a lake area-water level model. Finally, the lake water levels during 1984–2018 were estimated via the fitted lake area-water level model and the Landsat-derived lake area of each year.
3.4. Estimation of Lake Water Volumes
According to Duan’s study, the total water volume of a lake depends on a specific fixed minimum water volume and a variable component that varies with the water levels [6]. The main objective of this study is to estimate the relative water volume changes, rather than absolute values. The relative water volume changes can be used for further investigating the drivers. Hence, the mentioned water volume refers to the relative water volume of lakes, which has been widely used in previous studies [16,42,43]. By integrating ICESat-2 points and Landsat imagery, the water level and lake area were computed for each year and were integrated to estimate the lake water volume. First, yearly water levels were sorted in ascending order and yearly lake areas were sorted by the order of yearly water levels. Then, the total lake can be divided into a series of frustums with different volumes along the vertical direction (from the lower water levels to the higher water levels). The volume of each frustum can be calculated using following equation [44].
where h represents the water level difference between upper base (i.e., corresponds to the higher water level) and lower base (i.e., corresponds to the lower water level). si and si+1 correspond to lake areas of the upper base and lower base, respectively. The water volume ΔVyear1−year2 between two adjacent years (Hyear1 and Hyear2) can be estimated as follows.
Δvi are the frustums whose water levels of the upper and lower bases are both within the range of [Hyear2, Hyear1] (if Hyear1 > Hyear2) or [Hyear1, Hyear2] (if Hyear2 > Hyear1).
Then, lake water volumes during the study period were computed by accumulating all water volumes of the adjacent years from 1984 (i.e., the starting year of the Landsat TM/ETM+ data) to each year. It is noted that the water volume in 1984 can be considered as a constant or reference value. For instance, the lake water volume in 1987 can be obtained by accumulating ΔV1984–1985, ΔV1985–1986, ΔV1986–1987, and the water volume reference value in 1984. Finally, we can obtain Lake Mead’s water volumes for all years between 1984 and 2018.
4. Results
4.1. Lake Water Level Estimation and Validation
First, applying the MNDWI method, yearly Lake Mead boundaries between 1984 and 2018 with the polyline format were extracted from all available Landsat TM/ETM+ images, and, for example, in Figure 1, blue curves illustrate the Lake Mead boundary in 2016. Second, the signal photons were detected by the DBSCAN method. Figure 4a,b illustrate the lidar photons and the corresponding satellite image in the case area (i.e., the brown box in Figure 1). In Figure 4a, the green line corresponds to one of the ICESat-2 lidar ground tracks on 12/02/2019, the blue curve corresponds to Landsat derived annual lake boundary in 2016, and the basemap (i.e., Sentinel-2 imagery) was captured on 11/22/2016. In Figure 4b, red points represent raw data points, blue circles represent the ICESat-2 results with the highest confidence value (most likely signal photons with the confidence value of 4), and green points represent the signal photons from our results. The photons in Figure 4b are illustrated in along-track distance, which correspond to the green line in Figure 4a. We can find that our results obtained a better performance than the ATL03 results (i.e., the confidence parameter from ATL03 datasets), where more noise photons remained. It should be noted that when the Sentinel-2 imagery was captured on 11/22/2016, the water level (1077.8 feet from the in situ data) was approximately 2.4 m lower, compared to the water level (1085.8 feet from the in situ data) on 12/02/2019, when the ICESat-2 passed over Lake Mead. Consequently, some lidar points on underwater bottom (in Figure 4b) correspond to land surfaces (in Figure 4a). Then, the elevation of lidar points that were below the water surface was corrected using Equation (5). After the bathymetric correction, the ICESat-2 sensor can capture signal photons reflected from underwater bottoms up to 10 m in Lake Mead in Figure 4b.
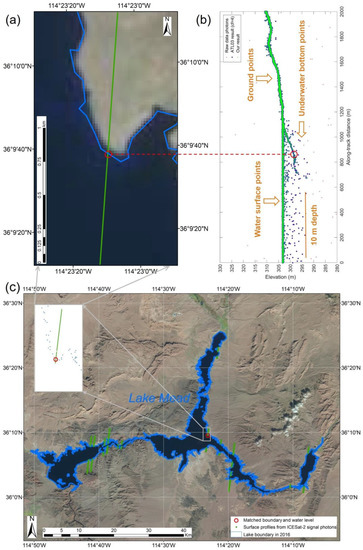
Figure 4.
(a) Satellite imagery, ICESat-2’s laser ground track, and Landsat derived annual lake boundary in a case area (corresponding to the brown box in Figure 1). (b) ICESat-2 lidar raw data points (captured on 12/02/2019) and the detected along-track surface profile in the case area. (c) Landsat-derived annual lake boundary in 2016 matched with the ICESat-2-derived along-track surface profiles. The inset of (c) also corresponds to the case area. In (a), the green line represents one of the ICESat-2 lidar ground tracks on 12/02/2019, the blue curve represents the annual lake boundary in 2016, and the basemap (i.e., Sentinel-2 imagery) was captured on 11/22/2016. Note that, when the Sentinel-2 imagery was captured on 11/22/2016, the water level (1077.8 feet from the in situ data) was approximately 2.4 m lower than the water level (1085.8 feet from the in situ data) on 12/02/2019, when ICESat-2 flew over the Lake Mead. In (b), the raw data points, signal photons from ATL03 standard results, and our detected signal photons are demonstrated in along-track distance, and the detected signal photons correspond to the green line in (a), and the green line in the inset of (c). Some lidar points obtained on 12/02/2019 on the underwater bottom in (b) correspond to land surfaces in (a), because these locations were above the water surface on 11/22/2016, when the basemap image was captured. In (a–c), the red circle corresponds to the location where Landsat-derived lake boundary in 2016 was matched with the ICESat-2-derived along-track surface profile. The red dashed line across (a) and (b) indicates the matching principle, i.e., the water/land boundary pixel (a) on the ICESat-2’s laser ground track corresponds to the ICESat-2’s points (b) on the underwater bottom; therefore, the corresponding ICESat-2’s points at this water/land boundary pixel will be selected to calculate the water level in 2016. In (c), blue points and green points represent the lake boundaries and the detected surface profiles from lidar signal photons, respectively.
Third, the Landsat-derived lake boundaries were matched with ICESat-2 profiles for estimating lake water levels. Specifically, Figure 4c illustrates how to match the lake boundary in 2016 (the blue points), with one of the surface profiles from the detected ICESat-2 lidar photons (the green points) from Figure 4b. In Figure 4a–c, the red circle corresponds to the location where Landsat-derived lake boundary in 2016 was matched with the ICESat-2-derived along-track surface profile. The selected lidar photons near the red circle (within a radius of 10 m in horizontal) in Figure 4b were used for further estimating lake water levels. Although the radius of 10 m is not a short distance, the lake boundary generated from the Landsat images has a lower spatial resolution (with a 30 m pixel). As illustrated using green lines in Figure 4c, 153,292 ICESat-2 topographic points were extracted and used near the shore of Lake Mead. These lidar points were captured on four different dates and generated 11 along-track topography profiles (one profile did not have valid data near the shore). For each flight over the study area, three strong laser beams were used.
Fourth, the lake water levels in early years were determined with the lake bottom profile derived from ICESat-2 data collected in 2018 and 2019. Since the water level of Lake Mead dropped dramatically from 1984 to 2018, the lake surface retreated significantly. During the process, the area once under water gradually exposed to air and occupied by shrubs/scrubs. Therefore, the location of lake boundary in early years, e.g., 1984, is now covered by shrubs/scrubs. These shrubs/scrubs were also captured by the ICESat-2 sensor in 2018 and 2019 and were on the ICESat-2 lake bottom profile. In other words, the water levels in early years determined from the ICESat-2 bottom profile do not represent the real water levels at that time, but the canopy of the shrubs/scrubs in 2018 or 2019. These water levels are erroneous and should be excluded from the linear regression model between lake water level and lake water surface. In this study, the NLCD 2016 product was used to represent the shrub/scrub cover surrounding Lake Meade in 2018 and 2019, and to further exclude the erroneous lake levels. For the locations of lake boundary during the whole study period, percentages of shrub/scrub cover were calculated and illustrated in Figure 5a. According to the shrub/scrub percentage curve in Figure 5a, estimated water levels (by the matching process) during the period of 2007–2018 (i.e., percentages of lake boundaries covered by shrubs/scrubs from NLCD 2016 product are less than 10%) were selected and combined with the Landsat-derived lake areas over 2007–2018 to construct the linear regression model (i.e., lake area-water level model). To make a comparison, all estimated water levels during the whole period of 1984–2018 were used to fit the other linear regression model. Figure 5c,d show the scatter plots and the regression results with and without water levels in early years (from 1984 to 2006), respectively. After discarding the data in early years that may be contaminated by shrubs/scrubs, Figure 5d shows a better regression result with an R2 of 0.96 and RMSE (Root-mean-square error) of 0.79 m.
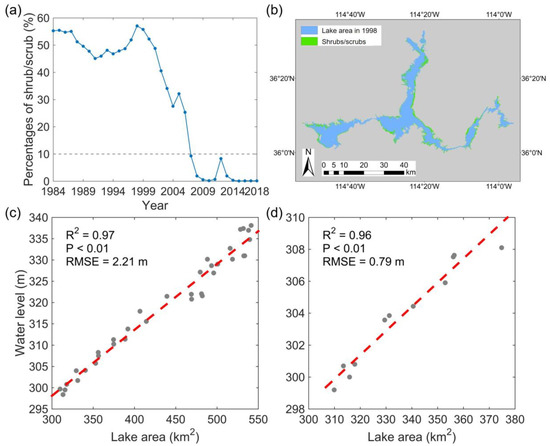
Figure 5.
(a) Percentages of lake boundaries covered by shrubs/scrubs (from the National Land Cover Database (NLCD) 2016 product) between 1984 and 2018. (b) Spatial distribution of shrubs/scrubs around Lake Mead in 1998 with the maximum shrubs/scrubs percentage between 1984 and 2018. Relationships and regression results between lake areas extracted from Landsat data and water levels extracted from ICESat-2 data during 1984–2018 (c) and 2007–2018 (d). In sub-figure (a), percentages of shrubs/scrubs along the shoreline of Lake Mead during 2007–2018 are less than 10% (i.e., gray dotted line), and the data of this period were selected to fit the level/area relationship in (d). In sub-figure (b), green areas correspond to shrubs/scrubs, blue areas correspond to the water surface, and gray areas correspond to the background.
Next, the fitted lake area-water level model was used to estimate yearly water levels during 1984–2018 by inputting the yearly Landsat-derived water areas. Figure 6a,b indicate a good consistency between our estimated water levels and in situ measurements with R2 = 1.00, p = 0.00, and RMSE = 1.06 m, which proves the reliability and accuracy of the derived model in Figure 5d. It is notable that the systematic offset between water levels from our estimations and in situ data was removed to make them comparable (the in situ water levels are based on the benchmark above sea level and in units of feet, whereas the estimated water levels from ICESat-2 data are based on the WGS84 ellipsoidal height and in units of meters). According to our calculations, during the study period, the change rates of the lake water levels calculated by our results and the in situ measurements are −1.36 m/year and −1.29 m/year, respectively. Lake Mead’s water level decreased from 1984 to 1991 (change rate = −1.85 m/year); increased from 1992 to 1998 (change rate = 1.83 m/year); and decreased from 1999 to 2018 (change rate = −1.93 m/year). We can observe similar results from the in situ measurements with water level change rates of −1.49 m/year, 1.64 m/year and −1.91 m/year during 1984–1991, 1992–1998, and 1999–2018. Our results indicate the decrease–increase–decrease temporal characteristics of Lake Mead’s water levels during 1984−2018.
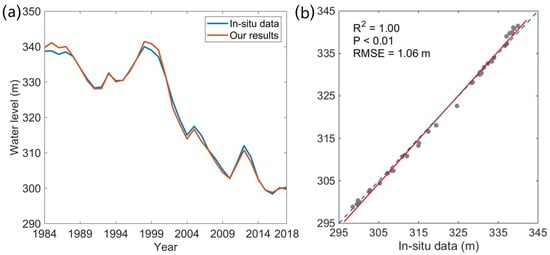
Figure 6.
Estimations and validations of yearly Lake Mead’s water levels from ICESat-2 data and in situ data from 1984 to 2018. (a) Yearly water levels derived from our results and in situ data. (b) Relationship between the yearly water levels derived from our results and in situ data. In sub-figure (b), the correlation between results from our method and the in situ measurements is 1.00 with an RMSE (Root-mean-square error) of 1.06 m, and the blue dotted line is the 1:1 line.
4.2. Lake Water Volume Estimation and Validation
Based on the Landsat imagery, yearly areas of Lake Mead were calculated. Between 1984 and 2018, the maximum lake area is 541.27 km2 in 1998; the median lake area is 468.90 km2 in 1991; and the minimum lake area is 309.84 km2 in 2016 (illustrated in Figure 7). Then, water volumes were calculated via the method by combining water areas and water levels of Lake Mead using Equation (7). To make our estimated lake water volumes and in situ data comparable, their systematic offset was removed. As shown in Figure 8, the estimated yearly lake water volumes show a good agreement with the in situ data (R2 = 1.00, p = 0.00, and RMSE = 0.36 km3). During the study period, change rates of the lake water volumes calculated by our results and the in situ measurements are −0.57 km3/year and −0.58 km3/year, respectively. The Lake Mead’s water volume decreased from 1984 to 1991 (change rate = −0.94 km3/year); increased from 1992 to 1998 (change rate = 0.92 km3/year); and decreased from 1999 to 2018 (change rate = −0.79 km3/year). We can observe similar results from the in situ measurements with lake water volume change rates of −0.85 km3/year, 0.94 km3/year, and −0.81 km3/year during 1984–1991, 1992–1998, and 1999–2018. Our results suggest decrease–increase–decrease temporal characteristics of Lake Mead’s water volumes during 1984–2018, which is in accordance with the temporal changes of lake water levels.
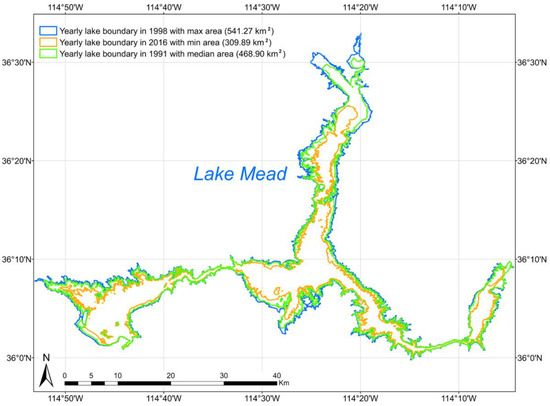
Figure 7.
Yearly lake boundaries with the maximum, minimum, and median areas between 1984 and 2018. According to our calculations, the maximum lake area, median lake area, and minimum lake area are 541.27 km2 in 1998; 468.90 km2 in 1991; and 309.84 km2 in 2016, respectively.
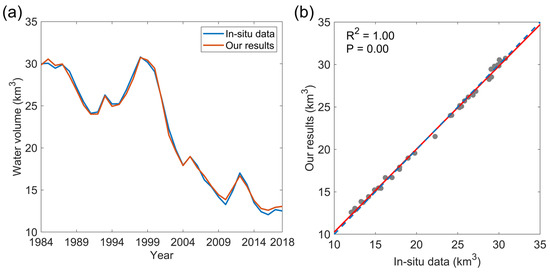
Figure 8.
Comparison between the yearly Lake Mead’s water volumes from our results and the in situ measurements. (a) Yearly water volumes derived from our results and in situ data. (b) Comparison between the yearly water volumes derived from our results and in situ data. The correlation coefficient between our results and the in situ data is 1.00 with an RMSE of 0.36 km3. In sub-figure (b), the blue dotted line is the 1:1 line. Note that the unit of water volumes from the in situ measurements were converted from acre feet to cubic kilometers.
To further characterize Lake Mead’s water volume changes year by year, the first-order difference of yearly water volumes was calculated as the interannual variation of Lake Mead’s water volumes during 1984–2018 and illustrated in Figure 9. We can observe that the interannual variation in Lake Mead’s water volumes from our results is well in accordance with that from in situ measurements (R2 = 0.94, p = 0.00, and RMSE = 0.37 km3). This good agreement indicates that our method by integrating Landsat imagery between 1984 and 2018 and recent ICESat-2 data (in 2018 and 2019) achieved a good performance of annual scale and long-term monitoring of changes of lake water levels and volumes for over 30 years, even though the yearly lake water volumes highly fluctuated.
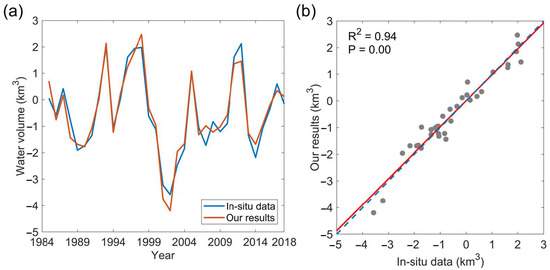
Figure 9.
Comparison between the interannual variations in Lake Mead’s water volumes obtained from our results and the in situ measurements. (a) Interannual variations in water volumes derived from our results and in situ data. (b) Comparison between the interannual variations in water volumes derived from our results and in situ data. The correlation coefficient between two results is 0.94 with an RMSE of 0.37 km3. In sub-figure (b), the blue dotted line is the 1:1 line.
5. Discussions
5.1. Performance Analysis of ICESat-2 Data
For the detected surface profiles on ground or vegetation covered surface from the ICESat-2 datasets, the accuracy of these lidar points (even covered with forest) has been verified to satisfy 0.85 m in vertical and 5 m in horizontal, because most errors have been corrected (i.e., the atmospheric delay, solid tide, and systematic pointing bias, etc.) [26]. For detected points on the underwater bottom, the bathymetric errors have not been corrected in the ATL03 product. Parrish et al. [24] developed a significant approach to correct the bathymetric error arising from the refraction effect in water column, and, in this paper, the bathymetric error arising from the wave effect was further corrected. The RMS (root mean square) wave height of the water surface is 0.12 m in Figure 4b. A 0.12 m RMS wave height corresponds to 1 sigma, i.e., the significant wave height (SWH) in local areas can be over 0.36 m. If the wave effect on the water surface is not considered, some errors will be introduced to the bathymetric results. As illustrated in Figure 6a, the water levels in 2015 and 2016 were lower than those in 2018 and 2019 when ICESat-2 flew over Lake Mead. The water levels in 2015 and 2016 were computed by matching the lidar points on the underwater bottom with lake boundaries. These water levels are well in accordance with the in situ water levels, which can prove that the bathymetry results from ICESat-2 are reliable.
5.2. Importance of Water Level/Volume at Annual Scale
The water level and volume of lakes can change by different drivers at different temporal scales. In many applications, scholars focused on the contribution of various drivers (i.e., natural forces and human activities) on water level/volume changes of lakes over a long-term. For these drivers, such as the precipitation, temperature, vegetation, GDP, and population, some of them were not organized at a diurnal scale, but at other temporal scales, such as monthly, seasonal, and annual scales. The quantitative attribution analysis should be conducted at the same time scale. The annual scale is sufficient to investigate drivers that control the water level/volume changes over a long-term (e.g., over 30 years in this study). Moreover, annual water level/volume changes may omit some intra-annual changes, such as seasonal fluctuations and abrupt changes induced by extreme rainfalls.
5.3. Difference from Classical Studies Using Satellite Lidars
There is a significant difference between classical ICESat/ICESat-2-based studies and this study. In these previous studies on ICESat/ICESat-2-based water level estimations, water levels of lakes and reservoirs across different areas were directly extracted from ICESat or/and ICESat-2 product (after data filtering) and achieved very high accuracies [15,45,46,47,48,49,50]. Unlike the above studies, the water level was estimated in an indirect way in this study. Specifically, ICESat-2 data were first used to extract accurate along-track topography profiles around the shore of lake, and then the annual lake boundary derived from Landsat data was matched with the ICESat-2-derived topography profiles, to obtain the annual water level in that year.
Compared to ICESat lidar with a larger footprint, ICESat-2 lidar has a very small footprint and a green laser source, and thus exhibits a high potential to accurately characterize the ground/underwater topography. Additionally, ICESat-2 can provide six along-track topography profiles from three strong and three weak beams, which can cover many small lakes where only a few laser footprints were available for ICESat. In this study, after data processing and error correction, only three strong laser beams with higher signal-to-noise ratios were used. The results indicate that four days’ ICESat-2 observations were sufficient to obtain an acceptable water level/volume result over a long-term. Therefore, for other lakes, the temporal resolution of ICESat-2 is not the key point, but whether the laser ground tracks pass over is. Fortunately, the spatial coverage of ICESat-2 is several times larger than that of ICESat benefitting from the multiple laser beams. This study provides a new way to conduct the long-term water level/volume observations (over 30 years), especially for small lakes, while direct ICESat/ICESat-2 water level observations can only cover a very limited period.
In addition, benefitting from the bathymetric capacity and much denser ground/bottom points, the simulated ICESat-2 data (based on the airborne MABEL data) [51,52] or measured ICESat-2 data [40,53,54,55] were used to obtain the along-track underwater bottom points and further generate the bathymetric maps with satellite images, e.g., the Landsat, Sentinel-2, and GSWD (Global Surface Water Dataset) products [4]. Although these used datasets and some steps of the method (e.g., detecting the signal photons) are similar to this study, the specific applications and other steps (e.g., the data fusion) are quite different.
5.4. Comparison with the Hydroweb Database
To further perform a comparison between annual water levels/volumes derived from our method and the previous method via direct satellite altimeter observations, water level and volume results of Lake Mead derived from multiple satellite altimeters were downloaded from the Hydroweb (http://hydroweb.theia-land.fr/). Then, the water level and volume results from the Hydroweb were processed into annual water levels and volumes for comparing with our results. Figure 10a illustrates the annual water levels from in situ data, our results, and the Hydroweb database over 2000–2014 (i.e., the available period of water levels from the Hydroweb database). For the annual water levels, our results (R2 = 0.99, p = 0.00, RMSE = 0.92 m) exhibit a better consistency with in situ data compared to the results from the Hydroweb database (R2 = 0.99, p = 0.00, RMSE = 1.05 m). Figure 10b illustrates the annual water volumes from in situ data, our results, and the Hydroweb database over 2003–2014 (i.e., the available period of water volumes from the Hydroweb database). For the annual water volumes, our results (R2 = 0.99, p = 0.00, RMSE = 0.26 km3) also exhibit a better consistency with in situ data compared to that from the Hydroweb database (R2 = 0.99, p = 0.00, RMSE = 0.30 km3). Note that the estimated annual water levels and volumes of lakes can be used to quantify the contribution of natural forces and human activities (e.g., precipitation, temperature, vegetation, GDP, and population) to long-term temporal changes of water levels and volumes. Moreover, the main objective of this study is to monitor the water level/volume changes over a long-term (i.e., dated back to the 1980s in the Landsat imagery), which is no longer limited by the time span of satellite altimeters (i.e., such as the Hydroweb database, which was only available after 2000).
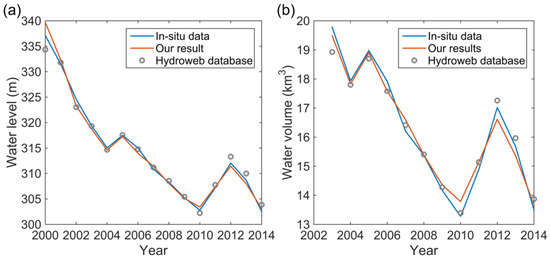
Figure 10.
Comparisons between in situ data, our results, and the Hydroweb database of water levels (a) and water volumes (b) at an annual scale for Lake Mead.
5.5. Further Considerations
Compared to the previous study using the airborne MABEL photon-counting lidars and Landsat imagery [14], benefiting from the longer time span, global spatial coverage, and good bathymetric capacity of ICESat-2 datasets, we have conducted a monitoring of lake water levels and volumes with a similar accuracy and a longer time span. In addition, the spaceborne ICESat-2 lidar captured signal photons reflected from underwater bottoms up to approximately 10 m in Lake Mead, and this depth is dependent on the water clarity [24,56]. It means that the ICESat-2 lidar (at 532 nm) is able to detect signal photons of underwater bottoms and obtain bathymetric information in shallow waters, which cannot be achievable by the classical satellite laser (at 1064 nm) and radar altimeters. Specifically, these bathymetric data can be used to predict that if the water level further decreases within 10 m in Lake Mead, how much water volume will be lost. Using the ICESat-2 datasets with a global coverage and our method, to accurately monitor changes of annual water levels and volumes of lakes and reservoirs is potentially achievable over a long-term period. It should be noted that there are two limitations of this method. First, ICESat-2 bathymetric photons are not available when the water clarity is low. Second, if lakes did not experience significant water level changes over a long-term period (e.g., less than 1 m), the precise linear regression between lake water levels and water surfaces cannot be established.
6. Conclusions
In this study, a method was used to accurately monitor the annual scale and long-term changes of lake water levels and volumes, with only satellite remotely sensed data (i.e., Landsat imagery and ICESat-2 data), and Lake Mead in the USA was selected to conduct a case study to demonstrate the performance of this method. The yearly lake boundaries during 1984–2018 were first extracted with a dynamic thresholding method derived from the yearly Landsat-based median MNDWI composites. Then, ground/underwater bottom surface profiles were detected from the ICESat-2 data using a surface detecting algorithm. Next, the NLCD 2016 land-cover map was used to select available ICESat-2 derived surface profiles without shrubs/scrubs. Yearly water levels during 2007–2018 with lower percentages of shrubs/scrubs were generated for matching the detected surface profiles with corresponding lake boundaries in each year. A linear relationship between water levels and lake areas was established to estimate yearly water levels between 1984 and 2018. Finally, yearly water volumes were calculated using the lake areas and water levels during different years. With ICESat-2 data during 2018–2019 and Landsat TM/ETM+ images during 1984–2018, yearly water levels and volumes of Lake Mead can be estimated. During the study period from 1984 to 2018, the lake water volume results agree well with the in situ data, i.e., the R2 and RMSE of the water volumes were 1.00 and 0.36 km3, respectively, and the change rates of the water volumes calculated by our results and the in situ measurements are −0.57 km3/year and −0.58 km3/year, respectively.
With new ICESat-2 photon-counting lidar/altimetry datasets and classical Landsat imagery, lake water levels and volumes can be derived from only several measurements of the satellite altimetry data. Before this study, with only satellite remotely sensed data, it is difficult to accurately monitor annual scale and long-term changes of lake water levels/volumes for over 35 years and dated back to 1980s, mainly limited by the time span of available satellite altimetry data. For the ICESat-2 photon-counting lidar, we found that it exhibits a great potential to accurately characterize the Earth’s surface topography and has captured signal photons reflected from underwater bottoms up to approximately 10 m in Lake Mead. The depth would be larger if the water clarity is better. In the future, using our method, the ICESat-2 datasets, and other historical satellite data (e.g., Landsat imagery and Sentinel-2 imagery) with a global spatial coverage, it can monitor long-term changes of lake water levels and volumes for many lakes and reservoirs with good water qualities. Moreover, based on satellite derived water level/volume results over a long period, further works can be performed to elevate the scientific investigation, such as modelling spatial-temporal characteristics of water level changes, investigating reasons of water fluctuations, and analyzing regional water table changes.
Author Contributions
Conceptualization, N.X. and Y.M.; methodology, N.X., W.Z., and Y.M.; software, N.X. and W.Z.; validation, N.X., D.S., and Y.M.; writing—original draft preparation, N.X.; writing—review and editing, Y.M., W.Z., X.H.W., F.Y., and D.S.; supervision, Y.M., X.H.W., and F.Y.; project administration, Y.M. and X.H.W.; funding acquisition, Y.M. and F.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Nanjing Normal University Startup Research Foundation [Grant number 184080H202B254]; the National Natural Science Foundation of China [Grant number 41801261]; the National Science and Technology Major Project [Grant numbers 11-Y20A12-9001-17/18, 42-Y20A11-9001-17/18]; the National Key Research and Development Program of China [Grant numbers 2017YFC1404104, 2017YFC1404100]; the China Postdoctoral Science Foundation [Grant number 2020T130481]; and the Fundamental Research Funds for the Central Universities [Grant number 2042020kf1050].
Acknowledgments
We thank the Goddard Space Flight Center for distributing the ICESat-2 data, the Google Earth Engine platform for distributing the Landsat data, the “lakemead.water-data.com” for distributing the in situ measurement data, and the Hydroweb database for distributing the water levels and volumes derived from multiple satellite sensors. We thank reviewers’ helpful comments and suggested text revisions that have improved this paper significantly. This is publication No. 81 of the Sino Australian Research Consortium for Coastal Management (previously the Sino-Australian Research Centre for Coastal Management).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Khan, S.I.; Hong, Y.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite remote sensing and hydrologic modeling for flood inundation mapping in Lake Victoria basin: Implications for hydrologic prediction in ungauged basins. IEEE Trans. Geosci. Remote Sens. 2010, 49, 85–95. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48, W09504. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Shang, X.; Zhao, J.; Zhang, H. Obtaining high-resolution seabed topography and surface details by co-registration of side-scan sonar and multibeam echo sounder images. Remote Sens. 2019, 11, 1496. [Google Scholar] [CrossRef]
- Yang, F.; Bu, X.; Ma, Y.; Lu, X.; Wang, M.; Shi, B. Geometric calibration of multibeam bathymetric data using an improved sound velocity model and laser tie points for BoMMS. Ocean Eng. 2017, 145, 230–236. [Google Scholar] [CrossRef]
- Yang, F.; Su, D.; Ma, Y.; Feng, C.; Yang, A.; Wang, M. Refraction correction of airborne LiDAR bathymetry based on sea surface profile and ray tracing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6141–6149. [Google Scholar] [CrossRef]
- Peng, D.; Guo, S.; Liu, P.; Liu, T. Reservoir storage curve estimation based on remote sensing data. J. Hydrol. Eng. 2006, 11, 165–172. [Google Scholar] [CrossRef]
- Wang, X.W.; Gong, P.; Zhao, Y.; Xu, Y.; Cheng, X.; Niu, Z.; Luo, Z.; Huang, H.; Sun, F.; Li, X. Water-level changes in China’s large lakes determined from ICESat/GLAS data. Remote Sens. Environ. 2013, 132, 131–144. [Google Scholar] [CrossRef]
- Cai, X.; Feng, L.; Hou, X.; Chen, X. Remote sensing of the water storage dynamics of large lakes and reservoirs in the Yangtze River basin from 2000 to 2014. Sci. Rep. 2016, 6, 36405. [Google Scholar] [CrossRef]
- Tapia-Silva, F.O.; López-Caloca, A.A. Calculating long-term changes in Lake Chapala’s area and water volume using remote sensing and field data. J. Appl. Remote Sens. 2018, 12, 042805. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Sun, J.; Wang, X.H.; Yang, F.; Li, S. Estimating water levels and volumes of lakes dated back to the 1980s using Landsat imagery and photon-counting lidar datasets. Remote Sens. Environ. 2019, 232, 111287. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lv, A. monitoring the fluctuation of Lake Qinghai using multi-source remote sensing data. Remote Sens. 2014, 6, 10457–10482. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s lake level and volume changes from NASA’s ICESat/ICESat-2 and Landsat missions. Geophys. Res. Lett. 2019, 46, 13107–13118. [Google Scholar] [CrossRef]
- Brenner, A.C.; DiMarzio, J.R.; Zwally, H.J. Precision and accuracy of satellite radar and laser altimeter data over the continental ice sheets. IEEE Trans. Geosci. Remote Sens. 2007, 45, 321–331. [Google Scholar] [CrossRef]
- McGill, M.; Markus, T.; Scott, V.S.; Neumann, T. The multiple altimeter beam experimental Lidar (MABEL): An airborne simulator for the ICESat-2 mission. J. Atmos. Ocean. Tech. 2013, 30, 345–352. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The ice, cloud, and land elevation satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Kaufmann, G.; Amelung, F. Reservoir induced deformation and continental rheology in vicinity of Lake Mead, Nevada. J. Geophys. Res. Solid Earth 2000, 105, 16341–16358. [Google Scholar] [CrossRef]
- Benotti, M.J.; Stanford, B.D.; Snyder, S.A. Impact of drought on wastewater contaminants in an urban water supply. J. Environ. Qual. 2010, 39, 1196–1200. [Google Scholar] [CrossRef] [PubMed]
- Barnett, T.P.; Pierce, D.W. When will Lake Mead go dry? Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinsk, M. Validation of ICESat-2 ATLAS bathymetry and analysis of ATLAS’s bathymetric mapping performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A. Ice, Cloud, and Land Elevation Satellite—2 (ICESat-2) Project, Algorithm Theoretical Basis Document (ATBD) for Global Geolocated Photons ATL03; Goddard Space Flight Center: Greenbelt, MD, USA, 2019.
- Neuenschwander, A.L.; Magruder, L.A. Canopy and terrain height retrievals with ICESat-2: A first look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Zhang, J.; Kerekes, J. An adaptive density-based model for extracting surface returns from photon-counting laser altimeter data. IEEE Geosci. Remote Sens. Lett. 2014, 12, 726–730. [Google Scholar] [CrossRef]
- Wickham, J.; Homer, C.; Vogelmann, J.; McKerrow, A.; Mueller, R.; Herold, N.; Coulston, J. The multi-resolution land characteristics (MRLC) consortium—20 years of development and integration of USA national land cover data. Remote Sens. 2014, 6, 7424–7441. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Sagar, S.; Roberts, D.; Bala, B.; Lymburner, L. Extracting the intertidal extent and topography of the Australian coastline from a 28-year time series of Landsat observations. Remote Sens. Environ. 2017, 195, 153–169. [Google Scholar] [CrossRef]
- Almonacid-Caballer, J.; Sánchez-García, E.; Pardo-Pascual, J.E.; Balaguer-Beser, A.A.; Palomar-Vázqueza, J. Evaluation of annual mean shoreline position deduced from Landsat imagery as a mid-term coastal evolution indicator. Mar. Geol. 2016, 372, 79–88. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Zhang, B.; Shen, Q.; Ye, H.; Wang, S.; Lu, Z. A simple automated dynamic threshold extraction method for the classification of large water bodies from landsat-8 OLI water index images. Int. J. Remote Sens. 2018, 39, 3429–3451. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F.; Hoffmann, J.; Markus, T. Testing the ice-water discrimination and freeboard retrieval algorithms for the ICESat-2 mission. Remote Sens. Environ. 2016, 183, 13–25. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Xi, X.; Luo, S.; Li, G.; Tian, J.; Wang, H. Estimating the vegetation canopy height using micro-pulse photon-counting LiDAR data. Opt. Express 2018, 26, A520–A540. [Google Scholar] [CrossRef] [PubMed]
- Popescu, S.C.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K.M. Photon counting LiDAR: An adaptive ground and canopy height retrieval algorithm for ICESat-2 data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.; Sun, J.; Li, G.; Wang, X.H.; Li, S.; Xu, N. Photon-counting lidar: An adaptive signal detection method for different land cover types in coastal areas. Remote Sens. 2019, 11, 471. [Google Scholar] [CrossRef]
- Degnan, J.J. Photon-counting multikilohertz microlaser altimeters for airborne and spaceborne topographic measurements. J. Geodyn. 2002, 34, 503–549. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Busker, T.; Roo, A.; Gelati, E.; Schwatke, C.; Adamovic, M.; Bisselink, B.; Pekel, J.F.; Cottam, A. A global lake and reservoir volume analysis using a surface water dataset and satellite altimetry. Hydrol. Earth Syst. Sci. 2019, 23, 669–690. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Abarca-del-Río, R.; Berge-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake volume monitoring from space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef]
- Nahin, P. An Imaginary Tale: The Story of the Square Root of Negative One; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Jasinski, M.; Stoll, J.; Hancock, D.; Robbins, J.; Nattala, J.; Pavelsky, T.; Morrison, J.; Arp, C.; Jones, B.; Ondrusek, M.; et al. Algorithm Theoretical Basis Document (ATBD) for Inland Water Data Products ATL13 Version 1; Goddard Space Flight Center: Greenbelt, MD, USA, 2019.
- Dandabathula, G.; Verma, M.; Satyanarayana, P.; Rao, S.S. Evaluation of ICESat-2 ATL08 data product: Performance assessment in inland water. Eur. J. Environ. Earth Sci. 2020, 1. [Google Scholar] [CrossRef]
- Ryan, J.C.; Smith, L.C.; Cooley, S.W.; Pitcher, L.H.; Pavelsky, T.M. Global characterization of inland water reservoirs using ICESat-2 altimetry and climate reanalysis. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Dandabathula, G.; Rao, S.S. Validation of ICESat-2 surface water level product ATL13 with near real time gauge data. Hydrology 2020, 8, 19. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Bai, Y. Performance assessment of ICESat-2 laser altimeter data for water-level measurement over lakes and reservoirs in China. Remote Sens. 2020, 12, 770. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Jasinski, M.; Zhang, S.; Stoll, J. Deriving high-resolution reservoir bathymetry from ICESat-2 prototype photon-counting lidar and landsat imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7883–7893. [Google Scholar] [CrossRef]
- Forfinski-Sarkozi, N.A.; Parrish, C.E. Active-passive spaceborne data fusion for mapping nearshore bathymetry. Photogramm. Eng. Remote Sens. 2019, 85, 281–295. [Google Scholar] [CrossRef]
- Albright, A.; Glennie, C. Nearshore bathymetry from fusion Sentinel-2 and ICESat-2 observations. IEEE Geosci. Remote Sens. Lett. 2020. [Google Scholar] [CrossRef]
- Armon, M.; Dente, E.; Shmilovitz, Y.; Mushkin, A.; Cohen, T.J.; Morin, E.; Enzel, Y. Determining bathymetry of shallow and ephemeral desert lakes using satellite imagery and altimetry. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhou, H.; Zhang, W.; Zhang, Z.; Wang, X.H. A method to derive bathymetry for dynamic water bodies using ICESat-2 and GSWD data sets. IEEE Geosci. Remote Sens. Lett. 2020. [Google Scholar] [CrossRef]
- Jasinski, M.F.; Stoll, J.D.; Cook, W.B.; Ondrusek, M.; Stengel, E.; Brunt, K. Inland and near-shore water profiles derived from the high-altitude multiple altimeter beam experimental lidar (MABEL). J. Coast. Res. 2016, 76, 44–55. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).