Stand Characterization of Eucalyptus spp. Plantations in Uruguay Using Airborne Lidar Scanner Technology
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Data
2.3. Airborne LiDAR Data Acquisition and Processing
2.4. Variable Selection and Statistical Analysis of the Parametric Methods
2.5. Variable Selection and k-NN Models
2.6. fModel Assessment and Validation
2.7. Segmentation Method
2.8. Unsupervised Evaluation of the Segmentation Method
3. Results
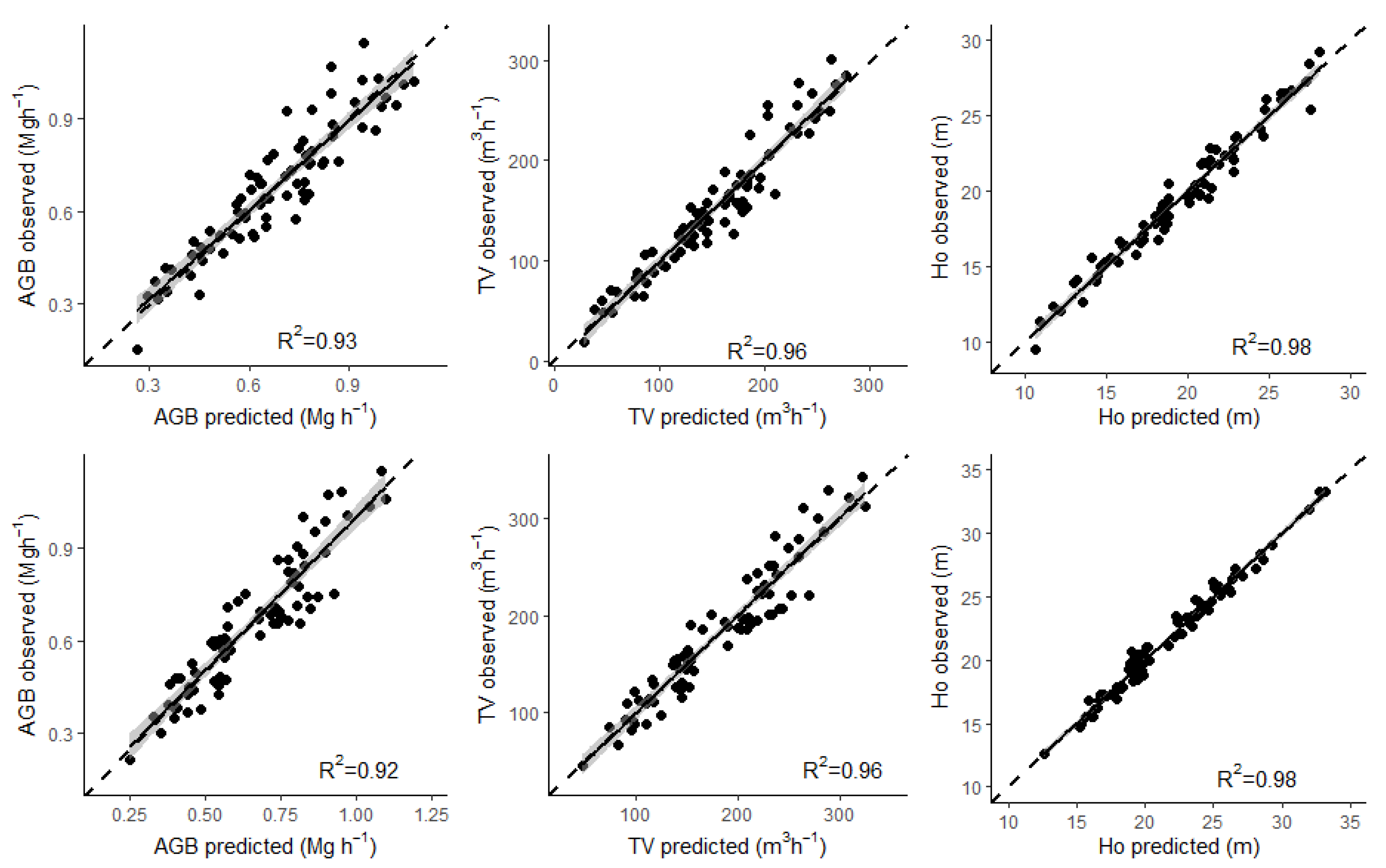
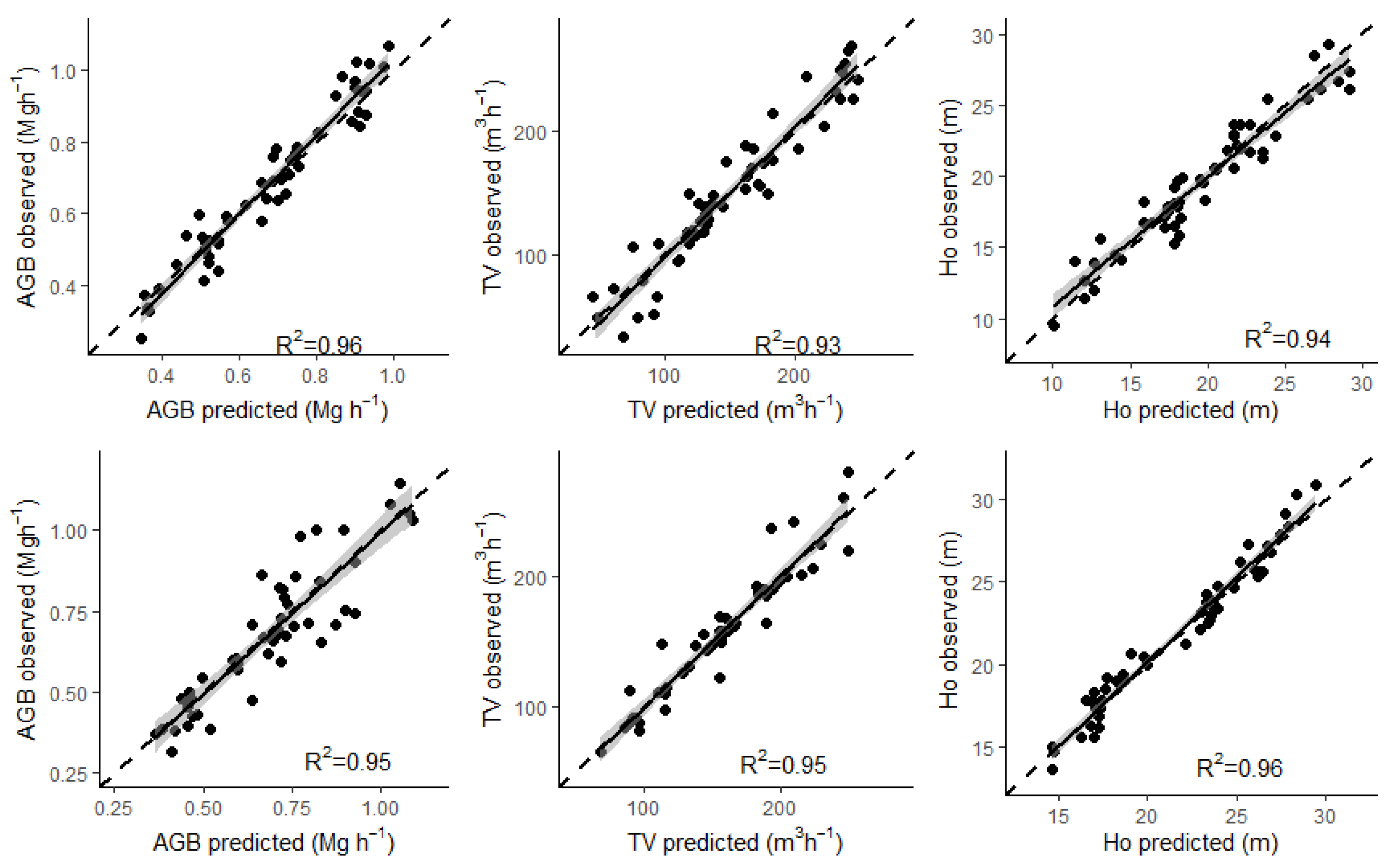
3.1. Parametric and Non-Parametric Models for Ho, TV and AGB
3.2. Imputation AGB, TV and Ho Models and Their Precision
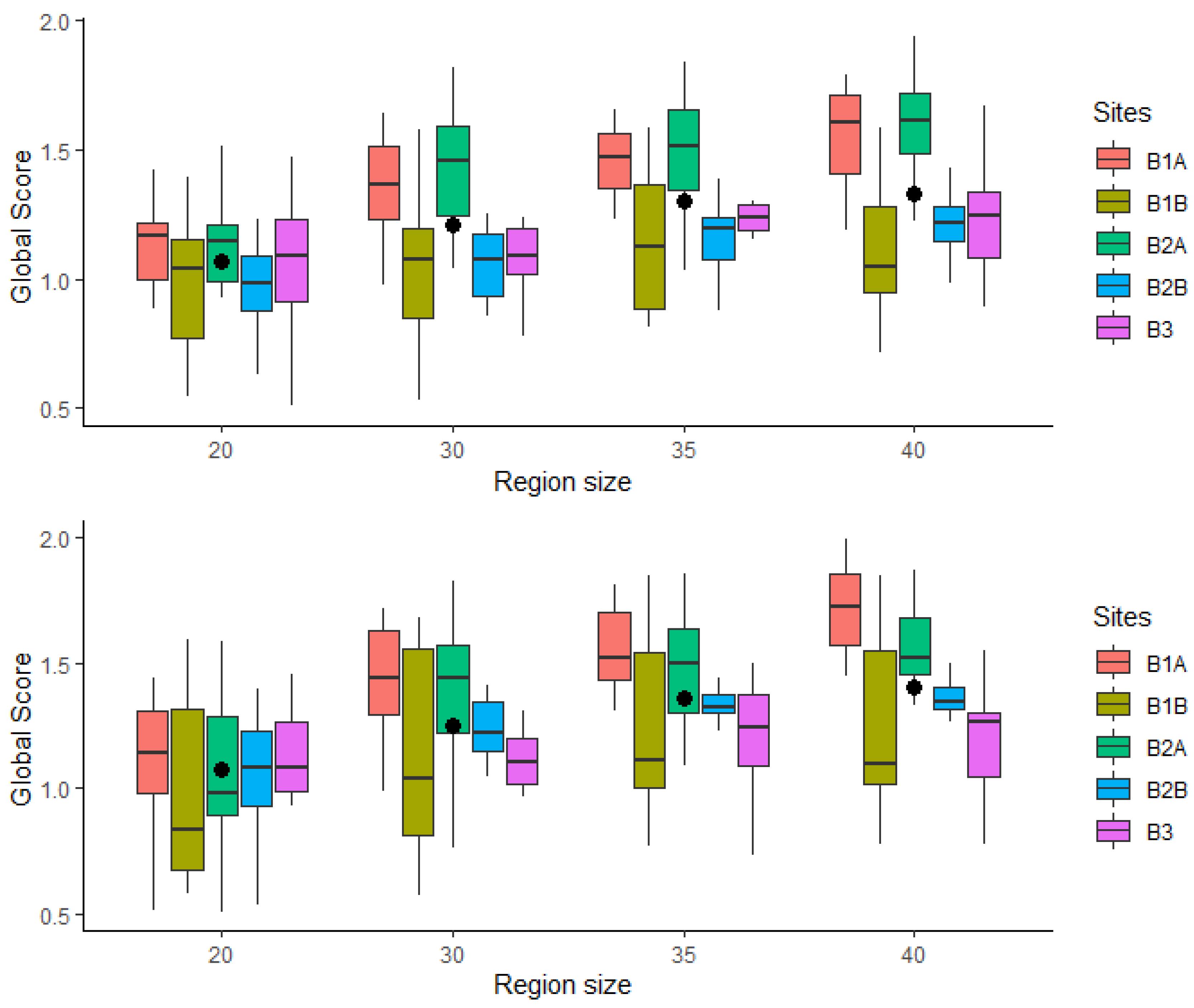
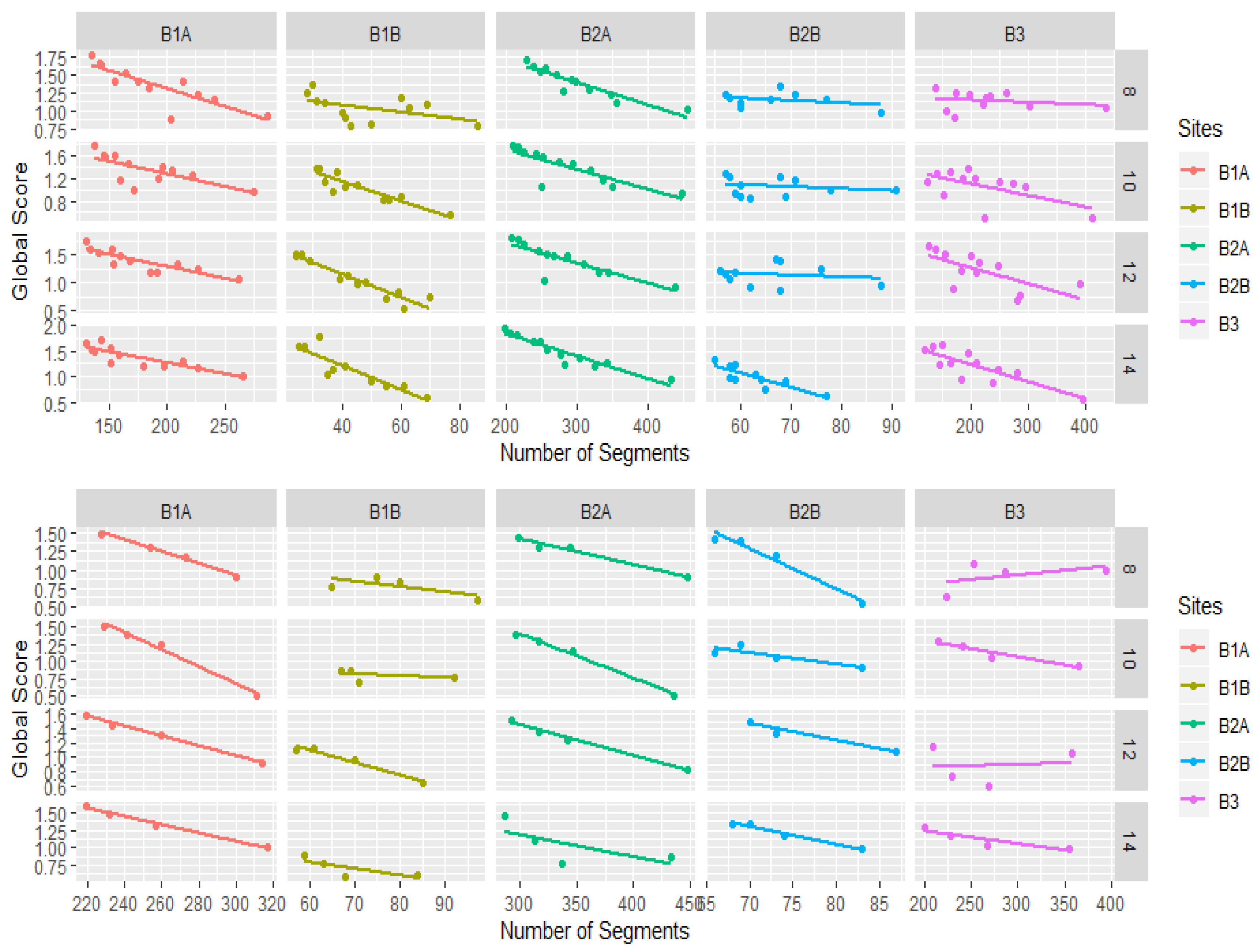
3.3. Segmentation
4. Discussion
4.1. Assmann Dominant Height, Total Volume, and Above Ground Biomass Modeling
4.2. Segmentations
4.3. Applications in Forest Management
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hawbaker, T.J.; Gobakken, T.; Lesak, A.; Trømborg, E.; Contrucci, K.; Radeloff, V. Light detection and ranging-based measures of mixed hardwood forest structure. For. Sci. 2010, 56, 313–326. [Google Scholar]
- Hościło, A.; Lewandowska, A. Mapping Forest Type and Tree Species on a Regional Scale Using Multi-Temporal Sentinel-2 Data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef]
- Naesset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Arellano-Pérez, S.; Castedo-Dorado, F.; Hevia, A.; Vega, J.A.; Vega-Nieva, D.; Álvarez-González, J.G.; Ruiz-González, A.D. Modelling the vertical distribution of canopy fuel load using national forest inventory and low-density airbone laser scanning data. PLoS ONE 2017, 12, e0176114. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; Mulverhill, C.; Liu, H.; Pang, Y.; Li, Z. Prediction of Diameter Distributions with Multimodal Models Using LiDAR Data in Subtropical Planted Forests. Forests 2019, 10, 125. [Google Scholar] [CrossRef]
- Nelson, R. How did we get here? An early history of forestry lidar1. Can. J. Remote Sens. 2013, 39, S6–S17. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.-P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Næsset, E.; McRoberts, R.E.; Ståhl, G.; Andersen, H.-E.; Gobakken, T.; Ene, L.; Nelson, R. Statistical rigor in LiDAR-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2016, 173, 98–108. [Google Scholar] [CrossRef]
- Garcia-Gutierrez, J.; Gonzalez-Ferreiro, E.; Riquelme-Santos, J.C.; Miranda, D.; Dieguez-Aranda, U.; Navarro-Cerrillo, R.M. Evolutionary feature selection to estimate forest stand variables using LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 119–131. [Google Scholar] [CrossRef]
- O’Hara, K.L.; Nagel, L.M. The stand: Revisiting a central concept in forestry. J. For. 2013, 111, 335–340. [Google Scholar] [CrossRef]
- Dechesne, C.; Mallet, C.; Le Bris, A.; Gouet, V.; Hervieu, A. Forest stand segmentation using airborne lidar data and very high resolution multispectral imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2016, 41, 207–214. [Google Scholar] [CrossRef]
- Haara, A.; Haarala, M. Tree species classification using semi-automatic delineation of trees on aerial images. Scand. J. For. Res. 2002, 17, 556–565. [Google Scholar] [CrossRef]
- Sanchez-Lopez, N.; Boschetti, L.; Hudak, A. Semi-Automated Delineation of Stands in an Even-Age Dominated Forest: A LiDAR-GEOBIA Two-Stage Evaluation Strategy. Remote Sens. 2018, 10, 1622. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Castaño, J.P.; Giménez, A.; Ceroni, M.; Furest, J.; Aunchayna, R.; Bidegain, M. Caracterización Agroclimática del Uruguay 1980–2009; Serie Técnica INIA 193; Instituto de Investigaciones Agropecuarias: Montevideo, Uruguay, 2011. [Google Scholar]
- Andrés, H.; Rafael, N.; Jorge, F.; Maurizio, B.; Cecilia, R. Modelling Taper, Total and Merchantable Stem Volume Considering Stand Density Effects to Eucalyptus Grandis and Eucalyptus Dunnii in Uruguay. iForest 2020, in press. [Google Scholar]
- McGaughey, R.J. FUSION/LDV: Software for LiDAR Data Analysis and Visualization. February 2013–FUSION Version 3.30; USDA Forest Service, Pacific Northwest Research Station, University of Washington: Seattle, WA, USA, 2013. [Google Scholar]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Liesenberg, V.; Bernett, L.G.; Scheraiber, C.F.; Schoeninger, E.R. Estimating Stand Height and Tree Density in Pinus taeda plantations using in-situ data, airborne LiDAR and k-Nearest Neighbor Imputation. An. Acad. Bras. Ciênc. 2018, 90, 295–309. [Google Scholar] [CrossRef]
- Lumley, T. Using Fortran Code by Alan Miller. Leaps: Regression Subset Selection, R Package Version 2.9; Available online: http://CRAN.R-project.org/package=leaps2009 (accessed on 1 August 2020).
- R Development Core Team. R Core Development Team A Language and Environment for Statistical Computing: Reference Index Version 3.5.1; R Development Core Team: Vienna, Austria, 2013. [Google Scholar]
- Mallows, C.L. Some comments on Cp. Technometrics 2000, 42, 87–94. [Google Scholar]
- Zhao, F.; Guo, Q.; Kelly, M. Allometric equation choice impacts lidar-based forest biomass estimates: A case study from the Sierra National Forest, CA. Agric. For. Meteorol. 2012, 165, 64–72. [Google Scholar] [CrossRef]
- Elzhov, T.V.; Mullen, K.M.; Spiess, A.-N.; Bolker, B.; Mullen, M.K.M.; Suggests, M. Package ‘minpack.lm.’ Title R Interface Levenberg-Marquardt Nonlinear Least-Sq. Algorithm Found MINPACK Plus Support Bounds’. 2016. Available online: https://cran.rproject.org/web/packages/minpack.lm/minpack.lm.pdf (accessed on 20 November 2020).
- Quinn, G.P.; Keough, M.J. Experimental Design and Data Analysis for Biologists; Cambridge University Press: Cambridge, UK, 2002; ISBN 1139432893. [Google Scholar]
- Crookston, N.L.; Finley, A.O. YaImpute: An R Package for kNN Imputation. J. Stat. Softw. 2008, 23, 1–16. [Google Scholar] [CrossRef]
- Zald, H.S.J.; Wulder, M.A.; White, J.C.; Hilker, T.; Hermosilla, T.; Hobart, G.W.; Coops, N.C. Integrating Landsat pixel composites and change metrics with lidar plots to predictively map forest structure and aboveground biomass in Saskatchewan, Canada. Remote Sens. Environ. 2016, 176, 188–201. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking lidar and forest modeling to assess biomass estimation across scales and disturbance states. Remote Sens. Environ. 2017, 205, 199–209. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Int. Jt. Conf. Artif. Intell. 1995, 2, 1137–1143. [Google Scholar]
- Andersen, H.-E.; McGaughey, R.J.; Reutebuch, S.E. Estimating Forest Canopy Fuel Parameters Using LIDAR Data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Qgis, D.T. QGIS Geographic Information System, Open Source Geospatial Foundation. 2009. Available online: https://scholar.google.com/scholar_lookup?title=QGIS%20Geographic%20Information%20System&author=QGIS%20Development%20Team&publication_year=2009#d=gs_cit&u=%2Fscholar%3Fq%3Dinfo%3AK9pErfIkywoJ%3Ascholar.google.com%2F%26output%3Dcite%26scirp%3D0%26hl%3Des (accessed on 20 November 2020).
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Wu, Z.; Heikkinen, V.; Hauta-Kasari, M.; Parkkinen, J.; Tokola, T. Forest Stand Delineation Using a Hybrid Segmentation Approach Based on Airborne Laser Scanning Data; Springer: Berlin/Heidelberg, Germany, 2013; pp. 95–106. [Google Scholar]
- Varo-martínez, M.Á.; Navarro-cerrillo, R.M.; Hernández-clemente, R. Semi-automated stand delineation in Mediterranean Pinus sylvestris plantations through segmentation of LiDAR data: The influence of pulse density. Int. J. Appl. Earth Obs. Geoinf. 2017, 56, 54–64. [Google Scholar] [CrossRef]
- Grybas, H.; Melendy, L.; Congalton, R.G. A comparison of unsupervised segmentation parameter optimization approaches using moderate-and high-resolution imagery. GIScience Remote Sens. 2017, 54, 515–533. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Xiao, P.; He, G.; Zhu, L. Segmentation quality evaluation using region-based precision and recall measures for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2015, 102, 73–84. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, P.; Feng, X. An unsupervised evaluation method for remotely sensed imagery segmentation. IEEE Geosci. Remote Sens. Lett. 2011, 9, 156–160. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Mora, B.; Wulder, M.A.; White, J.C.; Hobart, G. Modeling stand height, volume, and biomass from very high spatial resolution satellite imagery and samples of airborne LIDAR. Remote Sens. 2013, 5, 2308–2326. [Google Scholar] [CrossRef]
- Böck, S.; Immitzer, M.; Atzberger, C. On the Objectivity of the Objective Function—Problems with Unsupervised Segmentation Evaluation Based on Global Score and a Possible Remedy. Remote Sens. 2017, 9, 769. [Google Scholar] [CrossRef]
- Yang, L.; Mansaray, L.R.; Huang, J.; Wang, L. Optimal segmentation scale parameter, feature subset and classification algorithm for geographic object-based crop recognition using multisource satellite imagery. Remote Sens. 2019, 11, 514. [Google Scholar] [CrossRef]
- Shao, G.; Shao, G.; Gallion, J.; Saunders, M.R.; Frankenberger, J.R.; Fei, S. Improving Lidar-based aboveground biomass estimation of temperate hardwood forests with varying site productivity. Remote Sens. Environ. 2018, 204, 872–882. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Bolton, D.K.; Tompalski, P.; Bater, C.W. Three decades of forest structural dynamics over Canada’s forested ecosystems using Landsat time-series and lidar plots. Remote Sens. Environ. 2018, 216, 697–714. [Google Scholar] [CrossRef]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Lo, C.S.; Lin, C. Growth-competition-based stem diameter and volume modeling for tree-level forest inventory using airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2216–2226. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Görgens, E.B.; García-Gutiérrez, J.; Rodriguez, L.C.E.; Tomé, M.; González-Ferreiro, E. Comparison of ALS based models for estimating aboveground biomass in three types of Mediterranean forest. Eur. J. Remote Sens. 2016, 49, 185–204. [Google Scholar] [CrossRef]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass. Remote Sens. 2019, 11, 338. [Google Scholar] [CrossRef]

| Field Attributes | Min | Mean | Max | Stdev | |
|---|---|---|---|---|---|
| E. grandis (n = 76) | Dbh (cm) | 10.65 | 15.49 | 19.33 | 1.81 |
| TH (m) | 12.57 | 21.69 | 33.30 | 4.46 | |
| G (m2 ha−1) | 8.97 | 20.28 | 29.79 | 4.52 | |
| AGB (Mg ha−1) | 215.2 | 653.3 | 1175 | 213.2 | |
| TV (m3 ha−1) | 45.01 | 185.37 | 342.12 | 67.71 | |
| Age | 4.5 | 6.8 | 9.5 | 1.5 | |
| N (tree ha−1) | 634 | 1041 | 1336 | 144 | |
| E. dunnii (n = 75) | Dbh (cm) | 10.83 | 15.27 | 19.38 | 1.53 |
| TH (m) | 9.52 | 19.55 | 29.22 | 4.23 | |
| G (m2 ha−1) | 0.76 | 20.51 | 33.79 | 5.41 | |
| AGB (Mg ha−1) | 153.3 | 686.7 | 1296 | 218.2 | |
| TV (m3 ha-1) | 18.81 | 154.73 | 300.60 | 64.49 | |
| Age | 4.5 | 6.3 | 8.4 | 1.2 | |
| N (tree ha−1) | 669 | 1070 | 1432 | 159 |
| E. grandis | E. dunnii | |||
|---|---|---|---|---|
| Metrics | grmsd | Metrics | grmsd | |
| AGB | CRR | 0.461 | Elev.MO | 0.466 |
| Elev.MO | 0.479 | ARA2/TFR | 0.476 | |
| Elev.P75 | 0.562 | PFRAM | 0.511 | |
| Elev.P75 | 0.547 | |||
| TV | Elev.P75 | 0.556 | Elev.P75 | 0.394 |
| PFRAMO | 0.567 | Elev.MO | 0.401 | |
| ARA2 | 0.568 | ARA2/TFR | 0.410 | |
| Elev.MAX | 0.580 | |||
| Ho | Elev.MAX | 0.303 | ARAMO | 0.343 |
| CRR | 0.313 | Elev.P75 | 0.394 | |
| Elev.P75 | 0.349 | |||
| E. dunnii | E. grandis | ||||||
|---|---|---|---|---|---|---|---|
| RMSE | nRMSE | R2 | RMSE | nRMSE | R2 | ||
| Ho | Fit | 1.38 | 7.12 | 0.94 | 1.16 | 5.31 | 0.97 |
| Cross Validation | 2.00 | 10.22 | 0.90 | 1.08 | 4.98 | 0.97 | |
| TV | Fit | 18.43 | 16.28 | 0.93 | 20.04 | 15.06 | 0.93 |
| Cross Validation | 20.75 | 18.15 | 0.89 | 24.77 | 17.44 | 0.84 | |
| AGB | Fit | 71.2 | 10.37 | 0.96 | 70.2 | 11.89 | 0.95 |
| Cross Validation | 112.2 | 17.08 | 0.87 | 110 | 17.09 | 0.85 |
| Sites | Spatial Radius | Range Radius | Min Size of Region | AGB Band | TV Band | Ho Band | Two-Band Average | Number Segments | Average Area (ha) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| wVnorm | MInorm | GS | wVnorm | MInorm | GS | wVnorm | MInorm | GS | wVnorm | MInorm | GS | ||||||
| B1A | |||||||||||||||||
| 8 | 4 | 20 | 0.93 | 0.00 | 0.93 | 0.87 | 0.00 | 0.87 | 0.90 | 0.00 | 0.90 | 300 | 2.19 | ||||
| 8 | 4 | 20 | 0.95 | 0.00 | 0.95 | 0.90 | 0.00 | 0.90 | 0.93 | 0.00 | 0.93 | 287 | 2.28 | ||||
| B1B | |||||||||||||||||
| 14 | 4 | 30 | 0.62 | 0.30 | 0.91 | 0.00 | 0.24 | 0.24 | 0.31 | 0.27 | 0.57 | 68 | 3.02 | ||||
| 12 | 4 | 30 | 0.79 | 0.15 | 0.94 | 0.00 | 0.12 | 0.12 | 0.39 | 0.14 | 0.53 | 61 | 3.36 | ||||
| B2A | |||||||||||||||||
| 10 | 4 | 20 | 0.02 | 0.97 | 1.00 | 0.02 | 0.00 | 0.02 | 0.02 | 0.49 | 0.51 | 436 | 1.68 | ||||
| 10 | 4 | 20 | 0.04 | 0.93 | 0.97 | 0.03 | 0.85 | 0.88 | 0.03 | 0.89 | 0.92 | 449 | 1.63 | ||||
| B2B | |||||||||||||||||
| 8 | 4 | 20 | 0.00 | 0.95 | 0.95 | 0.02 | 0.09 | 0.12 | 0.01 | 0.52 | 0.53 | 83 | 1.68 | ||||
| 14 | 4 | 20 | 0.01 | 0.77 | 0.78 | 0.02 | 0.46 | 0.48 | 0.02 | 0.61 | 0.63 | 77 | 1.81 | ||||
| B3 | |||||||||||||||||
| 8 | 4 | 40 | 0.50 | 0.02 | 0.53 | 0.38 | 0.02 | 0.40 | 0.44 | 0.02 | 0.46 | 224 | 3.19 | ||||
| 10 | 4 | 40 | 0.44 | 0.07 | 0.51 | 0.48 | 0.01 | 0.49 | 0.46 | 0.04 | 0.50 | 225 | 3.18 | ||||
| Block | Total Block Area (ha) | Segment Number Manual | Average Segment Area (ha) | Segment Number AGB | Average Segment Area (ha) | Segment Number TV | Average Segment Area (ha) |
|---|---|---|---|---|---|---|---|
| B1A | 654.7 | 380 | 1.72 | 300 | 2.18 | 287 | 2.28 |
| B1B | 205.9 | 80 | 2.57 | 68 | 3.03 | 61 | 3.38 |
| B2A | 731.9 | 425 | 1.72 | 436 | 1.68 | 449 | 1.63 |
| B2B | 139.4 | 102 | 1.37 | 83 | 1.68 | 77 | 1.81 |
| B3 | 716.6 | 302 | 2.37 | 224 | 3.20 | 225 | 3.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirigoyen, A.; Varo-Martinez, M.A.; Rachid-Casnati, C.; Franco, J.; Navarro-Cerrillo, R.M. Stand Characterization of Eucalyptus spp. Plantations in Uruguay Using Airborne Lidar Scanner Technology. Remote Sens. 2020, 12, 3947. https://doi.org/10.3390/rs12233947
Hirigoyen A, Varo-Martinez MA, Rachid-Casnati C, Franco J, Navarro-Cerrillo RM. Stand Characterization of Eucalyptus spp. Plantations in Uruguay Using Airborne Lidar Scanner Technology. Remote Sensing. 2020; 12(23):3947. https://doi.org/10.3390/rs12233947
Chicago/Turabian StyleHirigoyen, Andrés, Mª Angeles Varo-Martinez, Cecilia Rachid-Casnati, Jorge Franco, and Rafael Mª Navarro-Cerrillo. 2020. "Stand Characterization of Eucalyptus spp. Plantations in Uruguay Using Airborne Lidar Scanner Technology" Remote Sensing 12, no. 23: 3947. https://doi.org/10.3390/rs12233947
APA StyleHirigoyen, A., Varo-Martinez, M. A., Rachid-Casnati, C., Franco, J., & Navarro-Cerrillo, R. M. (2020). Stand Characterization of Eucalyptus spp. Plantations in Uruguay Using Airborne Lidar Scanner Technology. Remote Sensing, 12(23), 3947. https://doi.org/10.3390/rs12233947







