Parametric Models to Characterize the Phenology of the Lowveld Savanna at Skukuza, South Africa
Abstract
1. Introduction
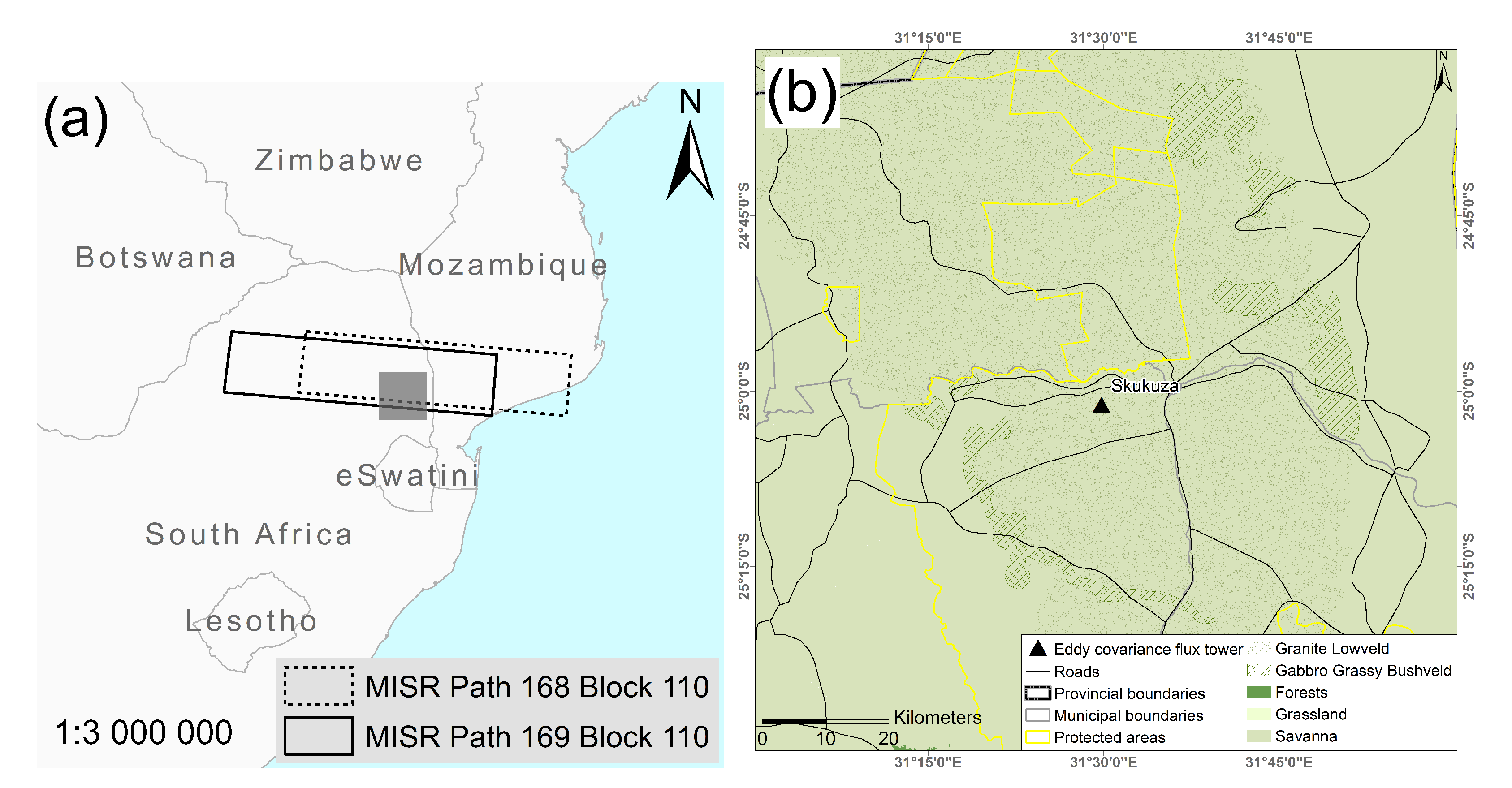
2. Study Area
3. Data Collections
3.1. Satellite Measurements
3.1.1. Background
- Major advances in understanding the processes of radiation transfer in complex environments resulted in the design and implementation of much improved algorithms. These aimed to effectively account for processes unrelated to vegetation (such as atmospheric clouds and aerosols, anisotropic effects, contributions to the measured signals due to variations in soil moisture, etc.) and to deliver reliable and accurate products to describe plant processes. The Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) is a case in point, since it has been identified as one of the Essential Climate Variables (ECV) by the Global Climate Observing System (GCOS) [20]. These developments, in turn, led to a more quantitative representation of plant phenology (in [21,22,23]).
- The technology of measuring reflected radiation on spaceborne platforms has improved drastically, and is currently able to deliver up to hundreds of spectral bands at spatial resolutions of the order of tens of meters or less, sometimes on a daily basis, or to acquire data from multiple directions or in multiple polarizations. Data fusion with observations obtained with different instruments (e.g., LiDARs: see [24,25,26]) or in entirely different spectral regions (e.g., microwaves: see [27,28,29]) have also been explored, though much remains to be done in order to provide a holistic description of the environment, or of plant phenology in particular.
- Progress in the field of information technology delivered computing, networking and data archiving resources and capabilities orders of magnitude faster and more performant than even a few decades ago, and permitted the investigation of complex issues. Although the drive to acquire more and better observations continues unabated, the major bottleneck today concerns the actual analysis of those data and the extraction of useful information from the immense archives that have already been accumulated.
3.1.2. Multi-Angular Observations
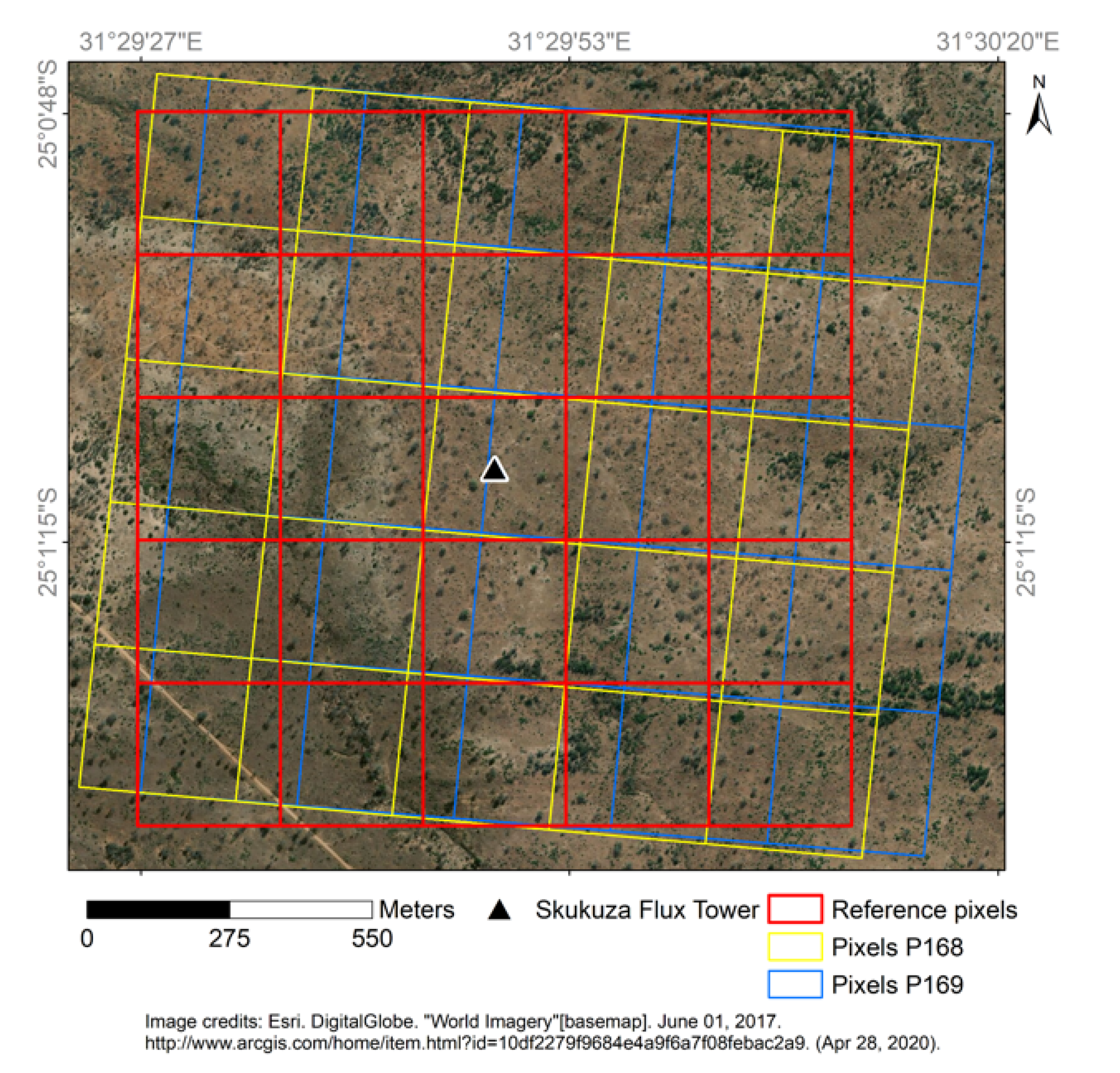
3.1.3. MISR-HR FAPAR Product for Skukuza
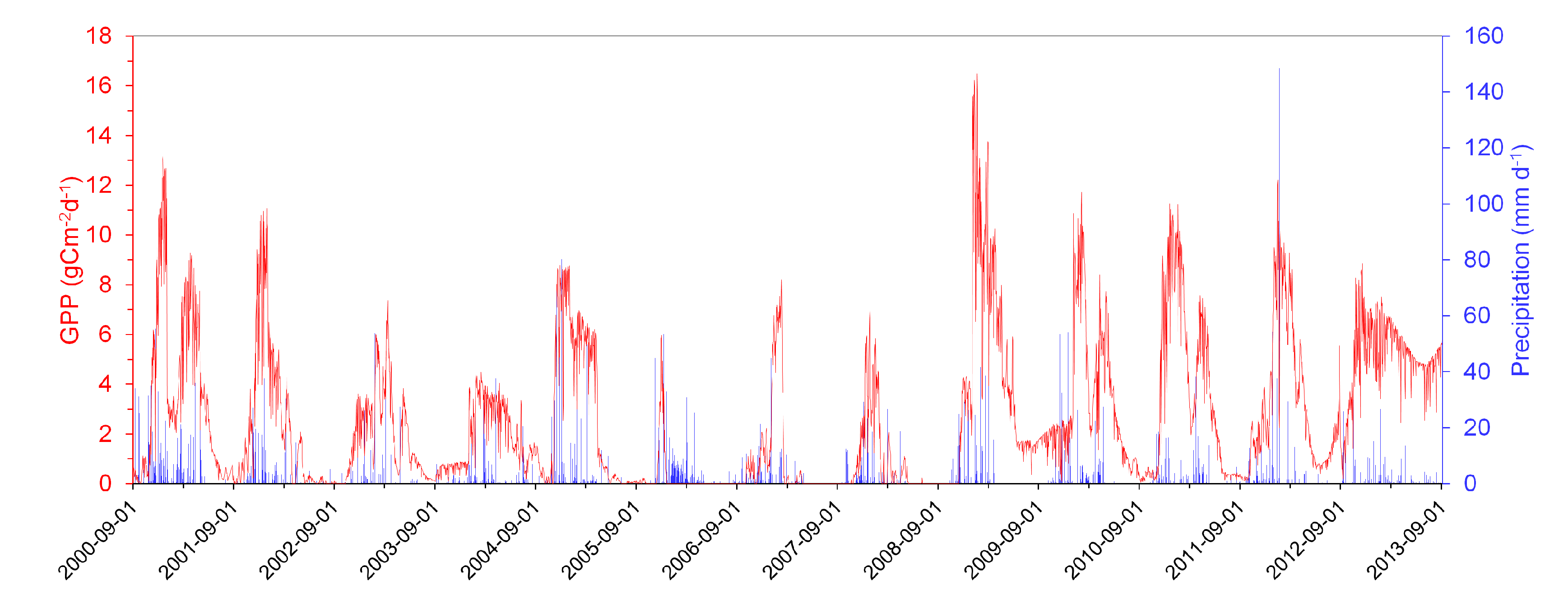
3.2. Flux Tower Observations
4. Data Processing
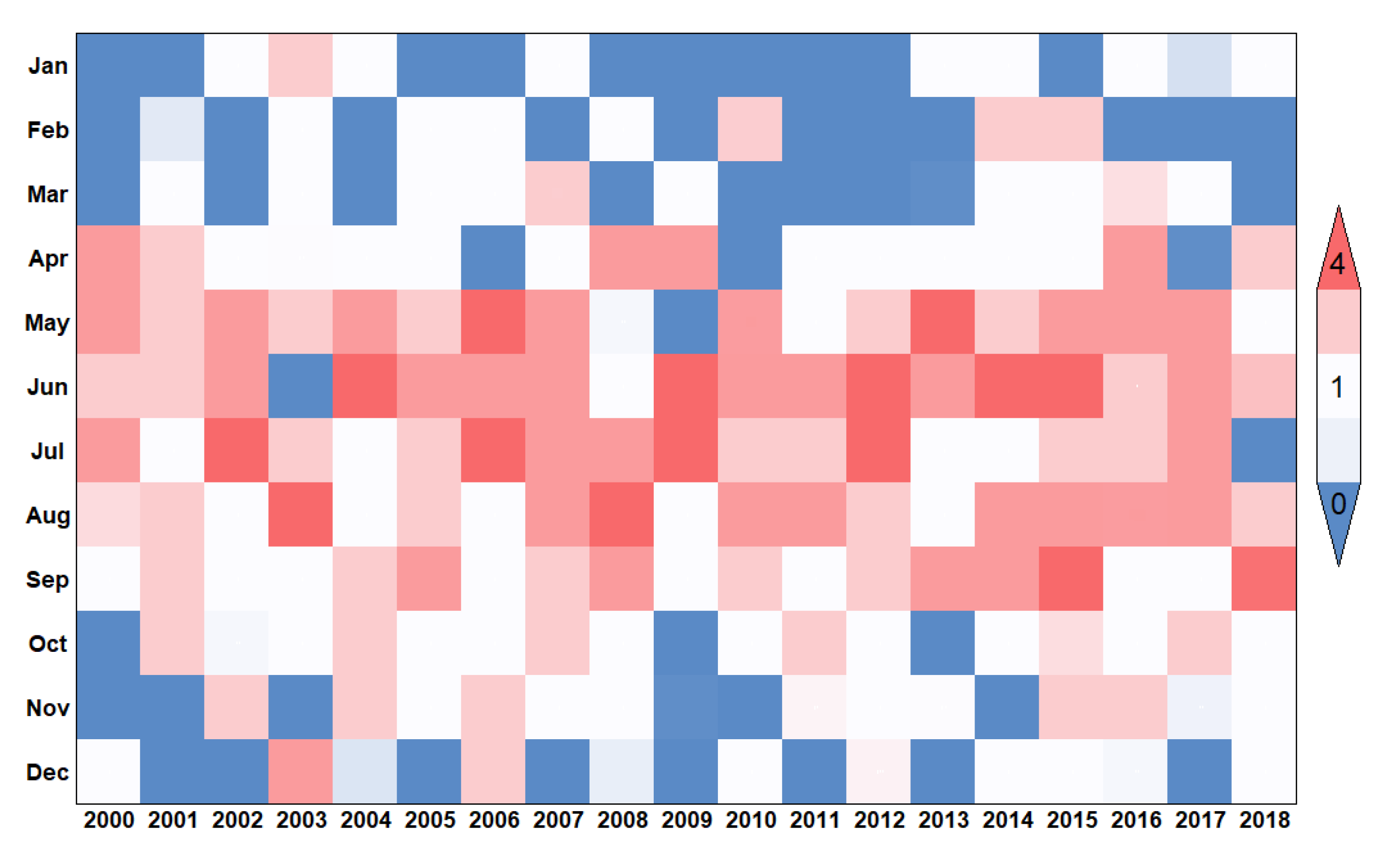
4.1. Measurement Uncertainties and Missing Data
4.2. Pre-Processing
4.2.1. Screening Outliers
4.2.2. Assembling the FAPAR Data Cube
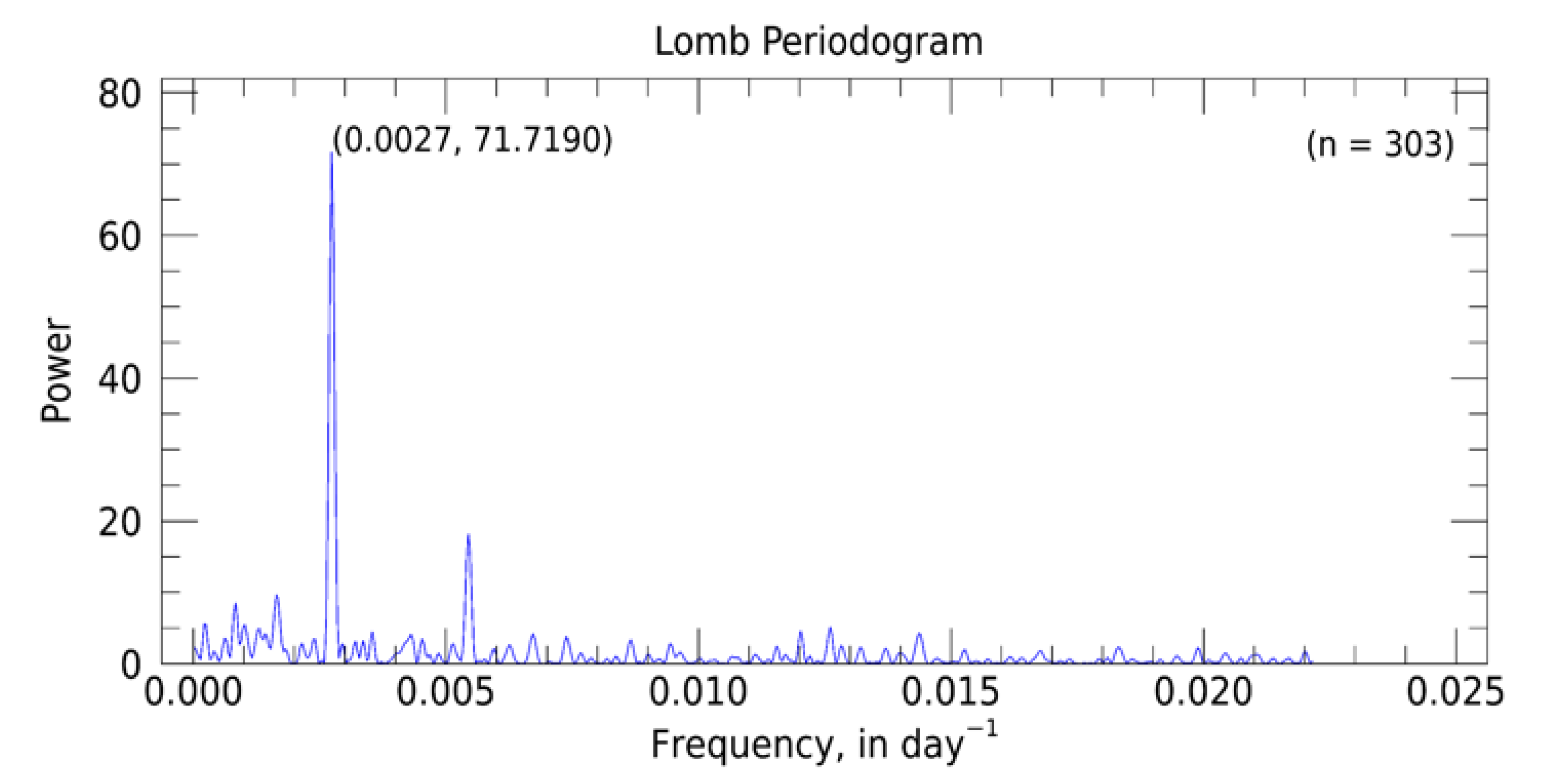
4.2.3. Identifying Individual Vegetative Seasons
- compute the median of the entire FAPAR record,
- search, from the start of the record, the date of the first observation whose value is lower than this threshold,
- define a time interval equal to 1/3 of the expected length of the vegetative period (as determined from the Lomb-Scargle algorithm), starting on this date, and
- set the start date of the first vegetative season to the date of acquisition of the minimum FAPAR value within this limited time period.
- add the expected average length of the vegetative season to the starting date just identified to estimate a nominal end date,
- define a new limited time window located around that nominal end date, extending 1/6 of the expected length of the vegetative season on either side of that nominal date, and
- set the end date of the vegetative season to the date of acquisition of the minimum FAPAR value within this limited time period.
4.3. Modeling Phenology
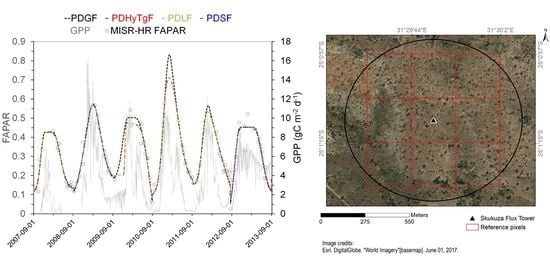
5. Results and Discussion
5.1. Simulation Capability
5.2. Ecological Effectiveness
5.2.1. Comparing Daily Values
5.2.2. Comparing Seasonally Integrated Values
5.2.3. Comparison Outcome
- The GPP estimates derived from the flux tower measurements exhibit a very high day-to-day variability, as a result of fluctuations in local conditions, including turbulence. While progressively larger values are expected during the vegetation growth phase than during senescence, there is no expectation that successive values generate a smooth sequence.
- By contrast, vegetation growth and senescence occurs as a generally slow, smooth process, with more branches and leaves occurring during the rainy season, and the plants wilting progressively during the dry season. Hence, it makes sense to fit a smooth model through the FAPAR data, while this would not be appropriate for the GPP data, at least on a daily time scale.
- Inspecting again Figure 11, it is seen that FAPAR and GPP both increase quickly and together at the start of the rainy seasons, but that the decrease in FAPAR tends to lag behind the decline in GPP: plants continue to appear photosynthetically active from space longer than the in situ measurements of CO2 indicate.
- GPP values measured at the Skukuza flux tower range from 0.0 to about 16 gC m−2 d−1, while FAPAR rarely drops below 0.1 or raises above 0.6 at this site: these variables experience quite different ranges of variability.
- As expected, the PDHyTgF (Hyperbolic Tangent) and the PDLF (Logistic) models generate essentially the same traces, since their parameters can be adjusted to generate the same values; however, they exhibit somewhat different levels of numerical efficiency, as will be seen shortly in Section 5.3.
5.3. Numerical Efficiency
5.3.1. Successful Inversions
5.3.2. Iterations
5.3.3. Computing Time
5.3.4. Simulation Effectiveness
5.4. Discussion
- Spatial analysis: Terrestrial ecosystems exhibit a high degree of spatial variability, due to the large number of plant species (especially in protected environments, such as the Kruger National Park), combined with a potentially similar variability in soil properties. These spatial fluctuations may be further enhanced by patchy precipitations, in particular in convective systems. However, spatial patterns may subsist over periods of weeks or more, because plants remain in place. Hence, if relevant spatial correlations can be established (e.g., by kriging), it may be possible to infer the likely value of FAPAR at one location where it is missing on the basis of its value at another location, provided both places share a common evolution.
- Temporal analysis: When excessively long gaps arise in the remote sensing data, it may be sufficient to interpolate the missing values on the basis of the last value available before and the first value after the gap. This approach tends to underestimate the actual variability of the variable (FAPAR in this case), as it will never generate higher (or lower) values than those effectively observed.
- Other sources: It may also be possible to ingest other data products. Indeed, FAPAR products are available from other instruments, such as NASA’s MODIS instrument (over the period of interest here). However, that approach carries its own set of complexities, as the algorithms used to generate these products (including to implement atmospheric corrections) are different so that the products may not match, or may introduce systematic biases or shifts.
- As far as the future is concerned, a particularly promising approach consists in operating constellations of identical instruments, in order to expand the number of opportunities to observe the surface despite the cloud coverage.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
Abbreviations
| ASAR | Advanced Synthetic Aperture Radar |
| ASDC | Atmospheric Science Data Center |
| ATSR | Along-Track Scanning Radiometer |
| CEOS | Committee on Earth Observation Satellites |
| CSIR | Council for Scientific and Industrial Research |
| EC | Eddy Covariance |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ECV | Essential Climate Variable |
| EOS | End Of (vegetative) Season |
| EO | Earth Observation |
| EPSG | European Petroleum Survey Group |
| ERA | ECMWF Re-Analysis |
| FAPAR | Fraction of Absorbed Photosynthetically Active Radiation |
| GCOS | Global Climate Observing System |
| IPCC | Intergovernmental Panel on Climate Change |
| JRC | Joint Research Centre |
| JRC-TIP | Joint Research Centre Two-stream Inversion Package |
| LAI | Leaf Area Index |
| LiDAR | Light Detection And Ranging |
| LOS | Length Of (vegetative) Season |
| MISR | Multi-angle Imaging SpectroRadiometer |
| MISR-HR | Multi-angle Imaging SpectroRadiometer High Resolution |
| NASA | National Aeronautics and Space Administration |
| NDVI | Normalized Difference Vegetation Index |
| PDGF | Parametric Double Gaussian Function |
| PDHyTgF | Parametric Double Hyperbolic Tangent Function |
| PDLF | Parametric Double Logistic Function |
| PDSF | Parametric Double Sine Function |
| POLDER | Polarization and Directionality of Earth’s Reflectances |
| RPV | Rahman, Pinty, Verstraete |
| SOM | Space Oblique Mercator |
| SOS | Start Of (vegetative) Season |
| SRES | Special Report on Emissions Scenarios |
Appendix A. The MISR Instrument and MISR-HR Products
Appendix A.1. The MISR Instrument
Appendix A.2. The MISR-HR Processing System
- The Ancillary Geographic Product (Earth Science Data Type or ESDT identifier: MIANCAGP) contains information on the latitude, longitude, and altitude distribution of each Block within the corresponding Path, as well as a scene classifier, for each 1100 m pixel, on the SOM map projection grid.
- The Geometric Parameters Product (ESDT identifier: MI1B2GEOP) contains information on the applicable illumination and observation geometry (zenith and azimuth angles), as well as the scatter (angular distance between the Sun and camera directions) and glitter (angular distance to specular reflection) angles for each of the 9 cameras.
- The L1B2 Terrain-projected Product (ESDT identifier: MI1B2T), in either Global or Local Mode, contains the calibrated Georectified Radiance Product (GRP) values measured by the MISR instrument, i.e., at the nominal ‘Top of the Atmosphere’ (ToA).
- The Level 2 Land Product (ESDT identifier: MIL2ASL) contains the standard MISR Level 2 Land products, at the nominal ‘Bottom of the Atmosphere’ (BoA), i.e., after taking into account the contribution of the atmosphere to the observed radiance.
- A sharpening algorithm is then applied to this updated L1B2 GRP product to generate the L1B3 product, i.e., the 36 bidirectional spectral reflectance data channels at the nominal Top of the Atmosphere (ToA), at the full spatial resolution of the instrument (275 m). This product resembles the MISR Local Mode product, except that (1) it can be generated everywhere (and does not depend on Local Mode acquisitions), (2) the data values in the 24 non-red, off-nadir data channels are obviously reconstructed (since the only available observations are at the spatial resolution of 1100 m), and (3) the swath width of the L1B3 product does not exceed that of the nadir camera since the latter is used in this reconstruction.
- An algorithm is then applied to the L1B3 product to estimate the bidirectional spectral reflectance factor (BRF) of the surface, sometimes also called Bottom of the Atmosphere (BoA) reflectance. This process takes into account the contribution of the atmosphere itself to the original measurements and yields 36 data channels at the native spatial resolution of the instrument.
- The parametric bidirectional reflectance model of Rahman et al. [49] is subsequently inverted against the nine surface directional measurements available for each location, in the four spectral bands, to document the spectral anisotropy of the surface. Three model parameters are retrieved in each band, together with estimates of their associated uncertainties: a base reflectance , which determines the brightness level of the reflectance, the Minnaert parameter k, which defines the bowl or bell shape of the reflectance as a function of the geometry of illumination and observation, and the asymmetry parameter , which controls whether the reflectance is predominantly due to forward or backward scattering (also see [114]).
- Those RPV results are spectrally and directionally integrated to generate the broadband albedos in the visible (VIS) and near-infrared (NIR) broadband regions required by the next step. These intermediary results are physically contained in the output files of the last processing step.
- Finally, the Joint Research Centre (JRC) Two-stream Inversion Package (TIP) is inverted against the albedos just computed to offer a complete description of the radiation fluxes at the surface, specifically through estimates of the reflectance, transmittance and absorptance of the plant canopy, in addition to estimates of the Leaf Area Index (LAI), the Fraction of Absorbed Photosynthetically Active Radiation (FAPAR), and optical properties of the leaves, as well as the implied albedo of the underlying surface. This inversion procedure also delivers estimates of the variance associated with each output variable, and the final value of the goodness of fit criterion, which can be used to cull data items that are obviously wrong or of doubtful reliability [76].
Appendix B. Parametric Double S-Shaped Functions
Appendix B.1. Parametric Double Gaussian Function
- ∘
- is the value of the Parametric Double Gaussian Function at argument x, returned by the IDL function pd_gaus_f,
- ∘
- is the value of the first Parametric Gaussian Function at argument x, using parameters to and provided as the output positional parameter pgf1, and
- ∘
- is the value of the second Parametric Gaussian Function at argument x, using parameters to and provided as the output positional parameter pgf2.
- ∘
- = Base value of , i.e., asymptotic value when .
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the maximum of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Standard deviation of .
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the maximum of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Standard deviation of .
Appendix B.2. Hyperbolic Tangent Functions
- ∘
- is the value of the Parametric Double Hyperbolic Tangent Function at argument x, returned by the IDL function pd_hytg_f,
- ∘
- is the value of the first Parametric Hyperbolic Tangent Function at argument x, using parameters to and provided as the output positional parameter phtf1, and
- ∘
- is the value of the second Parametric Hyperbolic Tangent Function at argument x, using parameters to and provided as the output positional parameter phtf2.
- ∘
- = Base value of , i.e., asymptotic value when .
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the inflection point of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Slope of at the inflection point.
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the inflection point of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Slope of at the inflection point.
Appendix B.3. Logistic Functions
- ∘
- is the value of the Parametric Double Logistic Function at argument x, returned by the IDL function pd_logi_f,
- ∘
- is the value of the first Parametric Logistic Function at argument x, using parameters to and provided as the output positional parameter plf1, and
- ∘
- is the value of the second Parametric Logistic Function at argument x, using parameters to and provided as the output positional parameter plf2.
- ∘
- = Base value of , i.e., asymptotic value when .
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the inflection point of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Slope of at the inflection point.
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the inflection point of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Slope of at the inflection point.
Appendix B.4. Sine Functions
- ∘
- is the value of the Parametric Double Sine Function at argument x, returned by the IDL function pd_sine_f,
- ∘
- is the value of the first Parametric Sine Function at argument x, using parameters to and provided as the output positional parameter psf1, and
- ∘
- is the value of the second Parametric Sine Function at argument x, using parameters to and provided as the output positional parameter psf2.
- ∘
- = Base value of , i.e., asymptotic value when .
- ∘
- = Amplitude of (positive for an increase, negative for a decrease), independently from the base value.
- ∘
- = Phase shift along the x axis for the start of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Phase shift along the x axis for the end of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Amplitude of , independently from the base value.
- ∘
- = Phase shift along the x axis for the start of : a positive (negative) value shifts the function to the right (left) of .
- ∘
- = Phase shift along the x axis for the end of : a positive (negative) value shifts the function to the right (left) of .
Appendix B.5. Prior Values
- Compute the mean value mid_y of the biogeophysical variable across the entire season.
- Identify the start fst_x_during and end lst_x_during of the period during which the input signal is higher than mid_y.
- Locate the largest value x_fst_max_y_during of this biogeophysical variable within this restricted period. The function also handles cases where there may be more than one instance of such a large value.
- Identify the start and end of the initial and final periods when the biogeophysical variable is lower than the mean value: fst_x_before, lst_x_before, fst_x_after and lst_x_after, respectively.
- Compute the mean values mean_before, mean_during and mean_after of the biogeophysical variable during the initial, peak and final periods characterized above.
- For all four models, set the prior value of parameter to mean_before, the prior value of parameter to (mean_during−mean_before), and the prior value of parameter to (mean_after− mean_during).
- For the PDGF model, set the prior values of parameter to fst_x_during, parameter to ((x_fst_max_y_during − lst_x_before) / 3.0), parameter to lst_x_during, and parameter to ((fst_x_after − x_lst_max_y_during) / 3.0).
- For the PDHyTgF model, set the prior values of parameter to (lst_x_before + ((fst_x_during - lst_x_before) / 2.0)), parameter to ((fst_y_during − lst_y_before) / delta_x), where delta_x is (fst_x_during − lst_x_before), parameter to (lst_x_during + ((fst_x_after − lst_x_during) / 2.0)), and parameter to (ABS(fst_y_after − lst_y_during) / delta_x).
- For the PDLS model, set the prior values of parameter to (lst_x_before + ((fst_x_during - lst_x_before) / 2.0)), parameter to (2.0 × (fst_y_during − lst_y_before) / delta_x), where delta_x is (fst_x_during − lst_x_before), parameter to (lst_x_during + ((fst_x_after − lst_x_during) / 2.0)), and parameter to (2.0 × ABS(fst_y_after − lst_y_during) / delta_x).
- For the PDSF model, set the prior values of parameter to fst_x_before, parameter to x_fst_max_y_during, parameter to x_lst_max_y_during, parameter to lst_x_after.
References
- Friedlingstein, P.; Cadule, P.; Piao, S.; Ciais, P.; Sitch, S. The African contribution to the global climate-carbon cycle feedback of the 21st century. Biogeosciences 2010, 7, 513–519. [Google Scholar] [CrossRef]
- Adole, T.; Dash, J.; Rodriguez-Galiano, V.; Atkinson, P.M. Photoperiod controls vegetation phenology across Africa. Commun. Biol. 2019, 2, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.D.; Lister, D.H.; Osborn, T.J.; Harpham, C.; Salmon, M.; Morice, C.P. Hemispheric and large-scale land-surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. Atmos. 2012, 117, 1–29. [Google Scholar] [CrossRef]
- Engelbrecht, F.; Adegoke, J.; Bopape, M.J.; Naidoo, M.; Garland, R.; Thatcher, M.; McGregor, J.; Katzfey, J.; Werner, M.; Ichoku, C.; et al. Projections of rapidly rising surface temperatures over Africa under low mitigation. Environ. Res. Lett. 2015, 10, 085004. [Google Scholar] [CrossRef]
- Archer, E.R.M.; Engelbrecht, F.A.; Hänsler, A.; Landman, W.; Tadross, M.; Helmschrot, J. Seasonal prediction and regional climate projections for southern Africa. In Climate Change and Adaptive Land Management in Southern Africa—Assessments, Changes, Challenges, and Solutions; Revermann, R., Krewenka, K.M., Schmiedel, U., Olwoch, J.M., Jörg, H., Jürgens, N., Eds.; Klaus Hess Publishers: Göttingen, Germany; Windhoek, Namibia, 2018; Volume 6, pp. 14–21. [Google Scholar] [CrossRef]
- Kutsch, W.L.; Hanan, N.; Scholes, R.J.; McHugh, I.; Kubheka, W.; Eckhardt, H.; Williams, C. Response of carbon fluxes to water relations in a savanna ecosystem in South Africa. Biogeosciences 2008, 5, 1797–1808. [Google Scholar] [CrossRef]
- Twine, W.C.; Moshe, D.; Netshiluvhi, T.; Siphugu, V. Consumption and direct-use values of savanna bio-resources used by rural households in Mametja, a semi-arid area of Limpopo province, South Africa. S. Afr. J. Sci. 2003, 99, 467–473. [Google Scholar]
- Shackleton, C.M.; Shackleton, S.E. The importance of non-timber forest products in rural livelihood security and as safety nets: A review of evidence from South Africa. S. Afr. J. Sci. 2004, 100, 658–664. [Google Scholar]
- Main, R.; Mathieu, R.; Kleynhans, W.; Wessels, K.; Naidoo, L.; Asner, G.P. Hyper-Temporal C-Band SAR for Baseline Woody Structural Assessments in Deciduous Savannas. Remote Sens. 2016, 8, 661. [Google Scholar] [CrossRef]
- Kalema, V.N.; Witkowski, E.T.F. Land-use impacts on woody plant density and diversity in an African savanna charcoal production region. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2012, 8, 231–247. [Google Scholar] [CrossRef]
- Matsika, R.; Erasmus, B.F.N.; Twine, W.C. Double jeopardy: The dichotomy of fuelwood use in rural South Africa. Energy Policy 2013, 52, 716–725. [Google Scholar] [CrossRef]
- Erasmus, B.F.N.; Coetzer, K.; Mambo, J.; Archer, E.R.M.; Fisher, J.T.; Asner, G.P. Environmental change in Bushbuckridge. In Observation on Environmental Change in South Africa; Sun Media Publishing: Stellenbosch, South Africa, 2011; pp. 1–5. Available online: https://researchspace.csir.co.za/dspace/handle/10204/6742 (accessed on 14 October 2020).
- Mucina, L.; Rutherford, M.C. (Eds.) The Vegetation of South Africa, Lesotho and Swaziland Number 19 in Strelitzia; South African National Biodiversity Institute: Pretoria, South Africa, 2006. [Google Scholar]
- Venter, F.J.; Scholes, R.J.; Eckhardt, H.C. The Abiotic Template and Its Associated Vegetation Pattern. In The Kruger Experience: Ecology and Management of Savanna Heterogeneity; du Toit, J.T., Rogers, K.H., Biggs, H.C., Eds.; Island Press: Washington, DC, USA, 2003; pp. 83–129. [Google Scholar]
- Sankaran, M.; Ratnam, J.; Hanan, N. Woody cover in African savannas: The role of resources, fire and herbivory. Glob. Ecol. Biogeogr. 2008, 17, 236–245. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; Technical report; Texas A&M University, Remote Sensing Center: College Station, TX, USA, 1973. [Google Scholar]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 1 January 1974; Volume 1, pp. 309–317. [Google Scholar]
- Committee on Planetary Biology; Space Science Board; Commission on Physical Sciences, Mathematics, and Resources; National Research Council. Remote Sensing of the Biosphere; Number 12344; National Academy Press: Washington, DC, USA, 1986; p. 148. [Google Scholar]
- Tang, J.; Körner, C.; Muraoka, H.; Piao, S.; Shen, M.; Thackeray, S.J.; Yang, X. Emerging opportunities and challenges in phenology: A review. Ecosphere 2016, 7, 1–17. [Google Scholar] [CrossRef]
- Gobron, N.; Verstraete, M.M. FAPAR—Fraction of Absorbed Photosynthetically Active Radiation (FAPAR); Technical Report T10–GTOS 65; Global Terrestrial Observing System (GTOS): Rome, Italy, 2009. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Butt, B.; Turner, M.D.; Singh, A.; Brottem, L. Use of MODIS NDVI to evaluate changing latitudinal gradients of rangeland phenology in Sudano-Sahelian West Africa. Remote Sens. Environ. 2011, 115, 3367–3376. [Google Scholar] [CrossRef]
- Buitenwerf, R.; Rose, L.; Higgins, S.I. Three decades of multi-dimensional change in global leaf phenology. Nat. Clim. Chang. 2015, 5, 364–368. [Google Scholar] [CrossRef]
- Kellndorfer, J.M.; Walker, W.S.; LaPoint, E.; Kirsch, K.; Bishop, J.; Fiske, G. Statistical fusion of lidar, InSAR, and optical remote sensing data for forest stand height characterization: A regional-scale method based on LVIS, SRTM, Landsat ETM+, and ancillary data sets. J. Geophys. Res. 2010, 115, 1–10. [Google Scholar] [CrossRef]
- Naidoo, L.; Cho, M.A.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and LiDAR data in a Random Forest data mining environment. Isprs J. Photogramm. Remote Sens. 2012, 69, 167–179. [Google Scholar] [CrossRef]
- Mahlangu, P.; Mathieu, R.; Wessels, K.; Naidoo, L.; Verstraete, M.M.; Asner, G.; Main, R. Indirect Estimation of Structural Parameters in South African Forests Using MISR-HR and LiDAR Remote Sensing Data. Remote Sens. 2018, 10, 1537. [Google Scholar] [CrossRef]
- Haack, B.N.; Herold, N.D.; Bechdol, M.A. Radar and Optical Data Integration for Land-Use/Land-Cover Mapping. Photogramm. Eng. Remote Sens. 2000, 66, 709–716. [Google Scholar]
- Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.R.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E.T.A.; et al. A Review of the Application of Optical and Radar Remote Sensing Data Fusion to Land Use Mapping and Monitoring. Remote Sens. 2016, 8, 70. [Google Scholar] [CrossRef]
- Lopes, M.; Frison, P.L.; Durant, S.M.; Schulte to Bühne, H.; Ipavec, A.; Lapeyre, V.; Pettorelli, N. Combining optical and radar satellite image time series to map natural vegetation: Savannas as an example. Remote Sens. Ecol. Conserv. 2020, 6, 316–326. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Jolly, W.M.; Nemani, R.; Running, S.W. A generalized, bioclimatic index to predict foliar phenology in response to climate. Glob. Chang. Biol. 2005, 11, 619–632. [Google Scholar] [CrossRef]
- Piao, S.; Tan, J.; Chen, A.; Fu, Y.H.; Ciais, P.; Liu, Q.; Janssens, I.A.; Vicca, S.; Zeng, Z.; Jeong, S.J.; et al. Leaf onset in the northern hemisphere triggered by daytime temperature. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Workie, T.G.; Debella, H.J. Climate change and its effects on vegetation phenology across ecoregions of Ethiopia. Glob. Ecol. Conserv. 2018, 13, e00366. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B. Global vegetation phenology from Moderate Resolution Imaging Spectroradiometer (MODIS): Evaluation of global patterns and comparison with in situ measurements. J. Geophys. Res. Biogeosci. 2006, 111, G04017. [Google Scholar] [CrossRef]
- Verger, A.; Filella, I.; Baret, F.; Peñuelas, J. Vegetation baseline phenology from kilometric global LAI satellite products. Remote Sens. Environ. 2016, 178, 1–14. [Google Scholar] [CrossRef]
- Adole, T.; Dash, J.; Atkinson, P.M. A systematic review of vegetation phenology in Africa. Ecol. Inform. 2016, 34, 117–128. [Google Scholar] [CrossRef]
- Verbesselt, J.; Somers, B.; Lhermitte, S.; Jonckheere, I.; Van Aardt, J.; Coppin, P. Monitoring herbaceous fuel moisture content with SPOT VEGETATION time-series for fire risk prediction in savanna ecosystems. Remote Sens. Environ. 2007, 108, 357–368. [Google Scholar] [CrossRef]
- Coetzer, K.L.; Erasmus, B.F.N.; Witkowski, E.T.F.; Bachoo, A.K. Land-cover change in the Kruger to Canyons Biosphere Reserve (1993–2006): A first step towards creating a conservation plan for the subregion. S. Afr. J. Sci. 2010, 106, 1–10. [Google Scholar] [CrossRef]
- Coetzer, K.L.; Erasmus, B.F.N.; Witkowski, E.T.F.; Reyers, B. The Race for Space: Tracking Land-Cover Transformation in a Socio-ecological Landscape, South Africa. Environ. Manag. 2013, 52, 595–611. [Google Scholar] [CrossRef] [PubMed]
- Madonsela, S.; Cho, M.A.; Ramoelo, A.; Mutanga, O. Remote sensing of species diversity using Landsat 8 spectral variables. ISPRS J. Photogramm. Remote Sens. 2017, 133, 116–127. [Google Scholar] [CrossRef]
- Wessels, K.J.; Mathieu, R.; Erasmus, B.F.N.; Asner, G.P.; Smit, I.P.J.; Van Aardt, J.A.N.; Main, R.; Fisher, J.; Marais, W.; Kennedy-Bowdoin, T.; et al. Impact of communal land use and conservation on woody vegetation structure in the Lowveld savannas of South Africa. For. Ecol. Manag. 2011, 261, 19–29. [Google Scholar] [CrossRef]
- Fisher, J.T.; Witkowski, E.T.F.; Erasmus, B.F.N.; van Aardt, J.A.N.; Asner, G.P.; Wessels, K.J.; Mathieu, R. Human-modified landscapes: Patterns of fine-scale woody vegetation structure in communal savannah rangelands. Environ. Conserv. 2012, 39, 72–82. [Google Scholar] [CrossRef]
- Fisher, J.T.; Witkowski, E.T.F.; Erasmus, B.F.N.; Mograbi, P.J.; Asner, G.P.; van Aardt, J.A.N.; Wessels, K.J.; Mathieu, R. What lies beneath: Detecting sub-canopy changes in savanna woodlands using a three-dimensional classification method. Appl. Veg. Sci. 2015, 18, 528–540. [Google Scholar] [CrossRef]
- Cho, M.A.; Mathieu, R.; Asner, G.P.; Naidoo, L.; van Aardt, J.; Ramoelo, A.; Debba, P.; Wessels, K.; Main, R.; Smit, I.P.J.; et al. Mapping tree species composition in South African savannas using an integrated airborne spectral and LiDAR system. Remote Sens. Environ. 2012, 125, 214–226. [Google Scholar] [CrossRef]
- Diner, D.J.; Asner, G.P.; Davies, R.; Knyazikhin, Y.; Muller, J.P.; Nolin, A.W.; Pinty, B.; Schaaf, C.B.; Stroeve, J. New Directions in Earth Observing: Scientific Applications of Multiangle Remote Sensing. Bull. Am. Meteorol. Soc. 1999, 80, 2209–2228. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Hunt, L.A.; Scholes, R.J.; Clerici, M.; Pinty, B.; Nelson, D.L. Generating 275 m Resolution Land Surface Products From the Multi-Angle Imaging SpectroRadiometer data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3980–3990. [Google Scholar] [CrossRef]
- Pinty, B.; Andredakis, I.; Clerici, M.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Widlowski, J.L. Exploiting the MODIS albedos with the Two-stream Inversion Package (JRC–TIP): 1. Effective Leaf Area Index, Vegetation, and Soil Properties. J. Geophys. Res. 2011, 116, D09105. [Google Scholar] [CrossRef]
- Pinty, B.; Clerici, M.; Andredakis, I.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Widlowski, J.L. Exploiting the MODIS albedos with the Two-stream Inversion Package (JRC–TIP): 2. Fractions of Transmitted and Absorbed Fluxes in the Vegetation and Soil Layers. J. Geophys. Res. 2011, 116, D09106. [Google Scholar] [CrossRef]
- Rahman, H.; Pinty, B.; Verstraete, M.M. Coupled Surface-Atmosphere Reflectance (CSAR) Model. 2. Semiempirical Surface Model Usable With NOAA Advanced Very High Resolution Radiometer Data. J. Geophys. Res. 1993, 98, 20791–20801. [Google Scholar] [CrossRef]
- Lavergne, T.; Kaminski, T.; Pinty, B.; Taberner, M.; Gobron, N.; Verstraete, M.M.; Vossbeck, M.; Widlowski, J.L.; Giering, R. Application to MISR land products of an RPV model inversion package using adjoint and Hessian codes. Remote Sens. Environ. 2007, 107, 362–375. [Google Scholar] [CrossRef]
- Clerici, M.; Vossbeck, M.; Pinty, B.; Kaminski, T.; Taberner, M.; Lavergne, T.; Andredakis, I. Consolidating the Two-Stream Inversion Package (JRC-TIP) to Retrieve Land Surface Parameters From Albedo Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 286–295. [Google Scholar] [CrossRef]
- Chernetskiy, M.; Gómez-Dans, J.; Gobron, N.; Morgan, O.; Lewis, P.; Truckenbrodt, S.; Schmullius, C. Estimation of FAPAR over Croplands Using MISR Data and the Earth Observation Land Data Assimilation System (EO-LDAS). Remote Sens. 2017, 9, 656. [Google Scholar] [CrossRef]
- Pinty, B.; Jung, M.; Kaminski, T.; Lavergne, T.; Mund, M.; Plummer, S.; Thomas, E.; Widlowski, J.L. Evaluation of the JRC-TIP 0.01° products over a mid-latitude deciduous forest site. Remote Sens. Environ. 2011, 115, 3567–3581. [Google Scholar] [CrossRef]
- D’Odorico, P.; Gonsamo, A.; Pinty, B.; Gobron, N.; Coops, N.; Mendez, E.; Schaepman, M.E. Intercomparison of fraction of absorbed photosynthetically active radiation products derived from satellite data over Europe. Remote Sens. Environ. 2014, 142, 142–154. [Google Scholar] [CrossRef]
- Kaminski, T.; Pinty, B.; Voßbeck, M.; Lopatka, M.; Gobron, N.; Robustelli, M. Consistent retrieval of land surface radiation products from EO, including traceable uncertainty estimates. Biogeosciences 2017, 14, 2527–2541. [Google Scholar] [CrossRef]
- Gobron, N.; Marioni, M.; Robustelli, M.; Vermote, E. Can We Use the QA4ECV Black-sky Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) using AVHRR Surface Reflectance to Assess Terrestrial Global Change? Remote Sens. 2019, 11, 3055. [Google Scholar] [CrossRef]
- Swinbank, W.C. The measurement of vertical transfer of heat and water vapor by eddies in the lower atmosphere. J. Meteorol. 1951, 8, 135–145. [Google Scholar] [CrossRef]
- Friend, A.D.; Arneth, A.; Kiang, N.Y.; Lomas, M.; Ogée, J.; Rödenbeck, C.; Running, S.W.; Santaren, J.D.; Sitch, S.; Viovy, N.; et al. FLUXNET and modelling the global carbon cycle. Glob. Chang. Biol. 2007, 13, 610–633. [Google Scholar] [CrossRef]
- Baldocchi, D.D. ‘Breathing’ of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Scholes, R.J.; Gureja, N.; Giannecchinni, M.; Dovie, D.; Wilson, B.; Davidson, N.; Piggott, K.; McLoughlin, C.; Van der Velde, K.; Freeman, A.; et al. The environment and vegetation of the flux measurement site near Skukuza, Kruger National Park. Koedoe 2001, 44, 73–83. [Google Scholar] [CrossRef]
- Archibald, S.A.; Kirton, A.; van der Merwe, M.R.; Scholes, R.J.; Williams, C.A.; Hanan, N. Drivers of inter-annual variability in Net Ecosystem Exchange in a semi-arid savanna ecosystem, South Africa. Biogeosciences 2009, 6, 251–266. [Google Scholar] [CrossRef]
- Annegarn, H.J.; Otter, L.; Swap, R.J.; Scholes, R.J. Southern Africa’s ecosystem in a test-tube: A perspective on the Southern African Regional Science Initiative (SAFARI 2000). S. Afr. J. Sci. 2002, 98, 111–113. [Google Scholar]
- Otter, L.B.; Scholes, R.J.; Dowty, P.; Privette, J.; Caylor, K.; Ringrose, S.; Mukelabai, M.; Frost, P.; Hanan, N.; Totolo, O.; et al. The Southern African Regional Science Initiative (SAFARI 2000): Wet season campaigns. S. Afr. J. Sci. 2002, 98, 131–137. [Google Scholar]
- Shugart, H.H.; Macko, S.A.; Lesolle, P.; Szuba, T.A.; Mukelabai, M.M.; Dowty, P.; Swap, R.J. The SAFARI 2000—Kalahari Transect Wet Season Campaign of year 2000. Glob. Chang. Biol. 2004, 10, 273–280. [Google Scholar] [CrossRef]
- Nickless, A.; Archibald, S.A.; Van der Merwe, M.R.; Scholes, R.J.; Williams, C.A.; Hanan, N. Estimation of net ecosystem exchange at the Skukuza flux site, Kruger National Park, South Africa. In Proceedings of the Open Science Conference on “Africa and Carbon Cycle: The CarboAfrica Project, Accra, Ghana, 25–27 November 2008; pp. 23–32. [Google Scholar]
- Majozi, N.P.; Mannaerts, C.M.; Ramoelo, A.; Mathieu, R.; Nickless, A.; Verhoef, W. Analysing surface energy balance closure and partitioning over a semi-arid savanna FLUXNET site in Skukuza, Kruger National Park, South Africa. Hydrol. Earth Syst. Sci. 2017, 21, 3401–3415. [Google Scholar] [CrossRef]
- Pastorello, G.Z.; Papale, D.; Chu, H.; Trotta, C.; Agarwal, D.A.; Canfora, E.; Baldocchi, D.D.; Torn, M.S. A New Data Set to Keep a Sharper Eye on Land-Air Exchanges. EOS 2017, 98. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Reed, B.C.; Schwartz, M.D.; Xiao, X. Remote Sensing Phenology. In Phenology of Ecosystem Processes; Springer: New York, NY, USA, 2009; pp. 231–246. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, J.; Yan, H.; Wu, W.; Biradar, C. Land Surface Phenology: Convergence of Satellite and CO2 Eddy Flux Observations. In Phenology of Ecosystem Processes: Applications in Global Change Research; Noormets, A., Ed.; Springer Science + Business Media, LLC: Berlin, Germany, 2009; pp. 247–270. [Google Scholar] [CrossRef]
- McCloy, K.R. Development and Evaluation of Phenological Change Indices Derived from Time Series of Image Data. Remote Sens. 2010, 2, 2442–2473. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- MacBean, N.; Maignan, F.; Peylin, P.; Bacour, C.; Bréon, F.M.; Ciais, P. Using satellite data to improve the leaf phenology of a global terrestrial biosphere model. Biogeosciences 2015, 12, 7185–7208. [Google Scholar] [CrossRef]
- Alessandri, A.; Catalano, F.; De Felice, M.; Van Den Hurk, B.; Reyes, F.D.; Boussetta, S.; Balsamo, G.; Miller, P.A. Multi-scale enhancement of climate prediction over land by increasing the model sensitivity to vegetation variability in EC-Earth. Clim. Dyn. 2017, 49, 1215–1237. [Google Scholar] [CrossRef]
- Liu, Z.; Verstraete, M.M.; de Jager, G. Handling outliers in model inversion studies: A remote sensing case study using MISR-HR data in South Africa. S. Afr. Geogr. J. 2018, 100, 122–139. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in FORTRAN 77: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Hocke, K.; Kämpfer, N. Gap filling and noise reduction of unevenly sampled data by means of the Lomb-Scargle periodogram. Atmos. Chem. Phys. 2009, 9, 4197–4206. [Google Scholar] [CrossRef]
- Moreno, Á.; García-Haro, F.J.; Martínez, B.; Gilabert, M.A. Noise Reduction and Gap Filling of fAPAR Time Series Using an Adapted Local Regression Filter. Remote Sens. 2014, 6, 8238–8260. [Google Scholar] [CrossRef]
- Ma, M.; Veroustraete, F. Reconstructing pathfinder AVHRR land NDVI time-series data for the Northwest of China. Adv. Space Res. 2006, 37, 835–840. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. A multisensor fusion approach to improve LAI time series. Remote Sens. Environ. 2011, 115, 2460–2470. [Google Scholar] [CrossRef]
- Pan, Z.; Hu, Y.; Cao, B. Construction of smooth daily remote sensing time series data: A higher spatiotemporal resolution perspective. Open Geospat. Data Softw. Stand. 2017, 2, 1–11. [Google Scholar] [CrossRef][Green Version]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Eilers, P.H.C. A Perfect Smoother. Anal. Chem. 2003, 75, 3631–3636. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Eklundh, L.; Jönsson, P. TIMESAT: A Software Package for Time-Series Processing and Assessment of Vegetation Dynamics. In Remote Sensing Time Series; Kuenzer, C., Dech, S., Wagner, W., Eds.; Number 22 in Remote Sensing and Digital Image Processing; Springer: Cham, Switherland, 2015; pp. 141–158. [Google Scholar] [CrossRef]
- Azzali, S.; Menenti, M. Mapping vegetation-soil-climate complexes in southern Africa using temporal Fourier analysis of NOAA-AVHRR NDVI data. Int. J. Remote Sens. 2000, 21, 973–996. [Google Scholar] [CrossRef]
- Bradley, B.A.; Jacob, R.W.; Hermance, J.F.; Mustard, J.F. A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite NDVI data. Remote Sens. Environ. 2007, 106, 137–145. [Google Scholar] [CrossRef]
- Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
- Sakamoto, T.; Wardlow, B.D.; Gitelson, A.A.; Verma, S.B.; Suyker, A.E.; Arkebauer, T.J. A Two-Step Filtering approach for detecting maize and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2010, 114, 2146–2159. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Gerard, F.F.; George, C.T.; Hayman, G.; Chavana-Bryant, C.; Weedon, G.P. Leaf phenology amplitude derived from MODIS NDVI and EVI: Maps of leaf phenology synchrony for Meso- and South America. Geosci. Data J. 2020, 7, 13–26. [Google Scholar] [CrossRef]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations–application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. III-Fourier transforms, autocorrelation functions, and cross-correlation functions of unevenly spaced data. Astrophys. J. 1989, 343, 874–887. [Google Scholar] [CrossRef]
- Fourier, J. Théorie Analytique de la Chaleur; Firmin Didot, Père et Fils: Paris, France, 1822; p. 639. [Google Scholar]
- Hmimina, G.; Dufrêne, E.; Pontailler, J.Y.; Delpierre, N.; Aubinet, M.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; Granier, A.; et al. Evaluation of the potential of MODIS satellite data to predict vegetation phenology indifferent biomes: An investigation using ground-based NDVI measurements. Remote Sens. Environ. 2013, 132, 145–158. [Google Scholar] [CrossRef]
- Meroni, M.; Marinho, E.; Sghaier, N.; Verstraete, M.M.; Léo, O. Remote Sensing Based Yield Estimation in a Stochastic Framework – Case Study of Durum Wheat in Tunisia. Remote Sens. 2013, 5, 539–557. [Google Scholar] [CrossRef]
- Meroni, M.; Verstraete, M.M.; Rembold, F.; Urbano, F.; Kayitakire, F. A phenology-based method to derive biomass production anomalies for food security monitoring in the Horn of Africa. Int. J. Remote Sens. 2014, 35, 2472–2492. [Google Scholar] [CrossRef]
- Tan, B.; Morisette, J.T.; Wolfe, R.E.; Gao, F.; Ederer, G.A.; Nightingale, J.; Pedelty, J.A. An Enhanced TIMESAT Algorithm for Estimating Vegetation Phenology Metrics From MODIS Data. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 361–371. [Google Scholar] [CrossRef]
- Cho, M.A.; Ramoelo, A.; Dziba, L. Response of Land Surface Phenology to Variation in Tree Cover during Green-Up and Senescence Periods in the Semi-Arid Savanna of Southern Africa. Remote Sens. 2017, 9, 689. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Pinty, B.; Myneni, R.B. Potential and Limitations of Information Extraction on the Terrestrial Biosphere From Satellite Remote Sensing. Remote Sens. Environ. 1996, 58, 201–214. [Google Scholar] [CrossRef]
- Gong, Z.; Kawamura, K.; Ishikawa, N.; Goto, M.; Wulan, T.; Alateng, D.; Yin, T.; Ito, Y. MODIS normalized difference vegetation index (NDVI) and vegetation phenology dynamics in the Inner Mongolia grassland. Solid Earth 2015, 6, 1185–1194. [Google Scholar] [CrossRef]
- Diner, D.J.; Bruegge, C.J.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.W.; Gordon, H.R.; Sellers, P.J.; Clark, J.; Daniels, J.A.; et al. MISR: A Multiangle Imaging SpectroRadiometer for Geophysical and Climatological Research from EOS. IEEE Trans. Geosci. Remote Sens. 1989, 27, 200–214. [Google Scholar] [CrossRef]
- Diner, D.J.; Beckert, J.C.; Reilly, T.H.; Ackerman, T.P.; Bruegge, C.J.; Conel, J.E.; Davies, R.; Gerstl, S.A.W.; Gordon, H.R.; Kahn, R.A.; et al. Multi-angle Imaging SpectroRadiometer (MISR) Instrument Description and Experiment Overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Diner, D.J.; Verstraete, M.M.; Martonchik, J.V. Foreword to Special Section on MISR. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1447–1448. [Google Scholar] [CrossRef]
- Diner, D.J.; Braswell, B.H.; Davies, R.; Gobron, N.; Hu, J.; Jin, Y.; Kahn, R.A.; Knyazikhin, Y.; Loeb, N.; Muller, J.P.; et al. The value of multiangle measurements for retrieving structurally and radiatively consistent properties of clouds, aerosols, and surfaces. Remote Sens. Environ. 2005, 97, 495–518. [Google Scholar] [CrossRef]
- Bull, M.; Matthews, J.; McDonald, D.; Menzies, A.; Moroney, C.; Mueller, K.; Paradise, S.; Smyth, M. Data Products Specifications; Technical Report JPL D-13963, Revision S; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2011. [Google Scholar]
- Verstraete, M.M.; Hunt, L.A.; De Lemos, H.; Di Girolamo, L. Replacing Missing Values in the Standard MISR Radiometric Camera-by-Camera Cloud Mask (RCCM) Data Product. Earth Syst. Sci. Data 2020, 12, 611–628. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Hunt, L.A.; Jovanovic, V.M. Improving the usability of the Multi-angle Imaging SpectroRadiometer (MISR) L1B2 Georectified Radiance Product (2000–present) in land surface applications. Earth Syst. Sci. Data 2020, 12, 1321–1346. [Google Scholar] [CrossRef]
- Engelsen, O.; Pinty, B.; Verstraete, M.M.; Martonchik, J.V. Parametric Bidirectional Reflectance Factor Models: Evaluation, Improvements and Applications; Technical Report EUR 16426 EN; EC Joint Research Centre: Ispra, Italy, 1996. [Google Scholar]
- Pinty, B.; Widlowski, J.L.; Gobron, N.; Verstraete, M.M.; Diner, D.J. Uniqueness of Multiangular Measurements—Part I: An Indicator of Subpixel Surface Heterogeneity From MISR. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1560–1573. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J.L.; Diner, D.J. Uniqueness of Multiangular Measurements—Part II: Joint Retrieval of Vegetation Structure and Photosynthetic Activity From MISR. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1574–1592. [Google Scholar] [CrossRef]
- Armston, J.D.; Scarth, P.F.; Phinn, S.R.; Danaher, T.J. Analysis of multi-date MISR measurements for forest and woodland communities, Queensland, Australia. Remote Sens. Environ. 2007, 107, 287–298. [Google Scholar] [CrossRef]
- Van den Hoof, C.; Verstraete, M.M.; Scholes, R.J. Differing Responses to Rainfall Suggest More Than One Functional Type of Grassland in South Africa. Remote Sens. 2018, 10, 2055. [Google Scholar] [CrossRef]
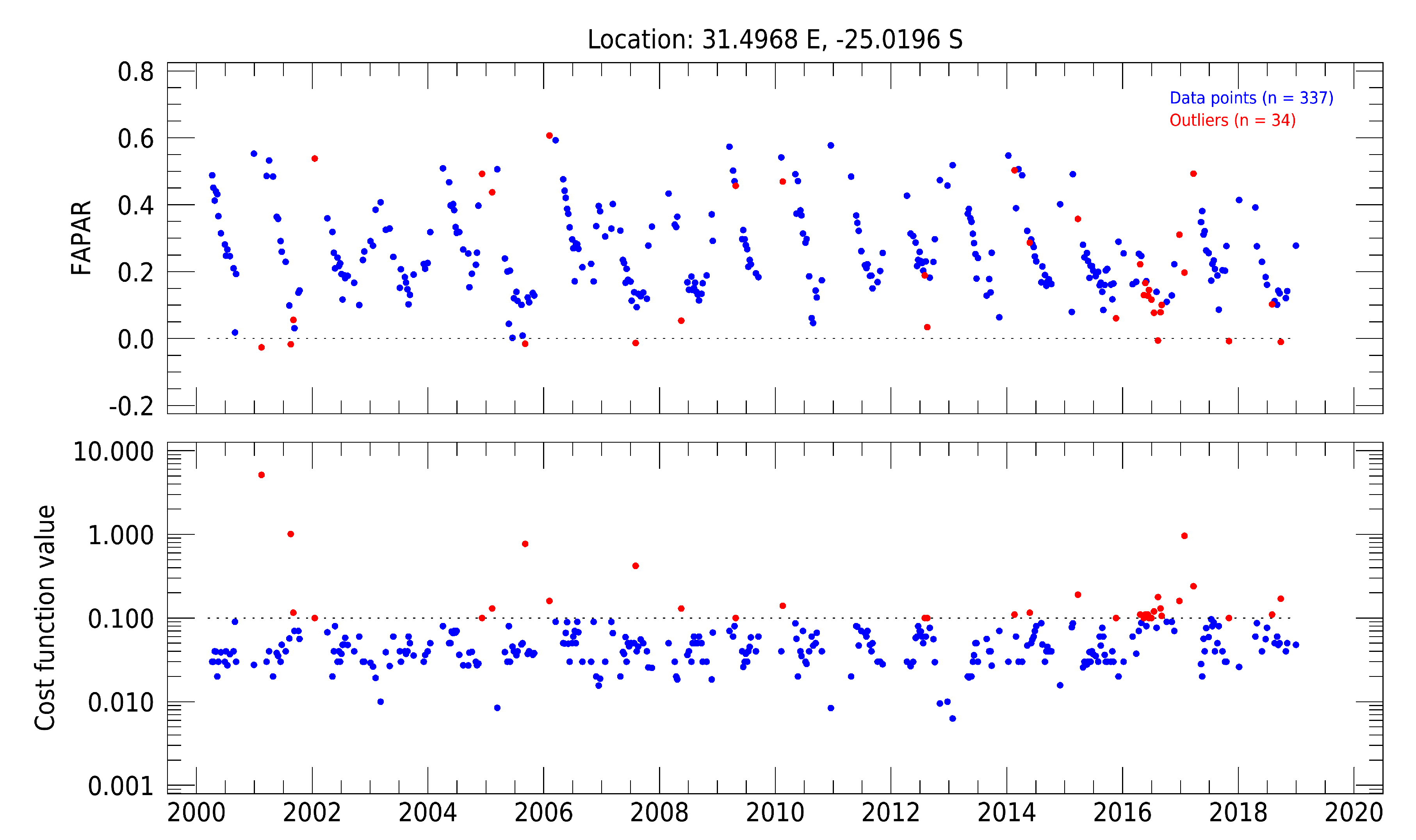
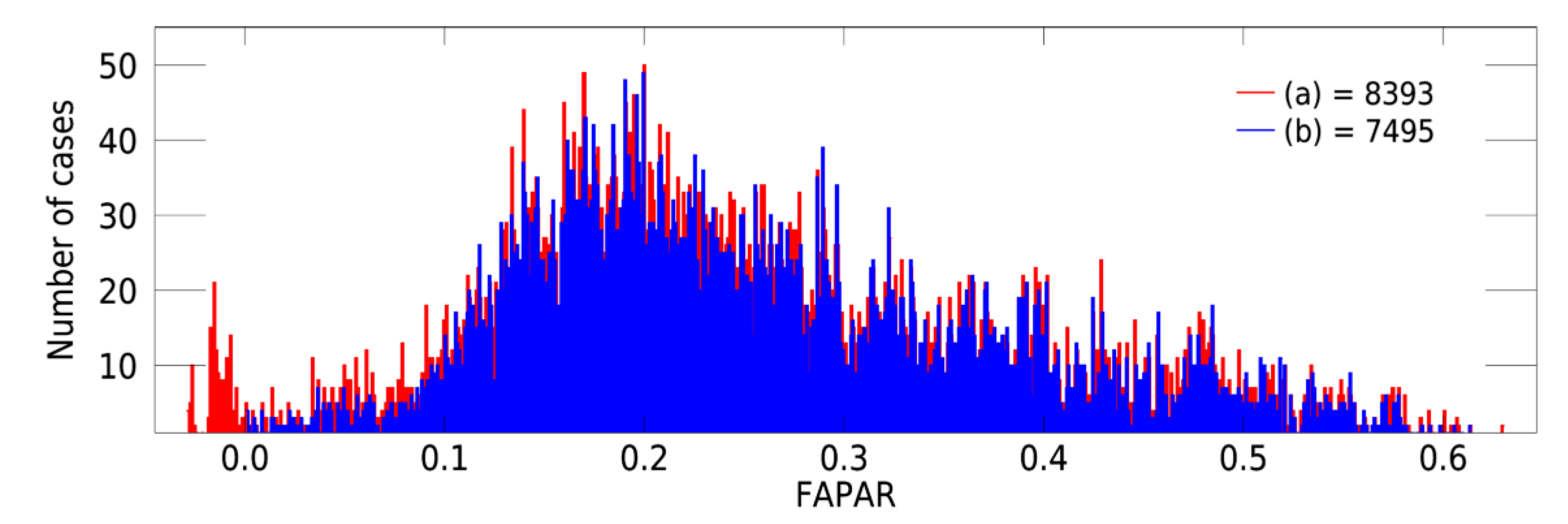

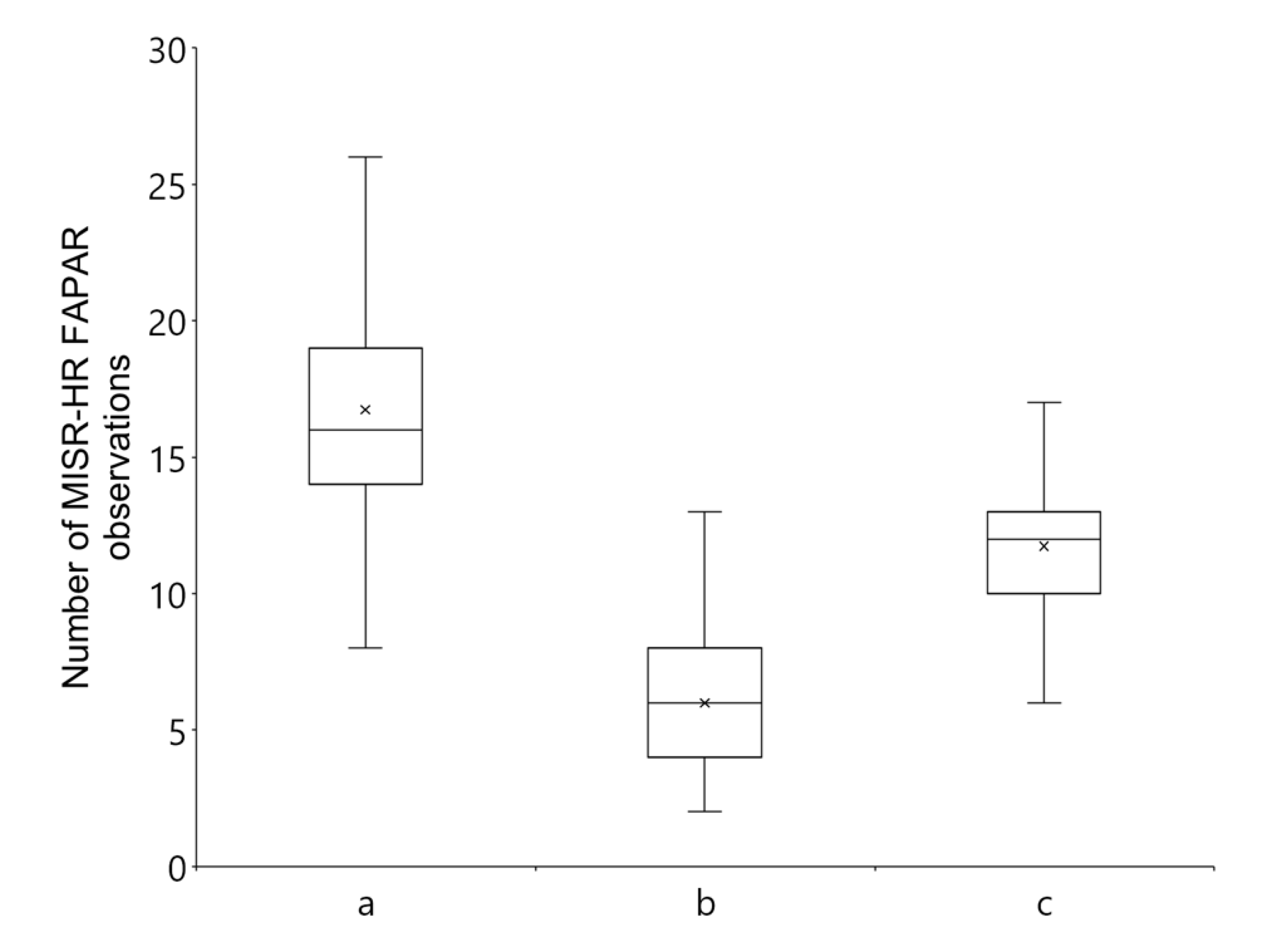
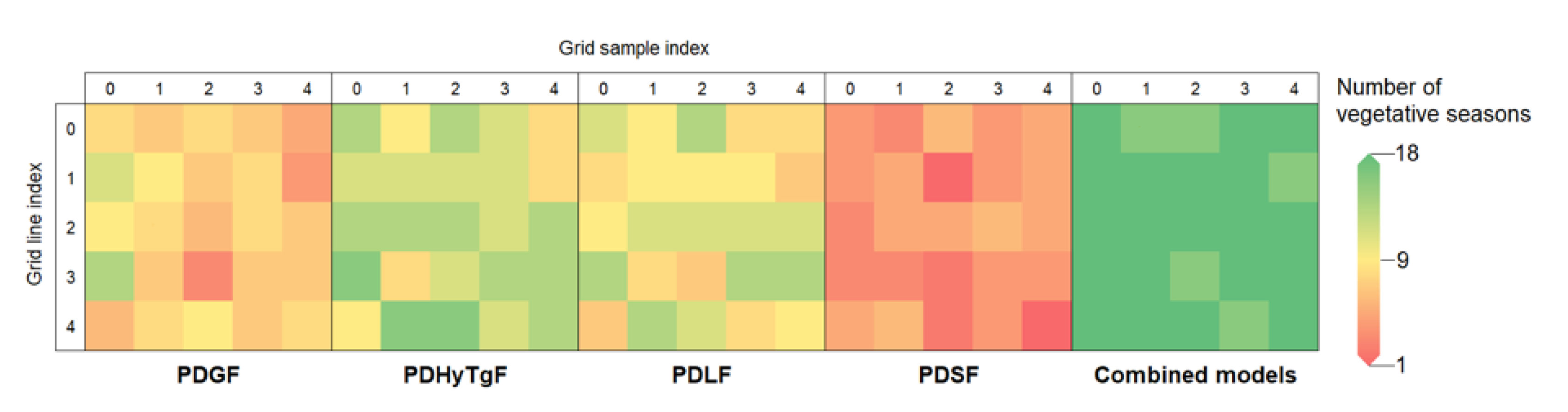
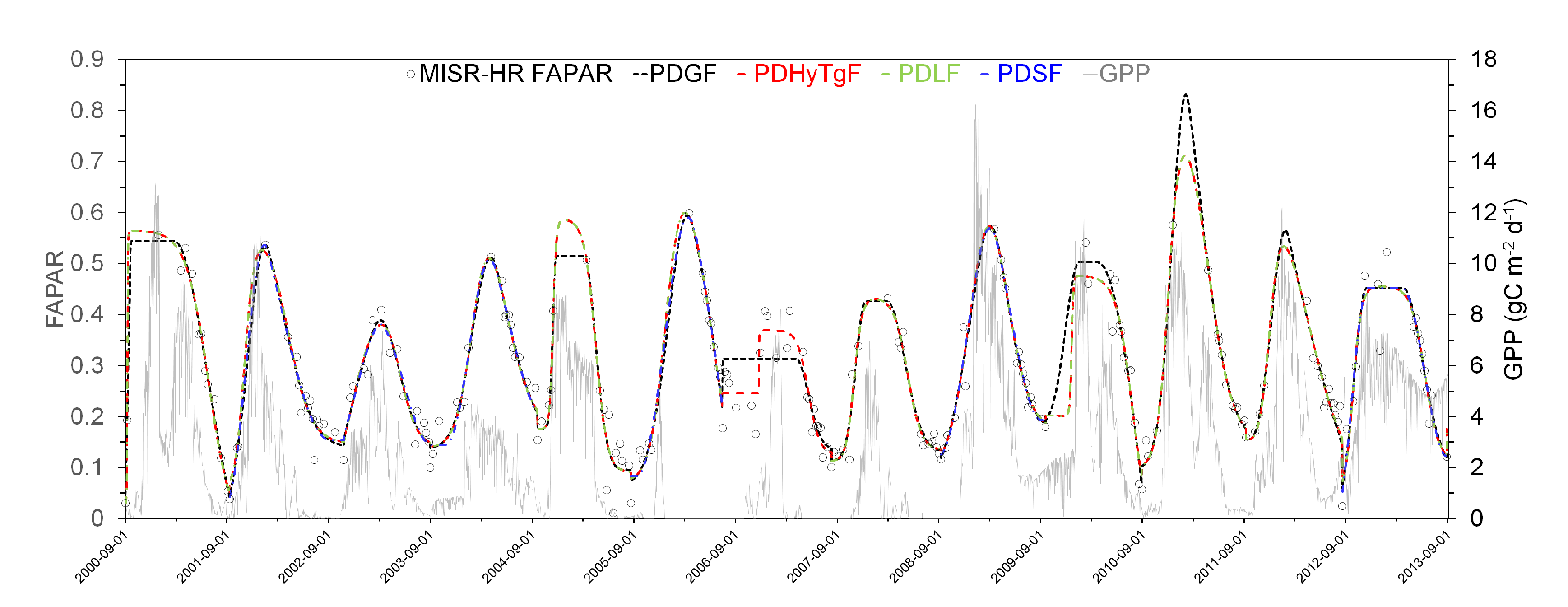

| Threshold | 0.1 | 0.08 | 0.06 | 0.04 |
|---|---|---|---|---|
| Outliers | 34 | 59 | 110 | 211 |
| Remaining | 303 | 278 | 227 | 126 |
| SOS/EOS | Vegetative Season | Season Length | GPP % | PDGFr | PDHyTgFr | PDLFr | PDSFr | Combinedr |
|---|---|---|---|---|---|---|---|---|
| 2000–08–31 | ||||||||
| 2001–09–10 | 1 | 375 | 99.2 | 0.56 | 0.52 | 0.52 | B | 0.56 |
| 2002–10–24 | 2 | 409 | 86.8 | 0.72 | 0.78 | 0.78 | 0.74 | 0.72 |
| 2003–08–31 | 3 | 311 | 100 | 0.71 | 0.70 | 0.70 | 0.70 | 0.71 |
| 2004–09–18 | 4 | 384 | 100 | 0.81 | 0.82 | 0.82 | 0.82 | 0.81 |
| 2005–08–20 | 5 | 336 | 94.6 | 0.92 | 0.93 | 0.93 | B | 0.93 |
| 2006–07–15 | 6 | 329 | 24.9 | A | A | A | A | A |
| 2007–08–10 | 7 | 391 | 41.4 | A | A | AB | AB | A |
| 2008–09–06 | 8 | 393 | 45.3 | A | A | A | AB | A |
| 2009–09–16 | 9 | 375 | 82.1 | 0.79 | 0.80 | 0.80 | 0.80 | 0.79 |
| 2010–08–27 | 10 | 345 | 100 | 0.69 | 0.72 | 0.72 | B | 0.69 |
| 2011–09–06 | 11 | 375 | 100 | 0.80 | 0.82 | 0.82 | B | 0.80 |
| 2012–09–01 | 12 | 361 | 100 | 0.82 | 0.80 | 0.80 | B | 0.82 |
| 2013–08–26 | 13 | 359 | 100 | 0.56 | 0.56 | 0.56 | 0.55 | 0.56 |
| SOS/EOS | Vegetative Season | Integrated GPP | CFAPAR | ||||
|---|---|---|---|---|---|---|---|
| PDGF | PDHyTgF | PDLF | PDSF | Combined | |||
| 2001–09–10 | |||||||
| 2002-10-24 | 2 | 815.25 | 117.72 | 122.26 | 122.26 | 118.50 | 117.72 |
| 2003–08–31 | 3 | 656.65 | 84.19 | 84.14 | 84.14 | 84.40 | 84.19 |
| 2004–09–18 | 4 | 682.33 | 119.50 | 119.91 | 119.91 | 119.24 | 119.50 |
| 2005–08–20 | 5 | 1043.88 | 105.95 | 111.70 | 111.70 | 111.70 | |
| 2009–09–16 | 9 | 1522.03 | 130.12 | 130.87 | 130.87 | 130.44 | 130.12 |
| 2010–08–27 | 10 | 1185.21 | 129.29 | 117.07 | 117.07 | 129.29 | |
| 2011–09–06 | 11 | 1314.19 | 155.09 | 148.36 | 148.36 | 155.09 | |
| 2012–09–01 | 12 | 1178.08 | 116.34 | 115.56 | 115.56 | 116.34 | |
| r | 0.65 | 0.62 | 0.62 | 0.65 | 0.65 | ||
| p-value | 0.35 | 0.38 | 0.38 | 0.35 | 0.35 | ||
| Successes | PDGF | PDHyTgF | PDLF | PDSF |
|---|---|---|---|---|
| Number | 309 | 382 | 355 | 224 |
| Proportion (%) | 68.6 | 84.8 | 78.8 | 49.7 |
| Iterations | PDGF | PDHyTgF | PDLF | PDSF | ||||
|---|---|---|---|---|---|---|---|---|
| Cases | s | u | s | u | s | u | s | u |
| Minimum | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 1 |
| 25th percentile | 7 | 1 | 8 | 2 | 8 | 1 | 7 | 1 |
| Median | 10 | 2 | 12 | 2 | 12 | 3 | 9 | 2 |
| Mean | 20.8 | 3 | 18.6 | 7.2 | 18.7 | 7.2 | 10.8 | 4 |
| 25th percentile | 14 | 3 | 19 | 4 | 19.5 | 4 | 11 | 3 |
| Maximum | 71 | 8 | 53 | 27 | 53 | 27 | 25 | 13 |
| Iterations | PDGF | PDHyTgF | PDLF | PDSF | ||||
|---|---|---|---|---|---|---|---|---|
| Cases | s | u | s | u | s | u | s | u |
| Minimum | 1.00008 | 1.00008 | 1.00008 | 1.33341 | 1.00000 | 1.00008 | 1.00008 | 1.00008 |
| 25th percentile | 1.66675 | 1.66675 | 1.66683 | 1.66675 | 1.66675 | 1.66675 | 1.66683 | 1.33341 |
| Median | 2.00008 | 2.00008 | 2.00016 | 2.00016 | 2.00016 | 1.66683 | 2.00016 | 1.66683 |
| Mean | 2.26680 | 2.53349 | 2.66686 | 2.13346 | 2.26680 | 2.06678 | 2.46685 | 1.93348 |
| 75th percentile | 2.00016 | 2.33349 | 2.33357 | 2.33349 | 2.33349 | 2.00016 | 2.33349 | 2.00016 |
| Maximum | 4.66708 | 5.66708 | 6.33383 | 3.33357 | 4.33365 | 4.00023 | 5.33372 | 3.66700 |
| PDGF | PDHyTgF | PDLF | PDSF |
|---|---|---|---|
| 0.022 | 0.020 | 0.018 | 0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Lemos, H.; Verstraete, M.M.; Scholes, M. Parametric Models to Characterize the Phenology of the Lowveld Savanna at Skukuza, South Africa. Remote Sens. 2020, 12, 3927. https://doi.org/10.3390/rs12233927
De Lemos H, Verstraete MM, Scholes M. Parametric Models to Characterize the Phenology of the Lowveld Savanna at Skukuza, South Africa. Remote Sensing. 2020; 12(23):3927. https://doi.org/10.3390/rs12233927
Chicago/Turabian StyleDe Lemos, Hugo, Michel M. Verstraete, and Mary Scholes. 2020. "Parametric Models to Characterize the Phenology of the Lowveld Savanna at Skukuza, South Africa" Remote Sensing 12, no. 23: 3927. https://doi.org/10.3390/rs12233927
APA StyleDe Lemos, H., Verstraete, M. M., & Scholes, M. (2020). Parametric Models to Characterize the Phenology of the Lowveld Savanna at Skukuza, South Africa. Remote Sensing, 12(23), 3927. https://doi.org/10.3390/rs12233927