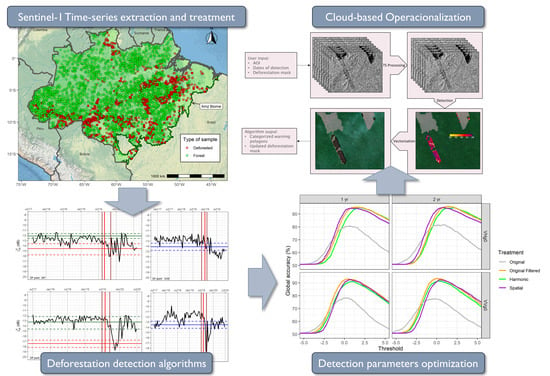
Optimizing Near Real-Time Detection of Deforestation on Tropical Rainforests Using Sentinel-1 Data
Abstract
1. Introduction
2. State of the Art
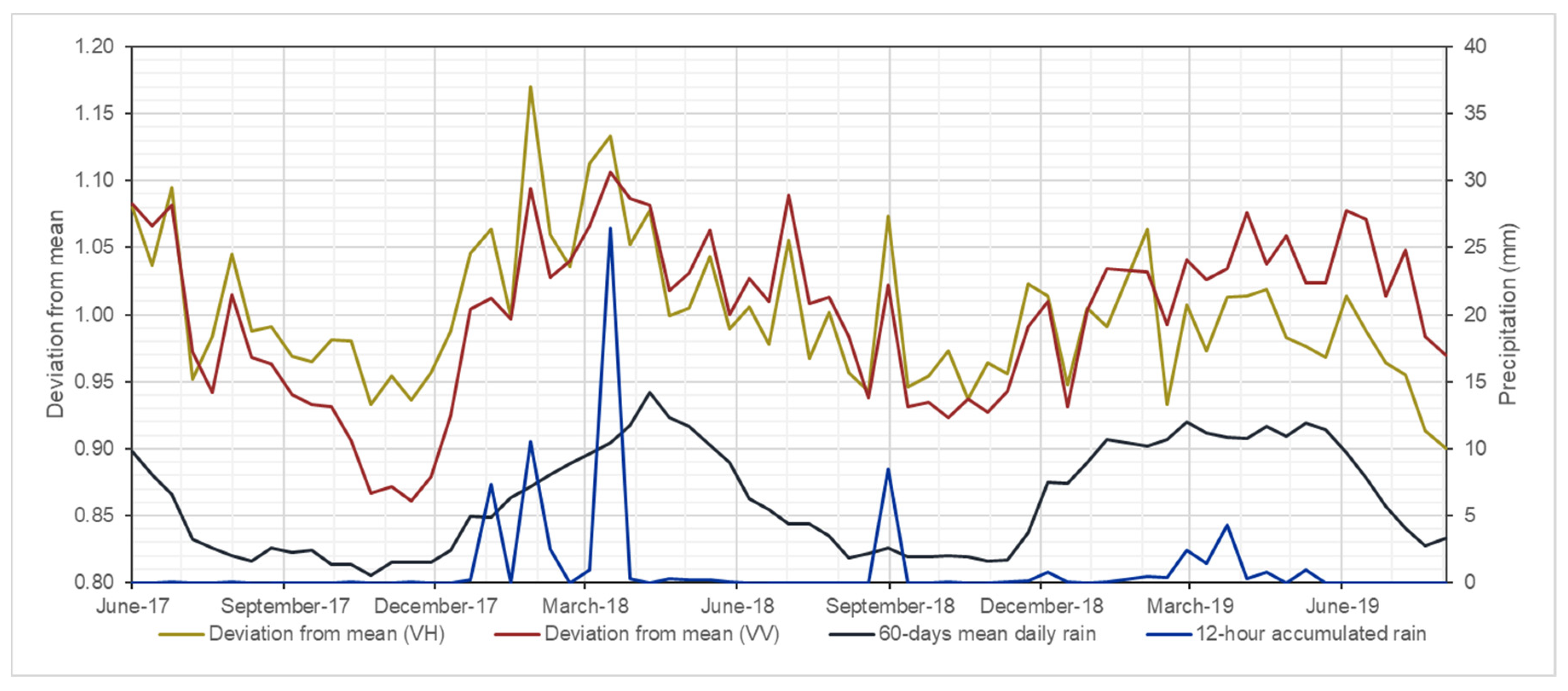
2.1. SAR Instability Mitigation
2.2. Deforestation Detection with SAR
3. Materials and Methods
3.1. Materials
3.1.1. SAR Data
- Orbit file correction: Updates orbit metadata with a restituted orbit file.
- GRD border noise removal: Removes low-intensity noise and invalid data on scene edges.
- Thermal noise removal: Removes additive noise in sub-swaths to help reduce discontinuities between sub-swaths for scenes in multi-swath acquisition modes.
- Radiometric calibration: Computes backscatter intensity using sensor calibration parameters in the GRD metadata.
- Terrain correction (orthorectification): Converts data from ground range geometry, which does not take terrain into account, to normalized backscatter coefficient using the SRTM 30 m DEM.
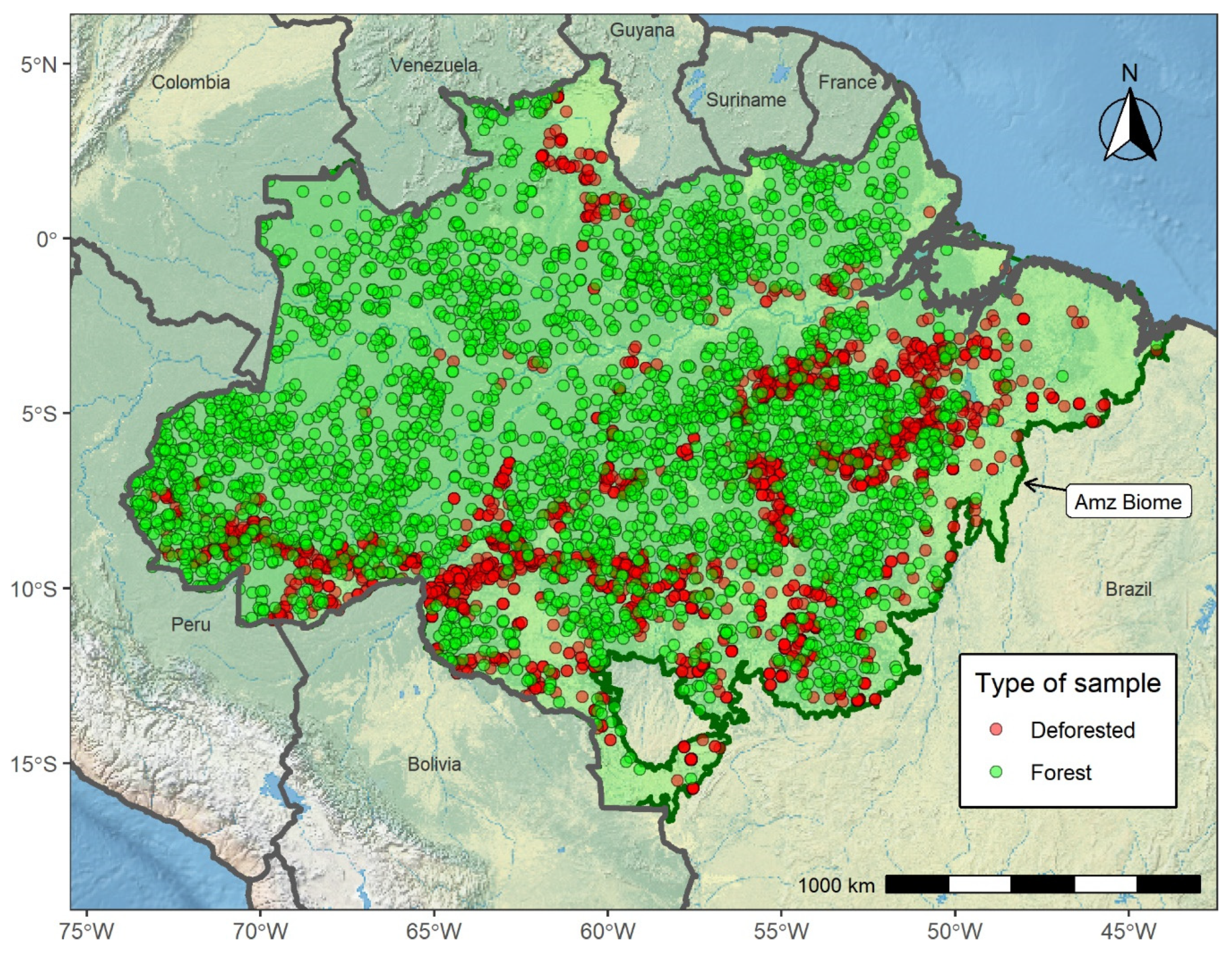
3.1.2. Sampling Spaces
3.2. Methods
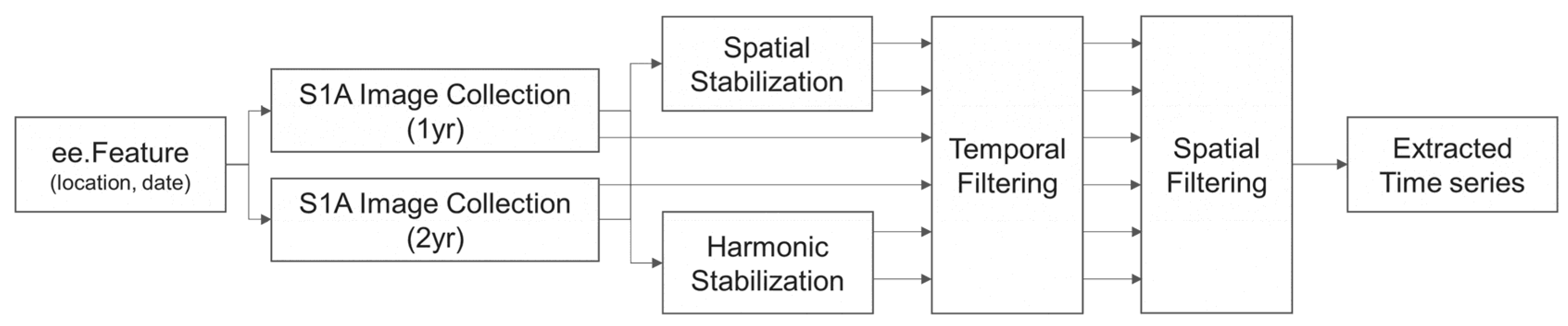
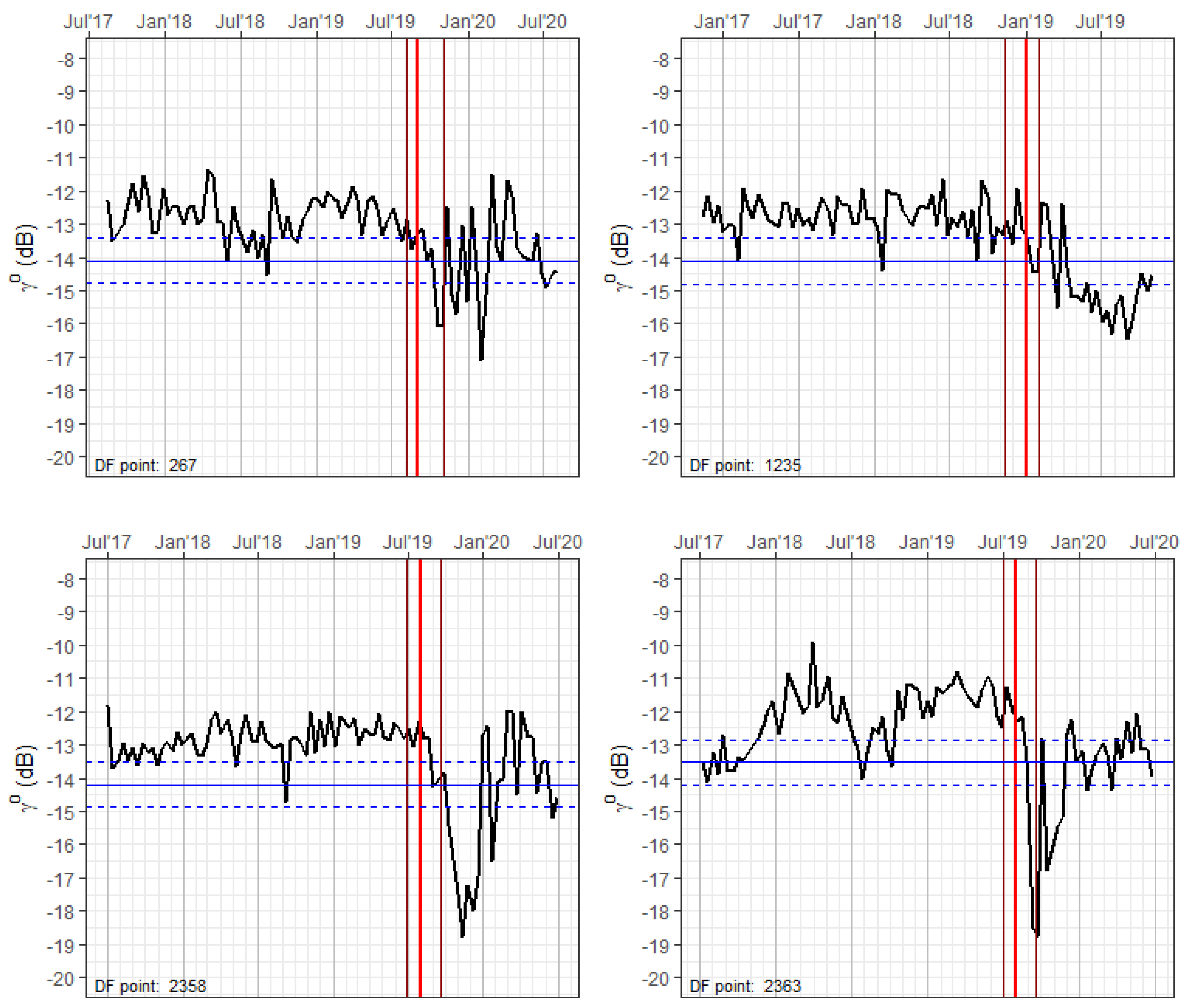
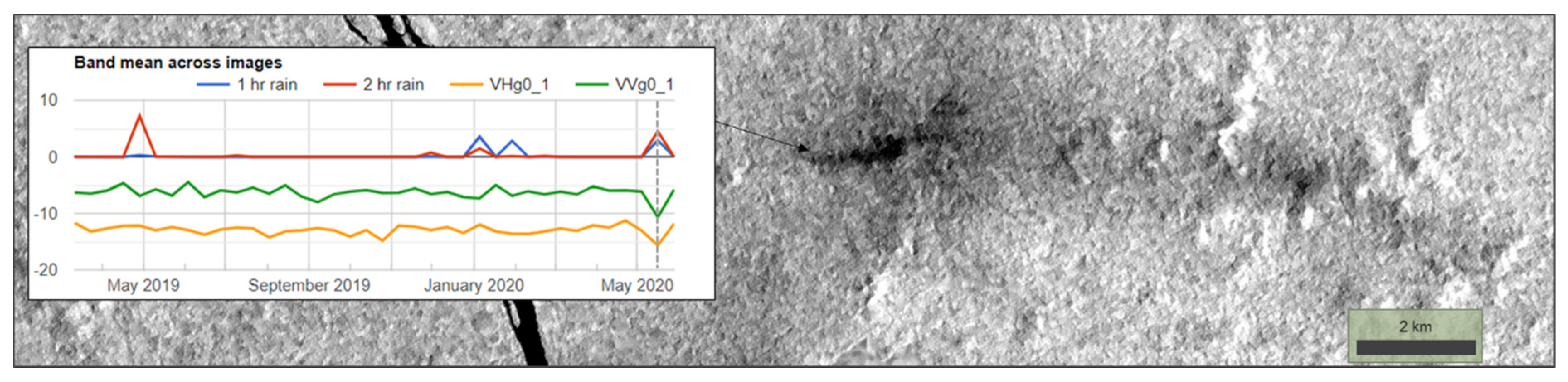
3.2.1. Time Series Stabilization
- Masking of all the available images of the interest area, leaving only the forest pixels unmasked. The forest mask is computed from previous knowledge of the deforestation history of the area and then applied to all the sensor images of the interest area.
- For every pixel of each image, the mean forest backscattering value is computed as the forest spatial mean of a 5 km radius neighborhood. This radius value was fixed considering the general spacing of the deforestation patches of the colonization roads of the Brazilian Amazon (the well-known ”fishbones”).
- For every image, the correction coefficient is computed as the ratio between the forest spatial mean to the temporal mean of the same forest mean computed along the entire time series.
- The final, stabilized backscatter value is computed by dividing the actual backscattering value by the correction coefficient.
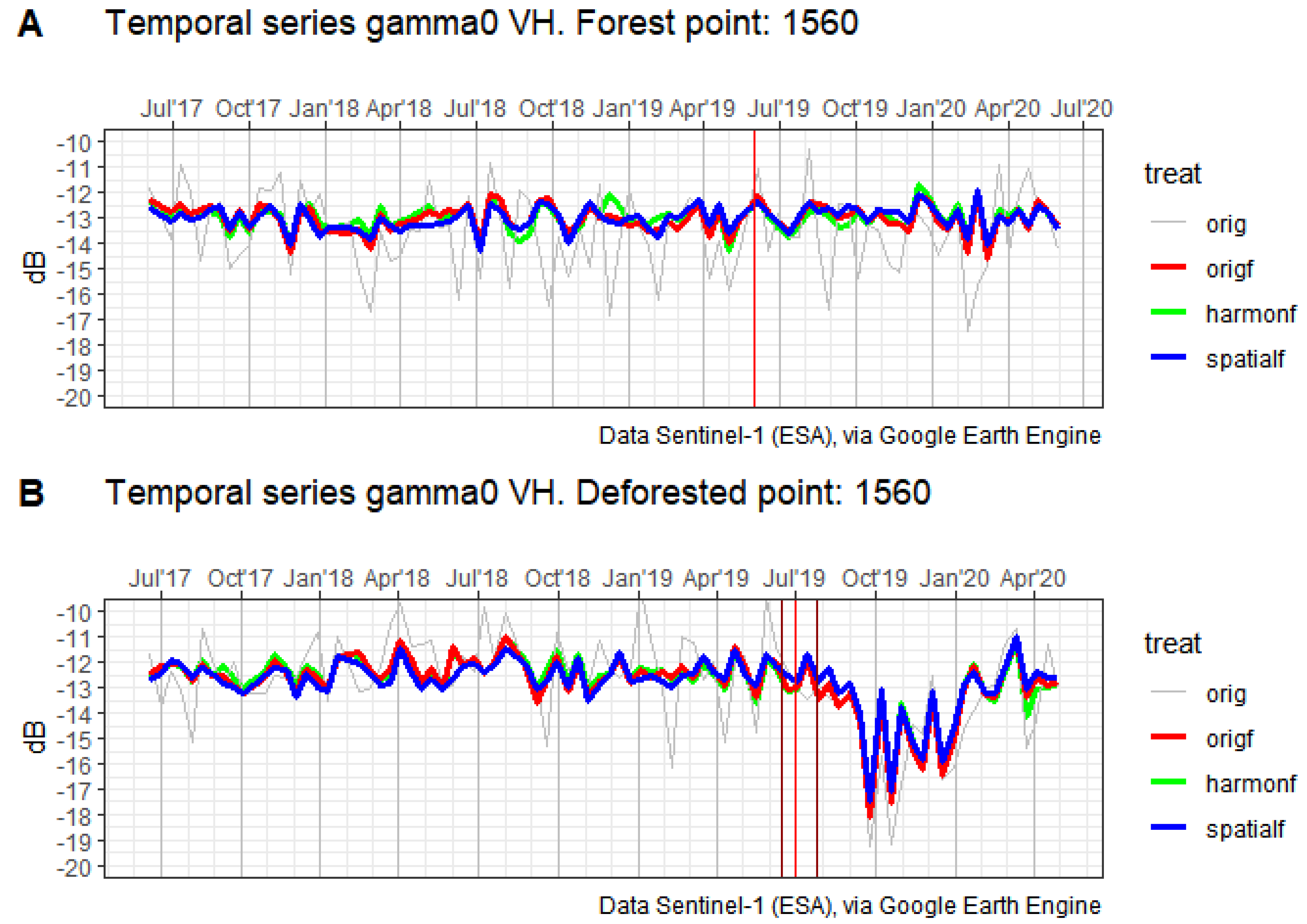
3.2.2. Time Series Filtering
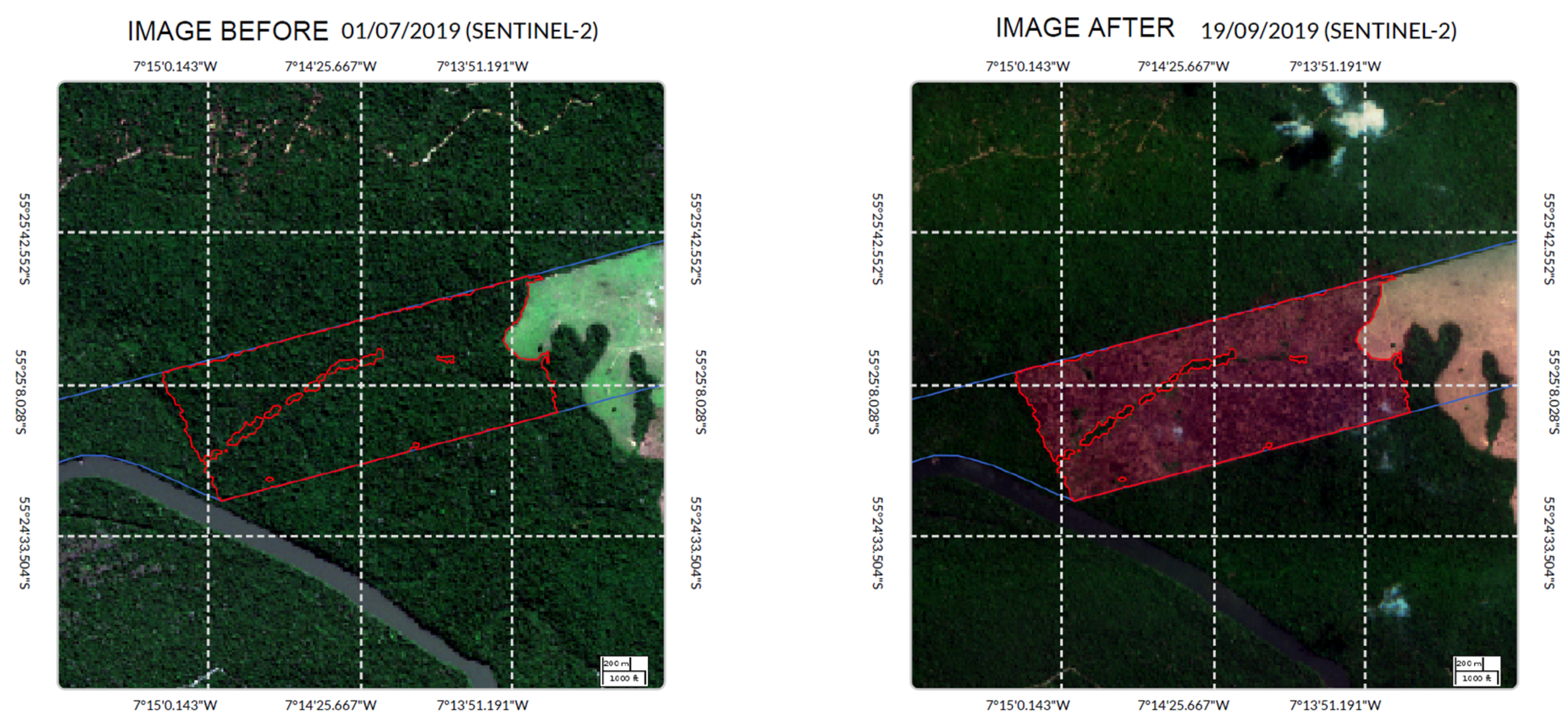
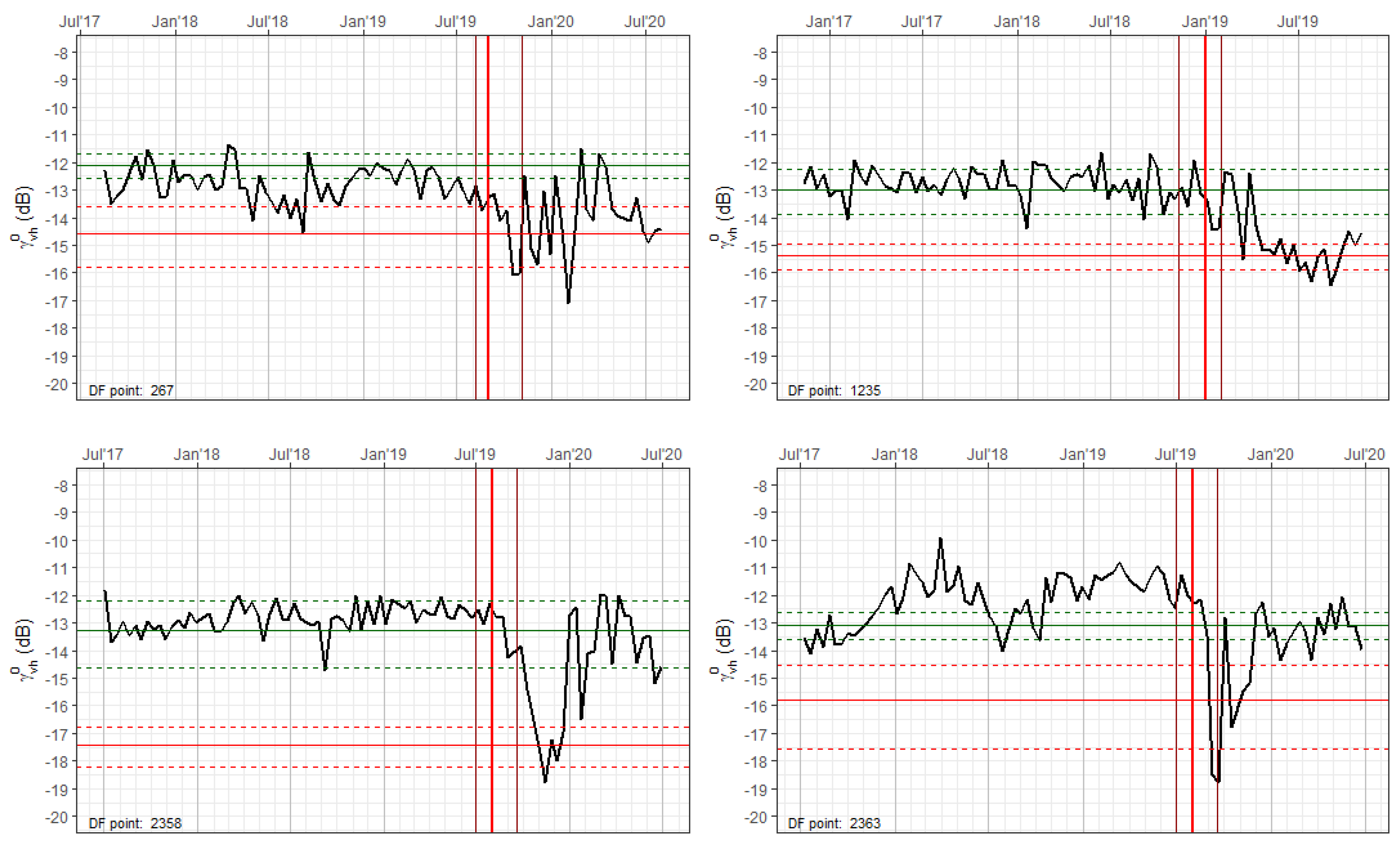
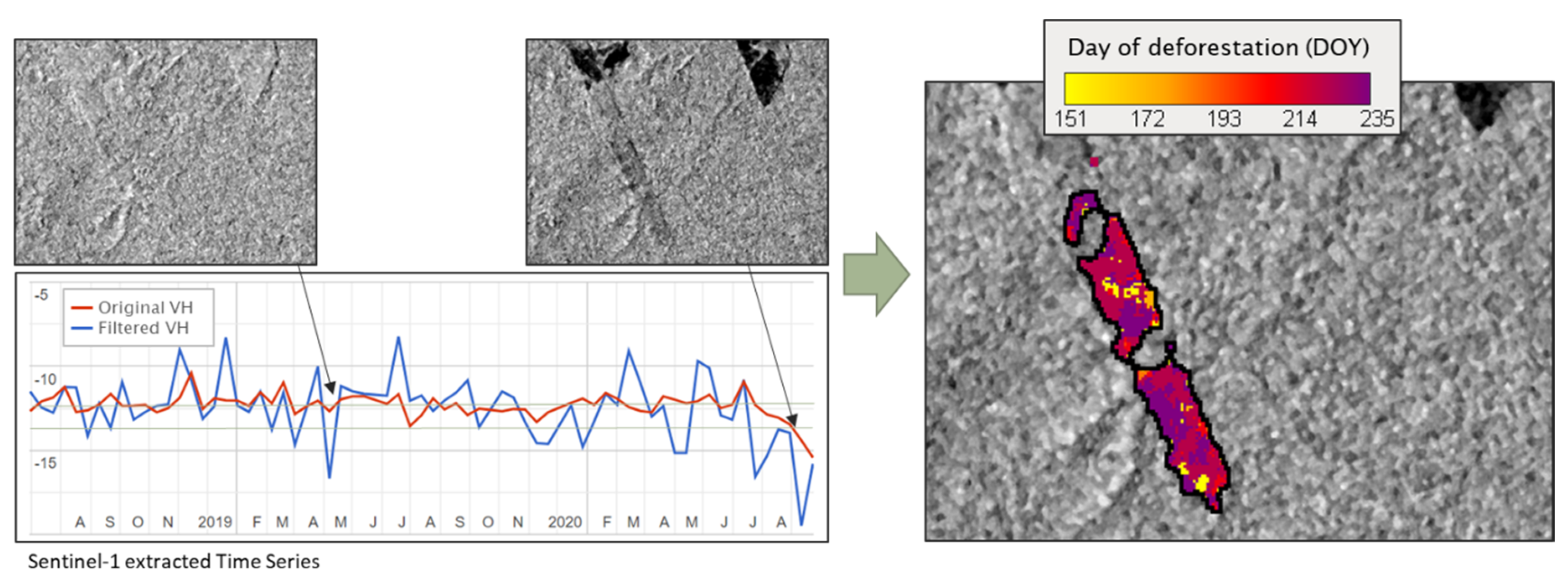
3.2.3. Deforestation Detection
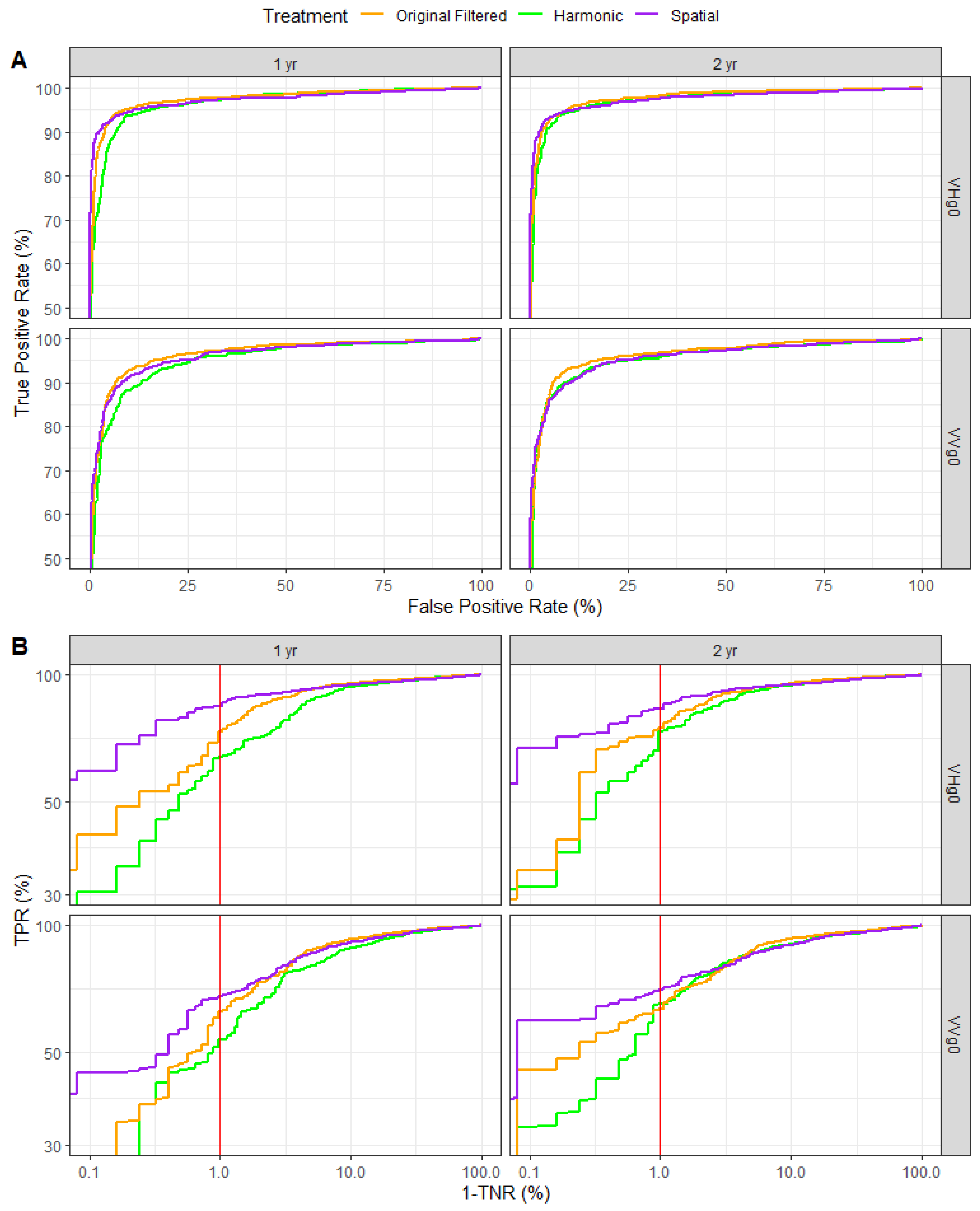
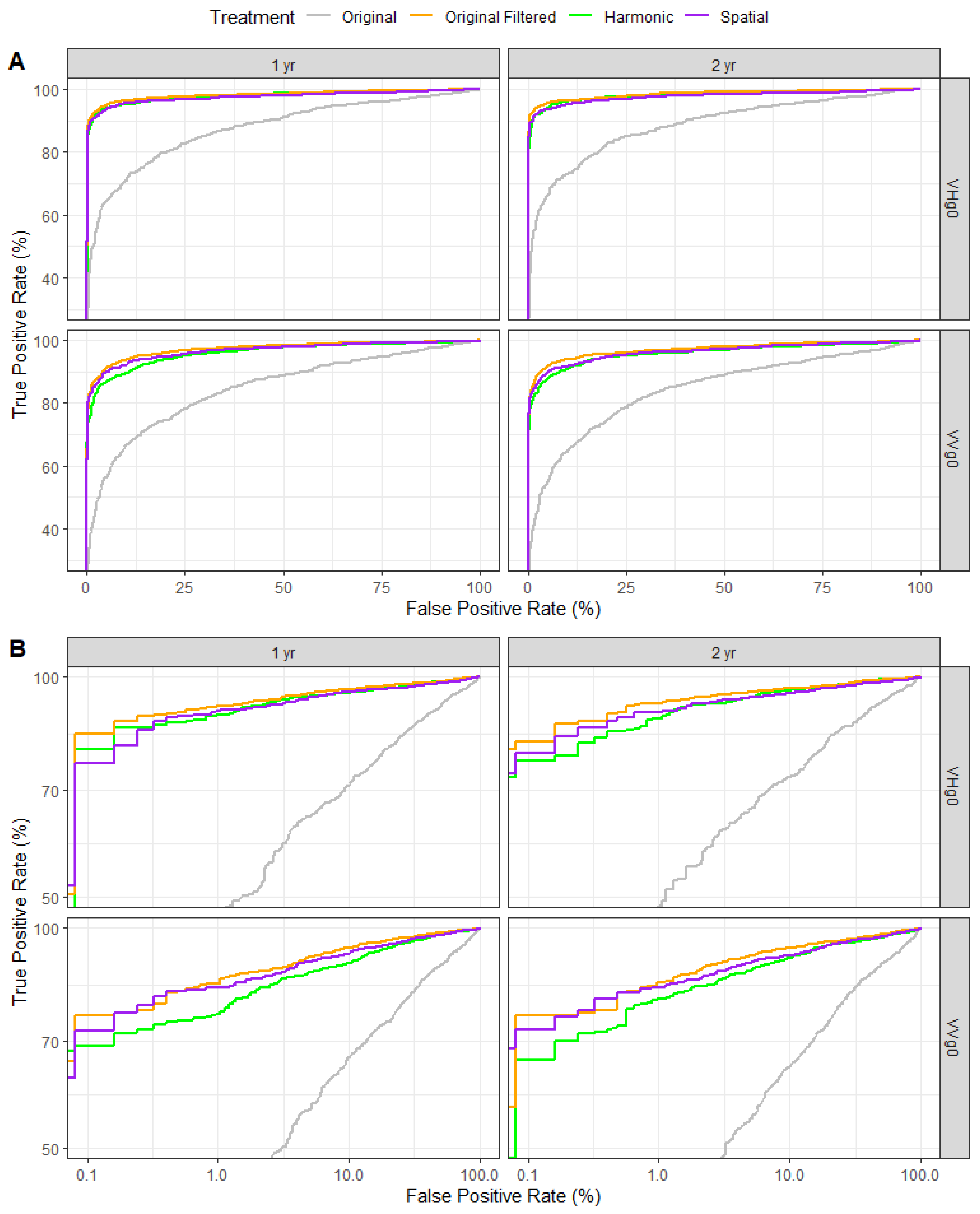
3.2.4. Detection Validation
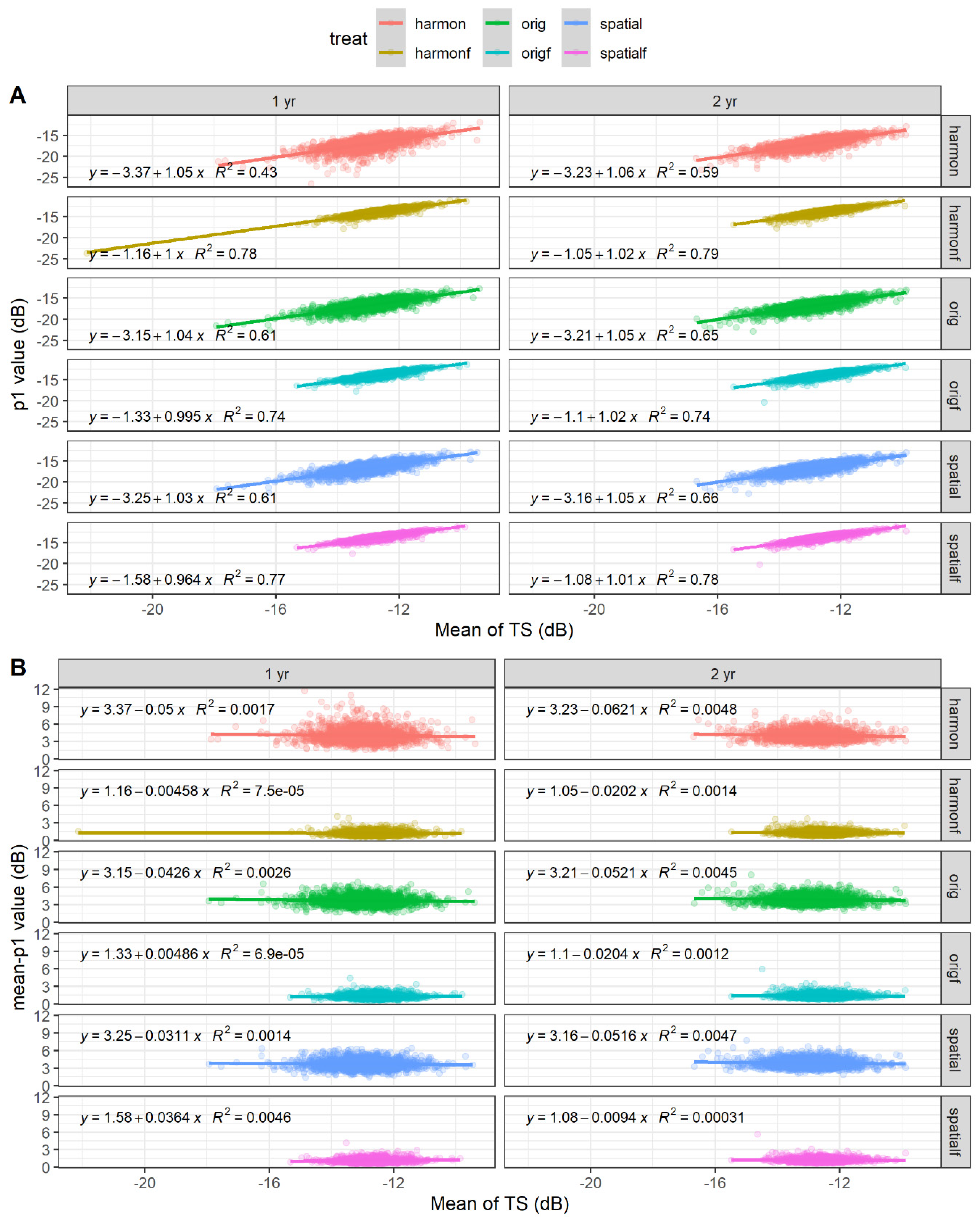
- Original backscattering values;
- Stabilized values;
- Filtered values.
- TP = True Positives, or the number of deforested locations classified as deforested;
- TN = True Negatives, or the number of forested locations classified as non-deforested;
- FP = False Positives, or the number of forested locations classified as deforested;
- FN = False Negatives, or the number of deforested locations classified as non-deforested
3.3. Code Availability
- Earth Engine Javascript Code Editor: Definition of the sampling locations.
- Earth Engine Python API: Extraction of filtered and stabilized time series at the selected locations.
- R [103]: Analysis of the results.
4. Results
- orig—original Sentinel-1 backscattering samples.
- origf—original TS filtered.
- harmon—original TS stabilized using harmonic fitting.
- harmonf—original TS stabilized using harmonic fitting and then filtered.
- spatial—original TS stabilized using spatial stabilization.
- spatialf—original TS stabilized using spatial stabilization and then filtered
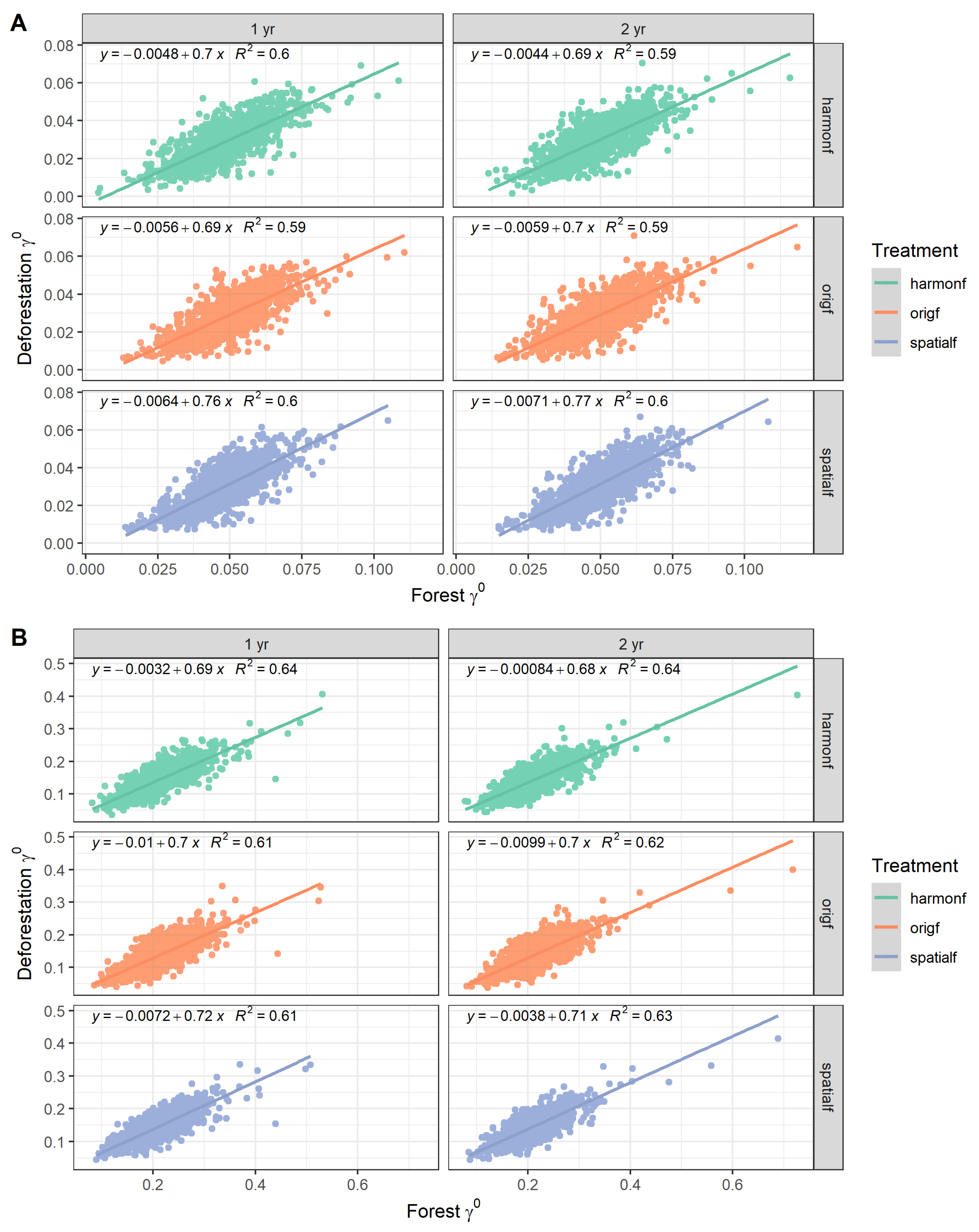
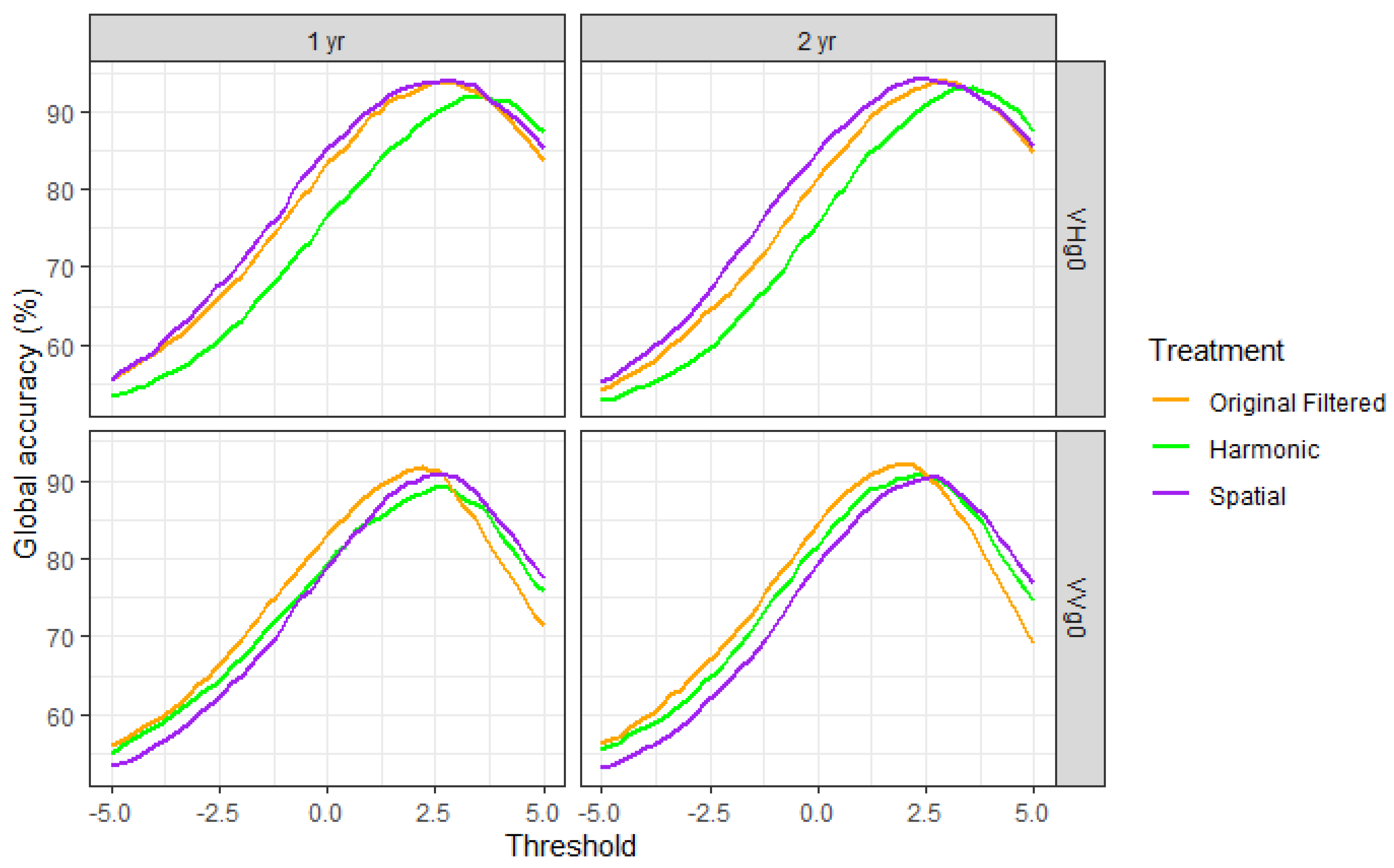
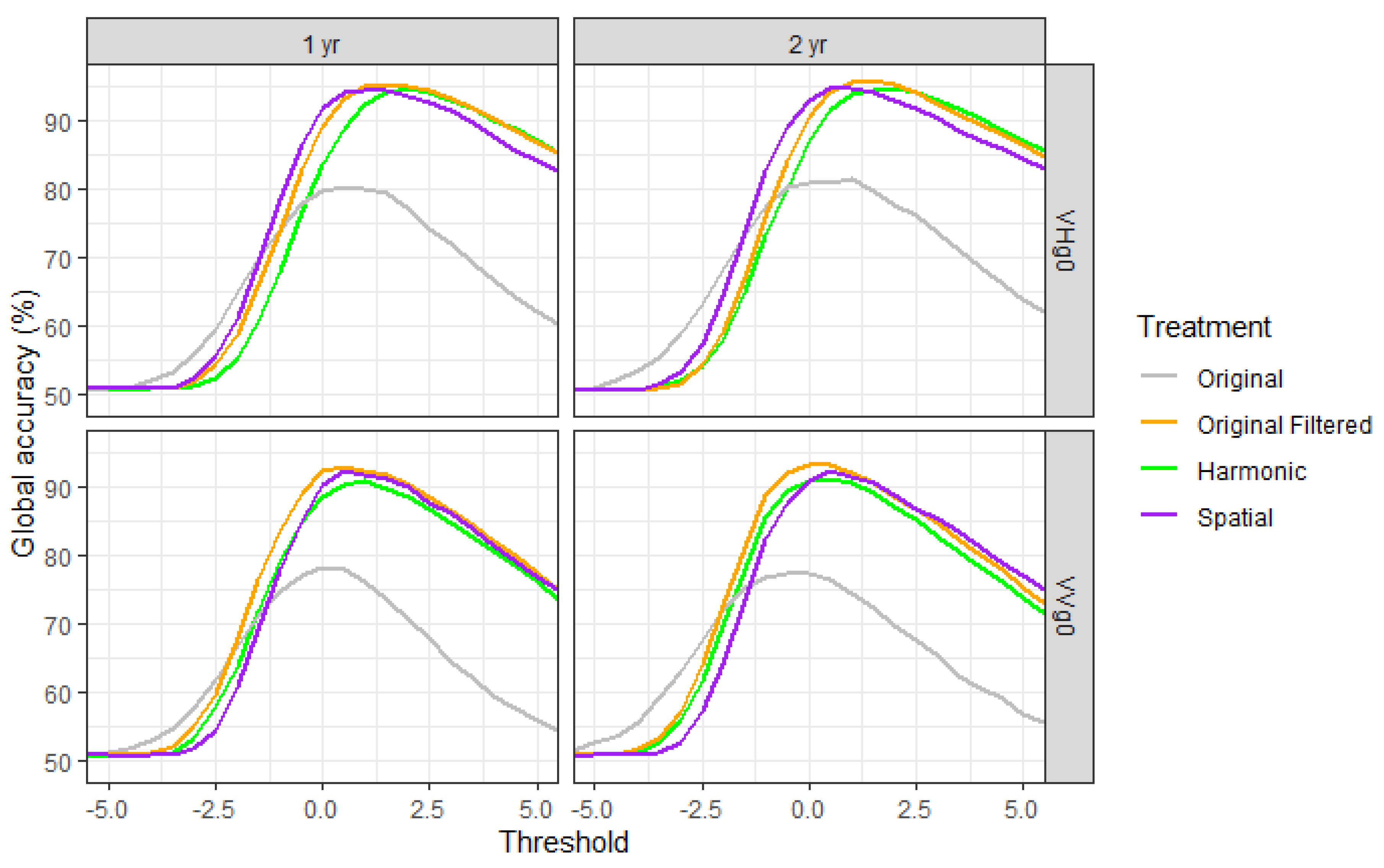
4.1. Detection of Deforestation
- Forest_mean = mean value of the validation TS samples before the deforestation date.
- Treatment_distance_mean = mean of the distances between the mean and the p1 value of the training dataset TS, for every treatment.
- Treatment_distance_sd = standard deviation of the distances between the mean and the p1 value of the training dataset TS, for every treatment.
- Central threshold = Forest_mean-Treatment_distance_mean.
- For thresholding_factor = −5 to 5:
- Threshold = Central_threshold-(Treatment_distance_sd*thresholding_factor).
- Flag TS samples < Threshold.
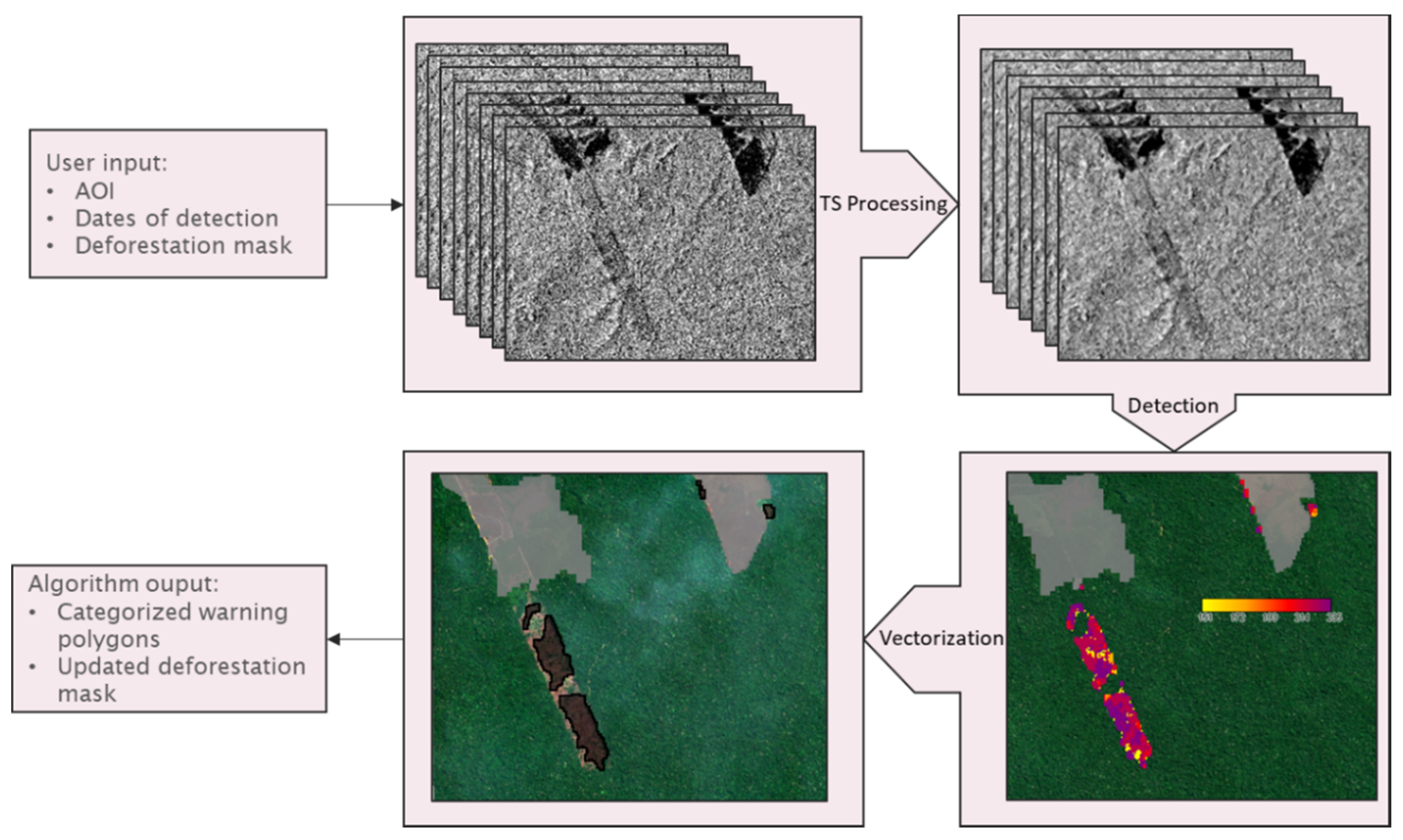
4.2. Algorithm Scalation to Support an EWS
5. Discussion
- Forest canopy with little or no damage.
- Initial deforestation, where some tree trunks and standing trees remain.
- Fire removes vegetation and promotes double bounce (remaining standing trees with bare soil) returns to the sensor.
- Pasture grows with increasing precipitation and remnants of burned vegetation
- Pasture reaches a decimetric height and becomes hardly distinguishable from the original forest cover for SAR-C incoherent signal.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- We Lost a Football Pitch of Primary Rainforest Every 6 Seconds in 2019. Available online: https://blog.globalforestwatch.org/data-and-research/global-tree-cover-loss-data-2019 (accessed on 30 June 2020).
- Monitoramento do Desmatamento da Floresta Amazônica Brasileira por Satélite. Available online: http://www.obt.inpe.br/OBT/assuntos/programas/amazonia/prodes (accessed on 10 July 2020).
- Early Warning Systems for Deforestation: An Explainer. Available online: https://blog.globalforestwatch.org/data-and-research/early-warning-systems-for-deforestation-an-explainer (accessed on 27 September 2019).
- Soares-Filho, B.; Moutinho, P.; Nepstad, D.; Anderson, A.; Rodrigues, H.; Garcia, R.; Dietzsch, L.; Merry, F.; Bowman, M.; Hissa, L.; et al. Role of Brazilian Amazon protected areas in climate change mitigation. Proc. Natl. Acad. Sci. USA 2010, 107, 10821–10826. [Google Scholar] [CrossRef] [PubMed]
- Assunção, J.; Gandour, C.; Rocha, R. DETERring Deforestation in the Brazilian Amazon: Environmental Monitoring and Law Enforcement TL-May. Clim. Policy Initiat. Rep. 2013, 1–36. Available online: https://climatepolicyinitiative.org/wp-content/uploads/2013/05/DETERring-Deforestation-in-the-Brazilian-Amazon-Environmental-Monitoring-and-Law-Enforcement-Technical-Paper.pdf (accessed on 30 October 2019).
- Nepstad, D.; McGrath, D.; Stickler, C.; Alencar, A.; Azevedo, A.; Swette, B.; Bezerra, T.; DiGiano, M.; Shimada, J.; Da Motta, R.S.; et al. Slowing Amazon deforestation through public policy and interventions in beef and soy supply chains. Science 2014, 344, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Finer, B.M.; Novoa, S.; Weisse, M.J.; Petersen, R.; Mascaro, J.; Souto, T.; Stearns, F.; Martinez, R.G. Combating deforestation: From satellite to intervention. Science 2018, 360, 1303–1305. [Google Scholar] [CrossRef] [PubMed]
- Indonesian Ban on Clearing New Swaths of Forest to be Made Permanent. Available online: https://news.mongabay.com/2019/06/indonesian-ban-on-clearing-new-swaths-of-forest-to-be-made-permanent (accessed on 20 June 2020).
- Hansen, M.C.; Krylov, A.; Tyukavina, A.; Potapov, P.V.; Turubanova, S.; Zutta, B.; Ifo, S.; Margono, B.; Stolle, F.; Moore, R. Humid tropical forest disturbance alerts using Landsat data. Environ. Res. Lett. 2016, 11, 034008. [Google Scholar] [CrossRef]
- Reiche, J.; Lucas, R.; Mitchell, A.L.; Verbesselt, J.; Hoekman, D.H.; Haarpaintner, J.; Kellndorfer, J.M.; Rosenqvist, A.; Lehmann, E.A.; Woodcock, C.E.; et al. Combining satellite data for better tropical forest monitoring. Nat. Clim. Chang. 2016, 6, 120–122. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Alparone, L.; Bianchi, T. A tutorial on speckle reduction in synthetic aperture radar images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Davies, K.; Smith, E.K. Ionospheric effects on satellite land mobile systems. IEEE Antennas Propag. Mag. 2002, 44, 24–31. [Google Scholar] [CrossRef]
- Bouvet, A.; Le Toan, T.; Floury, N.; MacKlin, T. An end-to-end error model for classification methods based on temporal change or polarization ratio of SAR intensities. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3521–3538. [Google Scholar] [CrossRef]
- Atlas, D.; Rosenfeld, D.; Wolff, D.B. C-band attenuation by tropical rainfall in Darwin, Australia, using climatologically tuned Ze-R relations. J. Appl. Meteorol. 1993, 32, 426–430. [Google Scholar] [CrossRef]
- Kasilingam, D.; Lin, I.I.; Lim, H.; Khoo, V.; Alpers, W.; Lim, T.K. Investigation of tropical rain cells with ERS SAR imagery and ground-based weather radar. In Proceedings of the Third ERS Symposium on Space at the Service of our Environment, Florence, Italy, 14–21 March 1997; Guyenne, T.D., Danesy, D., Eds.; European Space Agency, ESA Publications Division: Noordwijk, The Netherlands, 1997; Volume 414, pp. 1603–1608. [Google Scholar]
- Lin, I.I.; Kasilingam, D.; Alpers, W.; Lim, T.K.; Lim, H.; Khoo, V. A quantitative study of tropical rain cells from ERS SAR imagery. In Proceedings of the International Geoscience and Remote Sensing Symposium, Singapore, 3–8 August 1997; Stein, T.I., Ed.; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1997; pp. 1527–1529. [Google Scholar]
- Dobson, M.C.; Pierce, L.; McDonald, K.; Sharik, T. Seasonal change in radar backscatter from mixed conifer and hardwood forests in northern Michigan. Dig.-Int. Geosci. Remote Sens. Symp. 1991, 3, 1121–1124. [Google Scholar] [CrossRef]
- Henderson, F.M.; Lewis, A.J. Principles and Applications of Imaging Radar, Manual of Remote Sensing, 3rd ed.; John Wiley and Sons, Inc.: Somerset, NJ, USA, 1999; Volume 2. [Google Scholar]
- De Jong, J.; Klaassen, W.; Ballast, A. Rain storage in forests detected with ERS tandem mission SAR. Remote Sens. Environ. 2000, 72, 170–180. [Google Scholar] [CrossRef]
- Cisneros Vaca, C.; Van Der Tol, C. Sensitivity of sentinel-1 to rain stored in temperate forest. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; IGARSS: Valencia, Spain, 2018; pp. 5330–5333. [Google Scholar]
- Quegan, S.; Toan, L.; T, Y.; J, J.; Ribbes, F.; Floury, N. Multitemporal ERS SAR analysis applied to forest mapping. Remote Sens. Environ. 2000, 38, 741–753. [Google Scholar] [CrossRef]
- Danklmayer, A.; Doring, B.R.J.; Schwerdt, M.; Chandra, M. Assessment of atmospheric propagation effects in SAR images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3507–3518. [Google Scholar] [CrossRef]
- Moore, R.K.; Mogili, A.; Fang, Y.; Beh, B.; Ahamad, A. Rain measurement with SIR-C/X-SAR. Remote Sens. Environ. 1997, 59, 280–293. [Google Scholar] [CrossRef]
- Koyama, C.N.; Watanabe, M.; Hayashi, M.; Shimada, M. The effect of precipitation and soil moisture variations on (partial) polarimetric L-band SAR backscatter in tropical forest regions. In Proceedings of the International Geoscience and Remote Sensing Symposium, Singapore, 3–8 August 2017; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2017; pp. 2450–2453. [Google Scholar]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Bazzi, H. Synergic use of Sentinel-1 and Sentinel-2 images for operational soil moisture mapping at high spatial resolution over agricultural areas. Remote Sens. 2017, 9, 1292. [Google Scholar] [CrossRef]
- Benninga, H.-J.F.; van der Velde, R.; Su, Z. Impacts of Radiometric Uncertainty and Weather-Related Surface Conditions on Soil Moisture Retrievals with Sentinel-1. Remote Sens. 2019, 11, 2025. [Google Scholar] [CrossRef]
- Doblas, J.; Carneiro, A.; Shimabukuro, Y.; Sant’Anna, S.; Aragão, L. Assessment of rainfall influence on sentinel-1 time series on amazonian tropical forests aiming deforestation detection improvement. In Proceedings of the IEEE Latin American GRSS ISPRS Remote Sensing Conference (LAGIRS), Santiago de Chile, Chile, 22–27 March 2020; IEEE: Santiago de Chile, Chile, 2020; pp. 397–402. [Google Scholar]
- Reiche, J.; Verhoeven, R.; Verbesselt, J.; Hamunyela, E.; Wielaard, N.; Herold, M. Characterizing tropical forest cover loss using dense Sentinel-1 data and active fire alerts. Remote Sens. 2018, 10, 777. [Google Scholar] [CrossRef]
- Reiche, J.; Hamunyela, E.; Verbesselt, J.; Hoekman, D.; Herold, M. Improving near-real time deforestation monitoring in tropical dry forests by combining dense Sentinel-1 time series with Landsat and ALOS-2 PALSAR-2. Remote Sens. Environ. 2017, 204, 147–161. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Angelliaume, S. Analysis of Sentinel-1 radiometric stability and quality for land surface applications. Remote Sens. 2016, 8, 406. [Google Scholar] [CrossRef]
- Doblas, J.; Carneiro, A.; Shimabukuro, Y.; Sant’anna, S.; Aragão, L.; Pereira, F.R.S. Stabilization of sentinel-1 sar time-series using climate and forest structure data for early tropical deforestation detection. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 89–96. [Google Scholar] [CrossRef]
- FAO. Global Forest Resources Assessment 2020-Key Findings; Food and Agriculture Organization of the United nations: Rome, Italy, 2020. [Google Scholar] [CrossRef]
- FAO. Global Forest Resources Assessment 2020: Terms and Definition; Food and Agriculture Organization of the United nations: Rome, Italy, 2020. [Google Scholar]
- INPE. Metodologia Utilizada nos Projetos PRODES e DETER; INPE: São José dos Campos, Brazil, 2019. [Google Scholar]
- Almeida-Filho, R.; Rosenqvist, A.; Shimabukuro, Y.E.; Dos Santos, J.R. Evaluation and perspectives of using multitemporal L-band SAR data to monitor deforestation in the Brazilian Amazônia. IEEE Geosci. Remote Sens. Lett. 2005, 2, 409–412. [Google Scholar] [CrossRef]
- Shimabukuro, Y.E.; Almeida-Filho, R.; Kuplich, T.M.; de Freitas, R.M. Quantifying optical and SAR image relationships for tropical landscape features in the Amazônia. Int. J. Remote Sens. 2007, 28, 3831–3840. [Google Scholar] [CrossRef]
- Whittle, M.; Quegan, S.; Uryu, Y.; Stüewe, M.; Yulianto, K. Detection of tropical deforestation using ALOS-PALSAR: A Sumatran case study. Remote Sens. Environ. 2012, 124, 83–98. [Google Scholar] [CrossRef]
- Watanabe, M.; Koyama, C.; Hayashi, M.; Kaneko, Y.; Shimada, M. Development of early-stage deforestation detection algorithm (advanced) with PALSAR-2/ScanSAR for JICA-JAXA program (JJ-FAST). Int. Geosci. Remote Sens. Symp. 2017, 2017, 2446–2449. [Google Scholar] [CrossRef]
- Tanase, M.A.; Villard, L.; Pitar, D.; Apostol, B.; Petrila, M.; Chivulescu, S.; Leca, S.; Borlaf-Mena, I.; Pascu, I.S.; Dobre, A.C.; et al. Synthetic aperture radar sensitivity to forest changes: A simulations-based study for the Romanian forests. Sci. Total Environ. 2019, 689, 1104–1114. [Google Scholar] [CrossRef] [PubMed]
- Joshi, N.; Mitchard, E.T.A.; Woo, N.; Torres, J.; Moll-Rocek, J.; Ehammer, A.; Collins, M.; Jepsen, M.R.; Fensholt, R. Mapping dynamics of deforestation and forest degradation in tropical forests using radar satellite data. Environ. Res. Lett. 2015, 10, 034014. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Ballère, M.; Koleck, T.; Le Toan, T. Use of the SAR Shadowing Effect for Deforestation Detection with Sentinel-1 Time Series. Remote Sens. 2018, 10, 1250. [Google Scholar] [CrossRef]
- Rahman, M.M.; Sumantyo, J.T.S. Mapping tropical forest cover and deforestation using synthetic aperture radar (SAR) images. Appl. Geomatics 2010, 2, 113–121. [Google Scholar] [CrossRef]
- Balzter, H.; Cole, B.; Thiel, C.; Schmullius, C. Mapping CORINE land cover from Sentinel-1A SAR and SRTM digital elevation model data using random forests. Remote Sens. 2015, 7, 14876–14898. [Google Scholar] [CrossRef]
- Pereira, L.O.; Freitas, C.C.; Sant’Anna, S.J.S.; Reis, M.S. ALOS/PALSAR Data Evaluation for Land Use and Land Cover Mapping in the Amazon Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5413–5423. [Google Scholar] [CrossRef]
- Angelis, C.F.; Freitas, C.C.; Valeriano, D.M.; Dutra, L.V. Multitemporal analysis of land use/land cover JERS-1 backscatter in the Brazilian tropical rainforest. Int. J. Remote Sens. 2002, 23, 1231–1240. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Soares, J.V.; Alves, D.S. Mapping deforestation and land use in Amazon rainforest by using SIR-C imagery. Remote Sens. Environ. 1997, 59, 191–202. [Google Scholar] [CrossRef]
- Mercier, A.; Betbeder, J.; Rumiano, F.; Baudry, J.; Gond, V.; Blanc, L.; Bourgoin, C.; Cornu, G.; Ciudad, C.; Marchamalo, M.; et al. Evaluation of Sentinel-1 and 2 Time Series for Land Cover Classification of Forest–Agriculture Mosaics in Temperate and Tropical Landscapes. Remote Sens. 2019, 11, 979. [Google Scholar] [CrossRef]
- Cassol, H.L.G.; Shimabukuro, Y.E.; Beuchle, R.; Aragão, L.E.O.C. Sentinel-1 Time-Series Analysis For Detection Of Forest Degradation By Selective Logging. In Proceedings of the Simpósio Brasileiro de Sensoriamento Remoto; INPE: Santos, SP, Brazil, 2019; pp. 755–758. [Google Scholar]
- Varghese, A.O.; Suryavanshi, A.; Joshi, A.K. Analysis of different polarimetric target decomposition methods in forest density classification using C band SAR data. Int. J. Remote Sens. 2016, 37, 694–709. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-Component Scattering Model for Polarimetric SAR Image Decomposition based on Asymmetric Covariance Matrix. IEEE Trans. Geosci. Remote Sens. 2005, 104, 1699–1706. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Wiederkehr, N.C.; Gama, F.F.; Santos, J.R.; Mura, J.C.; Bispo, P.C.; Liesenberg, V. Análise de imagens polarimétricas do sensor ALOS/PALSAR-2 para discriminação do uso e cobertura da terra em região de influência da Floresta Nacional do Tapajós. In Proceedings of the XXVII Congr. Bras. Cartogr., Rio de Janeiro, Brazil, 6–9 November 2017; SBC: Rio de Janeiro, Brazil, 2017; pp. 654–658. [Google Scholar]
- Gama, F.F.; Paradella, W.R.; Mura, J.C.; Santos, A.R. dos Técnicas de interferometria radar na detecção de deformação superficial utilizando dados orbitais. In Proceedings of the Anais XVI Simposio Brasileiro de Sensoriamento Remoto-SBSR, Foz do Iguaçu, Brazil, 13–18 April 2013; INPE: Foz de Iguaçu, Brazil, 2013; pp. 6917–6922. [Google Scholar]
- Hagberg, J.O.; Ulander, L.M.H.; Askne, J. Repeat-pass SAR interferometry over forested terrain. IEEE Trans. Geosci. Remote Sens. 1995, 33, 331–340. [Google Scholar] [CrossRef]
- Askne, J.I.H.; Dammert, P.B.G.; Ulander, L.M.H.; Smith, G. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens. 1997, 35, 25–35. [Google Scholar] [CrossRef]
- Luckman, A.; Baker, J.; Wegmuller, U. Repeat-pass interferometric coherence measurements of tropical forest from JERS and ERS satellites. In Proceedings of the IGARSS ’98. Sensing and Managing the Environment. 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings: (Cat. No.98CH36174), Seattle, WA, USA, 6–10 July 1998; Volume 4, pp. 1828–1830. [Google Scholar]
- Strozzi, T.; Wegmuller, U.; Luckman, A.; Balzter, H. Mapping deforestation in Amazon with ERS SAR interferometry. Int. Geosci. Remote Sens. Symp. 1999, 2, 767–769. [Google Scholar] [CrossRef]
- Luckman, A.; Baker, J.; Wegmüller, U. Repeat-pass interferometric coherence measurements of disturbed tropical forest from JERS and ERS satellites. Remote Sens. Environ. 2000, 73, 350–360. [Google Scholar] [CrossRef]
- Gaboardi, C. Utilização de Imagem de Coerência SAR Para Classificação Do Uso Da Terra: Floresta Nacional Do Tapajós. Ph.D. Thesis, Instituto Nacional de Pesquisas Espaciais (INPE), Sao Jose dos Campos, Brazil, 11 June 2002. [Google Scholar]
- Hamadi, A.; Villard, L.; Borderies, P.; Albinet, C.; Koleck, T.; Le Toan, T. Comparative Analysis of Temporal Decorrelation at P-Band and Low L-Band Frequencies Using a Tower-Based Scatterometer over a Tropical Forest. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1918–1922. [Google Scholar] [CrossRef]
- El Idrissi Essebtey, S.; Villard, L.; Borderies, P.; Koleck, T.; Monvoisin, J.P.; Burban, B.; Le Toan, T. Temporal Decorrelation of Tropical Dense Forest at C-Band: First Insights From the TropiScat-2 Experiment. IEEE Geosci. Remote Sens. Lett. 2019, 1–5. [Google Scholar] [CrossRef]
- Diniz, J.M. Avaliação do Potencial Dos Dados Polarimétricos Sentinel-1A Para Mapeamento Do Uso e Cobertura da Terra na Região de Ariquemes (RO). Master’s Thesis, Instituto Nacional de Pesquisas Espaciais (INPE), Sao Jose dos Campos, Brazil, 15 February 2019. [Google Scholar]
- Sica, F.; Pulella, A.; Nannini, M.; Pinheiro, M.; Rizzoli, P. Repeat-pass SAR interferometry for land cover classification: A methodology using Sentinel-1 Short-Time-Series. Remote Sens. Environ. 2019, 232, 111277. [Google Scholar] [CrossRef]
- Cihlar, J.; Pultz, T.J.; Gray, A.L. Change detection with synthetic aperture radar. Int. J. Remote Sens. 1992, 13, 401–414. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, D.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Bruzzone, L.; Prieto, D.F. Automatic Analysis of the Difference Image for Unsupervised Change Detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Kittler, J.; Illingworth, J. Minimum Error Thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An Unsupervised Approach Based on the Generalized Gaussian Model to Automatic Change Detection in Multitemporal SAR Images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Reiche, J.; de Bruin, S.; Hoekman, D.; Verbesselt, J.; Herold, M. A Bayesian approach to combine landsat and ALOS PALSAR time series for near real-time deforestation detection. Remote Sens. 2015, 7, 4973–4996. [Google Scholar] [CrossRef]
- Frontiers in Forest Monitoring: Research Horizons for Global Forest Watch. Available online: https://www.youtube.com/watch?v=aM227q31uZ8 (accessed on 15 August 2020).
- Pirrone, D.; Bovolo, F.; Bruzzone, L. A Novel Framework Based on Polarimetric Change Vectors for Unsupervised Multiclass Change Detection in Dual-Pol Intensity SAR Images. IEEE Trans. Geosci. Remote Sens. 2020, 1–16. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.; Schou, J.; Skriver, H. A test statistic in the complex wishart distribution and its application to change detection in polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 4–19. [Google Scholar] [CrossRef]
- Yang, W.; Yang, X.; Yan, T.; Song, H.; Xia, G.S. Region-Based Change Detection for Polarimetric SAR Images Using Wishart Mixture Models. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6746–6756. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.A.; Skriver, H. Determining the Points of Change in Time Series of Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3007–3024. [Google Scholar] [CrossRef]
- Muro, J.; Canty, M.; Conradsen, K.; Hüttich, C.; Nielsen, A.A.; Skriver, H.; Remy, F.; Strauch, A.; Thonfeld, F.; Menz, G. Short-term change detection in wetlands using Sentinel-1 time series. Remote Sens. 2016, 8, 795. [Google Scholar] [CrossRef]
- Cloude, S.R. The Dual Polarisation Entropy / Alpha Decomposition. In Proceedings of the 3rd International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, Frascati, Italy, 22–26 January 2007; pp. 1–6. [Google Scholar]
- Ji, K.; Wu, Y. Scattering mechanism extraction by a modified Cloude-Pottier decomposition for dual polarization SAR. Remote Sens. 2015, 7, 7447–7470. [Google Scholar] [CrossRef]
- Khati, U.; Kumar, V.; Bandyopadhyay, D.; Musthafa, M.; Singh, G. Identification of forest cutting in managed forest of Haldwani, India using ALOS-2/PALSAR-2 SAR data. J. Environ. Manag. 2018, 213, 503–512. [Google Scholar] [CrossRef]
- Lavalle, M. A new automated algorithm for detecting forest disturbances with the dual-polarimetric SAR alpha angle. Int. Geosci. Remote Sens. Symp. 2017, 2017, 5299–5302. [Google Scholar] [CrossRef]
- Wahl, D.E.; Yocky, D.A.; Jakowatz, C.V.; Simonson, K.M. A New Maximum-Likelihood Change Estimator for Two-Pass SAR Coherent Change Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2460–2469. [Google Scholar] [CrossRef]
- Rizzoli, P.; Bello, J.L.B.; Pulella, A.; Sica, F.; Zink, M. A Novel Approach to Monitor Deforestation in the Amazon Rainforest by Means of Sentinel-1 and Tandem-X Data. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, {IGARSS} 2018, Valencia, Spain, 22–27 July 2018; pp. 192–195. [Google Scholar]
- White, R.G. Change detection in SAR imagery. Int. J. Remote Sens. 1991, 12, 339–360. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, J.; Liu, J.; Miao, Q.; Jiao, L. Change Detection in Synthetic Aperture Radar Images Based on Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 125–138. [Google Scholar] [CrossRef]
- Gong, M.; Yang, H.; Zhang, P. Feature learning and change feature classification based on deep learning for ternary change detection in SAR images. ISPRS J. Photogramm. Remote Sens. 2017, 129, 212–225. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A Deep Convolutional Coupling Network for Change Detection Based on Heterogeneous Optical and Radar Images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Lv, N.; Chen, C.; Qiu, T.; Sangaiah, A.K. Deep Learning and Superpixel Feature Extraction Based on Contractive Autoencoder for Change Detection in SAR Images. IEEE Trans. Ind. Inform. 2018, 14, 5530–5538. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, L.; Liang, M.; Liu, F.; Yang, S.; Hou, B. Fast unsupervised deep fusion network for change detection of multitemporal SAR images. Neurocomputing 2019, 332, 56–70. [Google Scholar] [CrossRef]
- Xu, S.; Mu, X.; Chai, D.; Zhang, X. Remote sensing image scene classification based on generative adversarial networks. Remote Sens. Lett. 2018, 9, 617–626. [Google Scholar] [CrossRef]
- Zhu, X.X.; Montazeri, S.; Ali, M.; Hua, Y.; Wang, Y.; Mou, L.; Shi, Y.; Xu, F.; Bamler, R. (In Press.) Deep Learning Meets SAR. Available online: https://arxiv.org/pdf/2006.10027.pdf (accessed on 1 September 2020).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Sentinel-1 Algorithms. Available online: https://developers.google.com/earth-engine/guides/sentinel1 (accessed on 10 July 2020).
- Woodhouse, I.H. Introduction to Microwave Remote Sensing; CRC Press: Boca Raton, FL, USA, 2006; ISBN 0-415-27123-1. [Google Scholar]
- About Sentinel-1 Radiometric Terrain Correction in Preprocessing. Available online: https://groups.google.com/g/google-earth-engine-developers/c/3-q0TEwa-Tk (accessed on 10 July 2019).
- Vollrath, A.; Mullissa, A.; Reiche, J. Angular-based radiometric slope correction for Sentinel-1 on google earth engine. Remote Sens. 2020, 12, 1867. [Google Scholar] [CrossRef]
- Assis, L.F.F.G.; Ferreira, K.R.; Vinhas, L.; Maurano, L.; Almeida, C.; Carvalho, A.; Rodrigues, J.; Maciel, A.; Camargo, C. TerraBrasilis: A Spatial Data Analytics Infrastructure for Large-Scale Thematic Mapping. ISPRS Int. J. Geo-Inf. 2019, 8, 513. [Google Scholar] [CrossRef]
- Diniz, C.G.; de Almeida Souza, A.A.; Santos, D.C.; Dias, M.C.; da Luz, N.C.; de Moraes, D.R.; Maia, J.S.; Gomes, A.R.; da Silva Narvaes, I.; Valeriano, D.M.; et al. DETER-B: The New Amazon Near Real-Time Deforestation Detection System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3619–3628. [Google Scholar] [CrossRef]
- Quegan, S.; Yu, J.J. Filtering of multichannel SAR images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2373–2379. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Quegan, S.; Tansey, K.; Page, S. Sentinel-1 observation frequency significantly increases burnt area detectability in tropical SE Asia. Environ. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Cozzolino, D.; Verdoliva, L.; Scarpa, G.; Poggi, G. Nonlocal CNN SAR image despeckling. Remote Sens. 2020, 12, 1006. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: New York, NY, USA, 2001; ISBN 978-0-471-05669-0. [Google Scholar]
- Scrucca, L.; Fop, M.; Murphy, T.B.; Raftery, A.E. Mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models. R J. 2016, 8, 289–317. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Rees, G. The Remote Sensing Data Book; Cambridge University Press: Cambridge, UK, 1999; ISBN 052148040X. [Google Scholar]
- Weisse, M.J.; Noguerón, R.; Eduardo, R.; Vicencio, V.; Castillo Soto, D.A. Use of Near-Real-Time Deforestation Alerts: A Case Study from Peru; World Resources Institute: Washington, DC, USA, 2019. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]

| Effect | Band | Ref | |||
|---|---|---|---|---|---|
| X | C | L | P | ||
| Faraday Rotation | - - | - | + | ++ | [12] |
| Raincells | ++ | + (−2 to −2.4 dB@80 mm/hr) | - | - | [22,23] |
| Rain interception | + + 2 to +3 dB | - +1 to +1.5 dB | - +1 to +2 dB | - - | [17,24] |
| Soil moisture | NR | - 0.11–0.5 dB/[vol%] (VV) 0.08–0.01 dB/[vol%] (VH) | + +1 dB (HH) +2 dB (HV) | NR | [24,25] |
| Band | Polarization | Backscattering Change | Reference | Forest Type and Location |
|---|---|---|---|---|
| C | VH | −2.0 dB | [28] | Tropical forest with dry season (Riau, Indonesia) |
| VV | −2.0 dB | [41] | ||
| −2.57 dB | [29] | Dry tropical forest (Santa Cruz, Bolivia) | ||
| L | HH | +1.2 dB | [38] | Early deforestation stage, tropical rainforest (Uyacali, Peru) |
| −5.0 dB | [36] | Completed deforestation, tropical rainforest w/dry season (Rondônia, Brazil) | ||
| −1.0 to −2.0 dB | [42] | Tropical rainforest (Bangladesh) | ||
| HV | −11.0 dB | [29] | Dry tropical forest (Santa Cruz, Bolivia) | |
| −2.3 to −3.0 dB | [40] | Tropical rainforest (Madre de Dios, Peru) | ||
| −6.0 dB | [42] | Tropical rainforest (Bangladesh) | ||
| −1.2 dB | [38] | Completed deforestation, tropical rainforest (Uyacali, Peru) |
| Characteristic | Value |
|---|---|
| Observation satellite | Sentinel-1A (S1A) |
| SAR band | C-band (5.405 GHz, 5.625 cm) |
| Acquisition mode | Interferometric Wide Swath (IW) |
| Orbit mode | Descending |
| Image product | GRD, high resolution |
| Multilooking | 4 × 1 |
| Spatial resolution | 10 m * |
| Revisit time | 12 days |
| Period | Pol. | Treatment | Threshold Factor | DF | F | TP | FP | ACC (%) | TNR (%) | TPR (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 yr | VHg0 | spatialf | 2.36 | 1280 | 1239 | 1186 | 48 | 94.36 | 96.13 | 92.66 |
| 1 yr | VHg0 | spatialf | 2.74 | 1281 | 1239 | 1173 | 43 | 94.01 | 96.53 | 91.57 |
| 2 yr | VHg0 | origf | 2.82 | 1280 | 1239 | 1192 | 65 | 93.93 | 94.75 | 93.12 |
| 1 yr | VHg0 | origf | 2.58 | 1281 | 1239 | 1205 | 80 | 93.81 | 93.54 | 94.07 |
| 1 yr | VHg0 | origf | 2.56 | 1281 | 1239 | 1206 | 81 | 93.81 | 93.46 | 94.15 |
| 2 yr | VHg0 | harmonf | 3.28 | 1280 | 1239 | 1197 | 88 | 93.21 | 92.9 | 93.52 |
| 1 yr | VHg0 | harmonf | 3.32 | 1281 | 1239 | 1194 | 111 | 92.14 | 91.04 | 93.21 |
| 1 yr | VHg0 | harmonf | 3.26 | 1281 | 1239 | 1198 | 115 | 92.14 | 90.72 | 93.52 |
| 1 yr | VHg0 | harmonf | 3.24 | 1281 | 1239 | 1199 | 116 | 92.14 | 90.64 | 93.60 |
| 2 yr | VVg0 | origf | 2.08 | 1280 | 1239 | 1159 | 77 | 92.14 | 93.79 | 90.55 |
| Period | Pol. | Treatment | Threshold Factor | DF | F | TP | FP | ACC (%) | TNR (%) | TPR (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 yr | VHg0 | spatialf | 4.36 | 1281 | 1239 | 1011 | 6 | 89.05 | 99.52 | 78.92 |
| 2 yr | VHg0 | spatialf | 4.56 | 1280 | 1239 | 986 | 6 | 88.09 | 99.52 | 77.03 |
| 2 yr | VHg0 | origf | 5.06 | 1280 | 1239 | 887 | 6 | 84.16 | 99.52 | 69.3 |
| 2 yr | VVg0 | spatialf | 4.2 | 1280 | 1239 | 847 | 6 | 82.57 | 99.52 | 66.17 |
| 2 yr | VVg0 | spatialf | 4.18 | 1280 | 1239 | 847 | 6 | 82.57 | 99.52 | 66.17 |
| 2 yr | VHg0 | harmonf | 6.36 | 1280 | 1239 | 751 | 7 | 78.72 | 99.44 | 58.67 |
| 2 yr | VVg0 | origf | 4.02 | 1280 | 1239 | 750 | 6 | 78.72 | 99.52 | 58.59 |
| 1 yr | VHg0 | origf | 5.84 | 1281 | 1239 | 747 | 6 | 78.57 | 99.52 | 58.31 |
| 1 yr | VVg0 | spatialf | 4.96 | 1281 | 1239 | 724 | 6 | 77.66 | 99.52 | 56.52 |
| 1 yr | VHg0 | harmonf | 7.22 | 1281 | 1239 | 667 | 6 | 75.4 | 99.52 | 52.07 |
| Period | Pol. | Treatment | Threshold Factor | DF | F | TP | FP | ACC (%) | TNR (%) | TPR (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 yr | VHg0 | origf | 1.4 | 1280 | 1239 | 1200 | 23 | 95.91 | 98.14 | 93.75 |
| 1 yr | VHg0 | origf | 1.4 | 1281 | 1239 | 1203 | 38 | 95.40 | 96.93 | 93.91 |
| 1 yr | VHg0 | origf | 1.38 | 1281 | 1239 | 1204 | 39 | 95.40 | 96.85 | 93.99 |
| 1 yr | VHg0 | origf | 1.36 | 1281 | 1239 | 1205 | 40 | 95.40 | 96.77 | 94.07 |
| 1 yr | VHg0 | harmonf | 1.9 | 1281 | 1239 | 1193 | 37 | 95.04 | 97.01 | 93.13 |
| 2 yr | VHg0 | spatialf | 0.96 | 1280 | 1239 | 1176 | 22 | 95.00 | 98.22 | 91.88 |
| 2 yr | VHg0 | harmonf | 2.12 | 1280 | 1239 | 1172 | 22 | 94.84 | 98.22 | 91.56 |
| 2 yr | VHg0 | harmonf | 2.1 | 1280 | 1239 | 1173 | 23 | 94.84 | 98.14 | 91.64 |
| 2 yr | VHg0 | harmonf | 2.08 | 1280 | 1239 | 1174 | 24 | 94.84 | 98.06 | 91.72 |
| 2 yr | VHg0 | harmonf | 2.06 | 1280 | 1239 | 1175 | 25 | 94.84 | 97.98 | 91.80 |
| Period | Pol. | Treatment | Threshold Factor | DF | F | TP | FP | ACC (%) | TNR (%) | TPR (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 yr | VHg0 | origf | 2.36 | 1280 | 1239 | 1147 | 6 | 94.48 | 99.52 | 89.61 |
| 1 yr | VHg0 | origf | 2.5 | 1281 | 1239 | 1144 | 6 | 94.33 | 99.52 | 89.31 |
| 1 yr | VHg0 | spatialf | 1.86 | 1281 | 1239 | 1133 | 6 | 93.89 | 99.52 | 88.45 |
| 2 yr | VHg0 | spatialf | 1.74 | 1280 | 1239 | 1125 | 6 | 93.61 | 99.52 | 87.89 |
| 1 yr | VHg0 | harmonf | 2.98 | 1281 | 1239 | 1115 | 7 | 93.13 | 99.44 | 87.04 |
| 2 yr | VHg0 | harmonf | 3.46 | 1280 | 1239 | 1084 | 7 | 91.94 | 99.44 | 84.69 |
| 1 yr | VVg0 | spatialf | 1.8 | 1281 | 1239 | 1055 | 7 | 90.75 | 99.44 | 82.36 |
| 1 yr | VVg0 | origf | 1.88 | 1281 | 1239 | 1050 | 6 | 90.6 | 99.52 | 81.97 |
| 1 yr | VVg0 | origf | 1.86 | 1281 | 1239 | 1050 | 6 | 90.6 | 99.52 | 81.97 |
| 2 yr | VVg0 | spatialf | 1.58 | 1280 | 1239 | 1043 | 6 | 90.35 | 99.52 | 81.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doblas, J.; Shimabukuro, Y.; Sant’Anna, S.; Carneiro, A.; Aragão, L.; Almeida, C. Optimizing Near Real-Time Detection of Deforestation on Tropical Rainforests Using Sentinel-1 Data. Remote Sens. 2020, 12, 3922. https://doi.org/10.3390/rs12233922
Doblas J, Shimabukuro Y, Sant’Anna S, Carneiro A, Aragão L, Almeida C. Optimizing Near Real-Time Detection of Deforestation on Tropical Rainforests Using Sentinel-1 Data. Remote Sensing. 2020; 12(23):3922. https://doi.org/10.3390/rs12233922
Chicago/Turabian StyleDoblas, Juan, Yosio Shimabukuro, Sidnei Sant’Anna, Arian Carneiro, Luiz Aragão, and Claudio Almeida. 2020. "Optimizing Near Real-Time Detection of Deforestation on Tropical Rainforests Using Sentinel-1 Data" Remote Sensing 12, no. 23: 3922. https://doi.org/10.3390/rs12233922
APA StyleDoblas, J., Shimabukuro, Y., Sant’Anna, S., Carneiro, A., Aragão, L., & Almeida, C. (2020). Optimizing Near Real-Time Detection of Deforestation on Tropical Rainforests Using Sentinel-1 Data. Remote Sensing, 12(23), 3922. https://doi.org/10.3390/rs12233922