Carrier Phase-Based Ionospheric Gradient Monitor Under the Mixed Gaussian Distribution
Abstract
1. Introduction
2. Test Statistic for the IGM
3. Minimum Detectable Error
3.1. Gaussian Distribution
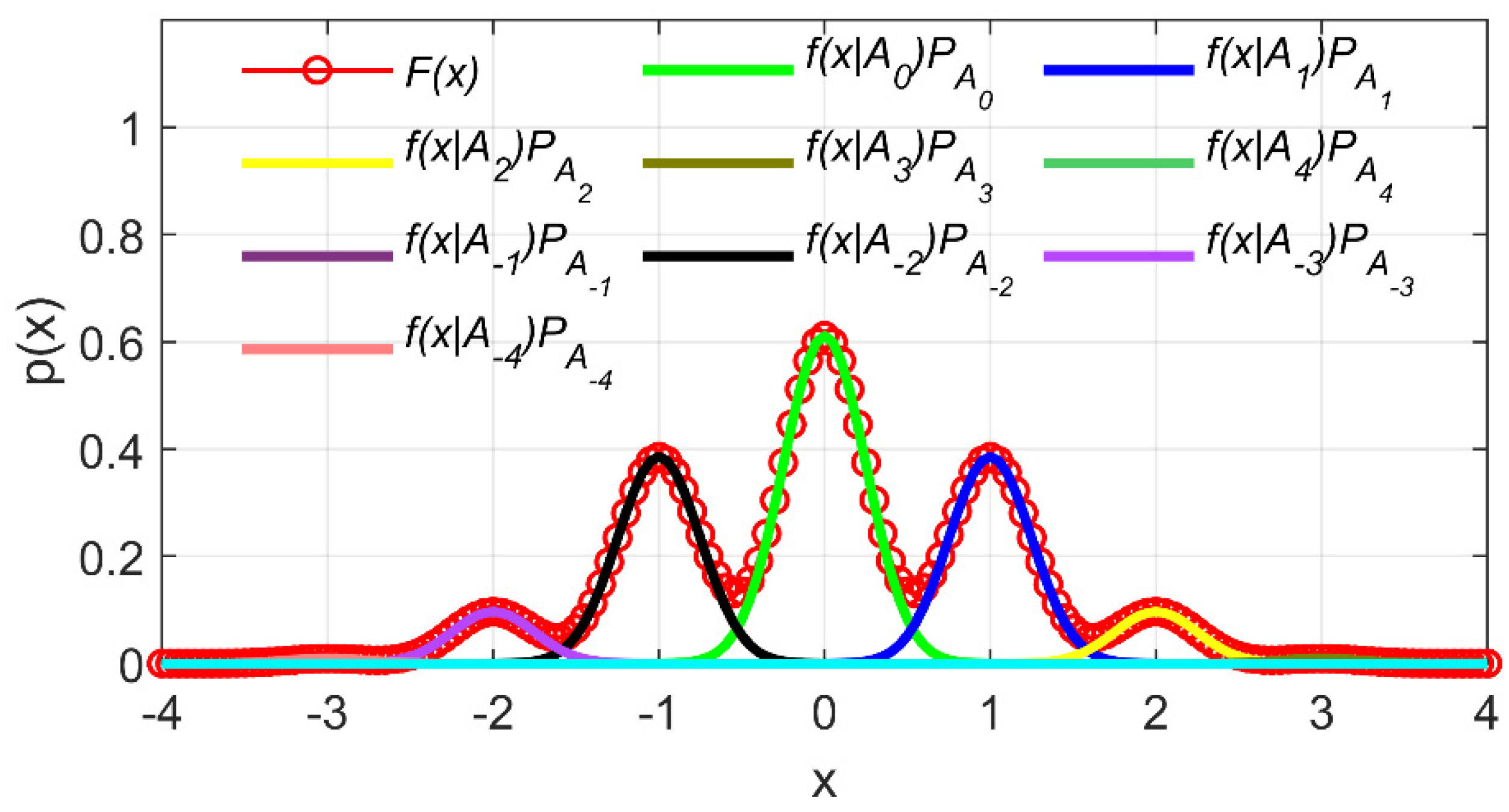
3.2. Mixed Gaussian Distribution
4. Benefits of Dual Frequency
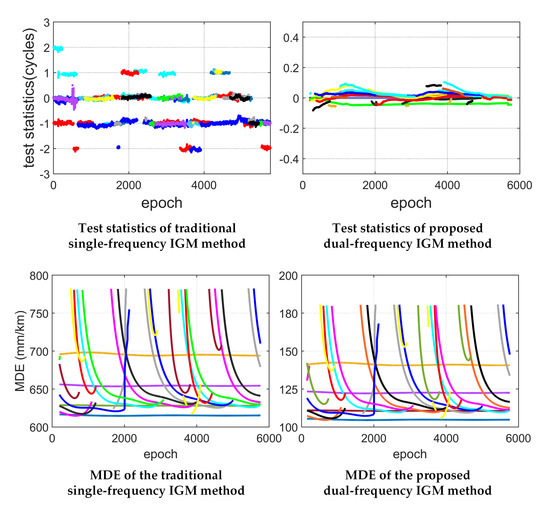
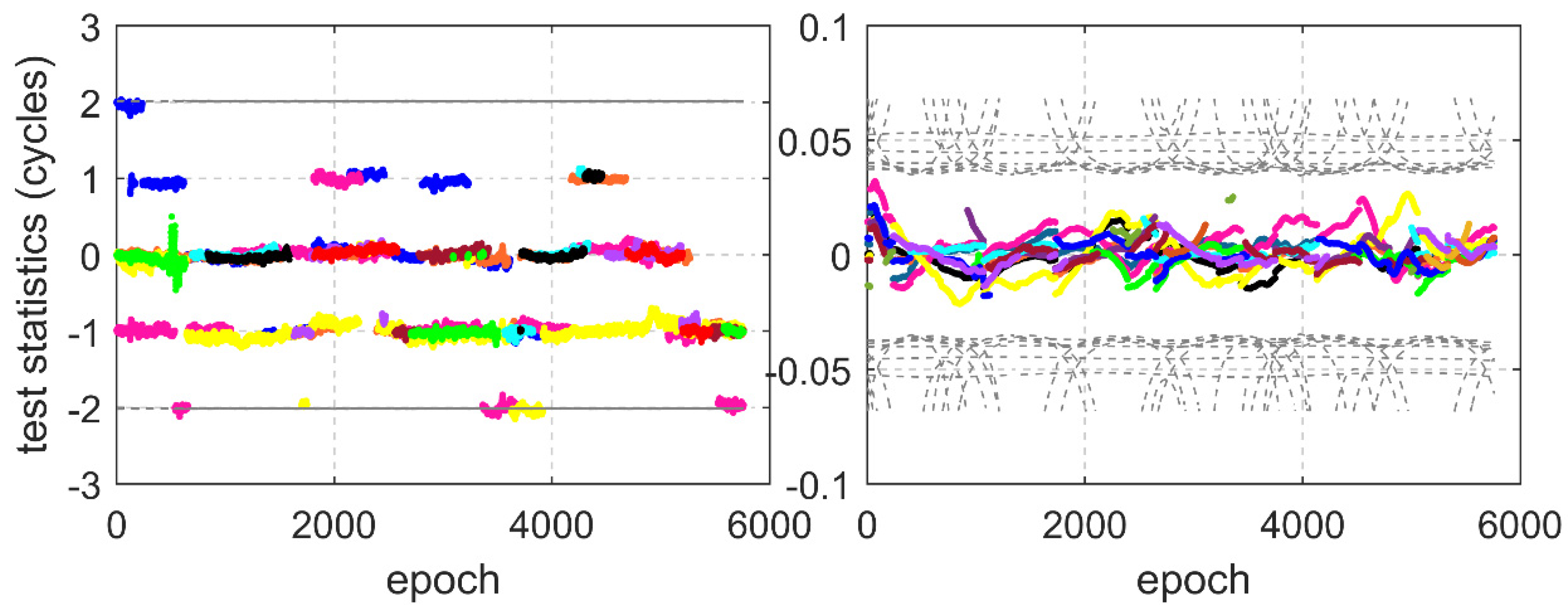
5. Experiment and Discussion
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nicola, M.; Falco, G.; Ferre, R.M.; Lohan, E.-S.; de la Fuente, A.; Falletti, E. Collaborative Solutions for Interference Management in GNSS-Based Aircraft Navigation. Sensors 2020, 20, 4085. [Google Scholar] [CrossRef] [PubMed]
- Salabert, P.; Inst, N. The future of GNSS in Civil Aviation: Opportunities and challenges ION GNSS+2017. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 25–29 September 2017; pp. 2742–2757. [Google Scholar]
- Felux, M.; Dautermann, T.; Becker, H. GBAS landing system—precision approach guidance after ILS. Aircr. Eng. Aerosp. Technol. 2013, 85, 382–388. [Google Scholar] [CrossRef]
- Saito, S.; Sunda, S.; Lee, J.; Pullen, S.; Supriadi, S.; Yoshihara, T.; Terkildsen, M.; Lecat, F.; Studies, I.A.I. Ionospheric delay gradient model for GBAS in the Asia-Pacific region. Gps Solut. 2017, 21, 1937–1947. [Google Scholar] [CrossRef]
- Hoffmann, H.O.; Walton, R.O. Integration of the ground-based augmentation system in continuous descent operations. Navig. J. Inst. Navig. 2018, 65, 571–580. [Google Scholar] [CrossRef]
- Jing, J.; Khanafseh, S.; Chan, F.-C.; Langel, S.; Pervan, B. Detecting Ionospheric Gradients for GBAS Using a Null Space Monitor. In Proceedings of the 2012 Ieee/Ion Position Location and Navigation Symposium, Myrtle Beach, CA, USA, 23–26 April 2012; pp. 1125–1133. [Google Scholar]
- Khanafseh, S.; Pullen, S.; Warburton, J. Carrier Phase Ionospheric Gradient Ground Monitor for GBAS with Experimental Validation. Navig. J. Inst. Navig. 2012, 59, 51–60. [Google Scholar] [CrossRef]
- Jung, S.; Lee, J. Long-term ionospheric anomaly monitoring for ground based augmentation systems. Radio Sci. 2012, 47. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, S.; Zhu, Y.; Xin, P. Assessment of Ionospheric Gradient Impacts on Ground-Based Augmentation System (GBAS) Data in Guangdong Province, China. Sensors 2017, 17, 2313. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, F.; Li, L.; Ding, J.; Zhao, Y. GBAS Ionospheric Anomaly Monitoring Based on a Two-Step Approach. Sensors 2016, 16, 763. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Li, Q.; Fang, K. Impact of anomalous ionospheric gradients on GBAS in the low-latitude region of China. GPS Solut. 2020, 25, 2. [Google Scholar] [CrossRef]
- Gratton, L.; Pervan, B. Carrier Phase Airborne and Ground Monitors for Ionospheric Front Detection for Category III LAAS. In Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation, Fort Worth, TX, USA, 26–29 September 2006; pp. 359–366. [Google Scholar]
- Liu, L.; Wan, W.; Ning, B.; Pirog, O.M.; Kurkin, V.I. Solar activity variations of the ionospheric peak electron density. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Jia, C.; Zhao, L.; Li, L.; Li, H.; Cheng, J.; Li, Z. Improving the Triple-Carrier Ambiguity Resolution with a New Ionosphere-Free and Variance-Restricted Method. Remote Sens. 2017, 9, 1108. [Google Scholar] [CrossRef]
- Murphy, T.; Naerlich, S. SARPs for GNSS Elements and Signals (GBAS). In Proceedings of the Navigation Systems Panel (NSP) Working Group of the Whole Meeting, Montreal, QC, Canada, 11–27 May 2010. [Google Scholar]
- Luo, M.; Pullen, S.; Datta-Barua, S.; Zhang, G.; Walter, T.; Enge, P. LAAS Study of Slow-Moving Ionosphere Anomalies and Their Potential Impacts. Proc. ION GNSS 2005, 2005, 2337–2349. [Google Scholar]
- Pullen, S.; Park, Y.S.; Enge, P. Impact and mitigation of ionospheric anomalies on ground-based augmentation of GNSS. Radio Sci. 2009, 44. [Google Scholar] [CrossRef]
- Kim, M.; Choi, Y.; Jun, H.-S.; Lee, J. GBAS ionospheric threat model assessment for category I operation in the Korean region. Gps Solut. 2015, 19, 443–456. [Google Scholar] [CrossRef]
- Lee, J.; Yoon, M.; Pullen, S.; Gillespie, J.; Mathur, N.; Cole, R.; de Souza, J.R.; Doherty, P.; Pradipta, R.; Inst, N. Preliminary Results from Ionospheric Threat Model Development to Support GBAS Operations in the Brazilian Region. In Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, FL, USA, 14–18 September 2015; pp. 1500–1506. [Google Scholar]
- Gratton, L.; Chan, F.-C.; Pervan, B. Algorithms for Airborne Ionospheric Front Detection in LAAS Using Carrier Phase and INS Measurements. In Proceedings of the 2005 National Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; pp. 131–139. [Google Scholar]
- Patel, J.; Khanafseh, S.; Pervan, B. Detecting Hazardous Spatial Gradients at Satellite Acquisition in GBAS. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3214–3230. [Google Scholar] [CrossRef]
- Circiu, M.-S.; Meurer, M.; Felux, M.; Gerbeth, D.; Thoelert, S.; Vergara, M.; Enneking, C.; Sgammini, M.; Pullen, S.; Antreich, F. Evaluation of GPS L5 and Galileo E1 and E5a Performance for Future Multifrequency and Multiconstellation GBAS. Navig. J. Inst. Navig. 2017, 64, 149–163. [Google Scholar] [CrossRef]
- Jiang, Y.; Milner, C.; Macabiau, C. Code carrier divergence monitoring for dual-frequency GBAS. Gps Solut. 2017, 21, 769–781. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 105–108. [Google Scholar] [CrossRef]
- Khanafseh, S.; Patel, J.; Pervan, B.; Inst, N. Ephemeris Monitor for GBAS Using Multiple Baseline Antennas with Experimental Validation. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 25–29 September 2017; pp. 4197–4209. [Google Scholar]
- Teunissen, P.J.G. Integer estimation in the presence of biases. J. Geod. 2001, 75, 399–407. [Google Scholar] [CrossRef]
- Verhagen, S.; Li, B.; Teunissen, P.J.G. Ps-LAMBDA: Ambiguity success rate evaluation software for interferometric applications. Comput. Geosci. 2013, 54, 361–376. [Google Scholar] [CrossRef]
- Li, L.; Shi, H.; Jia, C.; Cheng, J.; Li, H.; Zhao, L. Position-domain integrity risk-based ambiguity validation for the integer bootstrap estimator. Gps Solut. 2018, 22. [Google Scholar] [CrossRef]
- Hu, G.; Abbey, D.A.; Castleden, N.; Featherstone, W.E.; Earls, C.; Ovstedal, O.; Weihing, D. An approach for instantaneous ambiguity resolution for medium- to long-range multiple reference station networks. Gps Solut. 2005, 9, 1–11. [Google Scholar] [CrossRef]
- Jia, C.; Zhao, L.; Li, L.; Cheng, J.; Li, H. Ionosphere-free Multi-carrier Ambiguity Resolution Method Based on Ambiguity Linear Constraints. Acta Geod. Cartogr. Sin. 2018, 47, 930–939. [Google Scholar] [CrossRef]
- Jing, J.; Khanafseh, S.; Langel, S.; Pervan, B.; Inst, N. Detection and Isolation of Ionospheric Fronts for GBAS. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014; pp. 3526–3531. [Google Scholar]
- Pullen, S.; Cassell, R.; Johnson, B.; Brenner, M.; Weed, D.; Cypriano, L.; Topland, M.; Stakkeland, M.; Pervan, B.; Harris, M.; et al. Impact of Ionospheric Anomalies on GBAS GAST D Service and Validation of Relevant ICAO SARPs Requirements. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 25–29 September 2017; pp. 2085–2105. [Google Scholar]
- Li, L.; Jia, C.; Zhao, L.; Yang, F.; Li, Z. Integrity monitoring-based ambiguity validation for triple-carrier ambiguity resolution. Gps Solut. 2017, 21, 797–810. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Success probability of integer GPS ambiguity rounding and bootstrapping. J. Geod. 1998, 72, 606–612. [Google Scholar] [CrossRef]
- Li, L.; Liu, X.; Jia, C.; Cheng, C.; Li, J.; Zhao, L. Integrity monitoring of carrier phase-based ephemeris fault detection. Gps Solut. 2020, 24. [Google Scholar] [CrossRef]
- Jin, Y.; Oksavik, K. GPS Scintillations and Losses of Signal Lock at High Latitudes During the 2015 St. Patrick’s Day Storm. J. Geophys. Res. Space Phys. 2018, 123, 7943–7957. [Google Scholar] [CrossRef]
- Zakharov, V.I.; Yasyukevich, Y.V.; Titova, M.A. Effect of magnetic storms and substorms on GPS slips at high latitudes. Cosm. Res. 2016, 54, 20–30. [Google Scholar] [CrossRef]
- Wu, Y.; Jin, S.G.; Wang, Z.M.; Liu, J.B. Cycle slip detection using multi-frequency GPS carrier phase observations: A simulation study. Adv. Space Res. 2010, 46, 144–149. [Google Scholar] [CrossRef]


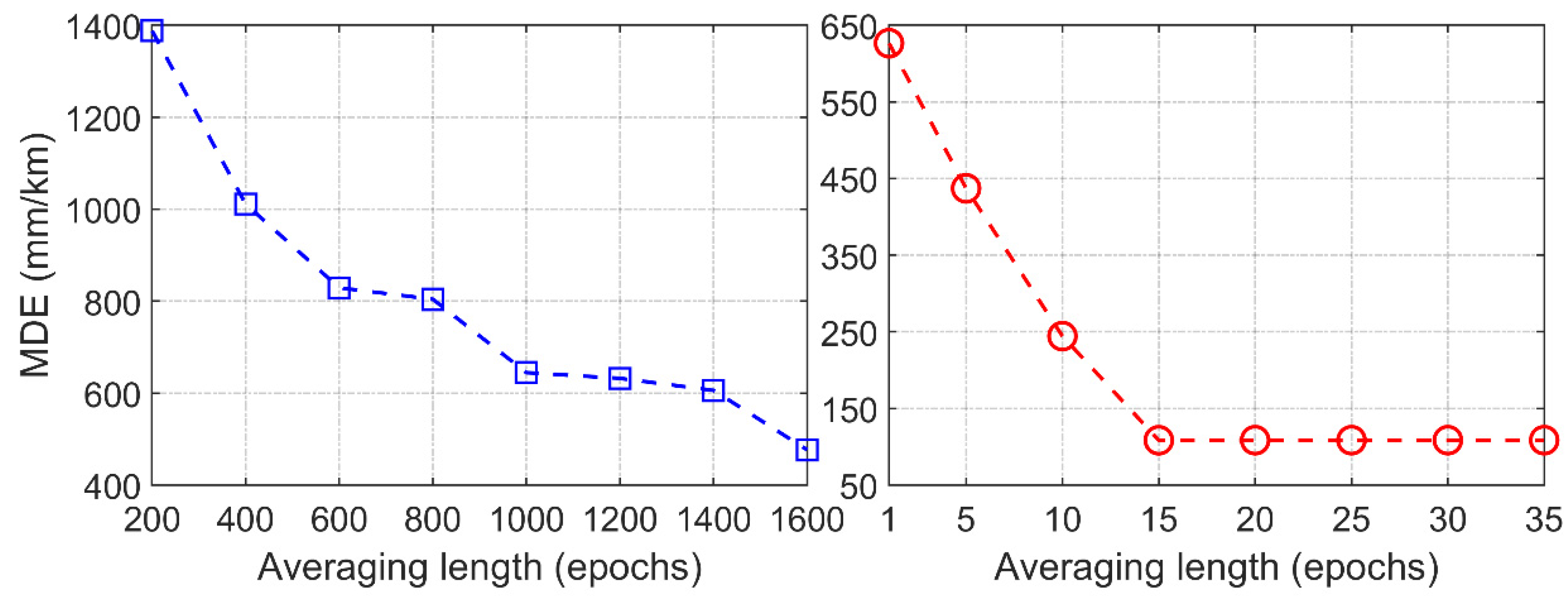




| Averaging Length | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | 1600 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 91.83% | |
| 0 | 0 | 96.68% | 100% | 100% | 100% | 100% | 8.17% | |
| 0 | 100% | 3.32% | 0 | 0 | 0 | 0 | 0 | |
| 99.45% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.55% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Averaging Length | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | 1600 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 86.11% | 98.24% | 99.88% | 99.99% | |
| 0 | 93.88 | 100% | 100% | 13.89% | 1.76% | 0.12% | 0.01% | |
| 93.04% | 3.06% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 6.96% | 3.06% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Instantaneous IGM | SF-IGM | DF-IGM | |
|---|---|---|---|
| PFA (%) | 0 | 0.19 | 0 |
| Ionospheric Gradients (mm/km) | PMD (%) | ||
|---|---|---|---|
| Instantaneous IGM | SF-IGM | DF-IGM | |
| 60 | 94.55 | 1 | 15.64 |
| 90 | 55.27 | 98.54 | 1.82 |
| 120 | 11.27 | 89.45 | 1.09 |
| 150 | 70.55 | 78.55 | 0.72 |
| 180 | 89.82 | 44.36 | 0.01 |
| 210 | 76.36 | 35.27 | 0 |
| 240 | 48.00 | 26.91 | 0 |
| 270 | 35.27 | 14.18 | 0 |
| 300 | 9.82 | 4.36 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Li, J.; Li, L.; Jiang, C.; Qi, B. Carrier Phase-Based Ionospheric Gradient Monitor Under the Mixed Gaussian Distribution. Remote Sens. 2020, 12, 3915. https://doi.org/10.3390/rs12233915
Cheng J, Li J, Li L, Jiang C, Qi B. Carrier Phase-Based Ionospheric Gradient Monitor Under the Mixed Gaussian Distribution. Remote Sensing. 2020; 12(23):3915. https://doi.org/10.3390/rs12233915
Chicago/Turabian StyleCheng, Jianhua, Jiaxiang Li, Liang Li, Chao Jiang, and Bing Qi. 2020. "Carrier Phase-Based Ionospheric Gradient Monitor Under the Mixed Gaussian Distribution" Remote Sensing 12, no. 23: 3915. https://doi.org/10.3390/rs12233915
APA StyleCheng, J., Li, J., Li, L., Jiang, C., & Qi, B. (2020). Carrier Phase-Based Ionospheric Gradient Monitor Under the Mixed Gaussian Distribution. Remote Sensing, 12(23), 3915. https://doi.org/10.3390/rs12233915