Analytical Computation of the Spatial Resolution in GNSS-R and Experimental Validation at L1 and L5

Abstract

Global navigation satellite systems reflectometry (GNSS-R) is a relatively novel remote sensing technique, but it can be understood as a multi-static radar using satellite navigation signals as signals of opportunity. The scattered signals over sea ice, flooded areas, and even under dense vegetation show a detectable coherent component that can be separated from the incoherent component and processed accordingly. This work derives an analytical formulation of the response of a GNSS-R instrument to a step function in the reflectivity using well-known principles of electromagnetic theory. The evaluation of the spatial resolution then requires a numerical evaluation of the proposed equations, as the width of the transition depends on the reflectivity values of two regions. However, it is found that results are fairly constant over a wide range of reflectivities, and they only vary faster for very high or very low reflectivity gradients. The predicted step response is then satisfactorily compared to airborne experimental results at L1 (1575.42 MHz) and L5 (1176.45 MHz) bands, acquired over a water reservoir south of Melbourne, in terms of width and ringing, and several examples are provided when the transition occurs from land to a rough ocean surface, where the coherent scattering component is no longer dominant.

1. Introduction

Global navigation satellite systems reflectometry (GNSS-R) is a relatively new remote sensing technique that uses navigation signals as signals of opportunity in a multi-static radar configuration [1].

The spatial resolution of GNSS-R instruments was first analyzed in [2], and it was estimated from the dimensions of the area determined by the intersection of the first iso-delay and iso-Doppler lines. In this case, for a Low Earth Orbit (LEO) satellite at 700 km, the predicted spatial resolution for an instrument using the GPS L1 C/A (Coarse/Acquisition) code would be in the range of 36 to 54 km, for elevation angles from 90° to 40°.

Later on, the definition of spatial resolution was revised and “an effective spatial resolution derived as a function of measurement geometry and delay–Doppler (DD) interval, and as a more appropriate representation of resolution than the geometric resolution previously used in the literature” was proposed in [3]. This effective spatial resolution was defined following an approach similar to the definition of effective bandwidth used in filter theory. An increase in the effective spatial resolution is observed for increasing incidence angle, receiver altitude, and delay–Doppler window. With this definition, the effective spatial resolution is estimated to range from 25 to 37 km for a 700 km height receiver (Figure 4, [3]).

The above definitions implicitly assume that the scattering is incoherent, as the radar equation used is the one that corresponds to surface scattering. However, the development of advanced GNSS-R receivers, capable of processing the coherent component and separating it from the incoherently scattered component, showed that much finer features can be distinguished [4,5]. In fact, when coherent scattering occurs, the GNSS reflectivity values have a very high spatial resolution, as most of the power is mainly coming from the first Fresnel zone [6], an ellipse of semi-major axis a (Equation (1a)) and semi-minor axis b (Equation (1b)):

$$a=\sqrt{\lambda \frac{R_T·R_R}{R_T+R_R}}$$

(1a)

$$b=\frac{a}{cos\left({\theta }_i\right)},$$

(1b)

where λ is the electromagnetic wavelength, R_T and R_R are the distances from the transmitter and receiver to the specular reflection point, and θ_i is the incidence angle. This means that even from an LEO satellite, the spatial resolution can be as small as ~400–500 m.

In [7] the spatial resolution under coherent scattering was theoretically analyzed in detail, including the effect of the different Fresnel zones. It was shown that up to ~45° most of the power is coming from an area determined by the first Fresnel zone, although a power equivalent to the one received in free-space conditions is actually coming from a region ~0.58–0.62 times the first Fresnel zone. However, significant contributions from regions farther away than the first Fresnel zone also contribute to the received power, making its interpretation more difficult. This region was ~800 m away at a 60° elevation angle for an LEO satellite at 500 km height.

In this work, we have gone one step further and analyzed the spatial resolution from a theoretical point of view, using known principles of electromagnetism. The use of these results makes it possible to compute in a very compact form the expression of the ringings and oscillations observed when the specular reflection point transitions from the land into the ocean or vice versa. Analytical results are validated with airborne experimental data gathered at L1 and L5 with the Microwave Interferometric Reflectometer (MIR) instrument when crossing the coastline [8].

2. Methodology

The scattering geometry is shown in Figure 1, where the receiver (R) and transmitter (T) lie in the YZ plane, and are at heights h_R and h_T over a flat surface. R_T and R_R are the distances to the origin of coordinates where the specular reflection point is, and θ_i is the incidence angle, which for the specular reflection point (origin of coordinates) is equal to the reflected angle θ_r. The different disks represent the Fresnel zones, with the odd ones (1, 3, 5, etc.) colored dark gray, and the even ones (2, 4, 6, etc.) colored white.

In what follows, a few principles of electromagnetism are reviewed. They will be used to compute a closed-form solution of the GNSS-R response to a step function, such as in the transition between water and the ocean.

2.1. Review of Some Basic Principles of Electromagnetism

2.1.1. Principle of Equivalence and Image Theory

The principle of equivalence [9] allows us to compute the solutions in the region of interest (half-space in front of the conducting plane) by replacing the plane conductor with the images of the dipoles. The image sources must satisfy the boundary condition that the tangential electric field at the conducting surface should be zero. The total electric field above the conducting plane (Figure 2) is then computed as the sum of the one created by the original currents and the image ones, while the total electric field below the conducting plane is zero. Applying this principle to our problem, the transmitter can be replaced by its “image” underneath the plane, as illustrated in Figure 3.

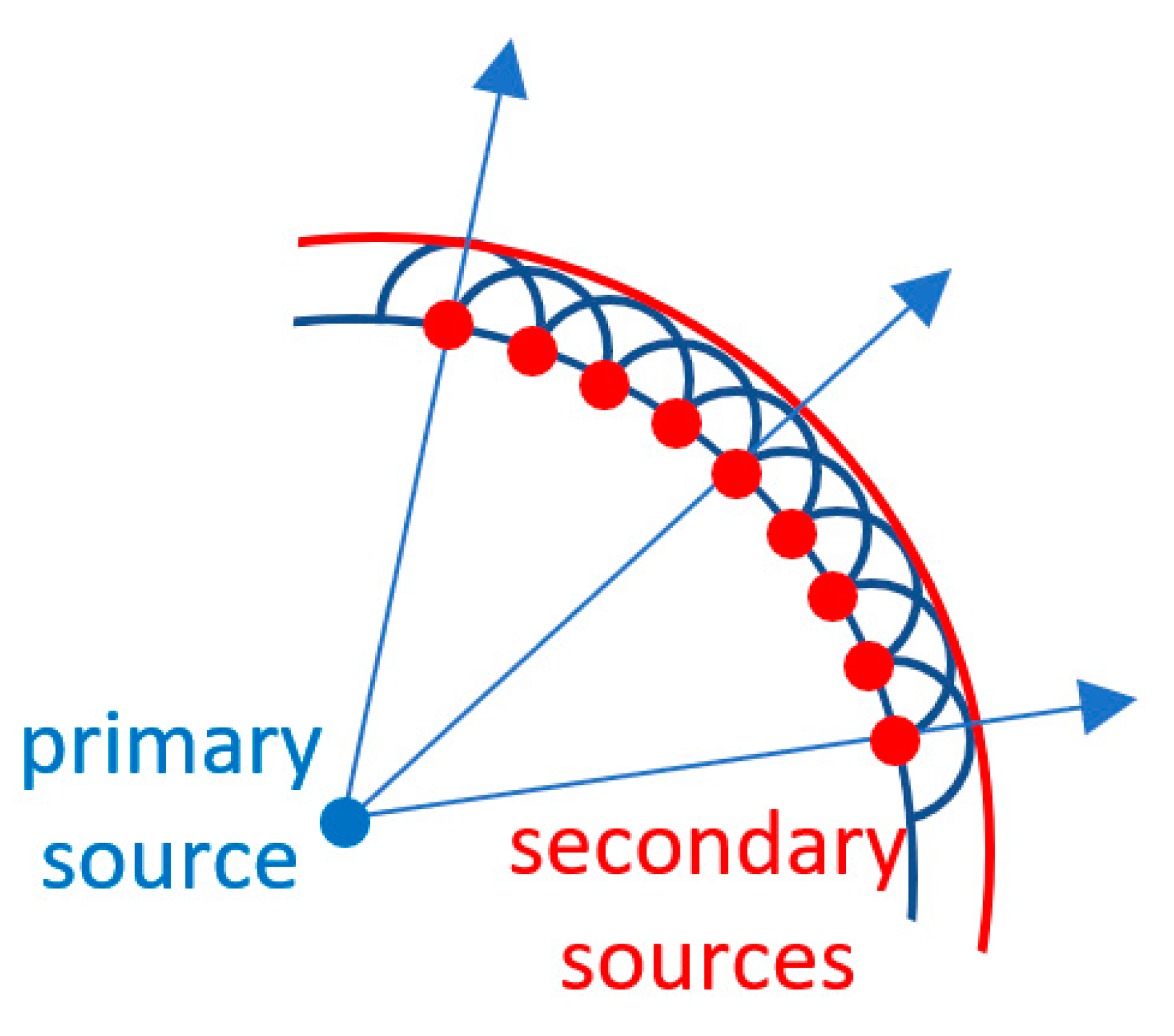
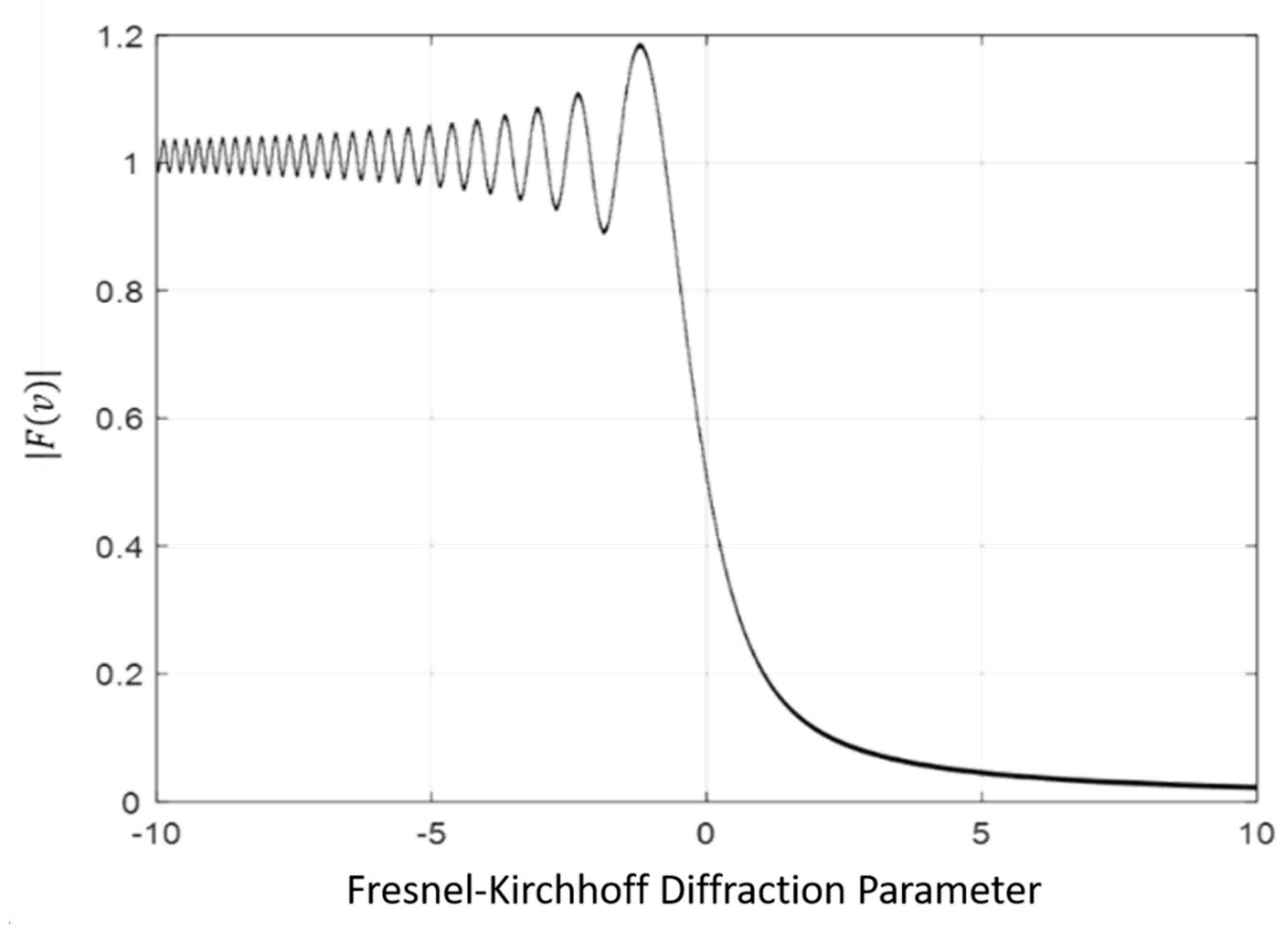
2.1.2. The Huygens Principle and Knife-Edge Diffraction

The Huygens principle states that every point (red dots in Figure 4) on a primary wave front (blue curve in Figure 4) may be regarded as a new source of spherical secondary waves, and that at each point in space these waves propagate in every direction at a speed and frequency equal to that of the primary wave, and in such a way that the primary wave front at some later time is the envelope of these secondary waves (red curve in Figure 4).

The Huygens principle can be applied to compute the electric fields when part of the trajectory is partially obstructed by a conducting plane as illustrated in Figure 5, leaving a clearance h with respect to the line of sight. This academic case is known as the “knife-edge diffraction”, and it is used in radio communications to assess the propagation losses with respect to the free space caused by the obstruction by a mountain, building, etc. In the latter this will represent the transition from one medium to another [6].

The development of an analytical solution can be found in many text books, and only the final result is provided below:

$$E_{diff}=E_{free space}·F\left(v\right)$$

(2)

where:

$$F\left(v\right)\widehat{=}\frac{1+j}{2}\left[{{\displaystyle \int }}_v^{\infty }cos\left(\frac{\pi }{2}{t}^2\right)dt-j{{\displaystyle \int }}_v^{\infty }sin\left(\frac{\pi }{2}{t}^2\right)dt\right]= \frac{1+j}{2}\left\{\left[\frac{1}{2}-C\left(v\right)\right]-j\left[\frac{1}{2}-S\left(v\right)\right]\right\},$$

(3)

$C\left(v\right)$ and $S\left(v\right)$ are the so-called Fresnel integrals, which are given be:

$$C\left(v\right)={{\displaystyle \int }}_0^{\nu }cos\left(\frac{\pi }{2}{t}^2\right)dt,$$

(4a)

$$S\left(v\right)={{\displaystyle \int }}_0^{\nu }sin\left(\frac{\pi }{2}{t}^2\right)dt,$$

(4b)

and $v$ is the Fresnel–Kirchhoff parameter:

$$v=h·\sqrt{\frac{2·\left(R_T+R_R\right)}{\lambda ·R_T·R_R}}$$

(5)

Figure 6 shows the absolute value of $F\left(v\right)$ in Equation (3) in linear units. When h = 0, half of the electric field is blocked, which translates into a power loss of 6 dB with respect to the free-space conditions. Note the ringing for h < 0 due to the different Fresnel zones being blocked or not and contributing to the total electric field with different phases.

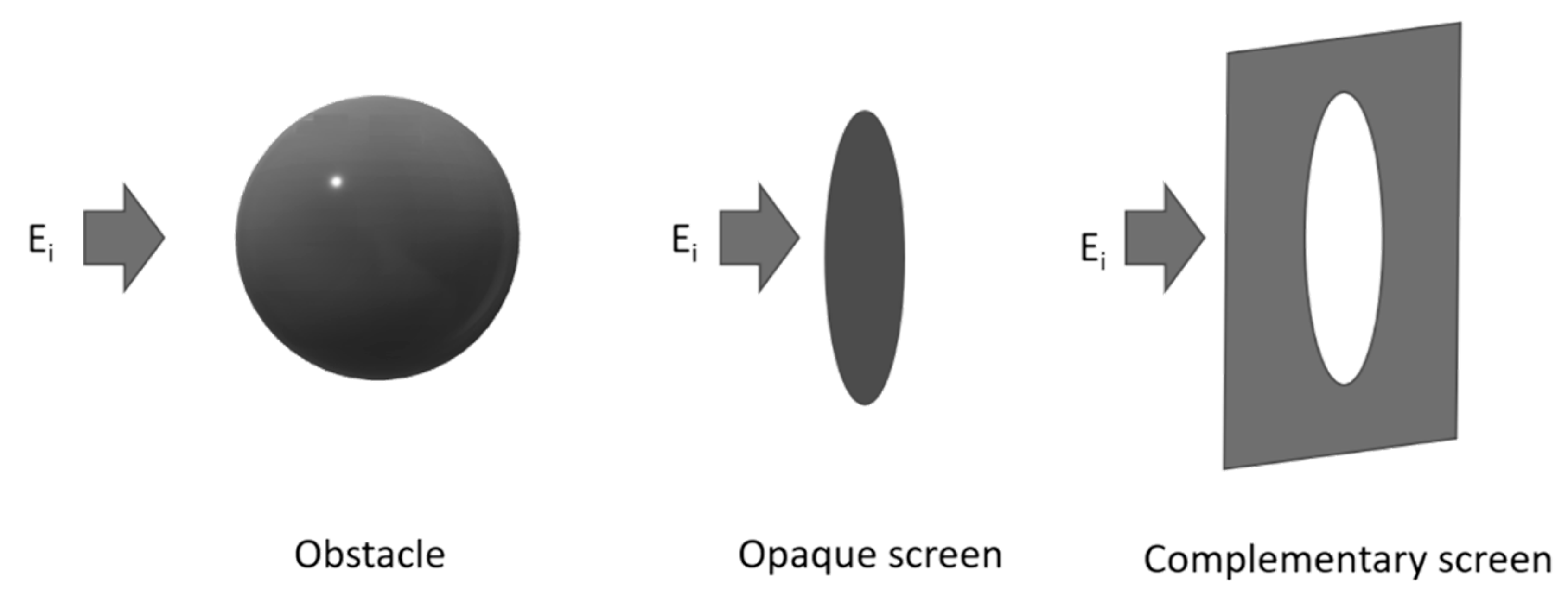
2.1.3. Babinet’s Principle

Babinet’s principle [10] states that the diffraction pattern from an opaque body is identical to that from a hole of the same size and shape, except for the overall forward beam intensity. The concept is expressed graphically in Figure 7 [11].

Babinet’s principle can be used to compute the electric field diffracted when the signal emitted by the transmitter’s image is diffracted by the light-gray opaque area in the z = 0 plane (the white area being “transparent”), and when it is diffracted by the white opaque area in the z = 0 plane (the light-gray area now being “transparent”).

2.1.4. Principle of Superposition

Once the electric fields diffracted by the semi-plane (the white area in the plane z = 0 in Figure 5) are computed, the electric fields diffracted by the complementary semi-plane (the light-gray area in the plane z = 0 in Figure 5), when it is not opaque, can be computed using Babinet’s principle, and then the total electric field arriving at the receiver can be computed as the sum of both.

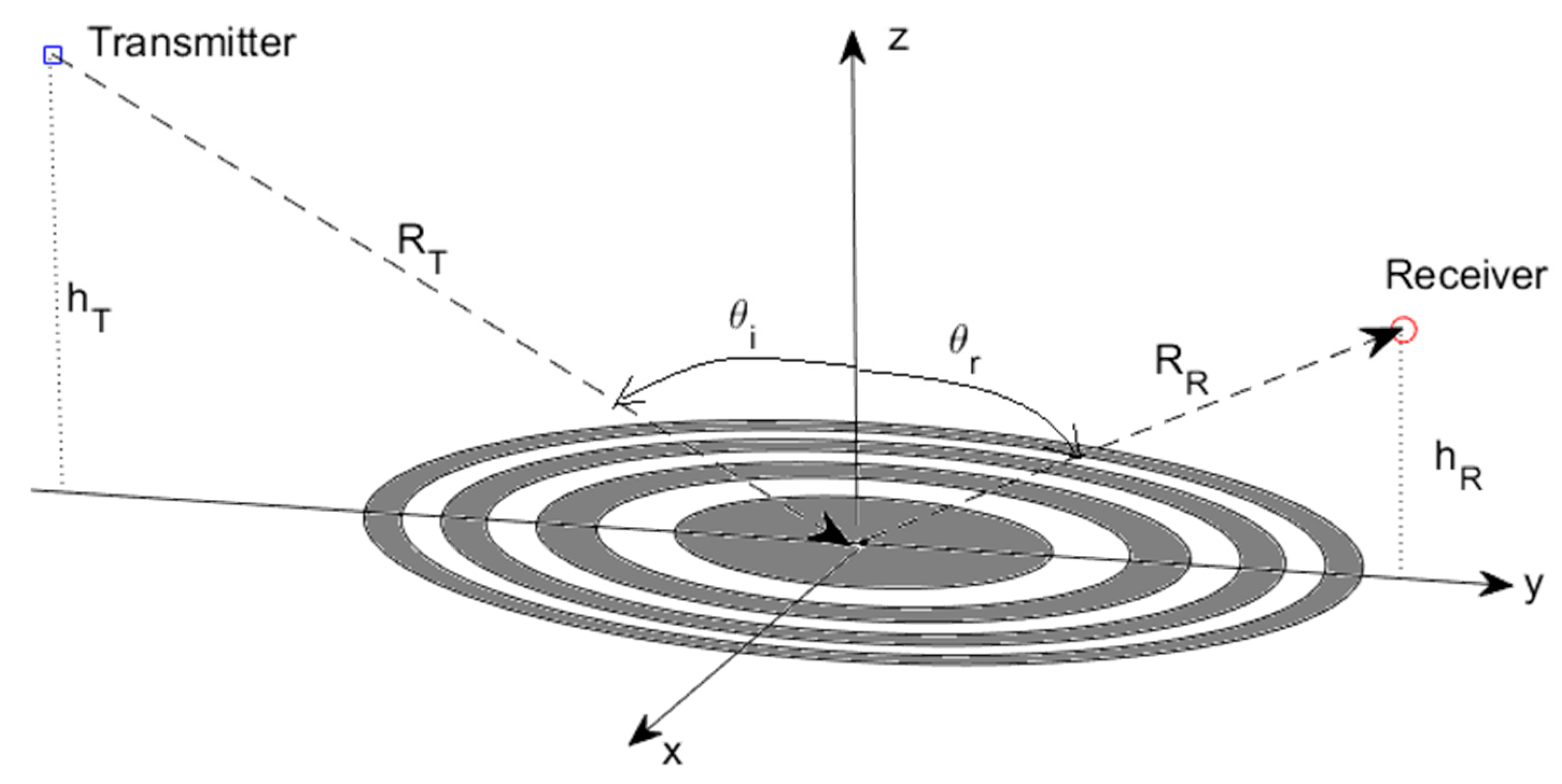
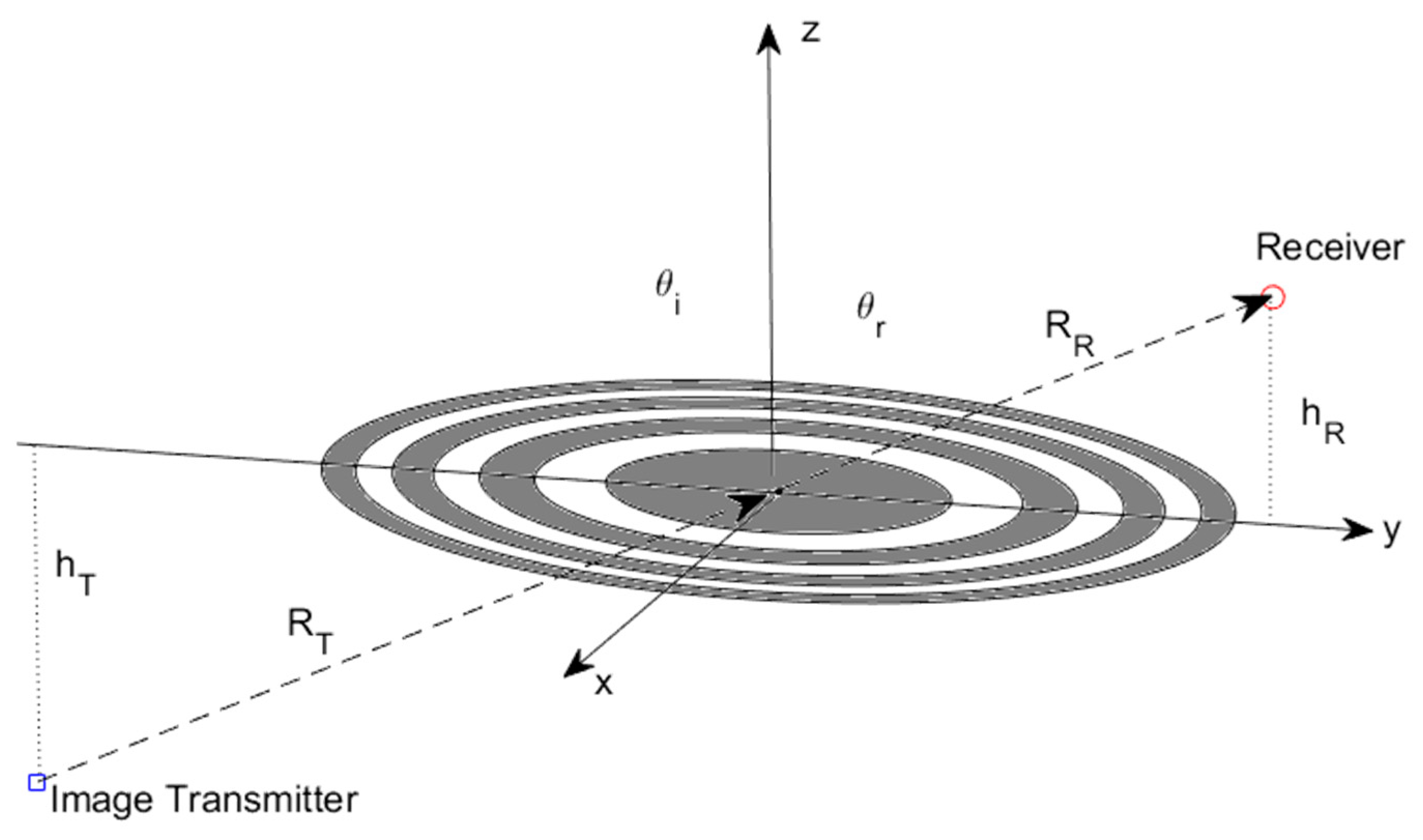
2.2. Computation of the Electric Field Scattered by the Discontinuity between Two Media

Assuming that an electromagnetic wave impinges over the z = 0 plane around (x,y,z) = (0,0,0), where the specular reflection point is, and:

• The extension of the Fresnel reflection zones is small enough (a few hundred meters from a low Earth orbiter) so that the variations of the local incidence angle can be neglected over a few Fresnel zones;
• The plane z = 0 is composed of two flat half-planes of different materials, and thus exhibiting different reflection coefficients; and
• The transmission coefficient for the wave emitted by the image transmitter (Figure 5) is equal to the reflection coefficient evaluated at the local incidence angle at the origin.

Then, as illustrated in Figure 8, the total electric field can be immediately computed as the sum of the following two terms:

$$E_{diff}=E_{free space}·\left[F\left(v\right)·\rho \left({\epsilon }_{r,1}, {\theta }_i\right)+F\left(-v\right)·\rho \left({\epsilon }_{r,2}, {\theta }_i\right)\right],$$

(6)

where $\rho \left({\epsilon }_{r,n}, {\theta }_i\right)$ is the Fresnel reflection coefficient, and ${\epsilon }_{r,n}$ is the dielectric constant of the half-plane n. The received power is proportional to the square of the absolute value of Equation (6).

$$P_{diff}=P_{free space}·{\left|F\left(v\right)·\rho \left({\epsilon }_{r,1}, {\theta }_i\right)+F\left(-v\right)·\rho \left({\epsilon }_{r,2}, {\theta }_i\right)\right|}^2,$$

(7)

Following Equation (7), an example is shown in Figure 9. The red and blue lines correspond to $\left|F\left(v\right)\right|$ and $\left|F\left(-v\right)\right|$ in decibels. The black line corresponds to the square of the absolute value of the term within brackets in Equation (7), computed for $\rho \left({\epsilon }_{r,1}, {\theta }_i\right)=\frac{2}{3}$, and $\rho \left({\epsilon }_{r,2}, {\theta }_i\right)=\sqrt{0.1}$, which corresponds to the normalized peak power that would be collected by a GNSS-R instrument.

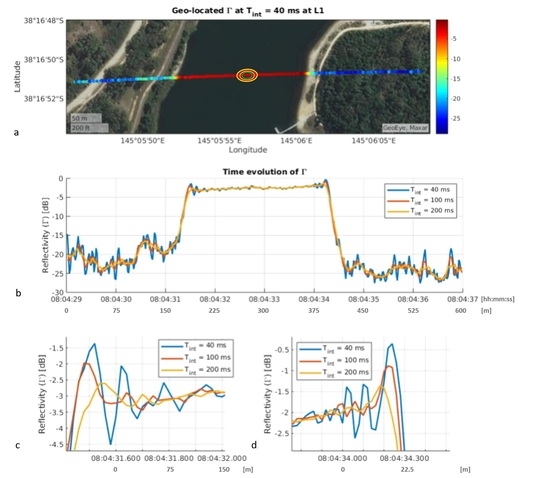
3. Results

3.1. Spatial Resolution Computation

Based on the above results the spatial resolution of a GNSS-R system can now be defined as the width of the transition from the 10% above ${\left|\rho \left({\epsilon }_{r,2}, {\theta }_i\right)\right|}^2\triangleq {\left|{\rho }_{max}\right|}^2$, and 90% of ${\left|\rho \left({\epsilon }_{r,1}, {\theta }_i\right)\right|}^2\triangleq {\left|{\rho }_{min}\right|}^2$

$${\left|F\left(v_{90\%}\right)·{\rho }_{max}+F\left(-v_{90\%}\right)·{\rho }_{min}\right|}^2=0.9· {\left|{\rho }_{max}\right|}^2,$$

(8a)

$${\left|F\left(v_{10\%}\right)·{\rho }_{max}+F\left(-v_{10\%}\right)·{\rho }_{min}\right|}^2=1.1· {\left|{\rho }_{min}\right|}^2$$

(8b)

The solution of the above equations has to be performed numerically, and it actually depends on the values of ${\rho }_{min}$ and ${\rho }_{max}$. The difference between $v_{10\%}$ and $v_{90\%}$ leads to the width of $v$, $\Delta v=v_{10\%}-v_{90\%}$, which is linked to the spatial resolution by means of Equation (9). For the sake of simplicity, assuming an airborne GNSS-R instrument, so that $R_T\gg R_R$, and approximating $R_R\approx h_R/cos\left({\theta }_i\right)$, the following is an approximated formula for the spatial resolution:

$$\Delta v=\Delta x\sqrt{\frac{2·cos\left({\theta }_i\right)}{\lambda ·h_R}}\Rightarrow \Delta x=\Delta v\sqrt{\frac{\lambda ·h_R}{2·cos\left({\theta }_i\right)}}.$$

(9)

Figure 10 shows the evolution of $\Delta v=v_{10\%}-v_{90\%}$ as a function of $\Delta \rho ={\rho }_{min}/{\rho }_{max}$ in decibels. It varies from 0.74 for ${\rho }_{min}/{\rho }_{max}= -3 \mathrm{dB}$ to 1.7 for ${\rho }_{min}/{\rho }_{max}= -20 \mathrm{dB}.$ This means that for a plane flying at h_R = 1000 m height, at GPS L1/Galileo E1 (λ = 19 cm), the spatial resolution ranges from 7.2 m/cos(θ_i) to 16.6 m/cos(θ_i), depending on the contrast of the reflection coefficients in the transition.

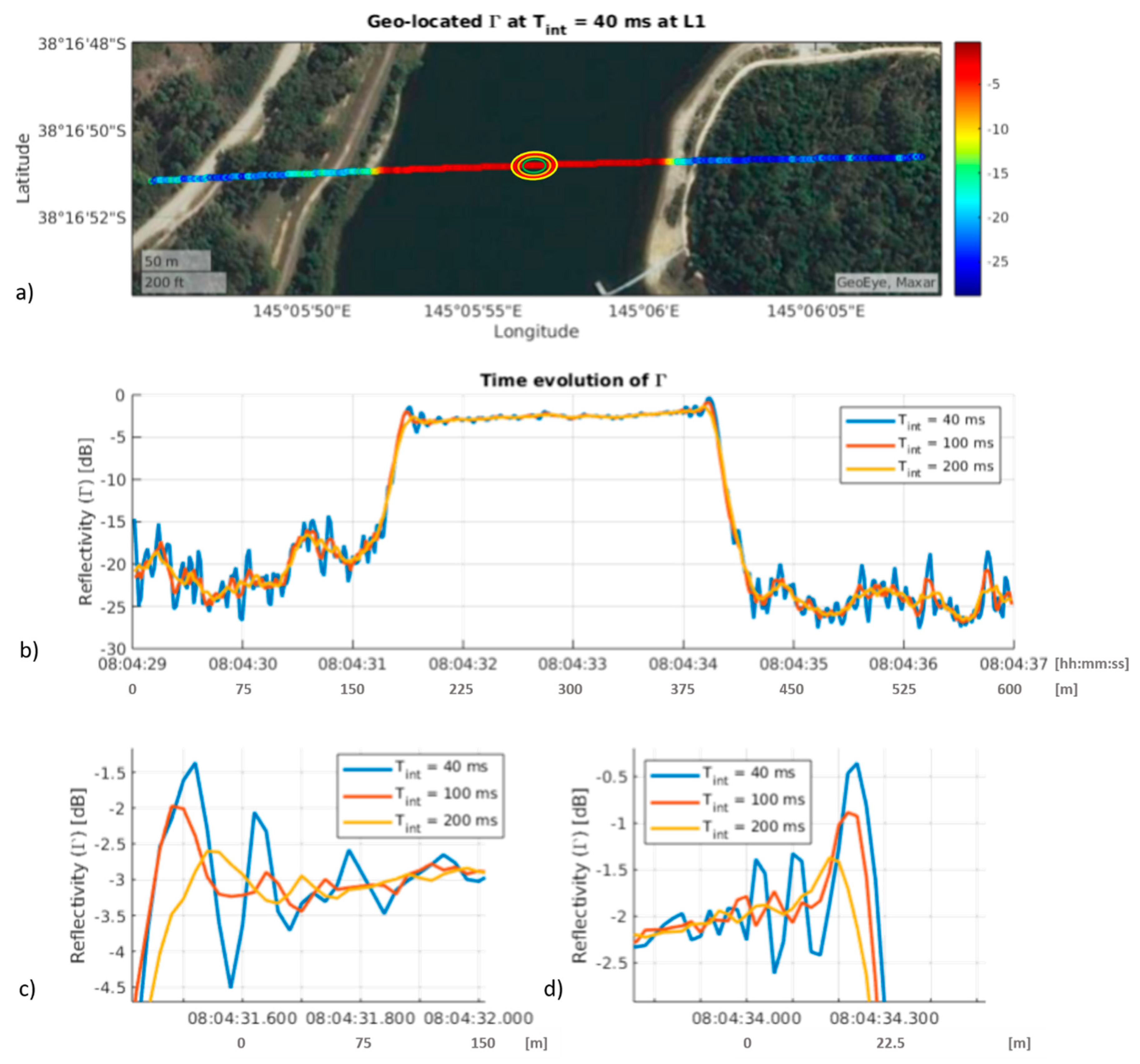
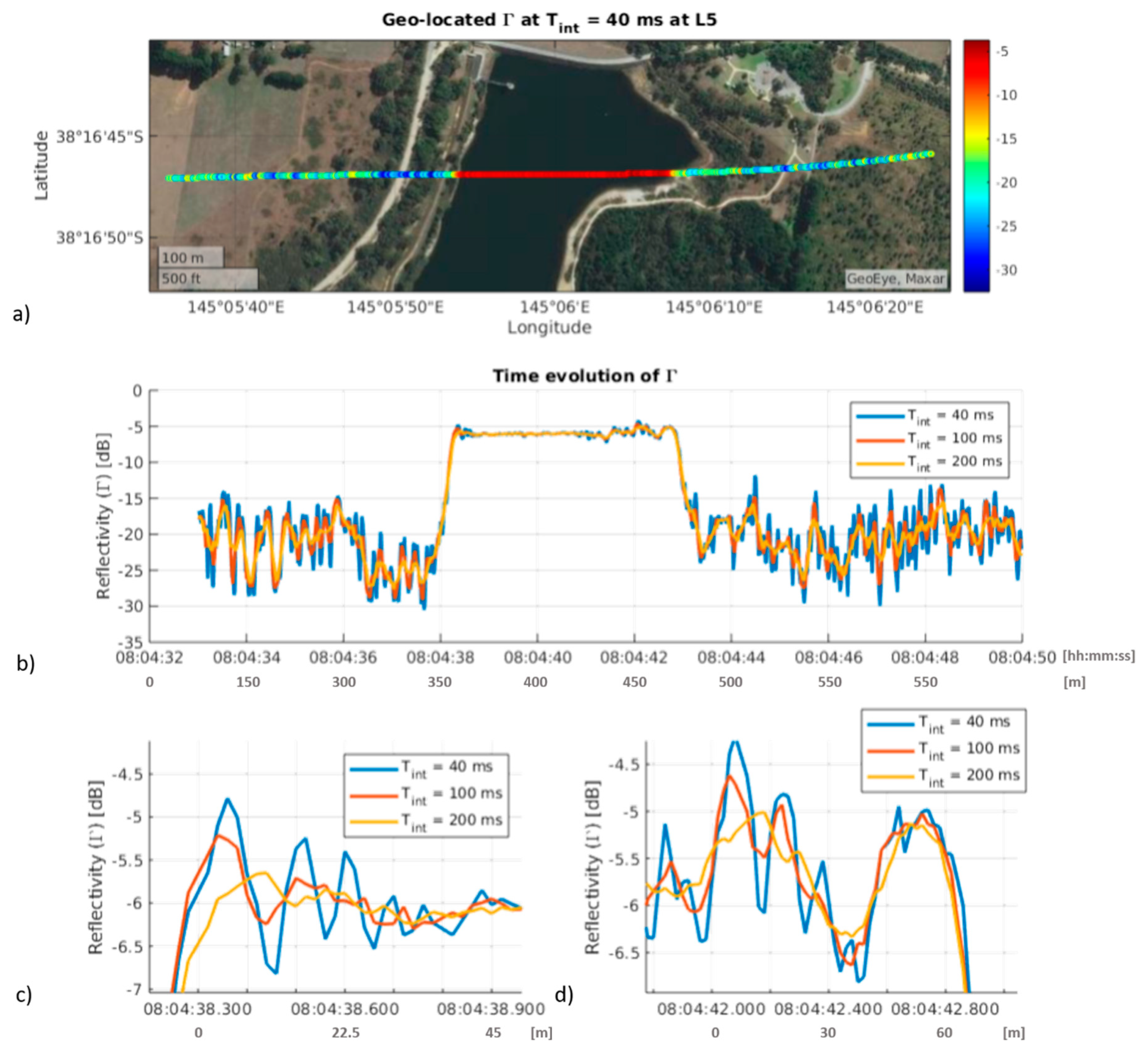
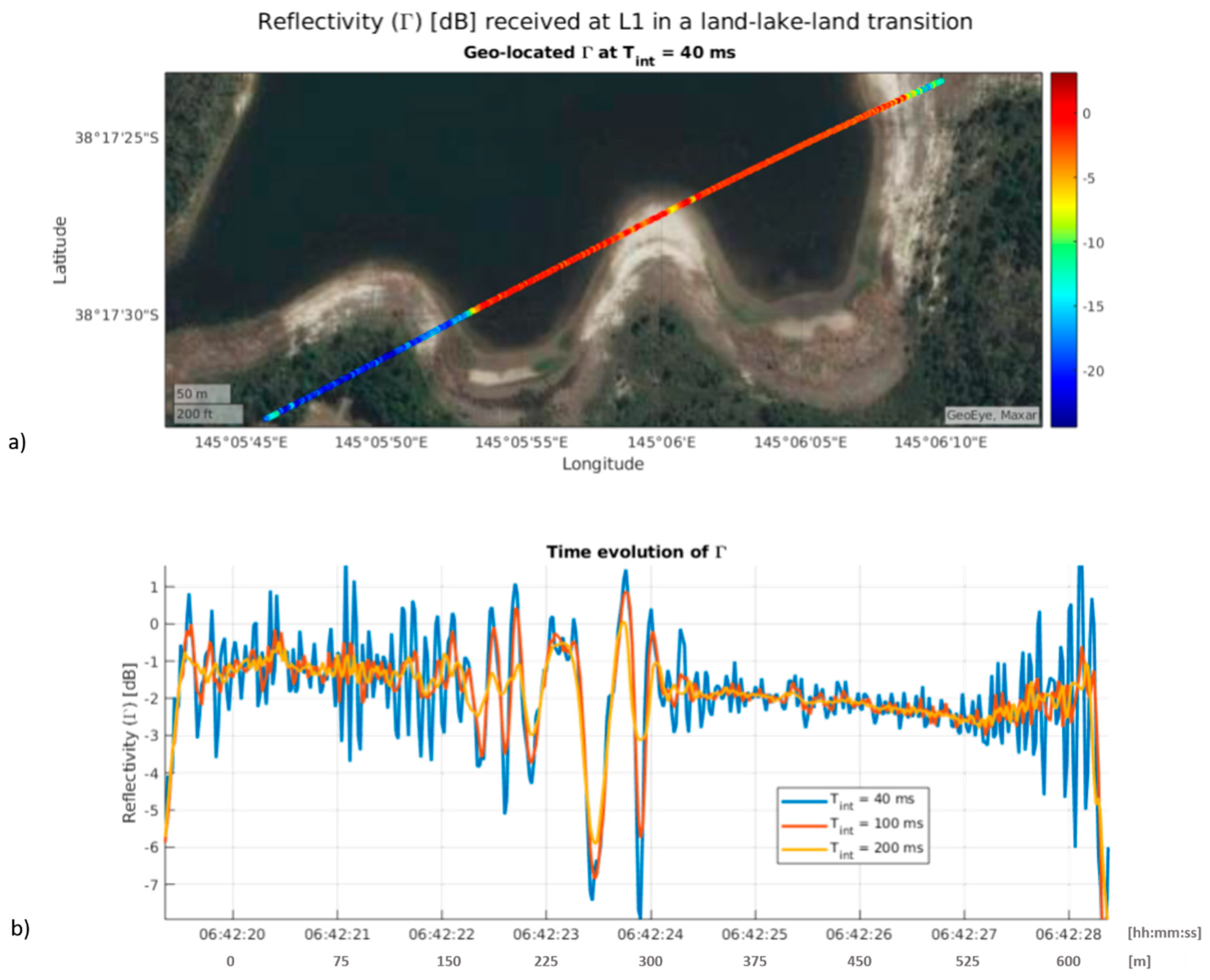
3.2. Experimental Validation

Figure 11 shows the measured reflectivity (Γ) in a transition between land and calm water in the Devilbend Reservoir, south of Melbourne, Victoria, Australia. The data was acquired during one of the test flights of the MIR [8] instrument on 30 April 2018. The top plot corresponds to one of the four beams at GPS L1, and the bottom plot at L5. Flight speed was 75 m/s, flight height was h_R = 1000 m, and GNSS-R data were coherently integrated for 1 ms (GPS L1 C/A code), and incoherently for T_inc = 20, 40, 100, and 200 ms. At 20 ms, the blurring produced by the aircraft movement is 1.5 m, which is negligible compared to the best spatial resolution computed in Section 3.1. Inspecting Figure 11, at 20 and 40 ms incoherent integration time, one can clearly observe some reflectivity ripples that are reminiscent of those seen in Figure 9. At 100 ms, the blurring is 7.5 m, which is now comparable to the best spatial resolution, and the ripples can no longer be appreciated. At 200 ms the reflectivity plot is even smoother. In the land part (left part of the plots), note that the L5 reflections exhibit a more marked fading pattern than the L1 ones. This may be because L5 penetrates a bit more in the land (and vegetation), and it is moister soil underneath the surface. Although it is not very clear, the width of the reflectivity step is approximately 0.3 s, which corresponds roughly to 22.5 m, as compared to the 20.7 m predicted value using Equation (9) and Figure 10 for a ~−15 dB reflectivity.

Taking a closer look to the periodicity of the ripples, it can be observed that the period in Figure 11b is larger than that in Figure 11a, as it can be inferred from Equation (5), and Figure 6 and Figure 9, parameterized in terms of $v$. In Figure 11a, the separation between consecutive peaks in time is ~100 ms, while in Figure 11b it is ~130 ms, which, for an aircraft speed of v = 75 m/s corresponds to 7.50 and 9.75 m, respectively. More detailed results are shown in

Table 1. Peak positions in Figure 6 and peak spacing ($\Delta v$ ), peak positions in time for L1 and L5 beams, time spacing and estimated peak spacing in $v$.

${\mathit{v}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s}}$	$\left|\mathsf{\Delta }{\mathit{v}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s}}\right|$	${\mathit{t}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s}, \mathit{L}1}$ [s]	$\mathsf{\Delta }{\mathit{t}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s}, \mathit{L}1}$ [ms]	$\mathsf{\Delta }{\widehat{\mathit{v}}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s},\mathit{L}1}$	${\mathit{t}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s}, \mathit{L}5}$ [s]	$\mathsf{\Delta }{\mathit{t}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s}, \mathit{L}5}$ [ms]	$\mathsf{\Delta }{\widehat{\mathit{v}}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}\mathit{s},\mathit{L}5}$
−1.22	-	Not visible	-	-	7.140	-
−2.34	1.12	13.290	-	-	7.310	170	0.95
−3.08	0.74	13.400	110	0.71	7.450	140	0.67
−3.68	0.60	13.500	100	0.65	7.570	120	0.78
−4.18	0.50	13.580	80	0.52	7.700	130	0.67

for several peaks. Replacing $\Delta x\left(t\right)$ by ${\mathrm{v}}_{\perp }·\Delta t$ in Equation (10), where ${\mathrm{v}}_{\perp }=\mathrm{v}·\cos \left(\mathsf{\phi }\right),$ $\mathsf{\phi }$ being the angle formed between the aircraft ground-track and the coastline, one obtains:

$$\Delta v={\mathrm{v}}_{\perp }·\Delta t\sqrt{\frac{2·cos\left({\theta }_i\right)}{\lambda ·h_R}}.$$

(10)

Assuming h_R = 1000 m, θ_i = 45°, and substituting $\Delta t$ for the time difference between consecutive peaks in Figure 11 (except for roundoff errors due to the discrete sampling), this ratio closely matches the squared root of the ratio of the wavelengths at L1 and L5: $\sqrt[]{1575.42 \mathrm{MHz}/1176.45 \mathrm{MHz}}=1.16$. Other sources of error are variations of the flight height (approximately h_R = 1000 m), variations of the incidence angle, and most likely the fact that the velocity vector is not perpendicular to the coastline (as implicitly assumed in Figure 5).

These results are corroborated by many other transitions. In what follows a few more examples are presented to illustrate this effect. A minimum incoherent integration time of 40 ms is used, since blurring is still negligible, and these results are almost identical to when 20 ms is used.

Figure 12 shows a geo-located double transition from land–calm water–land, the temporal evolution of the reflection coefficient at L1, and two zooms around the transitions for different incoherent integration times. Figure 13 shows another example at L5. Note that for large incoherent integration times (i.e., 200 ms) the ringings cannot be identified for both the L1 and L5 examples.

Figure 14 presents another example on the same flight. In this case, there is an additional transition to a small portion of a peninsula being crossed by the GNSS-R track. It can be noticed that at short integration times, some ripples are produced when changing from land to water, at the beginning and the end of the track. In addition, in the central part, when passing over the peninsula the combination of the different responses produces very large amplitude ripples. In this case, large incoherent integration times (i.e., 200 ms) are not blurring the ripples in the center of the image. However, if even larger integration times were used (i.e., 1 s) no ringings could be identified.

Finally, Figure 15 shows another double transition when passing over Sorrento, south of Melbourne. The left part corresponds to an open ocean area (Sorrento ocean beach), while the right part of the image is inside Port Phillip Bay (Sorrento front beach). Looking at the ocean–land transition in Figure 15c on the left-hand side, the reflectivity step is larger, but longer over time, and reflectivity values are noisy because of the increased surface roughness and speckle noise associated with a mostly incoherent scattering. The ripples described in the previous sections and illustrated in the previous examples can no longer be identified. However, as compared to the ocean side in Figure 15c, in Figure 15d the reflectivity step is smaller (calm water), but shorter in time (i.e., sharper), and similar ripples to the lake case can now be identified.

4. Discussion

To the authors’ best knowledge, this is the first analytical study of the response of a GNSS-R system to a reflectivity step. The analytical expression of the measured reflectivity $\hat{\mathsf{\Gamma }}$ can be derived from Equation (7):

$$\hat{\mathsf{\Gamma }}={\left|F\left(v\right)·\rho \left({\epsilon }_{r,1}, {\theta }_i\right)+F\left(-v\right)·\rho \left({\epsilon }_{r,2}, {\theta }_i\right)\right|}^2,$$

(11)

with $v$ given by Equation (5). It shows a smooth transition between ${\left|\rho \left({\epsilon }_{r,1}, {\theta }_i\right)\right|}^2$ and ${\left|\rho \left({\epsilon }_{r,2}, {\theta }_i\right)\right|}^2$, and ripples associated to different Fresnel zones passing from one area to the other one. The width of the transition, as measured from the 10% above the lowest reflectivity values to 90% of the highest reflectivity value, has been found to be dependent on the amplitude of the reflectivity step itself, although it is quite flat for a wide range of reflectivity steps (Figure 10): $\Delta v\approx 1.5$

$$\Delta x=\Delta v\sqrt{\frac{\lambda ·h_R}{2·cos\left({\theta }_i\right)}}\approx 1.5\sqrt{\frac{\lambda ·h_R}{2·cos\left({\theta }_i\right)}}.$$

(12)

The spatial resolution and the position of the peaks of the ripples was validated using airborne data at the L1 and L5 bands.

It is worth mentioning that the theoretical analysis assumes that coherent scattering is the dominant mechanism, which is the case when transitioning from land to/from calm water. However, when transitioning into open ocean, where incoherent scattering is more important, the presence of the ripples is not that evident, and the reflectivity exhibits random fluctuations associated mostly to the speckle noise.

These results should allow us to improve the determination of the extent of the flooded areas using GNSS-R observations as in [12,13,14,15], and they can also be used to dynamically optimize the coherent and incoherent integration times in future GNSS-R instruments (airborne or spaceborne) depending on the application or target area, as opposed to the approach implemented in past and current missions (1 ms coherent integration time, and 1 s incoherent integration time) such as UK TDS-1 [16] and NASA CyGNSS [17] missions.

5. Conclusions

In this study, the GNSS-R response to a step function in the reflectivity was derived analytically using known principles of electromagnetism. However, the evaluation of the Fresnel integrals has to be performed numerically. Analytical/numerical predictions match well with the experimental results at L1 and L5, acquired during an airborne experiment using the MIR (Microwave Interferometric Reflectometer) instrument over a water reservoir south of Melbourne and in a transition from the ocean into Port Phillip Bay, in terms of width and ringing, if incoherent integration times multiplied by the speed of the aircraft are shorter than the width of the Fresnel zone. Larger incoherent integration times blur the step response and degrade the achievable spatial resolution. Considering the size of the first Fresnel zone (tens of meters from a plane, to a few hundred meters from a spacecraft) the analysis presented is applicable to most coastlines.