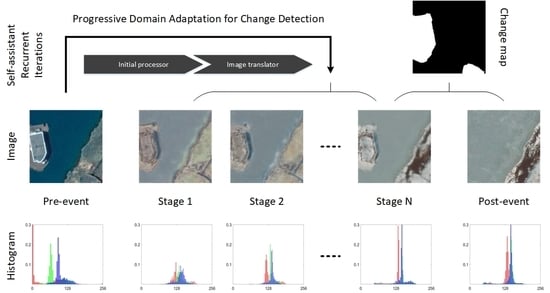
Progressive Domain Adaptation for Change Detection Using Season-Varying Remote Sensing Images

Abstract

The development of artificial intelligence technology has prompted an immense amount of researches on improving the performance of change detection approaches. Existing deep learning-driven methods generally regard changes as a specific type of land cover, and try to identify them relying on the powerful expression capabilities of neural networks. However, in practice, different types of land cover changes are generally influenced by environmental factors at different degrees. Furthermore, seasonal variation-induced spectral differences seriously interfere with those of real changes in different land cover types. All these problems pose great challenges for season-varying change detection because the real and seasonal variation-induced changes are technically difficult to separate by a single end-to-end model. In this paper, by embedding a convolutional long short-term memory (ConvLSTM) network into a conditional generative adversarial network (cGAN), we develop a novel method, named progressive domain adaptation (PDA), for change detection using season-varying remote sensing images. In our idea, two cascaded modules, progressive translation and group discrimination, are introduced to progressively translate pre-event images from their own domain to the post-event one, where their seasonal features are consistent and their intrinsic land cover distribution features are retained. By training this hybrid multi-model framework with certain reference change maps, the seasonal variation-induced changes between paired images are effectively suppressed, and meanwhile the natural and human activity-caused changes are greatly emphasized. Extensive experiments on two types of season-varying change detection datasets and a comparison with other state-of-the-art methods verify the effectiveness and competitiveness of our proposed PDA.

1. Introduction

Change detection is one of the critical research branches in the field of remote sensing. It is concerned with the detection and quantitative analyses of the changes in land cover types from bi-temporal or multi-temporal remote sensing images [1,2,3]. In recent years, change detection techniques have been extensively utilized in various applications, such as disaster assessment [4], land cover change mapping [5,6], resource and environmental monitoring [7,8,9], and urban planning [10,11]. The emergence of high spatial and high spectral resolution remote sensing imagery provides richer information of the Earth surface and offers the opportunities to promote the performance of change detection methods. On the other hand, particular challenges arise in better utilizing the abundance of spatial and spectral information in the current change detection tasks [12].

Recently, the development of artificial intelligence has provided new ideas for remote sensing image processing applications. With the powerful capability in terms of implicit feature expression, numerous neural networks have been applied for change detection tasks and witnessed the impressive performance. Following a two-step workflow, the current change detection methods can be generally seen as composed of two steps: feature extraction and decision making. Feature extraction intends to learn the discriminative features of changes from co-registered images, and decision making aims to identify the changed regions by analyzing these features. According to different feature extraction models, current deep learning-driven methods can be broadly classified into three classes: original image-based, image arithmetical-based, and image transformation-based, respectively.

Original image-based methods generally regard change detection as a specific type of semantic classification task and attempt to separate the changed and unchanged regions directly from paired images or their simple concatenation, merely with an end-to-end semantic labeling network. Lyu et al. (2016) [13] proposed a transferable change detection method by applying a recurrent neural network (RNN) with long short-term memory (LSTM) [14] to detect both binary and multi-class land cover changes. Hou et al. (2020) [15] integrated a W-Net model and a generative adversarial network (GAN) to build a CDGAN for change detection tasks, where the W-Net model was specifically designed to adapt to the characteristics of bi-temporal images. Gao et al. (2019) [16] designed a channel weighting-based deep cascade network to detect changes in synthetic aperture radar (SAR) images. Wang et al. (2019) [17] exploited a convolutional neural network (CNN) [18] to build a deep neural network to achieve sub-pixel level change detection results from hyperspectral imagery. These methods are advantageous at their direct and straightforward feature extraction model structures. However, changes in different land cover categories may have completely diverse characteristics, thus detecting them with an end-to-end semantic labeling network is theoretically inappropriate.

Image arithmetical-based methods generally first calculate the image differencing [19], image rationing [20], image regression [21], or analyze the change vector (CVA) [22], then apply a network to produce pixel-level change maps with the above image features. Gao et al. (2016) [23] introduced a PCANet and combined it with conventional methods to recognize the changed pixels in multi-temporal SAR images. Taking difference images as prior knowledge for sampling the training samples, Gong et al. (2017) [24] applied a GAN [25] to generate the change maps. Gong et al. (2017) [26] integrated a stacked autoencoder (SAE) [27], a CNN model, and the fuzzy c-means algorithms to learn the robust features of land cover changes from multi-temporal SAR images. Taking the difference images as auxiliary data, Yang et al. (2019) [28] designed a transferred deep learning-based framework to detect changes without references. Remarkably, these methods are specifically intended for SAR images, which are insensitive to negative influences of atmospheric and illumination conditions. However, for optical remote sensing images, the pixel-level difference images practically involve considerable noise and redundancy. Meanwhile, they may have lost the intrinsic land cover information. Therefore, directly applying these methods in optical images may lead to unsatisfactory performance.

Image transformation-based methods generally first translate the spectral combinations of the pre-event images to those of the post-event images, or translate them to a third feature space with a network, then identify the changed regions by comparing the paired translated images. Zhang et al. (2016) [29] proposed a hierarchical change detection framework in which a deep neural network was exploited to differentiate the unchanged regions from the changed regions. Zhan et al. (2017) [30] introduced a deep Siamese convolutional network (DSCN) to detect changes with a contrastive loss. Inspired by the Siamese network, Liu et al. (2018) [31] developed a symmetric deep convolutional network to eliminate the discrepancies between the optical image domain and SAR image domain, and successfully detected the changes based on heterogeneous bi-temporal imagery. Integrating the ideas of dual learning and Siamese network, Fang et al. (2019) [32] introduced a dual learning-based Siamese framework (DLSF) to simultaneously achieve the cross-domain translation between paired images and the detection of changed regions in two domains. Zhan et al. (2018) [33] introduced an iterative feature mapping network to transform the high-level features of multi-source images into a common high-dimensional feature space, aiming to shrink the difference of unchanged regions and enlarge that of changed ones. Niu et al. (2019) [34] first proposed a GAN-based network to translate optical images with the paired SAR images as targets, then introduced an approximation network to highlight changes in heterogeneous images. Ma et al. (2019) [35] first adopted a pixel-level mapping method to transform paired images into each other’s feature space, then designed a capsule network to recognize the changed pixels. These methods are able to guarantee the distribution consistencies of land cover categories in the paired unchanged regions, by eliminating the domain differences of bi-temporal remote sensing images. Transformation models are the most optimal for change detection in optical or multi-source remote sensing images, because they can effectively process various high-dimensional data even with diverse patterns.

In general, current change detection methods are designed based on the assumption that the appearances of the paired unchanged regions should be similar, and distinctive discrepancies should exist only in real changed regions. Nevertheless, for season-varying remote sensing images, due to different imaging sensors, capture times, and atmospheric and illumination conditions, it is tough to differentiate the seasonal spectral variation from the real changes, leading to entirely different appearances, no matter in the changed or unchanged regions. On the other hand, the changes that occur on diverse land cover categories may appear different to some extent, making it difficult to distinguish real changes from other season-induced changes using an end-to-end model. Therefore, it is quite essential to perform modeling for the seasonal variation of the pre- and post-event images, and facilitate eliminating the season-induced changes and highlighting the real changes. Along with this way, land cover features are first distilled from the pre-event images, and then they are composed with similar seasonal style features as the post-event images. During this process, the appearances of the unchanged regions in the post-event images are able to act as reliable references for those in the registered pre-event ones. At this point, it is easy to separate real changed regions from not only the unchanged ones, but also other season-induced changed ones, by directly comparing the translated and post-event images, or using a simple change decision making strategy.

According to the above analyses, in this research, we embed a convolutional LSTM (ConvLSTM) network in a cGAN, and introduce a novel image transformation-based method, named progressive domain adaptation (PDA), for change detection using season-varying remote sensing images. And the framework of our idea is composed of two cascaded modules, which are progressive translation and group discrimination, respectively. The former aims to progressively translate pre-event images from their own domain to the post-event one and maintaining the essential characteristics of land cover types. Meanwhile, the latter aims to evaluate the seasonal domain consistency of two groups of translated and post-event images. The proposed hybrid multi-model framework is trained to implement the cross-season translation in a one-sided fashion. The spectral variation caused by seasonal changes can be effectively suppressed, and the distinct real changes between paired images are highlighted. The major contributions of our research are summarized as follows:

• We develop a novel image transformation-based method that accommodated the specific demand for change detection tasks using season-varying remote sensing images. In this method, we emphasize the distribution consistencies of land cover categories in the paired unchanged regions.
• We propose a hybrid multi-model framework integrating strategies of ConvLSTM network and cGAN model. To the best of our knowledge, there has been no research into combing these two networks for change detection and especially for season-varying change detection
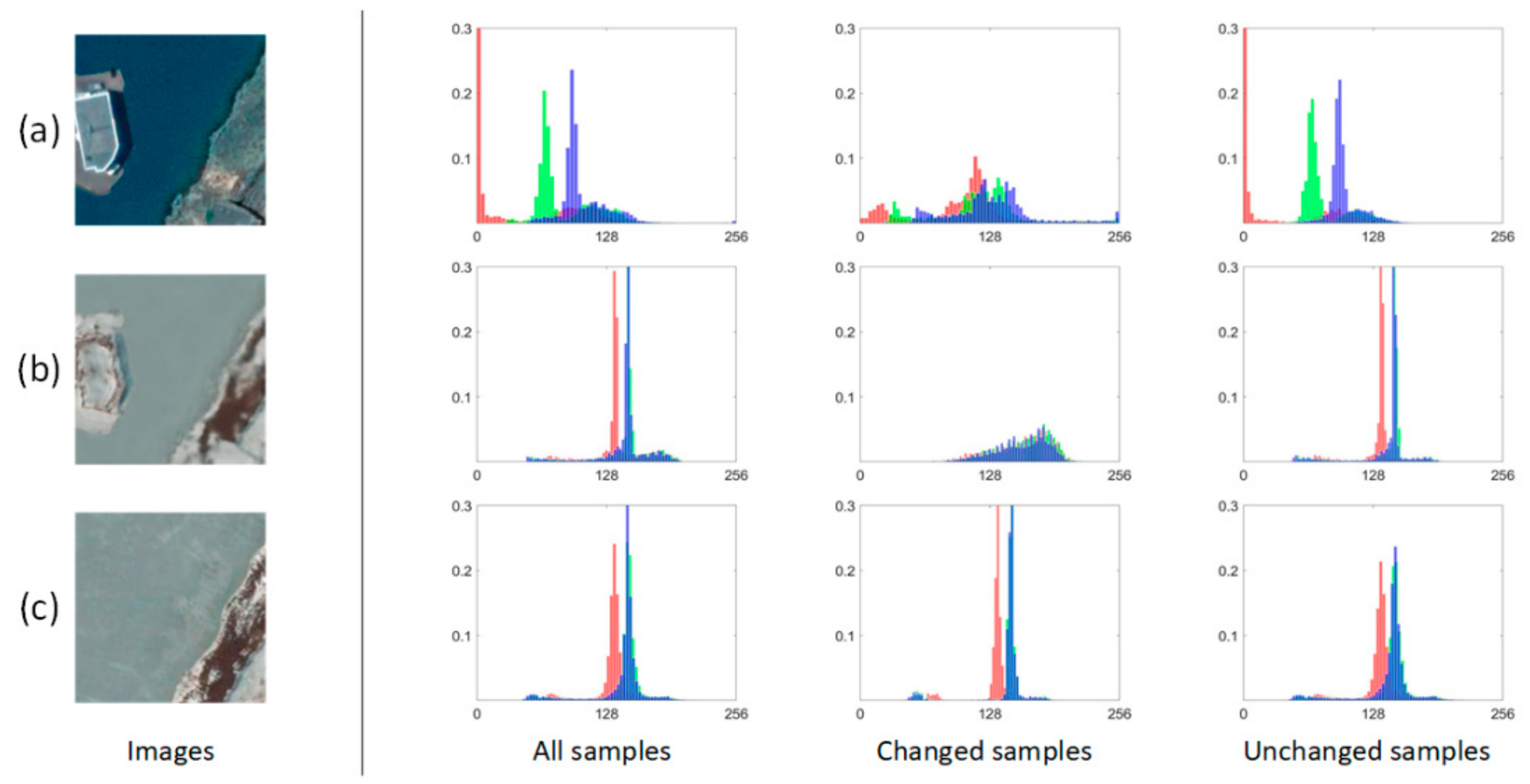
• We adopt a semantic stabilization strategy specifically for the original and translated images, to guarantee the distribution consistencies of land cover categories between them.
• Observing multiple constraints, we design a new full objective comprise of domain adversarial, cross-consistency, self-consistency, and identity losses to enforce satisfactory change detection results.

The structure of this paper is arranged as follows. In the next section, a brief description of the research background is presented. In Section 3, the methodology and implementation details of the proposed PDA are introduced. In Section 4, the experimental results, including domain adaptation and change detection, are discussed. Relative analyses to verify the effectiveness and superiority of our models are provided in Section 5. We end this paper with a summary and concluding remarks.

2. Background

2.1. Convolutional Long Short-Term Memory Network

As a specific RNN structure, LSTM is mainly innovative at the memory cell, which essentially acts as an accumulator of the state information, and is accessed, written, and cleared by several self-parameterized controlling gates. Based on this, LSTM has proven powerful and robust for modeling the long-range dependencies in one-dimensional general-purpose sequence data. Along this way, to explore the relationship in two-dimensional paired image data, convolutional blocks are embedded in LSTM units, to form the ConvLSTM model. With a new image input, the memory cell status will accumulate its information if the input gate is activated, and the past cell status will be forgotten in this process if the forget gate is activated. Meanwhile, the output gate will control whether the latest cell output is propagated to the final state. The primary advantage of utilizing this memory cell and gates is that the gradient is able to be trapped in the cell and be prevented from vanishing, which is a critical problem for conventional vanilla RNN models. The interaction of all states and gates along the time dimension is formulated as Equation (1).

$$\left\{\begin{array}{c}{i}_t=\sigma \left(W_{xi}⊛X_t+W_{hi}⊛H_{t-1}+W_{ci}\otimes C_{t-1}+b_i\right)\\ f_t=\sigma \left(W_{xf}⊛X_t+W_{hf}⊛H_{t-1}+W_{cf}\otimes C_{t-1}+b_f\right)\\ C_t=f_t\otimes C_{t-1}+i_t\otimes \tanh \left(W_{xc}⊛X_t+W_{hc}⊛H_{t-1}+b_c\right)\\ o_t=\sigma \left(W_{xo}⊛X_t+W_{ho}⊛H_{t-1}+W_{co}\otimes C_t+b_0\right)\\ H_t=o_t\otimes \tanh \left(C_t\right)\end{array}\right.$$

(1)

where $⊛$ indicates the convolution operation and $\otimes$ indicates the Hadamard product. $X_t$, $C_t$, and $H_t$ are the feature inputs, cell outputs, and hidden states, while $i_t$, $f_t$, and $o_t$ are the input, forget, and output gates, respectively.

ConvLSTM network was proposed for precipitation nowcasting [36] for the first time. Recently, with the powerful capability of feature expression on multi-temporal image sequences or video, ConvLSTM network attracts lots of research interests in many applications, including rain removal [37,38], image classification [39,40], moving target indication [41], and Earth surface monitoring [42]. It is suggested that this model is theoretically appropriate for domain adaptation.

2.2. Conditional Generative Adversarial Network

Extended from the preliminary GAN architecture, cGAN adopts conditional settings to provide controls on the generating modes. Here the conditionings are generally based on class labels or data modality, and they directly guide the data generation process. This specific adversarial mechanism helps to reduce the randomness of the generator, and improve the stability of the discriminator. For image translation tasks, given a pair of data with similar information capacities, cGAN tries to learn a global mapping model $G:\left(x,z\right)\to y$, from input image $x$ and auxiliary condition information $z$ to output image $y$. During this process, a discriminator $D$ tries to learn a strict decision rule, which can always identify the given output image $y$ as a “real” image, but identify the generated image $G\left(x\right)$ as a “fake” image. In this two-player antagonistic game, the continuous updates of these two opponent models are incentivized by an objective function, as expressed in Equation (2).

$${\mathcal{L}}_{cGAN}\left(G,D\right)={\mathbb{E}}_{y~P_{data}\left(y\right)}\left[\log D\left(y|z\right)\right]+{\mathbb{E}}_{x~P_{data}\left(x\right)}\left[\log \left(1-D\left(G\left(x|z\right)\right)\right)\right]$$

(2)

where the parameters of $G$ are updated to minimize this function, while those of $D$ are updated to maximize it. The main solution to this objective is expressed as Equation (3).

$$G^{*}=\arg \underset{G}{\min }\underset{D}{\max }{\mathcal{L}}_{cGAN}\left(G,D\right)$$

(3)

The adversarial learning method based on cGAN was first proposed for image labeling using multi-modal framework [43], and displayed stronger performance than conventional GAN. Due to its specific mechanism, cGAN has become an effective and popular tool for image generation-based tasks recently. With or without references, this type of framework has been widely applied in many applications, such as image-to-image translation [44], single image super-resolution [45], and cross-domain semantic segmentation [46]. Relevant researches have verified that cGAN is the mainstream backbone for domain adaptation.

2.3. Image-To-Image Translation

The idea of image-to-image translation goes back at least to image analogies tasks described by Hertzmann et al. (2001) [47], who employ a non-parametric texture model on input-output training image pairs. With this strategy, more recent approaches utilize datasets of input-output examples to learn parametric translation functions using a fully convolutional network (FCN) [48]. For example, given two groups of images as the inputs, the primary goal is to learn a pixel-level mapping model that is able to translate one of them to be near the other one, making them appear similar in color distribution, texture characteristics, or contextual information.

Current image-to-image translation approaches can be divided into two main categories, which are paired and unpaired, respectively. The former one pursues pixel-level alignment between paired images in two different but relevant datasets, and generally builds on the framework of pix2pix [44] or pix2pixHD [49]. With the supervision of references, these well-trained mapping models are able to produce detailed and precise translated images, but maybe out of generalization to some extent. The latter one pursues global feature-level similarity between unpaired images in two different and irrelevant datasets. Without the supervision of references, training these mapping models generally requires more implicit constraints. Kim et al. (2017) [50], Yi et al. (2017) [51], and Zhu et al. (2017) [52] consider the cycle-consistency of original and reconstructed images, to prevent image information loss in the translation process. References [53,54,55] apply disentangled representation theory to explore the latent content and style attributes of unpaired images, aiming to guarantee the invariance of content attributes in the translation process. In practice, these well-trained mapping models are advantageous in knowledge distillation, feature decomposition, and style transfer, since they are more robust and stable than those in paired image-to-image translation approaches.

For change detection, in registered bi-temporal images, the unchanged regions can be regarded as paired image parts meanwhile the changed regions can be regarded as unpaired ones. Therefore, in this particular case, unpaired image-to-image translation strategies can be considered to facilitate the elimination of domain discrepancies in remote sensing images.

3. Methodology

In this section, we begin with the discussion of the modeling problem of change detection task with season-varying co-registered images. After that, the overview of our framework architecture is given, and the corresponding new loss functions are interpreted in detail. In the end, specific implementation details, including the network architectures, training details, and predicting details, are introduced.

3.1. Problem Statement

Change detection task is mainly concerned with the identification and quantitative analyses of the changes of land cover types from co-registered bi-temporal remote sensing images $I_1$ and $I_2$. Although $I_1$ and $I_2$ are acquired in the same area, various positions, imaging conditions, atmospheric conditions, and even phenological shifts may lead to the spectral variation of the same land cover type between bi-temporal images. The land cover samples in these two images distribute dissimilarly and irregularly in the chromatic space, no matter changed or unchanged ones they are, as illustrated in Figure 1a,c. Remarkably, both the changed and unchanged samples have completely diverse distributions on the multi-channel histograms, making it difficult to detect changes using a simple decision-making strategy, or an end-to-end deep learning model. In order to highlight the features of the real changes between co-registered images and suppress interference of the spectral discrepancies of the same land cover types, a ConvLSTM network and a cGAN model are integrated to form a domain translation framework, to distill the land cover knowledge from the pre-event images, thereafter, progressively adjust the distributions of seasonal style features from the original domain to post-event one in the chromatic space, as illustrated in Figure 1b,c. At this stage, all the land cover samples follow an analogous distribution on the multi-channel histograms, where the changed ones appear diverse while the unchanged ones remain consistent. In this way, the changed and unchanged regions can be significantly differentiated by directly comparing the paired translated and post-event images, or by using a simple decision-making strategy.

Based on the above discussion, we develop a hybrid multi-model framework to simulate the process of our PDA, which includes an initial processor $Pr$, an image translator $Tr$, a semantic categorizer $Ca$, and a domain discriminator $D$, respectively. The processor is a traditional encoder-decoder network, which aims to extract features from the pre-event images, and provide an initially processed image for later image translation. The translator is a convolutional LSTM network, which aims to first extract features from the pre-event images, then translate them from their own domain to the post-event one. The categorizer is a pre-trained semantic segmentation network that guarantees the consistent distribution of land cover categories between the original and translated images. The discriminator is a simple down-sampling network that judges whether those two groups of translated and post-event images belong to the same seasonal domain.

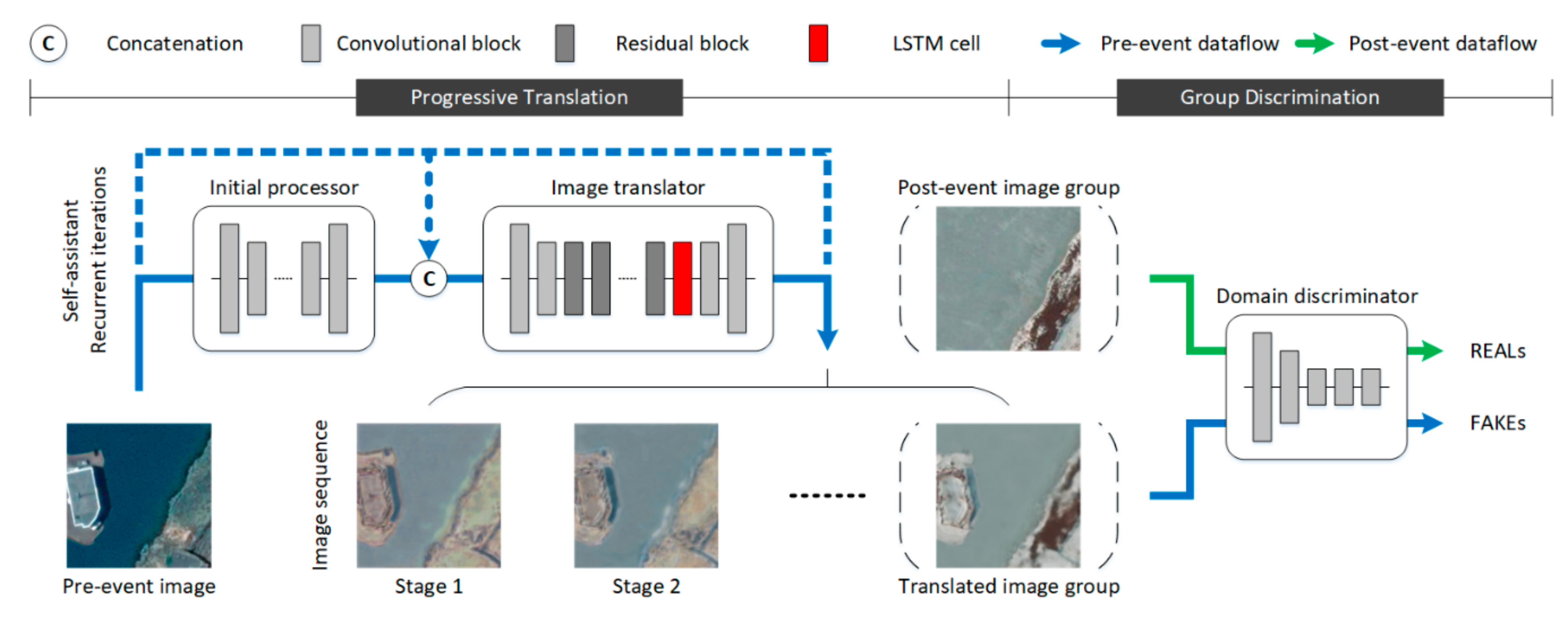
3.2. Framework Architecture

A multi-model framework is specifically designed to drive our proposed PDA, as illustrated in Figure 2. It is composed of two cascaded modules, namely, progressive translation and group discrimination, respectively. As the inputs of this framework, pre-event images are first forwarded to the former module, being progressively processed as the translated images. Thereafter, two groups of unpaired translated and post-event images are forwarded to the latter module, being discriminated whether they belong to the same seasonal domain. Detailed mechanisms of these two modules are introduced and interpreted in the following subsections.

3.2.1. Progressive Translation

As previously discussed, prevent the intrinsic characteristics of each land cover from season-varying changes is essential for better identification of the real land cover changes. Therefore, we utilize the translation module to alleviate the domain discrepancy between bi-temporal images progressively. It is achieved by an initial processor and an image translator, as illustrated in Figure 3, where pre-event images serve as the inputs of the module, and image sequences serve as the outputs.

Given a pre-event image $I_1$ as the input of this module, the initial processor produces a feature map as the primal guidance image for later image translation. For the entire translation process, this feature map can be regarded as the translated image at stage 0, defined as $I_{1\to 2}^{\left(0\right)}=Pr\left(I_1\right)$, its size is identical to those of the input image. Thereafter, taking the pre-event image as the self-assistant criteria, the image translator recurrently processes the concatenation of the pre-event and translated images as an image sequence, where multiple images can be regarded as the stage 1 to $N$ of the progressive translation process, as defined in Equation (4).

$$I_{1\to 2}^{\left(n\right)}=Tr\left(I_1,I_{1\to 2}^{\left(n-1\right)}\right) n=1,2,\dots ,N$$

(4)

where $I_{1\to 2}^{\left(n\right)}$ is the translated image produced by the image translator at recurrent time stage $n$, and $\left(·,·\right)$ denotes element-wise concatenation. Along this way, as the output of this module, the ultimate translated image is defined as $I_{1\to 2}^{\left(N\right)}$. At this point, the unchanged regions in the translated domain resemble those in the corresponding post-event domain, as formulated in Equation (5).

$$\left(1-CM\right)\otimes I_{1\to 2}^{\left(N\right)}\approx \left(1-CM\right)\otimes I_2$$

(5)

where $CM$ is the reference map for the change detection task. Its width and height are identical to those of the input images $I_1$ and $I_2$, yet it only has one channel to record the status of each pixel. In the binary reference map $CM$, value 1 indicates that the pixel belongs to the changed regions, while value 0 indicates that this pixel region is not changed. The symbol $\otimes$ in Equation (5) denotes the operation of element-wise multiplication. Moreover, the distributions of land cover categories in the pre-event and translated images have to be completely consistent, as formulated in Equation (6).

$$Ca\left(I_1\right)\approx Ca\left(I_{1\to 2}^{\left(N\right)}\right)$$

(6)

In this module, when training, the semantic categorizer and the aforementioned two constraints will simultaneously facilitate updating the initial processor and image translator until they are able to correctly translate the pre-event images to be near the post-event ones in the unchanged regions. When testing, nevertheless, only the initial processor and image translator are utilized to achieve the progressive domain adaptation.

3.2.2. Group Discrimination

In order to ensure the specific season associated image domain of the translated image data set is in keeping with those of the original post-event data set, a group discrimination module is utilized to evaluate if any two unpaired images have a similar appearance in the above two data set, respectively. It is achieved by a domain discriminator, as illustrated in Figure 4, where two groups of translated and post-event images serve as the inputs of the module, and discrimination matrices serve as the outputs.

Given two paired translated image $I_{1\to 2}$ and post-event image $I_2$ as the inputs of this module, two image collectors separately store them for later domain discrimination. As the pre-event images are continuously translated, these two collectors will continuously store them in a stochastic order. Thereafter, taking two unpaired translated and post-event images that are randomly selected from the above two image groups as the inputs, the domain discriminator evaluates whether they belong to the same seasonal domain. As the adversary of the initial processor and image translator that is mentioned in the previous subsection, the discriminator attempts to identify the post-event images as real images, while to identify the translated images as fake ones, as expressed in Equation (7).

$$\left\{\begin{array}{c}D\left(\left\{I_2\right\}\right)=TRUEs\\ D\left(\left\{I_{1\to 2}\right\}\right)=FALSEs\end{array}\right.$$

(7)

where $TRUE$ and $FALSE$ refer to the situation if the pixel is in the translated image or in the post-event image, and correspond to 1 and 0 in binary code, respectively, and $\left\{\cdot \right\}$ denotes the image group.

In combination with its constraint, the group discrimination module is trained dynamically to feedback to the initial processor and the domain translator. As long as the group discrimination module converging to the optimal solution, the initial processor and image translator are able to correctly translate the pre-event images from domain $T_1$ to $T_2$. When testing, nevertheless, the domain discriminator does not participate in the change detection process.

3.3. Loss Function

With the multi-model framework, a novel objective function composed of four specific terms is proposed in this research: (1) domain adversarial loss to match the global domain distributions of translated and post-event image groups; (2) cross-consistency loss to represent the pixel discrepancy of paired translated and post-event images in the unchanged regions; (3) self-consistency loss to represent the land cover category discrepancy of pre-event images and the corresponding translated ones; (4) identity loss to regularize the image translator to perform an identity mapping for post-event images.

3.3.1. Domain Adversarial Loss

As the principal loss of our framework, domain adversarial loss is derived from the basic adversarial loss in cGANs [43]. It is set to facilitate training the initial processor and image translator to hamper the domain discriminator from distinguishing the images of the translated domain from those of the post-event domain, when these images are in the same domain. In this research, we apply a domain adversarial loss in the post-event domain for the translated and post-event image groups, as formulated in Equation (8).

$${\mathcal{L}}_{dom}\left(Pr,Tr,D,T_1,T_2\right)={\mathbb{E}}_{I_2~T_2}\left[\log D\left(\left\{I_2\right\}\right)\right]+{\mathbb{E}}_{I_1~T_1}\left[\log \left(1-D\left(\left\{G\left(I_1\right)\right\}\right)\right)\right]$$

(8)

where $G\left(\cdot \right)$ is the simplified expression of the progressive translation module with the involvement of $Pr$ and $Tr$, and it satisfies $\mathrm{G}\left(I_1\right)=I_{1\to 2}$. In this loss function, $Pr$ and $Tr$ try to translate the pre-event images from domain $T_1$ to $T_2$, making them display similar seasonal appearances to the post-event images, while $D$ tries to separate them in the post-event domain, as depicted in Equation (7). Therefore, the domain adversarial loss is regarded as the mathematical formulation of a min-max problem, and can be defined as $\underset{\mathrm{Pr},Tr}{\min }\underset{D}{\max }{\mathcal{L}}_{dom}\left(Pr,Tr,D,T_1,T_2\right)$. In the min-max problem, the initial processor and image translator aim to minimize this domain adversarial loss function, while the domain discriminator aims to maximize it on the contrary.

3.3.2. Cross-Consistency Loss

With the progressive translation module, the appearances of paired translated and post-event images in the unchanged regions should be visually consistent, and distinctive discrepancies should exist only in the changed regions. Therefore, inspired by the cross-consistency loss in DLSF [32], we introduce a perceptual cross-consistency loss to ensure the accurate cross-season mapping only in the paired unchanged regions. Based on Equation (5), the cross-consistency loss can be formulated as Equation (9).

$${\mathcal{L}}_{cross}\left(Pr,Tr,T_2\right)={\mathbb{E}}_{I_{1\to 2},I_2~T_2}\left[{\displaystyle \sum }_n^N{\theta }^{N-n}\cdot ||\left(1-CM\right)\otimes {\left(I_{1\to 2}^{\left(n\right)}-I_2\right)||}_2\right]$$

(9)

where $\Vert \cdot {\Vert }_2$ is the L2 distance loss, and ${\theta }^{N-n}$ is a progressive weight specifically for the translated image at stage 1 to N. Minimizing this loss encourages the initial processor and image translator to achieve better mapping, especially in the paired unchanged regions.

3.3.3. Self-Consistency Loss

After the progressive translation process, the overall distribution of land cover categories in the translated images should remain invariant with that of the paired pre-event ones, even though they are in different seasonal domains. Therefore, we introduce a rigorous self-consistency loss derived from the LogSoftmax function in FCN [48], to avoid the displacement and distortion of land cover information in the cross-season mapping. Based on Equation (6), the self-consistency loss can be formulated as Equation (10).

$${\mathcal{L}}_{self}\left(Pr,Tr,Ca,T_1,T_2\right)={\mathbb{E}}_{I_1~T_1,I_{1\to 2}~T_2}\left[||Ca\left(I_1\right)-Ca{\left(I_{1\to 2}^{\left(N\right)}\right)||}_1\right]$$

(10)

where $\Vert \cdot {\Vert }_1$ represents the loss function using L1 norm. Minimizing this loss encourages the initial processor and image translator to achieve content-invariant mapping, no matter in changed or unchanged regions.

3.3.4. Identity Loss

Problems arise when the well-trained models for image-to-image translation tasks are generally stochastic and not unique, owing to the powerful expression capabilities of neural networks. Addressing this issue, Taigman et al. (2017) [56] propose an identity loss to regularize the generator to be near an identity mapping when real samples of the target domain are provided. Moreover, various unsupervised domain adaptation methods have used this kind of loss function, such as CycleGAN [52] and DistanceGAN [57]. In this research, to stabilize training the initial processor and image translator, we adopt an identity loss to ensure that the progressive translation module would keep the post-event images as invariant, and this can be formulated as Equation (11).

$${\mathcal{L}}_{idt}\left(Pr,Tr,T_2\right)={\mathbb{E}}_{I_2~T_2}\left[||G\left(I_2\right)-I_2||{}_1\right]$$

(11)

where $\Vert \cdot {\Vert }_1$ represents the loss function in L1 norm. The minimization of this loss function promotes the convergence of our initial processor and image translator. Along with the convergence procedure, the randomness of the initial processor and image translator is also restrained.

Finally, the objective function of our PDA is constituted by the four losses mentioned above functions, as formulated in Equation (12).

$$\begin{gathered} \mathcal{L}\left(Pr,Tr,Ca,D\right)={\lambda }_{dom}\cdot {\mathcal{L}}_{dom}\left(Pr,Tr,D,T_1,T_2\right) \\ +{\lambda }_{cross}\cdot {\mathcal{L}}_{cross}\left(Pr,Tr,T_2\right) \\ +{\lambda }_{self}\cdot {\mathcal{L}}_{self}\left(Pr,Tr,Ca,T_1,T_2\right) \\ +{\lambda }_{idt}\cdot {\mathcal{L}}_{idt}\left(Pr,Tr,T_2\right) \end{gathered}$$

(12)

where $\lambda$ represents the parameters used to adjust the importance of the four losses, therefore, the season-varying change detection problem can be modeled as in Equations (13) and (14).

$$P{r}^{*},T{r}^{*}=\arg \underset{\mathrm{Pr},Tr}{\min }\mathcal{L}\left(Pr,Tr,Ca,D\right)$$

(13)

$$D^{*}=\arg \underset{D}{\max }\mathcal{L}\left(Pr,Tr,Ca,D\right)$$

(14)

Guided by certain reference change maps, we keep the semantic categorizer constant, and train the initial processor, image translator, and domain discriminator simultaneously. When predicting, however, only the initial processor and image translator are used for change detection.

3.4. Implementation

3.4.1. Network Architecture

The proposed PDA is driven by four neural networks, namely an initial processor, an image translator, a semantic categorizer, and a domain discriminator, respectively. However, only three of them participate in the training process, and their architectures are described in Figure 5. Derived from Encoder-Decoder [58], the initial processor comprises six convolutional, one convolutional layer, and one TanH activation. This model conducts down-sampling operation, and up-sampling operation once respectively to the input image patches and generate the feature maps with the size of $256\times 256$. Applying ResNet [59] as the backbone, the image translator comprises two convolutional blocks and five residual blocks, followed by an LSTM cell, a convolutional block, a convolutional layer, and a Tanh activation. This model also conducts one down-sampling and one up-sampling on the input concatenation patches, but for multiple recurrent times. Furthermore, it produces an image sequence, where the size of all the translated images is identical to those of the original images. Because the input translated and post-event images are unpaired, a Markovian discrimination strategy [60] is adopted to model only the high-frequency features for the domain discriminator. Moreover, our discriminator is a PatchGAN that conducts four-fold down-sampling on the input image patches by reference to the discriminator in pix2pix [44]. All the weights and biases of their layers are initialized using the strategy of Xavier [61] in the aforementioned models. In addition, for the semantic categorizer, we suggest utilizing a pre-trained VGG-16 [62] model, which is trained on ImageNet [63] dataset.

3.4.2. Training Details

For all the experiments, our proposed PDA is trained by simultaneously minimizing its four component networks to optimal solutions iteratively by updating the associated full objective $\mathcal{L}\left(Pr,Tr,Ca,D\right)$. In this research, according to the implementations in Attentive GAN [37] and Progressive Recurrent Network [38], we set $N$, $n,$ and $\theta$ to 6, 4, and 0.8, respectively, in Equation (9). In addition, we set ${\lambda }_{dom}$ to 0.01, and set ${\lambda }_{cross}$ to 1, meanwhile set both ${\lambda }_{self}$ and ${\lambda }_{idt}$ to 0.1 in Equation (12), based on the implementations in DLSF [32] and CycleGAN [52]. The least-squares loss [64] specifically for ${\mathcal{L}}_{dom}$, instead of the negative log likelihood loss in basic GANs is chosen in our experiments to enforce a stabilized training. In addition, the volumes of two image collectors in the group discrimination module are both set to 50.

A hierarchical learning strategy in the optimization procedure is utilized in our research considering the complexity of this hybrid multi-model framework. In each epoch, paired image patches are first forwarded into all the networks in sequence. Thereafter, for the backward propagation, the initial processor, image translator, and domain discriminator are updated alternately, but the semantic categorizer remains constant. The overview of the training process concerning the forward and backward propagations in one epoch is presented in

Table 1. Overview of the training process for the proposed hybrid multi-model framework.

Inputs:	$\mathbf{Paired} \mathbf{Pre}-\mathbf{Event} \mathbf{Images}: {\mathit{I}}_1~{\mathit{T}}_1$ $\mathbf{Paired} \mathbf{Post}-\mathbf{Event} \mathbf{Images}: {\mathit{I}}_2~{\mathit{T}}_2$ $\mathbf{Corresponding} \mathbf{Reference} \mathbf{Change} \mathbf{Maps}: \mathit{C}\mathit{M}$
for$epoch\leftarrow 1 to epoc{h}_{max}$do $\mathrm{forward} I_1$$\mathrm{into} Pr$$\mathrm{to} \mathrm{produce} I_{1\to 2}^{\left(0\right)}$ $\mathrm{forward} I_1$$\mathrm{and} I_{1\to 2}^{\left(0\right)}$$\mathrm{into} Tr$$$$\mathrm{times} \mathrm{to} \mathrm{produce} I_{1\to 2}$ $\mathrm{forward} I_1$$\mathrm{and} I_{1\to 2}$$\mathrm{into} Ca$ $\mathrm{forward} \left\{I_{1\to 2}\right\}$$\mathrm{and} \left\{I_2\right\}$$$ $\mathrm{update}$$\mathrm{with} {\mathcal{L}}_{dom}\left(Pr,Tr,D,T_1,T_2\right)$ $\mathrm{update} Pr$$\mathrm{and} Tr$$\mathrm{with} \mathcal{L}\left(Pr,Tr,Ca,D\right)$ end for
Outputs:	$\mathrm{Well}-\mathrm{trained} \mathrm{initial} \mathrm{processor}: P{r}^{*}$ $\mathrm{Well}-\mathrm{trained} \mathrm{image} \mathrm{translator}: T{r}^{*}$

.

3.4.3. Predicting Details

The proposed PDA produces three well-trained networks, among which the initial processor and image translator are utilized for predicting. Like the training process, the two models will simultaneously achieve the progressive image translation from the pre-event domain to the post-event one. At this stage, the paired translated and post-event images are difficult to separate by the domain discriminator, indicating that our models are able to realize the cross-season translation. In the end, to decide the changed regions, we perform pixel-level similarity measurement on paired translated and post-event images, and then produce a predicted change map, as expressed in Equation (15).

$$P\left(i,j\right)=||I_{1\to 2}^{\left(N\right)}\left(i,j\right)-I_2{\left(i,j\right)||}_2$$

(15)

where $P$ is the predicted change map, which reflects the change probabilities of all pixels. The value of a pixel located at $\left(i,j\right)$ is large means that this pixel may be part of a changed region; otherwise, it may be part of an unchanged region. In this research, the final change detection result is calculated by the pixel-level binarization of the predicted change map, with the adaptive threshold.

4. Experiments

In this section, the datasets description, baseline methods, and evaluation metrics about all the experiments are first introduced. Thereafter, the relevant experimental setup is interpreted in detail. Finally, the experimental results of our PDA and other comparative methods are presented.

4.1. Datasets Description

All the season-varying remote sensing images are high-resolution optical real images, obtained by Google Earth (DigitalGlobe), and they involve massive season-induced changes [65]. According to the extent of seasonal differences, we divide them into two different types, which are image pairs with minor seasonal variation and ones with major seasonal variation, respectively.

The first type of dataset includes 4 multi-temporal remote sensing images with minor seasonal variation. As shown in Figure 6, in this dataset, these registered images have the same dimension of $4275\times 2700$, with the same spatial resolution of approximately 0.05 m per pixel. Remarkably, the corresponding references are in binary format, where the changes mainly include plenty of new buildings, several mobile vehicles, and a few vegetation covers. In the training process, each image can be regarded as the pre-event or post-event image, regardless of its chronological order.

The second type of dataset includes 3 couples of bi-temporal remote sensing images with major seasonal variation. As shown in Figure 7, in this dataset, the former two image pairs have the same dimension as ones in dataset I, with different spatial resolutions of approximate 0.22 and 0.52 m per pixel, and the latter image pair has the dimension of $1900\times 1000$, with the spatial resolution of approximate 0.5 m per pixel. Compared with those in dataset I, the changes in dataset II include more roads and vehicles, but fewer vegetation covers. In the training process, different from dataset I, we suggest regarding the images without snow cover as the pre-event images and regarding the images with snow cover as the post-event images.

4.2. Baseline Methods

In order to testify the effectiveness of our PDA in season-varying change detection, several state-of-the-art methods are selected to carry out comparative analysis and discussions. As the most popular classic model for unsupervised change detection in remote sensing, CVA [22] is the representative of conventional methods. In the comparison, we exploit the pixel-level change vector analysis method together with the threshold provided by K-means clustering algorithm. Derived from CNN, GETNET [17] is the representative of deep learning-driven methods based on original image. The features extracted by our proposed model are able to facilitate the supervised change detection by carefully designed network architecture and loss function. In addition, PCANet [23] and GAN [24] are the representatives of ones based on image arithmetical, while DSCN [30] and DSFL [32] are the representatives of ones based on image transformation. Remarkably, for the above competitors, only the models in GETNET and PCANet are end-to-end frameworks, and the ones in other methods are all hybrid multi-model frameworks.

4.3. Evaluation Metrics

Three commonly used metrics are selected as the evaluator to quantify the performance of our proposed PDA as well as to prove its effectiveness and robustness by comparison of its results with all the comparative deep learning-driven change detection methods.

Let $TP$ denotes the number of changed pixels correctly labeled, $TN$ denotes the number of unchanged ones correctly labeled, $FP$ denotes the number of unchanged ones incorrectly labeled, and $FN$ denotes the number of changed ones incorrectly labeled. Then, overall accuracy (OA), Kappa coefficient (KC), and F1 Score (F1) are defined as follows.

Overall accuracy: The overall accuracy is defined as the ratio of correctly recognized samples divided by the total number of all samples, and is often used to quantify the total capabilities of the change detection models, as expressed in Equation (16).

$$OA=\frac{TP+TN}{TP+TN+FP+FN}$$

(16)

Kappa coefficient: This index is a statistical measurement that represents the consistency between the experimental result and corresponding ground truth, as formulated in Equation (17).

$$KC=\frac{p_0-p_e}{1-p_e}$$

(17)

where $p_0$ indicates the true consistency, which is equal to $OA$ here, and $p_e$ indicates the theoretical consistency, as expressed in Equation (18).

$$p_e=\frac{\left(TP+FP\right)\left(TP+FN\right)+\left(TN+FP\right)\left(TN+FN\right)}{{\left(TP+TN+FP+FN\right)}^2}$$

(18)

F1 score: This index is a statistical magnitude that represents the harmonic average of the precision and recall rates. It is commonly used to assess the performance of neural network models, as expressed in Equation (19).

$$F1=\frac{2TP}{2TP+FP+FN}$$

(19)

It can be concluded that, the change detection performance gets better when the values of the above three evaluation metrics become larger.

4.4. Experimental Setup

We perform six groups of experiments on two types of datasets described in Section 4.1, which are between paired images I-a and I-b, I-b and I-c, I-c and I-d, II-1a and II-1b, II-2a and II-2b, and II-3a and II-3b, respectively. For each pair of images, we utilize three-quarters of the areas as the training areas, while leaving one-quarter of them as the testing areas. Before the experiments, to verify the effectiveness and competitiveness of this method, several pre-process operations are required to conduct on the season-varying remote sensing images as follows:

• To boost the convergence of the weight and bias parameters in the initial processor, image translator, and domain discriminator, we perform instance normalization on all the channels of remote sensing images, from 0 to 255 to −1 to 1.
• Since the original remote sensing images are of large scale, which is inconvenient for computation, the original training and testing images are processed into small image patches with the same size of $256\times 256$ through randomly cutting them with certain overlaps and rotations.
• Specifically, for the paired pre-event and translated image patches, which are forwarded to the semantic categorizer, we perform mean-subtraction normalization on each band of them in two different seasonal domains.

In our experiment, we set 200 epochs with the batch size of 1 to make the proposed models converge, using Adaptive Moment Estimation (Adam) [66] as the optimizer with the initial learning rate of $2\times {10}^{-4}$. In addition, the learning rate is set to a constant value for the first half of the total epochs, then linearly decayed to 0 for the other half. The decay rates for the moment estimates are set to 0.9 and 0.999, and the epsilon is set to ${10}^{-8}$.

The experiments based on our proposed PDA are completely performed on a computer, which is equipped with Intel i7 CPU, 32GB RAM, and NVIDIA GTX 1080 GPU. With the Python platform, we utilize a PyTorch 0.4+ environment and other dependencies, including torchvision, visdom, and dominate etc., to compile the programs. When training, the time for an iteration on two paired image patches is approximately 0.70 s. Nevertheless, when testing, the time for one pair is just 0.21 s. More detailed information about our experiments, including the training times and testing rates, is presented in

Table 2. Experimental information of our PDA.

Image Pair	Sample Number	Training Time	Testing Rate
I-a & I-b I-b & I-c I-c & I-d	1683	64.78 h	0.21 s/pair
II-1a & II-1b II-2a & II-2b	1308	50.50 h
II-3a & II-3b	936	36.55 h

.

4.5. Results Presentation

With the six couples of bi-temporal remote sensing images in two types of datasets, the binary format change detection results of the proposed PDA and several competitors are presented in Figure 8 and 9, respectively, where the pixels in white and black indicate the changed and unchanged regions. As can be seen, with different degrees of seasonal variation, the testing results on dataset I are generally better than those on dataset II.

For image pairs with minor seasonal variation, the appearances of changes are still structurally simple and distinct in the chromatic space, even CVA is able to give rough positions and outlines of the changed regions, though numerous errors and noises are contained, as shown in Figure 8c. Due to the limited capabilities on feature expression, the end-to-end frameworks, GETNET and PCANet, are able to give approximate shapes of changes but ambiguous outlines, as shown in Figure 8d,e. Although they are insensitive to image noises, abundant image details are overlooked. Different from end-to-end frameworks, GAN gives better results than PCANet, though they are both based on image arithmetical, as shown in Figure 8f. Nevertheless, its resistance ability to noises is weaker. As the pioneer image transformation-based method, DSCN is able to learn certain implicit information, to benefit detecting subtle changes, but with massive holes, as shown in Figure 8g. Integrating ideas of dual learning and Siamese network, DLSF achieves better results than DSCN, as shown in Figure 8h. Compared with DLSF, our proposed PDA displays competitive results, as shown in Figure 8i. It is notable that, the testing results of our PDA are slightly better than those of DLSF for the first and third image pairs. However, the testing result of our PDA is slightly worse than that of DLSF for the second image pair.

For image pairs with major seasonal variation, the appearances of changes are more uncertain and complex in the chromatic space, leading to unstable and poor change detection results by CVA, as shown in Figure 9c. On the other hand, the end-to-end frameworks, GETNET and PCANet, give entirely unsatisfactory results. Furthermore, their resistance abilities to noises are far weaker than those on dataset I, as shown in Figure 9d,e. In comparison, GAN is able to give better results, but with more incorrect detections, as shown in Figure 9f. Remarkably, the three methods based on image transformation still perform well for this dataset. Although containing more holes, DSCN can give correct positions and outlines of changed regions, as shown in Figure 9g. Different from DSCN, DLSF and our proposed PDA can give more accurate and robust results, as shown in Figure 9h,i. It is notable that, the boundaries of the changed regions generated by our PDA model are clearer and smoother than those by DLSF, and there are fewer negative influences from noises, specifically for the first and third image pairs.

The evaluation metrics OA, KC, and F1 values are calculated and summarized based on the change detection results generated by our proposed PDA and other comparative methods with the two types of datasets in

Table 3. Quantitative results of the comparative methods. The best values are in bold, and (−) denotes that the value is negative.

Image Pair	Metric	CVA	GETNET	PCANet	GAN	DSCN	DLSF	PDA
I-a & I-b	OA	0.8540	0.8981	0.9212	0.9069	0.8863	0.9225	0.9311
	KC	0.2058	0.6479	0.6516	0.6874	0.6649	0.7820	0.7383
	F1	0.2855	0.7092	0.6959	0.7421	0.7340	0.8313	0.7784
I-b & I-c	OA	0.7684	0.8786	0.8918	0.8706	0.7818	0.8946	0.8761
	KC	0.3505	0.7483	0.7536	0.6284	0.4627	0.7711	0.7329
	F1	0.4675	0.8501	0.8332	0.7074	0.5955	0.8525	0.8297
I-c & I-d	OA	0.8514	0.8911	0.9063	0.9134	0.4034	0.9146	0.9347
	KC	0.3084	0.6077	0.6658	0.7405	−	0.7513	0.7815
	F1	0.3921	0.6710	0.7212	0.7939	0.2616	0.8045	0.8210
II-1a & II-1b	OA	0.4748	0.5337	0.5819	0.9041	0.8094	0.9158	0.9272
	KC	−	0.0605	0.0821	0.7006	0.5368	0.6703	0.7535
	F1	0.1492	0.2275	0.2583	0.7581	0.6602	0.7167	0.7974
II-2a & II-2b	OA	0.4738	0.6806	0.7218	0.8642	0.7925	0.8892	0.9150
	KC	−	0.2195	0.2876	0.6057	0.3469	0.5940	0.7102
	F1	0.0792	0.3763	0.4310	0.6894	0.4475	0.6565	0.7610
II-3a & II-3b	OA	0.3701	0.4123	0.4328	0.7815	0.8176	0.8575	0.8994
	KC	−	−	−	0.4587	0.5043	0.5341	0.6577
	F1	0.2148	0.2851	0.2936	0.5937	0.6114	0.6136	0.7185

. Compared with CVA, GETNET, PCANet, GAN, DSCN, and DLSF, our PDA achieves the competitive OA, KC, and F1 values on dataset I, and achieves the highest values on dataset II.

5. Discussion

For deep learning-driven change detection methods based on hybrid multi-model frameworks, the experimental performances are primarily controlled by two decisive factors: network architecture and loss function. Meanwhile, for a one-sided translation model, the translation direction can also influence the experimental results. Therefore, in this section, we discuss the details of designing the aforementioned two factors and the selection of translation direction. The robustness and uniqueness of our method are verified through extensive experiments.

5.1. Design of Network Architectures

For different image processing tasks, deep neural networks are generally designed with diverse structures. Networks equipped with extensive and complex blocks have stronger abilities on feature expression and representation, but they may easily result in data over-fitting to some extent. On the contrary, networks equipped with few and simple blocks improve the efficiency and generalization, but their limited expression and representation abilities are likely to reduce the utilization of image information. In RNN-typed neural networks, the recurrent block is a plug-and-play component, and plays a significant role in image analysis related tasks. The structural volume and recurrent number of this block determine the performance of the model. Taking our image translator as the backbone, we conduct several comparative experiments, utilizing multiple different image translator but the same initial processor, semantic categorizer, and domain discriminator. The image translators are mainly different at the residual block number and the recurrent time. The translation results on two typical types of dataset are illustrated in Figure 10 and Figure 11.

As can be seen, with the increase of the residual block number and recurrent time in the image translators, the qualities of the translated images become distinctly better, leading to more accurate and precise change detection results. Remarkably, for image pairs with minor seasonal variation, the image translator only with five residual blocks and four recurrent iterations are strong enough to achieve satisfactory domain adaptation results, as depicted in the first patch in Figure 10b. Nevertheless, for image pairs with major seasonal variation, the image translator with at least five residual blocks and six recurrent iterations are able to perform complete and correct domain adaptation results, as depicted in the third patch in Figure 11b. Therefore, in this research, we designed the image translator with five residual blocks and six recurrent iterations to ensure the effectiveness and robustness of our proposed PDA, for change detection using all types of season-varying remote sensing images.

5.2. Design of Loss Functions

Loss functions generally act as the driven force to lead the proposed PDA model towards an optimal solution. Hence the loss functions are required to be designed carefully. In order to verify the effectiveness and uniqueness of our loss functions, several ablation studies are conducted separately for all the experiments with our proposed PDA. The testing OAs driven by five diverse loss function combinations are calculated and summarized in

Table 4. Ablation studies of the full objective for our six experiments.

Loss Combination	I-a & I-b	I-b & I-c	I-c & I-d	II-1a & II-1b	II-2a & II-2b	II-3a & II-3b
dom	0.3870	0.3429	0.3764	0.2691	0.2566	0.2302
dom+self	0.5171	0.4744	0.4993	0.4212	0.3930	0.3687
dom+corss	0.8146	0.7372	0.8205	0.7643	0.7469	0.7013
dom+cross+self	0.9057	0.8553	0.9120	0.8478	0.8117	0.8025
dom+cross+self+idt	0.9311	0.8761	0.9347	0.9272	0.9150	0.8994

. The specific effects of each loss function are discussed at the end.

It is worth noticing that the testing OAs on all the image pairs increase gradually when the full objective becomes more complex. It is confirmed that complex constraints can lead to stronger generalization ability of our models.

As shown in the three rows in the middle of Table 4, it is clear that the addition of the self-consistency loss can modestly promote the performance, while the addition of the cross-consistency loss can prominently improve the performance. Remarkably, the second combination represents an unsupervised change detection method, and the third combination represents a simplified mode of our PDA. The different increases in OAs indicate that the reference change maps and cross-domain constraints are essential for our models, and the self-supervision constraint can effectively facilitate our models better realizing the translation between bi-temporal remote sensing images.

As shown in the last two rows of Table 4, it is clear that the addition of the identity loss can slightly promote the performance. Furthermore, the increase on dataset II are more prominent than that on dataset I. The different increases in OAs indicate that this constraint is more significant for the translation between the paired images with major seasonal variation. Practically, the identity loss is widely adopted in unsupervised domain adaptation or unpaired image-to-image translation, to make the training process rid of model oscillations.

5.3. Selection of Translation Direction

With one-sided image-to-image translation networks, the dataflow between the paired images generally has two opposite directions to be selected. Taking our domain adaptation for example, in the training process, we can directly translate the pre-event images from their own seasonal domain to the post-event one, or regard the post-event images as the pre-event images and translate them in reverse order. In our experiments, we observe that the change detection results on dataset II are far more sensitive to the dataflow directions than those on dataset I. More precisely, utilizing the same change detection framework, the testing results obtained by the translation from the images without snow cover to the ones with snow cover are distinctly better than those obtained by the translation from the images with snow cover to the ones without snow cover. With this phenomenon, we make in-depth analyses on the training processes of our three experiments on dataset II. The convergence curves of all the comparative experiments are illustrated in Figure 12.

It is noteworthy that the convergence procedure of the full objectives and discrimination losses in Figure 12b are generally more stable than that in Figure 12a. It is confirmed that those translations with the direction, from the images without snow cover to the ones with snow cover, are positive to facilitate the change detection.

Based on the first image translation direction, adopting the training visualization technique, we have observed more details in the training process. For image pair II-1a & II-1b, the discriminator is always unstable, as depicted in the first column in Figure 12a, making the generator sometimes fails to perform complete and correct translations, even in the late period of the training process. On the contrary, for image pair II-3a & II-3b, the generator is always unstable, as depicted at epochs 48 and 102 in the third column in Figure 12a, leading to a difficult convergence procedure. Remarkably, for image pair II-2a & II-2b, the discriminator suddenly stops working after an update, and the loss of it eventually still fluctuates around 0.01, as depicted in the second column in Figure 12a. Without the supervision of the discriminator, the framework has led to data over-fitting, and is finally unable to achieve the cross-season translation. Theoretically, the images without snow cover generally involve more detailed features of land cover categories than the ones with snow cover. Regarding the former ones as the pre-event images, the translation is a type of dimension-reducing operation, conversely, the translation is a type of dimension-increasing operation. In the case of insufficient input features, forcing neural networks to generate image information that does not exist is logically and practically not appropriate. Therefore, for change detection using image pairs with major seasonal variation, it is suggested to regard the images without snow cover as the pre-event ones, and regard the images with snow cover as the post-event ones.

6. Conclusions

In this research, we integrated strategies of ConvLSTM network and cGAN, and then developed a novel image transformation-based approach named PDA, for supervised change detection using season-varying remote sensing images. With the proposed initial processor and image translator, we successfully distilled features of land cover categories from the pre-event images, then achieved the translation progressively from the pre-event domain to the post-event one. During this cross-season translation, the seasonal differences of paired unchanged regions are effectively suppressed, and the changed regions are distinctly highlighted. Extensive experiments were conducted on two types of season-varying change detection datasets. The presented discussions and comparative analysis verify the effectiveness and competitiveness of the PDA model proposed in this paper.

Nevertheless, our method still involves certain limitations. In the training process, the irregular distribution of seasonal characteristics will drive the strict loss functions to mislead the models. For example, in the images of winter, some of the buildings and roads are covered by snow, while some of them are not. These uncertain appearances confuse the models, leading to continuous oscillations on the convergence curves. In addition, the negative effect of land cover shadows on our method is much greater than that on other deep learning-driven methods, because the original image will be concatenated to the input ones for every recurrent iteration in the progressive translation. Therefore, in future studies, we plan to explore certain self-adaptive constraints, to facilitate our model’s better resistance against the negative influences of the aforementioned two problems.