Abstract
Automatic building categorization and analysis are particularly relevant for smart city applications and cultural heritage programs. Taking a picture of the facade of a building and instantly obtaining information about it can enable the automation of processes in urban planning, virtual city tours, and digital archiving of cultural artifacts. In this paper, we go beyond traditional convolutional neural networks (CNNs) for image classification and propose the HierarchyNet: a new hierarchical network for the classification of urban buildings from all across the globe into different main and subcategories from images of their facades. We introduce a coarse-to-fine hierarchy on the dataset and the model learns to simultaneously extract features and classify across both levels of hierarchy. We propose a new multiplicative layer, which is able to improve the accuracy of the finer prediction by considering the feedback signal of the coarse layers. We have quantitatively evaluated the proposed approach both on our proposed building datasets, as well as on various benchmark databases to demonstrate that the model is able to efficiently learn hierarchical information. The HierarchyNet model is able to outperform the state-of-the-art convolutional neural networks in urban building classification as well as in other multi-label classification tasks while using significantly fewer parameters.
1. Introduction
Over the past few centuries, there has been a radical shift in the organization of human societies marked by urbanization. According to the United Nations’ World Urbanization Prospects, in 2018, 55% of the world’s population lived in urban areas. This proportion is expected to increase to 68% by 2050 [1]. As the world continues to urbanize, it is crucial to analyze urban areas in order to obtain meaningful information to adequately guide urban development. Urban area analysis is a key issue at the core of numerous applications such as urban planning and management, urban visualization and population estimation. In our work, we investigate one specific aspect: building classification. Extensive research work has already been conducted on the detection and localization of buildings in remote sensing images [2,3,4,5,6], but only a few existing methods deal with the automated analysis and characterization of the extracted buildings [7]. In fact, limited research has analyzed buildings from a street-level perspective which is what the present work is concerned with. This article focuses on land-use classification at the level of individual buildings. It introduces a new approach for the classification of buildings in urban environments based on photographs of their facades. The proposed method can be integrated within a remote sensing data processing pipeline for virtual city modeling, providing specific information about the functionality and the architectural styles of the buildings.
Our work focuses on two main aspects of urban building categorization: functional purpose and architectural style. These two characteristics are useful in a number of applications such as: real-estate valuation, declaration as a monument, virtual city tours, etc. However, the classification of urban buildings in terms of function or style is often challenging for multiple reasons.
As for functional analysis, even for a human observer, the classification of urban buildings from photographs of their facades is not straightforward. As can be observed from the sample photographs in Figure 1, buildings fulfilling different functions can be confused with one another: e.g., an apartment building can be confused with an office building and vice versa due to their similar shapes, materials, and myriad of windows (see Figure 1b,c). Additionally, buildings fulfilling a similar general function are often difficult to differentiate: e.g., buildings with religious and spiritual purposes can showcase similar design features (cupolas, towers, elaborately decorated facades, etc.) making them hard to distinguish (see church, mosque, and synagogue in Figure 1d–f) from an image where revealing signs (Christian cross, Star of David etc.) are concealed.

Figure 1.
Some examples of building images.
Regarding architectural style analysis, precisely distinguishing among different styles can require special background knowledge in architecture. In addition to this, one building can display numerous architectural styles due to aesthetic and design choices and/or renovations and refurbishments throughout the years. It can thus be really hard to identify the correct architectural category of buildings. In this work, we consequently label buildings based only on the predominant style. Later on, future research can be conducted with the aim of segmenting and recognizing the different architectural styles present on a building.
To extract relevant features for building classification we propose a convolutional neural network based approach. Our model uses a baseline flat CNN feature extractor such as the VGG-16 [8]. At the top of the network, classifier branches are added following a coarse-to-fine paradigm which is reflected in a pre-defined class hierarchy. Our proposed model is thus an instance of multitask learning with the objective of solving a coarse classification along with a finer one. Setting up such a hierarchy helps the model to first solve the easier coarse classification before using this prior knowledge to guide the fine classifier through an intermediary custom multiplicative layer. This way, the model can distinguish between buildings falling under different coarse classes, for instance a residential building vs. a religious one, before using this knowledge to decide which fine class the building belongs to.
Contributions
To summarize the two main contributions of this research, it:
- proposes a new approach to the multi-label hierarchical classification of buildings—which can also be extended to other applications—which requires significantly less parameters than other existing hierarchical networks;
- solves the urban building classification problem better than state-of-the-art models as demonstrated in a new carefully designed dataset.
2. Literature Review
2.1. Building Recognition
The analysis of buildings has been an active area of research in computer vision in recent years. The majority of projects have, however, focused on satellite and aerial imagery [9]. These methods focus on the detection of building footprints [10], and the detection and segmentation of land covers [11]. In [12], the authors use deep learning techniques to map building functions using both aerial and street view images. For the fusion of the heterogeneous input data, an ensemble of models trained using each image type independently is implemented. For building type classification, only four classes are used: residential, public, industrial, and commercial.
With a similar objective, many methods have been developed for the extraction of buildings from remote sensing data. For instance, in [7], the authors introduce a new classification scheme for building types which integrates input information from different sources: building height information is extracted from LiDAR point clouds, while textural, spectral, and geometric information are obtained from high-resolution remote sensing images. The combination of this information is then used for segmentation which then provides input information for a better classification of building types. The authors use data from two Chinese urban villages and focus on the building types: villa, apartment building, low-rise building, carport, factory, and keep an additional class for all non-buildings.
In [13], the authors develop deep neural network based methods to semantically segment urban land and label land use at a pixel level. Both high-resolution aerial images and ground-level street view images are used, and are of New York City. Semantic features are extracted from sparsely distributed street view images through a deep neural network-based method. These features are processed and fused with the ones obtained from aerial images through a deep neural network to segment land use across 13 different categories such as public facilities and institutions, parking facilities, vacant land, commercial and office buildings, etc.
Unlike the approaches summarized above, our proposed method focuses on a more fine-grained classification of building types. Our model could be added to a remote sensing pipeline to provide a more precise analysis of the resulting extracted buildings given photographs of their facades. Coupling the information extracted using remote sensing technologies such as building height [7], and surrounding roads and neighboring buildings [14,15], with the outputs of our proposed network, one can obtain a complementary and more comprehensive analysis of land covers and the individual buildings as well.
Despite image classification being a hot research topic in the computer vision community, not much work has been reported in relation to fine grained analysis urban land use and street-level categorization from digital images. The authors of [16] propose a convolutional neural network called the Street-Frontage-Net (SFN) for the evaluation of street frontage quality using Google Street View images as well as 3D-model generated street view images. SFN aims at classifying street facades as either active if they contain windows and doors or blank if they only have walls, fences, and garages with a focus on images from the city of London. SFN is further developed in [17]. These works focus on street frontage quality and its impact on urban design as street facades can convey information regarding a neighborhood’s house prices and aesthetics. Although these papers establish street-level analysis from images, they focus on overall street facades, only taking into consideration the presence or absence of certain building characteristics such as doors and windows. In the present article, our objective is to classify buildings from their facades and gain information about their actual functions and styles.
Research in building classification has mostly been concerned with their architectural styles. Architecture combines artistic sensibility with practical scientific factors to design and create buildings. Architectural styles evolve with time, capturing and reflecting the progress of aesthetic trends, and the social, technological, cultural, historical, as well as socioeconomic circumstances of those who made them. Thus, the analysis of the architectural styles of buildings can be informative, and some research has been conducted in this direction. Shalunts et al. propose an approach that relies on clustering and learning local features along with integrating the knowledge used by architects to classify windows of different architecture styles, at the level of the training stage [18]. The same authors also classified building domes into three architecture types: Romanesque, Gothic, and Baroque in [19]. They have promising results, but the dataset used was quite small -only a few hundred cropped images which focused on specific elements (facade windows or domes). In contrast, the present paper simultaneously investigates both the function and overall architectural style of given buildings.
A recent paper proposes a model of classifying the architectural styles of historical Mexican buildings across three categories: Prehispanic, Colonial, and Modern [20]. Their method uses a deep convolutional neural network whose input is composed of sparse features in conjunction with primary color pixel values to increase its accuracy. Their results are promising in the specific database used, and have shown that the inclusion of sparse features has definitely improved the accuracy of the network. For our project, a more challenging task is faced as this work’s goal of functional classification of buildings is not restricted to a specific geographical area, but rather uses images of buildings from all around the world, calling for more diversity to be accounted for. Only about 284 images from the Mexican buildings dataset are made available through the MexCulture142 set. A few of these images have also been included in our proposed dataset.
Regarding the classification of buildings based on their functional purpose, Li et al. proposed a method to predict the type of buildings (residential vs. non-residential building) from Google Street View images based on Histograms of Oriented Gradients, Scale Invariant Feature Transform (SIFT) and Fisher Vectors [21]. In the framework of our research, the objective is to determine the function of a building using a hierarchical CNN-based model. Instead of focusing on a binary classification (residential vs. non-residential), our aim is to make a more detailed functionality classification across 10 different classes.
To the best of our knowledge and based on our literature review, we found that the questions posed by the present article have not yet been answered in the scale and context we provide. We propose a model which is able to extract features and solve building classification tasks in terms of functional purpose and architectural style using a coarse-to-fine hierarchical structure with a custom multiplicative layer which uses prior knowledge to make more informed fine-level decisions about the class of the given image from collected sets of building facade images from all around the world, with no geographical restrictions.
2.2. Convolutional Neural Network Schemes
In their paper [22], Yan et al. introduce Hierarchical Deep CNNs (HD-CNNs) by incorporating deep convolutional neural networks into a hierarchy of categories for general image classification. Given a classification task, it is decomposed into two stages following the coarse-to-fine classification paradigm. First, a coarse category classifier is used to separate easy classes from each other, then difficult classes (i.e., subclasses whose instances are more challenging to separate) are distinguished using fine category classifiers. HD-CNNs present a great contribution in that they represent the first method embedding a hierarchical class structure with CNNs to obtain better results. This method can achieve lower error compared to its building block CNN alone at the cost of an affordable increase in complexity. However, the training strategy on which it relies can be time-consuming since two steps are required: first, the coarse and fine classifiers need to be pre-trained, and second, they need to be fine-tuned. In addition, this model is not scalable to a hierarchical classification with more than two levels.
A more recent hierarchical CNN model called Branch CNN (B-CNN) was introduced in 2017 by Zhu and Bain [23]. The authors presented a scalable method in which multiple branch classifiers share the same main convolution workflow. Each branch makes a prediction corresponding to a level of a pre-defined class tree. These branches learn autonomously, and there is no direct connection between the coarse and fine branches. The authors reported promising results from experiments with benchmark datasets such as CIFAR-10, CIFAR-100, and MNIST. This work is related to our own since our proposed hierarchical model, HierarchyNet, relies on a main convolutional network for feature extraction which then branches out into different classifiers, each corresponding to a class tree level. However, unlike the B-CNN, our proposed HierarchyNet branches out at the same level, and it is able to use the coarser prediction as an explicit input. As shown later, our approach can guide better the fine classifier in solving the urban building classification task using a custom multiplicative layer.
A different potential technique of leveraging the defined class hierarchy for an image classification task using a CNN is through curriculum learning. This machine learning method is inspired by how human acquire new skills whereas one first masters simpler concepts, before getting into progressively more difficult ones. In formal academic settings, curricula are commonly built based on this idea. Following a curriculum in training a neural network was first presented in 1993 [24]. Then in 2009, Bengio, Louradour et al. formally defined curriculum based training [25]. The authors show that training first on easier samples before presenting the model with the remaining samples with increasing difficulty through different experiments. Their work investigates the effects of adopting curriculum based learning to SVMs, a perceptron, as well as a three-layer NN using a toy image dataset. These experiments proved that curriculum learning can improve the appropriately-trained models’ generalization, accuracy, and convergence speed. Consequently, given a coarse-to-fine class tree, it is possible to apply curriculum training to image classification such as the coarser levels are considered as easier to learn and are used to pre-train the model, and fine-tuning progressively on the more difficult fine level classes. In our proposed method, we introducte all hierarchy levels at once in a multi-task learning context without pre-training the model. In particular, it can be challenging to specifically rank which classes and instances to introduce in terms of increasing difficulty following the pretraining phase. The HierarchyNet model relies on loss weights modification schemes in order to control and alternate the model’s focus between the simpler coarse classification task and the fine one.
3. Proposed Datasets
To our knowledge, the majority of existing public image datasets related to the classification of buildings are based on satellite imagery. Nonetheless, two datasets with architectural-style classes and images of building facades were found online: one called MexCulture142, which contains 284 images of Mexican buildings divided into 142 subclasses of: prehispanic, colonial, and modern styles [20], and the other is a 25-class dataset of different architectural styles which contains 4794 images in total, with 60 to 300 per class [26]. However, only about 20% of all these images across the two datasets combined were appropriate for our research purpose. We only kept colored photographs of building facades that fall under our chosen functional purpose or style classes.
Due to the lack of publicly available extensive datasets, we collected images manually as well as using automated scripts. We extensively relied on the google_ images_download Python script (Available at https://pypi.org/project/google_images_download/) which, given a set of keywords, is uses the Google images search engine to download relevant images. We also web scraping techniques were used to build a new relevant dataset from scratch. Images were therefore collected from multiple sources through Google images, as well as the Wikimedia collection and the real-estate website Zillow (A sample of the code written for web-scraping is provided in: https://github.com/salmatfq/Scraping-Website-For-Images).
3.1. Urban Buildings—Functional Purposes
For the classification of urban buildings based on functionality, a new extensive dataset of 6297 images was built. The images are divided across 10 classes: Mosque, Church, Synagogue, Buddhist Temple, House, Apartment Building, Office Building, Mall, Store (includes retail stores such as grocery supermarkets, department stores, and clothing brands stores), and Restaurant (also includes cafes). Following the coarse-to-fine paradigm, we define a class tree, shown in Figure 2, based on a simple semantic taxonomy where:
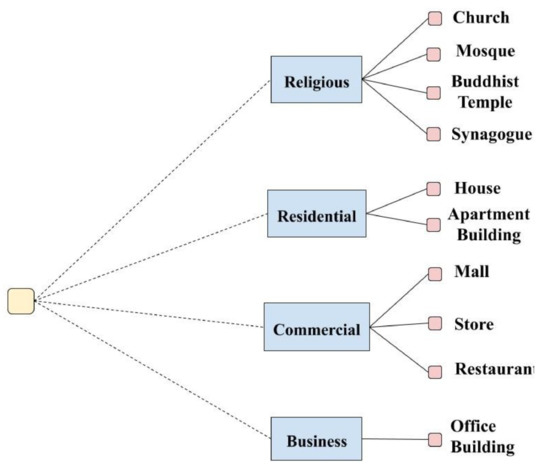
Figure 2.
Hierarchical class tree for buildings’ functions.
- Residential: consists of buildings where people live and reside: mainly houses and apartment buildings
- Commercial: consists of those buildings with a commercial purpose: grocery stores, retail and department stores, restaurants, cafes, and malls
- Business: mainly includes office buildings, and corporate headquarters.
- Religious: consists of buildings with a religious spiritual purpose.
For future use, we denote by the number of fine classes (subclasses), and the number of coarse classes (superclasses). In the current context: and . The hierarchy given in Figure 1 can be conceptualized as a mapping .
3.2. Urban Buildings—Architectural Styles
For architectural style classification, we built a smaller dataset to perform additional experiments with the proposed method. The dataset has a total of 1,033 images spread out across 15 different style classes, namely: Maya-Aztec, Greek-Roman, Egyptian, Persian, Romanesque, Gothic, Byzantine, Renaissance, Baroque, Tudor, Georgian, Victorian, Futuristic, Post Modern, and Communist. We established the class tree by dividing these fine classes across historical time periods as shown in Figure 3.
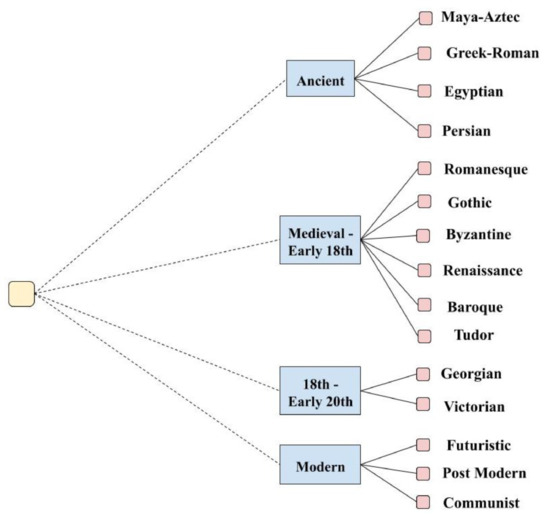
Figure 3.
Hierarchical class tree for buildings’ architectural styles.
4. Proposed Method: HierarchyNet
Our HierarchyNet model is inspired by the Branch Convolutional Neural Network (B-CNN) which was proposed by Xinqi Zhu and Michael Bain in 2017 [23]. Similarly to the B-CNN structure, our objective is to improve upon the target classification by introducing a coarse-to-fine non-overlapping hierarchical tree of classes that is reflected in the model’s architecture: given the prior knowledge of hierarchical relations among classes, the model is a CNN structure that uses multiple branch classifiers along the main convolutional workflow, each one corresponding to a different hierarchical level in the pre-defined class tree. With a baseline CNN as the backbone, internal output branches are added to make multiple predictions ordered from coarse to fine.
The goal is not to solve the multi-label classification task per se since the coarse class can be trivially implied given the fine one, but rather it is to use the prior knowledge from the coarse prediction for a better fine classification. To achieve this, the B-CNN model leverages the intrinsic hierarchical characteristic of CNNs’ feature extraction; lower layers capture low-level features, while higher layers extract high-level features as explicitly shown by Zeiler and Fergus through visualizations of a CNN’s layers during training [27]. The B-CNN model makes use of this by branching out at different levels of the baseline CNN feature extractor such that the coarsest-level branch only relies on the lowest convolutional layers while the finest-level branch is at the very top of the network. The Branch Training strategy (BT-strategy) is proposed to adjust the model’s parameters and successively learn coarse to fine concepts by shifting the loss weights of different level outputs as the learning progresses [23]. The authors show that the B-CNN model performs better than a flat CNN. Its fine branch implicitly benefits from the prior knowledge obtained from the coarse branch(es). However, the branch structure that makes the strength of this model also comes with a few limitations; depending on the classification task on-hand, the location of the different branch classifiers along the main convolutional workflow is a design decision that may require multiple experiments to figure out. In addition to this, the dense layers for each branch classifier bring additional parameters that may make the model memory-costly and time-consuming.
In contrast, the HierarchyNet is able to handle the above mentioned limitations. It is built on the premise of explicitly using the prior knowledge obtained from the coarse branch as input to the fine branch to guide it accordingly. For instance, if the coarse branch predicts that the building is residential, then this can be used as an explicit input for the fine branch to give higher consideration to the consequent children classes of the predicted coarse label, i.e., “House” and “Apartment Building” in this case. It follows that the coarse prediction should be reliable in order to guide the fine classifier into making a more informed decision. Consequently, the HierarchyNet branches out into the coarse and fine branches at the same level, at the top of the baseline network, so the entire convolutional workflow learns parameters that are useful for both tasks (the coarse and fine classifications). In solving these tasks, the model computes two probability distributions with its corresponding softmax layers. Given one image , the model-parameterized by learnable weights and biases -computes the conditional probabilities of the image belonging to each coarse class and fine class.
In order to explicitly account for the coarse prediction in the decision of the fine classifier using the hierarchical label tree in Figure 3 for example, consider the probability of outputting a fine class with given an image x fed to the network parameterized by as the probability of outputting its corresponding parent coarse class with and that out of that class’s subclasses, the subclass coinciding with is indeed chosen, with n indexing the subclasses of . Formally, it can be formulated as:
The proposed method aims at enforcing the inherent coarse-to-fine relationship during the learning process: the prediction of the fine class relies on the coarse class predicted and which one of its subclasses in the label tree is most likely to correspond to the image x. With simple probability notions, it is possible to express in terms of . Assume A and B are two dependent events. The intersection of A and B is defined by:
Therefore, the conditional probability of B given A is:
Applying , to Equation (1), we get the following:
Accordingly, the coarse prediction can be explicitly used to inform the fine classifier following the coarse-to-fine paradigm through the defined label tree. The HierarchyNet incorporates Equation (2) in the model structure using a custom multiplicative layer as pictured in Figure 4.
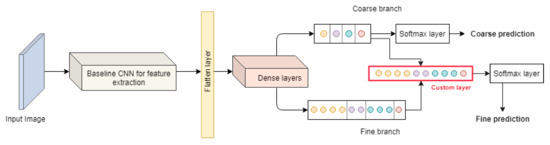
Figure 4.
Proposed Model - Two-level Hierarchy.
Let and be two resulting tensors containing the coarse classes logits and the sub-classes logits respectively. First, needs to be divided into sub-vectors with , such that each resulting has elements, i.e., the number of fine classes that the corresponding coarse class i is mapped to according to the defined label tree. Then, for each , the scalar multiplication
is performed, with the scalar being the ith element of . Finally, the results are concatenated into one vector of elements.
The custom multiplicative layer, as shown in Figure 4, takes two inputs: the tensor of coarse classes logits which is obtained from a fully connected layer with neurons, and the tensor of sub-classes logits which in turn is obtained from a fully connected layer with neurons.
The proposed model branches out into coarse and fine branches at the same level, at the top of the backbone network. The model extracts features from a given image by passing it through the baseline CNN model, and then routes the features through fully connected layers before splitting into two different branches corresponding to the coarse and fine levels of the pre-defined class tree structure. For the coarse branch, the model outputs the coarse logits which are then normalized by a softmax layer to get the model’s interpretable coarse classes predictions. Similarly, for the fine branch, it gets the sub-classes logits. At this point, the coarse branch gives an explicit feedback to the fine classifier by routing its coarse logits as input to the multiplicative layer alongside the sub-classes logits to compute products as expressed in Equation (2). The results are routed to a softmax layer to obtain the fine classes predictions.
For the loss function of the -level branch classifier, denoted simply by , cross entropy is used. As an instance of multitask-learning, it is possible to use loss weights as needed to guide the model’s learning. Hence, the model’s overall loss for each sample i is simply the weighted sum of both losses, similarly to the loss function of the B-CNN model:
where:
- i denotes the sample in the mini-batch (mini-batch gradient descent is the optimization technique used)
- K is the number of levels in the label tree
- is the loss weight corresponding to the level contributing to the loss function
- The term is the cross entropy loss of the sample on the class tree level
Since in our application we defined a two-level hierarchy of the classes, we use , furthermore we allow that the parameters be dynamically changed during the training process over the consecutive epochs.
5. Experiments
In this section, the proposed HierarchyNet is tested and compared to corresponding flat classifiers and B-CNN [23] structures in solving urban buildings classification problems. For a more robust evaluation, we also apply our model to other applications using well-established benchmark datasets. Our network and experiments are implemented in Python 3.6 using Tensorflow 1.15 and Keras 2.3. Our models are trained on one machine with one NVIDIA Tesla P100 16GB PCIe GPU using the online cloud-based Jupyter notebook service Google Colaboratory. Our experiments have also shown that the training time for the HierarchyNet on one image is about 10 ms.
5.1. Two-Level Urban Buildings Classification—Functional Purposes
As an initial experiment for the classification of urban buildings based on their functional purposes, the VGG-16 model, pre-trained on ImageNet, is used to solve two tasks separately:
- Task A: a 4-class classification across the classes: Business, Residential, Religious, Commercial
- Task B: a more detailed classification with the 10 fine classes: Mosque, Church, House, Office Building, ...
The pre-trained network is fine-tuned for each task accordingly. Table 1 summarizes the results of the two tasks:

Table 1.
VGG-16’s average performance on tasks A and B.
As shown in Table 1, it is easier for the regular VGG-16 network to classify images across broader classes (Task A), compared to more specific ones (Task B). This behavior is expected as it is generally much easier to discern a church from an office building than from a building fulfilling a similar religious function like a synagogue for instance. Additionally, broader classes are less numerous than finer ones which leaves less room for error.
Hierarchical models such as the B-CNN and our proposed model both-albeit differently-aim to leverage the relative ease of performing the coarser classification task to improve the target fine classification. In order to compare the performance of our proposed network to the B-CNN approach in a more representative way, we used the same VGG-16 baseline model in our HierarchyNet, as in the original B-CNN model [23]. Stochastic Gradient Descent (SGD) with momentum 0.9 is the optimizer used for both models which are trained within 50 epochs. The BT-strategy of the B-CNN model starts with initial loss weights being , which is then adjusted to after 15 epochs, and finally to after 25 epochs. The HierarchyNet method, on the other hand, uses a reversed BT-strategy for this task. The loss weights are initialized to: and in order to emphasize learning features relevant to the fine classification and slow down the convergence of the coarse branch, then after 15 epochs, they are adjusted to . The results of the comparison are presented below in Table 2. The proposed multi-label hierarchical model is more accurate than the B-CNN in classifying urban buildings across both levels of the hierarchy.

Table 2.
Performance comparison of the B-CNN and the proposed HierarchyNet approaches using VGG-16 backbone networks for the building functional purpose classification task. Bold values mark the best results.
Table 2 shows that the HierarchyNet (HN) outperforms the B-CNN and achieves more than 10% higher accuracy at the coarse level, and around 2.2% at the fine level. Since the finer classification is more challenging than the coarse one, a higher loss is indeed expected from both models at the fine level. We can also observe in Table 2, that the proposed HN model has a higher loss than the B-CNN model at the fine branch, which is a consequence of the fact that our custom multiplicative layer propagates the error of the coarse branch to the fine one. This phenomenon affects the HN’s fine softmax output’s distribution more significantly than in the B-CNN model where the two branches are more independent. However, we can also conclude that this increased loss does not decrease the classification accuracy. Since cross entropy is not a bounded loss, a single false prediction (outlier) which is classified extremely badly (the network is too confident) can explode the loss value, yielding a high loss since the total loss is averaged, but at the same time the accuracy of HN still surpasses that of the B-CNN.
We have designed the structure of the proposed HN model in a way that we have added the coarse branch at the top of the backbone network, alongside the fine one, so the coarse classifier can benefit from the entire convolutional workflow, leading it to reach a better performance. Furthermore, as a result of using the proposed multiplicative custom layer, the prior knowledge of the coarse class is routed to inform the fine branch better, resulting in the HierarchyNet’s better overall accuracy.
In order to illustrate the effect of the HN’s custom layer, suppose we set the loss weights to and in Equation (3), making the models ignore the fine branch classification, and only focus on learning the coarse classification. Both the B-CNN and HN models have a similar behavior in this case as can be seen from Figure 5a,b respectively.
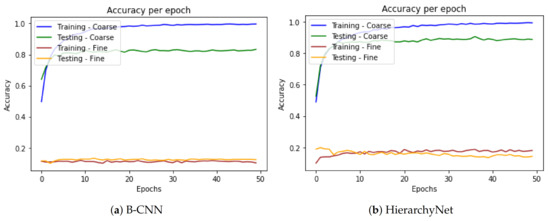
Figure 5.
Accuracy per epoch when the loss weights are 1 and 0 respectively for the coarse and fine branches.
In contract, if we set and , it nullifies the learning process of the coarse branch. In this case, as can be observed from Figure 6, the models behave differently. The HN’s fine classifier has a slower learning process since this branch is reliant on the coarse branch via the custom multiplicative layer. When the coarse classifier provides unreliable input due to the loss weights setting, it consequently impedes on the fine classifier’s learning process. In contrast, the B-CNN model, with and , merely converges to a flat CNN.
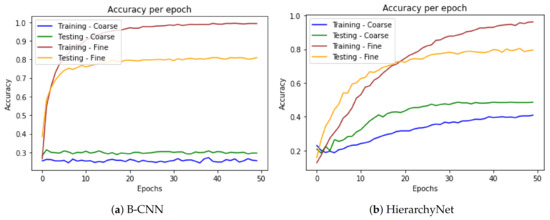
Figure 6.
Accuracy per epoch when the loss weights are 0 and 1 respectively for the coarse and fine branches.
In the B-CNN model, the information gained from the coarse prediction is implicit. It benefits from the fact that lower-level layers of CNNs learn generic patterns, and as they get deeper, higher-level features are learned by branching out at different points of the baseline neural network. Therefore, the deeper levels of the network can focus on solely solving the fine classification task.
On the other hand, the HierarchyNet makes coarse and fine predictions at the same level. The network tries to find a trade-off between learning features that are relevant for the coarse classification along with those relevant for the fine classification while decreasing the overall loss. It also explicitly takes the coarse logits as input to the custom layer in order to include this information in making the fine classification decision. This explains why the coarse branch is so crucial to the fine branch training process which leads to the behavior observed in Figure 6b.
Consider a balanced test set of 1260 building photographs, on average, the HierarchyNet is able to correctly classify 1178 images in terms of the coarse class, and 1052 in terms of the fine class, compared to only 1051 for the B-CNN at the coarse level and 993 at the fine level. Once the coarse class is correctly classified, the HierarchyNet is able to predict the correct fine class for up to 88.45% of these images, whereas out of the remaining images, up to 94.85% of them are assigned a wrong fine label that is actually the wrong subclass of the previously predicted correct coarse superclass. In contrast, the B-CNN only gives the correct fine class to 83.06% of the images to which it has correctly assigned the coarse label, and out of the remaining well-classified images at the coarse level, only 74.01% are given a fine label that is the child of the correct coarse parent. This illustrates the impact of the custom layer which characterizes our proposed method. It is able to route the prior knowledge of the coarse classifier to inform the fine classifier.
Figure 7 provides examples of building images that the HierarchyNet could correctly classify across both hierarchical levels whereas the B-CNN failed at both. In total, there are 30 such cases out of the 1260 images in the set.

Figure 7.
Building photographs correctly classified by the HierarchyNet on both hierarchical levels but not by the B-CNN model.
On the other hand, there are some buildings that have posed problems to both models. Examples of these images are provided in Figure 8. In fact, both models predicted the same fine label to 83% of these images. These samples are arguably challenging to classify even from a human perspective.

Figure 8.
Challenging samples which were given the same wrong fine label by both the HierarchyNet and the B-CNN models.
Using a hierarchical approach and routing the prior knowledge from the coarse branch to benefit the fine one through the additional custom layer contributes to the HierarchyNet’s superior performance in solving the urban buildings classification task, compared to a flat network as well as to a different hierarchical model such as the B-CNN. However, this particular characteristic can also limit the proposed model’s performance. Although placing the coarse branch at the top of the model grants it access to the full convolutional power of the underlying network thus making more accurate, it can still be prone to making some mistakes which are then disseminated to the fine classifier through the additional layer. Indeed, when the predicted coarse and fine classes are both incorrect, in 97% of such cases, the wrong fine class is actually one of the sub-classes of the wrong predicted coarse one for the HN model.
To experiment with a different baseline network for building function classification, we implemented our proposed method based on the ResNet50 network [28]. As a flat classifier, the ResNet50 model is able to achieve a higher accuracy of about 83.41% when solving the fine classification task compared to the VGG-16 model which only reaches 78.22% (see Task B in Table 1). A more powerful backbone network results in an even better performance of the HierarchyNet model as illustrated in Table 3 which presents a comparison between a ResNet50-based HierarchyNet and a regular ResNet50.

Table 3.
Average performance of ResNet50 and corresponding HierarchyNet in the building functional purpose classification task.
Our experiments with a ResNet50 backbone are limited to proving that the proposed hierarchical method outperforms the base model. Comparing the HN to a corresponding B-CNN model with a ResNet50 backbone is not a trivial task. The B-CNN structure relies on branching out at different levels of the main baseline convolutional workflow which requires the backbone network to be fully implemented and the branches to be hard coded. In contrast, the HierarchyNet provides more flexibility and convenience since it can be used with an out-of-the-box backbone network with only its top layers being altered.
5.2. Two-Level Urban Buildings Classification–Architectural Styles
For the classification task of urban buildings based on their architectural style, we use a VGG-16 backbone for both the reference B-CNN technique and the proposed HN. Models are trained for 100 epochs. Table 4 summarizes the obtained results. As noted earlier, discriminating between different architectural styles from photographs of buildings is a more challenging task. Additionally, we have 15 target fine classes, and a smaller dataset for this task. The overall lower performance of all three models compared to the functional purpose classification task as presented in Table 1 and Table 2 in this task reflects these constraints.

Table 4.
Performance comparison of the B-CNN and the proposed HierarchyNet approaches using VGG-16 backbone networks for the architectural style classification task. Bold values mark the best results.
Given a test set of 207 images, 183 images were given the correct coarse label, and out of these about 80% were consequently given a correct fine label. Figure 9 provides examples of such images that the model correctly classified on both hierarchical levels. As for the remaining 20% of these images for which the model predicted the right coarse class but the wrong fine class, only 2 were assigned a fine class that is not a subclass of the previously predicted superclass. These images are shown in Figure 10.

Figure 9.
Sample images that were correctly labeled by the HN model on the coarse and fine levels.

Figure 10.
Sample images with a correctly predicted coarse label but a wrong fine label which is not a subclass of the former.
5.3. Performance on Other Public Benchmark Datasets
Although our primary aim for the development of the proposed HierarchyNet approach has been to efficiently solve the urban building classification task, the network architecture itself can be applied to various other applications as well. For a more robust analysis, further experiments are conducted to evaluate the proposed model on well-known datasets: MNIST, CIFAR-10, CIFAR-100.
For the sake of comparison, we use the same baseline convolutional networks as in the B-CNN paper [23]. The backbone feature extractors are summarized in Table 5.

Table 5.
Baseline networks [23].
Each configuration relies on -sized filters with stride 1. The activation functions are ReLUs. Max pooling is applied over -sized patches with stride 2. Base model C corresponds to the VGG-16 model pre-trained on the ImageNet dataset.
5.3.1. MNIST
The MNIST dataset [29] contains gray-scale images of hand-written digits. The images are divided into a training set of 60,000 samples and a test set of 10,000. For hierarchical classification, we use the same class tree as in [23] based on the similarity of the shapes of the digits. We also use the same base model A as used in [23] for this dataset.
5.3.2. CIFAR-10
CIFAR-10 [30] is a 10-class dataset with a total of 60,000 -pixel RGB images. Each image belongs to 1 of 10 possible classes: airplane, automobile, bird, cat, deer, dog, frog, horse, ship and truck. The dataset comes with a predefined split into 50,000 training images and 10,000 test ones. As in [23], base models B and C are used for CIFAR-10.
5.3.3. CIFAR-100
CIFAR-100 [30] is a 100-class dataset of images. Each class contains 600 -pixel RGB images. This dataset comes with a pre-defined coarse-to-fine class tree since the 100 fine classes are grouped into 20 coarse classes. Similarly to CIFAR-10, base models B and C are used for this dataset.
5.3.4. Results on Benchmark Datasets
Table 6 summarizes the results of our experiments on all datasets with B-CNN models, HierarchyNet models, and corresponding backbone networks. We rely on the results of Zhu and Bain for the benchmark datasets as our reference and build the HierarchyNet networks using the same base models. For both CIFAR-10 and CIFAR-100, a two-level hierarchy is used in contrast to the three-level one adopted by the B-CNN authors. Since the HierarchyNet is structurally different, and the primary objective of introducing a hierarchy is to be able to use the prior knowledge from a coarse classification task to improve upon the target fine classification, it suffices to use two levels. The results summarized below show that the HierarchyNet is able to reach a similar performance than the B-CNN. In the majority of experiments, the HierarchyNet outperformed the flat base model as well as the corresponding B-CNN.

Table 6.
Performance comparison of the B-CNN and HierarchyNet models with different baselines networks (A, B, and C) on different datasets. Bold values mark the best results.
For the MNIST dataset, HierarchyNet A was trained for 50 epochs with similar specifications as base model A and B-CNN A: an SGD optimizer was used with a learning rate initialized to 0.01 which is decreased to 0.002 after 28 epochs and then to 0.0004 after 35 epochs. As this dataset is made of small gray-scale images, all models are able to achieve a high accuracy, still the HN slightly outperfoms the other two with 99.47% compared to 99.2% for base model A and 99.4% for B-CNN A.
For CIFAR-10, both HierarchyNet B and HierarchyNet C rely on the same training procedure as the corresponding base and B-CNN models: they are trained for 60 epochs and the optimizer used is SGD with an initial learning rate of 0.003 which is dropped to 0.0005 after 42 epochs and 0.0001 after 52 epochs. The loss weights are initialized to and starting epoch 15, they are changed to . In both experiments, the HierarchyNet has a higher accuracy than the corresponding models.
CIFAR-100 classification represents a more difficult task with its 100 target fine classes and 20 coarse classes. All models are trained for 80 epochs following the same learning rate scheme adopted in [23]: initialized as 0.001, the learning rate is then adjusted to 0.0002 after epoch 55 and 0.00005 at epoch 70. Experimentally, we found that for this dataset, the HierarchyNet works best with no loss weights. Since even the coarse classification is a challenging one in this case, better results were achieved when the learning was not hindered by implementing loss weights. The results for CIFAR-100 along with the other two benchmark datasets are presented in Table 6. Backbone model B only gets 51% accuracy while the HierarchyNet B reaches up to 55.64% and the B-CNN B gets an even higher accuracy: 57.59%. Conversely, with base model C, the HierarchyNet C surpasses both corresponding models with 64.65% in comparison to 64.42% and 62.92% for the base model C, and B-CNN C respectively.
HierarchyNet B reaches an average coarse branch accuracy of 67.6% while HierarchyNet C achieves 76.11%. As discussed earlier, the proposed model’s fine branch performance is dependent on its coarse branch which explains the HierarchyNet’s lower performance in the CIFAR-100 classification with backbone B. In the B-CNN structure, branches are more independent, as subsequent convolutional layers to a given branch can be more “specialized” in solving the next branch classification, which helps it with such as a task as CIFAR-100 in that it can still make better fine predictions in spite of a poorer coarse branch classifier.
Note that for both CIFAR-10 and CIFAR-100, the gaps in accuracy between B models compared to C models is higher. The backbone model C is deeper than the baseline convolutional model B as can be seen from Table 5. Additionally, base model C is in fact the VGG-16 network initialized with ImageNet pre-trained parameters. Therefore, with transfer learning, C models are able to fine tune the weights more easily and start their learning procedure from a better standpoint than B models.
We have concluded that the proposed HN can deal with different classification tasks, and exhibits around state-of-the-art (SoA) performance for various well known benchmark problems. However its real benefits (i.e., significant improvements vs. SoA) can be exploited by applying it for a complex classification problem such as urban area classification where the margins between the classes are small. For example, as we have stated before, in urban building classification small differences such as a small religious symbol can distinguish between a church and a commercial building, so by utilizing the hierarchy learning capability of the network we can widen the distance of the margins between the classes.
5.4. Parameter Sharing
Formulating classification problems as a coarse-to-fine hierarchical one can be viewed as an instance of multitask learning. Indeed, the HierarchyNet’s convolutional feature extractor and dense layers are all fully shared across two tasks (coarse classification and fine classification). The model hence relies on a strong parameter sharing scheme justified by the existing relationship between the two tasks which can be inferred from the label tree defined for the given problem. Parameter sharing in multitask learning often yields better generalization and generalization error bounds compared to using different layers for each task [31]. Table 7 provides a comparison of the number of parameters in different models used for the urban buildings categorization tasks.

Table 7.
Total number of parameters per model.
For buildings classification based on functional purposes, compared to the B-CNN structure, the HierarchyNet configuration only added about 6,475,918 parameters (vs. the 64,448,782 parameters added in the B-CNN) to the baseline conv. network. The B-CNN needed about 10 times more parameters than our proposed model. Similarly, for the architectural style classification, the B-CNN model required approximately 58 million more parameters compared to only 13 million for the HierarchyNet. The significantly lower number of parameters used by the proposed HierarchyNet is due to the stronger parameter sharing scheme it relies on. As can be observed from the HierarchyNet prototype in Figure 4, not only do the coarse and fine branches rely on the same baseline CNN feature extractor; but they also share fully connected layers. This parameter sharing scheme gives our proposed model a stark advantage over the B-CNN in that it uses fewer parameters while providing a similar or superior performance. With this important reduction in the model’s memory requirements and footprint, the HierarchyNet is better suited for usage in mobile apps specialized in city touring, cultural artifact archiving, etc.
6. Conclusions
In hereby solving the urban building classification tasks, experimentation with different model configurations has led to the development of a novel hierarchical model that performs better than its well-established counterpart, the Branch Convolutional Neural Network. Following a defined label structure that relies on the coarse-to-fine paradigm, the proposed model explicitly incorporates prior knowledge obtained from a coarser level as input to the finer level via a custom multiplicative layer thereby improving the accuracy of the overall model in solving urban building categorization tasks while using significantly less parameters. Consequently, the HierarchyNet can for instance be used within a virtual city tour phone application to provide information on the get-go to tourists who simply need to snap a picture of the facade of a building of interest. It can even be further fine-tuned for major cities. Beyond building classification, experiments with benchmark datasets have proven that the HierarchyNet model is applicable to different use cases. Looking forward, other avenues of research could focus on the model’s theoretical framework and further benefit the literature by extending the proposed model to adapt to potentially more complex label trees to solve more intricate tasks (e.g., a combined classification of architectural style, functional purpose, and state) at once. Future research should also consider further development of the proposed model using curriculum based learning to improve the model’s accuracy and generalization. It would be interesting to pre-train the HierarchyNet on instances which are easy to classify across both hierarchical levels before fine tuning the network with those instances which get misclassified among the subclasses of the correct parent class so as to boost its fine branch’s discrimination abilities. Finally, in the present article, we used predefined class hierarchies that we established. It can be useful to experiment with different unsupevised learning techniques such as spectral clustering to obtain learned class hierarchies and evaluate their impact on the HierarchyNet.
Author Contributions
All authors contributed to the conceptualization, methodology, and writing—editing the paper. Further specific contributions: software, S.T.; data acquisition S.T. and B.N.; validation and comparative state-of-the-art analysis, S.T.; supervision B.N. and C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Artificial Intelligence National Laboratory (MILAB); by the National Research, Development and Innovation Fund, under grants K-120233 and 2018-2.1.3-EUREKA-2018-00032; by the European Union and the Hungarian Government from the project ‘Intensification of the activities of HU-MATHS-IN—Hungarian Service Network of Mathematics for Industry and Innovation’ under grant number EFOP-3.6.2-16-2017-00015 (B.N., C.B.); by the National Excellence Program under Grant 2018-1.2.1-NKP-00008, and by the Michelberger Master Award of the Hungarian Academy of Engineering (C.B.); as well as by the ÚNKP-20-4 New National Excellence Program of the Ministry of Human Capacities (B.N.).
Conflicts of Interest
The authors declare no conflict of interest.
References
- 2018 Revision of World Urbanization Prospects. Available online: https://www.un.org/development/desa/publications/2018-revision-of-world-urbanization-prospects.html (accessed on 8 December 2020).
- You, Y.; Wang, S.; Ma, Y.; Chen, G.; Wang, B.; Shen, M.; Liu, W. Building detection from VHR remote sensing imagery based on the morphological building index. Remote Sens. 2018, 10, 1287. [Google Scholar] [CrossRef]
- Zhang, P.; Ke, Y.; Zhang, Z.; Wang, M.; Li, P.; Zhang, S. Urban land use and land cover classification using novel deep learning models based on high spatial resolution satellite imagery. Sensors 2018, 18, 3717. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wu, L.; Xie, Z.; Chen, Z. Building extraction in very high resolution remote sensing imagery using deep learning and guided filters. Remote Sens. 2018, 10, 144. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Liu, Q.; Liu, X.; Wang, W. CNN based suburban building detection using monocular high resolution Google Earth images. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 661–664. [Google Scholar]
- Vakalopoulou, M.; Karantzalos, K.; Komodakis, N.; Paragios, N. Building detection in very high resolution multispectral data with deep learning features. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 25–29 July 2015; pp. 1873–1876. [Google Scholar]
- Huang, Y.; Zhuo, L.; Tao, H.; Shi, Q.; Liu, K. A novel building type classification scheme based on integrated LiDAR and high-resolution images. Remote Sens. 2017, 9, 679. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. ISPRS J. Photogramm. Remote. Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Cohen, J.P.; Ding, W.; Kuhlman, C.; Chen, A.; Di, L. Rapid building detection using machine learning. Appl. Intell. 2016, 45, 443–457. [Google Scholar] [CrossRef]
- Muhr, V.; Despotovic, M.; Koch, D.; Döller, M.; Zeppelzauer, M. Towards Automated Real Estate Assessment from Satellite Images with CNNs. In Proceedings of the Forum Media Technology, Pölten, Austria, 29–30 November 2017. [Google Scholar]
- Hoffmann, E.J.; Wang, Y.; Werner, M.; Kang, J.; Zhu, X.X. Model fusion for building type classification from aerial and street view images. Remote Sens. 2019, 11, 1259. [Google Scholar] [CrossRef]
- Cao, R.; Zhu, J.; Tu, W.; Li, Q.; Cao, J.; Liu, B.; Zhang, Q.; Qiu, G. Integrating aerial and street view images for urban land use classification. Remote Sens. 2018, 10, 1553. [Google Scholar] [CrossRef]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Dalla Mura, M. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, Z.; Feng, Y.; Chen, Z. Road extraction from high-resolution remote sensing imagery using deep learning. Remote Sens. 2018, 10, 1461. [Google Scholar] [CrossRef]
- Law, S.; Shen, Y.; Seresinhe, C. An application of convolutional neural network in street image classification: The case study of London. In Proceedings of the 1st Workshop on Artificial Intelligence and Deep Learning for Geographic Knowledge Discovery, Redondo Beach, CA, USA, 7–10 November 2017; pp. 5–9. [Google Scholar]
- Law, S.; Seresinhe, C.; Shen, Y.; Gutiérrez-Roig, M. Street-Frontage-Net: Urban image classification using deep convolutional neural networks. Int. J. Geogr. Inf. Sci. 2018, 34, 1–27. [Google Scholar] [CrossRef]
- Shalunts, G.; Haxhimusa, Y.; Sablatnig, R. Architectural Style Classification of Building Facade Windows. In Advances in Visual Computing; Bebis, G., Boyle, R., Parvin, B., Koracin, D., Wang, S., Kyungnam, K., Benes, B., Moreland, K., Borst, C., DiVerdi, S., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 280–289. [Google Scholar]
- Shalunts, G.; Haxhimusa, Y.; Sablatnig, R. Architectural Style Classification of Domes. In Advances in Visual Computing; Bebis, G., Boyle, R., Parvin, B., Koracin, D., Fowlkes, C., Wang, S., Choi, M.H., Mantler, S., Schulze, J., Acevedo, D., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 420–429. [Google Scholar]
- Montoya Obeso, A.; Benois-Pineau, J.; Ramirez, A.; Vázquez, M. Architectural style classification of Mexican historical buildings using deep convolutional neural networks and sparse features. J. Electron. Imaging 2016, 26, 011016. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Li, W. Building block level urban land-use information retrieval based on Google Street View images. GISci. Remote Sens. 2017, 54, 819–835. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, H.; Piramuthu, R.; Jagadeesh, V.; DeCoste, D.; Di, W.; Yu, Y. HD-CNN: Hierarchical deep convolutional neural networks for large scale visual recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–10 December 2015; pp. 2740–2748. [Google Scholar]
- Zhu, X.; Bain, M. B-CNN: Branch Convolutional Neural Network for Hierarchical Classification. arXiv 2017, arXiv:1709.09890. [Google Scholar]
- Elman, J.L. Learning and development in neural networks: The importance of starting small. Cognition 1993, 48, 71–99. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 41–48. [Google Scholar]
- Xu, Z.; Tao, D.; Zhang, Y.; Wu, J.; Tsoi, A.C. Architectural Style Classification Using Multinomial Latent Logistic Regression. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; pp. 600–615. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features From Tiny Images; Technical report; Department of Computer Science, Univsersity of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning. 2016. Available online: http://www.deeplearningbook.org (accessed on 21 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).