UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning
Abstract
1. Introduction
- (1)
- A UAV motion model is constructed, and the UAV maneuvering target tracking is defined as an MDP. Based on TD3 algorithm, a decision-making framework is established to control the course and velocity of UAV. Through the decision-making framework, autonomous real-time maneuvering target tracking can be realized.
- (2)
- In order to make the UAV quickly adapt to the tracking of multiple uncertain target motion modes, a deep reinforcement learning algorithm, meta-TD3, is developed by combining DRL and meta-learning. A multi-task experience replay buffer is proposed, which contains several replay buffers of different tasks. A multi-task meta-learning update method is developed which breaks the original DRL network update. In this way, DRL model can learn multiple tasks at the same time and perform meta-learning on weights obtained by training from multiple tasks. Through these, meta-TD3 can overcome the shortcomings of DRL and enable UAV to quickly adapt to an uncertain environment and realize target tracking quickly and efficiently.
- (3)
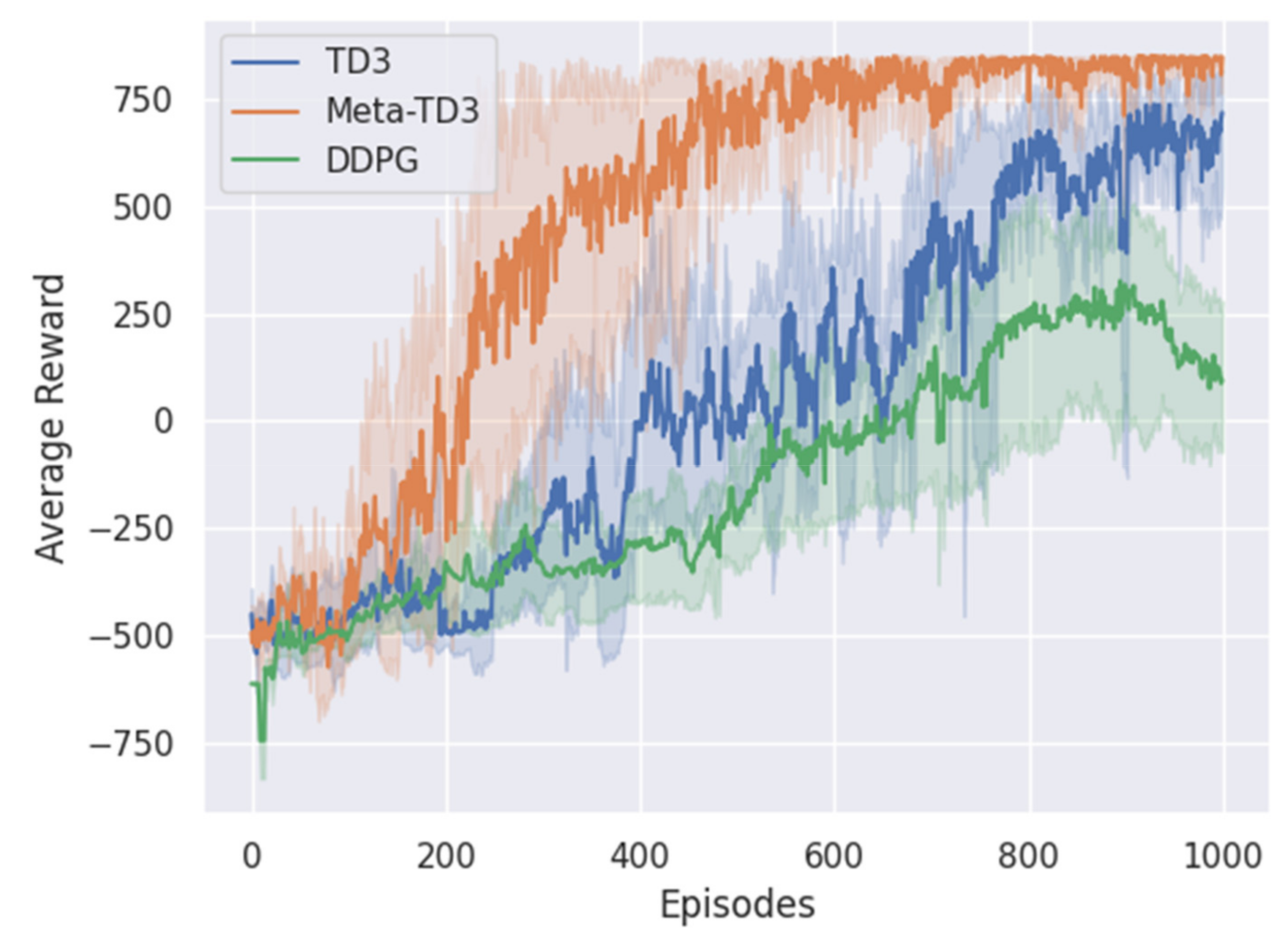
- Through a series of experiments, compared with the state-of-the-art algorithms DDPG and TD3, the performance, training efficiency and the generalization capability of meta-TD3 have been verified. In the UAV target tracking problem, Meta-TD3 only requires a few steps to train to enable the UAV to adapt to the new target movement mode more quickly and maintain a better tracking effect.
2. Problem Formulation
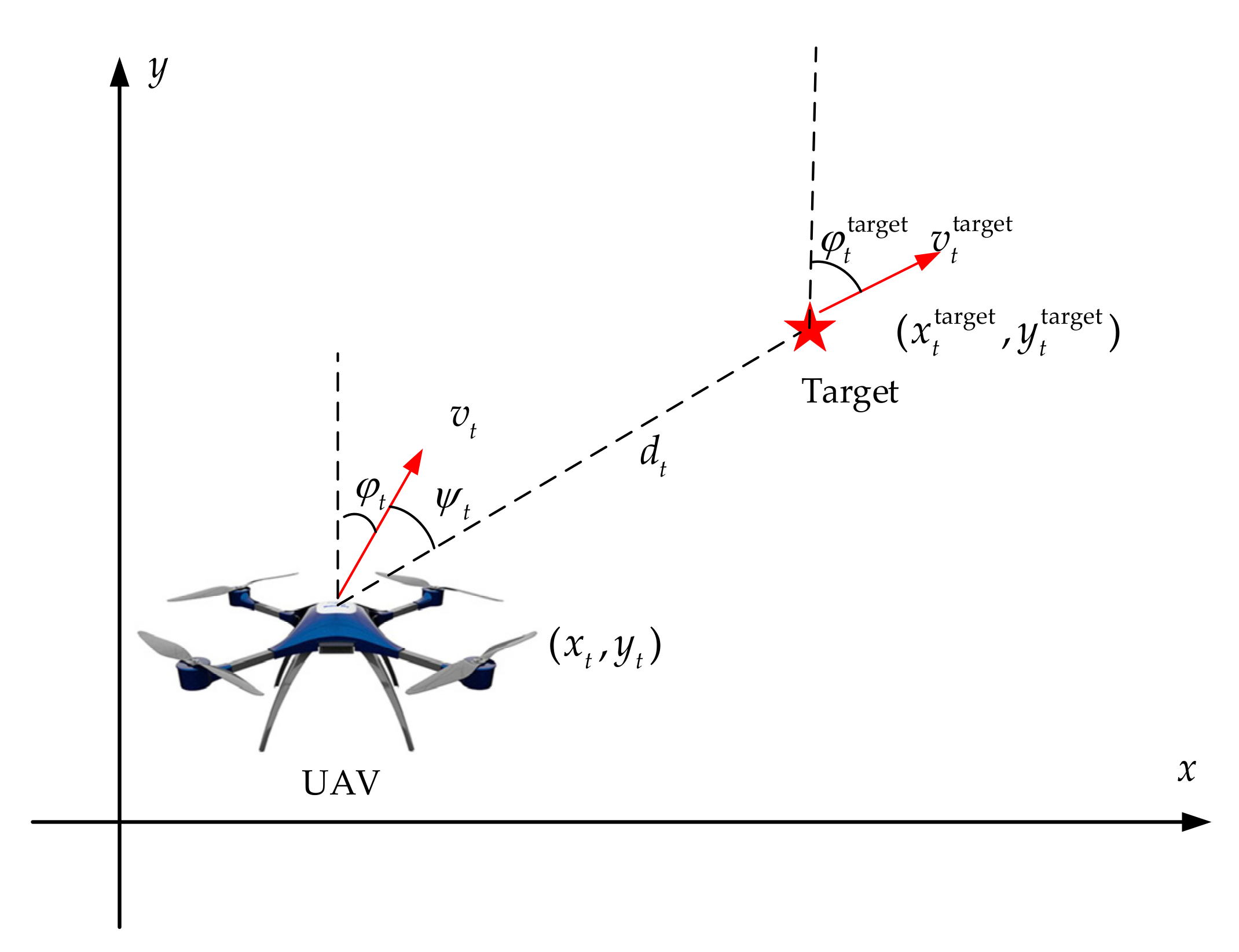
2.1. UAV Motion Model
2.2. Target Tracking Model Based on Reinforcement Learning
2.2.1. State Space
2.2.2. Action Space
2.2.3. Reward Shaping
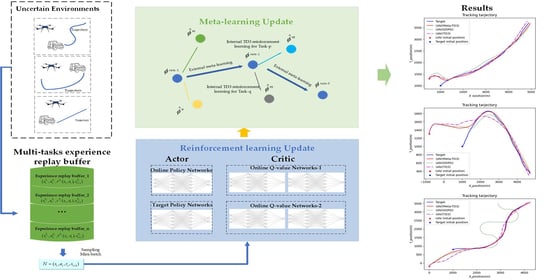
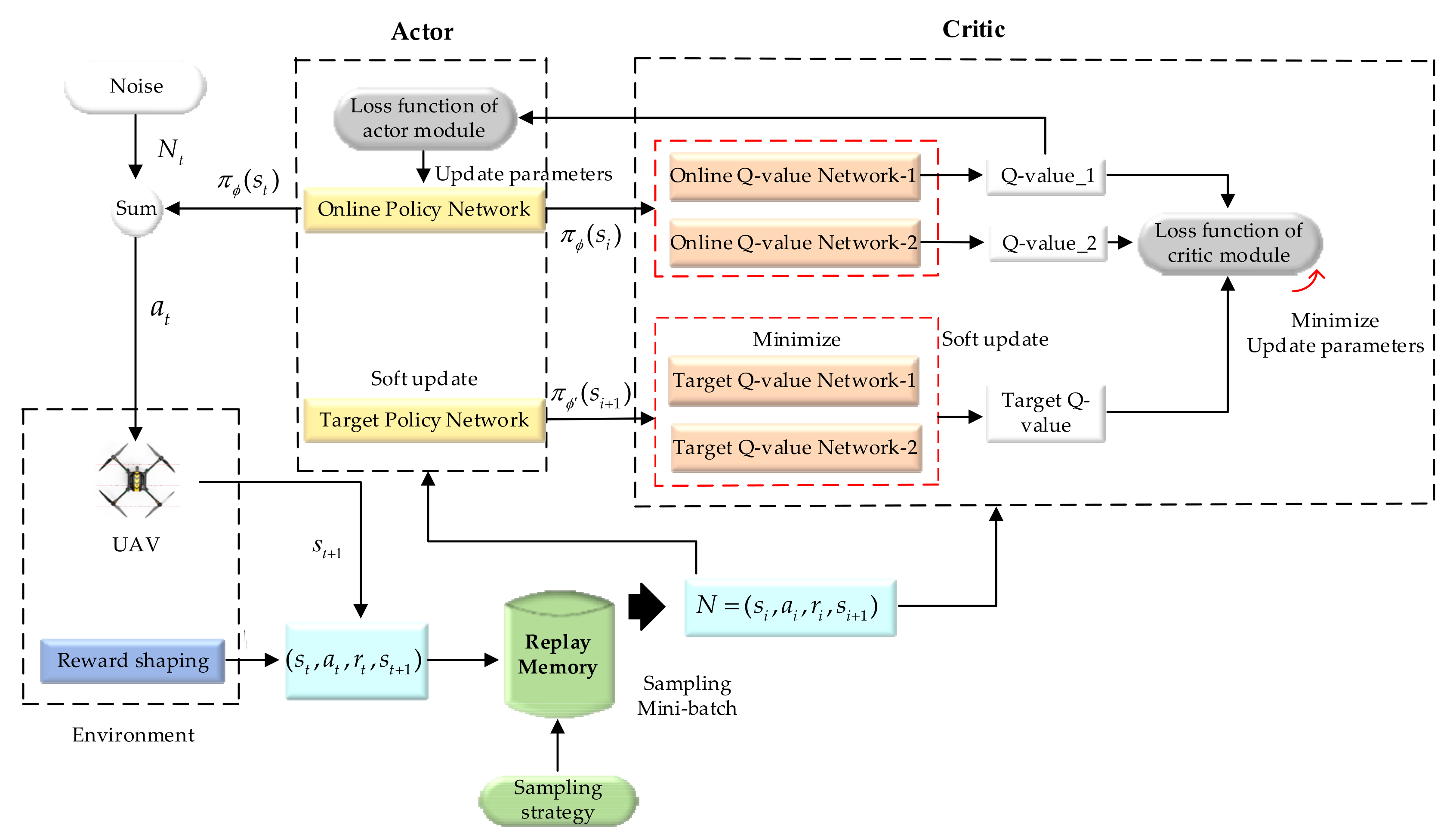
3. Meta-TD3 for Target Tracking Model
3.1. UAV Motion Model
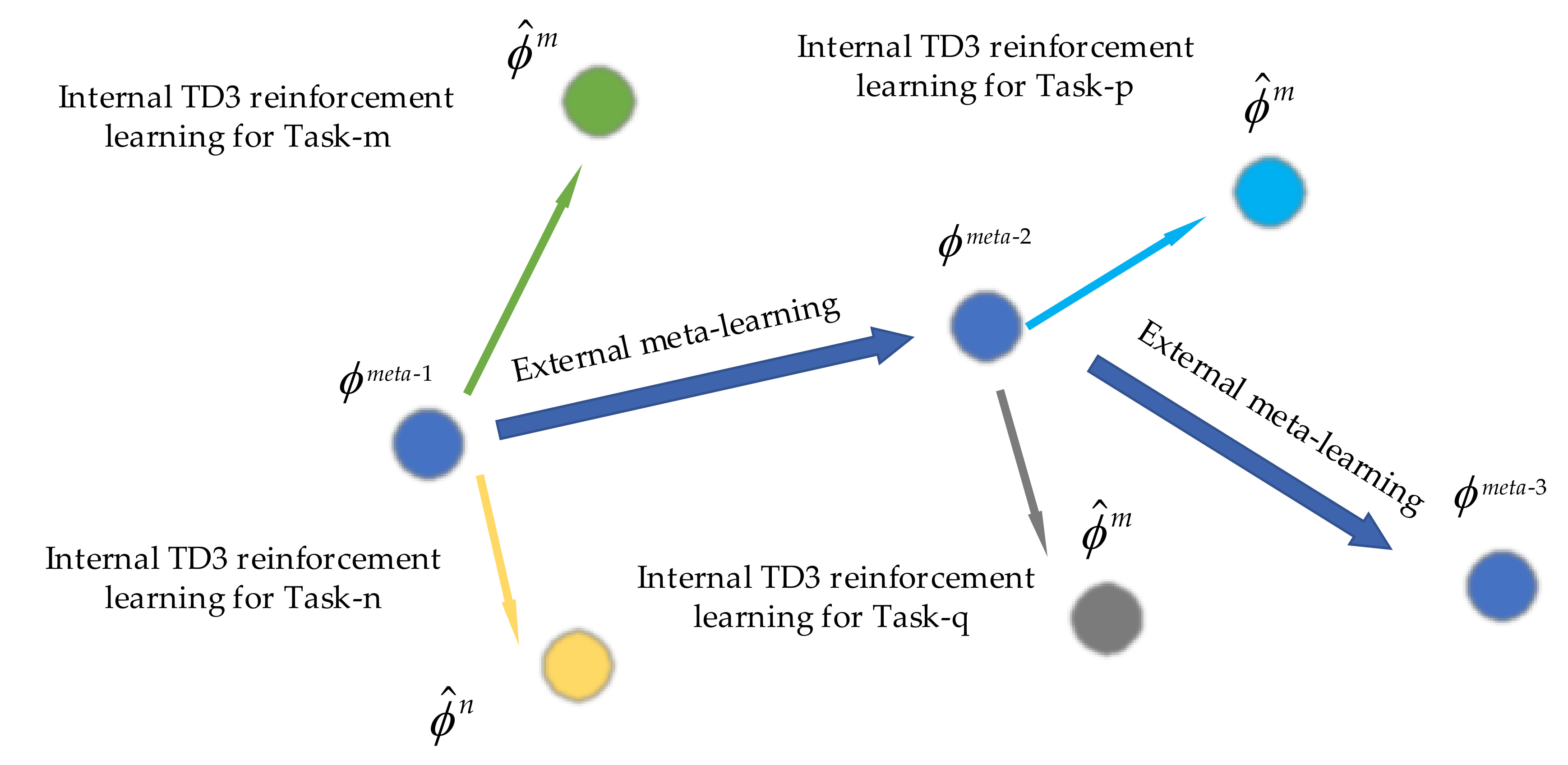
3.2. Multi-Tasks Experience Replay Buffer and Meta-Learning Update
3.2.1. Multi-Tasks Setting
3.2.2. Meta-Learning Update Method
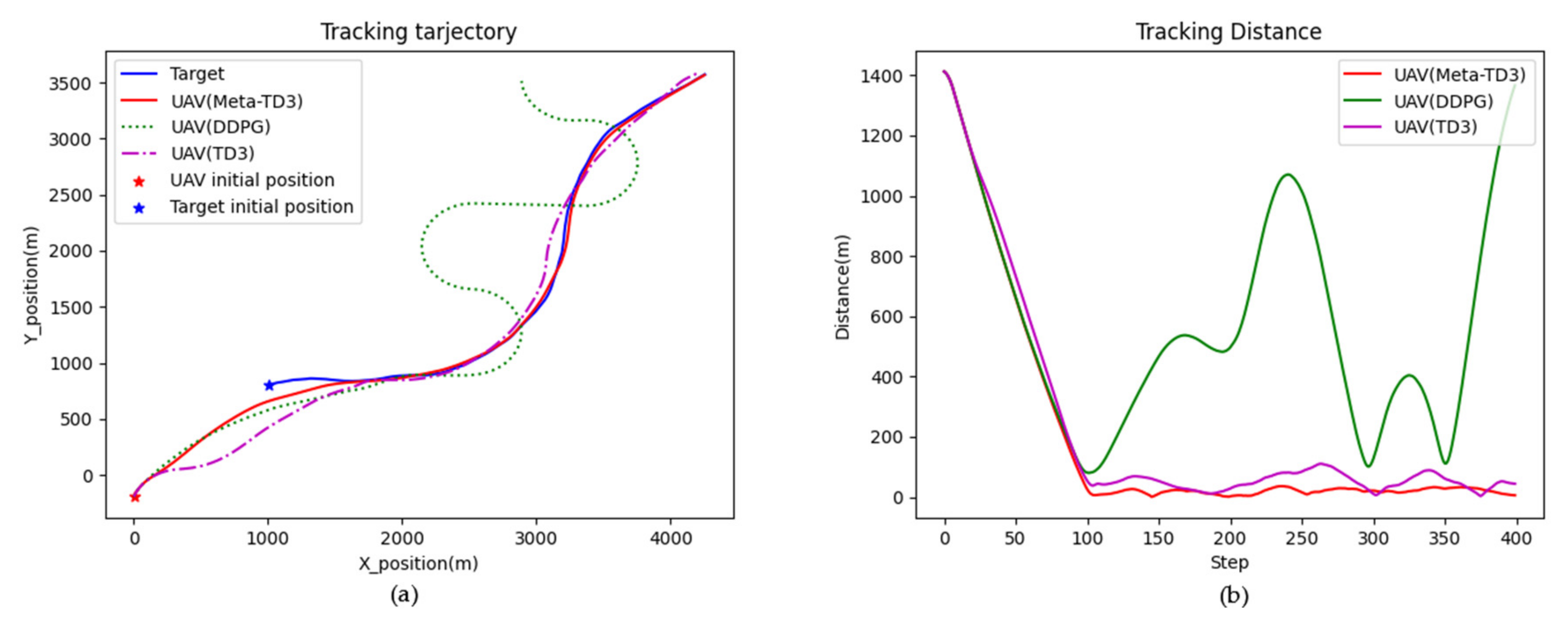
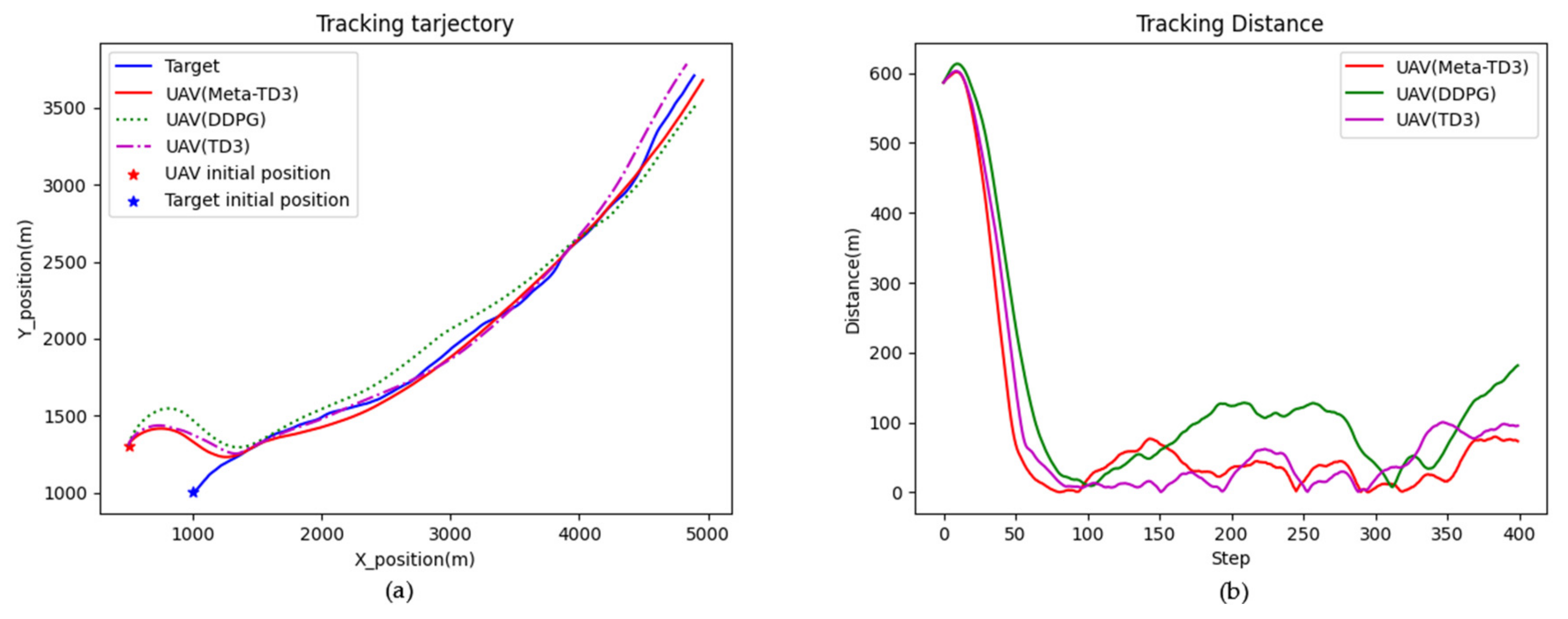
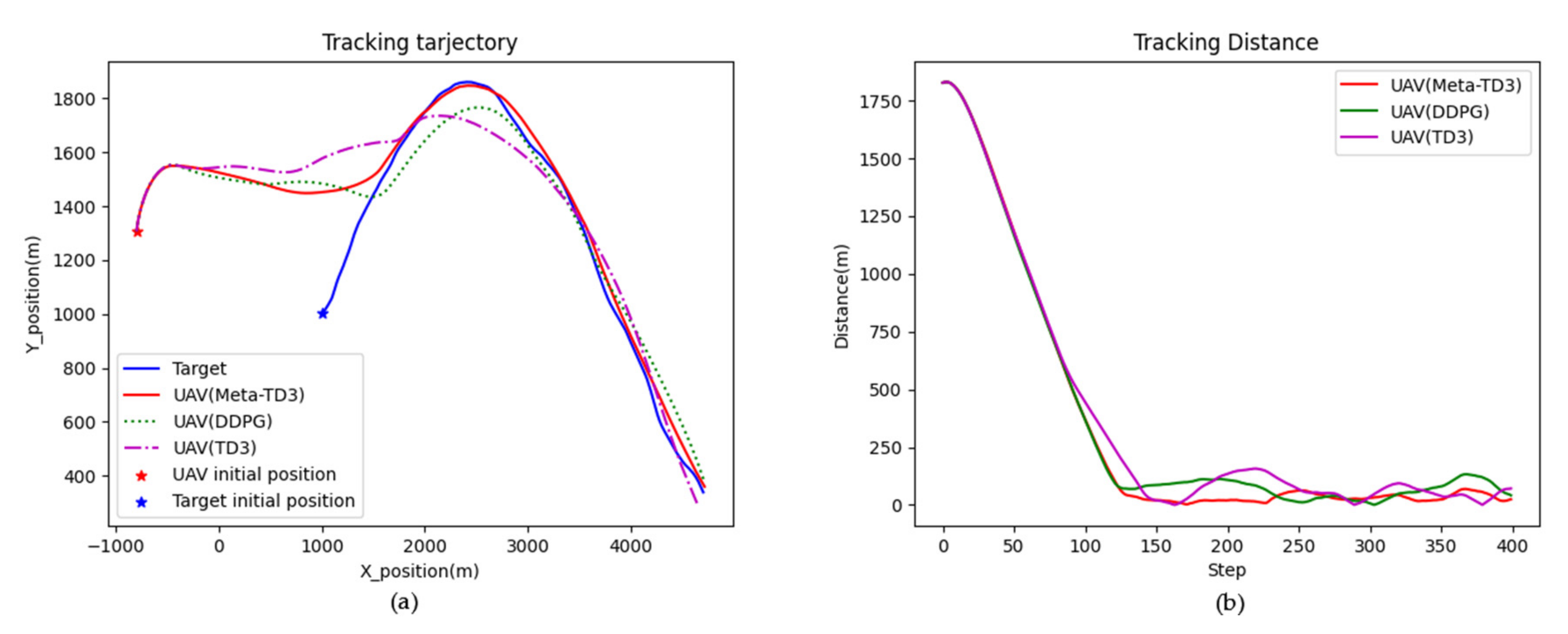
4. Results
4.1. Experimental Platform and Environment Setting
4.2. Model Training and Testing
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fu, C.; Carrio, A.; Olivares-Mendez, M.A.; Suarez-Fernandez, R.; Campoy, P. Robust real-time vision-based aircraft tracking from unmanned aerial vehicles. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; IEEE; Piscataway, NJ, USA, 2014; pp. 5441–5446. [Google Scholar]
- Olivares-Mendez, M.A.; Fu, C.; Ludivig, P.; Bissyandé, T.F.; Kannan, S.; Zurad, M.; Annaiyan, A.; Voos, H.; Campoy, P. Towards an autonomous vision-based unmanned aerial system against wildlife poachers. Sensors 2015, 15, 31362–31391. [Google Scholar] [CrossRef] [PubMed]
- Birk, A.; Wiggerich, B.; Bülow, H.; Pfingsthorn, M.; Schwertfeger, S. Safety, security, and rescue missions with an unmanned aerial vehicle (UAV). J. Intell. Robot. Syst. 2011, 64, 57–76. [Google Scholar] [CrossRef]
- Fu, C.; Carrio, A.; Campoy, P. Efficient visual odometry and mapping for unmanned aerial vehicle using ARM-based stereo vision pre-processing system. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 957–962. [Google Scholar]
- Li, B.; Wu, Y. Path Planning for UAV Ground Target Tracking via Deep Reinforcement Learning. IEEE Access 2020, 8, 29064–29074. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Yang, Y.; Wang, H.; Ding, Z.; Sari, H.; Adachi, F. Deep reinforcement learning for UAV navigation through massive MIMO technique. IEEE Trans. Veh. Technol. 2019, 69, 1117–1121. [Google Scholar] [CrossRef]
- Wu, C.; Ju, B.; Wu, Y.; Lin, X.; Xiong, N.; Xu, G.; Li, H.; Liang, X. UAV autonomous target search based on deep reinforcement learning in complex disaster scene. IEEE Access 2019, 7, 117227–117245. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Shen, Y.; Zhang, X. Autonomous navigation of UAVs in large-scale complex environments: A deep reinforcement learning approach. IEEE Trans. Veh. Technol. 2019, 68, 2124–2136. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019. [Google Scholar]
- Wan, K.; Gao, X.; Hu, Z.; Wu, G. Robust Motion Control for UAV in Dynamic Uncertain Environments Using Deep Reinforcement Learning. Remote. Sens. 2020, 12, 640. [Google Scholar] [CrossRef]
- Bhagat, S.; Sujit, P.B. UAV Target Tracking in Urban Environments Using Deep Reinforcement Learning. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 694–701. [Google Scholar]
- Hayat, S.; Yanmaz, E.; Brown, T.X.; Bettstetter, C. Multi-objective UAV path planning for search and rescue. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5569–5574. [Google Scholar]
- Mukherjee, A.; Misra, S.; Sukrutha, A.; Raghuwanshi, N.S. Distributed aerial processing for IoT-based edge UAV swarms in smart farming. Comput. Netw. 2020, 167, 107038. [Google Scholar] [CrossRef]
- Yang, B.; Cao, X.; Yuen, C.; Qian, L. Offloading Optimization in Edge Computing for Deep Learning Enabled Target Tracking by Internet-of-UAVs. IEEE Internet Things J. 2020, 1. [Google Scholar] [CrossRef]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep reinforcement learning that matters. arXiv 2017, arXiv:1709.06560. [Google Scholar]
- Zhang, A.; Wu, Y.; Pineau, J. Natural environment benchmarks for reinforcement learning. arXiv 2018, arXiv:1811.06032. [Google Scholar]
- Liu, H.; Socher, R.; Xiong, C. Taming maml: Efficient unbiased meta-reinforcement learning. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 4061–4071. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. arXiv 2017, arXiv:1703.03400. [Google Scholar]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-sgd: Learning to learn quickly for few-shot learning. arXiv 2017, arXiv:1707.09835. [Google Scholar]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Imanberdiyev, N.; Fu, C.; Kayacan, E.; Chen, I.-M. Autonomous navigation of UAV by using real-time model-based reinforcement learning. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar]
- Zhou, D.; Schwager, M. Vector field following for quadrotors using differential flatness. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6567–6572. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 1057–1063. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Roderick, M.; MacGlashan, J.; Tellex, S. Implementing the deep q-network. arXiv 2017, arXiv:1711.07478. [Google Scholar]
- Yadav, A.K.; Gaur, P. AI-based adaptive control and design of autopilot system for nonlinear UAV. Sadhana 2014, 39, 765–783. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Policy gradient methods for robotics. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2219–2225. [Google Scholar]
- Lin, L.-J. Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. Meta-learning with memory-augmented neural networks. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1842–1850. [Google Scholar]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building machines that learn and think like people. Behav. Brain Sci. 2017, 40, e253. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Harley, T.; Lillicrap, T.P.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]


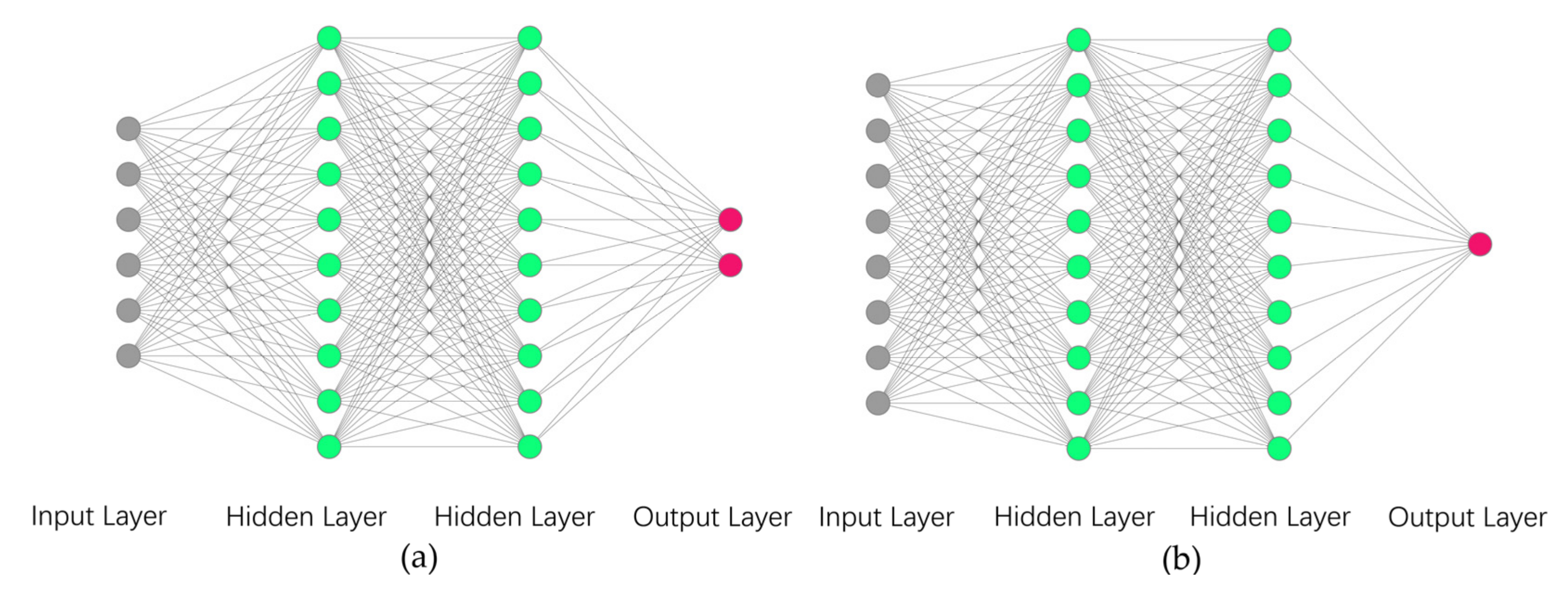


| Algorithm: Meta-TD3 |
| 1: Require: distribution over tasks |
| 2: Require: meta-learning steps size hyperparameters |
| 3: Initialize meta-critic networks , , and meta-actor network with random parameters , , |
| 4: Initialize critic networks , , and actor network , , |
| 5: Initialize target networks , , |
| 6: Sample batch of tasks |
| 7: Initialize replay buffer |
| 8: For do |
| 9: for do |
| 10: Select action with exploration noise |
| 11: Observe reward and new state |
| 12: Store transition in |
| 13: Sample mini-batch of N transitions from |
| 14: , |
| 15: Update critics |
| 16: if t mod update_policy_freq then |
| 17: Update by the deterministic policy gradient: |
| 18: |
| 19: Update the target networks: |
| 20: , , |
| 21: The neural network parameters of task :, , |
| 22: if t mod meta_update_freq then |
| 23: , |
| 24: |
| 25: end for |
| 26: , , |
| 27: , , |
| 28: end for |
| Environment | Meta-TD3 | TD3 | DDPG |
|---|---|---|---|
| Task 1 | 847.24 | 717.66 | 95.04 |
| Task 2 | 1027.45 | 946.38 | −20.42 |
| Task 3 | 715.84 | 154.12 | 275.26 |
| Environment | Meta-TD3 | TD3 | DDPG |
|---|---|---|---|
| Task 1 | 0.79 | 1.46 | 22.60 |
| Task 2 | 0.58 | 4.11 | 45.77 |
| Task 3 | 2.02 | 2.99 | 6.90 |
| Environment | Meta-TD3 | TD3 | DDPG |
|---|---|---|---|
| Task 1 | 40.91 | 334.75 | 660.72 |
| Task 2 | 85.63 | 150.80 | 274.12 |
| Task 3 | 88.77 | 321.42 | 160.01 |
| Environment | Meta-TD3 | TD3 | DDPG |
|---|---|---|---|
| Task 1 | 400 ± 50 | 950 ± 20 | |
| Task 2 | 350 ± 30 | 900 ± 50 | |
| Task 3 | 500 ± 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Gan, Z.; Chen, D.; Sergey Aleksandrovich, D. UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning. Remote Sens. 2020, 12, 3789. https://doi.org/10.3390/rs12223789
Li B, Gan Z, Chen D, Sergey Aleksandrovich D. UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning. Remote Sensing. 2020; 12(22):3789. https://doi.org/10.3390/rs12223789
Chicago/Turabian StyleLi, Bo, Zhigang Gan, Daqing Chen, and Dyachenko Sergey Aleksandrovich. 2020. "UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning" Remote Sensing 12, no. 22: 3789. https://doi.org/10.3390/rs12223789
APA StyleLi, B., Gan, Z., Chen, D., & Sergey Aleksandrovich, D. (2020). UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning. Remote Sensing, 12(22), 3789. https://doi.org/10.3390/rs12223789