Long-Range Automatic Detection, Acoustic Signature Characterization and Bearing-Time Estimation of Multiple Ships with Coherent Hydrophone Array
Abstract
1. Introduction
2. Methods
2.1. Experiment, Instrumentation and Acoustic Data Collection
2.2. Temporal Coherence Analysis of Ship Tonal Sound Using MMSC
2.3. Spectral Coherence Analysis of Ship Cavitation Noise Using CSC
2.4. Ship Sound’s Energetics Analysis with PSD
3. Results
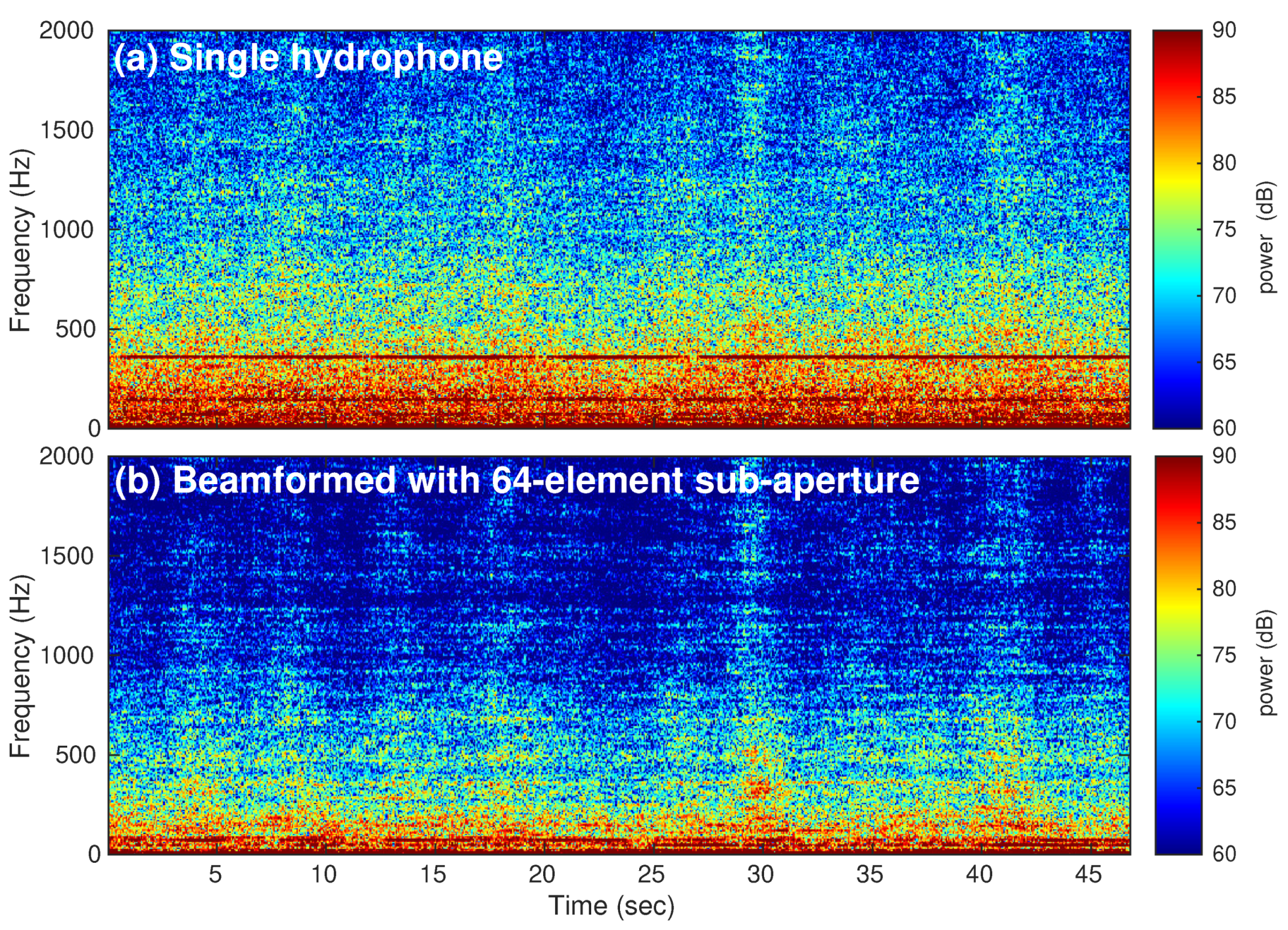
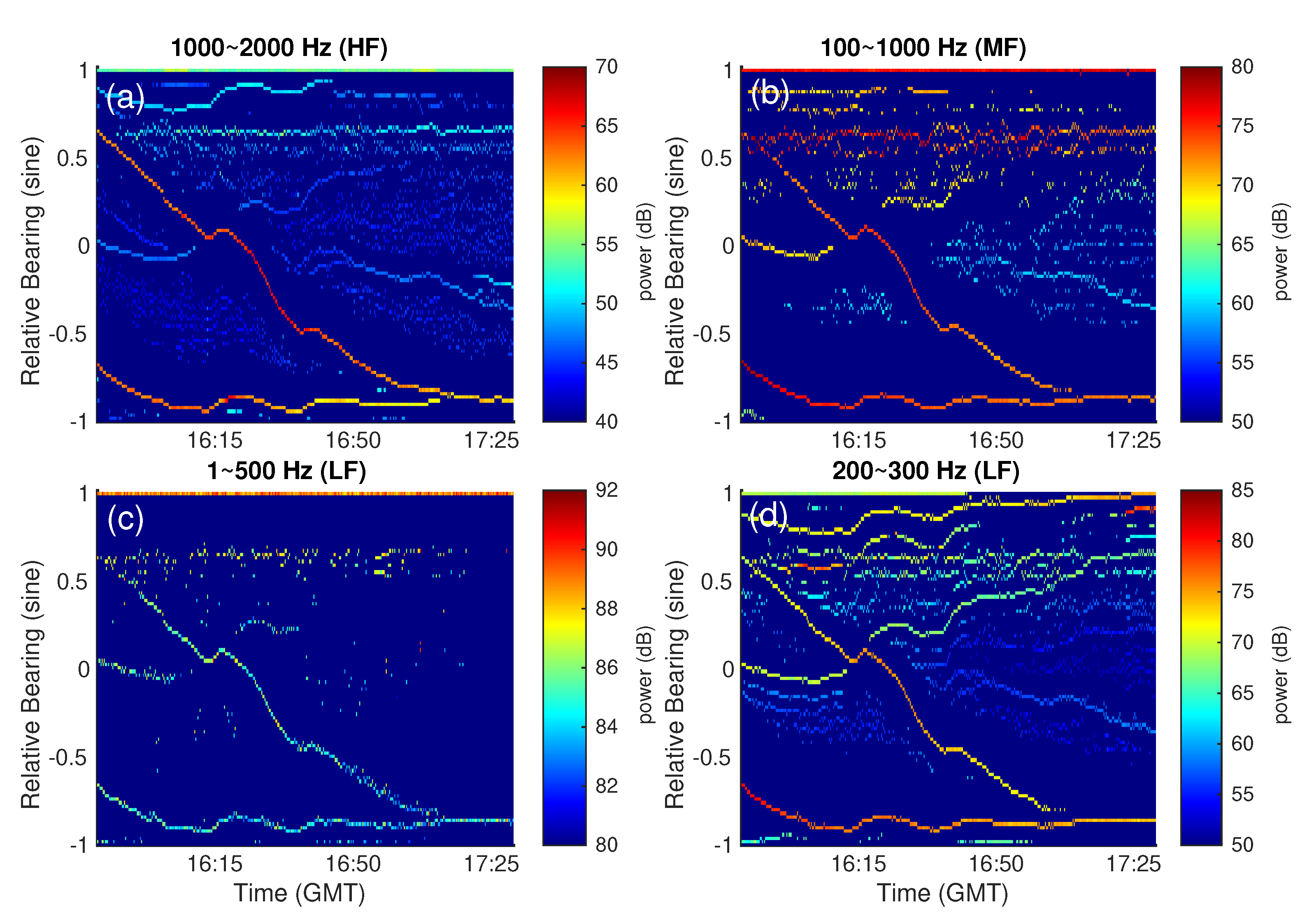
3.1. Beamform Analysis of Coherent Hydrophone Array Data
3.2. Machinery Tonal Sound Analysis via MMSC
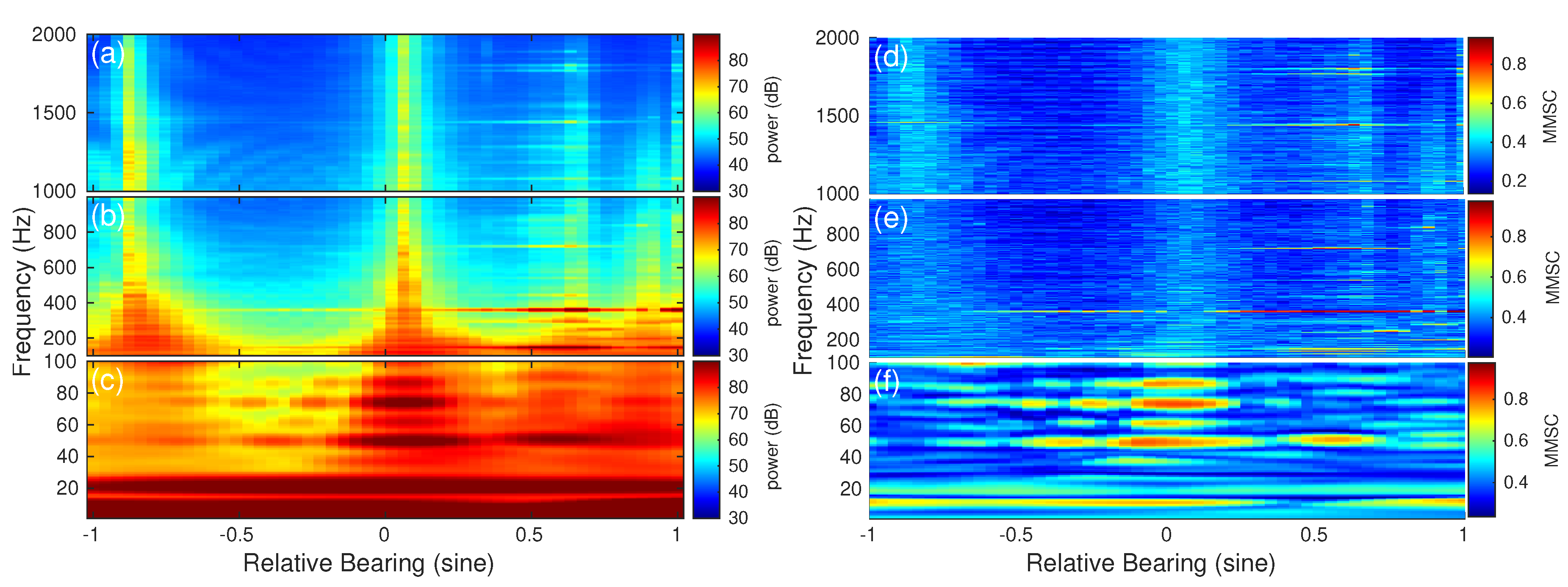
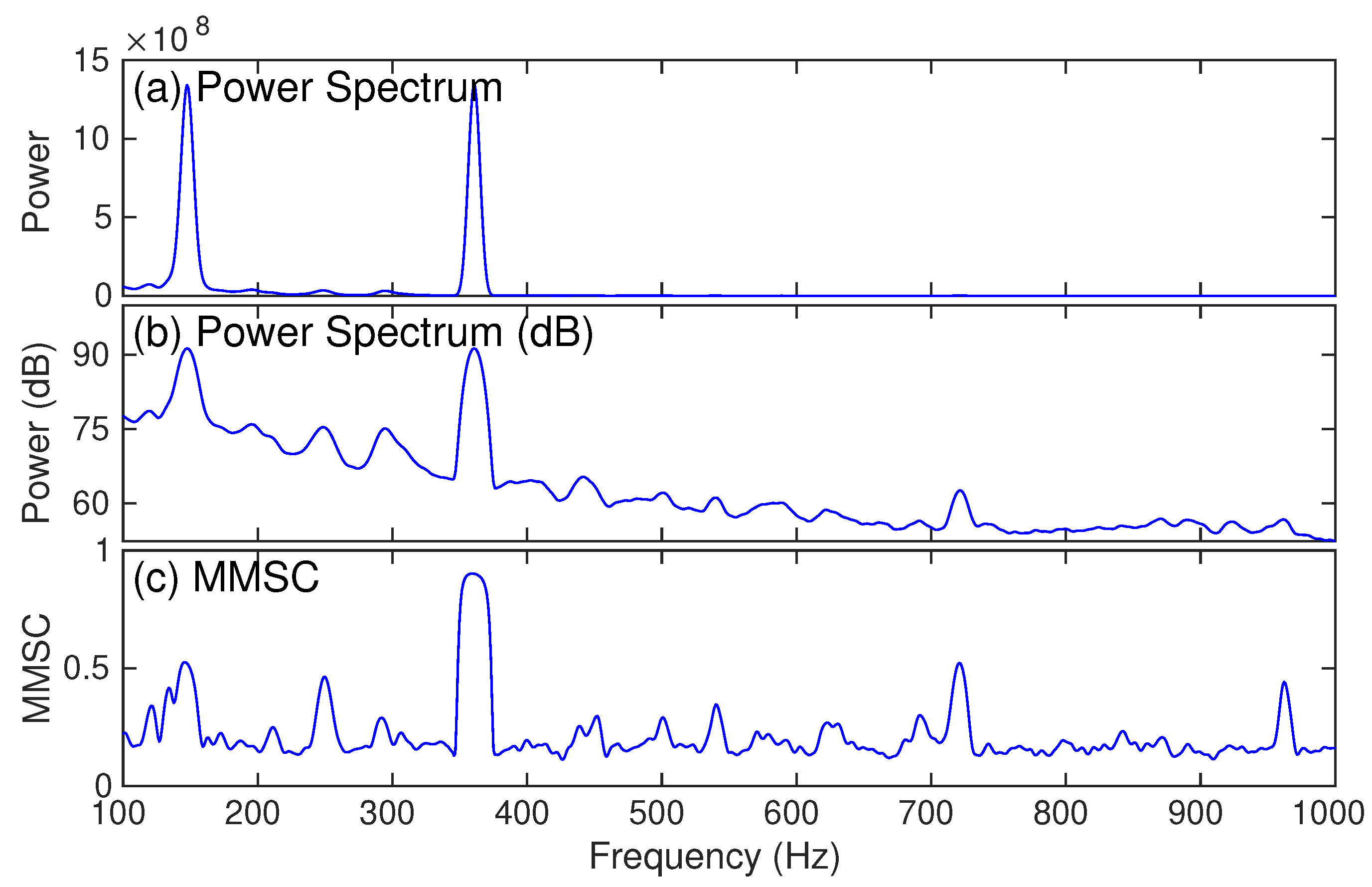
3.2.1. Comparing MMSC with Conventional Power Spectrum Analysis
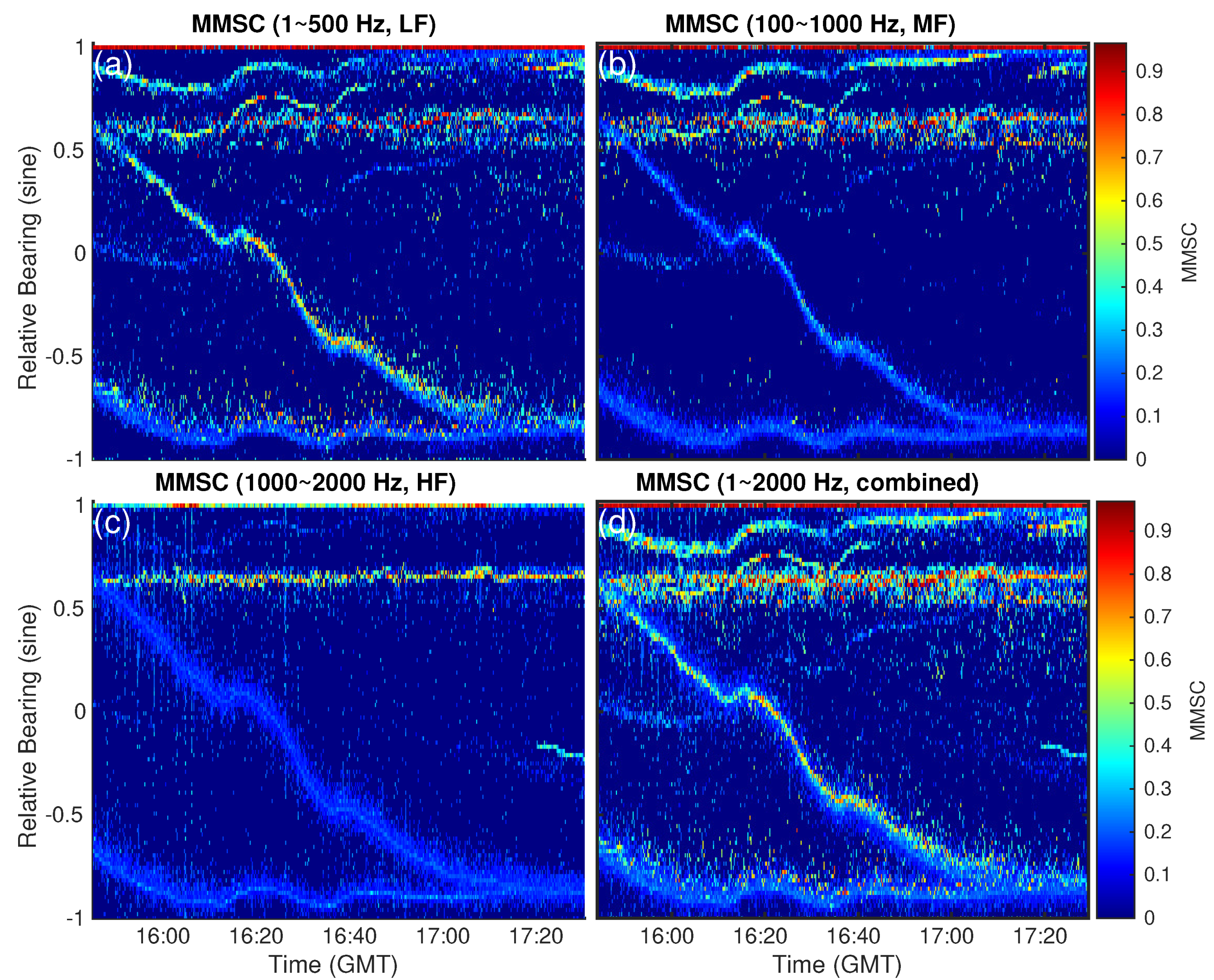
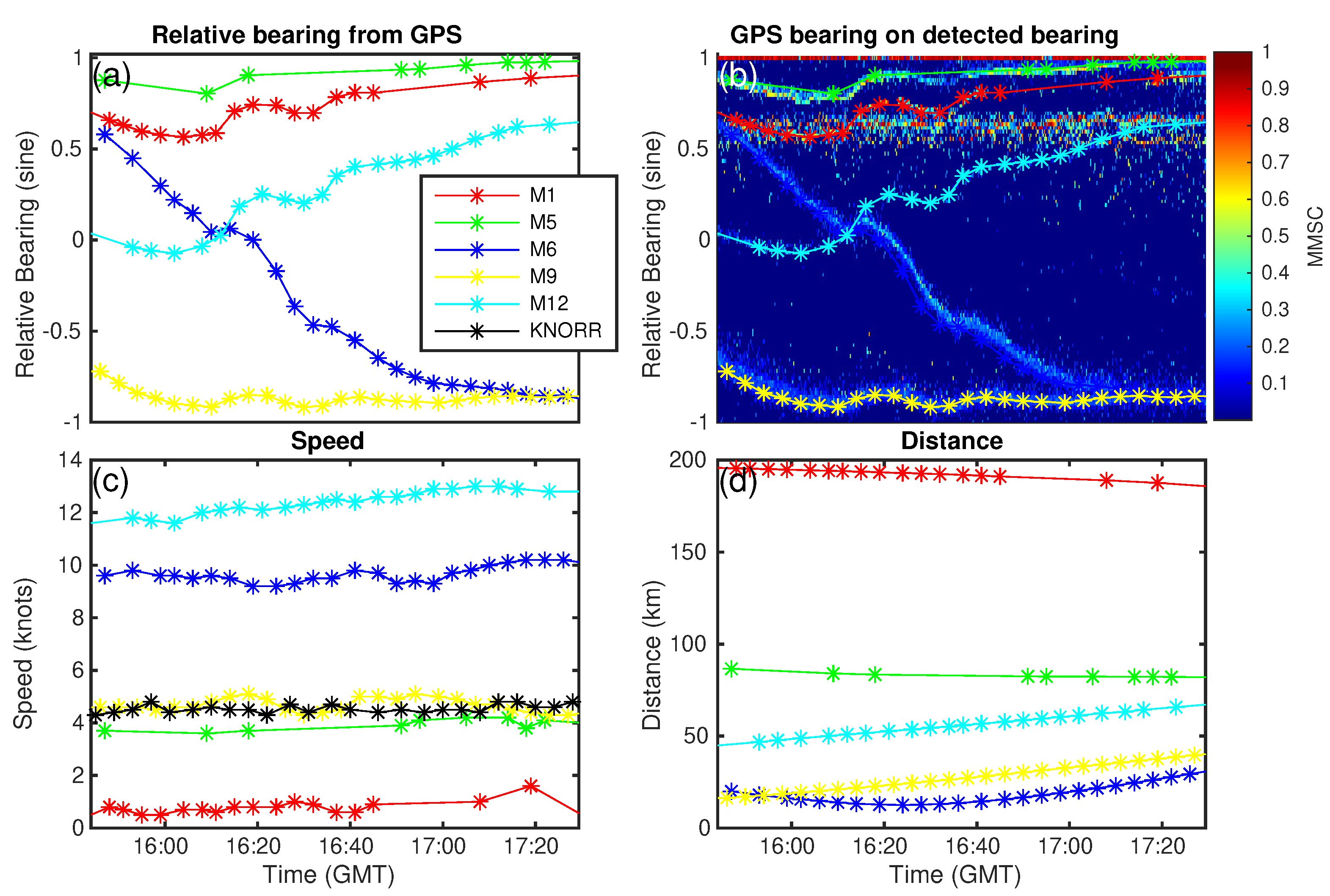
3.2.2. Bearing Estimation of Targets from MMSC
3.2.3. Individual Ship’s Tonal Sound Signature in Different Time Period
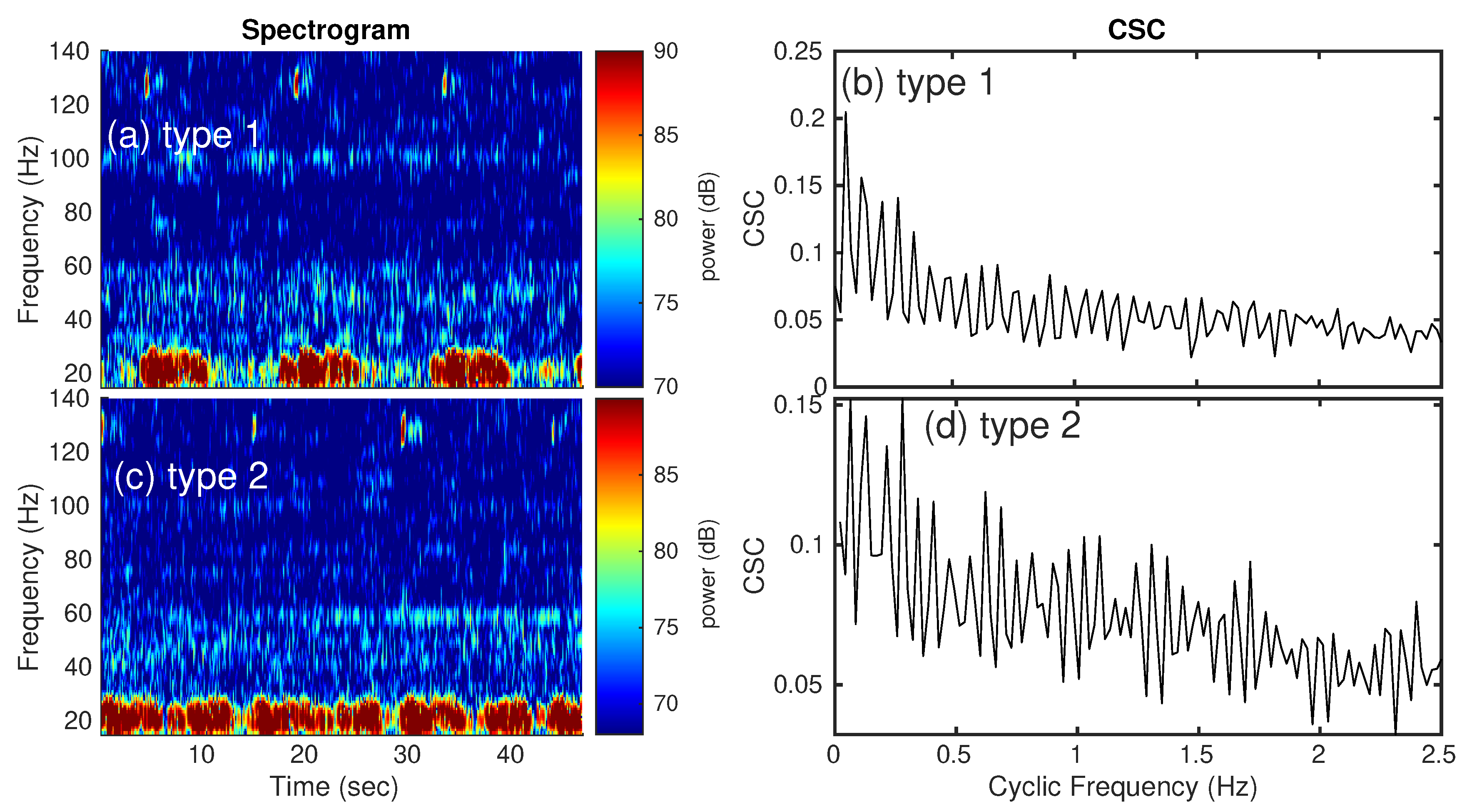
3.3. Propeller Noise Analysis via CSC
3.3.1. Received Broadband Cavitation Noise Overview
3.3.2. Bearing-Time Trajectory Estimation for Targets from CSC Analysis
3.3.3. Individual Ship’s CSC Signature in Different Time Period
3.4. General Energy Analysis of Ship-Radiated Underwater Sound via PSD
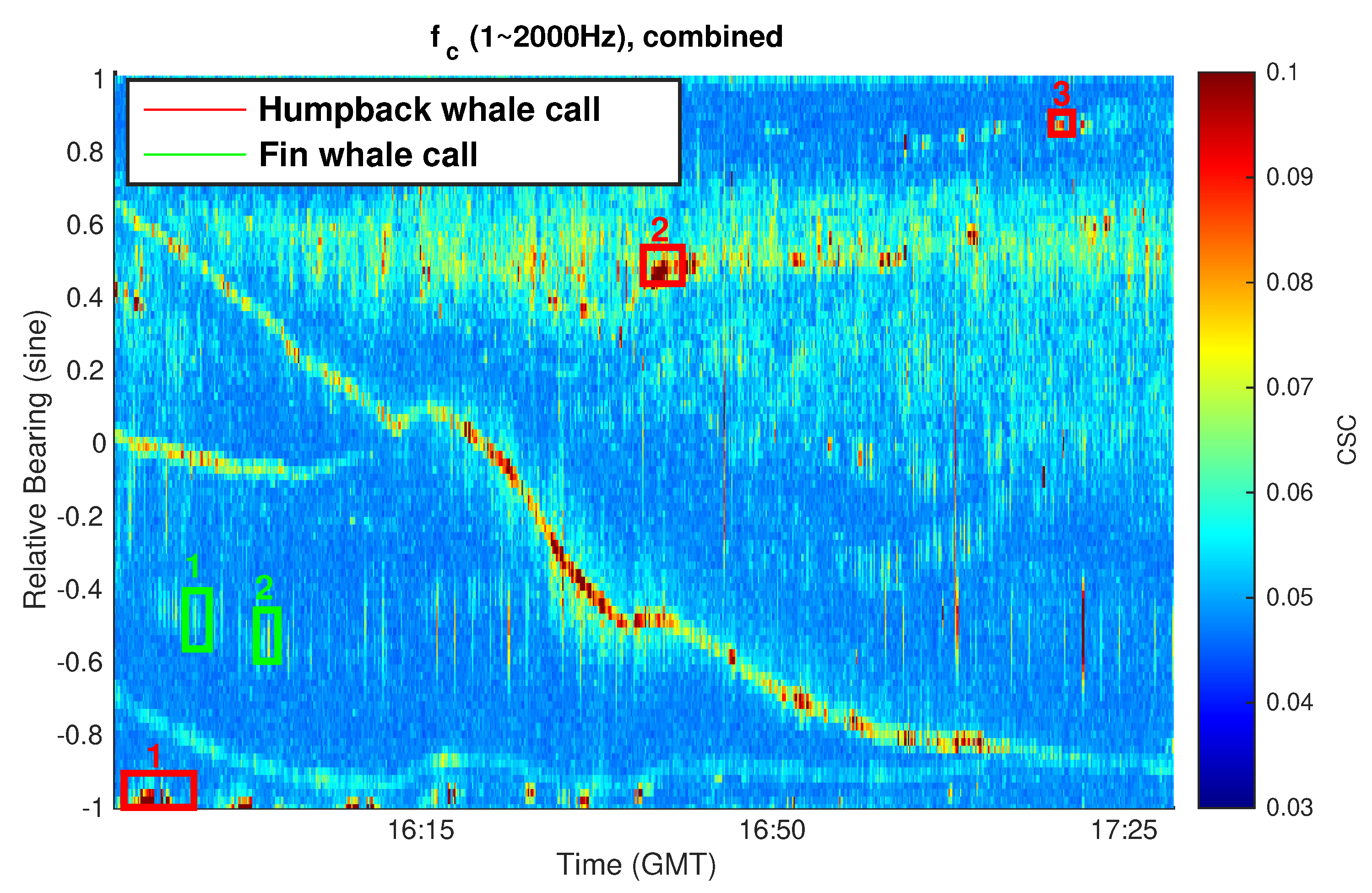
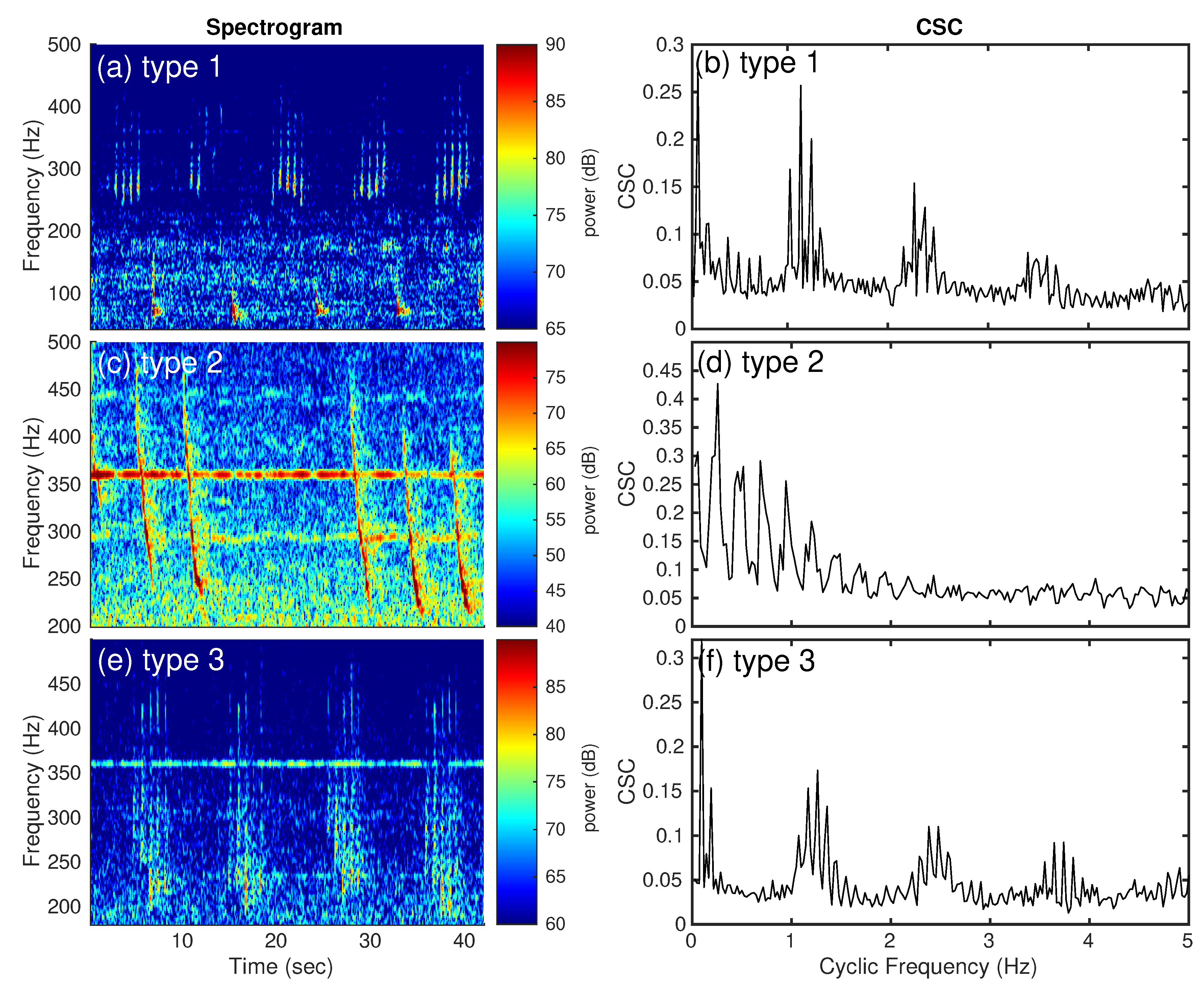
3.5. Marine Mammal Vocalization Analysis via CSC
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
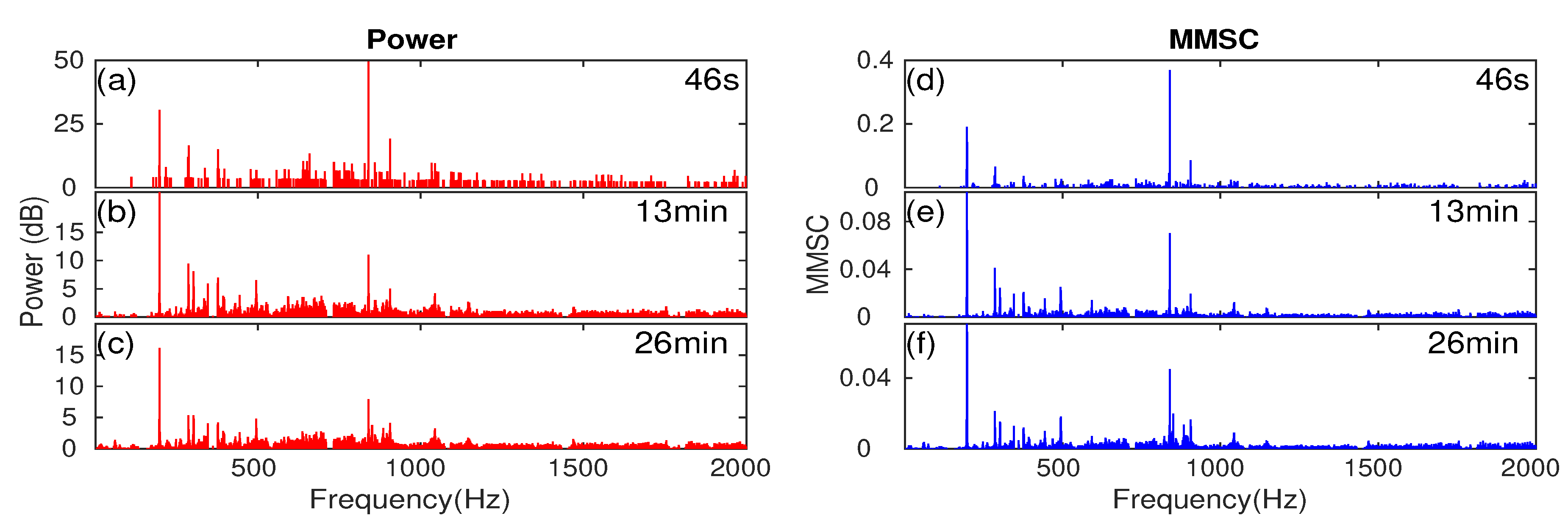
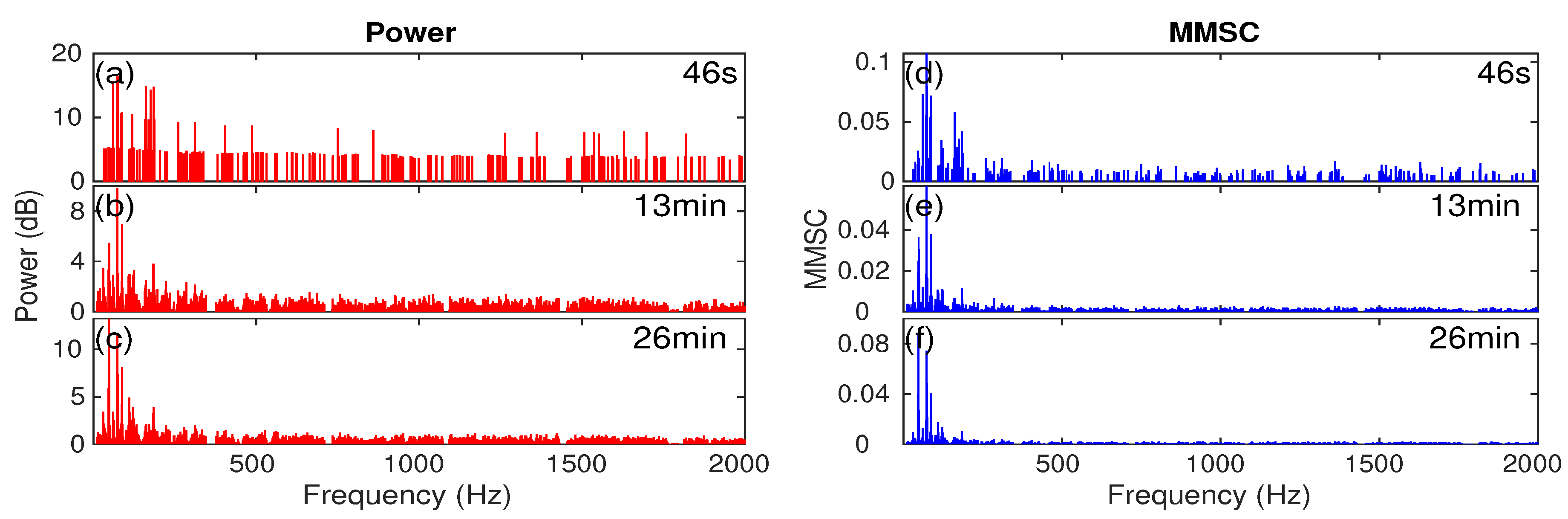
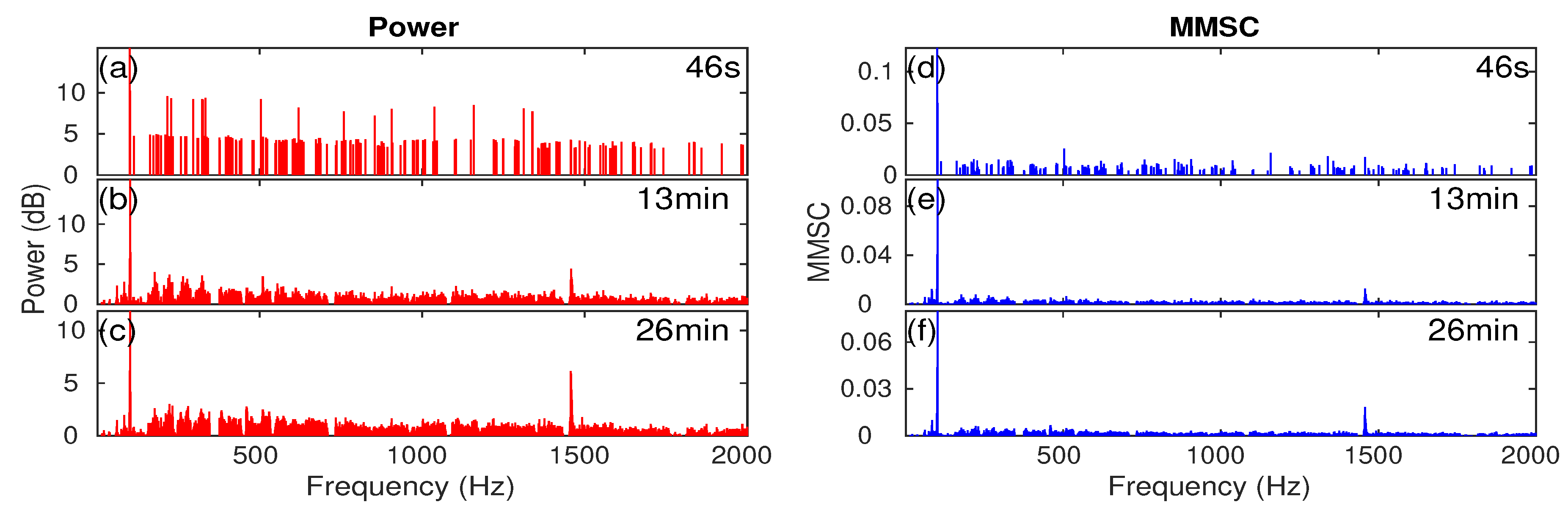
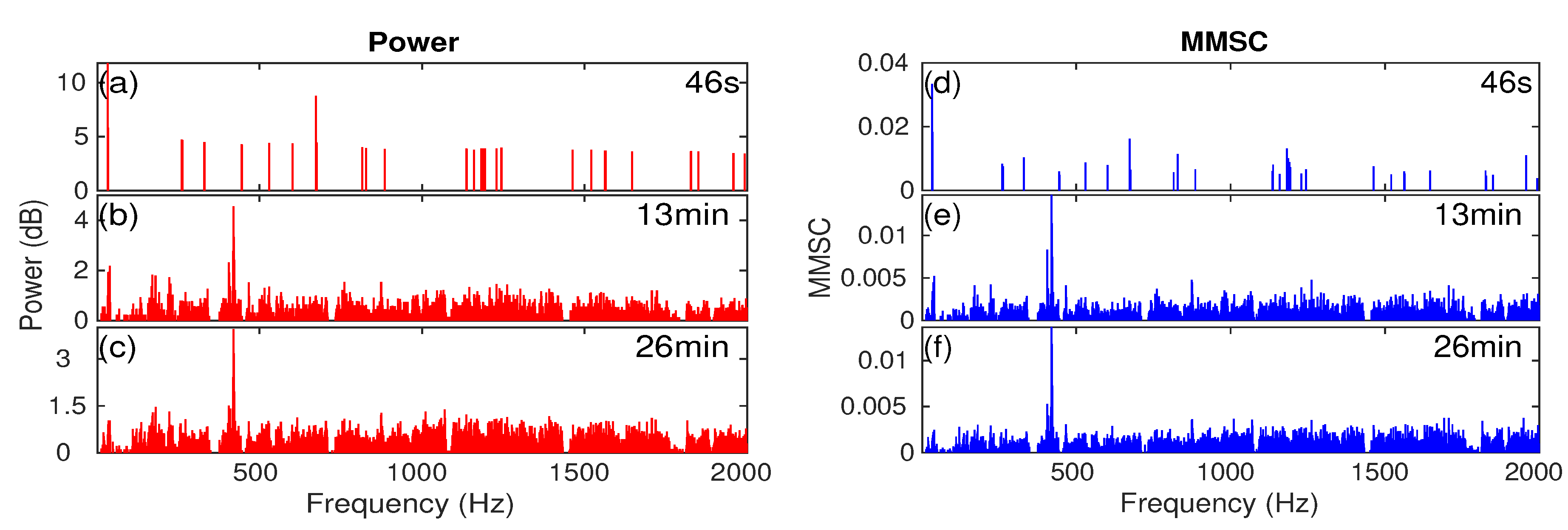
Appendix A. Individual Ship’s Tonal Sound Signature in Different Time Period
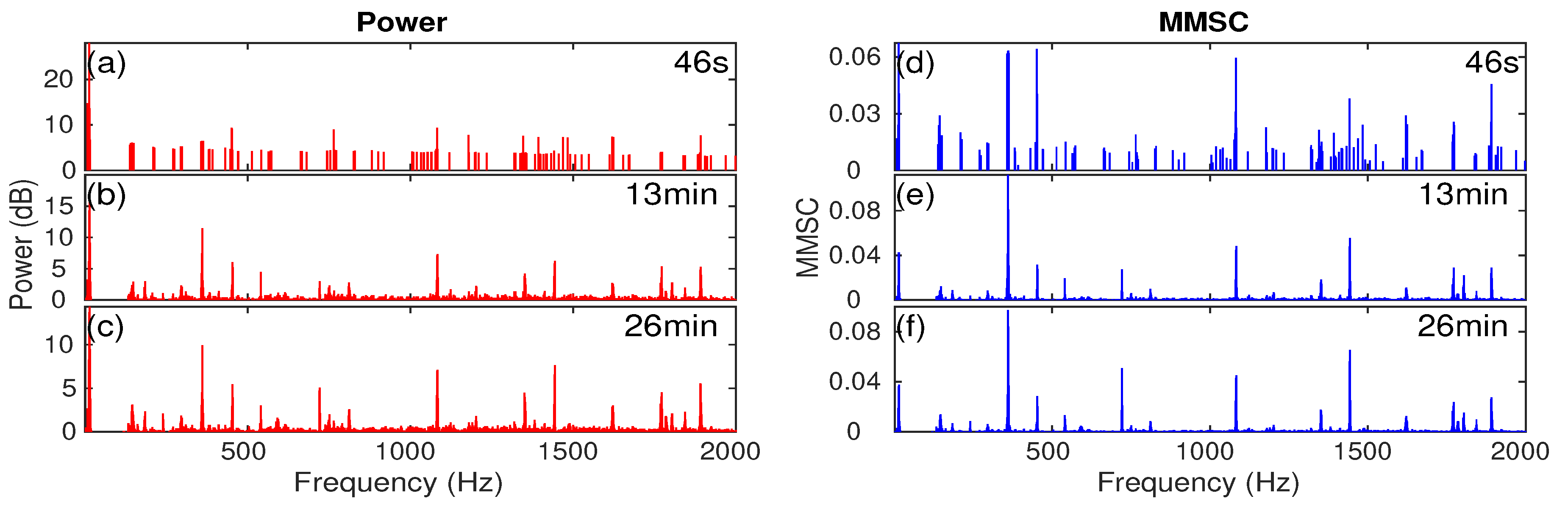
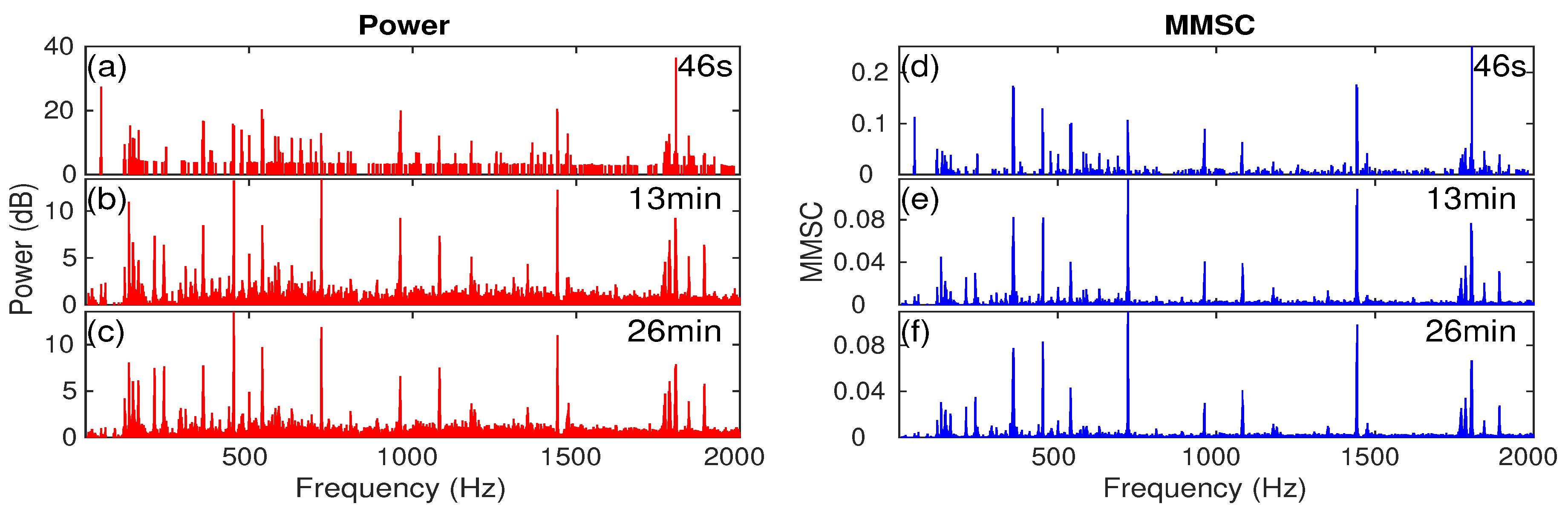
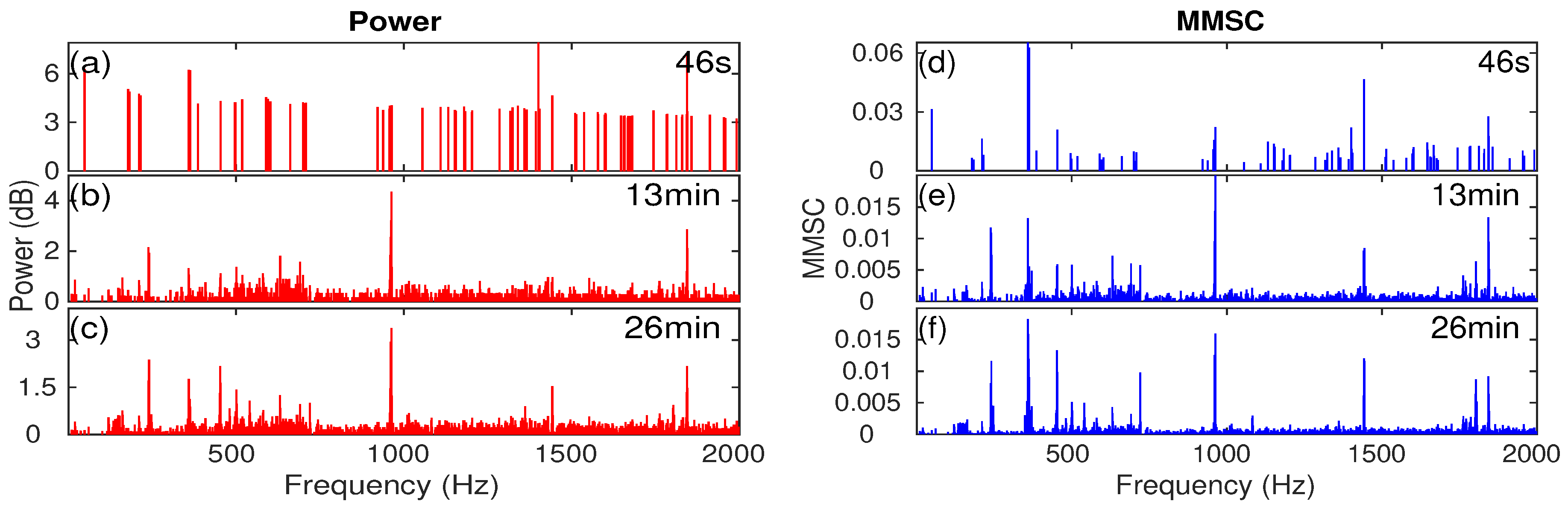
References
- Bergmann, P.G.; Major, J.; Wildt, R. Physics of Sound in the Sea; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Arveson, P.T.; Vendittis, D.J. Radiated noise characteristics of a modern cargo ship. J. Acoust. Soc. Am. 2000, 107, 118–129. [Google Scholar] [CrossRef] [PubMed]
- Bruno, M.; Chung, K.; Salloum, H.; Sedunov, A.; Sedunov, N.; Sutin, A.; Graber, H.; Mallas, P. Concurrent use of satellite imaging and passive acoustics for maritime domain awareness. In Proceedings of the 2010 International Waterside Security Conference (WSS), Carrara, Italy, 3–5 November 2010. [Google Scholar]
- Chung, K.W.; Sutin, A.; Sedunov, A.; Bruno, M. DEMON acoustic ship signature measurements in an urban harbor. Adv. Acoust. Vib. 2011, 2011, 952798. [Google Scholar] [CrossRef]
- Fillinger, L.; Sutin, A.; Sedunov, A. Acoustic ship signature measurements by cross-correlation method. J. Acoust. Soc. Am. 2010, 129, 774–778. [Google Scholar] [CrossRef] [PubMed]
- Leal, N.; Leal, E.; Sanchez, G. Marine vessel recognition by acoustic signature. ARPN J. Eng. Appl. Sci. 2015, 10, 9633–9639. [Google Scholar]
- Ogden, G.L.; Zurk, L.M.; Jones, M.E.; Peterson, M.E. Extraction of small boat harmonic signatures from passive sonar. J. Acoust. Soc. Am. 2011, 129, 3768–3776. [Google Scholar] [CrossRef]
- Wales, S.C.; Heitmeyer, R.M. An ensemble source spectra model for merchant ship-radiated noise. J. Acoust. Soc. Am. 2002, 111, 1211–1231. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; Peninsula Publising: Los Atlos, CA, USA, 1983. [Google Scholar]
- Wenz, G.M. Acoustic ambient noise in the ocean: Spectra and sources. J. Acoust. Soc. Am. 1962, 34, 1936–1956. [Google Scholar] [CrossRef]
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar] [CrossRef]
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godø, O.R.; Nero, R.W.; Jech, J.M. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 2009, 323, 1734–1737. [Google Scholar] [CrossRef]
- Wang, D.; Garcia, H.; Huang, W.; Tran, D.D.; Jain, A.D.; Yi, D.H.; Gong, Z.; Jech, J.M.; Godø, O.R.; Makris, N.C.; et al. Vast assembly of vocal marine mammals from diverse species on fish spawning ground. Nature 2016, 531, 366–370. [Google Scholar] [CrossRef]
- Mohebbi-Kalkhoran, H.; Zhu, C.; Schinault, M.; Ratilal, P. Classifying humpback whale calls to song and non-song vocalizations using bag of words descriptor on acoustic data. In Proceedings of the 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 865–870. [Google Scholar]
- MacLennan, D.N.; Simmonds, E.J. Fisheries Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 5. [Google Scholar]
- Vieira, M.; Amorim, M.; Sundelöf, A.; Prista, N.; Fonseca, P.J. Underwater noise recognition of marine vessels passages: Two case studies using hidden Markov models. ICES J. Mar. Sci. 2019, 77, 2157–2170. [Google Scholar] [CrossRef]
- Stojanovic, M. Underwater acoustic communications. In Proceedings of the InElectro/95 International, Professional Program Proceedings, Boston, MA, USA, 21–23 June 1995; pp. 435–440. [Google Scholar]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Dambra, R.; Firenze, E. Underwater radiated noise of a small vessel. In Proceedings of the 22nd International Congress on Sound and Vibration, Florence, Italy, 12–16 July 2015; pp. 12–16. [Google Scholar]
- Hildebrand, J.A. Anthropogenic and natural sources of ambient noise in the ocean. Mar. Ecol. Prog. Ser. 2009, 395, 5–20. [Google Scholar] [CrossRef]
- Merchant, N.D.; Witt, M.J.; Blondel, P.; Godley, B.J.; Smith, G.H. Assessing sound exposure from shipping in coastal waters using a single hydrophone and Automatic Identification System (AIS) data. Mar. Pollut. Bull. 2012, 64, 1320–1329. [Google Scholar] [CrossRef]
- Vasconcelos, R.O.; Amorim, M.C.P.; Ladich, F. Effects of ship noise on the detectability of communication signals in the Lusitanian toadfish. J. Exp. Biol. 2007, 210, 2104–2112. [Google Scholar] [CrossRef]
- Slabbekoorn, H.; Dooling, R.J.; Popper, A.N.; Fay, R.R. Effects of Anthropogenic Noise on Animals; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Codarin, A.; Wysocki, L.E.; Ladich, F.; Picciulin, M. Effects of ambient and boat noise on hearing and communication in three fish species living in a marine protected area (Miramare, Italy). Mar. Pollut. Bull. 2009, 58, 1880–1887. [Google Scholar] [CrossRef]
- Ona, E.; Godø, O.R.; Handegard, N.O.; Hjellvik, V.; Patel, R.; Pedersen, G. Silent research vessels are not quiet. J. Acoust. Soc. Am. 2007, 121, EL145–EL150. [Google Scholar] [CrossRef]
- Mitson, R. Underwater noise radiated by research vessels. ICES Mar. Sci. Symp. 1993, 196, 147–152. [Google Scholar]
- Mitson, R.B.; Knudsen, H.P. Causes and effects of underwater noise on fish abundance estimation. Aquat. Living Resour. 2003, 16, 255–263. [Google Scholar] [CrossRef]
- Hawkins, A.D.; Pembroke, A.E.; Popper, A.N. Information gaps in understanding the effects of noise on fishes and invertebrates. Rev. Fish Biol. Fish. 2015, 25, 39–64. [Google Scholar] [CrossRef]
- Veirs, S.; Veirs, V.; Wood, J.D. Ship noise extends to frequencies used for echolocation by endangered killer whales. PeerJ 2016, 4, e1657. [Google Scholar] [CrossRef] [PubMed]
- Erbe, C.; Dunlop, R.; Dolman, S. Effects of noise on marine mammals. In Effects of Anthropogenic Noise on Animals; Springer: Berlin/Heidelberg, Germany, 2018; pp. 277–309. [Google Scholar]
- Makris, N.C.; Godø, O.R.; Yi, D.H.; Macaulay, G.J.; Jain, A.D.; Cho, B.; Gong, Z.; Jech, J.M.; Ratilal, P. Instantaneous areal population density of entire Atlantic cod and herring spawning groups and group size distribution relative to total spawning population. Fish Fish. 2019, 20, 201–213. [Google Scholar] [CrossRef]
- Garcia, H.A.; Zhu, C.; Schinault, M.E.; Kaplan, A.I.; Handegard, N.O.; Godø, O.R.; Ahonen, H.; Makris, N.C.; Wang, D.; Huang, W.; et al. Temporal–spatial, spectral, and source level distributions of fin whale vocalizations in the Norwegian Sea observed with a coherent hydrophone array. ICES J. Mar. Sci. 2019, 76, 268–283. [Google Scholar] [CrossRef]
- Zhu, C.; Garcia, H.; Kaplan, A.; Schinault, M.; Handegard, N.O.; Godø, O.R.; Huang, W.; Ratilal, P. Detection, localization and classification of multiple mechanized ocean vessels over continental-shelf scale regions with passive ocean acoustic waveguide remote sensing. Remote Sens. 2018, 10, 1699. [Google Scholar] [CrossRef]
- Duane, D.; Cho, B.; Jain, A.D.; Godø, O.R.; Makris, N.C. The Effect of Attenuation from Fish Shoals on Long-Range, Wide-Area Acoustic Sensing in the Ocean. Remote Sens. 2019, 11, 2464. [Google Scholar] [CrossRef]
- Seri, S.G.; Zhu, C.; Schinault, M.; Garcia, H.; Handegard, N.O.; Ratilal, P. Long Range Passive Ocean Acoustic Waveguide Remote Sensing (POAWRS) of Seismo-acoustic Airgun Signals Received on a Coherent Hydrophone Array. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019; pp. 1–8. [Google Scholar]
- Garcia, H.A.; Couture, T.; Galor, A.; Topple, J.M.; Huang, W.; Tiwari, D.; Ratilal, P. Comparing performances of five distinct automatic classifiers for fin whale vocalizations in beamformed spectrograms of coherent hydrophone array. Remote Sens. 2020, 12, 326. [Google Scholar] [CrossRef]
- Pollara, A.; Sutin, A.; Salloum, H. Improvement of the Detection of Envelope Modulation on Noise (DEMON) and its application to small boats. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–10. [Google Scholar]
- Antoni, J.; Hanson, D. Detection of surface ships from interception of cyclostationary signature with the cyclic modulation coherence. IEEE J. Ocean. Eng. 2012, 37, 478–493. [Google Scholar] [CrossRef]
- Sichun, L.; Desen, Y. DEMON feature extraction of acoustic vector signal based on 3/2-D spectrum. In Proceedings of the 2007 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, China, 23–25 May 2007; pp. 2239–2243. [Google Scholar]
- Hanson, D.; Antoni, J.; Brown, G.; Emslie, R. Cyclostationarity for ship detection using passive sonar: Progress towards a detection and identification framework. In Proceedings of the Acoustics, Adelaide, Australia, 23–25 November 2009; pp. 1–8. [Google Scholar]
- Antoni, J. Cyclostationarity by examples. Mech. Syst. Signal Process. 2009, 23, 987–1036. [Google Scholar] [CrossRef]
- Antoni, J.; Xin, G.; Hamzaoui, N. Fast computation of the spectral correlation. Mech. Syst. Signal Process. 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Gardner, W. Measurement of spectral correlation. IEEE Trans. Acoust. Speech, Signal Process. 1986, 34, 1111–1123. [Google Scholar] [CrossRef]
- Hanson, D.; Antoni, J.; Brown, G.; Emslie, R. Cyclostationarity for passive underwater detection of propeller craft: A development of DEMON processing. In Proceedings of the Acoustics 2008, Geelong, Victoria, Australia, 24–26 November 2008; pp. 24–26. [Google Scholar]
- Kay, S.M. Modern Spectral Estimation; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Goodman, J. Statistical Optics; Willey: New York, NY, USA, 1988. [Google Scholar]
- Pollara, A.; Sutin, A.; Salloum, H. Modulation of high frequency noise by engine tones of small boats. J. Acoust. Soc. Am. 2017, 142, EL30–EL34. [Google Scholar] [CrossRef] [PubMed]
- Becker, K.; Preston, J. The ONR five octave research array (FORA) at Penn State. In Proceedings of the Oceans 2003. Celebrating the Past... Teaming Toward the Future (IEEE Cat. No. 03CH37492), San Diego, CA, USA, 22–26 September 2003; Volume 5, pp. 2607–2610. [Google Scholar]
- Wang, D.; Ratilal, P. Angular resolution enhancement provided by nonuniformly-spaced linear hydrophone arrays in ocean acoustic waveguide remote sensing. Remote Sens. 2017, 9, 1036. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Gold, B. Theory and Application of Digital Signal Processing; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1975; 777p. [Google Scholar]
- Woods Hole Oceanographic Institution. RV KNORR Propeller Image. 2020. Available online: https://www.whoi.edu/multimedia/r-v-knorr/ (accessed on 25 February 2020).
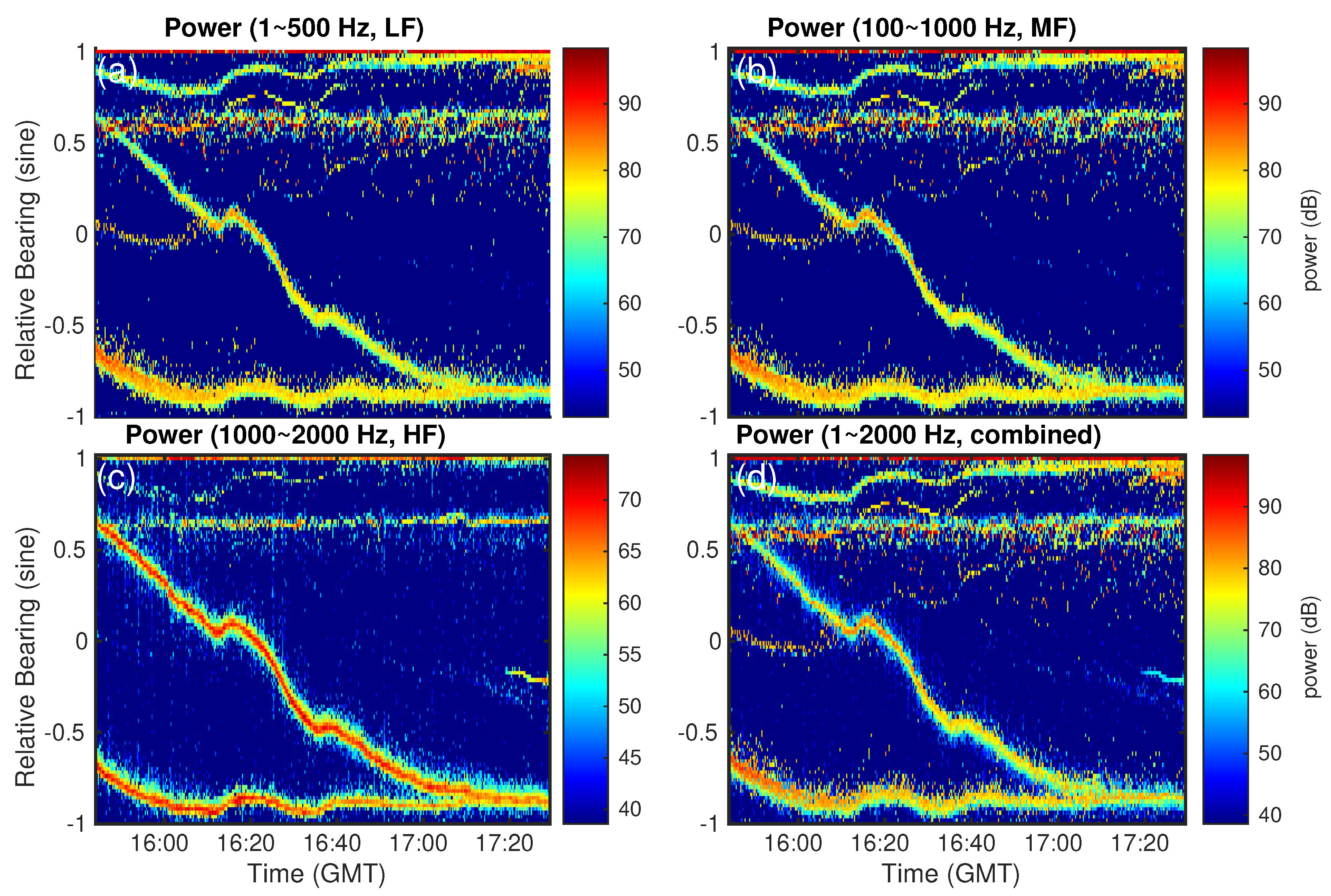
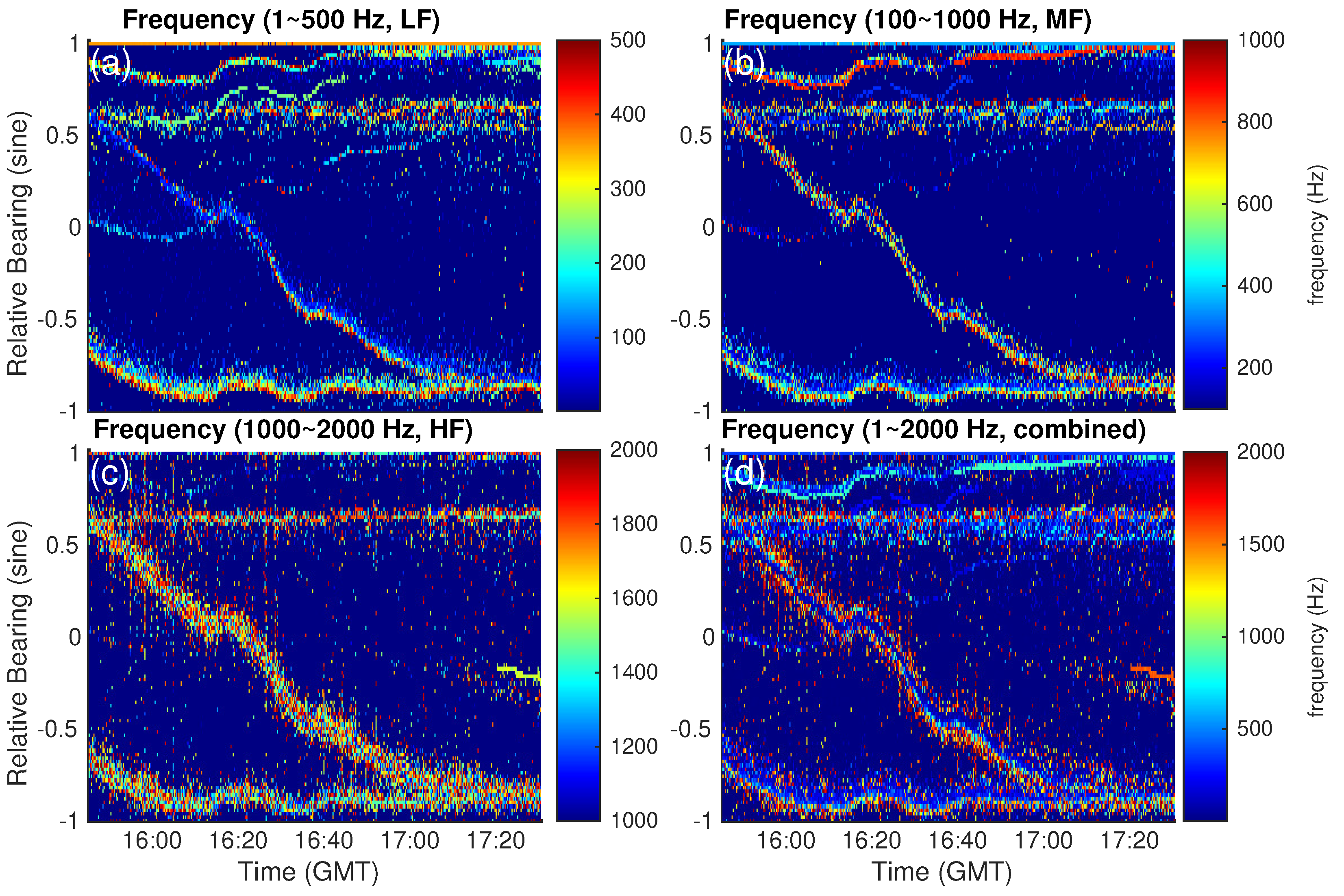
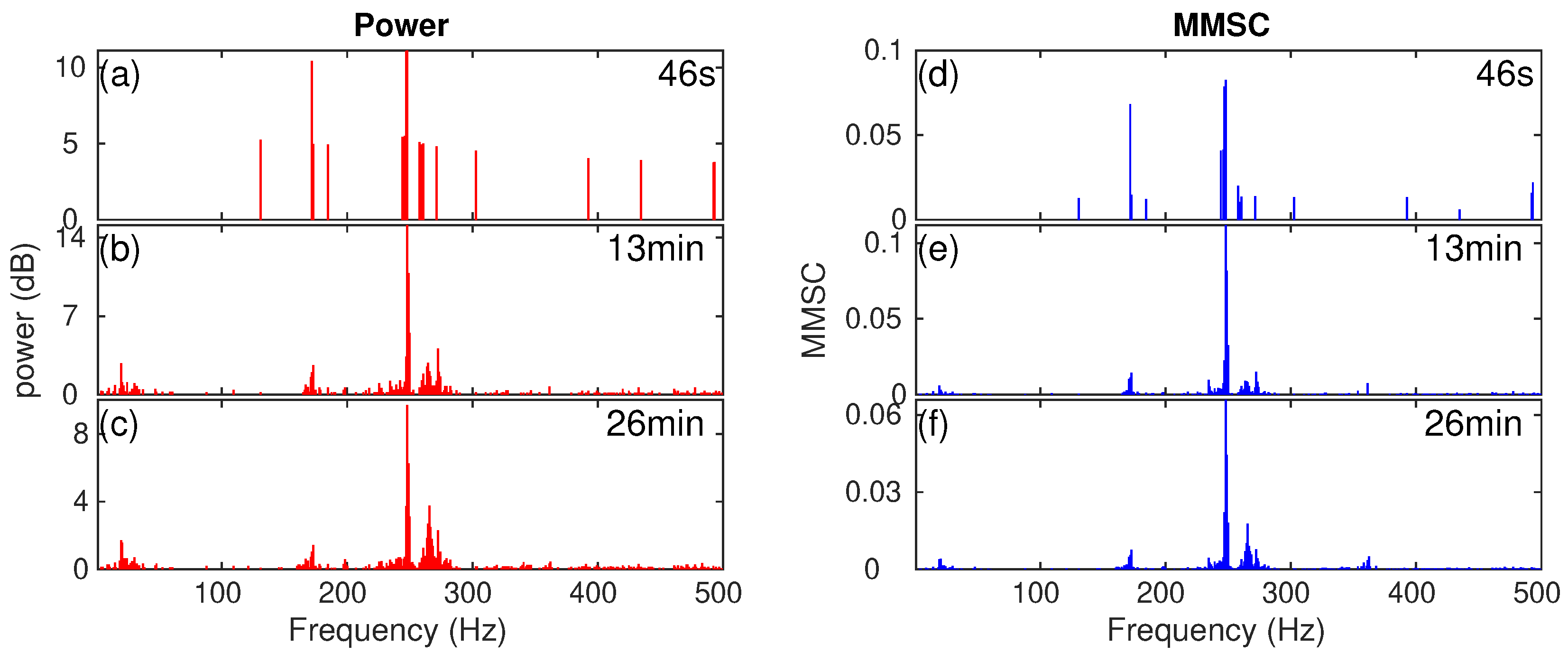
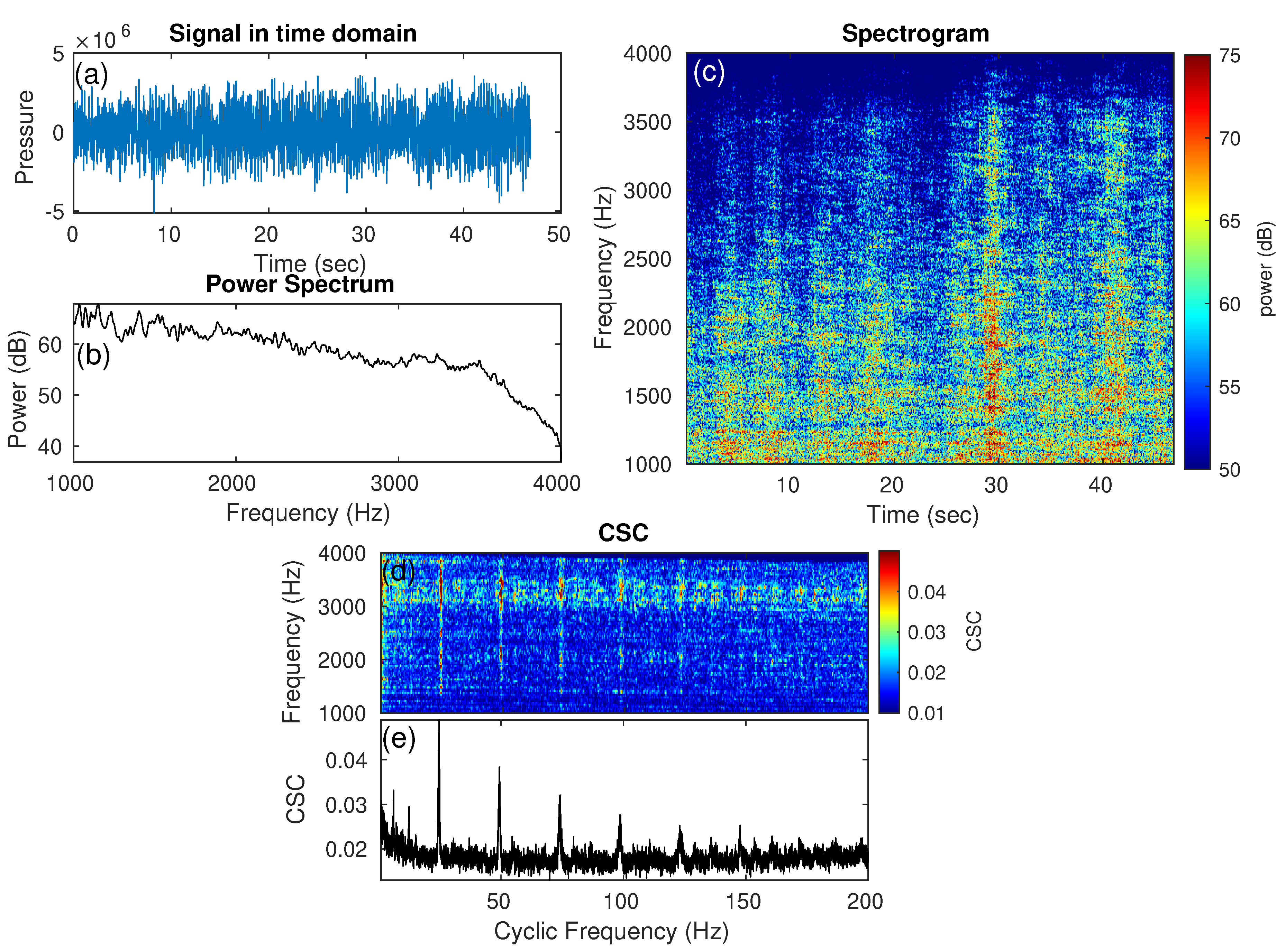
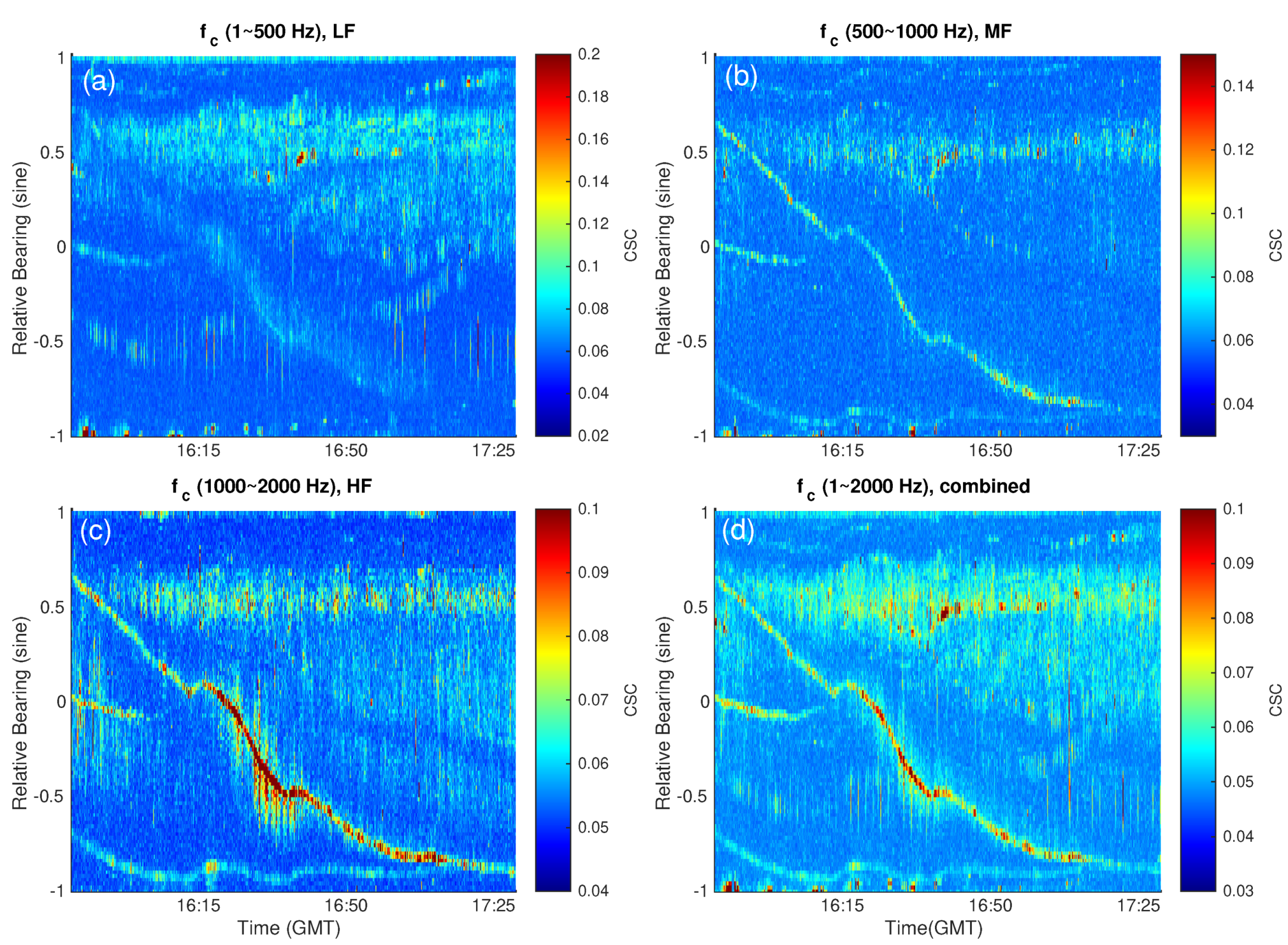
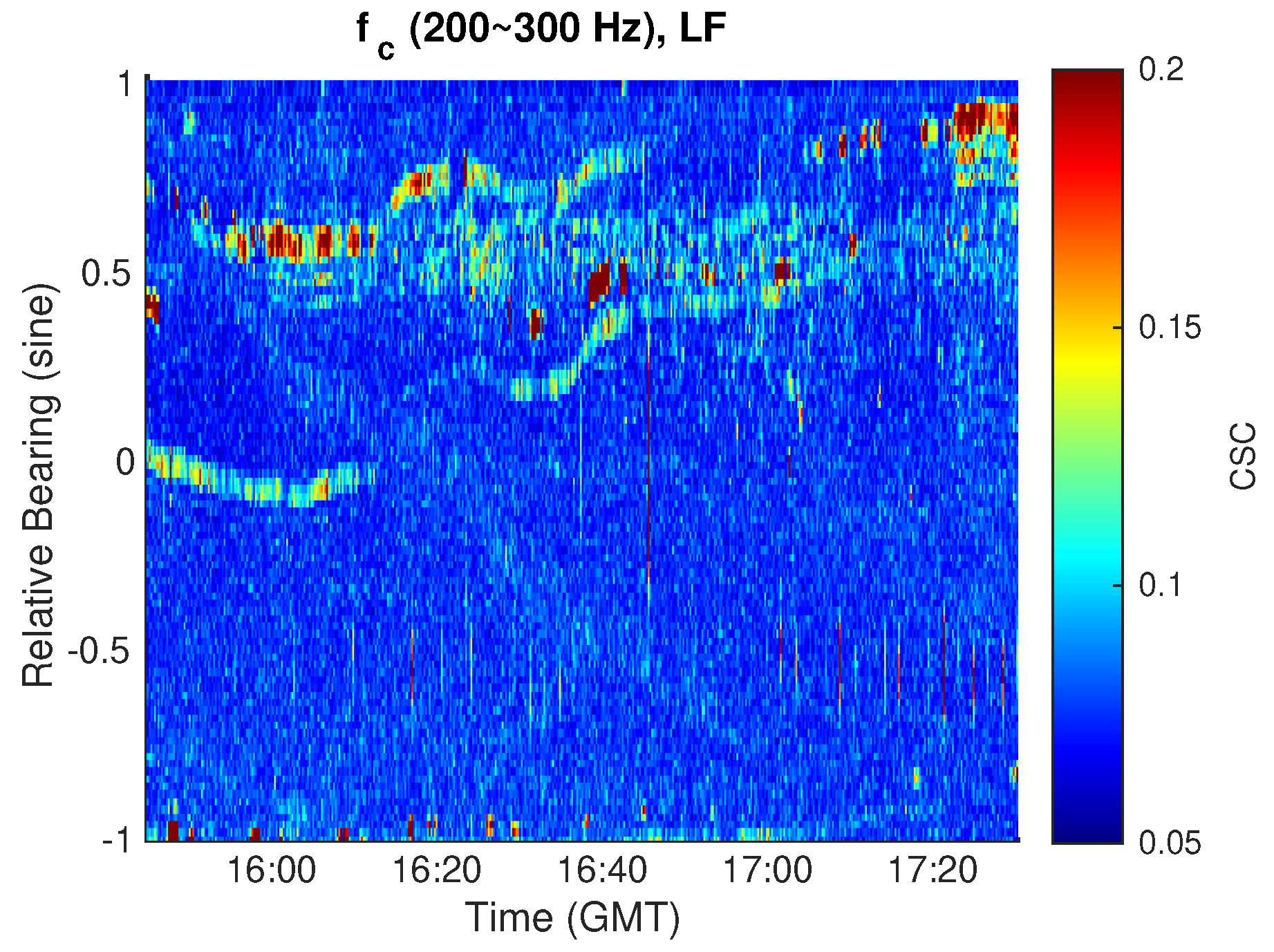
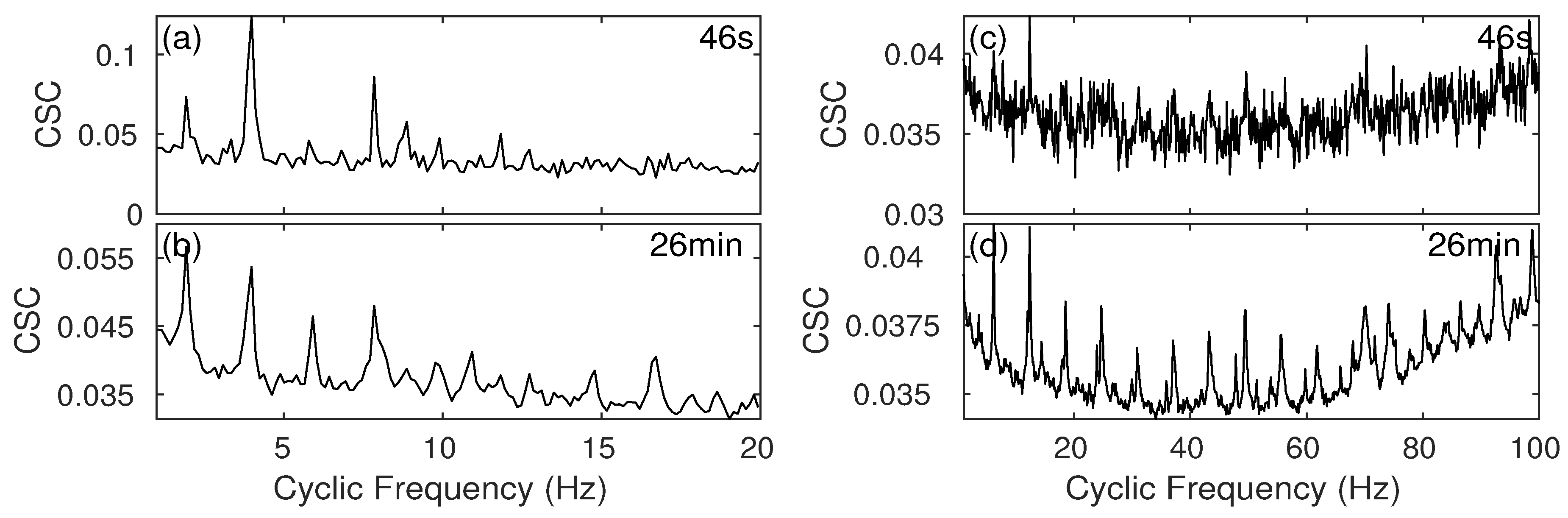
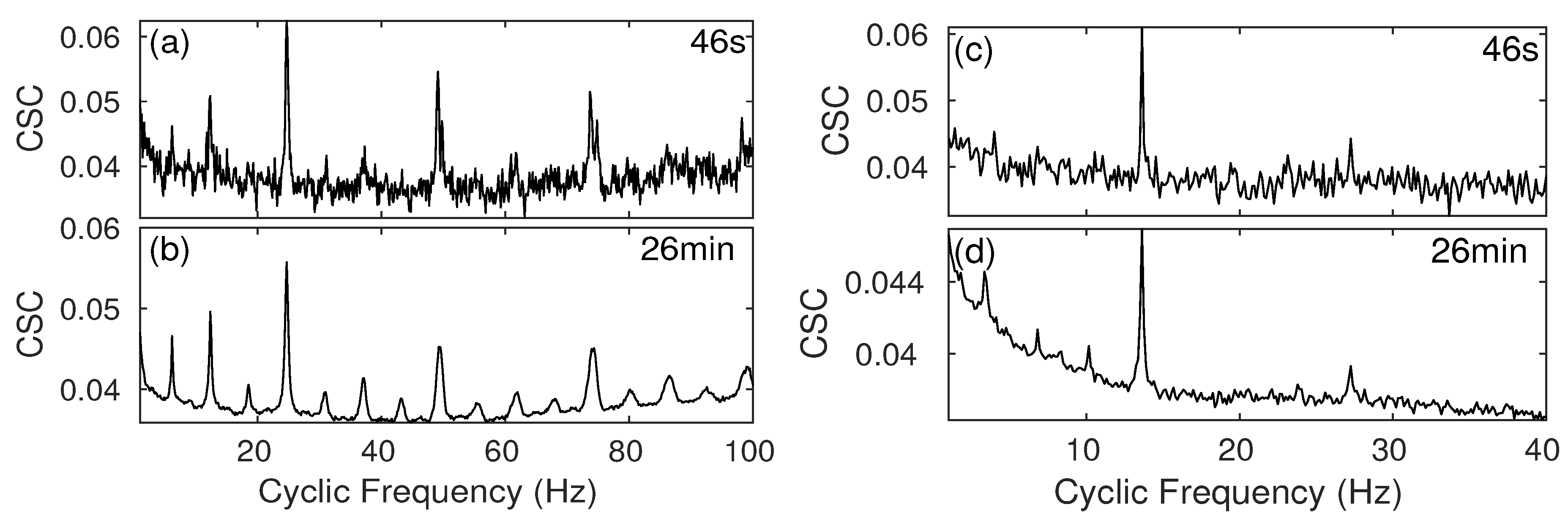
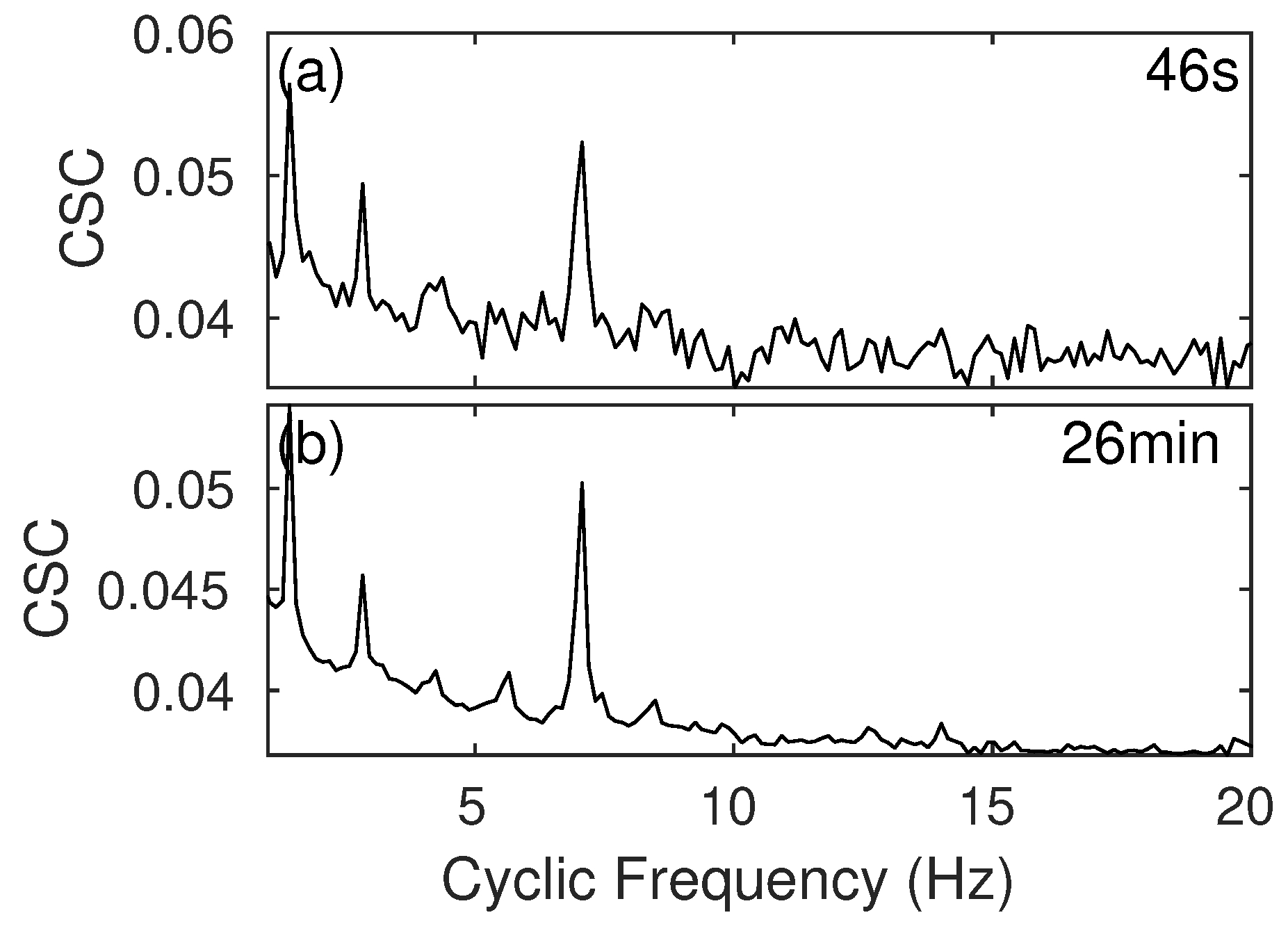
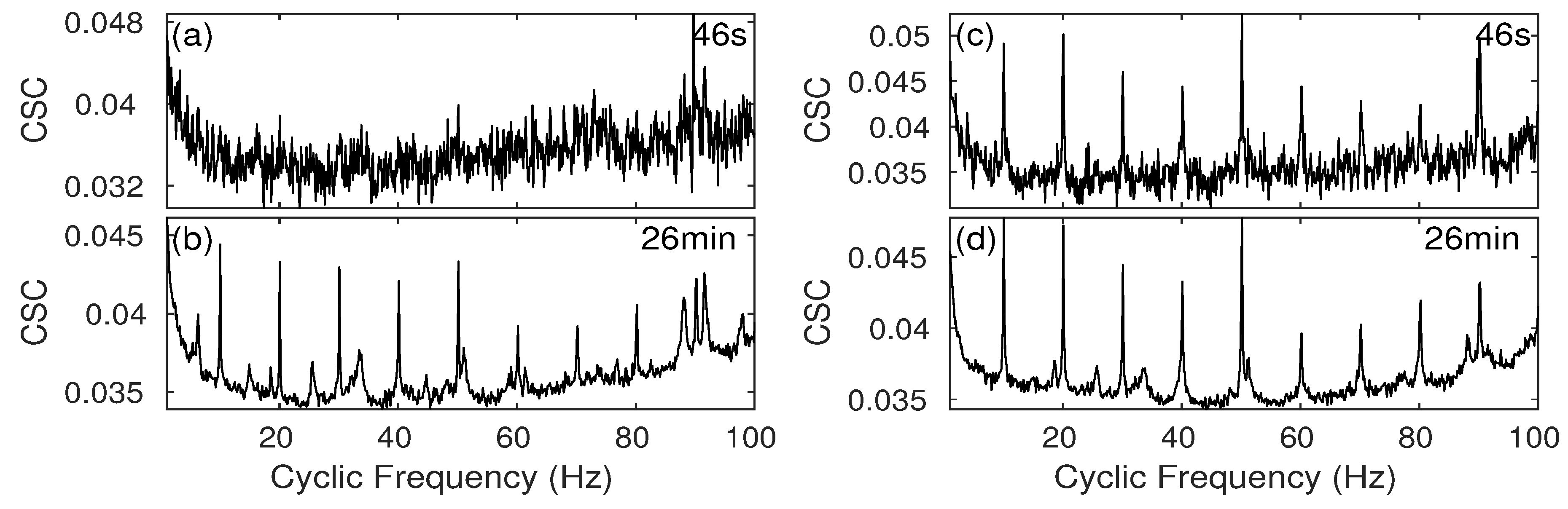
| Vessel | fcarrier Hz | Time Period |
|---|---|---|
| M1 | 200–300 | t1 |
| M5 | 1–2000 | t2 |
| M6 | 1–2000 | t1 |
| M9 | 1000–2000 | t1 |
| M12 | 1–2000 | t2 |
| KNORR (direct arrival) | 1000–2000 | t1 |
| KNORR (seafloor reflected) | 1000–2000 | t1 |
| From GPS | From Acoustic Signals | |||||
|---|---|---|---|---|---|---|
| Vessel No. | Vessel Type | Speed (Knots) | Distance (km) | fshaft (Hz) | fblade-pass (Hz) | Blade Number |
| M1 | SAR | 0.78 ± 0.16 | 192.4 ± 0.6 | 1.92 | 7.84 | 4 |
| M5 | F | 3.7 | 83.38 | 2.06 | 6.17 | 3 |
| M6 | F | 9.4 ± 0.2 | 13.2 ± 0.7 | 6.17 | 24.68 | 4 |
| M9 | F | 4.6 ± 0.3 | 25.4 ± 1.9 | 3.34 | 13.62 | 4 |
| M12 | CG | 12.3 ± 0.1 | 54.3 ± 1.8 | 1.41 | 7.06 | 5 |
| KNORR | RV | 4.5 ± 0.2 | 0.2-0.3 | 10.03 | 50.13 | 5 |
| Call Category | Description | Fundamental Cyclic Frequency (Call Rate) (Hz) | Call Interval (sec) |
|---|---|---|---|
| Humpback Type 1 | Clicks and lower frequency Downsweeps combined | 0.1068 1.132 | 9.36 0.88 |
| Humpback Type 2 | Higher frequency Downsweeps only | 0.0427 0.2136 | 23.41 4.68 |
| Humpback Type 3 | Clicks only | 0.095 1.263 | 10.492 0.7918 |
| Fin Type 1 | Sparse 20 Hz calls mixed with 130 Hz calls | 0.064 | 15.625 |
| Fin Type 2 | Dense 20 Hz calls mixed with 130 Hz calls | 0.064 0.2782 | 15.625 3.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Seri, S.G.; Mohebbi-Kalkhoran, H.; Ratilal, P. Long-Range Automatic Detection, Acoustic Signature Characterization and Bearing-Time Estimation of Multiple Ships with Coherent Hydrophone Array. Remote Sens. 2020, 12, 3731. https://doi.org/10.3390/rs12223731
Zhu C, Seri SG, Mohebbi-Kalkhoran H, Ratilal P. Long-Range Automatic Detection, Acoustic Signature Characterization and Bearing-Time Estimation of Multiple Ships with Coherent Hydrophone Array. Remote Sensing. 2020; 12(22):3731. https://doi.org/10.3390/rs12223731
Chicago/Turabian StyleZhu, Chenyang, Sai Geetha Seri, Hamed Mohebbi-Kalkhoran, and Purnima Ratilal. 2020. "Long-Range Automatic Detection, Acoustic Signature Characterization and Bearing-Time Estimation of Multiple Ships with Coherent Hydrophone Array" Remote Sensing 12, no. 22: 3731. https://doi.org/10.3390/rs12223731
APA StyleZhu, C., Seri, S. G., Mohebbi-Kalkhoran, H., & Ratilal, P. (2020). Long-Range Automatic Detection, Acoustic Signature Characterization and Bearing-Time Estimation of Multiple Ships with Coherent Hydrophone Array. Remote Sensing, 12(22), 3731. https://doi.org/10.3390/rs12223731







