Modeling and Theoretical Analysis of GNSS-R Soil Moisture Retrieval Based on the Random Forest and Support Vector Machine Learning Approach
Abstract
1. Introduction
2. Theoretical Background
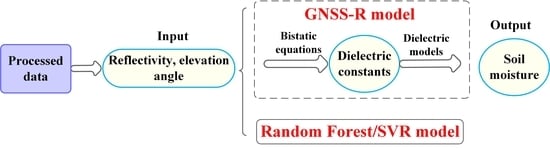
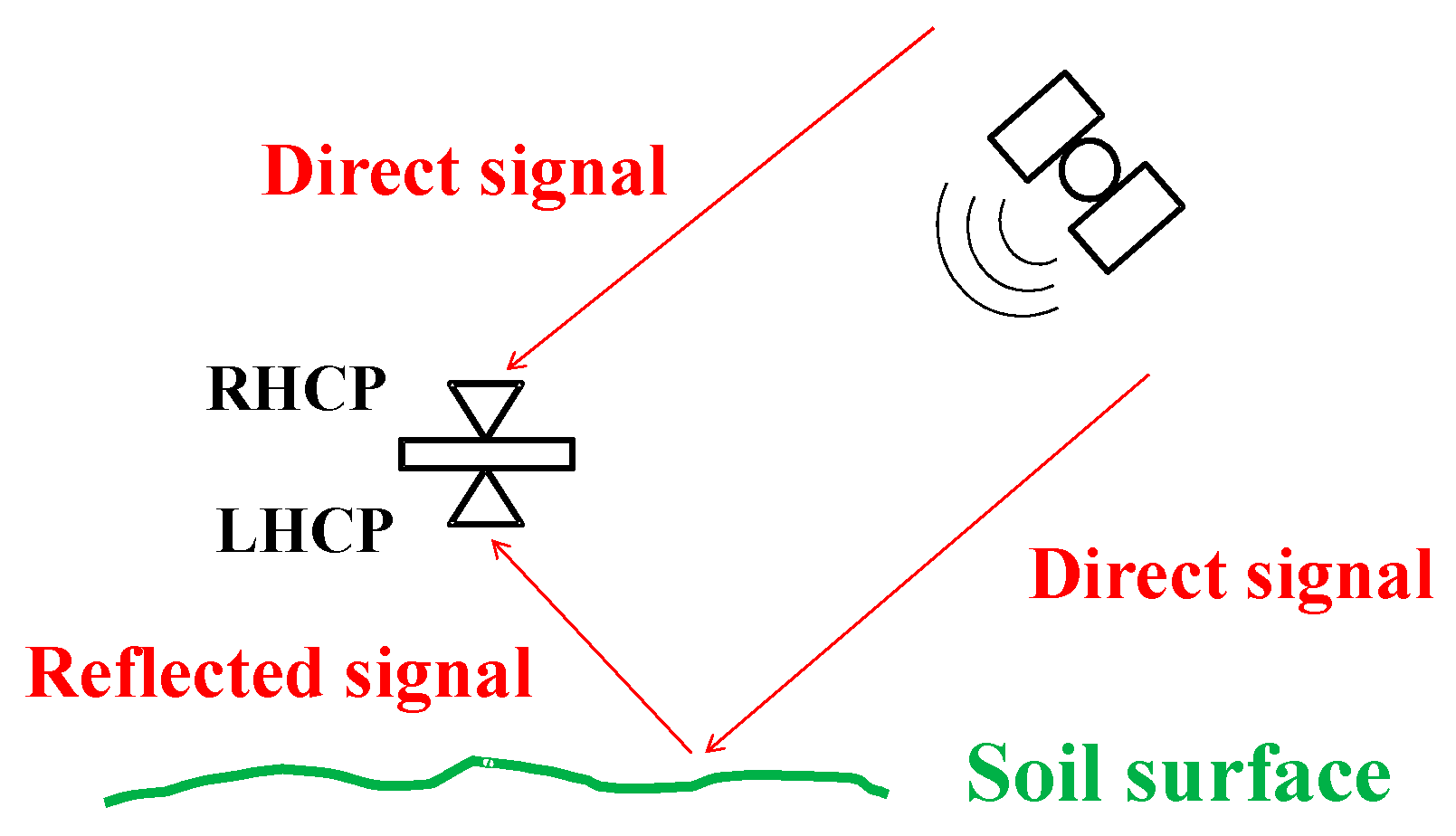
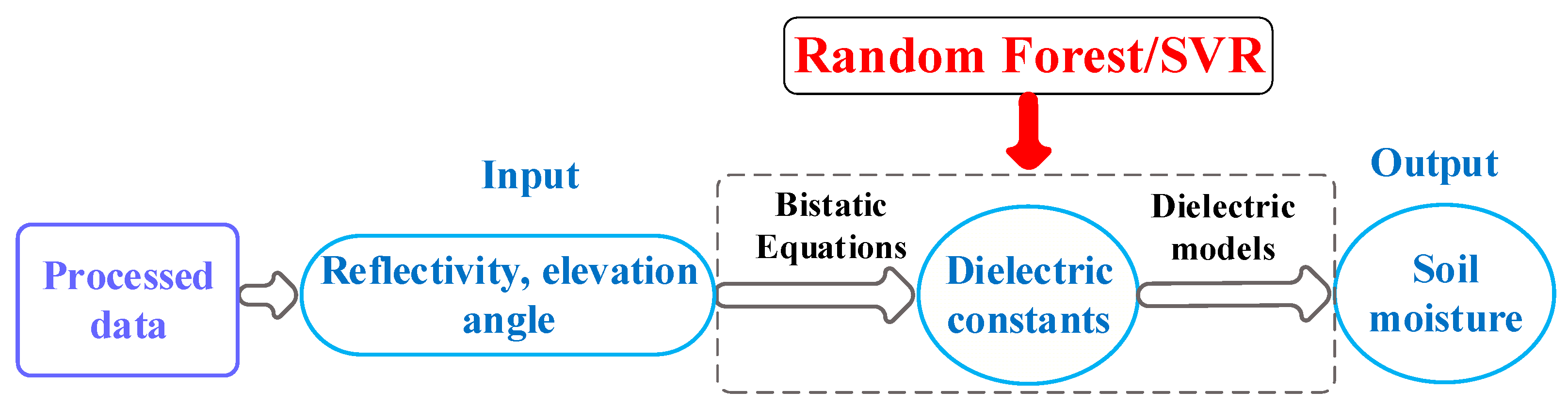
2.1. Soil Moisture Retrieval Process from Bistatic GNSS-R
2.2. Support Vector Machines
2.3. Random Forest
3. Methodology
3.1. RF and SVMs Models for GNSS-R Soil Moisture Retrieval
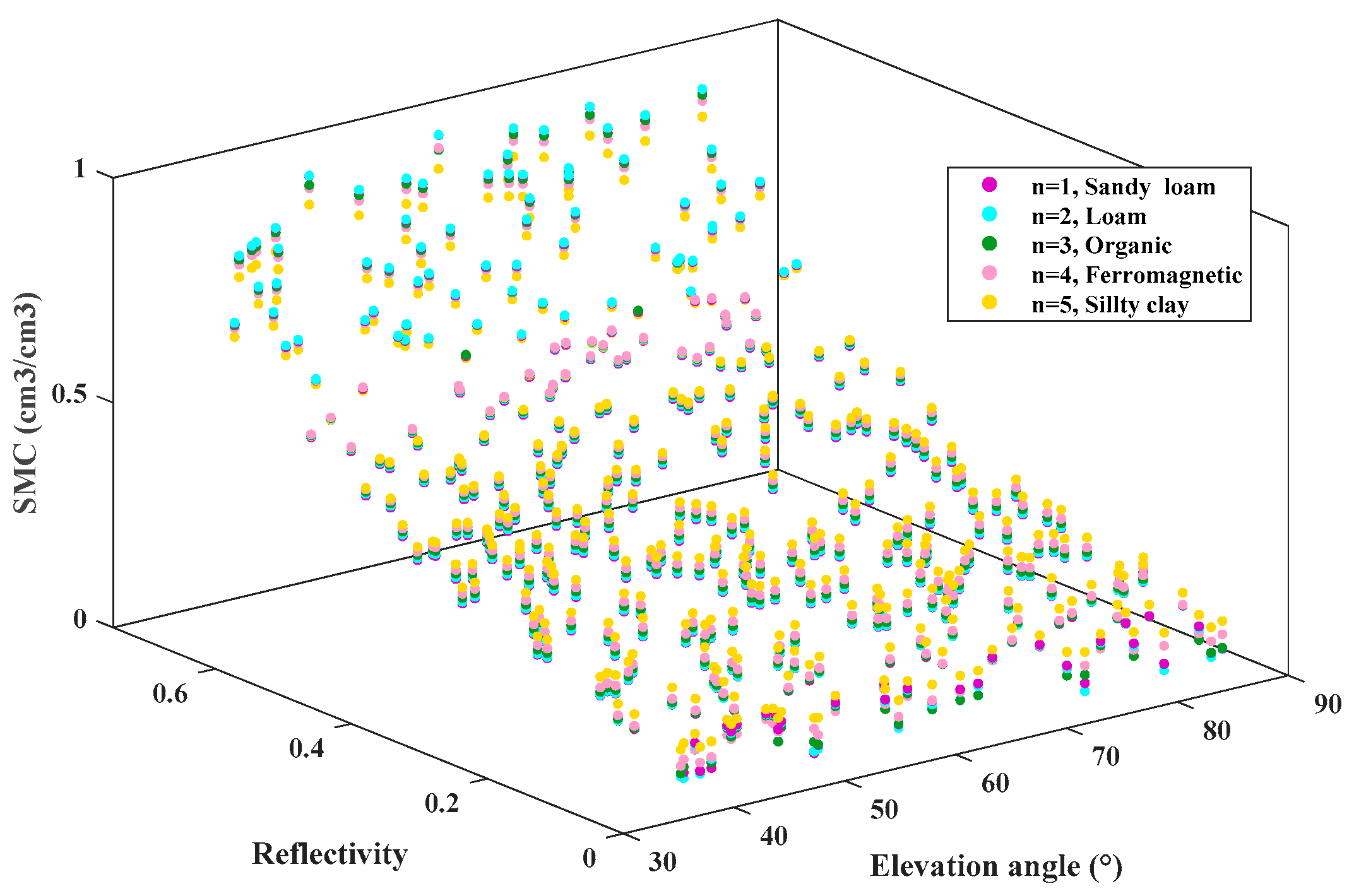
3.2. Simulated GNSS-R Dataset for Training Regression Models
- , Reflectivity (from 0–0.8)
- , Elevation angle (from 35 degrees to 85 degrees)
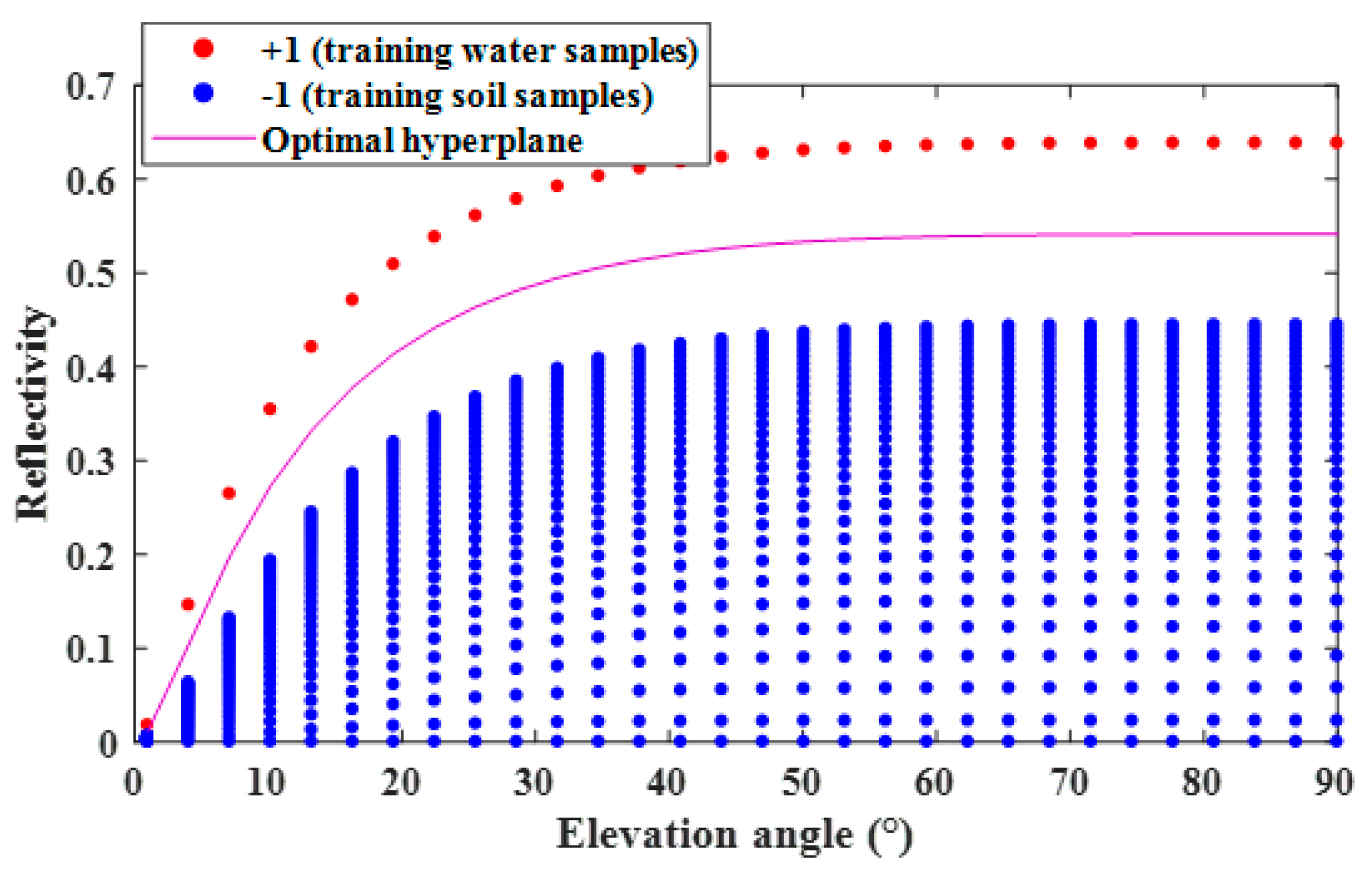
3.3. Simulated GNSS-R Dataset for Training Classification Models
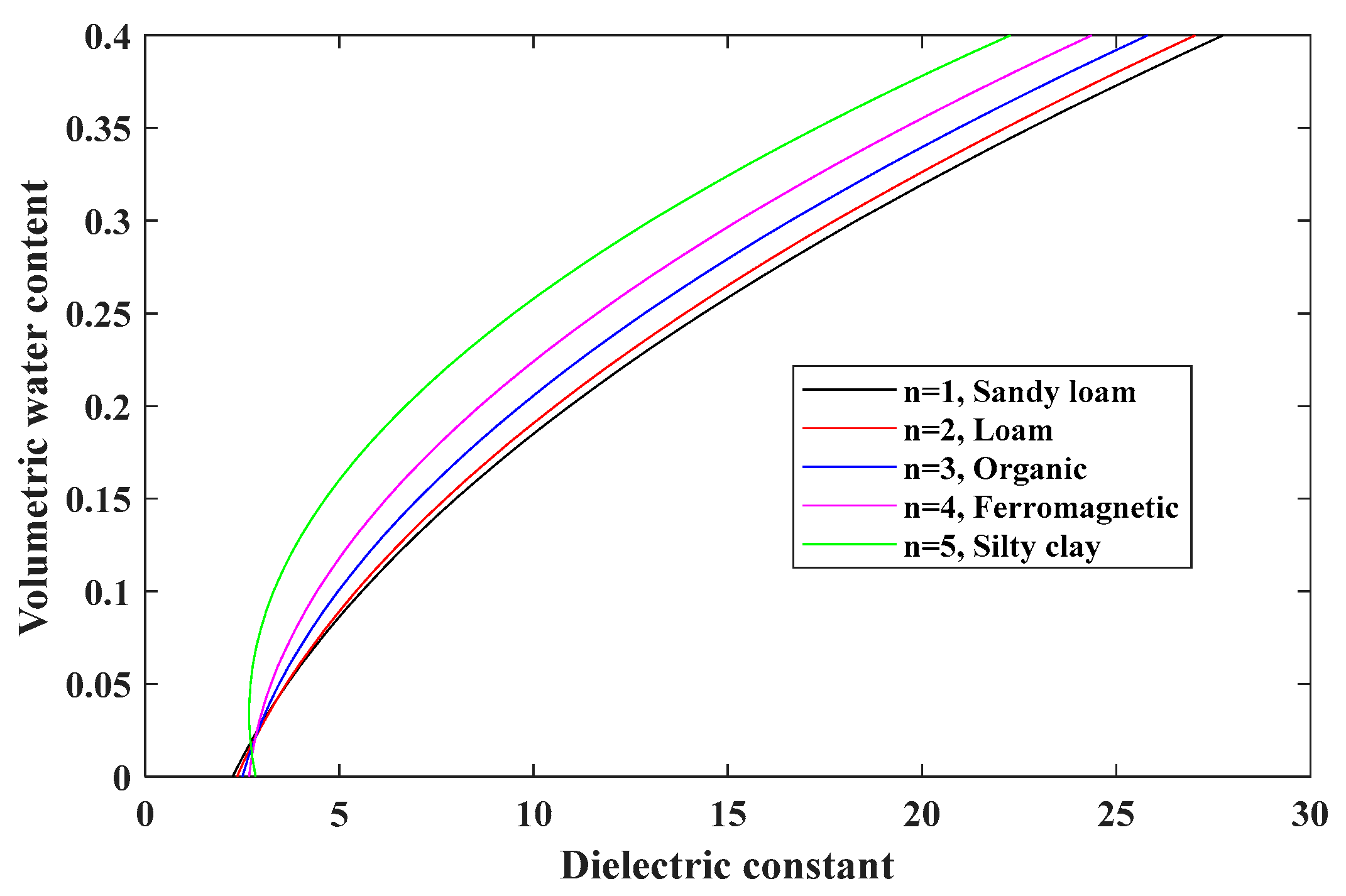
- , Dielectric constant, soils (from 1 to 25, with a step size of 1), water (78)
- , Elevation angle (from 0 degrees to 90 degrees, with a step size of 3)
4. Experiments and Data
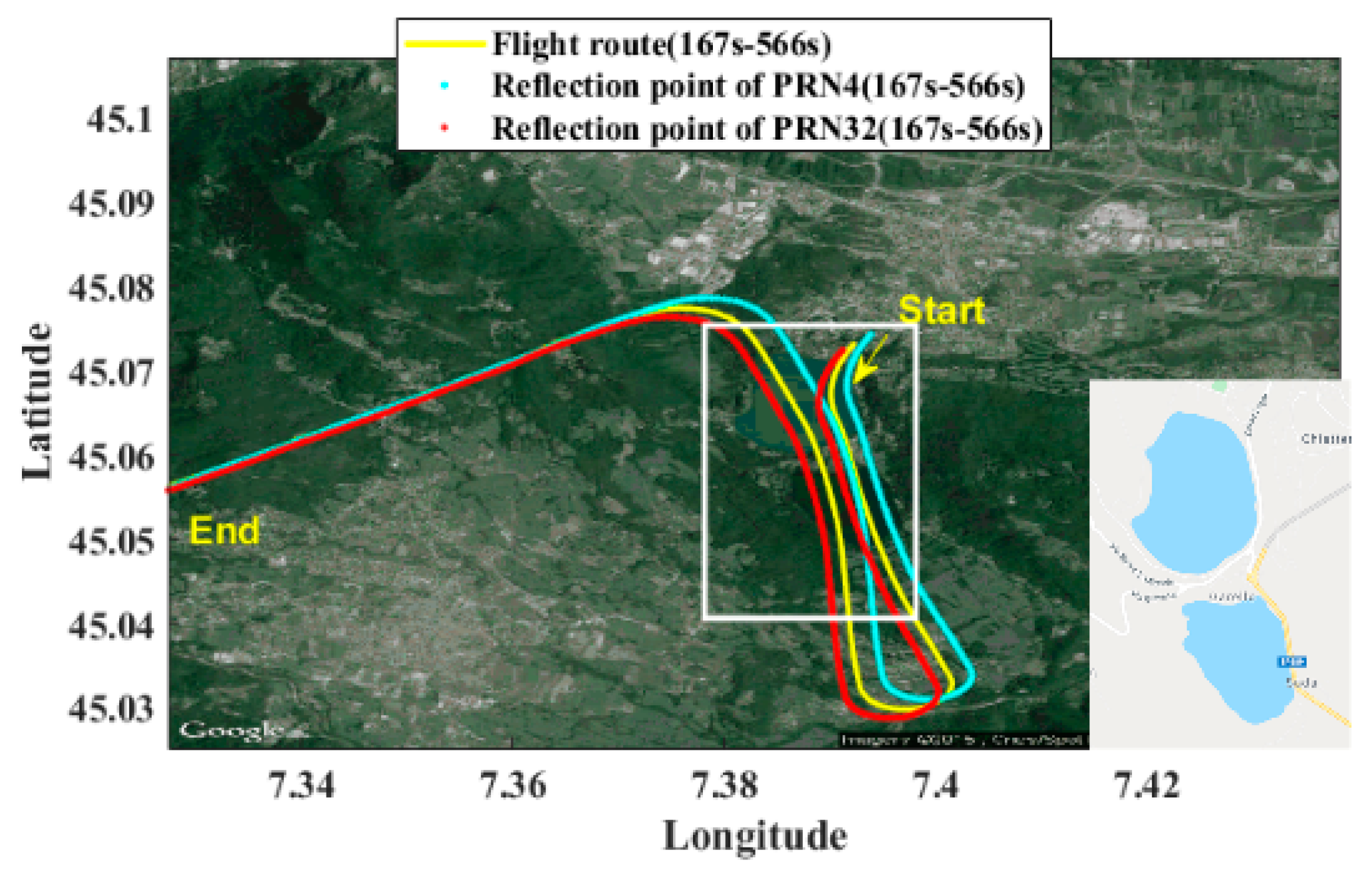
4.1. Airborne Experimental Data
4.2. In Situ Experimental Data
5. Results and Analysis
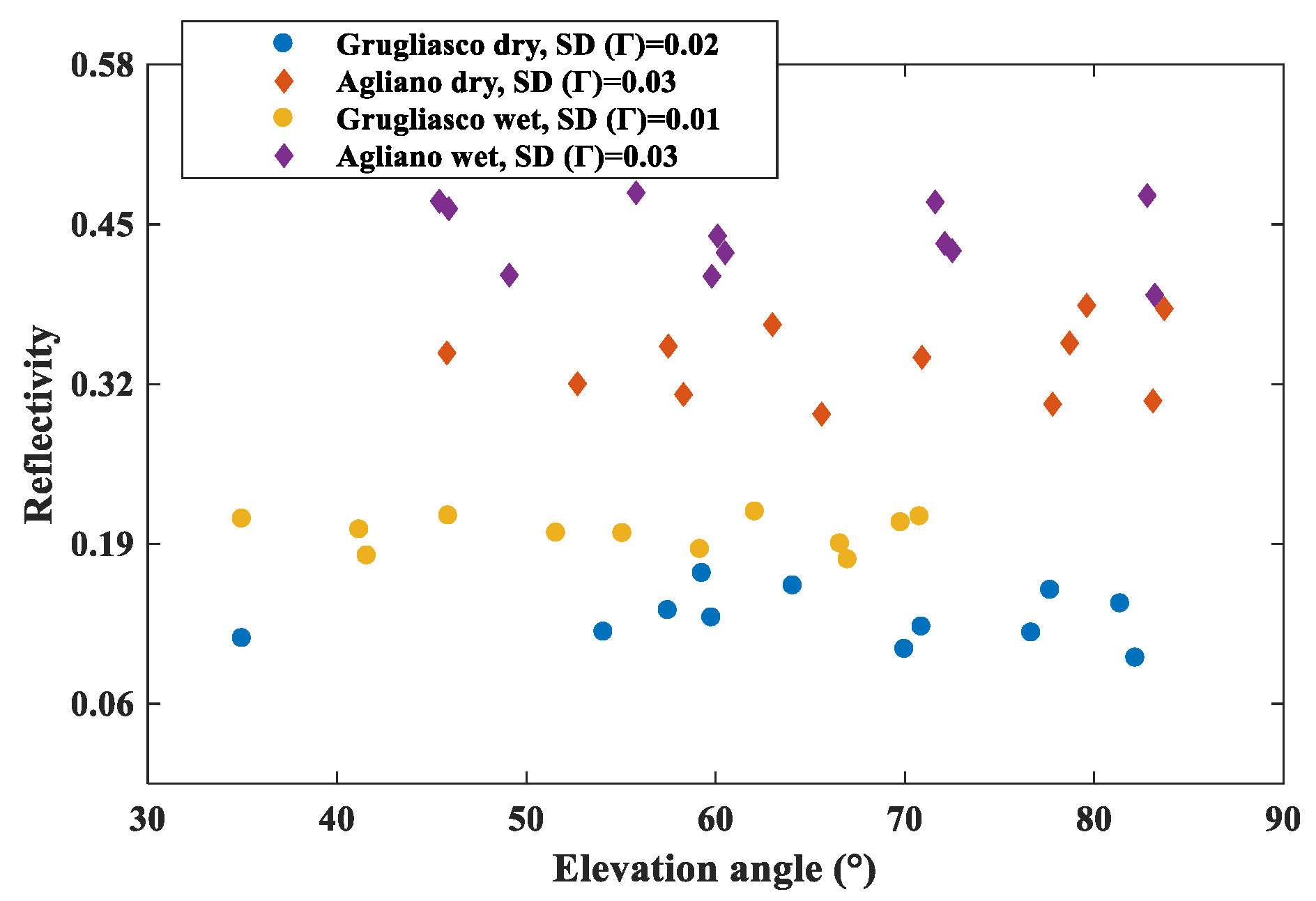
5.1. In Situ Experiments
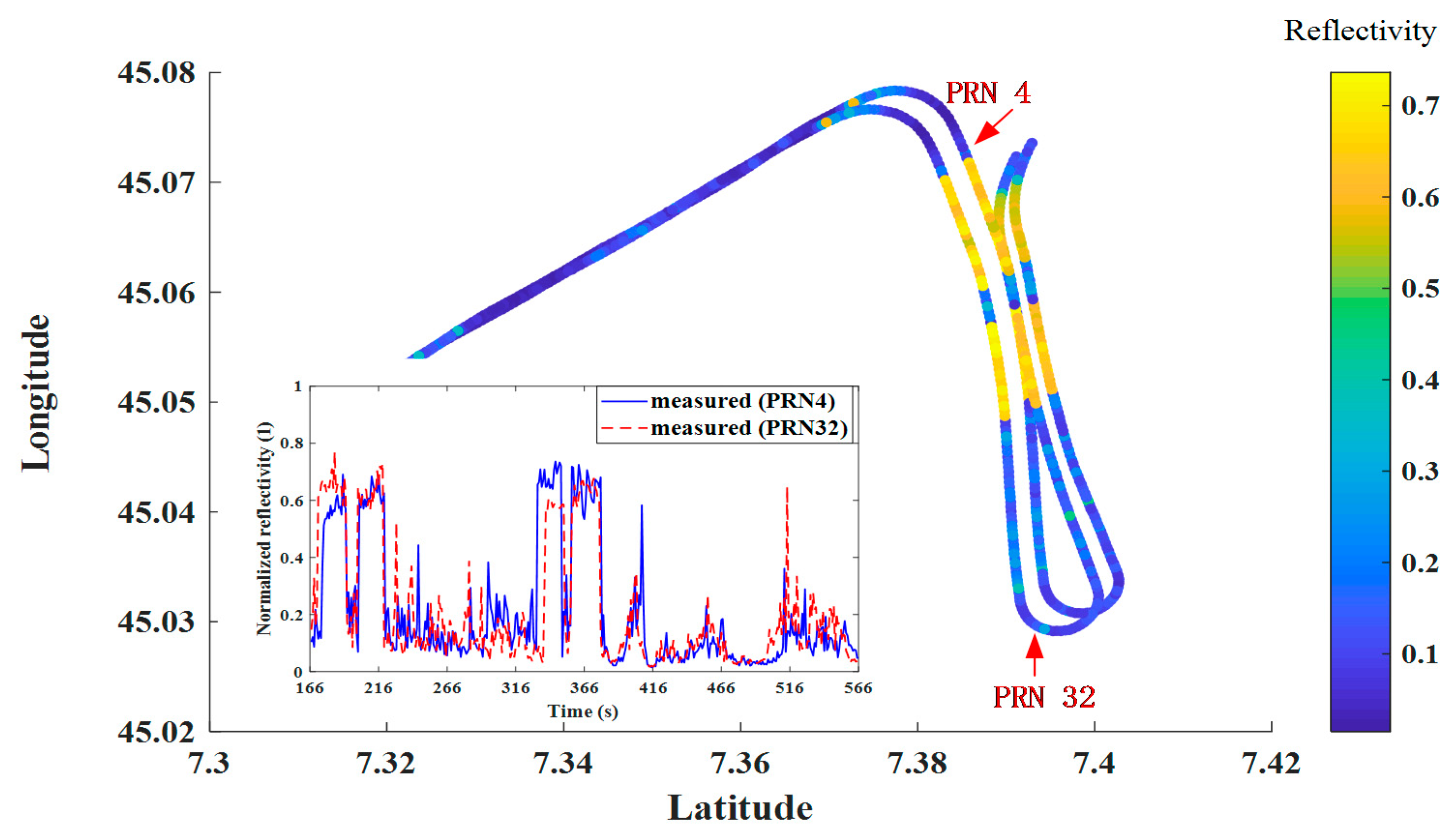
5.2. Airborne Experiments
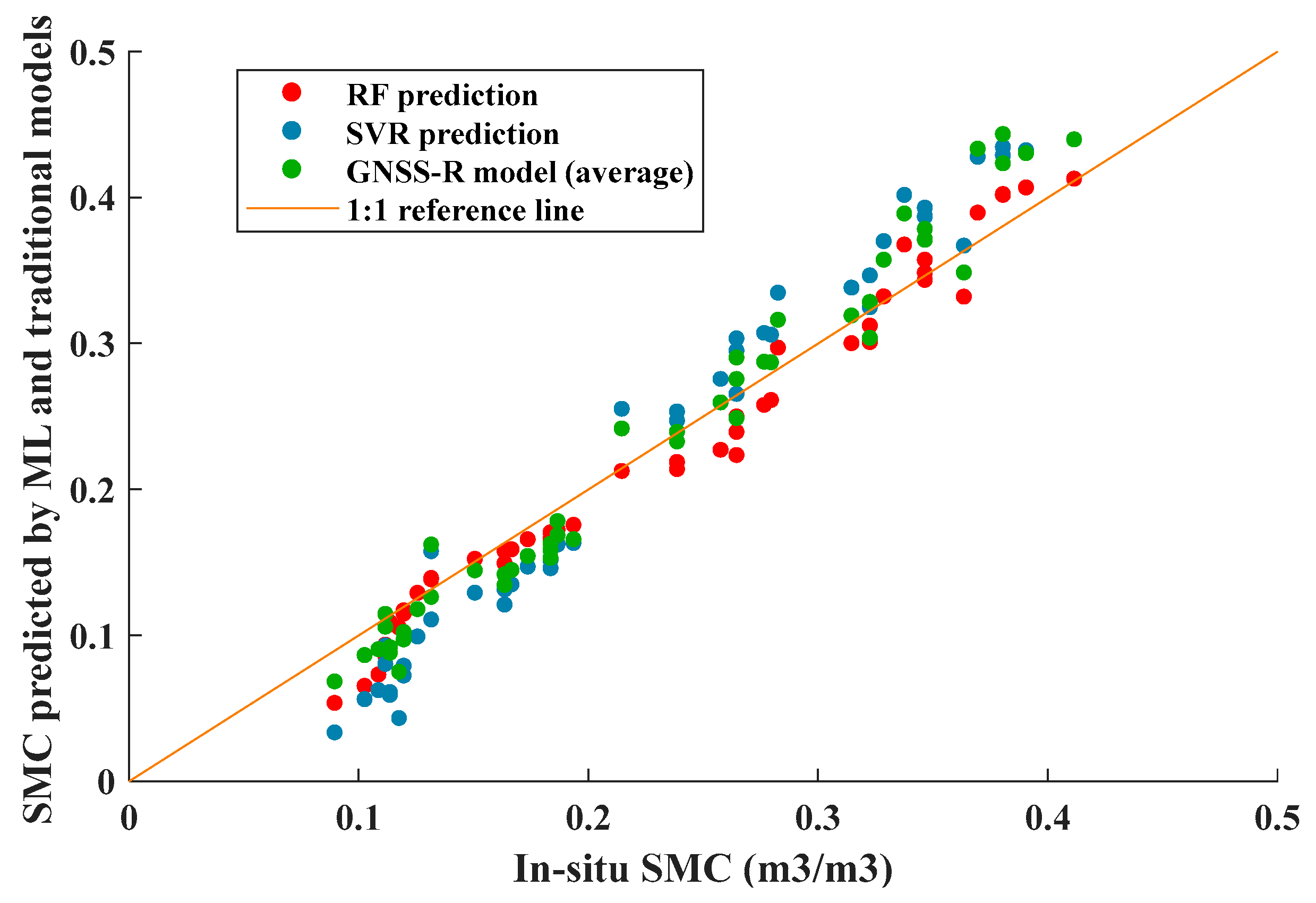
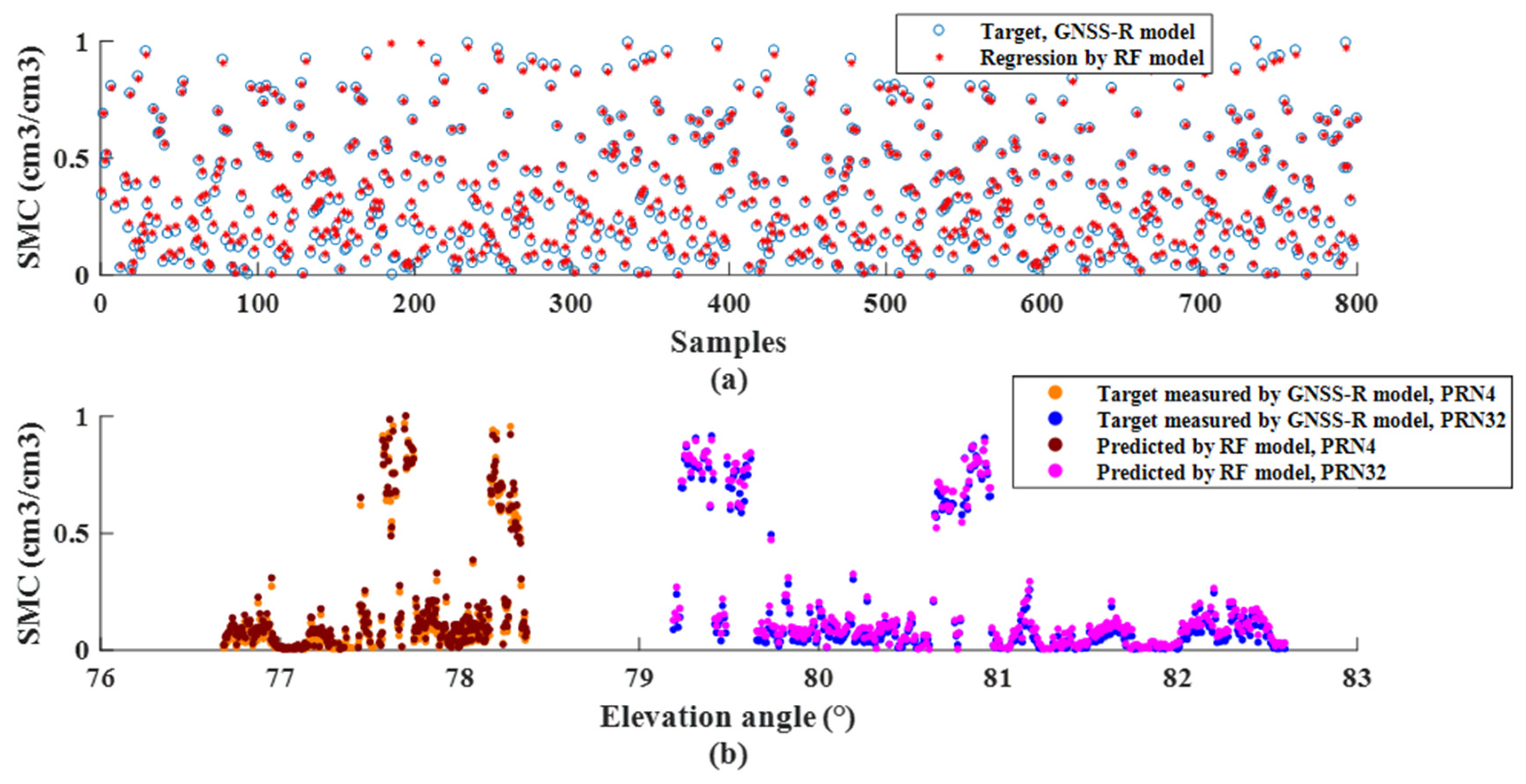
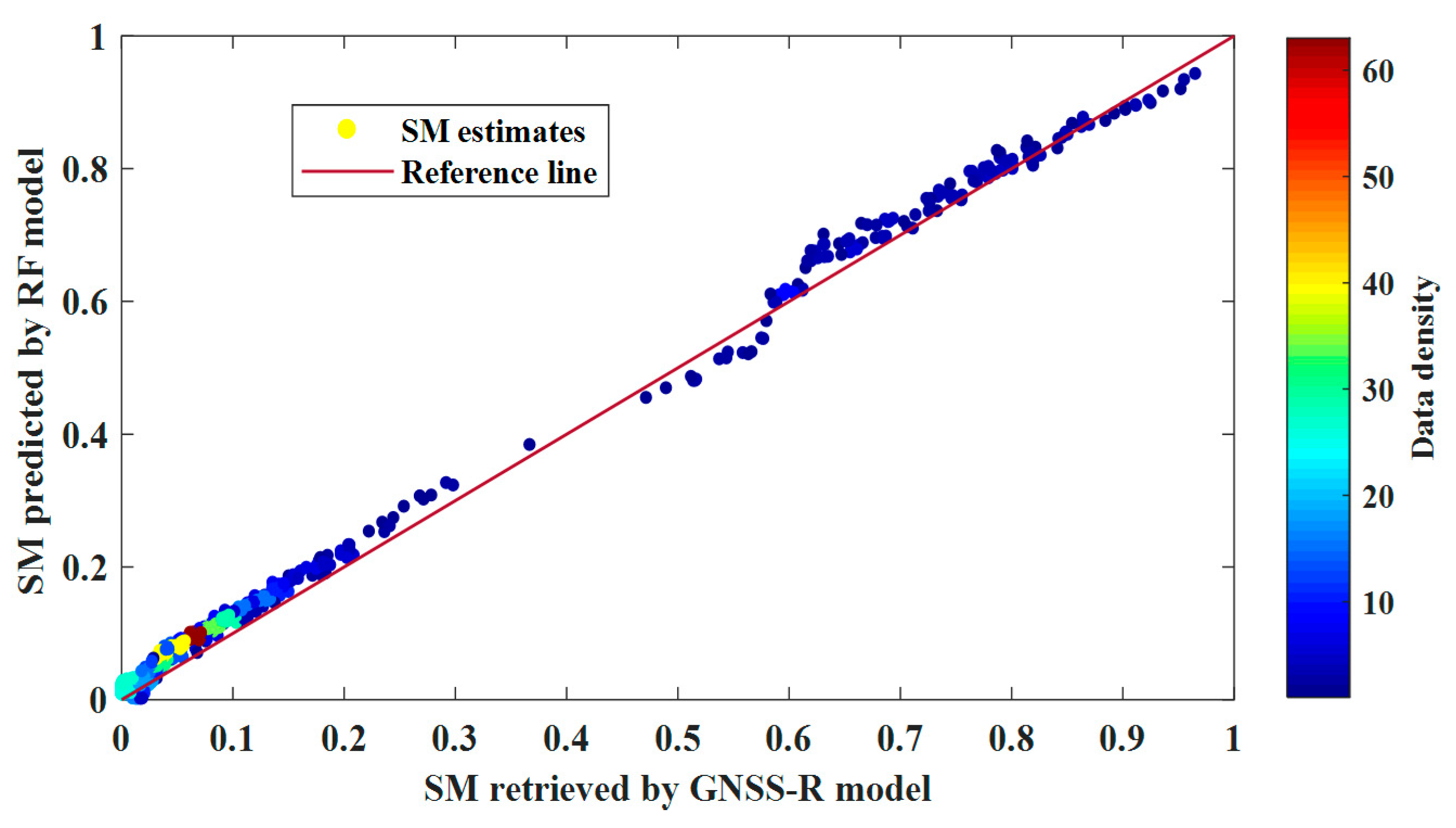
5.2.1. SMC Regression Predictions
5.2.2. Open Water Classification
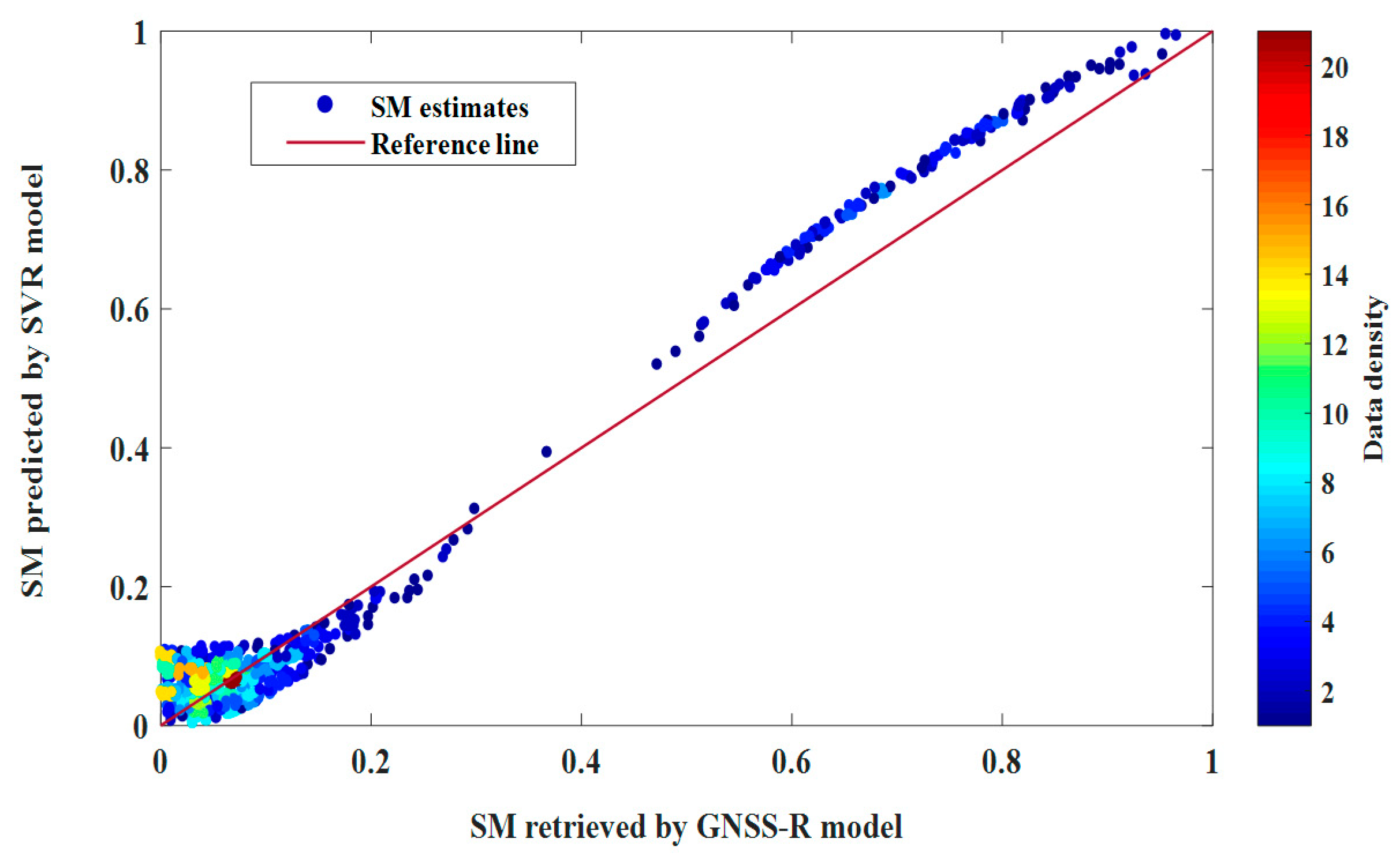
6. Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wigneron, J.P.; Calvet, J.C.; Pellarin, T.; Van De Griend, A.A.; Berger, M.; Ferrazzoli, P. Retrieving near-surface soil moisture from microwave radiometric observations: Current status and future plans. Remote Sens. Environ. 2003, 85, 489–506. [Google Scholar] [CrossRef]
- Jin, S.G.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 16. [Google Scholar] [CrossRef]
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Garrison, J.L.; Katzberg, S.J.; Hill, M.I. Effect of sea roughness on bistatically scattered range coded signals from the Global Positioning System. Geophys. Res. Lett. 1998, 25, 2257–2260. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geoence Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Lowe, S.; Kroger, P.; Franklin, G.; Labrecque, J.; Lerma, J.; Lough, M.; Marcin, M.; Muellerschoen, R.; Spitzmesser, D.; Young, L. A delay/Doppler-mapping receiver system for GPS-reflection remote sensing. IEEE Trans. Geoence Remote Sens. 2002, 40, 1150–1163. [Google Scholar] [CrossRef]
- Marchan-Hernandez, J.F.; Rodriguez-Alvarez, N.; Camps, A.; Bosch-Lluis, X.; Ramos-Perez, I.; Valencia-Domènech, E. Correction of the Sea State Impact in the L-Band Brightness Temperature by Means of Delay-Doppler Maps of Global Navigation Satellite Signals Reflected Over the Sea Surface. IEEE Trans. Geoence Remote Sens. 2008, 46, 2914–2923. [Google Scholar] [CrossRef]
- Jin, S.G.; Feng, G.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, 24–28. [Google Scholar] [CrossRef]
- Jin, S.G.; Qian, X.; Kutoglu, H. Snow Depth Variations Estimated from GPS-Reflectometry: A Case Study in Alaska from L2P SNR Data. Remote Sens. 2016, 8, 63. [Google Scholar] [CrossRef]
- Li, X.; Zheng, K.; Li, X.; Liu, G.; Ge, M.; Wickert, J.; Schuh, H. Real-time capturing of seismic waveforms using high-rate BDS, GPS and GLONASS observations: The 2017 Mw 6.5 Jiuzhaigou earthquake in China. GPS Solut. 2019, 23, 17. [Google Scholar] [CrossRef]
- Edokossi, K.; Calabia, A.; Jin, S.; Molina, I. GNSS in Reflectometry and Remote Sensing of Soil Moisture: A Review of Measurement Techniques, Methods, and Applications. Remote Sens. 2020, 12, 614. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Castellví, J.; Corbera, J.; Ascaso, E. Single-Pass Soil Moisture Retrievals Using GNSS-R: Lessons Learned. Remote Sens. 2020, 12, 2064. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsu, C.C. Extreme Gradient Boosting Model for Rain Retrieval using Radar Reflectivity from Various Elevation Angles. Remote Sens. 2020, 12, 2203. [Google Scholar] [CrossRef]
- Masters, D.; Zavorotny, V.; Katzberg, S.; Emery, W. GPS signal scattering from land for moisture content determination. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000. [Google Scholar]
- Masters, D.; Axelrad, P.; Katzberg, S. Initial results of land-reflected GPS bistatic radar measurements in SMEX02. Remote Sens. Environ. 2004, 92, 507–520. [Google Scholar] [CrossRef]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Masters, D. Utilizing calibrated GPS reflected signals to estimate soil reflectivity and dielectric constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A. A Physical Model for GPS Multipath Caused by Land Reflections: Toward Bare Soil Moisture Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 3, 100–110. [Google Scholar] [CrossRef]
- Larson, K.M.; Braun, J.J.; Small, E.E.; Zavorotny, V.U.; Gutmann, E.D.; Bilich, A. GPS Multipath and Its Relation to Near-Surface Soil Moisture Content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 91–99. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-Llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-Llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil moisture retrieval using GNSS-R techniques: Experimental results over a bare soil field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Egido, A.; Caparrini, M.; Ruffini, G.; Paloscia, S.; Santi, E.; Guerriero, L.; Pierdicca, N.; Floury, N. Global Navigation Satellite Systems Reflectometry as a Remote Sensing Tool for Agriculture. Remote Sens. 2012, 4, 2356–2372. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Amèzaga, A.; Vidal, D.; Olivé, R.; Munoz, J.F.; Camps, A. First polarimetric GNSS-R measurements from a stratospheric flight over boreal forests. Remote Sens. 2015, 7, 13120–13138. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Braun, J.J. Sensing vegetation growth with reflected GPS signals. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Ramos-Perez, I.; Valencia, E.; Park, H.; Vall-Llossera, M. Vegetation water content estimation using GNSS measurements. IEEE Geosci. Remote Sens. Lett. 2011, 9, 282–286. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L.; Pierdicca, N.; Rahmoune, R. Forest biomass monitoring with GNSS-R: Theoretical simulations. Adv. Space Res. 2011, 47, 1823–1832. [Google Scholar] [CrossRef]
- Gleason, S. Detecting bistatically reflected GPS signals from low earth orbit over land surfaces. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3086–3089. [Google Scholar]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Portal, G.; Rossato, L. Sensitivity of TDS-1 GNSS-R reflectivity to soil moisture: Global and regional differences and impact of different spatial scales. Remote Sens. 2018, 10, 1856. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Sensitivity of CyGNSS bistatic reflectivity and SMAP microwave radiometry brightness temperature to geophysical parameters over land surfaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 107–122. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CYGNSS wind speed retrieval uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 87–97. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil moisture sensing using spaceborne GNSS reflections: Comparison of CYGNSS reflectivity to SMAP soil moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-series retrieval of soil moisture using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Calabia, A.; Molina, I.; Jin, S. Soil Moisture Content from GNSS Reflectometry Using Dielectric Permittivity from Fresnel Reflection Coefficients. Remote Sens. 2020, 12, 122. [Google Scholar] [CrossRef]
- Wu, X.; Dong, Z.; Jin, S.; He, Y.; Song, Y.; Ma, W.; Yang, L. First Measurement of Soil Freeze/Thaw Cycles in the Tibetan Plateau Using CYGNSS GNSS-R Data. Remote Sens. 2020, 12, 2361. [Google Scholar] [CrossRef]
- Zribi, M.; Motte, E.; Baghdadi, N.; Baup, F.; Dayau, S.; Fanise, P.; Guyon, D.; Huc, M.; Wigneron, J.P. Potential Applications of GNSS-R Observations over Agricultural Areas: Results from the GLORI Airborne Campaign. Remote Sens. 2018, 10, 1245. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, Q.; Shen, H.; Liu, T.; Li, T.; Yue, L.; Shi, X.; Zhang, L. Estimating snow depth by combining satellite data and ground-based observations over Alaska: A deep learning approach. J. Hydrol. 2020, 585, 124828. [Google Scholar] [CrossRef]
- Jia, Y.; Jin, S.; Savi, P.; Gao, Y.; Tang, J.; Chen, Y.; Li, W. GNSS-R soil moisture retrieval based on a XGboost machine learning aided method: Performance and validation. Remote Sens. 2019, 11, 1655. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Ashourloo, D.; Aghighi, H.; Matkan, A.A.; Mobasheri, M.R.; Rad, A.M. An investigation into machine learning regression techniques for the leaf rust disease detection using hyperspectral measurement. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4344–4351. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Detecting sea ice from TechDemoSat-1 data using support vector machines with feature selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1409–1416. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Liu, J.; Hyyppä, J.; Yu, X.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Zhu, L.; Liang, X.; Wang, Y.; Hyyppä, H. A novel GNSS technique for predicting boreal forest attributes at low cost. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4855–4867. [Google Scholar] [CrossRef]
- Min, M.; Bai, C.; Guo, J.; Sun, F.; Liu, C.; Wang, F.; Xu, H.; Tang, S.; Li, B.; Di, D.; et al. Estimating summertime precipitation from Himawari-8 and global forecast system based on machine learning. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2557–2570. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, S.; Yue, L.; Li, T.; Shen, H.; Zhang, L. Monitoring the Variation of Vegetation Water Content with Machine Learning Methods: Point–Surface Fusion of MODIS Products and GNSS-IR Observations. Remote Sens. 2019, 11, 1440. [Google Scholar] [CrossRef]
- Tan, K.; Ma, W.; Wu, F.; Du, Q. Random forest–based estimation of heavy metal concentration in agricultural soils with hyperspectral sensor data. Environ. Monit. Assess. 2019, 191, 446. [Google Scholar] [CrossRef]
- Wang, J.R.; Schmugge, T.J. An empirical model for the complex dielectric permittivity of soils as a function of water content. IEEE Trans. Geosci. Remote Sens. 1980, 288–295. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House: Norwood, MA, USA, 1987. [Google Scholar]
- Stutzman, W.L. Polarization in Electromagnetic Systems; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Behari, J. Microwave Dielectric Behaviour of Wet Soils; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hong, S.; Shin, I. A physically-based inversion algorithm for retrieving soil moisture in passive microwave remote sensing. J. Hydrol. 2011, 405, 24–30. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.K. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, 25–34. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Moser, G.; Serpico, S.B. Automatic parameter optimization for support vector regression for land and sea surface temperature estimation from remote sensing data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 909–921. [Google Scholar] [CrossRef]
- Okujeni, A.; Van der Linden, S.; Jakimow, B.; Rabe, A.; Verrelst, J.; Hostert, P. A comparison of advanced regression algorithms for quantifying urban land cover. Remote Sens. 2014, 6, 6324–6346. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. Training v-support vector regression: Theory and algorithms. Neural Comput. 2002, 14, 1959–1977. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pei, Y.; Notarpietro, R.; De Mattia, S.; Savi, P.; Dovis, F.; Pini, M. Remote sensing of soil based on a compact and fully software GNSS-R receiver. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS + 2013), Nashville, TN, USA, 16–20 September 2013; pp. 56–61. [Google Scholar]
- Pei, Y.; Notarpietro, R.; Savi, P.; Cucca, M.; Dovis, F. A fully software Global Navigation Satellite System reflectometry (GNSS-R) receiver for soil monitoring. Int. J. Remote Sens. 2014, 35, 2378–2391. [Google Scholar] [CrossRef]
- Ulaby, F.T. Microwave Remote Sensing Active and Passive-Volume III: From Theory to Applications; Artech House: London, UK, 1986. [Google Scholar]
- Jia, Y.; Savi, P. Sensing soil moisture and vegetation using GNSS-R polarimetric measurement. Adv. Space Res. 2017, 59, 858–869. [Google Scholar] [CrossRef]
- Istituto SuperioreMario Boella (ISMB), Torino, Italy. Available online: http://www.ismb.it/ (accessed on 9 November 2020).
- Falletti, E.; Margaria, D.; Nicola, M.; Povero, G.; Gamba, M.T. N-FUELS and SOPRANO: Educational tools for simulation, analysis and processing of satellite navigation signals. In Proceedings of the 2013 IEEE Frontiers in Education Conference (FIE), Oklahoma City, OK, USA, 23–26 October 2013; pp. 303–308. [Google Scholar]
- Savi, P.; Maio, I.A.; Ferraris, S. The role of probe attenuation in the time-domain reflectometry characterization of dielectrics. Electromagnetics 2010, 30, 554–564. [Google Scholar] [CrossRef]


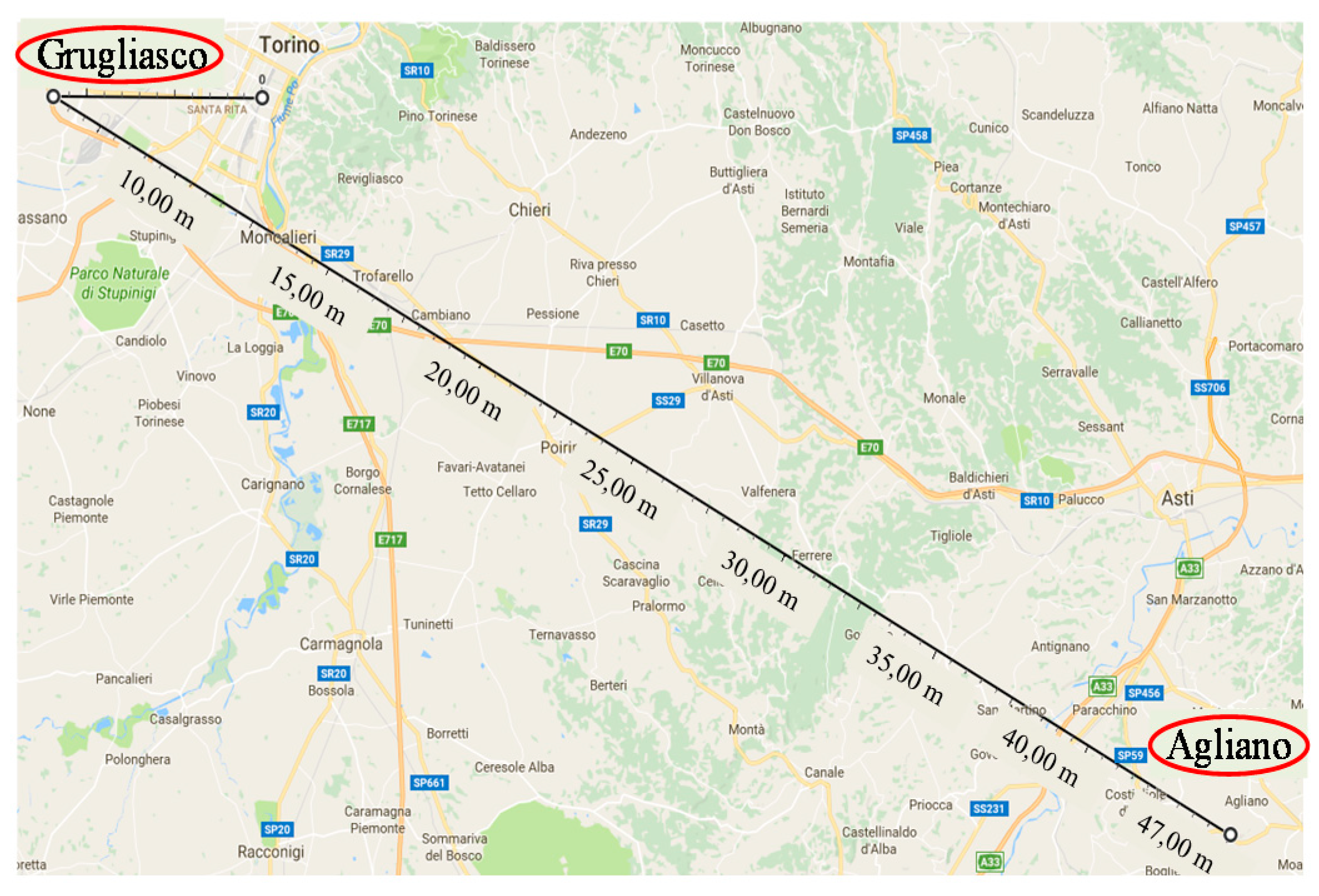




| Date | Soil Condition | Location | |
|---|---|---|---|
| Before rain | 27 January 2016 | dry | Grugliasco |
| 4 February 2016 | dry | Agliano | |
| After rain | 3 March 2016 | wet | Grugliasco |
| 7 March 2016 | wet | Agliano |
| SMC (m3/m3) | Dry, Grugliasco | Dry, Agliano | Wet, Grugliasco | Wet, Agliano | ||||
|---|---|---|---|---|---|---|---|---|
| Ground-Truth | 0.11 | 0.28 | 0.16 | 0.36 | ||||
| mean | rmse | mean | rmse | mean | rmse | mean | rmse | |
| RF model | 0.10 | 0.02 | 0.27 | 0.03 | 0.16 | 0.02 | 0.39 | 0.05 |
| SVR model | 0.07 | 0.05 | 0.32 | 0.06 | 0.16 | 0.03 | 0.45 | 0.10 |
| GNSS-R (n = 1) | 0.08 | 0.04 | 0.25 | 0.04 | 0.13 | 0.03 | 0.37 | 0.04 |
| GNSS-R (n = 2) | 0.08 | 0.04 | 0.26 | 0.04 | 0.13 | 0.03 | 0.38 | 0.04 |
| GNSS-R (n = 3) | 0.09 | 0.03 | 0.27 | 0.03 | 0.15 | 0.02 | 0.39 | 0.05 |
| GNSS-R (n = 4) | 0.10 | 0.02 | 0.29 | 0.03 | 0.16 | 0.01 | 0.40 | 0.06 |
| GNSS-R (n = 5) | 0.14 | 0.03 | 0.31 | 0.04 | 0.20 | 0.04 | 0.42 | 0.07 |
| Average (GNSS-R) | 0.10 | 0.02 | 0.27 | 0.03 | 0.15 | 0.01 | 0.39 | 0.05 |
| In-Situ Meas. | RMSE (m3/m3) | CC |
|---|---|---|
| RF | 0.02 | 0.92 |
| SVR | 0.04 | 0.82 |
| GNSS-R (average) | 0.03 | 0.80 |
| PRN Number | Azimuth (°) | Elevation Angle (°) |
|---|---|---|
| 4 | 49 | 76.6 |
| 32 | 222 | 80.1 |
| PRN32 and 4 | RMSE (cm3/cm3) | CC |
|---|---|---|
| RF | 0.02 | 0.99 |
| SVR | 0.08 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Jin, S.; Savi, P.; Yan, Q.; Li, W. Modeling and Theoretical Analysis of GNSS-R Soil Moisture Retrieval Based on the Random Forest and Support Vector Machine Learning Approach. Remote Sens. 2020, 12, 3679. https://doi.org/10.3390/rs12223679
Jia Y, Jin S, Savi P, Yan Q, Li W. Modeling and Theoretical Analysis of GNSS-R Soil Moisture Retrieval Based on the Random Forest and Support Vector Machine Learning Approach. Remote Sensing. 2020; 12(22):3679. https://doi.org/10.3390/rs12223679
Chicago/Turabian StyleJia, Yan, Shuanggen Jin, Patrizia Savi, Qingyun Yan, and Wenmei Li. 2020. "Modeling and Theoretical Analysis of GNSS-R Soil Moisture Retrieval Based on the Random Forest and Support Vector Machine Learning Approach" Remote Sensing 12, no. 22: 3679. https://doi.org/10.3390/rs12223679
APA StyleJia, Y., Jin, S., Savi, P., Yan, Q., & Li, W. (2020). Modeling and Theoretical Analysis of GNSS-R Soil Moisture Retrieval Based on the Random Forest and Support Vector Machine Learning Approach. Remote Sensing, 12(22), 3679. https://doi.org/10.3390/rs12223679