Aboveground Biomass Changes in Tropical Montane Forest of Northern Borneo Estimated Using Spaceborne and Airborne Digital Elevation Data
Abstract
1. Introduction
2. Materials and Methods
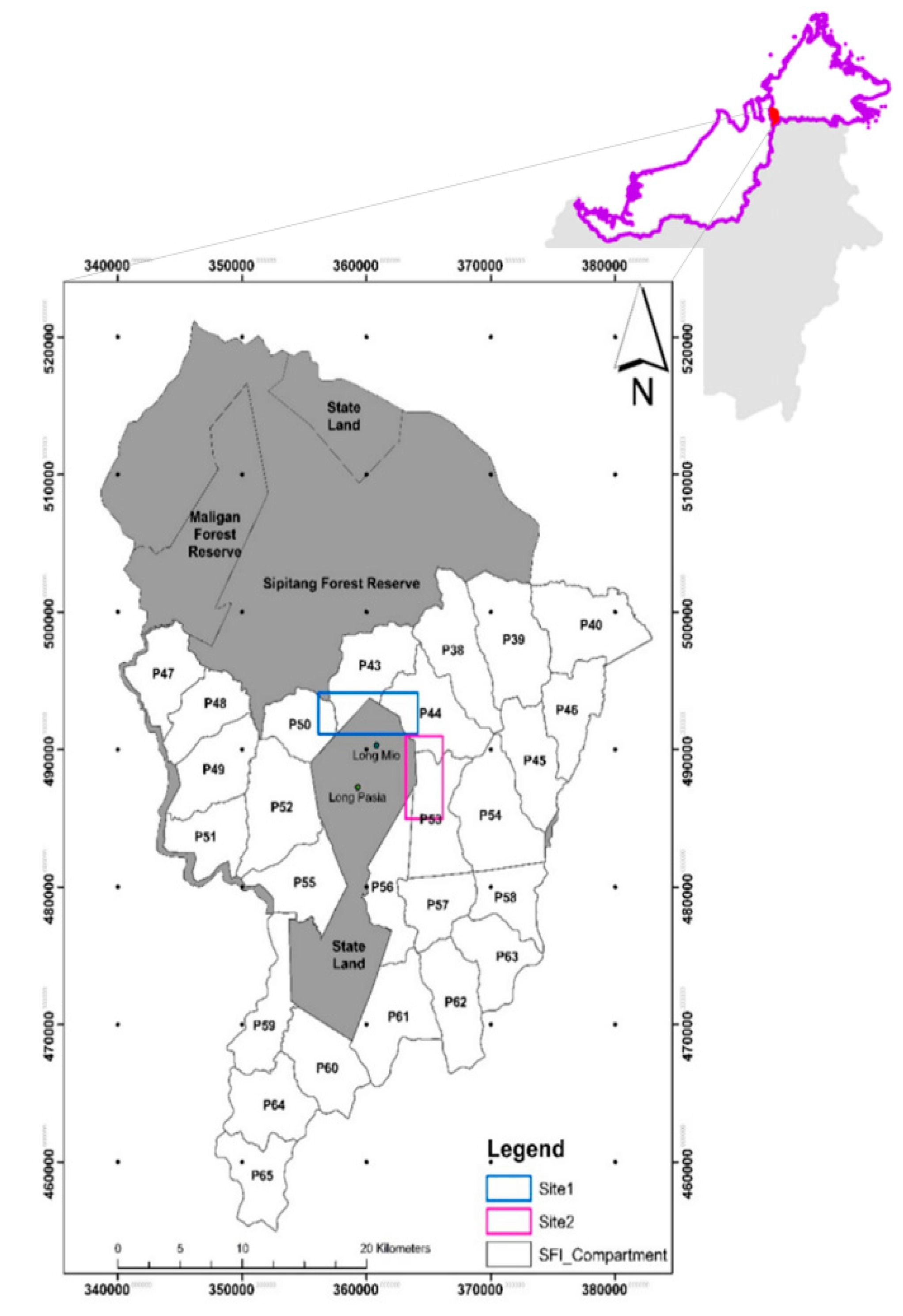
2.1. Study Area
2.2. Field Measurement
2.3. SRTM Data
2.4. LiDAR Data
2.5. Remotely Sensed Digital Elevation Data Processing
2.6. AGB Estimation Models
3. Results
3.1. Field Measurements
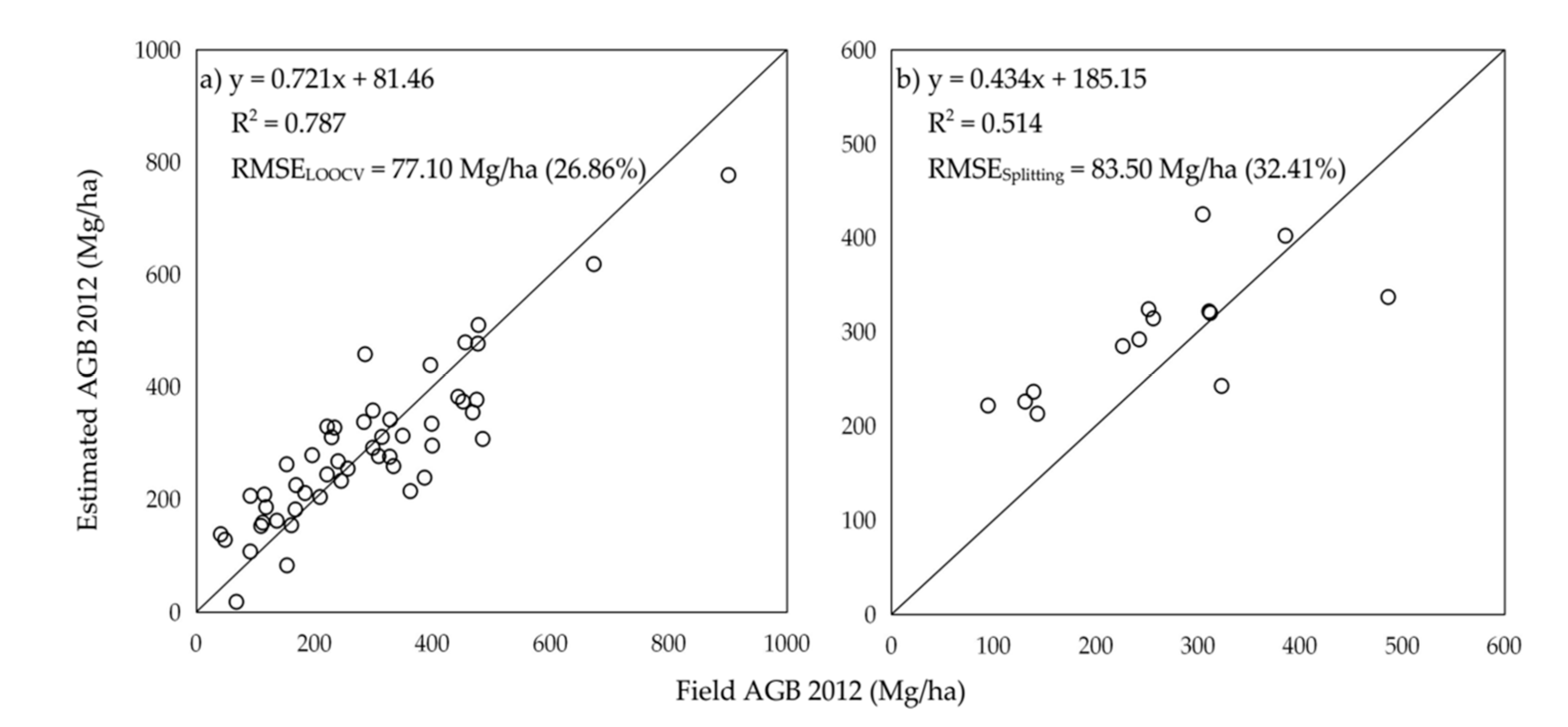
3.2. AGB Estimation
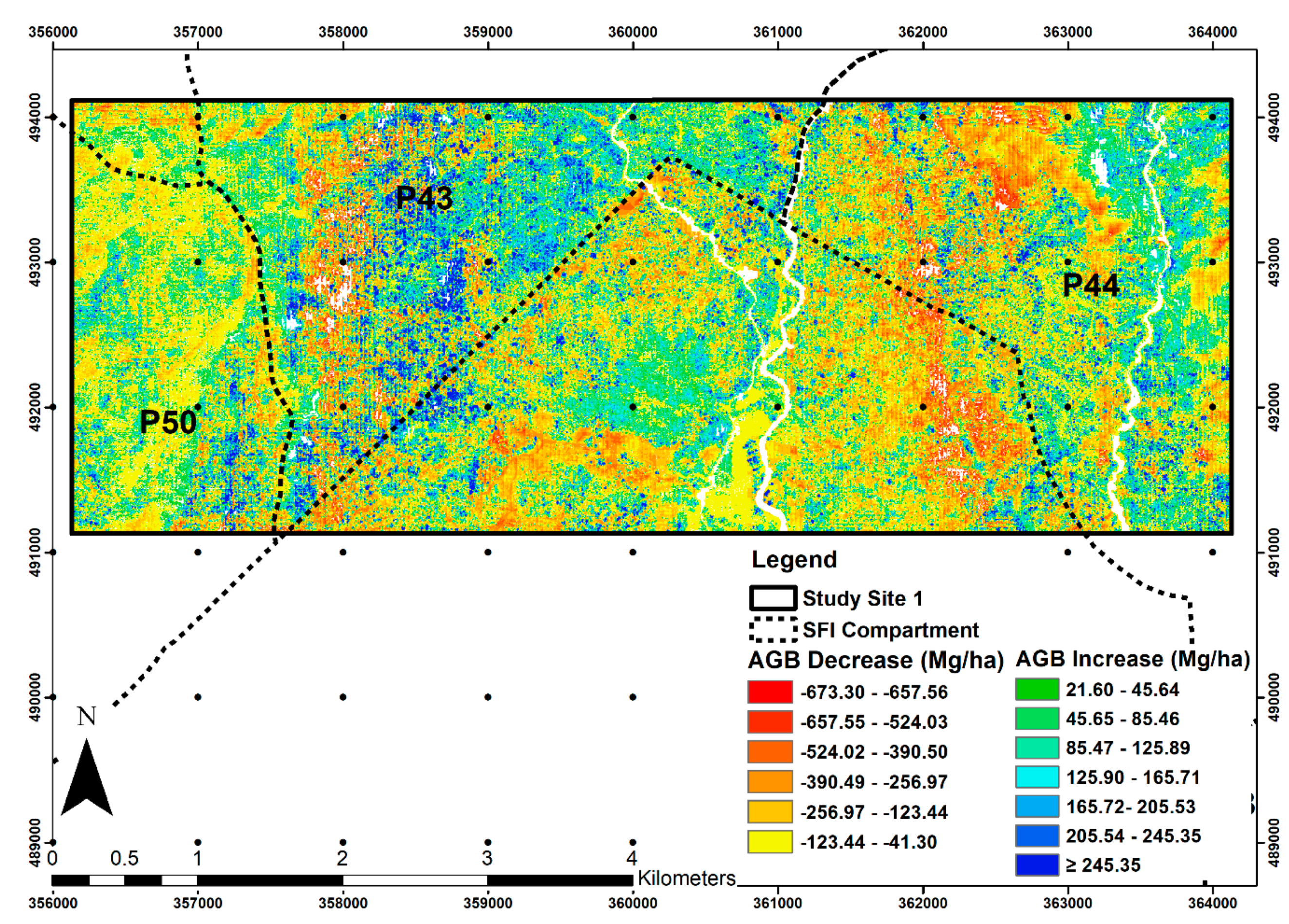
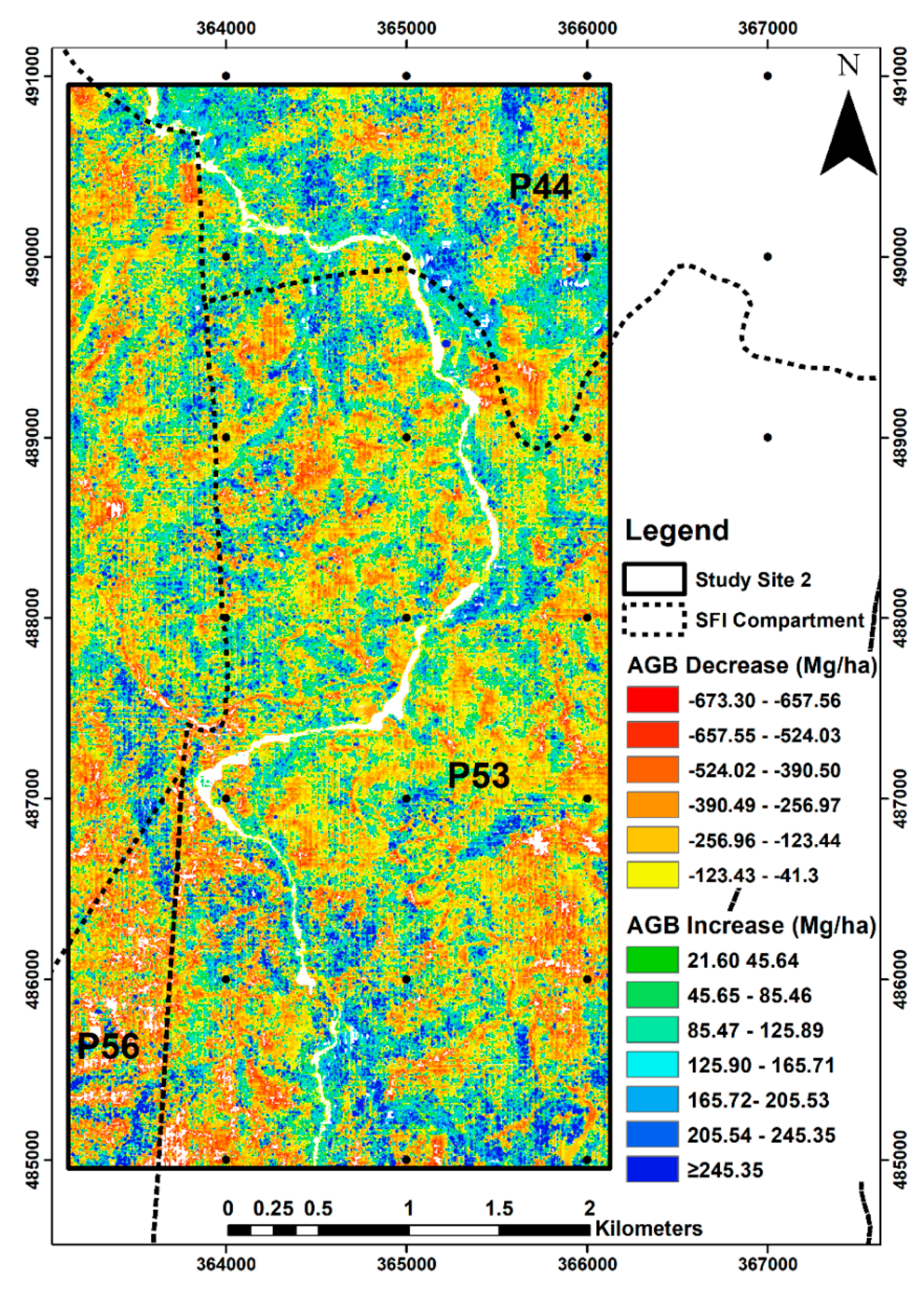
3.3. Above-Ground Biomass Changes
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Le Quéré, C.; Raupach, M.R.; Canadell, J.G.; Marland, G.; Bopp, L.; Ciais, P.; Conway, T.J.; Doney, S.C.; Feely, R.A.; Foster, P.; et al. Trends in the sources and sinks of carbon dioxide. Nat. Geosci. 2009, 2, 831–836. [Google Scholar] [CrossRef]
- Eggleston, S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. (Eds.) 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Hayama, Japan, 2006; Volume 5. [Google Scholar]
- Langner, A.; Samejima, H.; Ong, R.C.; Titin, J.; Kitayama, K. Integration of carbon conservation into sustainable forest management using high resolution satellite imagery: A case study in Sabah, Malaysian Borneo. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 305–312. [Google Scholar] [CrossRef]
- Gaveau, D.L.A.; Salim, M.A.; Hergoualc’H, K.; Locatelli, B.; Sloan, S.; Wooster, M.; Marlier, M.E.; Molidena, E.; Yaen, H.; DeFries, R.; et al. Major atmospheric emissions from peat fires in Southeast Asia during non-drought years: Evidence from the 2013 Sumatran fires. Sci. Rep. 2014, 4, srep06112. [Google Scholar] [CrossRef] [PubMed]
- Broich, M.; Hansen, M.; Potapov, P.V.; Wimberly, M.C. Patterns of tree-cover loss along the Indonesia–Malaysia border on Borneo. Int. J. Remote Sens. 2013, 34, 5748–5760. [Google Scholar] [CrossRef]
- Maycock, C.R.; Nilus, R. Overview of the permanent vegetation plot network in Sabah. In Developing a Network of Long-Term Research Field Stations to Monitor Environmental Changes and Ecosystem Responses in Asian Forests; Kamata, N., Kuraji, K., Owari, T., Guan, B.T., Eds.; The University of Tokyo Forests Press: Tokyo, Japan, 2019; pp. 157–168. [Google Scholar]
- Stern, N. The Economics of Climate Change; Cambridge University Press: Cambridge, UK, 2007; p. 712. [Google Scholar]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm. Remote Sens. 2010, 65, 581–590. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R.; Adam, E. Intra-and-Inter Species Biomass Prediction in a Plantation Forest: Testing the Utility of High Spatial Resolution Spaceborne Multispectral RapidEye Sensor and Advanced Machine Learning Algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved forest biomass estimates using ALOS AVNIR-2 texture indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Balzter, H.; Rowland, C.S.; Saich, P. Forest canopy height and carbon estimation at Monks Wood National Nature Reserve, UK, using dual-wavelength SAR interferometry. Remote Sens. Environ. 2007, 108, 224–239. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests—The potential of combined X- and L-band SAR data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; Woodhouse, I.H.; Nangendo, G.; Ribeiro, N.S.; Williams, M.; Ryan, C.M.; Lewis, S.L.; Feldpausch, T.R.; Meir, P. Using satellite radar backscatter to predict above-ground woody biomass: A consistent relationship across four different African landscapes. Geophys. Res. Lett. 2009, 36, 36. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.; Lewis, S.L.; Feldpausch, T.R.; Woodhouse, I.; Sonke, B.; Rowland, C.S.; Meir, P. Measuring biomass changes due to woody encroachment and deforestation/degradation in a forest–savanna boundary region of central Africa using multi-temporal L-band radar backscatter. Remote Sens. Environ. 2011, 115, 2861–2873. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.V.; dos Santos, J.R.; Freitas, C.D.C.; Araujo, L.S. Tropical forest measurement by interferometric height modeling and P-band radar backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 45. [Google Scholar] [CrossRef]
- Bhang, K.J.; Schwartz, F.W.; Braun, A. Verification of the Vertical Error in C-Band SRTM DEM Using ICESat and Landsat-7, Otter Tail County, MN. IEEE Trans. Geosci. Remote Sens. 2006, 45, 36–44. [Google Scholar] [CrossRef]
- Hofton, M.; Dubayah, R.; Blair, J.B.; Rabine, D. Validation of SRTM Elevations over Vegetated and Non-vegetated Terrain Using Medium Footprint Lidar. Photogramm. Eng. Remote Sens. 2006, 72, 279–285. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q. A practical method for SRTM DEM correction over vegetated mountain areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 216–228. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Simard, M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2012, 34, 668–681. [Google Scholar] [CrossRef]
- Goïta, K.; Mouloungou, J.; Bénié, G.B. Estimation of aboveground biomass and carbon in a tropical rain forest in Gabon using remote sensing and GPS data. Geocarto Int. 2017, 34, 243–259. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.T.; Vona, J.; Clutter, M. Vegetation height estimation from Shuttle Radar Topography Mission and National Elevation Datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.-K.; Feliciano, E.; Trettin, C.C.; Simard, M. A Comparison of Mangrove Canopy Height Using Multiple Independent Measurements from Land, Air, and Space. Remote Sens. 2016, 8, 327. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. For. 2000, 98, 44–46. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; Van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2011, 168, 1147–1160. [Google Scholar] [CrossRef]
- Hayashi, M.; Saigusa, N.; Yamagata, Y.; Hirano, T. Regional forest biomass estimation using ICESat/GLAS spaceborne LiDAR over Borneo. Carbon Manag. 2015, 6, 19–33. [Google Scholar] [CrossRef]
- Keller, M.; Lefsky, M.A.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest biomass mapping from lidar and radar synergies. Remote Sens. Environ. 2011, 115, 2906–2916. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S. Hierarchical watershed segmentation of canopy height model for multi—Scale forest inventory. Proc. ISPRS Work. Group Laser Scanning 2007, XXXVI, 436–442. [Google Scholar]
- Phua, M.-H.; Hue, S.W.; Ioki, K.; Hashim, M.; Bidin, K.; Musta, B.; Suleiman, M.; Yap, S.W.; Maycock, C. Estimating Logged-Over Lowland Rainforest Aboveground Biomass in Sabah, Malaysia Using Airborne LiDAR Data. Terr. Atmos. Ocean. Sci. 2016, 27, 481. [Google Scholar] [CrossRef][Green Version]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.; Burslem, D.F.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.-H.; et al. Area-based vs tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Phua, M.-H.; Johari, S.A.; Wong, O.C.; Ioki, K.; Mahali, M.; Nilus, R.; Coomes, D.A.; Maycock, C.R.; Hashim, M. Synergistic use of Landsat 8 OLI image and airborne LiDAR data for above-ground biomass estimation in tropical lowland rainforests. For. Ecol. Manag. 2017, 406, 163–171. [Google Scholar] [CrossRef]
- Skowronski, N.S.; Clark, K.L.; Gallagher, M.; Birdsey, R.A.; Hom, J.L. Airborne laser scanner-assisted estimation of aboveground biomass change in a temperate oak–pine forest. Remote Sens. Environ. 2014, 151, 166–174. [Google Scholar] [CrossRef]
- Takagi, K.; Yone, Y.; Takahashi, H.; Sakai, R.; Hojyo, H.; Kamiura, T.; Nomura, M.; Liang, N.; Fukazawa, T.; Miya, H.; et al. Forest biomass and volume estimation using airborne LiDAR in a cool-temperate forest of northern Hokkaido, Japan. Ecol. Inform. 2015, 26, 54–60. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Indirect and direct estimation of forest biomass change using forest inventory and airborne laser scanning data. Remote Sens. Environ. 2015, 164, 36–42. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Gregoire, T.G.; Næsset, E.; Øyen, B.-H. Detection of biomass change in a Norwegian mountain forest area using small footprint airborne laser scanner data. J. Ital. Stat. Soc. 2012, 22, 113–129. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.; Martinuzzi, S.; Falkowski, M.J. Quantifying aboveground forest carbon pools and fluxes from repeat LiDAR surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- De Moura, Y.M.; Balzter, H.; Galvão, L.S.; Dalagnol, R.; Espírito-Santo, F.; Santos, E.G.; García, M.; Bispo, P.D.C.; De Oliveira, R.C.; Shimabukuro, Y.E. Carbon Dynamics in a Human-Modified Tropical Forest: A Case Study Using Multi-Temporal LiDAR Data. Remote Sens. 2020, 12, 430. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Tymen, B.; Blanc, L.; Fauset, S.; Feldpausch, T.R.; Monteagudo, A.; Phillips, O.L.; Richard, H.; Chave, J. Using repeated small-footprint LiDAR acquisitions to infer spatial and temporal variations of a high-biomass Neotropical forest. Remote Sens. Environ. 2015, 169, 93–101. [Google Scholar] [CrossRef]
- Vaz, J. An Analysis of International Law, National Legislation, Judgements, and Institutions as they Interrelate with Territories and Areas Conserved by Indigenous Peoples and Local Communities: No. 15 Malaysia; Natural Justice in Bangalore and Kalpavriksh: Delhi, India, 2012. [Google Scholar]
- Wong, W.V.C.; Tsuyuki, S.; Ioki, K.; Phua, M.H. Accuracy assessment of global topographic data (SRTM & ASTER GDEM) in comparison with lidar for tropical montane forest. In Proceedings of the 35th Asian Conference on Remote Sensing 2014, ACRS 2014: Sensing for Reintegration of Societies, Nay Pyi Taw, Myanmar, 27–31 October 2014; pp. 27–31. [Google Scholar]
- Simard, M.; Zhang, K.; Rivera-Monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castañeda-Moya, E.; Twilley, R.R.; Rodriguez, E. Mapping Height and Biomass of Mangrove Forests in Everglades National Park with SRTM Elevation Data. Photogramm. Eng. Remote Sens. 2006, 72, 299–311. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Giancristofaro, R.A.; Salmaso, L. Model Performance Analysis and Model Validation in Logistic Regression. Statistica 2007, 63, 375–396. [Google Scholar] [CrossRef]
- Vanclay, J.K.; Skovsgaard, J. Evaluating forest growth models. Ecol. Model. 1997, 98, 1–12. [Google Scholar] [CrossRef]
- Baskerville, G.L. Use of Logarithmic Regression in the Estimation of Plant Biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Jochem, A.; Hollaus, M.; Rutzinger, M.; Höfle, B.; Schadauer, K.; Maier, B. Estimation of aboveground biomass using airborne LiDAR data. In Proceedings of the 10th International Conference on LiDAR Applications for Assessing Forest Ecosystems (Silvilaser 2010), Freiburg, Germany, 14–17 September 2010; pp. 14–17. [Google Scholar]
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A comparison of lidar, radar, and field measurements of canopy height in pine and hardwood forests of southeastern North America. For. Ecol. Manag. 2009, 257, 1136–1147. [Google Scholar] [CrossRef]
- Mascaró, J.; Asner, G.P.; Muller-Landau, H.C.; Van Breugel, M.; Hall, J.; Dahlin, K. Controls over aboveground forest carbon density on Barro Colorado Island, Panama. Biogeosciences 2011, 8, 1615–1629. [Google Scholar] [CrossRef]
- Ioki, K.; Tsuyuki, S.; Hirata, Y.; Phua, M.-H.; Wong, W.V.C.; Ling, Z.-Y.; Saito, H.; Takao, G. Estimating above-ground biomass of tropical rainforest of different degradation levels in Northern Borneo using airborne LiDAR. For. Ecol. Manag. 2014, 328, 335–341. [Google Scholar] [CrossRef]
- Sabah Forestry Department. Identification of Potential Protected Areas: Ulu Padas Sabah Biodiversity Conservation Project Final Report; Sabah Forestry Department: Sandakan, Malaysia, 1998.
- Markesteijn, L.; Poorter, L. Seedling root morphology and biomass allocation of 62 tropical tree species in relation to drought- and shade-tolerance. J. Ecol. 2009, 97, 311–325. [Google Scholar] [CrossRef]
- Spracklen, D.V.; Righelato, R. Carbon storage and sequestration of re-growing montane forests in southern Ecuador. For. Ecol. Manag. 2016, 364, 139–144. [Google Scholar] [CrossRef]
- Kitayama, K.; Aiba, S.-I. Ecosystem structure and productivity of tropical rain forests along altitudinal gradients with contrasting soil phosphorus pools on Mount Kinabalu, Borneo. J. Ecol. 2002, 90, 37–51. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Voustianiouk, A. Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics. Remote Sens. Environ. 2006, 104, 409–415. [Google Scholar] [CrossRef]
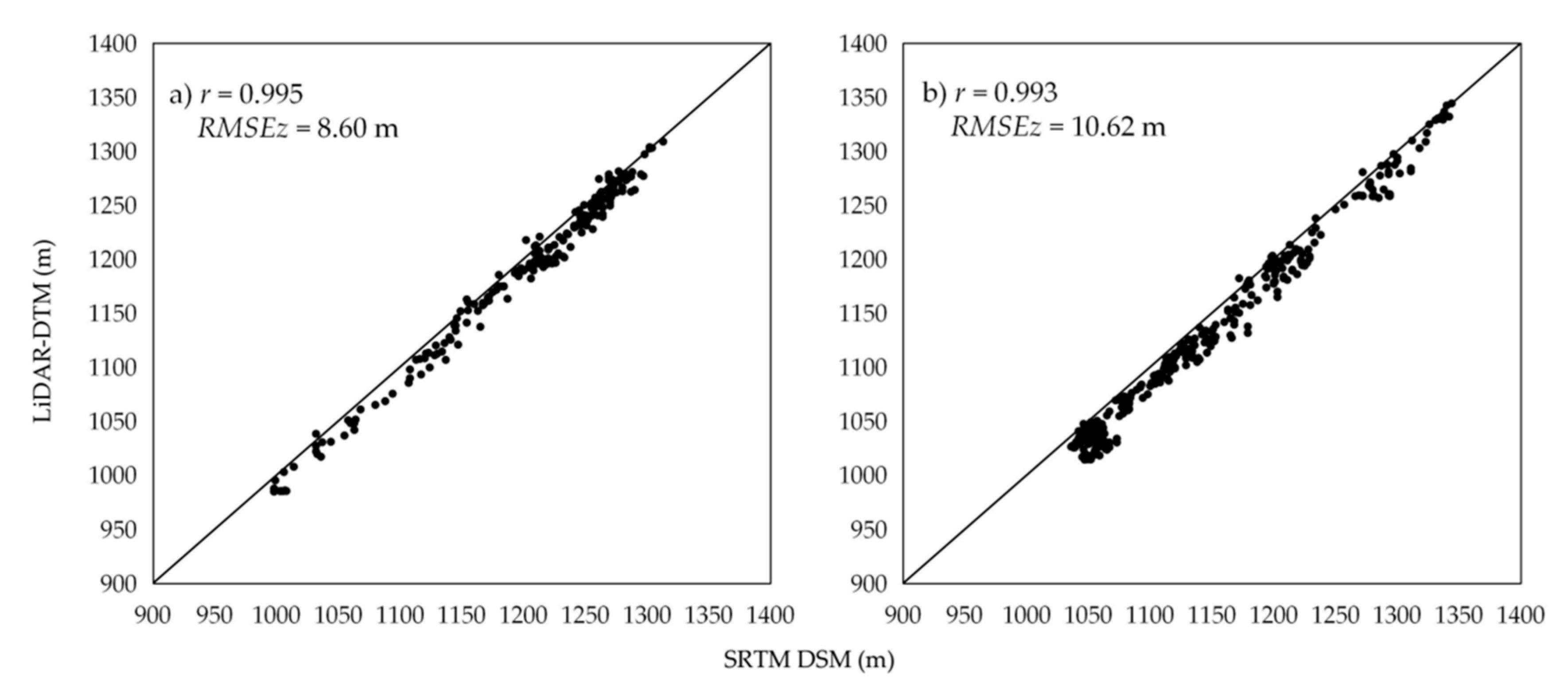
| Measures | Study Site 1 | Study Site 2 |
|---|---|---|
| r | 0.995 ** | 0.993 ** |
| RMSE | 8.60 m | 10.62 m |
| biasz | 6.66 m | 8.93 m |
| rbiasz | 0.56% | 0.79% |
| Resolution | Mean Height (m) | LiDAR CHM (m) | SRTM CHM (m) | |
|---|---|---|---|---|
| 1 m | Mean height (m) | 1 | ||
| LiDAR CHM (m) | 0.875 ** | 1 | ||
| SRTM CHM (m) | 0.846 ** | 0.906 ** | 1 | |
| 5 m | Mean height (m) | 1 | ||
| LiDAR CHM (m) | 0.874 ** | 1 | ||
| SRTM CHM (m) | 0.844 ** | 0.918 ** | 1 | |
| 10 m | Mean height (m) | 1 | ||
| LiDAR CHM (m) | 0.861 ** | 1 | ||
| SRTM CHM (m) | 0.838 ** | 0.860 ** | 1 | |
| 30 m | Mean height (m) | 1 | ||
| LiDAR CHM (m) | 0.701 ** | 1 | ||
| SRTM CHM (m) | 0.839 ** | 0.683 ** | 1 |
| (Constant) | Coefficient | ||||||
|---|---|---|---|---|---|---|---|
| Resolution | Model | R2 | Std. Error of the Estimate | t | Sig. | t | Sig. |
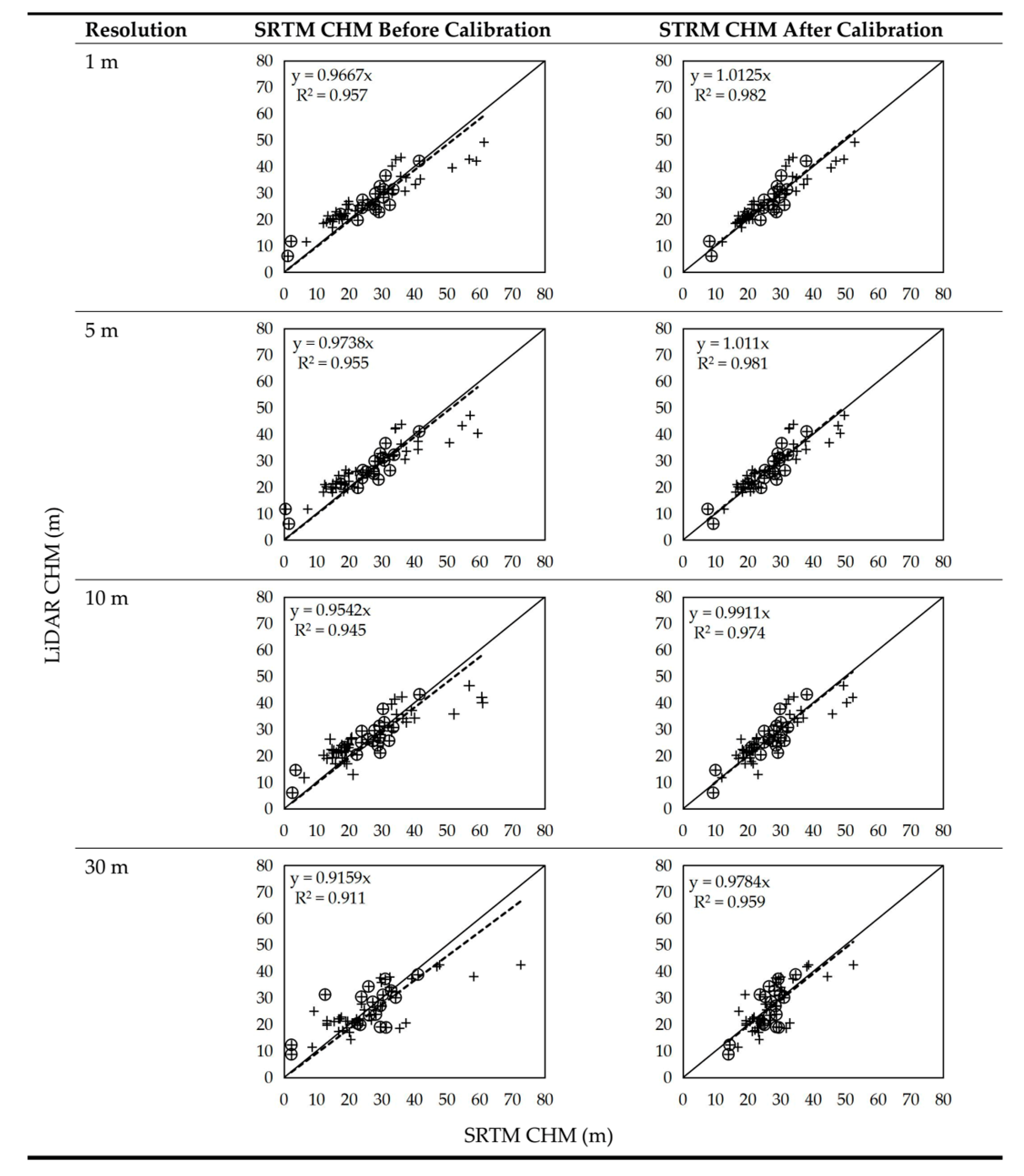
| 1 m | SRTM CHMCal = 0.747(SRTM CHM) + 6.9367 | 0.821 | 3.607 | 2.917 | 0.001 | 8.564 | 0.000 |
| 5 m | SRTM CHMCal = 0.7418(SRTM CHM) + 7.2375 | 0.843 | 3.366 | 3.328 | 0.004 | 9.284 | 0.000 |
| 10 m | SRTM CHMCal = 0.7394(SRTM CHM) + 7.3553 | 0.740 | 4.312 | 2.472 | 0.025 | 6.755 | 0.009 |
| 30 m | SRTM CHMCal = 0.5557(SRTM CHM) + 12.032 | 0.467 | 6.236 | 2.994 | 0.009 | 3.745 | 0.002 |
| Site | DBH, (cm) | Tree Height, (m) | Wood Density, (g/cm3) | AGB, (Mg/ha) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max * | SD ** | Mean | Max * | SD ** | Mean | Max * | SD ** | Mean | Max * | SD ** | |
| 1 | 19.33 | 109.90 | 4.68 | 17.66 | 65.90 | 2.32 | 0.61 | 1.05 | 0.04 | 292.15 | 901.29 | 164.45 |
| 2 | 18.98 | 122.10 | 3.61 | 17.03 | 29.35 | 4.53 | 0.58 | 1.06 | 0.04 | 243.01 | 468.04 | 118.01 |
| Resolution | Model | EF | RMSEModel (Mg/ha) | Relative RMSEModel (%) |
|---|---|---|---|---|
| 1 m | Ln(AGB) = 1.721[Ln(CHMmean 1 m)] + 0.1719 | 0.798 | 74.10 | 25.81 |
| 5 m | Ln(AGB) = 1.6813[Ln(CHMmean 5 m)] + 0.29 | 0.768 | 79.28 | 27.62 |
| 10 m | Ln(AGB) = 1.719[Ln(CHMmean 10 m)] + 0.167 | 0.797 | 74.04 | 25.79 |
| 30 m | Ln(AGB) = 0.501[Ln(CHMmean 30 m)] + 3.961 | 0.288 | 139.10 | 48.45 |
| AGB Increase (Mg/ha) | ||||
|---|---|---|---|---|
| Minimum | Mean | Maximum | SD 1 | |
| Overall | 21.60 | 125.29 | 901.30 | 39.82 |
| Managed forests | 82.50 | 122.57 | 901.30 | 34.67 |
| Village areas | 21.60 | 99.70 | 137.65 | 33.54 |
| AGB Decrease (Mg/ha) | ||||
| Overall | −41.30 | −390.50 | −673.30 | 133.53 |
| Managed forests | −95.45 | −158.97 | −673.30 | 58.42 |
| Village areas | −41.30 | −154.90 | −274.10 | 8.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loh, H.Y.; James, D.; Ioki, K.; Wong, W.V.C.; Tsuyuki, S.; Phua, M.-H. Aboveground Biomass Changes in Tropical Montane Forest of Northern Borneo Estimated Using Spaceborne and Airborne Digital Elevation Data. Remote Sens. 2020, 12, 3677. https://doi.org/10.3390/rs12223677
Loh HY, James D, Ioki K, Wong WVC, Tsuyuki S, Phua M-H. Aboveground Biomass Changes in Tropical Montane Forest of Northern Borneo Estimated Using Spaceborne and Airborne Digital Elevation Data. Remote Sensing. 2020; 12(22):3677. https://doi.org/10.3390/rs12223677
Chicago/Turabian StyleLoh, Ho Yan, Daniel James, Keiko Ioki, Wilson Vun Chiong Wong, Satoshi Tsuyuki, and Mui-How Phua. 2020. "Aboveground Biomass Changes in Tropical Montane Forest of Northern Borneo Estimated Using Spaceborne and Airborne Digital Elevation Data" Remote Sensing 12, no. 22: 3677. https://doi.org/10.3390/rs12223677
APA StyleLoh, H. Y., James, D., Ioki, K., Wong, W. V. C., Tsuyuki, S., & Phua, M.-H. (2020). Aboveground Biomass Changes in Tropical Montane Forest of Northern Borneo Estimated Using Spaceborne and Airborne Digital Elevation Data. Remote Sensing, 12(22), 3677. https://doi.org/10.3390/rs12223677






