New Higher-Order Correction of GNSS RO Bending Angles Accounting for Ionospheric Asymmetry: Evaluation of Performance and Added Value
Abstract
1. Introduction
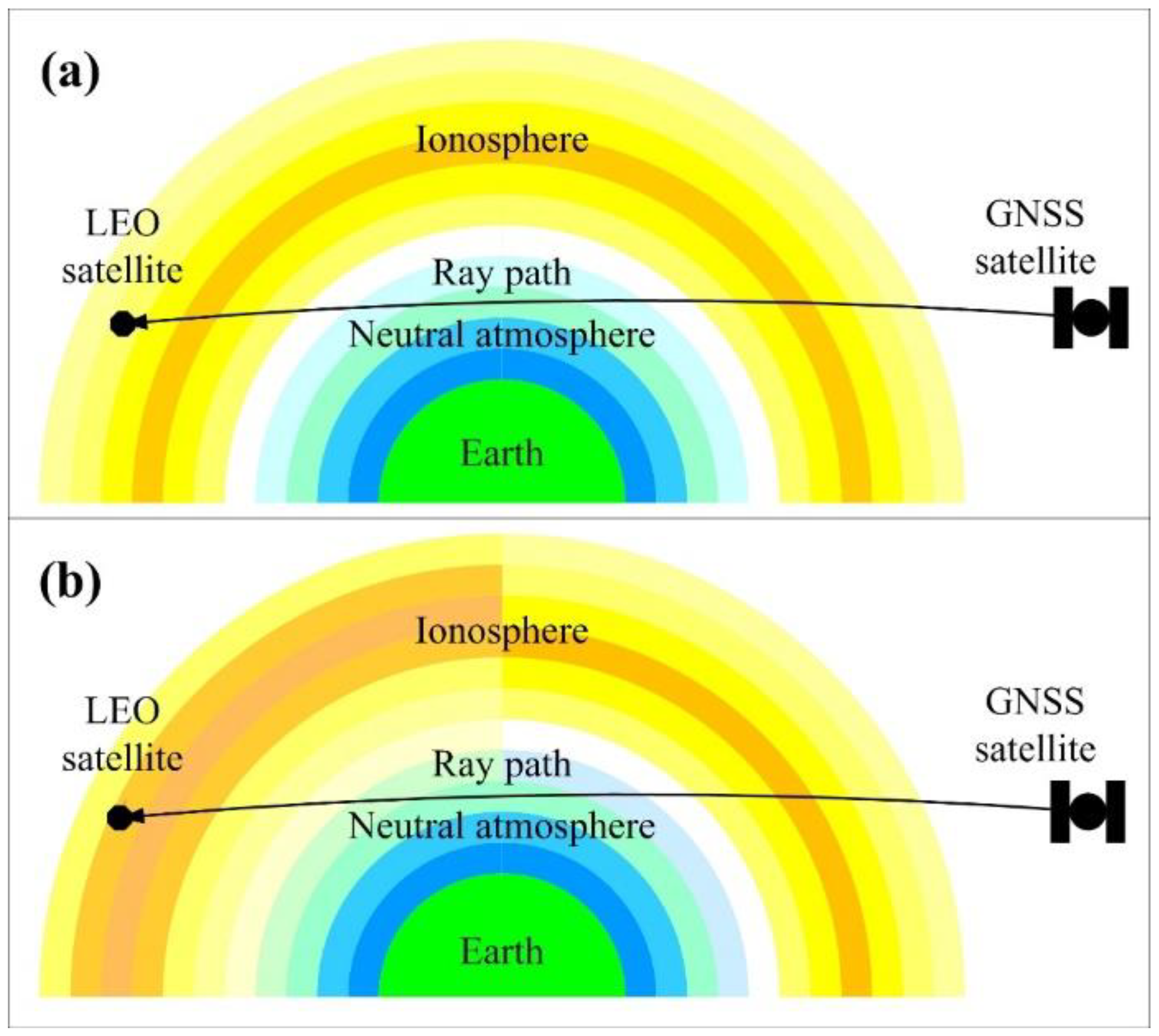
2. Correction Approach and Implementation Setup
2.1. Formulation of Bi-Local RIE Model
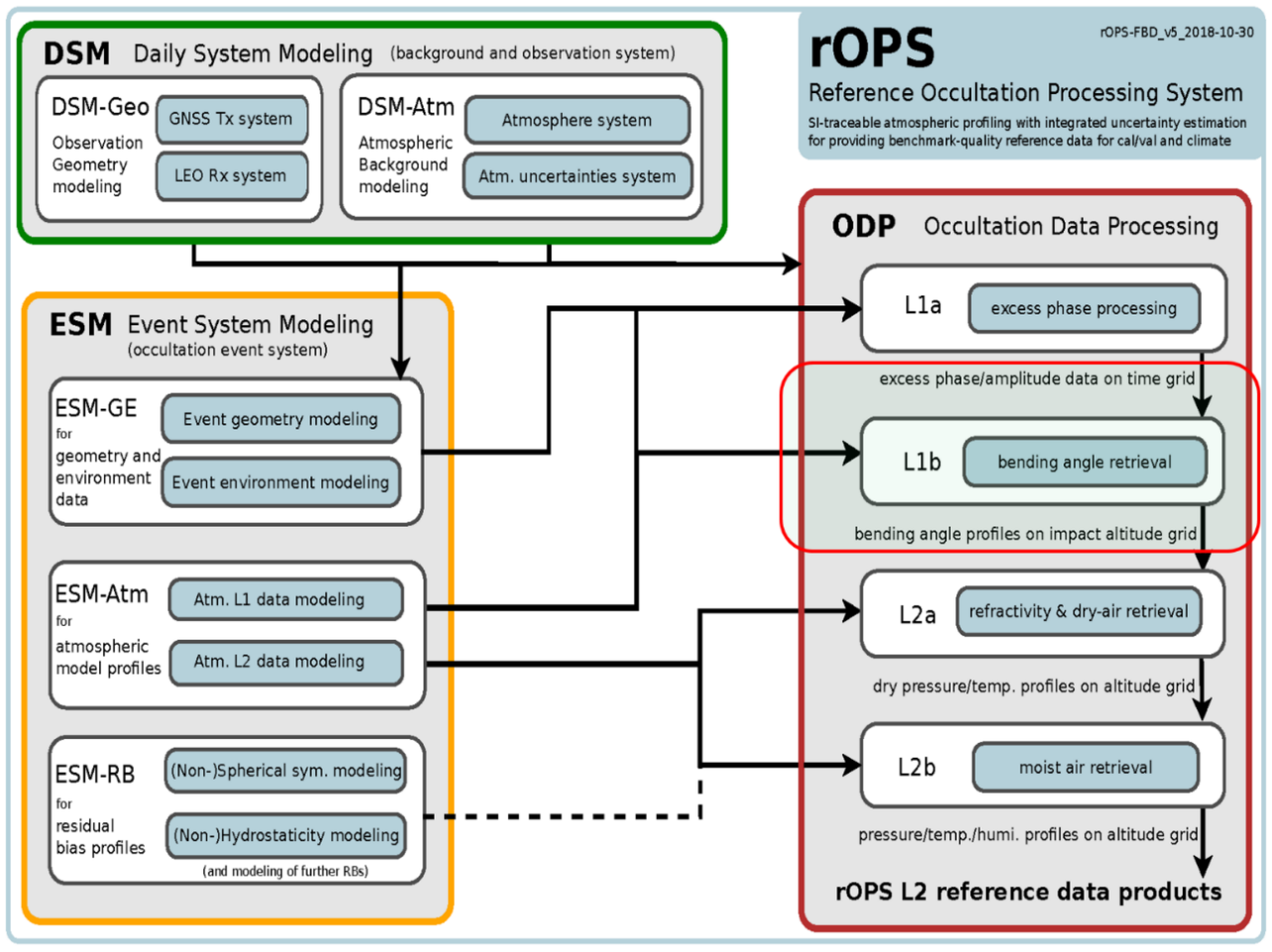
2.2. Processing Setup for the Bi-Local Correction in the rOPS
2.2.1. rOPS as the System for RIE Correction Evaluation
2.2.2. Implementation of the Bi-Local Correction Approach
2.3. Setup of the Performance Evaluation Simulations
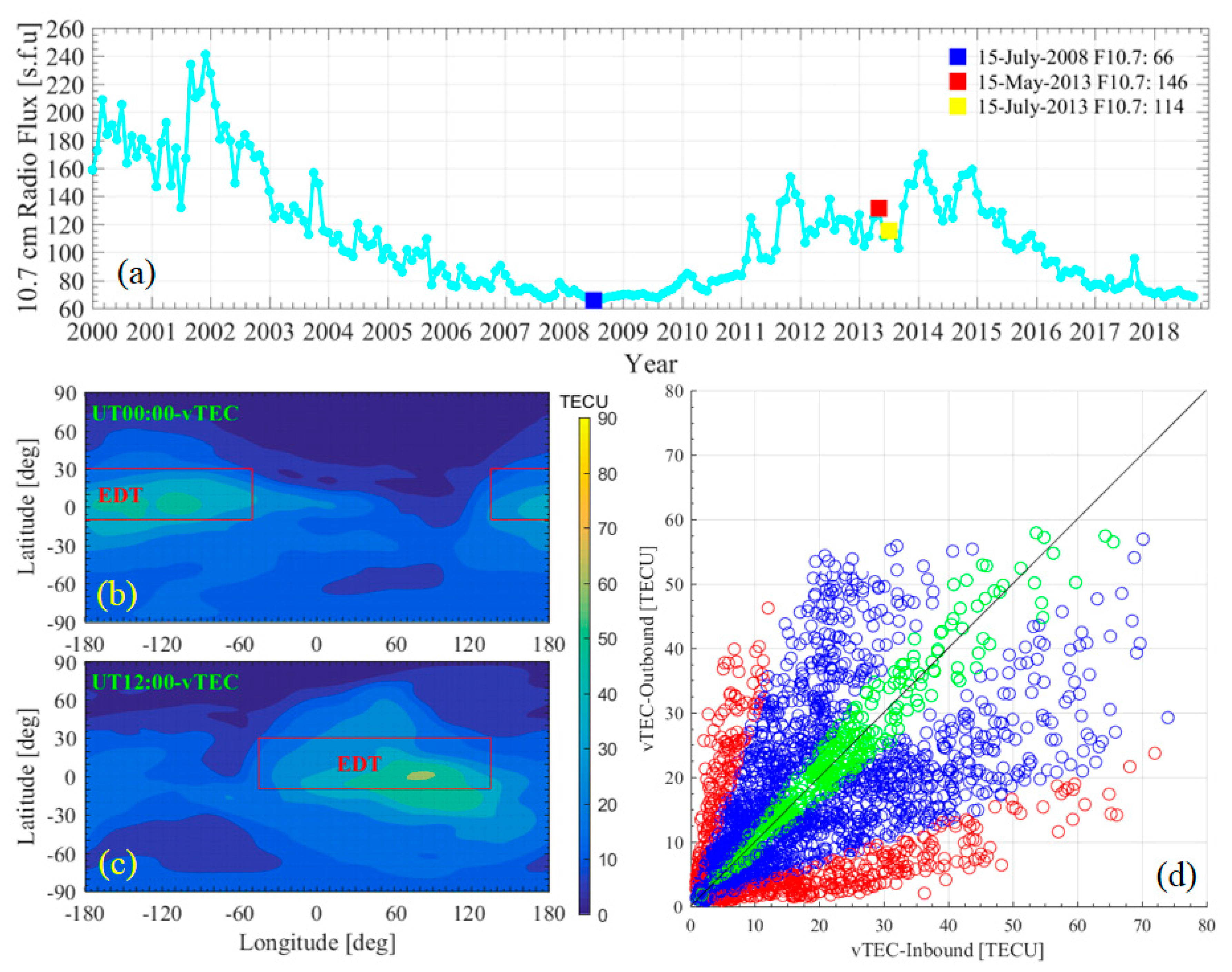
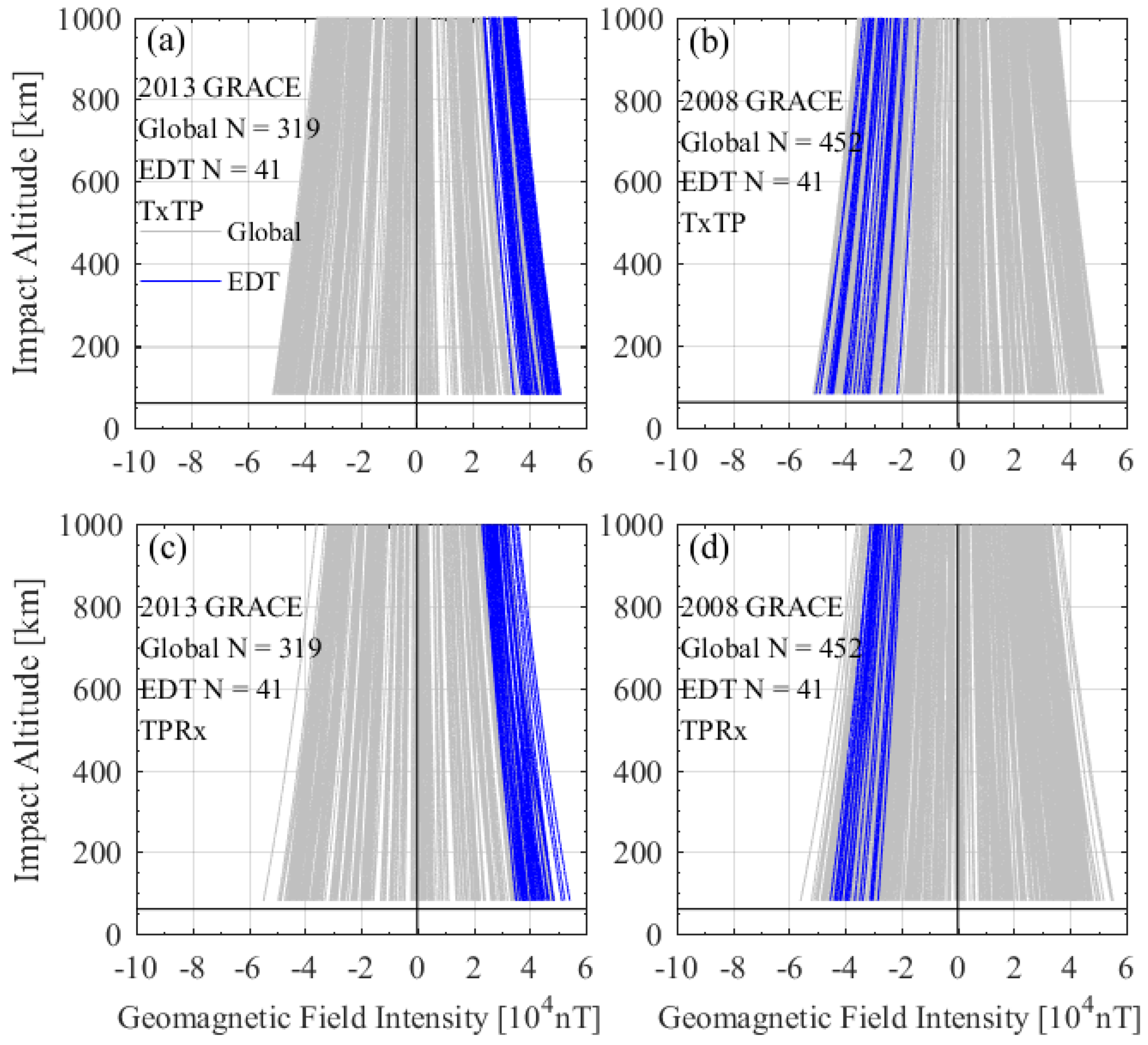
2.3.1. Solar and Ionospheric Conditions
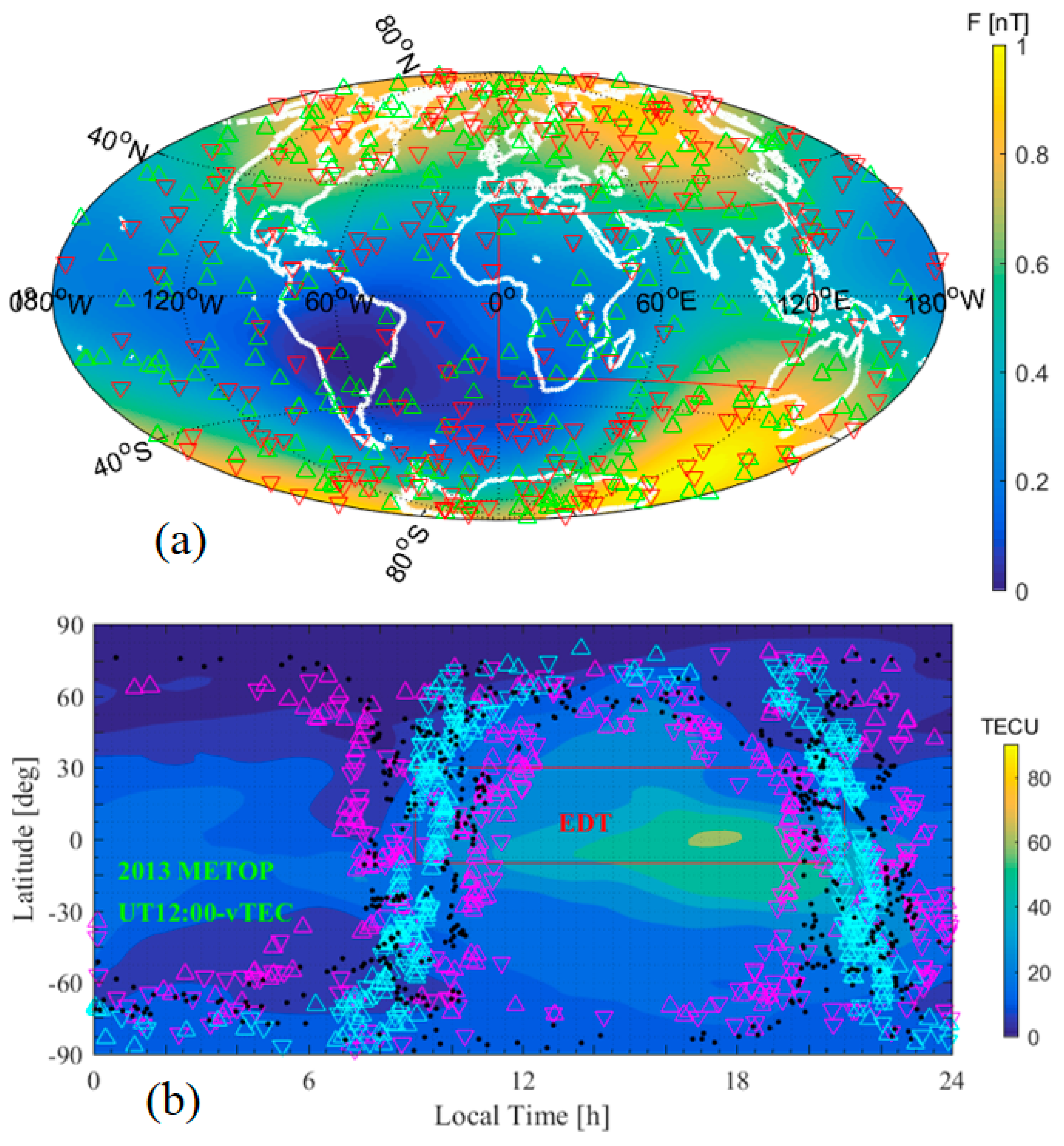
2.3.2. Geomagnetic Conditions
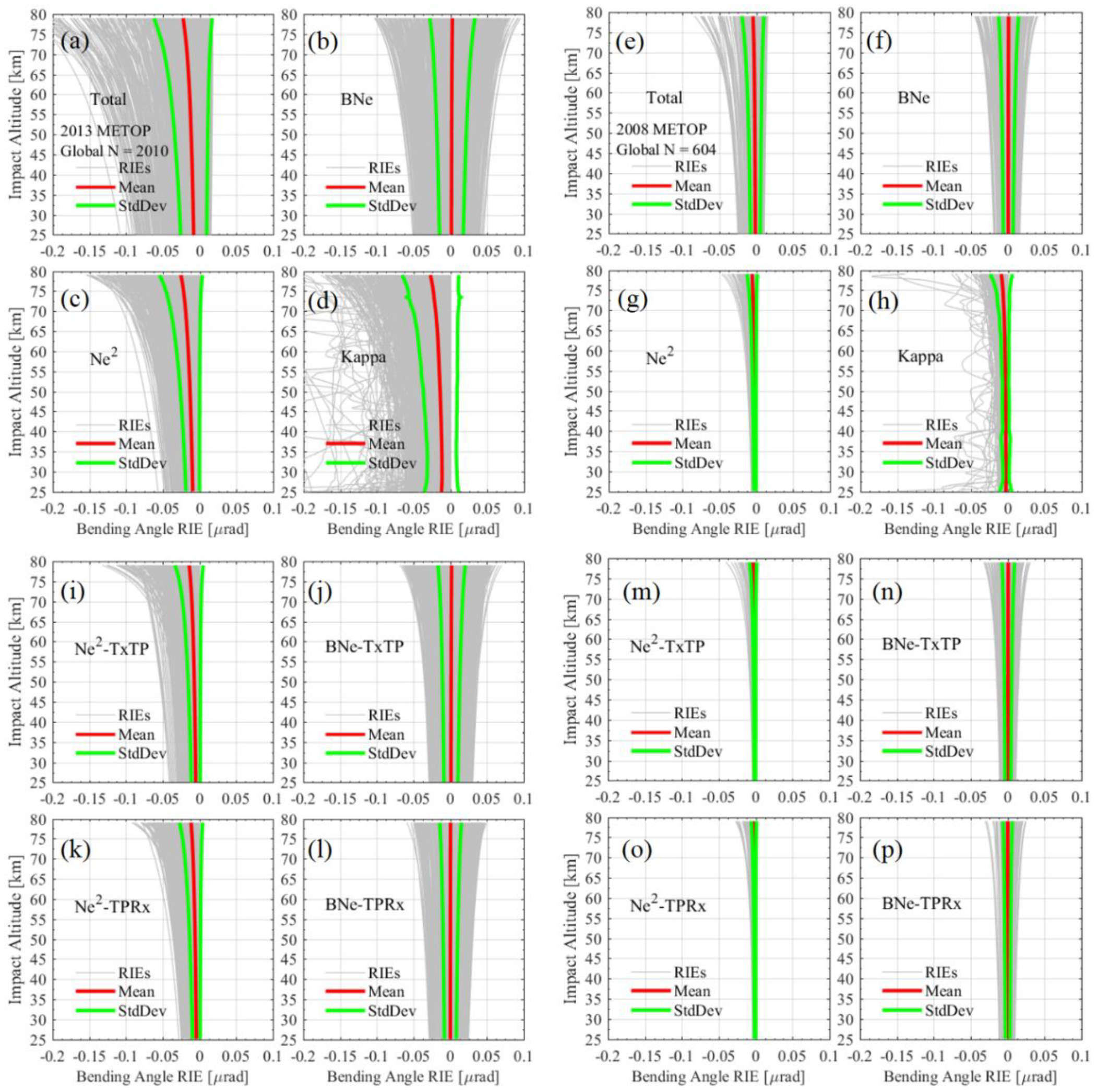
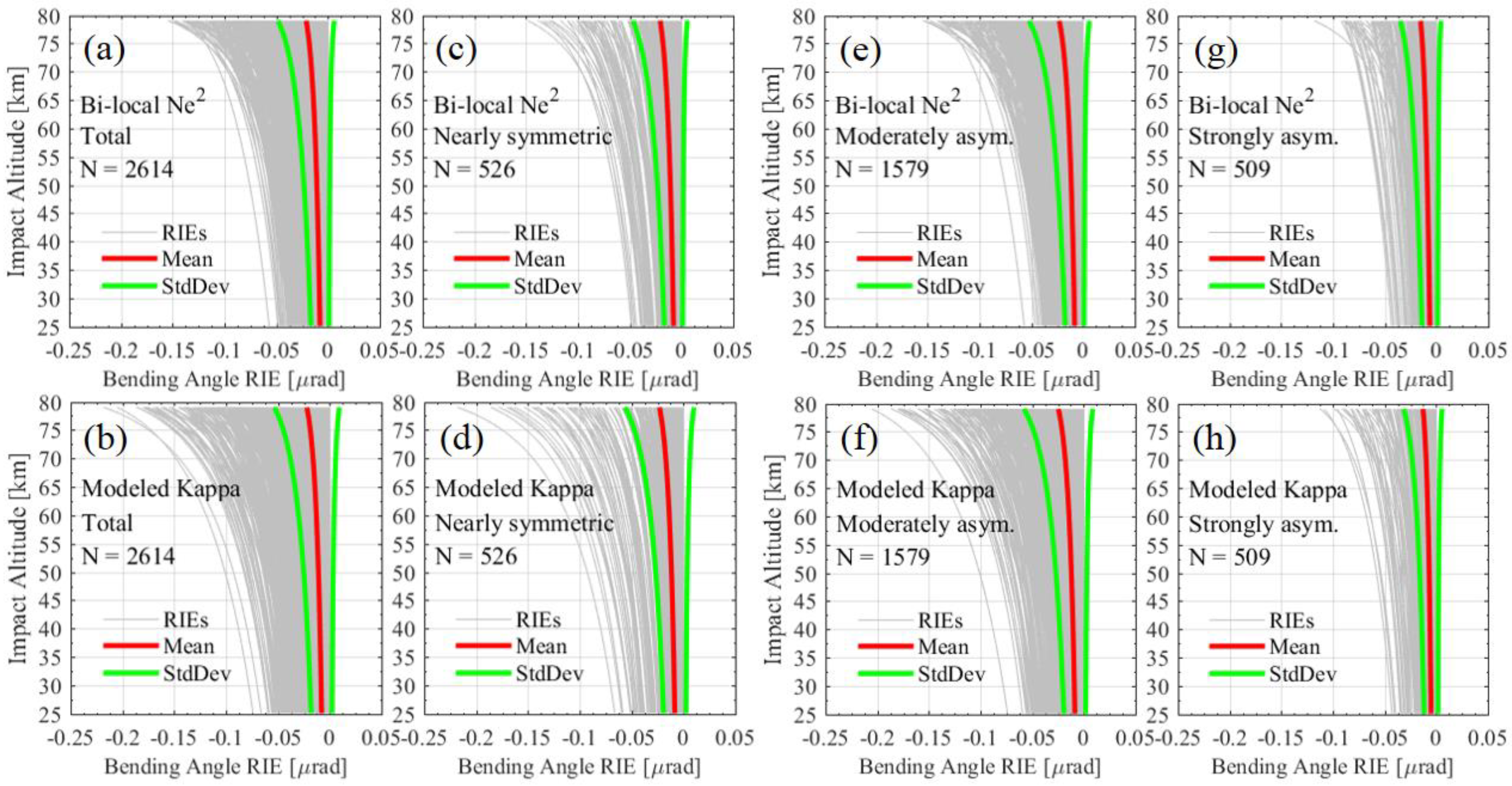
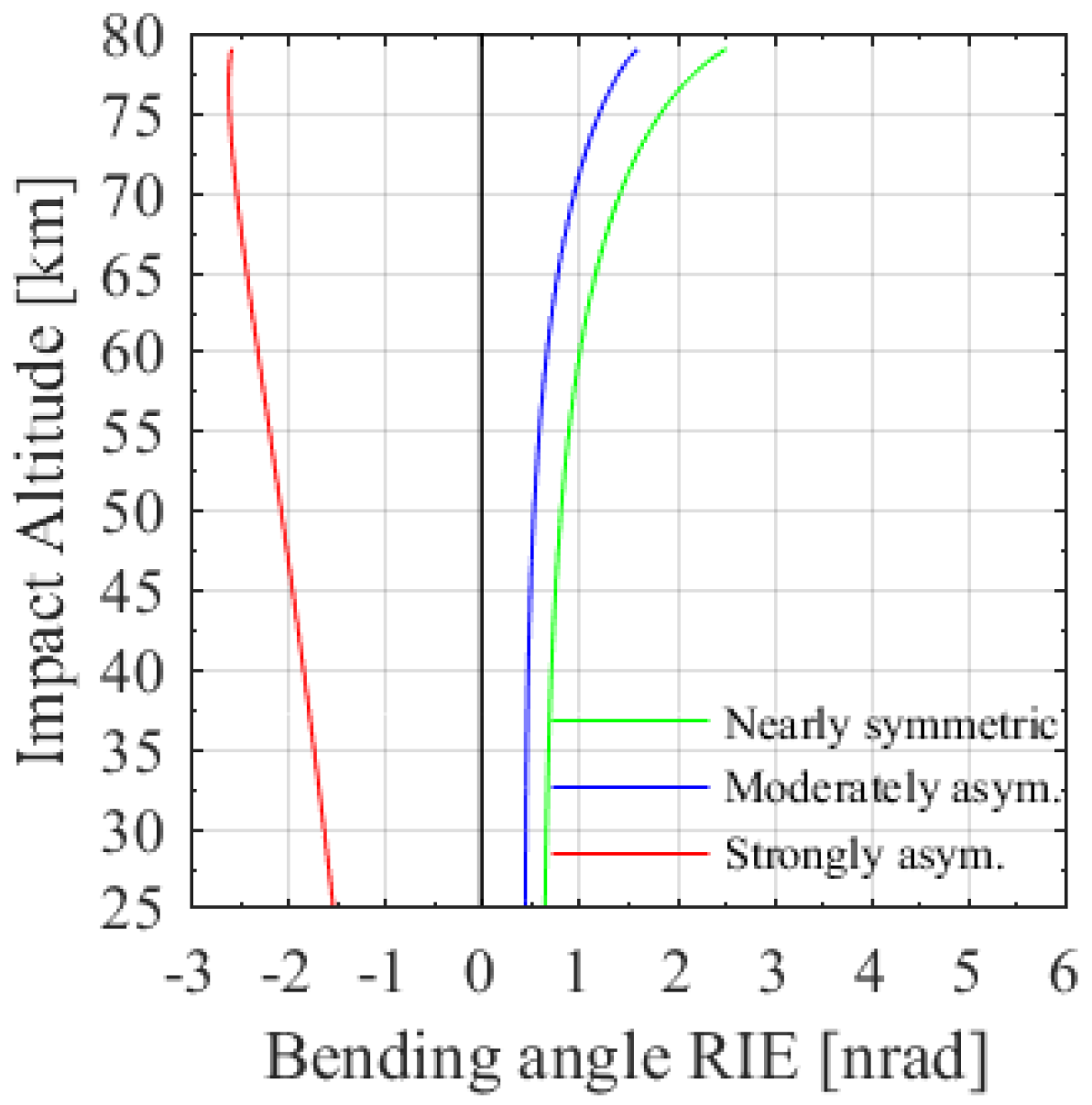
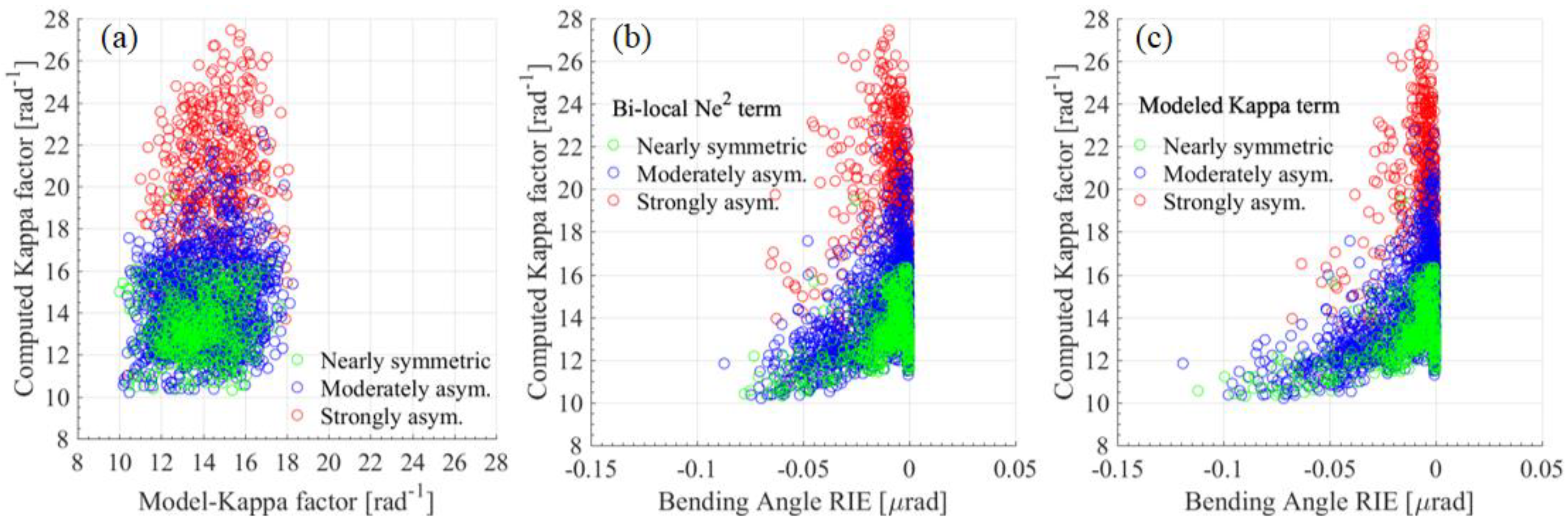
3. Results
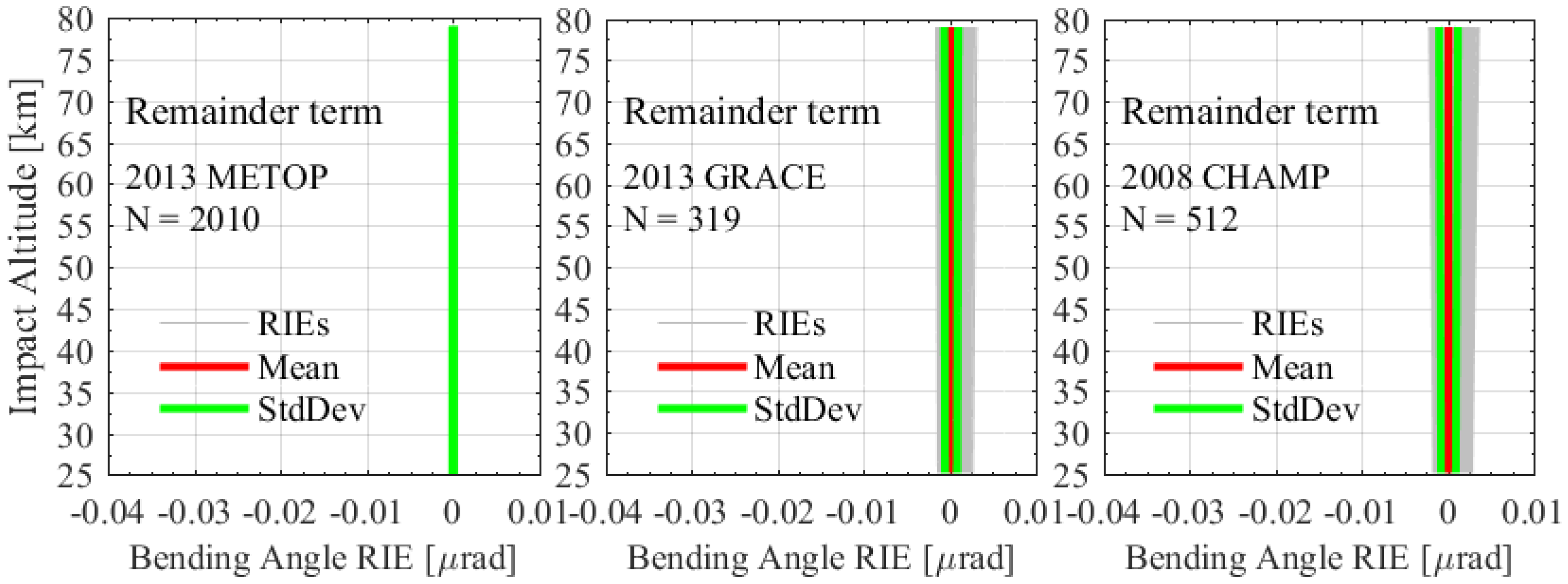
3.1. Statistical Ensemble of Bending Angle RIE Profiles
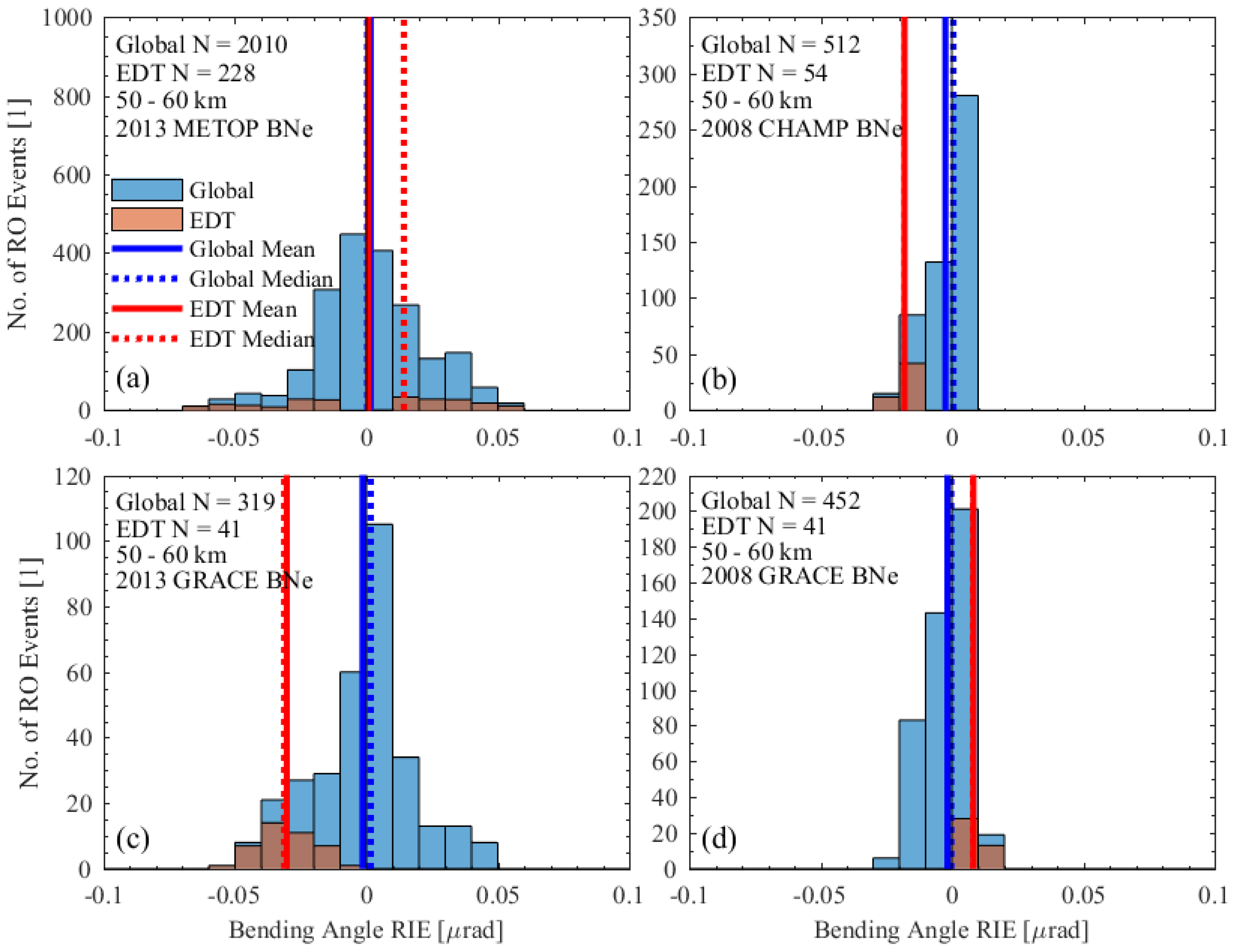
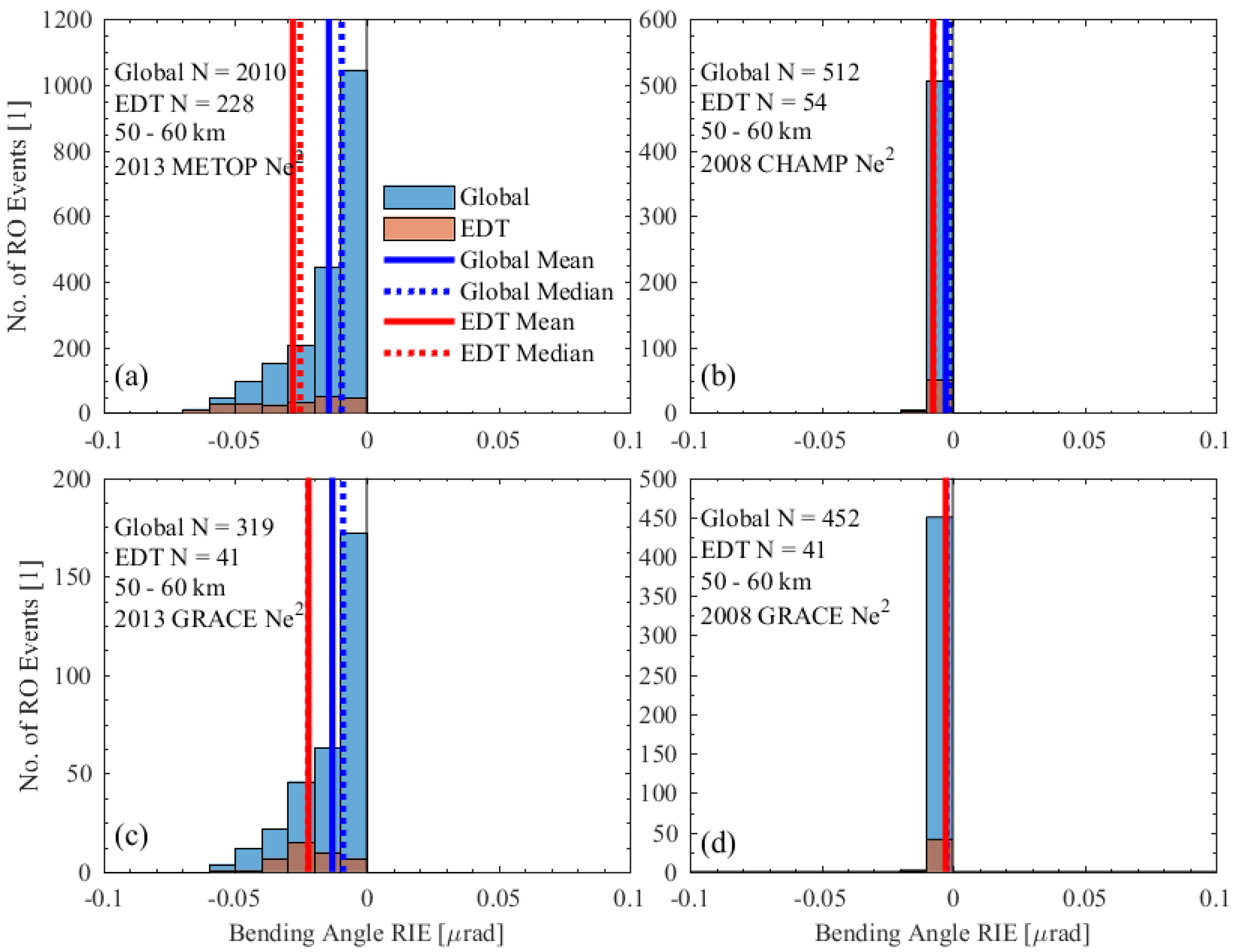
3.2. Statistical Results Inspected by Histograms
4. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Melbourne, W.G.; Davis, E.S.; Duncan, C.B.; Hajj, G.A.; Hardy, K.R.; Kursinski, E.R.; Meehan, T.K.; Young, L.E.; Yunck, T.P. The Application of Spaceborne GPS to Atmospheric Limb Sounding and Global Change Monitoring; JPL Publication 94-18; Jet Propulsion Laboratory: Pasadena, CA, USA, 1994; p. 147. [Google Scholar]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing earth’s atmosphere with radio occultation measurements using the global positioning system. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Steiner, A.K.; Lackner, B.C.; Ladstädter, F.; Scherllin-Pirscher, B.; Foelsche, U.; Kirchengast, G. GPS radio occultation for climate monitoring and change detection. Radio Sci. 2011, 46, RS0D24. [Google Scholar] [CrossRef]
- Lackner, B.C.; Steiner, A.K.; Hegerl, G.C.; Kirchengast, G. Atmospheric climate change detection by radio occultation data using a fingerprinting method. J. Clim. 2011, 24, 5275–5291. [Google Scholar] [CrossRef]
- Anthes, R.A.; Rocken, C.; Kuo, Y.H. Applications of COSMIC to meteorology and climate. Terr. Atmos. Ocean. Sci. 2000, 11, 115–156. [Google Scholar] [CrossRef]
- Gobiet, A.; Kirchengast, G. Advancements of global navigation satellite system radio occultation retrieval in the upper stratosphere for optimal climate monitoring utility. J. Geophys. Res. 2004, 109, D24110. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Bai, W.H.; Liu, C.L.; Liu, Y.; Du, Q.F.; Wang, X.Y.; Yang, G.L.; Liao, M.; Yang, Z.D.; Zhang, X.X.; et al. The Fengyun-3c radio occultation sounder GNOS: A review of the mission and its early results and science applications. Atmos. Meas. Tech. 2018, 11, 5797–5811. [Google Scholar] [CrossRef]
- Buontempo, C.; Jupp, A.; Rennie, M. Operational NWP assimilation of GPS radio occultation data. Atmos. Sci. Lett. 2008, 9, 129–133. [Google Scholar] [CrossRef]
- Healy, S.B. Forecast impact experiment with GPS radio occultation measurements. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Vorobev, V.V.; Krasilnikova, T.G. An estimation of accuracy of the atmospheric refractive-index recovery from measurements of doppler shifts at frequencies used in the navstar system. Izv. Fiz Atmos. Okeana 1994, 29, 626–633. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Ionospheric bending correction for GNSS radio occultation signals. Radio Sci. 2011, 46, RS0D06. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Sun, Y.Q.; Bai, W.H.; Du, Q.F.; Wang, X.Y.; Meng, X.G.; Wang, D.W.; Cai, Y.R.; Wu, D.; et al. Study of bending angle residual ionosphric error in real RO data. Int. Geosci. Remote Sens. 2016, 4171–4174. [Google Scholar]
- Mannucci, A.J.; Ao, C.O.; Pi, X.; Iijima, B.A. The impact of large scale ionospheric structure on radio occultation retrievals. Atmos. Meas. Tech. 2011, 4, 2837–2850. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Zhang, K.F.; Norman, R.; Li, Y.; Zhang, S.C.; Carter, B.; Fritzer, J.; Schwaerz, M.; Choy, S.L.; et al. Characterisation of residual ionospheric errors in bending angles using GNSS RO end-to-end simulations. Adv. Space Res. 2013, 52, 821–836. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Zhang, K.; Norman, R.; Li, Y.; Zhang, S.C.; Fritzer, J.; Schwaerz, M.; Wu, S.Q.; Tan, Z.X. Quantifying residual ionospheric errors in GNSS radio occultation bending angles based on ensembles of profiles from end-to-end simulations. Atmos. Meas. Tech. 2015, 8, 2999–3019. [Google Scholar] [CrossRef]
- Syndergaard, S. On the ionosphere calibration in GPS radio occultation measurements. Radio Sci. 2000, 35, 865–883. [Google Scholar] [CrossRef]
- Healy, S.B.; Culverwell, I.D. A modification to the standard ionospheric correction method used in GPS radio occultation. Atmos. Meas. Tech. 2015, 8, 3385–3393. [Google Scholar] [CrossRef]
- Danzer, J.; Healy, S.B.; Culverwell, I.D. A simulation study with a new residual ionospheric error model for GPS radio occultation climatologies. Atmos. Meas. Tech. 2015, 8, 3395–3404. [Google Scholar] [CrossRef]
- Bassiri, S.; Hajj, G.A. Higher-order ionospheric effects on the GPS observables and means of modeling them. Adv. Astronaut. Sci. 1993, 82, 1071–1086. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Higher order ionospheric propagation effects on GPS radio occultation signals. Adv. Space. Res. 2010, 46, 162–173. [Google Scholar] [CrossRef]
- Danzer, J.; Scherllin-Pirscher, B.; Foelsche, U. Systematic residual ionospheric errors in radio occultation data and a potential way to minimize them. Atmos. Meas. Tech. 2013, 6, 2169–2179. [Google Scholar] [CrossRef]
- Qu, X.C.; Li, Z.H.; An, J.C.; Ding, W.W. Characteristics of second-order residual ionospheric error in GNSS radio occultation and its impact on inversion of neutral atmospheric parameters. J. Atmos. Sol. Terr. Phys. 2015, 130, 159–171. [Google Scholar] [CrossRef]
- Zeng, Z.; Sokolovskiy, S.; Schreiner, W.; Hunt, D.; Lin, J.; Kuo, Y.H. Ionospheric correction of GPS radio occultation data in the troposphere. Atmos. Meas. Tech. 2016, 9, 335–346. [Google Scholar] [CrossRef]
- Zeng, Z.; Sokolovskiy, S. Effect of sporadic E clouds on GPS radio occultation signals. Geophys. Res. Lett. 2010, 37, L18817(1–5). [Google Scholar] [CrossRef]
- Angling, M.J.; Elvidge, S.; Healy, S.B. Improved model for correcting the ionospheric impact on bending angle in radio occultation measurements. Atmos. Meas. Tech. 2018, 11, 2213–2224. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Sun, Y.Q.; Zhang, K.F.; Norman, R.; Schwaerz, M.; Bai, W.H.; Du, Q.F.; Li, Y. Analysis of ionospheric structure influences on residual ionospheric errors in GNSS radio occultation bending angles based on ray tracing simulations. Atmos. Meas. Tech. 2018, 11, 2427–2440. [Google Scholar] [CrossRef]
- Danzer, J.; Schwaerz, M.; Kirchengast, G.; Healy, S.B. Sensitivity analysis and impact of the Kappa-Correction of residual ionospheric biases on radio occultation climatologies. Earth Space Sci. 2020, 7. [Google Scholar] [CrossRef]
- Syndergaard, S.; Kirchengast, G. A bi-local estimation approach for residual ionospheric correction of radio occultation bending angles. Presented at EUMETSAT ROM SAF-IROWG International Workshop, Elsinore, Denmark, 19–25 September 2019; Fri, 20 Sep; Poster P23. Available online: http://www.romsaf.org/romsaf-irowg-2019/en/content/21/program-agenda-by-day (accessed on 8 September 2020).
- Leitinger, R.; Kirchengast, G. Easy to use global and regional ionospheric models—A report on approaches used in Graz. Acta Geodaet. Geophys. Hung. 1997, 32, 329–342. [Google Scholar]
- Thébault, E.; Finlay, C.C.; Beggan, C.D.; Alken, P.; Aubert, J.; Barrois, O.; Bertrand, F.; Bondar, T.; Boness, A.; Brocco, L.; et al. International geomagnetic reference field: The 12th generation. Earth Planets Space 2015, 67. [Google Scholar] [CrossRef]
- Feltens, J. The international GPS service (IGS) ionosphere working group. Adv. Space Res. 2003, 31, 635–644. [Google Scholar] [CrossRef]
- Petrie, E.J.; Hernández Pajares, M.; Spalla, P.; Moore, P.; King, M.A. A review of higher order ionospheric refraction effects on dual frequency GPS. Surv. Geophys. 2011, 32, 197–263. [Google Scholar] [CrossRef]
- Kirchengast, G.; Schwärz, M.; Schwarz, J.; Scherllin-Pirscher, B.; Pock, C.; Innerkofler, J.; Proschek, V.; Steiner, A.K.; Danzer, J.; Ladstädter, F.; et al. The reference occultation processing system approach to interpret GNSS radio occultation as SI-traceable planetary system refractometer. Presented at OPAC-IROWG International Workshop, Leibnitz, Austria, 8–14 September 2016; Available online: http://wegcwww.unigraz.at/opacirowg2016/data/public/files/opacirowg2016_Gottfried_Kirchengast_presentation_261.pdf (accessed on 8 September 2020).
- Kirchengast, G.; Schwärz, M.; Angerer, B.; Schwarz, J.; Innerkofler, J.; Proschek, V.; Ramsauer, J.; Fritzer, J.; Scherllin-Pirscher, B.; Rieckh, T.; et al. Reference OPS DAD—Reference Occultation Processing System (rOPS) Detailed Algorithm Description; Technical Report for ESA and FFG No. 1/2018, Doc-Id: WEGC-rOPS-2018-TR01, Issue 2.0; Wegener Center, University of Graz: Graz, Austria, 2018. [Google Scholar]
- Schwarz, J. Benchmark Quality Processing of Radio Occultation Data with Integrated Uncertainty Propagation; Scientific Report No. 77-2018; Wegener Center Verlag: Graz, Austria, 2018. [Google Scholar]
- Schwarz, J.; Kirchengast, G.; Schwärz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From excess phase to atmospheric bending angle profiles. Atmos. Meas. Tech. 2018, 11, 2601–2631. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kirchengast, G. Uncertainty propagation through wave optics retrieval of bending angles from GPS radio occultation: Theory and simulation results. Radio Sci. 2015, 50, 1086–1096. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kirchengast, G. Wave-optics uncertainty propagation and regression-based bias model in GNSS radio occultation bending angle retrievals. Atmos. Meas. Tech. 2018, 11, 111–125. [Google Scholar] [CrossRef]
- Schwarz, J.; Kirchengast, G.; Schwärz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From bending angle to dry-air atmospheric profiles. Earth Space Sci. 2017, 4, 200–228. [Google Scholar] [CrossRef]
- Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Schwärz, M.; Nielsen, J.K.; Ho, S.P.; Yuan, Y.B. A new algorithm for the retrieval of atmospheric profiles from GNSS radio occultation data in moist air and comparison to 1DVar retrievals. Remote Sens. 2019, 11, 2729. [Google Scholar] [CrossRef]
- Innerkofler, J.; Kirchengast, G.; Schwärz, M.; Pock, C.; Jäggi, A.; Andres, Y.; Marquardt, C. Precise orbit determination for climate applications of GNSS radio occultation including uncertainty estimation. Remote Sens. 2020, 12, 1180. [Google Scholar] [CrossRef]

| Variable | Unit | Description |
|---|---|---|
| φ, λ | degree | Location (i.e., latitude, longitude) of the RO event |
| UT | s | Reference time of the RO event |
| Rc, hG | m | Radius of curvature (WGS84 1) and geoid undulation (EGM2008 2) |
| fk | Hz | (GPS) Transmitter signal carrier frequency, elements fk (L1 and L2 signals) |
| za | m | Impact altitude (profile, joint one for L1 and L2) |
| α1 | rad | Bending angle of L1 signal (profile) |
| α2 | rad | Bending angle of L2 signal (profile) |
| F10.7 | s.f.u. | Solar flux index |
| rT | m | Position vector of Tx satellite for ref.altitude 3 (ECEF 4: x y z) |
| vT | m/s | Velocity vector of Tx satellite for ref.altitude (ECEF: vx vy vz) |
| rR | m | Position vector of Rx satellite for ref.altitude (ECEF: x y z) |
| vR | m/s | Velocity vector of Rx satellite for ref.altitude (ECEF: vx vy vz) |
| sTR | m | Straight line unit vector from Tx (rT) to Rx (rR) (ECEF: x y z) |
| xI350T | m | Position vector of ion.mean-altitude point 5 inbound (ECEF and Geodetic) |
| xI350R | m | Position vector of ion.mean-altitude point outbound (ECEF and Geodetic) |
| TECU | vTEC of ion.mean-altitude point inbound (from IGS) | |
| TECU | vTEC of ion.mean-altitude point outbound (from IGS) |
| Variable | Unit | Description |
|---|---|---|
| m−3 | Electron density inbound/outbound, calculated using NeUoG model. NeUoG inputs: height (km), latitude (deg), longitude (deg), time (UT) and F10.7 (s.f.u.); we use impact altitude for z. | |
| nT | Geomagnetic field strength along the ray path inbound/outbound derived from the total geomagnetic field vector B (X, Y, Z), which is obtained using the IGRF-12 model; then computed by B// = B⋅sTR. | |
| TECU (1016m−2) | Integration of Ne from 80 km to 2000 km inbound/outbound | |
| m−3 | Ne(z) = (vTECIGS/vTECNeUoG)⋅NeNeUoG(z) inbound/outbound, which is the observational TEC-adjusted Ne(z) |
| Constant | Unit | Description |
|---|---|---|
| C | m3s−1 | 40.308, basic ionization constant in the ion.refractive index equation |
| K | m3T−1s−3 | 1.1283 × 1012, magnetic term constant in the ion.refractive index equation |
| Variable | Unit | Description |
|---|---|---|
| rad | Total residual ionospheric error (RIE) from Equation (7), i.e., | |
| rad | Total geomagnetic residual term–based on Equation (8) with Tx-to-TP geomagnetic residual term–from 1st integral in Equation (8) TP-to-Rx geomagnetic residual term–from 2nd integral in Equation (8) Rx-local geomagnetic residual term–from last term in Equation (8) | |
| rad | Total squared electron density residual term–based on Equation (8) with Tx-to-TP squared electron density residual term–from 1st integral in Equation (8) TP-to-Rx squared electron density residual term–from 2nd integral in Equation (8) Rx-local squared electron density residual term–from last term in Equation (8) | |
| rad | LEO electron density residual term–last term in Equation (7) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Kirchengast, G.; Syndergaard, S.; Schwaerz, M.; Danzer, J.; Sun, Y. New Higher-Order Correction of GNSS RO Bending Angles Accounting for Ionospheric Asymmetry: Evaluation of Performance and Added Value. Remote Sens. 2020, 12, 3637. https://doi.org/10.3390/rs12213637
Liu C, Kirchengast G, Syndergaard S, Schwaerz M, Danzer J, Sun Y. New Higher-Order Correction of GNSS RO Bending Angles Accounting for Ionospheric Asymmetry: Evaluation of Performance and Added Value. Remote Sensing. 2020; 12(21):3637. https://doi.org/10.3390/rs12213637
Chicago/Turabian StyleLiu, Congliang, Gottfried Kirchengast, Stig Syndergaard, Marc Schwaerz, Julia Danzer, and Yueqiang Sun. 2020. "New Higher-Order Correction of GNSS RO Bending Angles Accounting for Ionospheric Asymmetry: Evaluation of Performance and Added Value" Remote Sensing 12, no. 21: 3637. https://doi.org/10.3390/rs12213637
APA StyleLiu, C., Kirchengast, G., Syndergaard, S., Schwaerz, M., Danzer, J., & Sun, Y. (2020). New Higher-Order Correction of GNSS RO Bending Angles Accounting for Ionospheric Asymmetry: Evaluation of Performance and Added Value. Remote Sensing, 12(21), 3637. https://doi.org/10.3390/rs12213637






