Multisensor Characterization of the Incandescent Jet Region of Lava Fountain-Fed Tephra Plumes

Abstract

Explosive basaltic eruptions eject a great amount of pyroclastic material into the atmosphere, forming columns rising to several kilometers above the eruptive vent and causing significant disruption to both proximal and distal communities. Here, we analyze data, collected by an X-band polarimetric weather radar and an L-band Doppler fixed-pointing radar, as well as by a thermal infrared (TIR) camera, in relation to lava fountain-fed tephra plumes at the Etna volcano in Italy. We clearly identify a jet, mainly composed of lapilli and bombs mixed with hot gas in the first portion of these volcanic plumes and here called the incandescent jet region (IJR). At Etna and due to the TIR camera configuration, the IJR typically corresponds to the region that saturates thermal images. We find that the IJR is correlated to a unique signature in polarimetric radar data as it represents a zone with a relatively high reflectivity and a low copolar correlation coefficient. Analyzing five recent Etna eruptions occurring in 2013 and 2015, we propose a jet region radar retrieval algorithm (JR3A), based on a decision-tree combining polarimetric X-band observables with L-band radar constraints, aiming at the IJR height detection during the explosive eruptions. The height of the IJR does not exactly correspond to the height of the lava fountain due to a different altitude, potentially reached by lapilli and blocks detected by the X-band weather radar. Nonetheless, it can be used as a proxy of the lava fountain height in order to obtain a first approximation of the exit velocity of the mixture and, therefore, of the mass eruption rate. The comparisons between the JR3A estimates of IJR heights with the corresponding values recovered from TIR imagery, show a fairly good agreement with differences of less than 20% in clear air conditions, whereas the difference between JR3A estimates of IJR height values and those derived from L-band radar data only are greater than 40%. The advantage of using an X-band polarimetric weather radar in an early warning system is that it provides information in all weather conditions. As a matter of fact, we show that JR3A retrievals can also be obtained in cloudy conditions when the TIR camera data cannot be processed.

1. Introduction

Explosive eruptions eject large volumes of volcanic particles (i.e., tephra) having different size from micrometers to meters. During the most intense explosive events, volcanic ash can reach the stratosphere, sometimes encircling the globe (e.g., Cordon Caulle 2011 eruption, Chile) [1]. In the eruptive column, tephra is mixed with gas (e.g., water and CO₂) that controls the dynamics of explosive eruptions [2]. This mixture rises first due to gas expansion (gas-thrust region) and then to buoyancy after the sufficient entrainment of air (convective region). When the mixture eventually reaches the atmospheric density, it starts spreading horizontally (umbrella region) [2]. Tephra are deposited thousands of kilometers from the vent, affecting communities at variable temporal and spatial scales [3,4].

The dynamics of eruption columns has been widely studied and, thanks to the increase of computational resources, new 3D models of turbulent eruptive columns have been developed [5,6,7]. However, the dynamics of lava fountain-fed tephra plumes, typically emitted during basaltic explosive eruptions, remains poorly understood. Lava fountains have an inner hotter part and consist of a mixture of liquid clots, pyroclasts and magmatic gases [8] that develop from the volcanic vent rising up to several hundreds of meters [8,9]. Due to the presence of a hot inner core (i.e., the lava fountain), volcanic plumes formed above lava fountains are characterized by more complex structures and dynamics with respect to plumes directly sourced at volcanic vents [10]. A full characterization of lava fountains is, therefore, critical to constrain these complex plumes.

Geophysical monitoring is crucial for operational forecasting of volcanic plumes because it can provide eruption source parameters, such as plume height, mass eruption rate (MER), and erupted mass, in near real-time (e.g., [11,12,13]). The capacity to monitor volcanic activity in all weather conditions is the major advantage of using a complementary set of remote sensing systems. Visible calibrated images can be extensively used to estimate eruption column height [14]. MER can be evaluated using a combination of infrasound measurements and thermal infrared (TIR) images [15]. An L-band ground-based Doppler radar (i.e., VOLDORAD 2B, [16,17]) has been used to study plume dynamics [16] and estimate the MER [17]. Furthermore, erupted mass can be estimated by X-band radars [18], capable of scanning the volcanic plumes at high spatial resolution (less than a few hundred meters) and with a relatively short temporal sampling.

Among the worldwide volcanoes producing lava fountain-fed volcanic plumes, Mt. Etna is one of the most active and best monitored [19,20]. During the last ten years, more than fifty lava fountain events have occurred at Etna. For some of these events, and thanks to the multidisciplinary studies which used different remote sensing sensors, a full characterization has been made [21]. Moreover, lava fountain dynamics has also been extensively studied using thermal cameras of the permanent monitoring system of the Istituto Nazionale di Geofisica e Vulcanologia, Osservatorio Etneo (INGV-OE) (e.g., [20,22,23]). The lava fountain is clearly visible because the pixels within the thermal images are saturated [20,23,24]. It is important to stress that the saturated region detected by thermal-infrared camera does not perfectly correspond to the lava fountain, due to hot pyroclasts that might reach higher altitudes or lower levels when covered by volcanic ash. Mainly for this reason, hereafter we named the saturated region as the incandescent jet region (IJR), previously indicated simply as Incandescent Region in [25]. The IJR is generally characterized by large-size tumbling particles (from a few to several millimeters) [26]. Even though important information on the exit velocities, heights of lava fountains, and bulk volumes of pyroclasts at the source can be obtained from thermal data, thermal cameras cannot work properly under bad weather conditions and also when the lava fountains are darkened by volcanic ash.

In this work, we explore for the first time the potential use of a dual-polarization X-band weather radar to detect and distinguish the IJR formed during Etna explosive eruptions. The paper is organized as follows. Section 2 describes the instruments used in our study, i.e., the TIR camera as well as the X-band and L-band radars. Section 3 presents an overview of the algorithms developed to distinguish the IJR at Etna volcano. Section 4 describes the Etna case studies, while results are shown in Section 5, and conclusions in Section 6.

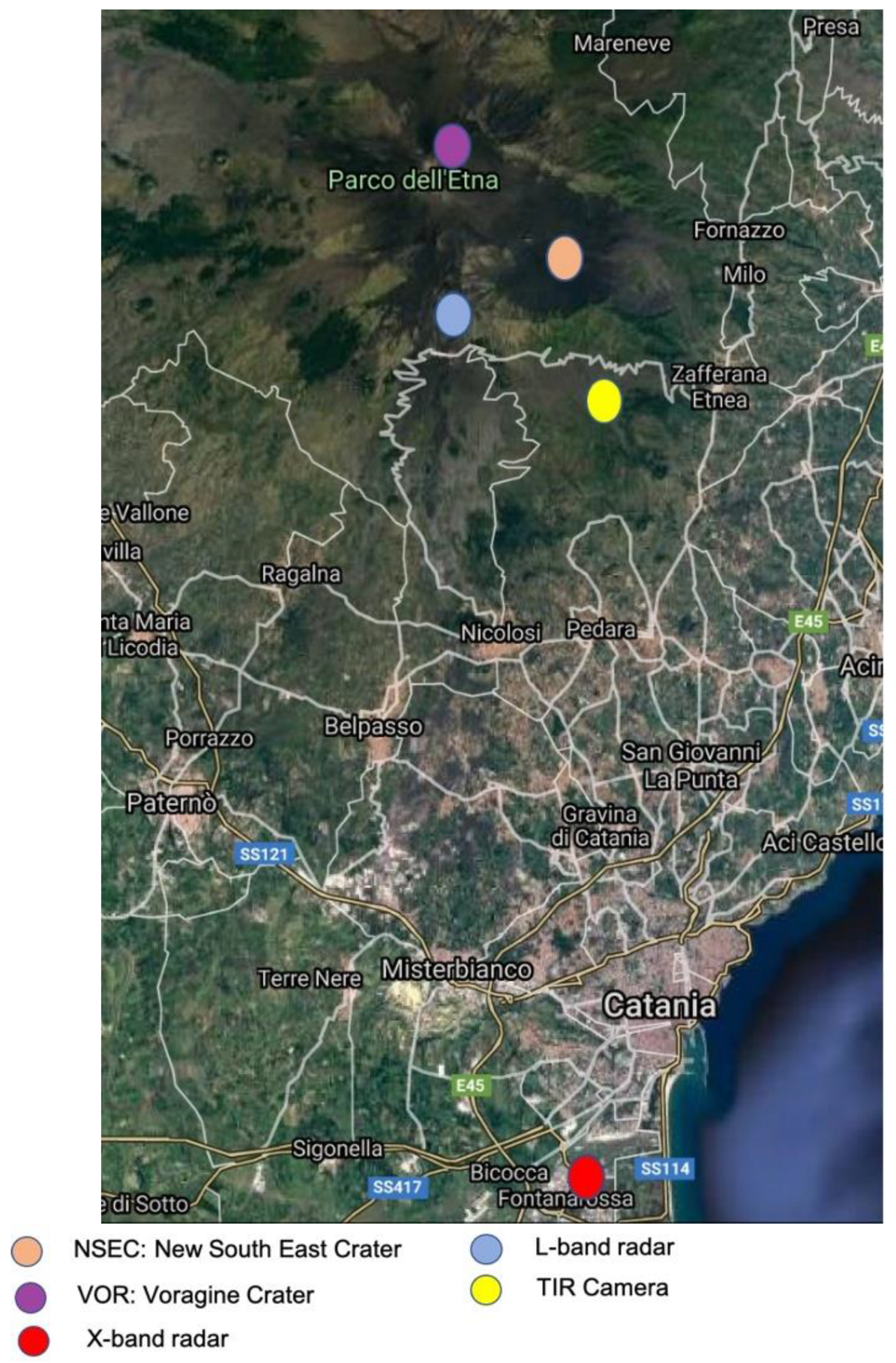
2. Instruments

We consider in this work three ground-based remote sensing systems, permanently monitoring Etna’s summit craters (see Figure 1): (i) the video thermal-infrared camera (hereinafter called TIR camera); (ii) the VOLDORAD-2B L-band Doppler radar (hereinafter called L-band radar); (iii) the X-band polarimetric weather radar (hereinafter called X-band radar or WR). They are located on the south east flank of two of Etna’s summit craters, the New South East crater (NSEC) and the Voragine (VOR) crater, as shown in Figure 1.

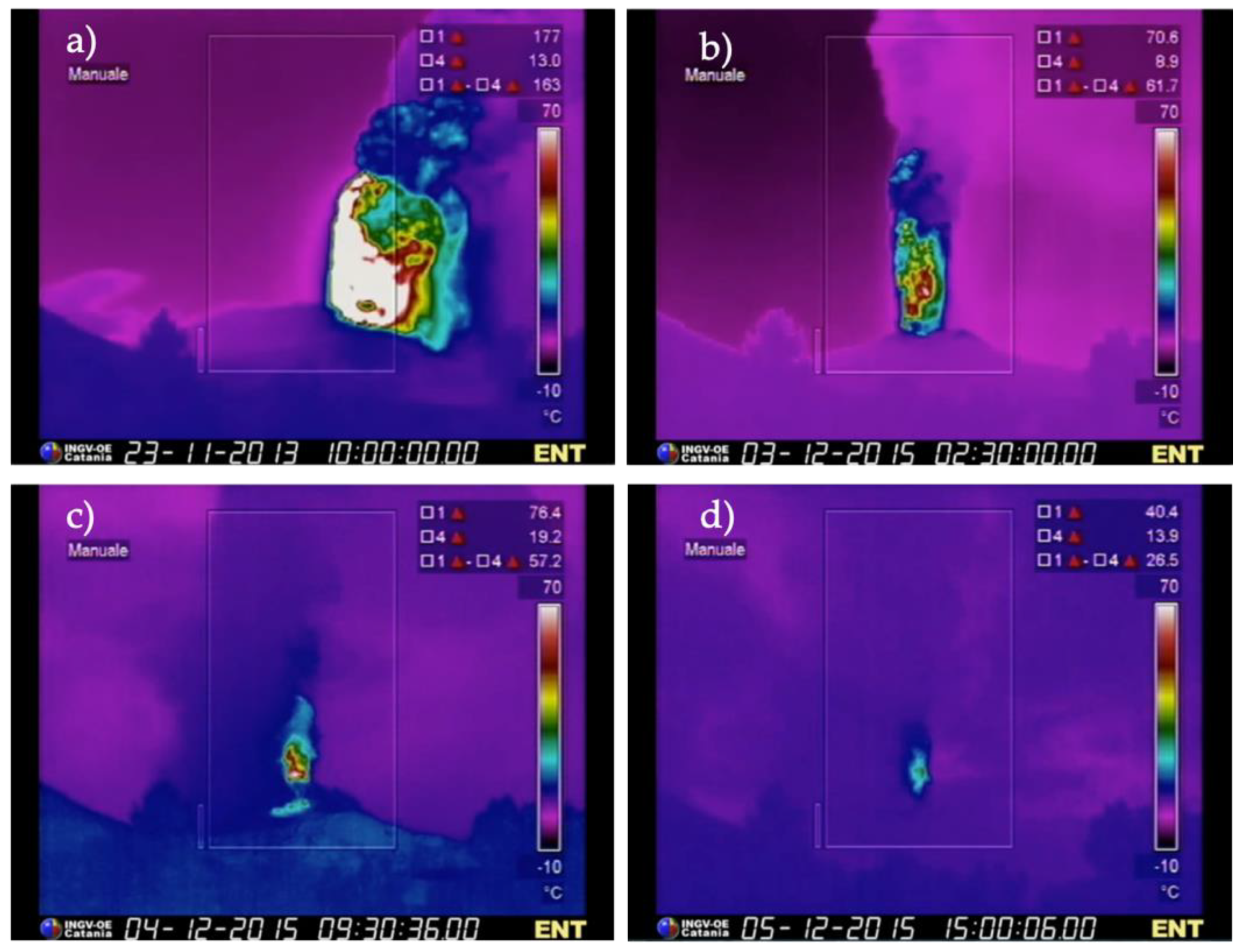
2.1. Thermal Infrared Camera

The thermal-infrared camera is located at ∼15 km (Nicolosi) south from the Etna summit craters and belongs to the video-monitoring network system of the INGV-OE. The TIR camera provides a time series of 640 × 480-pixel images with a spatial resolution of a few meters [22,27] and a thermal sensitivity of 80 mK at 25 °C. The images are displayed with a fixed color scale with a range of −10 to 70 °C. Radiometric data, recorded between 0 and 500 °C, are processed in real-time by a custom written code (i.e., NewSaraterm) [27,28].

The top height of the IJR can be detected by selecting the saturated portion of the measured brightness imagery. The saturation of the camera depends on the properties of the camera and on environmental factors; different thermal surveillance cameras at Etna might, therefore, be saturated in different conditions [20]. Most procedures, used to identify the IJR, are based on setting a suitable threshold to the vertical spatial gradients and/or to edge-contour detection filters. Selecting the TIR camera frames at time intervals of 1 min, it is possible to derive the IJR top height in each image, as described in [20,22,23,25,29].

2.2. The L-Band VOLDORAD-2B Doppler Radar

The VOLDORAD is a fixed-pointing L-band radar (i.e., wavelength of 23.5 cm) that aims at the near-vent detection of erupted material during Etna’s explosive events. This Doppler radar measures both the radial velocity v_r and the received backscattered power that characterizes the amount of detected tephra at high time resolution (i.e., 0.2 s). From the observation geometry, it is possible to convert v_r into exit velocity v_ex (i.e., v_ex = 3.89 v_r) [16,17,28], whereas from the specifications of the L-band radar and the radar constant, the backscattered power can be transformed into the L-band reflectivity factor Z_hh [15,17].

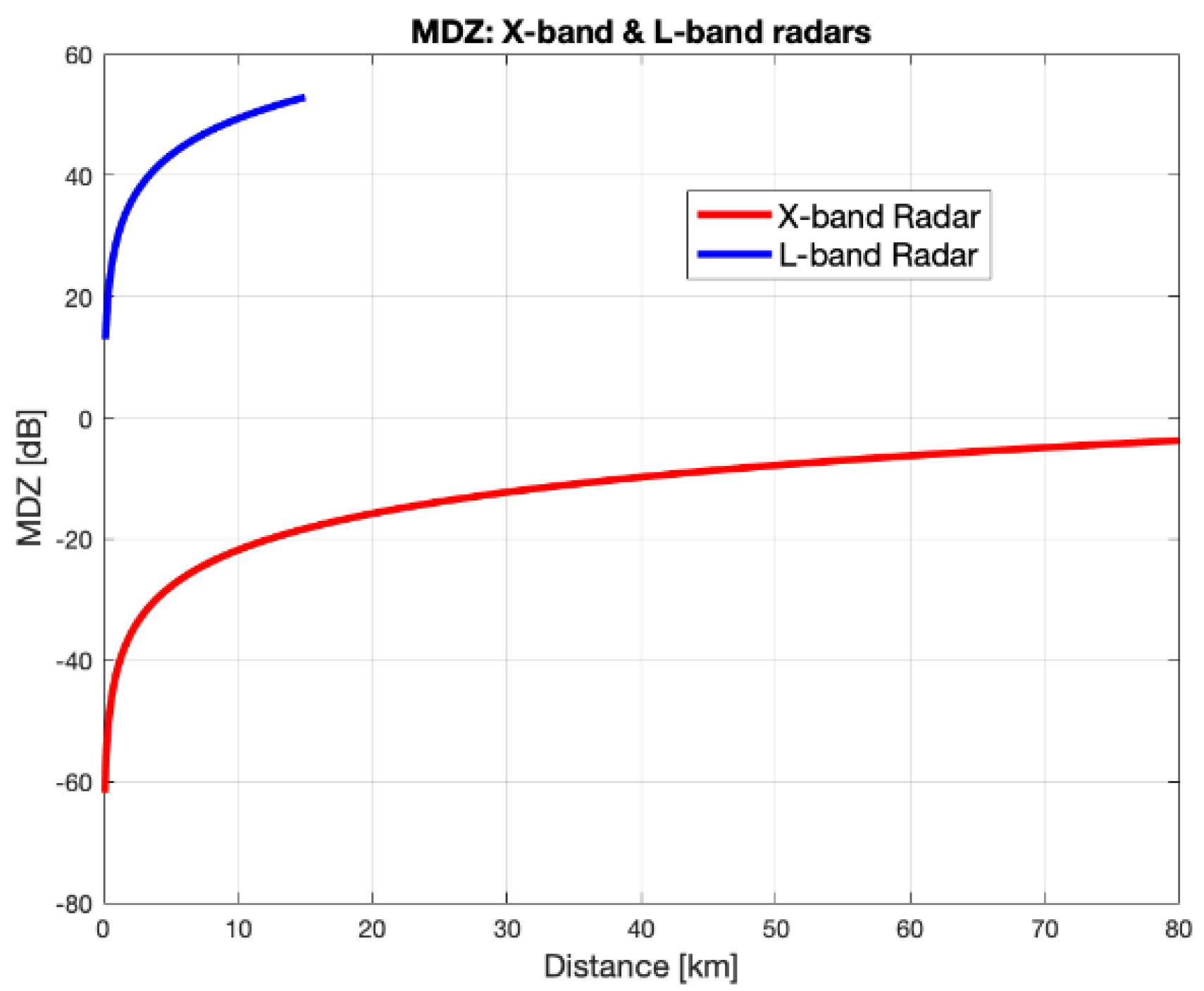
2.3. The X-Band Polarimetric Weather Radar

The X-band radar is a dual-polarization scanning radar of the Italian weather radar network [30]. This system has the following features: wavelengths of about 3.1 cm (9.6 GHz), transmitted peak power of 50 kW, half-power beam width of 1.3°, and permittivity factor of ash particles (equal to 0.39 with respect to 0.93 of water particles) [12,31]. The X-band radar performs a 3-D scan of the surrounding scene as a function of range, azimuth, and elevation with five azimuthal scans per minutes. The X-band radar acquisitions consist of data volumes having a selected area of about 160 × 160 km² wide and 20 km height for each considered event. The data volume cross sections are sampled along 12 elevation angles plus a vertical one with a time resolution of 10 min. X-band radar is located at a distance of about 32 km from the NSEC and 33 km from the VOR (see Figure 1).

Generally, microwave weather radars are able to monitor power level variations to determine reflectivity with high accuracy. The calibration of the weather radar equipment is a mandatory procedure with which it is possible to configure the system in a suitable way to carry out quantitative measurements of the reflectivity of a known target. Figure 2 shows the sensitivity of X-band (red line) and L-band (blue line) radars, i.e., the minimum detectable reflectivity (MDZ) for a specified scattering volume at a given distance from radar [12], knowing the operational specifications of both radars. The range of each radar varies according to its specifications. In fact, the L-band radar maximum observable distance is 15 km with a sensitivity ranging from 15 dBZ to 55 dBZ, whereas the X-band radar the maximum observable distance is about 80 km with an MDZ ranging from −58 dBZ to −3 dBZ.

3. Methods

Processing and retrieval methodologies will be illustrated in the following paragraphs for the TIR camera, L-band radar, and X-band radar.

3.1. Thermal-Infrared Camera Algorithms

At Etna, the height of the IJR is identified as the top height of the saturated thermal infrared region, extracted from the thermal-infrared products or images of the TIR camera as shown in Figure 3. The main assumption is that, during lava fountain events, the saturated region of thermal images mainly represents sustained jets of hot tephra and gas [23]. Thermal-infrared camera measurements are hence processed to extract the H_IJR from the recorded thermal-infrared brightness temperature imagery T_TIR over the eruptive time interval. The TIR camera algorithm is relatively simple and based on a brightness temperature gradient algorithm larger than a given threshold, as tested in [29]. The height of the IJR does not necessarily correspond to the height of the lava fountain because it is mostly associated with the hot region characterized by large clasts. The IJR can also be higher than the lava fountain. Nonetheless, it is worth mentioning that, for simplicity, previous studies have associated the IJR to the lava fountain [22,23,27].

The IJR height detection from TIR camera images is derived by imposing a thermal infrared condition $C_{TIR}$, i.e., looking for the height above the crater and along the axis z centered on the vent such that the C_TIR is satisfied:

$$h_{IJR}^{TIR}\left(x,y,t\right) = z | C_{TIR}$$

(1)

where the vertical bar stands for “conditioned to” and (x,y) are the horizontal coordinates. The various conditions $C_{TIR}$ are discussed in the next paragraphs. Using a reference target in the TIR camera images with a known position, we can derive a scale factor and convert the TIR image coordinates from pixel numbers to meters. Starting from the time sequence of TIR camera images we can apply the threshold algorithms in order to extract the lava fountain edges, defined by a high temperature change, in each intensity image.

The first TIR condition $C_{TIR}$ uses the Canny edge detection [32], looking for local maxima of the TIR temperature gradient, above the vent, by means of the derivative of a Gaussian filter. The Canny method applies two thresholds, shown in

Table 1. Thermal-infrared camera threshold values for the IJR height detection algorithms.

Threshold	Value
tTIR (K)	>315
tT1	0.45
tT2	0.35

, for the gradient detection: a high threshold t_T1 for low-edge sensitivity and a lower threshold t_T2 for high-edge sensitivity. Both values are used in order to set the standard deviation of the Gaussian filter. By using two thresholds, the Canny method is less likely than other methods to be fooled by image noise, and more likely to detect true weak edges. In summary, the first TIR condition imposes that the temperature gradient $\nabla T_{TIR}\left(s, t\right)$ along the vertical axis z is included between t_T1 and t_T2 as expressed by:

$$C_{TIR}^{\nabla \mathrm{T}} = \left\{t_{T2} < \nabla T_{TIR}\left(x,y, t\right) < t_{T1}\right\}$$

(2)

where ($x, y, z, t$) indicate the three coordinates (x,y,z) and the time instant t, whereas the curly brackets stand for a set of rules to be satisfied. This TIR camera approach, supported by (2), is hereinafter named TIR Camera-Edge.

The second TIR condition is obtained by choosing the suitable temperature gradient threshold values t_TIR. The H_IJR is derived in conditions of good atmospheric visibility as the maximum height of the image saturated region above the vent whose contour is identified by a rapid temperature variation rather than a fixed temperature value, according to the relation:

$$C_{TIR}^T = \left\{T_{TIR}\left(x,y,z,t\right) > t_{TIR}\right\}$$

(3)

where t_TIR is the TIR camera temperature threshold (see Table 1). This approach, supported by (3), is hereinafter named TIR Camera.

In both previous methods, the IJR height from TIR imagery at a given instant can be extracted as the mean of all h_IJR in (1) satisfying the corresponding TIR condition, that is:

$$H_{IJR}^{TIR}\left(t\right) = Mean \left\{h_{IJR}^{TIR}\left(x,y,t\right)\right\}$$

(4)

where Mean is the average operator over (x,y) coordinates.

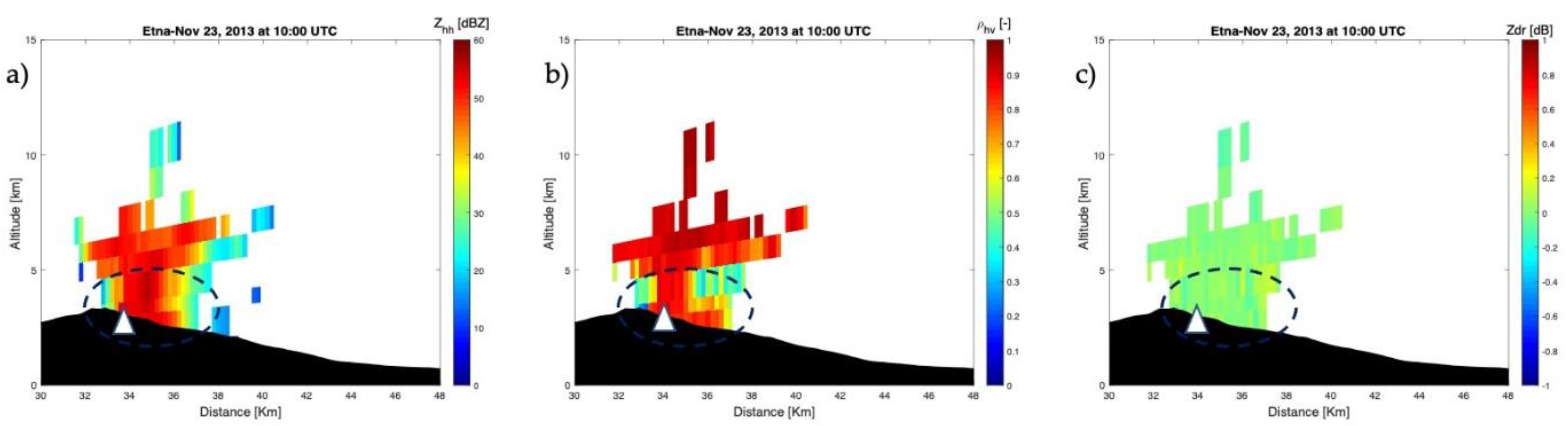
3.2. Simulated X-Band Radar Responses

In order to better understand the radar response, we introduce and discuss the main polarimetric radar observables:

(i).

The reflectivity factor Z_hh, expressed in units of mm⁶ m⁻³ or commonly as decibels dBZ. Z_hh, is equal within Rayleigh scattering conditions to the integral of the sixth-order moment of the detected particle size distribution, i.e., N(D)D⁶dD, with N(D) the number distribution (m⁻³) of particle with diameter D (mm) and size interval dD (mm);

(ii).

The differential reflectivity Z_dr related to the ratio of reflectivity between the horizontal and vertical polarizations, expressed in dB;

(iii).

The copolar correlation coefficient ρ_hv is a measure of the correlation degree between horizontally and vertically polarized echoes, hence a measure of the variety of particle shapes in a pulse volume between horizontal (H) and vertical (V) polarization radar returns [33].

Starting from the assumptions on the dielectric microphysical model of the tephra particles dispersion, we use the Tephra Particle Ensemble Scattering Simulator (TPESS) for distinguishing tephra orientation, concentration, and typology inside eruptive columns [12,13]. The TPESS simulator is run at X-band frequency for three dimensional tephra classes: coarse ash (CA, particle sizes between 0.063 mm and 2 mm), fine lapilli (FL, particle sizes between 2 mm and 4 mm), and medium lapilli (ML, particle sizes between 4 mm and 16 mm) [34,35] and generated at specific concentration: medium concentration (MC, mass density between 10⁻¹ and 10⁰ g/m³), high or large concentration (LC, mass density between 10⁰ and 10¹ g/m³) and very high concentration or intense (IC, mass density between 10¹ and 3∙10¹ g/m³). The particle average orientations are oblate (red), prolate (blue), and tumbling (green).

In Figure 4, we show the scatterplots of Z_hh as a function of ρ_hv and Z_dr. These values are derived from a Monte Carlo generation in the framework of TPESS [13,32,36]. The copolar correlation coefficient shows a response that changes with the increase of particle size and according to the particle orientation (Figure 4). In fact, the largest variations are due to oblate particles, which show a decreasing copolar correlation coefficient as a function of particle size. This superposition, among the particle’s orientation states, makes distinguishing among the three different orientations (oblate, prolate, and tumbling) quite difficult. With increasing particle size, the Z_dr signature of the three orientations tends to be merged but they remain distinguishable among each other.

3.3. Microwave Radar Algorithms

We use the Volcanic Advanced Radar Retrieval (VARR, previously termed as volcanic ash radar retrieval, e.g., [12,13]) to analyze the time series of X-band radar data in order to quantitatively estimate the tephra particle category, mass concentration, MERs and plume height every ten minutes within eruptive columns [13]. The VARR methodology, supported by numerical simulations of plume coupled with lava fountain [10], has been improved in order to consider the strong heterogeneity of the volcanic jet, e.g., composition in microlite, vesicle content, or spindle composition [37].

In contrast with X-band radar and TIR camera that can provide a more direct estimate of H_IJR, from L-band radar data we can derive directly the tephra exit velocity v_ex as a normal projection of the measured radial Doppler velocities [17,25]. However, the latter can be used to retrieve H_IJR, based on the Torricelli’s equation [2]. This equation, also deducible from energy conservation, can provide an estimate of H_IJR associated with the vertically directed outflow velocity v_ex of a constant jet from the eruptive vent, and vice-versa. Indeed, the Torricellli equation is a valid approximation when most of the pyroclasts are sufficiently large to be considered as being uniformly accelerated projectiles that do not enter into the upper convective region of the plume [2,25] as well as atmospheric density variations and drag effects are negligible. Under these assumptions, at each timestep t using for the L-band fixed-pointing radar we can write:

$$H_{IJR}^L\left(t\right) = v_{ex}^2\left(t\right)/2g$$

(5)

where g (m/s²) is the Earth gravity acceleration and the superscript L stands for L-band radar.

The multisensor approach to IJR height detection and retrieval aims at:

(1)

Exploring X-band radar data potential to detect and estimate the height of the IJR from its polarimetric signatures.

(2)

Integrating X-band radar estimates with the IJR height retrievals from L-band estimates used as a constraint.

(3)

Comparing X-band radar and TIR camera observations in order to better understand the link between the IJR and the lava fountains and to reduce errors in their respective IJR height estimates.

Physically speaking, we can consider the IJR area as a turbulent volume above the crater in which the gas represents the driving component of the pyroclastic jet. In this region, based on the polarimetric X-band synthetic signatures discussed in the previous Section 3.2, the copolar correlation coefficient should show lower values at lower altitudes within the jet region and tends to increase as the turbulent motion decreases. At the same time, the reflectivity factor should reach quite high values (say, greater than 45 dBZ at X band), related to the increase in the heterogeneity of tephra coarse particles being pushed out of the crater at high speed. From Figure 4, in particular, we should expect a significant decrease of Z_hh near the top of the IJR due to the decrease of the average particle size in the plume-fed by lava fountain, as well as a decrease of ρ_hv due to the predominant tumbling effect and turbulence within the eruption column. This behavior is typical of the transition zone between the lava fountains and the convective zone of volcanic plumes [2]. Moreover, near the top of IJR, the Z_dr values tend to increase due to larger non-spherical particles and reduced turbulence inducing less tumbling above the lava fountain. This is the physical rationale of the incandescent jet region radar retrieval algorithm (JR3A) approach, based on the analysis of the vertical gradients of polarimetric observables Z_hh and ρ_hv as well as L-band estimates if available.

The JR3A methodology is a decision approach for detecting H_JIR, based on the following steps:

(i) Select an area A_WR = (Δx, Δy) within the Cartesian horizontal coordinates x and y (derived from the radar projected azimuth and range coordinates at the lowest elevation), centered on volcanic vent expected position and define a volume V_WR = (A_WR, Δz) = (Δx,Δy,Δz) where vertical interval Δz above the vent extends preliminarily up to the expected maximum IJR height. In this work (Δx, Δy) are set to less than 3 km and Δz is set equal to 3 km (an IJR higher than 3 kilometers is improbable).

(ii) Calculate the mean value and standard deviation of Z_hh and ρ_hv within the selected volume V_WR and compute the standardized values of $Z_{hh}^{\prime }$ and ${\mathsf{\rho }}_{hv}^{\prime }$, centered with respect to respective mean values and divided with respect to standard deviation of Z_hh and ρ_hv. Then select within the volume V_WR, the incandescent jet-region sub-volume V_IJR verifying a combined polarimetric condition $C_{POL}^{Z,\rho }$, i.e., both $Z_{hh}^{\prime }$(x,y,t) lower than t_z and ${\mathsf{\rho }}_{hv}^{\prime }$(x,y,t). lower than t_ρ, that is similarly to (2) and (3):

$$C_{POL}^{Z,\rho } = \left\{Z_{hh}^{\prime }\left(x,y,t\right) < t_Z {\displaystyle \cup } {\mathsf{\rho }}_{hv}^{\prime }\left(x,y,t\right)< t_{\rho }\right\}$$

(6)

where the polarimetric thresholds values, used in this work for the X-band radar, are t_z = 2 and t_ρ = 1 (both adimensional).

(iii) Compute the vertical gradient ∇ along z for each column (x∈Δx, y∈Δy) within the volume V_WR at each time step (depending on the scanning radar sampling time) of the reflectivity factor, named $\nabla Z_{hh}^{ }$(x,y,t), and of the copolar correlation coefficient, named $\nabla {\mathsf{\rho }}_{hv}^{ }$(x,y,t).

(iv) Search for the IJR heights $h_{IJR}^X\left(x,y\right)$ above the crater and along the vertical coordinate axis z, such that previous conditions in (6) are satisfied on X-band radar reflectivity and copolar correlation coefficient, where the superscript X stands for X-band radar.

(v) Apply the Torricelli equation in (5) to the exit velocity v_ex normal to the crater surface, derived from the L-band radar measurements, to estimate the IJR height $H_{IJR}^L$;

(vi) Select the set heights $h_{IJR}^X\left(x,y,t\right)$ corresponding $\nabla Z_{hh}^{ }\left(x,y,t\right)$ and $\nabla {\mathsf{\rho }}_{hv}^{ }\left(x,y,t\right)$ different to zero within the X-band radar volume, minimizing the difference between $H_{IJR}^L$, derived from L-band radar velocities measurements ([25,38]), and each height $h_{IJR}^X\left(x,y,t\right)$ of X-band radar volumes, that is we can write:

$$h_{IJR}^{WR}\left(x,y,t\right) = Min\left\{h_{IJR}^X\left(x,y,t\right) - H_{IJR}^L\right\}$$

(7)

where Min is the minimization operator over (x,y) and WR stands for X-band weather radar. If L-band radar data are not available, this step can be skipped.

(vii) Compute the maximum height within all estimates in (7) and add the uncertainty Δh_HPBW representing the half-opening of the radar beam with respect to its boresight, namely at each time step we can obtain:

$$H_{IJR}^{WR}\left(t\right) = Max\left\{h_{IJR}^{WR}\left(x,y,t\right) + ∆h_{HPBW}\right\}$$

(8)

where Max is the maximum operator over (x,y). It should be noted that $H_{IJR}^{WR}\left(t\right)$ is the altitude above the summit crater (in the Etna case, about 3 km above sea level), whereas the half cross-section Δh_HPBW of the radar main-beam along the vertical above the crater is range dependent (in our case, around 300 m [25]).

4. Etna Case Studies

The recent paroxysmal activity at Etna was characterized by more than 150 lava fountain-fed tephra plume events lasting from 20 min up to several hours. Typically, these ash-rich events generate sustained plumes whose heights often exceed 10 km above sea level (a.s.l.) and usually impact the local population and air traffic [19,39,40,41]. Here, we analyzed 5 paroxysmal episodes that occurred between 2013 and 2015.

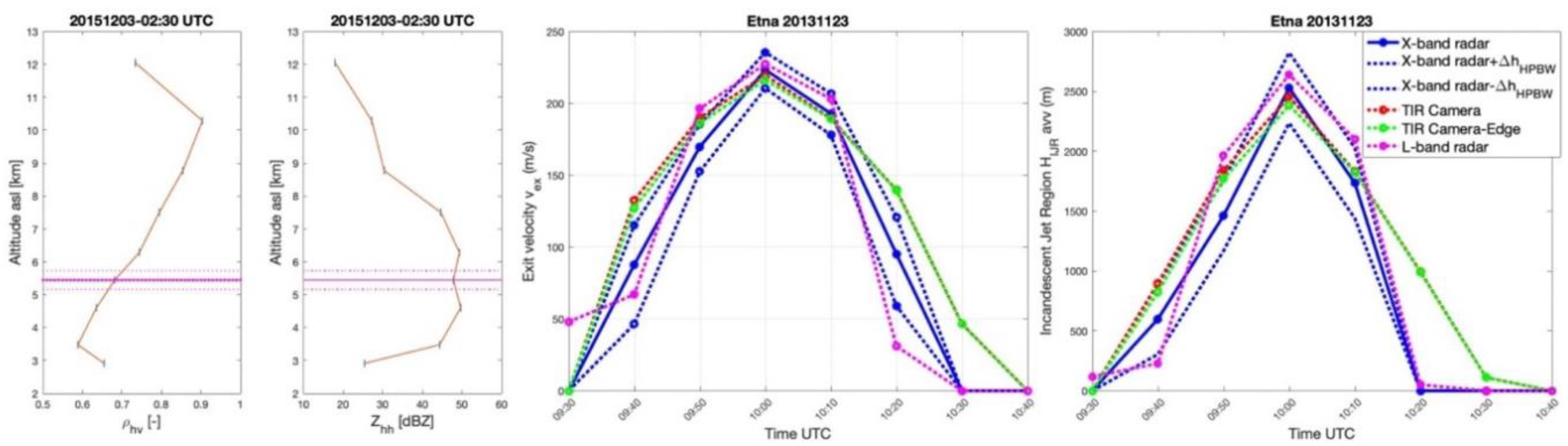
4.1. Paroxysm of 23 November 2013

On 23 November 2013 a lava fountain produced an intense explosive activity from the NSEC (Figure 5) for about an hour. Previous studies on this event focused on the eruptive processes and tephra volumes [22], integration of observational data [41], tephra fallout characterization [42], plume dynamics [43] and total grain-size distribution retrievals [25,44]. Figure 5 shows the range-height distribution of reflectivity factor, copolar correlation coefficient and differential reflectivity. Looking at these measurements, close to the NSEC, we notice a column showing increasing Z_hh values (pixels in red/orange) above the crater and decreasing values of ρ_hv (pixels in green/blue). A similar trend is shown in the Z_hh and Z_dr signatures. For the 23 November 2013 eruption, shown in Figure 5, the lowest values of ρ_hv are observed only in the lateral parts of the first portion of the eruptive column. As observed by [43], ρ_hv displays a notably low signature above the crater during the violent phase of the explosive activity corresponding to what we call the IJR.

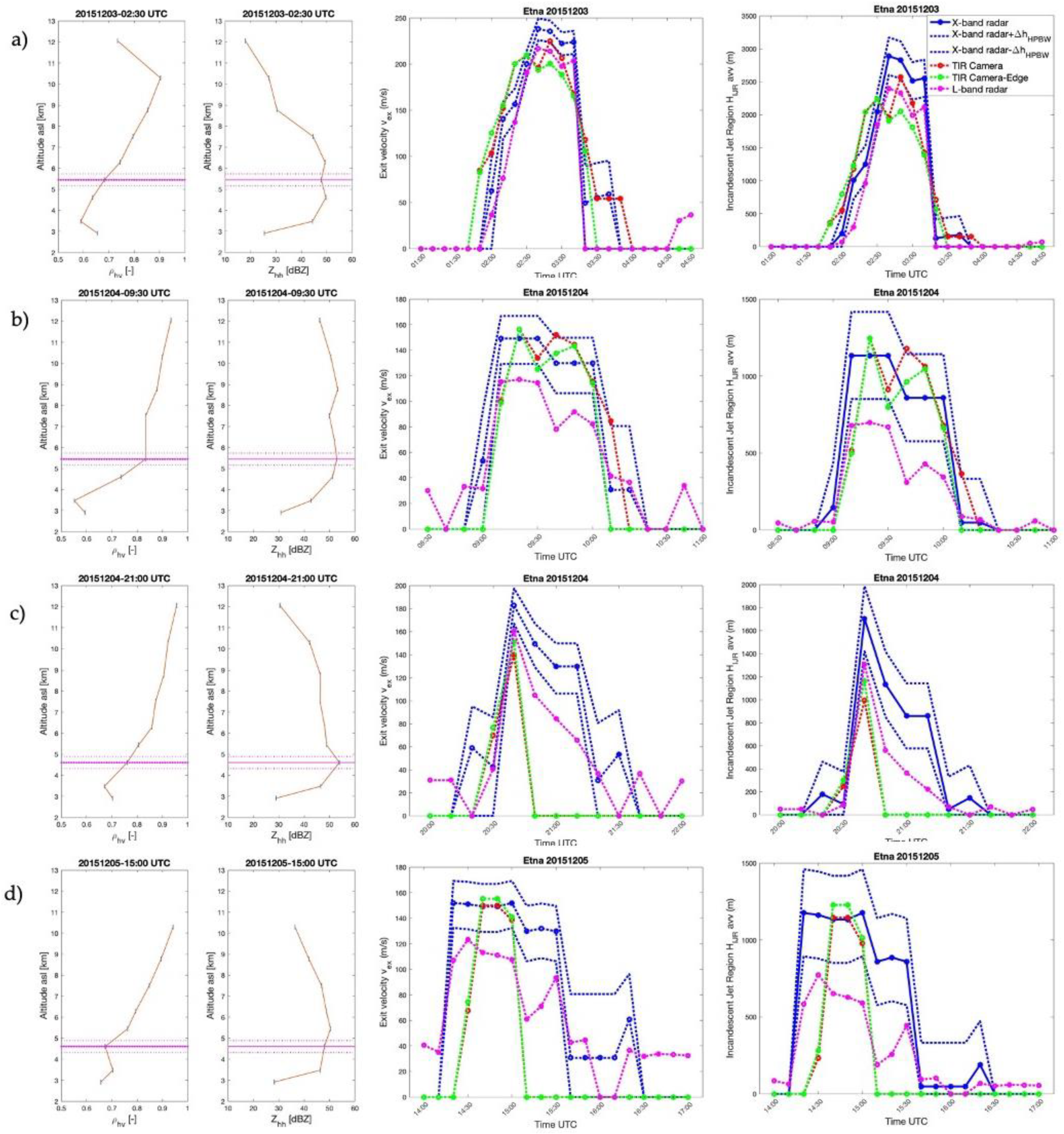
4.2. Paroxysms on 3–5 December 2015

Starting in the second half of October 2015, the VOR produced an intra-crater Strombolian activity that progressively increased and culminated in four lava fountains on 3, 4 and 5 December. These episodes, each lasting 50–60 min, generated eruptive columns reaching 15 km asl [45]. Figure 6 shows the RHI (from left to right) of the range-height distribution of reflectivity factor, copolar correlation coefficient and differential reflectivity for those events on 3 December 2015 at 02:30 UTC (a), on 4 December 2015 at 09:30 UTC (b), 4 December 2015 at 21:00 UTC (c) and on 5 December 2015 at 15:00 UTC (d). In the case of the 2015 events, the different polarimetric responses of the IJR are also visible in the RHI patterns. In particular, the lava fountain and the eruption column are well detectable since, corresponding to high Z_hh value near the crater, moderate values of ρ_hv and a high Z_dr are observed for each event.

5. Results

In this section, we will demonstrate the potential of using X-band polarimetric radar observables, such as ρ_hv jointly with Z_hh, together with L-band radar constraints, to detect and estimate the IJR height. As anticipated, we will compare radar-based retrievals of IJR height with the estimates extracted from the TIR camera.

The left panels of Figure 7 (related to 23 November 2013 paroxysm) and Figure 8 (related to 3, 4, and 5 December 2015 events) show the horizontally averaged vertical profile at a certain time of Z_hh and ρ_hv at the instant of maximum X-band radar H_JIR estimates (above the vent). The vertical profile of ρ_hv gradually increases with altitude, whereas the Z_hh profiles initially increase at middle altitude and then decrease as they reach the plume top height. The drop of ρ_hv in the far side of the column is likely related to a low signal-to-noise ratio (SNR), as it corresponds to low reflectivity values [46]. A general increase in the copolar correlation coefficient with increasing altitudes can be due to a reduction of turbulent motion. Interestingly, the lowest value of ρ_hv coincides with the top of the IJR. Based on radar signatures shown in Figure 4, the IJR internal patterns of Z_hh and ρ_hv are associated with the behavior of a jet dominated by ballistic blocks, bombs, and lapilli. Moreover, these signatures could be related to the relative amplification of particle heterogeneity due to the reduction of size sorting depending on the vertical velocity [30]. The continuous lines in the left panels of Figure 7 and Figure 8 identify the H_IJR (as the center height of the radar beam) in function of time (as indicated in the title of each panel). The dashed lines represent the two edges of the main-beam aperture at the same height, i.e., the uncertainty of the H_IJR estimates.

The central and right-hand panels of Figure 7 and Figure 8, panels a–d, show the comparisons among the time-series of v_ex and H_IJR, derived respectively from the TIR camera (TIR Camera and TIR Camera-Edge), X-band and L-band radar. In detail, the central panel of Figure 7 shows an increasing trend of v_ex with a maximum value of 215–225 m/s at 10:00 UTC. In the left-hand panel, a similar increasing trend of TIR camera-derived H_IJR starting from 9:30 UTC is observed with a peak of 2500 m at 10:00 UTC, using the TIR Camera algorithm as expressed in (2), then decreasing to a few meters at 10:30 UTC, and a peak of 2460 m, using the TIR Camera algorithm as expressed in (3), at 10:00 UTC, decreasing similarly to previous estimation. The X-band radar observes H_IJR only from 09:30–10:20 UTC with a final estimate between 10:00 UTC of 2530 m above the vent. An uncertainty Δh_HPBW (about 300 m) is associated to X-band radar retrievals and expressed as a function of half power beam width. Accordingly, this uncertainty is plotted in each panel as dashed lines indicated by H_IJR +/− Δh_HPBW. The height peaks observed by each sensor method show a very similar value of 2500 m. This minimal difference among retrievals is probably due to the X-band radar sensitivity to the microphysical characteristics of the detected particle, according to the combination of radar observables.

In the panel (a) of the central part of Figure 8, each v_ex values range between 200 and 250 m/s from 02:00 to 03:20 UTC, highlighting a good agreement among values obtained by all methods, with the greatest value detected by the X-band radar and lowest by the L-band radar; in (b) the variability of v_ex detected by the X-band radar incorporates the TIR camera values from 09:00 until 10:10 UTC with values ranging between 130 and 170 m/s, whereas the L-band velocities show the lowest values; in (c) all retrievals indicate a peak value of 140–200 m/s at the same time, i.e., 20:40 UTC. In this case, the time range detected by TIR camera is limited to 20:30 until 20:50 UTC; in (d) Similarly, the variability of v_ex detected by the X-band radar incorporates the TIR camera values between 09:00 and 10:10 UTC, whereas the L-band shows the lowest values that range between 130 and 170 m/s from 14:20 to 15:10 UTC.

In the panel (a) on the right of Figure 8 there is a longer temporal extension of the H_IJR from the TIR camera (01:30 and 03:30 UTC), while for the radar the IJR-detected interval is between 01:50–03:50 UTC. The maximum of IJR height is obtained by X-band radar estimates at 02:30 UTC, with a value of 2900 m ± 300 m (Δh_HPBW) and two TIR camera peaks of 2250 m at 02:20 and of 2600 m at 02:40 UTC. In the right panel (b) a temporal agreement is observed in the identification of heights among the various methods between 09:00 and 10:30 UTC. The peaks for the TIR camera are at 09:20 UTC with a value around 1300 m. The X-band radar estimate presents a constant value of 1150 m ± 300 m (Δh_HPBW) between 09:10 and 09:30 UTC. On the evening of 4 December 2015, right panel (c) the TIR camera estimates are limited to a small interval between 20:20 and 20:50 UTC with a peak at 20:40 UTC of about 1000 m and 1150 m. The X-band radar estimates, instead, present a longer time interval going from 20:10 to 21:40 UTC with a peak of 1700 m ± 300 m (Δh_HPBW) at 20:40 UTC. Similarly to the previous case, on 5 December 2015 (right panel (d)), the incandescent region height estimates from TIR camera show a consistent estimate only between 14:20 and 15:10 UTC, probably for the poor visibility due to weather clouds and an H_IJR value of 1150 m and 1250 m.

The X-band radar, thanks to its scanning capacity in elevation and azimuth and little sensitivity to small water droplets of non-precipitating clouds, provides an estimate of H_IJR within the interval between 14:10 UTC to 16:30 UTC. Its estimated height between 14:10 UTC and 15:10 UTC is quite constant (about 1200 m ± 300 m (Δh_HPBW)) and with a secondary peak of 200 m at 16:20 UTC. It should be noted that a temperature drop detected by the TIR camera of about ten degrees has been observed, correlated to some meteorological phenomenon, as confirmed by the video cameras of INGV-OE, that is interposed between the TIR camera and the eruptive plume with consequent lowering of the H_IJR identification thresholds. Observing the various H_IJR retrievals from the X-band radar compared to those obtained from the TIC camera, it emerges that the radar can detect the IJR observed by the camera. If we take into account the discretization of the altitudes detected by the X-band radar, due to the observation angle and the distance between the radar and the volcanic plume, and given its uncertainty relative to the Δh_HPBW, the H_IJR estimates of the X-band radar are quite similar to the TIR camera estimates.

The lower estimates of the TIR camera, especially between 20:00 and 22:00 UTC on 4 December and during the 5 December 2015 events (Figure 8c,d) are mainly due to bad weather conditions. Indeed, the presence of meteorological water clouds in Etna’s summit area results in a strong degradation of the detected brightness temperature. For this reason, the detected heights are limited to narrow time intervals with respect to what was detected by the two radars. This variation is less evident when comparing both X-band radar and L-band radar estimates, although the X-band radar polarimetric signatures appear significantly cleaner in November 2013, due to the absence of any meteorological phenomenon at the same time as the eruption, than in December 2015 (see Figure 7 and Figure 8), as well as for a different resolution of the radar beam.

In addition, we quantified the vertical gradient variability of reflectivity factor and copolar correlation coefficient involved in the H_IJR determination (panel a) in the Figure 9a). The values of ∇Z_hh follow the range (7.20 dBZ +/− 8.50 dBZ), whereas the values of ∇ρ_hv are in within (−0.06 +/− 0.16). In Figure 9b, the bars of vertical gradient of reflectivity factor and copolar correlation coefficient, related to five events, are plotted in different colors. Moreover, to quantify the difference in the IJR height estimates with the two sensors, we compute the difference between the retrievals $H_{IJR}^{WR}\left(t\right)$, derived from X-band radar using (8), and $H_{IJR}^{TIR}$ from TIR camera using (4) (TIR Camera algorithm), as expressed below:

$$\delta H_{WR-TIR}\left(t\right) = H_{IJR}^{WR}\left(t\right) - H_{IJR}^{TIR}\left(t\right)$$

(9)

The few higher values, shown in the tail of the histogram, ranging between 590 m and 1180 m and with mean value of 890 m, are related to the limited operativity of the TIR camera instrument for lava fountain detection due to the occurrence of meteorological clouds, as described before (Figure 9c). The X-band radar generally guarantees a “microwave” visibility of both plume and lava fountain activity in the cases of limited view conditions as during an explosive activity, thanks to the very good receiver sensitivity and effective penetration into volcanic jets and plumes.

The comparison of the results, obtained for the event of 23 November 2013 and 3–5 December 2015, shows a promising agreement. Our comparative analyses of the polarimetric radar measurements provides estimates of the IJR heights. Here, we might validate the use of such heights to retrieve first order estimates of MER during paroxysms at Etna [20,25,30]. Indeed, MER can be derived using the area of the eruptive vent, the magma-gas mixture density and the exit velocity (surface flux approach in [25]). If we consider the IJR height as a proxy for the height of the lava fountain [22,23,27], it can then be related to an exit velocity v_ex through the well-known Torricelli equation for a non-viscous ballistic flow [25,26,27]. When making this assumption, it is, however, important to bear in mind that the IJR can be higher than the lava fountains due to hot blocks, bombs, and lapilli that reach higher levels or lower levels when covered by volcanic ash.

Assuming that lava fountains feed the associated tephra plumes, the retrieved MER can be used to estimate the total mass of tephra emitted during a paroxysmal episode at Etna. Part of them will build the scoria cone [28,47] while the finest particles will feed the eruption column.

6. Conclusions

Describing lava fountain-fed tephra plumes and quantifying their dynamics is crucial to monitoring and hazard assessment but it is by no means trivial. The thermal-infrared camera provides 2D information on the near-source environment of the eruptive columns at Etna. However, the internal structure of the eruption column cannot be investigated, and thermal images suffer from severe degradation when meteorological clouds are present. The L-band radar with fixed pointing on the eruptive crater can only scan the first portion of the plume. On the contrary, X-band radar can scan the entire eruptive column in 3D volumes, providing accurate information of its geometrical and microphysical parameters with less weather restrictions. In this study, we also confirm the capacity of X-band radar to investigate the lava fountains and tephra plume activity during explosive eruptions.

Our analyses have shown how the patterns of the polarimetric observables Z_hh and ρ_hv, as detected from the X-band radar, provide a good estimate of the IJR height when compared to those obtained from the TIR camera. The radar signature of IJR is compatible with a jet of blocks, bombs, and lapilli. As previously discussed, the IJR can be of different height with respect to the lava fountain due to hot blocks, bombs and lapilli that reach higher levels or lower levels when covered by volcanic ash. Nonetheless, for the sake of simplicity, and in agreement with previous studies [22,23,27], the height of IJR has been used as a proxy for the height of the lava fountain in order to derive the exit velocity of the mixture. The exit velocity of the mixture can then be used to determine the associated MER and total erupted mass. In any case, it is important to also stress that the IJR and the lava fountain cannot be considered as a proxy of the gas thrust region of the associated plume [10].

In this work, we have demonstrated the importance of the combined use of TIR camera, X-band polarimetric and L-band Doppler radars for the characterization of paroxysmal activity at Etna. Further quantitative information should be obtained from multi-sensor strategies to investigate the link between lava fountains and IJR at other volcanoes and or eruptive events.