Improving Soil Thickness Estimations Based on Multiple Environmental Variables with Stacking Ensemble Methods
Abstract
1. Introduction
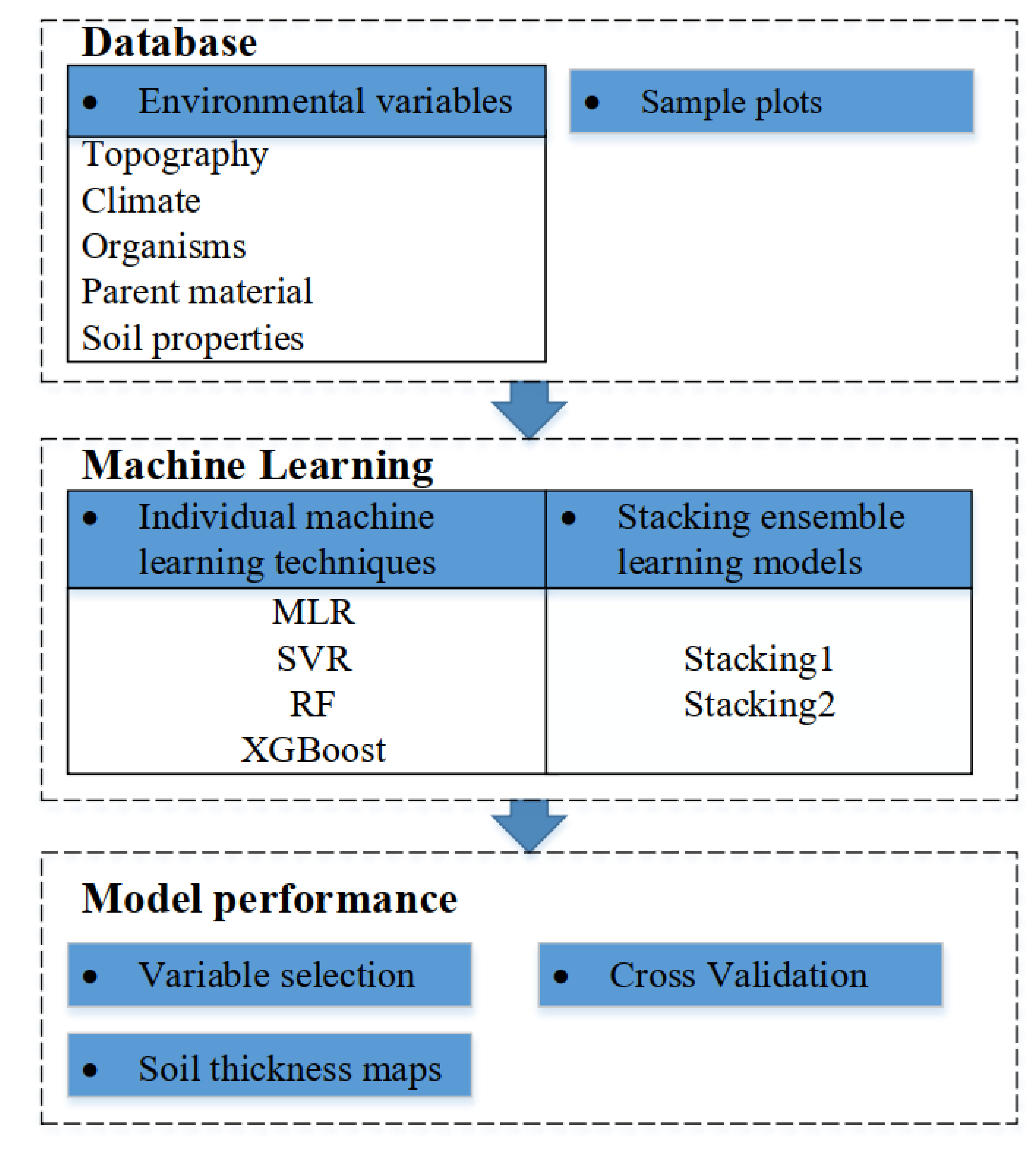
2. Material and Methods
2.1. Study Area
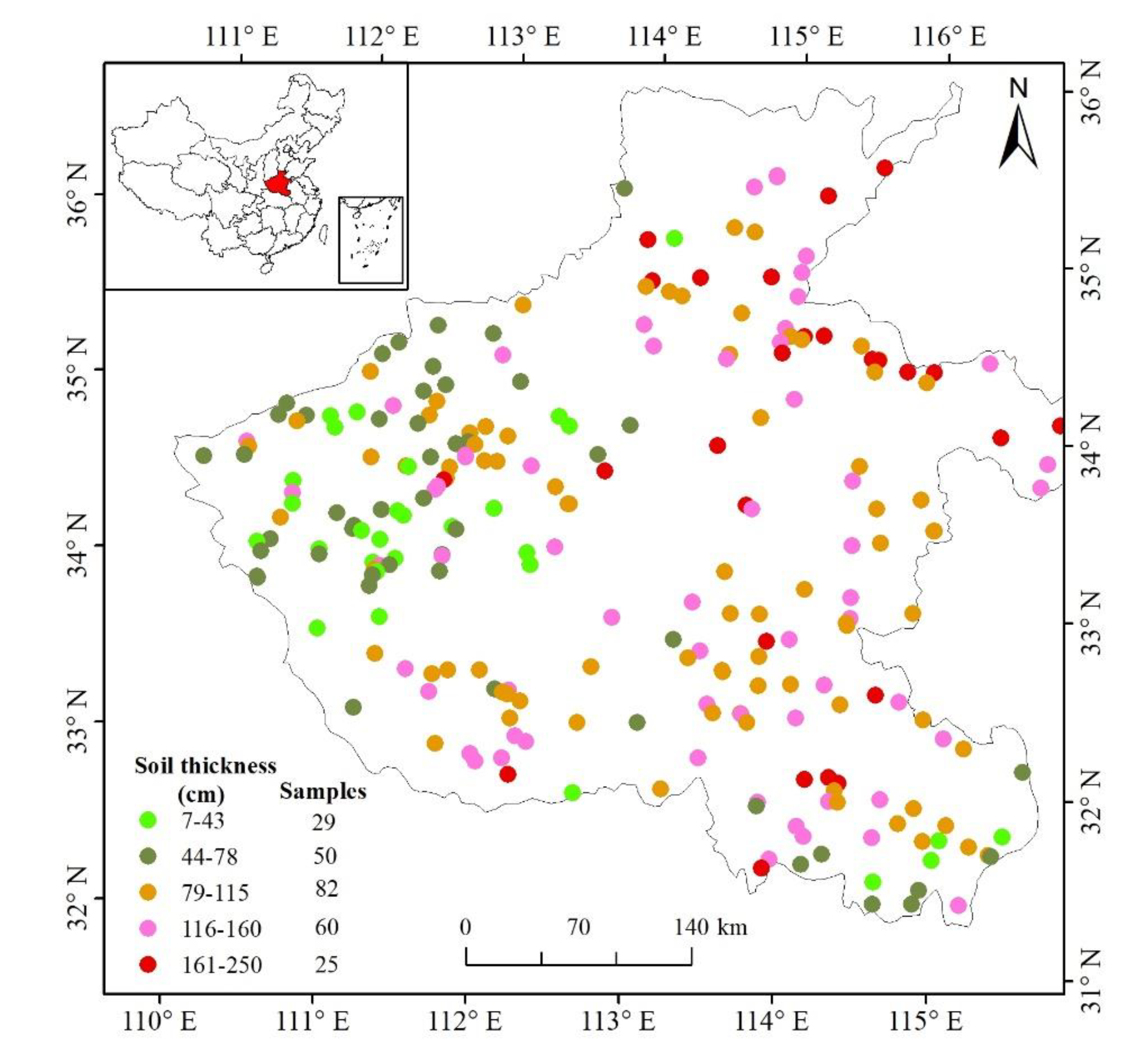
2.2. Soil Dataset
2.3. Environmental Factors
2.3.1. Topography
2.3.2. Climate
2.3.3. Vegetation
2.3.4. Geological and Soil Environment
2.4. Individual Machine Learning Techniques
2.4.1. Multiple Linear Regression
2.4.2. Support Vector Regression
2.4.3. Random Forest
2.4.4. Extreme Gradient Boosting
2.5. Stacking Ensemble Learning Models
2.6. Model Evaluation
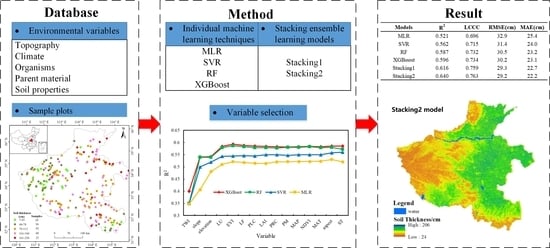
3. Result
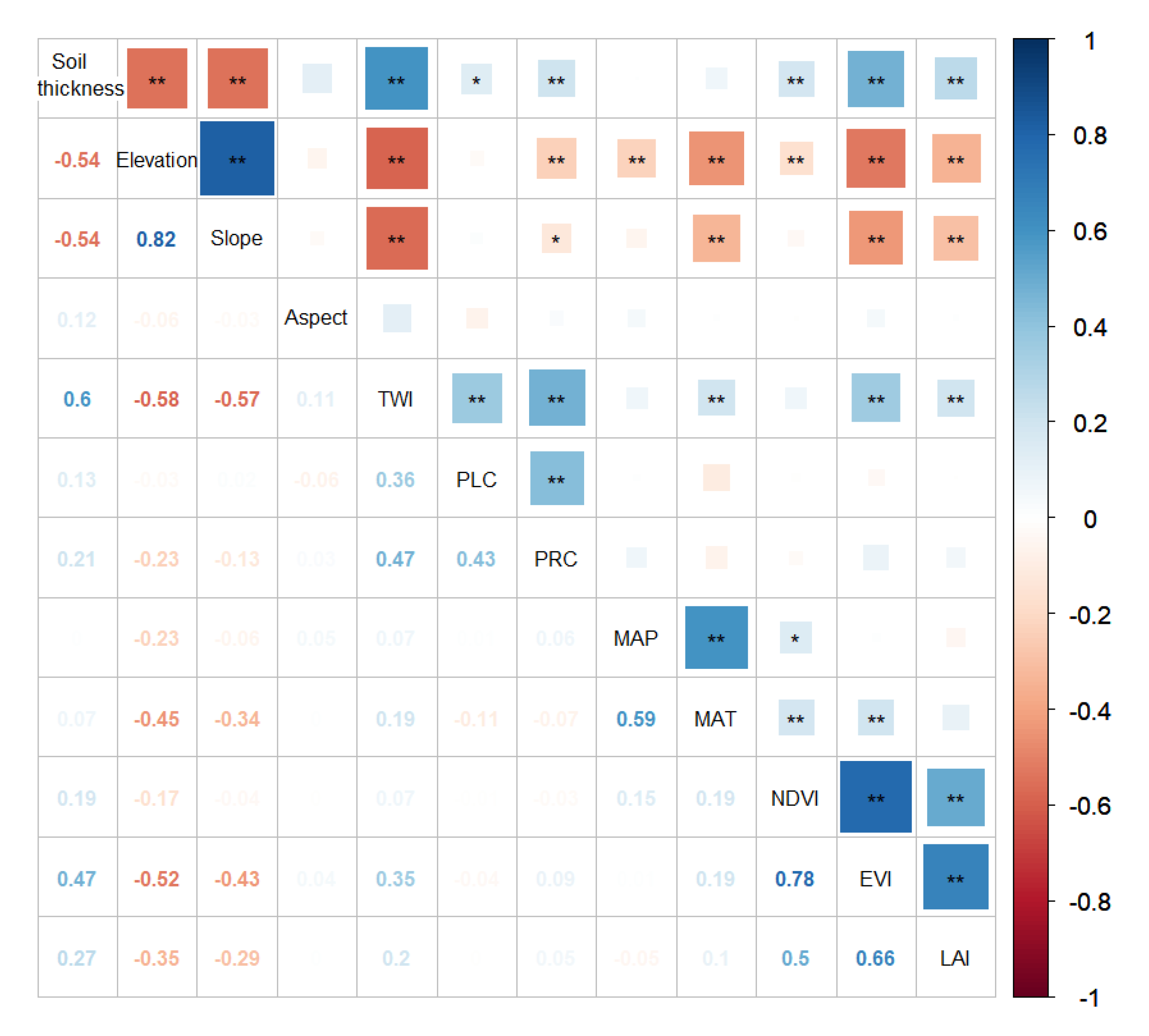
3.1. The Relationships between Soil Thickness and Environmental Factors
3.2. Performances of Four Individual Machine Learning (ML) Models
3.3. Best Environmental Variables
3.4. Performances of Stacking Ensemble Models
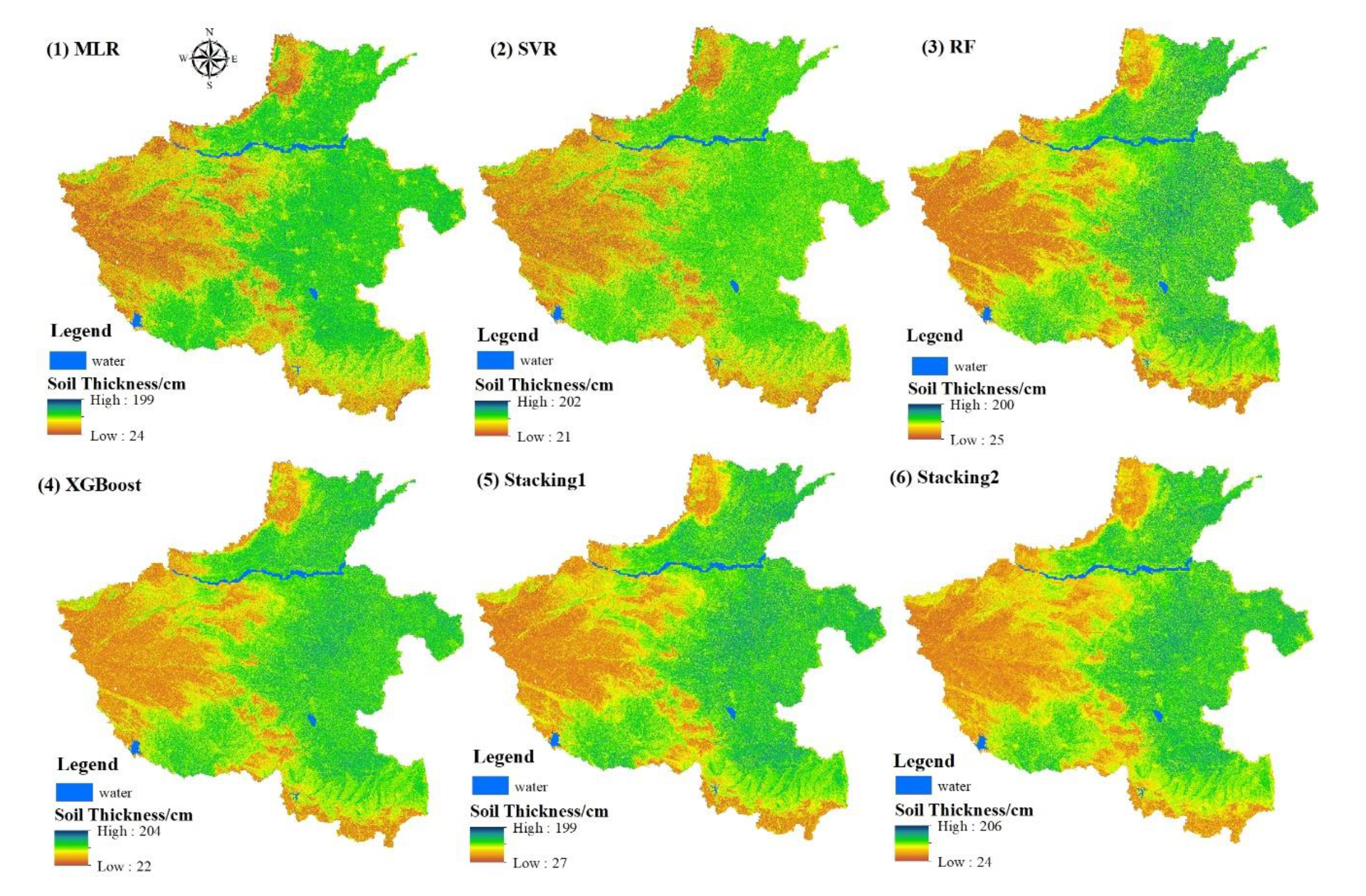
3.5. Spatial Distribution of Soil Thickness
4. Discussion
4.1. The Performance of Environmental Variables
4.2. The Importance of Variable Selection
4.3. The Performance of Ensemble Methods
4.4. The Performance of Predictions
4.5. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vogel, H.; Bartke, S.; Daedlow, K.; Helming, K.; Kögel-Knabner, I.; Lang, B.; Rabot, E.; Russell, D.; Stößel, B.; Weller, U.; et al. A systemic approach for modeling soil functions. Soil 2018, 4, 83–92. [Google Scholar] [CrossRef]
- Meyer, M.D.; North, M.P.; Gray, A.N.; Harold, S.J.Z. Influence of soil thickness on stand characteristics in a Sierra Nevada mixed-conifer forest. Plant Soil. 2007, 294, 113–123. [Google Scholar] [CrossRef]
- Gochis, D.J.; Vivoni, E.R.; Watts, C.J. The impact of soil depth on land surface energy and water fluxes in the North American Monsoon region. J. Arid Environ. 2010, 74, 564–571. [Google Scholar] [CrossRef]
- Liang, W.; Chan, M. Spatial and temporal variations in the effects of soil depth and topographic wetness index of bedrock topography on subsurface saturation generation in a steep natural forested headwater catchment. J. Hydrol. 2017, 546, 405–418. [Google Scholar] [CrossRef]
- Chan, H.C.; Chang, C.C.; Chen, P.A.; Lee, J.T. Using multinomial logistic regression for prediction of soil depth in an area of complex topography in Taiwan. Catena 2019, 176, 419–429. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, F.; Song, X. Recent progress and future prospect of digital soil mapping: A review. J. Integr. Agric. 2017, 16, 2871–2885. [Google Scholar] [CrossRef]
- Hartemink, A.E.; McBratney, A. A soil science renaissance. Geoderma 2008, 148, 123–129. [Google Scholar] [CrossRef]
- Lacoste, M.; Mulder, V.L.; Richer-de-Forges, A.C.; Martin, M.P.; Arrouays, D. Evaluating large-extent spatial modeling approaches: A case study for soil depth for France. Geoderma Reg. 2016, 7, 137–152. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Savin, I.Y.; Zhogolev, A.V.; Prudnikova, E.Y. Modern Trends and Problems of Soil Mapping. Eurasian Soil Sci. 2019, 52, 471–480. [Google Scholar] [CrossRef]
- Kuriakose, S.L.; Devkota, S.; Rossiter, D.G.; Jetten, V.G. Prediction of soil depth using environmental variables in an anthropogenic landscape, a case study in the Western Ghats of Kerala, India. Catena 2009, 79, 27–38. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Jafari, A.; Finke, P.A.; Vande Wauw, J.; Ayoubi, S.; Khademi, H. Spatial prediction of USDA- great soil groups in the arid Zarand region, Iran: Comparing logistic regression approaches to predict diagnostic horizons and soil types. Eur. J. Soil Sci. 2012, 63, 284–298. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Jafari, A.; Bagheri Bodaghabadi, M.; Ayoubi, S.; Taghizadeh-Mehrjardi, R.; Toomanian, N.; Kerry, R.; Xu, M. Conventional and digital soil mapping in Iran: Past, present, and future. Catena 2020, 188, 104424. [Google Scholar] [CrossRef]
- Cavazzi, S.; Corstanje, R.; Mayr, T.; Hannam, J.; Fealy, R. Are fine resolution digital elevation models always the best choice in digital soil mapping? Geoderma 2013, 195–196, 111–121. [Google Scholar] [CrossRef]
- Hengl, T.; Nikolić, M.; MacMillan, R.A. Mapping efficiency and information content. Int. J. Appl. Earth Obs. 2013, 22, 127–138. [Google Scholar] [CrossRef]
- Kim, J.S.; Grunwald, S.; Rivero, R.G. Soil Phosphorus and Nitrogen Predictions Across Spatial Escalating Scales in an Aquatic Ecosystem Using Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6724–6737. [Google Scholar] [CrossRef]
- Li, Y.; Chao, L.; Li, M. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Samuel-Rosa, A.; Heuvelink, G.B.M.; Vasques, G.M.; Anjos, L.H.C. Do more detailed environmental covariates deliver more accurate soil maps? Geoderma 2015, 243–244, 214–227. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, F.; Zhao, Y.; Song, X.; Zhang, G. An integrated method of selecting environmental covariates for predictive soil depth mapping. J. Integr. Agric. 2019, 18, 301–315. [Google Scholar] [CrossRef]
- Emadi, M.; Taghizadeh-Mehrjardi, R.; Cherati, A.; Danesh, M.; Mosavi, A.; Scholten, T. Predicting and Mapping of Soil Organic Carbon Using Machine Learning Algorithms in Northern Iran. Remote Sens. 2020, 12, 2234. [Google Scholar] [CrossRef]
- Sarkar, S.; Roy, A.K.; Martha, T.R. Soil depth estimation through soil-landscape modelling using regression kriging in a Himalayan terrain. Int. J. Geogr. Inf. Sci. 2013, 27, 2436–2454. [Google Scholar] [CrossRef]
- Tesfa, T.K.; Tarboton, D.G.; Chandler, D.G.; Mcnamara, J.P. Modeling soil depth from topographic and land cover attributes. Water Resour. Res. 2009, 45, W10438. [Google Scholar] [CrossRef]
- Han, X.; Liu, J.; Mitra, S.; Li, X.; Srivastava, P.; Guzman, S.M.; Chen, X. Selection of optimal scales for soil depth prediction on headwater hillslopes: A modeling approach. Catena 2018, 163, 257–275. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Sun, C.; Haase, D.; Lausch, A. Mapping of Soil Total Nitrogen Content in the Middle Reaches of the Heihe River Basin in China Using Multi-Source Remote Sensing-Derived Variables. Remote Sens. 2019, 11, 2934. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Modell. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Khaledian, Y.; Miller, B.A. Selecting appropriate machine learning methods for digital soil mapping. Appl. Math. Model. 2020, 81, 401–418. [Google Scholar] [CrossRef]
- Scarpone, C.; Schmidt, M.G.; Bulmer, C.E.; Knudby, A. Modelling soil thickness in the critical zone for Southern British Columbia. Geoderma 2016, 282, 59–69. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma. 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8. [Google Scholar] [CrossRef]
- Opitz, D.; Maclin, R. Popular Ensemble Methods: An Empirical Study. J Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Song, X.; Wu, H.; Ju, B.; Liu, F.; Yang, F.; Li, D.; Zhao, Y.; Yang, J.; Zhang, G. Pedoclimatic zone-based three-dimensional soil organic carbon mapping in China. Geoderma 2020, 363, 114145. [Google Scholar] [CrossRef]
- Riggers, C.; Poeplau, C.; Don, A.; Bamminger, C.; Höper, H.; Dechow, R. Multi-model ensemble improved the prediction of trends in soil organic carbon stocks in German croplands. Geoderma 2019, 345, 17–30. [Google Scholar] [CrossRef]
- Chen, S.; Mulder, V.L.; Heuvelink, G.B.M.; Poggio, L.; Caubet, M.; Román Dobarco, M.; Walter, C.; Arrouays, D. Model averaging for mapping topsoil organic carbon in France. Geoderma 2020, 366, 114237. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valavi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sens. 2020, 12, 1095. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Tran, T.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, J.; Chen, S.; Zhou, Y.; Liang, Z.; Wang, N.; Shi, Z. Fine-Resolution Mapping of Soil Total Nitrogen across China Based on Weighted Model Averaging. Remote Sens. 2020, 12, 85. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Toomanian, N.; Zeraatpisheh, M.; Amirian-Chakan, A.; Triantafilis, J. Digital Mapping of Soil Classes Using Ensemble of Models in Isfahan Region, Iran. Soil Syst. 2019, 3, 37. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Z.; Webster, R.; Zhang, G.; Zhou, Y.; Teng, H.; Hu, B.; Arrouays, D.; Shi, Z. A high-resolution map of soil pH in China made by hybrid modelling of sparse soil data and environmental covariates and its implications for pollution. Sci. Total Environ. 2019, 655, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Román Dobarco, M.; Arrouays, D.; Lagacherie, P.; Ciampalini, R.; Saby, N.P.A. Prediction of topsoil texture for Region Centre (France) applying model ensemble methods. Geoderma 2017, 298, 67–77. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, X. Multi-class Geomorphic Diversity and Its Relationship with Pedodiversity in Henan Province. Soils 2019, 51, 142–151. (In Chinese) [Google Scholar]
- Yi, C.; Li, D.; Zhang, G.; Zhao, Y.; Yang, J.; Liu, F.; Song, D. Criteria for partition of soil thickness and case studies. Acta Pedol. Sin. 2015, 52, 220–227. (In Chinese) [Google Scholar]
- Wei, K. Soil Geography of Henan; Henan Science and Technology Press: Zhengzhou, China, 1995. (In Chinese) [Google Scholar]
- Wei, K. Soils of Henan Province; China Agriculture Press: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Conrad, O.; Olaya, V. SAGA-GIS Module Library Documentation (v2.2.3). Module Valley Depth. Available online: http://www.sagagis.org/saga_tool_doc/2.2.3/index.html (accessed on 2 January 2020).
- Piao, S.; Jingyun, F.; Zhou, L.; Qinghua, G.; Henderson, M.; Wei, J.; Yan, L.; Shu, T. Interannual variations of monthly and seasonal normalized difference vegetation index (NDVI) in China from 1982 to 1999. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Mehnatkesh, A.; Ayoubi, S.; Jalalian, A.; Sahrawat, K.L. Relationships between Soil Depth and Terrain Attributes in a Semi Arid Hilly Region in Western Iran. J. Mt. Sci. 2013, 10, 163–172. [Google Scholar] [CrossRef]
- Li, A.; Tan, X.; Wu, W.; Liu, H.; Zhu, J. Predicting active-layer soil thickness using topographic variables at a small watershed scale. PLoS ONE 2017, 12, e183742. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, F.; Jiang, Z.; Li, W.; Zhang, J.; Zeng, F.; Li, H. Relationship between soil depth and terrain attributes in karst region in Southwest China. J. Soils Sediment 2014, 14, 1568–1576. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. Available online: http://www.R-project.org (accessed on 12 December 2019).
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Meyer, D.; Wien, F.T. Support Vector Machines—The Interface to Libsvm in Package e1071. Available online: https://cran.r-project.org/web/packages/e1071/index.html (accessed on 25 November 2019).
- Breiman, L.; Cutler, A. Breiman and Cutler’s Random Forests for Classification and Regression. Available online: https://cran.r-project.org/web/packages/randomForest/ (accessed on 25 March 2018).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tan, Y. Extreme Gradient Boosting. 2020. Available online: https://cran.r-project.org/web/packages/xgboost/xgboost.pdf. (accessed on 30 July 2020).
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R.; Narasimhan, B.; Tay, K.; Simon, N.; Qian, J. Lasso and Elastic-Net Regularized Generalized Linear Models. Available online: https://cran.r-project.org/web/packages/glmnet/index.html (accessed on 30 July 2020).
- Ridgeway, G. Gbm: Generalized Boosted Regression Models. Available online: https://cran.r-project.org/web/packages/gbm/index.html (accessed on 30 July 2020).
- Gessler, P.E.; Chadwick, O.A.; Chamran, F.; Holmes, K. Modeling soil-landscape and ecosystem properties using terrain attributes. Soil Sci. Soc. Am. J. 2000, 64, 2046–2050. [Google Scholar] [CrossRef]
- Ho, J.; Lee, K.T.; Chang, T.; Wang, Z.; Liao, Y. Influences of spatial distribution of soil thickness on shallow landslide prediction. Eng. Geol. 2012, 124, 38–46. [Google Scholar] [CrossRef]
- Maynard, J.J.; Levi, M.R. Hyper-temporal remote sensing for digital soil mapping: Characterizing soil-vegetation response to climatic variability. Geoderma 2017, 285, 94–109. [Google Scholar] [CrossRef]
- Swain, S.; Abeysundara, S.; Hayhoe, K.; Stoner, A.M.K. Future changes in summer MODIS-based enhanced vegetation index for the South-Central United States. Ecol. Inform. 2017, 41, 64–73. [Google Scholar] [CrossRef]
- Chen, S.; Mulder, V.L.; Martin, M.P.; Walter, C.; Lacoste, M.; Richer-de-Forges, A.C.; Saby, N.P.A.; Loiseau, T.; Hu, B.; Arrouays, D. Probability mapping of soil thickness by random survival forest at a national scale. Geoderma 2019, 344, 184–194. [Google Scholar] [CrossRef]
- Malone, B.; Searle, R. Improvements to the Australian national soil thickness map using an integrated data mining approach. Geoderma 2020, 377, 114579. [Google Scholar] [CrossRef]
- Paul, S.S.; Coops, N.C.; Johnson, M.S.; Krzic, M.; Chandna, A.; Smukler, S.M. Mapping soil organic carbon and clay using remote sensing to predict soil workability for enhanced climate change adaptation. Geoderma 2020, 363, 114177. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Li Liu, D.; Simpson, M.; McGowen, I.; Sides, T. Estimating soil organic carbon stocks using different modelling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
- Dietterich, T.G. An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
- McCaffrey, D.F.; Ridgeway, G.; Morral, A.R. Propensity Score Estimation with Boosted Regression for Evaluating Causal Effects in Observational Studies. Psychol. Methods 2004, 9, 403–425. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Ge, Y.; Avitabile, V.; Heuvelink, G.B.M.; Wang, J.; Herold, M. Fusion of pan-tropical biomass maps using weighted averaging and regional calibration data. Int. J. Appl. Earth Obs. 2014, 31, 13–24. [Google Scholar] [CrossRef]
- Somarathna, P.D.S.N.; Minasny, B.; Malone, B.P. More Data or a Better Model? Figuring Out What Matters Most for the Spatial Prediction of Soil Carbon. Soil Sci. Soc. Am. J. 2017, 81, 1413–1426. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, G.; Sheng, J.; Weindorf, D.C.; Wu, H.; Xuan, J.; Yan, A.; Gu, Z. Estimating effective soil depth at regional scales: Legacy maps versus environmental covariates. J. Plant Nutr. Soil Sci. 2018, 181, 167–176. [Google Scholar] [CrossRef]
- Siewert, M.B. High-resolution digital mapping of soil organic carbon in permafrost terrain using machine learning: A case study in a sub-Arctic peatland environment. Biogeosciences 2018, 15, 1663–1682. [Google Scholar] [CrossRef]
- Li, C.; Li, M.; Li, Y.; Qian, P. Estimating aboveground forest carbon density using Landsat 8 and field-based data: A comparison of modelling approaches. Int. J. Remote Sens. 2020, 41, 4269–4292. [Google Scholar] [CrossRef]
- Pahlavan-Rad, M.R.; Khormali, F.; Toomanian, N.; Brungard, C.W.; Kiani, F.; Komaki, C.B.; Bogaert, P. Legacy soil maps as a covariate in digital soil mapping: A case study from Northern Iran. Geoderma 2016, 279, 141–148. [Google Scholar] [CrossRef]
- Valavi, R.; Elith, J.; Lahoz Monfort, J.J.; Guillera Arroita, G. blockCV: An R package for generating spatially or environmentally separated folds for k-fold cross-validation of species distribution models. Methods Ecol. Evol. 2018, 10, 225–232. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
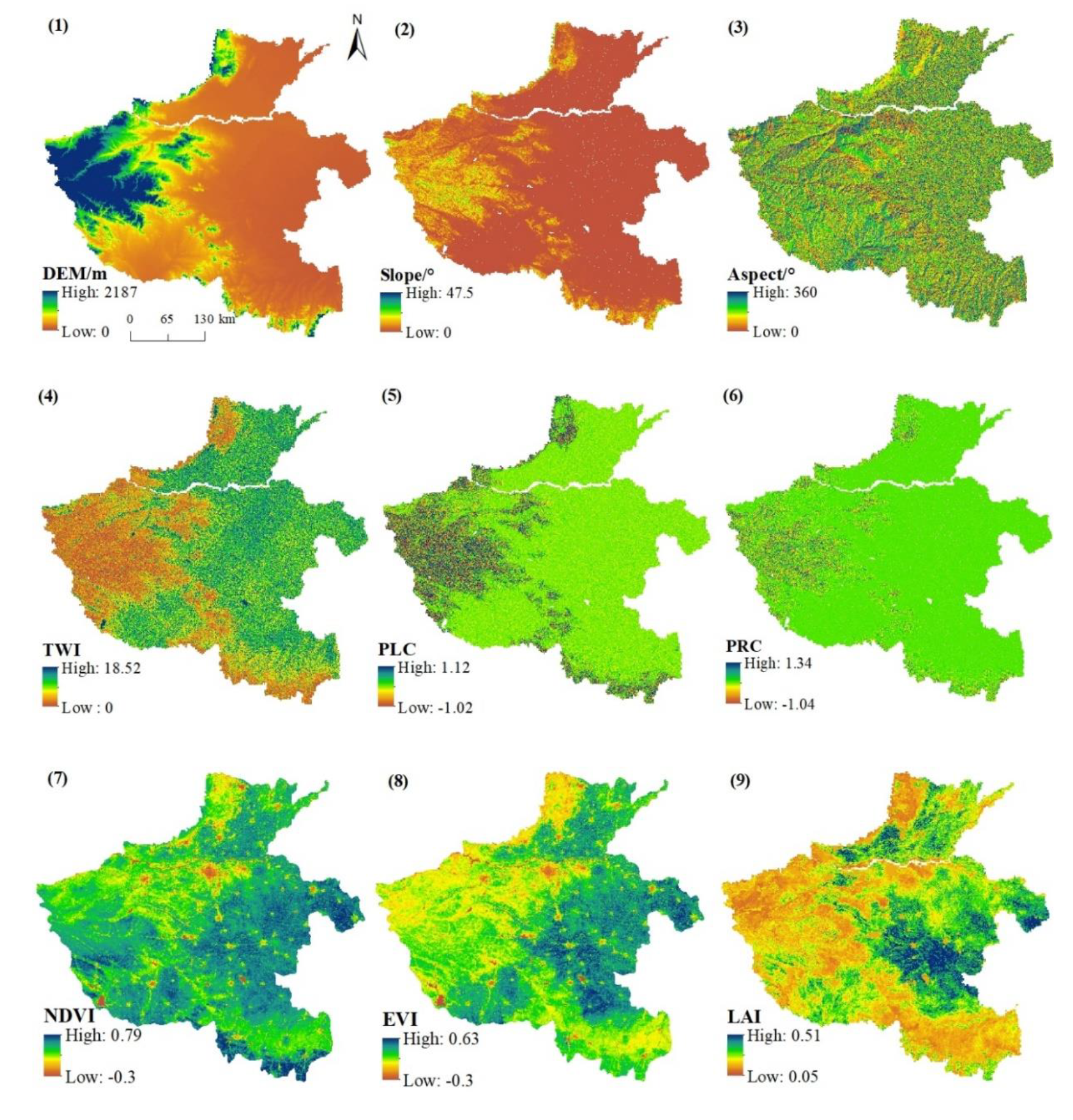
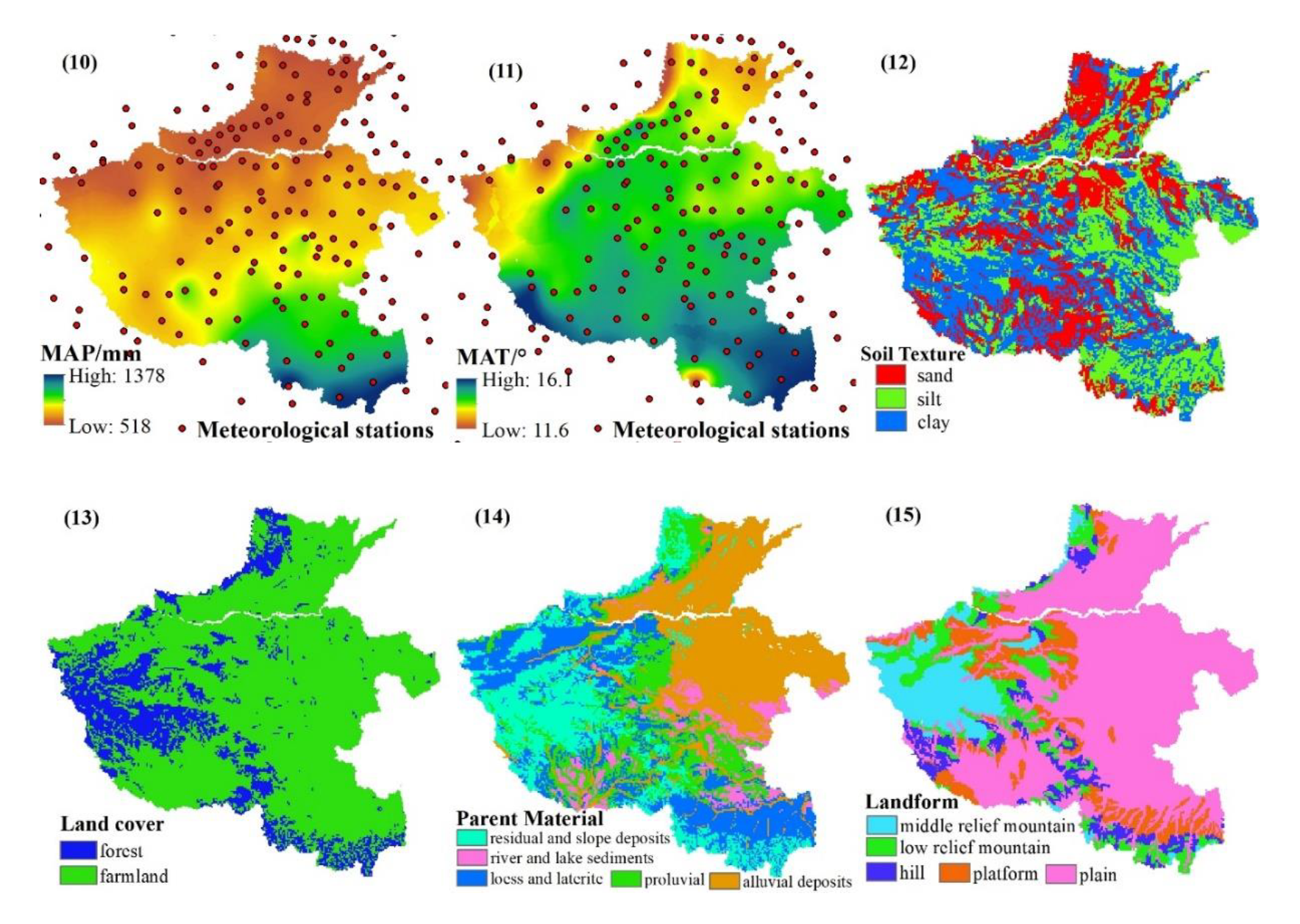





| Variable | Abbreviation | Soil Forming Factor | Resolution |
|---|---|---|---|
| Elevation | elevation | Topography | 30 m |
| Slope | slope | Topography | 30 m |
| Aspect | aspect | Topography | 30 m |
| Topographic Wetness Index | TWI | Topography | 30 m |
| Plan Curvature | PLC | Topography | 30 m |
| Profile Curvature | PRC | Topography | 30 m |
| Mean Annual Precipitation | MAP | Climate | 250 m |
| Mean Annual Temperature | MAT | Climate | 250 m |
| Mean Annual Normalized Vegetation Index | NDVI | Organism | 250 m |
| Mean Annual Enhanced Vegetation Index | EVI | Organism | 250 m |
| Mean Annual Leaf Area Index | LAI | Organism | 1000 m |
| Variable | Abbreviation | Soil Forming Factor | Category |
|---|---|---|---|
| Landform | LF | Topography | Middle Relief Mountain, Low Relief Mountain Hill, Platform, Plain |
| Parent Material | PM | Parent Material | Residual and Slope Deposits, Proluvial, Loess and Laterite, Alluvial Deposits, River and Lake Sediments |
| Land Use | LU | Organism | Forest, Farmland |
| Soil Texture | ST | Soil Property | Sand, Silt, Clay |
| Models | R2 | LCCC | RMSE (cm) | MAE (cm) |
|---|---|---|---|---|
| MLR | 0.521 | 0.696 | 32.9 | 25.4 |
| SVR | 0.562 | 0.715 | 31.4 | 24.0 |
| RF | 0.587 | 0.732 | 30.5 | 23.2 |
| XGBoost | 0.596 | 0.734 | 30.2 | 23.1 |
| Stacking1 | 0.616 | 0.759 | 29.3 | 22.7 |
| Stacking2 | 0.640 | 0.763 | 29.2 | 22.2 |
| Model | Minimum (cm) | Maximum (cm) | Mean (cm) | Standard Deviation (cm) |
|---|---|---|---|---|
| MLR | 24 | 199 | 103.7 | 35.8 |
| SVR | 21 | 202 | 99.6 | 32.6 |
| RF | 25 | 200 | 104.5 | 36.2 |
| XGBoost | 22 | 204 | 105.5 | 34.4 |
| Stacking1 | 25 | 199 | 105.1 | 34.6 |
| Stacking2 | 24 | 206 | 105.1 | 34.5 |
| Model | Minimum (cm) | Maximum (cm) | Mean (cm) | Standard Deviation (cm) | Proportion of Total Area (%) | ||
|---|---|---|---|---|---|---|---|
| <10 cm | 10–20 cm | >20 cm | |||||
| Stacking2-MLR | −61.1 | 40.0 | 1.3 | 19.1 | 43.1 | 39.1 | 17.8 |
| Stacking2-SVR | 60.3 | 46.1 | 5.4 | 21.1 | 45.8 | 40.7 | 13.6 |
| Stacking2-RF | −35.2 | 20.4 | 0.6 | 11.0 | 69.6 | 23.4 | 7.0 |
| Stacking2-XGBoost | −29.4 | 17.4 | −0.5 | 8.9 | 79.3 | 16.8 | 3.9 |
| Stacking2-Stacking1 | −19.8 | 12.1 | 0.0 | 5.9 | 91.3 | 7.9 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Luo, J.; Jin, X.; He, Q.; Niu, Y. Improving Soil Thickness Estimations Based on Multiple Environmental Variables with Stacking Ensemble Methods. Remote Sens. 2020, 12, 3609. https://doi.org/10.3390/rs12213609
Li X, Luo J, Jin X, He Q, Niu Y. Improving Soil Thickness Estimations Based on Multiple Environmental Variables with Stacking Ensemble Methods. Remote Sensing. 2020; 12(21):3609. https://doi.org/10.3390/rs12213609
Chicago/Turabian StyleLi, Xinchuan, Juhua Luo, Xiuliang Jin, Qiaoning He, and Yun Niu. 2020. "Improving Soil Thickness Estimations Based on Multiple Environmental Variables with Stacking Ensemble Methods" Remote Sensing 12, no. 21: 3609. https://doi.org/10.3390/rs12213609
APA StyleLi, X., Luo, J., Jin, X., He, Q., & Niu, Y. (2020). Improving Soil Thickness Estimations Based on Multiple Environmental Variables with Stacking Ensemble Methods. Remote Sensing, 12(21), 3609. https://doi.org/10.3390/rs12213609