Assessing the Performance of a Low-Cost Thermal Camera in Proximal and Aerial Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Proximal Analysis
2.2. Aerial Analysis
2.2.1. Data Acquisition
2.2.2. Flight Altitude Analysis
2.2.3. Orthomosaic Generation and Blending Modes Analysis
2.3. Empirical Line Calibration
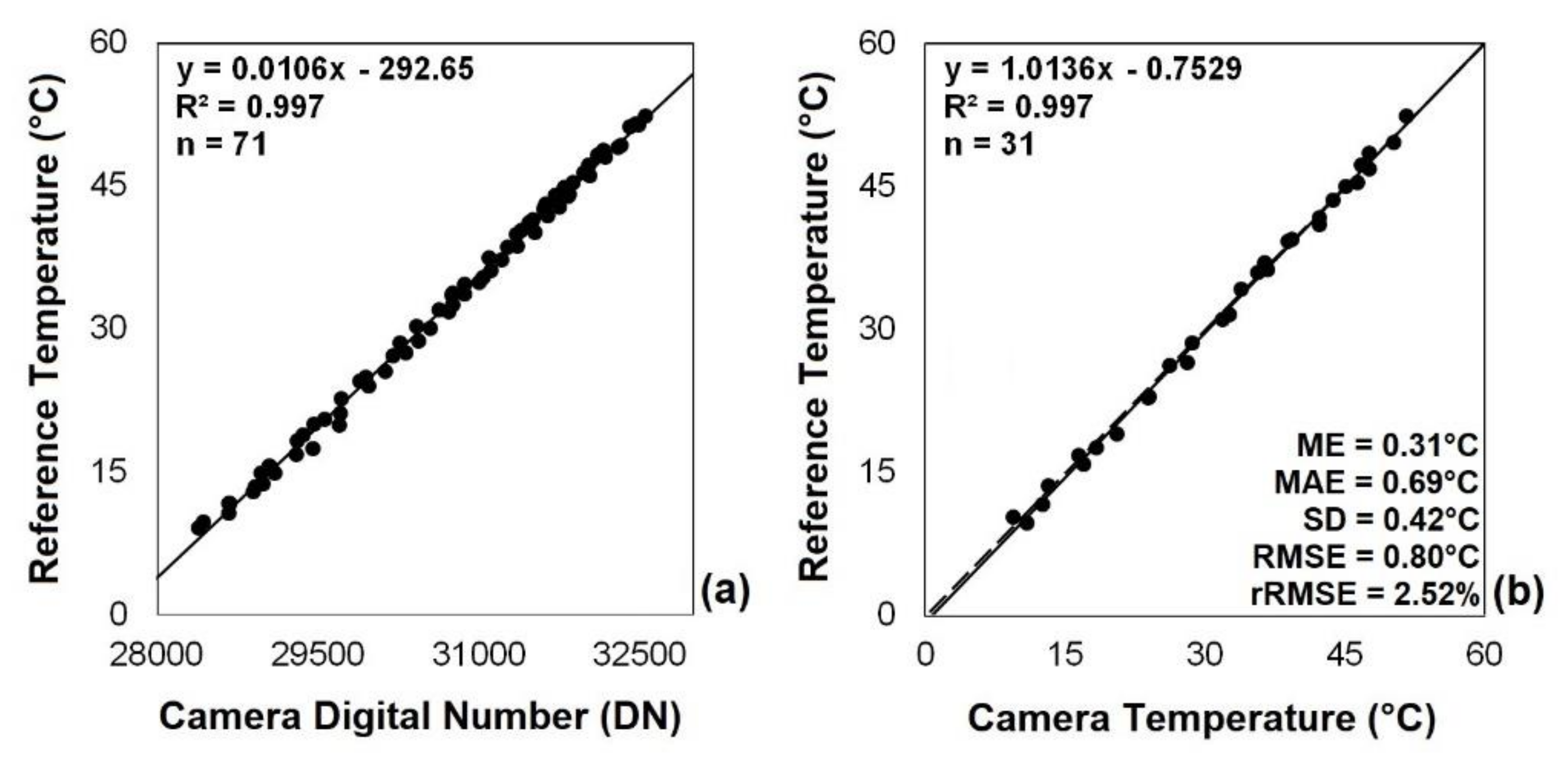
2.3.1. Proximal Calibration
2.3.2. Aerial Calibration
2.4. Statistical Analysis
3. Results
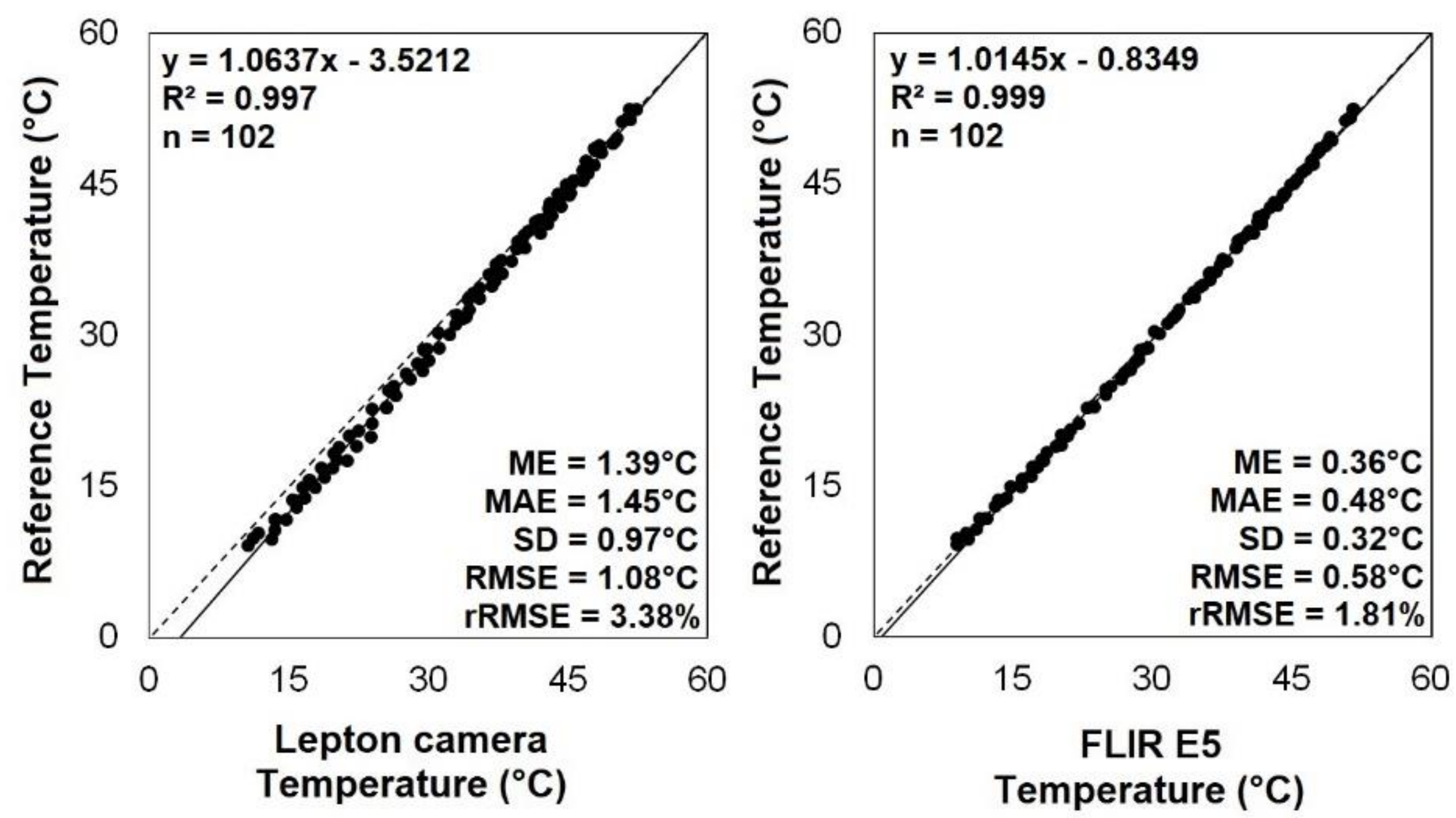
3.1. Proximal Analysis
3.2. Aerial Analysis
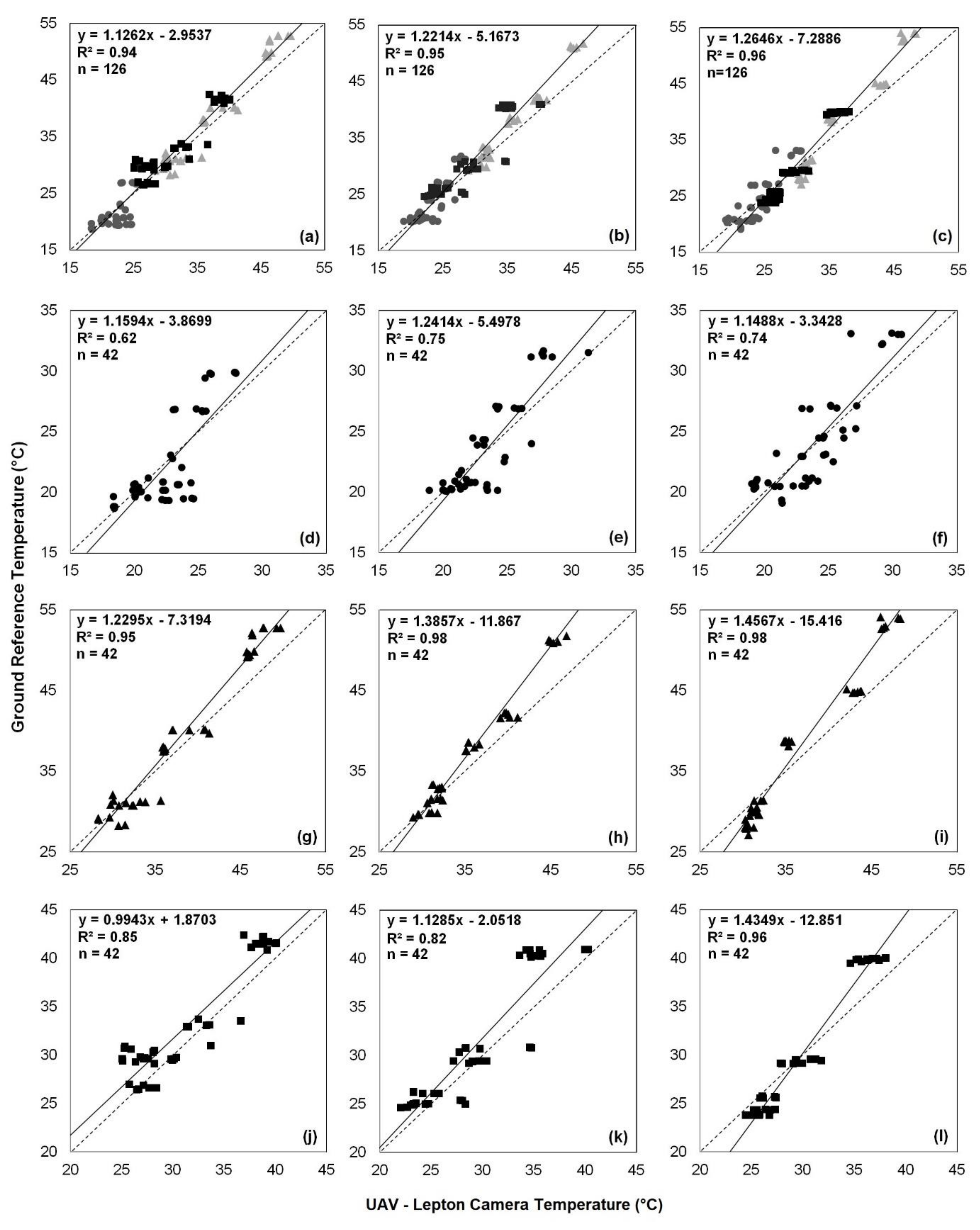
3.2.1. Flight Altitudes
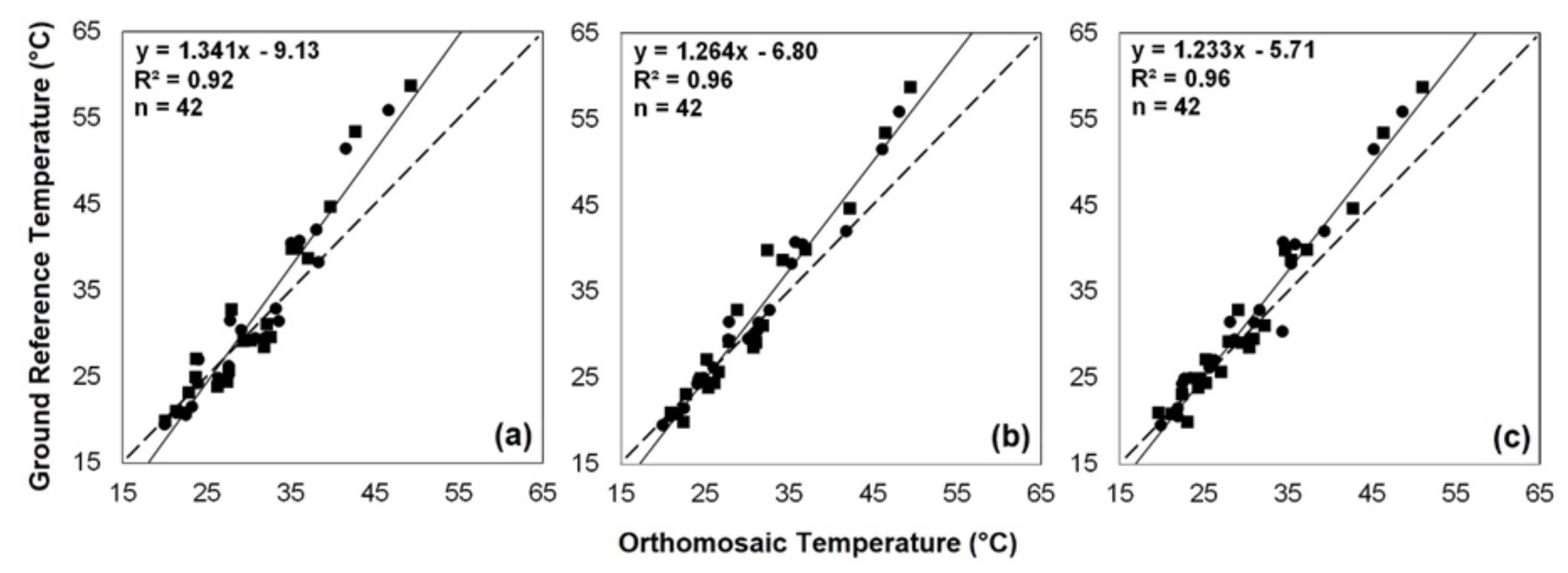
3.2.2. Blending Models
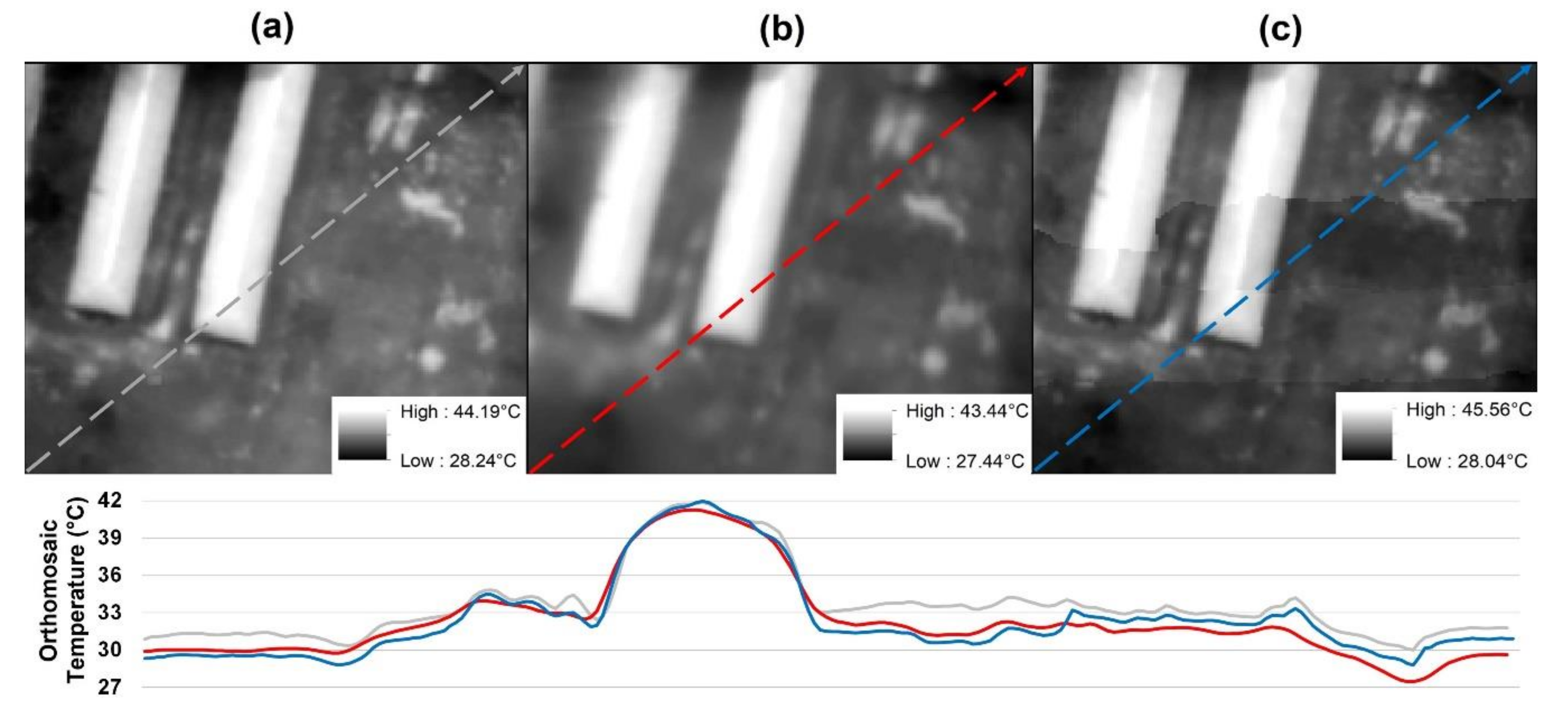
3.2.3. Co-registration Process
3.3. Calibration Strategies
3.3.1. Proximal Calibration
3.3.2. Aerial Calibration
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Prakash, A. Thermal Remote Sensing: Concepts, Issues and Applications. Int. Arch. Photogramm. Remote Sens. 2000, 33, 239–243. Available online: https://www.isprs.org/proceedings/XXXIII/congress/part1/239_XXXIII-part1.pdf (accessed on 21 July 2020).
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Baker, E.A.; Lautz, L.K.; McKenzie, J.M.; Aubry-Wake, C. Improving the accuracy of time-lapse thermal infrared imaging for hydrologic applications. J. Hydrol. 2019, 571, 60–70. [Google Scholar] [CrossRef]
- Eschbach, D.; Piasny, G.; Schmitt, L.; Pfister, L.; Grussenmeyer, P.; Koehl, M.; Skupinski, G.; Serradj, A. Thermal-infrared remote sensing of surface water–groundwater exchanges in a restored anastomosing channel (Upper Rhine River, France). Hydrol. Process. 2017, 31, 1113–1124. [Google Scholar] [CrossRef]
- Mundy, E.; Gleeson, T.; Roberts, M.; Baraer, M.; McKenzie, J.M. Thermal imagery of groundwater seeps: Possibilities and limitations. Groundwater 2017, 55, 160–170. [Google Scholar] [CrossRef]
- Flasse, S.P.; Ceccato, P. A contextual algorithm for AVHRR fire detection. Int. J. Remote Sens. 1996, 17, 419–424. [Google Scholar] [CrossRef]
- Quintano, C.; Fernandez-Manso, A.; Roberts, D.A. Burn severity mapping from Landsat MESMA fraction images and Land Surface Temperature. Remote Sens. Environ. 2017, 190, 83–95. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Aubrecht, D.M.; Helliker, B.R.; Goulden, M.L.; Roberts, D.A.; Still, C.J.; Richardson, A.D. Continuous, long-term, high-frequency thermal imaging of vegetation: Uncertainties and recommended best practices. Agric. For. Meteorol. 2016, 228, 315–326. [Google Scholar] [CrossRef]
- Klemas, V.V. Coastal and environmental remote sensing from unmanned aerial vehicles: An overview. J. Coast. Res. 2015, 31, 1260–1267. [Google Scholar] [CrossRef]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Perich, G.; Hund, A.; Anderegg, J.; Roth, L.; Boer, M.P.; Walter, A.; Liebisch, F.; Aasen, H. Assessment of multi-image unmanned aerial vehicle based high-throughput field phenotyping of canopy temperature. Front. Plant Sci. 2020, 11, 150. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Natarajan, S.; Basnayake, J.; Wei, X.; Lakshmanan, P. High-throughput phenotyping of indirect traits for early-stage selection in sugarcane breeding. Remote Sens. 2019, 11, 2952. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Zarco-Tejada, P.; Nicolás, E.; Nortes, P.A.; Alarcón, J.J.; Intrigliolo, D.S.; Fereres, E. Using high resolution UAV thermal imagery to assess the variability in the water status of five fruit tree species within a commercial orchard. Precis. Agric. 2013, 14, 660–678. [Google Scholar] [CrossRef]
- Martínez, J.; Egea, G.; Agüera, J.; Pérez-Ruiz, M. A cost-effective canopy temperature measurement system for precision agriculture: A case study on sugar beet. Precis. Agric. 2017, 18, 95–110. [Google Scholar] [CrossRef]
- Zhang, L.; Niu, Y.; Zhang, H.; Han, W.; Li, G.; Tang, J.; Peng, X. Maize canopy temperature extracted from UAV thermal and RGB imagery and its application in water stress monitoring. Front. Plant Sci. 2019, 10, 1–18. [Google Scholar] [CrossRef]
- Crusiol, L.G.T.; Nanni, M.R.; Furlanetto, R.H.; Sibaldelli, R.N.R.; Cezar, E.; Mertz-Henning, L.M.; Nepomuceno, A.L.; Neumaier, N.; Farias, J.R.B. UAV-based thermal imaging in the assessment of water status of soybean plants. Int. J. Remote Sens. 2020, 41, 3243–3265. [Google Scholar] [CrossRef]
- Santesteban, L.G.; Di Gennaro, S.F.; Herrero-Langreo, A.; Miranda, C.; Royo, J.B.; Matese, A. High-resolution UAV-based thermal imaging to estimate the instantaneous and seasonal variability of plant water status within a vineyard. Agric. Water Manag. 2017, 183, 49–59. [Google Scholar] [CrossRef]
- Matese, A.; Baraldi, R.; Berton, A.; Cesaraccio, C.; Di Gennaro, S.F.; Duce, P.; Facini, O.; Mameli, M.G.; Piga, A.; Zaldei, A. Estimation of Water Stress in grapevines using proximal and remote sensing methods. Remote Sens. 2018, 10, 114. [Google Scholar] [CrossRef]
- Hoffmann, H.; Nieto, H.; Jensen, R.; Guzinski, R.; Zarco-Tejada, P.; Friborg, T. Estimating evaporation with thermal UAV data and two-source energy balance models. Hydrol. Earth Syst. Sci. 2016, 20, 697–713. [Google Scholar] [CrossRef]
- Calderón, R.; Navas-Cortés, J.A.; Lucena, C.; Zarco-Tejada, P.J. High-resolution airborne hyperspectral and thermal imagery for early detection of Verticillium wilt of olive using fluorescence, temperature and narrow-band spectral indices. Remote Sens. Environ. 2013, 139, 231–245. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; Pérez-Porras, F.; de Larriva, J.E.M.; Frau, C.M.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P.; García-Ferrer, A. Drift correction of lightweight microbolometer thermal sensors on-board unmanned aerial vehicles. Remote Sens. 2018, 10, 615. [Google Scholar] [CrossRef]
- Olbrycht, R.; Więcek, B.; De Mey, G. Thermal drift compensation method for microbolometer thermal cameras. Appl. Opt. 2012, 51, 1788–1794. [Google Scholar] [CrossRef]
- Gómez-Candón, D.; Virlet, N.; Labbé, S.; Jolivot, A.; Regnard, J.L. Field phenotyping of water stress at tree scale by UAV-sensed imagery: New insights for thermal acquisition and calibration. Precis. Agric. 2016, 17, 786–800. [Google Scholar] [CrossRef]
- Nugent, P.W.; Shaw, J.A.; Pust, N.J. Correcting for focal-plane-array temperature dependence in microbolometer infrared cameras lacking thermal stabilization. Opt. Eng. 2013, 52, 061304. [Google Scholar] [CrossRef]
- Kelly, J.; Kljun, N.; Olsson, P.-O.; Mihai, L.; Liljeblad, B.; Weslien, P.; Klemedtsson, L.; Eklundh, L. Challenges and best practices for deriving temperature data from an uncalibrated UAV thermal infrared camera. Remote Sens. 2019, 11, 567. [Google Scholar] [CrossRef]
- Budzier, H.; Gerlach, G. Calibration of uncooled thermal infrared cameras. J. Sens. Sens. Syst. 2015, 4, 187–197. [Google Scholar] [CrossRef]
- Torres-Rua, A. Vicarious calibration of sUAS microbolometer temperature imagery for estimation of radiometric land surface temperature. Sensors 2017, 17, 1499. [Google Scholar] [CrossRef]
- Hammerle, A.; Meier, F.; Heinl, M.; Egger, A.; Leitinger, G. Implications of atmospheric conditions for analysis of surface temperature variability derived from landscape-scale thermography. Int. J. Biometeorol. 2017, 61, 575–588. [Google Scholar] [CrossRef]
- Meier, F.; Scherer, D.; Richters, J.; Christen, A. Atmospheric correction of thermal-infrared imagery of the 3-d urban environment acquired in oblique viewing geometry. Atmos. Meas. Tech. 2011, 4, 909–922. [Google Scholar] [CrossRef]
- Kay, J.E.; Kampf, S.K.; Handcock, R.N.; Cherkauer, K.A.; Gillespie, A.R.; Burges, S.J. Accuracy of lake and stream temperatures estimated from thermal infrared images. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 1161–1175. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator For A Single Thermal Band Earth-Sensing Instrument. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; pp. 3014–3016. Available online: https://atmcorr.gsfc.nasa.gov/Barsi_IGARSS03.PDF (accessed on 25 July 2020).
- Dillen, M.; Vanhellemont, M.; Verdonckt, P.; Maes, W.H.; Steppe, K.; Verheyen, K. Productivity, stand dynamics and the selection effect in a mixed willow clone short rotation coppice plantation. Biomass Bioenergy 2016, 87, 46–54. [Google Scholar] [CrossRef]
- Maes, W.H.; Huete, A.R.; Steppe, K. Optimizing the processing of UAV-based thermal imagery. Remote Sens. 2017, 9, 476. [Google Scholar] [CrossRef]
- Raza, S.-E.-A.; Smith, H.K.; Clarkson, G.J.J.; Taylor, G.; Thompson, A.J.; Clarkson, J.; Rajpoot, N.M. Automatic detection of regions in spinach canopies responding to soil moisture deficit using combined visible and thermal imagery. PLoS ONE 2014, 9, e9761. [Google Scholar] [CrossRef]
- Yahyanejad, S.; Rinner, B. A fast and mobile system for registration of low-altitude visual and thermal aerial images using multiple small-scale UAVs. ISPRS J. Photogramm. Remote Sens. 2015, 104, 189–202. [Google Scholar] [CrossRef]
- Aasen, H.; Bolten, A. Multi-temporal high-resolution imaging spectroscopy with hyperspectral 2D imagers—From theory to application. Remote Sens. Environ. 2018, 205, 374–389. [Google Scholar] [CrossRef]
- Aragon, B.; Johansen, K.; Parkes, S.; Malbeteau, Y.; Al-Mashharawi, S.; Al-Amoudi, T.; Andrade, C.F.; Turner, D.; Lucieer, A.; McCabe, M.F. A calibration procedure for field and UAV-based uncooled thermal infrared instruments. Sensors 2020, 20, 3316. [Google Scholar] [CrossRef]
- FLIR LEPTON: Engineering Datasheet. Available online: https://www.flir.com/globalassets/imported-assets/document/flir-lepton-engineering-datasheet.pdf (accessed on 12 July 2020).
- FLIR EX SERIES: Datasheet. Available online: https://flir.netx.net/file/asset/12981/original/attachment (accessed on 6 October 2020).
- MLX906014 Family: Datasheet Single and Dual Zone. Available online: https://www.melexis.com/-/media/files/documents/datasheets/mlx90614-datasheet-melexis.pdf (accessed on 6 October 2020).
- Testo 926: Datasheet. Available online: https://static-int.testo.com/media/ef/d7/e9ed0e5e694b/testo-926-Data-sheet.pdf (accessed on 6 October 2020).
- Buettner, K.J.; Kern, C.D. The determination of infrared emissivities of terrestrial surfaces. J. Geophys. Res. 1965, 70, 1329–1337. [Google Scholar] [CrossRef]
- Griggs, M. Emissivities of natural surfaces in the 8-to 14-micron spectral region. J. Geophys. Res. 1968, 73, 7545–7551. [Google Scholar] [CrossRef]
- Messina, G.; Modica, G. Applications of UAV thermal imagery in precision agriculture: State of the art and future research outlook. Remote Sens. 2020, 12, 1491. [Google Scholar] [CrossRef]
- Smigaj, M.; Gaulton, R.; Barr, S.L.; Suarez, J.C. Investigating the performance of a low-cost thermal imager for forestry applications. In Proceedings of the Image and Signal Processing for Remote Sensing XXII, Edinburgh, UK, 26–28 September 2016. [Google Scholar] [CrossRef]
- Ritter, M. Further Development of an Open-Source Thermal Imaging System in Terms of Hardware, Software and Performance Optimizations. Available online: https://github.com/maxritter/DIY-Thermocam (accessed on 12 July 2020).
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 17 July 2020).
- Verhoeven, G. Taking computer vision aloft—Archaeological three-dimensional reconstructions from aerial photographs with photoscan. Archaeol. Prospect. 2011, 18, 67–73. [Google Scholar] [CrossRef]
- Pech, K. Generation of Multitemporal Thermal Orthophotos from UAV Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, 305–310. Available online: https://core.ac.uk/download/pdf/206789497.pdf (accessed on 7 July 2020). [CrossRef]
- Osroosh, Y.; Khot, L.R.; Peters, R.T. Economical thermal-RGB imaging system for monitoring agricultural crops. Comput. Electron. Agric. 2018, 147, 34–43. [Google Scholar] [CrossRef]
- Smigaj, M.; Gaulton, R.; Suarez, J.C.; Barr, S.L. Use of miniature thermal cameras for detection of physiological stress in conifers. Remote Sens. 2017, 9, 957. [Google Scholar] [CrossRef]
- Berk, A.; Bernsten, L.S.; Robertson, D.C. MODTRAN: A Moderate Resolution Model for LOWTRAN7; GL-TR-89-0122; Air Force Geophysics Laboratory: Hanscom AFB, MA, USA, 1989; Available online: https://apps.dtic.mil/sti/pdfs/ADA185384.pdf (accessed on 23 July 2020).
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN 5: A reformulated atmospheric band model with auxiliary species and practical multiple scattering options: Update. Algorithms Technol. Multispectr. Hyperspectr. Ultraspectr. Imag. XI 2005, 5806, 662. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A major upgrade of the MODTRAN radiative transfer code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 113–119. [Google Scholar] [CrossRef]
- Sugiura, R.; Noguchi, N.; Ishii, K. Correction of low-altitude thermal images applied to estimating soil water status. Biosyst. Eng. 2007, 96, 301–313. [Google Scholar] [CrossRef]
- Deery, D.M.; Rebetzke, G.J.; Jimenez-Berni, J.A.; James, R.A.; Condon, A.G.; Bovill, W.D.; Hutchinson, P.; Scarrow, J.; Davy, R.; Furbank, R.T. Methodology for high-throughput field phenotyping of canopy temperature using airborne thermography. Front. Plant Sci. 2016, 7, 1808. [Google Scholar] [CrossRef]
- Ribeiro-Gomes, K.; Hernández-López, D.; Ortega, J.F.; Ballesteros, R.; Poblete, T.; Moreno, M.A. Uncooled thermal camera calibration and optimization of the photogrammetry process for UAV applications in agriculture. Sensors 2017, 17, 2173. [Google Scholar] [CrossRef]
- Song, B.; Park, K. Verification of accuracy of unmanned aerial vehicle (UAV) land surface temperature images using in-situ data. Remote Sens. 2020, 12, 288. [Google Scholar] [CrossRef]
- Sun, L.; Chang, B.; Zhang, J.; Qiu, Y.; Qian, Y.; Tian, S. Analysis and measurement of thermal-electrical performance of microbolometer detector. In Proceedings of the SPIE Optoelectronic Materials and Devices II, Wuhan, China, 19 November 2007. [Google Scholar] [CrossRef]
- Pestana, S.; Chickadel, C.C.; Harpold, A.; Kostadinov, T.S.; Pai, H.; Tyler, S.; Webster, C.; Lundquist, J.D. Bias correction of airborne thermal infrared observations over forests using melting snow. Water Resour. Res. 2019, 55, 11331–11343. [Google Scholar] [CrossRef]
Publisher's Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |




| Sensor | Detector Type | Resolution | Detector Sensitivity | Field of View | Spectral Range | Temperature Range | Reported Accuracy | |
|---|---|---|---|---|---|---|---|---|
| FLIR Lepton 3.5 | Focal Plane Array—Uncooled VOx Microbolometer | 160 × 120 | 0.05 °C | 71° × 57° | 8–14 µm | −10 to +140 °C | ±5 °C or 5% | |
| FLIR E5 | Focal Plane Array—Uncooled Microbolometer | 120 × 90 | 0.1 °C | 45° × 34° | 7.5–13 µm | −20 to +250 °C | ±2 °C or 2% | |
| MLX-90614BAA | Infra Red Sensitive Thermopile | - | 0.02 °C | 10° | - | −70 to +380 °C | ±0.5 °C (0 °C to 50 °C) | |
| Testo 926 | Type T thermocouple (Cu-CuNi) | - | 0.1 °C | - | - | −50 to +400 °C | ±0.3 °C |
| Mission ID | Date | Start Time | Elapsed Time | N° of Images | AGL | GSD | Tair | RH | SR | Wind |
|---|---|---|---|---|---|---|---|---|---|---|
| m | cm px−1 | °C | % | W m−2 | m s−1 | |||||
| A | 18 March 2020 | 7:18:10 | 11:06 | 1313 | 35 | 21.2 | 21.4 | 89.4 | 172.4 | 0.9 |
| B | 18 March 2020 | 14:17:40 | 11:02 | 1302 | 35 | 21.9 | 31.5 | 53.3 | 583.4 | 1.3 |
| C | 17 March 2020 | 17:27:10 | 11:06 | 1306 | 35 | 21.5 | 30.1 | 55.9 | 171.4 | 1.8 |
| D | 18 March 2020 | 7:34:22 | 05:24 | 666 | 65 | 40.2 | 22.3 | 85.4 | 230.9 | 0.8 |
| E | 18 March 2020 | 14:07:42 | 05:26 | 675 | 65 | 41.5 | 32.2 | 51.8 | 862.0 | 1.5 |
| F | 17 March 2020 | 17:41:52 | 05:24 | 691 | 65 | 42.0 | 29.7 | 57.3 | 101.2 | 1.5 |
| G | 18 March 2020 | 7:44:36 | 03:26 | 433 | 100 | 62.8 | 22.5 | 84.9 | 260.8 | 0.9 |
| H | 18 March 2020 | 13:57:50 | 03:26 | 436 | 100 | 65.3 | 32.1 | 52.4 | 914.0 | 1.6 |
| I | 17 March 2020 | 17:51:56 | 03:24 | 447 | 100 | 66.6 | 29.5 | 58.6 | 69.9 | 1.4 |
| Flight Altitude (m) | Mission ID | n | R² | ME | MAE | SD | RMSE | rRMSE |
|---|---|---|---|---|---|---|---|---|
| °C | % | |||||||
| 35 | A | 42 | 0.62 ** | 0.24 | 1.90 | 1.49 | 2.41 | 10.70 |
| B | 42 | 0.95 ** | −1.28 | 2.32 | 1.49 | 2.75 | 7.09 | |
| C | 42 | 0.85 ** | −1.69 | 2.26 | 1.54 | 2.72 | 8.19 | |
| Overall | 126 | 0.94 ** | −0.91 | 2.16 | 1.51 | 2.63 | 8.35 | |
| 65 | D | 42 | 0.75 ** | −0.17 | 1.65 | 1.25 | 2.06 | 8.71 |
| E | 42 | 0.98 ** | −2.63 | 2.91 | 2.60 | 3.88 | 9.64 | |
| F | 42 | 0.82 ** | −1.72 | 2.61 | 1.94 | 3.24 | 10.43 | |
| Overall | 126 | 0.95 ** | −1.50 | 2.39 | 2.06 | 3.15 | 9.96 | |
| 100 | G | 42 | 0.74 ** | −0.22 | 1.85 | 1.25 | 2.23 | 9.23 |
| H | 42 | 0.98 ** | −2.15 | 3.57 | 2.71 | 4.47 | 10.99 | |
| I | 42 | 0.96 ** | −0.22 | 1.94 | 1.30 | 2.33 | 7.69 | |
| Overall | 126 | 0.96 ** | −0.87 | 2.46 | 2.03 | 3.18 | 10.04 | |
| Blending Mode | Mission ID | n | Model | R² | ME | MAE | SD | RMSE | rRMSE |
|---|---|---|---|---|---|---|---|---|---|
| °C | % | ||||||||
| Mosaic | D | 7 | y = 1.637x − 14.43 | 0.87 * | −0.34 | 1.67 | 1.31 | 2.07 | 8.78 |
| E | 7 | y = 1.888x − 30.83 | 0.95 ** | −2.56 | 4.01 | 3.98 | 5.45 | 13.57 | |
| F | 7 | y = 1.764x − 22.48 | 0.96 ** | −0.67 | 2.59 | 1.75 | 3.05 | 9.86 | |
| G | 7 | y = 1.769x − 16.53 | 0.95 ** | −1.15 | 1.62 | 1.81 | 2.33 | 9.64 | |
| H | 7 | y = 1.814x − 28.10 | 0.97 ** | −2.72 | 4.86 | 3.74 | 5.97 | 14.71 | |
| I | 7 | y = 1.798x − 24.10 | 0.99 ** | 0.00 | 2.48 | 1.57 | 2.88 | 9.52 | |
| Overall | 42 | y = 1.341x−9.13 | 0.92 ** | −1.24 | 2.87 | 2.36 | 3.93 | 12.43 | |
| Average | D | 7 | y = 1.551x − 12.56 | 0.97 ** | −0.26 | 1.20 | 1.12 | 1.58 | 6.73 |
| E | 7 | y = 1.369x − 11.89 | 0.97 ** | −2.13 | 2.37 | 3.01 | 3.66 | 9.11 | |
| F | 7 | y = 1.317x − 8.01 | 0.96 ** | −1.38 | 1.66 | 1.90 | 2.42 | 7.81 | |
| G | 7 | y = 1.602x − 13.91 | 0.94 ** | −0.39 | 1.36 | 1.45 | 1.91 | 7.89 | |
| H | 7 | y = 1.508x − 16.82 | 0.98 ** | −2.52 | 3.92 | 3.02 | 4.81 | 11.86 | |
| I | 7 | y = 1.495x − 14.02 | 0.84 * | −0.68 | 2.56 | 2.16 | 3.25 | 10.75 | |
| Overall | 42 | y = 1.264x − 6.80 | 0.96 ** | −1.23 | 2.18 | 2.11 | 3.14 | 9.93 | |
| Disabled | D | 7 | y = 1.414x − 9.19 | 0.94 ** | −0.39 | 1.22 | 1.03 | 1.55 | 6.59 |
| E | 7 | y = 1.401x − 12.32 | 0.99 ** | −2.71 | 3.01 | 2.65 | 3.88 | 9.67 | |
| F | 7 | y = 1.087x − 0.96 | 0.78 * | −1.61 | 2.77 | 2.18 | 3.43 | 11.09 | |
| G | 7 | y = 1.365x − 8.06 | 0.84 * | −0.55 | 1.65 | 1.34 | 2.06 | 8.53 | |
| H | 7 | y = 1.449x − 15.18 | 0.98 ** | −2.11 | 3.48 | 2.67 | 4.26 | 10.51 | |
| I | 7 | y = 1.386x − 10.64 | 0.96 ** | −0.73 | 1.73 | 1.58 | 2.26 | 7.49 | |
| Overall | 42 | y = 1.233x − 5.71 | 0.96 ** | −1.35 | 2.31 | 1.91 | 3.08 | 9.74 | |
| Mission ID | Number of Photos | Without Co-Registering | With Co-Registering | ||
|---|---|---|---|---|---|
| Aligned Photos (%) | Tie Points | Aligned Photos (%) | Tie Points | ||
| D | 527 | 46.1 | 1978 | 79.7 | 4294 |
| E | 518 | 38.6 | 1396 | 89.4 | 3499 |
| F | 543 | 25.2 | 1175 | 81.4 | 3625 |
| Overall | - | 36.7 | 1516 | 83.5 | 3806 |
| G | 350 | 51.7 | 1075 | 87.4 | 1940 |
| H | 346 | 28.0 | 526 | 83.2 | 1544 |
| I | 339 | 31.9 | 898 | 87.0 | 1687 |
| Overall | - | 37.2 | 833 | 85.9 | 1724 |
| Method | Calibration | Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | Model | R² | n | R² | ME | MAE | SD | RMSE | rRMSE | |
| °C | % | |||||||||
| Proximal a | 71 | y = 0.0106x − 292.65 | 0.99 ** | 18 | 0.98 ** | −2.75 | 2.81 | 1.96 | 3.40 | 10.71 |
| General b | 180 | y = 0.0125x − 347.39 | 0.95 ** | 18 | 0.98 ** | 0.15 | 0.99 | 0.87 | 1.31 | 4.12 |
| 65 m c | 90 | y = 0.0122x − 337.21 | 0.95 ** | 9 | 0.99 ** | 1.28 | 1.29 | 0.93 | 1.56 | 4.93 |
| 100 m d | 90 | y = 0.0129x − 359.05 | 0.96 ** | 9 | 0.99 ** | 0.57 | 1.23 | 1.26 | 1.32 | 4.16 |
| 7–8 h e | 60 | y = 0.0126x − 351.29 | 0.76 ** | 6 | 0.94 * | −1.34 | 1.34 | 0.90 | 1.57 | 6.74 |
| 13–14 h f | 60 | y = 0.0144x − 408.19 | 0.98 ** | 6 | 0.98 ** | −1.27 | 1.46 | 1.41 | 1.94 | 4.81 |
| 17–18 h g | 60 | y = 0.0124x − 346.06 | 0.86 ** | 6 | 0.98 ** | −1.35 | 1.60 | 0.57 | 1.68 | 5.37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acorsi, M.G.; Gimenez, L.M.; Martello, M. Assessing the Performance of a Low-Cost Thermal Camera in Proximal and Aerial Conditions. Remote Sens. 2020, 12, 3591. https://doi.org/10.3390/rs12213591
Acorsi MG, Gimenez LM, Martello M. Assessing the Performance of a Low-Cost Thermal Camera in Proximal and Aerial Conditions. Remote Sensing. 2020; 12(21):3591. https://doi.org/10.3390/rs12213591
Chicago/Turabian StyleAcorsi, Matheus Gabriel, Leandro Maria Gimenez, and Maurício Martello. 2020. "Assessing the Performance of a Low-Cost Thermal Camera in Proximal and Aerial Conditions" Remote Sensing 12, no. 21: 3591. https://doi.org/10.3390/rs12213591
APA StyleAcorsi, M. G., Gimenez, L. M., & Martello, M. (2020). Assessing the Performance of a Low-Cost Thermal Camera in Proximal and Aerial Conditions. Remote Sensing, 12(21), 3591. https://doi.org/10.3390/rs12213591






