Abstract
Chlorophyll content, as the primary pigment driving photosynthesis, is directly affected by many natural and anthropogenic disturbances and stressors. Accurate and timely estimation of canopy chlorophyll content (CCC) is essential for effective ecosystem monitoring to allow for successful management interventions to occur. Hyperspectral remote sensing offers the possibility to accurately estimate and map canopy chlorophyll content. In the past, research has predominantly focused on the use of hyperspectral data on canopy chlorophyll content retrieval of crops and grassland ecosystems. Therefore, in this study, a temperate mixed forest, the Bavarian Forest National Park in Germany, was chosen as the study site. We compared different statistical models (narrowband vegetation indices (VIs), partial least squares regression (PLSR) and random forest (RF)) in their accuracy to predict CCC using airborne hyperspectral data. The airborne hyperspectral imagery was acquired by the AisaFenix sensor (623 bands; 3.5 nm spectral resolution in the visible near-infrared (VNIR) region, and 12 nm spectral resolution in the shortwave infrared (SWIR) region; 3 m spatial resolution) on July 6, 2017. In situ leaf chlorophyll content and leaf area index measurements were sampled from the upper canopy of coniferous, mixed, and deciduous forest stands in July and August 2017. The study yielded the highest retrieval accuracies with PLSR (root mean square error (RMSE) = 0.25 g/m2, R2 = 0.66). It further indicated specific spectral regions within the visible (390–400 nm and 470–540 nm), red edge (680–780 nm), near-infrared (1050–1100 nm) and shortwave infrared regions (2000–2270 nm) that were important for CCC retrieval. The results showed that forest CCC can be mapped with relatively high accuracies using image spectroscopy.
1. Introduction
Chlorophyll is the primary pigment driving photosynthesis. Its content is affected by anthropogenic and natural stressors, such as water or nutrient shortage or oversupply, insects, herbivores, pollution or diseases [1,2,3]. Therefore, plant chlorophyll content is typically used as a bioindicator of vegetation state [4,5,6,7]. Further, it is a crucial measure of ecosystem functioning and has therefore been suggested as an Essential Biodiversity Variable (EBV) to monitor progress towards the Aichi Biodiversity Targets [8,9].
Remote sensing technologies offer the possibility of detecting changes in chlorophyll content with a high spatial coverage over short time periods, allowing consistent monitoring of ecosystems [10]. Optical remote sensing of chlorophyll content is based on the principle that leaf reflection is influenced by water, chlorophyll and dry matter content, and the internal structure of the leaf [7,11,12]. Stress-induced by environmental or anthropogenic stressors alters the composition and content of the biophysical and biochemical properties of vegetation which can be detected by different regions of the electromagnetic spectrum [6,13,14].
Methods for assessing plant traits include physical/deductive models (i.e., radiative transfer models) and statistical/empirical models (e.g., vegetation indices and multivariate analysis techniques) [15]. While radiative transfer models are often considered more accurate than vegetation indices, they are complex and difficult to calibrate as they require measurements of several biophysical parameters [16]. Vegetation indices (VIs) are commonly used to identify relationships between spectral signatures of vegetation and specific biophysical and biochemical parameters by mathematically relating two or more spectral bands [17,18]. Combining spectral bands rather than using individual bands minimizes solar irradiance and soil background [19]. Thus, VIs have proven to be a simple but effective method in assessing vegetation stress and estimating vegetation traits [20,21,22,23].
The application of multispectral broadband indices (>10 nm) has shown to be restricted when dense canopies reach a saturation point [24]. Narrowband indices calculated from hyperspectral images can overcome this problem by allowing a more precise selection of specific spectral regions from an almost continuous spectrum which is sensitive to specific vegetation parameters such as chlorophyll [25,26]. Further, narrowband vegetation indices have been used to detect vegetation stress and estimate chlorophyll content [5,23,26,27,28,29,30]. As such, [26] achieved an accurate assessment of grassland CCC (R2 = 0.69) using a narrowband soil adjusted vegetation index. Haboudane et al. [27] integrated the Modified Chlorophyll Absorption in Reflectance Index (MCARI) and the Transformed Chlorophyll Absorption in Reflectance Index (TCARI) to predict crop CCC from PROSAIL simulated hyperspectral data. Inoue et al. [5] compared multivariable regression models and narrowband indices for CCC estimation of different vegetation types (crops and grasslands). They achieved the highest accuracy using a narrowband simple ratio index using wavelengths from the infrared and red-edge regions (815 nm and 704 nm).
The high spectral resolution of hyperspectral images, however, also leads to high dimensionality and collinearity of predictor variables (spectral bands) [14,31,32]. Multivariate statistical analysis techniques, such as partial least squares regression (PLSR), and the non-parametric statistical classifier random forest (RF), are designed to process data with high dimensionalities and are suitable for analysing highly collinear datasets [33,34].
A multitude of research has focused on the accurate retrieval of leaf chlorophyll content (LCC) and CCC using various remote sensing data sources and methods. At the leaf level, estimates of chlorophyll have been achieved for broad leaves and needles [7,29,35]. At the canopy level, most research has focused on crop and grassland ecosystems [5,26,36,37,38,39] with only limited research on forest CCC [40]. Moreover, research directed at forest CCC has concentrated on physical models such as radiative transfer model inversion over statistical models such as vegetation indices [3,41].
Recently, [42] compared different methods for retrieving CCC in the same forest as our study site using Sentinel-2 satellite imagery. They compared both vegetation indices, non-parametric statistical approaches, and radiative transfer model inversions. Their results suggested that statistical approaches outperformed physical models.
In this study, we investigate the potential of airborne hyperspectral data to estimate forest canopy chlorophyll content using narrowband vegetation indices as well as multivariate methods, including PLSR and RF regression. The predictive performance of all models was determined using in situ data.
2. Materials and Methods
2.1. Study Site
The Bavarian Forest National Park (BFNP) is located in south-eastern Germany (49°3’19’’N, 13°12’9’’E). It was established in 1970 as Germany’s first National Park. In 1997, the original park area (Rachel-Lusen region) was increased by the former forestry enterprise Zwiesel and Regen and some privately-owned areas. The park covers 24,369 ha and together with the Bohemian Forest/Šumava (Czech Republic) it forms the largest continuous strictly protected area of forests in Central Europe totalling 900 km2 [43].
The mean elevation is 930 m with the highest peak reaching 1453 m. The park can be divided into three distinct forest types [43]. The highlands are characterised by sub-alpine spruce forest which is almost exclusively dominated by Norway spruce (Picea abies). Hillsides (700–1050 m) contain mountain mixed forests dominated by Norway spruce, European beech (Fagus sylvatica) and silver fir (Albies alba). Valley bottoms are characterised by alluvial spruce forests with Norway spruce being the dominant tree type [44].
2.2. Data Collection and Processing
2.2.1. Hyperspectral
The airborne hyperspectral imagery was acquired by the AisaFenix sensor (SPECIM, Spectral Imaging Ltd, Oulu, Finland) during a flight campaign of the European Facility for Airborne Research in Environmental and Geo-sciences (EUFAR) on 6 July 2017. The AisaFenix sensor provides 623 spectral bands at 3.5 nm spectral resolution in the visible near-infrared (VNIR) region (380–970 nm), and 12 nm spectral resolution in the shortwave infrared (SWIR) region (970–2500 nm) at a 3 m spatial resolution. The 29 flight lines were atmospherically corrected with a radiative transfer approach and the application of a bidirectional reflectance distribution function (BRDF) within the ATCOR4 software. The flight lines were geometrically corrected using a digital elevation model (DEM) from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) to apply the rough terrain model within ATCOR4. A mosaic of images was generated from the atmospherically and geometrically corrected flight lines for two sites within the National Park (Figure 1). The flight lines and mosaics were georeferenced to WGS1984 UTM Zone 33N. All corrections and mosaics were generated by the Natural Environment Research Council Airborne Research Facility (NERC-ARF).
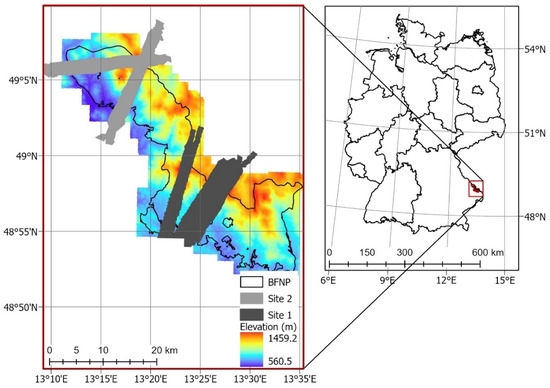
Figure 1.
Location of Bavarian Forest National Park (source: Park administration office) and hyperspectral transects.
2.2.2. Field Data
Biophysical and biochemical parameters across 40 plots were collected from coniferous, broadleaf and mixed forest stands using stratified random sampling in July and August 2017 [45]. A Leica 1200 differential Global Positioning System (GPS) (geometric accuracy of sub-meter after post-processing) was used to record the centre location of each 30 × 30 m north-oriented plot.
Leaf/needle samples were collected from the upper canopy. Sunlit leaves/needles from the upper canopy were collected using a crossbow, and shaded leaves/needles from the lower canopy were collected with extendable secateurs [46]. Leaf chlorophyll content (LCC) was measured immediately with the handheld CCM-300 chlorophyll content meter (OPTI-SCIENCES, Hudson, NY, USA). Leaf area index (LAI) was measured with the LAI 2200 Plant Canopy Analyzer (Li-COR Inc, Lincoln, NE). Three readings were taken from above the canopy and five below [7,42]. LCC was weighted by species biomass for each plot [40]. Canopy chlorophyll content (total of chlorophyll a and b pigments per square meter ground area (g/m2) [37]) was obtained by multiplying the average LAI and LCC per plot [26,36]. Table 1 describes the statistics of the collected field data.

Table 1.
Descriptive statistics of the in situ measurements: leaf area index (LAI), leaf canopy content (LCC) and canopy chlorophyll content (CCC) (n = 30). Ten of the 40 plots were not included in the analysis as they were outside the image extent or covered by clouds.
2.3. Methods
2.3.1. Hyperspectral Vegetation Indices
The methodological framework is outlined in Figure 2. The average spectrum of all pixels within a radius of 4 pixels around the centroid of the field plots (27 × 27 m to avoid edge effects) was extracted from each corresponding flight line. Where a field plot was covered by multiple flight lines, the reflectance was extracted from all cloudless lines and averaged for each plot. Ten of the 40 plots were not included in the analysis as they were outside the image extent, covered by clouds in all flight lines or affected by georeferencing errors. The statistical software R was used for the computation of all models and model validation [47].
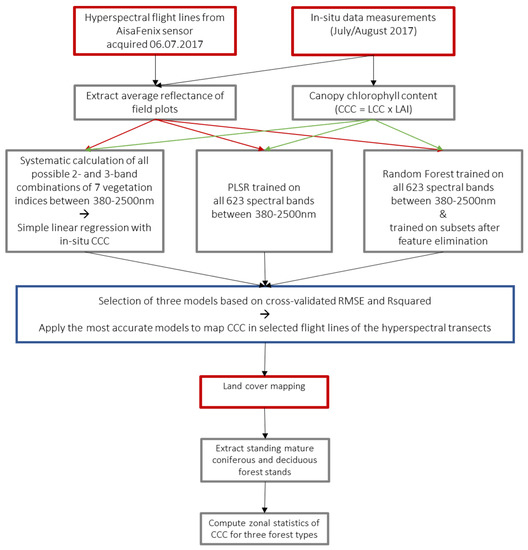
Figure 2.
Methodological framework of the study. Red rectangles are representing input data, grey analysis steps and blue outputs.
Narrowband vegetation indices were calculated systematically for all possible two-band combinations of 623 bands between 380 nm and 2500 nm (623 × 622 = 387,506 wavelength combinations) for narrowband normalised difference vegetation index (nNDVI), narrowband simple ratio index (nSRI), narrowband carotenoid reflectance index (nCRI), narrowband modified simple ratio index (nMSR), narrowband optimised soil adjusted vegetation index (nOSAVI), and narrowband Datt derivative index (nDD) which uses the first derivative of the spectrum. The first derivative was calculated after the spectra were smoothed using the Savitzky–Golay filter from the “prospectr” package in R with a window size of 11, and second-degree polynomial order [48].
The two-band indices were calculated according to the formulae below:
where R is the reflectance value at wavelengths λ1 and λ2, respectively, and D is the first derivative value at wavelengths 1 and 2, respectively.
Additionally, all possible three-band combinations of 623 bands between 380 nm and 2500 nm (623 × 622 × 621 = 240,641,226 wavelength combinations) were calculated for narrowband MERIS terrestrial chlorophyll index (nMTCI) according to formula (7):
where R is the reflectance value at wavelengths λ1, λ2 and λ3, respectively. All narrowband VIs were calculated in R [47].
The normalised difference vegetation index (NDVI) was originally developed to quantify vegetation state [49]; it is commonly used for chlorophyll content as the normalised difference between red and near-infrared wavelengths are sensitive to the amount of photosynthetically active vegetation [20]. Simple ratio indices (SRI) [50] are the simplest way to combine wavebands with [51] introducing one of the first SRIs by taking the ratio of near-infrared and red wavelengths to estimate leaf area index. In a review of several vegetation indices and other models, Inoue et al. [5] demonstrated that an SRI using 815 nm for the NIR region combined with either 704 nm from the red-edge region or 578 nm from the green region was the most robust method of assessing CCC. The carotenoid reflectance index (CRI) is based on SRI and was introduced to account for differences in leaf structure between different plant species from different climatic regions [52]. The modified simple ratio index was proposed as a non-linear function of NDVI—less sensitive to geometrical and optical variations of plant canopies compared to NDVI [53]. The optimised soil adjusted vegetation index (OSAVI) belongs to the group of soil adjusted indices which include a canopy background adjustment factor aimed at reducing the effect of soil on reflectance values in areas with sparse vegetation [54]. The soil adjusted vegetation index was originally introduced by [24] and uses an adjustment factor of 0.5. The transformed soil adjusted vegetation index (TSAVI) further evolved this concept by using the slope and intercept of the soil line as well as a coefficient value 0.08 to minimise soil effects [55]. OSAVI was subsequently suggested as a simplified version of TSAVI that does not require prior knowledge about the soil line [54]. It includes an adjustment factor of 0.16 as this was found to reduce soil noise for both low and high canopy cover environments. Datt derivative index (DD) [56] uses the first derivative spectrum and therefore the slope and curvature of reflectance curves rather than individual reflectance values [57]. It thereby aims to reduce the variations of scatter caused by variations in canopy density, leaf structure and soil background [56]. Consequently, derivative indices have reduced sensitivity to soil background reflection [58]. MERIS terrestrial chlorophyll index (MTCI) was developed for the Medium Resolution Imaging Spectrometer (MERIS) as a simple substitute for red edge inflection point (REIP) calculations [59]. REIP is defined as the wavelength at the point of the steepest slope between peak absorption in the green region and maximum reflectance in the near-infrared region. The REIP changes its position towards shorter or longer wavelengths depending on chlorophyll and water content [60]. MTCI was found not to saturate at high chlorophyll content, unlike REIP and traditional vegetation indices. MTCI and its successor OLCI Terrestrial Chlorophyll Index are therefore used as a standard global terrestrial product by the European Space Agency (ESA) [61].
2.3.2. Regression Models for VIs
Simple linear regression models were fitted between the measured CCC from 30 field sites and all possible two-band combinations of nNDVI, nSRI, nCRI, nMSR, nOSAVI, and nDD, and all possible three-band combinations of nMTCI [26]. The coefficient of determination (R2) was used to rank the wavelength combinations for each index. Cross-validated coefficient of determination and cross-validated root mean square error were calculated using the train function of the “caret” package in R [62].
2.3.3. Partial Least Squares Regression
Partial least squares regression (PLSR) is one of the most widely adopted multivariate statistical analysis techniques for hyperspectral data and is frequently used as a predictive model for environmental variables [21,26,63]. PLSR is a regression method that iteratively chooses linear combinations of the predictor variables which have the maximum correlation with the response variable [64]. It thereby minimises the dimensionality of datasets and breaks the variables into independent, uncorrelated components [65]. PLSR is designed to process data with high dimensionalities and can use all variables (i.e., spectral bands) simultaneously [21,26]. Further, PLSR is capable of handling data where the number of predictors exceeds the number of observations and where predictors are highly correlated [66]. Rännar et al. [67] introduced the so-called “wide kernel pls” specifically for this case.
The “wide kernel pls” regression model was trained on all 623 spectral bands from 380 nm to 2500 nm. The reflectance values were scaled prior to model fitting by dividing each variable by its standard deviation.
PLSR, like other multivariate methods, can be prone to overfitting through selecting too many components. If this is the case, the model does not include wavelengths that are causally related to the vegetation parameter of interest. Consequently, a regression may appear strong and statistically significant, but may not be applicable to datasets other than the one used for building the model. Therefore, choosing the optimal number of components is a critical step in model building. Overfitting is related to model bias and variance, with overfitted models typically showing low bias and high variance [68]. Thus, one of the most common methods when choosing the optimal number of components to be included in the model is based on an evaluation of the variance through cross-validation.
Here, we selected the number of components of the PLSR model based on the root mean square error (RMSE) between the measured and predicted CCC values using leave-one-out cross-validation. To prevent overfitting, components were only added to the model if they decreased the RMSE of cross-validation by >2% [26,69].
The PLSR model was calculated using the “caret” package in R [62] and verified using the “pls” package in R [70].
2.3.4. Random Forest
The Random Forest algorithm (RF) is a non-parametric statistical analysis tool that is based on the classification and regression trees (CART) method [71]. It consists of a large number of individual decision trees that work as an ensemble [66]. RF uses bagging (bootstrap aggregation) to ensure a low correlation between models created by different trees. Bagging creates random combinations of the predictor variables, where the same variable can be selected multiple times, to build the individual trees [72]. In each tree, the data are split into in-bag (training) and out-of-bag (testing) samples, and each tree predicts the out-of-bag sample. The predictions of all trees are averaged in order to prevent overfitting of individual trees and to reduce the overall model variance [73]. In each tree, the variables to split the samples are selected randomly [71]. The number of splits (mtry), as well as the number of trees (ntree), need to be optimised.
RF is capable of dealing with complex relationships between predictors and responses, noisy data and data with a large number of variables [71]. It can therefore be used for the prediction of environmental variables from remote sensing data including hyperspectral images [74,75,76].
The RF model was trained on all 623 spectral bands from 380 nm to 2500 nm in the “caret” package in R [62]. mtry and ntree were tuned empirically to generate the lowest RMSE using leave-one-out cross-validation [77]. Input variables (i.e., spectral bands) were selected based on their variable importance which is computed as the average increase in the squared residuals of the out-of-bag samples when a predictor variable is permuted.
Correlated predictor variables can affect the performance of the random forest algorithm [78,79]. Therefore, two feature elimination methods were additionally tested.
Firstly, random forest recursive feature elimination (RF-RFE) was implemented in the “caret” package in R. Random feature elimination (RFE) [80] iteratively trains the random forest model and ranks input variables based on their mean decrease of accuracy (MDA). MDA is calculated by randomly adding input variables and assessing how much the prediction accuracy decreases with each added variable—a larger decline in prediction accuracy corresponds with a higher importance of that variable. During each iteration, the input variable with the lowest MDA is removed [81]. Based on the RFE process, 50 spectral bands were selected and subsequently used to train the random forest algorithm. mtry and ntree were tuned empirically to generate the lowest RMSE using leave-one-out cross-validation.
Secondly, the spectral bands with the highest variable importance of the original RF model with 623 predictors were determined using the varImp function in the “caret” package in R. Subsequently, the random forest algorithm was fitted with only the most important spectral bands based on this method (n = 38). mtry and ntree were tuned empirically to generate the lowest RMSE using leave-one-out cross-validation.
2.3.5. Validation
Cross-validation was used to verify and compare all models. In cross-validation, one part of the dataset is used to fit the model, and the remaining part is used to test it [73]. In leave-one-out cross-validation (LOOCV), n − 1 samples are used for model fitting and models are validated by the remaining one sample [82]. The procedure is repeated n times so that each sample is used for both model fitting and testing. In this study, 29 samples were used to fit the model, and this was repeated 30 times in the R packages used to compute each model. LOOCV is understood to give an approximately unbiased test error and is an effective validation method for small datasets where it is not feasible to split the data into training and test samples [63,83]. In this study, cross-validated root mean square error (RMSE) and coefficient of determination (R2) were used to rank the models, with
where y = predicted values, z = measured values. This is a common method for comparing different models [35].
2.3.6. Mapping Canopy Chlorophyll Content
The most accurate multivariate method, the most accurate 2-band combination VI, and the most accurate 3-band combination VI were selected and inverted to map the CCC of two selected flight lines. The inversion of the VIS was performed in R by applying the regression function to the flight lines. The PLSR inversion was performed by using the predict function in “caret” [62].
A land cover map available from the national park administration was used to analyse the distribution of CCC for standing coniferous, deciduous, and mixed stands for each map by computing the zonal statistics of CCC for each group in ArcGIS Pro 2.5. A description of the land cover classes can be found in [84].
3. Results
3.1. Model Selection
3.1.1. Narrowband Vegetation Indices
The optimal band combinations with CCC for all seven tested vegetation indices were determined by computing the coefficient of determination (R2) for all possible waveband combinations. All indices with the optimal combination were significantly correlated with CCC (p < 0.01) (Table 2).

Table 2.
RMSE and R2 of the most accurate band combinations for all tested narrowband vegetation indices. Leave-one-out cross-validation was used to verify the models. All listed models were statistically significant (p < 0.01). Vegetation indices are listed by lowest cross-validated RMSE in descending order. R (nm) is the reflectance at the corresponding wavelength λ.
The highest retrieval accuracy for CCC was obtained with the narrowband MERIS terrestrial chlorophyll index (nMTCI) (RMSE = 0.27 g/m2, R2 = 0.61), comprising a three-band combination. The most accurate nMTCI was based on two wavelengths in the shortwave infrared region (1820 nm and 1997 nm) combined with one wavelength from the blue region (390 nm) (Figure 3). All well-performing band combinations of nMTCI were based on either wavelength 1 from the green region and wavelength 2 from the red edge/NIR region combined with all possible spectral regions for wavelength 3 except shortwave infrared (blue rectangle); or based on combinations with all three bands located in the red edge (red circle).
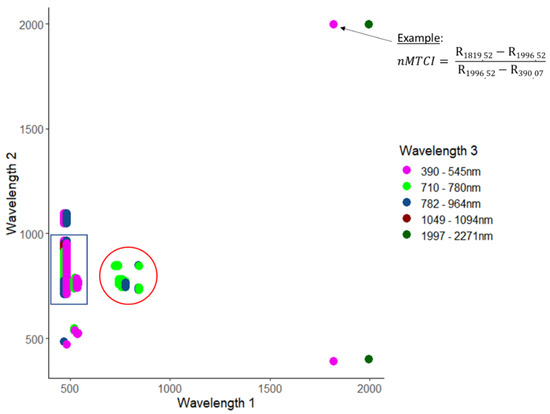
Figure 3.
3-D correlation matrix of CCC and narrowband MERIS terrestrial chlorophyll index (MTCI) for all combinations of wavelengths that yielded R2 values of 0.6 or higher (not cross-validated). The arrow in the top right corner points to the location that indicates the index with the optimal wavelength combination. The blue rectangle indicates the band combinations with wavelength 1 in the green region, wavelength 2 in the red edge region and wavelength 3 in one of the listed regions except shortwave infrared. The red circle shows the band combinations with all three wavelengths in the red edge.
The narrowband Datt derivative index (nDD) yielded the highest retrieval accuracy of the two-band combination indices (RMSE = 0.28 g/m2, R2 = 0.580), with one wavelength in the green region and one in the red edge region. Figure 4 shows the 2-D correlation matrix for nDD with all R2 values of CCC and the calculated nDD values. The vertical and horizontal black lines specify the location of the red edge region between 680 nm and 780 nm. It shows that most of the R2 hotspots occur in this region.
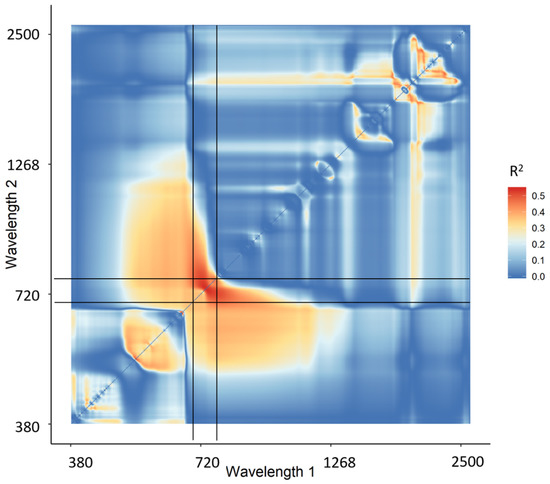
Figure 4.
2-D correlation plot of R2 of canopy chlorophyll content and narrowband Datt derivative index (not cross-validated). The vertical and horizontal black lines indicate the red edge region between 680–780 nm.
The optimal band combinations of nNDVI, nSRI, nMSR and nOSAVI were all located in the red edge. They performed equally well at predicting CCC, and there was no statistically significant difference in their retrieval accuracy (p > 0.05).
3.1.2. PLSR
The optimal number of components for partial least squares regression was chosen through leave-one-out cross-validation. The optimal number of components selected was five components. PLSR outperformed all other models by yielding both lower RMSE and higher R2 (RMSE = 0.25 g/m2, R2 = 0.66).
3.1.3. Random Forest
The optimal tuning parameters for the random forest algorithm were determined with leave-one-out cross-validation. mtry = 11 and ntree = 50 yielded the lowest RMSE for the model using all 623 bands. Despite tuning parameter optimisation, the random forest was the least accurate of all tested models (RMSE = 0.42 g/m2) and had a low correlation with CCC (R2 = 0.07).
Both feature elimination methods improved the random forest model. Recursive feature elimination with 50 spectral bands yielded an RMSE = 0.40 g/m2 and R2 = 0.12.
The variable importance algorithm returned that 38 spectral bands explained 50% of the overall importance. Fitting the random forest algorithm with those 38 bands achieved the same metrics as the method using recursive feature elimination with 50 bands. The spectral bands selected with the two models were not the same.
3.1.4. Model Comparison
Three models were selected for upscaling to the hyperspectral transect and further analysis. PLSR was chosen as the most accurate multivariate method, nMTCI with wavelength 1 = 1819.52 nm, wavelength 2 = 1996.52 nm and wavelength 3 = 390.07 nm was selected as the most accurate three-band combination vegetation index, and nDD with wavelength 1 = 528.83 nm and wavelength 3 = 735.02 nm was selected as the most accurate two-band combination vegetation index. Note that in the following figures, only these three selected models are displayed.
Figure 5 displays the relationship between the measured in situ CCC, and the values predicted by the three models. PLSR shows the least variation around the dotted line which indicates the 1:1 relationship between predicted and measured values. Figure 5b,c approach an asymptote and thus indicate a curvilinear relationship between measured and predicted values by PLSR and nDD. All three models predicted the same mean CCC as the in situ CCC (µ = 1.64), and a slightly higher median CCC (Figure 5d).
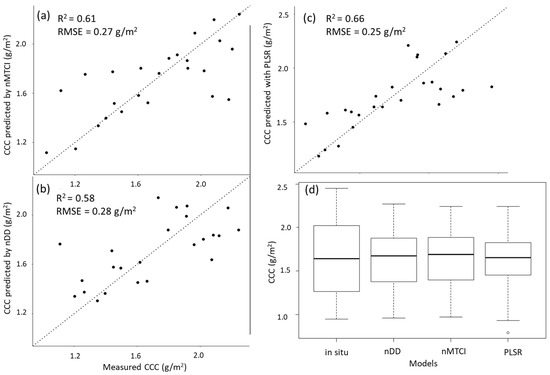
Figure 5.
Scatterplot of the in situ CCC and predicted values made by (a) nMTCI with optimal wavelength combinations, (b) nDD with optimal wavelength combinations, and (c) Partial least squares regression (PLSR) with five components. The dotted line shows the 1:1 relationship between predicted and measured values. (d) Boxplot of in situ and predicted CCC (g/m2) using the three selected models. Mean CCC was 1.64 g/m2 for all models as well as in situ CCC. The median predicted CCC was 1.67 g/m2, 1.69 g/m2 and 1.65 g/m2 for nDD, nMTCI and PLSR, respectively. The median in situ CCC was 1.64 g/m2.
3.2. Mapping Canopy Chlorophyll Content
The three selected models were used to map CCC along two flight lines; the lines were selected due to low cloud cover. Flight line 193 (FL193) is in the northern part of the Bavarian Forest National Park (Figure 1, site 2). Flight line 143 is located in the southern part of the national park which is also known as the Rachel-Lusen region (Figure 1, site 1). The CCC maps produced with PLSR were more accurate at distinguishing between adjacent areas with different land cover classes. Figure 6 shows a close-up of one flight line (FL193). It displays changes in CCC (mapped with PLSR) which correspond to different land cover classes (Figure 6b) as well as areas where deadwood was recorded (Figure 6c). Areas of high CCC coincide with deciduous and mixed forest, while areas of lower CCC coincided with areas with deadwood or salvage locked areas. The complete CCC maps of flight lines 143 and 193 can be found in the Appendix A (Figure A1, Figure A2 and Figure A3).
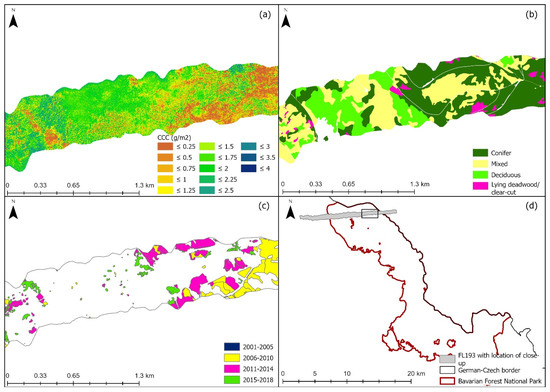
Figure 6.
Close up of eastern site of light line 193; (a) Canopy chlorophyll content map derived with PLSR, (b) Land cover classification map, (c) Deadwood classification map, (d) Location plan of flight line 193 and the close-up in relation to the Bavarian Forest National Park. Forest classification map from land cover map. Deadwood classification map from infestation map (obtained from aerial photographs) available from the national park administration [85].
Table 3 summarises the basic statistics of the predicted CCC for deciduous, mixed, and coniferous forest stands using the three selected models, as well as the in situ measurements (n = 30). All models estimated higher CCC for deciduous areas compared to mixed and coniferous stands. The estimated values are similar for all models and in the same range as the in situ measurements.

Table 3.
Mean and standard deviation of in situ and estimated canopy chlorophyll content (g/m2) using the three selected models for standing deciduous, mixed, and coniferous forest stands.
4. Discussion
This study related airborne hyperspectral data with in situ measurements of canopy chlorophyll content to compare different models in their accuracy to predict canopy chlorophyll content (CCC). The results show that forest canopy chlorophyll content can be mapped with relatively high accuracies using hyperspectral remote sensing data.
The highest retrieval accuracy was achieved with the multivariate analysis method partial least squares regression (PLSR) using five components (RMSE = 0.25 g/m2, R2 = 0.66). The improvement in retrieval accuracy and the precision of PSLR compared to vegetation indices and other regression methods have been observed with [26] finding PLSR improved CCC estimations from an R2 of 0.68 using a narrowband vegetation index to 0.74 with PLSR [5,21,86]. Atzberger et al. [38] reported an improvement from an R2 of 0.57 using principal component analysis (PCA) to 0.82 with PLSR. It is important to note that these results are from studies on grasslands or crops and thus cannot be compared to those obtained in this forest study. However, the relative accuracy improvement of PLSR over other methods is comparable. The selected number of components included in the PLSR model is also comparable to other studies which included five and six components respectively [42,86].
In addition to PLSR, the most accurate vegetation index, narrowband MERIS terrestrial chlorophyll index, as well as the most accurate two-band VI, narrowband Datt derivative index, were selected for further analysis and mapping. They yielded relatively higher RMSE and lower R2 than PLSR (RMSE = 0.27 g/m2, R2 = 0.61, and RMSE = 0.28 g/m2, R2 = 0.58, respectively). All three of the selected models robustly predicted the central tendency of the in situ CCC.
The predicted versus measured values plots of PLSR and nDD (Figure 5b,c) indicated a curvilinear relationship with higher CCC values approaching an asymptote indicating that the predictions at higher CCC values are less accurate using either of these models.
The total CCCs averaged across the three forest types were 1.55 g/m2, 1.64 g/m2 and 1.46 g/m2 for estimations with PLSR, nMTCI and nDD, respectively. Ali et al. [42] compared CCC values estimated by four models for the Bavarian Forest National Park and yielded mean CCC between 1.46–1.59 g/m2 for the entire park. The total mean CCC estimated with the models in this study fall into the same range of predictions.
Further, all three selected models showed a difference in CCC between coniferous, mixed, and deciduous stands which agrees with previous research confirming that chlorophyll content tends to be higher in deciduous trees compared to conifers during summer [87]. This indicates that all three models predicted the relative distribution of CCC over the study sites, as well as the order of magnitude of absolute values, correctly.
All CCC maps indicated similar patterns in the distribution of CCC, and these patterns matched the spatial arrangement of land cover classes. The visual analysis indicated that the maps produced with PLSR were more accurate in differentiating between adjacent zones with different land cover classes (A2 & A3).
This study highlighted the importance of different spectral regions for CCC retrieval. The visible region between 390–400 nm and between 470–540 nm, the red edge region, as well as the near-infrared region between 1050–1100 nm and the shortwave infrared region between 2000–2270 nm were identified as important for estimating CCC.
The visible spectrum between 400 nm and 700 nm is understood to be linked to pigments such as chlorophyll a and b [88,89]. Furthermore, spectral bands in the blue and green regions have been linked to leaf chlorophyll content [5,26]. A multitude of studies has revealed the significance of the red edge for chlorophyll estimations at canopy [2,5,37,90,91,92,93,94,95]. VIs using wavelengths of the red edge region had higher accuracy than the traditional NDVI which is based on wavelengths at the chlorophyll absorption centre around 670 nm and the maximum reflection in the NIR plateau around 800 nm. This confirms previous findings that wavelengths in the red edge region are more sensitive to CCC than the chlorophyll absorption wavelengths [35,96,97,98].
The spectral area between 700 nm and 1100 nm has been associated with leaf structure [11,99,100]. The red-edge region overlaps the visible and NIR regions (680–780 nm). Therefore, the importance of the red edge spectrum identified in this study, stresses that canopy chlorophyll content is influenced by both pigment content and the internal leaf structure [60].
The shortwave infrared region (SWIR) has been shown to be one of the most important spectral areas for leaf area index (LAI) estimations [19,101,102]. Canopy chlorophyll content is defined as the product of leaf area index and leaf chlorophyll content, and most of the variation in CCC is caused by variations in LAI [26]. Therefore, the result of this study which illustrated the importance of the SWIR for CCC retrieval is reasonable considering the significance of LAI for CCC.
Ali et al. [42] correlated Sentinel-2 imagery with CCC using the same in situ measurements as presented in this study and obtained the highest coefficient of determination with PLSR (RMSE = 0.22 g/m2, R2 = 0.78), and a slightly lower RMSE of 0.21 g/m2 (R2 = 0.75) with a modified simple ratio index using bands in the NIR and red edge region. Based on the results of [42], it was expected that the present study would achieve higher retrieval accuracies due to the finer spatial and spectral resolution of the airborne hyperspectral data. Although the wavebands of Sentinel-2 have wider bandwidth compared to those from the SPECIM hyperspectral sensor, the heterogeneity within the plots, effects of reflectance from the plots’ neighbouring pixels as well as noise in the data, are averaged when using Sentinel-2 imagery. Consequently, detailed information about plot characteristics may be lost compared to using hyperspectral data. Further, the field sample set used in our study was slightly different from the ones used by [42]. As such, [42] eliminated eight field plots (out of 40) due to cloud cover in the Sentinel-2 image. These plots were not identical with our removed ten plots (out of 40) due to cloud cover and because the plots were not covered by the flight lines. Therefore, plausibly explaining a slight difference in our obtained accuracy. Additionally, the Sentinel-2 image used by [42] was acquired on July 13 while the hyperspectral image was obtained on 6 July. The field measurements were sampled during several field campaigns in July and August. Thus, the Sentinel-2 image was taken closer to the sampling of the reference in situ data than the hyperspectral image. Lindner [103] and [104] observed an increase in chlorophyll content in spruce needles during July and August. Therefore, estimated accuracies may be improved by ensuring that there is no time lag between the acquisition of images and reference in situ data.
It was surprising that the random forest algorithm achieved the lowest accuracy and had a low correlation with CCC. The random forest recursive feature elimination (RF-RFE) and variable importance methods improved model performance but were still less accurate when compared with all other tested models. When comparing random forest regression with the performance of vegetation indices, or machine learning algorithms such as artificial neural networks or support vector regression, previous studies identified the high potential of random forest for biomass and nitrogen estimations [74,75,105]. Random forest regression has also been applied to predict chlorophyll content. While some studies found that RF was superior to other models [106,107], other research reported, as here, lower accuracy [108]. Shah et al. [76] used established VIs to train the RF algorithm and determine the variable importance. In a second step, they iteratively reduced the number of predictors by eliminating less important VIs. They found that using only one-quarter of the original VIs improved the accuracy. Similarly, [79] concluded that RFE improved accuracy for datasets with highly correlated predictor variables. Darst et al. [78] on the other hand inferred that RF-RFE was not an appropriate method for data with high dimensionality as they did not find that it improved the effect of highly correlated variables.
This study supports the conclusion that feature elimination using RF-RFE or variable importance may improve model performance. However, other dimensionality reduction techniques coupled with the random forest algorithm may yield higher accuracies for canopy chlorophyll content retrieval using hyperspectral sensing data. According to [109] subsampling by the RF algorithm may result in an increased variance of the estimates when the sample size is small (though we note this is also true for VIs and PLSR). We do not consider our sample size in this study to be very small (i.e., n = 30 is considered statistically to be a reasonable compromise size [110])—especially when compared to similar studies that used the RF model. For example, ref. [75] used 28 samples with an RF model and EO-1 Hyperion hyperspectral data to estimate sugarcane leaf nitrogen concentration. Tan et al. [111] used 30 samples to estimate heavy metal concentration in agricultural soils using RF and hyperspectral data. In another study, ref. [112] used only 14 samples in an RF model to estimate forest biomass using RISAT-1 PolSAR and Terrestrial LiDAR Data.
Early detection of stress or disturbances is often necessary for successful management interventions. This may be difficult to achieve due to the temporal aspects of the disturbance as well as the revisiting frequencies of remote sensing platforms.
Various stressors and disturbances, such as drought, insects, herbivores, pollution, or snow breakage, have a direct effect on chlorophyll content. Here we take the example of bark beetles to illustrate the potential practical constraints of canopy chlorophyll content as a metric for forest ecosystem functioning. Bark beetle development occurs under the bark of the host tree and takes less than two months in the case of the European spruce bark beetle [113]. In order to be pragmatic and useful for land managers, the detection of bark beetle infestation must occur in a timely manner that allows for affected trees to be identified and removed before the next generation of beetles leave their host trees and swarm to surrounding areas [113,114]. Early detection is impeded by infested trees not showing visual symptoms and biophysical and biochemical changes being subtle [115,116]. Consequently, there is a very limited time to detect changes in canopy chlorophyll content and identify infestation hot spots using remote sensing technologies.
Furthermore, the biochemical response in vegetation to stress is similar irrespective of the factors leading to the stress, and it is difficult to separate the causes for alterations in chlorophyll content [117,118]. Therefore, certain stress or disturbance factor can only be deduced and confirmed based on prior knowledge about the site including baseline conditions regarding leaf properties along with natural variability, potential stressors, and their ecological/climatic niches.
5. Conclusions
The study accurately estimated canopy chlorophyll content using airborne hyperspectral imagery and mapped canopy chlorophyll content for transects of the Bavarian Forest National Park in Germany. Therefore, the study has demonstrated that forest canopy chlorophyll content can be mapped, which is important for forest ecosystem monitoring and management.
The retrieval accuracy may be improved in future studies by ensuring that image acquisition and field data sampling temporarily coincide to prevent a time lag between the corresponding data. Further, the ability of new sensors such as the spaceborne hyperspectral sensors EnMAP or HYPXIM, or the high-resolution lidar instrument JEDI, as well as the integration of active and passive remote sensors may enhance the retrieval accuracy of canopy chlorophyll content and allow for the timely detection of forest ecosystem stressors and disturbances.
Author Contributions
Conceptualization, J.M.H., A.K.S., R.D. and M.H.; methodology, A.K.S. and R.D.; software, J.M.H. and H.-C.C.; analysis, J.M.H.; validation, J.M.H., A.K.S., R.D. and M.H.; resources, R.D. and H.-C.C.; data curation, T.W.G.; writing—original draft preparation, J.M.H.; writing—review and editing, J.M.H., A.K.S., R.D., M.H., H.-C.C. and T.W.G.; supervision, A.K.S. and H.-C.C.; funding acquisition, A.K.S. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Horizon 2020 research and innovation programme - 396 European Commission ’BIOSPACE Monitoring Biodiversity from Space’ project (Grant 397 agreement ID 834709, H2020-EU.1.1.). The authors acknowledge the support of the “Data Pool Forestry” data sharing initiative of the Bavarian Forest National Park.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
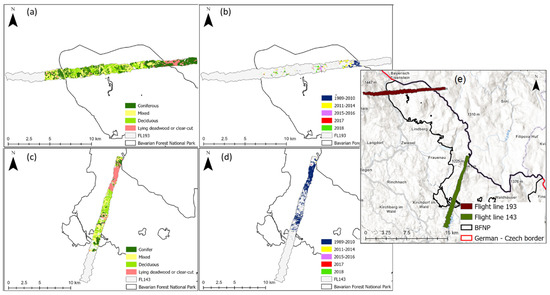
Figure A1.
(a) Flight line 193: Forest classification map, (b) Flight line 193: Deadwood classification map, (c) Flight line 143: Forest classification map (d) Flight line 143: Deadwood classification map, (e) Location plan of flight line 193 and 143 in relation to the Bavarian Forest National Park. Forest classification map from land cover map available from the national park administration. Deadwood classification map from infestation map (obtained from aerial photographs) available from the national park administration.
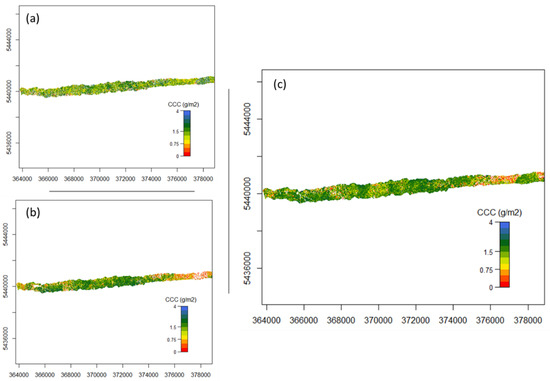
Figure A2.
Flight line 193 mapped CCC (a) using nMTCI with wavelength 1 =1819.52 nm, wavelength 2 = 1996.52 nm and wavelength 3 = 390.07 nm, (b) using nDD with wavelength 1 = 528.83 nm and wavelength 3 = 735.02 nm, and (c) using PLSR.
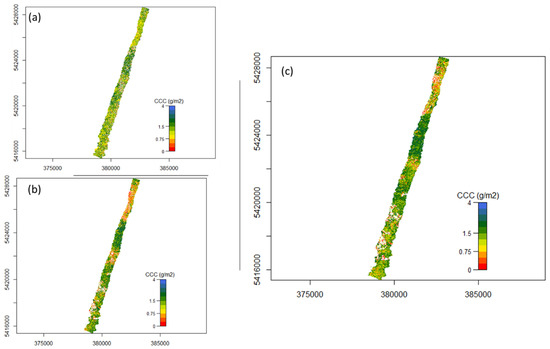
Figure A3.
Flight line 149 mapped CCC (a) using nMTCI with wavelength 1=1819.52 nm, wavelength 2 = 1996.52 nm and wavelength 3 = 390.07 nm, (b) using nDD with wavelength 1 = 528.83 nm and wavelength 3 = 735.02 nm, and (c) using PLSR.
References
- Björkman, O.; Powles, S.B. Inhibition of photosynthetic reactions under water stress: Interaction with light level. Planta 1984, 161, 490–504. [Google Scholar] [CrossRef] [PubMed]
- Le Maire, G.; François, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Yang, X.; Yu, Y.; Fan, W. Chlorophyll content retrieval from hyperspectral remote sensing imagery. Environ. Monit. Assess. 2015, 187, 456. [Google Scholar] [CrossRef] [PubMed]
- Clevers, J.G.P.W.; Kooistra, L. Using Hyperspectral Remote Sensing Data for Retrieving Canopy Chlorophyll and Nitrogen Content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 5, 574–583. [Google Scholar] [CrossRef]
- Inoue, Y.; Guérif, M.; Baret, F.; Skidmore, A.; Gitelson, A.; Schlerf, M.; Darvishzadeh, R.; Olioso, A. Simple and robust methods for remote sensing of canopy chlorophyll content: A comparative analysis of hyperspectral data for different types of vegetation. Plant Cell Environ. 2016, 39, 2609–2623. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Keydan, G.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Abdullah, H.; Cherenet, E.; Ali, A.; Wang, T.; Nieuwenhuis, W.; Heurich, M.; Vrieling, A.; O’Connor, B.; et al. Mapping leaf chlorophyll content from Sentinel-2 and RapidEye data in spruce stands using the invertible forest reflectance model. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 58–70. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Pettorelli, N. Agree on biodiversity metrics to track from space: Ecologists and space agencies must forge a global monitoring strategy. Nature 2015, 523, 403–406. [Google Scholar] [CrossRef]
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential Biodiversity Variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef]
- Homolová, L.; Malenovský, Z.; Clevers, J.G.; García-Santos, G.; Schaepman, M.E. Review of optical-based remote sensing for plant trait mapping. Ecol. Complex. 2013, 15, 1–16. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.K.; Van Duren, I.; Heiden, U.; Heurich, M. Estimating leaf functional traits by inversion of PROSPECT: Assessing leaf dry matter content and specific leaf area in mixed mountainous forest. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 66–76. [Google Scholar] [CrossRef]
- Abdullah, H.; Skidmore, A.K.; Darvishzadeh, R.; Heurich, M. Timing of red-edge and shortwave infrared reflectance critical for early stress detection induced by bark beetle (Ips typographus, L.) attack. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101900. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. The stress concept in plants: An introduction. Ann. N. Y. Acad. Sci. 1998, 851, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Meentemeyer, R.K. Remote Sensing of Forest Damage by Diseases and Insects. In Remote Sensing for Sustainability; CRC Press, Taylor & Francis Group: Boca Raton, Florida, 2016; pp. 145–162. [Google Scholar]
- Skidmore, A.K. Taxonomy of Environmental Models in the Spatial Sciences. In Environmental Modelling with GIS and Remote Sensing; Taylor & Francis: London, UK, 2010; pp. 8–24. [Google Scholar]
- Atzberger, C.; Richter, K.; Vuolo, F.; Darvishzadeh, R.; Schlerf, M. Why Confining to Vegetation Indices? Exploiting the Potential of Improved Spectral Observations Using Radiative Transfer Models. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XIII; International Society for Optics and Photonics, SPIE Remote Sensing: Prague, Czech Republic, 2011. [Google Scholar]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.K.; Abkar, A.A. Leaf Area Index derivation from hyperspectral vegetation indicesand the red edge position. Int. J. Remote Sens. 2009, 30, 6199–6218. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef]
- Misurec, J.; Kopačková-Strnadová, V.; Zuzana, L.; Campbell, P.K.E.; Albrechtová, J. Detection of Spatio-Temporal Changes of Norway Spruce Forest Stands in Ore Mountains Using Landsat Time Series and Airborne Hyperspectral Imagery. Remote Sens. 2016, 8, 92. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Koch, B. An angular vegetation index for imaging spectroscopy data—Preliminary results on forest damage detection in the Bavarian National Park, Germany. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 308–321. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.M.; Miller, J.R.; Noland, T.L. Leaf chlorophyll content retrieval from airborne hyperspectral remote sensing imagery. Remote Sens. Environ. 2008, 112, 3234–3247. [Google Scholar] [CrossRef]
- Lawrence, R.; Labus, M. Early Detection of Douglas-Fir Beetle Infestation with Subcanopy Resolution Hyperspectral Imagery. West. J. Appl. For. 2003, 18, 202–206. [Google Scholar] [CrossRef]
- Grossman, Y.; Ustin, S.; Jacquemoud, S.; Sanderson, E.; Schmuck, G.; Verdebout, J. Critique of stepwise multiple linear regression for the extraction of leaf biochemistry information from leaf reflectance data. Remote Sens. Environ. 1996, 56, 182–193. [Google Scholar] [CrossRef]
- De Jong, S.M.; Pebesma, E.; Lacaze, B. Above-ground biomass assessment of Mediterranean forests using airborne imaging spectrometry: The DAIS Peyne experiment. Int. J. Remote Sens. 2003, 24, 1505–1520. [Google Scholar] [CrossRef]
- Atzberger, C.; Jarmer, T.; Schlerf, M.; Kötz, B.; Werner, W. Spectroradiometric Determination of Wheat Bio-Physical Variables: Comparison of Different Empirical-Statistical Approaches. In Proceedings of the Remote Sensing in Transitions, Proc. 23rd EARSeL Symposium, Ghent, Belgium, 2–5 June 2003. [Google Scholar]
- Immitzer, M.; Atzberger, C. Early Detection of Bark Beetle Infestation in Norway Spruce (Picea abies, L.) using WorldView-2 Data Frühzeitige Erkennung von Borkenkä ferbefall an Fichten mittels WorldView-2 Satellitendaten. Photogramm. Fernerkund. Geoinf. 2014, 2014, 351–367. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrene, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Matkan, A.A.; Ahangar, A.D. Inversion of a Radiative Transfer Model for Estimation of Rice Canopy Chlorophyll Content Using a Lookup-Table Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1222–1230. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Wu, C.; Wang, L.; Niu, Z.; Gao, S.; Wu, M. Nondestructive estimation of canopy chlorophyll content using Hyperion and Landsat/TM images. Int. J. Remote Sens. 2010, 31, 2159–2167. [Google Scholar] [CrossRef]
- Gara, T.W.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Heurich, M. Accurate modelling of canopy traits from seasonal Sentinel-2 imagery based on the vertical distribution of leaf traits. ISPRS J. Photogramm. Remote Sens. 2019, 157, 108–123. [Google Scholar] [CrossRef]
- Sampson, P.H.; Zarco-Tejada, P.J.; Mohammed, G.H.; Miller, J.R.; Noland, T.L. Hyperspectral remote sensing of forest condition: Estimating chlorophyll content in tolerant hardwoods. For. Sci. 2003, 49, 381–391. [Google Scholar]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.; Gara, T.W.; O’Connor, B.; Roeoesli, C.; Heurich, M.; Paganini, M. Comparing methods for mapping canopy chlorophyll content in a mixed mountain forest using Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 87, 102037. [Google Scholar] [CrossRef]
- Heurich, M.; Neufanger, M. Die Wälder des Nationalparks Bayerischer Wald: Ergebnisse der Waldinventur 2002/2003 im Geschichtlichen und Waldökologischen Kontext; Nationalparkverwaltung Bayerischer Wald: Grafenau, Germany, 2005. [Google Scholar]
- Cailleret, M.; Heurich, M.; Bugmann, H. Reduction in browsing intensity may not compensate climate change effects on tree species composition in the Bavarian Forest National Park. For. Ecol. Manag. 2014, 328, 179–192. [Google Scholar] [CrossRef]
- Gara, T. Quantitative Remote Sensing of Essential Biodiversity Variables; University of Twente: Enschede, The Netherlands, 2019. [Google Scholar]
- Gara, T.W.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Heurich, M. Evaluating the performance of PROSPECT in the retrieval of leaf traits across canopy throughout the growing season. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101919. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. 2018. Available online: https://www.r-project.org/ (accessed on 13 February 2012).
- Stevens, A.; Ramirez-Lopez, L. An Introduction to the Prospectr Package; R Package Vignette R Package Version 0.1.3. 2013. Available online: https://github.com/l-ramirez-lopez/prospectr (accessed on 29 October 2020).
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Sympoisum, Washington, DC, USA, 10–14 December 1974; NASA: Greenbelt, MD, USA. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of the Shortgrass Prairie. In Eighth International Symposium on Remote Sensing of Enviroment; University of Michigan: Ann Arbor, MI, USA, 1972. [Google Scholar]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.G.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Datt, B. Visible/near infrared reflectance and chlorophyll content in Eucalyptus leaves. Int. J. Remote Sens. 1999, 20, 2741–2759. [Google Scholar] [CrossRef]
- Datt, B.; Paterson, M. Vegetation-soil spectral mixture analysis. In IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120); IEEE: Honolulu, HI, USA, 2000; Volume 5, pp. 1936–1938. [Google Scholar] [CrossRef]
- Kochubey, S.M.; Kazantsev, T.A. Derivative vegetation indices as a new approach in remote sensing of vegetation. Front. Earth Sci. 2012, 6, 188–195. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P. Evaluation of the MERIS terrestrial chlorophyll index (MTCI). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and Regression Training; R package Version 6.0-85. 2020. Available online: https://github.com/topepo/caret/ (accessed on 29 October 2020).
- Ramoelo, A.; Skidmore, A.K.; Cho, M.A.; Mathieu, R.; Heitkönig, I.M.; Dudeni-Tlhone, N.; Schlerf, M.; Prins, H. Non-linear partial least square regression increases the estimation accuracy of grass nitrogen and phosphorus using in situ hyperspectral and environmental data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 27–40. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Geladi, P.; Hadjiiski, L.; Hopke, P.K. Multiple regression for environmental data: Nonlinearities and prediction bias. Chemom. Intell. Lab. Syst. 1999, 47, 165–173. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Rännar, S.; Lindgren, F.; Geladi, P.; Wold, S. A PLS kernel algorithm for data sets with many variables and fewer objects. Part 1: Theory and algorithm. J. Chemom. 1994, 8, 111–125. [Google Scholar] [CrossRef]
- Gowen, A.A.; Downey, G.; Esquerre, C.; O’Donnell, C.P. Preventing over-fitting in PLS calibration models of near-infrared (NIR) spectroscopy data using regression coefficients. J. Chemom. 2011, 25, 375–381. [Google Scholar] [CrossRef]
- Kooistra, L.; Salas, E.; Clevers, J.; Wehrens, R.; Leuven, R.; Nienhuis, P.; Buydens, L. Exploring field vegetation reflectance as an indicator of soil contamination in river floodplains. Environ. Pollut. 2004, 127, 281–290. [Google Scholar] [CrossRef]
- Mevik, B.H.; Wehrens, R.; Liland, K.H. Pls: Partial Least Squares and Principal Component Regression; R Package Version 2.7-2. 2019. Available online: https://github.com/bhmevik/pls (accessed on 29 October 2020).
- Breiman, L.; Last, M.; Rice, J. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer Classification and Regression Tree Techniques: Bagging and Random Forests for Ecological Prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Hastie, T. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Friedman, J., Hastie, T., Tibshirani, R., Eds.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Ahmed, F.B.; Ismail, R. Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data. Int. J. Remote Sens. 2013, 34, 712–728. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Darst, B.F.; Malecki, K.C.; Engelman, C.D. Using recursive feature elimination in random forest to account for correlated variables in high dimensional data. BMC Genet. 2018, 19, 65. [Google Scholar] [CrossRef]
- Gregorutti, B.; Michel, B.; Saint-Pierre, P. Correlation and variable importance in random forests. Stat. Comput. 2017, 27, 659–678. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Bahl, A.; Hellack, B.; Balas, M.; Dinischiotu, A.; Wiemann, M.; Brinkmann, J.; Luch, A.; Renard, B.Y.; Haase, A. Recursive feature elimination in random forest classification supports nanomaterial grouping. NanoImpact 2019, 15, 100179. [Google Scholar] [CrossRef]
- Lachenbruch, P.A.; Mickey, M.R. Estimation of Error Rates in Discriminant Analysis. Technometrics 1968, 10, 1–11. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Gonzalez, R.S.; Latifi, H.; Weinacker, H.; Dees, M.; Koch, B.; Heurich, M. Integrating LiDAR and high-resolution imagery for object-based mapping of forest habitats in a heterogeneous temperate forest landscape. Int. J. Remote Sens. 2018, 39, 8859–8884. [Google Scholar] [CrossRef]
- Heurich, M.; Ochs, T.; Andresen, T.; Schneider, T. Object-orientated image analysis for the semi-automatic detection of dead trees following a spruce bark beetle (Ips typographus) outbreak. Eur. J. For. Res. 2010, 129, 313–324. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.; Corsi, F.; Van Wieren, S.E.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Li, Y.; He, N.; Hou, J.; Xu, L.; Liu, C.; Zhang, J.; Wang, Q.; Zhang, X.; Wu, X. Factors Influencing Leaf Chlorophyll Content in Natural Forests at the Biome Scale. Front. Ecol. Evol. 2018, 6, 1–10. [Google Scholar] [CrossRef]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Carter, G.A.; Knapp, A.K. Leaf optical properties in higher plants: Linking spectral characteristics to stress and chlorophyll concentration. Am. J. Bot. 2001, 88, 677–684. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Noland, T.L.; Mohammed, G.H.; Sampson, P.H. Scaling-up and model inversion methods with narrowband optical indices for chlorophyll content estimation in closed forest canopies with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1491–1507. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote Estimation of Crop Chlorophyll Content Using Spectral Indices Derived From Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Eitel, J.U.; Vierling, L.A.; Litvak, M.E.; Long, D.S.; Schulthess, U.; Ager, A.A.; Krofcheck, D.; Stoscheck, L. Broadband, red-edge information from satellites improves early stress detection in a New Mexico conifer woodland. Remote Sens. Environ. 2011, 115, 3640–3646. [Google Scholar] [CrossRef]
- Curran, R. Satellite-borne lidar observations of the Earth: Requirements and anticipated capabilities. Proc. IEEE 1989, 77, 478–490. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Tong, A.; He, Y. Remote Sensing of Grassland Chlorophyll Content: Assessing the Spatial-Temporal Performance of Spectral Indices. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; Institute of Electrical and Electronics Engineers (IEEE); pp. 2846–2849. [Google Scholar]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Darvishzadeh, R.; Heiden, U.; Heurich, M.; Wang, T. Leaf Nitrogen Content Indirectly Estimated by Leaf Traits Derived From the PROSPECT Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3172–3182. [Google Scholar] [CrossRef]
- Abdullah, H.; Skidmore, A.K.; Darvishzadeh, R.; Heurich, M. Sentinel-2 accurately maps green-attack stage of European spruce bark beetle (Ips typographus, L.) compared with Landsat-8. Remote Sens. Ecol. Conserv. 2018, 5, 87–106. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Lee, K.-S.; Cohen, W.B.; Kennedy, R.E.; Maiersperger, T.K.; Gower, S.T. Hyperspectral versus multispectral data for estimating leaf area index in four different biomes. Remote Sens. Environ. 2004, 91, 508–520. [Google Scholar] [CrossRef]
- Lindner, S. Seasonal Variation of Pigments in Needles: A Study of Scots Pine and Norway Spruce Seedlings Grown under Different Nursery Conditions. In Studia Forestalia Suecica; Skogshogskolan Royal College of Forestry Stockholm: Stockholm, Sweden, 1972; Volume 100. [Google Scholar]
- Senser, M.; Beck, E. Seasonal changes in structure and function of spruce chloroplasts. Planta 1975, 126, 1–10. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Liang, L.; Qin, Z.; Zhao, S.; Di, L.; Zhang, C.; Deng, M.; Lin, H.; Zhang, L.; Wang, L.; Liu, Z. Estimating crop chlorophyll content with hyperspectral vegetation indices and the hybrid inversion method. Int. J. Remote Sens. 2016, 37, 2923–2949. [Google Scholar] [CrossRef]
- Cavallo, D.P.; Cefola, M.; Pace, B.; Logrieco, A.F.; Attolico, G. Contactless and non-destructive chlorophyll content prediction by random forest regression: A case study on fresh-cut rocket leaves. Comput. Electron. Agric. 2017, 140, 303–310. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Liu, M.; Wang, C.; Xia, X. A hyperspectral index sensitive to subtle changes in the canopy chlorophyll content under arsenic stress. Int. J. Appl. Earth Obs. Geoinf. 2015, 36, 41–53. [Google Scholar] [CrossRef]
- Fassnacht, F.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques; John Wiley & Sons: New York, NY, USA, 1963. [Google Scholar]
- Tan, K.; Ma, W.; Wu, F.; Du, Q. Random forest–based estimation of heavy metal concentration in agricultural soils with hyperspectral sensor data. Environ. Monit. Assess. 2019, 191, 446. [Google Scholar] [CrossRef]
- Mangla, R.; Kumar, S.; Nandy, S. Random Forest Regression Modelling for Forest Aboveground Biomass Estimation Using RISAT-1 PolSA;R and Terrestrial LiDAR Data. In Lidar Remote Sensing for Environmental Monitoring XV; Volume 9879, p. 98790. Available online: https://www.researchgate.net/publication/305015564 (accessed on 29 October 2020).
- Wermelinger, B. Ecology and management of the spruce bark beetle Ips typographus—A review of recent research. For. Ecol. Manag. 2004, 202, 67–82. [Google Scholar] [CrossRef]
- Abdullah, H.; Darvishzadeh, R.; Skidmore, A.; Groen, T.A.; Heurich, M. European spruce bark beetle (Ips typographus, L.) green attack affects foliar reflectance and biochemical properties. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 199–209. [Google Scholar] [CrossRef]
- Niemann, K.O.; Visintini, F. Assessment of Potential for Remote Sensing Detection of Bark Beetle-Infested Areas during Green Attack: A Literature Review; Mountain Pine Beetle Initiative Working Paper 2005-2; Natural Resources Canada, Canadian Forest Service, Pacific Forestry Centre: Victoria, BC, Canada.
- Foster, A.C.; Walter, J.A.; Shugart, H.H.; Sibold, J.; Negron, J. Spectral evidence of early-stage spruce beetle infestation in Engelmann spruce. For. Ecol. Manag. 2017, 384, 347–357. [Google Scholar] [CrossRef]
- Lausch, A.; Heurich, M.; Gordalla, D.; Dobner, H.-J.; Gwillym-Margianto, S.; Salbach, C. Forecasting potential bark beetle outbreaks based on spruce forest vitality using hyperspectral remote-sensing techniques at different scales. For. Ecol. Manag. 2013, 308, 76–89. [Google Scholar] [CrossRef]
- Deshayes, M.; Guyon, D.; Jeanjean, H.; Stach, N.; Jolly, A.; Hagolle, O. The contribution of remote sensing to the assessment of drought effects in forest ecosystems. Ann. For. Sci. 2006, 63, 579–595. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).