Influence of DEM Elaboration Methods on the USLE Model Topographical Factor Parameter on Steep Slopes
Abstract
1. Introduction
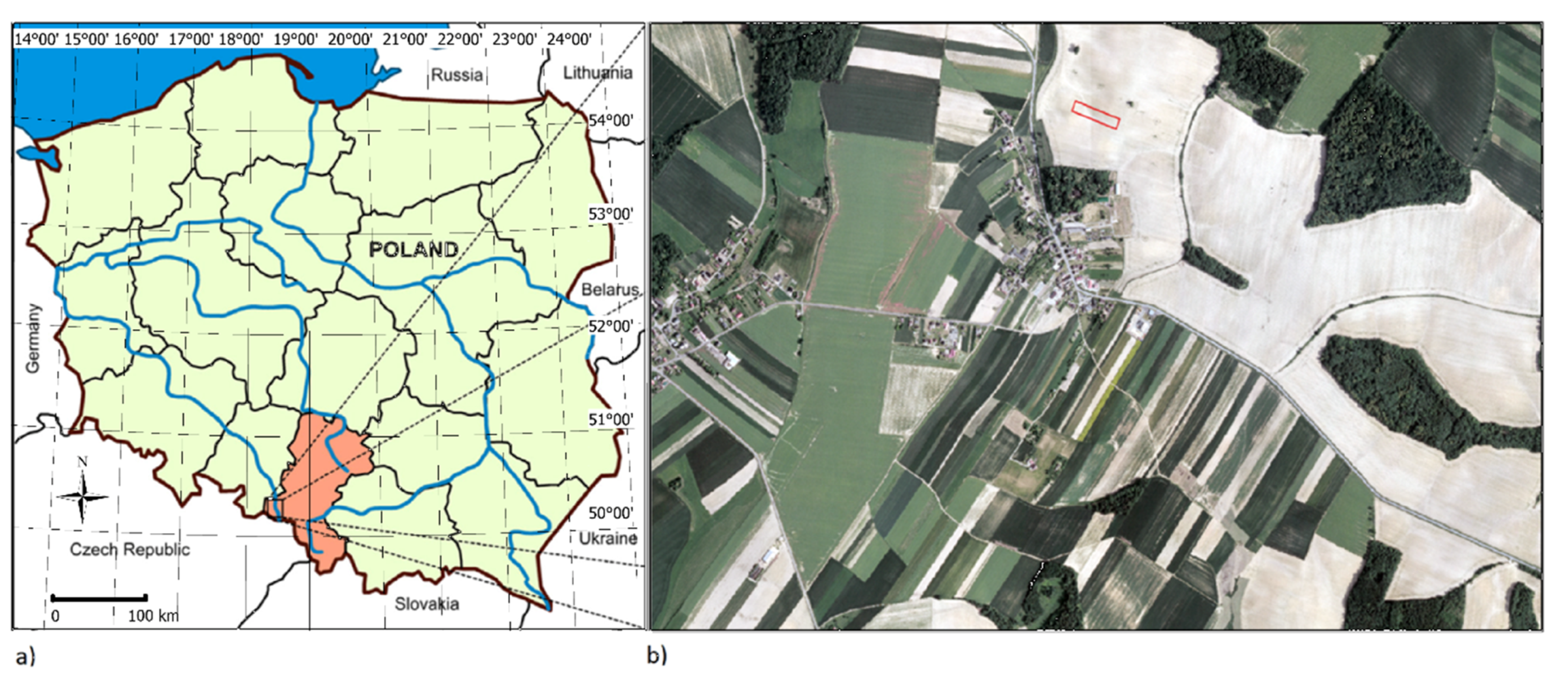
2. Materials and Methods
3. Source of DEMs
3.1. Aerial Photographs (APs)
3.2. Aerial Laser Scans (ALSs)
3.3. Terrestrial Laser Scans (TLSs)
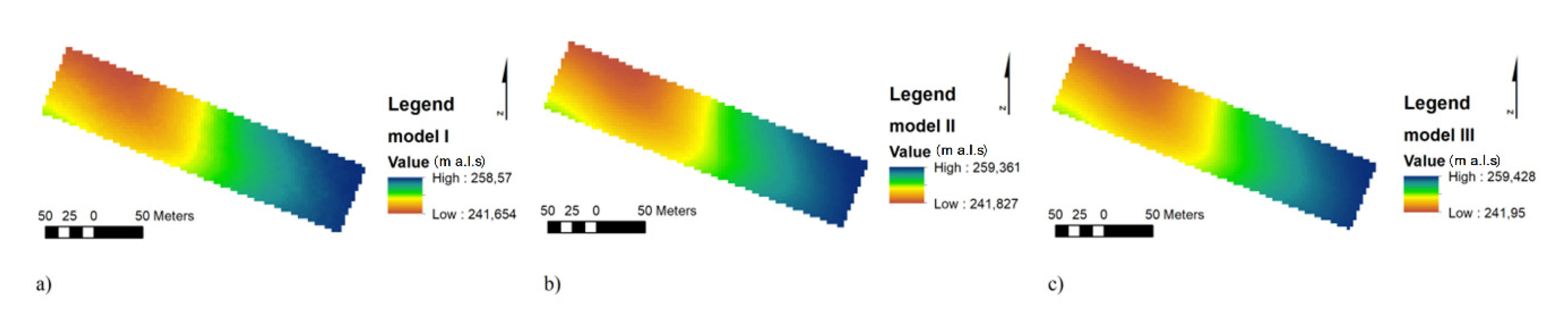
3.4. DEMs Generation
3.5. LSUSLE Calculations
- S = 10.8 × sin θ + 0.03, where: slope gradient < 0.09
- S = 16.8 × sin θ − 0.5, where: slope gradient ≥ 0.09
3.6. Statistical Analysis
4. Results and Discussion
- Model I: 193.804, 19.328,
- Model II: 167.787, 6.934, and
- Model III 160.240,
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ballabio, C.; Borrelli, P.; Spinoni, J.; Meusburger, K.; Michaelides, S.; Beguería, S.; Klik, A.; Petan, S.; Janeček, M.; Olsen, P.; et al. Mapping monthly rainfall erosivity in Europe. Sci. Total. Environ. 2017, 579, 1298–1315. [Google Scholar] [CrossRef]
- Ryczek, M.; Boroń, K.; Klatka, S.; Kruk, E. Wykorzystanie technik GIS do oceny zagrożenia erozją wodną na przykładzie rolniczej zlewni potoku Mątny w Beskidzie Wyspowym. Zesz. Nauk. Uniw. Przyr. Wroc. Rol. 2010, 96, 163–174. (In Polish) [Google Scholar]
- Halecki, W.; Kruk, E.; Ryczek, M. Evaluation of soil erosion in the Mątny stream catchment in the West Carpathians using the G2 model. Catena 2018, 164, 116–124. [Google Scholar] [CrossRef]
- Halecki, W.; Kruk, E.; Ryczek, M. Influence of various use scenarios on soil loss in the Mątny stream catchment in the Gorce, West Carpathians region. Land Use Policy 2018, 73, 363–372. [Google Scholar] [CrossRef]
- Shi, Z.; Ai, L.; Fang, N.; Zhu, H. Modeling the impacts of integrated small watershed management on soil erosion and sediment delivery: A case study in the Three Gorges Area, China. J. Hydrol. 2012, 438–439, 156–167. [Google Scholar] [CrossRef]
- Thomas, Z.; Abbott, B.W.; Troccaz, O.; Baudry, J.; Pinay, G. Proximate and ultimate controls on carbon and nutrient dynamics of small agricultural catchments. Biogeosciences 2016, 13, 1863–1875. [Google Scholar] [CrossRef]
- Karamage, F.; Zhang, C.; Ndayisaba, F.; Shao, H.; Kayiranga, A.; Sun, B.; Nahayo, L.; Nyesheja, E.M.; Tian, G. Extent of Cropland and Related Soil Erosion Risk in Rwanda. Sustainability 2016, 8, 609. [Google Scholar] [CrossRef]
- Halecki, W.; Młyński, D.; Ryczek, M.; Kruk, E.; Radecki-Pawlik, A. The application of Artificial Neural Network (ANN) to assessment of soil salinity and temperature variability in agricultural areas of a mountain catchment. Polish J. Environ. Study 2017, 6, 2545–2554. [Google Scholar] [CrossRef]
- Dabral, P.P.; Baithuri, N.; Pandey, A. Soil Erosion Assessment in a Hilly Catchment of North Eastern India Using USLE, GIS and Remote Sensing. Water Resour. Manag. 2008, 22, 1783–1798. [Google Scholar] [CrossRef]
- Bahadur, K.C.K. Mapping soil erosion susceptibility using remote sensing and GIS: A case of the Upper Nam Wa Watershed Nan Province. Thai. Environ. Geol. 2009, 57, 695–705. [Google Scholar] [CrossRef]
- Wójcik, A.; Klapa, P.; Mitka, B.; Piech, I. The use of TLS and UAV methods for measurement of the repose angle of granular materials in terrain conditions. Measurement 2019, 146, 780–791. [Google Scholar] [CrossRef]
- Mitka, B. Comparative analysis of geospatial data received by TLS and UAV technologies for the quarry. In Proceedings of the 18th International Multidisciplinary Scientific Geoconference SGEM: Photogrammetry and Remote Sensing, Albena, Bulgaria, 30 June–9 July 2018; Volume 30, pp. 57–64. [Google Scholar]
- Tompalski, P.; White, J.C.; Coops, N.C.; Wulder, M.A. Demonstrating the transferability of forest inventory attribute models derived using airborne laser scanning data. Remote Sens. Environ. 2019, 227, 110–124. [Google Scholar] [CrossRef]
- Bożek, P.; Janus, J. The Influence of Elevation Data Generalization on the Accuracy of the RUSLE Model. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 374–377. [Google Scholar]
- Bigdeli, B.; Amirkolaee, H.A.; Pahlavani, P. DTM generation from the point cloud using a progressive geodesic morphology and a modified Particle Swarm Optimization. Int. J. Remote. Sens. 2018, 39, 8450–8481. [Google Scholar] [CrossRef]
- Picu, I.A.C. Updating Geospatial Data by Creating a High Resolution Digital Surface Model. J. Appl. Eng. Sci. 2018, 8, 51–58. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; Supersedes Agriculture Handbook No. 282; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978; pp. 4–11.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation(RUSLE); Agriculture Handbook 703; US Department of Agriculture: Washington, DC, USA, 1997; pp. 1–251.
- Liu, B.Y.; Zhang, K.L.; Xie, Y. An Empirical Soil Loss Equation. In Proceedings of the 12th International SoilConservation Organization Conference, Beijing, China, 26–31 May 2002; Tsinghua Press: Beijing, China, 2002; pp. 143–149. [Google Scholar]
- Zhang, H.; Yao, Z.; Yang, Q.; Li, S.; Baartman, J.E.; Gai, L.; Yao, M.; Yang, X.; Ritsema, C.J.; Geissen, V. An integrated algorithm to evaluate flow direction and flow accumulation in flat regions of hydrologically corrected DEMs. Catena 2017, 151, 174–181. [Google Scholar] [CrossRef]
- Wilson, J.P.; Lam, C.S.; Deng, Y. Comparison of the performance of flow-routing algorithms used in GIS-based hydrologic analysis. Hydrol. Process. 2007, 21, 1026–1044. [Google Scholar] [CrossRef]
- Ligonja, P.J.; Shrestha, R.P. Soil Erosion Assessment in Kondoa Eroded Area in Tanzania using Universal Soil Loss Equation, Geographic Information Systems and Socioeconomic Approach. Land Degrad. Dev. 2013, 26, 367–379. [Google Scholar] [CrossRef]
- Van Remortel, R.; Maichle, R.; Hickey, R. Computing the LS factor for the Revised Universal Soil Loss Equation through array-based slope processing of digital elevation data using a C++ executable. Comput. Geosci. 2004, 30, 1043–1053. [Google Scholar] [CrossRef]
- McCool, D.K.; Brown, L.C.; Foster, G.R.; Mutchler, C.K.; Meyer, L.D. Revised Slope Steepness Factor for the Universal Soil Loss Equation. Trans. ASAE 1987, 30, 1387–1396. [Google Scholar] [CrossRef]
- McCool, D.K.; Foster, G.R.; Mutchler, C.K.; Meyer, L.D. Revised slope length factor for the Universal Soil Los Equation. Trans. ASAE 1989, 32, 1571–1576. [Google Scholar] [CrossRef]
- Liu, H.; Kiesel, J.; Hörmann, G.; Fohrer, N. Effects of DEM horizontal resolution and methods on calculating the slope length factor in gently rolling landscapes. Catena 2011, 87, 368–375. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences 2015, 5, 117–126. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the revised universal soil loss equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Moore, I.D.; Burch, G.J. Physical Basis of the Length-slope Factor in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Griffin, M.L.; Beasley, D.B.; Fletcher, J.J.; Foster, G.R. Estimating soil loss on topographically nonuniform field and farm units. J. Soil Water Conserv. 1988, 43, 326–331. [Google Scholar]
- Desmet, P.J.J.; Govers, G. A GIS procedure for the automated calculation of the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Mitasova, H.; Mitas, L.; Brown, W.M.; Johnson, D.M. Terrain Modeling and Soil Eorsion Simulationa for Fort Hood and Fort Polk Test Areas; Geographic Modeling and Systems Laboratory, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1999; pp. 10–11. [Google Scholar]
- Nearing, M.A. A single, continuous function for slope steepness influence on soil loss. Soil Sci. Soc. Am. J. 1997, 61, 917–919. [Google Scholar] [CrossRef]
- Winchell, M.F.; Jackson, S.H.; Wadley, A.M.; Srinivasan, R. Extension and validation of a geographic information system-based method for calculating the Revised Universal Soil Loss Equation length-slope factor for erosion risk assessments in large watersheds. J. Soil Water Conserv. 2008, 63, 105–111. [Google Scholar] [CrossRef]
- Rodriguez, J.L.G.; Suarez, M.C.G. Methodology for estimating the topographic factor LS of RUSLE3D and USPED using GIS. Geomorphology 2012, 175–176, 98–106. [Google Scholar] [CrossRef]
- Hickey, R. Slope Angle and Slope Length Solutions for GIS. Cartography 2000, 29, 1–8. [Google Scholar] [CrossRef]
- Van Remortel, R.D.; Hamilton, M.E.; Hickey, R.J. Estimating the LS Factor for RUSLE through Iterative Slope Length Processing of Digital Elevation Data within Arclnfo Grid. Cartography 2001, 30, 27–35. [Google Scholar] [CrossRef]
- Galdino, S.; Sano, E.E.; Andrade, R.G.; Grego, C.R.; Nogueira, S.F.; Bragantini, C.; Flosi, A.H.G. Large-scale Modeling of Soil Erosion with RUSLE for Conservationist Planning of Degraded Cultivated Brazilian Pastures. Land Degrad. Dev. 2015, 27, 773–784. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comp. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Orlandini, S.; Moretti, G.; Gavioli, A. Analytical basis for determining slope lines in grid digital elevation models. Water Resour. Res. 2014, 50, 526–539. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Modelling Erosion and Deposition: Topographic Effects. Trans. ASAE 1986, 29, 1624–1630. [Google Scholar] [CrossRef]
- Orlandini, S.; Moretti, G.; Corticelli, M.A.; Santangelo, P.E.; Capra, A.; Rivola, R.; Albertson, J.D. Evaluationof flow direction methods against field observations of overland flow dispersion. Water Resour. Res. 2012, 48, 13. [Google Scholar] [CrossRef]
- Feng, T.; Chen, H.; Polyakov, V.O.; Wang, K.; Zhang, X.; Zhang, W. Soil erosion rates in two karst peak-cluster depression basins of northwest Guangxi, China: Comparison of the RUSLE model with 137Cs measurements. Geomorphology 2016, 253, 217–224. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, S.; Varghese, J. Estimation of Soil Erosion for a Himalayan Watershed Using GIS Technique. Water Resour. Manag. 2001, 15, 41–54. [Google Scholar] [CrossRef]
- Lee, S. Soil erosion assessment and its verification using the Universal Soil Loss Equation and Geographic Information System: A case study at Boun, Korea. Environ. Earth Sci. 2004, 45, 457–465. [Google Scholar] [CrossRef]
- Yoshino, K.; Ishioka, Y. Guidelines for soil conservation towards integrated basen managenment for sustainable development: A new approach based on the assessment of soil loss risk using remote sensing and GIS. Paddy Water Environ. 2005, 3, 235–247. [Google Scholar] [CrossRef]
- Bhattarai, R.; Dutta, D. Estimation of Soil Erosion and Sediment Yield Using GIS at Catchment Scale. Water Resour. Manag. 2006, 21, 1635–1647. [Google Scholar] [CrossRef]
- Lee, G.S.; Choi, I.H. Scaling effect for the quantification of soil loss using GIS spatial analysis. KSCE J. Civ. Eng. 2010, 14, 897–904. [Google Scholar] [CrossRef]
- Zhang, J.; DeAngelis, D.L.; Zhuang, J. GIS-Based ER-USLE Model to Predict Soil Loss in Cultivated Land; Springer: Berlin, Germany, 2011; pp. 65–80. [Google Scholar]
- Perović, V.; Životić, L.; Kadović, R.; Đorđević, A.; Jaramaz, D.; Mrvić, V.; Todorović, M. Spatial modelling of soil erosion potential in a mountainous watershed of South-eastern Serbia. Environ. Earth Sci. 2012, 68, 115–128. [Google Scholar] [CrossRef]
- Chen, Y.; Miller, J.R.; Francis, J.; Russell, G. Projected regime shift in Arctic cloud and water vapor feedbacks. Environ. Res. Lett. 2011, 6, 044007. [Google Scholar] [CrossRef]
- Mhangara, P.; Kakembo, V.; Lim, K.J. Soil erosion risk assessment of the Keiskamma catchment, South Africa using GIS and remote sensing. Environ. Earth Sci. 2011, 65, 2087–2102. [Google Scholar] [CrossRef]
- Prasannakumar, V.; Shiny, R.; Geetha, N.; Vijith, H. Spatial prediction of soil erosion risk by remote sensing, GIS and RUSLE approach: A case study of Siruvani river watershed in Attapady valley, Kerala, India. Environ. Earth Sci. 2011, 64, 965–972. [Google Scholar] [CrossRef]
- Kumar, S.; Kushwaha, S.P.S. Modelling soil erosion risk based on RUSLE-3D using GIS in a Shivalik sub-watershed. J. Earth Syst. Sci. 2013, 122, 389–398. [Google Scholar] [CrossRef]
- Saygin, S.D.; Ozcan, A.U.; Basaran, M.; Timur, O.B.; Dolarslan, M.; Yılman, F.E.; Erpul, G. The combined RUSLE/SDR approach integrated with GIS and geostatistics to estimate annual sediment flux rates in the semi-arid catchment, Turkey. Environ. Earth Sci. 2013. [Google Scholar] [CrossRef]
- Mashimbye, Z.; De Clercq, W.P.; Van Niekerk, A. An evaluation of digital elevation models (DEMs) for delineating land components. Geoderma 2014, 213, 312–319. [Google Scholar] [CrossRef]
- Available online: http://www.gugik.gov.pl/pzgik/zamow-dane (accessed on 20 September 2020).
- Moore, I.D.; Turner, A.K.; Wilson, J.P.; Jenson, S.K.; Band, L.E. GIS and land-surface-subsurface process modeling. Environ. Model. GIS 1993, 20, 196–230. [Google Scholar]
- Pilesjö, P.; Hasan, A. A Triangular Form-based Multiple Flow Algorithm to Estimate Overland Flow Distribution and Accumulation on a Digital Elevation Model. Trans. GIS 2013, 18, 108–124. [Google Scholar] [CrossRef]
- Molnár, D.K.; Julien, P.Y. Estimation of upland erosion using GIS. Comput. Geosci. 1998, 24, 183–192. [Google Scholar] [CrossRef]
- Wilson, D.J.; Gallant, J.C. Digital terrain analysis. In Terrain Analysis: Principles and Applications; Wilson, D.J., Gallant, J.C., Eds.; John Willey & Sons, INC: New York, NY, USA, 2000; pp. 1–27. [Google Scholar]
- McCool, D.K.; Foster, G.R.; Weesies, G.A. Slope Length and Steepness Factors (LS). In Agricultural Research Service (USDAARS) Handbook 703; United States Department of Agriculture: Washington, DC, USA, 1997. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Rahnama, M.; Barani, G.A. Application of Rainfall-runoff Models to Zard River Catchment’s. Am. J. Environ. Sci. 2005, 1, 86–89. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow forecasting through conceptual models-Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Risse, L.M.; Nearing, M.A. Evaluation of WEPP ant its comparison with USLE and RUSLE. Trans. ASAE 2000, 43, 1129–1135. [Google Scholar] [CrossRef]
- Dawson, C.; Abrahart, R.J.; Shamseldin, A.Y.; Wilby, R. Flood estimation at ungauged sites using artificial neural networks. J. Hydrol. 2006, 319, 391–409. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
- Arge, L.; Chase, J.S.; Halpin, P.; Toma, L.; Vitter, J.S.; Urban, D.; Wickremesinghe, R. Efficient Flow Computation on Massive Grid Terrain Datasets. GeoInformatica 2003, 7, 283–313. [Google Scholar] [CrossRef]
- Bhowmik, A.K.; Metz, M.; Schafer, R.B. An automated, objective and open source tool for streamthreshold selection and upstream riparian corridor delineation. Environ. Model Softw. 2015, 63, 240–250. [Google Scholar] [CrossRef]
- Magalhães, S.V.G.; Andrade, M.V.A.; Franklin, W.R.; Pena, G.C. A New Method for Computing the Drainage Network Based on Raising the Level of an Ocean Surrounding the Terrain. Adv. Cartogr. GIS 2012, 391–407. [Google Scholar] [CrossRef]
- Metz, M.; Mitasova, H.; Harmon, R.S. Efficient extraction of drainage networks from massive, radar-based elevation models with least cost path search. Hydrol. Earth Syst. Sci. 2011, 15, 667–678. [Google Scholar] [CrossRef]
- Yao, Y.Z.; Shi, X. Alternatingscanningordersandcombiningalgorithms toimprove the efficiency of flow accumulation calculation. Int. J. Geogr. Inf. Sci. 2015, 29, 1214–1239. [Google Scholar] [CrossRef]
- Yao, Y.; Tao, H.; Shi, X. Multi-types weeping for improving the efficiency off low accumulation calculation. In Proceedings of the 20th International Conference on Geoinformatics (GEOINFORMATICS), Hong Kong, China, 15–17 June 2012; pp. 1–4. [Google Scholar]
- Su, C.; Yu, W.-B.; Feng, C.-J.; Yu, C.-N.; Huang, Z.-C.; Zhang, X.-C. An Efficient Algorithm for Calculating Drainage Accumulation in Digital Elevation Models Based on the Basin Tree Index. IEEE Geosci. Remote Sens. Lett. 2014, 12, 424–428. [Google Scholar] [CrossRef]
- Bai, R.; Li, T.; Huang, Y.; Li, J.; Wang, G. An efficient and comprehensive method for drainage network extraction from DEM with billions of pixels using a size-balanced binary search tree. Geomorphology 2015, 238, 56–67. [Google Scholar] [CrossRef]
- Moretti, G.; Orlandini, S. Automatic delineation of drainage basins from contour elevation data using skeleton construction techniques. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef]
- Gallant, J.C.; Wilson, J.P. Primary Topographic Attributes, Terrain Analysis: Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley and Sons: New York, NY, USA, 2000; pp. 51–85. [Google Scholar]
- Zandbergen, P.A. The effect of cell resolution on depressions in Digital Elevation Models. Appl. GIS 2006, 2, 04.1–04.35. [Google Scholar] [CrossRef]
- Jensen, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Zhu, D. A Comparative Study of Single and Dual Polarisation Quantitative Weather Radar in the Context of Hydrological Modelling Structure. Ph.D. Thesis, University of Bristol, Bristol, UK, 2009. [Google Scholar]
- MacMillan, R.A.; Martin, T.C.; Earle, T.J.; McNabb, D.H. Automatic analysis and classification of landforms using high resolution digital elevation data: Applications and issues. Can. J. Remote Sens. 2003, 29, 592–606. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Creed, I.F. Removal of artefact depressions from digital elevation models: Towards a minimum impact approach. Hydrol. Process. 2005, 19, 3113–3126. [Google Scholar] [CrossRef]
- Thompson, J.A.; Bell, J.C.; Butler, C.A. Digital elevation model resolution: Effectson terrain attribute calculation and quantitative soil-landscape modeling. Geoderma 2001, 100, 67–89. [Google Scholar] [CrossRef]
- Zhang, W.; Montgomery, D.R. Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Wang, X. A cross-scale comparison of drainage basin characteristics derived from digital elevation models. Earth Surf. Process. Landf. 1999, 24, 557–562. [Google Scholar] [CrossRef]
- Quinn, P.; Beven, K.; Chevallier, P.; Planchon, O. The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
- Wolock, D.M.; Price, C.V. Effects of digital elevation model map scale and data resolution on a topography-based watershed model. Water Resour. Res. 1994, 30, 3041–3052. [Google Scholar] [CrossRef]
- Bolstad, P.V.; Stowe, T. An Evaluation of DEM Accuracy: Elevation, Slope, and Aspect. Photogram. Eng. Remote Sens. 1994, 60, 1327–1332. [Google Scholar]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total. Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
- Stone, R.P.; Hilborn, D. Factsheet, Universal Soil Loss Equation (USLE); Ministry of Agriculture, Food and Rural Affairs: Guelph, ON, Canada, 2000.
- Available online: http://www.omafra.gov.on.ca/english/engineer/facts/12-051.htm (accessed on 20 September 2020).



| Method | Equation | Components Description |
|---|---|---|
| Wishmeier and Smith [17] | λ is the cumulative slope length; m is a variable slope-length exponent m = 0.5 if β > 0.05; m = 0.4 if 0.03 < β > 0.05; m = 0.3 if 0.01 < β > 0.03; and m = 0.2 if β < 0.01 | |
| McCool et al. [24] | , , | L is the slope length coefficient; 22.13 is the USLE unit plot length in meters; β is the ratio of rill to inter-rill erosion for conditions when the soil is moderately susceptible to both rill and inter-rill erosion; and θ is the slope angle |
| Moore and Wilson [28] | AS is the unit contributing area (m); θ is the slope in radians; S as above; m value range: 0.4–0.56; and n value range: 1.2–1.30 | |
| Moore and Burch [29] | m = 0.4 (value range: 0.4–0.6); n = 1.3 (value range: 1.22–1.3) | |
| Griffin et al. [30] | L, S, m is as above, AS is the unit contributing area (m) m = 0.4 (value range: 0.2–0.6); and n = 1.3 (value range: 1.0–1.3) | |
| Desmet and Govers [31] | D is the raster resolution; A(i,j) is the unit area at the entrance to cell (i,j); m is the exponent of slope length indicator; and x is the coefficient correcting the path length of flow through raster cells depending on flow direction and calculated based on exposure | |
| Nearing [33] | S as above; D is the grid cell size in meters; x(i,j) = sin a(i,j) + cos a(i,j); ai is the aspect direction of the grid cell (i,j); and m is related to the F ratio of the rill to inter-rill erosion | |
| Yoshino and Ishioka [47] | l is the slope length (m); s is slope %; m is dependent on slope %, where: m = 0.5 for slope s ≤ 5%; m = 0.4 (3.5 < s < 4.5%); m = 0.3 (1% < s < 3%); and m = 0.2 (1.8% < s). The slope length l was defined as the length of a slope with the greatest incline in a given pixel | |
| Bhattarai and Dutta [48] | ;; S = 10.8∙sinθ + 0.03 for slopes < 9%; S = 16.8∙sinθ − 0.50 for slopes 9% | L, m, S, as above θ is slope inclination in degrees (°) |
| Lee and Choi [49] | ; ; | L, m, as above x is raster cell length; and θ is slope inclination in degrees (°) |
| Perovic et al. [51] | A is the supply area outflowing to a cell [m]; b is slope inclination in degrees (°); m and n are parameters (m = 0.4; n = 1.4); 0 is determined from USLE with a length of 22.1 m; and b0 is the parameter arising from the USLE model and equal to 0.09. | |
| Kumar and Kushwaha [55] | β(r) is slope inclination in degrees (°); m and n equal 0.6 and 1.3, respectively; Ar is the coefficient of network cells divided by the up-slope contributing area; and r(x,y) is the location of a given point | |
| Saygm et al. [56] | χ is the accumulation of surface flow calculated from a DEM using the delinearization module of the basin in the Arc View 9.2 program; λ is the dimension of the raster cell; and θ is the inclination in degrees (°) |
| Parameter | Method I | Method II | Method III | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean | St. Dev. | Min. | Max. | Mean | St. Dev. | Min. | Max. | Mean | St. Dev. | |
| DEM [m a.s.l] | 241.65 | 258.57 | 250.27 | 5.21 | 241.83 | 259.36 | 250.78 | 5.36 | 241.95 | 259.43 | 250.87 | 5.29 |
| S [-] | 0.06 | 4.17 | 1.85 | 0.80 | 0.22 | 3.66 | 1.95 | 0.79 | 0.12 | 3.57 | 1.93 | 0.78 |
| β [-] | 0.06 | 1.89 | 1.27 | 0.31 | 0.30 | 1.79 | 1.31 | 0.29 | 0.16 | 1.77 | 1.30 | 0.29 |
| m [-] | 0.06 | 0.65 | 0.55 | 0.08 | 0.23 | 0.64 | 0.56 | 0.07 | 0.14 | 0.64 | 0.56 | 0.07 |
| L [-] | 1.01 | 3.65 | 1.15 | 0.25 | 1.03 | 3.84 | 1.16 | 0.26 | 1.02 | 2.94 | 1.13 | 0.20 |
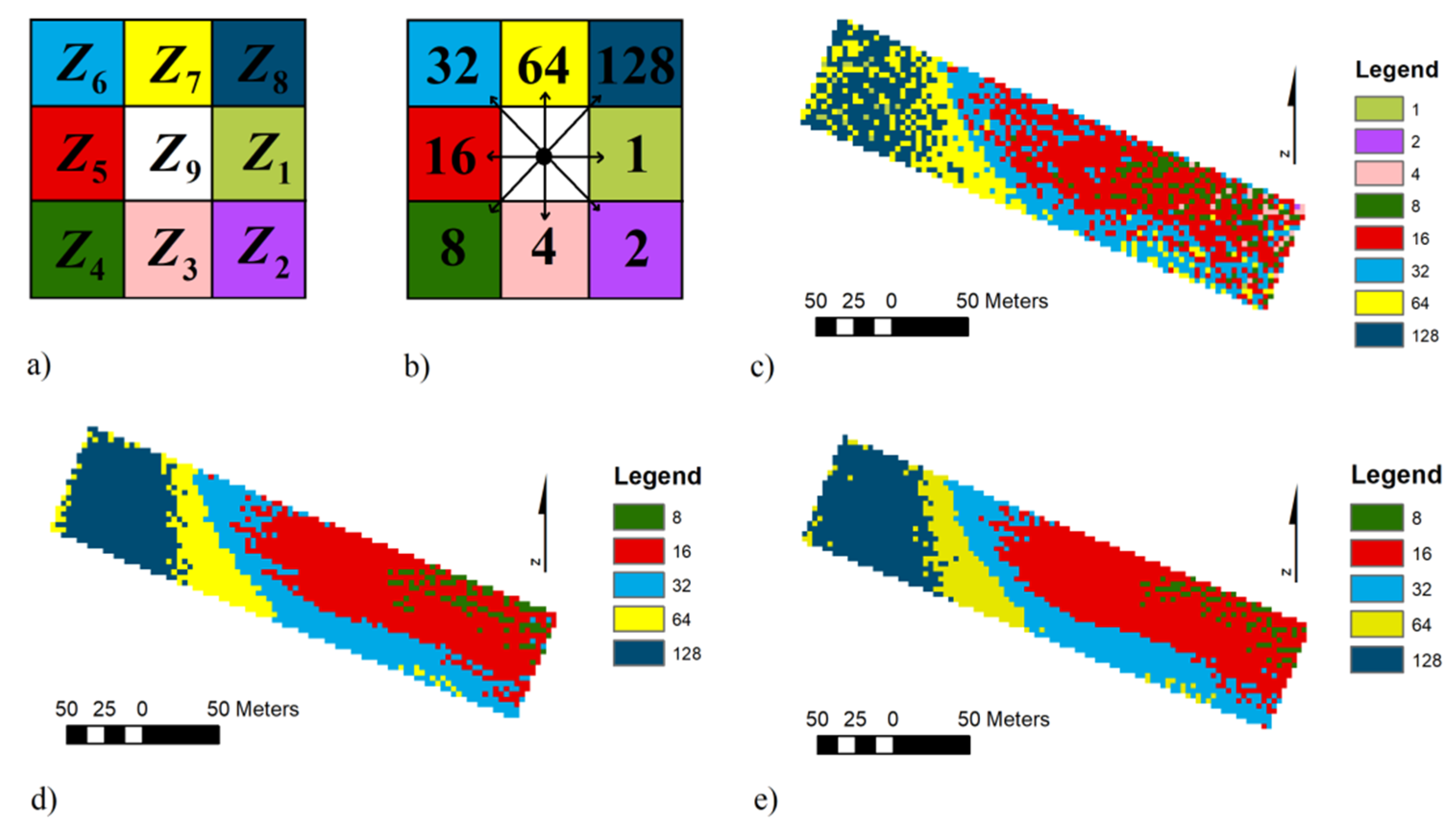
| FlowDir [-] | 1.00 | 128 | 46.50 | 41.27 | 8.00 | 128 | 49.47 | 43.85 | 8.00 | 128 | 50.40 | 44.45 |
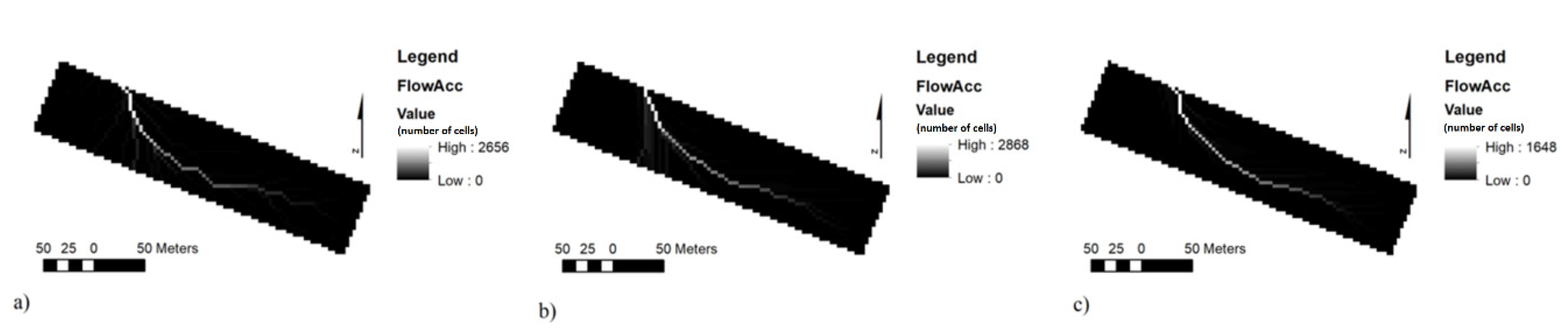
| Flow Acc [-] | 0.00 | 2656 | 46,70 | 213.55 | 0.00 | 2868 | 49.63 | 218.73 | 0.00 | 1648 | 30.02 | 143.68 |
| Slope [o] | 0.19 | 16.13 | 7.99 | 2.92 | 1.07 | 14.34 | 8.32 | 2.83 | 0.51 | 14.01 | 8.25 | 2.80 |
| LS [-] | 0.06 | 6.32 | 2.13 | 0.97 | 0.23 | 5.47 | 2.25 | 0.95 | 0.12 | 5.22 | 2.17 | 0.89 |
| Method | DEMs | |||
|---|---|---|---|---|
| MEP * [m] | RMSE * [m] | MPE * [%] | ME * [-] | |
| ALS vs. TLS | 0.104 | 0.194 | 0.042 | 0.999 |
| AP vs. TLS | 0.610 | 0.647 | 0.242 | 0.985 |
| ALS vs. AP | 0.507 | 0.576 | 0.201 | 0.988 |
| LS-Factors MEP * [-] RMSE * [-] MPE * [%] ME *[-] | ||||
| ALS vs. TLS | −0.089 | 0.412 | −5.374 | 0.784 |
| AP vs. TLS | 0.044 | 0.571 | −0.061 | 0.585 |
| ALS vs. AP | −0.133 | 0.606 | −13.535 | 0.600 |
| (a) | ||||||||||
| Model | MLP | Learning Algorithm | Activation Function- Perceptrons | Analysis of Quality and Errors of ANN | ||||||
| Quality | Error | |||||||||
| Hid-den | Out-put | l * | t * | v * | l * | t * | v * | |||
| I (AP) | 7-10-1 | BFGS488 | log. | tanh | 0.99998 | 0.99997 | 0.99998 | 0.000018 | 0.000024 | 0.000018 |
| II (ALS) | 7-8-1 | BFGS203 | log. | linear | 0.99999 | 0.99999 | 0.99999 | 0.000004 | 0.000005 | 0.000004 |
| III (TLS) | 7-12-1 | BFGS422 | tanh | expon. | 1.00000 | 1.00000 | 1.00000 | 0.000000 | 0.000000 | 0.000000 |
| (b) | ||||||||||
| Model | MLP | Learning Algorithm | Models Efficiency Measures | |||||||
| MEP * | RMSE * | MPE * | ME * | r * | ||||||
| - | - | % | - | - | ||||||
| I (AP) | 7-10-1 | BFGS488 | 0.0017 | 0.3988 | −2.5596 | 0.8296 | 0.9108 | |||
| II (ALS) | 7-8-1 | BFGS203 | 6 × 10−6 | 0.0018 | −0.0084 | 0.9999 | 0.9999 | |||
| III (TLS) | 7-12-1 | BFGS422 | 0.0002 | 0.3082 | −1.4001 | 0.8795 | 0.9378 | |||
| Model | I—AP | II—ALS 7-8-1 | III—TLS 7-12-1 | |||||
|---|---|---|---|---|---|---|---|---|
| MLP | 7-10-1 | |||||||
| Parameter | Share | Parameter | Share | Parameter | Share | |||
| Relative [-] | Absolute [%] | Relative [-] | Absolute [%] | Relative [-] | Absolute [%] | |||
| S | 47,846.9 | 50.7 | S | 144,751.5 | 67.2 | S | 3,838,295.5 | 45.6 |
| Slope [°] | 26.801.8 | 28.4 | L | 24,354.8 | 11.3 | Slope [°] | 3,591,172.6 | 42.6 |
| β | 8670.2 | 9.2 | β | 22,335.5 | 10.4 | m | 510,529.7 | 6.1 |
| FlowAcc. | 6549.6 | 6.9 | m | 19,413.4 | 9.0 | L | 256,630.0 | 3.0 |
| L | 3961.3 | 4.2 | Slope [°] | 4453.1 | 2.1 | β | 229,728.8 | 2.7 |
| m | 607.4 | 0.6 | FlowDir. | 1.2 | 0.0 | FlowDir. | 2.0 | 0.0 |
| FlowDir. | 1.1 | 0.0 | FlowAcc. | 1.0 | 0.0 | FlowAcc. | 1.0 | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruk, E.; Klapa, P.; Ryczek, M.; Ostrowski, K. Influence of DEM Elaboration Methods on the USLE Model Topographical Factor Parameter on Steep Slopes. Remote Sens. 2020, 12, 3540. https://doi.org/10.3390/rs12213540
Kruk E, Klapa P, Ryczek M, Ostrowski K. Influence of DEM Elaboration Methods on the USLE Model Topographical Factor Parameter on Steep Slopes. Remote Sensing. 2020; 12(21):3540. https://doi.org/10.3390/rs12213540
Chicago/Turabian StyleKruk, Edyta, Przemysław Klapa, Marek Ryczek, and Krzysztof Ostrowski. 2020. "Influence of DEM Elaboration Methods on the USLE Model Topographical Factor Parameter on Steep Slopes" Remote Sensing 12, no. 21: 3540. https://doi.org/10.3390/rs12213540
APA StyleKruk, E., Klapa, P., Ryczek, M., & Ostrowski, K. (2020). Influence of DEM Elaboration Methods on the USLE Model Topographical Factor Parameter on Steep Slopes. Remote Sensing, 12(21), 3540. https://doi.org/10.3390/rs12213540






