Abstract
Many debris-covered glaciers are broadly distributed across High Mountain Asia and have made a number of contributions to water circulation for Qinghai-Tibet Plateau (QTP). The formation of large supraglacial lakes poses risks for glacier lake outburst floods (GLOFs). Therefore, it is important to monitor the movement of glaciers and to analyze their spatiotemporal characteristics. In this study we take Cuolangma glaciers in the central Himalayas as study targets, where glacier No.1 is a lake-terminating debris-covered glacier and glacier No.2 is a land-terminating debris-covered glacier. The 3D deformation time series is firstly estimated by using the Pixel Offset-Small Baseline Subsets (PO-SBAS) based on the ascending and descending Sentinel-1 datasets spanning from January to December 2018. Then the horizontal and vertical time series displacements are obtained to show their spatiotemporal features. The velocities of glacier No.1 in horizontal and vertical direction were up to 16.00.04 m/year and 3.40.42 m/year, respectively, and the ones of the glacier No.2 were 12.00.07 m/year and 2.00.27 m/year, respectively. Next, the correlation between the precipitation and the surface velocity suggests that the glacier velocity does not show a clear association with daily precipitation alone. Finally, the debris-covered glaciers evolution is evaluated which shows that the tongue of the glacier No.1 is wasting away and the transition of glacier No.2 from land-terminating to lake-terminating is a probable scenario in the later period of glacier wastage. This research can significantly serve for glacier multidimensional monitoring and the mitigation of hazardous disaster caused by debris-covered glaciers in the central Himalayas.
1. Introduction
Mountain glaciers are one of the most sensitive natural indicators for climate changes in the Himalayas [1]. The melting water of mountain glaciers is one main live resource for downstream people, especially for the arid and inland areas. Furthermore, debris-covered glaciers play a significant role in water-cycles in High Mountain Asia (HMA), altering glacier melting and their spatial patterns [2]. Shrinking of Himalayan debris-covered glaciers poses challenges to societies, such as the increasing changes of seasonal runoff caused by the glacier melting and the increasing risk of glacier lake outburst floods (GLOFs) caused by the expansion of unstable glacial lakes [3]. The percentage of debris-covered glaciers are roughly 10% in the Himalayas [2] and their tongues are generally situated in the lowest elevation with the increasing number of glacial lakes at the terminate [4]. Additionally, previous studies show that mass loss of debris-covered tongues were at the same rates as debris-free glaciers [5,6,7], but the lake-terminating glaciers mass loss were more negative than land-terminating glaciers over the period of 2001–2015. [3]. The principal reason may be the significant increased rate of supraglacial lakes melting [2].
The estimation of debris-covered glacier flow velocity provides better insight into glacier spatiotemporal evolution. The variation of glacier flow velocity and the mass balance are largely determined by their susceptibility to climate change. Recent studies show that flow velocities are 100–200 m/year near Bhutan on the north side of Himalayas whereas the maximum flow velocities on the south side is around tens of meters, emphasizing a great spatial variation of glacier velocity in the Himalayas [8,9,10]. However, the flow velocities for debris-covered tongues varied from 0 to 37 m/year on the south side of Everest region [10]. Additionally, the dynamic behaviors of lake-terminating glaciers are in contrast to the land-terminating glaciers in the Himalayas [4]. Since 2000, the Himalayas have experienced considerable reduction of flow velocities due to thinning and driving stress reduction [3]. Therefore, it is crucial to conduct multidimensional movement monitoring of debris-covered glacier.
Most of debris-covered glaciers are difficult to approach and study with regular in-situ measurements. Satellite remote sensing techniques including optical feature-tracking and interferometric synthetic aperture radar (InSAR) have been abroad used for mapping comprehensive, nonuniform, and frequent glacier velocities [11,12,13,14,15]. However, optical remote sensing is often hampered by the inclement weather conditions [16]. Phase-based InSAR and amplitude-based pixel-tracking methods have become significant instrument to study glacier movement in a tradition, low-priced manner [17]. Phase-based InSAR methods including differential InSAR(D-InSAR) and multiple aperture interferometry (MAI) are always affected by the loss of coherence caused by the large time interval of SAR image pairs and large gradient glacier movement [18,19]. In contrast, the amplitude-based pixel-tracking method can work very well to estimate glaciers displacements with rates ranging from decimeter per year to tens meter per year in both line-of-sight (LOS) and azimuth directions [20]. With accessible to multi-track SAR data, it is possible to acquire ascending and descending SAR data over the same region during the specific period, which can then be used to construct 3D deformation models of glaciers [21,22]. More importantly, the time series of 3D motion can also be derived with the pixel-offset small-baseline subset (PO-SBAS) technique [23]. In recent years, numerous geological disasters have occurred in the northern of Himalayas, Tibet, China [24,25]. Generally, it is fundamental to comprehend the full 3D flow pattern for interpreting of debris-covered glacier movement and particularly recognizing their evolution process [26]. However, what was the 3D debris-covered glacier deformation pattern and how did it change with time? And what was the relationship between the glacier movement and precipitation? How does a moraine-lake form in a debris-covered glacier? We take the Cuolangma glaciers as example to answer these questions.
In this study, we derive 3D time series displacement of two different terminus types of Cuolangma glaciers in the central Himalayas by applying PO-SBAS methods with Sentinel-1 imagery. We examine the 3D time series movement of Cuolangma glaciers in detail, where the one is a lake-terminating glacier and the other is a land-terminating glacier. Then the deformation features in terms of precipitation and seasonality are analyzed. A general explanation for evolution of debris-covered glaciers will trace the development of a glacial lake, verifying the role of lake-terminating debris-covered glacier in catastrophic disaster.
2. Study Area and Datasets
2.1. Study Area
Cuolangma glaciers are located at the Mid-Himalayas, which consists of a series of parallel ranges from the Ganges Basin to the QTP [16,27]. It should be stressed that the status of debris-covered glacier and its surroundings in the Himalayas have been paid much attention as the increased risks of GLOFs [16]. Since the 1980s reduced height of ice dam and accelerated accumulation of glacial lake water occurred with the rising temperatures [4]. In addition, the Mid-Himalayas provide waters for major rivers in Asia, including the Ganges, Indus, and Yangtze Rivers [27]. The prevailing westerlies and the Indian summer monsoon have a profound contribution to complicated climate pattern [28], as shown in Figure 1a. In summer, the Indian summer monsoon brings significant rainwater to the south side of Himalayas, resulting in annual precipitation of about 2500–3000 mm in the eastern Nyainqentanglha mountains [29]. In winter, the westerlies have played a determined role in precipitation in the west of Himalayas [6,28]. The two glaciers have debris covering in their ablation areas, which provides facilities for supraglacial ponds’ growth [16]. We take the two different type glaciers of Cuolangma glaciers as the study object. The location and topographic features can be seen in Figure 1, where Figure 1b and Figure 1c show the terrain of glacier No.1 and No.2, respectively. The area of glacier No.1 is 24 and the elevation varies from 5500 to 6100 m, while the area of glacier No.2 is 26 within the elevation from 4900 to 5800 m. The glacier No.1 is a lake-terminating glacier; the supraglacial ponds and lakes are typically studded on the tongues of the large debris-covered glacier [2]. However, the glacier No.2 is a land-terminating debris-covered glacier with the likely consequence of transiting into a lake-terminating glacier.
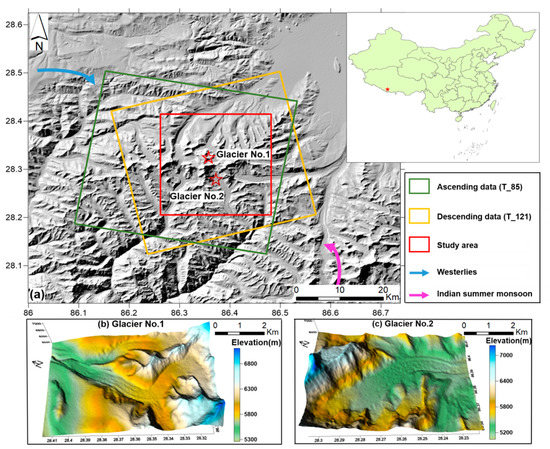
Figure 1.
Study area and SAR dataset coverages: (a) Spatial coverage of ascending and descending Sentinel-1 datasets represented on SRTM DEM; (b) The terrain of glacier No.1, (c) The terrain of glacier No.2.
2.2. Datasets
To generate 3D movement maps of the Cuolangma glaciers, we processed Sentinel-1 images acquired from both ascending and descending tracks with Interferometric Wide Swath (IWS) mode. The pixel spacing in the LOS and azimuth directions are 2.33 m and 13.96 m, respectively. Table 1 presents the principal parameters for SAR imagery, whilst Figure 1a shows their coverages superimposed on the SRTM DEM shaded relief image. In total, 30 ascending and 30 descending SAR images were acquired from tracks 85 and 121, respectively, spanning from January 2018 to December 2018. From these, a total of 173 high-quality offset pairs which meet the co-registration accuracy with 0.02 pixels, were selected as shown in Figure 2 including 85 ascending pairs and 88 descending pairs. Additionally, the daily rainfall products from the Global Precipitation Measurement (GPM, https://gpm.nasa.gov) were involved for triggering factor analysis.

Table 1.
The principal parameters of the synthetic aperture radar (SAR) datasets.
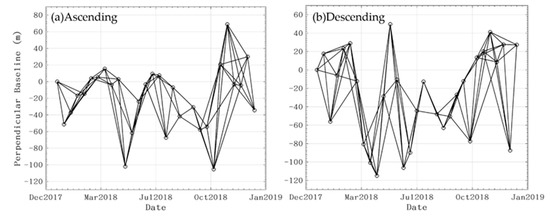
Figure 2.
The distributions of temporal and perpendicular baselines of ascending and descending offset pairs used in this study: (a) shows the offset pairs generated by ascending Sentinel-1 data; (b) shows the offset pairs generated by descending Sentinel-1 data.
3. Methods
Figure 3 illustrates the flowchart used to retrieve the time series of 3D glacier movement, including three steps: offset-tracking method, estimation of 3D displacement, and the time series of 3D displacement.
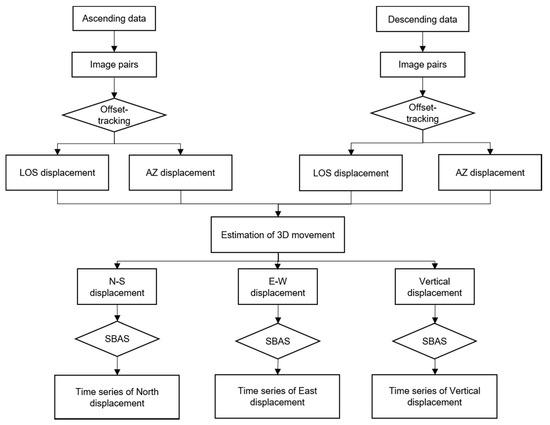
Figure 3.
Flowchart of 3D time series displacement estimation.
3.1. Offset-Tracking
Offset-tracking, including amplitude tracking and coherence tracking, is based on the calculation of the offsets in both range and azimuth directions by maximizing the cross-correlation of the SAR image patches, which have been used to measure surface displacement caused by seismic activity, coal exploration, and glacier movements. [18,20,30,31,32,33,34,35,36]. Amplitude tracking correlates two images using the amplitude information and is suitable for situations with clear ground features or poor coherence of the image pair. Coherence tracking correlates two images by calculating coherence within the given patch if no clear features are available [20]. The amplitude-based method is used in this study because it is more sensitive to large gradient displacement measurement as seen in the research area and it has a high computation efficiency [20,21,22,23,24].
Normally, the calculated total offsets contain four elements, that is, the offsets caused by (1) glacier movement, (2) differences in satellite orbit position, (3) ionospheric delays, and (4) the topographic relief [20]. The offsets caused by ionospheric delays are generally ignored for C-band Sentine-1 SAR images in mid and low-latitude areas [20,23,37]. Previous work [38,39] confirmed that topography errors can be calculated by this mathematical model, as shown in Equations (1) and (2):
where is the azimuth angle, is the look angle of the SAR images, is the slant range, is the azimuth pixel spacing, is the perpendicular baseline, is the slant-range pixel spacing, and is the topographic error. In this study, we estimate and remove the offsets caused by height difference based on Equations (1) and (2).
Three main steps are employed to estimate LOS and azimuth offsets by GAMMA [23,40]: (1) precise registration of SAR images, (2) the calculation of offsets, (3) the separation of the deformation signals from offset measurements. As the offset pairs with short temporal intervals ( days) and spatial baselines ( m) were used to obtain initial offset fields, we first chose the window size of 256256 pixels in azimuth and range directions. Then, the window sizes of 128128 pixels and 6464 pixels were used to refine the results adaptively [37]. We set the correlation coefficient (CRC) threshold at 0.2, and any patches below this value were masked. Lower CRC values usually appear for the offset pairs with large spatial baseline, large-gradient movement, and temporal changes in the surface scattering characteristics [23,37].
3.2. Estimation of 3D Deformation Fields
As the difference of acquisition dates between adjacent ascending and descending Sentinel-1 SAR data is only 3 days, it is reasonable to derive 3D time series movement by fusing ascending and descending SAR measurements. The range and azimuth offsets derived from SAR offset-tracking are the function of the real 3D surface deformations [23]. Taking the ascending images as an example, the ground-range (GR) deformation can be expressed as the function of north-south deformation and east-west deformation , whilst the LOS deformation is the function of vertical deformation and ground-range deformation , as shown in Equations (3) and (4) [23]:
where is azimuth angle of the SAR images, and is the look angle. Based on Equations (3) and (4), the relationship between LOS deformation and real 3D surface deformation can be deduced as follows [23,35]:
Meanwhile, the azimuth deformation can be expressed as the function of east-west and north-south deformations [23]:
Therefore, the real 3D deformation of the glacier can be retrieved using the azimuth and LOS offsets derived from ascending and descending images. For simplicity, the matrix form is shown below.
where
We use the least squares criterion () to obtain the optimal estimation of 3D displacements and error as follows,
3.3. Time Series of 3D Displacement
When we establish the adjustment model for the 3D (east-west, north-south, up-down) displacement, the 3D time series displacement can be estimated using the singular value decomposition (SVD). Taking the north-south direction as an example, we first generate M offset pairs with n+1 SAR images:
Second the north-south displacement between each offset pair is independently calculated using the offset-tracking method and the estimation of 3D displacement.
where are the north-south displacement between each offset pair.
Next, in the M offset pairs, the acquisition orders of primary and secondary images are and (), respectively. If the primary and secondary images are ranged in order, thus,
Equation (11) includes M equations with N unknown parameters and can be rewritten in matrix form as:
where A = , each row of matrix A [] corresponds to an offset pair.
Finally, SVD is used to solve Equation (12) to derive the time series deformation of the glacier in north-south direction. Similarly, the time series of other two directions can be achieved in a similar way.
4. Results and Analyses
4.1. 3D Glacier Velocities Fields
In this study, the 3D glacier velocities were derived by PO-SBAS method to better explain their complicated movement. Figure 4 shows the horizontal and vertical velocity of these two glaciers. The map indicates that the most active part of glacier No.1 in horizontal velocity is at the downstream part. While the most active part of the glacier No.2 is at the upper part. Identically, as for the vertical component, the downward velocity happens in the western of the two profiles (AA′, BB′), while the upward velocity occurs in the eastern part.

Figure 4.
The 3D velocities maps and optical images of the two glaciers. Color represents the vertical velocity and arrows represents the horizontal velocity. (a) the 3D velocities for glacier No.1; (b) the 3D velocities for glacier No.2; (c) Landsat-8 image of glacier No.1 in 2018; the red rectangle indicates the stable region; (d) Landsat-8 image of glacier No.2 in 2018.
Figure 5 illustrates the relationship between the elevation and the glacier surface velocity, vertical velocity. The four profiles are shown in Figure 4, in which AA′ and CC′ are the flow direction of glacier No.1 and glacier No.2 respectively; BB′ and DD′ intersect the flow profiles of glacier No.1 and glacier No.2 at their widest places. The error bar represents the standard deviation (STD) of the 3D velocities in the range parallel to the selected profiles.
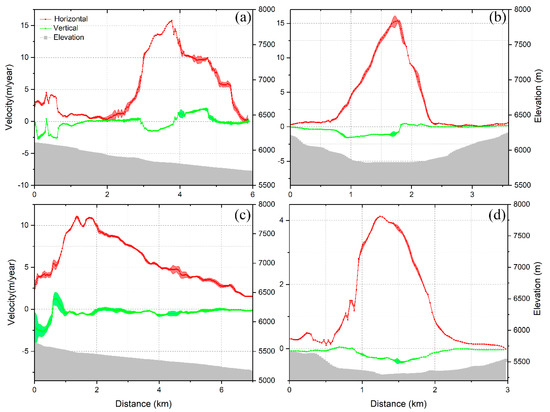
Figure 5.
3D velocities and elevations of glacier No.1 and glacier No.2 in 2018, where red and green lines represent the horizontal and vertical annual velocity, respectively. Profiles of AA′ and BB′ are shown on Figure 4a and profiles of CC′ and DD′ are shown on Figure 4b. The error bar indicated the standard deviation of the velocity in the area near the selected profiles. (a) Profile A-A′; (b) Profile B-B′; (c) Profile C-C′; (d) Profile D-D′.
The horizontal velocity is increasing gradually from the upper part to the middle part, with a maximum annual velocity of 15.770.04 m/year. Immediately, the glacier flows towards the lower section. At a distance of 5 km from the initial point along profile AA′, the horizontal velocity is up to 14.460.12 m/year, which is the second maximum velocity, behind the middle part due to the narrow proglacial tongue in Figure 5a. The vertical velocity of mainstream direction is around zero as a whole except a significant abrupt change within 0.5 km. From the perspective of the STD of glacier velocity, the errors in horizontal and vertical directions are mainly distributed in two locations. Within 2 to 3 km, there is an obviously increased velocity in horizontal direction. Immediately afterwards, in the tongue part of 4.0 to 6.0 km, the horizontal velocity gradually slows down. At the same time, the velocity in vertical direction suddenly makes change. The upward velocity of 1.88 ± 0.23 m/year occurred and then the glacier experienced downward velocity of −0.25 ± 0.14 m/year. The unstable flow velocity at these locations of glacier No.1 may be due to the complicated mechanism between the tongue and the glacial lake.
The horizontal velocity along profile CC′ in Figure 5c firstly increased and gradually decreased, where the maximum velocity is 11.00.07 m/year at 2 km. The velocity in vertical direction for glacier No.2 is 2.00.27 m/year. The unstable flow velocity of profile CC′ mainly occurs within 1 km. The maximum velocity errors are 3.45 ± 0.34 m/year at 0.95 km and 1.40 ± 0.18 m/year at 0.9 km in horizontal and vertical directions, respectively. The reason may be that there is abundant ice at the upper part that is conducive to movement, while the terminus type is land with less ice mass exchange.
Figure 5b and d present that the 3D glacier velocities are the fastest in the mainstream and slower at the two edges along profiles BB′ and DD′ due to increasing frictional drag between the edge and the valley wall. The maximum horizontal velocities are 15.330.11 m/year increasing by 98% and 4.130.01 m/year increasing by 92% from edge to the mainstream of glacier No.1 and glacier No.2, respectively. The ice motion usually increases to maximum value in the mainstream direction and immediately decreases down to zero at the other edge [32]. The same characteristic can also be observed in vertical velocities. On the whole, the errors in the mainstream directions of profile AA′ and CC′ are obvious, but the changes of 3D velocities for profile BB′ and DD′ that are perpendicular to the mainstream directions are relatively stable. The horizontal velocity of glacier No.1 and No.2 clearly and intuitively reflect the spatial distribution of glacier surface, while the change of vertical velocity is more complicated. This is because the vertical velocity not only reflects the thinning or thickening of a glacier but includes the deformation of the glacial moraine.
4.2. Time Series of 3D Glacier Movement
Under the method described above, the time series of 3D glacier movement from January to December 2018 are retrieved. Figure 6 depicts the 3D displacement time series of glacier kinematics at No.1, and Figure 7 for glacier No.2. Color indicates the vertical displacement while the arrow represents the horizontal displacement of the two glaciers. It can be seen that the horizontal displacement of glacier No.1 gradually increased from January to December, showing the longer length arrows in Figure 6. The time series of horizontal motion of a glacier, shown by displacement vectors, is located at the center line of the middle of glacier No.1. The vertical motion shows that the lower part is increasingly downward. However, the upward occurs in the middle part by 77% from January to December due to the mass accumulation at the intersection of two glacier branches.
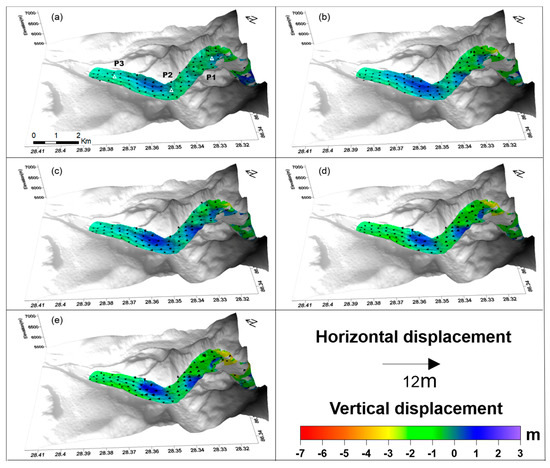
Figure 6.
Time series of 3D displacement for glacier No.1 from 23 January to 25 December, 2018. Color represents the vertical displacement and arrows represent the horizontal displacement. (a) 20180123–20180429; (b) 20180123–20180604; (c) 20180123–20180803; (d) 20180123–20181002; (e) 20180123–20181225.
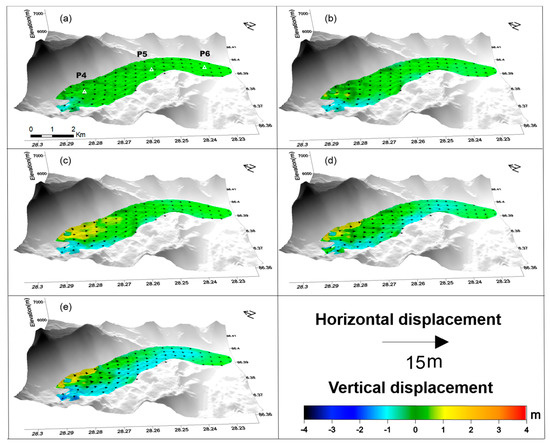
Figure 7.
Time series of 3D displacement for glacier No.2 from 23 January to 25 December, 2018. Color represents the vertical displacement and arrows represent the horizontal displacement. (a) 20180123–20180429; (b) 20180123–20180604; (c) 20180123–20180803; (d) 20180123–20181002; (e) 20180123–20181225.
The horizontal movement of glacier No.2 is mainly distributed in the upper part with the increased length of displacement vectors in Figure 7. The upward movement of glacier No.2 occurs at the eastern part, while the downward movement extensively focusses on the western part and the lower part of glacier in Figure 7.
In order to analyze the temporal deformation characteristics at different positions, we select six points (P1–P6 as shown in Figure 6a and Figure 7a) at front, middle, and the terminus of two glaciers. Figure 8 shows the time series displacement value; to avoid the influence of inconsistent precision, standard deviation (STD) of the 33 pixel around each point was estimated for horizontal and vertical direction which is indicated by error bars.
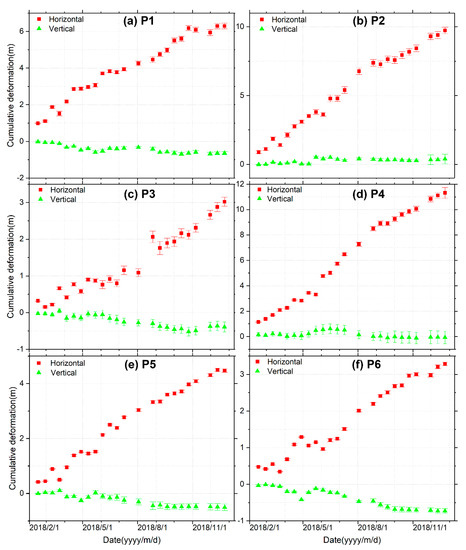
Figure 8.
3D deformation time series for points P1-P6. Red square and green triangle represent the horizontal and vertical time series movement, respectively. Locations of P1-P3 are shown on Figure 6a and P4-P6 are shown on Figure 7a. Negative values refer to downward movement. The red error bars indicated the STD of the average 33 pixels in horizontal directions and the green error bars indicated the errors for vertical direction. (a)–(f) represents the 3D time series displacement of points P1-P6, respectively.
At the front of the glacier No.1 and No.2, the time series of P1 and P4 are close to a linear tendency in horizontal and vertical directions. The horizontal displacement is 6.900.16 m on 25 December while the vertical displacement is –0.580.08 m (see Figure 8a). For the glacier No.2, the horizontal motion at point P4 increased with the maximum cumulative displacement of 11.320.43 m. The vertical deformation is around zero (see Figure 8d). For glacier No.1, the cumulative deformation of point P2 is 9.740.35 m in horizontal direction on 25 December. However, the deformation of the glacier with time is minimal in vertical directions (Figure 8b). Similarly, the dramatic displacement occurs in horizontal direction with 4.500.06 m at point P5 while the downward displacement is –0.510.12 m on 25 December for glacier No.2 (Figure 8e). There are some common characteristics at the termini of the two glaciers, i.e., the vertical change is negative, suggesting an upward phenomenon at the end of the glacier due to mass loss (Figure 8c,f).
4.3. Uncertainty Analysis
Errors in the PO-SBAS method results are mainly caused by offset-tracking and the 3D inversion method. Firstly, there are three main sources of error by means of offset-tracking: SAR image registration, geocoding, and topography [41,42]. In the process of offset-tracking method, we set the spatiotemporal threshold and the correlation coefficient threshold and used different window size to continuously refine the result of offset-tracking. The DEM errors were estimated and removed through Equations (1) and (2). So, the accuracy of co-registration was guaranteed within 0.02 pixels, which is approximately 0.3 m and 0.05 m in azimuth and LOS direction, respectively. The study area is located at towing mountains with hostile environments and blocked roads in winter, which makes it difficult to obtain the real observations by field survey, such as GPS, leveling data, etc. Based on the assumption that the movement of the non-ice region is zero theoretically [43], the STD of velocity was estimated in a stable region in Figure 4c, showing the result were 0.6 m/year and 0.2 m/year in horizontal and vertical direction, respectively. The values in a stable region are all much lower than the average velocities as shown in Figure 4, which indicates the reliability of the result.
Finally, in order to further confirm the quality of our 3D velocities results, we made comparison of glaciers velocity in horizontal direction between our results and the ones from published reference [44]. As the absence for time series velocities in published reference, the velocity in 2018 was used to make comparison. The published results from the reference were obtained by optical feature-tracking method with the resolution of 250 × 250 m. The surface velocity datasets could be downloaded from the website (https://its-live.jpl.nasa.gov/), which contain coordinates and annual surface velocity. Therefore, we used the six points that were discussed in the previous analysis due to the large difference in resolution. The six points can be seen in Figure 6a and Figure 7a and located at the upper, middle, and terminus of the two glaciers, respectively. The detailed process is to sample our surface velocity results to the same resolution as the reference dataset in 2018, comparing the differences and making statistics as shown in Table 2. The maximum difference is 1.73 m/year, and most of them are less than 1.27 m/year, which verifies the feasibility and reliability of our results.

Table 2.
Comparison of glaciers flow velocity in horizontal direction between our results and published ones (Dehecq et al. [44]).
5. Discussion
5.1. The Correlation between Precipitation and Glacier Surface Velocity
It is critical to investigate glacier movement caused by climatic conditions, including precipitation and temperature [44,45]. Fujita et al. [46] revealed that glaciers located in a summer-precipitation climate show higher sensitivity than those in a winter-precipitation climate. Both Shi et al. [47] and Liu et al. [48] proposed a glacier classification system for the Himalayas based upon their continentality. Maussion et al. [49] indicated that glacier velocities are impacted by the uncertainty of snowfall occurrence and magnitude in spring or summer with the Weather Research and Forecasting (WRF) model. They further proposed a new classification using an objective clustering approach based on precipitation seasonality. Precipitation seasonality importantly affected the climatic sensitivities of glacier different types [49]. However, because of the lack of meteorological documentation in the Himalayan climate, it is challenging to understand the precipitation factors.
To further analyze the relationship between precipitation and the glacier flow velocity, we conducted comparison for the glaciers No.1 and No.2. The daily precipitation is obtained from the Global Precipitation Measurement (GPM). The relationship between the flow velocities of two glaciers and the precipitation variation were discussed as shown in Figure 9. Firstly, as glacier No.1 and glacier No.2 are located on the leeward and windward sides of the Indian summer monsoon respectively, the precipitation patterns are significantly different. The peak of rainfall at glacier No.1 was 53 mm on 15 July. June to August was a period with abundant precipitation. The maximum daily rainfall at glacier No.2 was 39 mm on 21 August, and the period of abundant rainfall was in July. In summary, there are different precipitation patterns for these two glaciers. Secondly, the glacier No.1 had undergone apparent two acceleration processes: (I) during the period of 24 March to 29 April, the velocity increased from 5.70.6 m/year to 11.80.4 m/year; (II) during the period of 28 June to 27 August, the velocity increased from 10.70.5 m/year to 12.60.7 m/year, where the maximum rainfall is 53.1 mm on 15 July. As for glacier No.2, the conspicuous acceleration process can be found from 23 May to 10 July with the velocity increased from 5.70.3 m/year to 9.60.5 m/year. On the whole, the surface velocities of the two glaciers have experienced cyclical changes of an acceleration-deceleration-acceleration-deceleration stage. The daily rainfall during the acceleration period is abundant and the rainfall during the deceleration period is poor for glacier No.1. The reason may be that a large amount of surface meltwater and rainfall penetrate into the glacier bedrock in abundant rainfall period, resulting in the decrease of basal frication and increase of flow velocity. However, the horizontal velocity for glacier No.2 does not show a clear association with daily precipitation alone. Therefore, the glacier velocity cannot merely be attributed to daily precipitation. The casual factors of glacier movement are complex and interactional in the central Himalayas.
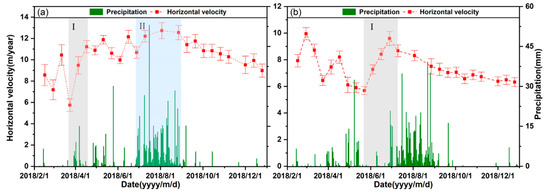
Figure 9.
Correlation between glaciers horizontal velocities and precipitation in 2018. (a) point P2 at glacier No.1; (b) point P4 at glacier No.2. Locations of points P2 and P4 are shown on Figure 6 and Figure 7, respectively. The error bars indicated by the STD of the average 3 × 3 pixels in horizontal direction.
5.2. 3D Glacier Movement with Seasonal Characteristics
Besides the variations in precipitation, different seasons also exert effects on glacier motion. As the glaciers in our study area are both summer-accumulation glaciers [49], they are more susceptible to increasing temperature. Therefore, the different responses to the same climate circumstance are generated by the different glacier accumulation types.
To make seasonal analysis, we chose four representative classifications, i.e., December to February (DJF), March to May (MAM), June to August (JJA), and September to November (SON). Note that in order to ensure cumulative deformation, “December” here refers to December in 2017. We used PO-SBAS method to connect December of 2017 with January and February of 2018. Figure 10 shows the contributions to the 3D glacier deformation in four different periods, where the seasonal deformation in horizontal and vertical directions is firstly analyzed. It is mostly dry in DJF because the precipitation has a spatially variability with 20–25% [49]. Furthermore, the results illustrate that the displacements are 0.820.10 m and 1.120.05 m in horizontal direction for glacier No.1 and No.2 respectively. In vertical direction, the displacement is –0.070.01 m in downward movement for glacier No.1 and 0.050.01 m in upward motion for glacier No.2. The precipitation in MAM is impacted by the variability of the Indian summer monsoon. It can be detected that the contribution for MAM to glacier No.1 3D movement is greater than that of the glacier No.2. For horizontal and upward direction, the displacements for glacier No.1 are 2.820.10 m and 0.300.07 m, respectively, while the displacements for glacier No.2 are 0.850.08 m and 0.070.04 m respectively. In JJA, the cycle patterns change severely with the highest precipitation in a year, both in India and central Himalayas [49]. The period of JJA for glacier No.1 is impacted by 3.600.24 m and –0.130.02 m in horizontal and downward directions, respectively. In this same period, glacier No.2 is affected by 2.380.30 m and –0.500.05 m in horizontal and downward directions, respectively. It is worth noting that the period in SON is limited by low precipitation. The displacements are 1.510.16 m and 0.280.02 m for glacier No.1 in horizontal and upward respectively, while the displacements are 1.340.08 m and –0.150.02 m for glacier No.2 in horizontal and downward, respectively. Overall, June to August is the most important period for 3D movement of glacier No.2, while for glacier No.1, the four seasonal periods all have a propound influence, especially in vertical direction.
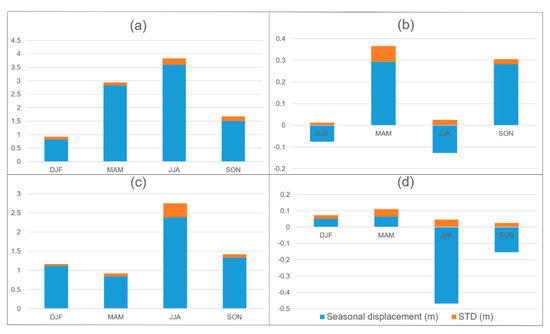
Figure 10.
Graph of the 3D glacier displacement in four different periods. (a) the horizontal displacement for glacier No.1; (b) the vertical displacement for glacier No.1; (c) the horizontal displacement for glacier No.2; (d) the vertical displacement for glacier No.2; DJF: December, January, February; MAM: March, April, May; JJA: June, July, August; SON: September, October, November. The positive values indicate upward movement while the negative values show downward movement, respectively.
We attribute the difference in two glaciers to their different glacier types, where glacier No.1 is a lake-terminating debris-covered glacier and glacier No.2 is a land-terminating debris-covered glacier. The abundant debris of the glacier No.1 not only provides facilities for the ice cliff and supraglacial ponds development but also creates complicated supraglacial, englacial, and subglacial drainage system components. Further, a supraglacial lake is developed at the lowest part of glacier No.1, which is combinedly produced by wind-driven surface currents and density-driven undercurrents to deliver power to the ice front and lake floor via melting ice [50]. Moreover, lake changes, an important source of GLOFs, had a temporally and spatially diversity effect on glacier movement.
5.3. The Evolution of Debris-Covered Glaciers
Debris-covered glaciers affect glacier length, ice motion, and mass balance in high-mountain regions [2,10,51,52]. The emergence of extensive debris cover means that the linkage of cause and effect is more complicated than on debris-free glaciers [2,4,53,54]. The recession of tongues on large debris-covered glaciers promotes the growth of supraglacial lakes, which brings about an increased risk of GLOFs. Therefore, it is meaningful and important to consider the evolution of debris-covered glaciers. The general conceptual model of the debris-covered glaciers’ evolution was advanced by Been et al. [2]. Three process regimes can be detected in Figure 11.
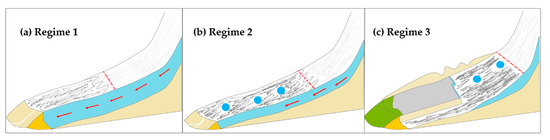
Figure 11.
Diagrammatic representation of debris-covered glacier regimes. (a) Regime 1: active ice flow; (b) Regime 2: downwasting ice; (c) Regime 3: calving retreat. Red arrows represent basal flowing, red dotted lines represent the equilibrium line altitudes (ELAS), blue circles represent small lakes, blue shadow represents the basal surface, light orange shadow represents the terrain, orange shadow represents the surface at the terminal of a glacier, the white strips at the terminal in (a,b) represent the flow of glacial melting, gray shading in (c) indicates a glacial lake, and green shadow indicates the surface at the terminal of a lake. (modified from Been et al. [2]).
In regime 1, the surfaces of glaciers are not extensively crevassed and the meltwater can be transferred to their terminus. The ablation phenomenon typically occurs in lower areas and the highest melt rates are located in the mid-ablation areas [2]. The mechanism for glacier No.1 in this study differ from the regime 1 in that there are evident crevasses in the tongue. With the increasing climatic warming, the balance between ice accumulation and ablation rates are altered on debris-covered glacier tongues, causing a transition to some characteristic cliffs. So, a new stage was formed called the regime 2. Consequently, mid-ablation zones are experiencing the increased mass loss and reduced ice accumulation. In turn, this result encourages glacier slowdown and stagnation [10]. Accordingly, the optical image in Figure 4c shows a large moraine-dammed lake and many small concave-up lakes that are facilitated by a reduction of glacier gradient. A lake can form immediately at part of the glacier surface and can expand rapidly by calving and melting above or below the waterline [2]. Therefore, the existence of a supraglacial lake is a dominant sign for determining whether a glacier is in regime 2 or regime 3. These large lakes provide sufficient convenience for potential glacier lake outburst floods. Therefore, the evolution of glacier No.1 or other lake-terminating debris-covered glaciers need to be carefully supervised henceforward.
6. Conclusions
In this study, the time series of the 3D movement of the Cuolangma glaciers in 2018 were estimated from multitrack SAR images by PO-SBAS method, where the one is a lake-terminating debris-covered glacier and the other is a land-terminating debris-covered glacier. Firstly, the multidimensional spatial pattern and temporal evolution of the two glaciers were characterized, which indicated the maximum cumulative displacement of lake-terminating glacier occurs at their middle part, while the maximum cumulative displacement of land-terminating glacier occurs at their upper section.
Then, the correlations analysis between glacier surface velocity and daily precipitation revealed that the surface velocity does not display a clear relationship with daily precipitation alone. In addition, the seasonal displacement shows that June to August exert the biggest contribution on 3D movement of land-terminating glaciers while the seasonal change of lake-terminating glaciers is not evident for their 3D movement. Moreover, the evolution of debris-covered glaciers was evaluated to better understand the formation for a glacial lake, providing reference for the prevention and management of glacial lake outburst floods in the central Himalayas.
More importantly, regarding the absence for vertical component by conventional offset-tracking method, the accuracy and temporal resolution of the glacier motion are limited. Time series of 3D movement for glaciers provide more comprehensive and accurate information for clarifying their movement process. PO-SBAS method for interpreting the 3D movement will be widely applied to more scenarios for different glaciers, such as the evolution of surge of glaciers, the mechanism of glacial lake outburst floods, and the work for disaster deduced by glacier motion. However, the PO-SBAS model could be further optimized with the help of in-situ measurements of glaciers in High Mountain Asia.
Author Contributions
Conceptualization, L.Y., C.Z., and Z.L.; methodology, L.Y. and C.Z.; software, L.Y.; validation, L.Y., C.Z., and C.Y.; data analysis, L.Y., C.Z., and Q.Z.; writing—original draft preparation, L.Y.; writing—review and editing, all the author.; funding acquisition, C.Z., Z.L., C.Y and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is jointly supported by the National Natural Science Foundation of China NSFC (Grant No. 41874005), China Geological Disaster Investigation Project (DD20190637) and the Fundamental Research Funds for the Central Universities (CHD, 300102269204, 300102269303), Shaanxi Provincial Natural Science Basic Research Project (2019JM-245).
Acknowledgments
The authors would like to thank the European Copernicus for providing the Sentinel-1 SAR data freely. The precipitation data was download from the website https://gpm.nasa.gov/. One-arc-second SRTM DEM is freely downloaded from https://e4ftl01.cr.usgs.gov/MODV6_Dal_D/SRTM/SRTMGL1.003/2000.02.11/. We are also indebted with editor Xiao Becky and three anonymous reviewers for their valuable remarks and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dyurgerov, M.B.; Meier, M.F. Twentieth century climate change: Evidence from small glaciers. Proc. Natl. Acad. Sci. USA 2000, 97, 1406–1411. [Google Scholar] [CrossRef] [PubMed]
- Been, D.I.; Bolach, T.; Hands, K.; Gulley, J.; Luckman, A.; Nicholson, L.I.; Quincey, D.; Thompson, S.; Toumi, R.; Wiseman, S. Response of debris-covered glaciers in the Mount Everest region to recent warming, and implications for outburst flood hazards. Earth Sci. Rev. 2012, 114, 156–174. [Google Scholar] [CrossRef]
- Maurer, J.M.; Schaefer, J.M.; Rupper, S.; Corley, A. Acceleration of ice loss across the Himalayas over the past 40 years. Sci. Adv. 2019, 56. [Google Scholar] [CrossRef] [PubMed]
- King, O.; Bhattacharya, A.; Bhambri, R.; Bolch, T. Glacial lakes exacerbate Himalayan glacier mass loss. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Slight mass gain of Karakoram glaciers in the early twenty-first century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
- Pellicciotti., F.; Stephan, C.; Miles, E.; Herreid, S.; Immerzeel, W.W.; Bolch, T. Mass-Balance changes of the debris-covered glaciers in the Langtang Himal, Nepal, from 1974 to 1999. J. Glaciol. 2015, 61, 373–386. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.; Meijer, S.W.; Shea, J.M.; Pellicciotti, F.; Immerzeel, W.M. Seasonal surface velocities of a Himalayan glacier derived by automated correlation of unmanned aerial vehicle imagery. Ann. Glaciol. 2016, 57, 103–113. [Google Scholar] [CrossRef]
- Kääb, A. Combination of SRTM3 and repeat ASTER data for deriving alpine glacier flow velocities in the Bhutan Himalaya. Remote Sens. Environ. 2005, 94, 463–474. [Google Scholar] [CrossRef]
- Quincey, D.J.; Luckman, A.; Benn, D. Quantification of Everest region glacier velocities between 1992 and 2002, using satellite radar interferometry and feature tracking. J. Glaciol. 2009, 55, 596–606. [Google Scholar] [CrossRef]
- Berthier, E.; Raup, B.; Scambos, T. New velocity map and mass-balance estimate of Mertz Glacier, East Antarctica, derived from Landsat sequential imagery. J. Glaciol. 2003, 49, 503–511. [Google Scholar] [CrossRef]
- Trouvé, E.; Vasile, G.; Gay, M.; Bombrun, L.; Grussenmeyer, P.; Landes, T.; Nicolas, J.; Bolon, P.; Petillot, I.; Julea, A. Combining airborne photographs and spaceborne SAR data to monitor temperate glaciers: Potentials and limits. IEEE Trans. Geosci. Remote Sens. 2007, 45, 905–924. [Google Scholar] [CrossRef]
- Tong, X.; Liu, S.; Li, R.; Xie, H.; Liu, S.; Qiao, G.; Feng, T.; Feng, T.; Tian, Y.; Ye, Z. Multi-Track extraction of two-dimensional surface velocity by the combined use of differential and multiple-aperture InSAR in the Amery Ice Shelf, East Antarctica. Remote Sens. Environ. 2018, 204, 122–137. [Google Scholar] [CrossRef]
- Sundal, A.V.; Shepherd, A.; Nienow, P.; Hanna, E.; Palmer, S.; Huybrechts, P. Melt-Induced speed-up of Greenland ice sheet offset by efficient subglacial drainage. Nature 2011, 469, 521–524. [Google Scholar] [CrossRef] [PubMed]
- Nobakht, M.; Motagh, M.; Wetzel, H.U.; Roessner, S.; Kaufmann, H. The Inylchek Glacier in Kyrgyzstan, Central Asia: Insight on surface kinematics from optical remote sensing imagery. Remote Sens. 2014, 6, 841–856. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.; Zhao, R.; Ding, X. Glacier mass balance in the Qinghai-Tibet Plateau and its surroundings from the mid-1970s to 2000 based on Hexagon KH-9 and SRTM DEMs. Remote Sens. Environ. 2018, 210, 96–112. [Google Scholar] [CrossRef]
- Jeremie, M.; Eric, R.; Bernd, S.; Romain, M. Comprehensive annual ice sheet velocity mapping using Landsat-8, Sentinel-1, and RADARSAT-2 data. Remote Sens. 2017, 9, 364. [Google Scholar]
- Luckman, A.; Quincey, D.; Bevan, S. The potential of satellite radar interferometry and feature tracking for monitoring flow rates of Himalayan glaciers. Remote Sens. Environ. 2007, 111, 172–181. [Google Scholar] [CrossRef]
- Erten, E.; Reigber, A.; Hellwich, O.; Prats, P. Glacier velocity monitoring by maximum likelihood texture tracking. IEEE Trans. Geosci. Remote Sens. 2009, 47, 394–405. [Google Scholar] [CrossRef]
- Strozzi, T.; Luckman, A.; Murray, T. Glacier motion estimation using SAR offset-tracking procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Engelhardt, H. Satellite radar interferometry for monitoring ice sheet motion: Application to an Antarctic ice stream. Science 1993, 262, 1525–1530. [Google Scholar] [PubMed]
- Bechor, N.B.D.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Wu, L.; Xu, B.; Hu, J.; Zhou, Y.; Miao, Z. Deriving a time series of 3D glacier motion to investigate interactions of a large mountain glacial system with its glacial lake: Use of Synthetic Aperture Radar Pixel Offset-Small Baseline Subset technique. J. Hydrol. 2018, 559, 596–608. [Google Scholar]
- Neelmeijer., J.; Motagh, M.; Wetzel, H.U. Estimating spatial and temporal variability in surface kinematics of the Inylchek glacier, central Asia, using TerraSAR–X data. Remote Sens. 2014, 6, 9239–9259. [Google Scholar]
- Dehecq, A.; Gourmelen, N.; Gardner, A.S.; Brun, F.; Goldberg, D.; Nienow, P.W.; Berthier, E.; Vincent, C.; Wagnon, P.; Trouve, E. Twenty-First century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 2019, 12, 22–27. [Google Scholar]
- Mohr, J.J.; Reeh, N.; Madsen, S. Three-Dimensional glacial flow and surface elevation measured with radar interferometry. Nature 1998, 391, 273–276. [Google Scholar]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar]
- Yao, T.; Yang, W. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 1580, 1–5. [Google Scholar]
- Xie, Z.C.; Liu, C.H. Introduction to Glaciology; Shanghai Popular Science Press: Shanghai, China, 2010. (In Chinese) [Google Scholar]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar]
- Yasuda, T.; Furuya, M. Short-Term glacier velocity changes at West Kunlun Shan, Northwest Tibet, detected by synthetic aperture radar data. Remote Sens. Environ. 2013, 128, 87–106. [Google Scholar]
- Bindschadler, R.; Vornberger, P.; Blankenship, D.; Scambos, T.; Jacobel, R. Surface velocity and mass balance of Ice Streams D and E, West Antarctica. J. Glaciol. 1996, 42, 461–475. [Google Scholar] [CrossRef]
- Bamler, R.; Eineder, M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 151–155. [Google Scholar] [CrossRef]
- Lai, P.; Vaka, D.; Rao, Y.S. Mapping surface flow velocities of Siachen and Gangotri glaciers using TerraSAR-X and Sentinel-1A data by intensity tracking. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 325–329. [Google Scholar] [CrossRef]
- Varugu, B.K.; Rao, Y.S. Glacier retreat monitoring from SAR coherence images: Application to Gangotri glacier. SPIE Asia Pac. Remote Sens. 2016, 987715. [Google Scholar] [CrossRef]
- Muhuri, A.; Bhattacharya, A.; Natsuaki, R.; Hirose, A. Glacier surface velocity estimation using stokes vector correlation. In Proceedings of the IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015. [Google Scholar]
- Liu, X.J.; Zhao, C.Y.; Zhang, Q.; Li, Z.H. Deformation of the Baige landslide, Tibet, China, revealed through the integration of cross-platform ALOS/PALSAR-1 and ALOS/PALSAR-2 SAR observations. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Ding, X.; Wang, Q.; Zhu, J.; Wang, C. Investigating mountain glacier motion with the method of SAR intensity-tracking: Removal of topographic effects and analysis of the dynamic patterns. Earth Sci. Rev. 2014, 138, 179–195. [Google Scholar] [CrossRef]
- Sansosti, E.; Berardino, P.; Manunta, M.; Serafino, F.; Fornaro, G. Geometrical SAR image registration. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2861–2870. [Google Scholar] [CrossRef]
- Raucoules, D.; De Michele, M.; Malet, J.P.; Ulrich, P. Time-Variable 3D ground displacements from High-Resolution Synthetic Aperture Radar (SAR). Application to La Valette landslide (South French Alps). Remote Sens. Environ. 2013, 139, 198–204. [Google Scholar] [CrossRef]
- Nag1ler, T.; Rott, H.; Hetzenecker, M.; Wuite, J.; Potin, P. The Sentinel-1 Mission: New opportunities for ice sheet observations. Remote Sens. 2015, 7, 9371–9389. [Google Scholar] [CrossRef]
- Strozzi, T.; Paul, F.; Wiesmann, A.; Schellenberger, T.; Kaab, A. Circum-Arctic changes in the flow of glaciers and ice caps from satellite SAR data between the 1990s and 2017. Remote Sens. 2017, 9, 947. [Google Scholar] [CrossRef]
- Yan, S.Y.; Liu, G.; Wang, Y.J.; Ruan Z., X. Accurate Determination of Glacier Surface Velocity Fields with a DEM-Assisted Pixel-Tracking Technique from SAR imagery. Remote Sens. 2015, 7, 10898–10916. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Troive, E. Deriving large-scale glacier velocities from a complete satellite archive: Application to the Pamir-Karakoram-Himalaya. Remote Sens. Environ. 2015, 162, 55–66. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Yi, S.; Sun, W.K. Consistent interannual changes in glacier mass balance and their relationship with climate variation on the periphery of the Tibetan Plateau. Geophys. J. Int. 2018, 214, 573–582. [Google Scholar] [CrossRef]
- Fujita, K. Effect of precipitation seasonality on climatic sensitivity of glacier mass balance. Earth Planet. Sci. Lett. 2008, 276, 14–19. [Google Scholar] [CrossRef]
- Shi, Y. Characteristics of late Quaternary monsoonal glaciation on the Tibetan Plateau and in East Asia. Quat. Int. 2002, 97, 79–91. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation seasonality and variability over the Tibetan Plateau as resolved by the high Asia reanalysis. J. Clim. 2013, 27, 1910–1927. [Google Scholar] [CrossRef]
- Chikita, K.; Jha, J.; Yamada, T. Sedimentary effects on the expansion of a Himalayan supraglacial lake. Glob. Planet. Chang. 2001, 28, 23–34. [Google Scholar] [CrossRef]
- Bolch, T.; Buchroithner, M.; Peters, J.; Baessler, M.; Bajracharya, S. Identification of glacier motion and potentially dangerous glacial lakes in the Everest region/Nepal using spaceborne imagery. Nat. Hazards Earth Syst. Sci. 2008, 1329–1340. [Google Scholar] [CrossRef]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 2011, 4, 156–159. [Google Scholar] [CrossRef]
- Anderson, L.S.; Anderson, R.S. Debris thickness patterns on debris-covered glaciers. Geomorphology 2017, 311, 1–12. [Google Scholar] [CrossRef]
- Fujita, K.; Sakai, A. Modelling runoff from a Himalayan debris-covered glacier. Hydrol. Earth Syst. Sci. 2014, 18, 2679–2694. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).