Drought Stress Detection in Juvenile Oilseed Rape Using Hyperspectral Imaging with a Focus on Spectra Variability
Abstract
1. Introduction
2. Material and Methods
2.1. Plant Material and Experimental Factors
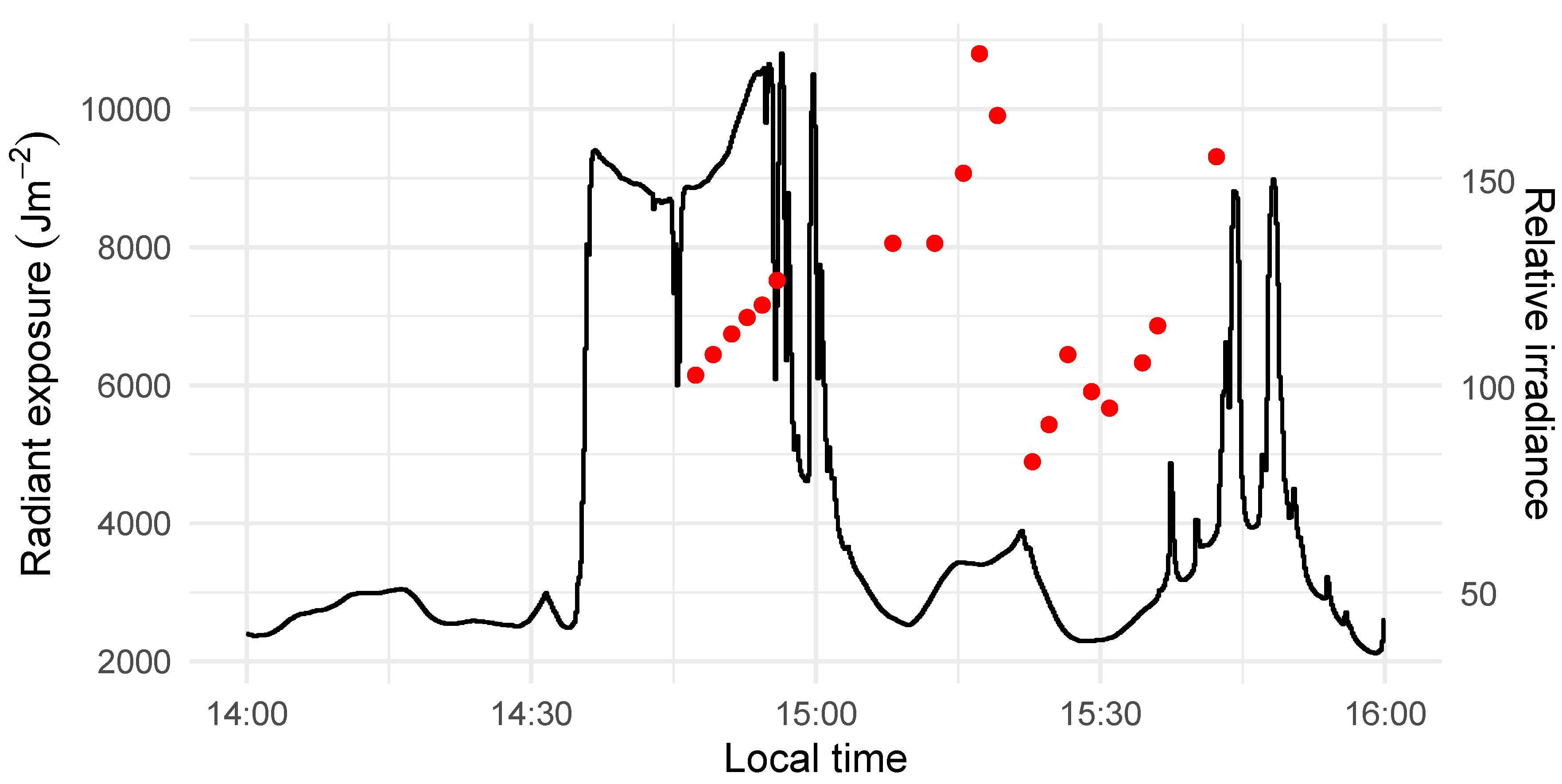
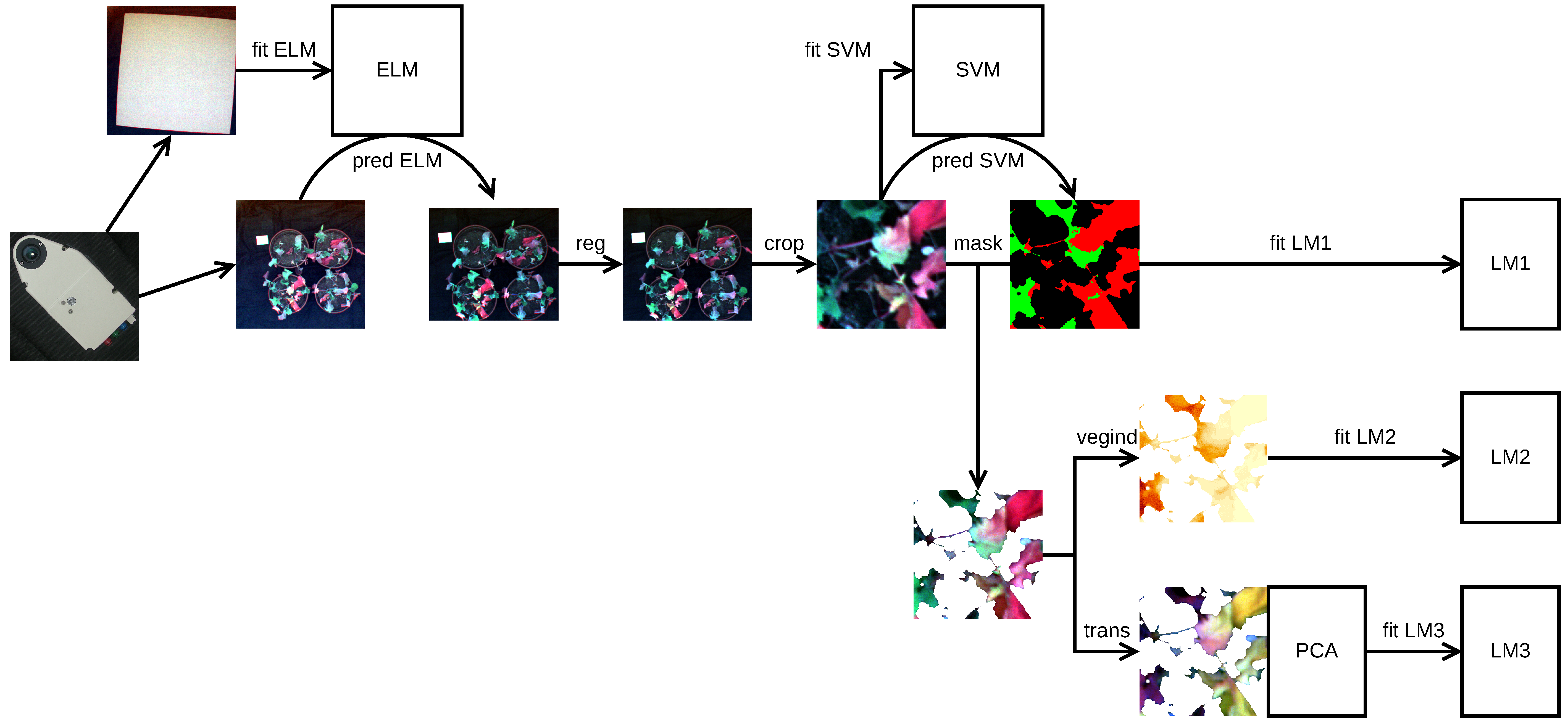
2.2. Image Acquisition and Pre-processing
2.3. Pixel Classification and Evaluation of Class Size Proportions
2.4. Vegetation Index and Full-Spectrum Analyses
2.5. Statistical Inference and Model Diagnostics
2.6. Reproducing the Study
3. Results
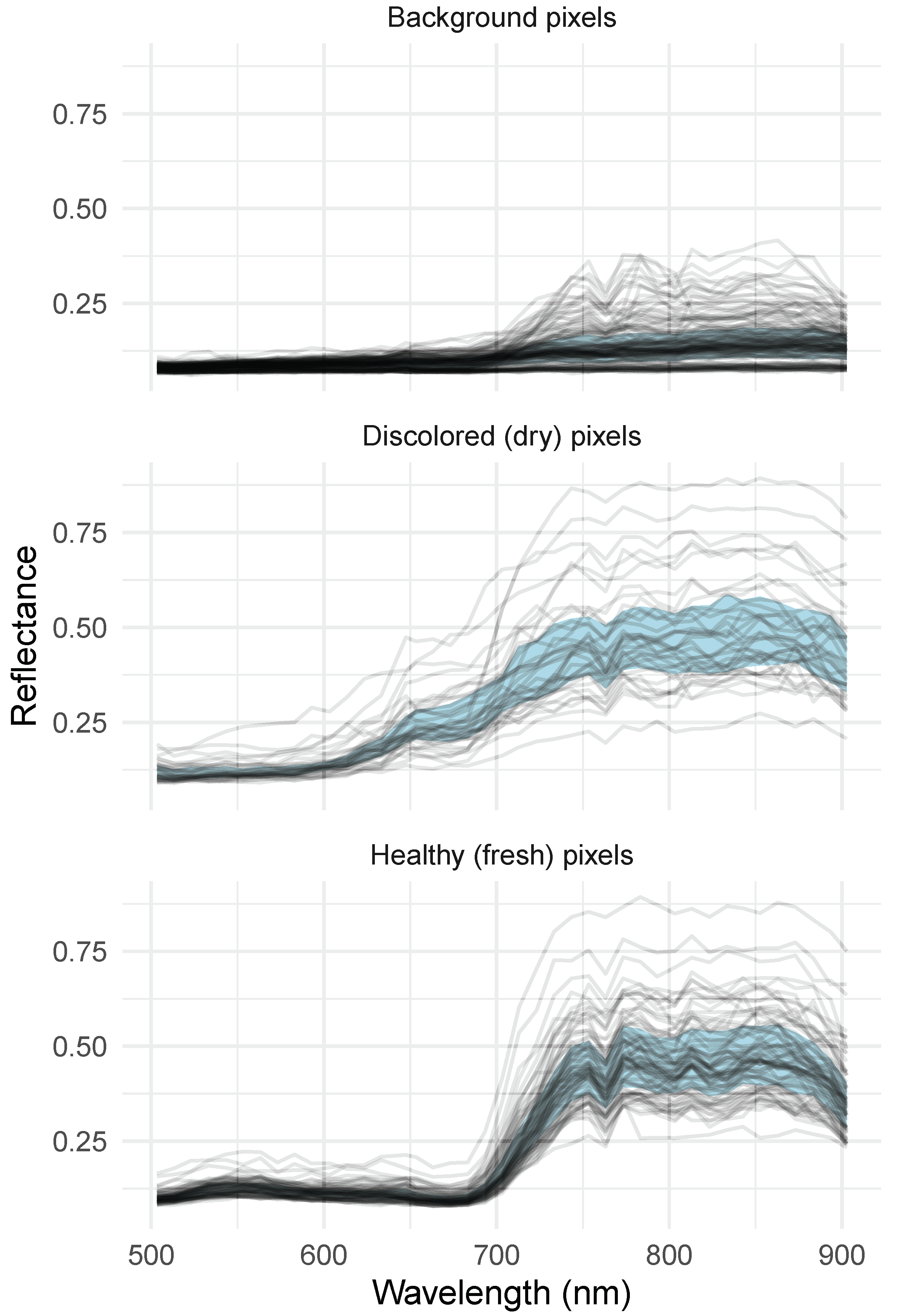
3.1. Image Segmentation and Dry Pixel Occurrence
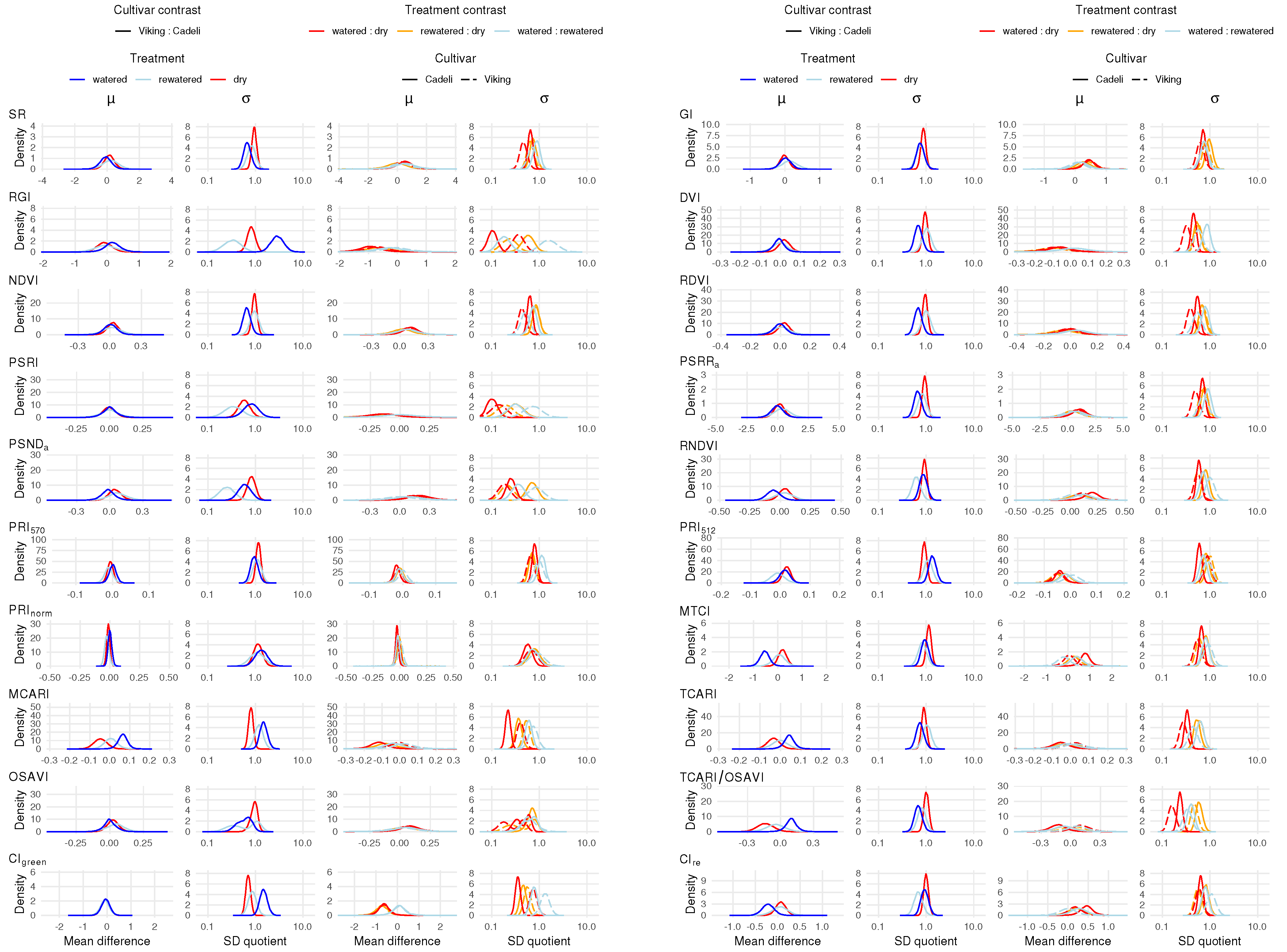
3.2. Vegetation Indexes
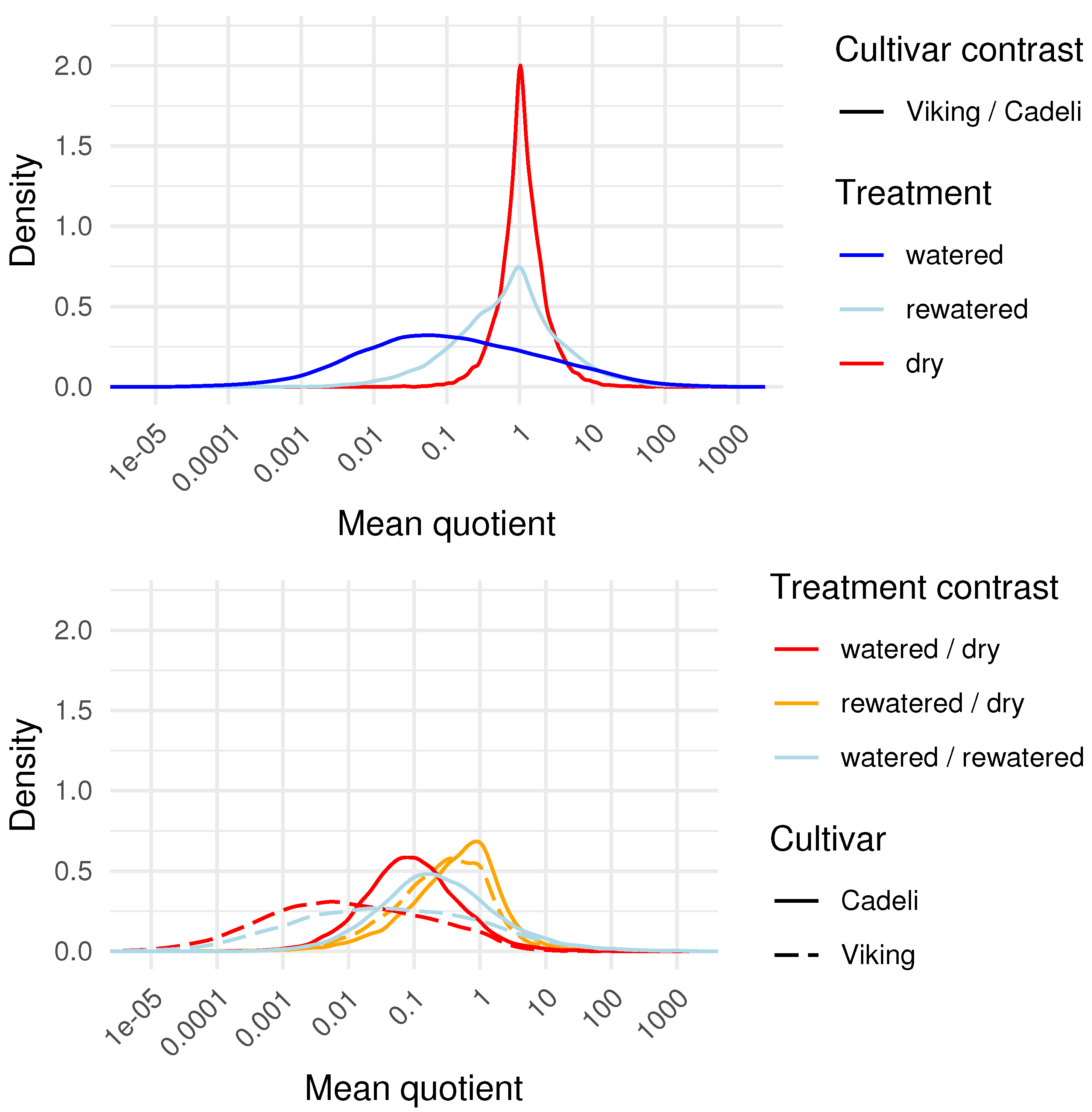
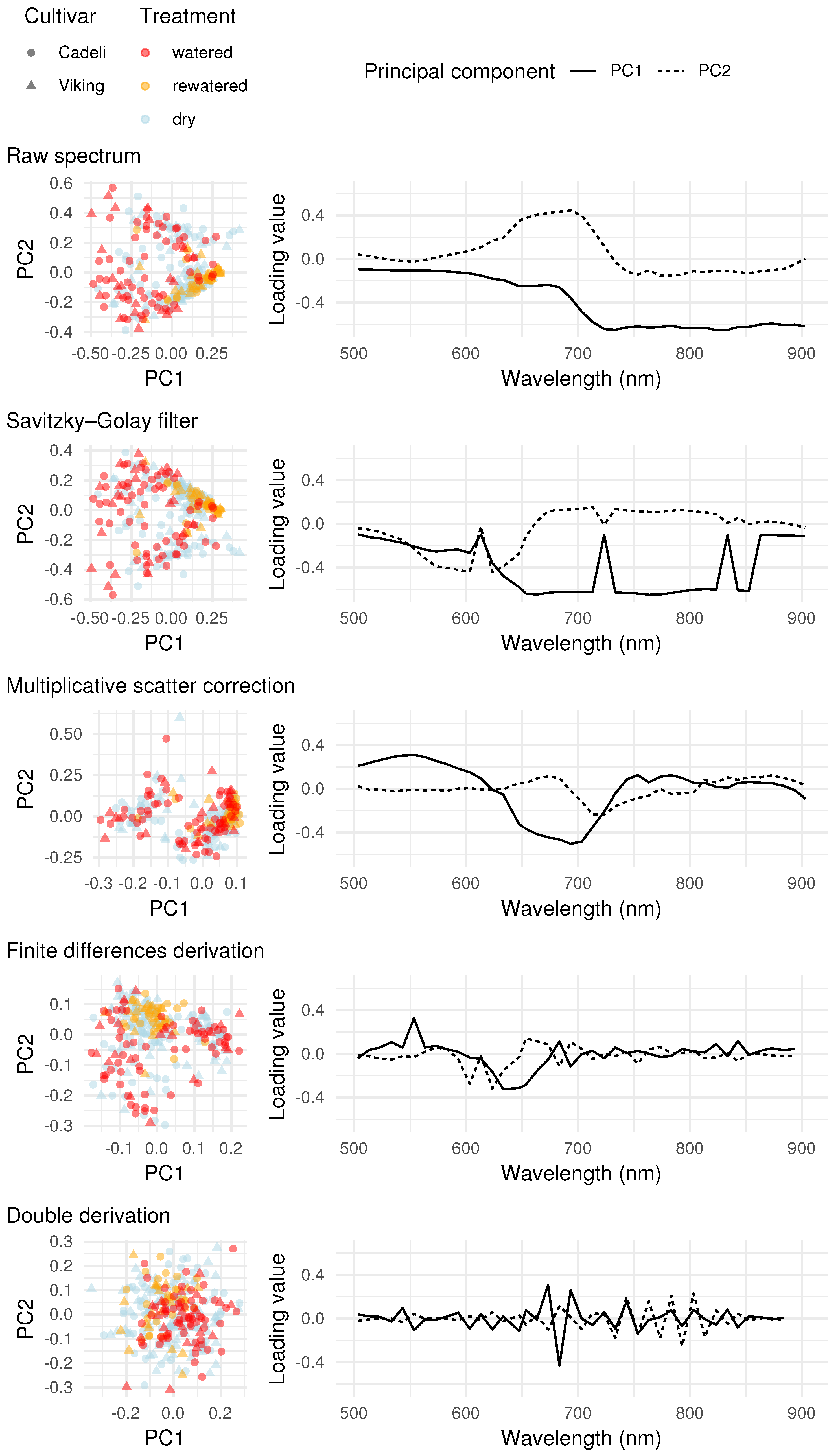
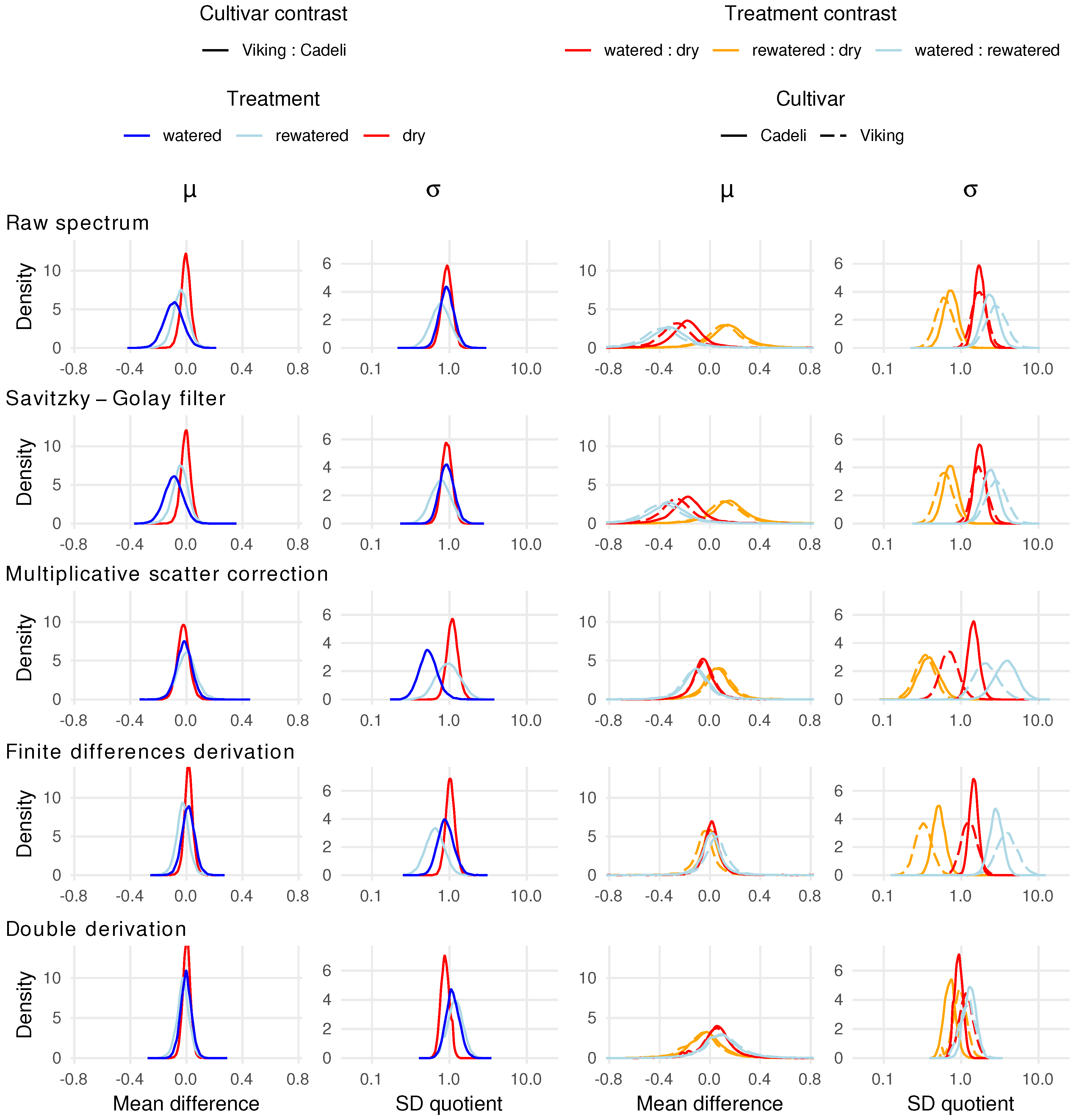
3.3. Full Spectrum Information
4. Discussion
4.1. Image Quality and Patterns Related to Segmentation
4.2. Vegetation Indexes
4.3. Full Spectrum Information
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lobell, D.B.; Schlenker, W.; Costa-Roberts, J. Climate Trends and Global Crop Production Since 1980. Science 2011, 333, 616–620. [Google Scholar] [CrossRef] [PubMed]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global Changes in Drought Conditions Under Different Levels of Warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Arnell, N.; Lowe, J.; Challinor, A.; Osborn, T. Global and regional impacts of climate change at different levels of global temperature increase. Clim. Chang. 2019, 155, 377–391. [Google Scholar] [CrossRef]
- Daryanto, S.; Wang, L.; Jacinthe, P.A. Global synthesis of drought effects on cereal, legume, tuber and root crops production: A review. Agric. Water Manag. 2017, 179, 18–33. [Google Scholar] [CrossRef]
- Sun, C.; Li, C.; Zhang, C.; Hao, L.; Song, M.; Liu, W.; Zhang, Y. Reflectance and biochemical responses of maize plants to drought and re-watering cycles. Ann. Appl. Biol. 2018, 172, 332–345. [Google Scholar] [CrossRef]
- Asaari, M.S.M.; Mertens, S.; Dhondt, S.; Inzé, D.; Wuyts, N.; Scheunders, P. Analysis of hyperspectral images for detection of drought stress and recovery in maize plants in a high-throughput phenotyping platform. Comput. Electron. Agric. 2019, 162, 749–758. [Google Scholar] [CrossRef]
- Behmann, J.; Steinrücken, J.; Plümer, L. Detection of early plant stress responses in hyperspectral images. ISPRS J. Photogramm. Remote Sens. 2014, 93, 98–111. [Google Scholar] [CrossRef]
- Linke, R.; Richter, K.; Haumann, J.; Schneider, W.; Weihs, P. Occurrence of repeated drought events: Can repetitive stress situations and recovery from drought be traced with leaf reflectance? Period. Biol. 2008, 110, 219–229. [Google Scholar]
- Buezo, J.; Sanz-Saez, Á.; Moran, J.F.; Soba, D.; Aranjuelo, I.; Esteban, R. Drought tolerance response of high-yielding soybean varieties to mild drought: Physiological and photochemical adjustments. Physiol. Plant. 2019, 166, 88–104. [Google Scholar] [CrossRef]
- Gilbert, M.E.; Zwieniecki, M.A.; Holbrook, N.M. Independent variation in photosynthetic capacity and stomatal conductance leads to differences in intrinsic water use efficiency in 11 soybean genotypes before and during mild drought. J. Exp. Bot. 2011, 62, 2875–2887. [Google Scholar] [CrossRef]
- Blum, A. Drought resistance, water-use efficiency, and yield potential—are they compatible, dissonant, or mutually exclusive? Aust. J. Agric. Res. 2005, 56, 1159–1168. [Google Scholar] [CrossRef]
- Raza, M.A.S.; Shahid, A.M.; Saleem, M.F.; Khan, I.H.; Ahmad, S.; Ali, M.; Iqbal, R. Effects and management strategies to mitigate drought stress in oilseed rape (Brassica napus L.): A review. Zemdirb. Agric. 2017, 104, 85–94. [Google Scholar] [CrossRef]
- Ashraf, M.; Harris, P. Photosynthesis under stressful environments: An overview. Photosynthetica 2013, 51, 163–190. [Google Scholar] [CrossRef]
- Flexas, J.; Bota, J.; Loreto, F.; Cornic, G.; Sharkey, T. Diffusive and metabolic limitations to photosynthesis under drought and salinity in C3 plants. Plant Biol. 2004, 6, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Urban, M.O.; Vašek, J.; Klíma, M.; Krtková, J.; Kosová, K.; Prášil, I.T.; Vítámvás, P. Proteomic and physiological approach reveals drought-induced changes in rapeseeds: Water-saver and water-spender strategy. J. Proteom. 2017, 152, 188–205. [Google Scholar] [CrossRef] [PubMed]
- Nakhforoosh, A.; Bodewein, T.; Fiorani, F.; Bodner, G. Identification of Water Use Strategies at Early Growth Stages in Durum Wheat from Shoot Phenotyping and Physiological Measurements. Front. Plant Sci. 2016, 7, 1155. [Google Scholar] [CrossRef] [PubMed]
- Roche, D. Stomatal conductance is essential for higher yield potential of C3 crops. Crit. Rev. Plant Sci. 2015, 34, 429–453. [Google Scholar] [CrossRef]
- Kim, Y.; Glenn, D.M.; Park, J.; Ngugi, H.K.; Lehman, B.L. Hyperspectral image analysis for water stress detection of apple trees. Comput. Electron. Agric. 2011, 77, 155–160. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Carter, G.A.; Knapp, A.K. Leaf optical properties in higher plants: Linking spectral characteristics to stress and chlorophyll concentration. Am. J. Bot. 2001, 88, 677–684. [Google Scholar] [CrossRef]
- Gill, S.S.; Tuteja, N. Reactive oxygen species and antioxidant machinery in abiotic stress tolerance in crop plants. Plant Physiol. Biochem. 2010, 48, 909–930. [Google Scholar] [CrossRef] [PubMed]
- Din, J.; Khan, S.; Ali, I.; Gurmani, A. Physiological and agronomic response of canola varieties to drought stress. J. Anim. Plant Sci. 2011, 21, 78–82. [Google Scholar]
- Munné-Bosch, S.; Alegre, L. Die and let live: Leaf senescence contributes to plant survival under drought stress. Funct. Plant Biol. 2004, 31, 203–216. [Google Scholar] [CrossRef] [PubMed]
- Govender, M.; Govender, P.J.; Weiersbye, I.M.; Witkowski, E.T.F.; Ahmed, F. Review of commonly used remote sensing and ground-based technologies to measure plant water stress. Water SA 2009, 35, 741–752. [Google Scholar] [CrossRef]
- Van der Werff, H.; van der Meijde, M.; Jansma, F.; van der Meer, F.; Groothuis, G.J. A Spatial-Spectral Approach for Visualization of Vegetation Stress Resulting from Pipeline Leakage. Sensors 2008, 8, 3733–3743. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Lowe, A.; Harrison, N.; French, A.P. Hyperspectral image analysis techniques for the detection and classification of the early onset of plant disease and stress. Plant Methods 2017, 13, 80. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Mishra, P.; Asaari, M.S.M.; Herrero-Langreo, A.; Lohumi, S.; Diezma, B.; Scheunders, P. Close range hyperspectral imaging of plants: A review. Biosyst. Eng. 2017, 164, 49–67. [Google Scholar] [CrossRef]
- Ge, Y.; Bai, G.; Stoerger, V.; Schnable, J.C. Temporal dynamics of maize plant growth, water use, and leaf water content using automated high throughput RGB and hyperspectral imaging. Comput. Electron. Agric. 2016, 127, 625–632. [Google Scholar] [CrossRef]
- Kumar, A.; Bharti, V.; Kumar, V.K.U.; Meena, P. Hyperspectral imaging: A potential tool for monitoring crop infestation, crop yield and macronutrient analysis, with special emphasis to Oilseed Brassica. J. Oilseed Brassica 2016, 7, 113–125. [Google Scholar]
- Bruning, B.; Liu, H.; Brien, C.; Berger, B.; Lewis, M.; Garnett, T. The Development of Hyperspectral Distribution Maps to Predict the Content and Distribution of Nitrogen and Water in Wheat (Triticum aestivum). Front. Plant Sci. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Römer, C.; Wahabzada, M.; Ballvora, A.; Pinto, F.; Rossini, M.; Panigada, C.; Behmann, J.; Léon, J.; Thurau, C.; Bauckhage, C.; et al. Early drought stress detection in cereals: Simplex volume maximisation for hyperspectral image analysis. Funct. Plant Biol. 2012, 39, 878–890. [Google Scholar] [CrossRef] [PubMed]
- Zarco-Tejada, P.; González-Dugo, V.; Berni, J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Zovko, M.; Žibrat, U.; Knapič, M.; Kovačić, M.B.; Romić, D. Hyperspectral remote sensing of grapevine drought stress. Precis. Agric. 2019, 20, 335–347. [Google Scholar] [CrossRef]
- Sabagh, A.E.; Hossain, A.; Barutçular, C.; Islam, M.S.; Ratnasekera, D.; Kumar, N.; Meena, R.S.; Gharib, H.S.; Saneoka, H.; da Silva, J.A.T. Drought and salinity stress management for higher and sustainable canola (‘Brassica napus’ L.) production: A critical review. Aust. J. Crop. Sci. 2019, 13, 88–96. [Google Scholar] [CrossRef]
- Xia, J.; Yang, Y.W.; Cao, H.X.; Zhang, W.; Xu, L.; Wang, Q.; Ke, Y.; Zhang, W.; Ge, D.; Huang, B. Hyperspectral Identification and Classification of Oilseed Rape Waterlogging Stress Levels Using Parallel Computing. IEEE Access 2018, 6, 57663–57675. [Google Scholar] [CrossRef]
- Högy, P.; Franzaring, J.; Schwadorf, K.; Breuer, J.; Schütze, W.; Fangmeier, A. Effects of free-air CO2 enrichment on energy traits and seed quality of oilseed rape. Agric. Ecosyst. Environ. 2010, 139, 239–244. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, G.; Long, W.; Zou, X.; Li, F.; Nishio, T. Recent progress in drought and salt tolerance studies in Brassica crops. Breed. Sci. 2014, 64, 60–73. [Google Scholar] [CrossRef]
- Bonjean, A.P.; Dequidt, C.; Sang, T. Rapeseed in China. OCL 2016, 23, D605. [Google Scholar] [CrossRef][Green Version]
- Kumar, A.; Bharti, V.; Kumar, V.; Meena, P.; Suresh, G. Hyperspectral imaging applications in rapeseed and mustard farming. J. Oilseeds Res. 2017, 34, 1–8. [Google Scholar]
- Majidi, M.; Rashidi, F.; Sharafi, Y. Physiological traits related to drought tolerance in Brassica. Int. J. Plant Prod. 2015, 9, 4. [Google Scholar]
- Tesfamariam, E.H.; Annandale, J.G.; Steyn, J.M. Water Stress Effects on Winter Canola Growth and Yield. Agron. J. 2010, 102, 658–666. [Google Scholar] [CrossRef]
- Müller, T.; Lüttschwager, D.; Lentzsch, P. Recovery from drought stress at the shooting stage in oilseed rape (Brassica napus). J. Agron. Crop. Sci. 2010, 196, 81–89. [Google Scholar] [CrossRef]
- Kosová, K.; Klíma, M.; Vítamvás, P.; Prášil, I.T. Odezva vybraných odrůd řepky na sucho a následná regenerace [Response of selected oilseed rape cultivars to drought and subsequent recovery]. Úroda 2018, 66, 19–25. [Google Scholar]
- Piekarczyk, J.; Sulewska, H.; Szymańska, G. Winter oilseed-rape yield estimates from hyperspectral radiometer measurements. Quaest. Geogr. 2011, 30, 77–84. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y. Rapid estimation of seed yield using hyperspectral images of oilseed rape leaves. Ind. Crop. Prod. 2013, 42, 416–420. [Google Scholar] [CrossRef]
- Kong, W.; Liu, F.; Zhang, C.; Zhang, J.; Feng, H. Non-destructive determination of Malondialdehyde (MDA) distribution in oilseed rape leaves by laboratory scale NIR hyperspectral imaging. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Kruschke, J.K.; Liddell, T.M. The Bayesian New Statistics: Hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective. Psychon. Bull. Rev. 2017, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Nansen, C. Use of Variogram Parameters in Analysis of Hyperspectral Imaging Data Acquired from Dual-Stressed Crop Leaves. Remote Sens. 2012, 4, 180–193. [Google Scholar] [CrossRef]
- Jay, S.; Hadoux, X.; Gorretta, N.; Rabatel, G. Potential of hyperspectral imagery for nitrogen content retrieval in sugar beet leaves. In Proceedings of the Proceedings International Conference of Agricultural Engineering, Zurich, Switzerland, 6–10 July 2014; pp. 1–8. [Google Scholar]
- Peteinatos, G.G.; Korsaeth, A.; Berge, T.W.; Gerhards, R. Using Optical Sensors to Identify Water Deprivation, Nitrogen Shortage, Weed Presence and Fungal Infection in Wheat. Agriculture 2016, 6, 24. [Google Scholar] [CrossRef]
- Van Zyl, C.J. Frequentist and Bayesian inference: A conceptual primer. New Ideas Psychol. 2018, 51, 44–49. [Google Scholar] [CrossRef]
- Zyphur, M.J.; Oswald, F.L. Bayesian estimation and inference: A user’s guide. J. Manag. 2015, 41, 390–420. [Google Scholar] [CrossRef]
- Che, X.; Xu, S. Bayesian data analysis for agricultural experiments. Can. J. Plant Sci. 2010, 90, 575–603. [Google Scholar] [CrossRef]
- Gelfand, A.E. Gibbs Sampling. J. Am. Stat. Assoc. 2000, 95, 1300–1304. [Google Scholar] [CrossRef]
- Visser, M.D.; McMahon, S.M.; Merow, C.; Dixon, P.M.; Record, S.; Jongejans, E. Speeding Up Ecological and Evolutionary Computations in R; Essentials of High Performance Computing for Biologists. PLoS Comput. Biol. 2015, 11, e1004140. [Google Scholar] [CrossRef] [PubMed]
- Bürkner, P.C. Advanced Bayesian Multilevel Modeling with the R Package brms. R J. 2018, 10, 395–411. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A Probabilistic Programming Language. J. Stat. Softw. 2017, 76, 1–32. [Google Scholar] [CrossRef]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Filzmoser, P.; Hron, K.; Reimann, C. Univariate statistical analysis of environmental (compositional) data: Problems and possibilities. Sci. Total Environ. 2009, 407, 6100–6108. [Google Scholar] [CrossRef]
- Roeder, A.H.; Cunha, A.; Burl, M.C.; Meyerowitz, E.M. A computational image analysis glossary for biologists. Development 2012, 139, 3071–3080. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Karimi, Y.; Prasher, S.; Madani, A.; Kim, S. Application of support vector machine technology for the estimation of crop biophysical parameters using aerial hyperspectral observations. Can. Biosyst. Eng. 2008, 50, 13–20. [Google Scholar]
- Bischl, B.; Richter, J.; Bossek, J.; Horn, D.; Thomas, J.; Lang, M. mlrMBO: A Modular Framework for Model-Based Optimization of Expensive Black-Box Functions. arXiv 2018, arXiv:1703.03373. [Google Scholar]
- Amigo, J.M.; Babamoradi, H.; Elcoroaristizabal, S. Hyperspectral image analysis. A tutorial. Anal. Chim. Acta 2015, 896, 34–51. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Jakulin, A.; Pittau, M.G.; Su, Y.S. A weakly informative default prior distribution for logistic and other regression models. Ann. Appl. Stat. 2008, 2, 1360–1383. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Peñuelas, J. Remote Sensing of Biomass and Yield of Winter Wheat under Different Nitrogen Supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.; De Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral Reflectance Changes Associated with Autumn Senescence of Aesculus hippocastanum L. and Acer platanoides L. Leaves. Spectral Features and Relation to Chlorophyll Estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Suárez, L.; Morales, F.; Zarco-Tejada, P.J. Assessing structural effects on PRI for stress detection in conifer forests. Remote Sens. Environ. 2011, 115, 2360–2375. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.; Suárez, L.; Berni, J.A.; Goldhamer, D.; Fereres, E. A PRI-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Daughtry, C.; Walthall, C.; Kim, M.; De Colstoun, E.B.; McMurtrey, J., III. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A. Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Anal. 2006, 1, 515–534. [Google Scholar] [CrossRef]
- Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Cumming, G. The New Statistics: Why and How. Psychol. Sci. 2014, 25, 7–29. [Google Scholar] [CrossRef]
- Courtès, L.; Wurmus, R. Reproducible and User-Controlled Software Environments in HPC with Guix; Euro-Par 2015: Parallel Processing Workshops; Hunold, S., Costan, A., Giménez, D., Alexandru, I., Ricci, L., Gómez Requena, M.E., Scarano, V., Verbanescu, A.L., Scott, S.L., Lankes, S., Eds.; Vienna University of Technology: Vienna, Austria, 2015; pp. 579–591. [Google Scholar] [CrossRef]
- Feldman, S.I. Make—A program for maintaining computer programs. Softw. Pract. Exp. 1979, 9, 255–265. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien, 2019. Available online: https://cran.r-project.org/package=e1071 (accessed on 21 October 2020).
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. mlr: Machine Learning in R. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. Discuss. 2015, 8. [Google Scholar] [CrossRef]
- Brenning, A.; Bangs, D.; Becker, M. RSAGA: SAGA Geoprocessing and Terrain Analysis. 2018. Available online: https://cran.r-project.org/package=RSAGA (accessed on 21 October 2020).
- Bradski, G. The OpenCV Library. Dobb’S J. Softw. Tools 2000, 25, 120–125. [Google Scholar]
- Honkavaara, E.; Khoramshahi, E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sens. 2018, 10, 256. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S.L. Leaf optical properties: A state of the art. In Proceedings of the 8th International Symposium of Physical Measurements & Signatures in Remote Sensing, Aussois, France, 8–12 January 2001; pp. 223–332. [Google Scholar]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote Estimation of Crop Chlorophyll Content Using Spectral Indices Derived from Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Gitelson, A.A. Hyperspectral Remote Sensing of Vegetation; chapter Remote Sensing Estimation of Crop Biophysical Characteristics at Various Scales; Thenkabail, P.S., Lyon, J.G., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 329–358. [Google Scholar]
- Perry, E.M.; Roberts, D.A. Sensitivity of Narrow-Band and Broad-Band Indices for Assessing Nitrogen Availability and Water Stress in an Annual Crop. Agron. J. 2008, 100, 1211–1219. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, J.R.; Riaño, D.; Carlisle, E.; Ustin, S.; Smart, D.R. Evaluation of Hyperspectral Reflectance Indexes to Detect Grapevine Water Status in Vineyards. Am. J. Enol. Vitic. 2007, 58, 302–317. [Google Scholar]
- Gutierrez, M.; Reynolds, M.P.; Raun, W.R.; Stone, M.L.; Klatt, A.R. Spectral Water Indices for Assessing Yield in Elite Bread Wheat Genotypes under Well-Irrigated, Water-Stressed, and High-Temperature Conditions. Crop Sci. 2010, 50, 197–214. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Rossini, M.; Fava, F.; Cogliati, S.; Meroni, M.; Marchesi, A.; Panigada, C.; Giardino, C.; Busetto, L.; Migliavacca, M.; Amaducci, S.; et al. Assessing canopy PRI from airborne imagery to map water stress in maize. ISPRS J. Photogramm. Remote Sens. 2013, 86, 168–177. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.; Fredeen, A.; Merino, J.; Field, C. Reflectance indices associated with physiological changes in nitrogen-and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Chou, S.; Chen, J.M.; Yu, H.; Chen, B.; Zhang, X.; Croft, H.; Khalid, S.; Li, M.; Shi, Q. Canopy-Level Photochemical Reflectance Index from Hyperspectral Remote Sensing and Leaf-level Non-photochemical Quenching as Early Indicators of Water Stress in Maize. Remote Sens. 2017, 9, 794. [Google Scholar] [CrossRef]
- Sun, H.; Feng, M.; Xiao, L.; Yang, W.; Wang, C.; Jia, X.; Zhao, Y.; Zhao, C.; Muhammad, S.K.; Li, D. Assessment of plant water status in winter wheat (Triticum aestivum L.) based on canopy spectral indices. PLoS ONE 2019, 14, e0216890. [Google Scholar] [CrossRef]
- Feng, W.; Qi, S.; Heng, Y.; Zhou, Y.; Wu, Y.; Liu, W.; He, L.; Li, X. Canopy Vegetation Indices from In situ Hyperspectral Data to Assess Plant Water Status of Winter Wheat under Powdery Mildew Stress. Front. Plant Sci. 2017, 8, 1219. [Google Scholar] [CrossRef]
- Pasban Eslam, B. Evaluation of Physiological Indices, Yield and its Components as Screening Techniques for Water Deficit Tolerance in Oilseed Rape Cultivars. J. Agric. Sci. Technol. 2009, 11, 413–422. [Google Scholar]
- Salvador, M.; Resmini, R. Data Mining for Geoinformatics; chapter Computation in Hyperspectral Imagery (HSI) Data Analysis: Role and Opportunities; Cervone, G., Lin, J., Waters, N., Eds.; Springer: New York, NY, USA, 2014; pp. 1–27. [Google Scholar]
- Danson, F.; Steven, M.; Malthus, T.; Clark, J. High-spectral resolution data for determining leaf water content. Int. J. Remote Sens. 1992, 13, 461–470. [Google Scholar] [CrossRef]

| Watering Regime | Cultivar | |
|---|---|---|
| Cadeli | Viking | |
| dry | 6 | 6 |
| rewatered | 3 (2) | 3 (2) |
| watered | 5(0) | 3(0) |
| Vegetation Index | Formula | Sensitivity | Reference |
|---|---|---|---|
| SR | Chl, fIPAR, LAI | [69] | |
| GI | Chl | [70] | |
| RGI | Chl | [70] | |
| DVI | LWC | [71] | |
| NDVI | Chl, fIPAR, LAI | [69] | |
| RDVI | fAPAR | [72] | |
| PSRI | Chl, Car | [73] | |
| PSSRa | Chl, Car | [74] | |
| PSNDa | Chl, Car | [74] | |
| RNDVI | Chl | [75] | |
| PRI570 | ΔF/Fm’ | [76] | |
| PRI512 | Gs, ᴪ, EPS | [77] | |
| PRInorm | Gs, ᴪ | [78] | |
| MTCI | Chl | [79] | |
| MCARI | Chl | [80] | |
| TCARI | Chl | [81] | |
| OSAVI | LAI | [82] | |
| TCARI/OSAVI | Chl | [81] | |
| CIgreen | Chl | [83] | |
| CIre | Chl | [83] |
| Observed Classes | Predicted Classes | ||
|---|---|---|---|
| b | d | f | |
| background | 26 | 0 | 1 |
| dry | 0 | 8 | 1 |
| fresh | 0 | 0 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żelazny, W.R.; Lukáš, J. Drought Stress Detection in Juvenile Oilseed Rape Using Hyperspectral Imaging with a Focus on Spectra Variability. Remote Sens. 2020, 12, 3462. https://doi.org/10.3390/rs12203462
Żelazny WR, Lukáš J. Drought Stress Detection in Juvenile Oilseed Rape Using Hyperspectral Imaging with a Focus on Spectra Variability. Remote Sensing. 2020; 12(20):3462. https://doi.org/10.3390/rs12203462
Chicago/Turabian StyleŻelazny, Wiktor R., and Jan Lukáš. 2020. "Drought Stress Detection in Juvenile Oilseed Rape Using Hyperspectral Imaging with a Focus on Spectra Variability" Remote Sensing 12, no. 20: 3462. https://doi.org/10.3390/rs12203462
APA StyleŻelazny, W. R., & Lukáš, J. (2020). Drought Stress Detection in Juvenile Oilseed Rape Using Hyperspectral Imaging with a Focus on Spectra Variability. Remote Sensing, 12(20), 3462. https://doi.org/10.3390/rs12203462





