Wavelength Selection Method Based on Partial Least Square from Hyperspectral Unmanned Aerial Vehicle Orthomosaic of Irrigated Olive Orchards
Abstract
1. Introduction
2. Materials and Methods
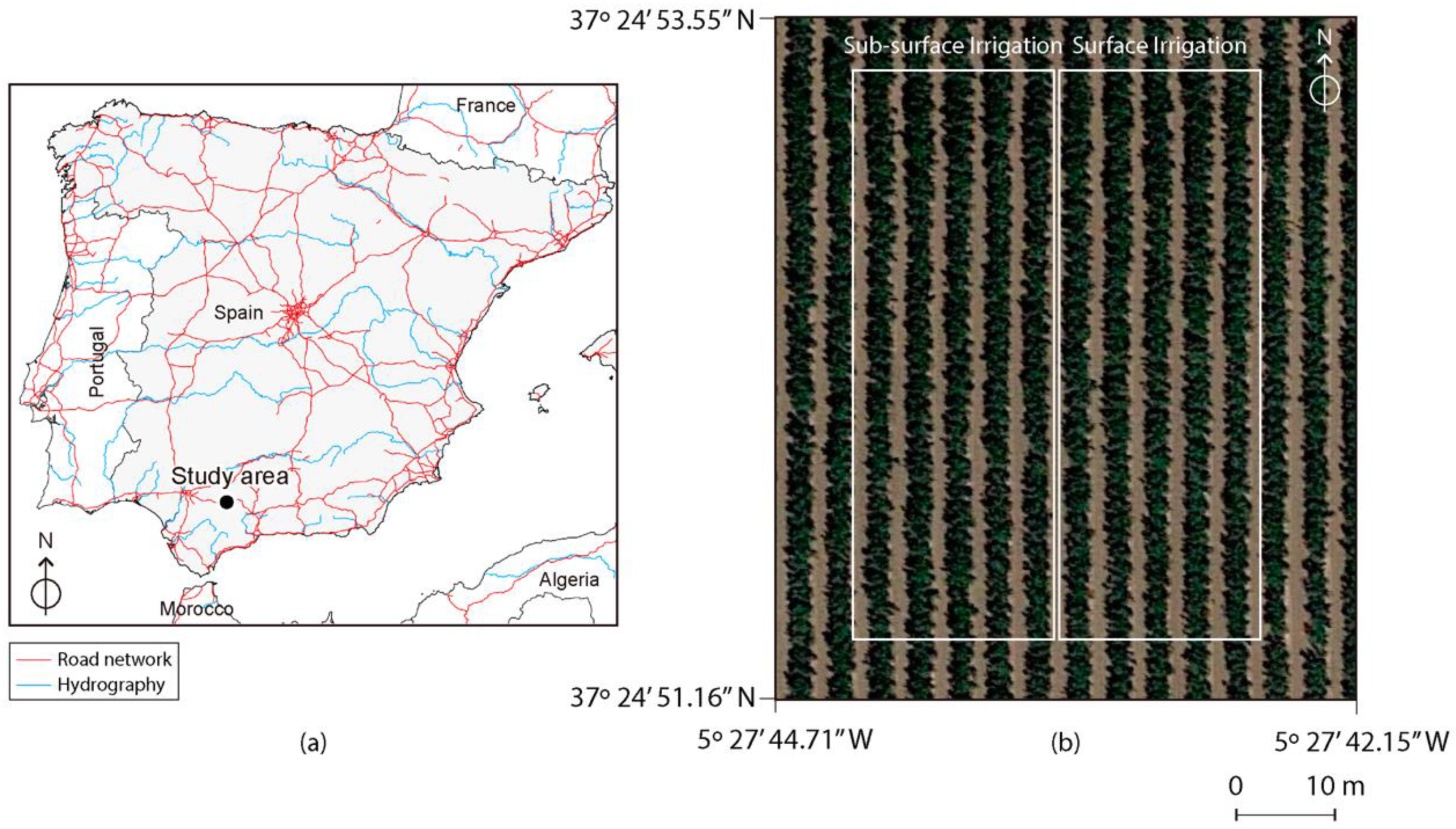
2.1. Study Area and UAV Flights
2.2. UAV Flights and Processing
2.3. Wavelength Selection Methods Used and Evaluation
2.4. Evaluation of Wavelength Selection Methods
2.5. Software
3. Results and Discussion
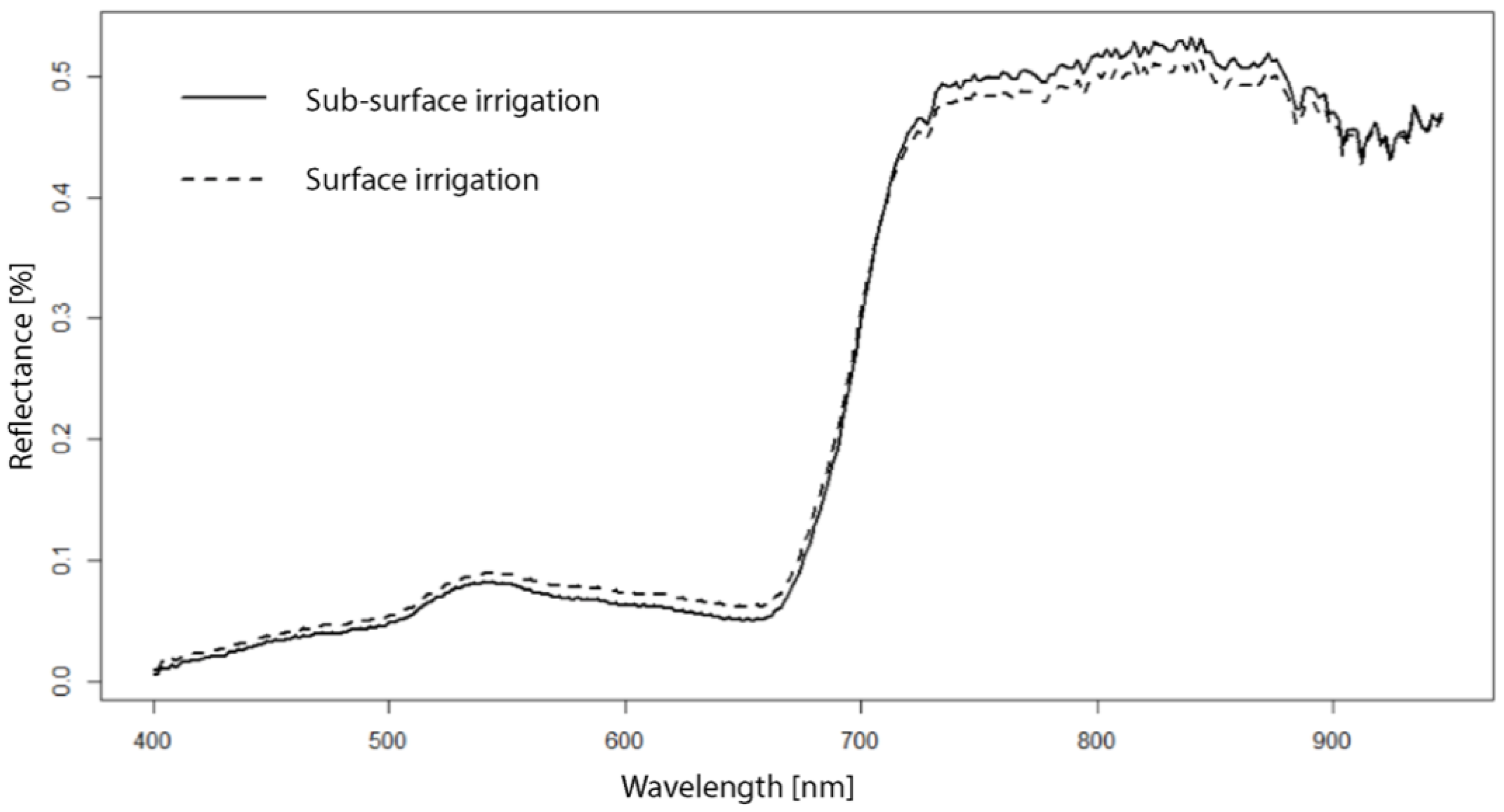
3.1. Spectral Reflectance Data
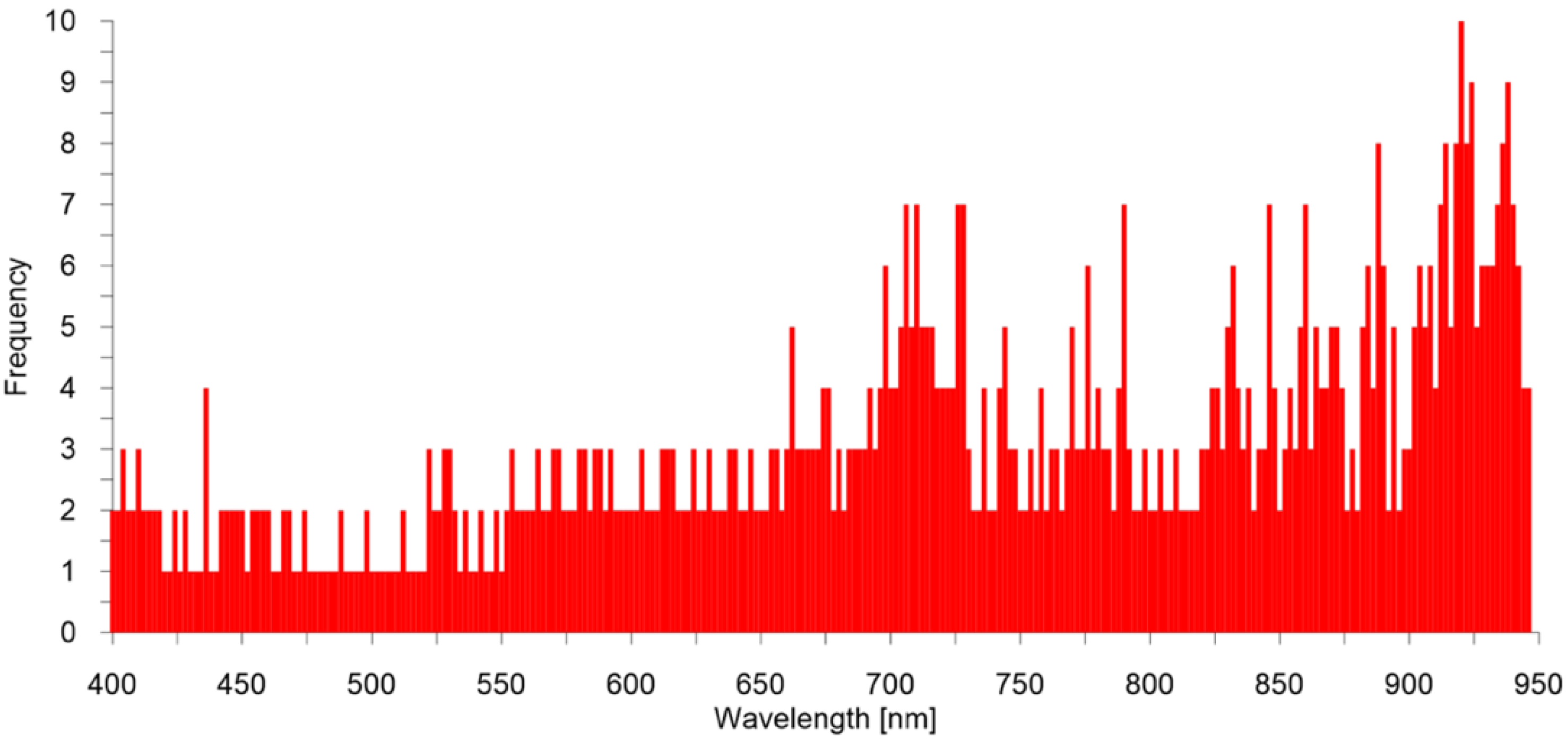
3.2. Wavelength Selection Results
3.3. Quality and Efficiency of Classification with Each Selection Method
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ozdogan, M.; Yang, Y.; Allez, G.; Cervantes, C. Remote sensing of irrigated agriculture: Opportunities and challenges. Remote Sens. 2010, 2, 2274–2304. [Google Scholar] [CrossRef]
- Cai, X.; Rosegrant, M.W. Global Water Demand and Supply Projections: Part 1. A Modeling Approach. Water Int. 2002, 27, 159–169. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Douglas, E.M.; Fekete, B.M.; Vörösmarty, C.J.; Schumann, A.H. Global irrigation water demand: Variability and uncertainties arising from agricultural and climate data sets. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Kueppers, L.M.; Snyder, M.A.; Sloan, L.C. Irrigation cooling effect: Regional climate forcing by land-use change. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Droogers, P.; Aerts, J. Adaptation strategies to climate change and climate variability: A comparative study between seven contrasting river basins. Phys. Chem. Earth 2005, 30, 339–346. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Dheeravath, V.; Biradar, C.M.; Gangalakunta, O.R.P.; Noojipady, P.; Gurappa, C.; Velpuri, M.; Gumma, M.; Li, Y. Irrigated area maps and statistics of India using remote sensing and national statistics. Remote Sens. 2009, 1, 50–67. [Google Scholar] [CrossRef]
- Escobar, R.F.; de la Rosa, R.; Leon, L.; Gomez, J.A.; Testi, F.; Orgaz, M.; Gil-Ribes, J.A.; Quesada-Moraga, E.; Trapero, A. Evolution and sustainability of the olive production systems. In Present and Future of the Mediterranean Olive Sector; CIHEAM/IOC: Zaragoza, Spain, 2013; Volume 106, pp. 11–41. ISBN 2-85352-512-0. [Google Scholar]
- Martínez, J.; Reca, J. Water use efficiency of surface drip irrigation versus an alternative subsurface drip irrigation method. J. Irrig. Drain. Eng. 2014, 140, 1–9. [Google Scholar] [CrossRef]
- Briggs, L.J.; Shantz, H.L. The water requirement of plants. In Bureau of Plant Industry Bulletin; Wiley: Akron, OH, USA, 1913; p. 96. [Google Scholar]
- Yu, L.; Gao, X.; Zhao, X. Global synthesis of the impact of droughts on crops’ water-use efficiency (WUE): Towards both high WUE and productivity. Agric. Syst. 2020, 177, 102723. [Google Scholar] [CrossRef]
- Tolk, J.; Howell, T.; Evett, S. Effect of mulch, irrigation, and soil type on water use and yield of maize. Soil Tillage Res. 1999, 50, 137–147. [Google Scholar] [CrossRef]
- Basso, B.; Ritchie, J.T. Evapotranspiration in High-Yielding Maize and under Increased Vapor Pressure Deficit in the US Midwest. Agric. Environ. Lett. 2018, 3, 170039. [Google Scholar] [CrossRef]
- Bota, J.; Tomás, M.; Flexas, J.; Medrano, H.; Escalona, J.M. Differences among grapevine cultivars in their stomatal behavior and water use efficiency under progressive water stress. Agric. Water Manag. 2016, 164, 91–99. [Google Scholar] [CrossRef]
- Michelon, N.; Pennisi, G.; Myint, N.O.; Orsini, F.; Gianquinto, G. Strategies for improved Water Use Efficiency (WUE) of field-grown lettuce (Lactuca sativa L.) under a semi-arid climate. Agronomy 2020, 10, 668. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Schull, M.; Turral, H. Ganges and Indus river basin land use/land cover (LULC) and irrigated area mapping using continuous streams of MODIS data. Remote Sens. Environ. 2005, 95, 317–341. [Google Scholar] [CrossRef]
- Toureiro, C.; Serralheiro, R.; Shahidian, S.; Sousa, A. Irrigation management with remote sensing: Evaluating irrigation requirement for maize under Mediterranean climate condition. Agric. Water Manag. 2017, 184, 211–220. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.J.; Baghdadi, N.; Segui, P.Q. Irrigation mapping using Sentinel-1 time series at field scale. Remote Sens. 2018, 10, 1495. [Google Scholar] [CrossRef]
- Jalilvand, E.; Tajrishy, M.; Hashemi, S.A.G.Z.; Brocca, L. Quantification of irrigation water using remote sensing of soil moisture in a semi-arid region. Remote Sens. Environ. 2019, 231, 111226. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.-J.; Torres-Sánchez, J.; Clavero-Rumbao, I.; García-Ferrer, A.; Peña, J.-M.; Borra-Serrano, I.; López-Granados, F. Assessing Optimal Flight Parameters for Generating Accurate Multispectral Orthomosaicks by UAV to Support Site-Specific Crop Management. Remote Sens. 2015, 7, 12793–12814. [Google Scholar] [CrossRef]
- Pageot, Y.; Baup, F.; Inglada, J.; Baghdadi, N.; Demarez, V. Detection of Irrigated and Rainfed Crops in Temperate Areas Using Sentinel-1 and Sentinel-2 Time Series. Remote Sens. 2020, 12, 3044. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Thenkabail, P.S.; Gumma, M.K.; Biradar, C.; Dheeravath, V.; Noojipady, P.; Yuanjie, L. Influence of resolution in irrigated area mapping and area estimation. Photogramm. Eng. Remote Sens. 2009, 75, 1383–1395. [Google Scholar] [CrossRef]
- Matese, A.; Toscano, P.; Di Gennaro, S.F.; Genesio, L.; Vaccari, F.P.; Primicerio, J.; Belli, C.; Zaldei, A.; Bianconi, R.; Gioli, B. Intercomparison of UAV, aircraft and satellite remote sensing platforms for precision viticulture. Remote Sens. 2015, 7, 2971–2990. [Google Scholar] [CrossRef]
- Eastman, J.R.; Sangermano, F.; Machado, E.A.; Rogan, J.; Anyamba, A. Global trends in seasonality of Normalized Difference Vegetation Index (NDVI), 1982–2011. Remote Sens. 2013, 5, 4799–4818. [Google Scholar] [CrossRef]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and Narrowband Multispectral Remote Sensing for Vegetation Monitoring from an Unmanned Aerial Vehicle Improved Evapotranspiration using Unmanned Aerial Vehicles View project High throughput and remote trait measurement View project Thermal and Nar. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Berra, E.F.; Gaulton, R.; Barr, S. Assessing spring phenology of a temperate woodland: A multiscale comparison of ground, unmanned aerial vehicle and Landsat satellite observations. Remote Sens. Environ. 2019, 223, 229–242. [Google Scholar] [CrossRef]
- Jay, S.; Baret, F.; Dutartre, D.; Malatesta, G.; Héno, S.; Comar, A.; Weiss, M.; Maupas, F. Exploiting the centimeter resolution of UAV multispectral imagery to improve remote-sensing estimates of canopy structure and biochemistry in sugar beet crops. Remote Sens. Environ. 2019, 231, 110898. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Nhamo, L.; van Dijk, R.; Magidi, J.; Wiberg, D.; Tshikolomo, K. Improving the accuracy of remotely sensed irrigated areas using post-classification enhancement through UAV capability. Remote Sens. 2018, 10, 712. [Google Scholar] [CrossRef]
- Qin, J.; Chao, K.; Kim, M.S.; Lu, R.; Burks, T.F. Hyperspectral and multispectral imaging for evaluating food safety and quality. J. Food Eng. 2013, 118, 157–171. [Google Scholar] [CrossRef]
- Park, B.; Lu, R. (Eds.) Hyperspectral Imaging Technology in Food and Agriculture; Springer US: New York, NY, USA, 2015; ISBN 9781493928354. [Google Scholar]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Yu, F.H.; Xu, T.Y.; Du, W.; Ma, H.; Zhang, G.S.; Chen, C.L. Radiative transfer models (RTMs) for field phenotyping inversion of rice based on UAV hyperspectral remote sensing. Int. J. Agric. Biol. Eng. 2017, 10, 150–157. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Li, C.; Li, Z.; Wang, Y.; Feng, H.; Xu, B. Estimation of Winter Wheat Above-Ground Biomass Using Unmanned Aerial Vehicle-Based Snapshot Hyperspectral Sensor and Crop Height Improved Models. Remote Sens. 2017, 9, 708. [Google Scholar] [CrossRef]
- Akhtman, Y.; Golubeva, E.I.; Tutubalina, O.V.; Zimin, M. Application of hyperspectural images and ground data for precision farming. Geogr. Environ. Sustain. 2017, 10, 117–128. [Google Scholar] [CrossRef]
- Bauer, M.E.; Daughtry, C.S.T.; Vanderbilt, V.C. Spectral-agronomic relationships of corn, soybean and wheat canopies. In Proceedings of the Signatures Spectrales D’objets En Teledetection, Avignon, France, 18–22 January 1981; pp. 261–272. [Google Scholar]
- Bohnenkamp, D.; Behmann, J.; Mahlein, A.K. In-field detection of Yellow Rust in Wheat on the Ground Canopy and UAV Scale. Remote Sens. 2019, 11, 2495. [Google Scholar] [CrossRef]
- Scherrer, B.; Sheppard, J.; Jha, P.; Shaw, J.A. Hyperspectral imaging and neural networks to classify herbicide-resistant weeds. J. Appl. Remote Sens. 2019, 13, 044516. [Google Scholar] [CrossRef]
- Rinaldi, M.; Castrignanò, A.; De Benedetto, D.; Sollitto, D.; Ruggieri, S.; Garofalo, P.; Santoro, F.; Figorito, B.; Gualano, S.; Tamborrino, R. Discrimination of tomato plants under different irrigation regimes: Analysis of hyperspectral sensor data. Environmetrics 2015, 26, 77–88. [Google Scholar] [CrossRef]
- Renzullo, L.J.; Blanchfield, A.L.; Powell, K.S. A method of wavelength selection and spectral discrimination of hyperspectral reflectance spectrometry. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1986–1994. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Enclona, E.A.; Ashton, M.S.; Van Der Meer, B. Accuracy assessments of hyperspectral waveband performance for vegetation analysis applications. Remote Sens. Environ. 2004, 91, 354–376. [Google Scholar] [CrossRef]
- Becker, B.L.; Lusch, D.P.; Qi, J. Identifying optimal spectral bands from in situ measurements of Great Lakes coastal wetlands using second-derivative analysis. Remote Sens. Environ. 2005, 97, 238–248. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Biging, G.S.; Larrieu, M.R. Extraction of red edge optical parameters from hyperion data for estimation of forest leaf area index. IEEE Trans. Geosci. Remote Sens. 2003, 41, 916–921. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.K.; Abkar, A.A. Leaf Area Index derivation from hyperspectral vegetation indicesand the red edge position. Int. J. Remote Sens. 2009, 30, 6199–6218. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Farrell, M.D.; Mersereau, R.M. On the impact of PCA dimension reduction for hyperspectral detection of difficult targets. IEEE Geosci. Remote Sens. Lett. 2005, 2, 192–195. [Google Scholar] [CrossRef]
- Koonsanit, K.; Jaruskulchai, C.; Eiumnoh, A. Band Selection for Dimension Reduction in Hyper Spectral Image Using Integrated InformationGain and Principal Components Analysis Technique. Int. J. Mach. Learn. Comput. 2012, 2, 248–251. [Google Scholar] [CrossRef]
- Burger, J.; Gowen, A. Data handling in hyperspectral image analysis. Chemom. Intell. Lab. Syst. 2011, 108, 13–22. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W.; Zhang, B. Optimized kernel minimum noise fraction transformation for hyperspectral image classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef]
- Menon, V.; Du, Q.; Fowler, J.E. Fast SVD with Random Hadamard Projection for Hyperspectral Dimensionality Reduction. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1275–1279. [Google Scholar] [CrossRef]
- Fordellone, M.; Bellincontro, A.; Mencarelli, F. Partial least squares discriminant analysis: A dimensionality reduction method to classify hyperspectral data. Stat. Appl. Ital. J. Appl. Stat. 2018, 31, 181–200. [Google Scholar] [CrossRef]
- Krishnan, A.; Williams, L.J.; McIntosh, A.R.; Abdi, H. Partial Least Squares (PLS) methods for neuroimaging: A tutorial and review. Neuroimage 2011, 56, 455–475. [Google Scholar] [CrossRef]
- Ray, S.S.; Das, G.; Singh, J.P.; Panigrahy, S. Evaluation of hyperspectral indices for LAI estimation and discrimination of potato crop under different irrigation treatments. Int. J. Remote Sens. 2006, 27, 5373–5387. [Google Scholar] [CrossRef]
- Mehmood, T.; Sæbø, S.; Liland, K.H. Comparison of variable selection methods in partial least squares regression. J. Chemom. 2020, 34. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). WIREs Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Lu, B.; He, Y. Evaluating empirical regression, machine learning, and radiative transfer modelling for estimating vegetation chlorophyll content using bi-seasonal hyperspectral images. Remote Sens. 2019, 11, 1979. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Mariotto, I.; Gumma, M.K.; Middleton, E.M.; Landis, D.R.; Huemmrich, K.F. Selection of hyperspectral narrowbands (hnbs) and composition of hyperspectral twoband vegetation indices (HVIS) for biophysical characterization and discrimination of crop types using field reflectance and hyperion/EO-1 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 427–439. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Thenkabail, P.; Lyon, J. (Eds.) Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Durif, G.; Modolo, L.; Michaelsson, J.; Mold, J.E.; Lambert-Lacroix, S.; Picard, F. High dimensional classification with combined adaptive sparse PLS and logistic regression. Bioinformatics 2018, 34, 485–493. [Google Scholar] [CrossRef]
- Deb, D.; Mackey, D.; Opiyo, S.O.; McDowell, J.M. Application of alignment-free bioinformatics methods to identify an oomycete protein with structural and functional similarity to the bacterial AvrE effector protein. PLoS ONE 2018, 13, 1–19. [Google Scholar] [CrossRef]
- Sampaio, P.S.; Soares, A.; Castanho, A.; Almeida, A.S.; Oliveira, J.; Brites, C. Optimization of rice amylose determination by NIR-spectroscopy using PLS chemometrics algorithms. Food Chem. 2018, 242, 196–204. [Google Scholar] [CrossRef]
- Li, J.; Tong, Y.; Guan, L.; Wu, S.; Li, D. Optimization of COD determination by UV–vis spectroscopy using PLS chemometrics algorithms. Optik 2018, 174, 591–599. [Google Scholar] [CrossRef]
- Luedeling, E.; Gassner, A. Partial Least Squares Regression for analyzing walnut phenology in California. Agric. For. Meteorol. 2012, 158–159, 43–52. [Google Scholar] [CrossRef]
- Song, S.; Gong, W.; Zhu, B.; Huang, X. Wavelength selection and spectral discrimination for paddy rice, with laboratory measurements of hyperspectral leaf reflectance Shalei. ISPRS J. Photogramm. Remote Sens. 2011, 66, 672–682. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Yu, X.; Wang, Y.; Deng, S.; Gao, J.-M. Rapid Determination of Lycium Barbarum Polysaccharide with Effective Wavelength Selection Using Near-Infrared Diffuse Reflectance Spectroscopy. Food Anal. Methods 2016, 9, 131–138. [Google Scholar] [CrossRef]
- Chen, H.; Xia, Z. Determination of total flavonoids in propolis based on NIR spectroscopy technology. Chin. J. Pharm. Anal. 2014, 34, 1868–1873. [Google Scholar]
- Eriksson, I.; Johansson, E.; Kettaneh-Wold, N.; Wold, S. Multi- and Megavariate Data Analysis. Principles and Applications; MKS Umetrics: Malmö, Sweden, 2002; Volume 16. [Google Scholar]
- Ding, X.-B.; Zhang, C.; Liu, F.; Song, X.L.; Kong, W.W.; He, Y. Determination of soluble solid content in strawberry using hyperspectral imaging combined with feature extraction methods. Spectroscopy Spectr. Anal. 2015, 35, 1020–1024. [Google Scholar]
- Pan, L.; Lu, R.; Zhu, Q.; Tu, K.; Cen, H. Predict compositions and mechanical properties of sugar beet using hyperspectral scattering. Food Bioprocess Technol. 2016, 9, 1177–1186. [Google Scholar] [CrossRef]
- Guzmán, E.; Baeten, V.; Pierna, J.A.F.; García-Mesa, J.A. Application of low-resolution Raman spectroscopy for the analysis of oxidized olive oil. Food Control. 2011, 22, 2036–2040. [Google Scholar] [CrossRef]
- Li, H.D.; Zeng, M.M.; Tan, B.-B.; Liang, Y.Z.; Xu, Q.S.; Cao, D.S. Recipe for revealing informative metabolites based on model population analysis. Metabolomics 2010, 6, 353–361. [Google Scholar] [CrossRef]
- Pan, T.; Chen, W.; Chen, Z.; Xie, J. Wavelength selection for NIR spectroscopic analysis of chemical oxygen demand based on different partial least squares models. Key Eng. Mater. 2011, 480–481, 393–396. [Google Scholar] [CrossRef]
- Zou, X.; Zhao, J.; Li, Y. Selection of the efficient wavelength regions in FT-NIR spectroscopy for determination of SSC of “Fuji” apple based on BiPLS and FiPLS models. Vib. Spectrosc. 2007, 44, 220–227. [Google Scholar] [CrossRef]
- Yang, Q.; Zhu, G.; Ren, P.; Long, S.; Yang, J. Wavelength selection for NIR spectroscopic analysis of chemical oxygen demand based on different partial least squares models. J. Anal. Sci. 2016, 32, 485–489. [Google Scholar]
- Fan, S.; Zhang, B.; Li, J.; Huang, W.; Wang, C. Effect of spectrum measurement position variation on the robustness of NIR spectroscopy models for soluble solids content of apple. Biosyst. Eng. 2016, 143, 9–19. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Lê Cao, K.A.; Rossouw, D.; Robert-Granié, C.; Besse, P. A sparse PLS for variable selection when integrating omics data. Stat. Appl. Genet. Mol. Biol. 2008, 7. [Google Scholar] [CrossRef] [PubMed]
- Bax, E.; Weng, L.; Tian, X. Speculate-correct error bounds for k-nearest neighbor classifiers. Mach. Learn. 2019, 108, 2087–2111. [Google Scholar] [CrossRef]
- Grove, A.J. General Convergence Results for Linear Discriminant Updates. Mach. Learn. 2001, 43, 173–210. [Google Scholar] [CrossRef]
- AbuZeina, D.; Al-Anzi, F.S. Employing fisher discriminant analysis for Arabic text classification. Comput. Electr. Eng. 2018, 66, 474–486. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Suarez, L.A.; Apan, A.; Werth, J. Detection of phenoxy herbicide dosage in cotton crops through the analysis of hyperspectral data. Int. J. Remote Sens. 2017, 38, 6528–6553. [Google Scholar] [CrossRef]
- Zhou, Q.; Huang, W.; Fan, S.; Zhao, F.; Liang, D.; Tian, X. Non-destructive discrimination of the variety of sweet maize seeds based on hyperspectral image coupled with wavelength selection algorithm. Infrared Phys. Technol. 2020, 109, 103418. [Google Scholar] [CrossRef]
- Xia, Z.; Zhang, C.; Weng, H.; Nie, P.; He, Y. Sensitive Wavelengths Selection in Identification of Ophiopogon japonicus Based on Near-Infrared Hyperspectral Imaging Technology. Int. J. Anal. Chem. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from Internet photo collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; de Castro, A.I.; Torres-Sánchez, J.; Triviño-Tarradas, P.; Jiménez-Brenes, F.M.; García-Ferrer, A.; López-Granados, F. Classification of 3D point clouds using color vegetation indices for precision viticulture and digitizing applications. Remote Sens. 2020, 12, 317. [Google Scholar] [CrossRef]
- Mesas-carrascosa, F.J.; Rumbao, I.C.; Alberto, J.; Berrocal, B.; Porras, A.G. Positional Quality Assessment of Orthophotos Obtained from Sensors Onboard Multi-Rotor UAV Platforms. Sensors 2014, 14, 22394–22407. [Google Scholar] [CrossRef] [PubMed]
- Barreto, M.A.P.; Johansen, K.; Angel, Y.; McCabe, M.F. Radiometric assessment of a UAV-based push-broom hyperspectral camera. Sensors 2019, 19, 4699. [Google Scholar] [CrossRef] [PubMed]
- van Zyl, J.J. The Shuttle Radar Topography Mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001, 48, 559–565. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L. The Python Language Reference; Python Software Foundation: Scotts Valley, CA, USA, 2011; p. 109. [Google Scholar]
- Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of variable selection methods for random forests and omics data sets. Brief. Bioinform. 2019, 20, 492–503. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Jain, A. A Complete Tutorial on Ridge and Lasso Regression in Python. Available online: https://www.analyticsvidhya.com/blog/2016/01/complete-tutorial-ridge-lasso-regression-python/ (accessed on 5 August 2020).
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Alba-Fernández, M.V.; Ariza-López, F.J.; Rodríguez-Avi, J.; García-Balboa, J.L. Statistical methods for thematic-accuracy quality control based on an accurate reference sample. Remote Sens. 2020, 12, 816. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2018. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R; RStudio: Boston, MA, USA, 2017. [Google Scholar]
- Mevik, B.H.; Wehrens, R. The pls package: Principal component and partial least squares regression in R. J. Stat. Softw. 2007, 18, 1–23. [Google Scholar] [CrossRef]
- Northrop, P.J.; Attalides, N.; Jonathan, P. Cross-validatory extreme value threshold selection and uncertainty with application to ocean storm severity. J. R. Stat. Soc. Ser. C Appl. Stat. 2017, 66, 93–120. [Google Scholar] [CrossRef]
- Kucheryavskiy, S. Mdatools—R package for chemometrics. Chemom. Intell. Lab. Syst. 2020, 198. [Google Scholar] [CrossRef]
- Li, H.D.; Xu, Q.S.; Liang, Y.Z. LibPLS: An integrated library for partial least squares regression and linear discriminant analysis. Chemom. Intell. Lab. Syst. 2018, 176, 34–43. [Google Scholar] [CrossRef]
- Chun, H.; Keleş, S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 3–25. [Google Scholar] [CrossRef]
- Friedman, J.; Trevor, H.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Calderón, R.; Navas-Cortés, J.A.; Lucena, C.; Zarco-Tejada, P.J. High-resolution airborne hyperspectral and thermal imagery for early detection of Verticillium wilt of olive using fluorescence, temperature and narrow-band spectral indices. Remote Sens. Environ. 2013, 139, 231–245. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Camino, C.; Beck, P.S.A.; Calderon, R.; Hornero, A.; Hernández-Clemente, R.; Kattenborn, T.; Montes-Borrego, M.; Susca, L.; Morelli, M.; et al. Previsual symptoms of Xylella fastidiosa infection revealed in spectral plant-trait alterations. Nat. Plants 2018, 4, 432–439. [Google Scholar] [CrossRef]
- Starzacher, A.; Rinner, B. Evaluating KNN, LDA and QDA classification for embedded online feature fusion. In Proceedings of the 2008 International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Sydney, NSW, Australia, 15–18 December 2008; IEEE: Piscataway Township, NJ, USA, 2008; pp. 85–90. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |




| Category | PLS Method | Reference |
|---|---|---|
| Filter | Loading Weights (LW-PLS) | [68] |
| Regression Coefficient (RC-PLS) | [69] | |
| Variable Importance in Projection (VIP-PLS) | [70] | |
| Wrapper | Genetic Algorithm (GA-PLS) | [71] |
| Uninformative Variable Elimination (UVE-PLS) | [72] | |
| Backward Variable Elimination (BVE-PLS) | [73] | |
| Subwindow Permutation Analysis (SwPA-PLS) | [74] | |
| Iterative Predictive Weighting (IPW-PLS) | [75] | |
| Regularized Elimination Procedure (REP-PLS) | [67] | |
| Backward Interval (BiPLS) | [76] | |
| Forward Interval (FiPLS) | [77] | |
| Competitive Adaptive Reweighted Sampling (CARS-PLS) | [78] | |
| Embedded | Sparse (S-PLS) | [80] |
| Sub-Surface Irrigation | Surface Irrigation | |
|---|---|---|
| Calibration set | 160 | 150 |
| Prediction set | 53 | 50 |
| Total | 213 | 200 |
| PLS Method | R Packages | Reference |
|---|---|---|
| Loading Weights (LW-PLS) | plsVarSel, pls | [67,101] |
| Regression Coefficient (RC-PLS) | plsVarSel, pls, threshr | [67,101,102] |
| Variable Importance in Projection (VIP-PLS) | plsVarSel, pls | [67,101] |
| Genetic Algorithm (GA-PLS) | plsVarSel | [67] |
| Uninformative Variable Elimination (UVE-PLS) | plsVarSel | [67] |
| Backward Variable Elimination (BVE-PLS) | plsVarSel | [67] |
| Subwindow Permutation Analysis (SwPA-PLS) | plsVarSel | [67] |
| Iterative Predictive Weighting (IPW-PLS) | plsVarSel | [67] |
| Regularized Elimination Procedure (REP-PLS) | plsVarSel | [67] |
| Backward Interval (BiPLS) | mdatools | [103] |
| Forward Interval (FiPLS) | mdatools | [103] |
| Competitive Adaptive Reweighted Sampling (CARS-PLS) | libPLSn | [104] |
| Sparse (S-PLS) | spls | [105] |
| Lasso | glmnet | [106] |
| Boruta | Boruta | [97] |
| Method | Number of Wavelengths | Wavelengths [nm] |
|---|---|---|
| LW-PLS | 5 | 882, 884, 890, 934, 942 |
| RC-PLS | 12 | 726, 728, 888, 904–908, 914, 920, 924, 928, 930–942 |
| VIP-PLS | 10 | 726, 888, 904, 906, 914, 924, 928, 936, 938, 942 |
| GA-PLS | 31 | 424, 428, 436, 442, 444, 458, 460, 522, 588, 612, 630, 640, 662, 698, 714, 716, 744, 758, 770, 780, 826, 846, 854, 860, 870, 878, 888, 912, 918, 920, 938 |
| UVE-PLS | 10 | 428, 696, 698, 700–704, 734, 792, 812, 856 |
| BVE-PLS | 69 | 686–734, 746, 776, 790, 840, 846, 848, 858, 860, 864–870, 880–890, 894–946 |
| SwPA-PLS | 77 | 410, 414, 418, 424, 436, 450, 466, 476, 490, 494, 496, 500, 506, 508, 518, 530–538, 542, 558, 562, 568, 576–580, 584, 588, 596, 612, 622–630, 640, 646, 648, 660, 668, 690, 702–706, 728, 738, 746, 752, 756, 768, 774, 782, 786, 804, 812, 822, 828, 836, 838, 848, 850, 856, 858, 860, 862, 874, 878, 882, 888, 896, 900, 904, 910, 914, 926, 936, 940 |
| IPW-PLS | 12 | 710, 790, 832, 846, 888, 914, 920–924, 936–940 |
| REP-PLS | 31 | 726, 728, 882, 884, 888, 890, 894, 898, 902–946 |
| BiPLS | 265 | 400–604, 624–946 |
| FiPLS | 54 | 660–676, 696–730, 768–784, 858–874, 912–928 |
| CARS | 2 | 436, 790 |
| S-PLS | 192 | 560–714, 720–946 |
| Lasso | 17 | 404, 662, 698, 704, 788, 844, 846, 858, 886, 904, 912, 918–922, 934–938 |
| Boruta | 29 | 430, 456, 464, 474, 636, 638, 644, 646, 650–660, 698, 774, 776, 780, 792, 794, 810, 816, 818, 838, 866, 868, 914, 930, 936 |
| All-together | 18 | 790, 814, 846, 860, 866, 868, 870, 882, 888, 892, 898, 902, 904, 920, 928, 934, 936, 940 |
| LDA | KNN | |||||||
|---|---|---|---|---|---|---|---|---|
| Method | OA (%) | A SDI (%) | A DI (%) | E | OA (%) | A SDI (%) | A DI (%) | E |
| All bands | 65.0 | 62.5 | 68.7 | - | 68.1 | 64.6 | 73.6 | - |
| LW-PLS | 62.5 | 57.5 | 70.7 | −2.9 | 54.8 | 51.7 | 61.1 | −13.1 |
| RC-PLS | 81.3 | 80.7 | 81.1 | 15.3 | 68.3 | 64.4 | 73.3 | 0.2 |
| VIP-PLS | 72.2 | 69.5 | 73.3 | 6.7 | 60.6 | 55.1 | 71.9 | −7.2 |
| GA-PLS | 85.2 | 83.6 | 87.6 | 17.7 | 69.2 | 65.4 | 73.0 | 1.0 |
| UVE-PLS | 66.5 | 61.9 | 72.8 | 1.0 | 63.5 | 59.9 | 70.1 | −4.4 |
| BVE-PLS | 79.0 | 78.5 | 79.5 | 10.5 | 65.4 | 61.7 | 71.1 | −2.0 |
| SwPA-PLS | 76.3 | 76.2 | 76.4 | 7.9 | 68.3 | 66.6 | 70.0 | 0.1 |
| IPW-PLS | 75.5 | 71.5 | 79.5 | 9.6 | 71.2 | 67.4 | 75.4 | 3.0 |
| REP-PLS | 69.3 | 67.9 | 71.3 | 3.5 | 59.6 | 54.5 | 71.1 | −7.5 |
| BiPLS | 70.2 | 68.3 | 72.1 | 0.2 | 69.2 | 64.2 | 75.2 | 0.0 |
| FiPLS | 80.1 | 81.6 | 79.0 | 12.0 | 66.3 | 63.5 | 70.1 | −1.4 |
| CARS | 66.0 | 60.1 | 76.1 | 1.0 | 63.5 | 60.1 | 67.9 | −4.6 |
| S-PLS | 75.3 | 75.3 | 75.3 | 3.0 | 69.2 | 66.2 | 72.2 | 0.5 |
| Lasso | 84.0 | 86.4 | 82.3 | 17.8 | 71.2 | 72.3 | 72.2 | 2.9 |
| Boruta | 78.0 | 76.4 | 80.2 | 11.6 | 74.0 | 73.5 | 75.6 | 5.3 |
| All-together | 82.5 | 78.6 | 85.3 | 15.9 | 69.2 | 65.3 | 74.9 | 1.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos-Rufo, A.; Mesas-Carrascosa, F.-J.; García-Ferrer, A.; Meroño-Larriva, J.E. Wavelength Selection Method Based on Partial Least Square from Hyperspectral Unmanned Aerial Vehicle Orthomosaic of Irrigated Olive Orchards. Remote Sens. 2020, 12, 3426. https://doi.org/10.3390/rs12203426
Santos-Rufo A, Mesas-Carrascosa F-J, García-Ferrer A, Meroño-Larriva JE. Wavelength Selection Method Based on Partial Least Square from Hyperspectral Unmanned Aerial Vehicle Orthomosaic of Irrigated Olive Orchards. Remote Sensing. 2020; 12(20):3426. https://doi.org/10.3390/rs12203426
Chicago/Turabian StyleSantos-Rufo, Antonio, Francisco-Javier Mesas-Carrascosa, Alfonso García-Ferrer, and Jose Emilio Meroño-Larriva. 2020. "Wavelength Selection Method Based on Partial Least Square from Hyperspectral Unmanned Aerial Vehicle Orthomosaic of Irrigated Olive Orchards" Remote Sensing 12, no. 20: 3426. https://doi.org/10.3390/rs12203426
APA StyleSantos-Rufo, A., Mesas-Carrascosa, F.-J., García-Ferrer, A., & Meroño-Larriva, J. E. (2020). Wavelength Selection Method Based on Partial Least Square from Hyperspectral Unmanned Aerial Vehicle Orthomosaic of Irrigated Olive Orchards. Remote Sensing, 12(20), 3426. https://doi.org/10.3390/rs12203426







