Bathymetric Inversion and Uncertainty Estimation from Synthetic Surf-Zone Imagery with Machine Learning
Abstract
1. Introduction
1.1. Physics-Based Bathymetric Inversion Methods
1.2. Machine Learning for Nearshore Bathymetry Inversion
1.3. Machine Learning Uncertainty
1.4. Objectives
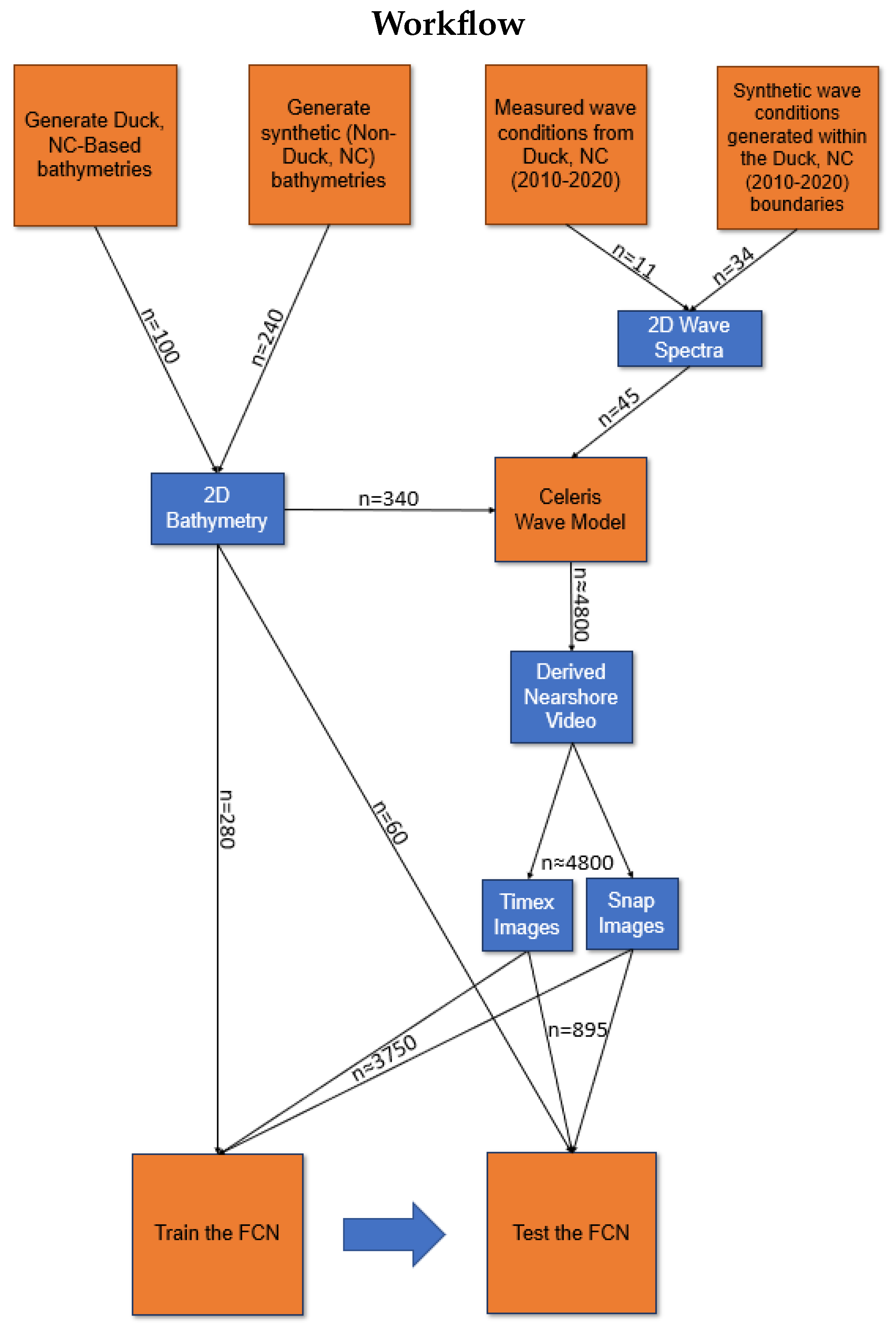
2. Methods
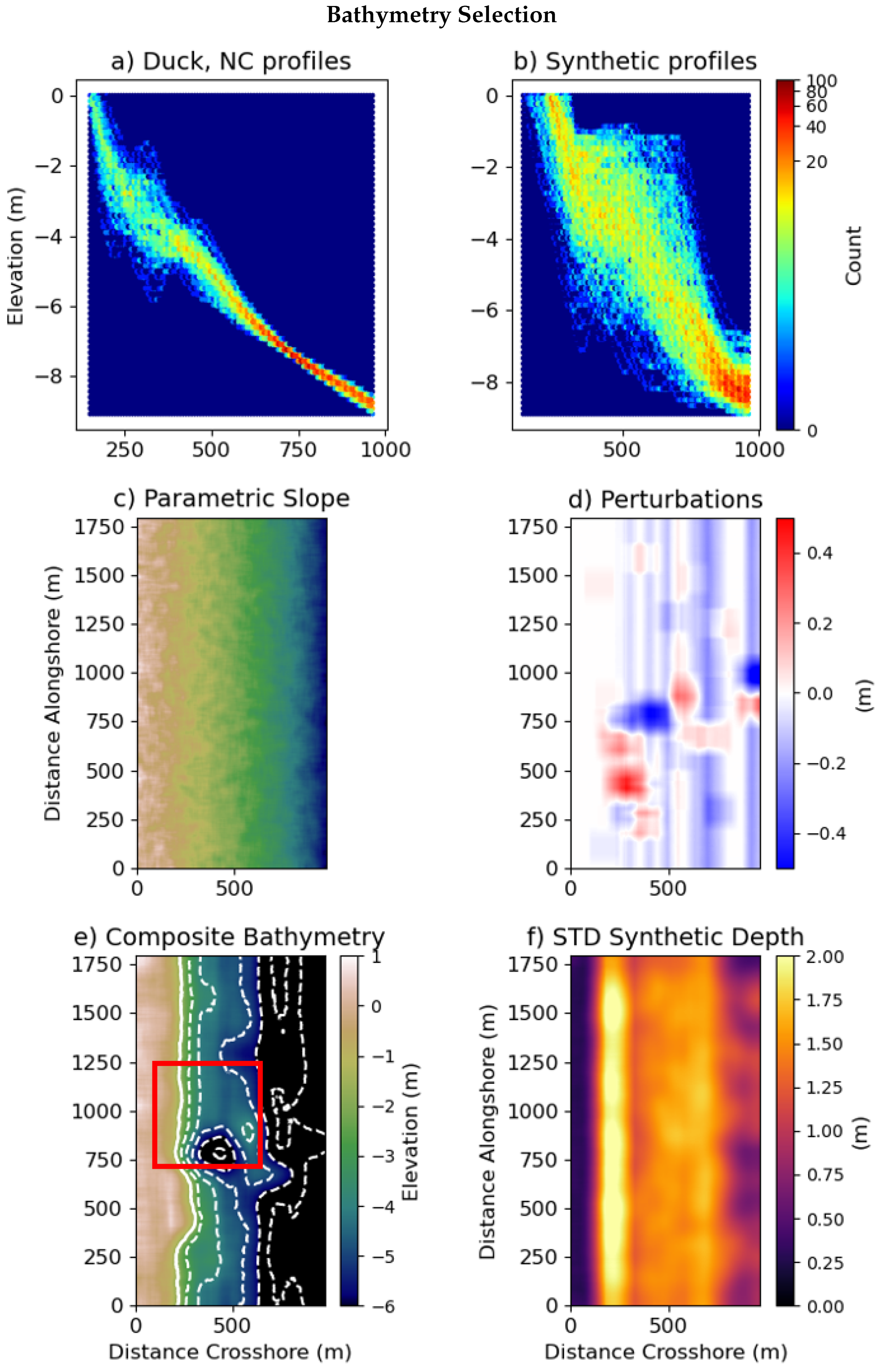
2.1. Synthetic Imagery Generation
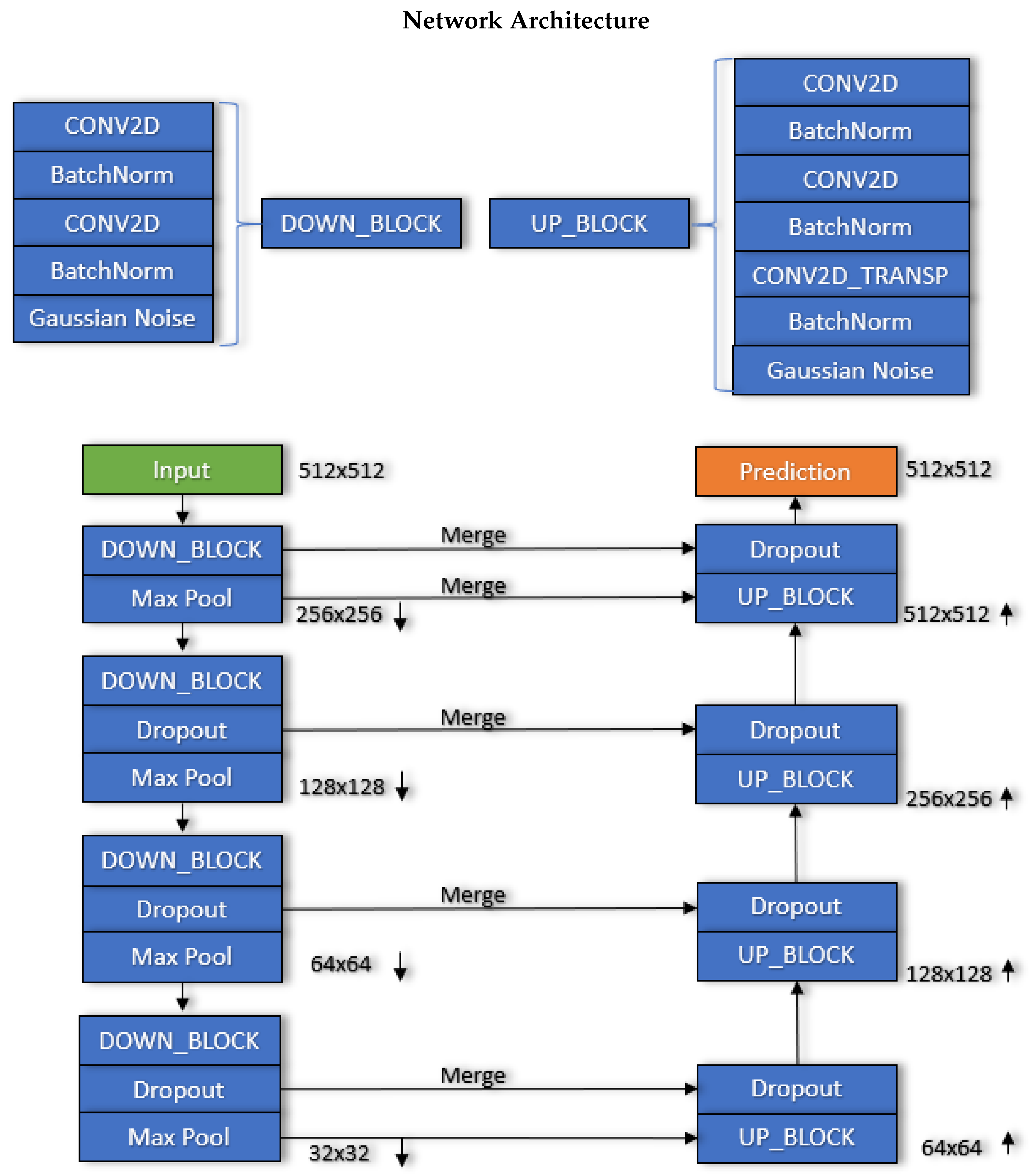
2.2. Network Architecture
2.3. FCNN Model Uncertainty
2.4. Training
3. Results
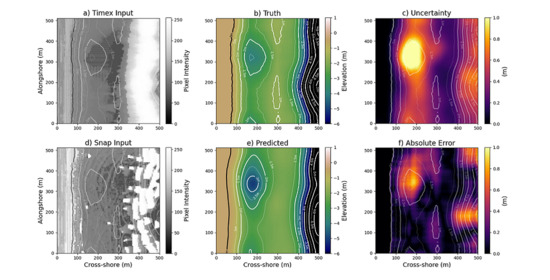
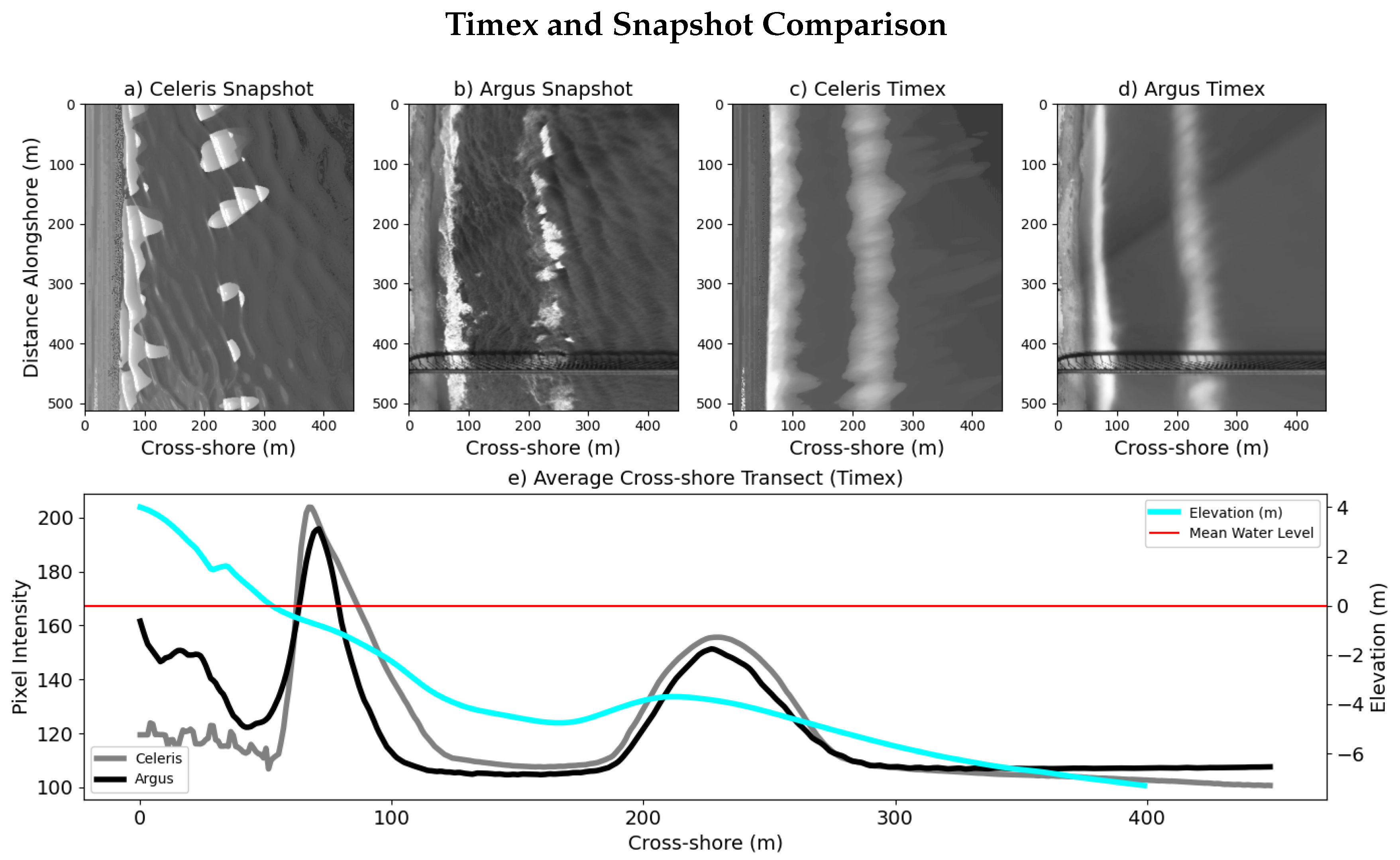
3.1. Input Feature Comparison
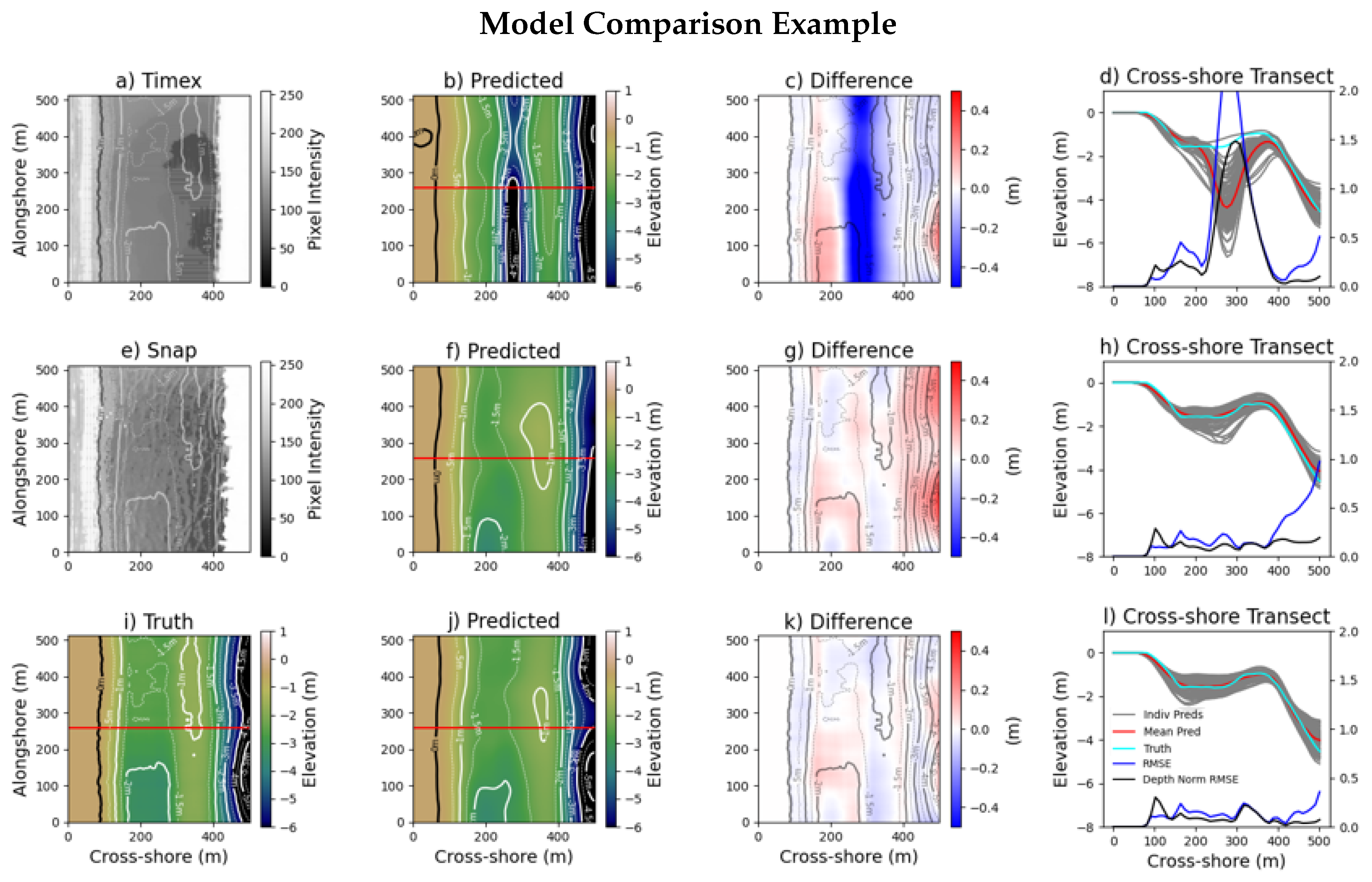
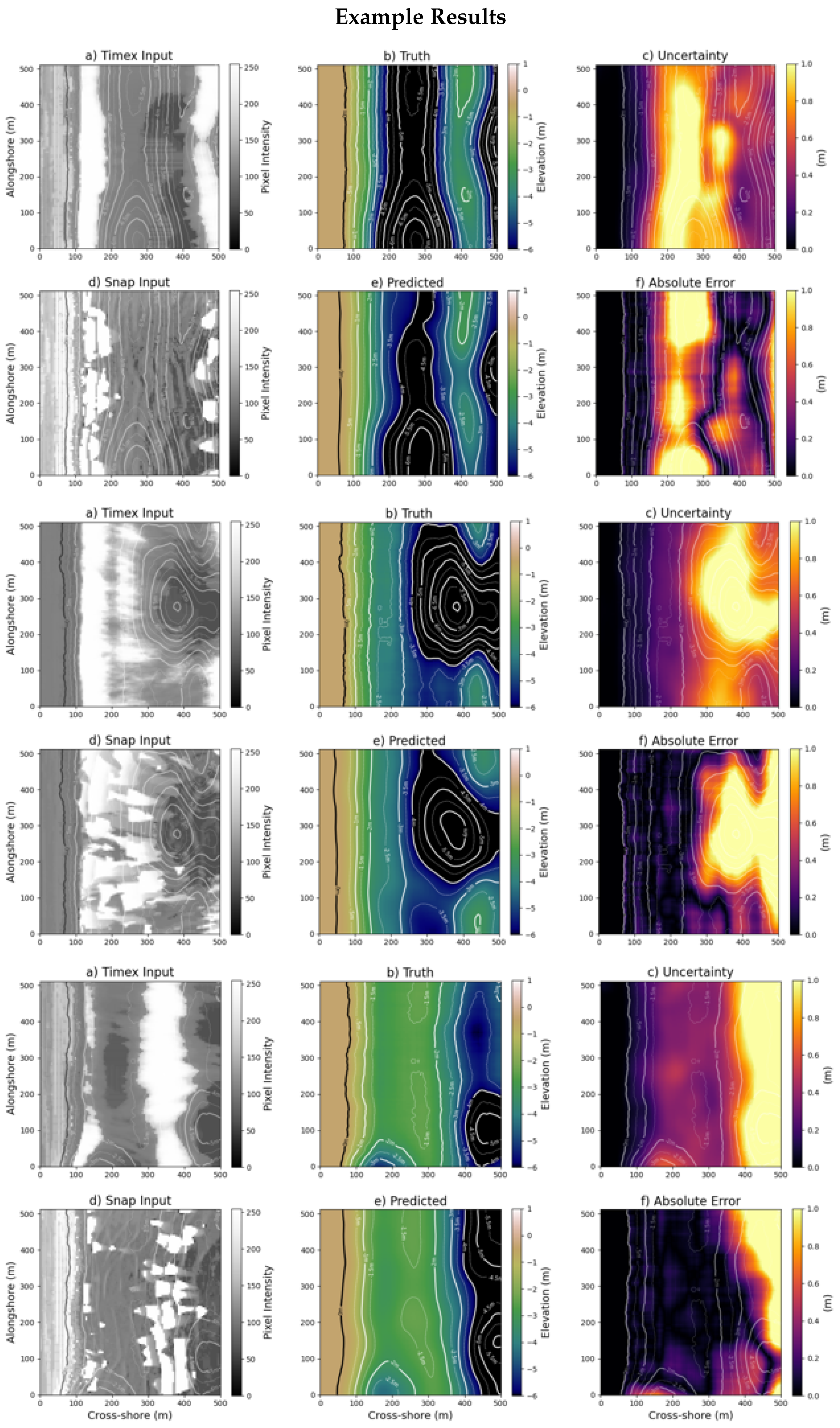
3.2. Example Predictions
4. Discussion
4.1. Wave Conditions
4.2. Activation Maps
4.3. Uncertainty Measurements
4.4. Future Work
5. Conclusions
6. Source Code
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Birkemeier, W.A.; Mason, C. The CRAB: A unique nearshore surveying vehicle. J. Surv. Eng. 1984, 110, 1–7. [Google Scholar] [CrossRef]
- Dugan, J.P.; Vierra, K.C.; Morris, W.D.; Farruggia, G.J.; Campion, D.C.; Miller, H.C. Unique vehicles used for bathymetry surveys in exposed coastal regions. In Proceedings of the US Hydrographic Conference Society National Meeting, Mobile, AK, USA, 26–29 April 1999. Available online: https://rb.gy/bftf3f (accessed on 14 October 2020).
- Dugan, J.P.; Morris, W.D.; Vierra, K.C.; Piotrowski, C.C.; Farruggia, G.J.; Campion, D.C. Jetski-based nearshore bathymetric and current survey system. J. Coast. Res. 2001, 107, 900–908. [Google Scholar]
- Komar, P.D.; Gaughan, M.K. Airy wave theory and breaker height prediction. Coast. Eng. 1973, 405–418. [Google Scholar] [CrossRef]
- Sallenger, A.H., Jr.; Holman, R.A.; Birkemeier, W.A. Storm-induced response of a nearshore-bar system. Mar. Geol. 1985, 64, 237–257. [Google Scholar] [CrossRef]
- Fredsøe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport; World Scientific: Singapore, 1992; Volume 3. [Google Scholar]
- Trenhaile, A.S. Coastal Dynamics and Landforms; Oxford University Press on Demand: Oxford, UK, 1997. [Google Scholar]
- Jackson, D.W.T.; Cooper, J.A.G.; Del Rio, L. Geological control of beach morphodynamic state. Mar. Geol. 2005, 216, 297–314. [Google Scholar] [CrossRef]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Holland, K.T.; Lalejini, D.M.; Spansel, S.D.; Holman, R.A. Littoral environmental reconnaissance using tactical imagery from unmanned aircraft systems. In Ocean Sensing and Monitoring II; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7678, p. 767806. Available online: https://rb.gy/ejbbmg (accessed on 14 October 2020).
- Holman, R.A.; Brodie, K.L.; Spore, N.J. Surf zone characterization using a small quadcopter: Technical issues and procedures. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2017–2027. [Google Scholar] [CrossRef]
- Holland, K.T.; Palmsten, M.L. Remote sensing applications and bathymetric mapping in coastal environments. Adv. Coast. Hydraul. 2018, 35, 375–411. [Google Scholar]
- Brodie, K.L.; Bruder, B.L.; Slocum, R.K.; Spore, N.J. Simultaneous Mapping of Coastal Topography and Bathymetry from a Lightweight Multicamera UAS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6844–6864. [Google Scholar] [CrossRef]
- Almar, R.; Bergsma, E.W.J.; Maisongrande, P.; de Almeida, L.P.M. Wave-derived coastal bathymetry from satellite video imagery: A showcase with Pleiades persistent mode. Remote Sens. Environ. 2019, 231, 111263. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R.; Maisongrande, P. Radon-Augmented Sentinel-2 Satellite Imagery to Derive Wave-Patterns and Regional Bathymetry. Remote Sens. 2019, 11, 1918. [Google Scholar] [CrossRef]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Sabour, S.; Brown, S.; Nicholls, R.; Haigh, I.; Luijendijk, A. Multi-decadal shoreline change in coastal Natural World Heritage Sites—A global assessment. Environ. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-resolution maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Jagalingam, P.; Akshaya, B.J.; Hegde, A.V. Bathymetry mapping using Landsat 8 satellite imagery. Procedia Eng. 2015, 116, 560–566. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Jay, S.; Guillaume, M. Regularized estimation of bathymetry and water quality using hyperspectral remote sensing. Int. J. Remote Sens. 2016, 37, 263–289. [Google Scholar] [CrossRef]
- Lin, Y.C.; Cheng, Y.T.; Zhou, T.; Ravi, R.; Hasheminasab, S.M.; Flatt, J.E.; Troy, C.; Habib, A. Evaluation of UAV LiDAR for mapping coastal environments. Remote Sens. 2019, 11, 2893. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Paavel, B.; Kutser, T. How much benthic information can be retrieved with hyperspectral sensor from the optically complex coastal waters? J. Appl. Remote Sens. 2020, 14, 16504. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. Ocean. 2000, 105, 22015–22033. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T.; Haller, M.C. Ocean wavenumber estimation from wave-resolving time series imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2644–2658. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. cBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. Ocean. 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Williams, W.W. The determination of gradients on enemy-held beaches. Geogr. J. 1947, 109, 76–90. [Google Scholar] [CrossRef]
- Lippmann, T.C.; Holman, R.A. Quantification of sand bar morphology: A video technique based on wave dissipation. J. Geophys. Res. Ocean. 1989, 94, 995–1011. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A.; Lippmann, T.C.; Stanley, J.; Plant, N. Practical use of video imagery in nearshore oceanographic field studies. IEEE J. Ocean. Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Aarninkhof, S.G.J.; Holman, R.A. Monitoring the nearshore with video. Backscatter 1999, 10, 8–11. [Google Scholar]
- Aarninkhof, S.G.J.; Turner, I.L.; Dronkers, T.D.T.; Caljouw, M.; Nipius, L. A video-based technique for mapping intertidal beach bathymetry. Coast. Eng. 2003, 49, 275–289. [Google Scholar] [CrossRef]
- Aarninkhof, S.G.J. Nearshore Bathymetry Derived from Video Imagery. Ph.D. Thesis, Delft University, Delft, The Netherlands, 2003. [Google Scholar]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Guedes, R.M.C.; Calliari, L.J.; Holland, K.T.; Plant, N.G.; Pereira, P.S.; Alves, F.N.A. Short-term sandbar variability based on video imagery: Comparison between Time–Average and Time–Variance techniques. Mar. Geol. 2011, 289, 122–134. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R. Video-based depth inversion techniques, a method comparison with synthetic cases. Coast. Eng. 2018, 138, 199–209. [Google Scholar] [CrossRef]
- Ghorbanidehno, H.; Lee, J.; Farthing, M.; Hesser, T.; Kitanidis, P.K.; Darve, E.F. Novel data assimilation algorithm for nearshore bathymetry. J. Atmos. Ocean. Technol. 2019, 36, 699–715. [Google Scholar] [CrossRef]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Wilson, G.W.; Özkan-Haller, H.T.; Holman, R.A. Data assimilation and bathymetric inversion in a two-dimensional horizontal surf zone model. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Wilson, G.W.; Özkan-Haller, H.T.; Holman, R.A.; Haller, M.C.; Honegger, D.A.; Chickadel, C.C. Surf zone bathymetry and circulation predictions via data assimilation of remote sensing observations. J. Geophys. Res. 2014, 119, 1993–2016. [Google Scholar] [CrossRef]
- Moghimi, S.; Özkan-Haller, H.T.; Wilson, G.W.; Kurapov, A. Data assimilation for bathymetry estimation at a tidal inlet. J. Atmos. Ocean. Technol. 2016, 33, 2145–2163. [Google Scholar] [CrossRef]
- Wilson, G.; Berezhnoy, S. Surfzone State Estimation, with Applications to Quadcopter-Based Remote Sensing Data. J. Atmos. Ocean. Technol. 2018, 35, 1881–1896. [Google Scholar] [CrossRef]
- Aarninkhof, S.G.J.; Ruessink, B.G.; Roelvink, J.A. Nearshore subtidal bathymetry from time-exposure video images. J. Geophys. Res. Ocean. 2005, 110. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Plant, N.; Cohen, A.; Roelvink, D.; Haller, M.C.; Catalán, P. Beach Wizard: Nearshore bathymetry estimation through assimilation of model computations and remote observations. Coast. Eng. 2008, 55, 1016–1027. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S.C.E. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef]
- Holland, T.K. Application of the linear dispersion relation with respect to depth inversion and remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2060–2072. [Google Scholar] [CrossRef]
- Catálan, P.A.; Haller, M.C. Remote sensing of breaking wave phase speeds with application to non-linear depth inversions. Coast. Eng. 2008, 55, 93–111. [Google Scholar] [CrossRef]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave celerity from video imaging: A new method. In Coastal Engineering 2008: (In 5 Volumes); World Scientific: Singapore, 2009; pp. 661–673. [Google Scholar]
- Haller, M.C.; Catalán, P.A. Remote sensing of wave roller lengths in the laboratory. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Kirby, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. FUNWAVE 1.0: Fully Nonlinear Boussinesq Wave Model-Documentation and User’s Manual; Research Report NO. CACR-98-06; University of Delaware: Newark, DE, USA, 1998. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In European Conference on Computer Vision; Springer: New York, NY, USA, 2006; pp. 430–443. [Google Scholar]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Tavakkol, S.; Lynett, P. Celeris: A GPU-accelerated open source software with a Boussinesq-type wave solver for real-time interactive simulation and visualization. Comput. Phys. Commun. 2017, 217, 117–127. [Google Scholar] [CrossRef]
- Saibaba, A.K.; Kitanidis, P.K. Fast computation of uncertainty quantification measures in the geostatistical approach to solve inverse problems. Adv. Water Resour. 2015, 82, 124–138. [Google Scholar] [CrossRef]
- Lee, J.; Yoon, H.; Kitanidis, P.K.; Werth, C.J.; Valocchi, A.J. Scalable subsurface inverse modeling of huge data sets with an application to tracer concentration breakthrough data from magnetic resonance imaging. Water Resour. Res. 2016, 52, 5213–5231. [Google Scholar] [CrossRef]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2002–2011. [Google Scholar]
- Dhamo, H.; Tateno, K.; Laina, I.; Navab, N.; Tombari, F. Peeking behind objects: Layered depth prediction from a single image. Pattern Recognit. Lett. 2019, 125, 333–340. [Google Scholar] [CrossRef]
- Eldesokey, A.; Felsberg, M.; Khan, F.S. Confidence propagation through cnns for guided sparse depth regression. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]
- Ghorbanidehno, H.; Lee, J.; Farthing, M.; Hesser, T.; Darve, E.F.; Kitanidis, P.K. Deep learning technique for fast inference of large-scale riverine bathymetry. Adv. Water Resour. 2020, 103715. [Google Scholar] [CrossRef]
- Stringari, C.E.; Harris, D.L.; Power, H.E. A novel machine learning algorithm for tracking remotely sensed waves in the surf zone. Coast. Eng. 2019, 147, 149–158. [Google Scholar] [CrossRef]
- Buscombe, D.; Carini, R.J.; Harrison, S.R.; Chickadel, C.C.; Warrick, J.A. Optical wave gauging using deep neural networks. Coast. Eng. 2020, 155, 103593. [Google Scholar] [CrossRef]
- Benshila, R.; Thoumyre, G.; Najar, M.A.; Abessolo, G.; Almar, R. A Deep Learning Approach for Estimation of the Nearshore Bathymetry A Deep Learning Approach for Estimation of the Nearshore. J. Coast. Res. 2020, 95, 1011–1015. [Google Scholar] [CrossRef]
- Kemker, R.; Luu, R.; Kanan, C. Low-Shot Learning for the Semantic Segmentation of Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6214–6223. [Google Scholar] [CrossRef]
- Kemker, R.; Salvaggio, C.; Kanan, C. Algorithms for semantic segmentation of multispectral remote sensing imagery using deep learning. ISPRS J. Photogramm. Remote Sens. 2018, 145, 60–70. [Google Scholar] [CrossRef]
- Chickadel, C.C. Remote Measurements of Waves and Currents over Complex Bathymetry. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2007. [Google Scholar]
- Splinter, K.D.; Holman, R.A. Bathymetry estimation from single-frame images of nearshore waves. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3151–3160. [Google Scholar] [CrossRef]
- Pitman, S.; Gallop, S.L.; Haigh, I.D.; Mahmoodi, S.; Masselink, G.; Ranasinghe, R. Synthetic Imagery for the Automated Detection of Rip Currents. J. Coast. Res. 2016, 75, 912–916. [Google Scholar] [CrossRef]
- Perugini, E.; Soldini, L.; Palmsten, M.L.; Calantoni, J.; Brocchini, M.C.E. Linear Depth Inversion Sensitivity to Wave Viewing Angle Using Synthetic Optical Video. Coast. Eng. 2019, 152, 103535. [Google Scholar] [CrossRef]
- Pereira, P.; Baptista, P.; Cunha, T.; Silva, P.A.; Romão, S.; Lafon, V. Estimation of the nearshore bathymetry from high temporal resolution Sentinel-1A C-band SAR data-A case study. Remote Sens. Environ. 2019, 223, 166–178. [Google Scholar] [CrossRef]
- Denker, J.S.; LeCun, Y. Transforming neural-net output levels to probability distributions. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1991; pp. 853–859. [Google Scholar]
- MacKay, D.J.C. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Graves, A. Practical variational inference for neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; pp. 2348–2356. [Google Scholar]
- Hron, J.; Matthews, A.G.d.G.; Ghahramani, Z. Variational Bayesian dropout: Pitfalls and fixes. arXiv 2018, arXiv:1807.01969. [Google Scholar]
- Pearce, T.; Zaki, M.; Brintrup, A.; Anastassacos, N.; Neely, A. Uncertainty in neural networks: Bayesian ensembling. arXiv 2018, arXiv:1810.05546. [Google Scholar]
- Teye, M.; Azizpour, H.; Smith, K. Bayesian uncertainty estimation for batch normalized deep networks. arXiv 2018, arXiv:1802.06455. [Google Scholar]
- Atanov, A.; Ashukha, A.; Molchanov, D.; Neklyudov, K.; Vetrov, D. Uncertainty estimation via stochastic batch normalization. In International Symposium on Neural Networks; Springer: New York, NY, USA, 2019; pp. 261–269. [Google Scholar]
- Kendall, A.; Badrinarayanan, V.; Cipolla, R. Bayesian segnet: Model uncertainty in deep convolutional encoder-decoder architectures for scene understanding. arXiv 2015, arXiv:1511.02680. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Gal, Y.; Hron, J.; Kendall, A. Concrete dropout. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3581–3590. [Google Scholar]
- Collins, A.; Brodie, K.L.; Bak, S.; Hesser, T.; Farthing, M.W.; Gamble, D.W.; Long, J.W. A 2D Fully Convolutional Neural Network for Nearshore And Surf-Zone Bathymetry Inversion from Synthetic Imagery of Surf-Zone using the Model Celeris. In Proceedings of the AAAI Spring Symposium: MLPS, Palo Alto, CA, USA, 23–25 March 2020. [Google Scholar]
- Brodie, K.L.; Collins, A.; Hesser, T.J.; Farthing, M.W.; Bak, A.S.; Lee, J.H. Augmenting wave-kinematics algorithms with machine learning to enable rapid littoral mapping and surf-zone state characterization from imagery. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications II. International Society for Optics and Photonics, San Francisco, CA, USA, 1–6 February 2020. [Google Scholar]
- Ayhan, M.S.; Berens, P. Test-time data augmentation for estimation of heteroscedastic aleatoric uncertainty in deep neural networks. In Proceedings of the 1st Conference on Medical Imaging with Deep Learning, Amsterdam, The Netherlands, 4–6 July 2018. [Google Scholar]
- Wang, C.; Principe, J.C. Training neural networks with additive noise in the desired signal. IEEE Trans. Neural Netw. 1999, 10, 1511–1517. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Holman, R.A.; Brodie, K.L.; Spore, N. Nearshore Measurements From a Small UAV. AGUOS 2016, 2016, 1067. [Google Scholar]
- Forte, M.F.; Birkemeier, W.A.; Mitchell, J.R. Nearshore Survey System Evaluation; Technical Report; ERDC-CHL. 2017. Available online: https://apps.dtic.mil/sti/citations/AD1045534 (accessed on 14 October 2020).
- Braud, I.; Obled, C. On the Use of Empirical Orthogonal Function (EOF) Analysis in the Simulation of Random Fields. Stoch. Hydrol. Hydraul. 1991, 5, 125–134. [Google Scholar]
- Hughes, S.A. The TMA Shallow-Water Spectrum Description and Applications. Technical Report; No. CERC-TR-84-7. 1984. Available online: https://erdc-library.erdc.dren.mil/jspui/handle/11681/12522 (accessed on 14 October 2020).
- Bouws, E.; Günther, H.; Rosenthal, W.; Vincent, C.L. Similarity of the wind wave spectrum in finite depth water: 1. Spectral form. J. Geophys. Res. Oceans 1985, 90, 975–986. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Holman, R.A.; Lalejini, D.M.; Edwards, K.; Veeramony, J. A parametric model for barred equilibrium beach profiles. Coast. Eng. 2014, 90, 85–94. [Google Scholar] [CrossRef]
- Holman, R.A.; Lalejini, D.M.; Holland, T. A parametric model for barred equilibrium beach profiles: Two-dimensional implementation. Coast. Eng. 2016, 117, 166–175. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: New York, NY, USA, 2015; pp. 234–241. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Mi, L.; Wang, H.; Tian, Y.; Shavit, N. Training-Free Uncertainty Estimation for Neural Networks. arXiv 2019, arXiv:1910.04858. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. Open Rev. 2016. Available online: https://openreview.net/forum?id=OM0jvwB8jIp57ZJjtNEZ (accessed on 14 October 2020).
- Dubost, F.; Adams, H.; Yilmaz, P.; Bortsova, G.; van Tulder, G.; Ikram, M.A.; Niessen, W.; Vernooij, M.; de Bruijne, M. Weakly Supervised Object Detection with 2D and 3D Regression Neural Networks. arXiv 2019, arXiv:1906.01891. [Google Scholar]
- Chen, L.; Chen, J.; Hajimirsadeghi, H.; Mori, G. Adapting Grad-CAM for embedding networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 2794–2803. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch. Open Rev. 2017. Available online: https://openreview.net/forum?id=BJJsrmfCZ (accessed on 14 October 2020).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A System for Large-Scale Machine Learning; OSDI: Boulder, CO, USA, 2016; Volume 16, pp. 265–283. [Google Scholar]
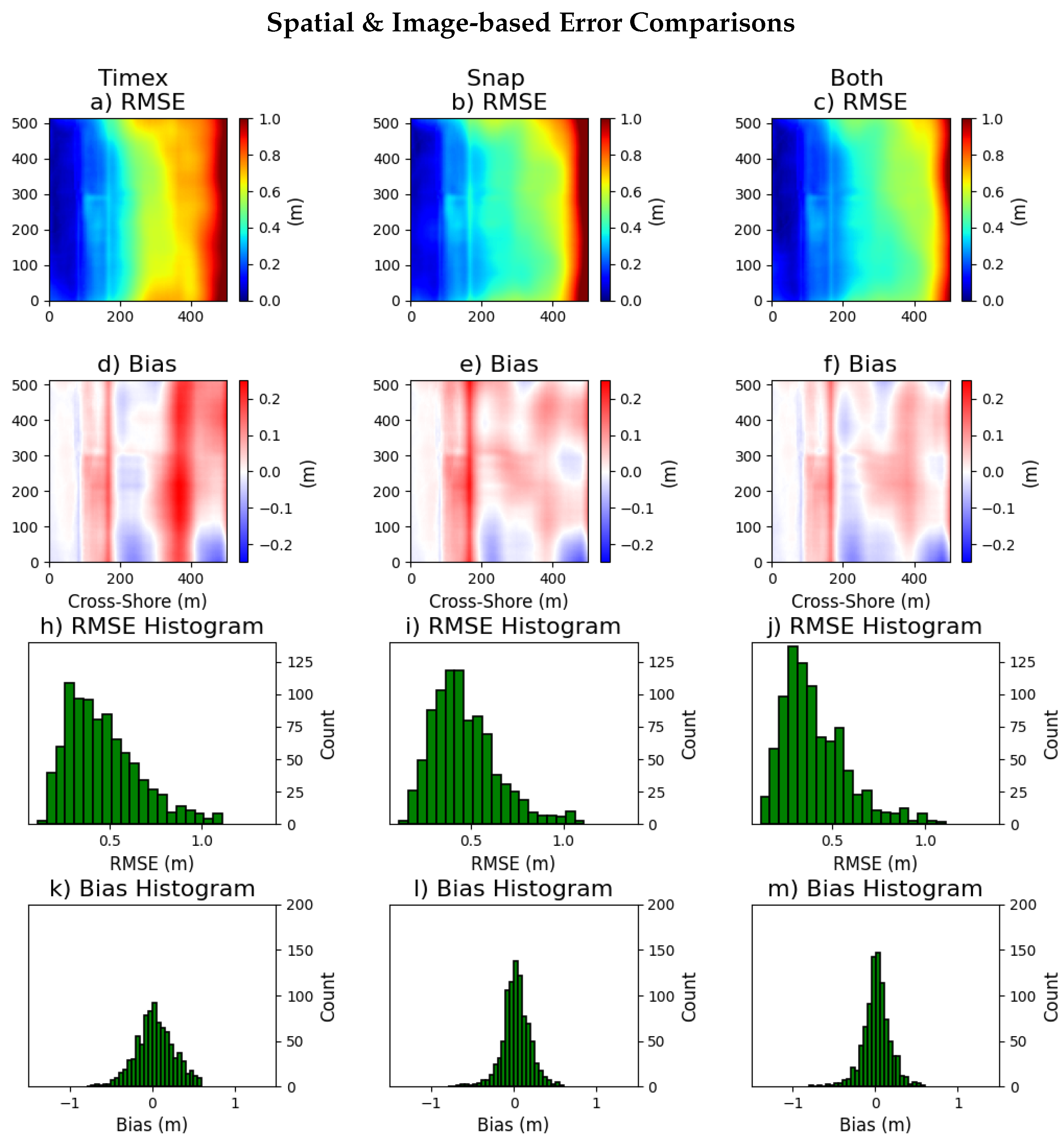
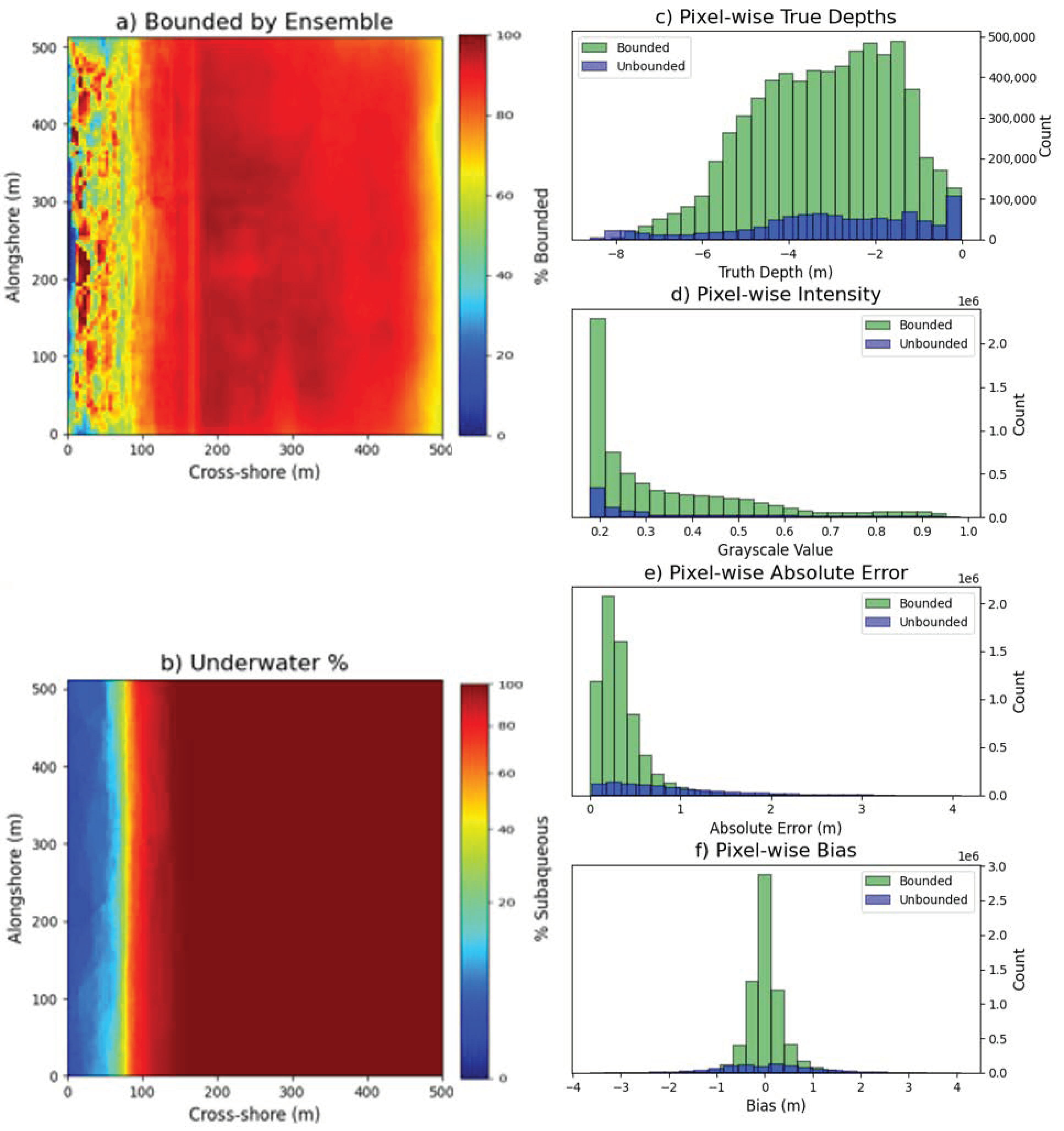
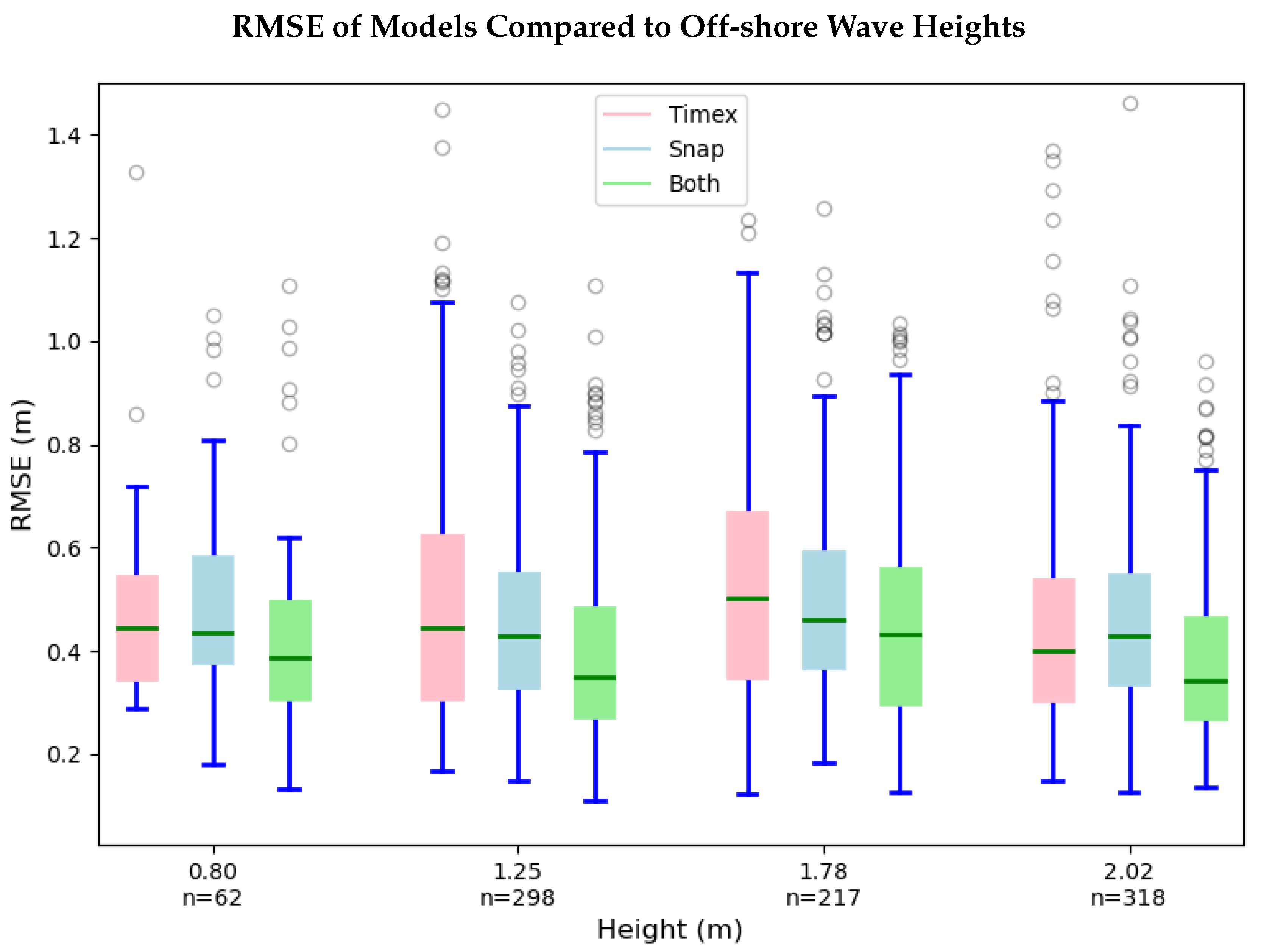

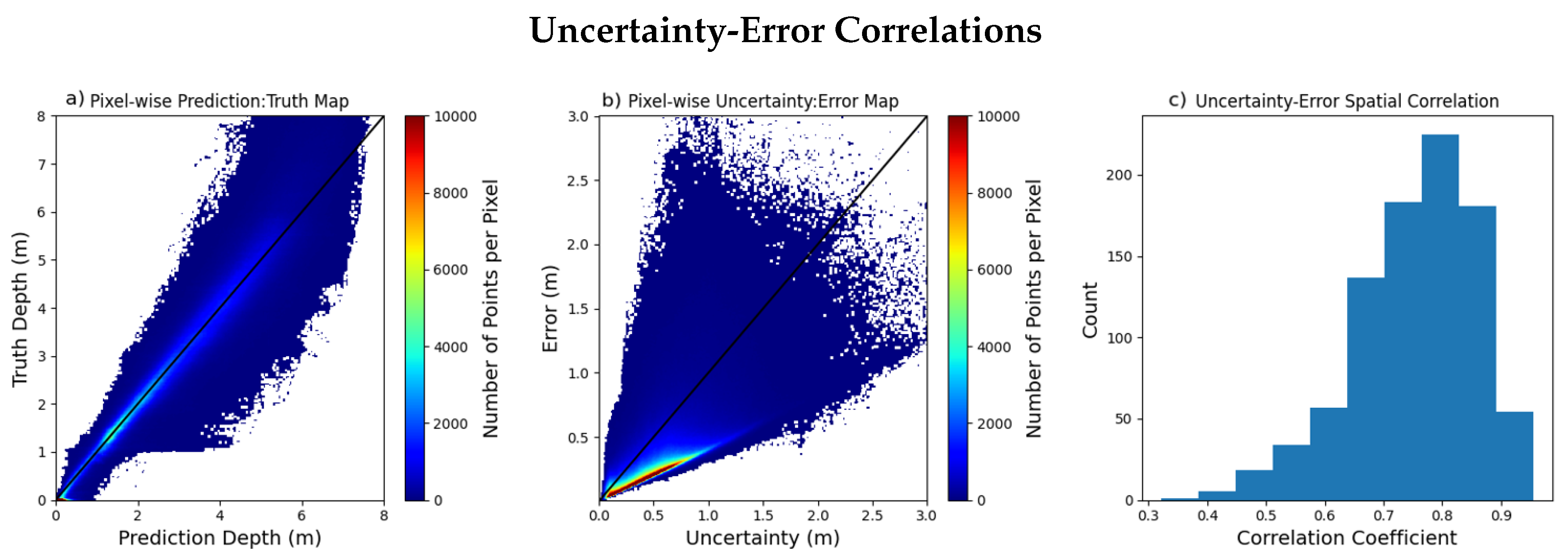
| Error Statistics by Input Features | ||||||
|---|---|---|---|---|---|---|
| Input Features | Bias (m) | MAE (m) | RMSE (m) | NRMSE | 90% Error (m) | Bounded % |
| Timex | 0.05 | 0.39 | 0.49 | 0.17 | 0.86 | 78 |
| snapshot | 0.04 | 0.35 | 0.44 | 0.15 | 0.79 | 82 |
| Both | 0.02 | 0.33 | 0.39 | 0.14 | 0.68 | 88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collins, A.M.; Brodie, K.L.; Bak, A.S.; Hesser, T.J.; Farthing, M.W.; Lee, J.; Long, J.W. Bathymetric Inversion and Uncertainty Estimation from Synthetic Surf-Zone Imagery with Machine Learning. Remote Sens. 2020, 12, 3364. https://doi.org/10.3390/rs12203364
Collins AM, Brodie KL, Bak AS, Hesser TJ, Farthing MW, Lee J, Long JW. Bathymetric Inversion and Uncertainty Estimation from Synthetic Surf-Zone Imagery with Machine Learning. Remote Sensing. 2020; 12(20):3364. https://doi.org/10.3390/rs12203364
Chicago/Turabian StyleCollins, Adam M., Katherine L. Brodie, Andrew Spicer Bak, Tyler J. Hesser, Matthew W. Farthing, Jonghyun Lee, and Joseph W. Long. 2020. "Bathymetric Inversion and Uncertainty Estimation from Synthetic Surf-Zone Imagery with Machine Learning" Remote Sensing 12, no. 20: 3364. https://doi.org/10.3390/rs12203364
APA StyleCollins, A. M., Brodie, K. L., Bak, A. S., Hesser, T. J., Farthing, M. W., Lee, J., & Long, J. W. (2020). Bathymetric Inversion and Uncertainty Estimation from Synthetic Surf-Zone Imagery with Machine Learning. Remote Sensing, 12(20), 3364. https://doi.org/10.3390/rs12203364