A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images
Abstract
1. Introduction
2. Method
2.1. Building Fine SBP Images
2.2. Characteristics of SBP Sediment Interface
- A sediment interface has lateral continuity; therefore, the pixels with high gray level representing interfaces in adjacent pings are continuous along lateral directions. Then the sediment interfaces can be approximated as line-like structures [14].
- Adjacent pings have different attitudes, incident energy, and signal–noise ratio (SNR); therefore the intensity imbalance often occurs along pings in SBP images.
2.3. Filtering Line-Like Sructures
- If both λ1 and λ2 are small, the analyzed region has approximately constant intensities.
- If one eigenvalue is high and the other low, there are small gray level changes in one direction and significant changes in the orthogonal direction, which indicates that there is a line-like structure.
- If both λ1 and λ2 are high, their gray level changes in both directions, which indicates the presence of a corner.
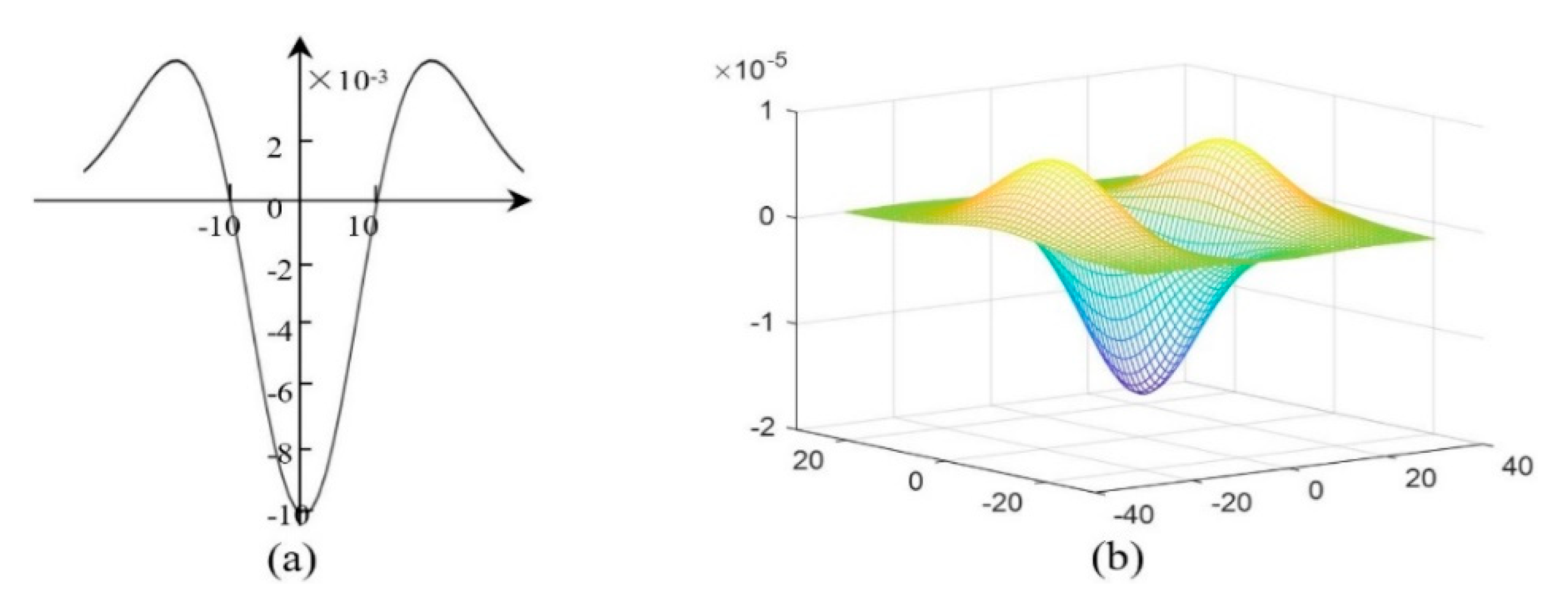
2.4. Suppression of Vertical Structures
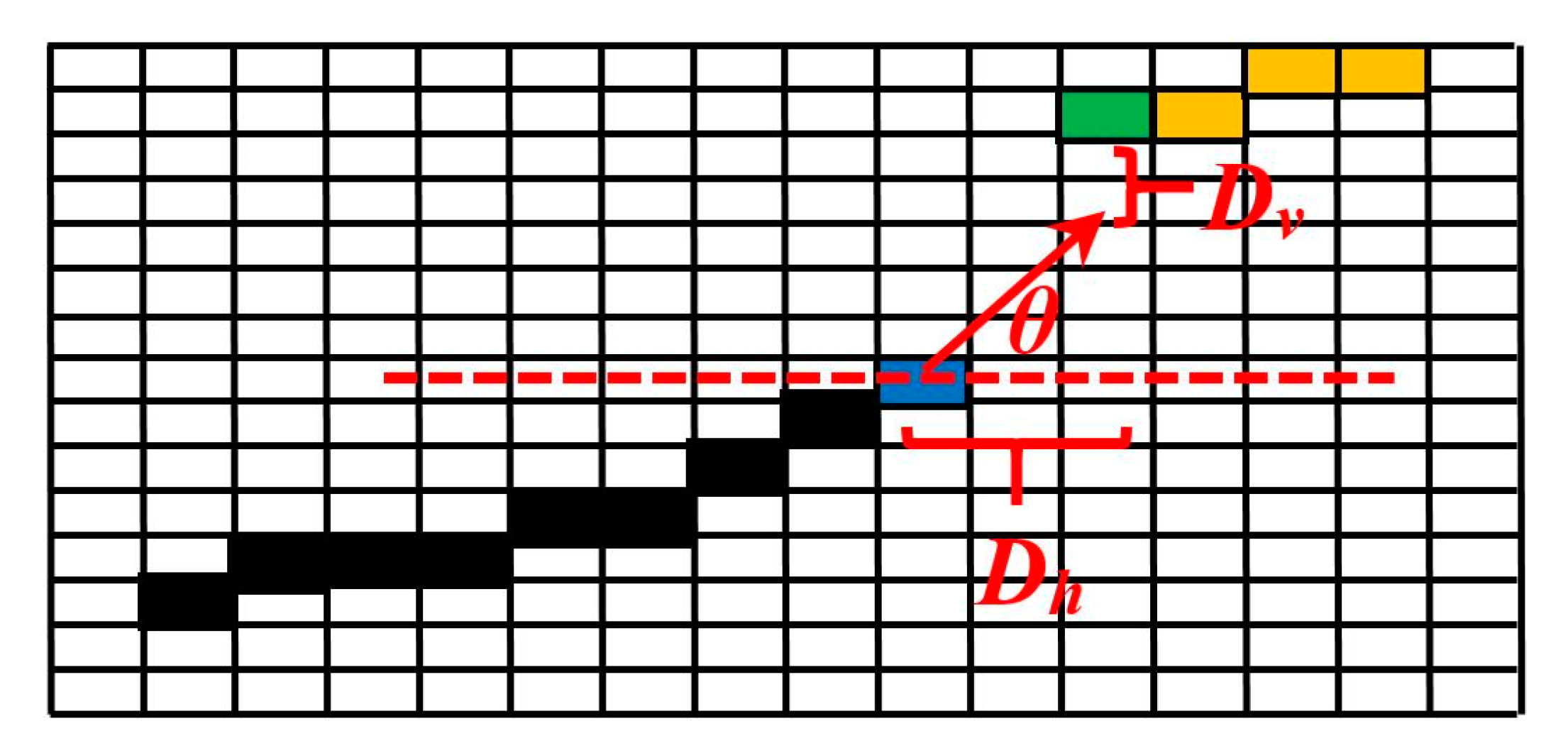
2.4.1. The Verticality Descriptor
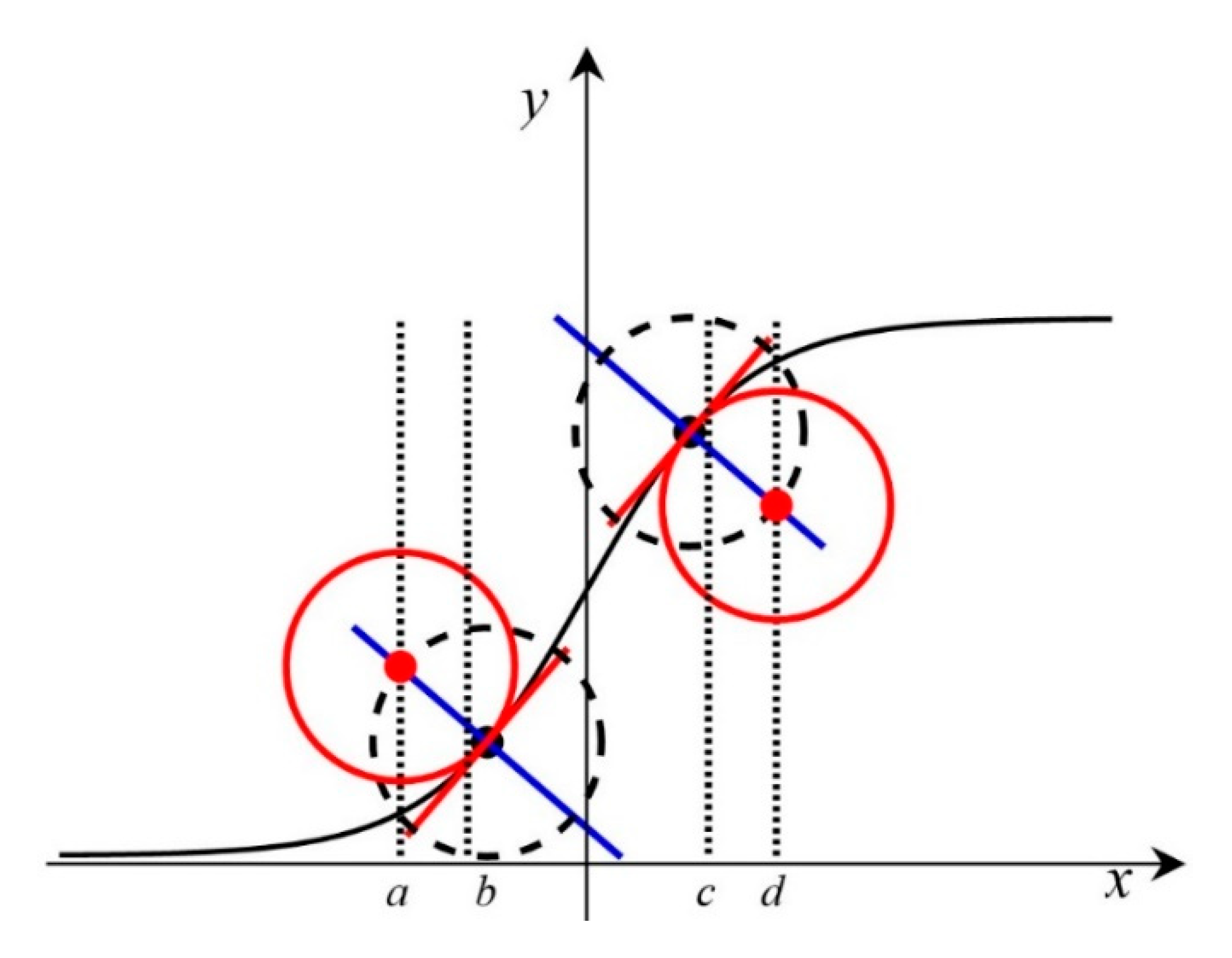
2.4.2. Definitions of the Key Points
2.4.3. Determination of the Final Vertical Suppression Model
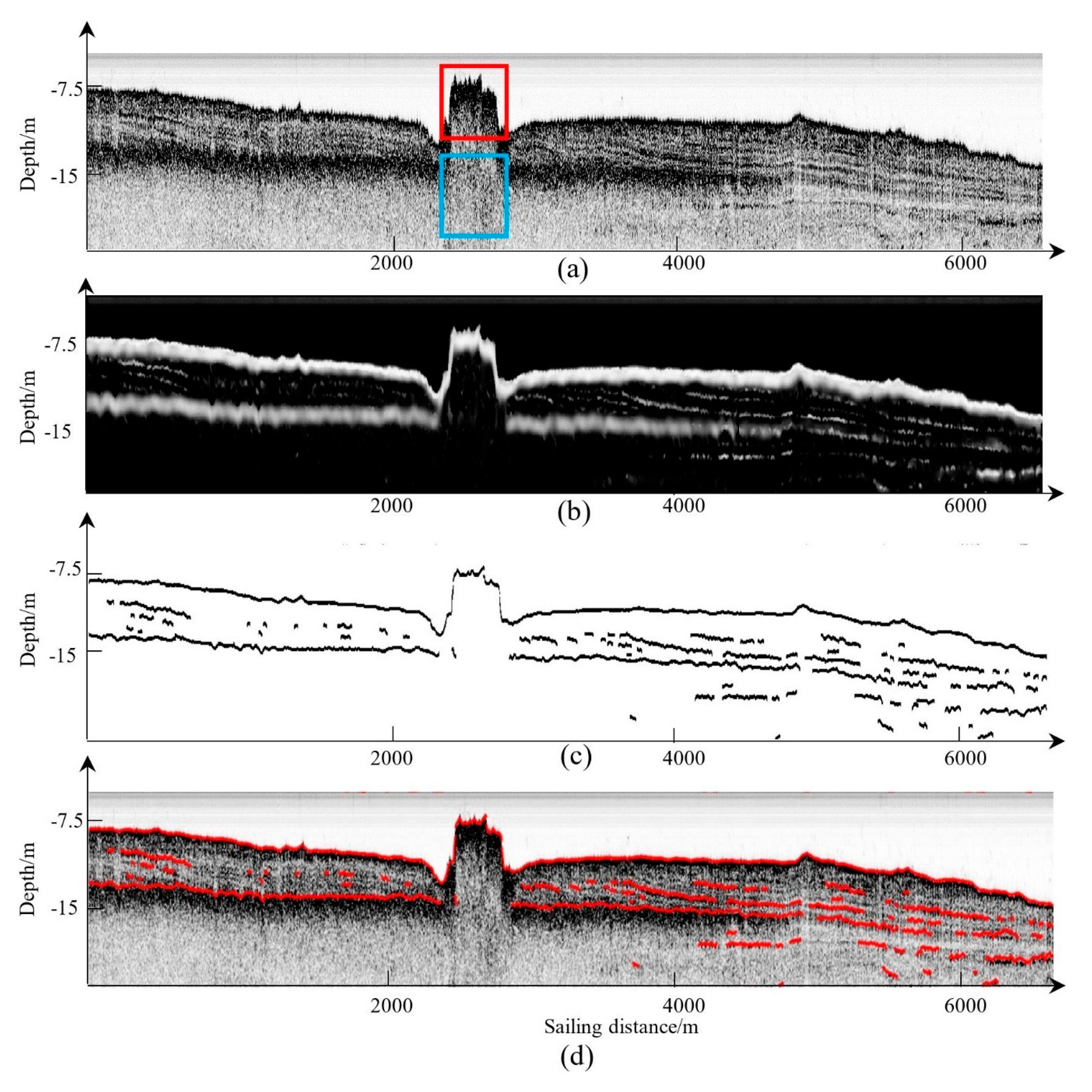
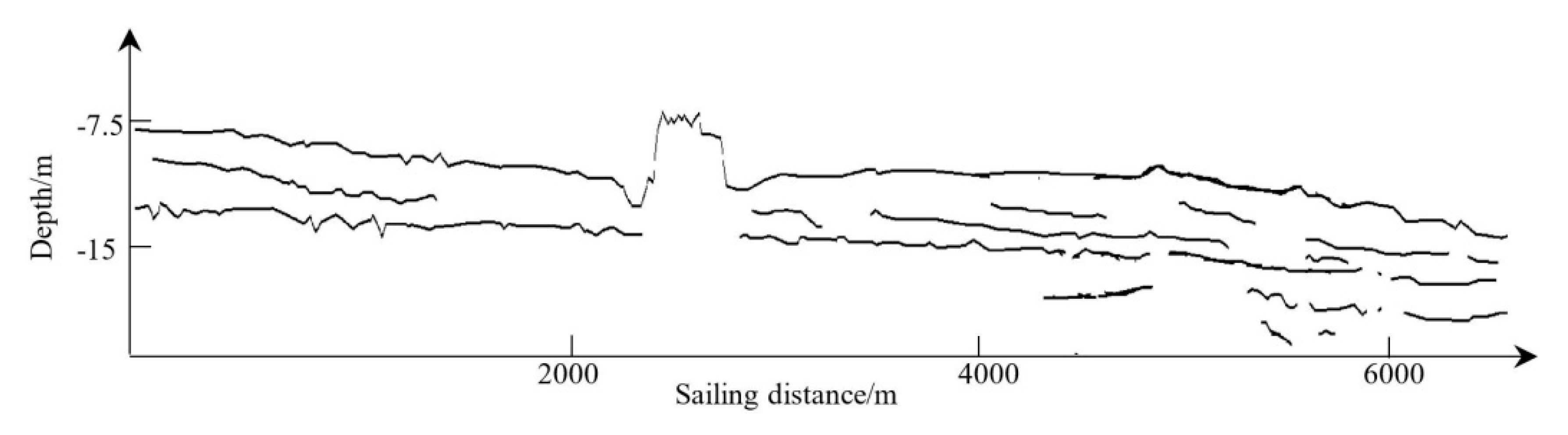
2.5. Horizon Picking and Linking
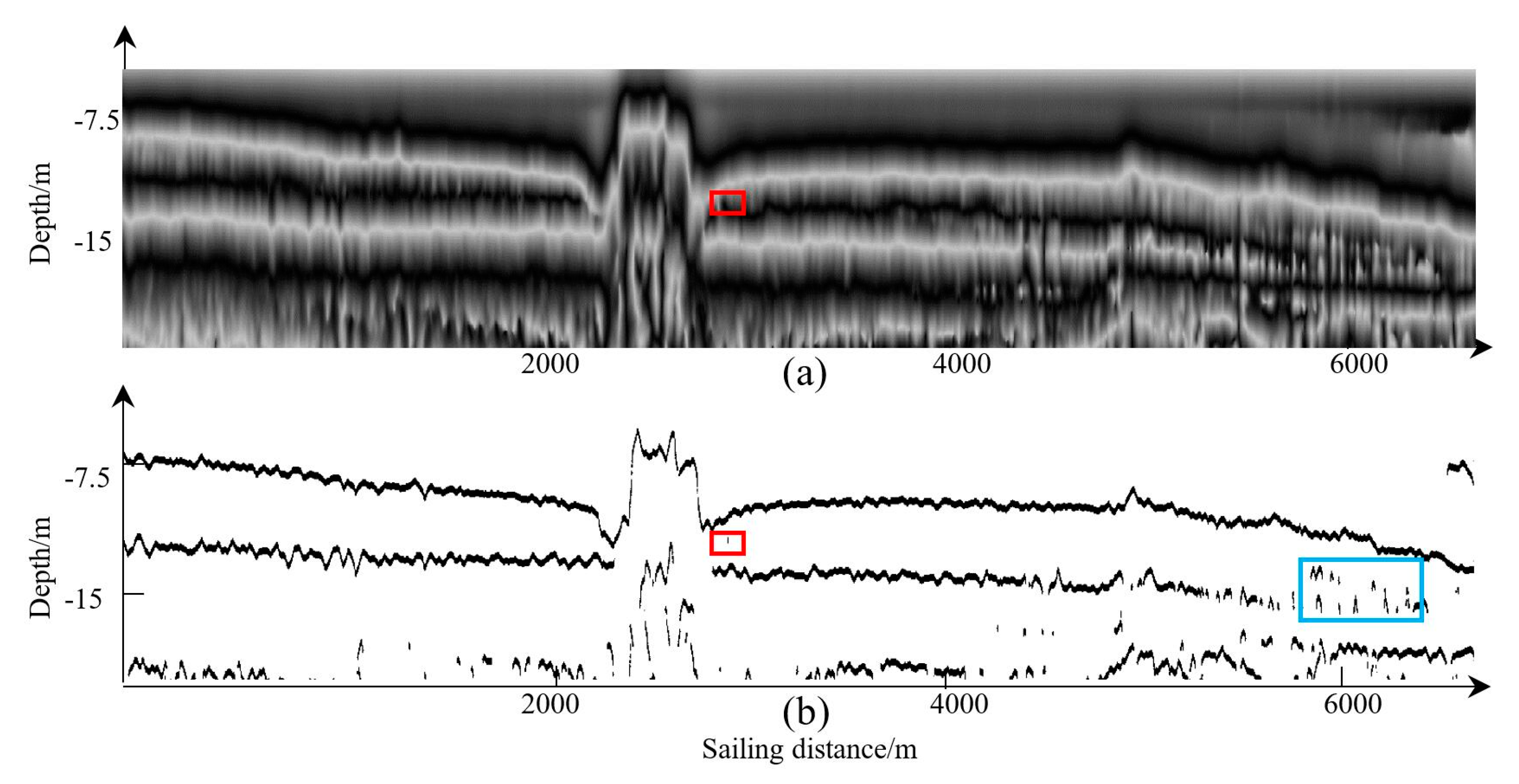
3. Experiment and Analysis
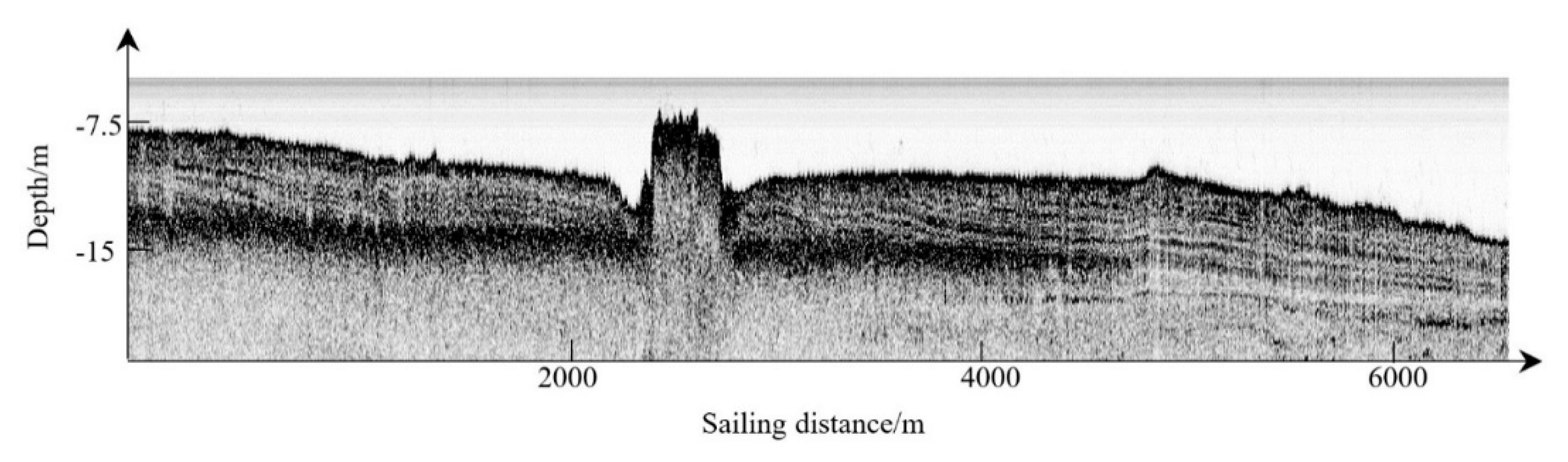
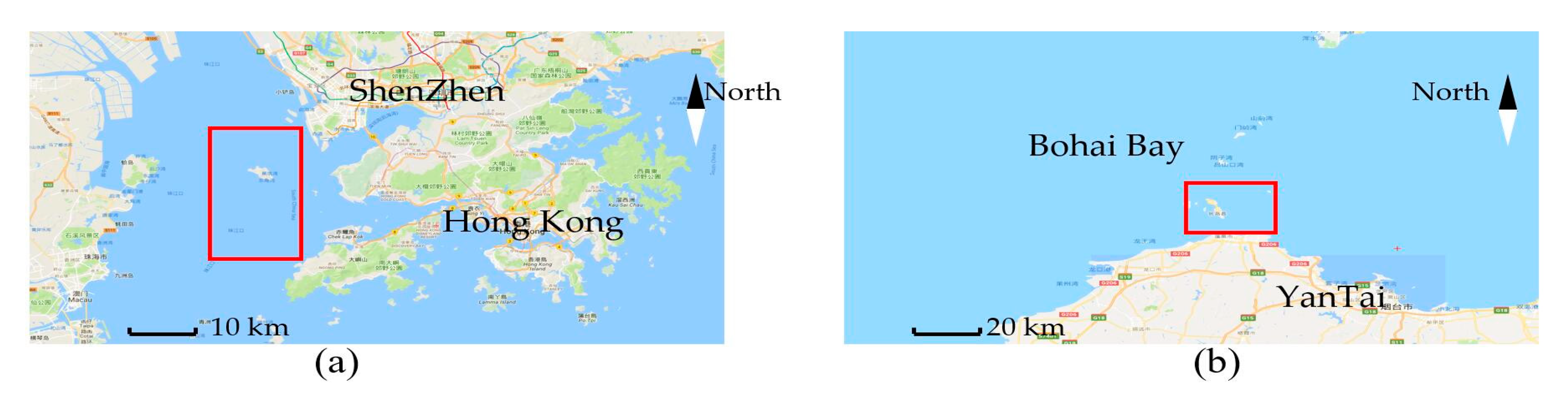
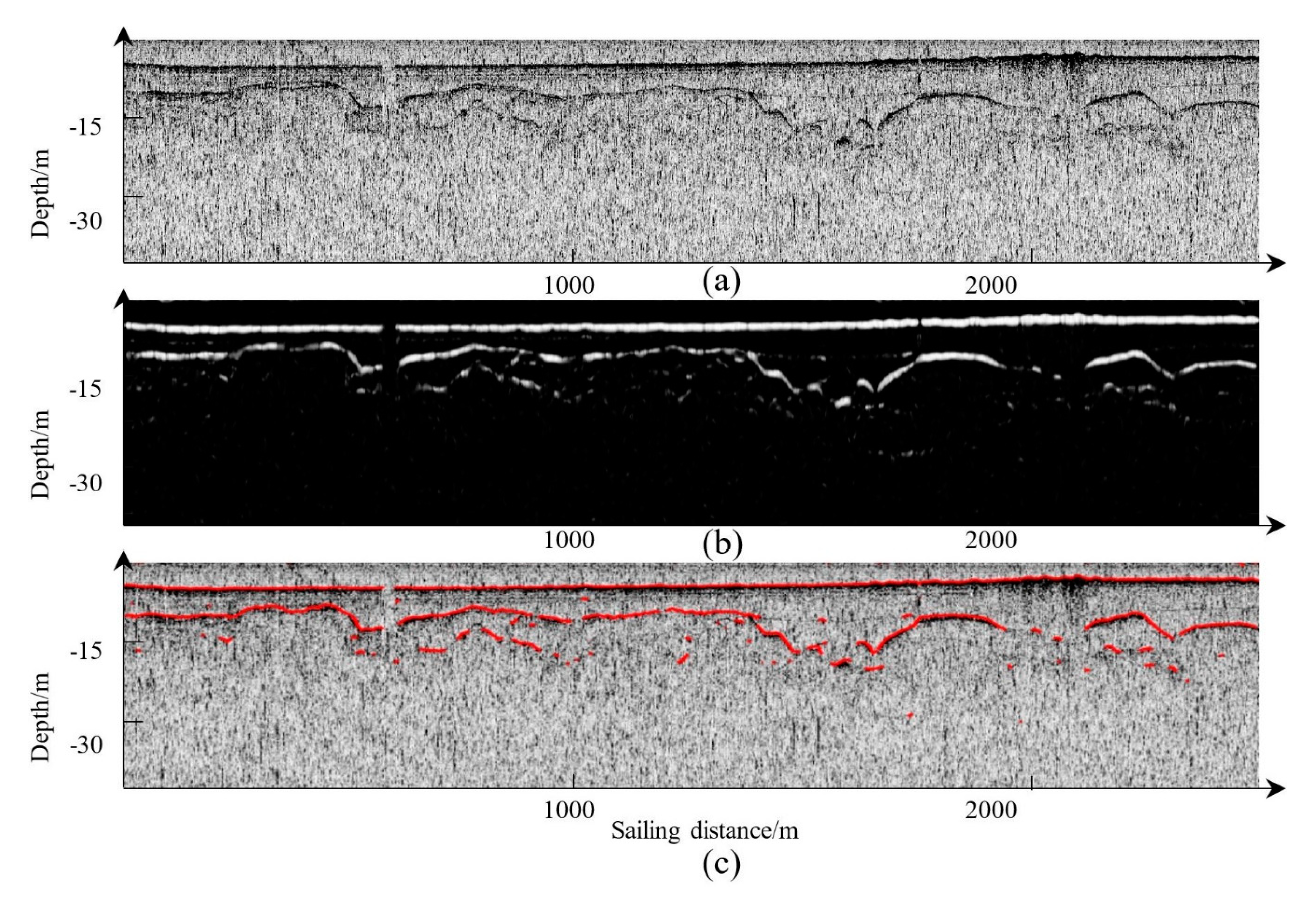
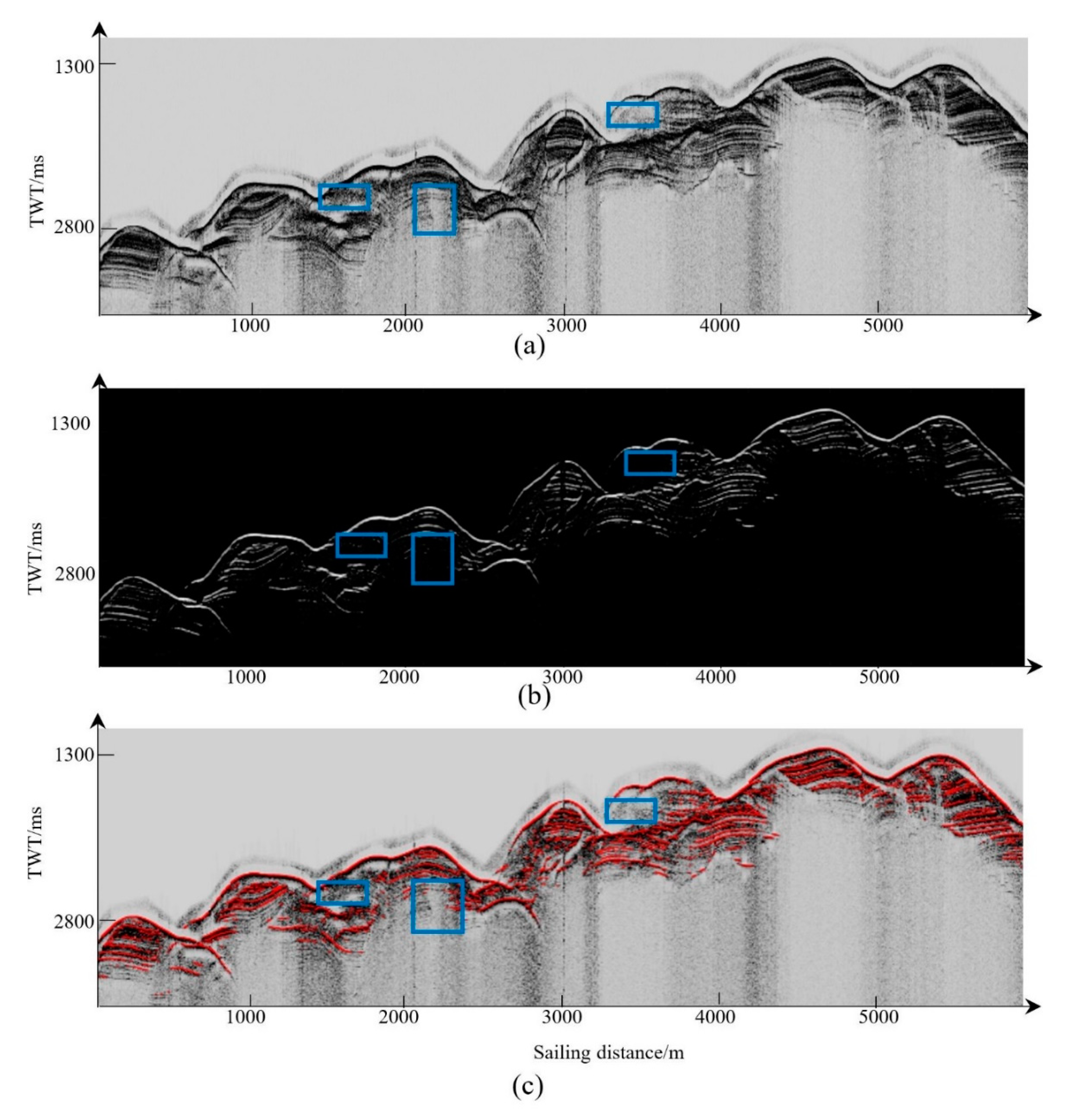
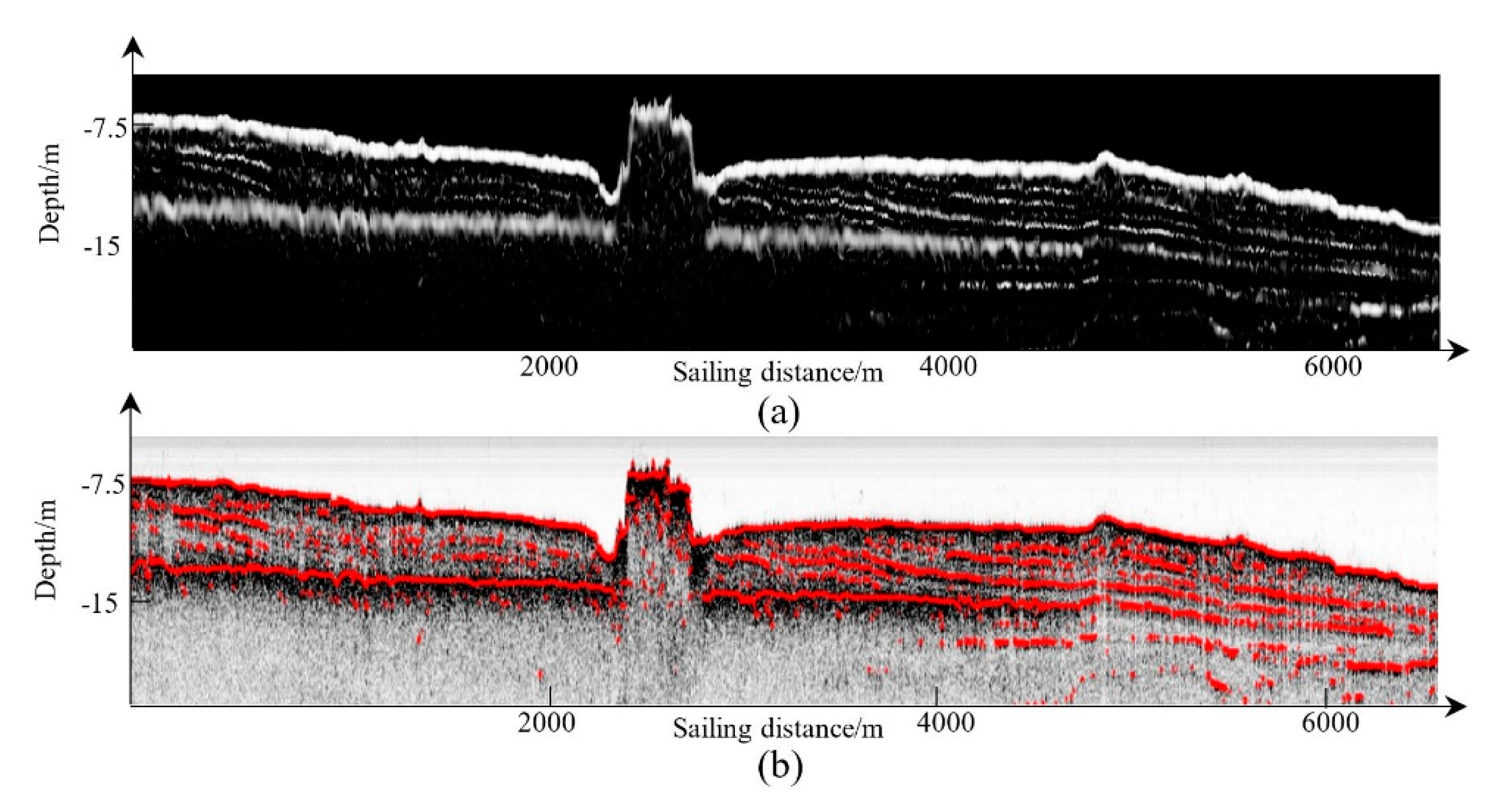
3.1. Horizon Picking on EdgeTech 3100P Data in Shenzhen
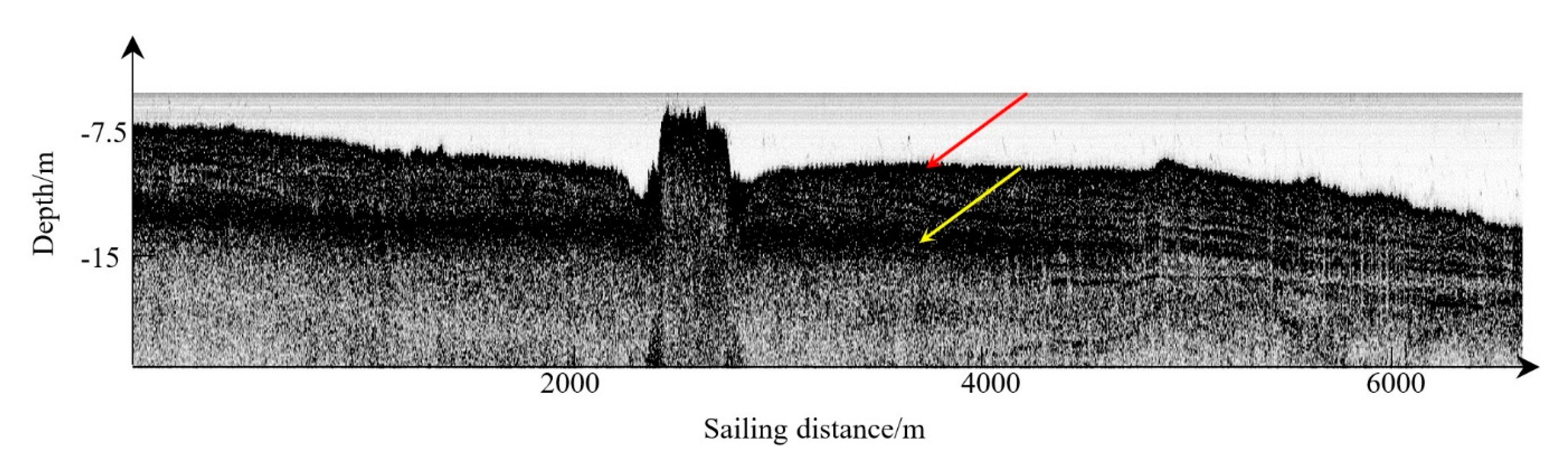
3.2. Horizon Picking on C-boom Data in Shenzhen
3.3. Horizon Picking on C-boom Data in Bohai Bay
3.4. Horizon Picking on Parasound P70 Data in the South China Sea
4. Results
5. Discussion
5.1. Scale Parameter
5.2. Vertical Exaggeration
5.3. S and RB in the Multi-Scale Filter
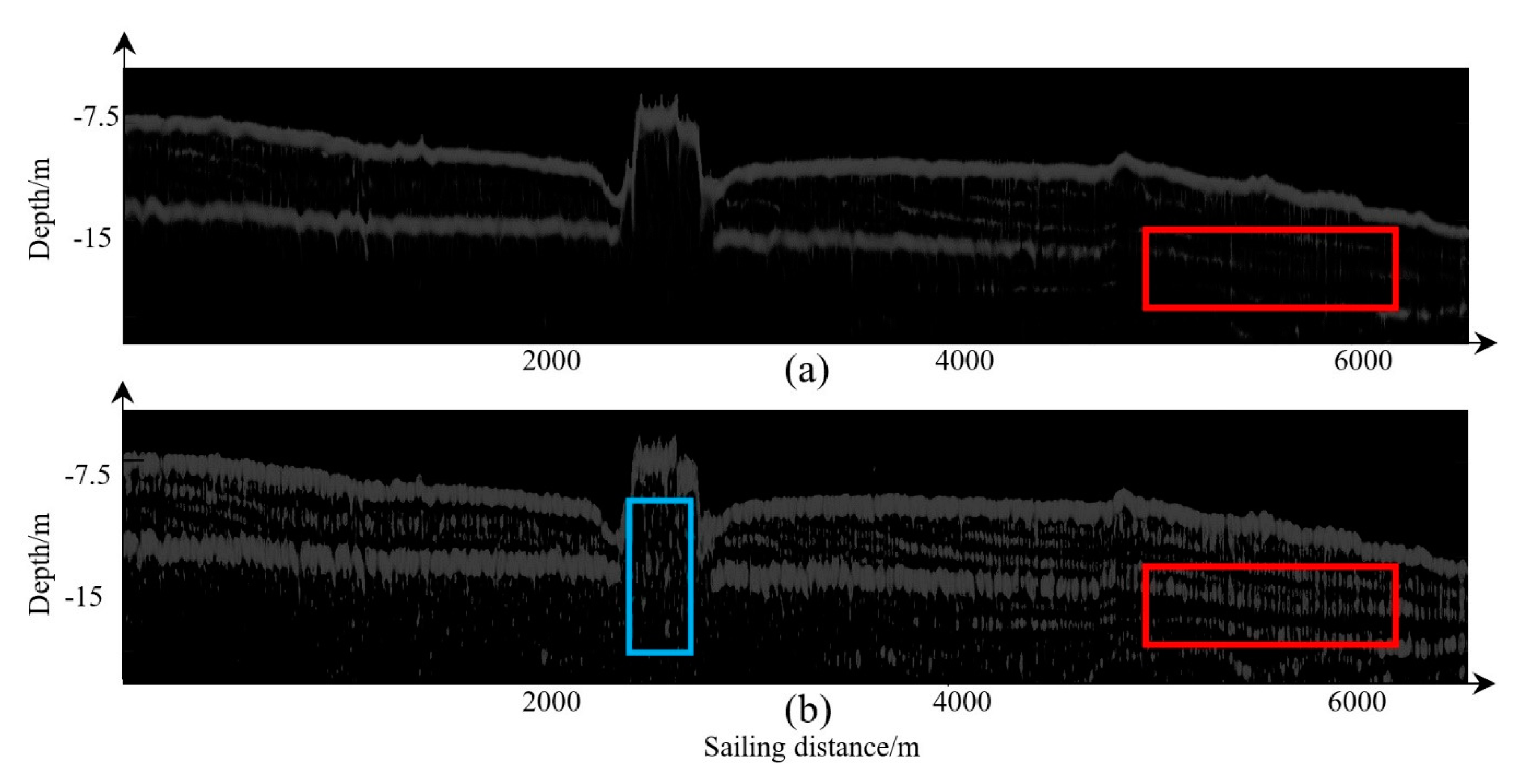
5.4. Comparison with the Method Using Local Phase
5.5. Applicability of the Proposed Method
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McGee, T.M. High-resolution marine reflection profiling for engineering and environmental purposes. Part A: Acquiring analogue seismic signals. J. Appl. Geophys. 1995, 33, 271–285. [Google Scholar] [CrossRef]
- Wilken, D.; Wunderlich, T.; Feldens, P.; Coolen, J.; Preston, J.; Mehler, N. Investigating the Norse Harbour of Igaliku (Southern Greenland) using an integrated system of side-scan sonar and high-resolution reflection seismics. Remote Sens. 2019, 11, 1889. [Google Scholar] [CrossRef]
- Lurton, X. An Introduction to Underwater Acoustic: Principles and Applications, 2nd ed.; Springer: Chichester, UK, 2010; pp. 372–379. [Google Scholar]
- Fakiris, E.; Blondel, P.; Papatheodorou, G.; Christodoulou, D.; Dimas, X.; Georgiou, N.; Kordella, S.; Dimitriadis, C.; Rzhanov, Y.; Geraga, M.; et al. Multi-frequency, multi-sonar mapping of shallow habitats—Efficacy and management implications in the National Marine Park of Zakynthos, Greece. Remote Sens. 2019, 11, 461. [Google Scholar] [CrossRef]
- Maroni, C.S.; Quinquis, A.; Vinson, S. Horizon picking on sub-bottom profiles using multiresolution analysis. Digit. Signal Prog. 2001, 11, 269–287. [Google Scholar] [CrossRef]
- Bondár, I. Seismic horizon detection using image processing algorithms. Geophys. Prospect. 1992, 40, 785–800. [Google Scholar] [CrossRef]
- Theuillon, G.; Stephan, Y.; Pacault, A. High-resolution geoacoustic characterization of the seafloor using a sub-bottom profiler in the gulf of lion. IEEE J. Ocean. Eng. 2009, 33, 240–254. [Google Scholar] [CrossRef]
- Dossi, M.; Forte, E.; Pipan, M. Automated reflection picking and polarity assessment through attribute analysis: Theory and application to synthetic and real ground-penetrating radar data. Geophysics 2015, 80, 23–35. [Google Scholar] [CrossRef]
- Forte, E.; Dossi, M.; Pipan, M.; Ben, A.D. Automated phase attribute-based picking applied to reflection seismics. Geophysics 2016, 81, 55–64. [Google Scholar] [CrossRef]
- Zhao, J.H.; Li, S.B.; Zhao, X.; Feng, J. A comprehensive horizon picking method on sub-bottom profiles by combining envelope, phase attributes, and texture analysis. Earth Space Sci. 2020, 7, e2019EA000680. [Google Scholar] [CrossRef]
- Baradello, L. An improved processing sequence for uncorrelated Chirp sonar data. Mar. Geophys. Res. 2014, 35, 337–344. [Google Scholar] [CrossRef]
- Kim, Y.J.; Koo, N.H.; Cheong, S.; Kim, J.K.; Chun, J.H.; Shin, S.R.; Riedel, H.; Lee, Y.H. A case study on pseudo 3-D Chirp sub-bottom profiler (SBP) survey for the detection of a fault trace in shallow sedimentary layers at gas hydrate site in the Ulleung Basin, East Sea. J. Appl. Geophys. 2016, 133, 98–115. [Google Scholar] [CrossRef]
- Hidalgo-Gato, M.C.; Barbosa, V.C.F. The monogenic signal of potential-field data: A Python implementation. Geophysics 2017, 82, 9–14. [Google Scholar] [CrossRef]
- Wang, W.; Ren, Q.; Li, J.; Ma, L. Hybrid method to extract sediment layered structure from sub-bottom profile. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC 2017), Xiamen, China, 22–25 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Mohamed, S. Sediment Classification Using Sub-Bottom Profiler. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale vessel enhancement filtering. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI1998), Boston, MA, USA, 11–13 October 1998; pp. 130–137. [Google Scholar] [CrossRef]
- Li, S.; Zhao, J.; Zhang, H.; Bi, Z.; Qu, S. A non-local low-rank algorithm for sub-bottom profile sonar image denoising. Remote Sens. 2020, 12, 2336. [Google Scholar] [CrossRef]
- Sun, G.Q.; Ling, G.H.; Huang, A.W.; Zhang, J. Five stages of logistic curve. J. Math. Med. 2012, 25, 269–270. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. Int. Conf. Netw. 2002, 760–766. [Google Scholar] [CrossRef]
- Zhao, J.; Li, S.; Zhang, H.; Feng, J. Comprehensive sediment horizon picking from subbottom profile data. IEEE J. Ocean. Eng. 2019, 44, 524–534. [Google Scholar] [CrossRef]
- Verbeek, N.; McGee, T. Characteristics of high-resolution marine reflection profiling sources. J. Appl. Geophys. 1995, 33, 251–269. [Google Scholar] [CrossRef]
- Garcia-Gil, S.; Vilas, F.; Garcia-Garcia, F. Shallow gas features in incised-valley fills (Rıa de Vigo, NW Spain): A case study. Cont. Shelf Res. 2002, 22, 2303–2315. [Google Scholar] [CrossRef]




| Precision | Recall | F-measure | Accuracy |
|---|---|---|---|
| 0.86 | 0.85 | 0.85 | 0.99 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhao, J.; Zhang, H.; Bi, Z.; Qu, S. A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images. Remote Sens. 2020, 12, 3322. https://doi.org/10.3390/rs12203322
Li S, Zhao J, Zhang H, Bi Z, Qu S. A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images. Remote Sensing. 2020; 12(20):3322. https://doi.org/10.3390/rs12203322
Chicago/Turabian StyleLi, Shaobo, Jianhu Zhao, Hongmei Zhang, Zijun Bi, and SiHeng Qu. 2020. "A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images" Remote Sensing 12, no. 20: 3322. https://doi.org/10.3390/rs12203322
APA StyleLi, S., Zhao, J., Zhang, H., Bi, Z., & Qu, S. (2020). A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images. Remote Sensing, 12(20), 3322. https://doi.org/10.3390/rs12203322







