Abstract
Marine remote sensing provides comprehensive characterizations of the ocean surface across space and time. However, cloud cover is a significant challenge in marine satellite monitoring. Researchers have proposed various algorithms to fill data gaps “below the clouds”, but a comparison of algorithm performance across several geographic regions has not yet been conducted. We compared ten basic algorithms, including data-interpolating empirical orthogonal functions (DINEOF), geostatistical interpolation, and supervised learning methods, in two gap-filling tasks: the reconstruction of chlorophyll a in pixels covered by clouds, and the correction of regional mean chlorophyll a concentrations. For this purpose, we combined tens of cloud-free images with hundreds of cloud masks in four study areas, creating thousands of situations in which to test the algorithms. The best algorithm depended on the study area and task, and differences between the best algorithms were small. Ordinary Kriging, spatiotemporal Kriging, and DINEOF worked well across study areas and tasks. Random forests reconstructed individual pixels most accurately. We also found that high levels of cloud cover led to considerable errors in estimated regional mean chlorophyll a concentration. These errors could, however, be reduced by about 50% to 80% (depending on the study area) with prior cloud-filling.
Keywords:
cloud-filling; gap-filling; interpolation; ocean color; satellite; data gaps; DINEOF; Kriging; supervised learning 1. Introduction
The world’s marine ecosystems are exposed to many anthropogenic pressures from climate change, fishing, pollution, and habitat destruction [1,2,3,4]. Consequently, monitoring how marine ecosystems change is more critical than ever. Since the launch of the Sea-viewing Wide Field-of-view Sensor (SeaWiFS) in 1997, the continuous availability of moderate-resolution, multi-spectral ocean color and thermal satellite imagery has expanded our ability to study and monitor marine phenomena at broad spatial scales [5]. However, climatologies based on satellite and ground observations indicate that, on average, more than two-thirds of the world’s oceans are covered by clouds at any given time [6,7]. Because electromagnetic radiation at visible, near- and thermal-infrared wavelengths is absorbed and scattered by clouds, essential marine satellite data products have significant gaps, limiting the ability to observe phenomena with high spatial and temporal variability.
Chlorophyll a (Chl a) concentration is a standard satellite data product serving as a proxy for phytoplankton biomass and essential input for models estimating marine primary production [8,9]. Although phytoplankton accounts for almost half of the world’s primary production [10], global analyses indicate that biomass is declining, especially in the open oceans, with important implications for, e.g., future fisheries [11]. At regional scales, receding sea ice has led to increased primary production [12,13] and the development of fall blooms in the Arctic Ocean [14], with the potential for fundamental changes of the marine food web [15]. In other regions, anthropogenic nutrient loadings have driven local increases in primary production, and in some cases caused eutrophication and coastal hypoxia, for example in the Baltic Sea [16,17,18] and the Gulf of Mexico [19]. Consequently, remote sensing of phytoplankton biomass is essential for monitoring marine ecosystems and the services they provide in a changing climate and amid other anthropogenic stressors.
Phytoplankton has long been known to form patches ranging in size from meters to 100 s of kilometers that rapidly change due to complex interactions between physical (e.g., transport by currents) and biological (e.g., grazing by zooplankton) processes [20,21]. If clouds frequently obscure satellite observations, important aspects of phytoplankton dynamics may be missed. Furthermore, if some parts of a study region have more frequent cloud cover than others, regional estimates of, e.g., total phytoplankton biomass and primary production, can be biased. For example, clear skies are more common over coastal waters [7]. Many coastal areas also have higher phytoplankton biomass and Chl a concentrations, as runoff from land provides nutrients to surface waters. If places with high Chl a also have less frequent cloud cover during satellite overpasses, the total regional or global phytoplankton biomass, and primary production will be overestimated because pixels with lower biomass will be cloud-covered and thus omitted from calculations more frequently. Such bias in spatial averages can be problematic if time series are used as climatologies, as input for ecosystem models, or for tracking variability and change in primary production [22].
Several research teams have developed gap-filling algorithms that can reduce the problems caused by cloud cover in marine satellite data. The most widely used algorithm is DINEOF (Data-Interpolating Empirical Orthogonal Functions [23]), which has been applied and tested in various studies, and allows the interpolation of single or several, correlated oceanographic variables [22,23,24,25,26,27,28,29]. Geostatistical interpolation is another common approach for filling gaps in spatial data [30]. For example, Saulquin et al. [31] used a sophisticated Kriging algorithm to create a gap-free global Chl a data product for Copernicus, the European Union’s earth observation program. Other proposed algorithms have used statistical learning and machine learning methods to estimate Chl a concentration for cloud-covered pixels, e.g., self-organizing maps (SOMs) [32] and random forests [33,34]. Such approaches predict values for pixels without data based on valid Chl a and other related variables in a spatiotemporal neighborhood.
Various studies in different marine regions have validated DINEOF, and researchers proposing other cloud-filling algorithms for marine satellite data have evaluated their performance based on example images with artificial clouds [22,32]. However, no quantitative comparison of the existing algorithms’ accuracy in a broad set of realistic situations and several globally representative study areas has been published. Consequently, which algorithms perform well under diverse conditions and for different applications remains unknown. Furthermore, recent technological advances (for example, the availability of software libraries for statistical and machine learning methods, and cloud computing services that allow the rental of the required computational resources as opposed to buying expensive hardware) make the application of powerful statistical and machine learning algorithms to fill gaps in ocean color data feasible for more researchers. We thus aim to answer three related research questions. First, how accurately can the existing and various new gap-filling algorithms predict Chl a concentrations “under the clouds”? Second, which of these algorithms can be recommended when considering accuracy, computational cost, and the manual effort required to use them? Third, for researchers interested in developing new methods, what (if any) are the shared properties of the best-performing algorithms?
We answer these questions based on analyses in four study areas of different sizes and a globally representative range of phytoplankton and cloud dynamics: The southern Beaufort Sea, the southern Chukchi Sea, part of the open equatorial Atlantic, and the Gulf of Mexico. To test different gap-filling algorithms, we combined mostly cloud-free images with clouds “transplanted” from other images. We then used the algorithms to reconstruct the pixels under the clouds for each combination of cloud-free image and transplanted cloud mask, while all other images (cloud-free or not) were left unmodified for use by the reconstruction algorithms. In contrast to previous research using a small number of clouds transplanted to a few example images for this purpose, we processed 750 to over 8000 combinations of mostly cloud-free images and transplanted clouds in each study area. We were thus able to quantify the algorithms’ performance in a wide range of realistic situations. The images with and without transplanted clouds are publicly available for testing future cloud-filling algorithms. Our source code is available online (https://doi.org/10.6084/m9.figshare.9782453).
2. Materials and Methods
2.1. Study Areas
We estimated errors of 10 cloud-filling algorithms in 4 study areas (Table 1, Figure 1 and Figure 2): the southern Beaufort Sea (BS), the southern Chukchi Sea (CS), a part of the tropical Atlantic (TA), and the Gulf of Mexico (GoM). These study areas span arctic to tropical latitudes, coastal and offshore waters, low and high primary productivity, and frequent cloud cover to relatively clear skies.

Table 1.
Overview of the study areas.
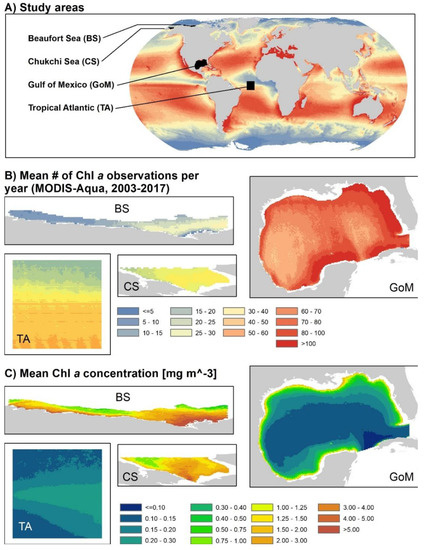
Figure 1.
The four study areas (A), their mean number of MODIS-Aqua Chl a observations in daily L3m data per year in 2003–2017 (B), as a proxy for data gaps caused by cloud cover), and their mean Chl a concentration (C) during the respective study seasons (1998–2017). Panel (A) has the same color scale as panel (B). Note that the number of observations in panels (A,B) are shown as an annual average, but our study period in the Beaufort Sea (BS) and Chukchi Sea (CS) covered only the summer months when observations are more frequent. Grey areas represent land.

Figure 2.
Percent of pixels that were visible during the study seasons (see Table 1) in 8-day composites (Tropical Atlantic, Beaufort Sea, Chukchi Sea) and 3-day composites (Gulf of Mexico) of binned MODIS-Aqua Chl a data.
Our study area in the BS covers the continental shelf north of Alaska and the Yukon Territories, between 156°W and 132°W. It is covered by sea ice from autumn until early summer; our analyses for the BS are thus limited to the ice-free summer months. Because of sea ice, lack of daylight in the winter, large solar zenith angles, and frequent cloud cover, valid ocean color observations are scarce. A bloom forms a few weeks after the sea ice retreats [35]. Additional blooms have recently been noted in the fall [14]. On average, Chl a concentrations exhibit a strong gradient when moving offshore, and are dominated by the Mackenzie River plume in the east. However, satellite-measured Chl a concentrations in the BS, and especially the Mackenzie plume, may be overestimated because of high colored dissolved organic matter (CDOM) concentrations and difficulties with atmospheric correction [36]. We excluded coastal waters with the highest average Chl a concentrations from the analysis.
Our study area in the CS stretches from the Siberian to the Alaskan coast, and northwards from the Bering Strait, from around 66.5°N to 68.5°N, but excluding a high-Chl a coastal band. It covers shelf waters mostly less than 50 m deep. Compared to the BS, the ice-free season begins several weeks earlier and ends several weeks later. However, the same challenges for ocean color remote sensing as in the BS apply: there are no data for much of the year, clouds are common during the summer, and Chl a concentrations estimated by standard ocean color algorithms can be inaccurate [37]. Overall, Chl a concentrations in the CS are rather high during the ice-free season. A large bloom forms every summer, and like in the BS and elsewhere in the Arctic, fall blooms are becoming more common [14].
Our study area in the TA is centered on the equator and located about halfway between South America and Africa (5°S to 5°N, 28°W to 18°W). It does not include any coastal waters, and depths exceed 5000 m in most locations. Atmospheric interferences are due to cloud cover associated with the Intertropical Convergence Zone (ITCZ) as well as haze due to seasonal transport of Saharan dust over the ocean. In contrast to the Arctic study areas, satellite observations of ocean color are possible year-round, but cloud cover is frequent and increases from south to north due to the presence of the ITCZ that moves northward in June. Primary production is seasonally nutrient-limited, and the highest mean Chl a concentrations are found in an upwelling band along the equator, which becomes wider when moving eastward and is associated with the Atlantic Cold Tongue. Chl a concentrations peak in July–August and exhibit a secondary peak in December–January [38]. Among our study areas, the TA has the lowest Chl a concentrations, on average <0.4 mg m−3.
Our study area in the GoM covers the whole basin, delineated in the east by the Florida Straits and the Yucatan Channel. We excluded a high- Chl a coastal band, following the 2 mg m−3 contour of the multi-year mean Chl a concentration. Chl a shows a strong gradient from the coasts to the offshore GoM, and coastal waters are affected by nutrient inputs from large rivers such as the Mississippi and the Atchafalaya [39]. The resulting increased phytoplankton biomass contributes to the seasonal formation of a hypoxic benthic “dead zone”, stretching far onto the continental shelf [19]. Chl a concentrations are lowest in the southeast, where the nutrient-poor Loop Current flows through the Gulf. Offshore, Chl a concentrations are highest in the winter and lowest in the late spring to early summer [40,41]. At finer spatiotemporal scales, Chl a concentrations vary due to extreme weather events affecting mixing [42], Loop Current eddies [40], and, possibly, industrial oil spills [43] and natural hydrocarbon seeps on the seafloor [44]. Satellite observations are possible year-round, and clear skies are much more frequent than in the TA. Nevertheless, considerable gaps exist in satellite imagery at finer temporal resolutions, and we hence tested gap-filling algorithms on 3-day composites in the GoM, as opposed to 8-day composites in the other study areas.
2.2. Satellite Data
All data used in this study are standard products obtained from public sources (Table 2). We downloaded SeaWiFS and MODIS-Aqua Chl a data for the BS and CS directly as L3b 8-day composites. The spatial resolution was 4 km (MODIS-Aqua) and 9 km (SeaWiFS); we reprojected the SeaWiFS data to the same 4 km grid. For the TA, we downloaded L3m 8-day composites at 9 km spatial resolution. For the Gulf of Mexico (GoM), which has lower levels of cloud cover overall, we downloaded daily 9 km L3m data and mosaicked them into 3-day composites. All data were downloaded for January 1998 to December 2017 (SeaWiFS: 1998–2002, MODIS-Aqua: 2003–2017). The BS, CS, and GoM include coastal waters where remotely sensed Chl a concentrations using the standard algorithm may be overestimated (e.g., by mistaking CDOM for Chl a). To avoid the domination of error estimates by pixels with very high Chl a concentrations, and evaluating the performance of gap-filling algorithms in situations where the original data may already be too inaccurate for many applications, we removed near-shore pixels where mean Chl a during the study period was higher than 2 mg m−3 in the CS and GoM, and manually to exclude bays and other areas with high Chl a in the BS.

Table 2.
Overview of raw data sources. All data were mosaicked into 8-day (BS, CS, tropical Atlantic (TA)) or 3-day composites (Gulf of Mexico (GoM)), and resampled to the Chl a grid (BS, CS: 4 km spatial resolution; TA, GoM: 9 km spatial resolution). All data were downloaded on 17 August 2017 (BS, CS), 20 September 2018 (TA), 2 February 2019 (GoM, NARR data), and 7 January 2019 (GoM, all other data).
We also used sea ice concentrations to exclude areas with summer ice in the BS and CS, and various other data products such as sea surface temperature for use as predictors in supervised learning algorithms. For these variables, we obtained daily data and resampled them to the same 4 km (BS, CS) and 9 km (TA, GoM) regular grid as Chl a (nearest neighbor method), and mosaicked them into 8-day (BS, CS, TA) and 3-day (GoM) composites.
2.3. Estimation of Algorithm Accuracy
2.3.1. Overview
Because the “best algorithm” may depend on its specific purpose, we estimated two error measures related to different gap-filling tasks for each algorithm. First, we estimated the root mean squared error (RMSE) of each algorithm’s prediction of the Chl a concentration for individual pixels under the clouds. This average error depends on the reconstructed pixels’ absolute errors. Second, we estimated the average RMSEs of the study areas’ mean Chl a concentrations before and after the filling algorithms had been applied. This average error depends on the reconstruction’s bias, as over- and underestimated pixel values cancel each other out in the calculation of the regional mean. In the following, the term “image” will refer to an individual 8-day (BS, CS, TA) or 3-day (GoM) composite. Overall, we followed the procedure described in pseudo-code below for each cloud-filling algorithm and study area (Figure 3):
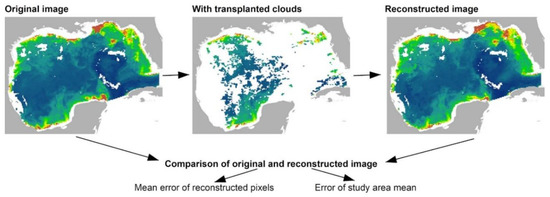
Figure 3.
We estimated the accuracy of each gap-filling algorithm (shown here: spatiotemporal Kriging) by adding clouds from cloudy images onto relatively cloud-free images, then using the algorithm to reconstruct the original image and calculate two error measures: the root mean squared error (RMSE) of the reconstructed pixels and the difference between the original and reconstructed image’s mean Chl a concentrations. We repeated this process for hundreds of combinations of original images and cloud masks in four study areas and thus were able to calculate the algorithms’ mean errors over many realistic situations.
- Identify a set of mostly cloud-free images ICF for the study area based on a threshold, e.g., 90% visible
- For each cloud-free image iCF ∈ ICF:
- For each image iC ∉ ICF (i.e., all images for the study area that are not cloud-free):
- Transplant clouds from iC onto iCF, but leave all other images unmodified
- Use the cloud-filling algorithm to reconstruct iCF
- Calculate reconstruction errors (mean per-pixel error and error of study area mean) for this combination of iCF and iC
- Average reconstruction errors over all combinations of iCF and iC
Details of each step are provided in the following sections. Note that only the image to be reconstructed, one at a time, was modified by transplanting clouds, while all other images were left unmodified for use by the cloud-filling algorithms, where applicable. All computations were performed in R [58] on a combination of local workstations and the Amazon Elastic Compute Cloud. All code used for processing and analysis is publicly available (see Introduction).
For some applications, Chl a values are commonly log-transformed; however, whether this is appropriate depends on the application. For example, after log-transforming values, multiplying mean concentration by volume would not yield the total mass anymore; in contrast, for statistical inference assuming a normal distribution, log-transformation may be required. Here, we calculated errors on untransformed data. However, some of the interpolation methods described below assume a normal distribution. In these cases, the data were first transformed as necessary, then interpolated, and finally transformed back before errors were calculated.
2.3.2. Cloud-Free Images and Cloudmasks
In this and the following subsections, we ignore the spatial structure of the satellite data and treat each image as a set of n pixels. For this purpose, we exclude land pixels, and other pixels that are by definition outside of the study area, i.e., the set I contains exactly the pixels that have an associated mean Chl a value shown in Figure 1 for the respective study area. In this study, we define an image as an 8-day (BS, CS, TA) or 3-day (GoM) composite. For a given image, we further define the function , that returns the remotely sensed Chl a concentration of a given pixel, as well as the function , which returns the respective sea ice concentration. We denote “no data” by the constant ; the subset of I containing pixels that have Chl a data as , and the subset of I containing pixels with sea ice as . We calculated the visible and the ice-free proportions of a given image as
There were no completely cloud-free images in the four study areas. We thus considered an image to be cloud-free if (BS, CS) or (TA and GoM, because only five and two images in these study areas respectively exceeded the 0.9 threshold). Furthermore, we considered an image ice-free if . It would be more precise to refer to these images as, e.g., “mostly cloud-free” and “mostly ice-free”, but for the sake of brevity, we omit the qualifier.
We extracted one cloud mask C from each ice-free image I that was not cloud-free. A pixel was included in the cloud mask only if it was in the study area, had no sea ice but also no Chl a data:
We assumed that all no-data pixels without ice and within a study area are the consequence of clouds, but there are other possible reasons for missing data (e.g., sun glint and failures of atmospheric correction). However, given the frequent cloud cover in our study areas, our assumption is not unreasonable. Furthermore, the comparison of various algorithms to fill significant data gaps, whatever their cause, is of interest.
Finally, we calculated the visible proportion of an image I and a cloud mask C (derived from a different image) as the proportion of pixels with data in the image that are not under the cloud mask:
Note that the visible proportion depends both on the cloud-free image and the cloudmask because the cloud-free images had small proportions of missing data, which can overlap with the cloudmasks but were ignored in all calculations.
2.3.3. Error Measures
We define a cloud-filling algorithm as a function that, for a given pixel, returns an estimated Chl a value based on some input data (which we omit from the notation for the sake of simplicity). For a given algorithm a, cloud-free image I and cloud mask C, we estimated the per-pixel root mean squared error (RMSE):
We estimated each algorithm’s overall RMSE for making per-pixel Chl a predictions as the mean of the per-pixel RMSEs of all combinations of cloud-free images and cloud masks:
where is the set of cloud-free images and is the set of cloud masks. Note that for a given algorithm, we first calculated the RMSE for each combination of cloud-free image and cloud mask, and then averaged these RMSEs to obtain a measure of the algorithm’s average performance over all combinations of images and cloud masks.
We also estimated how much (if at all) cloud-filling with different algorithms improved estimates of regional mean Chl a concentrations. For a given cloud-free image I, we defined the “true” mean Chl a concentration as
i.e., we assumed that the true mean is the mean of all pixels that have data. For the same image I, a cloud mask C, and a cloud-filling algorithm a, we calculated the estimated mean concentration as average of the original Chl a values outside the cloud mask and the algorithm’s estimates below the cloud mask:
To obtain an overall measure of the algorithm’s effect on estimated spatial means, we again calculated an RMSE:
Note that for the per-pixel errors, we calculated one RMSE per image and cloud mask (based on the difference of the pixels’ true vs. filled values), and then averaged these RMSEs across all image-cloud mask pairings. In contrast, for spatial means, each image and cloud mask yielded a single true and a single estimated value, which we then used to calculate the RMSE across all image-cloud mask pairings. Note that the per-pixel RMSE of a given image and cloud mask is also calculated only for pixels under a cloud mask (i.e., pixels that get filled), whereas the estimated spatial means consider both the original values outside the cloud mask and the estimated values under the cloud mask. Furthermore, when interpreting our results, it is important to keep in mind that for algorithm comparison, we assumed cloud-free pixels to be the “true” Chl a concentrations. In reality, satellite-retrieved Chl a estimates are subject to a variety of errors, for example, imperfect atmospheric correction, over-estimation in areas with high levels of CDOM, and the effects of local biological factors, such as pigment packaging [37]. Besides the two RMSEs estimated for each algorithm’s performance on all images and cloud masks, we also report as a running average function of the visible proportion (Equation (4)). For this purpose, we calculated it as in Equation (9), but including only combinations of images and cloud masks where was in the respective range.
2.4. Cloud-Filling Algorithms
2.4.1. Baselines for Comparison (Random Missing Pixels, Clouds but no Correction, Mean Model, Correction Factor)
We calculated different error estimates as baselines to which we compared the performance of the cloud-filling algorithms. As a baseline for the per-pixel error, we used a null model that fills all pixels under a cloud mask with the mean of Chl a values that are not under the cloud mask. Concerning the spatial mean of Chl a, clouds affect the estimates in two ways. First, if not all pixels in an image have data, the mean is estimated from a sample rather than the population, and the smaller the sample size (visible proportion), the higher the estimated mean’s variance. We approximated this component of the error by estimating the mean chlorophyll concentration with artificial “cloud masks” consisting of different proportions of randomly chosen pixels in each image (from 0% to 99% in steps of 1%, and averaging over 1000 random samples of pixels for each proportion). Second, clouds tend to obscure whole sub-regions of a study area, which means that under realistic cloud cover, the sample of pixels can be biased. We thus also report without any filling algorithm, i.e., the mean of pixels outside of the cloud mask, as a measure of the error of the regional mean caused by clouds if no gap-filling or other corrections are applied. Finally, we tested how much a simple correction factor (used instead of prior cloud-filling) improved estimates of the regional mean Chl a concentration. As described below, if the visible parts of the study area had below-average Chl a concentrations, the estimated mean was corrected upward. Conversely, if the visible pixels had a higher long-term average Chl a concentration than the whole study area, the estimated mean was corrected downward. We first calculated each pixel’s long-term mean Chl a using all images that were not cloud-free. We then calculated a corrected mean for each image and cloudmask as the mean of all visible pixels but multiplied by a correction factor: the quotient of the whole study area’s long-term mean and the visible pixels’ long-term mean.
2.4.2. Geostatistical Interpolation Methods
We tested the performance of four geostatistical interpolation methods to fill data gaps: linear temporal interpolation (TI), inverse-distance weighted interpolation (IDW), ordinary Kriging (OK), and spatiotemporal Kriging (STK). We implemented TI as follows. For each pixel under a cloud mask, we searched for the last and next images in which the pixel had data (within +/−8 composites). We then interpolated linearly between the two closest (previous and next in time) valid observations for the pixel. The long temporal search window was necessary to ensure that values could be interpolated in all situations. For IDW and OK, we used the implementation in the R package gstat [59]. We log-transformed the Chl a data (but errors were calculated on back-transformed Chl a concentrations, as for all other algorithms), and subtracted each pixel’s long-term mean for the respective study period before interpolation. For IDW, we used weights relative to the squared distance between pixel centroids. For OK, we first calculated a separate experimental, omnidirectional variogram for each image in the study period and season, combining distances between pixel centroids in 10 km bins. We then averaged the individual images’ semi-variances in each bin to create a sample variogram representing spatial autocorrelation over the whole study period. Finally, we fit an exponential variogram model to the combined sample variogram in each study area. To reduce computation times, we interpolated Chl a concentrations locally, including only the 50 closest visible pixels in the interpolation of each pixel under the cloudmask.
We also implemented spatiotemporal Kriging using the gstat package [60]. To achieve acceptable computational costs, we calculated experimental, omnidirectional spatiotemporal variograms using images from only one year. For each image from the study season in 2015, we sampled up to 1000 pixels (except for the GoM where we sampled 300 pixels due to higher temporal resolution), resulting in 7237 (BS), 13,995 (CS), 45,000 (TA), and 35,700 (GoM) pixels for estimation of the variogram. We used temporal bins covering the period of one composite (i.e., BS, CS, TA: 8 days; GoM: 3 days), and spatial bins that were 30 km wide, up to a cutoff distance of 300 km. We fit various theoretical, spatiotemporal variogram models to the experimental variogram for each study area, and chose the best-fitting model type, which was a sum-metric model in all four study areas. Finally, we interpolated locally, using the 80 closest pixels in space and time, with the conversion between time and space distances determined by the fitted theoretical variogram.
2.4.3. DINEOF
DINEOF (Data-Interpolating Empirical Orthogonal Functions) [23] may be the most widely used sophisticated gap-filling algorithm for marine satellite data. The central idea is to represent the data as a combination of a reduced number of spatial and temporal “modes” that capture most of the spatial and temporal variability (empirical orthogonal functions, EOFs). To calculate the EOFs, data gaps are first filled with an initial guess; the estimated EOFs are used to reconstruct better estimates for the data gaps and are then updated. This process is repeated iteratively, and the optimal number of EOFs is estimated using a held-out set of pixels. While software from the researchers who developed DINEOF is available online [61], there is at present no official implementation in R. However, R code for DINEOF is available as part of the sinkr package under development [62]. After comparing this unofficial implementation to descriptions of DINEOF in the literature, we modified it slightly by centering the field matrix on its mean before gap-filling, as described by [23,24]. We constrained the pixel values reconstructed by DINEOF to the range of observed values in the study period after noticing unrealistically high reconstructed values in some situations. While many researchers use DINEOF to reconstruct the values of all pixels in an image (including the pixels that had data in the first place), which reduces local noise and can thus be beneficial for some applications, we only filled pixels under the cloud mask and left those outside the cloud mask unchanged (consistent with how we calculated errors in regional means).
In our computational framework, using the sophisticated official DINEOF software was computationally not feasible for the larger study areas. We hence used the unofficial R implementation of DINEOF instead of the official software. However, we tested the original DINEOF software in our smallest study area, the BS, and sub-sets of the other study areas. We let the software calculate up to 30 modes with up to 1000 iterations and calculated reconstructions with and without temporal filtering as described by [63]. Because the official software did not achieve lower reconstruction errors in these tests, we used the less sophisticated, unofficial, but in our computational environment much faster R implementation for the algorithm comparison.
2.4.4. Self-Organizing Maps
Jouini et al. [32] proposed a gap-filling technique for ocean color data based on self-organizing maps (SOMs). The idea is to split the data into several “oceanographic situations”, represented by Chl a, sea surface temperature (SST), and sea level anomaly (SLA) in a 3 × 3 pixel neighborhood around a given pixel, as well as these values in the previous and the next image (i.e., a vector of 3 variables × 3 time steps × 9 pixels = 81 elements). A pixel with missing Chl a data is then filled with the mean Chl a values of situations that are similar, based on the Chl a, SST, and SLA observations in the spatiotemporal neighborhood that are available. The SOM itself is a 2-dimensional grid where each unit represents a set of similar oceanographic situations and is arranged so that similar sets of situations in the original, high-dimensional space are neighbors in the SOM. In each study area, we log-transformed Chl a and created a training data set by searching for neighborhoods consisting of 3 × 3 pixels that had complete Chl a data in 3 consecutive time steps; SST and SLA were available for all pixels in the data sources we used for these variables. We identified 55,511 (BS), 6616 (CS), 856,074 (TA) and 228,396 (GoM) such neighborhoods in which all 27 (9 per time step) pixels had Chl a data. We then used the R package kohonen [64] to train a SOM for each study area with dimensions 40 × 40 (BS), 25 × 25 (CS), 80 × 80 (TA), and 60 × 60 units (GoM). The training data were presented to each SOM 15,000 times, with a learning rate declining from 0.05 to 0.01 as iterations progressed. We used the Euclidean distance of the three variables (after normalization) in the spatiotemporal neighborhood as a metric of two situations’ similarity. Given the small number of training examples in the BS and CS, we added an iterative step in these two study areas [32]: We used the trained SOM to fill in all Chl a data, then used the filled Chl a data to create a new training data set. The resulting “filled” training sets contained 394,985 (BS) and 53,172 (CS) situations and were used to train larger SOMs for these study areas (BS: 80 × 80, CS: 60 × 60 units). To predict a Chl a value for a given grid cell without data, we identified the most similar unit in the SOM, and used the median Chl a concentration of this unit and its 8 neighbors, again as suggested by [32].
2.4.5. Supervised Learning
While SOMs, as used by [32], is an unsupervised learning approach, it appears more natural to predict missing Chl a values by means of supervised learning, with Chl a as a response (dependent) variable of a statistical regression model (see Section 4.3 for a summary of deep learning efforts for gap-filling of satellite data). Here, we trained two types of simple regression models: ridge regression (with the penalty multiplier determined by means of 10-fold cross-validation) and random forests (with 500 trees). The ridge regression models were trained with the glmnet package [65], and the random forests with randomForest [66,67].
While a detailed discussion of variable selection for machine learning is beyond the scope of this article, it is important to note that ridge regression and random forests as used here are designed to ignore any predictors (independent variables) that do not improve predictions for data excluded from model fitting. We hence included a wide range of predictors based on published machine learning algorithms for cloud-filling of Chl a data [32,34], algorithms for mapping the spatial distribution of phytoplankton communities based on environmental variables [68,69], as well as data availability (for example, values of the predictors had to be available where Chl a data had gaps). Specifically, we included latitude, longitude, day of the year, SST, SLA, cloud cover, wind speed (north-south and east-west separately as well as the corresponding scalar speed), water depth, distance to land and the 20-year mean Chl a concentration during the study season (Table 2). In addition, we included Chl a-based predictors to allow spatiotemporal interpolation: the mean Chl a concentration of the 1, 4, and 16 pixels that were closest in space in the image itself, in the previous and the next image. For random forests (which can represent interactions between predictors in a straightforward way), we additionally included the search distance required to find the respective number of visible pixels. For example, this could allow the models to learn to base predictions primarily on pixels with valid Chl a data if they exist nearby, but rely increasingly on covariates like SST and SLA if the closest Chl a observations are farther away (if such relationships exist in the training data). To compare the importance of Chl a observations in cloud-free parts of an image and its immediate neighbors in time versus the importance of the various covariates, we trained two versions of each regression model: one with only the covariates and one additionally including the Chl a based predictors. The training data were sampled from all images in the respective study season that were ice-free but not cloud-free, up to 2000 pixels per image, where the response and all predictors had data available. There were 46,088 (BS), 73,458 (CS), 345,585 (TA) and 428,875 (GoM) training observations.
3. Results
3.1. Per-Pixel Reconstruction Errors
Figure 4 shows example reconstructions calculated with the tested algorithms in the Tropical Atlantic. In addition to the R implementations of the algorithms tested here, Figure 4 also shows a reconstruction made with the original DINEOF software [61]. The absolute percentage difference between the two DINEOF reconstructions was 1.4%.
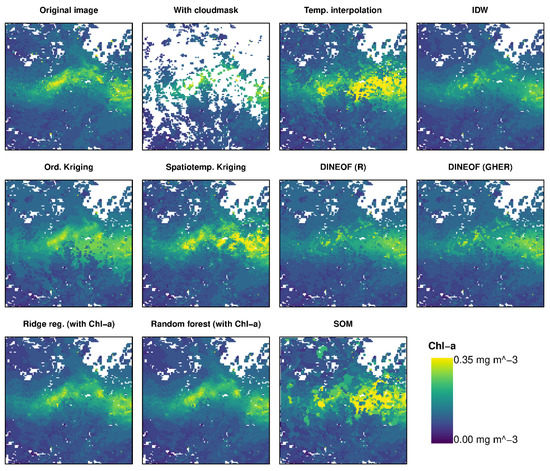
Figure 4.
Example of a mostly cloud-free image in the Tropical Atlantic (8-day composite for 26 June–3 July, 2001), an added cloud mask, and reconstructions of pixels under the cloud mask. The plot labeled DINEOF (R) shows a reconstruction made with the unofficial R implementation, whereas the plot labeled DINEOF (GHER) shows a reconstruction made with the official DINEOF software. Only pixels under the cloud mask were reconstructed. All others are shown with their original values.
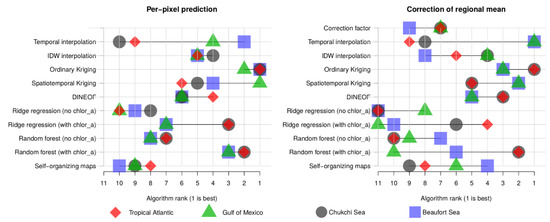
While some algorithms generated more accurate reconstructions than others in Figure 4, when analyzing reconstructions for many images and cloud-masks, none of the gap-filling algorithms outperformed the others consistently in all study areas in terms of the error of individual pixels (Figure 5). However, some algorithms had consistently lower errors than most others. In particular, ordinary Kriging and random forests that include Chl a as a predictor were among the top three algorithms in all four areas. In the TA, ordinary Kriging had the lowest RMSE (0.042 mg m−3, 41% of the RMSE of the null model). Ridge regression and a random forest that included Chl a as a predictor had only slightly higher RMSEs. In the GoM, spatiotemporal Kriging had the lowest RMSE (0.22 mg m−3, 54% of the null model). Random forests that included Chl a-based predictors for interpolation and ordinary Kriging had only slightly higher RMSEs. In the CS, ordinary Kriging had the lowest RMSE (0.96 mg m−3, 58% of the null model). The random forest that included Chl a-based predictors had only a slightly higher RMSE. In the BS, ordinary Kriging had the lowest RMSE (0.78 mg m−3, 43% of the null model). Temporal interpolation, the random forest with Chl a-based predictors, and spatiotemporal Kriging had only slightly higher RMSEs. Furthermore, it is worth noting that for random forests and ridge regression, the versions that included Chl a-based predictors, and thereby allow interpolation, consistently outperformed the versions that included only covariates such as SST and SLA.
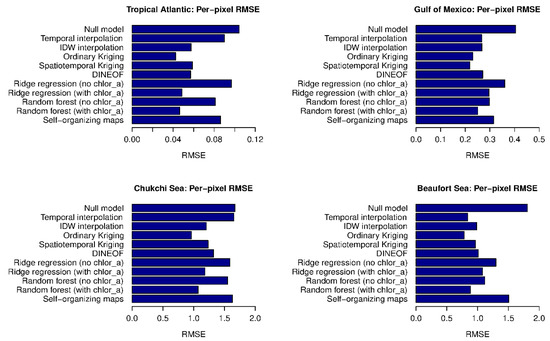
Figure 5.
Means of the algorithms’ per-pixel RMSEs in the four study areas (, Equation (6)). The null model filled all gap pixels with the mean of all pixels that had data. Because of different means and ranges of Chl a concentrations, RMSEs should not be compared across study areas.
3.2. Errors of Regional Means
Likewise, when the algorithms were used to improve estimates of the regional mean Chl a concentration, no algorithm consistently outperformed the others in all study areas (Figure 6). Nevertheless, the best algorithm in each area achieved remarkable reductions of the RMSE, compared to calculating mean Chl a concentrations without prior gap-filling. Similar to per-pixel RMSE reduction, some algorithms consistently worked well in improving regional mean estimates: ordinary Kriging, spatiotemporal Kriging, and DINEOF were among the five best-performing algorithms in all four areas. In the TA, ordinary Kriging had the lowest RMSE (0.004 mg m−3, 20% of the RMSE of calculating the regional mean without prior gap-filling). DINEOF, ridge regression, and the random forest that included Chl a as a predictor had only slightly higher RMSEs. In the GoM, temporal interpolation had the lowest RMSE (0.016 mg m−3, 27% of RMSE without gap-filling). Spatiotemporal Kriging and ordinary Kriging had only slightly higher RMSEs. In the CS, ordinary Kriging had the lowest RMSE (0.15 mg m−3, 42% of RMSE without gap-filling). Several other algorithms also reduced the RMSE considerably but less so than ordinary Kriging. In the BS, temporal interpolation had the lowest RMSE (0.08 mg m−3, 18% of RMSE without gap-filling). Several other algorithms also reduced the RMSE considerably, but less so than temporal interpolation. Again, random forests and ridge regression that included Chl a-based predictors consistently outperformed statistical models that only included potential covariates.
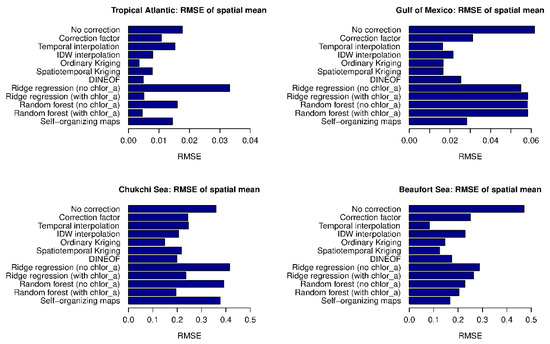
Figure 6.
The root mean squared errors (RMSEs) of regional mean Chl a concentrations calculated without prior gap-filling, and after gap-filling using the different algorithms in the four study areas (, Equation (9)).
3.3. Summary of Algorithm Accuracy
While no algorithm worked best in all study areas and for both gap-filling tasks, some algorithms performed consistently well, whereas the performance of others was more variable, depending on the study area and gap-filling task (Figure 7). For filling individual pixels, ordinary Kriging and random forests that included Chl a-based predictors were always among the best three algorithms. Spatiotemporal Kriging was the best algorithm in the GoM. Elsewhere, it was never among the best, but always among the better-performing algorithms. DINEOF and IDW interpolation were also never among the best, but always among the better algorithms. Given the often small differences in RMSE on which the ranking was based, these three algorithms should also be seen as working consistently well. Self-organizing maps, as well as random forests and ridge regression without Chl a-based predictors, were always among the five algorithms with the most substantial errors. Notably, linear temporal interpolation was one of the best algorithms in the BS and GoM, but one of the worst algorithms in the CS and TA.
3.4. Errors of Regional Means as a Function of Cloud Cover
The error in regional means calculated from data with gaps caused by clouds has two components (ignoring sources of error not related to data gaps; see Section 4.2). First, data gaps introduce error simply because the sample size (i.e., the number of pixels with data) decreases. We estimated this component of the error by calculating the means of the cloud-free images omitting different proportions of randomly selected pixels. This error was small and only increased steeply as the percentage of obscured pixels exceeded 90% (Figure 8, dashed black curves). Second, data gaps introduce error because clouds often cover continuous parts of the study area, which may, on average, have higher or lower Chl a concentrations than the mean for the visible parts of the region. The total error caused by realistically shaped data gaps was much larger and increased more steeply even at moderate levels of cloud cover (Figure 8, solid black curves). The colored curves in Figure 8 represent the different algorithms. The best algorithms, according to their RMSEmean (Figure 6), tended to perform well over the whole range of cloud cover. In some cases, the errors of spatial interpolation algorithms (ordinary Kriging and IDW interpolation) increased more steeply at very high levels of cloud cover than those of algorithms incorporating temporal interpolation or including other variables. As earlier discussed, a similar performance of several algorithms in each study area is also evident in Figure 8. At high levels of cloud cover, substantial improvements of the regional mean estimate were achieved by almost all algorithms, and even by multiplication with the simple correction factor.
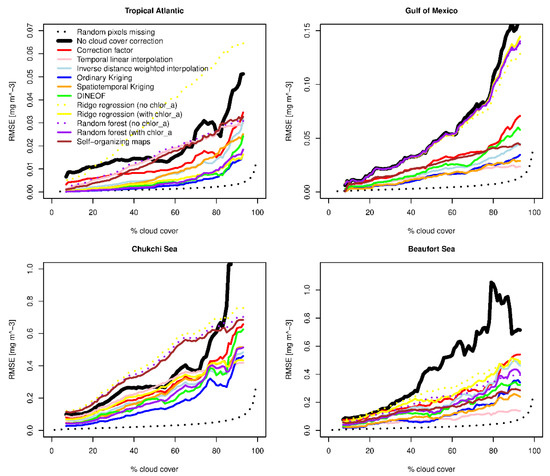
Figure 8.
Running means of the mean error of the regional mean Chl a concentration () as a function of cloud cover, calculated with and without prior cloud-filling.
4. Discussion
4.1. Algorithm Recommendations
We found that applying even simple cloud-filling algorithms before calculating spatial means of Chl a substantially reduced the means’ errors. Prior cloud-filling can thus be a straightforward way to improve regional time series derived from marine satellite data.
Ordinary Kriging was the only algorithm, of those tested here, that was among the best in all four study areas and for both gap-filling tasks. Overall, we found that the best algorithm depends on the study area, the purpose of the gap-filling, and the period covered by the images. For example, temporal interpolation was one of the best algorithms for both gap-filling tasks in the GoM and the BS, but one of the worst in the TA and CS. Random forests were one of the most accurate algorithms for reconstructing individual pixels in all study areas, but one of the least accurate algorithms for correcting the regional mean Chl a concentration in the GoM. One explanation is that the random forests were trained to minimize the RMSE of the predicted Chl a concentration for individual pixels, i.e., they were optimized for this task. Furthermore, when calculating the regional mean, errors in over- and under-estimated pixels cancel each other out. Hence, an algorithm with larger errors in individual pixels can be a better choice for correcting the mean if it is less biased. However, random forests are one of the most complicated algorithms tested in this study. Thus, it is possible that their limited accuracy in some cases could be overcome with additional tuning to the specifics of these study areas and tasks.
Hence, instead of identifying a single best algorithm, we provide guidance for algorithm selection—in particular for researchers who wish to use cloud-filling in their work, but cannot test a large number of cloud-filling algorithms or fine-tune an algorithm that is optimized for their project.
Besides their error statistics, the manual work required to use the algorithms and their computational costs are important considerations. Because these depend to some extent on the software and hardware environment, the implementation used, and the user’s familiarity with an algorithm, we do not provide quantitative benchmarks but note qualitatively that there were large differences between the algorithms. For example, temporal linear interpolation can be implemented with a few lines of code. In the largest study area (GoM), filling all combinations of cloud-free images and cloud masks took only minutes on our workstation, without any dedicated optimization efforts. In contrast, the implementation of spatiotemporal Kriging—while based on an existing library—required more manual work (for example, calculating sample variograms and fitting and testing different theoretical variogram models). Computation time for all combinations of cloud-free images and cloud masks in the GoM on the same workstation was almost two weeks. Random forests required considerable manual preparation (e.g., to generate the training data) and several days of computation time.
Three algorithms had above-average accuracy across all study areas and tasks: ordinary Kriging, spatiotemporal Kriging, and DINEOF. These algorithms are available in different software packages. Ordinary Kriging took moderate manual effort and computation time. DINEOF had larger errors and also required moderate computation time, but still worked consistently well and does not require prior manual steps such as the calculation of a variogram. Furthermore, DINEOF has been tested and found to perform well in many other settings [22,24,25,26,27,29,70]. Spatiotemporal Kriging, in contrast, was one the most time-consuming algorithms we tested, both in terms of manual effort and computation. However, we tested the algorithms on 8-day and 3-day composites. Daily imagery will have less spatial coverage, but temporally adjacent images are closer in time. Spatiotemporal interpolation may hence be worth the additional effort when filling data gaps in images with higher temporal resolution. Ordinary Kriging, spatiotemporal Kriging, and DINEOF are consequently good default choices for many applications. IDW interpolation is much faster but filled gaps less accurately than ordinary Kriging in all cases. This result is consistent with results for applications other than cloud-filling in satellite data, where Kriging has been shown to outperform IDW [71,72]. Other algorithms with more variable performance can still be suitable for specific study areas. For example, simple linear temporal interpolation worked well in the BS and the GoM. Both areas have strong gradients which persist over multiple images, and can thus be accurately interpolated from past and future observations. Furthermore, the overall less frequent cloud cover and higher temporal resolution in the GoM made it more likely that a pixel obscured by clouds had valid data in close temporal proximity. Supervised learning methods including predictors that allow spatiotemporal interpolation, in particular random forests, also showed much potential, but require careful training and testing.
Lastly, there are algorithms that we cannot recommend. Supervised learning that did not take Chl a concentrations in visible pixels and past and future images into account (and thus did not allow spatiotemporal interpolation) did not work well. Self-organizing maps, following the verbal algorithm description in [32], were the most time-consuming algorithms to implement and one of the most computationally demanding. This effort was, overall, not justified by the results, possibly because the algorithm only considered a small spatiotemporal neighborhood around each pixel.
4.2. Scope and Limitations of Study Design
We compared ten gap-filling algorithms in four oceanographically heterogeneous study areas, spanning coastal to offshore waters and Arctic to tropical latitudes; our Arctic study areas can be optically complex even offshore [73]. However, we excluded coastal waters with the highest Chl a concentrations from our analyses for two reasons. First, the global Chl a data product that we used as a foundation is often inaccurate in nearshore waters where colored dissolved organic matter and suspended particulate matter may account for most of the measured optical signal; comparing the accuracy of gap-filling algorithms for areas where the original data product may be inadequate for most applications would not be useful. Second, areas with permanently high Chl a concentrations would have a large influence on the mean of error estimates, as large absolute differences may occur. Excluding these areas was hence a compromise between testing the gap-filling algorithms with realistic regional scale-data and avoiding that reconstruction errors in waters with low Chl a are eclipsed by large absolute errors in highly productive waters. At the same time, ocean color remote sensing of productive, optically complex coastal waters is a crucial component of monitoring changes in the world’s oceans [74]. A test of DINEOF in the Canadian Salish Sea, including satellite-measured Chl a concentrations up to 40 mg m−3, found reasonable agreement between reconstructions and in-situ observations [29]. While beyond the scope of this article, a similar comparison of gap-filling algorithms for satellite data products optimized for highly productive nearshore waters would hence be a promising endeavor.
Our study design has several limitations, mostly arising from the fact that we tested many algorithms in several study areas. Specifically, we focused on relatively basic algorithms that require limited manual tuning efforts. For example, we used omnidirectional variograms for Kriging, assuming that spatial auto-correlation is independent of direction. In contrast, Saulquin et al. [31] implemented a more sophisticated Kriging-based algorithm. Among other improvements, their algorithm accounts for anisotropy (directional differences in spatial autocorrelation). This can improve interpolation, e.g., along coastal land-sea gradients. As another example, we tested simple, linear temporal interpolation, in contrast to Paul et al. [75], who interpolated in time using autocorrelation-based weights for past and future cloud-free observations. Furthermore, there are other algorithms that we did not test at all. For example, Buttlar et al. [76] proposed an algorithm that fills gaps with typical spatial and temporal patterns (similar to DINEOF) but makes explicit use of spatial structure. We also did not test multivariate DINEOF, which fills gaps in correlated oceanographic variables simultaneously [25]. Numerical oceanographic models have also been used to fill gaps in ocean color data [77] and can simulate physical and biological processes even in prolonged periods of cloud cover (such as winters at high latitudes) where interpolation approaches are likely to fail. However, such models do not yet exist for all ocean regions, and we hence focused on algorithms that use publicly available global satellite data as input.
We focused on algorithms for filling data gaps primarily caused by clouds in ocean color data (although some gaps in our data may have been caused by other phenomena such as sun glint and failures of atmospheric correction). Other gap-filling algorithms have been proposed for terrestrial satellite data and different types of data gaps [78,79,80,81,82]. For example, along-track stripes of missing data resulting from sensor malfunction in MODIS-Aqua band 6 can be reconstructed using data from neighboring bands. However, in contrast to many marine applications, terrestrial remote sensing often focuses on sharply delineated, categorical objects (e.g., individual buildings, or land cover patches). Our results cannot inform gap-filling for such applications. For example, while Kriging methods are one of our recommended approaches for ocean color gap-filling, spatial interpolation algorithms cannot appropriately reconstruct typical terrestrial surface textures [81].
A second limitation of our study design is that we tested algorithm performance by transplanting clouds from cloudy onto mostly cloud-free images, assuming that the original images were error-free. However, satellite instruments do not directly measure Chl a concentrations, but electromagnetic radiation detected by the sensor in different wavelength bands. These measurements have to be corrected for effects of the atmosphere and are then used to estimate Chl a, which is subject to different errors. For example, the optical signal from the water also depends on biological factors such as pigment packaging, and the concentrations of other optical water constituents such as colored dissolved organic matter [37]. In the TA, dust blown from deserts not accounted for by standard atmospheric correction algorithms is another potential error source [83]. Satellite-measured Chl a concentrations hence suffer from well-documented errors. For example, Lewis et al. [37] compared satellite estimates of Chl a against in situ measurements in the Chukchi Sea but extending further north than our study area. They reported an RMSE of 4.91 mg m−3 for the global MODIS OC3Mv6 algorithm, and 2.90 mg m−3 for a regionally optimized algorithm (including many coastal sampling stations affected by CDOM). In comparison, the best cloud-filling algorithm tested in this paper for the southern Chukchi Sea had per-pixel reconstruction errors of 1.00 mg m−3. Because of different study areas, the Chl a retrieval errors for visible pixels cannot be directly compared to the per-pixel reconstruction errors estimated in this study. However, the magnitude of these errors suggests that any additional errors introduced by gap-filling were not unreasonably large.
Finally, our approach implicitly assumes that Chl a concentrations are independent of cloud cover. In reality, however, clouds and phytoplankton interact. Clouds affect phytoplankton by limiting light available for photosynthesis [9]. Conversely, some phytoplankton taxa produce dimethylsulfide, which escapes to the atmosphere, is oxidized, and forms cloud condensation nuclei [84]. Hence, while much about the interactions between phytoplankton and atmospheric conditions remains unknown, Chl a concentrations obscured by persistent cloud cover can be different from those that would have occurred if the sky had been clear. Our method, based on transplanting clouds from cloudier days onto in fact sunlit waters, does not account for these possible errors.
Some of these limitations could be avoided by comparing cloud-filling algorithms based on in-situ measurements of Chl a. However, satellite-derived Chl a estimates in our study areas can be systematically over-estimated, e.g., because of high CDOM concentrations in coastal waters. In such a setting, a cloud-filling algorithm that systematically under-estimates values would appear to perform well—but in general, biased reconstructions are not a desirable property of an algorithm. Therefore, we decided to treat the reconstruction of missing data in satellite images as a problem that is separate from the accurate satellite retrieval of Chl a in the first place. Nevertheless, it is important to keep in mind that the error estimates presented in this paper do not represent the tested gap-filling algorithms’ skill in reconstructing real Chl a concentrations, but their skill in reconstructing the original images.
In summary, we chose several cloud-filling algorithms for inclusion in this comparison because they are widely used (e.g., DINEOF, Kriging), based on a unique idea (e.g., SOM), or promising for further research (e.g., supervised learning). Nevertheless, each of the tested algorithms could, in principle, be further improved and fine-tuned to the specifics of our study areas, and other algorithms worth testing exist. However, our focus on relatively easy-to-use algorithms can guide readers who cannot develop specialized cloud-filling algorithms but wish to apply such algorithms in their research. We also made the cloud-free images as well as the cloud masks publicly available. Consequently, researchers wishing to test other algorithms or fine-tuned versions of the algorithms tested here can conduct the same analyses using the same set of realistic test situations. Our results also guide the identification of other algorithms that may be promising for specific study regions and gap-filling problems (Section 4.1 and Section 4.3). Finally, the recommended generic algorithms that we identified can serve as a baseline for demonstrating performance gains by future algorithms.
4.3. Properties of the Best Algorithms
All of the recommended algorithms incorporated some form of interpolation of Chl a in space, time, or both. The importance of interpolation was further highlighted by the result that the two supervised learning algorithms tested here worked much better if predictors allowing spatiotemporal interpolation were included. Correlated oceanographic variables such as SST and SLA may sometimes allow the reconstruction of transient and small features that interpolation misses, and provide relevant information to fall back on if widespread cloud cover persists, but by themselves did not allow the accurate reconstruction of Chl a.
Random forests can represent non-linear relationships and interactions between predictors and consistently outperformed ridge regression. Given a large number of images available from ocean color missions and a large number of pixels in each image, sufficiently large training sets for such flexible models can normally be extracted. Furthermore, there is much room for improvements over our relatively basic supervised learning methods. First, remote sensing applications of supervised learning make increasing use of advances in deep learning [85], including the first deep-learning-based gap-filling algorithms for terrestrial [82,86] and marine satellite data [87]. In this comparison, we included only relatively easy-to-use supervised learning algorithms such as random forests, which require less computation time and tend to produce adequate predictions without the need for major manual tuning efforts [88]. The strong performance of random forests in terms of per-pixel reconstruction suggests that the further development of supervised learning algorithms for cloud-filling in marine satellite data is a promising undertaking. Second, it would be helpful to engineer features that allow the representation of anisotropy, for example, by including visible pixels for interpolation based on both distance and direction. Third, it would be promising to test hybrid methods, such as supervised learning methods that include interpolated values from geostatistical methods as predictors.
Merged multi-instrument data products like GlobColour can substantially reduce data gaps caused by clouds, compared to observations from a single instrument. Such data can thus make gap-filling superfluous in some applications. However, considerable gaps remain in merged products. For example, GlobColour data combining images from SeaWiFS, MODIS-Aqua, and MERIS covered about 25% of the global oceans each day from 2002–2009 [89]. Furthermore, some time periods are covered by only one moderate-resolution ocean color instrument (for example, the period from the launch of SeaWiFS in 1997 until the launch of MERIS and MODIS-Aqua in 2002). Consequently, gap-filling remains relevant even as high-quality, multi-instrument, merged data products become available, and new ocean color missions are launched.
5. Conclusions
- Data gaps caused by clouds lead to errors in estimated regional mean chlorophyll a concentrations. These errors can, however, be substantially reduced by prior gap-filling, even with simple algorithms.
- The best algorithm depends on the specific study area, data, and task. Ordinary Kriging, spatiotemporal Kriging, and DINEOF worked well across study areas and tasks, are available in various software packages and are thus recommended as generic gap-filling approaches for marine satellite data. The choice between these algorithms should take the data’s temporal resolution into account.
- Random forests including predictors that allow spatiotemporal interpolation reconstructed individual pixel values most accurately. This result suggests that the continued development of interpolating supervised learning methods for filling data gaps in marine satellite imagery is a promising direction for future research.
- The recommended cloud-filling algorithms allowed interpolation in space and/or time over relatively large distances. Correlated oceanographic variables such as SST and SLA may help to fill in local details, or serve as a backup if clouds are persistent and widespread, but did not by themselves allow the accurate reconstruction of Chl a.
Author Contributions
Conceptualization: A.S. (Andy Stock) and L.M.W.; methodology: A.S. (Andy Stock) and M.A.C.; data curation: G.L.V.D., A.S. (Andy Stock), and M.M.M.; software: A.S. (Andy Stock); formal analysis: A.S. (Andy Stock); writing—original draft preparation: A.S. (Andy Stock); writing—review and editing: all authors; visualization: A.S. (Andy Stock); supervision: F.M., K.R.A., A.S. (Ajit Subramaniam); project administration, L.M.W.; funding acquisition: F.M., K.R.A., A.S. (Ajit Subramaniam). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Stanford University’s Catalyst for Collaborative Solutions Program, NASA OBB grant NNX16AAJ08G, NSF OCE-1737128, the Earth Institute Postdoctoral Research Program at Columbia University, and the Gulf of Mexico Research Initiative’s “Ecosystem Impacts of Oil and Gas Inputs to the Gulf” (ECOGIG) program.
Acknowledgments
This study was conducted using publicly available data provided by NASA, NOAA, the E.U. Copernicus Marine Service, and IFREMER. This is ECOGIG contribution #554 and LDEO contribution #8451.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Halpern, B.S.; Frazier, M.; Afflerbach, J.; Lowndes, J.S.; Micheli, F.; O’Hara, C.; Scarborough, C.; Selkoe, K.A. Recent pace of change in human impact on the world’s ocean. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Pauly, D.; Christensen, V.; Guénette, S.; Pitcher, T.J.; Sumaila, U.R.; Walters, C.J.; Watson, R.A.; Zeller, D. Towards sustainability in world fisheries. Nature 2002, 418, 689–695. [Google Scholar] [CrossRef] [PubMed]
- Poloczanska, E.S.; Brown, C.J.; Sydeman, W.J.; Kiessling, W.; Schoeman, D.S.; Moore, P.J.; Brander, K.; Bruno, J.F.; Buckley, L.B.; Burrows, M.T.; et al. Global imprint of climate change on marine life. Nat. Clim. Chang. 2013, 3, 919–925. [Google Scholar] [CrossRef]
- Stock, A.; Crowder, L.B.; Halpern, B.S.; Micheli, F. Uncertainty analysis and robust areas of high and low modeled human impact on the global oceans. Conserv. Biol. 2018, 32, 1368–1379. [Google Scholar] [CrossRef] [PubMed]
- McClain, C.R. A decade of ocean color observations. Annu. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed]
- King, M.D.; Platnick, S.; Menzel, W.P.; Ackerman, S.A.; Hubanks, P.A. Spatial and Temporal Distribution of Clouds Observed by MODIS Onboard the Terra and Aqua Satellites. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 3826–3852. [Google Scholar] [CrossRef]
- Warren, S.; Eastman, R.; Hahn, C. CLOUDS AND FOG | Climatology. In Encyclopedia of Atmospheric Sciences; Elsevier: Amsterdam, The Netherlands, 2015; pp. 161–169. [Google Scholar]
- Carr, M.-E.; Friedrichs, M.A.; Schmeltz, M.; Aita, M.N.; Antoine, D.; Arrigo, K.R.; Asanuma, I.; Aumont, O.; Barber, R.P.; Behrenfeld, M.; et al. A comparison of global estimates of marine primary production from ocean color. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 741–770. [Google Scholar] [CrossRef]
- Lee, Z.; Marra, J.; Perry, M.J.; Kahru, M. Estimating oceanic primary productivity from ocean color remote sensing: A strategic assessment. J. Mar. Syst. 2015, 149, 50–59. [Google Scholar] [CrossRef]
- Field, C.B. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Boyce, D.G.; Dowd, M.; Lewis, M.R.; Worm, B. Estimating global chlorophyll changes over the past century. Prog. Oceanogr. 2014, 122, 163–173. [Google Scholar] [CrossRef]
- Arrigo, K.R.; Van Dijken, G.L.; Pabi, S. Impact of a shrinking Arctic ice cover on marine primary production. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef]
- Arrigo, K.R.; Van Dijken, G.L. Secular trends in Arctic Ocean net primary production. J. Geophys. Res. Space Phys. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Ardyna, M.; Babin, M.; Gosselin, M.; Devred, E.; Rainville, L.; Tremblay, J.-É. Recent Arctic Ocean sea ice loss triggers novel fall phytoplankton blooms. Geophys. Res. Lett. 2014, 41, 6207–6212. [Google Scholar] [CrossRef]
- Arrigo, K.R.; Van Dijken, G.L. Continued increases in Arctic Ocean primary production. Prog. Oceanogr. 2015, 136, 60–70. [Google Scholar] [CrossRef]
- Carstensen, J.; Andersen, J.H.; Gustafsson, B.G.; Conley, D.J. Deoxygenation of the Baltic Sea during the last century. Proc. Natl. Acad. Sci. USA 2014, 111, 5628–5633. [Google Scholar] [CrossRef]
- Fleming-Lehtinen, V.; Andersen, J.H.; Carstensen, J.; Łysiak-Pastuszak, E.; Murray, C.; Pyhälä, M.; Laamanen, M. Recent developments in assessment methodology reveal that the Baltic Sea eutrophication problem is expanding. Ecol. Indic. 2015, 48, 380–388. [Google Scholar] [CrossRef]
- Murray, C.J.; Muller-Karulis, B.; Carstensen, J.; Conley, D.J.; Gustafsson, B.G.; Andersen, J.H. Past, Present and Future Eutrophication Status of the Baltic Sea. Front. Mar. Sci. 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Rabalais, N.N.; Turner, R.E.; Wiseman, W.J. Gulf of Mexico hypoxia, a.k.a. ‘The dead zone’. Annu. Rev. Ecol. Syst. 2002, 33, 235–263. [Google Scholar] [CrossRef]
- Denman, K.L.; Dower, J.F. Patch Dynamics. Encycl. Ocean Sci. 2001, 348–355. [Google Scholar]
- Martin, A. Phytoplankton patchiness: The role of lateral stirring and mixing. Prog. Oceanogr. 2003, 57, 125–174. [Google Scholar] [CrossRef]
- Sirjacobs, D.; Alvera-Azcárate, A.; Barth, A.; Lacroix, G.; Park, Y.; Nechad, B.; Ruddick, K.; Beckers, J.-M. Cloud filling of ocean colour and sea surface temperature remote sensing products over the Southern North Sea by the Data Interpolating Empirical Orthogonal Functions methodology. J. Sea Res. 2011, 65, 114–130. [Google Scholar] [CrossRef]
- Beckers, J.M.; Rixen, M.; Rixen, M. EOF Calculations and Data Filling from Incomplete Oceanographic Datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Rixen, M.; Beckers, J. Reconstruction of incomplete oceanographic data sets using empirical orthogonal functions: Application to the Adriatic Sea surface temperature. Ocean. Model. 2005, 9, 325–346. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Beckers, J.-M.; Weisberg, R.H. Correction to Multivariate reconstruction of missing data in sea surface temperature, chlorophyll, and wind satellite fields. J. Geophys. Res. Space Phys. 2007, 112, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; He, R. Spatial and temporal variability of SST and ocean color in the Gulf of Maine based on cloud-free SST and chlorophyll reconstructions in 2003–2012. Remote. Sens. Environ. 2014, 144, 98–108. [Google Scholar] [CrossRef]
- Alvera-Azcaràte, A.; Vanhellemont, Q.; Ruddick, K.; Barth, A.; Beckers, J.M. Analysis of high frequency geostationary ocean colour data using DINEOF. Estuar. Coast. Shelf Sci. 2015, 159, 28–36. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M.; Liu, X.; Wang, M. Filling the Gaps of Missing Data in the Merged VIIRS SNPP/NOAA-20 Ocean Color Product Using the DINEOF Method. Remote Sens. 2019, 11, 178. [Google Scholar] [CrossRef]
- Hilborn, A.; Costa, M.P.F. Applications of DINEOF to Satellite-Derived Chlorophyll-a from a Productive Coastal Region. Remote. Sens. 2018, 10, 1449. [Google Scholar] [CrossRef]
- Urquhart, E.A.; Hoffman, M.J.; Murphy, R.R.; Zaitchik, B.F. Geospatial interpolation of MODIS-derived salinity and temperature in the Chesapeake Bay. Remote. Sens. Environ. 2013, 135, 167–177. [Google Scholar] [CrossRef]
- Saulquin, B.; Gohin, F.; D’Andon, O.F. Interpolated fields of satellite-derived multi-algorithm chlorophyll-a estimates at global and European scales in the frame of the European Copernicus-Marine Environment Monitoring Service. J. Oper. Oceanogr. 2018, 12, 47–57. [Google Scholar] [CrossRef]
- Jouini, M.; Lévy, M.; Crépon, M.; Thiria, S. Reconstruction of satellite chlorophyll images under heavy cloud coverage using a neural classification method. Remote. Sens. Environ. 2013, 131, 232–246. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Barnes, B.B.; Xie, Y.; Lin, G.; Qiu, Z. Improving ocean color data coverage through machine learning. Remote. Sens. Environ. 2019, 222, 286–302. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.-H.; Kim, H.-C.; Kim, B.-K.; Bae, D.; Jo, Y.-H.; Jo, N.; Lee, S.H. Reconstruction of Ocean Color Data Using Machine Learning Techniques in Polar Regions: Focusing on Off Cape Hallett, Ross Sea. Remote. Sens. 2019, 11, 1366. [Google Scholar] [CrossRef]
- Wang, J.; Cota, G.F.; Comiso, J.C. Phytoplankton in the Beaufort and Chukchi Seas: Distribution, dynamics, and environmental forcing. Deep. Sea Res. Part. II Top. Stud. Oceanogr. 2005, 52, 3355–3368. [Google Scholar] [CrossRef]
- Ben Mustapha, S.; Bélanger, S.; Larouche, P. Evaluation of ocean color algorithms in the southeastern Beaufort Sea, Canadian Arctic: New parameterization using SeaWiFS, MODIS, and MERIS spectral bands. Can. J. Remote. Sens. 2012, 38, 535–556. [Google Scholar] [CrossRef]
- Lewis, K.M.; Mitchell, B.; Van Dijken, G.; Arrigo, K. Regional chlorophyll a algorithms in the Arctic Ocean and their effect on satellite-derived primary production estimates. Deep. Sea Res. Part. II Top. Stud. Oceanogr. 2016, 130, 14–27. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Carton, J.A.; McClain, C.R. Variability of upwelling and chlorophyll in the equatorial Atlantic. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef]
- Fennel, K.; Hetland, R.; Feng, Y.; Dimarco, S. A coupled physical-biological model of the Northern Gulf of Mexico shelf: Model description, validation and analysis of phytoplankton variability. Biogeosciences 2011, 8, 1881–1899. [Google Scholar] [CrossRef]
- Muller-Karger, F.E.; Walsh, J.J.; Evans, R.H.; Meyers, M.B. On the seasonal phytoplankton concentration and sea surface temperature cycles of the Gulf of Mexico as determined by satellites. J. Geophys. Res. Space Phys. 1991, 96, 12645–12665. [Google Scholar] [CrossRef]
- Muller-Karger, F.E.; Smith, J.P.; Werner, S.; Chen, R.; Roffer, M.; Liu, Y.; Muhling, B.; Lindo, D.; Lamkin, J.; Cerdeira-Estrada, S.; et al. Natural variability of surface oceanographic conditions in the offshore Gulf of Mexico. Prog. Oceanogr. 2015, 134, 54–76. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. Observations of a Hurricane Katrina-induced phytoplankton bloom in the Gulf of Mexico. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Hu, C.; Weisberg, R.H.; Liu, Y.; Zheng, L.; Daly, K.L.; English, D.; Zhao, J.; Vargo, G.A. Did the northeastern Gulf of Mexico become greener after the Deepwater Horizon oil spill? Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- D’Souza, N.A.; Subramaniam, A.; Juhl, A.R.; Hafez, M.; Chekalyuk, A.; Phan, S.; Yan, B.; Macdonald, I.R.; Weber, S.C.; Montoya, J.P. Elevated surface chlorophyll associated with natural oil seeps in the Gulf of Mexico. Nat. Geosci. 2016, 9, 215–218. [Google Scholar] [CrossRef]
- NASA. Sea-Viewing Wide Field-of-View Sensor (SeaWiFS) Chlorophyll Data; 2014 Reprocessing; Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group: Washington, DC, USA, 2014.
- NASA. Moderate-Resolution Imaging Spectroradiometer (MODIS) Aqua Chlorophyll Data; Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group: Washington, DC, USA, 2014.
- NASA. Sea-Viewing Wide Field-of-View Sensor (SeaWiFS) Chlorophyll Data; 2018 Reprocessing; Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group: Washington, DC, USA, 2018.
- NASA. Moderate-Resolution Imaging Spectroradiometer (MODIS) Aqua Chlorophyll Data; 2018 Reprocessing; Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group: Washington, DC, USA, 2018.
- Meier, W.; Fetterer, F.; Savoie, M.; Mallory, S.; Duerr, R.; Stroeve, J. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 3; National Snow and Ice Data Center: Washington, DC, USA, 2017. [Google Scholar]
- Peng, G.; Meier, W.N.; Scott, D.J.; Savoie, M.H. A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring. Earth Syst. Sci. Data 2013, 5, 311–318. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- NOAA. High Resolution SST data provided by the NOAA/OAR/ESRL PSD. 2019. Available online: https://www.esrl.noaa.gov/psd/ (accessed on 10 February 2019).
- Copernicus. Global Ocean Gridded L4 Sea Surface Heights and Derived Variables Reprocessed (SEALEVEL_GLO_PHY_L4_REP_OBSERVATIONS_008_047). 2019. Available online: http://marine.copernicus.eu/services-portfolio/access-to-products/?option=com_csw&view=details&product_id=SEALEVEL_GLO_PHY_L4_REP_OBSERVATIONS_008_047 (accessed on 10 January 2019).
- NOAA. NCEP North American Regional Reanalysis: NARR. 2019. Available online: https://www.esrl.noaa.gov/psd/data/gridded/data.narr.html (accessed on 10 February 2019).
- Romanic, D.; Hangan, H.; Ćurić, M. Wind climatology of Toronto based on the NCEP/NCAR reanalysis 1 data and its potential relation to solar activity. Theor. Appl. Clim. 2016, 131, 827–843. [Google Scholar] [CrossRef]
- Mesinger, F.; DiMego, G.; Kalnay, E.; Mitchell, K.; Shafran, P.C.; Ebisuzaki, W.; Jović, D.; Woollen, J.; Rogers, E.; Berbery, E.H.; et al. North American Regional Reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.Y.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Development Core Team R. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-temporal geostatistics using gstat. R J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- GHER. “DINEOF”. 2016. Available online: http://modb.oce.ulg.ac.be/mediawiki/index.php/DINEOF (accessed on 27 February 2019).
- Taylor, M. Sinkr: Collection of Functions with Emphasis in Multivariate Data Analysis. R Package Version 0.6. 2017. Available online: https://github.com/marchtaylor/sinkr (accessed on 5 October 2020).
- Alvera-Azcárate, A.A.; Barth, D.S.; Beckers, J.M. Enhancing temporal correlations in EOF expansions for the reconstruction of missing data using DINEOF. Ocean Sci. 2009, 5, 475–485. [Google Scholar] [CrossRef]
- Wehrens, R.; Buydens, L.M. Self-and super-organizing maps in R: The Kohonen package. J. Stat. Softw. 2007, 21, 1–19. [Google Scholar] [CrossRef]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L.; Last, M.; Rice, J. Random Forests: Finding Quasars. Stat. Chall. Astron. 2006, 45, 243–254. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Stock, A.; Subramaniam, A. Accuracy of Empirical Satellite Algorithms for Mapping Phytoplankton Diagnostic Pigments in the Open Ocean: A Supervised Learning Perspective. Front. Mar. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Raitsos, D.E.; Lavender, S.; Maravelias, C.D.; Haralabous, J.; Richardson, A.J.; Reid, P.C. Identifying four phytoplankton functional types from space: An ecological approach. Limnol. Oceanogr. 2008, 53, 605–613. [Google Scholar] [CrossRef]
- Liu, X.; Wang, M. Gap Filling of Missing Data for VIIRS Global Ocean Color Products Using the DINEOF Method. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 4464–4476. [Google Scholar] [CrossRef]
- Murphy, R.R.; Curriero, F.C.; Ball, W.P. Comparison of Spatial Interpolation Methods for Water Quality Evaluation in the Chesapeake Bay. J. Environ. Eng. 2010, 136, 160–171. [Google Scholar] [CrossRef]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An Experimental Comparison of Ordinary and Universal Kriging and Inverse Distance Weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Lewis, K.M.; Arrigo, K.R. Ocean Color Algorithms for Estimating Chlorophyll a CDOM Absorption, and Particle Backscattering in the Arctic Ocean. J. Geophys. Res. Ocean. 2020, 125. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, Á.M.; Clementson, L.A.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining Phytoplankton Diversity from Ocean Color: A Scientific Roadmap for Future Development. Front. Mar. Sci. 2017, 4, 1–15. [Google Scholar] [CrossRef]
- Paul, S.; Willmes, S.; Gutjahr, O.; Preußer, A.; Heinemann, G. Spatial Feature Reconstruction of Cloud-Covered Areas in Daily MODIS Composites. Remote. Sens. 2015, 7, 5042–5056. [Google Scholar] [CrossRef]
- Buttlar, J.V.; Zscheischler, J.; Mahecha, M.D. An extended approach for spatiotemporal gapfilling: Dealing with large and systematic gaps in geoscientific datasets. Nonlinear Process. Geophys. 2014, 21, 203–215. [Google Scholar] [CrossRef]
- Konik, M.; Kowalewski, M.; Bradtke, K.; Darecki, M. The operational method of filling information gaps in satellite imagery using numerical models. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 68–82. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, C. Blind cloud and cloud shadow removal of multitemporal images based on total variation regularized low-rank sparsity decomposition. ISPRS J. Photogramm. Remote. Sens. 2019, 157, 93–107. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Optimizing and comparing gap-filling techniques using simulated NDVI time series from remotely sensed global data. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 93–111. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote. Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote. Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing Data Reconstruction in Remote Sensing Image With a Unified Spatial–Temporal–Spectral Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Gregg, W.W.; Casey, N.W. Global and regional evaluation of the SeaWiFS chlorophyll data set. Remote. Sens. Environ. 2004, 93, 463–479. [Google Scholar] [CrossRef]
- Andreae, M.O.; Cronin, J.; Pizzarello, S. Atmospheric Aerosols: Biogeochemical Sources and Role in Atmospheric Chemistry. Science 1997, 276, 1052–1058. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote. Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Wu, P.; Yin, Z.; Yang, H.; Wu, Y.; Ma, X. Reconstructing Geostationary Satellite Land Surface Temperature Imagery Based on a Multiscale Feature Connected Convolutional Neural Network. Remote. Sens. 2019, 11, 300. [Google Scholar] [CrossRef]
- Barth, A.; Alvera-Azcaràte, A.; Ličer, M.; Beckers, J.-M. DINCAE 1.0: A convolutional neural network with error estimates to reconstruct sea surface temperature satellite observations. Geosci. Model. Dev. 2020, 13, 1609–1622. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote. Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Maritorena, S.; D’Andon, O.H.F.; Mangin, A.; Siegel, D.A. Merged satellite ocean color data products using a bio-optical model: Characteristics, benefits and issues. Remote. Sens. Environ. 2010, 114, 1791–1804. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).