Hybrid Compact Polarimetric SAR for Environmental Monitoring with the RADARSAT Constellation Mission
Abstract
1. Introduction and Background
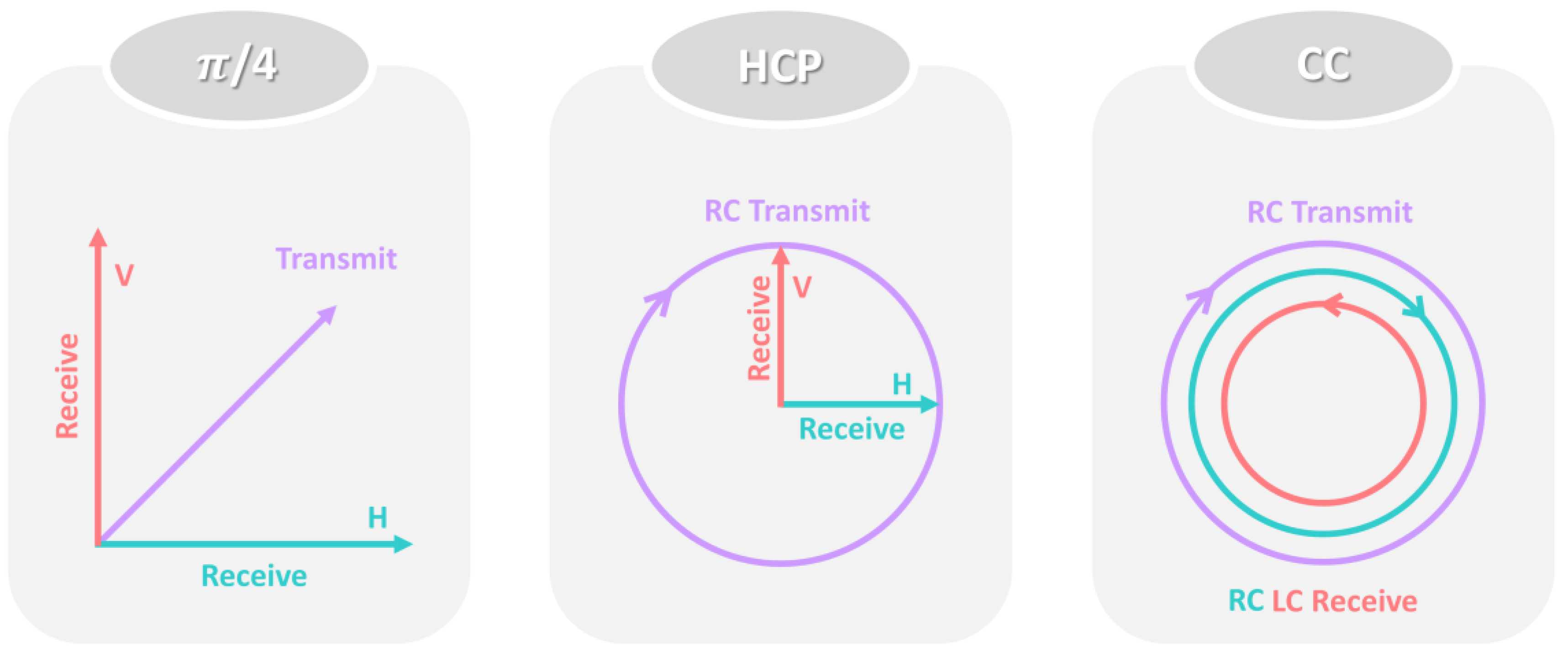
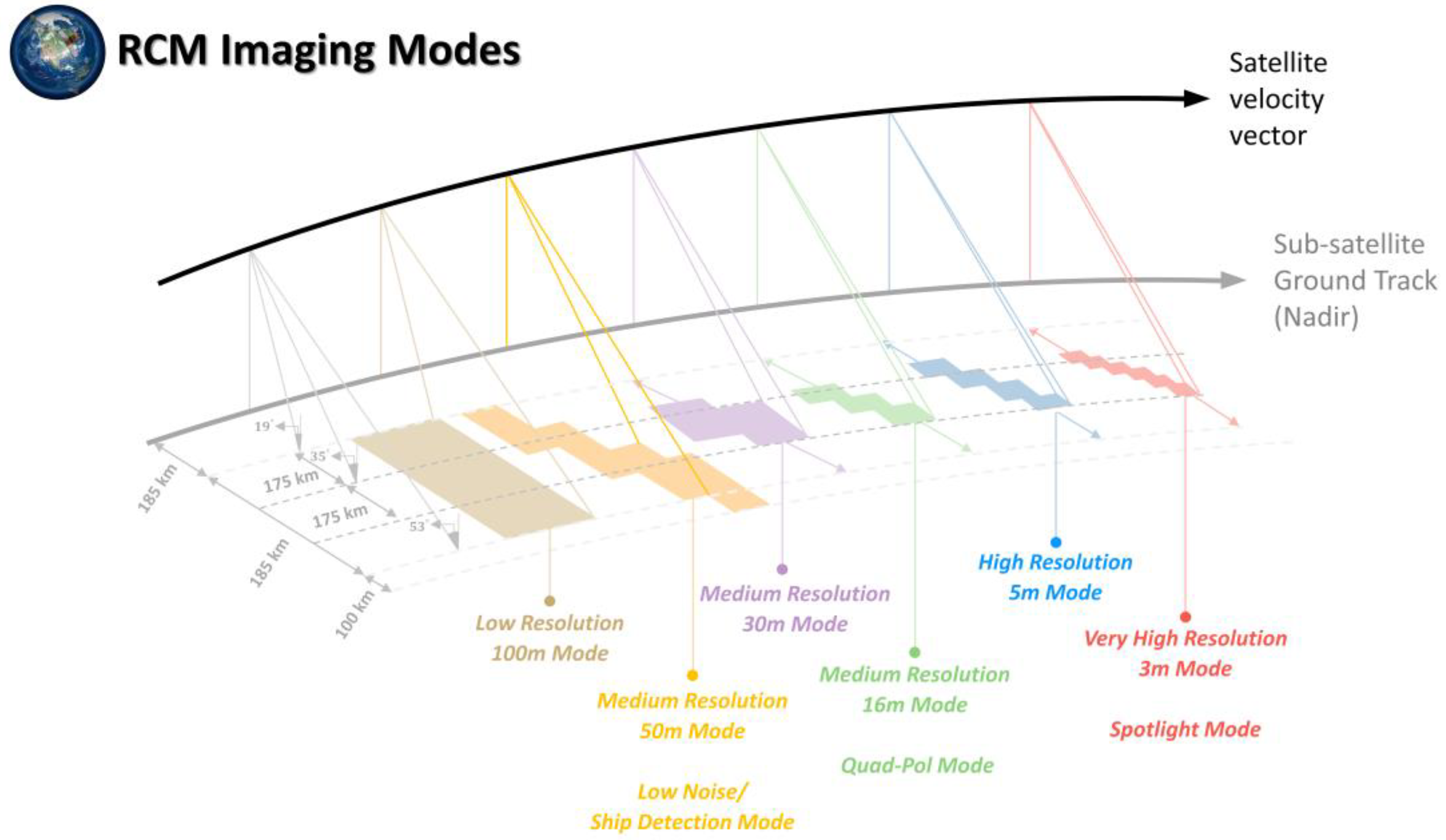
2. HCP SAR and RCM
3. HCP SAR Data Analyses
3.1. Analyses to be Avoided for HCP SAR Data
3.1.1. 3 × 3. Pseudo-Covariance
3.1.2. The Decomposition
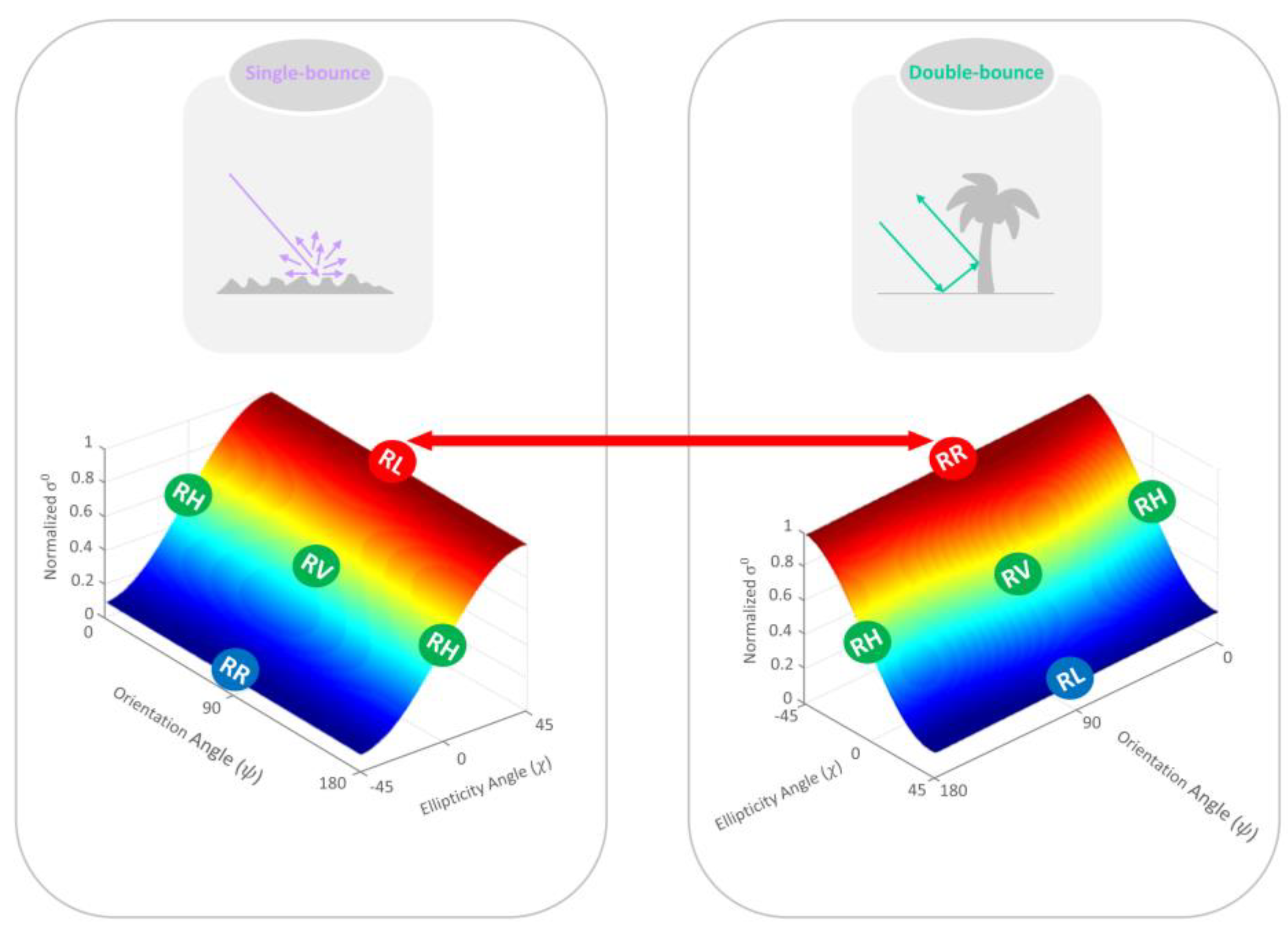
3.1.3. RH and RV Methods
3.2. Recommended Methodologies for HCP Data Analyses
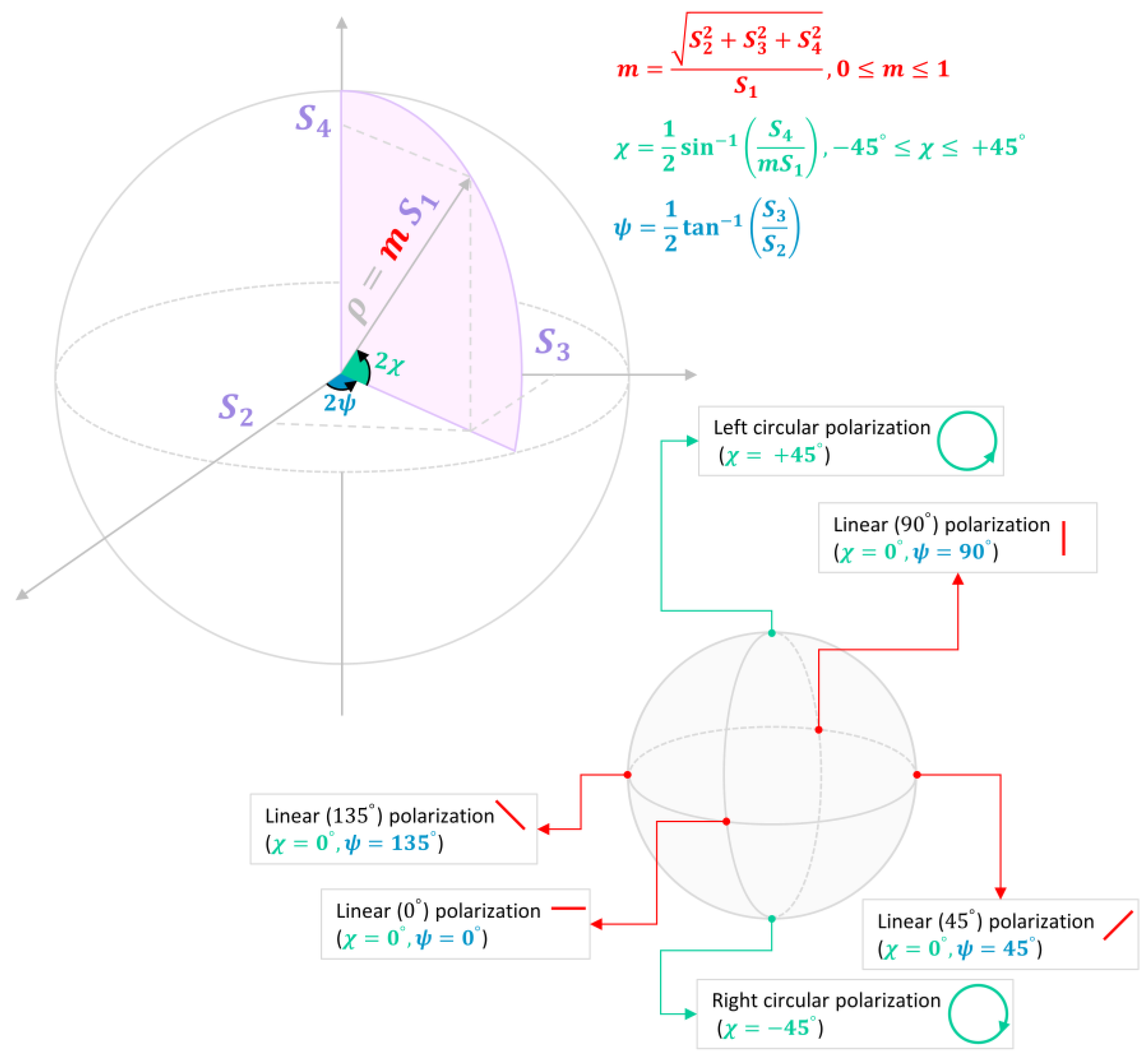
3.2.1. Stokes Vector and Stokes Child Parameters
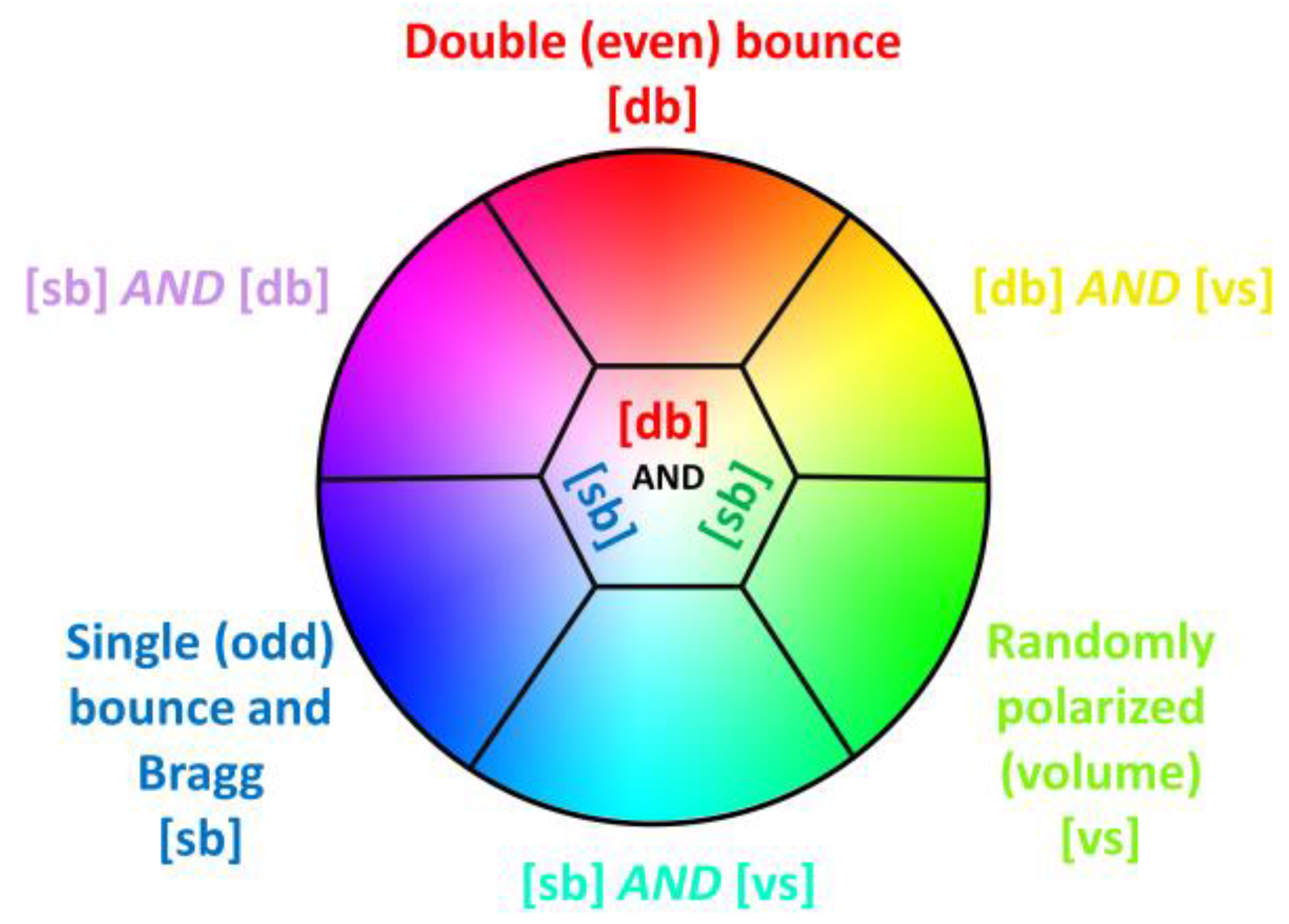
3.2.2. HCP SAR Decomposition
3.2.3. HCP SAR Image Classification
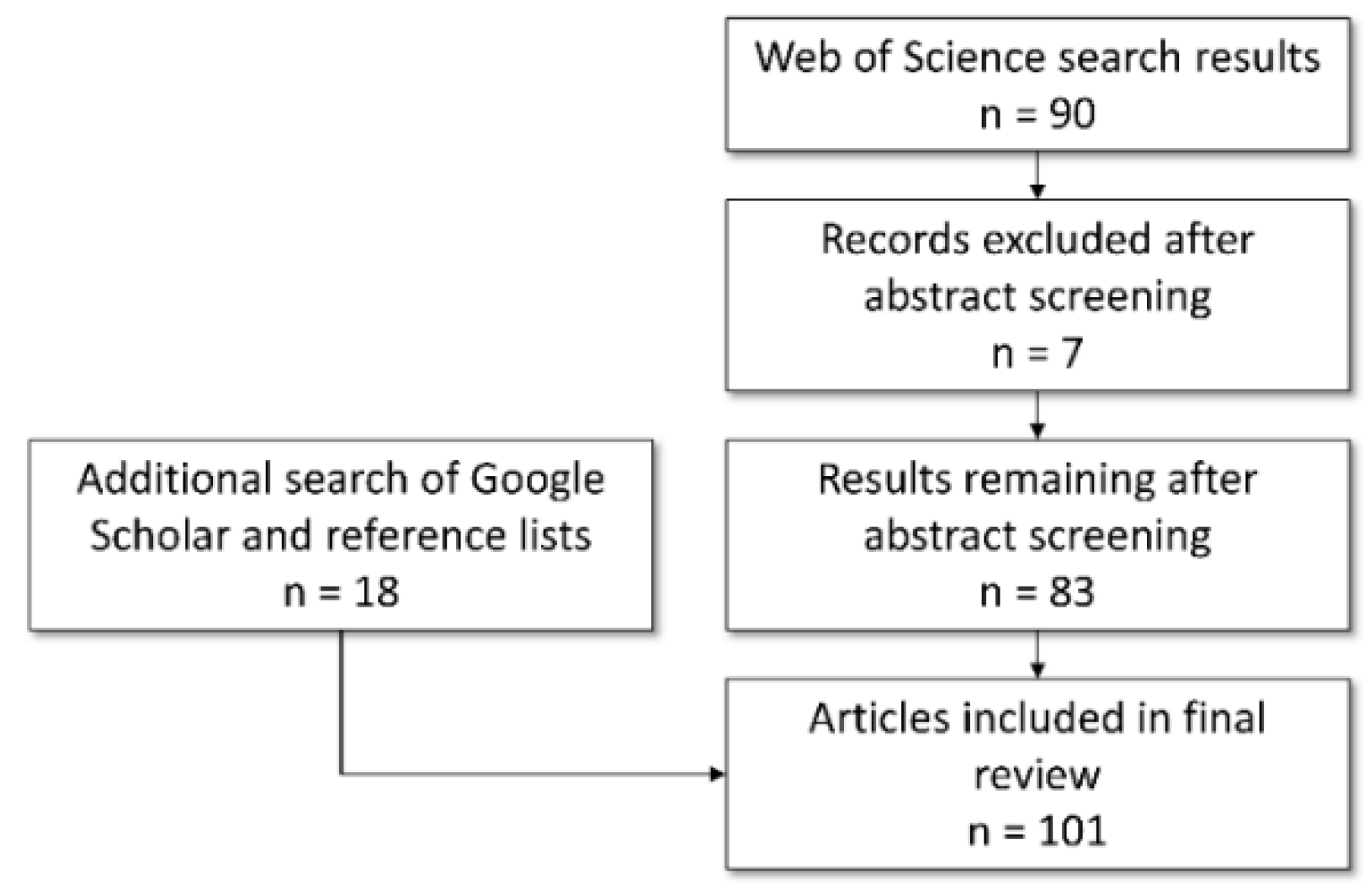
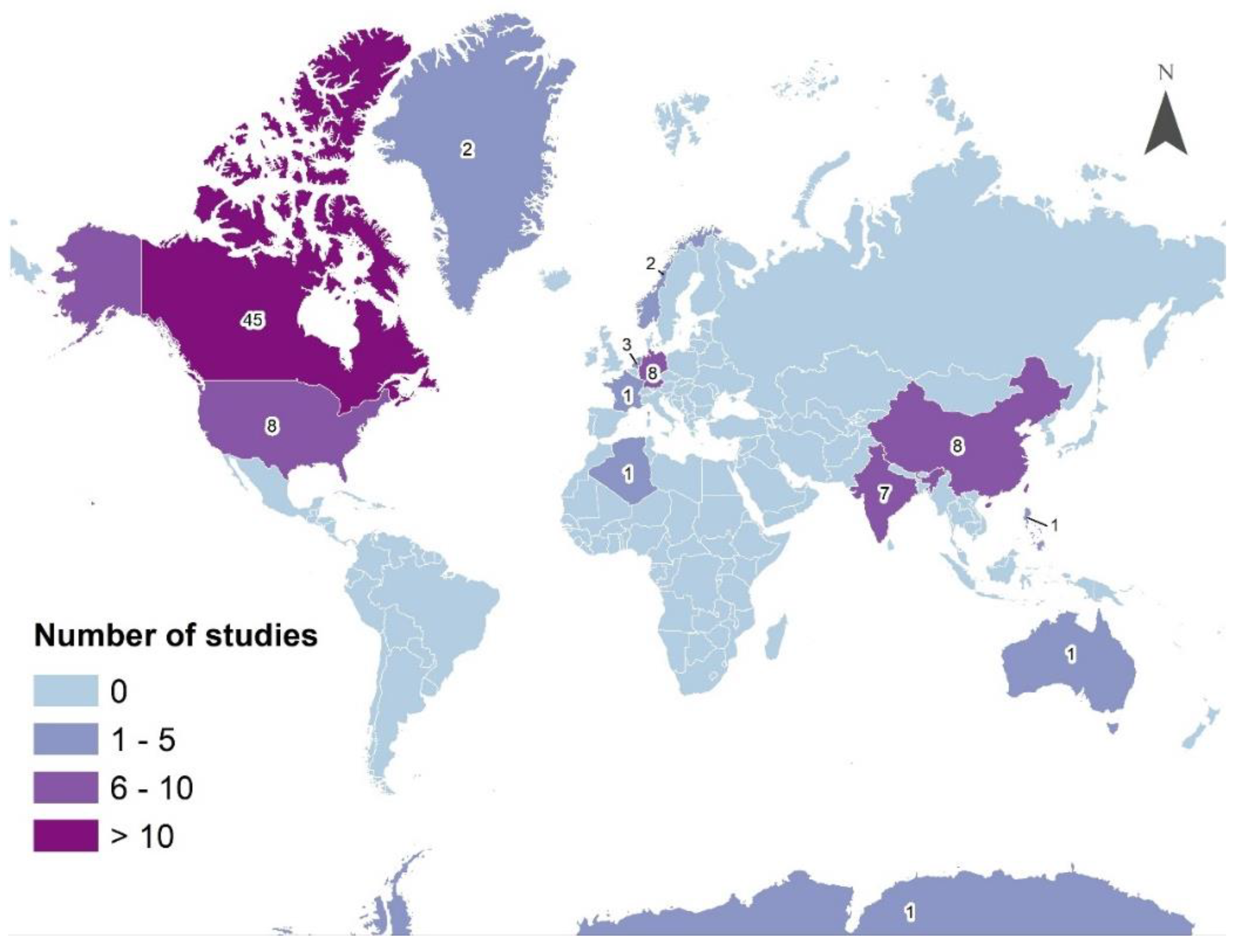
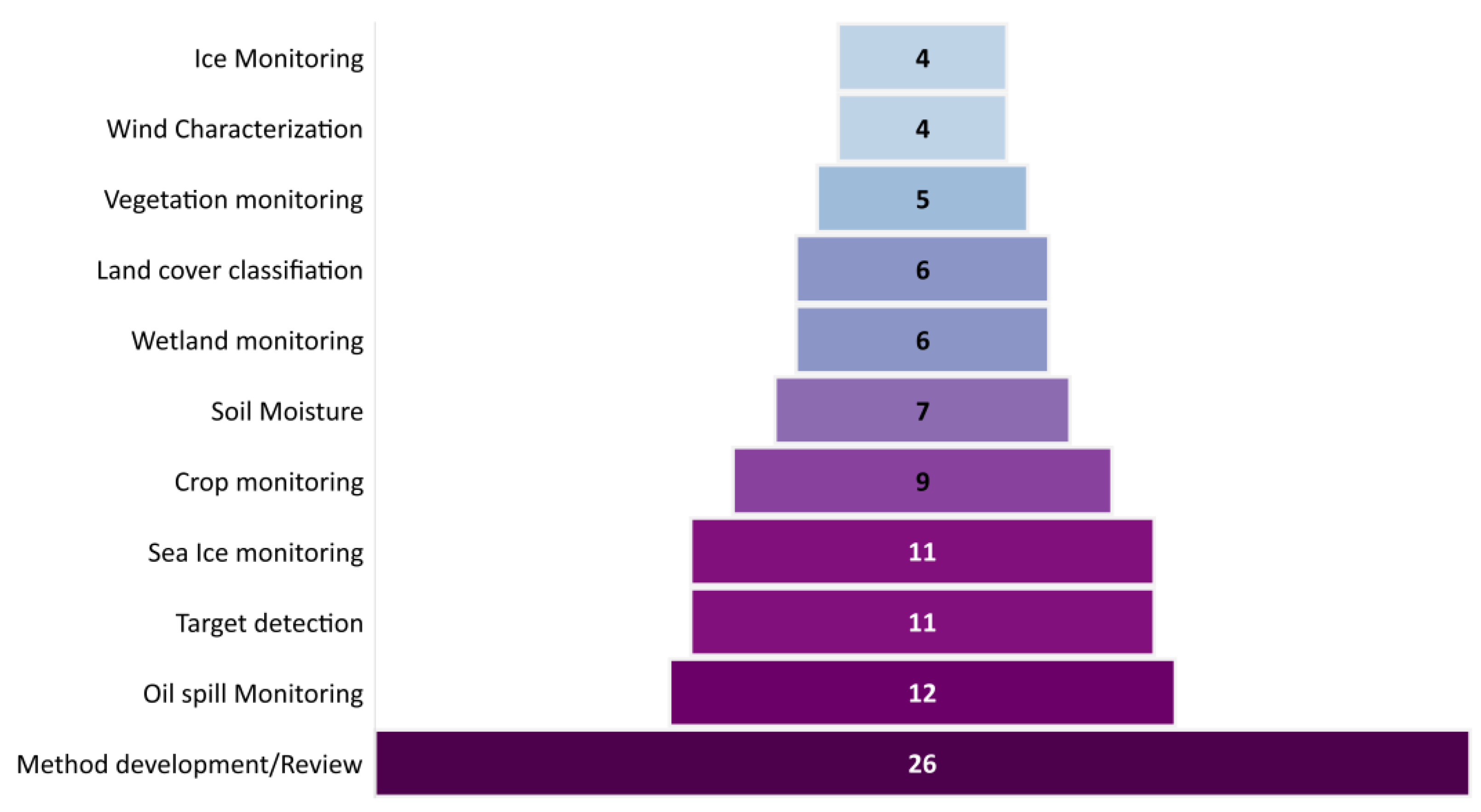
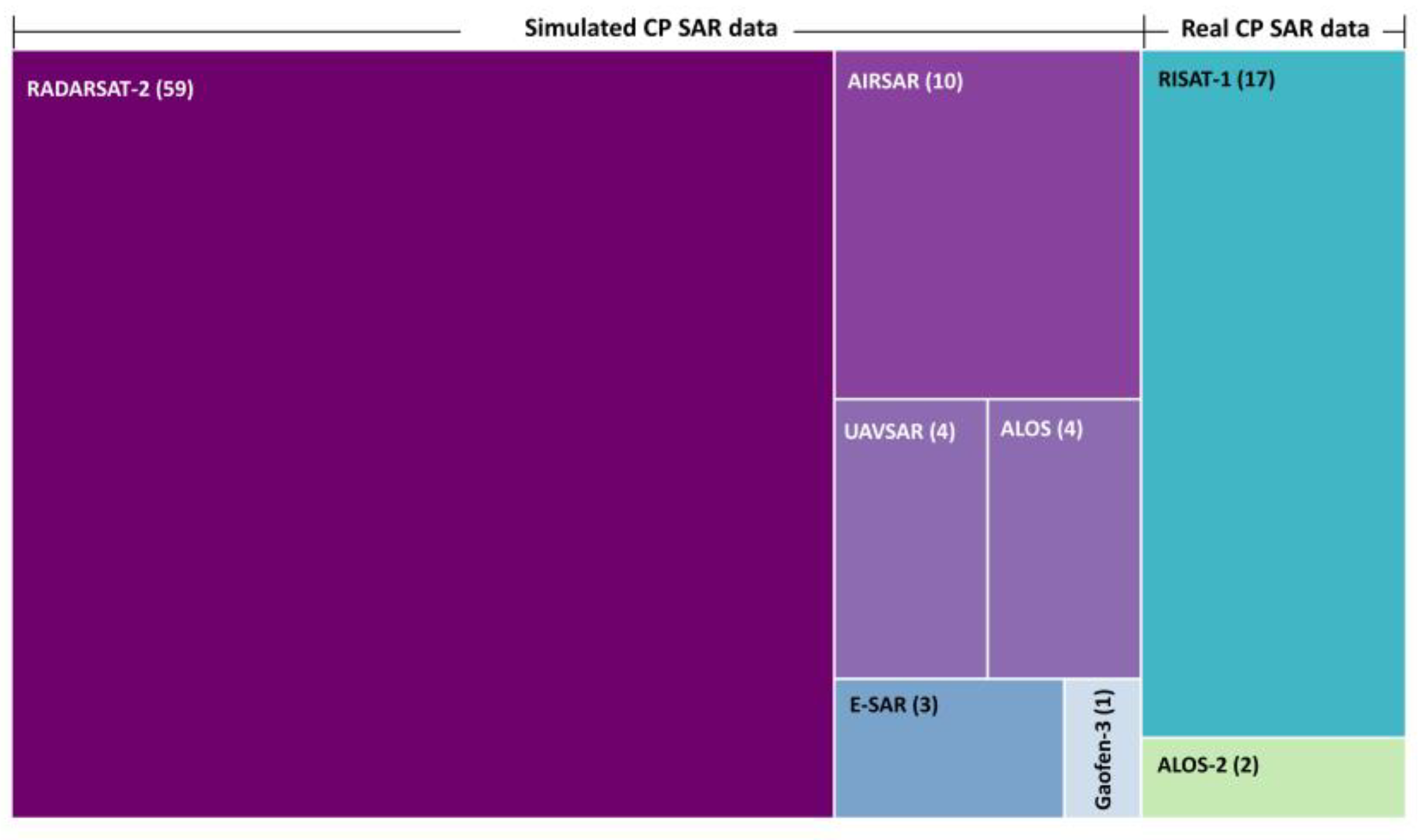
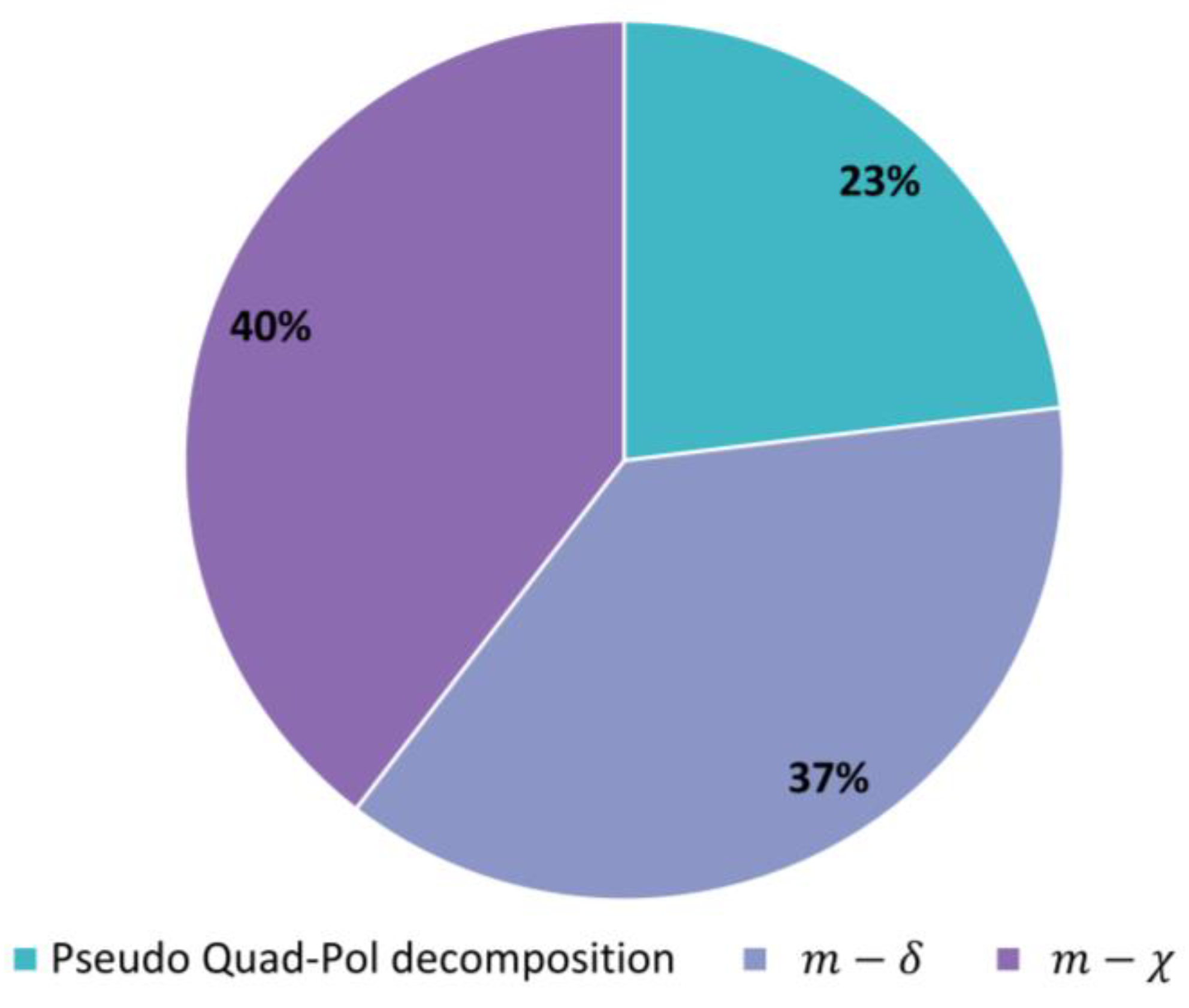
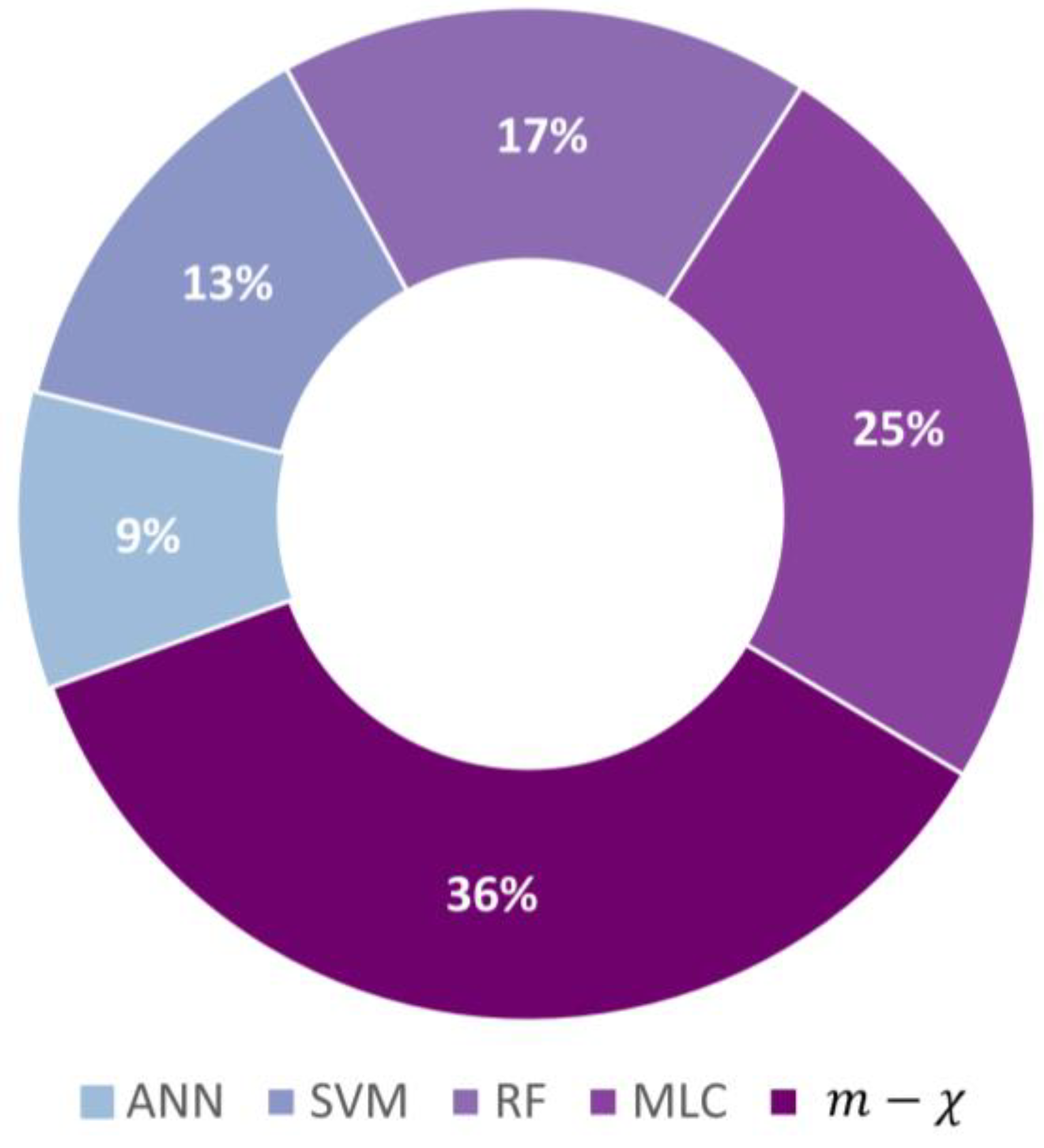
4. HCP Applications Overview: A Meta-Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- RADARSAT Constellation Mission. Available online: https://www.asc-csa.gc.ca/eng/satellites/radarsat/default.asp (accessed on 21 September 2020).
- Raney, R.K. Hybrid Dual-Polarization Synthetic Aperture Radar. Remote Sens. 2019, 11, 1521. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Wetland Water Level Monitoring Using Interferometric Synthetic Aperture Radar (InSAR): A Review. Can. J. Remote Sens. 2018, 44, 247–262. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Mahdianpari, M. Advanced Machine Learning Algorithms for Canadian Wetland Mapping Using Polarimetric Synthetic Aperture Radar (PolSAR) and Optical Imagery. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, October 2019. [Google Scholar]
- Mahdianpari, M.; Brisco, B.; Granger, J.E.; Mohammadimanesh, F.; Salehi, B.; Banks, S.; Homayouni, S.; Bourgeau-Chavez, L.; Weng, Q. The Second Generation Canadian Wetland Inventory Map at 10 Meters Resolution Using Google Earth Engine. Can. J. Remote Sens. 2020, 46, 360–375. [Google Scholar] [CrossRef]
- Ban, Y.; Zhang, P.; Nascetti, A.; Bevington, A.R.; Wulder, M.A. Near Real-Time Wildfire Progression Monitoring with Sentinel-1 SAR Time Series and Deep Learning. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef]
- Salberg, A.-B.; Rudjord, O.; Solberg, A.H.S. Oil Spill Detection in Hybrid-Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6521–6533. [Google Scholar] [CrossRef]
- Yin, J.; Yang, J.; Zhou, Z.-S.; Song, J. The Extended Bragg Scattering Model-Based Method for Ship and Oil-Spill Observation Using Compact Polarimetric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 3760–3772. [Google Scholar] [CrossRef]
- Zakhvatkina, N.; Smirnov, V.G.; Bychkova, I. Satellite SAR Data-based Sea Ice Classification: An Overview. Geoscience 2019, 9, 152. [Google Scholar] [CrossRef]
- Shirvany, R.; Chabert, M.; Tourneret, J.-Y. Ship and Oil-Spill Detection Using the Degree of Polarization in Linear and Hybrid/Compact Dual-Pol SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 885–892. [Google Scholar] [CrossRef]
- Touzi, R.; Vachon, P.W. RCM Polarimetric SAR for Enhanced Ship Detection and Classification. Can. J. Remote Sens. 2015, 41, 473–484. [Google Scholar] [CrossRef]
- Olsen, R.B.; Wahl, T. The role of wide swath SAR in high-latitude coastal management. Johns Hopkins APL Tech. Dig. 2000, 21, 136–140. [Google Scholar]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Homayouni, S.; Gill, E.W. The First Wetland Inventory Map of Newfoundland at a Spatial Resolution of 10 m Using Sentinel-1 and Sentinel-2 Data on the Google Earth Engine Cloud Computing Platform. Remote Sens. 2018, 11, 43. [Google Scholar] [CrossRef]
- Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.R.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E.T.A.; et al. A Review of the Application of Optical and Radar Remote Sensing Data Fusion to Land Use Mapping and Monitoring. Remote Sens. 2016, 8, 70. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-temporal, multi-frequency, and multi-polarization coherence and SAR backscatter analysis of wetlands. ISPRS J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Souyris, J.-C.; Imbo, P.; Fjortoft, R.; Mingot, S.; Lee, J.-S. Compact polarimetry based on symmetry properties of geophysical media: The /spl pi//4 mode. IEEE Trans. Geosci. Remote Sens. 2005, 43, 634–646. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Gill, E.; Molinier, M. A new fully convolutional neural network for semantic segmentation of polarimetric SAR imagery in complex land cover ecosystem. ISPRS J. Photogramm. Remote Sens. 2019, 151, 223–236. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Homayouni, S. Unsupervised wishart classfication of wetlands in Newfoundland, Canada using polsar data based on fisher linear discriminant analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 305–310. [Google Scholar] [CrossRef]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Boerner, W.M. PolSARPro v3. 0-Lecture Notes, Basic Concepts in Radar Polarimetry; European Space Agency: Noordwijk, The Netherlands, 2010.
- Van Zyl, J.J.; Zebker, H.A.; Elachi, C. Imaging radar polarization signatures: Theory and observation. Radio Sci. 1987, 22, 529–543. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F. The Effect of PolSAR Image De-speckling on Wetland Classification: Introducing a New Adaptive Method. Can. J. Remote Sens. 2017, 43, 485–503. [Google Scholar] [CrossRef]
- Van Zyl, J.J. Synthetic Aperture Radar Polarimetry; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 2. [Google Scholar]
- Buono, A.; Nunziata, F.; Migliaccio, M. Analysis of Full and Compact Polarimetric SAR Features Over the Sea Surface. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1527–1531. [Google Scholar] [CrossRef]
- Ainsworth, T.; Kelly, J.; Lee, J.-S. Classification comparisons between dual-pol, compact polarimetric and quad-pol SAR imagery. ISPRS J. Photogramm. Remote Sens. 2009, 64, 464–471. [Google Scholar] [CrossRef]
- Fobert, M.-A.; Spray, J.G.; Singhroy, V. Assessing the Benefits of Simulated RADARSAT Constellation Mission Polarimetry Images for Structural Mapping of an Impact Crater in the Canadian Shield. Can. J. Remote Sens. 2018, 44, 321–336. [Google Scholar] [CrossRef]
- Raney, R.K. Comparing Compact and Quadrature Polarimetric SAR Performance. IEEE Geosci. Remote Sens. Lett. 2016, 13, 861–864. [Google Scholar] [CrossRef]
- Charbonneau, F.J.; Brisco, B.; Raney, R.K.; McNairn, H.; Liu, C.; Vachon, P.W.; Shang, J.; DeAbreu, R.; Champagne, C.; Merzouki, A.; et al. Compact polarimetry overview and applications assessment. Can. J. Remote Sens. 2010, 36, S298–S315. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Brisco, B. An Assessment of Simulated Compact Polarimetric SAR Data for Wetland Classification Using Random Forest Algorithm. Can. J. Remote Sens. 2017, 43, 468–484. [Google Scholar] [CrossRef]
- Sabry, R.; Vachon, P.W. A Unified Framework for General Compact and Quad Polarimetric SAR Data and Imagery Analysis. IEEE Trans. Geosci. Remote Sens. 2013, 52, 582–602. [Google Scholar] [CrossRef]
- Stokes, G.G. On the composition and resolution of streams of polarized light from different sources. Trans. Camb. Philos. Soc. 1851, 9, 399. [Google Scholar]
- Raney, R.K.; Spudis, P.D.; Bussey, B.; Crusan, J.; Jensen, J.R.; Marinelli, W.; McKerracher, P.; Neish, C.; Palsetia, M.; Schulze, R.; et al. The Lunar Mini-RF Radars: Hybrid Polarimetric Architecture and Initial Results. Proc. IEEE 2011, 99, 808–823. [Google Scholar] [CrossRef]
- Raney, R.K.; Cahill, J.T.; Patterson, G.; Bussey, D.B.J. The m-chi decomposition of hybrid dual-polarimetric radar data with application to lunar craters. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Dabboor, M.; Geldsetzer, T. Towards sea ice classification using simulated RADARSAT Constellation Mission compact polarimetric SAR imagery. Remote Sens. Environ. 2014, 140, 189–195. [Google Scholar] [CrossRef]
- Aghabalaei, A.; Maghsoudi, Y.; Ebadi, H. Forest classification using extracted PolSAR features from Compact Polarimetry data. Adv. Space Res. 2016, 57, 1939–1950. [Google Scholar] [CrossRef]
- Dabboor, M.; Singha, S.; Montpetit, B.; Deschamps, B.; Flett, D. Pre-Launch Assessment of RADARSAT Constellation Mission Medium Resolution Modes for Sea Oil Slicks and Lookalike Discrimination. Can. J. Remote Sens. 2019, 45, 530–549. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Gill, E.W. Full and Simulated Compact Polarimetry SAR Responses to Canadian Wetlands: Separability Analysis and Classification. Remote Sens. 2019, 11, 516. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Mohammadimanesh, F.; McNairn, H.; Davidson, A.; Rezaee, M.; Salehi, B.; Homayouni, S. Mid-season Crop Classification Using Dual-, Compact-, and Full-polarization in Preparation for the Radarsat Constellation Mission (RCM). Remote Sens. 2019, 11, 1582. [Google Scholar] [CrossRef]
- Mathews, J.D. A short history of geophysical radar at Arecibo Observatory. Hist. Geo-Space Sci. 2013, 4, 19–33. [Google Scholar] [CrossRef]
- De Lisle, D.; Iris, S.; Arsenault, E.; Smyth, J.; Kroupnik, G. RADARSAT constellation mission status update. In Proceedings of the 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018; pp. 1–5. [Google Scholar]
- Harati-Mokhtari, A.; Wall, A.; Brookes, P.; Wang, J. Automatic Identification System (AIS): A human factors approach. J. Navig. 2007, 60, 373–389. [Google Scholar] [CrossRef]
- Cloude, S.R. A General Elliptical Formulation of Hybrid-POLSAR System Ambiguities. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1066–1069. [Google Scholar] [CrossRef]
- Boularbah, S.; Ouarzeddine, M.; Belhadj-Aissa, A. Investigation of the capability of the Compact Polarimetry mode to Reconstruct Full Polarimetry mode using RADARSAT2 data. Adv. Electromagn. 2012, 1, 19–28. [Google Scholar] [CrossRef]
- Raney, R. Hybrid-Polarity SAR Architecture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3397–3404. [Google Scholar] [CrossRef]
- Truong-LoI, M.-L.; Freeman, A.; Dubois-Fernandez, P.; Pottier, E. Estimation of Soil Moisture and Faraday Rotation from Bare Surfaces Using Compact Polarimetry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3608–3615. [Google Scholar] [CrossRef]
- Singha, S.; Ressel, R. Arctic Sea Ice Characterization Using RISAT-1 Compact-Pol SAR Imagery and Feature Evaluation: A Case Study Over Northeast Greenland. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3504–3514. [Google Scholar] [CrossRef]
- Kumar, V.; McNairn, H.; Bhattacharya, A.; Rao, Y.S. Temporal Response of Scattering from Crops for Transmitted Ellipticity Variation in Simulated Compact-Pol SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5163–5174. [Google Scholar] [CrossRef]
- Van Zyl, J. Unsupervised classification of scattering behavior using radar polarimetry data. IEEE Trans. Geosci. Remote Sens. 1989, 27, 36–45. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Pottier, E.; Cloude, S.R. Application of the H/A/alpha polarimetric decomposition theorem for land classification. In Proceedings of the Wideband Interferometric Sensing and Imaging Polarimetry; International Society for Optics and Photonics, San Diego, CA, USA, 8–14 February 1997; Volume 3120, pp. 132–143. [Google Scholar]
- Touzi, R. Target Scattering Decomposition in Terms of Roll-Invariant Target Parameters. IEEE Trans. Geosci. Remote Sens. 2007, 45, 73–84. [Google Scholar] [CrossRef]
- Doulgeris, A.P.; Anfinsen, S.N.; Eltoft, T. Classification with a Non-Gaussian Model for PolSAR Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2999–3009. [Google Scholar] [CrossRef]
- Yueh, S.; Kong, J.; Jao, J.; Shin, R.; Novak, L. K-Distribution and Polarimetric Terrain Radar Clutter. J. Electromagn. Waves Appl. 1989, 3, 747–768. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Lang, R.H.; Ranson, K.J. K-distribution for multi-look processed polarimetric SAR imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS’94-1994), Mono Lake, CA, USA, 8–12 August 1994; Volume 4, pp. 2179–2181. [Google Scholar]
- Cloude, S.R.; Goodenough, D.G.; Chen, H. Compact decomposition theory for L-Band satellite radar applications. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5097–5100. [Google Scholar]
- Li, H.; Perrie, W. Sea Ice Characterization and Classification Using Hybrid Polarimetry SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4998–5010. [Google Scholar] [CrossRef]
- Kumar, A.; Das, A.; Panigrahi, R.K. Hybrid-Pol Based Three-Component Scattering Model for Analysis of RISAT Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5155–5162. [Google Scholar] [CrossRef]
- Harmon, J.K.; Perillat, P.J.; Slade, M.A. High-resolution radar imaging of Mercury’s north pole. Icarus 2001, 149, 1–15. [Google Scholar] [CrossRef]
- Campbell, B.; Neish, C.; Campbell, D.; Carter, L.; Morgan, G.; Nolan, M.; Patterson, G.W.; Rivera-Valentin, E.; Taylor, P.; Whitten, J. Radar Astronomy for Planetary Surface Studies. Astro2020 Sci. White Pap. 2019, BAAS 51, 350. [Google Scholar]
- Geldsetzer, T.; Arkett, M.; Zagon, T.; Charbonneau, F.; Yackel, J.J.; Scharien, R. All-season Compact-Polarimetry C-band SAR Observations of Sea Ice. Can. J. Remote Sens. 2015, 41, 485–504. [Google Scholar] [CrossRef]
- White, L.; Millard, K.; Banks, S.; Richardson, M.; Pasher, J.; Duffe, J. Moving to the RADARSAT Constellation Mission: Comparing Synthesized Compact Polarimetry and Dual Polarimetry Data with Fully Polarimetric RADARSAT-2 Data for Image Classification of Peatlands. Remote Sens. 2017, 9, 573. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Espeseth, M.M.; Brekke, C.; Johansson, A.M. Assessment of RISAT-1 and Radarsat-2 for Sea Ice Observations from a Hybrid-Polarity Perspective. Remote Sens. 2017, 9, 1088. [Google Scholar] [CrossRef]
- Brisco, B.; Li, K.; Tedford, B.; Charbonneau, F.; Yun, S.; Murnaghan, K. Compact polarimetry assessment for rice and wetland mapping. Int. J. Remote Sens. 2012, 34, 1949–1964. [Google Scholar] [CrossRef]
- Uppala, D.; Venkata, R.K.; Poloju, S.; Rama, S.M.V.; Dadhwal, V.K. Discrimination of maize crop with hybrid polarimetric RISAT1 data. Int. J. Remote Sens. 2016, 37, 2641–2652. [Google Scholar] [CrossRef]
- Uppala, D.; Kothapalli, R.V.; Poloju, S.; Mullapudi, S.S.V.R.; Dadhwal, V.K. Rice Crop Discrimination Using Single Date RISAT1 Hybrid (RH, RV) Polarimetric Data. Photogramm. Eng. Remote Sens. 2015, 81, 557–563. [Google Scholar] [CrossRef]
- Paes, R.L.; Buono, A.; Nunziata, F.; Migliaccio, M. On the Sensitivity Analysis of the Compact-Polarimetry SAR Architectures for Maritime Targets Detection; Bostater, C.R., Mertikas, S.P., Neyt, X., Eds.; Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions; International Society for Optics and Photonics: Amsterdam, The Netherlands, 2014; p. 92401A. [Google Scholar]
- Singha, S. Potential of Compact Polarimetry for Operational Sea Ice Monitoring Over Arctic and Antarctic Region. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018), Valencia, Spain, 22–27 July 2018; pp. 7113–7116. [Google Scholar]
- Ponnurangam, G.G.; Jagdhuber, T.; Hajnsek, I.; Rao, Y.S. Soil Moisture Estimation Using Hybrid Polarimetric SAR Data of RISAT-1. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2033–2049. [Google Scholar] [CrossRef]
- Dasari, K.; Lokam, A. Exploring the Capability of Compact Polarimetry (Hybrid Pol) C Band RISAT-1 Data for Land Cover Classification. IEEE Access 2018, 6, 57981–57993. [Google Scholar] [CrossRef]
- Sabry, R.; Ainsworth, T.L. SAR Compact Polarimetry for Change Detection and Characterization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 898–909. [Google Scholar] [CrossRef]
- Buono, A.; Nunziata, F.; Migliaccio, M.; Li, X. Polarimetric Analysis of Compact-Polarimetry SAR Architectures for Sea Oil Slick Observation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5862–5874. [Google Scholar] [CrossRef]
- Atteia, G.; Collins, M. Ship detection performance using simulated dual-polarization RADARSAT constellation mission data. Int. J. Remote Sens. 2015, 36, 1705–1727. [Google Scholar] [CrossRef]
- Kumar, A.; Das, A.; Panigrahi, R.K. Hybrid-pol Decomposition Methods: A Comparative Evaluation and a New Entropy-based Approach. IETE Tech. Rev. 2019, 37, 296–308. [Google Scholar] [CrossRef]
| Attribute | Type | Category |
|---|---|---|
| First Author | Text | |
| Year | Numeric | |
| Publication | Text | |
| Title | Text | |
| Document Type | Text | Article, Conference, Review, Letter |
| Country | Text | |
| Polarization Mode | Class | π/4, CTLR, HCP |
| Simulated or Real | Class | Simulated, Real |
| Pseudo Quad | Class | Yes, No |
| Comparison of results with full or dual | Class | Full, Dual, Both |
| Classification Method | Class | classification, SVM, MLC, ANN, Random Forest, Thresholding |
| Decomposition Method | Class | , |
| Resolution | Numeric | |
| Features | List | Stokes Vector Components, like- and cross-polarized radar, degree of polarization (m), circular-polarization ratio (CPR), degree of linear polarization, polarization ratio, correlation coefficient, decomposition parameters, phase difference, conformity, alpha angle etc. |
| Number of Features | Numeric |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brisco, B.; Mahdianpari, M.; Mohammadimanesh, F. Hybrid Compact Polarimetric SAR for Environmental Monitoring with the RADARSAT Constellation Mission. Remote Sens. 2020, 12, 3283. https://doi.org/10.3390/rs12203283
Brisco B, Mahdianpari M, Mohammadimanesh F. Hybrid Compact Polarimetric SAR for Environmental Monitoring with the RADARSAT Constellation Mission. Remote Sensing. 2020; 12(20):3283. https://doi.org/10.3390/rs12203283
Chicago/Turabian StyleBrisco, Brian, Masoud Mahdianpari, and Fariba Mohammadimanesh. 2020. "Hybrid Compact Polarimetric SAR for Environmental Monitoring with the RADARSAT Constellation Mission" Remote Sensing 12, no. 20: 3283. https://doi.org/10.3390/rs12203283
APA StyleBrisco, B., Mahdianpari, M., & Mohammadimanesh, F. (2020). Hybrid Compact Polarimetric SAR for Environmental Monitoring with the RADARSAT Constellation Mission. Remote Sensing, 12(20), 3283. https://doi.org/10.3390/rs12203283







