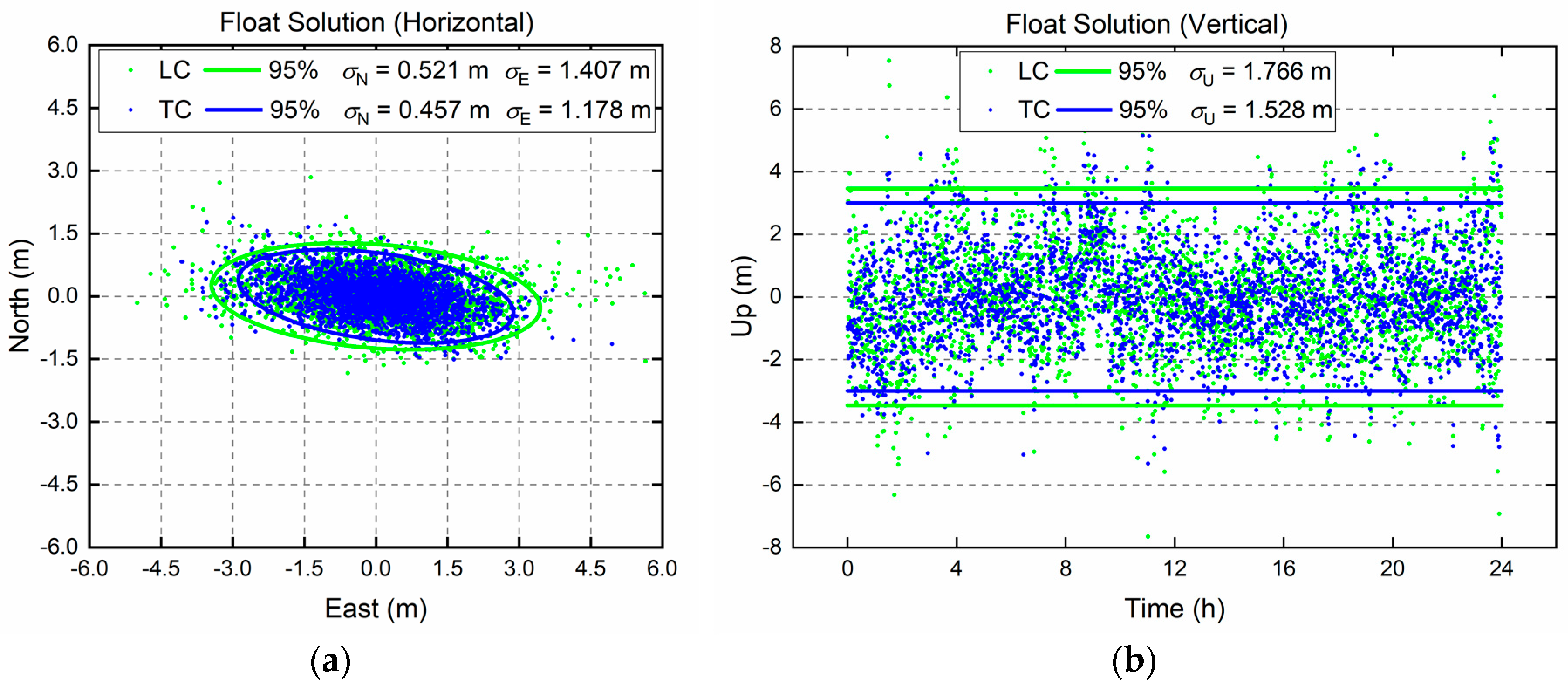
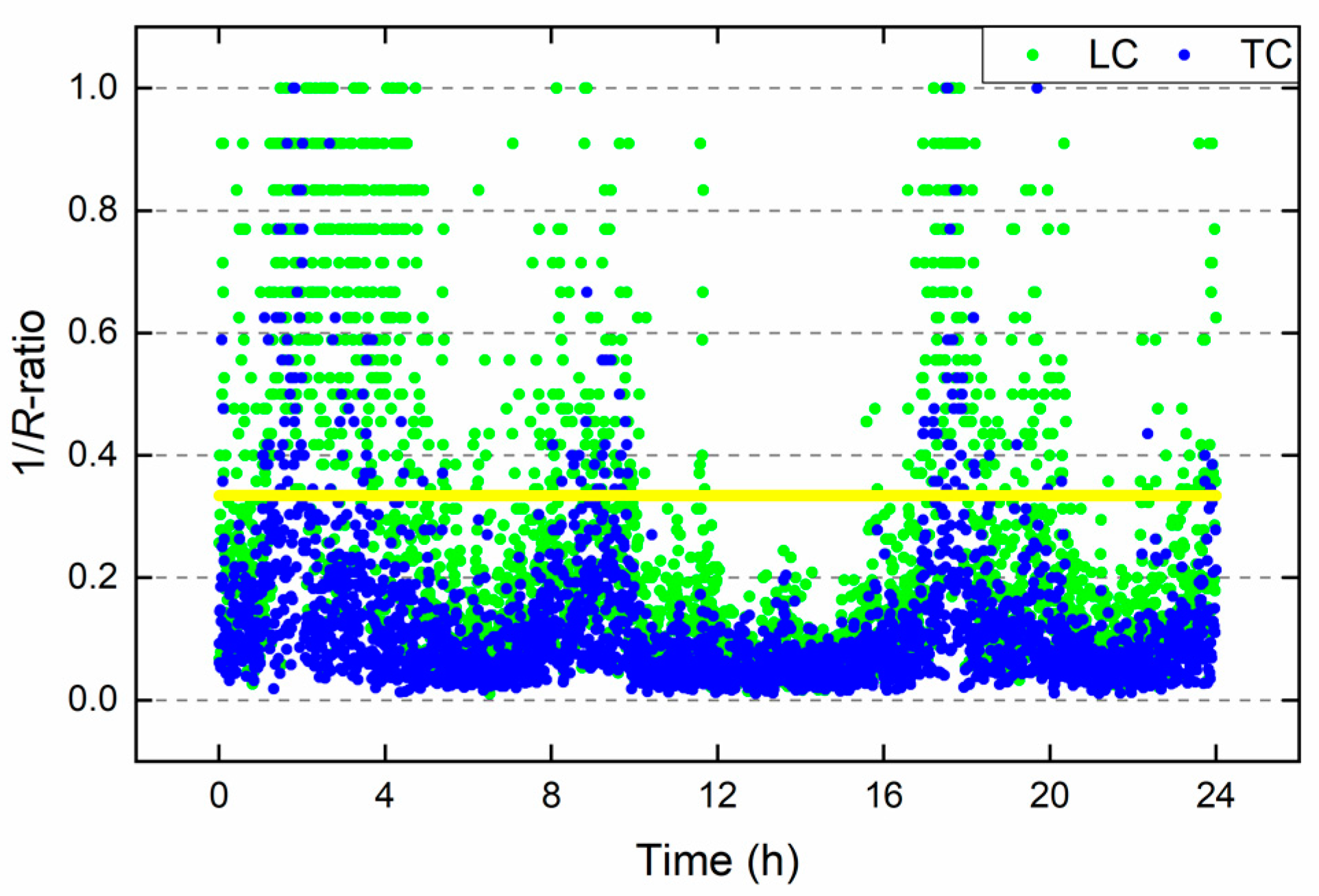
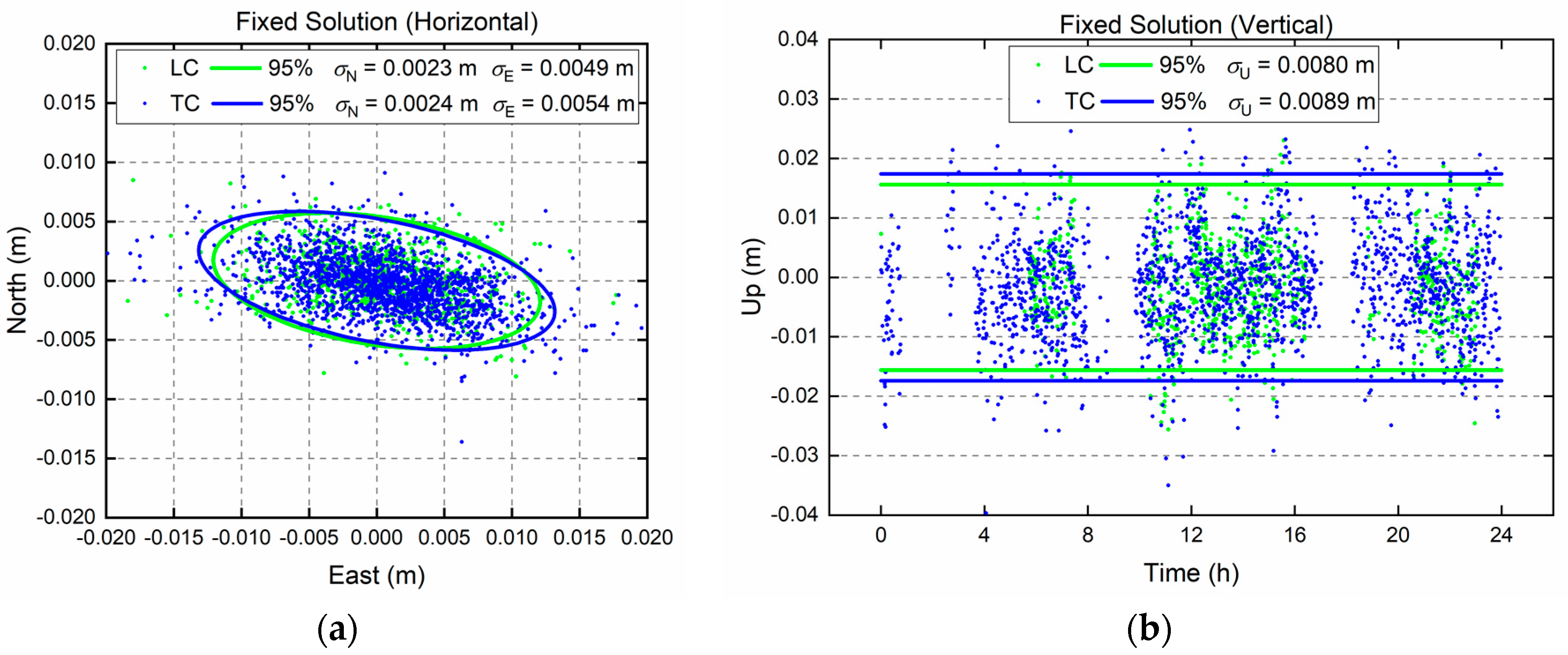
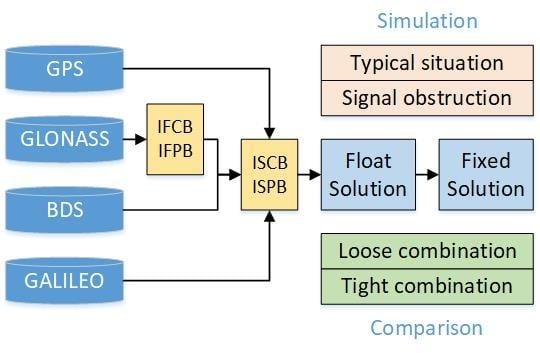
3.1. IFB Calibration
According to Equations (5) and (7), the pseudorange and carrier phase observation equations are biased by IFCB and IFPB, respectively, and these biases must be removed before the subsequent AR.
For the
IFCB, Shi et al. [
33] analyzed their characteristics and employed both the linear and quadratic frequency functions for different receivers. Zhou et al. [
34] used data from 132 International GNSS Service stations, estimated the
IFCB for each satellite with a datum constraint, and compared its performance with linear or quadratic polynomial functions. To simplify the model, in this paper only the linear function was adopted, i.e.,
, where
is the
IFCB rate in meters. Thus, the
IFCB in Equation (6) can be re-written as:
In this model, the
IFCB rate can be easily determined using the DD pseudorange observation expressions in Equation (5). In the following procedure, the code observables will be significantly down-weighted, and this will hardly cause noticeable bad effects on the solution [
16].
For the
IFPB, some researchers used the calibration strategy before the positioning process [
12,
13,
14], and others adopted the estimation strategy in the processing procedure [
15,
16,
17]. Since the
IFPB has a great impact on the AR, it should be precisely estimated. Herein, we will propose an easy-to-implement method to quickly determine the accurate
IFPB value.
As derived from the SD carrier phase observation equation in meters in Equation (3), we can obtain the DD carrier phase observation equation in cycles for the GLONASS as follows:
where
is the frequency difference between two satellites. Furthermore, the frequency can be expressed as a linear function of
, i.e.:
where
is the central frequency and
a is the constant coefficient. For the L1 signal, they are 1602 MHz and 9/16 MHz, respectively.
is then transformed to
. Since we know that
, if the precision of the estimated
can reach 10 ns, the largest bias caused by
will be smaller than 0.08 cycles and the ambiguity rounding can only be affected by the
IFPB.
Furthermore, the linear relationship between the
IFPB and
is given as [
11]:
where
is the
IFPB rate in meters. Combining Equations (15) and (16),
can be derived:
Benefitting from the previous research by Wanninger [
11], an empirical range of
that is less than 6 cm can be assumed as the tolerance, i.e.,
< 0.2 ns. For the single-frequency case, when the condition
is satisfied, the bias
is smaller than 0.322 cycles, and the bias caused by
is further reduced to no more than 0.006 cycles. As a result, for baselines with known coordinates for the base station and rover station, the total bias in Equation (14) will be no more than 0.33 cycles. If we temporarily ignore the effect of the hardware delay, the DD ambiguity can be estimated by directly rounding:
where
round(*) means the rounding off operation. In this way, the DD integer ambiguity is determined, and the next step is to calculate the
IFPB rate.
It should be mentioned that the efficiency of this algorithm is affected by two factors: the precision of and the limit of the IFPB rate. If the above limit of 6 cm for IFPB rate is used, the precision of can be as tolerant as 200 ns. On the other hand, considering there is no guarantee that the above critical value of the IFPB rate is the absolute limit, the IFPB rate that can be supported by our algorithm should be no larger than 9 cm, where the precision of should not exceed 10 ns. Otherwise, the DD integer ambiguity cannot be fixed to its right value and the algorithm is inapplicable.
According to Equation (16) and the definition of
IFPB in Equation (6), the
IFPB is expressed in a similar model as the
IFCB in Equation (13), i.e.,
. From the DD carrier phase observation equation in Equation (5), we can obtain the
IFPB rate as follows:
where the float DD ambiguity is converted to the combination of an integer DD ambiguity
and the SD ambiguity for the reference satellite
. The initial value of
can be easily calculated via Equation (3) when the hardware delays are ignored. The bias in the calculated
will be dramatically reduced due to the mm-level’s coefficient
. If no cycle slip occurs,
remains the same and the
IFPB rate can be determined.
Since there may be only a very few DD observables meeting
at a single epoch, the obtained
IFPB rates may be very noisy. Therefore, a sufficient duration is required to smooth the noisy
IFPB rates and achieve a relatively accurate initial value. After the initial
IFPB rate is calculated, the bias
in Equation (17) can thereby be calculated, and all DD ambiguity can then be re-estimated using the corresponding DD carrier phase observables:
Similarly, from Equation (19) we can get the
IFPB rate again at each epoch using all DD observables, and further obtain a much more accurate value through smoothing. In other word, the
IFPB rate is iterated from an initial value to a much more accurate value. The whole procedure is listed in
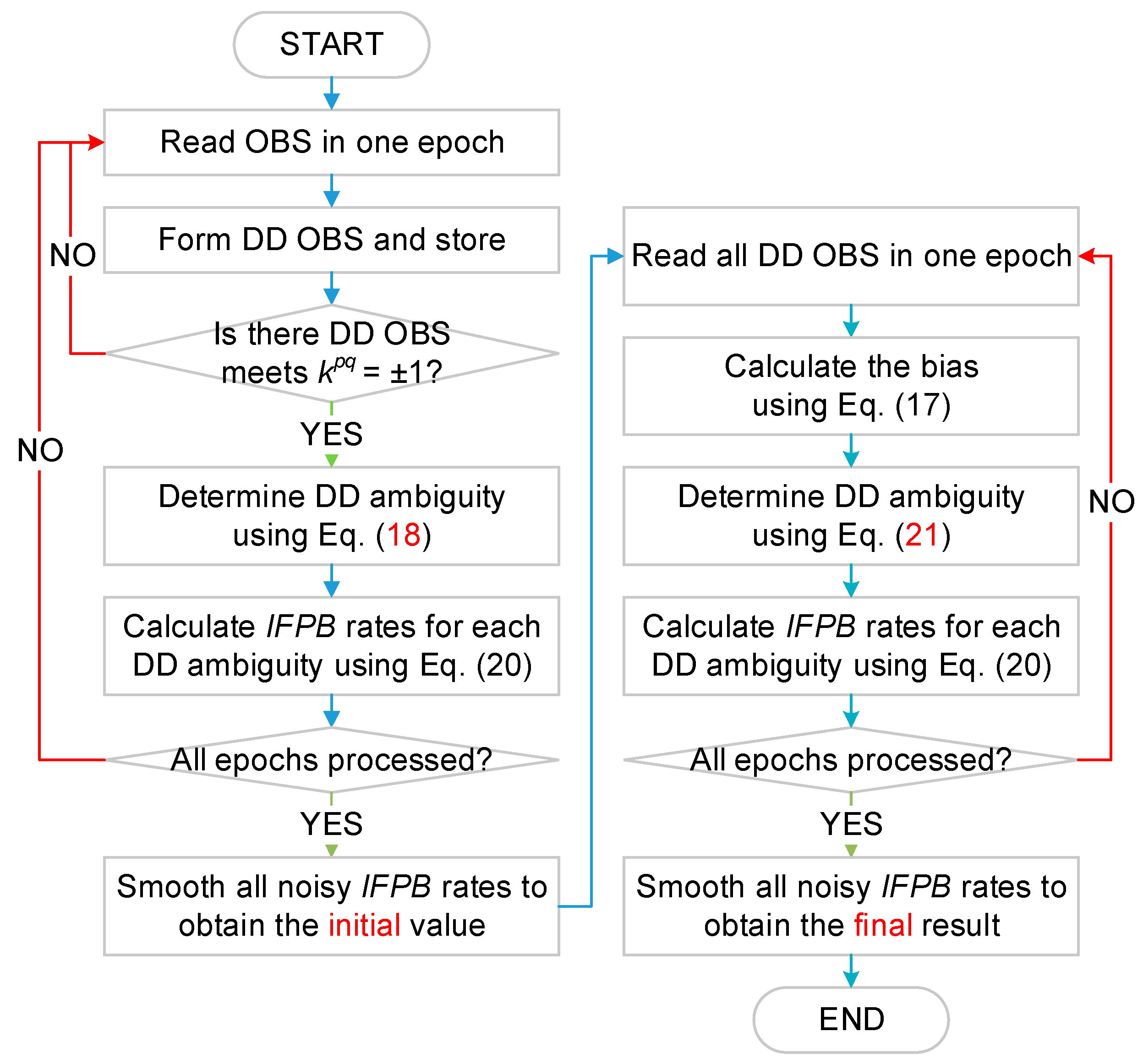
Figure 1.
Before applying the above procedure, some remarks should be made. The first is the inputs, where only the pair of observation data files with known coordinates can be used in our algorithm. The second is the condition difference to calculate the initial and the final IFPB rate. When we use DD observables to determine the DD ambiguity the first time, the condition must be satisfied. However, when we determine the DD ambiguity again after we obtained the initial IFPB rate, all DD observables were utilized to get more calculated IFPB rates and thus a more precise result.
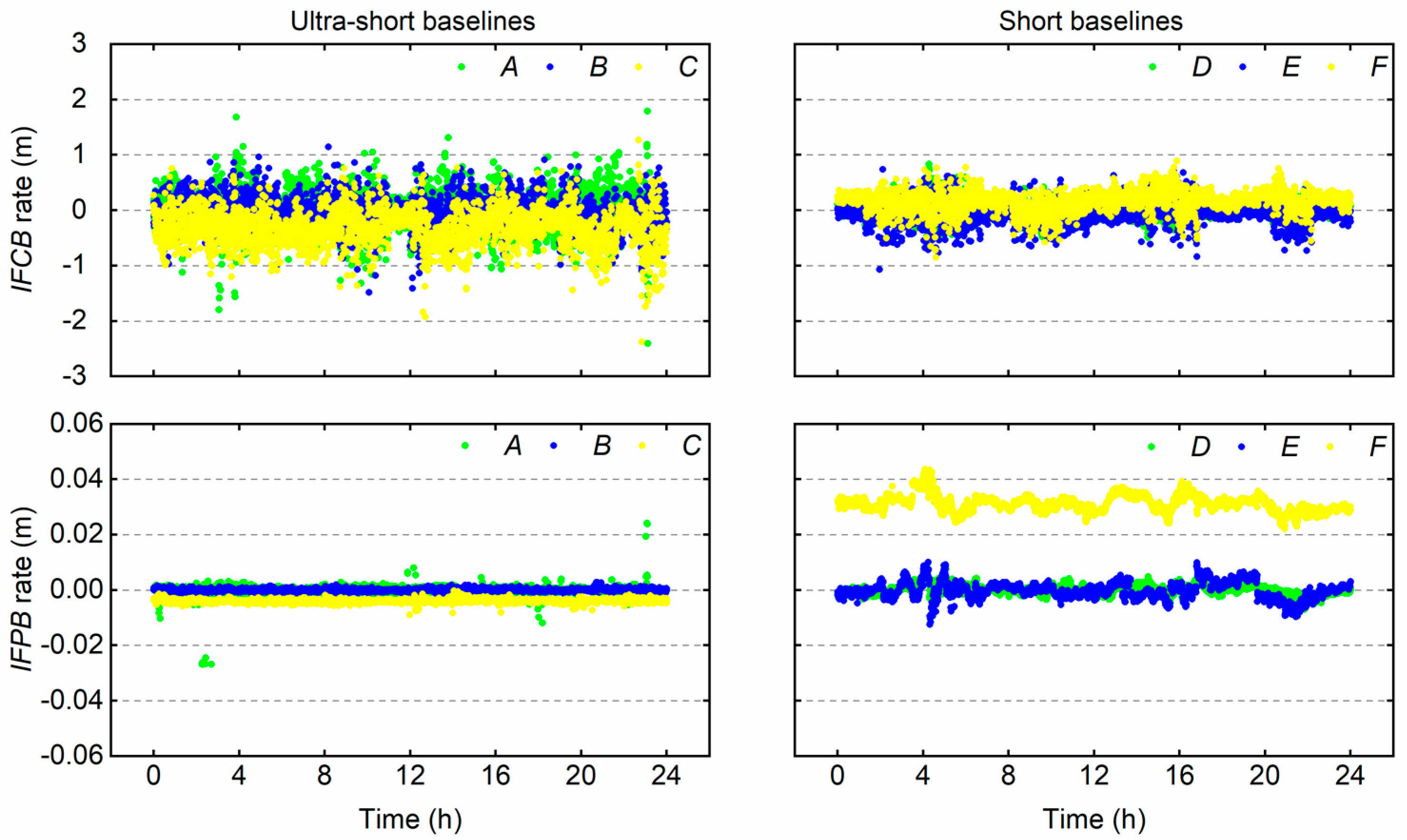
Taking the data in
Figure 2 as examples and using the above-proposed method, we obtained the epoch-by-epoch
IFCB rates and
IFPB rates, which are plotted in
Figure 2 The final smoothed
IFCB rates,
IFPB rates, and corresponding standard deviations (STDs) are listed in
Figure 2.
From
Figure 2, we can see that the IFB rates were very stable during one day’s observation session for all six baselines; thus, we can calibrate this bias using a pre-estimated value. Meanwhile, the
IFPB rates for all baselines with homogeneous receivers were almost normally distributed and the statistical results were close to zero, while the IFB rates for baselines with heterogeneous receivers were obviously biased.
Table 2 shows that the
IFPB rate for baseline
F reached up to 0.03 m. If
is larger than 3, the
IFPB for this baseline will exceed half cycle, and severely obstruct the subsequent AR. Furthermore, the STD values reflected that by adopting the proposed algorithm, we could obtain a 0.3-m-level
IFCB rate and a 0.003-m-level
IFPB rate.
After the
IFCB and
IFPB rates were determined, the
IFCB and
IFPB can be calculated and expressed as:
The calculated IFBs were then used for calibration in the tightly combined model.
3.2. ISB Estimation
Taking a tight combination between the GPS and GLONASS as an example, after the IFB is calibrated, the tightly combined observation equations can be re-written as:
From Equation (9), and considering the consistency of the hardware delays for all satellite pairs, we can regard both the
ISCB and
ISPB as short-term constants, which means their values remain unchanged for at least several hours of continuous operation [
23,
32]. The
ISCB can be easily estimated using a least-squares adjustment or Kalman filtering. As for the
ISPB, from Equation (22), we find the DD ambiguity has lost its integer nature. Therefore, a transformation similar to Equation (19) is employed to recover the integer nature, and the tightly combined DD carrier phase observation equation is re-expressed as follows:
Similarly, the float DD ambiguity is separated into the terms of and , and the initial value of can be calculated. If no cycle slip occurs, the reduced bias in the calculated will be absorbed into the ISPB.
Since the
ISPB and the DD ambiguity terms are also very difficult to separate, they will be regarded as one parameter and estimated together with the coordinates, or directly calculated using the following formula:
Herein, the geometry can be obtained when we estimate the ISCB. After rounding off, the integer part of the real ISPB is absorbed into the integer DD ambiguity, and the residual is changed to a constant value by multiplying the coefficient and then taken as the ISPB in cycles. Furthermore, if the determined ISPB is around ±0.5 cycles, one cycle is added to the ISPB around −0.5 cycles to make all results consistent.
For a tight combination between GPS and BDS, there may be a 0.5-cycles inter-satellite type bias in BDS between the geostationary orbit (GEO) satellites and the non-GEO satellites [
35], and this bias is corrected in advance. For a tight combination between GPS and Galileo, the overlapping frequency is used and the SD ambiguity term is eliminated, thus the model becomes simple.
The determined ISPBs for each pair of satellites are averaged together to one ISPB value at one epoch. For a short-term observation period, the ISPB can be further smoothed due to its stability to achieve its final value.
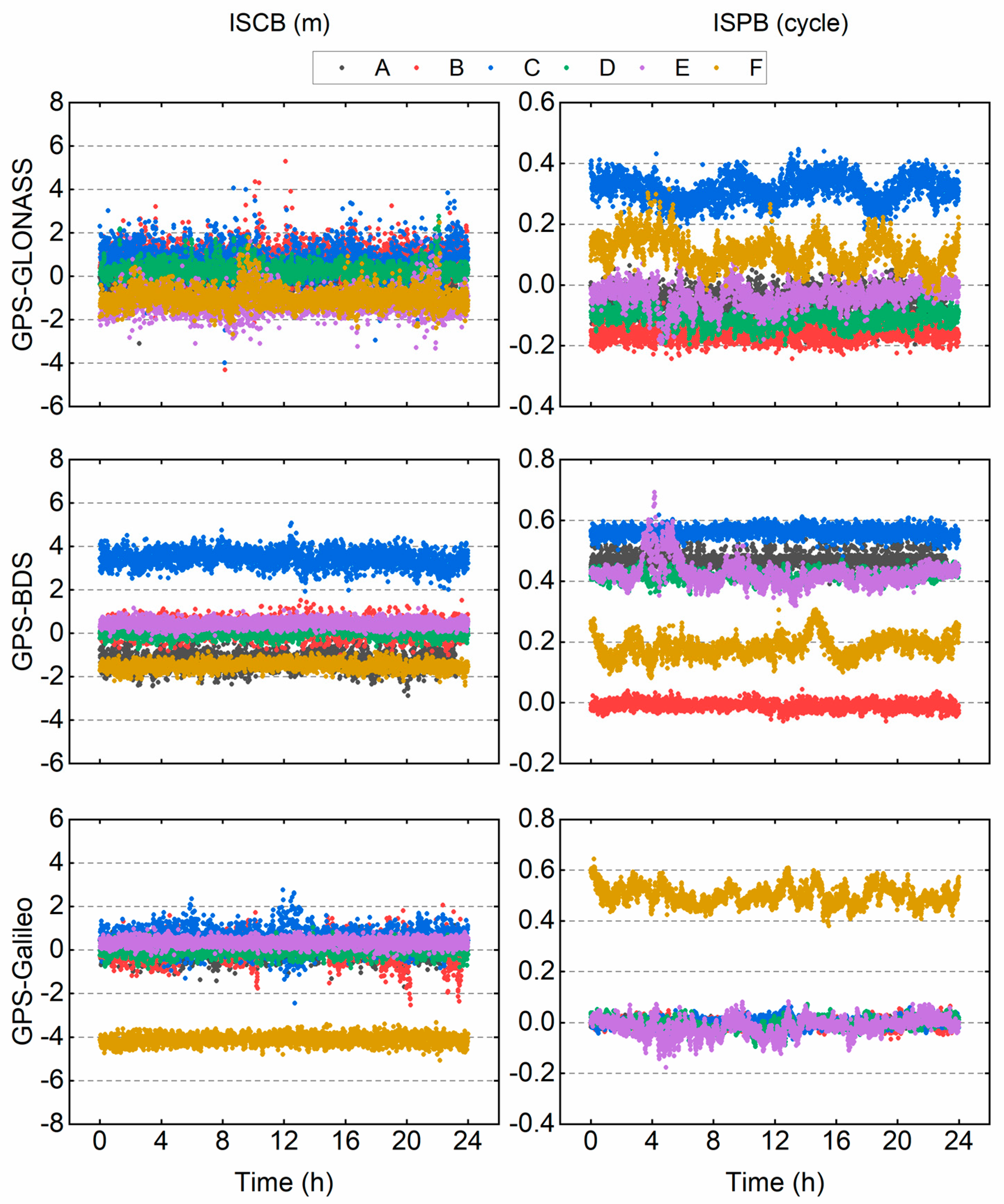
Using data in
Table 1 and the above method, we obtained the epoch-by-epoch
ISCB and
ISPB, which are plotted in
Figure 3. The final smoothed
ISCBs,
ISPBs, and corresponding STD values are listed in
Table 3.
From
Figure 3 and
Table 3, we can see that the ISB had a diurnal stability and could be corrected in advance. In addition, the
ISCB and
ISPB differ from one another, whether homogeneous or heterogeneous receivers are used. The
ISCB could be as large as 4 m and the
ISPB could reach up to 0.5 cycles. Such large biases will no doubt hamper the subsequent AR and must be removed. In the meantime, the given STD values show that the precision of the estimated
ISCB was almost at the same level as the code measurement noise, and the
ISCB between GPS and GLONASS was slightly larger than other inter-system pairs. This was reasonable due to the large code noise of GLONASS. As for
ISPB, for ultra-short baselines, the precision could be up to 0.015 cycles, and a general precision of 0.03 cycles was achieved.
What is interesting is that for most baselines, the ISPB values between GPS and Galileo were close to zero because of their identical frequency, with the only exception being for baseline F. This indicates that the ISPB may exist even if overlapping frequencies are used in tightly combined systems.