Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto
Abstract
1. Introduction
2. Methodology
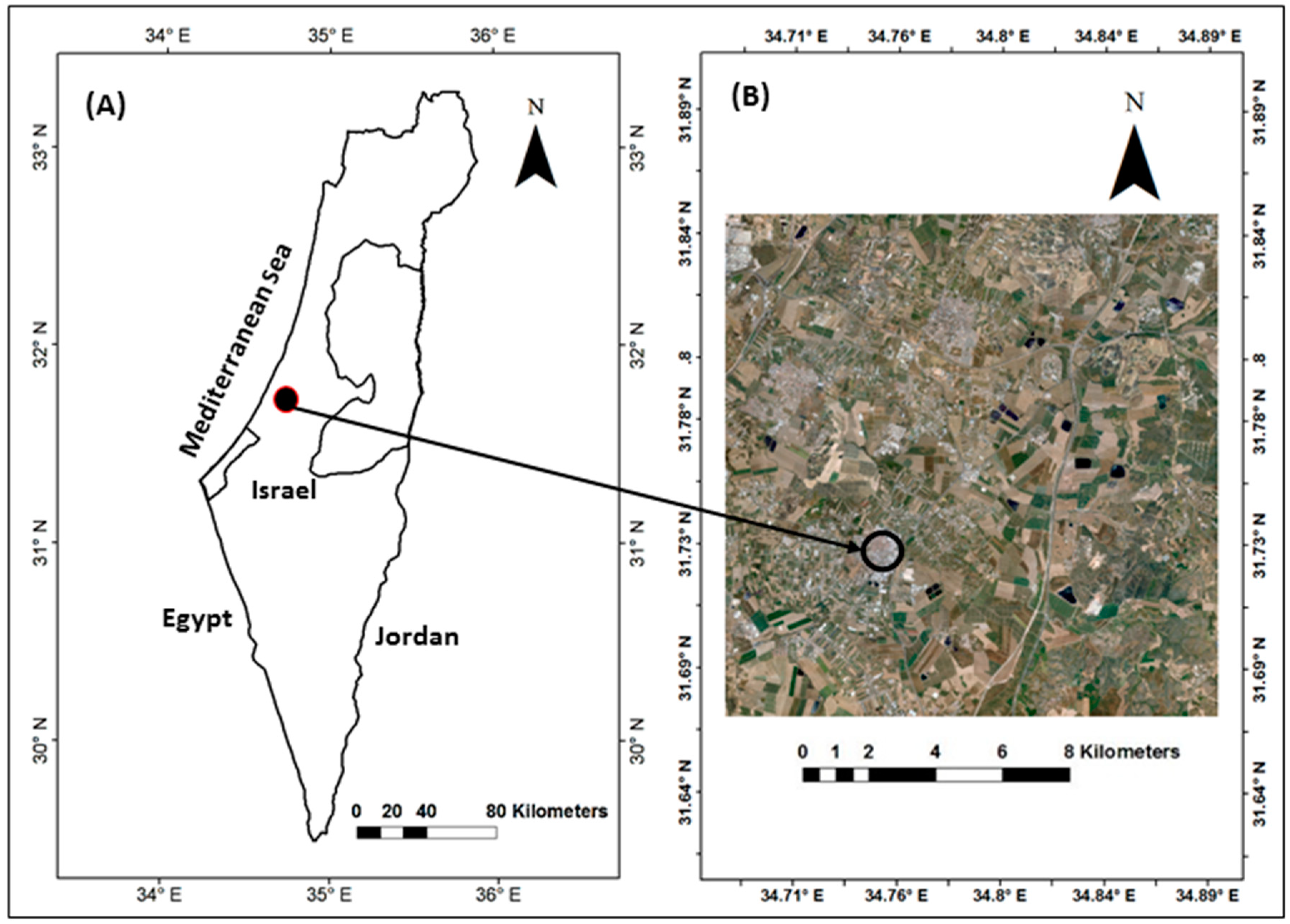
2.1. Study Area and Data Sources
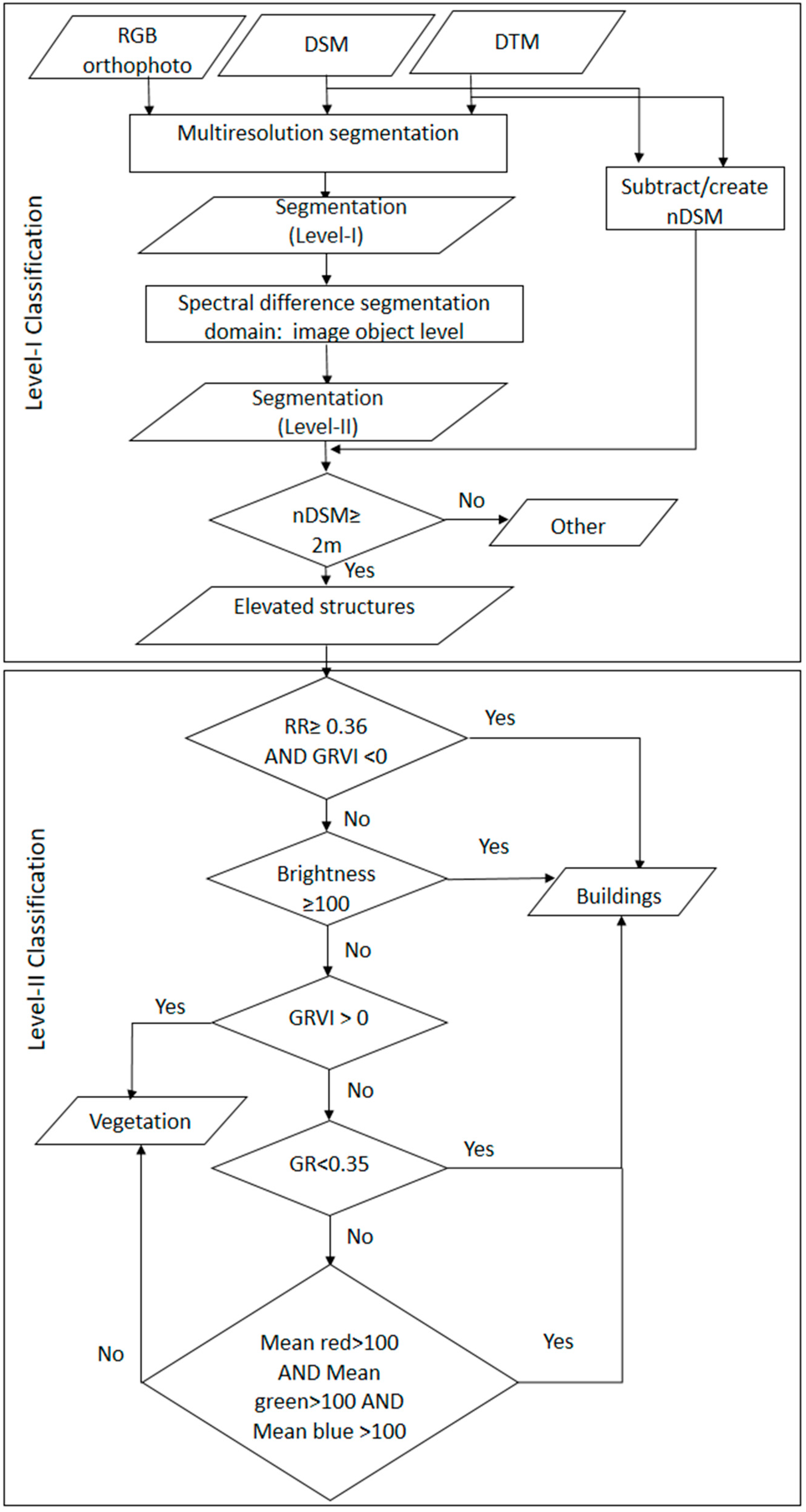
2.2. Classification
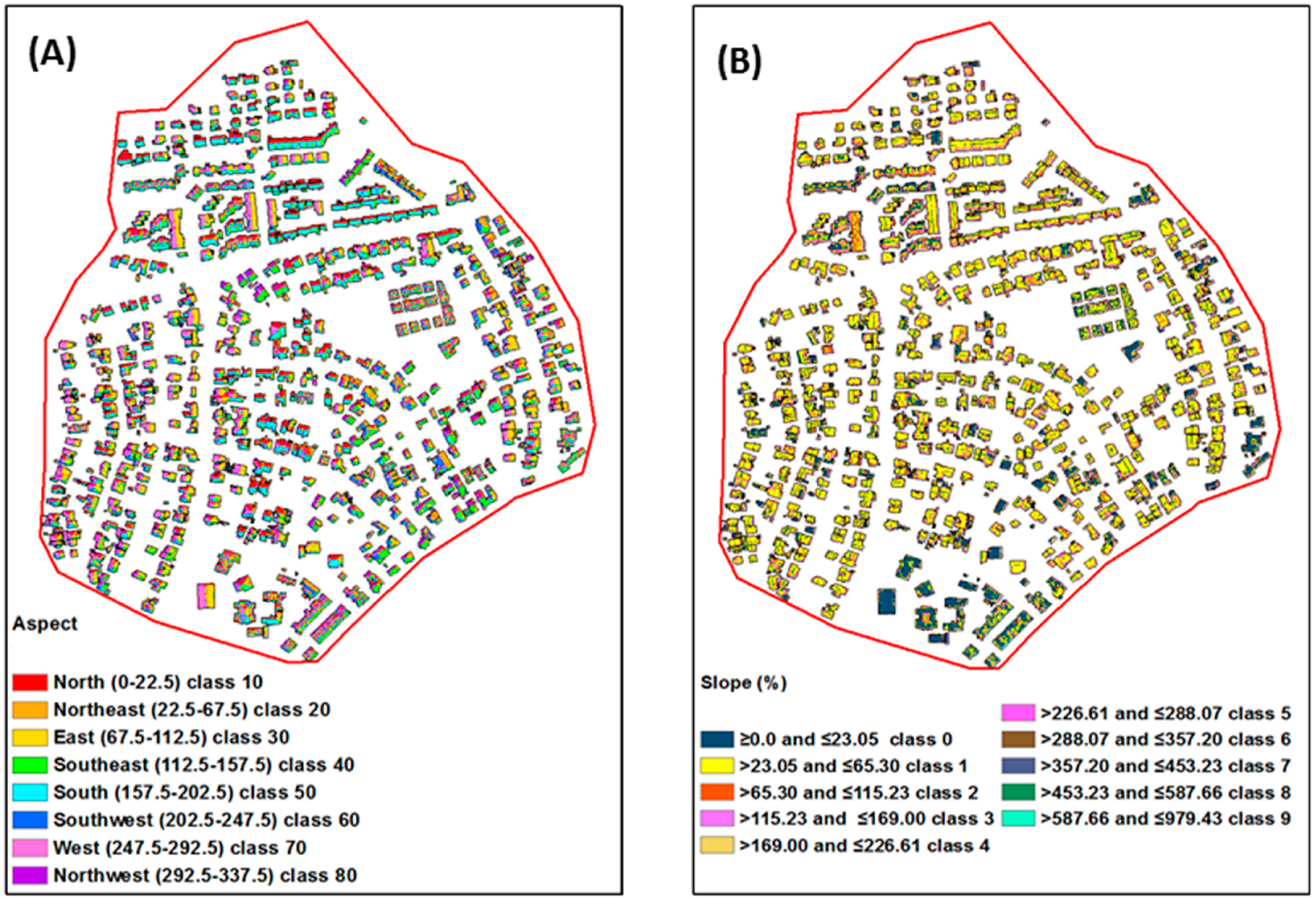
2.3. Aspect and Slope
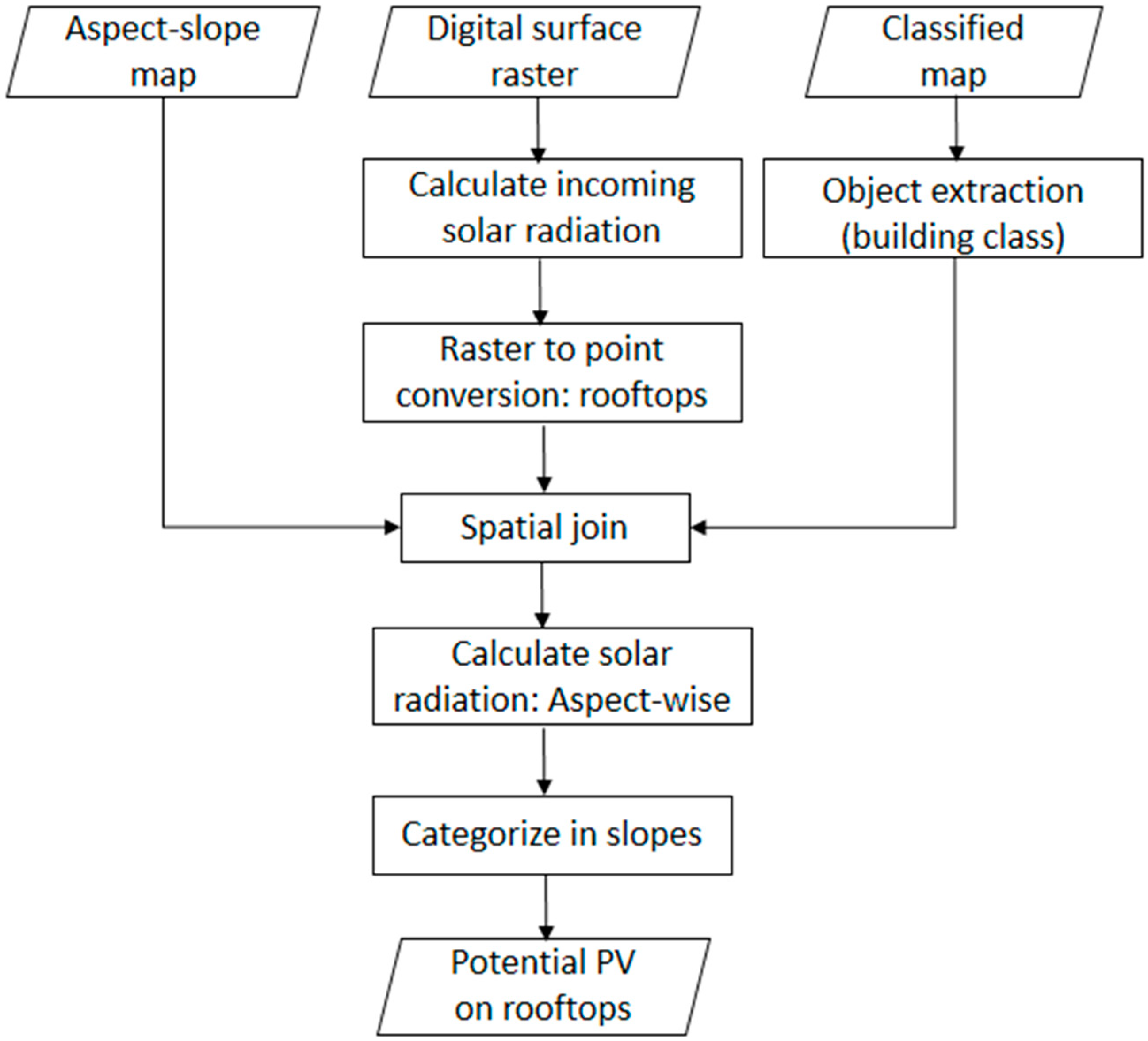
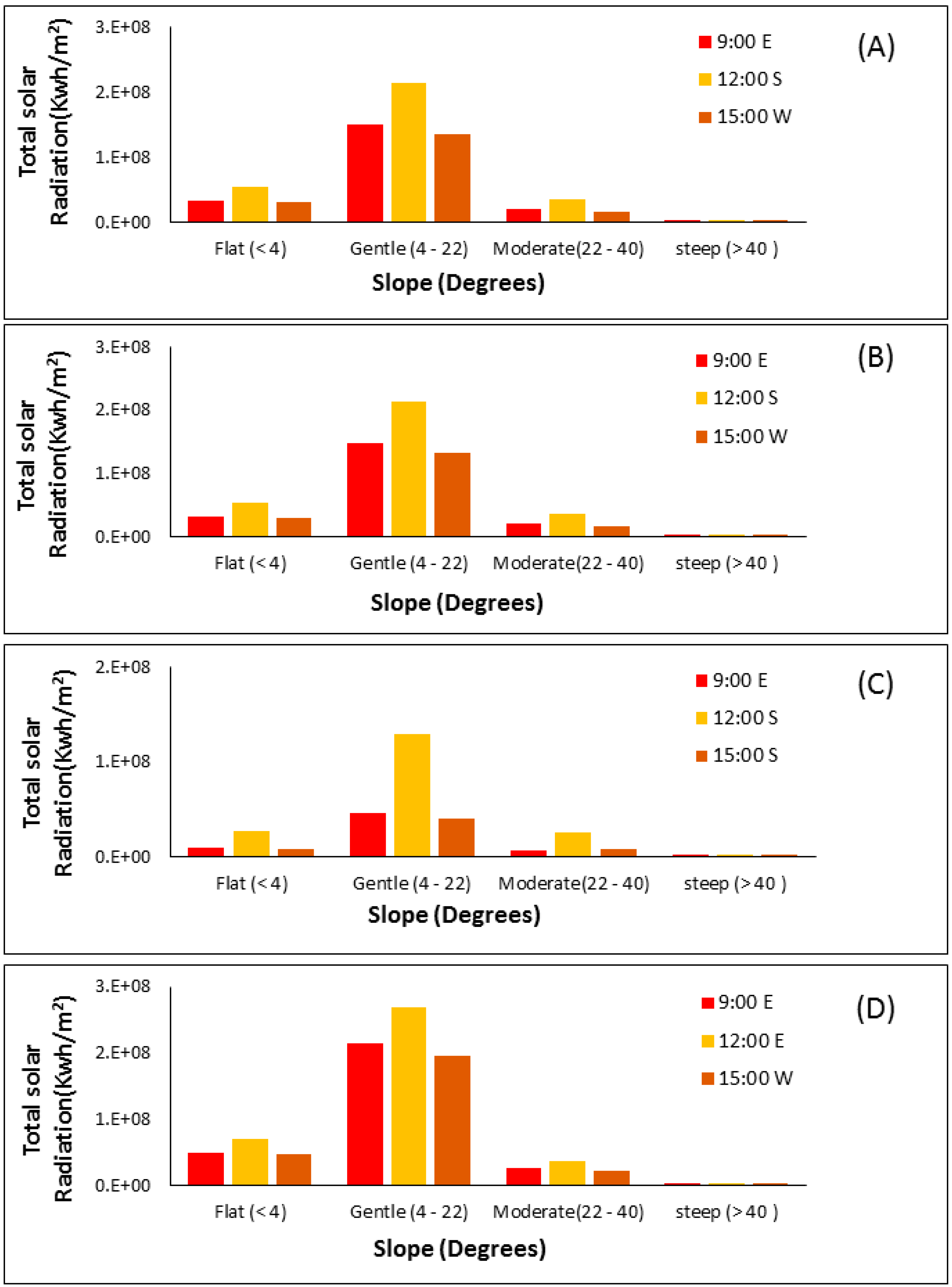
2.4. Solar Radiation
2.5. Spatial Analysis of Building Rooftops
3. Results and Discussion
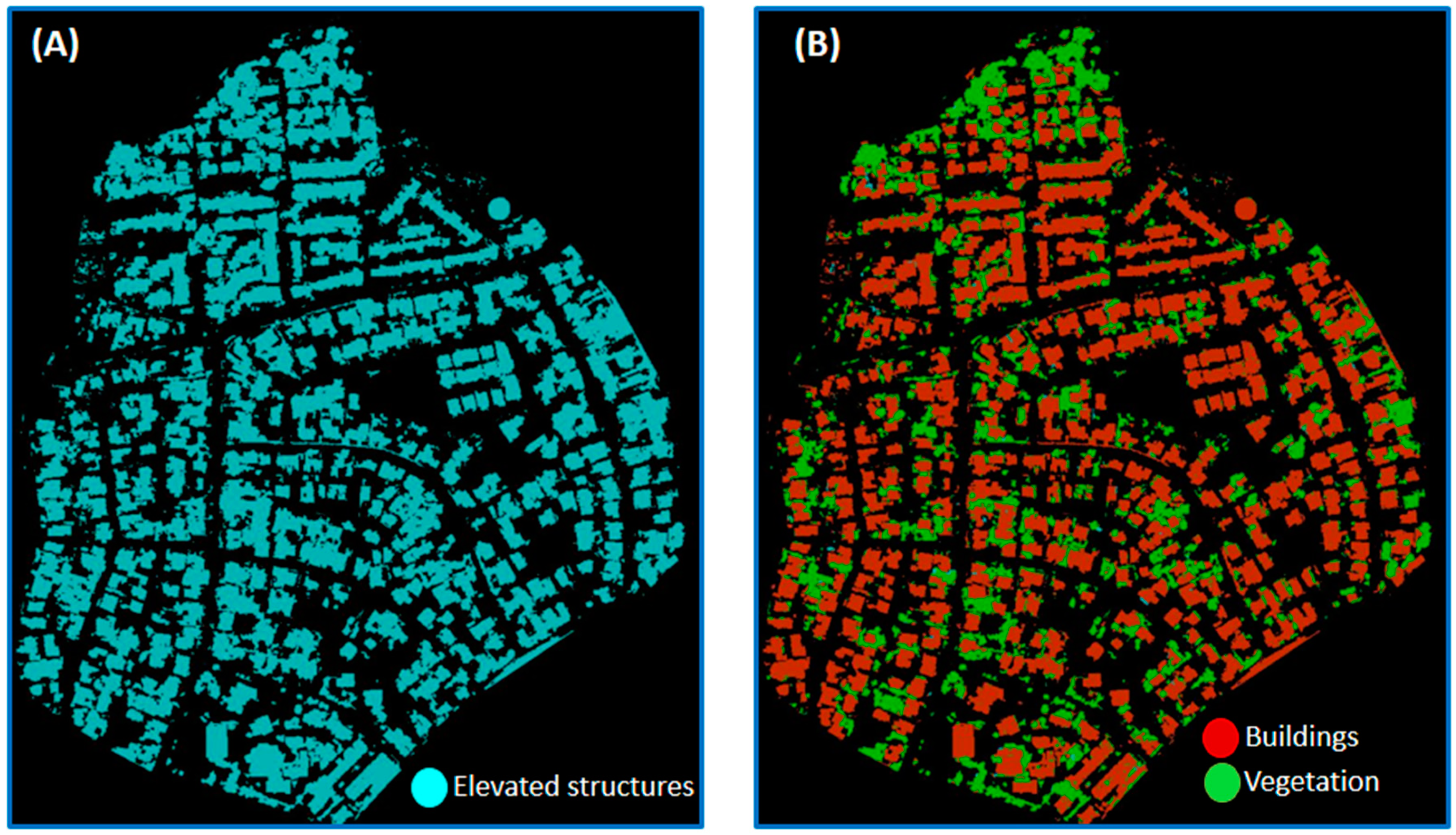
3.1. Classification and Accuracy Assessment
3.2. LiDAR Mapping
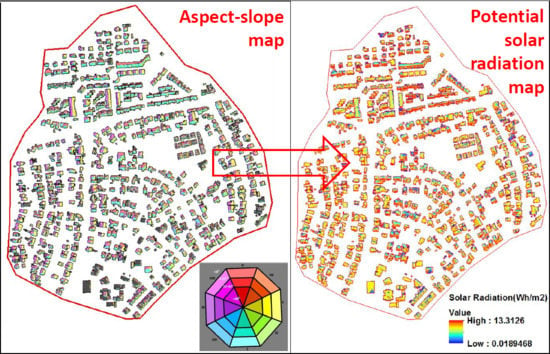
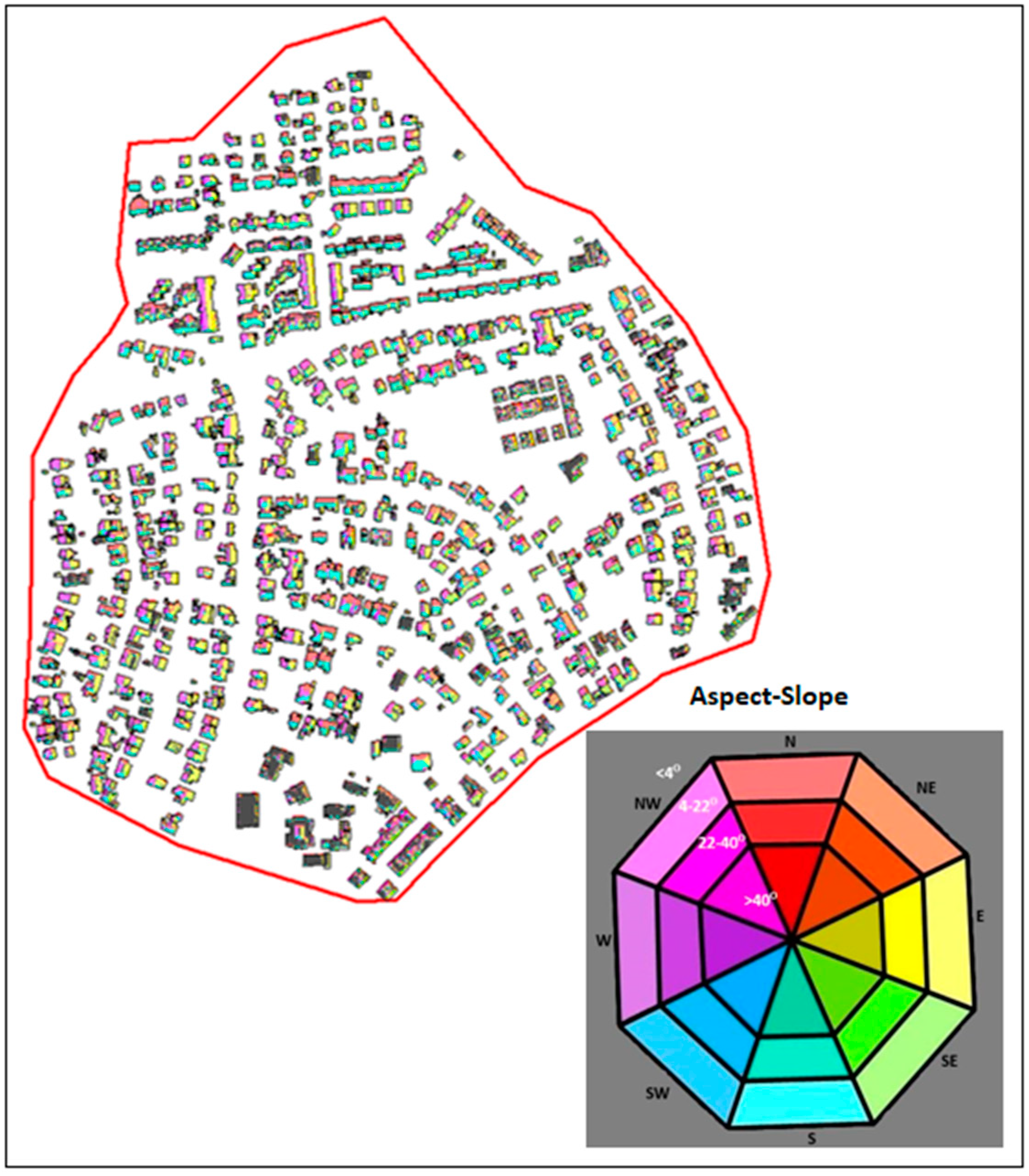
3.3. Visual Validation of Aspect-Slope Map
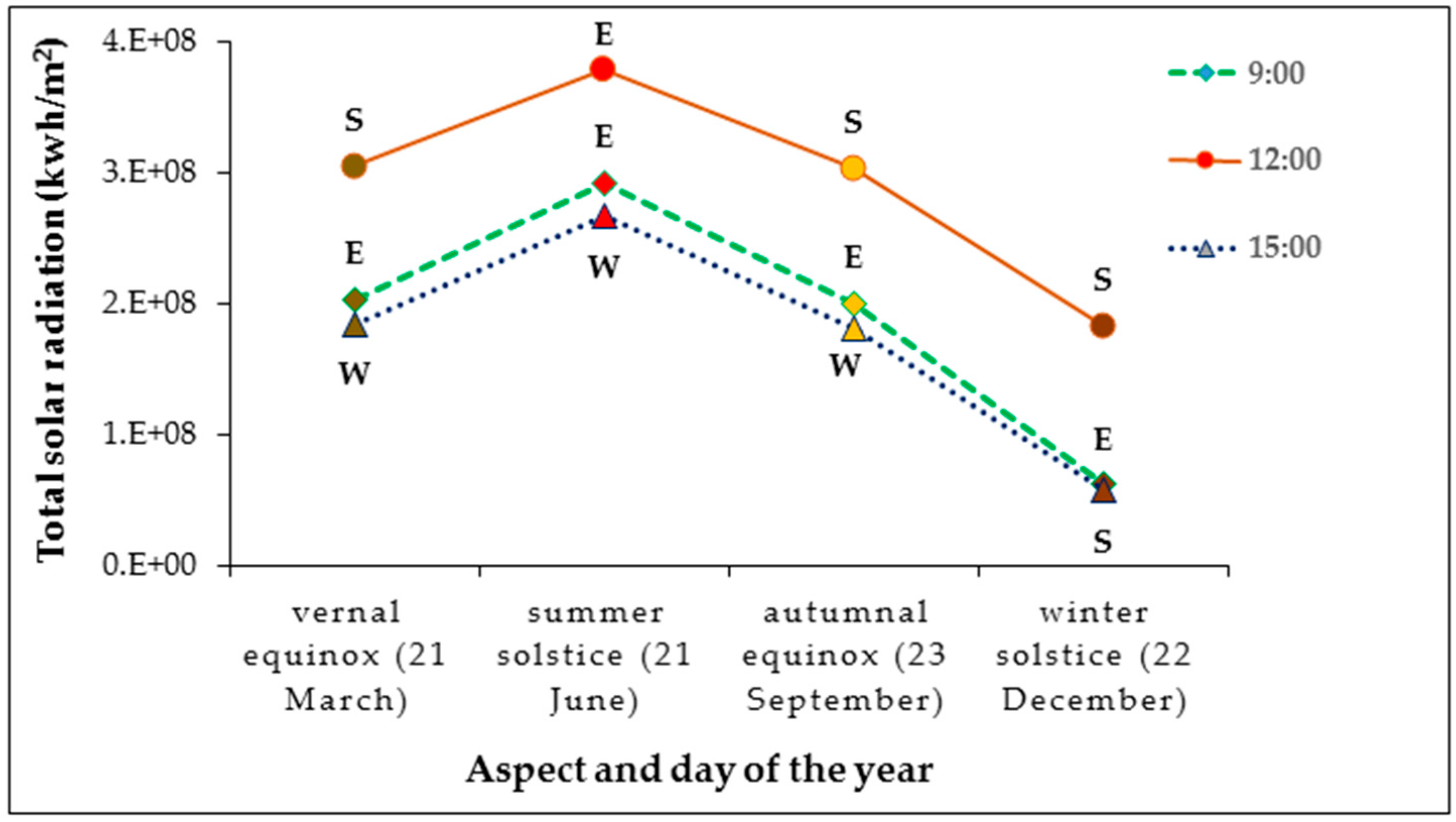
3.4. Spatio-Temporal Distribution of Solar Radiation
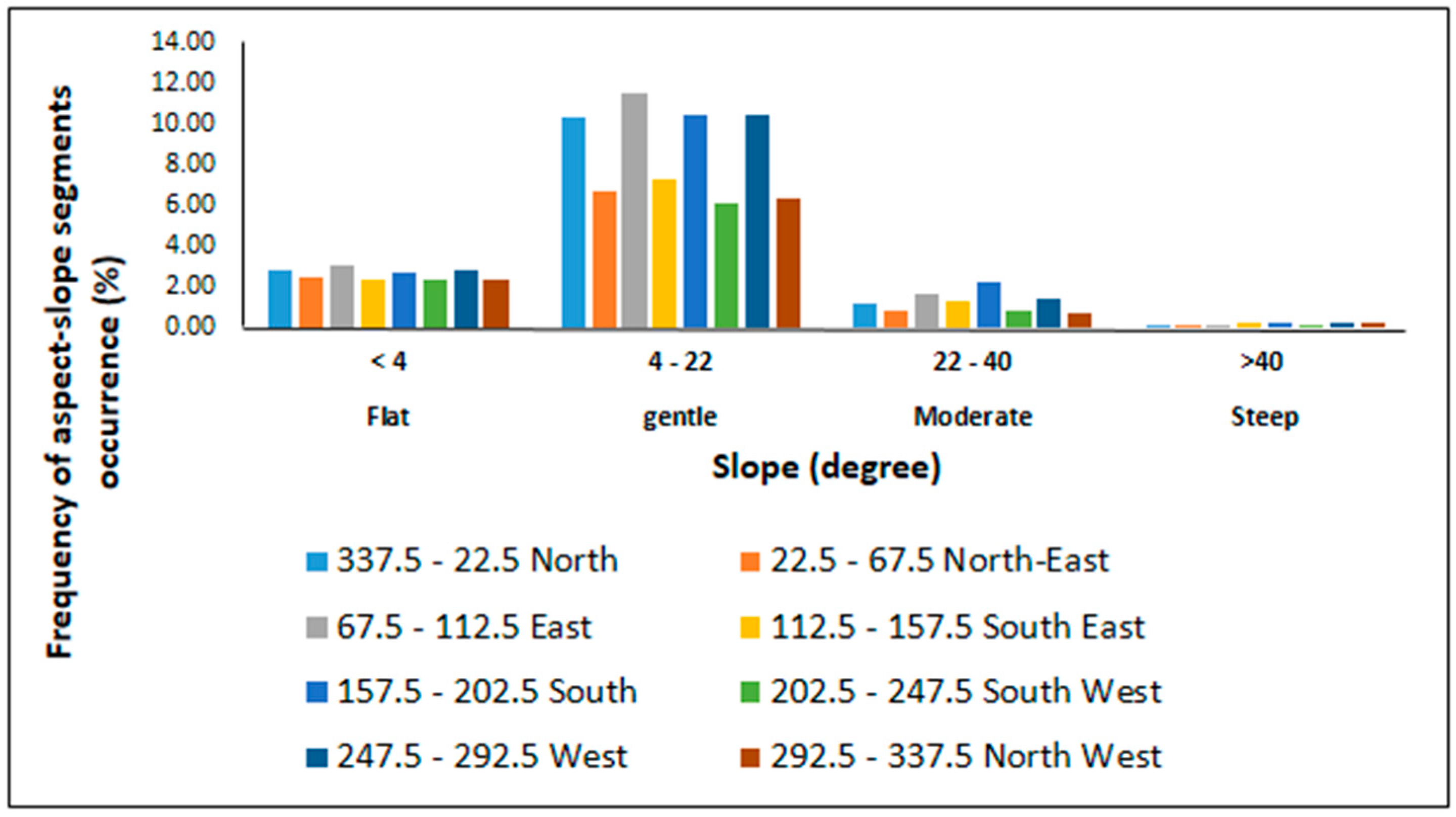
3.5. Spatial Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Olejarnik, P. IEA World Energy Outlook 2013; International Energy Agency: Paris, France, 2013; pp. 1–7. [Google Scholar]
- Ramachandra, T.V.; Shruthi, B.V. Spatial mapping of renewable energy potential. Renew. Sustain. Energy Rev. 2007, 11, 1460–1480. [Google Scholar] [CrossRef]
- York, R.; Bell, S.E. Energy transitions or additions?: Why a transition from fossil fuels requires more than the growth of renewable energy. Energy Res. Soc. Sci. 2019, 51, 40–43. [Google Scholar] [CrossRef]
- De L’Énergie, C.M. 2014 World Energy Issues Monitor; World Energy Council: London, UK, 2014. [Google Scholar]
- IRENA. Renewable Capacity Statistics 2019; International Renewable Energy Agency (IRENA): Masdar, Abu Dhabi, 2019; ISBN 978-92-9260-123-2. [Google Scholar]
- Lukač, N.; Žlaus, D.; Seme, S.; Žalik, B.; Štumberger, G. Rating of roofs’ surfaces regarding their solar potential and suitability for PV systems, based on LiDAR data. Appl. Energy 2013, 102, 803–812. [Google Scholar] [CrossRef]
- Solomon, A.A.; Bogdanov, D.; Breyer, C. Solar driven net zero emission electricity supply with negligible carbon cost: Israel as a case study for Sun Belt countries. Energy 2018, 155, 87–104. [Google Scholar] [CrossRef]
- D’Adamo, I. The profitability of residential photovoltaic systems. A new scheme of subsidies based on the price of CO2 in a developed PV market. Soc. Sci. 2018, 7, 148. [Google Scholar] [CrossRef]
- Karthick, A.; Kalidasa Murugavel, K.; Kalaivani, L.; Saravana Babu, U. Performance study of building integrated photovoltaic modules. Adv. Build. Energy Res. 2018, 12, 178–194. [Google Scholar] [CrossRef]
- Szabó, S.; Enyedi, P.; Horváth, M.; Kovács, Z.; Burai, P.; Csoknyai, T.; Szabó, G. Automated registration of potential locations for solar energy production with Light Detection and Ranging (LiDAR) and small format photogrammetry. J. Clean. Prod. 2016, 112, 3820–3829. [Google Scholar] [CrossRef]
- Fang, X.; Li, D. Solar photovoltaic and thermal technology and applications in China. Renew. Sustain. Energy Rev. 2013, 23, 330–340. [Google Scholar] [CrossRef]
- Zuo, J.; Zhao, Z.Y. Green building research-current status and future agenda: A review. Renew. Sustain. Energy Rev. 2014, 30, 271–281. [Google Scholar] [CrossRef]
- García-Cascales, M.S.; Lamata, M.T.; Sánchez-Lozano, J.M. Evaluation of photovoltaic cells in a multi-criteria decision making process. Ann. Oper. Res. 2012, 199, 373–391. [Google Scholar] [CrossRef]
- Lukač, N.; Seme, S.; Žlaus, D.; Štumberger, G.; Žalik, B. Buildings roofs photovoltaic potential assessment based on LiDAR (Light Detection And Ranging) data. Energy 2014, 66, 598–609. [Google Scholar] [CrossRef]
- Hofierka, J.; Kaňuk, J. Assessment of photovoltaic potential in urban areas using open-source solar radiation tools. Renew. Energy 2009, 34, 2206–2214. [Google Scholar] [CrossRef]
- Brito, M.C.; Gomes, N.; Santos, T.; Tenedório, J.A. Photovoltaic potential in a Lisbon suburb using LiDAR data. Sol. Energy 2012, 86, 283–288. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Zhou, J.; Ibrahim, A.N.; Li, M. An open-source 3D solar radiation model integrated with a 3D Geographic Information System. Environ. Model. Softw. 2015, 64, 94–101. [Google Scholar] [CrossRef]
- Palmero-Marrero, A.I.; Oliveira, A.C. Research on heating and cooling requirements of buildings with solar louvre devices. In Advances in Building Energy Research; Taylor & Francis Group: London, UK, 2010; ISBN 9781136532788. [Google Scholar]
- Lukač, N.; Žalik, B. GPU-based roofs’ solar potential estimation using LiDAR data. Comput. Geosci. 2013, 52, 34–41. [Google Scholar] [CrossRef]
- Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Evaluation of photovoltaic integration potential in a village. Sol. Energy 2015, 121, 152–168. [Google Scholar] [CrossRef]
- Bizjak, M.; Žalik, B.; Lukač, N. Evolutionary-driven search for solar building models using LiDAR data. Energy Build. 2015, 92, 195–203. [Google Scholar] [CrossRef]
- Hong, T.; Koo, C.; Kim, J.; Lee, M.; Jeong, K. A review on sustainable construction management strategies for monitoring, diagnosing, and retrofitting the building’s dynamic energy performance: Focused on the operation and maintenance phase. Appl. Energy 2015, 155, 671–707. [Google Scholar] [CrossRef]
- Carneiro, C.; Morello, E.; Ratti, C.; Golay, F. Solar radiation over the urban texture: Lidar data and image processing techniques for environmental analysis at city scale. Lect. Notes Geoinf. Cartogr. 2009, 319–340. [Google Scholar]
- Redweik, P.; Catita, C.; Brito, M. Solar energy potential on roofs and facades in an urban landscape. Sol. Energy 2013, 97, 332–341. [Google Scholar] [CrossRef]
- Šúri, M.; Huld, T.A.; Dunlop, E.D.; Ossenbrink, H.A. Potential of solar electricity generation in the European Union member states and candidate countries. Sol. Energy 2007, 81, 1295–1305. [Google Scholar] [CrossRef]
- Neteler, M.; Mitasova, H. Open Source GIS: A GRASS GIS Approach; Springer: New York, NY, USA, 2008; ISBN 9780387357676. [Google Scholar]
- Kodysh, J.B.; Omitaomu, O.A.; Bhaduri, B.L.; Neish, B.S. Methodology for estimating solar potential on multiple building rooftops for photovoltaic systems. Sustain. Cities Soc. 2013, 8, 31–41. [Google Scholar] [CrossRef]
- Jacques, D.A.; Gooding, J.; Giesekam, J.J.; Tomlin, A.S.; Crook, R. Methodology for the assessment of PV capacity over a city region using low-resolution LiDAR data and application to the City of Leeds (UK). Appl. Energy 2014, 124, 28–34. [Google Scholar] [CrossRef]
- Santos, T.; Gomes, N.; Freire, S.; Brito, M.C.; Santos, L.; Tenedório, J.A. Applications of solar mapping in the urban environment. Appl. Geogr. 2014, 51, 48–57. [Google Scholar] [CrossRef]
- Li, Y.; Ding, D.; Liu, C.; Wang, C. A pixel-based approach to estimation of solar energy potential on building roofs. Energy Build. 2016, 129, 563–573. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C. Estimating solar energy potentials on pitched roofs. Energy Build. 2017, 139, 101–107. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Wu, B.; Chen, L.; Mao, W.; Zhao, F.; Wu, J.; Wu, J.; Yu, B. Estimating roof solar energy potential in the downtown area using a GPU-accelerated solar radiation model and airborne LiDAR data. Remote Sens. 2015, 7, 17212–17233. [Google Scholar] [CrossRef]
- Bayrakci Boz, M.; Calvert, K.; Brownson, J.R.S. An automated model for rooftop PV systems assessment in ArcGIS using LIDAR. AIMS Energy 2015, 3, 401–420. [Google Scholar] [CrossRef]
- Wong, M.S.; Zhu, R.; Liu, Z.; Lu, L.; Peng, J.; Tang, Z.; Lo, C.H.; Chan, W.K. Estimation of Hong Kong’s solar energy potential using GIS and remote sensing technologies. Renew. Energy 2016, 99, 325–335. [Google Scholar] [CrossRef]
- Suomalainen, K.; Wang, V.; Sharp, B. Rooftop solar potential based on LiDAR data: Bottom-up assessment at neighbourhood level. Renew. Energy 2017, 111, 463–475. [Google Scholar] [CrossRef]
- Guide, U. eCognition Developer 8: Whats New; Trimble Navigation Limited: Sunnyvale, CA, USA, 2009. [Google Scholar]
- Segal, D.B. Use of Landsat multispectral scanner data for the definition of limonitic exposures in heavily vegetated areas (Montana, Idaho). Econ. Geol. 1983, 78, 711–722. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of green-red vegetation index for remote sensing of vegetation phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Fu, P.; Rich, P.M. Design and implementation of the solar analyst: An ArcView extension for modeling solar radiation at landscape scales. In Proceedings of the Nineteenth Annual ESRI User Conference, San Diego, CA, USA, 26–30 July 1999. [Google Scholar]
- Fu, P.; Rich, P.M. The Solar Analyst 1.0 User Manual; Helios Environmental Modeling Institute: Vermont Lawrence, KS, USA, 1999. [Google Scholar]
- Rich, P.M. Characterizing plant canopies with hemispherical photographs. Remote Sens. Rev. 1990, 5, 13–29. [Google Scholar] [CrossRef]
- Esri ArcGIS Help 10.1: Area Solar Radiation (Spatial Analyst). Available online: http://resources.arcgis.com/en/help/main/10.1/index.html#/Area_Solar_Radiation/009z000000t5000000/ (accessed on 21 November 2019).


| Domain | Image Layer Weights | Scale Parameter | Shape Factor | Compactness |
|---|---|---|---|---|
| Pixel level | R, G, B, DTM = 1, DSM = 3 | 10 | 0.5 | 0.7 |
| Original Aspect (in Degrees) Value | Re-Class Value |
|---|---|
| ≥0 and ≤22.5 | 10 |
| >22.5 and ≤67.5 | 20 |
| >67.5 and ≤112.5 | 30 |
| >112.5 and ≤157.5 | 40 |
| >157.5 and ≤202.5 | 50 |
| >202.5 and ≤247.5 | 60 |
| >247.5 and ≤292.5 | 70 |
| >292.5 and ≤337.5 | 80 |
| >337.5 and ≤360 | 10 |
| Original Slope (%) Value | Re-Class Value |
|---|---|
| ≥0.0 and ≤23.05 | 0 |
| >23.05 and ≤65.30 | 1 |
| >65.30 and ≤115.23 | 2 |
| >115.23 and ≤169.00 | 3 |
| >169.00 and ≤226.61 | 4 |
| >226.61 and ≤288.07 | 5 |
| >288.07 and ≤357.20 | 6 |
| >357.20 and ≤453.23 | 7 |
| >453.23 and ≤587.66 | 8 |
| >587.66 and ≤979.43 | 9 |
| Original Slope (%) Value | Re-Class Value | Slope in Degrees | Categorized Slope in Degrees | Description |
|---|---|---|---|---|
| ≥0.0 and ≤23.05 | 0 | 3.05 | <4° | Flat |
| >23.05 and ≤65.30 | 1 | 8.59 | 4–9° | Gentle slope |
| >65.30 and ≤115.23 | 2 | 14.93 | 9–15° | |
| >115.23 and ≤169.00 | 3 | 21.36 | 15–22° | |
| >169.00 and ≤226.61 | 4 | 27.67 | 22–28° | Moderate slope |
| >226.61 and ≤288.07 | 5 | 33.68 | 28–34° | |
| >288.07 and ≤357.20 | 6 | 39.57 | 34–40° | |
| >357.20 and ≤453.23 | 7 | 46.36 | 40–47° | Steep slope |
| >453.23 and ≤587.66 | 8 | 53.67 | 47–54° | |
| >587.66 and ≤979.43 | 9 | 66.19 | 54–67° |
| Classification/Reference Class | Buildings | Vegetation | Sum | User Accuracy (%) |
|---|---|---|---|---|
| Buildings | 52,720 | 328 | 53,048 | 99.38 |
| Vegetation | 537 | 47,651 | 48,188 | 98.89 |
| Unclassified | 523 | 1303 | 1826 | |
| Sum | 53,780 | 49,282 | ||
| Producer Accuracy (%) | 98.03 | 96.69 | ||
| Overall Accuracy 97.39 | ||||
| Kappa index of agreement 0.95 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, A.; Meir, I.A.; Karnieli, A. Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto. Remote Sens. 2020, 12, 223. https://doi.org/10.3390/rs12020223
Tiwari A, Meir IA, Karnieli A. Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto. Remote Sensing. 2020; 12(2):223. https://doi.org/10.3390/rs12020223
Chicago/Turabian StyleTiwari, Arti, Isaac A. Meir, and Arnon Karnieli. 2020. "Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto" Remote Sensing 12, no. 2: 223. https://doi.org/10.3390/rs12020223
APA StyleTiwari, A., Meir, I. A., & Karnieli, A. (2020). Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto. Remote Sensing, 12(2), 223. https://doi.org/10.3390/rs12020223