Variability of Diurnal Sea Surface Temperature during Short Term and High SST Event in the Western Equatorial Pacific as Revealed by Satellite Data
Abstract
1. Introduction
2. Dataset and Methods
2.1. SST Data Production
2.1.1. Diurnal SST Range and Foundation SST Estimates from Polar-Orbiting Satellite Data
2.1.2. Intercomparison Data from in situ and Geostationary Satellite Observations
In Situ SST Data
Geostationary Satellite-Based SST Data
2.2. Datasets for HE Analysis
3. Results
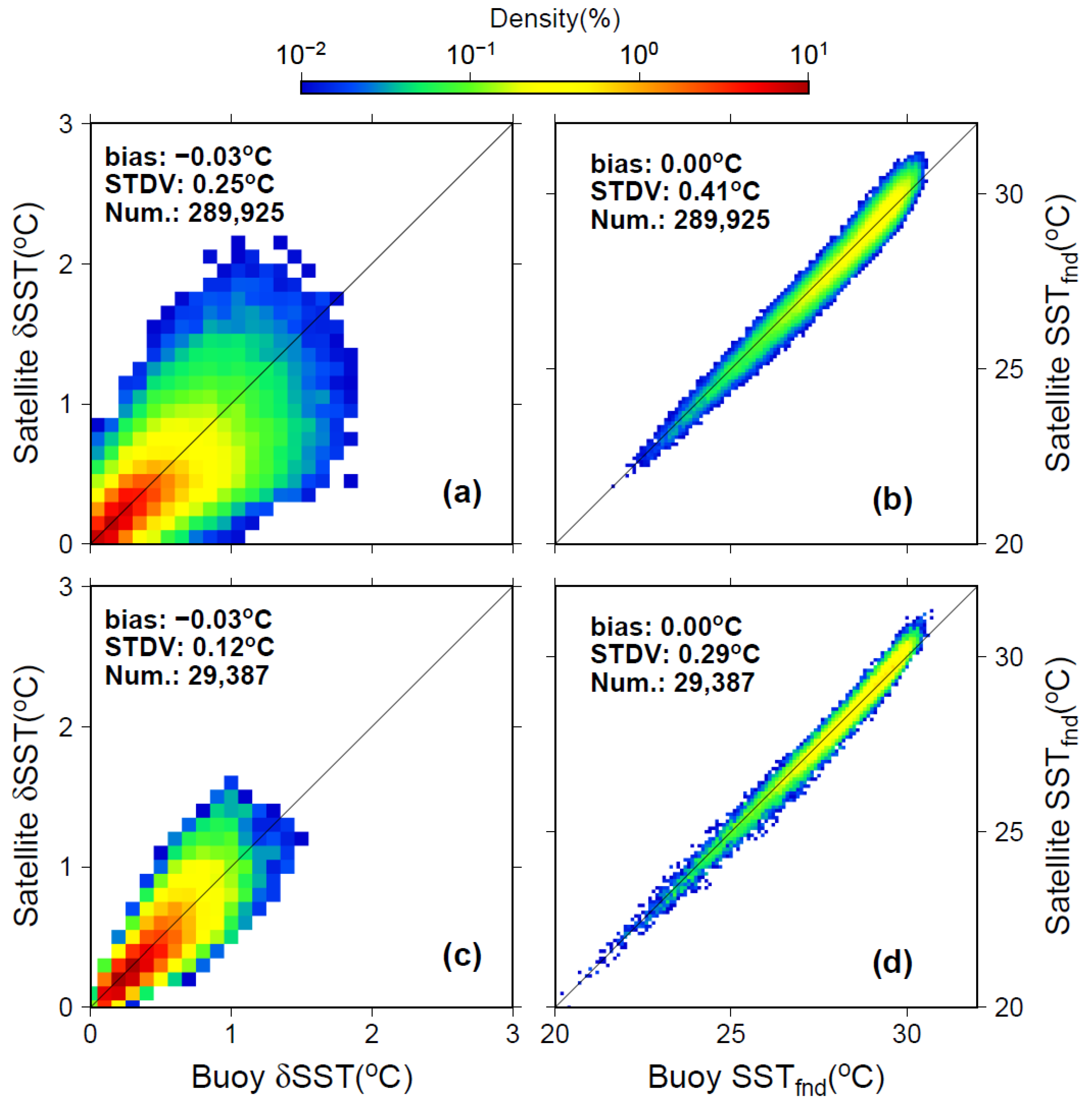
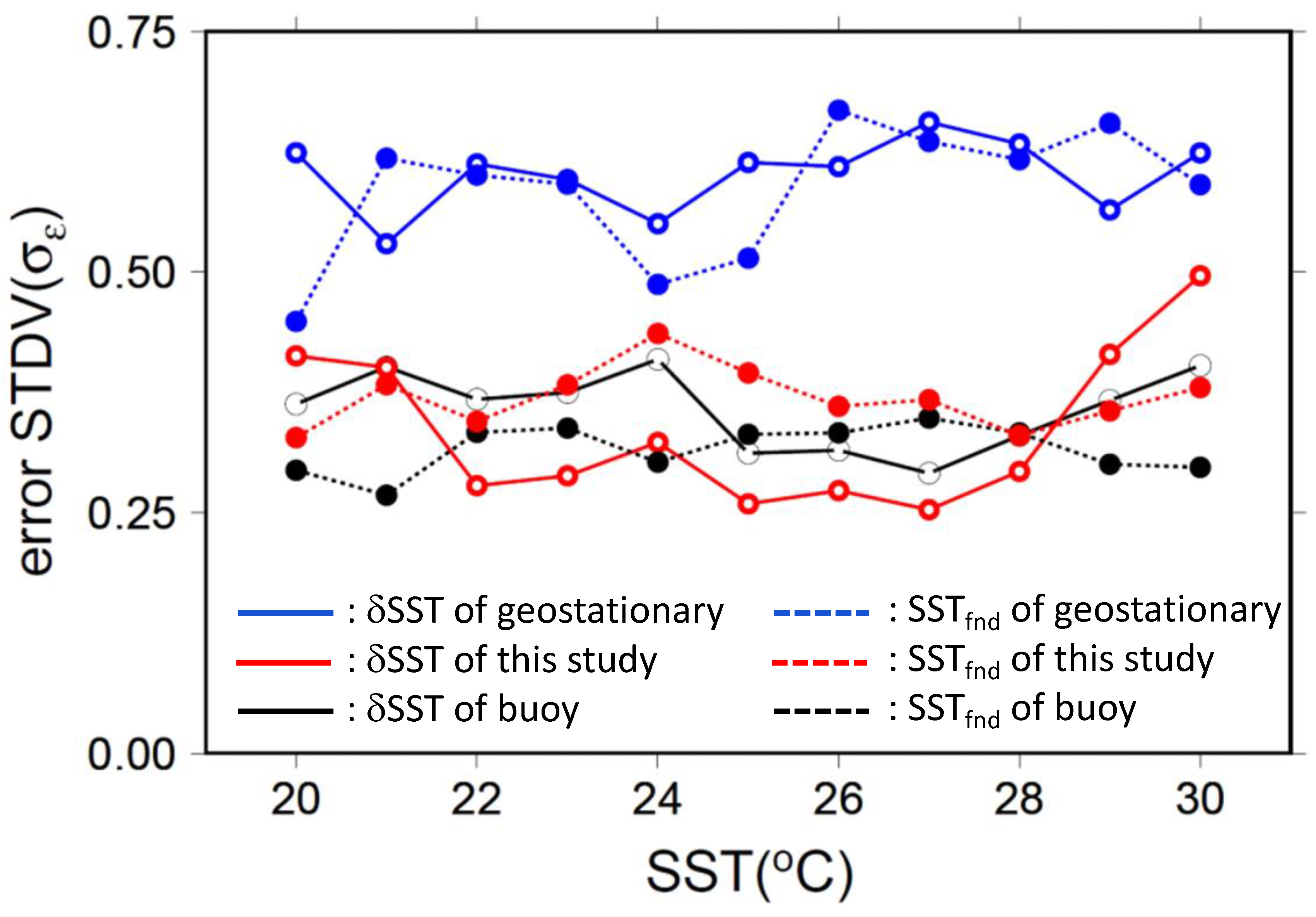
3.1. SST Validation
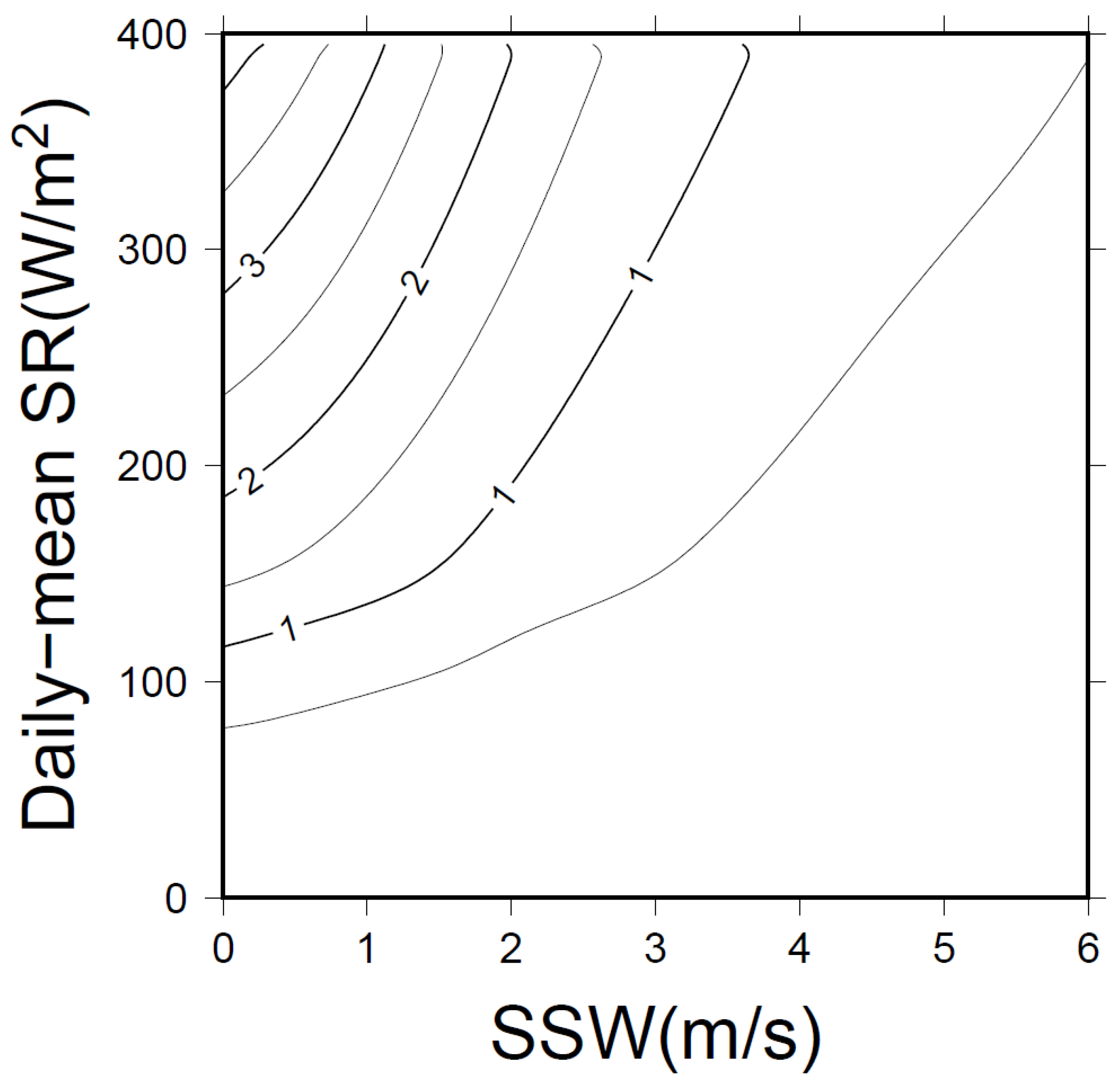
3.2. Relation between δSST Variability and HE in the Western Equatorial Pacific
4. Discussion
5. Conclusions
- (a)
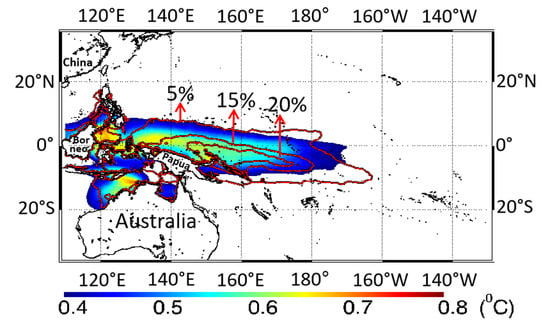
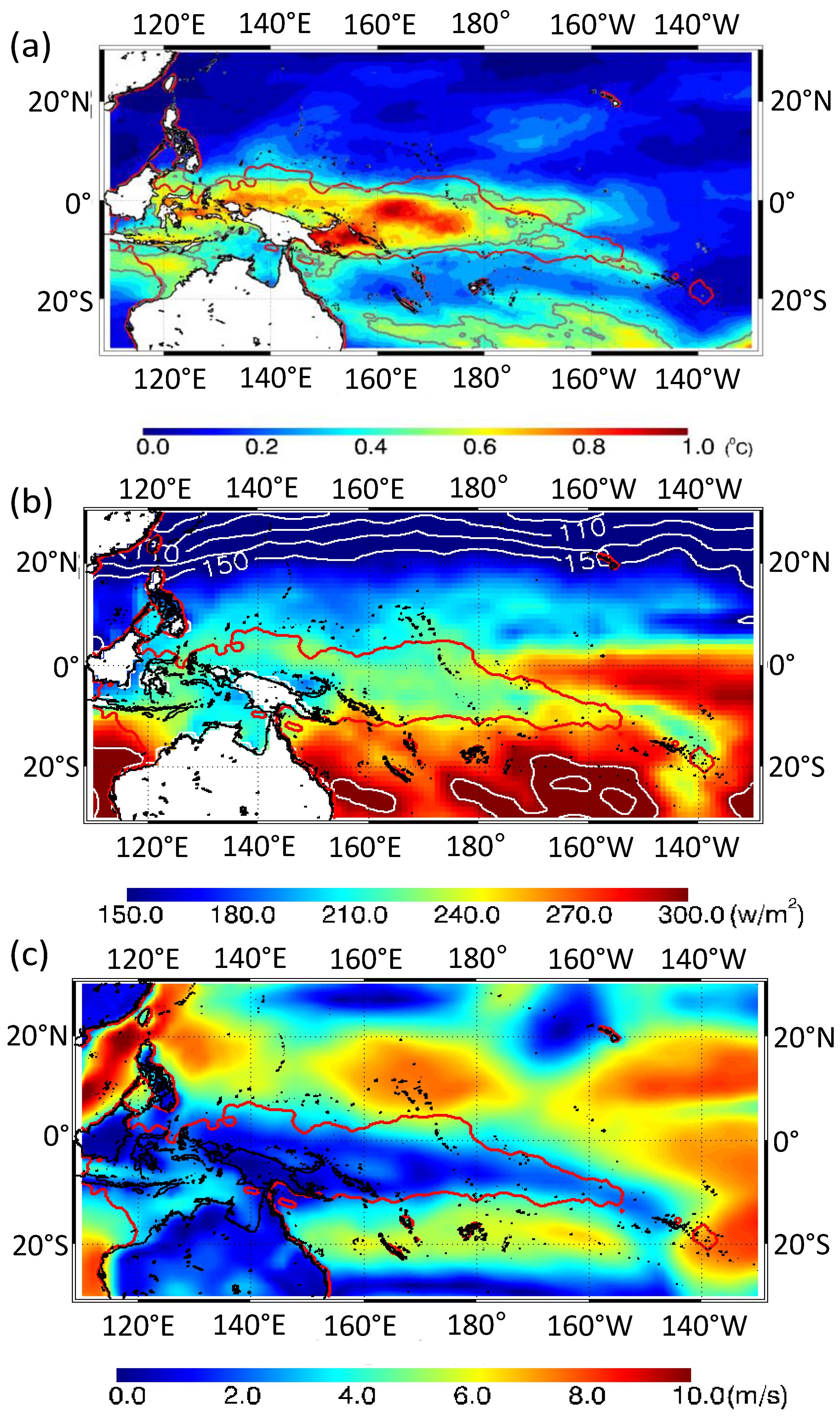
- In the case study, the area of HE041216 occurrence coincided well with the area of δSST of more than 0.5 °C.
- (b)
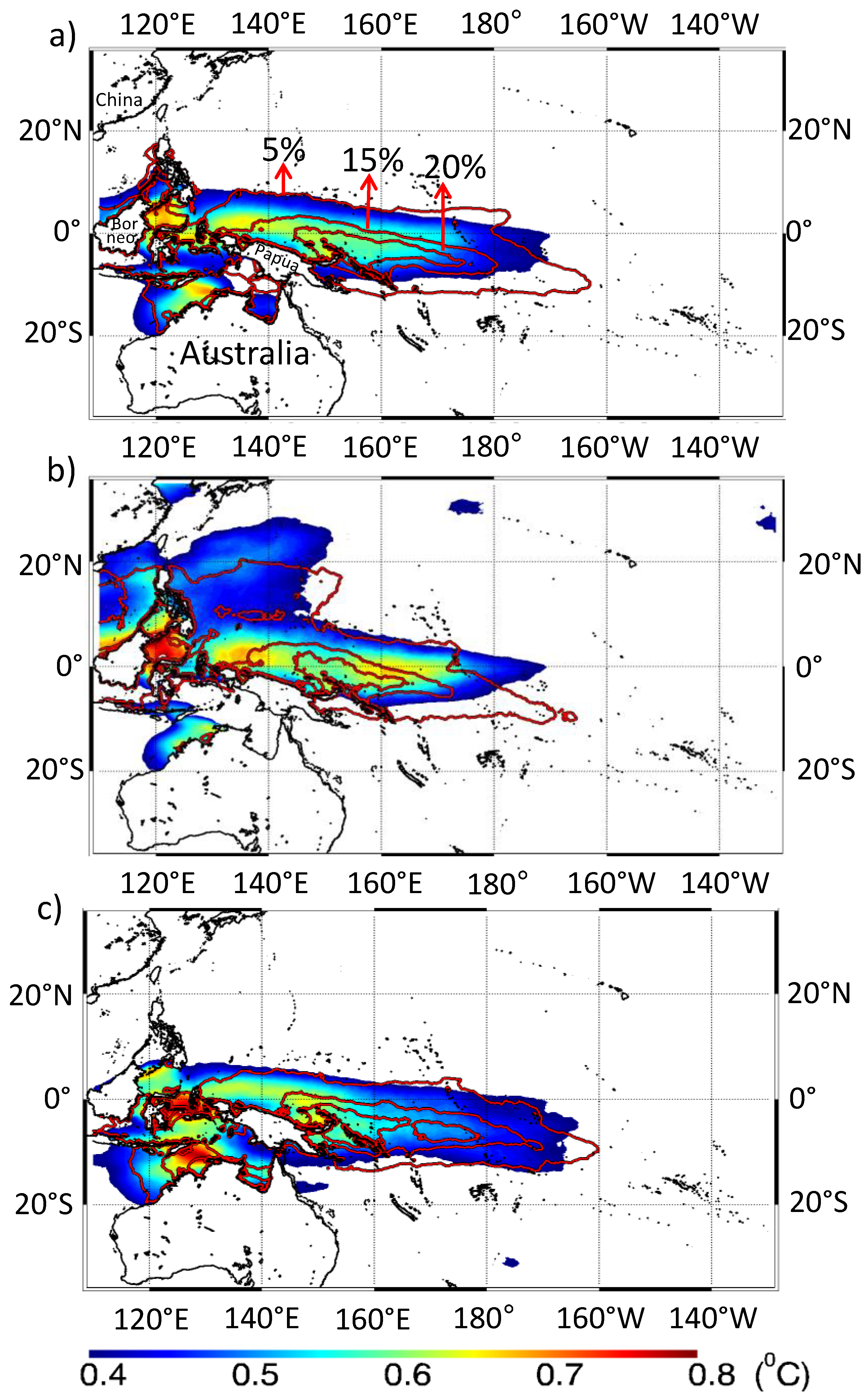
- The climatological mean of δSST shows that high δSST of more than 0.4 °C is distributed from 10°S to 10°N along the northern coast of New Guinea Island until 170°W. The high δSST distribution is collocated with the area of HE frequency occurrence of more than 5%.
- (c)
- During boreal summer (winter) the high δSST distribution shifts northward (southward).
- (d)
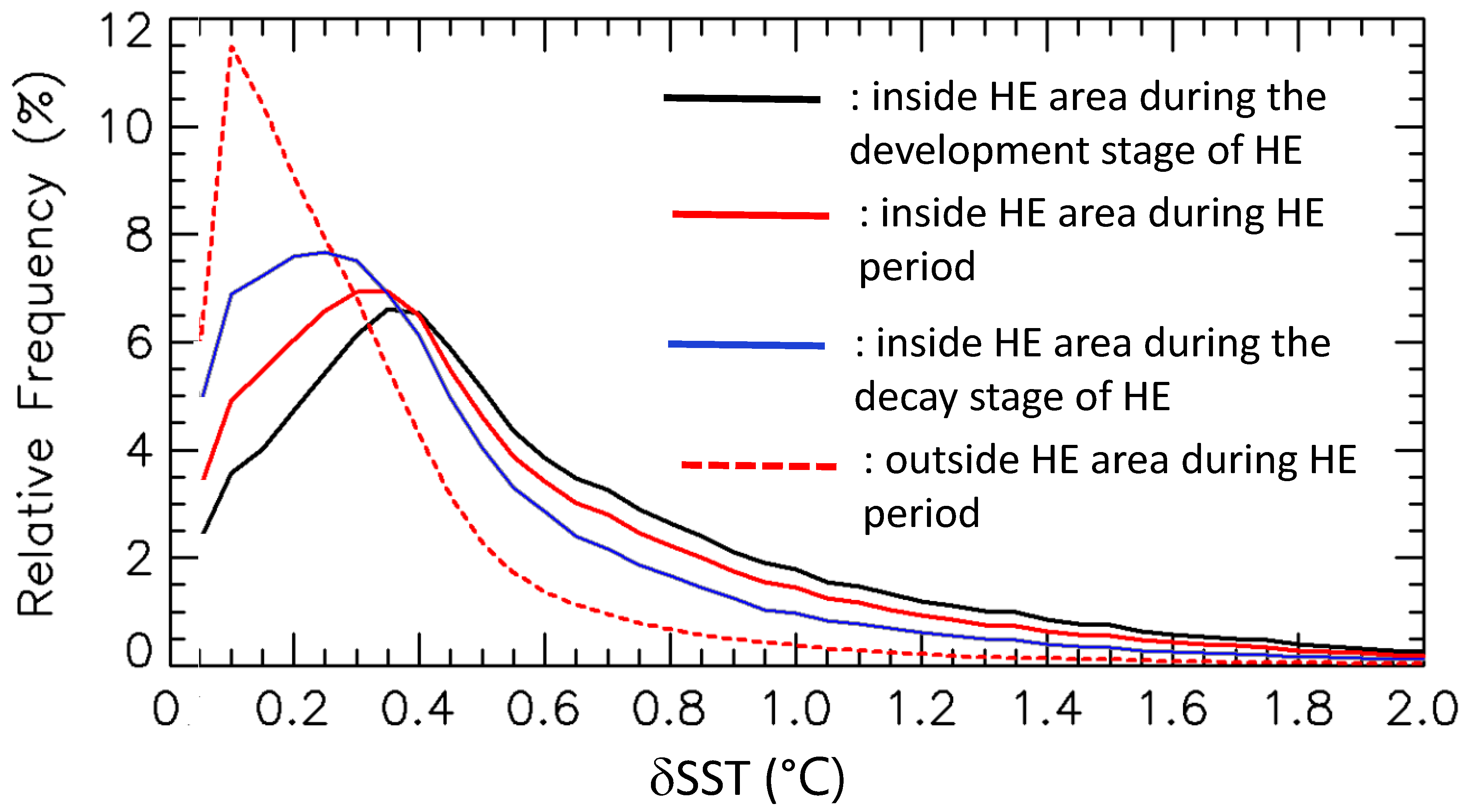
- The δSST inside HEs during the development stage is higher than the one during the decay stage.
- (e)
- High δSST can be a good indicator of HE occurrence in the western equatorial Pacific since both wind speed and solar radiation have been included for the calculation of δSST.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stramma, L.; Cornillon, P.; Weller, R.A.; Price, J.F.; Briscoe, M.G. Large Diurnal Sea Surface Temperature Variability: Satellite and In Situ Measurements. J. Phys. Oceanogr. 1986, 16, 827–837. [Google Scholar] [CrossRef]
- Price, J.F.; Weller, R.A.; Bowers, C.M.; Briscoe, M.G. Diurnal response of sea surface temperature observed at the long-term upper ocean study (34°N, 70°W) in the Sargasso Sea. J. Geophys. Res. 1987, 92, 14480. [Google Scholar] [CrossRef]
- Yokoyama, R.; Tanba, S.; Souma, T. Sea surface effects on the sea surface temperature estimation by remote sensing. Int. J. Remote Sens. 1995, 16, 227–238. [Google Scholar] [CrossRef]
- Wirasatriya, A.; Kawamura, H.; Koch, M.; Helmi, M. Satellite-borne detection of high diurnal amplitude of sea surface temperature in the seas west of the Tsugaru Strait, Japan, during Yamase wind season. J. Oceanogr. 2018, 75, 23–36. [Google Scholar] [CrossRef]
- Kawai, Y.; Kawamura, H. Evaluation of the Diurnal Warming of Sea Surface Temperature Using Satellite-Derived Marine Meteorological Data. J. Oceanogr. 2002, 58, 805–814. [Google Scholar] [CrossRef]
- Hosoda, K. Empirical method of diurnal correction for estimating sea surface temperature at dawn and noon. J. Oceanogr. 2013, 69, 631–646. [Google Scholar] [CrossRef]
- Bernie, D.J.; Guilyardi, E.; Madec, G.; Slingo, J.M.; Woolnough, S.J.; Cole, J. Impact of resolving the diurnal cycle in an ocean-atmosphere GCM. Part 2: A diurnally coupled CGCM. Clim. Dyn. 2008, 31, 909–925. [Google Scholar] [CrossRef]
- Kawai, Y.; Wada, A. Diurnal sea surface temperature variation and its impact on the atmosphere and ocean: A review. J. Oceanogr. 2007, 63, 721–744. [Google Scholar] [CrossRef]
- Clayson, C.A.; Chen, A. Sensitivity of a Coupled Single-Column Model in the Tropics to Treatment of the Interfacial Parameterizations. J. Clim. 2002, 15, 1805–1831. [Google Scholar] [CrossRef]
- Bernie, D.J.; Woolnough, S.J.; Slingo, J.M.; Guilyardi, É. Modeling Diurnal and Intraseasonal Variability of the Ocean Mixed Layer. J. Clim. 2005, 18, 1190–1202. [Google Scholar] [CrossRef]
- Li, W.; Yu, R.; Liu, H.; Yu, Y. Impacts of diurnal cycle of SST on the interseasonal variation of surface heat flux over the western Pacific warm pool. Adv. Atmos. Sci. 2001, 18, 793–806. [Google Scholar] [CrossRef]
- Kettle, H.; Merchant, C.J.; Jeffery, C.D.; Filipiak, M.J.; Gentemann, C.L. The impact of diurnal variability in sea surface temperature on the central Atlantic air-sea CO2 flux. Atmospheric Chem. Phys. Discuss. 2009, 9, 529–541. [Google Scholar] [CrossRef]
- Slingo, J.M.; Inness, P.; Neale, R.; Woolnough, S.; Yang, G.Y. Scale interactions on diurnal to seasonal timescales and their relevance to model systematic errors. Ann. Geophys. 2003, 46, 139–155. [Google Scholar]
- Dai, A.; Trenberth, K.E. The Diurnal Cycle and Its Depiction in the Community Climate System Model. J. Clim. 2004, 17, 930–951. [Google Scholar] [CrossRef]
- Bernie, D.J.; Guilyardi, É.; Madec, G.; Slingo, J.M.; Woolnough, S.J. Impact of resolving the diurnal cycle in an ocean–atmosphere GCM. Part 1: A diurnally forced OGCM. Clim. Dyn. 2007, 29, 575–590. [Google Scholar] [CrossRef]
- Hsu, J.-Y.; Hendon, H.; Feng, M.; Zhou, X. Magnitude and Phase of Diurnal SST Variations in the ACCESS-S1 Model During the Suppressed Phase of the MJOs. J. Geophys. Res. Oceans 2019, 124, 9553–9571. [Google Scholar] [CrossRef]
- Masson, S.; Terray, P.; Madec, G.; Luo, J.-J.; Yamagata, T.; Takahashi, K. Impact of intra-daily SST variability on ENSO characteristics in a coupled model. Clim. Dyn. 2011, 39, 681–707. [Google Scholar] [CrossRef]
- Qin, H.; Kawamura, H.; Kawai, Y. Detection of hot event in the equatorial Indo-Pacific warm pool using advanced satellite sea surface temperature, solar radiation, and wind speed. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Kawamura, H.; Qin, H.; Ando, K. In-situ diurnal sea surface temperature variations and near-surface thermal structure in the tropical hot event of the Indo-Pacific warm pool. J. Oceanogr. 2008, 64, 847–857. [Google Scholar] [CrossRef]
- Wirasatriya, A.; Kawamura, H.; Shimada, T.; Hosoda, K. Climatology of hot events in the western equatorial Pacific. J. Oceanogr. 2014, 71, 77–90. [Google Scholar] [CrossRef]
- Wirasatriya, A.; Kawamura, H.; Helmi, M.; Sugianto, D.N.; Shimada, T.; Hosoda, K.; Handoyo, G.; Putra, Y.D.G.; Koch, M. Thermal structure of hot events and their possible role in maintaining the warm isothermal layer in the Western Pacific warm pool. Ocean Dyn. 2020, 70, 771–786. [Google Scholar] [CrossRef]
- Kawai, Y.; Kawamura, H. Spatial and temporal variations of model-derived diurnal amplitude of sea surface temperature in the western Pacific Ocean. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Wentz, F.J. Satellite Measurements of Sea Surface Temperature Through Clouds. Science 2000, 288, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Chelton, D.B.; Esbensen, S.K.; Schlax, M.G.; Thum, N.; Freilich, M.H.; Wentz, F.J.; Gentemann, C.L.; McPhaden, M.J.; Schopf, P.S. Observations of coupling between surface wind stress and sea surface temperature in the eastern tropical Pacific. J. Clim. 2001, 14, 1479–1498. [Google Scholar] [CrossRef]
- Nonaka, M.; Xie, S. Covariations of Sea Surface Temperature and Wind over the Kuroshio and Its Extension: Evidence for Ocean-to-Atmosphere Feedback*. J. Clim. 2003, 16, 1404–1413. [Google Scholar] [CrossRef]
- Guan, L.; Kawamura, H. SST Availabilities of Satellite Infrared and Microwave Measurements. J. Oceanogr. 2003, 59, 201–209. [Google Scholar] [CrossRef]
- Hosoda, K. A review of satellite-based microwave observations of sea surface temperatures. J. Oceanogr. 2010, 66, 439–473. [Google Scholar] [CrossRef]
- Gentemann, C.; Meissner, T.; Wentz, F. Accuracy of Satellite Sea Surface Temperatures at 7 and 11 GHz. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1009–1018. [Google Scholar] [CrossRef]
- Hosoda, K.; Sakaida, F. Global Daily High-Resolution Satellite-Based Foundation Sea Surface Temperature Dataset: Development and Validation against Two Definitions of Foundation SST. Remote Sens. 2016, 8, 962. [Google Scholar] [CrossRef]
- Donlon, C.; Robinson, I.; Casey, K.S.; Vazquez-Cuervo, J.; Armstrong, E.; Arino, O.; Gentemann, C.; May, D.; Leborgne, P.; Piollé, J.; et al. The Global Ocean Data Assimilation Experiment High-resolution Sea Surface Temperature Pilot Project. Bull. Am. Meteorol. Soc. 2007, 88, 1197–1214. [Google Scholar] [CrossRef]
- Clayson, C.A.; Bogdanoff, A. The Effect of Diurnal Sea Surface Temperature Warming on Climatological Air–Sea Fluxes. J. Clim. 2013, 26, 2546–2556. [Google Scholar] [CrossRef]
- Gentemann, C.; Stuart-Menteth, A.; Wentz, F.J.; Donlon, C. Diurnal signals in satellite sea surface temperature measurements. Geophys. Res. Lett. 2003, 30, 1140. [Google Scholar] [CrossRef]
- Filipiak, M.J.; Merchant, C.J.; Kettle, H.; Le Borgne, P. An empirical model for the statistics of sea surface diurnal warming. Ocean Sci. 2012, 8, 197–209. [Google Scholar] [CrossRef]
- Clayson, C.A.; Weitlich, D. Variability of Tropical Diurnal Sea Surface Temperature*. J. Clim. 2007, 20, 334–352. [Google Scholar] [CrossRef]
- Morak-Bozzo, S.; Merchant, C.J.; Kent, E.C.; Berry, D.; Carella, G. Climatological diurnal variability in sea surface temperature characterized from drifting buoy data. Geosci. Data J. 2016, 3, 20–28. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Ando, K.; Bourles, B.; Freitag, H.P.; Lumpkin, R.; Masumoto, Y.; Murty, V.S.N.; Nobre, P.; Ravichandran, M.; Vialard, J.; et al. The Global Tropical Moored Buoy Array, Proceedings of the “OceanObs ’09: Sustained Ocean Observations and Information for Society”, Venice, Italy, 21–25 September 2009; Hall, J., Harrison, D.E., Stammer, D., Eds.; ESA Publication, WPP: Paris, France, 2010; p. 306. Available online: http://sunburn.aoml.noaa.gov/phod/docs/McPhadenTheGlobalTropical.pdf (accessed on 18 July 2020).
- NOAA/NESDIS. GOES Level 3 6 km Near Real Time SST 24 h. ver. 1. 2003. Available online: http://dx.doi.org/10.5067/GOES3-24HOR (accessed on 20 September 2016).
- Merchant, C.J.; Harris, A.R.; Maturi, E.; Maccallum, S. Probabilistic physically based cloud screening of satellite infrared imagery for operational sea surface temperature retrieval. Q. J. R. Meteorol. Soc. 2005, 131, 2735–2755. [Google Scholar] [CrossRef]
- Kurihara, Y.; Murakami, H.; Kachi, M. Sea surface temperature from the new Japanese geostationary meteorological Himawari-8 satellite. Geophys. Res. Lett. 2016, 43, 1234–1240. [Google Scholar] [CrossRef]
- Hosoda, K. Global space-time scales for day-to-day variations of daily-minimum and diurnal sea surface temperatures: Their distinct spatial distribution and seasonal cycles. J. Oceanogr. 2015, 72, 281–298. [Google Scholar] [CrossRef]
- Onogi, K.; Tsutsui, J.; Koide, H.; Sakamoto, M.; Kobayashi, S.; Hatsushika, H.; Matsumoto, T.; Yamazaki, N.; Kamahori, H.; Takahashi, K.; et al. The JRA-25 Reanalysis. J. Meteorol. Soc. Jpn. 2007, 85, 369–432. [Google Scholar] [CrossRef]
- Zhang, Y.; Oinas, V.; Rossow, W.B.; Lacis, A.A.; Mishchenko, M.I. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. J. Geophys. Res. 2004, 109, 1–27. [Google Scholar] [CrossRef]
- Wirasatriya, A.; Kawamura, H.; Shimada, T.; Hosoda, K. Atmospheric structure favoring high sea surface temperatures in the western equatorial Pacific. J. Geophys. Res. Atmos. 2016, 121, 11368–11381. [Google Scholar] [CrossRef]
- Emery, W.J.; Baldwin, D.J.; Schlüssel, P.; Reynolds, R.W. Accuracy of in situ sea surface temperatures used to calibrate infrared satellite measurements. J. Geophys. Res. 2001, 106, 2387–2405. [Google Scholar] [CrossRef]
- O’Carroll, A.; Eyre, J.R.; Saunders, R.W. Three-Way Error Analysis between AATSR, AMSR-E, and In Situ Sea Surface Temperature Observations. J. Atmospheric Ocean. Technol. 2008, 25, 1197–1207. [Google Scholar] [CrossRef]
- Lean, K.; Saunders, R. Validation of the ATSR reprocesiing for climate (ARC) dataset using data from drifting buoys and a three-way error analysis. J. Clim. 2013, 26, 4758–4772. [Google Scholar] [CrossRef]
- Gentemann, C.L. Three way validation of MODIS and AMSR-E sea surface temperatures. J. Geophys. Res. Oceans 2014, 119, 2583–2598. [Google Scholar] [CrossRef]
- Tu, Q.; Pan, D.; Hao, Z. Validation of S-NPP VIIRS Sea Surface Temperature Retrieved from NAVO. Remote Sens. 2015, 7, 17234–17245. [Google Scholar] [CrossRef]
- Cravatte, S.; Delcroix, T.; Zhang, D.; McPhaden, M.; Leloup, J. Observed freshening and warming of the western Pacific Warm Pool. Clim. Dyn. 2009, 33, 565–589. [Google Scholar] [CrossRef]
- Wang, H.-Y.; Tsang, L.M.; Lima, F.P.; Seabra, R.; Ganmanee, M.; Williams, G.A.; Chan, B.K.K. Spatial Variation in Thermal Stress Experienced by Barnacles on Rocky Shores: The Interplay Between Geographic Variation, Tidal Cycles and Microhabitat Temperatures. Front. Mar. Sci. 2020, 7, 1–14. [Google Scholar] [CrossRef]
- Meneghesso, C.; Seabra, R.; Broitman, B.R.; Wethey, D.S.; Burrows, M.T.; Chan, B.K.; Guy-Haim, T.; Ribeiro, P.A.; Rilov, G.; Santos, A.M.; et al. Remotely-sensed L4 SST underestimates the thermal fingerprint of coastal upwelling. Remote Sens. Environ. 2020, 237, 111588. [Google Scholar] [CrossRef]

| This Study (Blended Product) | Geostationary | Buoy | Number | This Study (Blended Product) | Geostationary | Buoy | Number | |
|---|---|---|---|---|---|---|---|---|
| δSST (daily) | δSST (10-day) | |||||||
| STDV (GOES) | 0.27 °C | 0.64 °C | 0.24 °C | 3317 | 0.14 °C | 0.39 °C | 0.02 °C | 528 |
| STDV (Himawari-8) | 0.35 °C | 0.58 °C | 0.36 °C | 610 | 0.19 °C | 0.31 °C | 0.06 °C | 86 |
| SSTfnd (daily) | SSTfnd (10-day) | |||||||
| STDV (GOES) | 0.47 °C | 0.55 °C | 0.42 °C | 2040 | 0.23 °C | 0.20 °C | 0.21 °C | 629 |
| STDV (Himawari-8) | 0.39 °C | 0.59 °C | 0.34 °C | 423 | 0.15 °C | 0.35 °C | 0.11 °C | 92 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wirasatriya, A.; Hosoda, K.; Setiawan, J.D.; Susanto, R.D. Variability of Diurnal Sea Surface Temperature during Short Term and High SST Event in the Western Equatorial Pacific as Revealed by Satellite Data. Remote Sens. 2020, 12, 3230. https://doi.org/10.3390/rs12193230
Wirasatriya A, Hosoda K, Setiawan JD, Susanto RD. Variability of Diurnal Sea Surface Temperature during Short Term and High SST Event in the Western Equatorial Pacific as Revealed by Satellite Data. Remote Sensing. 2020; 12(19):3230. https://doi.org/10.3390/rs12193230
Chicago/Turabian StyleWirasatriya, Anindya, Kohtaro Hosoda, Joga Dharma Setiawan, and R. Dwi Susanto. 2020. "Variability of Diurnal Sea Surface Temperature during Short Term and High SST Event in the Western Equatorial Pacific as Revealed by Satellite Data" Remote Sensing 12, no. 19: 3230. https://doi.org/10.3390/rs12193230
APA StyleWirasatriya, A., Hosoda, K., Setiawan, J. D., & Susanto, R. D. (2020). Variability of Diurnal Sea Surface Temperature during Short Term and High SST Event in the Western Equatorial Pacific as Revealed by Satellite Data. Remote Sensing, 12(19), 3230. https://doi.org/10.3390/rs12193230