Variational Based Estimation of Sea Surface Temperature from Split-Window Observations of INSAT-3D/3DR Imager
Abstract
1. Introduction
2. Data Used
2.1. Global Forecasting System (GFS) Forecasts
2.2. INSAT-3D/3DR L1B Data
2.3. In-situ SST Measurements
2.4. MUR Level-4 Daily Analysis GHRSST
3. Methodology
3.1. Cloud Masking
- If BT of TIR-1 channel is less than 275 K (sea-ice test). If the absolute difference between actual and simulated BTs is greater than 3 K.
- If the standard deviation of BTs in a FOR of 3 × 3 pixels centered at the given pixel is greater than 0.5 K.
- If the difference between TIR-1 and TIR-2 BTs is negative or greater than 5 K, (i.e., the valid range of the difference is 0–5 K),
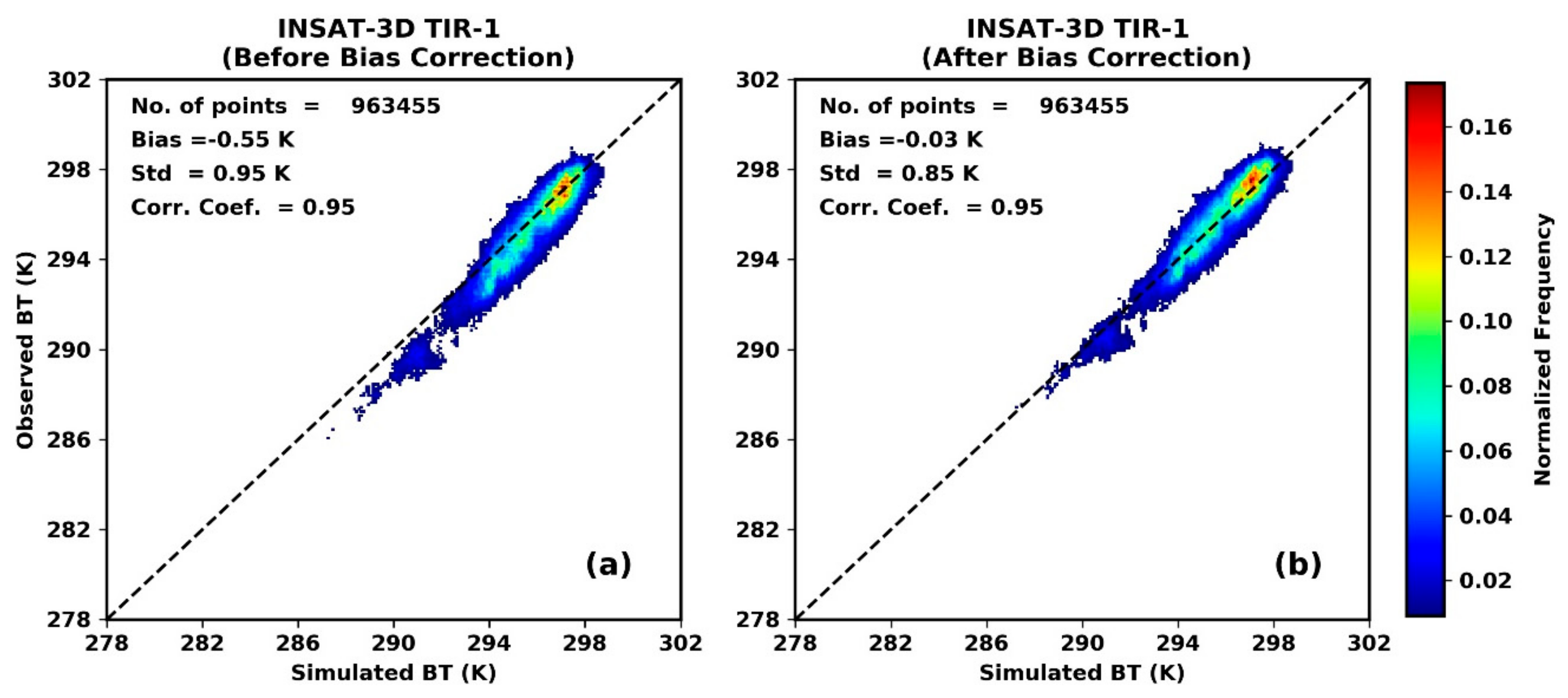
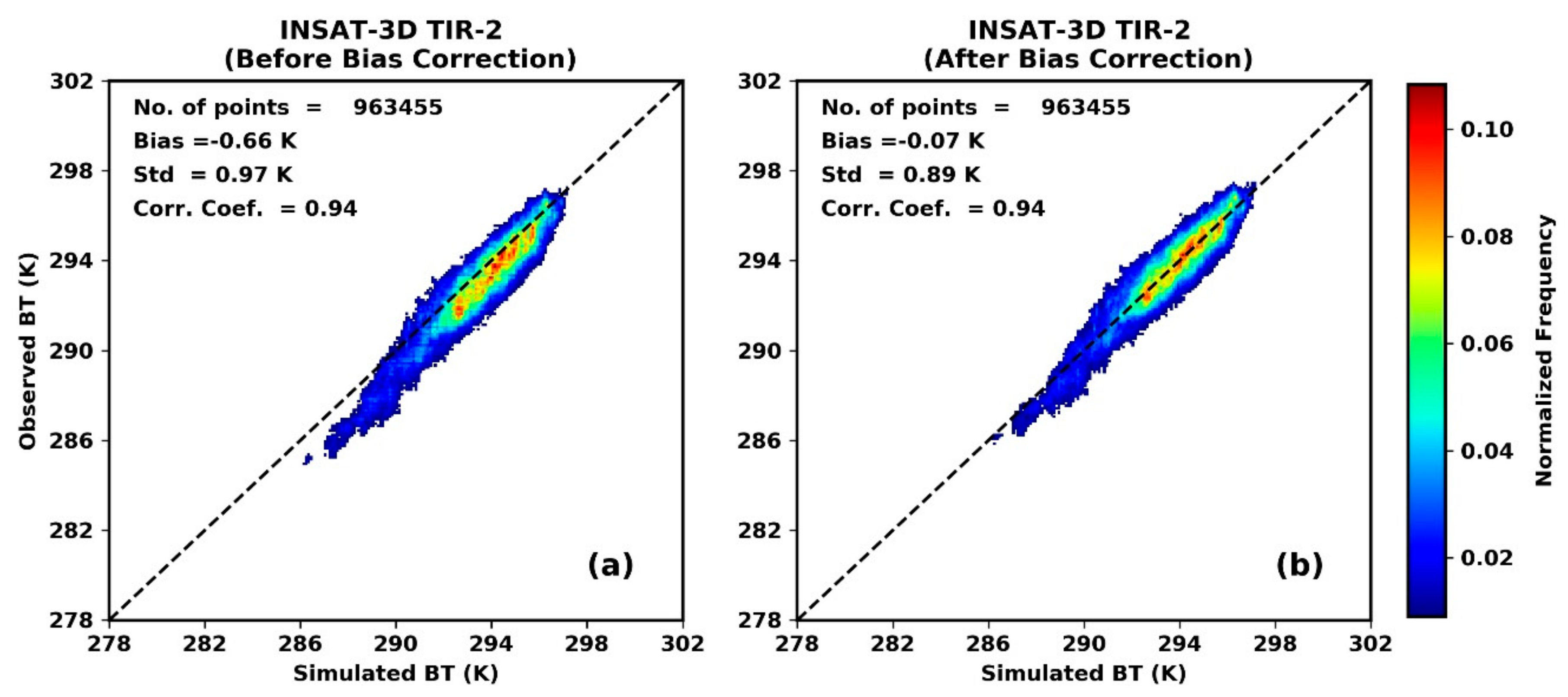
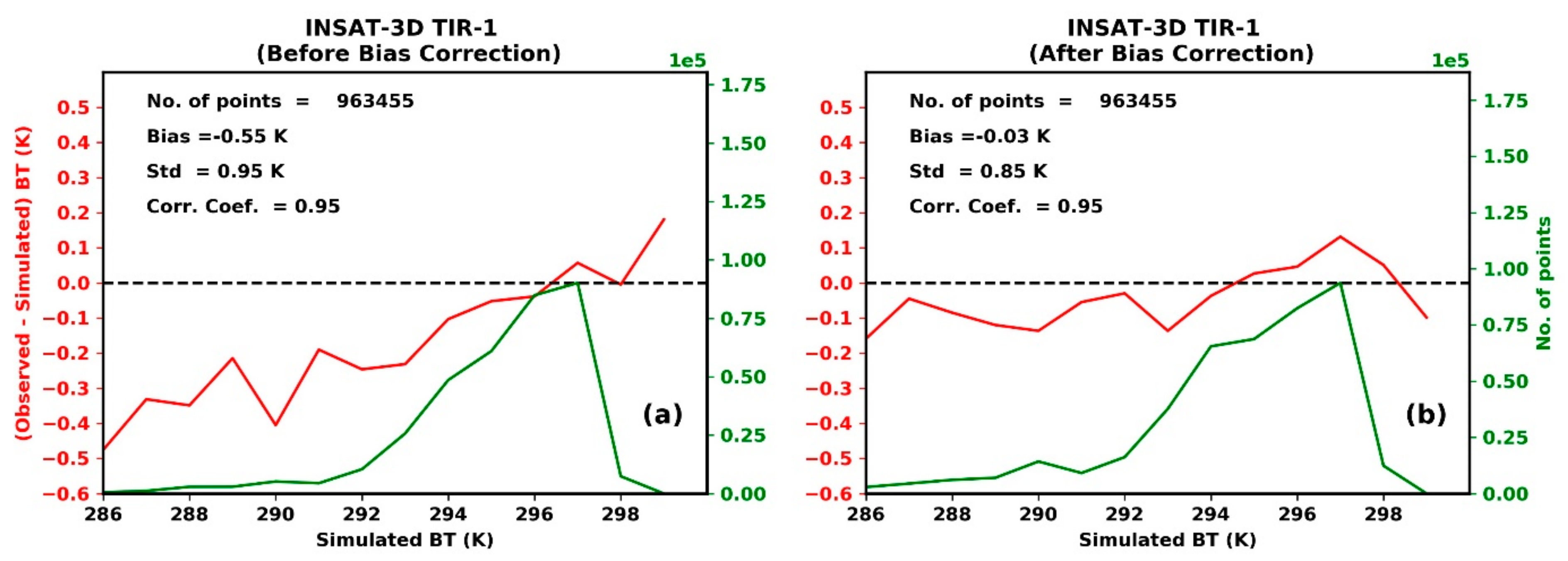
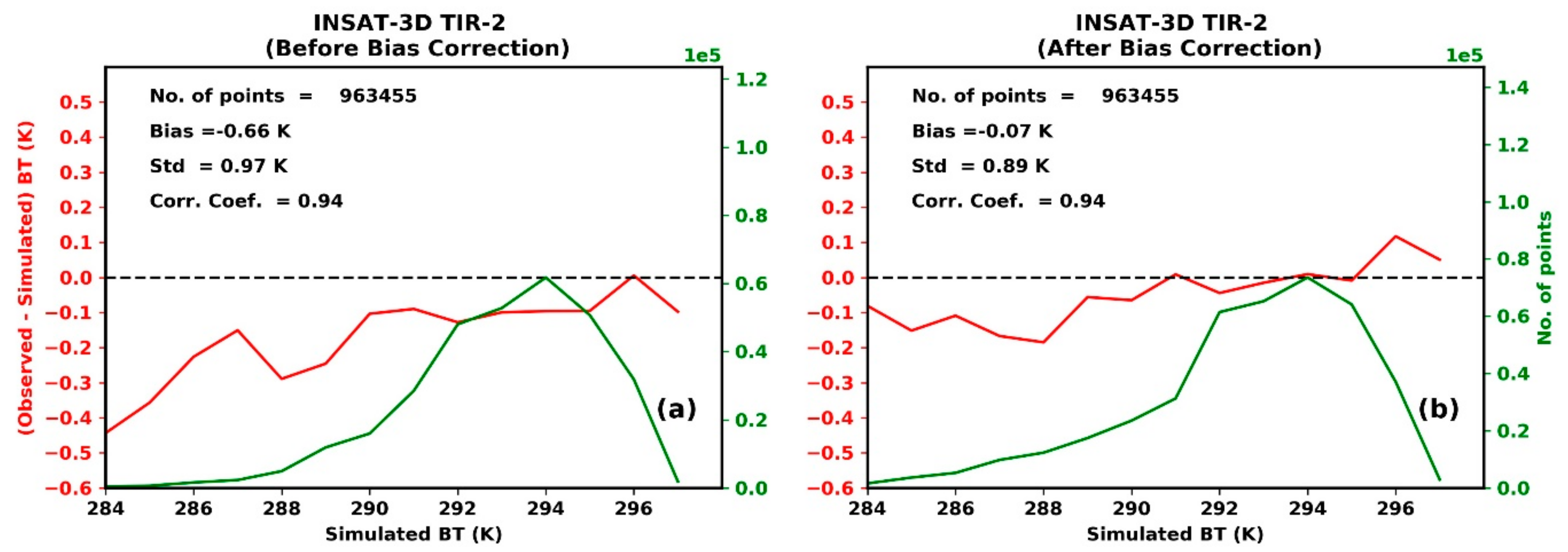
3.2. Bias Correction of the Observations
3.3. NLSST Algorithm
3.4. 1DVAR Algorithm
3.4.1. 1DVAR Setup
3.4.2. Convergence Testing
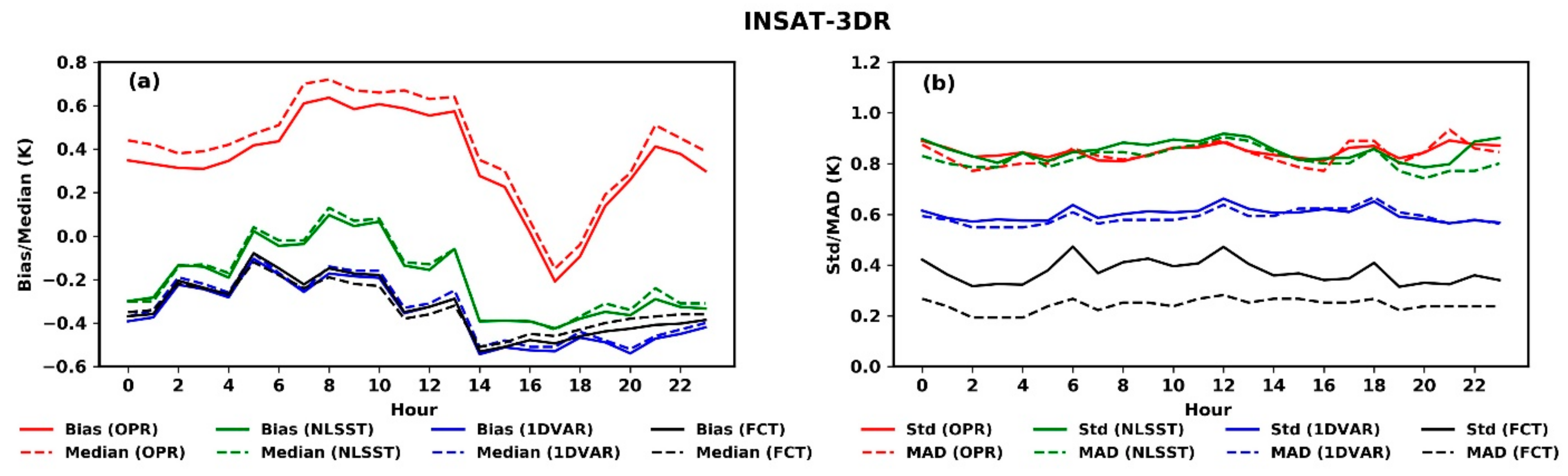
4. Results
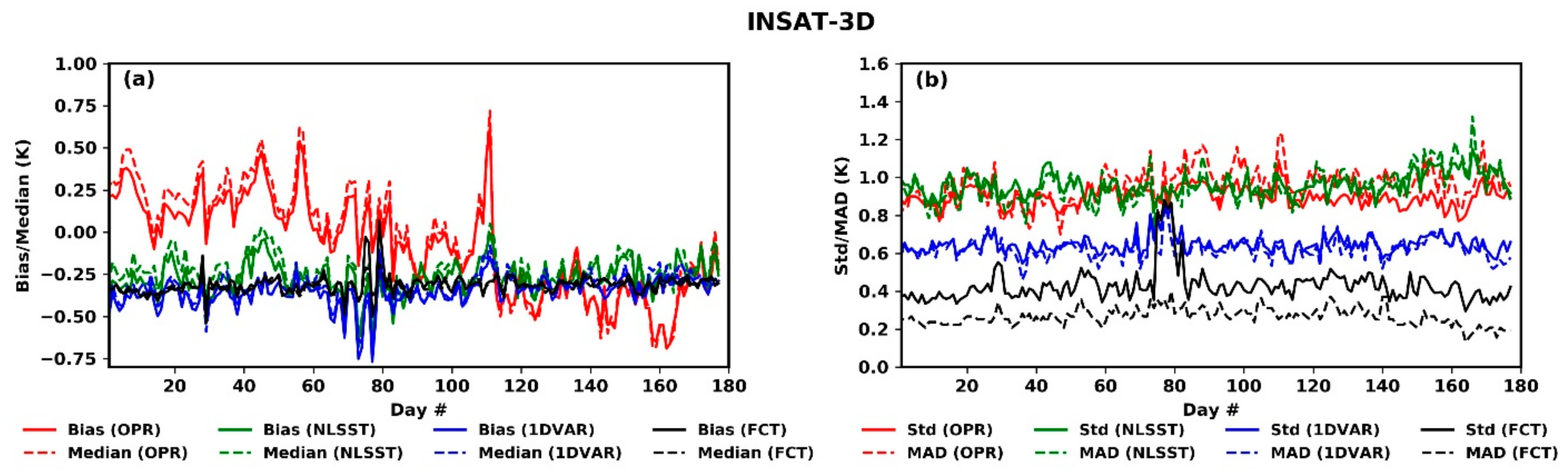
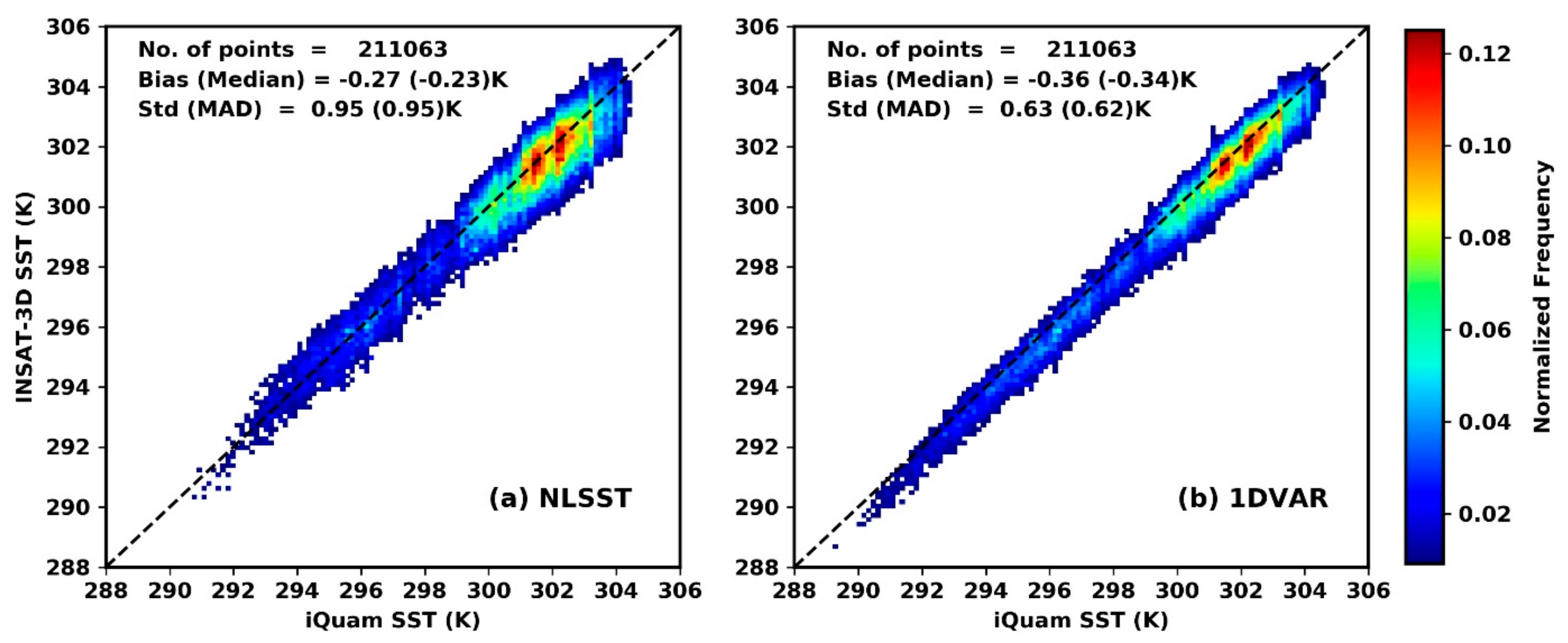
4.1. Validation Against iQuam SST Measurements
- Filtered data referred to hereafter as FILT_DATA.
- Entire matchup, referred to hereafter as NOFILT_DATA.
- The majority of the matchup dataset (>85%) is lying within 1 K of iQuam SST, leaving only <15% of it beyond this limit.
- Bias and Median do not show much difference indicating the robustness of the matchup data. The same outcome is endorsed by Std and MAD values being almost similar.
- For a larger population of the data, the 1DVAR SST shows Std (Bias) of 0.48 K (−0.23 K) whereas the NLSST gives 0.88 K (−0.15 K). However, SST accuracy with 0.95 K (−0.27 K) for the NLSST and 0.63 K (−0.36 K) for the 1DVAR, degrades slightly for the entire matchup. These values are without bulk-skin SST correction.
- The 1DVAR produces SST with greater accuracy and consistency than the NLSST, clearly seen when validated against iQuam SST.
- Both the algorithms demonstrate the consistent performance for all months, thereby ensuring their robustness.
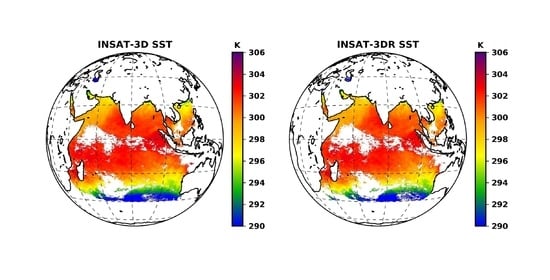
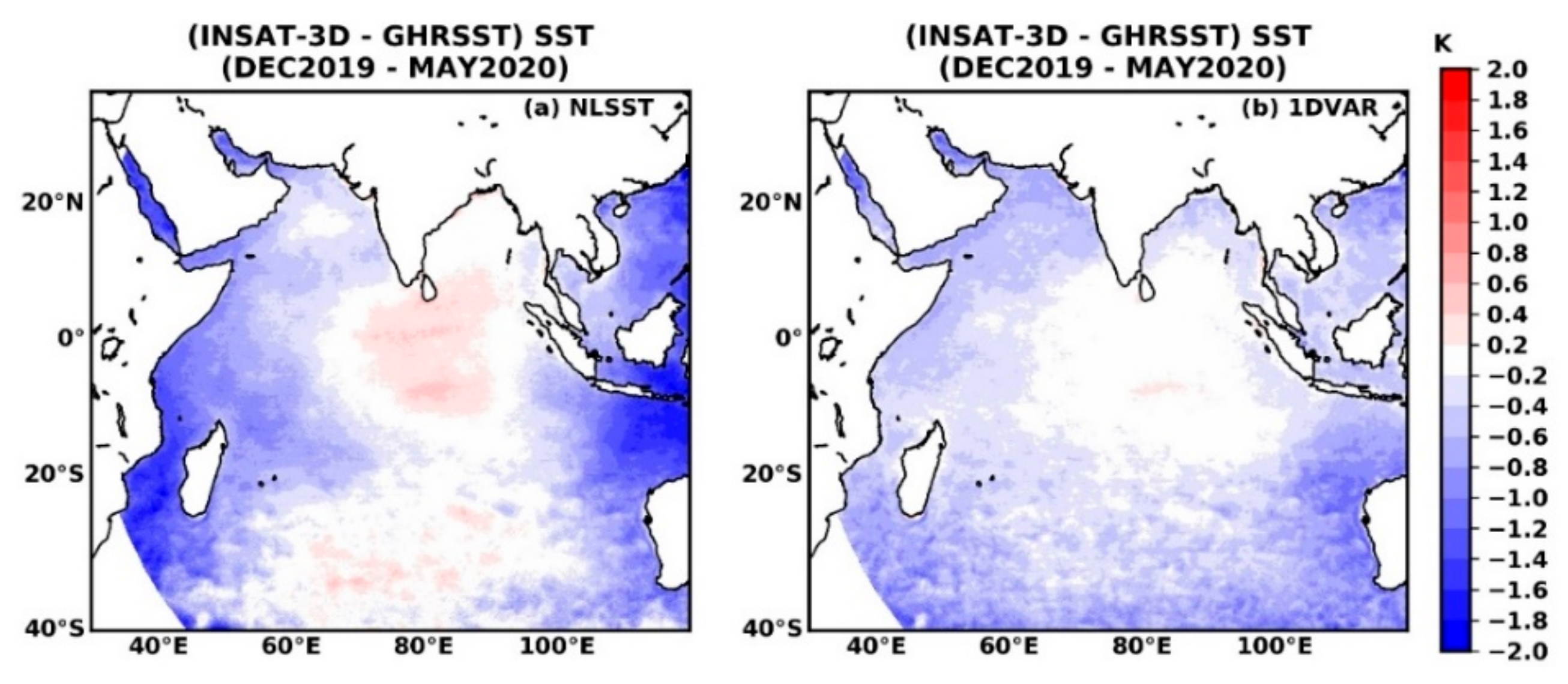
4.2. Comparison with MUR Level-4 Daily Analysis GHRSST Products
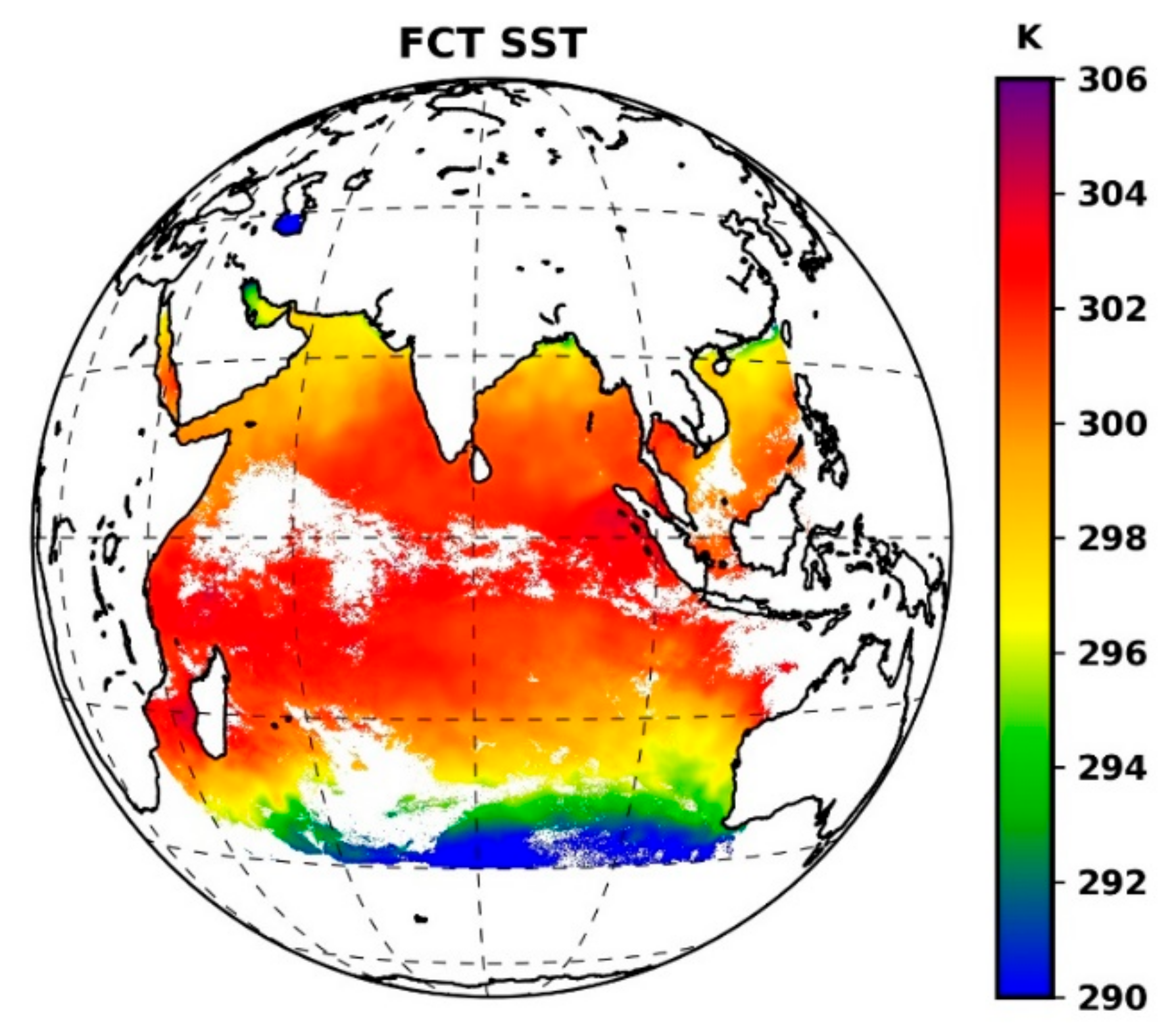
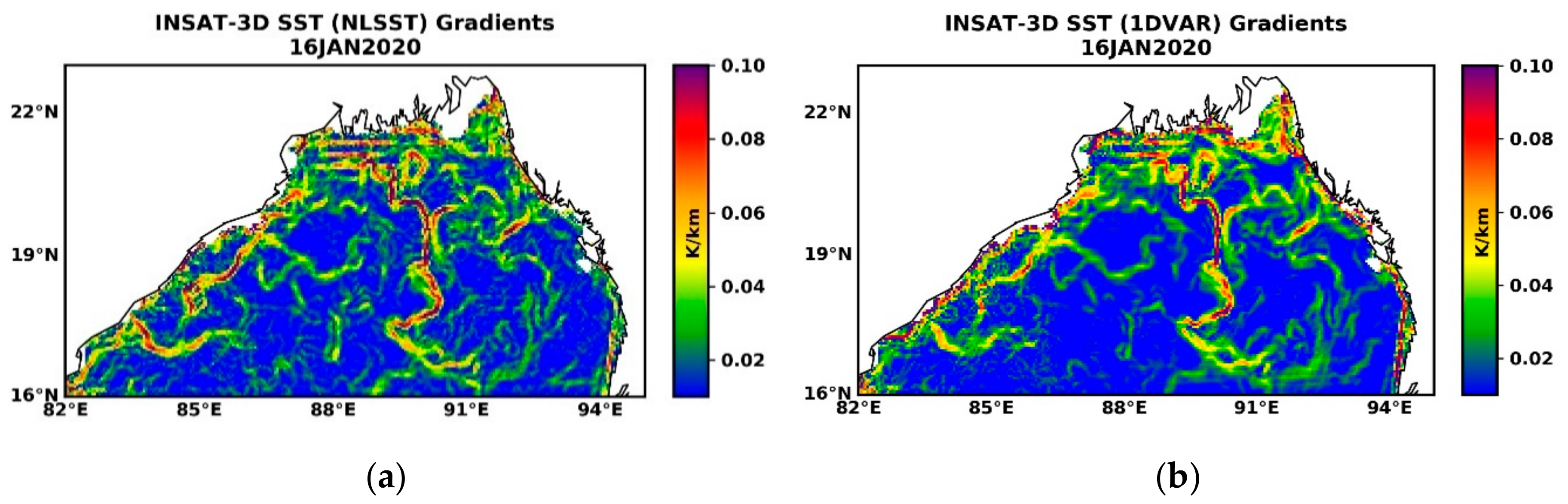
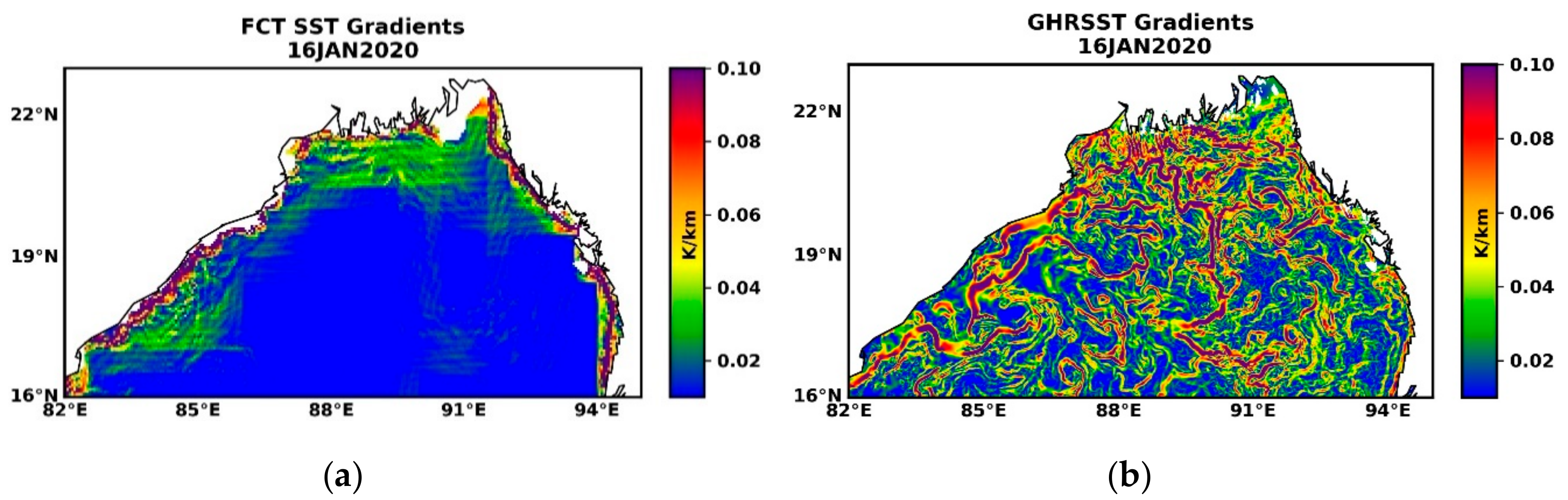
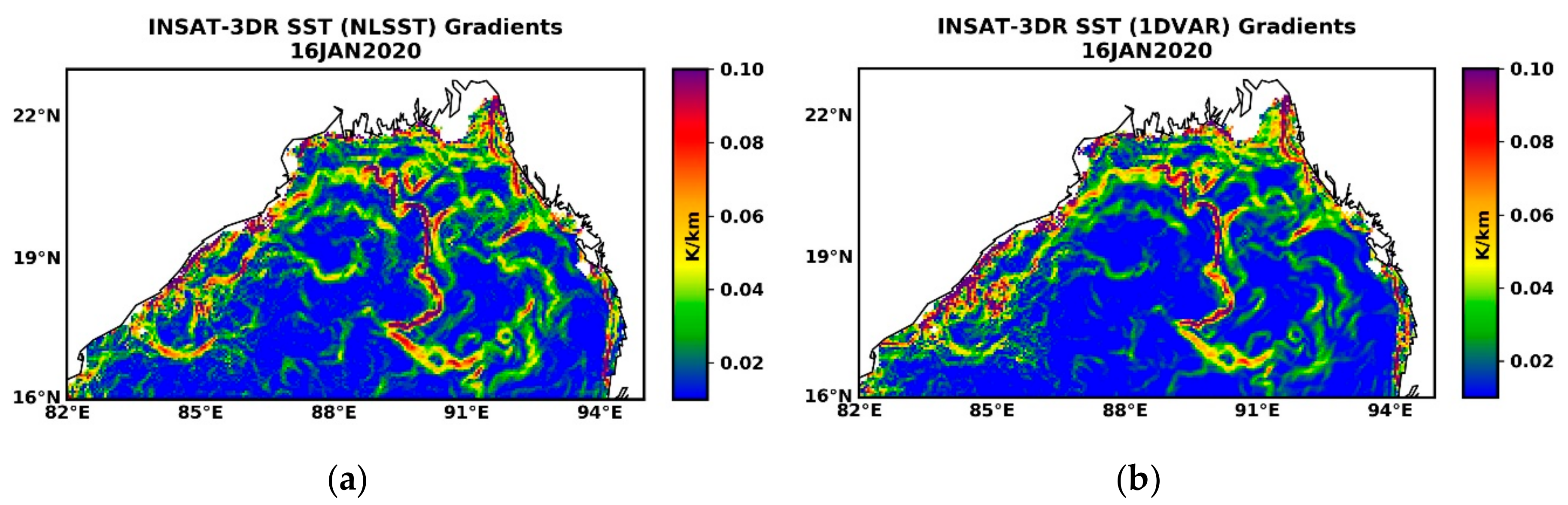
4.3. Thermal Gradients Derived from SST
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Yang, Q.; Nerger, L.; Losa, S.N.; Zhao, B.; Zheng, F.; Zhang, L.; Wu, L. Assimilating Copernicus SST Data into a Pan-Arctic Ice-Ocean Coupled Model with a Local SEIK Filter. J. Atmos. Ocean. Technol. 2017, 34, 1985–1999. [Google Scholar] [CrossRef]
- Brasnett, B.; Colan, D.S. Assimilating Retrievals of Sea Surface Temperature from VIIRS and AMSR2. J. Atmos. Ocean. Technol. 2016, 33, 361–375. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Antoine, D.; Bentamy, A.; Bonekamp, H.; Breivik, L.A.; Chapron, B.; Corlett, G.; Dibarboure, G.; Digiacomo, P.; Donlon, C.J.; et al. Use of satellite observations for operational oceanography: Recent achievements and future prospects. J. Oper. Oceanogr. 2015, 8 (Suppl. 1), 12–27. [Google Scholar] [CrossRef]
- Yang, C.-S.; Kim, S.H.; Ouchi, K.; Back, J.H. Generation of high resolution sea surface temperature using multi-satellite data for operational oceanography. Acta Oceanol. Sin. 2015, 34, 74–88. [Google Scholar] [CrossRef]
- Chelton, D.B.; Wentz, F.J. Global Microwave Satellite Observations of Sea Surface Temperature for Numerical Weather Prediction and Climate Research. Bull. Am. Meteorol. Soc. 2005, 86, 1097–1115. [Google Scholar] [CrossRef]
- Bentamy, A.; Piollé, J.F.; Grouazel, A.; Danielson, R.; Gulev, S.; Paul, F.; Azelmat, H.; Mathieu, P.P.; von Schuckmann, K.; Sathyendranath, S.; et al. Review and assessment of latent and sensible heat flux accuracy over the global oceans. Remote Sens. Environ. 2017, 201, 196–218. [Google Scholar] [CrossRef]
- O’Carroll, A.G.; Armstrong, E.M.; Beggs, H.M.; Bouali, M.; Casey, K.S.; Corlett, G.K.; Dash, P.; Donlon, C.J.; Gentemann, C.L.; Høyer, J.L.; et al. Observational Needs of Sea Surface Temperature. Front. Mar. Sci. 2019, 6, 420. [Google Scholar] [CrossRef]
- Ning, J.; Qing, X.; Wang, T.; Zhang, S. Upper Ocean Response to Super Typhoon Soudelor Revealed by Different SST Products. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Monzikova, A.K.; Kudryavtsev, V.N.; Reul, N.; Chapron, B. On the upper ocean response to tropical cyclones: Satellite microwave observation. In Proceedings of the Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017; pp. 2437–2444. [Google Scholar]
- Gentemann, C.L.; Donlon, C.J.; Stuart-Menteth, A.; Wentz, F.J. Diurnal signals in satellite sea surface temperature measurements. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Rayner, N.A.; Brohan, P.; Parker, D.E.; Folland, C.K.; Kennedy, J.J.; Vanicek, M.; Ansell, T.J.; Tett, S.F.B. Improved analyses of changes and uncertainties in sea surface temperature measured in situ since the mid-nineteenth century: The HadSST2 dataset. J. Clim. 2006, 19, 446–469. [Google Scholar] [CrossRef]
- Minnett, P.J.; Alvera-Azcárate, A.; Chin, T.M.; Corlett, G.K.; Gentemann, C.L.; Karagali Li, I.X.; Marsouin, A.; Marullo, S.; Maturi, E.; Santoleri, R.; et al. Half a century of satellite remote sensing of sea-surface temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]
- Donlon, C.; Rayner, N.; Robinson, I.; Poulter, D.J.S.; Casey, K.S.; Vazquez-Cuervo, J.; Armstrong, E.; Bingham, A.; Arino, O.; Gentemann, C.; et al. The Global Ocean Data Assimilation Experiment High-resolution Sea Surface Temperature Pilot Project. Bull. Am. Meteorol. Soc. 2007, 88, 1197–1213. [Google Scholar] [CrossRef]
- Donlon, C.; Casey, K.S.; Gentemann, C.; Harris, A. Successes and Challenges for the Modern Sea Surface Temperature Observing System. In Proceedings of the OceanObs’09: Sustained Ocean Observations and Information for Society, Venice, Italy, 21–25 September 2009. [Google Scholar]
- Wentz, F.J.; Gentemann, C.; Smith, D.; Chelton, D.B. Satellite Measurements of Sea Surface Temperature through Clouds. Science 2000, 288, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive. Volume 1-Microwave Remote Sensing Fundamentals and Radiometry; Addisoon-Wesley Publishing Company: Boston, MA, USA, 1981; ISBN 978-0890061909. [Google Scholar]
- Vázquez-Cuervo, J.; Armstrong, E.M.; Harris, A. The Effect of Aerosols and Clouds on the Retrieval of Infrared Sea Surface Temperatures. J. Clim. 2004, 17, 3921–3933. [Google Scholar] [CrossRef]
- Merchant, C.J.; Harris, A.R.; Murray, M.J.; Zavody, A.M. Toward the elimination of bias in satellite retrievals of skin sea surface temperature 1. Theory, modeling and inter-algorithm comparison. J. Geophys. Res. Ocean. 1999, 104, 23565–23578. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O.; Le Borgne, P.; Bellec, B. Saharan dust in night-time thermal imagery: Detection and reduction of related biases in retrieved sea surface temperature. Remote Sens. Environ. 2006, 104, 15–30. [Google Scholar] [CrossRef]
- Luo, B.; Minnett, P.J.; Gentemann, C.; Szczodrak, G. Improving satellite retrieved night-time infrared sea surface temperatures in aerosol contaminated regions. Remote Sens. Environ. 2019, 223, 8–20. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.; Williams, E.; Walsh, S.; Minnett, P.J. Alternating decision trees for cloud masking in MODIS and VIIRS NASA sea surface temperature products. J. Atmos. Ocean. Technol. 2019, 36, 387–407. [Google Scholar] [CrossRef]
- Gladkova, I.; Ignatov, A.; Shahriar, F.; Kihai, Y.; Hillger, D.; Petrenko, B. Improved VIIRS and MODIS SST Imagery. Remote Sens. 2016, 8, 79. [Google Scholar] [CrossRef]
- Embury, O.; Merchant, C.J.; Corlett, G.K. A reprocessing for climate of sea surface temperature from the along-track scanning radiometers: Initial validation, accounting for skin and diurnal variability effects. Remote Sens. Environ. 2012, 116, 62–78. [Google Scholar] [CrossRef]
- Maturi, E.; Harris, A.; Merchant, C.; Mittaz, J.; Potash, B.; Meng, W.; Sapper; J. NOAA’s sea surface temperature products from operational geostationary satellites. Bull. Am. Meteorol. Soc. 2008, 89, 1877–1888. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An Improved In Situ and Satellite SST Analysis for Climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Clayson, C.A.; Weitlich, D. Variability of tropical diurnal sea surface temperature. J. Clim. 2007, 20, 334–352. [Google Scholar] [CrossRef]
- Marullo, S.; Santoleri, R.; Banzon, V.; Evans, R.H.; Guarracino, M. A diurnal-cycle resolving sea surface temperature product for the tropical Atlantic. J. Geophys. Res. Ocean. 2010, 115, C05011. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Minnett, P.J.; LeBorgne, P.; Merchant, C.J. Multi-satellite measurements of large diurnal warming events. Geophys. Res. Lett. 2008, 35, L602. [Google Scholar] [CrossRef]
- Stuart-Menteth, A.C.; Robinson, I.S.; Welller, R.A.; Donlon, C.J. Sensitivity of the diurnal warm layer to meteorological fluctuations part 1: Observations. J. Atmos. Ocean Sci. 2005, 10, 193–208. [Google Scholar] [CrossRef]
- Zhang, H.; Beggs, H.; Majewski, L.; Wang, X.H.; Kiss, A. Investigating sea surface temperature diurnal variation over the Tropical Warm Pool using MTSAT-1R data. Remote Sens. Environ. 2016, 183, 1–12. [Google Scholar] [CrossRef]
- Zhang, H.; Beggs, H.; Wang, X.H.; Kiss, A.E.; Griffin, C. Seasonal patterns of SST diurnal variation over the Tropical Warm Pool region. J. Geophys. Res. Ocean. 2016, 121, 8077–8094. [Google Scholar] [CrossRef]
- Wu, X.; Menzel, W.P.; Wade, G.S. Estimation of Sea Surface Temperatures Using GOES-8/9 Radiance Measurements. Bull. Am. Meteor. Soc. 1999, 80, 1127–1138. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Marsouin, A.; Roquet, H. Optimal estimation of sea surface temperature from split-window observations. Remote Sens. Environ. 2008, 112, 2469–2484. [Google Scholar] [CrossRef]
- Walton, C.C.; Pichel, W.G.; Sapper, F.J.; May, D.A. The development and operational application of non-linear algorithms for the measurement of sea surface temperatures with NOAA polar orbiting environmental satellites. J. Geophys. Res. 1998, 103, 27999–28012. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Roquet, H.; Marsouin, A. Sea surface temperature from a geostationary satellite by optimal estimation. Remote Sens. Environ. 2009, 113, 445–457. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O. Simulation and Inversion of Satellite Thermal Measurements. In Experimental Methods in the Physical Sciences; Elsevier: Amsterdam, The Netherlands, 2014; Volume 47, pp. 489–526. ISBN 978-0-12-417011-7. [Google Scholar]
- Merchant, C.J.; Embury, O.; Roberts-Jones, J.; Fiedler, E.; Bulgin, C.E.; Corlett, G.K.; Good, S.; McLaren, A.; Rayner, N.; Morak-Bozzo, S.; et al. Sea surface temperature datasets for climate applications from Phase 1 of the European Space Agency Climate Change Initiative (SST CCI). Geosci. Data J. 2014, 1, 179–191. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Roquet, H.; Legendre, G. Extended optimal estimation techniques for sea surface temperature from the Spinning Enhanced Visible and Infra-Red Imager (SEVIRI). Remote Sens. Environ. 2013, 131, 287–297. [Google Scholar] [CrossRef]
- Ojha, S.P.; Singh, R. Physical retrieval of sea-surface temperature from INSAT-3D imager observations. Tellus A Dyn. Meteorol. Oceanogr. 2019, 71, 1–18. [Google Scholar] [CrossRef]
- Picart, S.S. Algorithm Theoretical Basis Document for MSG/SEVIRI Sea Surface Temperature Data Record, MSG SST Data Record Validation Report, Ver 1.3; SAF/OSI/CDOP2/MF/SCI/MA/256OSI-250; Meteo France: Paris, France, 2018; 20p. [Google Scholar] [CrossRef]
- Chin, T.M.; Vazquez-Cuervo, J.; Armstrong, E.M. A multi-scale high-resolution analysis of global sea surface temperature. Remote Sens. Environ. 2017, 200, 154–169. [Google Scholar] [CrossRef]
- Agarwal, N.; Sharma, R.; Thapliyal, P.; Gangwar, R.; Kumar, P.; Kumar, R. Geostationary satellite-observations for ocean applications. Curr. Sci. 2019, 117, 3. [Google Scholar] [CrossRef]
- Xu, F.; Ignatov, A. In situ SST Quality Monitor (iQuam). J. Atmos. Ocean. Technol. 2013, 31, 164–180. [Google Scholar] [CrossRef]
- Eyre, J.R. A Fast Radiative Transfer Model for Satellite Sounding Systems; ECMWF Technical Memorandum 176; European Centre for Medium Range Weather Forecasts: Reading, UK, 1991. [Google Scholar]
- Matricardi, M.; Chevallier, F.; Tjemkes, S. An Improved General Fast Radiative Transfer Model for the Assimilation of Radiance Observations; ECMWF Technical Memorandum 345; European Centre for Medium Range Weather Forecasts: Reading, UK, 2001. [Google Scholar]
- Saunders, R.W.; Matricardi, M.; Brunel, P. An improved fast radiative transfer model for assimilation of satellite radiance observations. Q. J. R. Meteorol. Soc. 1999, 125, 1407–1425. [Google Scholar] [CrossRef]
- Shukla, M.V.; Thapliyal, P.K. Development of a methodology to generate in-orbit electro-optical module temperature based calibration coefficients for INSAT-3D/3DR infrared imager channels. IEEE Trans. Geosci. Rem. Sens. 2020. [Google Scholar] [CrossRef]
- Dash, P.; Ignatov, A. Validation of clear-sky radiances over oceans simulated with MODTRAN4.2 and global NCEP GDAS fields against nighttime NOAA15-18 and MetOp-A AVHRR data. Remote Sens. Environ. 2008, 112, 3012–3029. [Google Scholar] [CrossRef]
- Chevallier, F.; Michele, S.D.; McNally, A.P. Diverse Profile Datasets from the ECMWF 91-Level Short-Range Forecast; NWPSAF-EC-TR-010; EUMETSAT: Darmstadt, Germany, 2006. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding—Theory and Practice; Series on Atmospheric Oceanic and Planetary Physics; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2000; Volume 2, ISBN 978-981-281-371-8. [Google Scholar]
- Rodgers, C.D. Retrieval of atmospheric temperature and composition from remote measurements of thermal radiation. R. Geophys. Space Phys. 1976, 14, 609–624. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013. [Google Scholar] [CrossRef]
- Donlon, C.J.; Nightingale, T.J.; Sheasby, T.; Turner, J.; Robinson, I.S.; Emergy, W.J. Implications of the oceanic thermal skin temperature Deviation at High Wind Speed. Geophys. Res. Lett. 1999, 26, 2505. [Google Scholar] [CrossRef]
- Jishad, M.; Sarangi, R.K.; Ratheesh, S.; Ali, S.M.; Sharma, R. Tracking fishing ground parameters in cloudy region using ocean colour and satellite-derived surface flow estimates: A study in the Bay of Bengal. J. Oper. Oceanogr. 2019. [Google Scholar] [CrossRef]




| Band # | Wavelength (μm) | Spatial Resolution @ Nadir (km) | SNR or NEDT * |
|---|---|---|---|
| 1 | 0.52–0.72 | 1 | 150:1 |
| 2 | 1.55–1.70 | 1 | 150:1 |
| 3 | 3.80–4.00 | 4 | 0.27 K@300 K |
| 4 | 6.50–7.00 | 8 | 0.18 K@230 K |
| 5 | 10.3–11.2 | 4 | 0.15 K@300 K |
| 6 | 11.5–12.5 | 4 | 0.25 K@300 K |
| Month | No. of Matchups (% of total) | CC * | Bias (K) | NLSST Median (K) | Std (K) | MAD (K) | CC * | Bias(K) | 1DVAR Median (K) | Std (K) | MAD (K) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| December 2019 | 54,116 (85.8) | 0.97 (0.97) | −0.28 (−0.15) | −0.22 (−0.09) | 0.94 (0.86) | 0.92 (0.82) | 0.99 (0.99) | −0.38 (−0.23) | −0.36 (−0.26) | 0.62 (0.48) | 0.64 (0.53) |
| January 2020 | 34,164 (87.5) | 0.96 (0.97) | −0.22 (−0.10) | −0.16 (−0.07) | 0.95 (0.87) | 0.92 (0.83) | 0.99 (0.99) | −0.35 (−0.22) | −0.32 (−0.24) | 0.61 (0.47) | 0.59 (0.50) |
| February 2020 | 37,732 (83.6) | 0.96 (0.96) | −0.35 (−0.22) | −0.32 − (0.18) | 0.92 (0.86) | 0.92 (0.85) | 0.98 (0.99) | −0.42 (−0.27) | −0.40 (−0.29) | 0.65 (0.46) | 0.62 (0.50) |
| March 2020 | 32,404 (87.7) | 0.96 (0.97) | −0.24 (−0.13) | −0.23 (−0.13) | 0.93 (0.87) | 0.93 (0.86) | 0.98 (0.99) | −0.33 (−0.21) | −0.32 (−0.23) | 0.62 (0.49) | 0.62 (0.53) |
| April 2020 | 28,877 (87.3) | 0.96 (0.98) | −0.27 (−0.17) | −0.25 (−0.15) | 0.94 (0.88) | 0.96 (0.90) | 0.99 (0.99) | −0.32 (−0.20) | −0.30 (−0.23) | 0.62 (0.49) | 0.62 (0.53) |
| May 2020 | 23,770 (87.9) | 0.98 (0.98) | −0.22 (−0.10) | −0.18 (−0.07) | 1.02 (0.95) | 1.05 (0.96) | 0.99 (0.99) | −0.30 (−0.19) | −0.27 (−0.19) | 0.63 (0.49) | 0.62 (0.53) |
| Overall | 211,063 (86.5) | 0.97 (0.9) | −0.27 (−0.15) | −0.23 (−0.12) | 0.95 (0.88) | 0.95 (0.86) | 0.99 (0.99) | −0.36 (−0.23) | −0.34 (−0.25) | 0.63 (0.48) | 0.62 (0.52) |
| Month | No. of Matchups (% of total) | CC * | Bias (K) | NLSST Median (K) | Std (K) | MAD (K) | CC * | Bias (K) | 1DVAR Median (K) | Std (K) | MAD (K) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| December 2019 | 40,286 (87.4) | 0.97 (0.98) | −0.26 (−0.15) | −0.21 (−0.11) | 0.83 (0.76) | 0.79 (0.71) | 0.99 (0.99) | −0.36 (−0.23) | −0.33 (−0.25) | 0.60 (0.46) | 0.59 (0.50) |
| January 2020 | 27,602 (88.3) | 0.98 (0.98) | −0.22 (−0.14) | −0.20 (−0.13) | 0.73 (0.68) | 0.77 (0.71) | 0.99 (0.99) | −0.37 (−0.26) | −0.36 (−0.28) | 0.58 (0.46) | 0.58 (0.50) |
| February 2020 | 32,486 (85.7) | 0.97 (0.98) | −0.24 (−0.15) | −0.22 (−0.13) | 0.73 (0.67) | 0.74 (0.70) | 0.98 (0.99) | −0.42 (−0.27) | −0.39 (−0.29) | 0.61 (0.45) | 0.59 (0.49) |
| March 2020 | 31,578 (87.7) | 0.97 (0.97) | −0.20 (−0.10) | −0.19 (−0.10) | 0.90 (0.84) | 0.87 (0.82) | 0.99 (0.99) | −0.35 (−0.23) | −0.33 (−0.25) | 0.61 (0.47) | 0.59 (0.50) |
| April 2020 | 29,428 (88.7) | 0.98 (0.98) | −0.08 (0.01) | −0.10 (−0.01) | 0.97 (0.91) | 0.95 (0.89) | 0.99 (0.99) | −0.25 (−0.14) | −0.22 (−0.15) | 0.63 (0.49) | 0.61 (0.53) |
| May 2020 | 21,581 (87.4) | 0.98 (0.98) | −0.04 (0.08) | −0.02 (0.09) | 1.07 (1.00) | 1.13 (1.04) | 0.99 (0.99) | −0.23 (−0.12) | −0.19 (−0.12) | 0.65 (0.50) | 0.65 (0.56) |
| Overall | 182,961 (87.6) | 0.98 (0.98) | −0.18 (−0.09) | −0.17 (−0.09) | 0.87 (0.81) | 0.85 (0.79) | 0.99 (0.99) | −0.34 (−0.21) | −0.31 (−0.23) | 0.62 (0.47) | 0.61 (0.52) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gangwar, R.K.; Thapliyal, P.K. Variational Based Estimation of Sea Surface Temperature from Split-Window Observations of INSAT-3D/3DR Imager. Remote Sens. 2020, 12, 3142. https://doi.org/10.3390/rs12193142
Gangwar RK, Thapliyal PK. Variational Based Estimation of Sea Surface Temperature from Split-Window Observations of INSAT-3D/3DR Imager. Remote Sensing. 2020; 12(19):3142. https://doi.org/10.3390/rs12193142
Chicago/Turabian StyleGangwar, Rishi Kumar, and Pradeep Kumar Thapliyal. 2020. "Variational Based Estimation of Sea Surface Temperature from Split-Window Observations of INSAT-3D/3DR Imager" Remote Sensing 12, no. 19: 3142. https://doi.org/10.3390/rs12193142
APA StyleGangwar, R. K., & Thapliyal, P. K. (2020). Variational Based Estimation of Sea Surface Temperature from Split-Window Observations of INSAT-3D/3DR Imager. Remote Sensing, 12(19), 3142. https://doi.org/10.3390/rs12193142